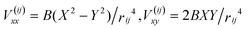Collective dynamics of small clusters of particles flowing in a quasi-two-dimensional microchannel†
William E.
Uspal
a and
Patrick S.
Doyle
*b
aDepartment of Physics, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
bDepartment of Chemical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: pdoyle@mit.edu
First published on 9th July 2012
Abstract
Spatially ordered equilibrium states – crystals – and their excitations – phonons – are the mainstay of condensed matter physics. Flowing, nonequilibrium crystalline states of microparticles and droplets are desirable for microfluidic logic, assembly, and control, and have been achieved in recent work via exploitation of viscous hydrodynamic interactions in geometric confinement. For the most part, these studies considered large ensembles of particles and, accordingly, large scale collective modes arising from small displacements of individual particles. Via theoretical modeling and computational simulations, we show that for small clusters of flowing particles tightly confined in a shallow, “quasi-two-dimensional” microchannel, new types of ordered behavior emerge, varying from steady states in which particles maintain their relative positions, to exquisitely coordinated collective motion with large particle displacements. These new collective behaviors require a thin channel geometry: strong confinement in one spatial direction and weak confinement in another. We elucidate principles and techniques for the a priori construction or rapid numerical discovery of these states, which could be exploited for the orchestration of particle motion in lab-on-a-chip devices and other applications.
1 Introduction
Imposing spatial and temporal order on flowing streams of particles is growing in practical significance for microfluidic applications. For bioanalysis, including on-chip flow cytometry1 and multiplexed assays with functionalized particles,2 the suspended objects must be individually distinguishable and addressable as they flow through a scanning region. Flowing, tunable lattices of particles are desirable for optofluidics3 and continuous fabrication of metamaterials or cell-laden microtissues.4 Order can be achieved by via hydrodynamic focusing with sheath flows5 or by positioning with external fields.6 However, these methods can be limited in generality and scalability. Recently, researchers have sought to understand how particles can organize themselves through forces generic to the flow of suspended objects through microchannels, such as viscous hydrodynamic interaction forces. For instance, trains of spherical particles at finite Reynolds number self-assemble into a lattice ordered both perpendicular to and along the direction of external flow, as determined by the balance of inertial lift and viscous hydrodynamic forces.7 This inertial ordering effect was exploited to efficiently encapsulate cells in droplets8 and for high throughput cytometry.9 In another study, simulations predict clustering, axial symmetry breaking, and alignment of deformable particles driven by fluid pressure drop in a tube.10 Particles optically driven around a ring will pair via an effective attraction that arises from the hydrodynamic interaction between them and the curvature of their trajectories.11 The flowing ordered states of these studies occur far from thermodynamic equilibrium, sustained by energy provided by the external forces or flow. While still lacking a settled body of theory, nonequilibrium self-organization offers a promising framework for engineering systems with new classes of programmable complexity.12Hydrodynamic interactions can be dramatically changed in the presence of confining boundaries.13–15 They take a novel form for flowing suspensions of particles with characteristic size comparable to the height of a confining slit, such that the particles are geometrically constrained to two-dimensional motion. In this “quasi-two-dimensional” (q2D) slit-like geometry, friction from the walls screens momentum flux from a force multipole. The leading far field hydrodynamic interaction is therefore determined by mass conservation as a source dipole.16–18 In contrast to hydrodynamic interactions in bulk fluid, this dipolar form lends itself to realization of crystalline states, since ensemble summations of velocity fluctuations converge even in the limit of infinite system size.19 Microfluidic crystals have been realized in q2D as flowing, ordered trains of droplets driven by external flow, exhibiting transverse and longitudinal acoustic waves (“phonons”) and nonlinear instabilities.20 Arrays of q2D particles form large scale patterns when driven by an external flow21 and sharp interfaces in sedimentation.22 The addition of side walls distinguishes the thin channel geometry, shown schematically in Fig. 1(a), from the slit, which is unbounded in the xy plane. The side walls screen the hydrodynamic interaction in the flow direction, modulating the dipolar form by an exponential decay, and modifying phonon dispersion relations for droplet trains.23 Recent efforts have examined jams and shock waves occurring in one-dimensional droplet trains24 and disordered two-dimensional droplet suspensions25 flowing in the thin channel geometry. A comprehensive review of this work is provided by Beatus et al.19
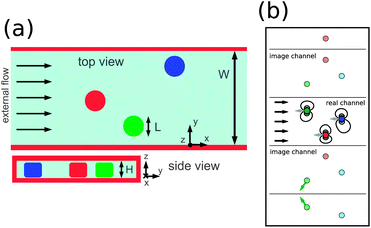 | ||
| Fig. 1 (a) In the thin channel geometry considered in this work, a cluster of N particles (here N = 3) is tightly confined in a gap of height H between plates normal to the z direction. They are free to move in x and y between side walls, where W is the width of the channel. The position of particle i is labelled by xi and yi in a frame fixed to the channel walls. The particles are driven by an external flow. (b) System of real and virtual particles used to derive the thin channel hydrodynamic interaction tensor. The real particles (dark colors) are subject to an external flow (black vectors) and are dressed by an infinite set of images (light colors) that are constructed iteratively, via mirror reflections across the real and virtual channel boundaries. Due to friction from the confining plates, each particle lags its own local flow field; gray vectors show the velocities of the real particles in frames moving with local flow. This relative motion gives rise to hydrodynamic disturbance fields (black streamlines) that couple the particles, and is dominated by motion in the direction opposed to that of external flow. We also show particle velocity in a frame moving with the particle cluster's center of mass for two of the virtual particles (green vectors). | ||
These studies examined large ensembles of particles, whether flowing in a linear train or a two dimensional swarm. Due to the size of these systems and the long-range nature of the dipolar interaction, the details of spatial microstructure average out of the description of collective behavior, permitting coarse-grained modeling via continuum approximations and mean-field theory. Moreover, for typical amplitudes of collective modes in these systems, the spatial displacement of an individual particle is generally small. For the dynamics of small clusters, on the other hand, we anticipate sensitive dependence on spatial configuration and larger, individualistic, and more complex excursions of single particles. Accordingly, cluster dynamics must be resolved at the single particle level. Recently, we showed theoretically that a pair of particles flowing in a thin channel will either scatter to infinity or oscillate together as a “quasiparticle” in a region of marginal stability, depending on the initial spatial configuration.26 In this paper, we study the emergent dynamics of clusters of multiple flowing rigid particles in a thin channel via theory and Lattice Boltzmann simulations. We find a rich variety of dynamical behaviors, including stable and metastable configurations in which particles maintain their relative positions, collective modes with relative particle displacements in two dimensions, cycles in which particles exchange positions, and stochastic cluster dispersion. We provide symmetry principles for the a priori construction of stable configurations and demonstrate techniques for rapid identification of more complex dynamical motifs. These findings could be used for control of highly confined particles in lab-on-a-chip devices, especially where complex motion of individual particles is desired. Furthermore, we suggest implications for the role of hydrodynamic interactions in hydrodynamic diffusion and irreversibility.
2 Theory and simulation method
2.1 Theoretical model
In a previous work, we developed a minimal theoretical model that treated the particles as coupled dipolar flow singularities, dressed by a set of virtual particles in order to impose the boundary conditions at the side walls.26 For a thin slit or channel, we take the flow field to have a parabolic dependence in z, where z is the channel direction with smallest geometric length, the height H. We consider the flow field U(r), where U(r) is flow relative to the walls, and r is position in the channel midplane z = H/2 in a frame fixed to the walls. We model the effect of the walls normal to z (the “plates”) through a frictional force with areal density γcHU(r), with γc = 8μ/H2, where μ is the bulk dynamic viscosity of the fluid. A rigid cylindrical particle of radius R (diameter L = 2R) confined between the plates will lag the local flow field, as its own friction coefficient γp, determined by the thin lubricating layers separating it from the plates, will be higher than γc. In the zero Reynolds number limit, the velocity of particle i, Upi, is determined by a force balance:| ζ(Upi − U(ri)) + γcπR2HU(ri) − γpπR2HUpi = 0 | (1) |
 | (2) |
Experimentally, α can determined from the velocity of a single particle driven by external flow through a slit or wide channel. This parameter is bounded by 0 < α < 1. For small (large) values of α, a particle significantly (barely) lags the local flow field.
In lagging the local flow, the particle creates a hydrodynamic disturbance. This can be understood most easily when the particle is considered in a frame moving with the local flow. In Fig. 2(b), a lagging particle is moving in −x with respect to the local flow (gray vector), and therefore pushes fluid away from its leading edge and draws fluid into its trailing edge (black streamlines). This dipolar disturbance can be modeled as due to a mass source and mass sink, i.e. a source dipole. Mass transport provides the leading order far-field flow disturbance in q2D, since momentum transport is damped by friction from the confining plates.17
 | ||
| Fig. 2 Fixed points obtained a priori via symmetry considerations, depicted in top down view. The first column shows particles in a frame moving in the center of mass when the theoretical model is integrated. In this frame, particles remain in fixed positions. Side walls are indicated by black lines. The second column shows particles in the center of mass frame for the corresponding Lattice Boltzmann simulations. Colors indicate the magnitude of the fluid velocity field. In the simulations, particles move slightly, but remain within one radius of their initial positions. Due to this motion, the fluid velocity field can be slightly asymmetric. (a) A “dimer column” for channel width W/L = 9. The LBM simulation is shown after the particles were advected downstream by xcm/L = 241 particle lengths at Re = 0.2, where xcm is the position of the center of mass in the flow direction. (b) A “column” fixed point and LBM simulation after advection by xcm/L = 833 particle lengths at Re = 0.2. (c) A “double column” fixed point and LBM simulation after advection by xcm/L = 524 particle lengths at Re = 0.2. | ||
For a system of N particles subject to a uniform external flow U0, the local flow field at particle i is determined through an implicit equation
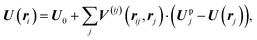 | (3) |
Modeling the thin channel geometry requires that the effect of side walls be included in V(ij). In analogy to electrostatics, the no-mass flux boundary condition at these walls can be enforced via the method of images. Each real particle is dressed by an infinite set of virtual particles, iteratively constructed by mirror reflections across the boundaries of real and virtual channels. The y component of particle velocity is negated in each successive reflection. (Fig. 1) Summing over these virtual particles gives the dressed self- and two body interactions for real particles. Particle pairs are now coupled by dipolar interactions that are screened in the flow direction over a length scale proportional to W, the distance between the side walls. (Appendix C) This screened dipolar field has been analogized to the field from a “leaky” capacitor, with the “leakiness” arising from the inherently discrete nature of the charge distribution.23 Moreover, the tensor now depends on particle position rj, since the disturbance field created by a particle now depends on its distance from the channel walls.
Eqn (2) and (3) can be rearranged into matrix form AUp = B, where Up is a vector containing all 2N particle velocities, A is a resistance matrix that includes all pairwise interactions, and B collects terms involving the external flow U0. Although A is constructed from pairwise interactions, inverting it solves a many-body problem for particle velocities; numerically, we can form A at each timestep, solve for Up, and integrate forward to the next timestep.
Substituting eqn (2) into eqn (3) and using the thin channel interaction tensor, we can identify two dimensionless parameters that govern particle dynamics. These are W/L, the dimensionless channel width, and a parameter β that characterizes the strength of hydrodynamic coupling between the particles. This parameter is
 | (4) |
Finally, we note that by approximating the local flow as uniform, we have neglected velocity gradients, even though the typical particle separation for our system is only a few particle diameters. However, the Faxén correction determining the contribution of velocity gradients to the force on a cylinder in a Brinkman medium was shown to be proportional to ∇2U(ri).29 Since the far field flow disturbance is the gradient of a potential ϕ that obeys Laplace's equation, ∇2ϕ = 0, this correction vanishes.
2.2 Lattice Boltzmann method
By construction, the theoretical model includes only far-field hydrodynamic interactions. We complement it with Lattice Boltzmann simulations. The Lattice Boltzmann Method (LBM) simulates hydrodynamics from the “bottom up,” through a coarse-grained model of populations of particles colliding and streaming on a grid. In the collision step, the populations at a fluid node relax to an equilibrium distribution that maximizes local entropy while conserving the collision invariants, density and momentum. These two macroscopic fields are computed for each node by taking moments of the local fluid populations. In the streaming step, populations are shifted to neighboring nodes along lattice links. For the correct choice of lattice architecture, this model recovers hydrodynamics for length scales larger than the grid spacing and time scales above the step size. Whereas with the singularity model, we took the dipolar form of hydrodynamic interactions as our starting point, in LBM, this form should emerge from the underlying lattice dynamics. Moreover, LBM naturally includes hydrodynamic near fields and the effects of finite inertia and easily handles complicated geometries. While in this work we consider rigid discs, deformable particles or particles with complicated shape can also be coupled to LBM.We use a D2Q9 grid with the popular single relaxation time (BGK) model, which is detailed extensively elsewhere.30,31 However, modifications are required to simulate q2D flow. We include the effect of the walls normal to z via a drag term linear in the local velocity. Such a term had been used in several previous LBM studies of Hele-Shaw flow.32,33 However, for the large flow domains and small channel heights we simulate, the pressure drop in the flow direction is substantial. In typical, weakly compressible BGK models, pressure and density are related by an equation of state, P = ρ/3. Large pressure drops introduce compressibility error. Moreover, continuity requires an increase in flow velocity between the inlet and outlet, (ρvx)left = (ρvx)right. This undesirable unidirectional extensional flow breaks the fore-aft symmetry of the velocity field in the Stokes regime, and would tend to align particle clusters with the flow. Therefore, we adopt the incompressible, “pressure-based” BGK model of Guo et al.34
Hereafter we apply the method of that work for a thin channel of height H. By construction, the numerical model is two dimensional, but we are interested in simulating a three dimensional system; therefore, we must take care with quantities that depend on spatial dimension. The mass density is fixed as ρ2D = 1. Therefore, ρ3D = 1/H. Dynamic viscosities μ3D and μ2D also depend on spatial dimension, but the kinematic viscosity ν does not: ν = μ3D/ρ3D = μ2D/ρ2D. From above, the force of friction on a column of fluid of height H, area A, and midplane velocity u is γcAHu, where γc = 8μ3D/H2. (Recall that we assume a Poiseuille profile in z, and u is the maximum of this profile.) Substituting μ3D = νρ3D and ρ3D = 1/H, we obtain A8ν/H2u. The area of a fluid node is, in lattice units, A = 1, so that 8ν/H2u is the frictional force we need to apply on a fluid node with local velocity u.
The fluid populations are designated gi, with equilibrium distributions given by
 | (5) |
In this model, the macroscopic fields are velocity and pressure, not velocity and density. We define λ ≡ 8ν/H2. The velocity at a node is computed as
 | (6) |
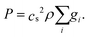 | (7) |
The collision step is
 | (8) |
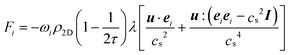 | (9) |
In comparison with weakly compressible BGK models, the incompressible BGK model introduces a new error term for unsteady flow that is ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (Ma2), where the Mach number Ma ≡ u/cs. However, as we simulate low Reynolds number flow, i.e. the quasi-steady regime, this term is small. For all simulations, we use relaxation time τ = 1 timesteps, so that the kinematic viscosity ν = 1/6 in LBM units.
(Ma2), where the Mach number Ma ≡ u/cs. However, as we simulate low Reynolds number flow, i.e. the quasi-steady regime, this term is small. For all simulations, we use relaxation time τ = 1 timesteps, so that the kinematic viscosity ν = 1/6 in LBM units.
Particles are included as a rigid discs. The discs are coupled to LBM fluid via transfer of momentum in the “bounce-back” boundary condition, using a first-order boundary interpolation method. This coupling determines the drag forces and drag torques on the disc. In Appendix B, we show that the coupling recovers the theoretical translational and rotational drag coefficients determined by Evans and Sackmann.27 LBM nodes within the boundaries are taken to be solid. As the discs move over the grid, LBM nodes are transferred between the solid and fluid domains, requiring removal or refill of fluid populations. In order to conserve momentum, this transfer requires calculation of additional forces on the discs, although we find that these forces do not significantly affect particle dynamics.
The discs are also subject to frictional forces and torques from the walls. The discs follow Newton's equations of motion, which are integrated via the DPD-VV scheme in Nikunen et al.35 This scheme adapts the familiar velocity Verlet numerical integration method for velocity dependent forces. We use the iterative version of this scheme, recalculating disc velocities, as well as the components of outgoing fluid populations that depend on the disc velocities, until a specified tolerance in the disc velocities is satisfied. However, we note that even a single pass seems accurate and numerically stable for rigid particles.
The discs are advected by the flow, and we are interested in dynamics over hundreds of advected particle lengths. For computational efficiency, we move the computed flow domain as a window containing the particles. In order that flow remain fully developed, a buffer of length W is maintained between the leftmost and rightmost particles and the boundaries. At the boundaries, we impose the velocity profile for steady flow in a thin channel via the method of Zou and He.36 The profile is given by:
 | (10) |
This profile is approximately uniform for most of the channel. Boundary layers at the channel walls satisfy the no-slip condition. When fluid nodes are added to the right edge of the domain, we extrapolate the local pressure and fill the nodes with equilibrium populations. We did not find variation of this method to have significant effect.
3 Results and discussion
The geometry of our quasi-two-dimensional system is shown in Fig. 1. A channel of width W and height H contains N discs of diameter L. The position of particle i is denoted by xi and yi. In the theoretical model, L = 1 is taken as the fundamental length scale, and U0 = 1 as the velocity scale. In simulations, we set L = 10 lattice lengths, and define a Reynolds number Re ≡ u0H/ν, where u0 is the maximum velocity at the channel boundaries, appearing in eqn (10). In both theoretical model and the simulations, we fix H/L = 2/3 for simplicity. We also fix the ratio of particle and channel friction coefficients as γp/γc = 25. The parameter β is therefore fixed as β = 1.82. In what follows, we generally consider the evolution of the cluster with the position of the center of mass in the flow direction, xcm ≡ 1/N∑ixi, instead of with time t. In the limit of Stokes flow, velocity can be arbitrarily rescaled (cf.eqn (3)), and therefore so can the dimensionless time tU0/L.3.1 Fixed points and oscillatory modes
Even before working with the equations of motion developed above, it is possible to construct special “fixed point” particle configurations on the basis of symmetry and the functional form of hydrodynamic interactions. These configurations are fixed points of the dynamical system constituted by eqn (2) and (3). Particles in these configurations maintain their relative positions as the cluster flows down the channel.Recall that our theoretical model imposed boundary conditions at the channel side walls via the method of images, in which each real particle is dressed by an infinite set of virtual particles. When the distinction between real and virtual particles is disregarded and all are considered together, they can be taken to be coupled through simple dipolar interactions, as in a slit, rather than through screened dipolar interactions, as restricting our attention to the real particles would require. If each particle is subject to the same local flow field, then there is no relative motion, and the particles maintain their spatial configuration in the center of mass frame. This is possible if each particle “looks like” every other particle through translational symmetry; relative motion would break this symmetry. In Fig. 2, we show three classes of fixed point that can be constructed through this principle: the “dimer column,” the “column,” and the “double column.” Each of these fixed points can be obtained for any number N of particles. As shown, Lattice Boltzmann simulations confirm that these are fixed points.
In order to illustrate the symmetry principle, in Fig. 3(a) we show the “dimer column” geometry for three particles, including nearby virtual particles. Each of the infinite set of real and virtual particles resembles the dipole in Fig. 3(b), moving in the negative x direction with respect to the local flow, and therefore contributing a component of velocity strictly in positive x to the other particles' local flow fields, which are identical to its own. By the image construction we obtain N(a + b) = 2W. Therefore, while rows (a) and (b) in Fig. 2, showing only real particles, appear quite distinct, we see that the “column” configuration is only the “dimer column” configuration with a = b. In the “double column,” particles now contribute components in y and −y to the local flow fields of other particles, due to the angular dependence of the dipolar form, but these components cancel because of the symmetry of the arrangement. (On the other hand, this would not be true of a “double dimer column,” which is therefore not a fixed point.) In view of the translational symmetry of the set of real and virtual particles, these fixed points can be regarded as “flowing crystals.”
 | ||
| Fig. 3 Geometric construction of the “dimer column” fixed point. In (a), three real particles are accompanied by an infinite set of virtual particles, the closest of which are at y = −a/2, y = W + b/2, and y = W + b/2 + a. These quantities are related by 3(a + b) = 2W. Each of the real and virtual particles is identical, resembling the particle shown in (b), moving in −x with respect to the local flow field and contributing components of velocity in positive x to the local flow fields of the other particles. The gray vector shows the velocity of a particle with respect to the local flow, while the black streamlines illustrate the dipolar disturbance field thus created. Because this configuration is one dimensional, the angular dependence of the dipolar form is not relevant here. | ||
As with crystals, these fixed points are associated with characteristic oscillatory modes, which can be obtained in the model via numerical calculation and diagonalization of the Jacobian matrix. Fig. 4 shows the two oscillatory modes of a three particle column. The eigenvalues of the Jacobian for these modes are strictly imaginary: the modes are marginally stable in linear theory. To further probe stability, we displace the particles from their fixed point positions along an eigenvector with finite amplitude and integrate the equations of motion. The initial displacement neither grows nor decays in time. This marginal stability, in which we obtain a nested set of closed orbits, recalls our earlier study of two particle dynamics, discussed in Appendix A. When we simulate the eigenmodes in Lattice Boltzmann, we find that the modes can either slowly grow or decay with time, i.e. the eigenvalues can have a small real part. This is not surprising, as Lattice Boltzmann is inherently a finite Reynolds number technique. Inertia increases the order of the differential equations governing particle dynamics, potentially affecting the stability of the dynamical states found for Re = 0. The effect of decreasing Re in the simulations is to decrease the significance of the effect, as we show quantitatively for the case of two particles in Appendix A.
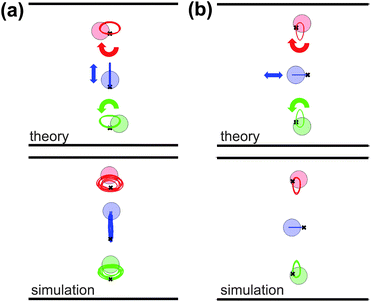 | ||
| Fig. 4 Oscillatory modes of a three particle column fixed point with W/L = 8 and lattice length a/L = 8/3. The top row shows trajectories found via numerical integration of the theoretical model, starting from an initial condition in which the particles are displaced from the fixed point along an eigenvector. In the bottom row we show the corresponding LBM simulations. Particles are shown in their final positions, while the crosses indicate initial positions. The red, blue, and green curves are the “tracks” showing particle positions over time. Arrows indicate the direction of particle motion. In the simulations, the oscillations in (a) slowly grow with time, while those in (b) slowly decay. As discussed in the text, this effect diminishes as Re is decreased. (a) Theory and simulation results after xcm/L = 482 advected particle lengths. For the simulations, Re = 0.2. The particles were initially displaced from the fixed point by Δy1 = −0.34L, where particle 1 is the green (bottom) particle; Δy2 = −0.68L, for the blue (middle) particle; and Δy3 = −0.34L for the red (top) particle. (b) Results after xcm/L = 205 advected particle lengths. For the simulations, Re = 0.05. The initial displacements from the fixed point are Δx1 = −0.22L, Δx2 = −0.43L, and Δx3 = −0.22L. In contrast with (a), here Re and xcm/L are too small for a discernible phase difference between theory and simulations. | ||
There are also fixed points for unbounded q2D flow (i.e. without side walls.) The case of N = 2 is trivial; the pair simply translates with fixed particle separation, and there are no oscillatory eigenmodes. At the other extreme are infinite one dimensional or two dimensional lattices. The lattices include those constructed above, with virtual particles replaced by real particles, as well as lattices that are periodic in the flow direction, as in Tlusty.37 These lattices do have eigenmodes, such as the “microfluidic phonons” of that work. However, infinite lattices can be destabilized by nonlinear instabilities, whereas the cluster fixed points constructed here are sustained for hundreds of advected particle lengths. We do not know of any fixed points for N = 3 or N = 4. For N = 5, there is a fixed point with particles arranged at the vertices of a regular pentagon. In the theoretical model, its Jacobian has only two eigenvalues of any significance: a pair of real numbers. There are no oscillatory collective modes, and the cluster is linearly unstable. The magnitude of the eigenvalue depends on the length scale of the pentagon. For instance, when the radius of the circumscribing circle is 3L, the cluster breaks up after approximately xcm/L = 240 particle lengths with even a very modest amount of noise applied to the initial particle positions. (Two separate noise terms were applied to the x and y positions of each particle, where the noise was uniformly distributed over the interval [−0.00025L,0.00025L].) Experimentally, the unbounded q2D geometry can only be approximately realized as a very wide channel. When the cluster is positioned in the center of a channel with W/L = 50, the residence length of the cluster is reduced even further, to xcm/L = 160. We suggest that the effect of the side walls should be considered for nearly all practical channel sizes.
3.2 Metastable states and stochastic dispersion
Within the theoretical model, fixed points constructed via symmetry considerations are marginally stable. There are still other, “metastable” configurations for which particles remain together for many advected lengths xcm/L before eventual break-up of the configuration, both in the theoretical model and in simulations. For instance, Fig. 5 shows LBM results for a “triangle” configuration. The cluster only disperses after xcm/L = 1047 advected particle lengths. Moreover, for much of this initial transient period, relative positions are roughly maintained, as in the first two panels. We find such steady metastable states by setting the relative particle velocities found viaeqn (2) and (3) to zero and solving the resulting algebraic equations numerically. These states provide new steady particle configuration geometries beyond the linear configurations of Fig. 2. | ||
| Fig. 5 Snapshots of simulation results for a metastable steady “triangle” configuration with Re = 0.2 and W/L = 8 at four values of the cluster center of mass xcm. Particle motion, initially limited to small excursions from the initial positions, grows in magnitude until the magenta and green particles pair. Ultimately, the red and green particles escape together. Colors indicate the magnitude of the fluid velocity. | ||
We characterize the eventual break-up and dispersion of the configuration via the quantity
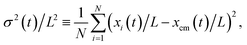 | (11) |
 | ||
| Fig. 6 Dispersion σ2/L2 with dimensionless time U0t/L for four trajectories of the metastable “triangle” configuration of Fig. 5, simulated with the Lattice Boltzmann method. For each trajectory, the initial particle positions are spatially perturbed by a displacement vector with magnitude 0.025L and random angle. The four trajectories break up at different times. | ||
To determine whether chaotic three body hydrodynamics can account for this sensitivity, we examine the three particle configuration of Fig. 7(a) by integrating the theoretical model. Recall that, by construction, this model contains only far-field hydrodynamics. We integrate several thousand trajectories, again with each starting with a small, random perturbation to the initial particle positions. (In this case, we apply two separate noise terms to the x and y positions of each particle, where the noise is uniformly distributed over the interval [−0.0125L,0.0125L].) We find two modes of cluster break-up: either the blue particle escapes from the red and green particles, (Fig. 7(a), top panel) or the blue and green particles escape together as a dimer and leave the red particle behind (Fig. 7(a), bottom panel). Qualitatively, this break-up can be understood on the basis of the so-called transverse “anti-drag” inherent in the dipolar form of hydrodynamic interactions. (Fig. 1(b)) The blue particle leaves the red and green particles behind when it is close to the lower wall, so that it is significantly sped up by interaction with its nearest image. Similarly, when two particles form a pair oriented perpendicular to the external flow – such as when the green and blue particles escape together – “anti-drag” increases the speed of the pair relative to that of a single particle. Once particles are separated by a distance comparable to W, their interaction is screened, and break-up is complete. The distribution of these escape pathways is shown in Fig. 7(b). This stochastic break-up process arises from sensitivity to initial particle positions, which can be quantified by measuring the characteristic time for exponential divergence of initially neighboring trajectories, as in Fig. 7(c).
![(a) Particle motion in the center of mass frame for two realizations of a metastable three particle configuration with W/L = 8, as determined by integration of the theoretical model. The two realizations differ by slight noise in the initial particle positions. A random perturbation uniformly distributed over the interval [−0.0125L,0.0125L] is applied to the x and y positions of each particle. The green (middle) particle pairs and escapes with either the red (left) particle, as shown in the first panel, or the blue (right) particle, as shown in the second panel. (b) Distribution of escape pathways for the three particle configuration. Bins are labeled by which two particles pair. For each trajectory, the initial particle positions are given a random perturbation, as in (a). The escape outcome is sensitive to this perturbation. (c) Euclidean distance Δ2(t) ≡ ∑i[(xi,A(t) − xi,B(t))2 + (yi,A(t) − yi,B(t))2] between the two realizations (trajectories in phase space) in (a) as a function of dimensionless time, where i indexes the three particles, and A and B label the two trajectories. For some initial transient period, both trajectories are bound as three particle configurations and diverge exponentially in phase space, Δ ∼ eΛU0t/L, with a Lyapunov exponent of Λ = 0.00185.](/image/article/2012/SM/c2sm25931a/c2sm25931a-f7.gif) | ||
| Fig. 7 (a) Particle motion in the center of mass frame for two realizations of a metastable three particle configuration with W/L = 8, as determined by integration of the theoretical model. The two realizations differ by slight noise in the initial particle positions. A random perturbation uniformly distributed over the interval [−0.0125L,0.0125L] is applied to the x and y positions of each particle. The green (middle) particle pairs and escapes with either the red (left) particle, as shown in the first panel, or the blue (right) particle, as shown in the second panel. (b) Distribution of escape pathways for the three particle configuration. Bins are labeled by which two particles pair. For each trajectory, the initial particle positions are given a random perturbation, as in (a). The escape outcome is sensitive to this perturbation. (c) Euclidean distance Δ2(t) ≡ ∑i[(xi,A(t) − xi,B(t))2 + (yi,A(t) − yi,B(t))2] between the two realizations (trajectories in phase space) in (a) as a function of dimensionless time, where i indexes the three particles, and A and B label the two trajectories. For some initial transient period, both trajectories are bound as three particle configurations and diverge exponentially in phase space, Δ ∼ eΛU0t/L, with a Lyapunov exponent of Λ = 0.00185. | ||
Our results on chaotic dispersion of three particle clusters recall a pioneering numerical study of the chaotic dynamics of three sedimenting spheres, represented mathematically as Stokeslets.39 Once again, unbounded q2D provides a point of contrast. Clusters of three particles in the unbounded geometry immediately break up as a dimer and a single particle. The bare dipolar form is not sufficient for three body chaotic dynamics. This does not rule out metastable states and chaotic dispersion for higher N in unbounded q2D, which could be explored with the techniques described here.
3.3 Cyclical dynamical motifs
The techniques discussed above are used to find configurations in which particles maintain their relative positions as the cluster flows down the channel, whether indefinitely, as with the marginally stable fixed points, or for many advected particle lengths, as with the metastable steady states. For the marginally stable fixed points, there are collective modes in which particles oscillate around their equilibrium positions. However, these are not the only ordered motions possible. There are metastable dynamical motifs in which particles follow cyclical paths. These configurations cannot be found by minimizing the particles' relative velocities, as above, since the particles are constantly in motion. Instead, we scan for these dynamical motifs by directly integrating the equations of motion for various initial particle configurations and sorting out trajectories for which the final configuration is close to the initial configuration in phase space. The simplicity of the theoretical model permits computation of thousands of trajectories overnight on a single processor. Candidate motifs can then be studied in greater detail via Lattice Boltzmann simulations. Via direct integration and LBM simulations, we find the “juggling” motif of Fig. 8(a), in which three particles cyclically exchange positions, and the “bowtie” configuration of Fig. 8(b). As metastable states, these configurations also eventually disperse.![Cyclical motifs for N = 3 particles discovered via a “brute force” search with the theoretical model and confirmed with LBM simulations. In a search, we sweep over initial spatial configurations of N particles, integrating the model forward in time for a specified time span and identifying candidate cycles as those with small Euclidean distance between the initial and final spatial configurations. The Euclidean distance d is defined as d2 ≡ ∑i[(xi(tfinal) − xi(0))2 + (yi(tfinal) − yi(0))2]. The simplicity of the model makes this approach computationally tractable. Colors indicate the magnitude of the fluid velocity field. (a) In the “juggling” motif, the three particles move clockwise, as indicated by the black arrow, cyclically exchanging positions. Particles pause in the bottom position, recalling how a juggler will momentarily have a ball in hand. Each exchange of particle positions occurs after about 115 advected particle lengths, so that the entire cycle takes about xcm/L = 345 lengths. (b) The “bowtie” motif. At first glance, it might appear that this motif is associated with a fixed point in which particles are positioned on the centerline, aligned with the flow. However, such a configuration would quickly disperse. Particles return roughly to their initial positions after approximately xcm/L = 960 particle lengths.](/image/article/2012/SM/c2sm25931a/c2sm25931a-f8.gif) | ||
| Fig. 8 Cyclical motifs for N = 3 particles discovered via a “brute force” search with the theoretical model and confirmed with LBM simulations. In a search, we sweep over initial spatial configurations of N particles, integrating the model forward in time for a specified time span and identifying candidate cycles as those with small Euclidean distance between the initial and final spatial configurations. The Euclidean distance d is defined as d2 ≡ ∑i[(xi(tfinal) − xi(0))2 + (yi(tfinal) − yi(0))2]. The simplicity of the model makes this approach computationally tractable. Colors indicate the magnitude of the fluid velocity field. (a) In the “juggling” motif, the three particles move clockwise, as indicated by the black arrow, cyclically exchanging positions. Particles pause in the bottom position, recalling how a juggler will momentarily have a ball in hand. Each exchange of particle positions occurs after about 115 advected particle lengths, so that the entire cycle takes about xcm/L = 345 lengths. (b) The “bowtie” motif. At first glance, it might appear that this motif is associated with a fixed point in which particles are positioned on the centerline, aligned with the flow. However, such a configuration would quickly disperse. Particles return roughly to their initial positions after approximately xcm/L = 960 particle lengths. | ||
4 Conclusions
Using a theoretical approach and Lattice Boltzmann simulations, we revealed new classes of nonequilibrium ordered states for small particle clusters flowing in quasi-two-dimensional channels. For several of these classes, particles maintain their relative configurations either indefinitely (the marginally stable configurations, which are fixed points of a dynamical system) or for hundreds of advected particle lengths (the steady metastable configurations.) The marginally stable configurations can be regarded as “flowing crystals,” since they are constructed by exploiting the translational symmetry of an infinite set of real and virtual particles. As with crystals, they have collective modes in which particles oscillate around their equilibrium positions. The oscillations are not strictly transverse or longitudinal, but occur in two dimensions. Moreover, these “crystals” may, in fact, be more stable than the one-dimensional trains and two-dimensional arrays examined in other studies, since the virtual particles are completely slaved to the real particles.Metastable states provide new configuration geometries in which particles remain in steady relative positions. They are sensitive to initial particle configuration, and their eventual break-up is characterized by individualistic particle motion. This sensitivity affects even a gross and discrete outcome, how three particles in a “triangle” split into a bound pair and an isolated particle. Moreover, sensitivity requires only three hydrodynamically interacting particles. Our system offers a facile experimental and theoretical platform for the study of irreversible behavior that arises from reversible equations of motion. For example, a possible line of investigation is the effect of number of particles N on the statistics of dispersion. For small N, the dynamically “sticky” metastable states could contribute to anomalous diffusion. For large N, the dimensionality of the particles' configuration space is large, and mean-field theory should be applicable. Furthermore, the metastable states can be harnessed for lab-on-a-chip devices. Consider Fig. 5. If a steady state with little relative motion is desired, the particles scarcely move as the cluster flows xcm/L = 582 particle lengths downstream, as shown by the second panel. For a HeLA cell with L = 20 μm, this corresponds to an advected length ∼1.1 cm, which is a typical microchannel length. For a channel twice as long, the three particles come to “mix” and closely interact through individualistic trajectories.
For other classes of metastable states – the cyclical dynamical motifs – particle motion is complex but still spatially and temporally ordered, with particle excursions occurring over many particle diameters in two dimensions.
We elucidated the principles for a priori construction of fixed points, as well as numerical techniques for rapid numerical discovery of metastable steady and cyclical states. These can be applied to any number N of particles; for the sake of brevity, we omitted results on N = 4, N = 5, and so on. Moreover, our findings and techniques suggest future directions of research incorporating other physical effects. Lattice Boltzmann can be coupled to deformable particles instead of rigid discs. For deformable particles, distant segments move relatively and interact hydrodynamically, and the collective behaviors revealed here could couple to the particles' internal elastic modes. Likewise, spring forces can be incorporated in the theoretical model. The particles can be made non-identical, either through varying particle size, or through varying the friction coefficient γp. Practically speaking, the latter might vary through the course of an experiment, either in a time invariant manner, through particle polydispersity, or transiently, through fluctuations in the z direction for weakly confined particles. If particles are non-identical, they no longer have the same interaction parameter β, and hydrodynamic interactions are no longer symmetric on the two particle level.11 For instance, when γp varies for three particles by ±10% for a “column” fixed point in the theoretical model, they no longer maintain steady relative positions, but adopt complicated quasi-periodic orbits. A limitation of the marginally stable fixed points constructed above is that they are not attractors for particle dynamics; that is, disordered suspensions of particles will not spontaneously “crystallize,” and access to the fixed points is limited by initial particle configuration. It is conceivable that particles could be induced to assemble when time reversal symmetry is broken, as when particles are deformable, and/or when particle symmetry is broken, as when particles have dissimilar size or shape. Our theoretical framework can also incorporate Brownian noise, and potentially be applied to the dynamics of macromolecules in slit-like confinement. Experimental evidence and theoretical arguments indicate that hydrodynamic interactions can be neglected in the mean-field limit for q2D confined macromolecules, although this still a subject of discussion.37,40 Our work suggests that hydrodynamics could significantly affect chain dynamics when the number of interacting segments N is small. We anticipate that this work will provide a starting point for further discovery of rich physics in q2D particle-laden flows.
5 Appendix A: two particle oscillations
The theoretical model was developed in a previous work, where it was applied to a system of two particles. It was found that, depending on the initial conditions, the two particles will either break apart and scatter to infinity, or remain together as a oscillatory bound state.26 These bound states are marginally stable orbits around two types of fixed point. The first type of fixed point has particle separation in the flow direction Δx = 0, where Δx ≡ x2 − x1, and Δy ≠ 0, where Δy ≡ y2 − y1. The center of mass position is on the channel centerline, ycm = W/2. For this type of fixed point, the particle separation vector r12 ≡ r2 − r1 is oriented at 90° with respect to the external flow. The second, 0° fixed point has ycm = W/2, Δx ≠ 0, and Δy = 0.We quantitatively compare Lattice Boltzmann and the theoretical model for two initial conditions and channel geometries that lead to oscillations around a 90° fixed point. For initial Δx = 0, Δy = 3L, ycm = W/2 + L, and W/L = 9, we find that LBM results at Re = 0.2 closely correspond to theoretical predictions, with very slight attenuation of amplitude over several wavelengths. This can be seen in Fig. 9 (left), which show particle positions y1 and y2 with center of mass position xcm.
 | ||
| Fig. 9 (left) Oscillation of a particle pair with initial Δy = 3L, initial Δx = 0 and initial center of mass position ycm = W/2 + L. The positions of the two particles in y are shown as a function of center of mass position xcm. The solid black curve shows LBM simulation results at Re = 0.2, and the dashed red curve shows the result of numerically integrating the theoretical model. These curves closely agree, though very slight attenuation in amplitude can be seen in the LBM results. (right) Simulation results for the particle pair, shown after advection by xcm/L = 859 particle lengths. The red and blue curves show particle positions at prior times, and crosses indicate initial particle positions. Colors indicate the magnitude of the fluid velocity field. | ||
On the other hand, decay of amplitude with xcm is much faster at Re = 0.2 for another, less dilute configuration with initial Δy = 2L, initial Δx = 0, and initial ycm = W/2 + L. Fig. 10 shows results for this trajectory and for other values of Re. Since yi is plotted against xcm instead of with time, these curves should overlap if the velocity scale is unimportant, i.e. in the absence of inertial effects. As Re is reduced, the effect diminishes in significance, and the trajectories approach overlap. We conclude that the marginal stability of the theoretical model can be recovered in the limit of Re → 0, although the inertial effect is more significant for configurations with closer contact between surfaces.
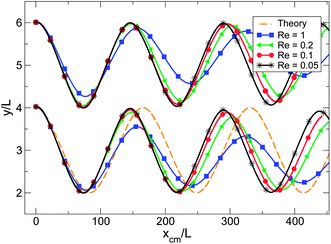 | ||
| Fig. 10 Oscillation of a particle pair with initial separation Δy = 2L, Δx = 0 and initial center of mass position ycm = W/2 + L for various values of Re. Particle positions in y are shown as a function of center of mass position xcm in the flow direction. As Re decreases, there is less decay of amplitude per wavelength. For clarity, we omitted the theoretical curve for one of the particles. | ||
We also show a trajectory at Re = 1, for which decay is rapid. For this trajectory, it can be easily seen that y1 and y2 drift towards focusing positions. This is reminiscent of the focusing effect exploited in inertial microfluidics.41 Inertia could provide another axis of control for particles flowing in q2D confinement, although the design rules, theory, and experimental results developed for weakly or moderately confined spheres may not be directly transferable to q2D particles.
Finally, we use this initial particle configuration and channel geometry to demonstrate the universality of our theoretical model and the effect of varying the parameter β. Since the hydrodynamic interaction term in eqn (3) is order β relative to the external flow U0, then the wavelength of oscillation of y1 or y2 with xcm should vary as β−1, since the particles' motion in y arises strictly from hydrodynamic interactions. For H/L = 2/3 and H/L = 1/3, we vary the value of γp to tune β, and find that λ/L, the wavelength of oscillation, does follow the predicted scaling, and that the data for both values of H/L collapse onto one curve (Fig. 11).
 | ||
| Fig. 11 The two particle configuration of Fig. 10 has an characteristic wavelength λ/L with which y1 and y2 oscillate as xcm increases. This wavelength λ/L scales with the hydrodynamic interaction parameter β with a fitted exponent of −0.963, close to the predicted value of −1. | ||
6 Appendix B: validation of q2D Lattice Boltzmann model
In order to test our q2D Lattice Boltzmann model quantitatively, we measure dimensionless drag forces and torques for comparison with the theoretical values derived in Evans and Sackmann.27 In the following, we use a square domain of side length 25L, while we vary disc size L and dimensionless height H/L. Larger values of L resolve more spatial detail, improving numerical accuracy, at the cost of greater computation time. We measure the dimensionless drag force Fx/4πμ2DU on a disc translating with fixed velocity U in a quiescent fluid. We fix Rep ≡ UpL/ν as Rep = 0.1. Likewise, we measure the dimensionless torque τ/4πR2μ2Dω on a disc rotating with fixed angular velocity ω in a quiescent fluid, keeping Reω = 0.1, where Reω ≡ 2ωR2/ν. The size of the domain allows us to neglect boundary effects. As Fig. 12 demonstrates, there is negligible improvement in accuracy when L is increased beyond the value L = 10 used throughout this work.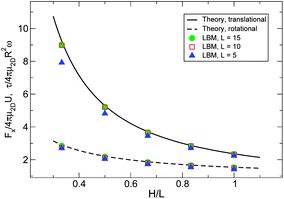 | ||
| Fig. 12 Dimensionless drag forces and torques vs. dimensionless channel height H/L for a disc translating or rotating in a quiescent fluid for various disc sizes L, where L characterizes the level of spatial coarse-graining. For L = 10, the disc size used in this study, there is negligible gain in accuracy with further improvement in resolution. | ||
7 Appendix C: hydrodynamic interaction tensor
As detailed in a previous work,26 a rigid particle of radius R in an unbounded q2D geometry can be modeled with the two dimensional Brinkman equation:| −∇P2D + μ2D∇2u − μHa2u = 0, | (12) |
 | (13) |
| X ≡ (xi − xj), Y ≡ (yi − yj) |
| V(ij)yx = V(ij)xy, V(ij)yy = −V(ij)xx. |
The tensor V(ij)αβ should be read as “the disturbance at particle i in direction α due to motion of particle j in direction β.”
To obtain V(ij)αβ for the thin channel geometry, we sum over particle images, as described in Section 2.1 and detailed in our previous work. This procedure introduces new self-interaction terms, and changes the form of the two particle coupling to be a screened dipolar interaction. The self-interaction (i = j) is determined as:
| V(ii)xx,far = −C/3, V(ii)yy,far = −V(ii)xx,far |
| V(ii)xy,far = 0, V(ii)yx,far = 0, V(ii)xx,near = −C/sin2(πyi/W) |
| V(ii)yy,near = V(ii)xx,near, V(ii)xy,near = 0,V(ii)yx,near = 0 |
| V(ii)αβ = V(ii)αβ,near + V(ii)αβ,far. |
For i ≠ j, the screened dipolar interaction is given by:
| X− ≡ π(xi − xj)/2W, Y± ≡ π(yi ± yj)/2W |
| V(ij)yx,far = V(ij)xy,far, V(ij)yy,far = −V(ij)xx,far |
| V(ij)yx,near = −V(ij)xy,near, V(ij)yy,near = V(ij)xx,near |
| V(ij)αβ = V(ij)αβ,near + V(ij)αβ,far |
For fixed Y+ and Y−, the two body interaction decays exponentially with screening length W/π or W/2π as |X−| → ∞.
Acknowledgements
This work was supported by the Institute for Collaborative Biotechnologies through through grant W911NF-09-0001 from the U.S. Army Research Office. The content of the information does not necessarily reflect the position or the policy of the Government, and no official endorsement should be inferred. We thank A. A. Alexeev and A. J. C. Ladd for valuable advice on the Lattice Boltzmann method.References
- S. H. Cho, J. M. Godin, C.-H. Chen, W. Qiao, H. Lee and Y.-H. Lo, Biomicrofluidics, 2010, 4, 043001 CrossRef.
- S. C. Chapin, D. C. Pregibon and P. S. Doyle, Lab Chip, 2009, 9, 3100–3109 RSC.
- D. Psaltis, S. R. Quake and C. Yang, Nature, 2006, 442, 381–386 CrossRef CAS.
- D. Choudhury, X. Mo, C. Iliescu, L. L. Tan, W. H. Ton and H. Yu, Biomicrofluidics, 2011, 5, 022203 Search PubMed.
- X. Mao, S.-C. S. Lin, C. Dong and T. J. Huang, Lab Chip, 2009, 8, 1583–1589 RSC.
- L. Wang, L. A. Flanagan, N. L. Jeon, E. Monuki and A. P. Lee, Lab Chip, 2007, 7, 1114–1120 RSC.
- W. Lee, H. Amini, H. A. Stone and D. Di Carlo, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 22413 CrossRef CAS.
- J. F. Edd, D. Di Carlo, K. J. Humphry, S. Köster, D. Irimia, D. A. Weitz and M. Toner, Lab Chip, 2008, 8, 1262–1264 RSC.
- S. C. Hur, H. T. K. Tseb and D. Di Carlo, Lab Chip, 2010, 10, 274–280 RSC.
- J. L. McWhirter, H. Noguchi and G. Gompper, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 6039 CrossRef CAS.
- Y. Sokolov, D. Frydel, D. G. Grier, H. Diamant and Y. Roichman, Phys. Rev. Lett., 2011, 107, 158302 CrossRef.
- G. M. Whitesides and B. Grzybowski, Science, 2002, 295, 2418 CrossRef CAS.
- M. P. Brenner, Phys. Fluids, 1999, 11, 754–772 CrossRef CAS.
- P. P. Lele, J. W. Swan, J. F. Brady, N. J. Wagner and E. M. Furst, Soft Matter, 2012, 7, 6844–6852 RSC.
- H. B. Eral, J. M. Oh, D. van den Ende, F. Mugele and M. H. G. Duits, Langmuir, 2010, 26, 16722–16729 CrossRef CAS.
- N. Liron and S. Mochon, J. Eng. Math., 1976, 10, 287–303 CrossRef.
- H. Diamant, J. Phys. Soc. Jpn., 2009, 78, 041002 CrossRef.
- B. Cui, H. Diamant, B. Lin and S. A. Rice, Phys. Rev. Lett., 2004, 92, 248301 CrossRef.
- T. Beatus, R. Bar-Ziv and T. Tlusty, Phys. Rep., 2012, 516, 103–145 CrossRef.
- T. Beatus, T. Tlusty and R. Bar-Ziv, Nat. Phys., 2006, 2, 743 CrossRef CAS.
- M. Baron, J. Blawzdziewicz and E. Wajnryb, Phys. Rev. Lett., 2008, 100, 174502 CrossRef CAS.
- A. Alvarez and R. Soto, J. Fluid Mech., 2005, 17, 093103 Search PubMed.
- T. Beatus, R. Bar-Ziv and T. Tlusty, Phys. Rev. Lett., 2007, 99, 124502 CrossRef.
- N. Champagne, E. Lauga and D. Bartolo, Soft Matter, 2011, 7, 11082–11085 RSC.
- T. Beatus, T. Tlusty and R. Bar-Ziv, Phys. Rev. Lett., 2009, 103, 114502 CrossRef.
- W. E. Uspal and P. S. Doyle, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 016325 CrossRef.
- E. Evans and E. Sackmann, J. Fluid Mech., 1988, 194, 553–561 CrossRef.
- D. Halpern and T. W. Secomb, J. Fluid Mech., 1991, 231, 545–560 CrossRef.
- D. Howells, J. Fluid Mech., 1974, 64, 449–475 CrossRef.
- A. J. C. Ladd and R. Verberg, J. Stat. Phys., 2001, 104, 1191–1251 CrossRef CAS.
- C. K. Aidun and J. R. Clausen, Annu. Rev. Fluid Mech., 2010, 42, 439–472 CrossRef.
- E. G. Flekkøy, U. Oxaal, J. Feder and T. Jøssang, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 52, 4952–4962 CrossRef.
- P. Grosfils, J. P. Boon, J. Chin and E. S. Boek, Philos. Trans. R. Soc. London, Ser. A, 2004, 362, 1723–1734 CrossRef.
- Z. L. Guo, C. G. Zheng and B. C. Shi, Prog. Comput. Fluid Dyn., 2009, 9, 225–230 CrossRef.
- P. Nikunen, M. Karttunen and I. Vattulainen, Comput. Phys. Commun., 2003, 153, 407–423 CrossRef CAS.
- Q. Zou and X. He, Phys. Fluids, 1997, 9, 1591–1598 CrossRef CAS.
- T. Tlusty, Macromolecules, 2006, 39, 3927–3930 CrossRef CAS.
- X. Xu, B. Lin, B. Cui, A. R. Dinner and S. A. Rice, J. Chem. Phys., 2010, 132, 084902 CrossRef.
- I. M. Jánosi, T. Tél, D. E. Wolf and J. A. C. Gallas, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 56, 2858 CrossRef.
- A. Balducci, P. Mao, J. Han and P. S. Doyle, Macromolecules, 2006, 39, 6273–6281 CrossRef CAS.
- D. Di Carlo, Lab Chip, 2009, 9, 3038–3046 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Videos corresponding to Fig. 5 and 8(a). See DOI: 10.1039/c2sm25931a |
| This journal is © The Royal Society of Chemistry 2012 |