Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Matrix-isolation IR spectra of iodotrifluoroethylene (C2F3I)†
Malte
Feßner
 ab,
Julien
Bloino
ab,
Julien
Bloino
 ab and
Christian
Merten
ab and
Christian
Merten
 *ab
*ab
aRuhr-Universität Bochum, Fakultät für Chemie und Biochemie, Organische Chemie II, Universitätsstraße 150, 44801 Bochum, Germany. E-mail: christian.merten@ruhr-uni-bochum.de; Web: https://www.mertenlab.de
bScuola Normale Superiore, Piazza dei Cavalieri 7, 56126 Pisa, Italy
First published on 25th March 2025
Abstract
The infrared spectra of iodotrifluoroethylene (ITFE) recorded under matrix-isolation (MI) conditions in para-hydrogen, neon and argon were investigated. The experimental spectra were analyzed by comparison with computed anharmonic spectra obtained in the second-order vibrational perturbation theory (VPT2) framework at the MP2 and revDSD-PBEP86-D3BJ levels of theory. In para-hydrogen and neon matrices, the experimentally observable bands in the range of 1800–650 cm−1 could be assigned to vibrational transitions of monomeric ITFE. The spectral resolution even allowed assignments of transitions arising from 13C-isotopologues and the observation of various higher-order resonances in the range up to ∼3550 cm−1. A comprehensive series of MI experiments in argon obtained by varying several experimental parameters revealed a dependence of the spectra on the deposition temperature. The spectra generally showed strong site-splitting effects due to the existence of different local environments around the ITFE molecule. Detailed analysis of the experimental spectra resulted in the identification of bands which are differently affected by matrix annealing. This observation led to the conclusion that ITFE occupies two major matrix sites of different stability. Calculations on ITFE dimers confirmed that spectral changes during annealing are due to the formation of dimers, which are stabilized through π–π interactions.
Introduction
Halogen bonding (XB) interactions1–6 are currently considered as alternative to classical Coulomb and hydrogen bonding interactions in various areas of chemistry. While applications typically make use of large electron-deficient molecules to increase the XB strength, it is more convenient to select neutral XB complexes of small donor and acceptor molecules as model systems for fundamental studies on XB interactions. Their reduced size makes easier the application of accurate theoretical models, while their lack of conformational dynamics and relatively simple electronic structure facilitate theoretical analyses. From an experimental perspective, the characterization of such weak intermolecular interactions in the solution phase is often challenging as they inevitably compete with solute–solvent interactions. Furthermore, IR spectroscopic signatures of complexes may sometimes only slightly deviate from those of the corresponding monomers, and hence will not be resolvable in broad solution phase spectra.Gas-phase spectroscopies and methods taking advantage of inert environments are thus the methods of choice for the characterization of such complexes. Rotational spectroscopy, for instance, has been utilized to gain insights into lone-pair (lp)⋯π interactions in complexes of C2F3Cl with water7 and ammonia8 or for C2H4⋯ClF,9 to name a few examples. Using liquid rare gases as solvents,10 Herrebout and co-workers investigated weakly bound complexes, among others,11,12 of CF3X (X = Cl, Br, I or H) with ethene and propene13 in liquid argon (LAr) and with benzene and toluene in liquid krypton (LKr) at 150 K.14 They also investigated C2F3X⋯N(CD3)3 (with X = F, Cl, Br, I) as model systems with potentially competing lp⋯π and halogen bonding interactions.15
The matrix isolation (MI) technique16,17 involves the trapping of weakly bound clusters in solid rare gas matrices, that are prepared by spraying mixtures of the target compounds and the host gas onto a cryogenic window, which is typically held at temperatures markedly below the melting point of the host gas. This procedure traps mostly complexes that are already formed in the gas phase. Through diffusion processes, that are initiated either due to excess thermal energy of the gas mixture during cooldown or by slightly warming the matrix after deposition, further complexation takes place. Due to the rigidity of the environment, large structural rearrangements are effectively suppressed, so that it is often possible to also trap thermodynamically less favourable clusters.18,19 Through MI-IR spectroscopy, C–Cl⋯π interactions between CCl4 and ethene20 (Ar and N2 matrix), as well as the complexes of CCl4 or CBr4 with acetone21 could be characterized, for instance.22–25
In a recent MI-IR study,26 we characterized complexes of iodotrifluoroethylene C2F3I (ITFE), the title compound of the present study, with N,N-dimethyl ferrocenyl amine. While the amine-derivative expectedly showed C–I⋯N interactions with ITFE, we also observed spectral signatures indicative of C–I⋯π halogen bonding and π⋯π interactions. The latter interactions could also be identified in MI-IR spectra of ITFE with the parent ferrocene. We also briefly characterized ITFE itself and discussed the spectral signatures of the monomer and some dimeric species. However, when studying complexes of ITFE with other XB-acceptors, we realized that the MI-IR spectra of pure ITFE were more complicated than we initially thought. In fact, we found a strong dependence of the spectra on the host gas and deposition temperature. In the present study, we thus further refine our picture of the structure of ITFE in cryogenic matrices (para-hydrogen, Ne, Ar) and revise earlier band assignments.
Results and discussion
ITFE possesses 12 fundamental vibrational transitions, of which five are predicted to occur in the spectral range above 600 cm−1, which is experimentally accessible to us. According to harmonic calculations,15,26,27 the observable fundamentals are the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching mode (νC
C stretching mode (νC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, 1770–1750 cm−1), the out-of-phase C–F stretching in
C, 1770–1750 cm−1), the out-of-phase C–F stretching in ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CFF (νCF2,oop, 1350–1300 cm−1), the C–F stretching of
CFF (νCF2,oop, 1350–1300 cm−1), the C–F stretching of ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CFI (νC–F, 1200–1150 cm−1), and in-phase stretching of C–F in
CFI (νC–F, 1200–1150 cm−1), and in-phase stretching of C–F in ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CFF (νCF2,ip, out-of-phase coupled to C–I stretching, around 1000 cm−1). At ∼650 cm−1, a fifth, very weak fundamental mode is predicted to arise from an in-plane bending motion of the entire molecule (νδ).
CFF (νCF2,ip, out-of-phase coupled to C–I stretching, around 1000 cm−1). At ∼650 cm−1, a fifth, very weak fundamental mode is predicted to arise from an in-plane bending motion of the entire molecule (νδ).
Experimental matrix-IR spectra of ITFE were recorded in para-hydrogen (pH2) and neon matrices deposited at 4 K, and in argon matrices prepared at various temperatures between 4 and 25 K. Upon inspection of the spectra (cf.Fig. 1), differences in band positions can be observed between the matrix host gases. Such matrix-induced band shifts are not unusual and arise from differences in the polarizabilities of the media as well as from packing effects.28,29 It is furthermore important to note that there are clearly more strong bands visible than the five fundamental transitions expected in this spectral range. In the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching range, one sharp band can be identified in the spectra recorded for pH2 and Ne, while there is at least one additional band visible in the Ar matrix. In fact, depending on the deposition temperature, up to five bands can be identified (see discussion below). In the spectral range where νCF2,oop lies, there are at least four bands identifiable in pH2, while even more weak features are found in the Ar matrix. Similar observations can be made in the other two highlighted spectral ranges.
C stretching range, one sharp band can be identified in the spectra recorded for pH2 and Ne, while there is at least one additional band visible in the Ar matrix. In fact, depending on the deposition temperature, up to five bands can be identified (see discussion below). In the spectral range where νCF2,oop lies, there are at least four bands identifiable in pH2, while even more weak features are found in the Ar matrix. Similar observations can be made in the other two highlighted spectral ranges.
To assign as many of the experimentally observed features as possible, we carried out spectral calculations at various levels of theory. In the following, we will first discuss the computational results in comparison to the spectra of ITFE recorded in pH2 and Ne, before subsequently moving to the spectra recorded in argon.
Band assignments in pH2 and Ne matrices
To identify the most suitable theoretical basis for the computation of the IR spectrum of ITFE, we first carried out calculations at the hybrid-DFT level using B3LYP30–32 in its dispersion corrected variant (D3BJ),33 at double-hybrid DFT levels with the B2PLYP-D3BJ34 and the revDSD-PBEP86-D3BJ35 functionals, and lastly using pure MP2.36–39 A triple-ζ basis set (def2TZVP40) was used for all calculations. As expected, the different levels of electronic structure theory gave different band positions in the harmonic approximation (cf. Fig. S1, ESI†). In line with previous observations,26,27,41 the B3LYP-D3BJ functional provided a good match for the three strong vibrational modes, that involve stretching motions of C–F bonds (νCF2,oop, νC–F, νCF2,ip), even without application of a frequency scaling factor, while the energy of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching mode was overestimated. After applying suitable uniform scaling factors, however, the spectrum computed at the MP2 level generally matched exceptionally well all four strong experimental band positions. In the order revDSD-PBEP86-D3BJ, B2PLYP-D3BJ, B3LYP-D3BJ, the other three methods led to increasingly strong deviations from the experimental band positions.
C stretching mode was overestimated. After applying suitable uniform scaling factors, however, the spectrum computed at the MP2 level generally matched exceptionally well all four strong experimental band positions. In the order revDSD-PBEP86-D3BJ, B2PLYP-D3BJ, B3LYP-D3BJ, the other three methods led to increasingly strong deviations from the experimental band positions.
As noted above, the experimental spectra show additional intense bands that are not associated with fundamental transitions (cf.Fig. 1, overview). In a study on halogen-bonding of ITFE in LKr,15 Herrebout et al. assigned some of them to combinations and overtones. However, due to the sharp bandwidth of the pH2-matrix measurement, significantly more bands could be resolved than in LKr. Hence, to complete the assignments, we computed the IR spectrum of ITFE including anharmonicity by means of second-order vibrational perturbation theory (VPT2) at all four computational levels.42–47 To our delight, the resulting IR spectrum obtained at either the MP2 or revDSD-PBEP86-D3BJ level reproduced many of the very small features that were missing in the harmonic spectrum (cf.Fig. 2 and Fig. S1 (ESI†) show the results for the other methods as well). Interestingly, revDSD-PBEP86-D3BJ in fact performed notably better than MP2 and almost perfectly matched many experimental band positions and relative intensities. It must be stressed that no frequency scaling factor was applied on top of the VPT2 energies.
 | ||
| Fig. 2 Experimental spectra of ITFE in a pH2 matrix deposited at 4 K compared to the computed anharmonic (VPT2) spectra obtained at the MP2 and revDSD-PBEP86-D3BJ levels of theory. Band labels refer to the excited modes and quanta (superscripts), when higher than 1. Colour-coded band assignments refer to 13C-isotopologues. Band broadening was simulated with Lorentzian functions and 0.5 cm−1 half-width at half-height. Instead of scaling the intensities of 13C-isotopologues to the actual natural abundancy of +1%, they were scaled to 10% for clarity. (*Fundamental 2 of 13C–FI and combination mode 9 + 3 overlap. For analysis and discussion see ESI.†) | ||
The most noteworthy band assignment is probably that of the very intense band at 1328 cm−1, which is a combination mode of the fundamentals 7 and 4. Yet, the VPT2 calculation on ITFE could not explain all small bands and distinct bands, such as those present at 1736 or 1723 cm−1, remained unexplained. As Herrebout et al. assigned one of them to a 13C-isotopologue,15 we computed the anharmonic spectra of ITFE with 13C at either position of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond. This allowed us to confirm the assignment of these two bands as the C
C bond. This allowed us to confirm the assignment of these two bands as the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching vibrations of the 13CFI and 13CFF isotopologues and to make further assignments for bands in the fingerprint region of the pH2-spectra (cf. colour-coded band assignments in Fig. 2 and Table 1). Notably, the anharmonic calculations even correctly predict minute energy shifts between vibrational states of different isotopologues (cf. ESI† for further discussions).
C stretching vibrations of the 13CFI and 13CFF isotopologues and to make further assignments for bands in the fingerprint region of the pH2-spectra (cf. colour-coded band assignments in Fig. 2 and Table 1). Notably, the anharmonic calculations even correctly predict minute energy shifts between vibrational states of different isotopologues (cf. ESI† for further discussions).
| ν exp/cm−1 | ν VPT2/cm−1 | Assignment | Origin |
|---|---|---|---|
| a Assignment supported by Geboes et al.15 | |||
| 652.8 | 654.5 | 5 | M |
| 906.6 | 913.3 | 11 + 10 | M |
| 939.1 | 943.9 | 8 + 1 | M |
| 974.2 | 976.4 | 7 + 5 | M |
| 984.8 | 989.7 | 4 (νCF2,ip) | 13C-FI |
| 1000.9 | 1006.3 | 4 (νCF2,ip) | 13C-F2 |
| 1004.5 | 1008.4 | 4 (νCF2,ip) | M |
| 1013.3 | 1014.2 | 62 | M |
| 1083.0 | 1126.7 | 102 | Ma |
| 1147.7 | 1149.9 | 3 (νC–F) | 13C-FI |
| 1153.2 | 1157.0 | 6 + 5 | 13C-FF |
| 1156.6 | 1159.4 | 6 + 5 | M |
| 1158.0 | 1161.3 | 6 + 5 | 13C-FI |
| 1174.5 | 1177.0 | 3 (νC–F) | 13C-FF |
| 1178.9 | 1180.9 | 3 (νC–F) | M |
| 1279.8 | 1276.2 | 2 (νCF2,oop) | 13C-FF |
| 1294.3 | 1295.9 | 9 + 3 | 13C-FI |
| 1303.8 | 1306.3 | 52 | M |
| 1315.8 | 1315.4 | 2 (νCF2,oop) | M |
| 1319.5 | 1322.7 | 2 (νCF2,oop) | 13C-FI |
| 1322.7 | 1322.8 | 9 + 1 | M |
| 1328.3 | 1334.2 | 7 + 4 | M |
| 1334.8 | 1337.4 | 7 + 62 | M |
| 1686.2 | 1685.1 | 6 + 3 | M |
| 1723.5 | 1738.3 | 1 (νC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) C) |
13C-FF |
| 1735.9 | 1747.9 | 1 (νC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) C) |
13C-FI |
| 1761.3 | 1773.6 | 1 (νC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) C) |
M |
| 1831.0 | 1832.0 | 5 + 3 | M |
It should be mentioned that ITFE possesses many more combination modes and overtones than those highlighted in the fingerprint region. Likewise, it must be acknowledged that the VPT2 calculations nicely reproduce these spectral features over a wide range (cf. Fig. S3, ESI†). The spectral intensities and computed spectra even allow the identification of the overtone of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching mode. The fundamental occurs at 1764 cm−1, while its overtone is experimentally found at 3524 cm−1.
C stretching mode. The fundamental occurs at 1764 cm−1, while its overtone is experimentally found at 3524 cm−1.
Comparing the spectrum recorded for the Ne matrix with the pH2 matrix reveals differences for only two peaks, the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching mode and C–F stretching of
C stretching mode and C–F stretching of ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CFI. Both appear highly structured, an indication of site splitting effects.48 Annealing of the Ne matrix at 9 K, a temperature at which the matrix is very close to evaporation, changed the band shapes only marginally, further stressing that this mode may be particularly prone to matrix site effects. We noticed that minor traces of water in the matrix led to a collapse of the site splitting (cf. Fig. S4, ESI†),49 so that matrix isolation studies on interactions of ITFE with other molecules in neon will most likely not show such strong splitting effects.
CFI. Both appear highly structured, an indication of site splitting effects.48 Annealing of the Ne matrix at 9 K, a temperature at which the matrix is very close to evaporation, changed the band shapes only marginally, further stressing that this mode may be particularly prone to matrix site effects. We noticed that minor traces of water in the matrix led to a collapse of the site splitting (cf. Fig. S4, ESI†),49 so that matrix isolation studies on interactions of ITFE with other molecules in neon will most likely not show such strong splitting effects.
Band assignments for ITFE in an Ar matrix
All bands observed in the experimental spectra in pH2 and Ne matrices can be assigned to monomeric ITFE. As noted above, in the context of a halogen bonding study, we have previously investigated the IR spectrum of ITFE in an Ar matrix and noted that the spectrum showed many additional bands not obviously assignable to the monomer. We thus concluded that a prominent band at 1758.7 cm−1 adjacent to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching band at 1760.4 cm−1 would arise from dimeric species.
C stretching band at 1760.4 cm−1 would arise from dimeric species.
For the present study, we have re-investigated the spectra of ITFE in an Ar matrix and carried out a comprehensive series of experiments, varying the concentration (i.e., the mixing ratio ITFE:Ar), the flow rate (i.e., deposition rates that determine the quality of the growth of the matrix), and the deposition temperature (i.e., the softness of the matrix during deposition). Interestingly, for a given deposition temperature, no differences were observed for concentrations ranging from 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 to 1
900 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3600 or by varying the flow rate (cf.Fig. 3a). Only the variation of the deposition temperature changed the spectral patterns. To our surprise, the aforementioned band at 1758.7 cm−1 occurred in all spectra and it showed approximately the same relative intensity (1
3600 or by varying the flow rate (cf.Fig. 3a). Only the variation of the deposition temperature changed the spectral patterns. To our surprise, the aforementioned band at 1758.7 cm−1 occurred in all spectra and it showed approximately the same relative intensity (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3) compared to the C
3) compared to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching band at 1760.4 cm−1 independent of the experimental parameters. In fact, a variation of the deposition temperature generated several additional bands (e.g., at 1763.6 and 1757.8 cm−1), while the bands at 1760.4 and 1758.7 cm−1 remained in a stable relative intensity ratio. Changes in the range around νCF2,oop (fundamental “2”) were weak and as this range was congested with contributions from several combination modes and overtones, it was not further considered in the analysis. The spectral signatures around νC–F and νCF2,ip, i.e. the fundamentals “3” and “4”, however, were found to differ notably depending on the deposition temperature, with the intensity ratio between the bands at 1004.7 and 1003.6 cm−1 showing the most prominent changes.
C stretching band at 1760.4 cm−1 independent of the experimental parameters. In fact, a variation of the deposition temperature generated several additional bands (e.g., at 1763.6 and 1757.8 cm−1), while the bands at 1760.4 and 1758.7 cm−1 remained in a stable relative intensity ratio. Changes in the range around νCF2,oop (fundamental “2”) were weak and as this range was congested with contributions from several combination modes and overtones, it was not further considered in the analysis. The spectral signatures around νC–F and νCF2,ip, i.e. the fundamentals “3” and “4”, however, were found to differ notably depending on the deposition temperature, with the intensity ratio between the bands at 1004.7 and 1003.6 cm−1 showing the most prominent changes.
 | ||
Fig. 3 (a) Experimental spectra of ITFE in an Ar matrix deposited at different temperatures and concentrations. The corresponding difference spectra are shown in Fig. S4 (ESI†). (b) Spectra of ITFE/Ar = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3600 after annealing at 35 K with band markers for the signatures discussed in the text. 3600 after annealing at 35 K with band markers for the signatures discussed in the text. | ||
After annealing of the matrices at 35 K (cf.Fig. 3b), the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching regions of the spectra taken at 10 K and higher converged to very similar band-shapes. New bands consistently occurred at 1763.6, 1757.8, 1757.2 and 1756.4 cm−1. The band at 1760.4 cm−1 generally decreased, but the band at 1758.7 cm−1 remained surprisingly constant in intensity. No other band was found to be equally robust upon annealing. On the contrary, around νC–F, new bands occurred at 1175.3 and 1174.0 cm−1, with the latter showing an interesting trend in intensity. The band pattern around νCF2,ip remained rather stable, but a slight change in relative intensity could nonetheless be noted.
C stretching regions of the spectra taken at 10 K and higher converged to very similar band-shapes. New bands consistently occurred at 1763.6, 1757.8, 1757.2 and 1756.4 cm−1. The band at 1760.4 cm−1 generally decreased, but the band at 1758.7 cm−1 remained surprisingly constant in intensity. No other band was found to be equally robust upon annealing. On the contrary, around νC–F, new bands occurred at 1175.3 and 1174.0 cm−1, with the latter showing an interesting trend in intensity. The band pattern around νCF2,ip remained rather stable, but a slight change in relative intensity could nonetheless be noted.
Site-splitting is commonly observed for the Ar-matrix,28,29,50,51 especially of small molecules. Several matrix-isolation studies have reported the existence of multiple matrix sites in Argon with different stabilities. For both carbon dioxide52 and dimethyl sulfate,53 for instance, two matrix sites are observed of which one is significantly more stable than the other. Given the discussed dependencies of the spectral patterns of ITFE in an Ar matrix on temperature and the changes upon annealing, we propose that monomeric ITFE resides in two major matrix sites of different stability. Accordingly, we interpret the bands at 1760.4 and 1758.7 cm−1 as C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching modes of ITFE molecules sitting in matrix pockets of different stability. It is remarkable, however, that the lower-energy band remains basically unaffected by annealing attempts, indicating a particularly high stability. For the other spectral regions, such direct assignments are more difficult, not least because of overlaps with combination states and overtones, and the occurrence of small site-splitting effects. Bands increasing in intensity during annealing should subsequently be considered the preferred dimeric species.
C stretching modes of ITFE molecules sitting in matrix pockets of different stability. It is remarkable, however, that the lower-energy band remains basically unaffected by annealing attempts, indicating a particularly high stability. For the other spectral regions, such direct assignments are more difficult, not least because of overlaps with combination states and overtones, and the occurrence of small site-splitting effects. Bands increasing in intensity during annealing should subsequently be considered the preferred dimeric species.
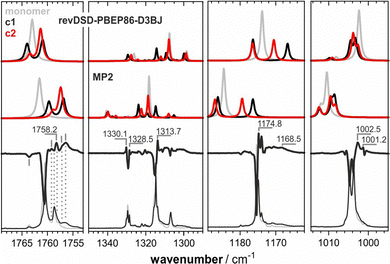
To assist in the assignment of further bands, we computed the IR spectra of ITFE dimers. To this end, geometry optimizations and IR spectra calculations were carried out on several dimer structures. Common to all low-energy dimers was the fact that they are stabilized by π–π interactions (cf.Fig. 4). Hence, they differed solely by the relative orientation of the molecules and molecular planes. The two lowest-energy structures (c1 and c2 in Fig. 4) are basically iso-energetic and thus equally likely to form during deposition and even more upon annealing. Other possible dimer geometries, involving C–I⋯π or C–I⋯I interactions, were found to be notably higher and thus were not considered in the analysis (cf. Fig. S8 and Table S1, ESI†).
 | ||
| Fig. 4 The four lowest-energy dimeric structures of ITFE considered in the analysis of the experimental matrix-IR spectra. Relative energies (in kcal mol−1) obtained from single-point calculations at the DLPNO-CCSD(T) level of theory54,55 on the revDSD-PBEP86-D3BJ optimized structures are given between parentheses. | ||
Each of the four lowest-energy dimers has characteristic spectral band shapes, which are independent of the level of theory and whether a harmonic or anharmonic approach was used (cf. Fig. S6, ESI† and Fig. 5, respectively). However, comparing the band positions relative to those of the ITFE monomer, they are found to differ significantly between computational levels. For instance, at the MP2 level, the two bands related to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching modes of each structure are consistently found at lower wavenumbers than the monomer. With revDSD-PBEP86-D3BJ, one of the two bands is predicted to be blue-shifted with respect to the monomer and the other one is red-shifted. At the anharmonic level, more contradicting predictions of the relative band positions were observed. For instance, with revDSD-PBEP86-D3BJ, the fundamental of mode 4 of the monomer (νCF2,ip, 1010–1000 cm−1) is at lower energy compared to those of the dimers, while the anharmonic MP2 calculations place it at higher energies. Hence, in addition to the need to consider that the monomer occupied two different matrix sites, the comparison between the experimental and computed spectra was further complicated by uncertainties in the computed band positions.
C stretching modes of each structure are consistently found at lower wavenumbers than the monomer. With revDSD-PBEP86-D3BJ, one of the two bands is predicted to be blue-shifted with respect to the monomer and the other one is red-shifted. At the anharmonic level, more contradicting predictions of the relative band positions were observed. For instance, with revDSD-PBEP86-D3BJ, the fundamental of mode 4 of the monomer (νCF2,ip, 1010–1000 cm−1) is at lower energy compared to those of the dimers, while the anharmonic MP2 calculations place it at higher energies. Hence, in addition to the need to consider that the monomer occupied two different matrix sites, the comparison between the experimental and computed spectra was further complicated by uncertainties in the computed band positions.
For this reason, we focussed our comparison of computed and experimental spectra on the data recorded for the 15 K deposition and especially on the difference spectrum (cf.Fig. 5). The latter spectrum amplifies spectral signatures of species generated and depleted during annealing. Bands of the lowest-energy dimers should occur as positive features, while negative bands are associated with higher-energy dimers and monomeric ITFE disappearing during annealing. In doing so, the new features in the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching region, i.e., the bands at 1759.2 and 1757.2 cm−1, could be reasonably well explained with the predicted two bands of dimers, which supports an assignment of the π–π c1 and π–π c2 to the bands at 1758.2/1756.5 and 1757.2 cm−1. Considering the predicted relative order of bands obtained from revDSD-PBEP86-D3BJ, the disappearing band at 1763.6 cm−1 may be assigned to the π–π c3 dimer (cf. Fig. S7 for an overview of all computed anharmonic spectra, ESI†). The growth of the broad features around 1170 cm−1 may also arise from the two lowest-energy dimers, but the new sharp bands cannot be assigned to any of the four dimer species. Likewise, the new features adjacent to νCF2,ip around 1002 cm−1 also agree well with the predicted band shapes of the two lowest-energy dimers. While the spectral calculations confirm that the spectra of ITFE in Ar matrices show mostly heavily site-split bands of the monomeric species, it must be concluded that the experimental and computational data do not allow for an unambiguous correlation of spectral features to specific dimeric species.
C stretching region, i.e., the bands at 1759.2 and 1757.2 cm−1, could be reasonably well explained with the predicted two bands of dimers, which supports an assignment of the π–π c1 and π–π c2 to the bands at 1758.2/1756.5 and 1757.2 cm−1. Considering the predicted relative order of bands obtained from revDSD-PBEP86-D3BJ, the disappearing band at 1763.6 cm−1 may be assigned to the π–π c3 dimer (cf. Fig. S7 for an overview of all computed anharmonic spectra, ESI†). The growth of the broad features around 1170 cm−1 may also arise from the two lowest-energy dimers, but the new sharp bands cannot be assigned to any of the four dimer species. Likewise, the new features adjacent to νCF2,ip around 1002 cm−1 also agree well with the predicted band shapes of the two lowest-energy dimers. While the spectral calculations confirm that the spectra of ITFE in Ar matrices show mostly heavily site-split bands of the monomeric species, it must be concluded that the experimental and computational data do not allow for an unambiguous correlation of spectral features to specific dimeric species.
Conclusions
In the present study, we investigated the IR spectra of ITFE recorded under matrix-isolation conditions in various host gases. The experimental spectra were analysed by means of anharmonic spectral calculations at the VPT2 level using different electronic structure calculation methods. For pH2 and Ne matrices, the experimental spectra matched very well computations on the ITFE monomer, and most experimentally observable bands could be assigned to fundamentals, combinations and overtones, or arising from the presence of 13C-isotopologues. This comparison stressed the need to go beyond harmonic spectral calculations to fully assign vibrational signatures, and simultaneously showcased the performance of the VPT2 approach to accurately account for resonances. In the case of argon matrices, additional bands were observed directly after deposition, and annealing resulted in significant spectral changes. A series of MI-experiments with varying deposition conditions allowed us to identify two matrix sites for the ITFE monomer, of which one was significantly more stable. It persisted during annealing, while ITFE in the less stable site formed dimers. Based on the computed spectra, only very few bands related to dimer species could be univocally assigned to the two lowest-energy structures (cf.Fig. 4). Spectral calculations also revealed that the exact shift of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching bands in dimer structures depended strongly on the chosen level of theory, which can be problematic for the precise assignment of such a highly sought band. In this context, the weak performance of a commonly used method such as MP2 was particularly unexpected, as it consistently underestimated the energies of the complexes’ bands.
C stretching bands in dimer structures depended strongly on the chosen level of theory, which can be problematic for the precise assignment of such a highly sought band. In this context, the weak performance of a commonly used method such as MP2 was particularly unexpected, as it consistently underestimated the energies of the complexes’ bands.
Our study led to two main conclusions for future studies on intermolecular interactions of ITFE. First, despite the very limited possibilities to anneal the matrix and thus to form larger amounts of intermolecularly bound clusters after deposition, pH2 and Ne are more suited as host gases than Ar. The bands arising from the additional argon matrix site bear the risk of overlapping with signatures of other complexes and cause unnecessary convolution of the spectra. Secondly, one should not rely solely on computed spectra from MP2 as the shifts of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching band caused by intermolecular interactions may be predicted incorrectly. As the performances of B3LYP-D3BJ, B2PLYP-D3BJ and revDSD-PBEP86-D3BJ were similar in terms of relative positions of the most sensitive C
C stretching band caused by intermolecular interactions may be predicted incorrectly. As the performances of B3LYP-D3BJ, B2PLYP-D3BJ and revDSD-PBEP86-D3BJ were similar in terms of relative positions of the most sensitive C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching bands, either of them should suffice to analyse the changes occurring in that spectral region.
C stretching bands, either of them should suffice to analyse the changes occurring in that spectral region.
Experimental details
Materials
ITFE was purchased from ABCR GmbH, Germany, in 97% purity and used without further purification. Gases were obtained from air liquide: H2 in 99.9999% purity, Ne in 99.999% purity and Ar in 99.999% purity.Matrix isolation IR spectroscopy
Experiments were carried out using either an APD Cryogenics DE-204SL for operation down to 10 K or a Janis SHI-4R cryostat operating down to 4 K. Ar depositions were carried out on both systems to ensure that spectral signatures are not instrument-dependent. para-Hydrogen (>99%) was generated using a home-built converter based on a Janis CCS-100/2004 cryostat.56 Sample mixtures were prepared in a standard gas manifold and sprayed onto a BaF2 window using a calibrated flow controller (MKS). Annealing of Ar matrices was done by slowly heating the window to 35 K, holding it at this temperature for 25 minutes, followed by a cooldown to the initial temperature. IR spectra were recorded at 0.2 cm−1 resolution using a Bruker INVENIO-R FT-IR spectrometer, accumulating 50 scans.Computational details
Geometry optimizations and IR spectra calculations were carried out at various levels of theory in the gas phase using Gaussian 16.57 Starting structures for the optimizations were generated manually, considering all possible relative orientations of the monomer species allowing for π⋯π, C–I⋯π, C–I⋯F and other interactions. Anharmonic calculations at the VPT2 level were carried out by first generating the necessary constants by numerical differentiation along mass-weighted normal coordinates, as implemented in Gaussian 16, with a constant step of 0.01 μ1/2 Å. Resonances in VPT2 were identified following the protocol described in ref. 58 with the same numerical thresholds. Removed terms were then reintroduced variationally and the final energies obtained by diagonalization of the generated polyads. A locally modified version of Gaussian was used for all VPT2 calculations. Spectra were simulated from the computed dipole strengths by assigning a Lorentzian band shape of 0.5 cm−1 half-width at half-height. Frequencies of the harmonic spectra were uniformly scaled as mentioned in the text. Single-point energies at the DLPNO-CCSD(T) level of theory were computed with ORCA 6.59–61 Structures were rendered using CylView.62Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany's Excellence Strategy (EXC-2033, project number 390677874), through the Research Training Group “Confinement Controlled Chemistry” (GRK 2376, project number 331085229), the DFG’s Heisenberg program (ME 4267/5-1; project no. 418661145), and a research grant (ME 4267/6-1; project no. 418662566), by the Boehringer Ingelheim Foundation through a Plus-3 grant, and by the Italian Ministry of University of Research (PRIN grant num. 2020HTSXMA).References
- R. L. Sutar, E. Engelage, R. Stoll and S. M. Huber, Angew. Chem., Int. Ed., 2020, 59, 6806–6810 CAS.
- G. Cavallo, P. Metrangolo, R. Milani, T. Pilati, A. Priimagi, G. Resnati and G. Terraneo, Chem. Rev., 2016, 116, 2478–2601 CrossRef CAS PubMed.
- L. C. Gilday, S. W. Robinson, T. A. Barendt, M. J. Langton, B. R. Mullaney and P. D. Beer, Chem. Rev., 2015, 115, 7118–7195 CrossRef CAS PubMed.
- S. H. Jungbauer, S. M. Walter, S. Schindler, L. Rout, F. Kniep and S. M. Huber, Chem. Commun., 2014, 50, 6281–6284 RSC.
- S. M. Huber, J. D. Scanlon, E. Jimenez-Izal, J. M. Ugalde and I. Infante, Phys. Chem. Chem. Phys., 2013, 15, 10350–10357 RSC.
- E. Corradi, S. V. Meille, M. T. Messina, P. Metrangolo and G. Resnati, Angew. Chem., Int. Ed., 2000, 39, 1782–1786 CrossRef CAS PubMed.
- Q. Gou, G. Feng, L. Evangelisti and W. Caminati, Angew. Chem., Int. Ed., 2013, 52, 11888–11891 CrossRef CAS PubMed.
- Q. Gou, L. Spada, Y. Geboes, W. A. Herrebout, S. Melandri and W. Caminati, Phys. Chem. Chem. Phys., 2015, 17, 7694–7698 RSC.
- H. I. Bloemink, J. H. Holloway and A. C. Legon, Chem. Phys. Lett., 1996, 250, 567–575 CrossRef CAS.
- W. Herrebout, in Halogen Bonding I - Impact on Materials Chemistry and Life Sciences, ed. P. Metrangolo and G. Resnati, Springer International Publishing, 2015 Search PubMed.
- D. Hauchecorne, A. Moiana, B. J. van der Veken and W. A. Herrebout, Phys. Chem. Chem. Phys., 2011, 13, 10204–10213 RSC.
- B. Michielsen, J. J. J. Dom, B. J. van der Veken, S. Hesse, M. A. Suhm and W. A. Herrebout, Phys. Chem. Chem. Phys., 2012, 14, 6469–6478 RSC.
- D. Hauchecorne, N. Nagels, B. J. van der Veken and W. A. Herrebout, Phys. Chem. Chem. Phys., 2012, 14, 681–690 RSC.
- N. Nagels, D. Hauchecorne and W. A. Herrebout, Molecules, 2013, 18, 6829–6851 CrossRef CAS PubMed.
- Y. Geboes, F. De Proft and W. A. Herrebout, J. Phys. Chem. A, 2015, 119, 5597–5606 Search PubMed.
- I. R. Dunkin, Chem. Soc. Rev., 1980, 9, 1–23 RSC.
- V. E. Bondybey, A. M. Smith and J. Agreiter, Chem. Rev., 1996, 96, 2113–2134 Search PubMed.
- C. Merten and Y. Xu, Chem. Phys. Chem., 2013, 14, 213–219 CrossRef CAS PubMed.
- C. Merten and Y. Xu, Angew. Chem., Int. Ed., 2013, 52, 2073–2076 CrossRef CAS PubMed.
- N. Ramanathan, K. Sundararajan, K. Vidya and E. D. Jemmis, Spectrochim. Acta, Part A, 2016, 157, 69–78 CrossRef CAS PubMed.
- P. Banerjee and I. Bhattacharya, Spectrochim. Acta, Part A, 2021, 250, 119355 CrossRef CAS PubMed.
- D. Pal, S. K. Agrawal, A. Chakraborty and S. Chakraborty, Phys. Chem. Chem. Phys., 2020, 22, 22465–22476 Search PubMed.
- D. Pal, A. Chakraborty and S. Chakraborty, Chem. Phys., 2022, 555, 111451 CrossRef CAS.
- B. Suryaprasad, S. Chandra, N. Ramanathan and K. Sundararajan, J. Mol. Struct., 2021, 1224, 129288 Search PubMed.
- P. Wang, N. Zhao and Y. Tang, J. Phys. Chem. A, 2017, 121, 5045–5055 CrossRef CAS PubMed.
- N. M. Kreienborg, F. Otte, C. Strohmann and C. Merten, Phys. Chem. Chem. Phys., 2023, 25, 15110–15114 RSC.
- N. M. Kreienborg and C. Merten, Phys. Chem. Chem. Phys., 2019, 21, 3506–3511 RSC.
- A. J. Barnes and H. E. Hallam, Q. Rev., Chem. Soc., 1969, 23, 392–409 RSC.
- A. J. Barnes and W. J. Orville-Thomas, FT-IR Matrix Isolation Studies, Dordrecht, 1980 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- S. Grimme, J. Chem. Phys., 2006, 124, 034108 CrossRef PubMed.
- G. Santra, N. Sylvetsky and J. M. L. Martin, J. Phys. Chem. A, 2019, 123, 5129–5143 CrossRef CAS PubMed.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483 Search PubMed.
- M. Head-Gordon, J. A. Pople and M. J. Frisch, Chem. Phys. Lett., 1988, 153, 503–506 CrossRef CAS.
- M. J. Frisch, M. Head-Gordon and J. A. Pople, Chem. Phys. Lett., 1990, 166, 275–280 CAS.
- M. Head-Gordon and T. Head-Gordon, Chem. Phys. Lett., 1994, 220, 122–128 CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 CAS.
- N. M. Kreienborg and C. Merten, Chem. – Eur. J., 2018, 24, 17948–17954 CAS.
- C. Merten, J. Bloino, V. Barone and Y. Xu, J. Phys. Chem. Lett., 2013, 4, 3424–3428 CAS.
- J. Bloino, M. Biczysko and V. Barone, J. Phys. Chem. A, 2015, 119, 11862–11874 CAS.
- J. Bloino, A. Baiardi and M. Biczysko, Int. J. Quantum Chem., 2016, 116, 1543–1574 CAS.
- Q. Yang, M. Mendolicchio, V. Barone and J. Bloino, Front. Astron. Space Sci., 2021, 8, 665232 Search PubMed.
- M. Fusè, G. Longhi, G. Mazzeo, S. Stranges, F. Leonelli, G. Aquila, E. Bodo, B. Brunetti, C. Bicchi, C. Cagliero, J. Bloino and S. Abbate, J. Phys. Chem. A, 2022, 126, 6719–6733 Search PubMed.
- N. M. Kreienborg, Q. Yang, C. H. Pollok, J. Bloino and C. Merten, Phys. Chem. Chem. Phys., 2023, 25, 3343–3353 CAS.
- S. Ostwald, M. A. Suhm and S. Coussan, Phys. Chem. Chem. Phys., 2019, 21, 1277–1284 Search PubMed.
- D. Forney, M. E. Jacox and W. E. Thompson, J. Mol. Spectrosc., 1993, 157, 479–493 CAS.
- J. Nieminen, J. Murto and M. Räsänen, Spectrochim. Acta, Part A, 1991, 47, 1495–1504 Search PubMed.
- I. D. Reva, S. G. Stepanian, L. Adamowicz and R. Fausto, J. Phys. Chem. A, 2001, 105, 4773–4780 CrossRef CAS.
- D. F. Dinu, M. Podewitz, H. Grothe, T. Loerting and K. R. Liedl, Phys. Chem. Chem. Phys., 2020, 22, 17932–17947 RSC.
- A. Borba, A. Gómez-Zavaglia, P. N. N. L. Simões and R. Fausto, Spectrochim. Acta, Part A, 2005, 61, 1461–1470 Search PubMed.
- C. Riplinger and F. Neese, J. Chem. Phys., 2013, 138, 034106 CrossRef PubMed.
- C. Riplinger, B. Sandhoefer, A. Hansen and F. Neese, J. Chem. Phys., 2013, 139, 134101 CrossRef PubMed.
- L. Andrews and X. Wang, Rev. Sci. Instrum., 2004, 75, 3039–3044 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. C.01, Wallingford, CT, 2016 Search PubMed.
- Q. Yang and J. Bloino, J. Phys. Chem. A, 2022, 126, 9276–9302 CrossRef CAS PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606 Search PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 Search PubMed.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- C. Y. Legault, CYLview 1.0b, Université de Sherbrooke, 2009 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Additional spectra plots, experimental spectra and computational data from VPT2 analysis. See DOI: https://doi.org/10.1039/d5cp00292c |
| This journal is © the Owner Societies 2025 |