Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Exceptional stability of ultrasmall cubic copper metal nanoclusters – a molecular dynamics study†
Nayana Edavan
Chathoth‡
 *a,
Hafila Khairun
S‡
*a,
Hafila Khairun
S‡
 a,
Manya
Krishna
a,
Manya
Krishna
 b and
Padmesh
Anjukandi
b and
Padmesh
Anjukandi
 *a
*a
aDepartment of Chemistry, Indian Institute of Technology, Palakkad-678623, Kerala, India. E-mail: 201914002@smail.iitpkd.ac.in; padmesh@iitpkd.ac.in
bDepartment of Chemistry, National Institute of Technology Meghalaya, Shillong, 793003, Meghalaya, India
First published on 3rd April 2024
Abstract
The fabrication of shape-selective coinage metal nanoclusters (MNCs) has promising applications due to their exceptional physical and chemical molecule-like properties. However, the stability of the specific geometry of the nanoclusters, such as their cubic shapes, is unclear and has been unraveled by assessing the nanoclusters' interactions with different environments. In this work, we investigate the morphological stability of cubic structured, coinage metal nanoclusters of varying sizes ranging from 14 to 1099 atoms. The impact of solvent environments like water and the presence of ionic liquids (IL) on the stabilization of the MNCs were assessed using molecular dynamics (MD) simulations. In general, smaller MNCs composed of less than 256 atoms encountered structural distortion easily compared to the larger ones, which preserved their cubic morphology with minimal surface aberrations in water. However, in the presence of 4M 1-butyl-1,1,1-trimethyl ammonium methane sulfonate [N1114][C1SO3] IL solution, the overall cubic shape of the MNCs was successfully preserved. Strikingly, it is observed that in contrast to the noble MNCs like Au and Ag, the cubic morphology for Cu MNCs with sizes less than 256 atoms exhibited significant stability even in the absence of IL.
1 Introduction
Nanoclusters (NCs) are a unique class of materials found in the ultrasmall size regime (1–3 nm in diameter), consisting of not more than a few hundred atoms. The exceptional physical and chemical molecule-like properties exhibited by nanoclusters are intrinsically different from their equivalent larger nanoparticles due to their ultrasmall size.1 Having control over factors like size, morphology, chemical composition, and surface structural characteristics, their mechanical, optical, electronic, magnetic, catalytic, electrochemical, and biological properties can be very well fine tuned.2 In view of these wide applications, the involvement of nanoclusters is growing rapidly in all sectors of application, including medicine, the food industry, energy materials, toxicology, the health care sector, electronics, and environmental applications.3 Most recently, the biocompatible and photoluminescent Pt nanoclusters have found biological applications, such as in bioimaging, enzyme-like activity and in cancer therapy.4 Furthermore, Ru nanoclusters are found to be employed as efficient multifunctional catalysts for zinc-air batteries.5 The ultra-small (see Fig. 1 for size to edge length dimension relation of Cu, Ag and Au MNCs) Au and Ag metal NCs are gaining efficacy owing to their stability, resistivity to oxidation under ambient conditions, low toxicities and high renal clearance rate.6 These properties enable them to be employed in bioimaging and analytical investigations of target molecules for in vivo disease therapy,7,8 catalysis,9 antimicrobial activity,10 and sensing applications.11 Copper MNCs, being comparatively smaller in size and more oxidatively reactive than Au and Ag, have recently gained importance in sensing,12 catalysis13 and also in the field of drug delivery, and bioimaging.14The manufacture of size and shape selective nanoclusters has attracted great significance in recent years due to their amazing and distinctive physicochemical features, which have found utilization in the advanced areas of chemistry and physics.15,16 Size, being an intrinsic property, imparts a strong influence towards their functionalities. For example, Pt NCs of 1.7 nm edge length are found to be particularly active for the hydrogenation of quinoline and thus superior to large-sized nanoparticles.17 Small sized nanoclusters are highly preferred in medical fields to enhance the efficiency of drug delivery and bioimaging.18,19 MNCs are also found to be versatile in their shape dependencies.20 Shapes like nanocubes (MNC images in Fig. 1 and Fig. S1 in ESI†) with sharp corners have attracted considerable attention among diverse nanostructural geometries as they are found to have distinct utilities. The confinement of cubic NC's photophysical properties in the visible region of the electromagnetic spectrum21 along with their high surface area to volume ratio enable functional advantages over the spherical nanoparticles,20 expanding their utilization in bioimaging and drug delivery applications. In addition to this, the compact crystalline cubic form of the NCs displays efficient photocatalytic degradation,22 strongest gas-sensing response,23 and excellent catalytic activity.24 Despite the prediction of enhanced applications of cubic morphologies, their preferentially weaker stability compared to the spherical geometries makes them quite challenging to synthesize. It is thus a crucial issue that needs to be addressed.
Understanding that the stabilization of cubic MNCs is a major hurdle in synthesizing them,25 various methods have been employed to date for the same, of which the prominent and most popular technique is the usage of various ligands. For example, the stabilization of MNCs is materialized with the help of proteins like bovine serum albumin (BSA) and human serum albumin (HSA).26,27 Short ssDNA has also been successfully used to stabilize fluorescent AgNCs.28 The most frequently used ligands in the stabilization of MNCs involve small thiol biomolecules, such as glutathione, self-assembled tripeptides, cysteine, and penicillamine.29 However, ionic liquids, typically composed of weakly coordinated large-sized cations and anions, have recently received much attention with multiple applications because of their various unique properties, such as high viscosity, high polarity, and thermal and chemical stability. For example, the catalytic system containing 1-butyl-3-methylimidazoliumbis(trifluoromethanesulfonyl)imide stabilized Ru nanoparticles are employed for hydrogenation30 purposes. Also, it has been reported that Au25 nanoclusters stabilized with an ionic liquid containing (3-mercaptopropyl)sulfonate as the anion and 1-decyl-3-methylimidazolium (DMIm) as the cation can serve as an accomplished enzymatic biosensor matrix for the detection of glucose.31
Understanding that the synthesis of shape-dependent MNCs is a fairly involved process. Herein, we specifically explore the cubic morphological stability of small, middle, and large-sized metal NCs (Cu, Ag, and Au) in water and ionic liquid [N1114][C1SO3](1-butyl-1,1,1-trimethyl ammonium methane sulfonate) using classical molecular dynamics (MD) simulations. Thus, with the help of an inclusive study of the stabilization of NCs, we envisage to provide an essential understanding of the size-dependent stabilization of these systems. To the best of our knowledge, only a few studies have been performed on the stabilization of cubic shaped coinage MNCs with different sizes in water and IL.
2 Methodology
Each shape contains a nanoparticle composed of a specific number of atoms that corresponds to the most stable configuration, sometimes referred to as the magic number.32 The cubic morphologies of coinage MNCs (Cu, Ag, and Au) follow the geometrical packing order of 14, 63, 108, 172, 256, 365, 500, 666, 864, and 1099 number of atoms, and were built using VESTA (visualization for electronic and structural analysis) software.33 In each case, the initial structure was taken as a perfect fcc cubic MNC (Fig. S1, ESI†). The edge lengths of each MNC containing a certain number of atoms were plotted and these were identified to be in the nanocluster regime as indicated in Fig. 1. The MNCs containing atoms N = 14, 63, 108, and 172 were identified to have dimensions less than 1.5 nm, thus classifying them as ultrasmall MNCs. To incorporate the IL in the simulation, 1-butyl-1,1,1-trimethylammonium methanesulfonate [N1114][C1SO3] (Fig. S2 in ESI†) was built using Avogadro34 and the forcefield parameters were obtained using an Automated force field topology builder (ATB).35 The Heinz group's Lennard–Jones parameters for MNCs were considered, which were used to maintain the non-bonded interactions of the metals.36 The Cu nanocluster was initially placed in the center of the cubic simulation box of 5 nm3 dimensions, and solvation was taken care of by the SPC/E (simple point charge) water model.37 Similar procedures were repeated for Ag and Au MNCs, respectively. In the case of the MNCs in the IL–water composition, 300 molecules (ion pairs) of the [N1114][C1SO3] IL were placed around the nanocluster within the MNC-water system of a 5 nm3 simulation box to maintain a concentration of 4M.38 Thus, MNCs in water and MNCs in IL–water mixture were energy minimized and equilibrated for 2 ns prior to the MD run for all systems. Further production simulations were carried out for 100 ns using GROMACS (Groningen machine for chemical simulations) 2020.1 version39 with the parameterized GROMOS 53a6 force field being utilized for all of the simulations.40 The trajectories of the simulation were analyzed using GROMACS utilities and the visualization of the molecular structures was carried out using visual molecular dynamics (VMD) 1.9.3 software.413 Results and discussion
Sixty sets of MD simulations including MNCs in water and MNCs in IL–water mixture of Cu, Ag, and Au MNCs of varying sizes (N = 14 to 1099) were carried out in order to investigate the stability of their cubic shape morphology, and they were found to be comparatively less stable than their spherical counterparts. The stability of a specific geometry was mapped based on the root mean square displacement (RMSD), solvent accessible surface area of the MNCs towards the solvent (SASA) and radial distribution function (RDF). For identifying the RMSD, the initial structure was taken as a perfect cubic structure of a particular size of the MNC chosen. RMSD provides the structural divergence of a given geometry or state from a preferred geometry and is calculated by the relation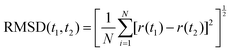 | (1) |
Radial distribution function, g(r), may be employed to analyze the structure of the MNCs. The radial distribution function (RDF) quantifies the atomic arrangement within a substance. This technique enables a direct examination of the interatomic distances and atomic displacements and determines the crystalline composition of a substance. The radial distribution function quantifies the variation in density with respect to distance from a chosen particle in a system of particles such as atoms and molecules. g(r) between particles A and B is given by eqn (2).
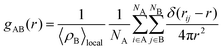 | (2) |
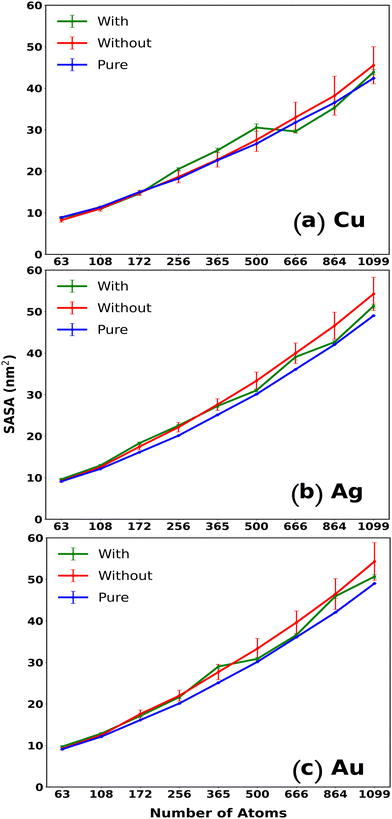
SASA, defined as the surface exhibiting van der Waals contact with the hypothetical center of a solvent sphere, can be extremely useful in understanding the exposed surface of the system and hence its reactivity. SASA has been efficiently utilized to assess the solvent exposed amino acid residues in proteins to define their stability.42 A similar approach can be utilized in the case of our MNCs to determine the extent of contact of the MNC surface with the solvent.43 A spherical geometry of the MNCs would provide a compact SASA owing to their distinct geometry, while that of a cube could be comparatively deviated due to high exposure of its surface to the solvent. Thus, SASA could qualitatively provide insight into the shape retainability of the MNCs and together, RMSD, RDF, and SASA could be an efficient analysis combination to describe the behavior of the cubic MNCs in water and water–IL systems.
3.1 Cu, Ag, and Au MNCs of varying N in water
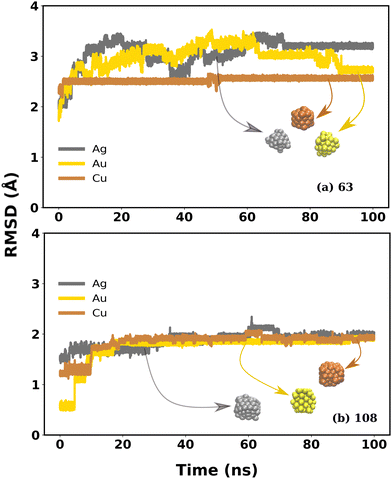
In order to assess the trend of the stability of a particular MNC with respect to size, the average RMSD with respect to each size from 63 to 1099 was calculated and plotted in Fig. 2 (see Fig. S3 in the ESI† for the 100 ns raw data of RMSD). The RMSD calculations for MNCs of varying sizes underline that the smaller MNCs (N < 256) exhibited huge structural deviations compared to the larger ones (N = 365 to 1099). The sudden increase of the average RMSD values from 1.0 to 3.0 Å as we descend from the larger to the smaller MNCs (from N = 256 to N = 63) apprise that the smaller NCs have got comparatively larger structural deviation compared to the larger ones. The insets in Fig. 2 represent the averaged structure of the MNCs of all sizes (the structures were visualized using VMD from which the snapshots of the averaged atomic coordinates were taken). A clear indication of how the larger MNCs retained their original cubic morphology with minor surface aberrations is evident from these images, whereas the smaller ones evolved into a structure in which the edges of the original cubic geometry were rounded, and the internal atomic arrangement was altered.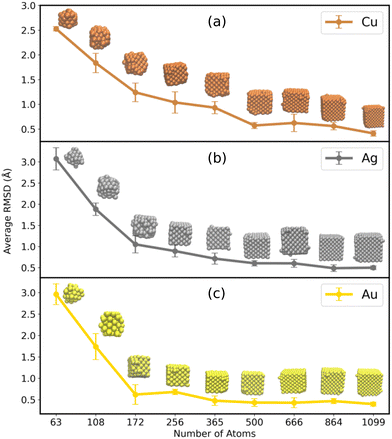 | ||
| Fig. 2 The time averaged RMSD of (a) Cu, (b) Ag, and (c) Au MNCs with respect to their sizes in bulk water. The RMSD averages were performed for 100 ns time of simulation. | ||
Appreciating that RMSD is capable enough in realizing the structural stabilization of the MNCs, it should also be noted that the RMSD, being related to the atomic positions, is indifferent to the atomic interchange within the MNC resulting in similar structures. As surface area is not dependent on the individual atoms and is only the virtue of the system's geometry, the accessible surface area could also be a handy tool to assess the shortcomings of the RMSD. Hence, to understand the overall stabilization of the MNCs in water, SASA was analyzed along the N for Cu, Ag, and Au MNCs and they were compared to the SASA of the original cubical structures of all the representative N. The evaluated SASA for varying N of Cu, Ag, and Au MNCs can be visualized in Fig. 3. The figure demonstrates that the SASA values for Au, Ag, and Cu MNCs in bulk water, as indicated by the red curve, increase as we move from smaller to larger structures, compared to the SASA values of a perfect fcc cubic structure, represented by the blue curve in Fig. 3. The higher SASA value observed in smaller MNCs in the bulk water can be attributed to the deviation from the cubic structure, as indicated by the higher RMSD (Fig. 2). On the other hand, in larger MNCs, despite the small RMSD observed in Fig. 2, the elevated SASA values are primarily caused by minor surface aberrations that result in an increase in the solvent accessible surface area.
Along with RMSD and SASA, the radial distribution function (RDF) can also be used to analyze the structure of the metal nanoclusters. In this study, the structural organization of MNCs was analyzed using RDF and plotted in Fig. S4 in the ESI.† The major initial peak corresponds to the mean distance between adjacent M–M atoms. Their high and sharp nature indicates a greater degree of remarkable local arrangement. It is clear that all MNCs have considerable structural stability in the core, which is reflected in their distinctive peaks (at a radius of 0.25 nm) suggesting an ordered nature. However, the smaller MNCs exhibit a slightly diffusive curve at larger distance indicating comparatively higher surface aberrations. These characterization indicators, such as RMSD, SASA, and RDF, indicate that the smaller MNCs of Au, Ag, and Cu deviate from the ideal cubic fcc structure notably than the bigger ones, which only experience slight deviation.
To discern the behavior of the small size NCs exhibiting larger structural aberrations, we explored the metal–metal interaction energies for the Cu, Ag, and Au NCs of various sizes (Fig. S5 in ESI†). It is observed that the increase in the size of the MNCs increases the metal–metal interaction energy, which indicates the existence of a strong and stable interplay between the metal atoms of higher morphologies. However, the smaller NC structures (N < 256) have comparatively weaker metal–metal interactions, which might be one of the reasons for its instability. Yet again, the ubiquitous presence of water in all chemical and biological environments suggests an inevitable interaction between water and the system, thus playing a vital role in various applications, such as heterogeneous catalysis, electrochemistry and drug delivery. The competition between the metal–metal and metal–water interaction (a stronger metal–water interaction suggests metal atoms going in to the solution phase) could be deterministic in stabilizing the MNCs in water. Thus, to look into the stability, we also probed the metal–water interaction energies. The distribution of interaction energies of MNCs with water over the simulation trajectory is represented in Fig. S6 in the ESI.† It is very well evident from the figure that the interaction energies between MNCs and water molecules yet again increases with increase in size. Thus, one might expect that the larger MNCs might disintegrate owing to the extensive interaction with water molecules. However, it should also be noted that the larger magnitude of the interaction between metal atoms of MNCs (Fig. S7 in ESI†) makes the larger cubic NC morphologies comparatively stable, as a result of which the impact of water on them becomes relatively insignificant. On the other hand, for smaller MNCs, there exists a strong competition between metal–metal and metal–water interactions, the latter being roughly one-fourth of the former. This sufficiently explains the cause of instabilities in small morphologies of sizes with N < 256 atoms, thus making it harder for us to devise a way to stabilize the small MNCs due to the huge structural deviations they exhibit from the original cubic structure.
3.2 Cu, Ag, and Au MNCs of varying N in an IL-water mixture
As it is evident from the previous section, water has a considerable impact on the shape of the smaller MNCs, and it is an utmost necessity to preserve their cubic structure as they find themselves very relevant, especially in drug delivery applications. There are various agents such as proteins, DNAs, surfactants, etc., which are readily employed in stabilizing the MNCs. However, the ILs have found massive applications along this line most recently, indebted to their enhanced fluorescence and stability, even without the help of additional surfactants.30 On this account, the stability of the MNCs in the presence of 4M [N1114][C1SO3] IL solution was analyzed. Similar to that of MNCs in water, the RMSD of the MNCs in the presence of IL–water mixture was calculated from the perfect cubic structure. The average RMSD of the MNC in the IL–water mixture can be found in Fig. 4 (the raw data for 100 ns of simulation is provided in Fig. S8 in ESI†). From the figure, it can be inferred that IL-protected MNCs of all sizes (including the ultrasmall MNCs) are sufficiently stabilized. This comprehends that small MNCs (N < 256) could substantially retain their cubic shape with less RMSD deviations i.e., < 1.5 Å in the presence of ILs along with larger MNCs. The RMSD plots thus affirm the stabilization of Cu, Ag, and Au MNCs in the presence of IL (the corresponding snapshots of the averaged structures are inserted for each of the sizes in Fig. 4).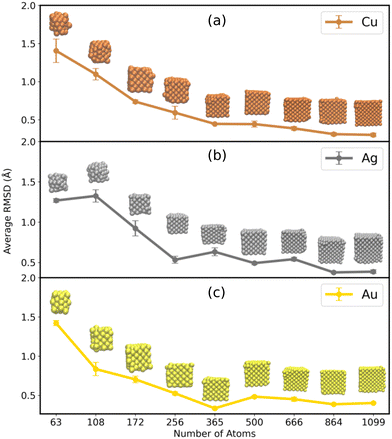 | ||
| Fig. 4 The time averaged RMSD of (a) Cu, (b) Ag, and (c) Au MNCs with respect to their sizes in the presence of a 4M IL–water mixture. The RMSD averages were performed for 100 ns time of simulation. | ||
SASA was also used to investigate the stabilization of the MNCs with the introduction of IL. The stability of the bigger MNCs is not considerably improved by adding 4M IL to the solvent (green curve in Fig. 3). This is consistent with our observations that the addition of any stabilizing material does not affect the stability of bigger MNCs, which are primarily stabilized by metal–metal interactions. In contrast, smaller cubic MNCs in ILs generally exhibit SASA values similar to the values of ideal fcc cubic structures, highlighting the fact that smaller MNCs are stabilized by ILs in contrast to larger ones. In the case of CuNCs of varying N (Fig. 3(a)), the smaller CuNCs with N < 256 atoms seem to be comparatively well stabilized in both water and water–IL mixtures. The CuNCs show a significant divergence from the AuNC and AgNC analogues in the SASA curves. With larger CuNCs (N > 256), they begin to display a comparable pattern to that observed with the larger Au and Ag NCs.
The structural stability of the MNCs was assessed by computing the RDF of metal-to-metal distance (Fig. S9 in ESI†). The core structure of all MNCs was intact, as seen by the strong and clear curve at approximately r = 2.5 nm. Smaller MNCs (N < 256) exhibit a diffusive curve at larger distances, indicating yet again a partial structural divergence from the cubic structure. At the same time, it is crucial to note that the presence of IL has stabilized the ultrasmall MNCs, as demonstrated by the RDF plot in Fig. S10 in the ESI.† The characteristic peak height of the RDF curve for metals in the presence of IL was found to be higher in all cases of ultrasmall MNCs, indicating that the metals are stabilized in the presence of IL. This indicates that the introduction of IL (as shown in Fig. S10 in ESI†) does indeed stabilize the MNCs. However, it is seen that smaller MNCs still exhibit small structural aberrations even when IL is present (as shown in Fig. S9 in ESI†), in contrast to larger MNCs.
Towards understanding the stabilization of MNCs in an IL–Water mixture, previous studies on the concept of stabilization of transition-MNCs in ILs were exploited. These are mainly concentrated towards the use of DLVO theory, which involves both surface adsorbed anion charge stabilization and steric stabilization.44 The essential electrostatic and steric (electrosteric) stabilization through the formation of an anion layer around the nanoparticles can be observed due to the interaction of these with the IL network.45 Interestingly, the stabilization of the MNCs with the use of ILs by the means of electrosteric interaction aligns with the above mentioned theory.46 Hence, the DLVO theory offers a foothold to explain the stabilization of MNCs in the presence of ILs without the use of additional surface-active agents. Thus, sustaining the shape of MNCs in the presence of IL can also be thought of as comparable to creating well-defined cubic shapes for MNCs with the help of effective stabilizing agents.
So as to decipher the stabilization mechanism of the MNCs by the anions of IL, the radial distribution function of the IL around the metal atoms was analyzed. g(r) of the IL around the MNCs for all the systems was computed by taking the center of mass of the anion, center of mass of the cation and center of mass of water molecule each to the center of mass of the metal atoms of the MNCs as plotted in Fig. 5. As can be visualized, the g(r) values for MNC with N = 63 to 256 suggest greater probability of finding the anion (Fig. 5(a)) in the first solvation shell followed by the cation (Fig. 5(b)). This supports the proximity of anions in close range with metals, which are electrophilic in nature and hence found to be in good agreement with the DLVO theory.46 Thus, it can be qualitatively inferred that the surface adsorbed anion could offer charge and steric stabilization to the MNCs. However, with the increase in size of the MNCs, for N > 256 the distribution of water molecules around them becomes more predominant than that of anions and cations of the IL as can be identified from Fig. 5(c). This highlights that ILs are comparatively more effective in facilitating surface-level interactions with the smaller MNCs as opposed to larger MNCs, thereby stabilizing the smaller MNCs.
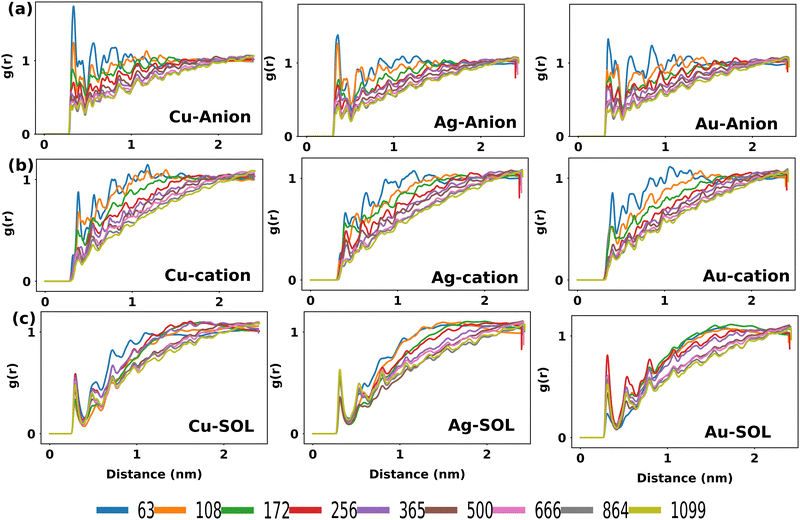 | ||
| Fig. 5 Radial distribution functions of (a) anions around Cu, Ag, and Au MNCs, (b) cations around Cu, Ag, and Au MNCs and (c) water molecules around Cu, Ag, and Au MNCs in 4M IL–water mixture. | ||
To further understand the extent of stabilization on MNCs offered by the ILs, the interaction energy between the metal atoms and water, the metal and the anions of the IL and the metal–metal interaction within the MNC were calculated (Fig. S11, S12, and S13 in the ESI† respectively). It is observed that the interaction energy between metal atoms and water (Fig. S11, ESI†) in the presence of the IL is weak compared to the metal–water interaction energy in water alone (Fig. S6 in ESI†). Thus, in accordance with the DLVO theory, the electrosteric stabilization provided by anions of the IL, in addition to a significant reduction in the interaction between MNCs and water, contributes to the preservation of the cubic shape of the smaller NCs. The stabilization of the MNCs in the presence of IL is also confirmed by the strong interaction of metals with anions which is represented in Fig. S12 of the ESI.† The presence of the anions around the MNCs (as accounted by the g(r) values) and their strong interaction with the metals, weakens the metal–water interaction and thus offers shape stability to the small cubic MNCs. However in the case of large morphologies, the interaction between the metal atoms is strong enough (Fig. S14 of the ESI†) compared to metal–anion interaction. Hence anions are predicted to have comparably less stabilization effect over large morphologies.
3.3 Revisiting small MNCs (N = 63 and 108) in water
Small morphologies of cubic MNCs, in general, undergo huge structural deviations compared to large ones as emphasized in the RMSD, RDF and SASA plots. Surprisingly, CuNCs with N = 63 and 108 whose size is small compared to that of Ag and Au MNCs composed of the same number of atoms, show a distinct behaviour. They exhibit comparatively smaller RMSD in the bulk water (<2.5 Å), whereas Ag and Au are identified to have higher RMSD in the range of 2.5–4.0 Å. The cubic shape of the CuNCs with N = 63 and 108 was also considerably retained compared to Ag and Au MNCs whose snapshots are inserted in Fig. 6(a).The SASA plot in Fig. S15 in the ESI† shows that the SASA values for perfect cubic (blue curve), bulk water (red curve), and IL–water mixture (green curve) for CuNCs with size N = 63 and 108 are similar, indicating that the cubic structures of CuNCs are retained to a greater extent, although not completely. In contrast, AuNCs and AgNCs with similar sizes have significantly different SASA values, indicating a comparatively higher structural divergence from the ideal cubic structure. Thus, SASA data confirm the additional stability of smaller CuNCs compared to AgNCs and AuNCs even in water. Their structural stability can also be visualized from the RDF plot shown in Fig. S16 in the ESI† One can see that a sharp, high, well-defined peak was observed in the case of CuNCs in bulk water, for N = 63 and 108 in contrast to the Ag and Au NCs. This confirms that the ultrasmall CuNCs have an ordered structure compared to AuNCs and AgNCs. Thus, the RMSD, SASA, and RDF values combined together indicate that the ultrasmall CuNCs are comparatively more stable than the Ag and Au analogue. The metal–water interaction energy of MNCs with N = 63 and 108 as represented in Fig. S17 of the ESI† can be used to describe this phenomenon. The metal atoms of Au and Ag have a relatively higher interaction with water, leading to their larger structural instability. However, the interaction between Cu MNCs and water is comparatively weaker than that of Au and Ag MNCs. This weak interaction significantly contributes to preserving the cubic structure to a considerable extent for the smaller morphologies of Cu.
3.4 MNCs with size N < 63
Analysis was conducted on the stability of MNCs (Ag, Au, and Cu) with N = 14 in the presence and absence of IL similar to those with N = 63 to 1099. The RMSD for 100 ns simulation for all the systems was calculated and given in Tables S1 and S2 in the ESI.† One can observe that the RMSD was found to be between 2.0 ± 5 Å in the bulk water. The RMSD has been reduced to 1.0 ± 5 Å in the presence of IL, confirming the stabilizing capability of the IL. A reduced RMSD value for MNCs with N = 14 in comparison to those with N = 63 to 1099 signifies enhanced stability. Nonetheless, it is evident from examining the trajectory that the MNC with N = 14 loses its cubic shape, and the RMSD is merely a result of the reduced atomic count. In order to examine the crystalline stability of the MNC, the RDF for the metal to metal distance was determined (Fig. S18 in ESI†). As depicted in Fig. S18 (ESI†), the RDF peak of all the MNCs (Ag, Au, and Cu) are broader and diffusive compared to that of the perfect fcc cubic crystal. This lacking of the characteristic sharp peaks indicates the disorder of the system and the lack of crystalline order in both bulk water and the IL–water mixture. The interaction energies between metal atoms, between the metal and water, and between the metal and anions were calculated and presented in Tables S1 and S2 in the ESI.† It is evident that the metal–water interaction is higher in the bulk water, which results in decreased stability of the systems. Comparable to MNCs with N = 63 to 1099, the metals interact strongly with the anions in the presence of IL, which stabilizes the cluster. These findings indicate that MNCs with a size less than 63 are comparatively less stable, making it challenging to synthesize them using standard methodologies such as bottom-up or top-down synthesis of nanoclusters.4 Conclusions
MD simulations were carried out on MNCs of Au, Ag, and Cu coinage metals of varied sizes in water and a 4M IL–water mixture to assess the stability of the cubic morphologies. The morphological stability of MNCs has been found to be significantly influenced by their size. According to MD simulations, MNCs with N > 256 atoms retained their cubic structure in water due to the significant interaction energy between the metal atoms of the MNC. However, when the size decreases, we see a general trend of increased structural instability in Ag, Au, and CuNCs. It is critical to preserve the cubical morphology of these three coinage metals as they are used in various applications such as sensing, bio-imaging, and more. In order to stabilize them, ionic liquid ([N1114][C1SO3]) was added to the system. We found that MNCs preserve their cubic morphology to a higher extent, although not completely, in the presence of ionic liquid due to steric stability and the restriction of surface atom mobility provided by the anions. Interestingly, within their structural instabilities, CuNCs with a size of N < 256 atoms exhibited higher ordered arrangement compared to AgNCs and AuNCs of similar sizes. This cubic morphological stability is due to the less contact between copper atoms and water, compared to Ag and Au MNCs. This suggests that, in contrast to Ag and Au, CuNCs have a higher chance of retaining their cubic structure during the synthesis of nanoclusters. We also examined MNCs with size N = 14 and observed that they were unstable and lost their cubic shape in both circumstances, indicating the difficulty in achieving a cubic shape early in the nucleation process during bottom-up synthesis. Finally, these results underline the size-dependent stability of cubic shape MNCs in water and ILs, providing insight into the cubic structure preservation and paving the way for its applications in diverse fields.Author contributions
P. A. conceptualized the work. P. A. and N. E. C. administered the work. N. E. C. and H. K. S. conducted the modeling and simulations of the systems. P. A., N. E. C., H. K. S. and M. K. contributed towards the result analysis and preparation of the draft manuscript.Conflicts of interest
The authors declare no competing interest.Acknowledgements
The authors thank IIT Palakkad for providing them with the CHANDRA supercomputing facility. P. A. also thank the Science and Engineering Research Board (SERB), India for the financial assistance through the SERB Core Research Grant (CRG/2022/007366).References
- X. Qu, Y. Li, L. Li, Y. Wang, J. Liang and J. Liang, J. Nanomater., 2015, 2015, 4 Search PubMed.
- N. Baig, I. Kammakakam and W. Falath, Mater. Adv., 2021, 2, 1821–1871 RSC.
- L. Trapiella-Alfonso, M. Tasso, G. R. Garca, D. Martn-Yerga and A. R. M. Bustos, Front. Chem., 2022, 10, 898480 CrossRef PubMed.
- F. Wu, Biomaterials, 2011, 32, 1611–1618 CrossRef PubMed.
- Y. Guo, D. Wu, M. Li, K. Wang, S. Zhang, G. He, H. Yin, C. Huang, B. Yang and J. Zhang, Small Sci., 2022, 2, 2200035 CrossRef CAS.
- H. Ding, D. Yang, C. Zhao, Z. Song, P. Liu, Y. Wang, Z. Chen and J. Shen, ACS Appl. Mater. Interfaces, 2015, 7, 4713–4719 CrossRef CAS PubMed.
- L. Nair, R. Nair, S. Shenoy, A. Thekkuveettil and R. Jayasree, J. Mater. Chem. B, 2017, 5, 8314–8321 RSC.
- N. Kundu, D. Mukherjee, T. K. Maiti and N. Sarkar, J. Phys. Chem. Lett., 2017, 8, 2291–2297 CrossRef CAS PubMed.
- J. Oliver-Messeguer, L. Liu, S. Garcia-Garcia, C. Canos-Gimenez, I. Dominguez, R. Gavara, A. Domenech-Carbo, P. Concepcion, A. Leyva-Perez and A. Corma, J. Am. Chem. Soc., 2015, 137, 3894–3900 CrossRef PubMed.
- Y. Xie, Y. Liu, J. Yang, Y. Liu, F. Hu, K. Zhu and X. Jiang, Angew. Chem., Int. Ed., 2018, 57, 3958–3962 CrossRef CAS PubMed.
- J. Li, J. Yu, Y. Huang, H. Zhao and L. Tian, ACS Appl. Mater. Interfaces, 2018, 10, 26075–26083 CrossRef CAS PubMed.
- A. Sebastian, B. R. Sarangi and S. S. Mojumdar, et al. , J. Photochem. Photobiol., A, 2023, 436, 114378 CrossRef CAS.
- M. A. Bhosale, S. C. Karekar and B. M. Bhanage, ChemistrySelect, 2016, 1, 6297–6307 CrossRef CAS.
- K. Babu Busi, M. Palanivel, K. Kanta Ghosh, W. Basu Ball, B. Gulyás, P. Padmanabhan and S. Chakrabortty, Nanomaterials, 2022, 12, 301 CrossRef CAS PubMed.
- H. Yang, J. Yan, Y. Wang, H. Su, L. Gell, X. Zhao, C. Xu, B. K. Teo, H. Hakkinen and N. Zheng, J. Am. Chem. Soc., 2017, 139, 31–34 CrossRef CAS PubMed.
- Y. Xia, Y. Xiong, B. Lim and S. E. Skrabalak, Angew. Chem., Int. Ed., 2009, 48, 60–103 CrossRef CAS PubMed.
- L. Bai, X. Wang, Q. Chen, Y. Ye, H. Zheng, J. Guo, Y. Yin and C. Gao, Angew. Chem., Int. Ed., 2016, 55, 15656–15661 CrossRef CAS PubMed.
- M. J. Mitchell, M. M. Billingsley, R. M. Haley, M. E. Wechsler, N. A. Peppas and R. Langer, Nat. Rev. Drug Discovery, 2021, 20, 101–124 CrossRef CAS PubMed.
- Z. Li, Q. Sun, Y. Zhu, B. Tan, Z. P. Xu and S. X. Dou, J. Mater. Chem. B, 2014, 2, 2793–2818 RSC.
- P. Jackson, S. Periasamy, V. Bansal and M. Geso, Australas. Phys. Eng. Sci. Med., 2011, 34, 243–249 CrossRef PubMed.
- M. T. Yaraki, S. D. Rezaei and Y. N. Tan, Phys. Chem. Chem. Phys., 2020, 22, 5673–5687 RSC.
- C. K. Govindappa, V. T. Venkatarangaiah and S. B. A. Hamid, Nano-Micro Lett., 2013, 5, 101–110 CrossRef CAS.
- X. Wan, J. Wang, L. Zhu and J. Tang, J. Mater. Chem. A, 2014, 2, 13641–13647 RSC.
- R. Xu, D. Wang, J. Zhang and Y. Li, Chem. – Asian J., 2006, 1, 888–893 CrossRef CAS PubMed.
- M. M. Blazhynska, A. Kyrychenko and O. N. Kalugin, Mol. Simul., 2018, 44, 981–991 CrossRef CAS.
- X. Le Guével, B. Hötzer, G. Jung, K. Hollemeyer, V. Trouillet and M. Schneider, J. Phys. Chem. C, 2011, 115, 10955–10963 CrossRef.
- P.-H. Chan and Y.-C. Chen, Anal. Chem., 2012, 84, 8952–8956 CrossRef CAS PubMed.
- J. T. Petty, J. Zheng, N. V. Hud and R. M. Dickson, J. Am. Chem. Soc., 2004, 126, 5207–5212 CrossRef CAS PubMed.
- N. Nishida, H. Yao, T. Ueda, A. Sasaki and K. Kimura, Chem. Mater., 2007, 19, 2831–2841 CrossRef CAS.
- A. S. Pensado and A. A. Pádua, Angew. Chem., Int. Ed., 2011, 50, 8683–8687 CrossRef CAS PubMed.
- K. Kwak, S. S. Kumar, K. Pyo and D. Lee, ACS Nano, 2014, 8, 671–679 CrossRef CAS PubMed.
- V. Y. Shevchenko and A. Madison, Glass Phys. Chem., 2002, 28, 40–43 CrossRef CAS.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 1–17 Search PubMed.
- A. K. Malde, L. Zuo, M. Breeze, M. Stroet, D. Poger, P. C. Nair, C. Oostenbrink and A. E. Mark, J. Chem. Theory Comput., 2011, 7, 4026–4037 CrossRef CAS PubMed.
- H. Heinz, R. Vaia, B. Farmer and R. Naik, J. Phys. Chem. C, 2008, 112, 17281–17290 CrossRef CAS.
- S. Prasad and M. Gupta, J. Mol. Liq., 2022, 347, 118342 CrossRef CAS.
- M. N. Jorabchi, M. Abbaspour, E. K. Goharshadi and S. Wohlrab, J. Mol. Liq., 2022, 360, 119447 CrossRef CAS.
- M. Barani, M. Reza Hajinezhad, S. Sargazi, M. Zeeshan, A. Rahdar, S. Pandey, M. Khatami and F. Zargari, Polymers, 2021, 13, 3153 CrossRef CAS PubMed.
- C. Oostenbrink, A. Villa, A. E. Mark and W. F. Van Gunsteren, J. Comput. Chem., 2004, 25, 1656–1676 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- R. Adamczak, A. Porollo and J. Meller, Proteins: Struct., Funct., Bioinf., 2005, 59, 467–475 CrossRef PubMed.
- P. Rama and Z. Abbas, Phys. Chem. Chem. Phys., 2022, 24, 3713–3721 RSC.
- J. Hierrezuelo, A. Sadeghpour, I. Szilagyi, A. Vaccaro and M. Borkovec, Langmuir, 2010, 26, 15109–15111 CrossRef CAS PubMed.
- C. Janiak, Z. Naturforsch. B, 2013, 68, 1059–1089 CrossRef CAS.
- M. Mamusa, J. Siriex-Plenet, F. Cousin, E. Dubois and V. Peyre, Soft Matter, 2014, 10, 1097–1101 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3tb02474a |
| ‡ N. E. C. and H. K. S. equally contributed in modelling, simulation and draft preparation. |
| This journal is © The Royal Society of Chemistry 2024 |

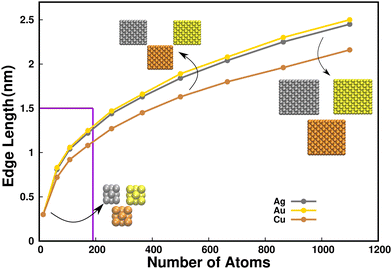
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500, and 1099 can be identified in the inset. It can also be identified here that structures with
500, and 1099 can be identified in the inset. It can also be identified here that structures with