Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Phase behavior of binary mixtures of hollow and regular microgels†
Alexander V.
Petrunin
 *a,
Tom
Höfken
a,
Stefanie
Schneider
*a,
Tom
Höfken
a,
Stefanie
Schneider
 a,
Pablo
Mota-Santiago
a,
Pablo
Mota-Santiago
 bc,
Judith E.
Houston
bc,
Judith E.
Houston
 d and
Andrea
Scotti
d and
Andrea
Scotti
 *e
*e
aInstitute of Physical Chemistry, RWTH Aachen University, 52056 Aachen, EU, Germany. E-mail: petrunin@pc.rwth-aachen.de
bAustralian Synchrotron, ANSTO, Clayton, Victoria, Australia
cMAX IV Laboratory, Lund University, P.O. Box 118, 22100 Lund, EU, Sweden
dEuropean Spallation Source ERIC, Box 176, SE-221 00 Lund, EU, Sweden
eDivision of Physical Chemistry, Lund University, SE-22100 Lund, Sweden. E-mail: andrea.scotti@fkem1.lu.se
First published on 4th October 2024
Abstract
Soft colloids are widely used to study glass transition, aging and jamming. A high size polydispersity is typically introduced in these systems to avoid crystal formation. Here, we use binary mixtures of hollow and regular microgels with comparable sizes to inhibit crystallization. The phase behavior of the mixture is probed as a function of the number fraction of hollow microgels and characterized by small-angle X-ray scattering. Molecular dynamic simulations are used to extract the particle–particle pair potential and obtain insight on their deformation. The results suggest that the high deformability of the hollow microgels offers an alternative route to maximize the entropy without crystal formation.
1 Introduction
Since more than a century, colloidal dispersions have been recognized as a model system to study the behavior of atoms and molecules.1 Their sizes are accessible by optical microscopy and scattering techniques, and the timescales of particle motion are slower compared to atoms or molecules, making it easy to follow the particle dynamics. Due to their capacity to crystallize and undergo glass transition, colloidal suspensions have become invaluable to tackle problems related to the liquid-to-crystal transition,2–4 crystallization kinetics,5–7 local structure and structural relaxation in glasses.3,8,9 To study the colloidal glasses, a high size polydispersity needs to be introduced to avoid crystal formation.10–13 However, increasing the size polydispersity can strongly change the particle dynamics14–16 and flow properties of the suspensions.17,18 Furthermore, the possibility of using soft deformable colloids has raised questions on the role of individual particle softness in phase transitions and in the formation of strong and fragile glasses.13,19,20 A plethora of model systems of soft spheres have been studied including polymer-grafted nanoparticles, block-copolymer micelles, star polymers, polysaccharide-based nanoparticles and other.21,22 Most of these colloids contain an incompressible core making the particles effectively harder once their polymeric shells are compressed.23,24 In addition, structure-specific effects including molecular exchange between block-copolymer micelles,25 interpenetration between star polymers leading to a dynamic arrest26,27 or even molecular weight distribution of grafted polymer chains25 can further complicate their use as soft particle models.Microgels, colloidal polymer networks of spherical shape,28 allow us to partially overcome these problems. Their core is not incompressible29 and the compressibilty of both the core and shell can be controlled via the synthesis protocol while maintaining a low size polydispersity.30 Due to their deformability, microgel suspensions with bimodal size distributions or with size polydispersity as high as 18% can form crystals.19,31,32 Suspensions of ultra-soft microgels demonstrated that softness does not suppress the crystallisation, but promotes the coexistence between face and body centered cubic crystals.33 Microgels have also been used to study glass and jamming transitions,34–36 as well the nature of fragility and strength in glasses.13,37 It was proposed that the deformability of soft colloids leads to strong glass formation because particle deformation allows for an anisotropic shape which promote directional interparticle interactions. In contrast, harder particles have more isotropic interaction since they retain their spherical shape making soft glasses.13,38
Hollow microgels have a solvent-filled cavity in the center39–41 and are similar to capsules or vesicles. Therefore, they do not conform to the common paradigm of soft colloids with a hard core and soft shell. The size of the cavity in hollow microgels, thickness of their shell and stiffness of the polymer network can be controlled by the synthesis protocol.41–45 Hollow microgels are more easily deformable than regular microgels with the same crosslinking density.46,47 When an osmotic stress is applied, they deswell by re-arranging the polymer network into the central cavity44 or buckle.45 Hollow microgels start to compress at osmotic pressure two orders of magnitude lower than what is observed for regular microgels synthesized with the same crosslinker content.44 Such high compressibility and deformability allow to easily maximize the entropy by reducing the colloidal volume fraction, so that crystallization is suppressed for hollow microgels, even when size polydispersity is sufficiently low.43 This fact is very appealing to study glass transition, jamming, and aging phenomena, because the undesirable formation of crystals can be avoided without introducing huge size disparities between the particles. Furthermore, hollow microgels can be used as “defects” in mixtures with regular microgels of the same size,32 so that the properties of the suspension are mostly determined by the latter, but crystallization is suppressed. Such systems would provide a better model to study molecular glass formers, for which size polydispersity is absent.48 Also, one can take advantage of the enhanced deformation of a few hollow “defects” to verify whether high particle deformability is related to the strong nature of the glass.13
Here, we report the phase behavior of binary mixtures of hollow and regular poly(N-isopropylacrylamide) (pNIPAM) microgels in water. Both the hollow and regular microgels are synthesized using the same amount of crosslinker agent (5 mol%) and have comparable sizes. This ensures that the polymeric networks of these microgels have similar modulus and the solvent-filled cavity is the only difference between them.28 Therefore, softness is a well-controlled parameter in our system. We demonstrate that increasing the fraction of hollow microgels in the binary mixture leads to a gradual inhibition of crystallization, whereas the structure factor in the fluid state changes only marginally. This is related to the high deformability of hollow microgels, which allows them to change shape and thus increase the entropy without crystal formation.
2 Experimental section
2.1 Microgel synthesis
The microgels were synthesized by precipitation polymerization in double-distilled Milli-Q water.49 To synthesize the regular microgels, 5.0924 g of N-isopropylacrylamide (NIPAM), 0.3652 g of the crosslinker N,N′-methylenebis(acrylamide) (BIS), and 0.0120 g of sodium dodecyl sulfate (SDS) were dissolved in 295 mL of double-distilled water filtered through a 0.2 μm regenerated cellulose membrane filter. The solution was heated to 70 °C and purged by nitrogen flow for 1 h under vigorous stirring. Simultaneously, 0.1265 g of the initiator potassium persulfate (KPS) was dissolved in 5 mL of double-distilled water and also purged with nitrogen. The reaction was initiated by transferring the KPS solution into the reaction mixture and then allowed to proceed for 4 h under vigorous stirring. After cooling to room temperature, the solution was purified by three-fold ultra-centrifugation at 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm, followed by redispersion in fresh double-distilled water. Freeze-drying was used for storage.
000 rpm, followed by redispersion in fresh double-distilled water. Freeze-drying was used for storage.
To synthesize the hollow microgels, cores-shell microgels containing sacrificial silica cores were obtained first. The cores were then etched away with NaOH yielding hollow microgels.39–41 Silica cores with 105 nm radius were obtained by the Stöber synthesis followed by surface functionalization, as described previously.43 To obtain core–shell microgels, 1.0967 g of NIPAM, 0.0787 g of BIS, and 0.0647 g of SDS were dissolved in 195 mL of filtered double-distilled water. 1.5 g of silica cores were dissolved in 4 mL of ethanol, redispersed by ultrasonication for 30 min, and added to the reaction mixture. The solution was heated to 70 °C and purged by nitrogen flow for 1 h under vigorous stirring. Simultaneously, 0.0860 g of KPS was dissolved in 5 mL of filtered double-distilled water and purged with nitrogen. The reaction was initiated by transferring the KPS solution into the reaction mixture and then allowed to proceed for 4 h under vigorous stirring. After cooling to room temperature, the core–shell microgels were purified by three-fold centrifugation at 5000 rpm, followed by redispersion in fresh double-distilled water, and then freeze-dried. To dissolve the silica cores, the freeze-dried core–shell microgels were redispersed in 100 mL of double-distilled water and 100 mL of 0.1 M NaOH solution was added. Dissolution was allowed to proceed for 3 days at room temperature under stirring. The resulting hollow microgels were purified by dialysis against 0.05 M NaOH solution for 3 days, and against deionized water for 1 week. Freeze-drying was used for storage.
2.2 Dynamic and static light scattering
Multi-angle dynamic light scattering (DLS) was used to determine the hydrodynamic radii of the microgels, Rh, as a function of temperature between T = 20 °C and T = 50 °C in water (refractive index n(λ0) = 1.33, where λ0 = 633 nm is the wavelength of the laser in vacuum). The temperature was controlled by a thermal bath filled with toluene to match the refractive index of glass. The scattering intensity was measured as a function of the scattering vector, q = 4πn/λ0sin(θ/2), where the scattering angle θ was changed between 30 °C and 110° in 10° increments.The intensity autocorrelation functions were analyzed with the second order cumulant method50 to obtain the q-dependent decay rates, Γ(q) = D0q2. Average diffusion coefficients D0 were obtained from linear fits of the data Γ(q) vs. q2 and then used to obtain the hydrodynamic radius from the Stokes–Einstein equation Rh = kBT/(6πηD0), where η is the viscosity of water at the temperature T and kB is the Boltzmann constant.
Static light scattering (SLS) measurements were performed on very dilute aqueous solutions of microgels (c < 0.01 wt%) using a SLS-Systemtechnik GmbH instrument equipped with a blue laser (λ = 407 nm) and a toluene bath at T = 20 °C. The scattering intensity was measured at angles between 30° and 150° with steps of 1°.
2.3 Viscometry
The viscosities of the microgel suspensions were measured at T = 20 °C as a function of weight concentration c using a 0c Ubbelohde viscometer (SI Analytics) and Lauda iVisc measuring stand. The dynamic viscosity at low concentrations (c < 0.25 wt%) were fitted with the Einstein-Batchelor equation:51 | (1) |
Furthermore, the molecular weights of the microgels Mw were estimated by combining viscometry and DLS results, as described previously:52,53
 | (2) |
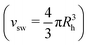 .
.
2.4 Phase behavior of the microgels
The samples were prepared by dilution from stock solutions of the two microgels in double-distilled water. Solutions were placed in closed glass vials further sealed with Parafilm and kept at T = 20 ± 1 °C for at least 4 months, some for ∼2 years. Crystals were detected by observing small iridescent spots in the samples, whereas homogeneous iridescence was assigned to the glassy state of the sample. In the case of fluid-crystal coexistence, the height of the crystal phase relative to the height of the sample was used as a measure of the fraction of crystals in the sample, x(crystals).54–56 A linear fit of x(crystals) vs. ζ was then used to determine the freezing point ζf and the melting point ζm. If either a plateau or a drop in x(crystals) was observed, two separate linear fits were used to determine ζf and ζm.2.5 Shear rheology
Rheological measurements were performed on the DHR-3 rheometer (TA Instruments) using a 40 mm 1° cone-plate geometry equipped with a solvent trap to prevent evaporation. To obtain the flow curves of the samples, shear rate sweeps were performed between 0.5 s−1 and 1000 s−1, but only the datapoints with torque τ > 1 μNm were kept. A shear rejuvenation protocol was applied prior to each measurement to erase any mechanical history and bring samples to a reproducible state. It consisted of applying a constant shear rate of 1000 s−1 for 1 min followed by 5 min equilibration (zero stress) at (20.0 ± 0.1) °C.The flow curves of the samples (viscosity η as function of shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) were fitted with the Cross equation:57
) were fitted with the Cross equation:57
 | (3) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) c is the critical shear rate halfway between η0 and η∞ and m is the shear-thinning exponent.
c is the critical shear rate halfway between η0 and η∞ and m is the shear-thinning exponent.
2.6 Small-angle scattering
The synchrotron small-angle X-ray scattering (SAXS) experiments were performed at the CoSAXS beamline at the 3 GeV ring of the MAX-IV Laboratory (Lund, Sweden).58 The q-range of interest in between 1 × 10−2 and 0.7 nm−1 was covered on CoSAXS using a sample-to-detector distance of 10 m with X-ray beam energy E = 12.4 keV. The instrument is equipped with an Eiger2 4M SAXS detector with pixel size of 75 μm × 75 μm. The data reduction software DAWN was used to convert the 2D images to 1D profiles.59The small-angle neutron scattering (SANS) measurements were performed using the D11 instrument at the Institut Laue-Langevin (ILL, Grenoble, France). Three configurations were used to cover a q-range between 2 × 10−2 and 1 nm−1: sample-to-detector distance, dSD = 34 m, 8 m, and 2 m, with the neutron wavelength λ = 0.6 nm. The instrument is equipped with a 3He detector. The wavelength resolution was Δλ/λ = 9% for all the measurements.
The scattering data in dilute state (ζ < 0.07) were fitted with the fuzzy-sphere model for regular microgels60 and the fuzzy core–shell model for hollow microgels42 using the customized Matlab-based software FitIt!.61 In the fuzzy-sphere model, a particle of radius R consists of a homogeneous core of radius Rc and a fuzzy shell of width 2σout, so that R = Rc + 2σout. This profile is obtained by convolution of a box function with a Gaussian of width 2σout. In the fuzzy core–shell model, a particle of radius R consists of a homogeneous core of radius Rc, an interpenetrating layer between the core and the shell of the length 2σin, a homogeneous shell of length wshell and a fuzzy outer surface of the length 2σout. The total particle radius is thus R = Rc + 2σin + wshell + 2σout. Size polydispersity is accounted for by convoluting the form factor with a Gaussian distribution of R. An additional Lorentzian term with an average meshsize ξ is then added to account for scattering from density inhomogeneities of the polymer network. Finally, the models are convolved with a Gaussian function that describes the instrument resolution62 and a constant background to account for incoherent scattering is added.
SLS and SAXS data were merged and fitted together, whereas the SANS data were fitted separately due to the different q-resolution.62
2.7 Molecular dynamics simulations
The simulated microgels have been modeled using a standard coarse grained bead-spring approach widely used for the modelling of uncharged and charged polymer networks.63,64 Monomer beads may have up to two bonds and crosslinker beads up to four. The initial network is generated by randomly arranging the beads inside a sphere or hollow sphere and afterwards connecting spatially close beads to each other, starting from the crosslinkers.65 Every bead not connected to the main network is deleted, leaving a single interconnected network. An equilibration is performed using molecular dynamics implemented in the software package LAMMPS and considering only excluded volume and bonding interactions. We use the Weeks–Chandler–Andersen potential between all beads to describe the short-range repulsion due to excluded volume: | (4) |
Here, σ is the bead diameter, which we chose to be 1 nm, r is the distance between beads and ε is the unit of energy and has a value of 1 kBT. Bonded monomers additionally interact via a finitely extensible nonlinear elastic (FENE) spring potential (eqn (5)).66
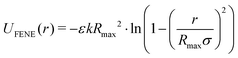 | (5) |
We chose a spring constant of k = 15, and a maximum bond extension of Rmax = 1.5σ. A Nosé–Hoover thermostat is used to keep the temperature constant at T = 298.15 K and time integration is performed with a timestep of 1 ns. Only two model microgels are simulated for our purposes: (i) regular microgels, consisting of a total number N = 150.000 of beads with 5% crosslink fraction and (ii) hollow microgels with a relative cavity radius of rc = 0.65, a number of beads of N = 100.000 and also 5% crosslink fraction.
3 Results and discussion
3.1 Microgel size and internal structure
Formation of colloidal crystals is well-known to be suppressed by polydispersity or size mismatch between the particles.10–13 For this reason, we first carefully check that the regular and hollow microgels used here have similar size and sufficiently low polydispersities. The hydrodynamic radii Rh obtained from multi-angle DLS are 223 ± 2 nm and 228 ± 3 nm for regular and hollow microgels, respectively. The temperature dependence of the Rh of the two microgels is shown in Fig. S1 (ESI†).We also obtain the form factors of the two microgels at T = 20 °C by measuring their dilute suspensions using small-angle X-ray scattering (SAXS, c = 0.3 wt%) and static light scattering (SLS, c < 0.01 wt%). Under these conditions, the scattering intensity is only proportional to the form factor P(q). Fig. 1 shows the form factors obtained with SAXS for the regular microgels (blue circles) and hollow microgels (orange squares). To expand the probed q-range, SLS data is also shown with green and red triangles for regular and hollow microgels, respectively. The form factors of the two microgels demonstrate distinctly different q-dependence, but both feature two well-defined minima and maxima allowing to describe their internal structure with good accuracy.
The combined form factors from SAXS and SLS were fitted using the fuzzy-sphere model for regular microgels60 and fuzzy core–shell model hollow microgels,42,67Fig. 1 (black solid lines). The fit parameters (see Experimental section) are summarized in Table 1. The inset in Fig. 1 shows radial distributions of relative polymer volume fraction ρ(r), which describes the internal structure of the microgels. As expected,60,68 the regular microgels have a densely crosslinked core (Rc = 69 ± 3 nm) and a large fuzzy shell (σout = 154 ± 7 nm), making them soft particles in the classical sense. In contrast, the hollow microgels have a solvent-filled cavity in their center (Rc = 78 ± 4 nm), internal and external fuzzy regions where polymer density gradually decays to zero (σin = 54 ± 3 nm and σout = 45 ± 2 nm) and a shell with homogeneous polymer density in between (wshell = 31 ± 2 nm). The size of the cavity is smaller than the hydrodynamic radius of the silica particles used as templates, Rh(SiO2) = 105 ± 3 nm, because after dissolution of the silica core the polymer network can swell into the cavity.42,43 Such a hollow architecture makes the hollow microgels different from the typical “hard core/soft shell” colloids.21,25 Additionally, the form factors were measured using small-angle neutron scattering (SANS), Fig. S2 (ESI†) and Table 1. The microgel radius R and internal structure determined by both methods agree within the experimental errors, however the polydispersity is likely overestimated by SANS due to the lower q-resolution of the method with respect to SAXS/SLS.62
| Microgel | R h (nm) | Static scattering method | R (nm) | R c (nm) | 2σin (nm) | w shell (nm) | 2σout | p (%) |
|---|---|---|---|---|---|---|---|---|
| Regular | 223 ± 2 | SAXS + SLS | 223 ± 11 | 69 ± 3 | — | — | 154 ± 7 | 5.6 ± 0.5 |
| SANS | 211 ± 10 | 65 ± 3 | — | — | 146 ± 7 | 13 ± 1 | ||
| Hollow | 228 ± 3 | SAXS + SLS | 208 ± 10 | 78 ± 4 | 54 ± 3 | 31 ± 2 | 45 ± 2 | 10 ± 1 |
| SANS | 211 ± 10 | 79 ± 4 | 52 ± 3 | 31 ± 2 | 49 ± 2 | 16 ± 1 |
Thus, using several scattering methods we verify that the two microgels have almost no size disparity and the only significant difference between them is the presence of a solvent-filled cavity. Also their polydispersity is sufficiently low, well below the crystallization limit for microgels p < 18%,53 so that the suppression of crystallization due to polydispersity effects can be ruled out in our system.
3.2 Phase behavior and shear rheology
We express the concentration of microgels as the generalized volume fraction ζ, which corresponds to the volume fraction of particles in their fully swollen state.54 Determining of the true volume fraction ϕ of soft deformable colloids is challenging, because they can change size and shape in response to crowding.69 So instead of ϕ, it is common to use ζ, which is proportional to weight fraction of polymer, c: ζ = kc, where k is the conversion constant.52–54 Here, the k values determined by viscometry are 10.5 ± 0.7 for regular microgels and 22 ± 2 for hollow microgels, Fig. S3 (ESI†). The higher value for the hollow microgels reflects that they occupy a larger volume for the same weight concentration, which is due to the solvent-filled cavity. The total generalized volume fraction of a binary mixture is a sum of the generalized volume fraction of regular microgels, ζr, and hollow microgels, ζh: ζ = ζr + ζh.Furthermore, we obtain molecular weights for regular and hollow microgels based on the viscometry data: (2.7 ± 0.1) × 109 g mol−1 for regular microgels and (1.3 ± 0.1) × 109 g mol−1 for hollow microgels. These values are used to calculate the number fraction of hollow microgels in the binary mixture, nh, as follows:
 | (6) |
Using the obtained values of ζ and nh, we plot the phase diagram of the binary mixtures, Fig. 2(a). Samples where crystals are observed from Bragg reflections are plotted with orange diamonds. Fig. 2(b) shows typical appearance of samples in the fluid, fluid/crystalline coexistence and glassy states for nh = 0.06 ± 0.01 and increasing ζ. Photographs of samples with other nh as a function of ζ are shown in Fig. S4(a) (ESI†). In the case of fluid-crystal coexistence, a clear boundary between the crystals (bottom phase) and the fluid (upper phase) formed after 1–3 months, allowing us to determine the freezing point ζf and the melting point ζm, Fig. S4(b) (ESI†).
For nh = 0, we observed a broad fluid-crystal coexistence region Δζ = ζm − ζf = 0.15 ± 0.04, with ζf = 0.55 ± 0.02 (freezing point, black exes) and ζm = 0.70 ± 0.02 (melting point, black pluses). Δζ is slightly broader than what was reported for similar microgels.53,54 The binary mixtures show crystals only in the coexistence region and fully crystalline samples are absent. Therefore, we define ζm as the volume fraction after the coexistence region, when the crystals disappear. Notably, for nh > 0.06 either a plateau or a drop in x(crystals) is observed with increasing ζ. The reason for such a drop is yet unclear and further studies are needed to clarify this observation. As nh increases, both ζf and ζm shift progressively to higher values until nh ≈ 0.23. For nh > 0.23, ζm depends weakly on nh while ζf continues to increase and, as a result, Δζ (shaded in blue) narrows and disappears at nh > 0.65. Similarly, a gradual inhibition of crystallization was observed in binary mixtures of large (l) and small microgels (s) with a size mismatch Rl/Rs ≈ 1.5.53 Furthermore, the kinetics of crystallization becomes slower with increasing nh. For nh = 0 crystals form within 1–2 days, while for nh ≥ 0.23 crystals appear after 2 weeks and form a stable fluid-crystal phase boundary after a few months.
The observed slowing down of the crystallization kinetics may be related to a general slowing down of the particle dynamics as the system approaches the glass transition, ζg.70 To determine the ζg in our system, we investigate the evolution of the zero-shear viscosity of individual regular and hollow microgels with increasing ζ. The value of the generalized volume fraction where the suspension viscosity diverges, ζ0, often coincides with glass transition, in particular for concentrated microgels suspensions,13,37,71 so it can be used as a good approximation for ζg.
Fig. 3(a) and (b) show the viscosity η as a function of shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) for suspensions of regular and hollow microgels, respectively, at different ζ. The samples show typical shear-thinning behavior, which can be fitted with eqn (3) (black solid lines) to obtain zero-shear viscosities η0. The results are plotted in Fig. 3(c) as relative viscosities, ηr = η0/ηs where ηs is the solvent viscosity, vs. generalized volume fraction ζ. For both regular and hollow microgels the curve ηrvs. ζ diverges. Such a course of the data can be described with good accuracy using the Quemada model:72
for suspensions of regular and hollow microgels, respectively, at different ζ. The samples show typical shear-thinning behavior, which can be fitted with eqn (3) (black solid lines) to obtain zero-shear viscosities η0. The results are plotted in Fig. 3(c) as relative viscosities, ηr = η0/ηs where ηs is the solvent viscosity, vs. generalized volume fraction ζ. For both regular and hollow microgels the curve ηrvs. ζ diverges. Such a course of the data can be described with good accuracy using the Quemada model:72
 | (7) |
 | ||
Fig. 3 (a) Shear viscosity η vs. shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) for suspensions of regular microgels with ζ = 0.45 ± 0.03 (circles), ζ = 0.50 ± 0.04 (squares), ζ = 0.55 ± 0.04 (upward triangles), ζ = 0.60 ± 0.04 (diamonds), ζ = 0.65 ± 0.05 (downward triangles). (b) Shear viscosity η vs. shear rate for suspensions of regular microgels with ζ = 0.45 ± 0.03 (circles), ζ = 0.50 ± 0.04 (squares), ζ = 0.55 ± 0.04 (upward triangles), ζ = 0.60 ± 0.04 (diamonds), ζ = 0.65 ± 0.05 (downward triangles). (b) Shear viscosity η vs. shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) for suspensions of hollow microgels with ζ= 0.49 ± 0.05 (circles), ζ= 0.57 ± 0.05 (squares), ζ= 0.62 ± 0.06 (upward triangles), ζ = 0.65 ± 0.05 (diamonds), ζ = 0.68 ± 0.06 (downward triangles), ζ = 0.70 ± 0.06 (left-pointing triangles), ζ = 0.74 ± 0.06 (right-pointing triangles). Black solid lines in (a) and (b) correspond to fits of the data using eqn (3). (c) Relative zero-shear viscosities η0/ηsvs. generalized volume fraction ζ for regular microgels (blue circles) and hollow microgels (orange upward triangles). Black solid and dashed lines correspond to fits of the data using eqn (7) for regular and hollow microgels, respectively. for suspensions of hollow microgels with ζ= 0.49 ± 0.05 (circles), ζ= 0.57 ± 0.05 (squares), ζ= 0.62 ± 0.06 (upward triangles), ζ = 0.65 ± 0.05 (diamonds), ζ = 0.68 ± 0.06 (downward triangles), ζ = 0.70 ± 0.06 (left-pointing triangles), ζ = 0.74 ± 0.06 (right-pointing triangles). Black solid lines in (a) and (b) correspond to fits of the data using eqn (3). (c) Relative zero-shear viscosities η0/ηsvs. generalized volume fraction ζ for regular microgels (blue circles) and hollow microgels (orange upward triangles). Black solid and dashed lines correspond to fits of the data using eqn (7) for regular and hollow microgels, respectively. | ||
We find ζ0,r = 0.703 ± 0.002 for regular microgels and ζ0,h = 0.802 ± 0.007 for hollow microgels. The presence of a cavity in hollow microgels delays the apparent glass transition by Δζ0 = ζ0,h − ζ0,r ≈ 0.1. For binary mixtures, one can expect a more complex behavior of the zero-shear viscosity, which is of high interest and should be addressed in a separate study. However, based on the results for regular and hollow microgels only, the viscosity divergence in binary mixtures is expected to occur between 0.7 < ζ0 < 0.8. This means that most of the samples studied here are below their apparent glass transition ζg ≈ ζ0 and the observed suppression of crystallization is not related to dynamical arrest.
3.3 Small-angle X-ray scattering
To probe the particle-to-particle arrangement, small-angle X-ray scattering (SAXS) was used. The effective structure factors of the concentrated suspensions S(q) are obtained from the measured scattering intensity I(q) as follows:73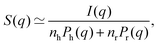 | (8) |
Fig. 4(a) shows the S(q) s of three binary mixtures with a fixed ζ ≃ 0.66 ± 0.01 and increasing values of nh: 0 (blue circles), 0.232 ± 0.001 (green triangles), and 0.342 ± 0.001 (red diamonds). Panels 4(b) and (c) show similar data for ζ ≃ 0.70 ± 0.01 and ζ ≃ 0.71 ± 0.01, respectively. These data are chosen to facilitate comparison; all structure factors measured in this work are shown in Fig. S5 (ESI†).
The positions of Bragg peaks of a face-centered cubic (fcc) lattice are indicated in Fig. 4 by the vertical dotted lines. Several Bragg reflections can be seen for suspensions of regular microgels (blue circles). With increasing nh, the higher-order peaks disappear, which reflects the loss of long-range (crystalline) order in the system. The first peak decreases its magnitude from S(qmax) ≈ 3 − 4 to S(qmax) ≤ 2.5, indicating that the suspensions are no longer crystalline according to the Hansen–Verlet criterion74,75: a system is crystalline when S(qmax) ≥ 2.85. The position of the first peak, which is related to the nearest-neighbor distance dnn between the microgels, shifts slightly to lower q with increasing nh. This shift is not immediately obvious from the structure factors in Fig. 4, but can be seen when dnn is plotted as a function of ζ, Fig. S6(a) (ESI†). This means that hollow microgels lead to a slightly larger dnn in the suspension with a constant ζ. The differences in dnn were only observed in samples with dominating fluid phase contribution in the S(q), whereas crystalline samples showed similar values of dnn independent of nh or ζ, Fig. S6(b) (ESI†). Details on dnn calculation and scaling with ζ are given in ESI,† Section S1.
Due to the slow crystallization kinetics, selected binary mixtures with different nh values were measured again by SAXS after 1 year. Fig. S7 (ESI†) shows that these samples have more pronounced and sharper Bragg peaks corresponding to the fcc lattice. The gradual disappearance of the shoulder of the first peak in the S(q) with increasing nh indicates increasing stacking disorder of hexagonal planes and a transition from predominantly fcc lattice to the random hexagonal close-packed (rhcp) lattice76 (see Section S1 for more details, ESI†). Furthermore, the height of Bragg peaks becomes smaller with increasing nh. These observations indicate that the inhibition of crystallization is not only of kinetic nature, but has thermodynamic origin related to the internal structure of hollow microgels.43 The SAXS results are supported by UV-Vis absorption spectroscopy, showing progressively smaller Bragg peaks with increasing nh, Fig. S8 (ESI†). Experimental details and analysis of the UV-Vis data can be found in ESI,† Section S2.
3.4 Molecular dynamic simulations
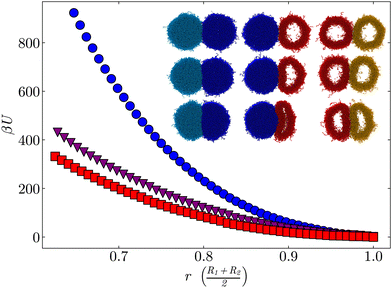
Molecular dynamics simulations of bead-spring microgels63,64,77 were performed to understand why crystallization is inhibited. We focus on two model microgels, one regular and one hollow. Due to the cavity, the two microgels have different masses with a ratio mr/mh ≈ 1.5, where mr and mh are the mass of the regular and hollow microgels, respectively. Their density profiles in equilibrium and representative snapshots are reported in Fig. S9 (ESI†). Both microgels have approximately the same size, with Rreg = 56.0 nm and Rhol = 54.6 nm. First, we aim to understand the difference in pair interactions between these microgels, to estimate the energy cost of deforming them. To probe the corresponding pair interaction potential, the microgel configurations need to be sampled in energetically highly unfavorable states. Therefore, umbrella sampling simulations, which apply an external bias to access these unfavorable states with sufficient statistical relevance, were conducted and the WHAM algorithm was applied.78,79Fig. 5 shows the potentials of mean force (PMF) between the different pairs of microgels. The interaction between two regular microgels (circles) is more unfavorable than the interaction between a regular and a hollow microgel (triangles) or between two hollow microgels (squares), especially at high deformation. Instead of increasing the density of the network, the hollow microgel is buckling due to the cavity.45 This requires a lower network deformation, making it entropically favorable and resulting in a lower interaction strength between hollow microgels. The interaction between a regular and a hollow microgel shows mainly a deformation of the hollow microgel facilitated by the anisotropic compression of the cavity. In contrast, the regular microgel barely facets.
To prove that such behavior is indeed expected, one can estimate the deformability of a homogeneous elastic capsule undergoing a small uniaxial deformation80 and compare it to the deformability of a simple Hertzian sphere. Let us consider a capsule with a shell thickness h similar to the hollow microgels studied here, h = 0.44R. When it is deformed by ≈10% of its initial radius, the resulting elastic energy is approximately 3 times less than for a Hertzian sphere of the same material and size, Fig. S10 (ESI†). This estimation is in qualitative agreement with the ratio of PMF that we obtained from the simulations, even though the model completely neglects the polymeric structure of the microgels. The latter should be included in the model to properly reproduce the results of the simulations, but this is beyond the scope of this study. The details about the calculation are given in ESI,† Section S3.
Next, a single hollow microgel surrounded by regular microgels is studied to probe the evolution with crowding of the size and shape of all the particles. To increase ζ, the box is progressively compressed. We average the results over multiple starting configuration since high density systems are prone to a poor sampling of the available configuration space. To compute the volume of a microgel, a triangulated surface mesh is created using the alpha shape algorithm.81 The degree of concavity of the shape is determined by the so called alpha parameter. We find that choosing an alpha parameter of 10 bead diameters prevents overestimating the volumes due to single dangling chains but still is able to capture the strong deformation of the hollow microgels (see Fig. S11, ESI†).
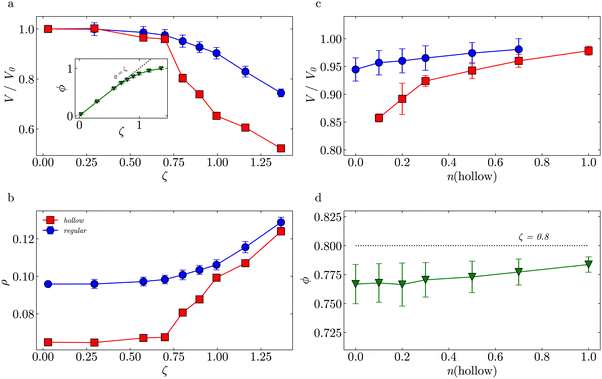
Fig. 6(a) shows the normalized volume of the regular (circles) and the hollow (squares) microgels V/V0. For ζ ⪅ 0.7, the volumes of both particles decrease rather similarly, i.e. there are low deformations. For ζ > 0.74, compression and deformation of both species of microgels become significant. This is reflected by the effective volume fraction (triangles) that deviates from the ϕ = ζ trend at ζ ≈ 0.7. We observe a stronger drop in V/V0 for the hollow microgels due to the cavity that makes them easier to be compressed with respect to their regular counterpart. Note that in experiments no crystals were observed at ζ > 0.74 (Fig. 2), which supports this interpretation.
Fig. 6(b) shows the evolution of the microgel density ρ vs. ζ. Both the hollow and regular microgel have a similar network density, as shown in their radial density profiles (see Fig. S9, ESI†). However, due to the missing mass in the cavity of the hollow network, the overall density, ρ = m/V, of the hollow microgel is lower under dilute conditions. The regular microgel contains 50% more beads than the hollow microgel, but has the same volume in the swollen state. As ζ-values increase, the hollow microgel becomes relatively more deformed than the regular one, as its cavity can be easily compressed. Once the cavity is fully compressed, the overall density becomes equivalent to the network density. Since both types of microgels have comparable crosslink fractions, their densities approach nearly the same value.
A further decrease of the microgel volume has the same entropic cost for both networks, therefore, the densities remain similar. This agrees with the reported rheological behavior of hard-soft binary mixtures of regular microgels with different crosslinker densities.82 The elastic moduli of those binary mixtures were mostly determined by the soft component that are compressed at low packing fractions, while both hard and soft microgels contributed to the elasticity at very dense packing.
Fig. 6(c) shows the effect of changing nh at a constant ζ = 0.8. An increase in nh leads to a higher V/V0 for all microgels. Due to their cavities, the additional hollow microgels are more easily compressed and deformed than the regular microgel, decreasing the deformation of all regular microgels. The cavity does not have to be deformed isotropically and the resulting non-spherical shapes occupy the solution volume more efficiently, which on average increases the V/V0 of hollow microgels. Fig. 6(d) shows that the effective ϕ of the suspension, which refers to both hollow and regular microgels, is also slightly increasing with increasing nh.
The simulations confirm that crowding leads to anisotropically deformed microgels, see Fig. 5 inset, therefore inhibiting the crystallization. To better understand it, we can make an analogy to the widely studied bidisperse or polydisperse mixtures of hard spheres10,83,84 or microgels.13,53 These suspensions have higher free volume than monodisperse ones, because smaller particles can explore the voids between bigger particles.14,85 This increases the overall entropy of the system and stabilizes the fluid state.11 Similarly, the high deformability of the hollow microgels allows the binary mixtures to pack more efficiently, providing an alternative way to increase the entropy without crystal formation. However, binary mixtures of hollow and regular microgels have almost no size disparity until ζ ≈ 0.7.
Concerning the initial shift of phase boundaries (Fig. 2(a)), previous studies showed that hollow microgels deswell below ζ = 0.7 in mixtures with both identical hollow43 and regular microgels.32 This osmotic deswelling can shift the ζf and ζm to higher values due to a decrease of the true volume fraction.31,56,86
4. Conclusions
The phase behavior of binary mixtures of hollow and regular microgels is presented in this study. We find that increasing the fraction of hollow microgels in a mixture, nh, first leads to a progressive shift of the phase boundaries followed by narrowing of the fluid-crystal coexistence region and complete disappearing of crystals at nh > 0.65. The kinetics of crystallization slows down significantly with increasing nh, but also even after an equilibration time of 1 year the binary mixtures with higher nh have smaller Bragg peaks and higher stacking disorder of hexagonal planes. The simulation results show that hollow microgels suppress crystal formation since their cavity allows them to buckle with a lower entropy penalty than by isotropically compressing the polymeric network. The resulting faceted particles can fill the space more efficiently, thus stabilizing the fluid state of the suspension.Studies of binary mixture of hollow and regular microgels can help us to investigate and better understand what is the role of size disparities, particle segregation, cluster formation on the properties of colloidal glasses and jammed suspensions. With these suspensions we can determine the exact effect of the deformability of individual particles on formation of soft or strong glasses and address whether or not the glass fragility depends on the rise of directional interactions.13,38 Given the absence of crystals above the melting point, further studies can be performed on this metastable supercooled fluid phase that can be used to explore the non-linear viscoelastic regime of colloidal dispersions.87 These hollow defects can be introduced to suppress crystal formation because of their internal structure and not due to size disparities. A systematic study of this new kind of defects can be done by finely tuning the extension of the cavity using external stimuli to partially collapse the hollow microgels making them similar to regular ones.
Data availability
All data used in this study are available at 10.22000/gDDeJtniERRQmiOx. The SANS data collected on D11 are available at doi.ill.fr/10.5291/ILL-DATA.9-11-1855 and doi.ill.fr/ILL-DATA.9-13-985.Conflicts of interest
There are no conflicts to declare.Acknowledgements
AS acknowledges financial support from the Knut and Alice Wallenberg Foundation (Wallenberg Academy Fellows). The authors gratefully acknowledge financial support from the Deutsche Forschungsgemeinschaft (DFG) withing the SFB 985 “Functional microgels and microgel systems”. The authors are grateful to A. Fernandez-Nieves for the valuable comments to the manuscript, and to W. Richtering and J. J. Crassous for fruitful discussions. We thank M. Brugnoni for synthesizing the regular microgels used in this work. We thank R. Schweins for the assistance during the SANS experiment at ILL (proposals 9-11-1855 and 9-13-985). We thank A. E. Terry and T. Plivelic for the assistance with the SAXS measurements that were performed on the CoSAXS beamline at the MAX IV laboratory (Lund, Sweden) under the proposals 20200777 and 20220526. The Research conducted at MAX IV, a Swedish national user facility, is supported by the Swedish Research Council under contract 2018-07152, the Swedish Governmental Agency for Innovation Systems under contract 2018-04969, and Formas under contract 2019-02496.Notes and references
- A. Einstein, Ann. Phys., 1905, 17, 208 Search PubMed.
- P. N. Pusey and W. Van Megen, Nature, 1986, 320, 340–342 CrossRef CAS.
- P. N. Pusey and W. van Megen, Phys. Rev. Lett., 1987, 59, 2083 CrossRef CAS PubMed.
- U. Gasser, E. R. Weeks, A. Schofield, P. Pusey and D. Weitz, Science, 2001, 292, 258–262 CrossRef CAS PubMed.
- K. Schätzel and B. J. Ackerson, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 48, 3766 CrossRef PubMed.
- S. Auer and D. Frenkel, Nature, 2001, 409, 1020–1023 CrossRef CAS PubMed.
- H. J. Schöpe, G. Bryant and W. Van Megen, J. Chem. Phys., 2007, 127, 084505 CrossRef PubMed.
- E. R. Weeks, J. C. Crocker, A. C. Levitt, A. Schofield and D. A. Weitz, Science, 2000, 287, 627–631 CrossRef CAS PubMed.
- G. Brambilla, D. El Masri, M. Pierno, L. Berthier, L. Cipelletti, G. Petekidis and A. B. Schofield, Phys. Rev. Lett., 2009, 102, 085703 CrossRef CAS PubMed.
- S. Henderson, T. Mortensen, S. M. Underwood and W. van Megen, Phys. A, 1996, 233, 102–116 CrossRef CAS.
- P. Pusey, E. Zaccarelli, C. Valeriani, E. Sanz, W. C. Poon and M. E. Cates, Philos. Trans. R. Soc., A, 2009, 367, 4993–5011 CrossRef CAS PubMed.
- P. Yunker, Z. Zhang, K. B. Aptowicz and A. G. Yodh, Phys. Rev. Lett., 2009, 103, 115701 CrossRef PubMed.
- J. Mattsson, H. M. Wyss, A. Fernandez-Nieves, K. Miyazaki, Z. Hu, D. R. Reichman and D. A. Weitz, Nature, 2009, 462, 83–86 CrossRef CAS PubMed.
- S. Williams and W. Van Megen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 041502 CrossRef CAS PubMed.
- W. Götze and T. Voigtmann, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 021502 CrossRef PubMed.
- J. M. Lynch, G. C. Cianci and E. R. Weeks, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 031410 CrossRef PubMed.
- P. F. Luckham and M. A. Ukeje, J. Colloid Interface Sci., 1999, 220, 347–356 CrossRef CAS PubMed.
- W. Richtering and H. Mueller, Langmuir, 1995, 11, 3699–3704 CrossRef CAS.
- A. S. J. Iyer and L. A. Lyon, Angew. Chem., 2009, 121, 4632–4636 CrossRef.
- D. Frenkel, Nature, 2009, 460, 465–466 CrossRef CAS.
- D. Vlassopoulos and M. Cloitre, Curr. Opin. Colloid Interface Sci., 2014, 19, 561–574 CrossRef CAS.
- H. Shamana, M. Grossutti, E. Papp-Szabo, C. Miki and J. R. Dutcher, Soft Matter, 2018, 14, 6496–6505 RSC.
- D. Parisi, E. Buenning, N. Kalafatakis, L. Gury, B. C. Benicewicz, M. Gauthier, M. Cloitre, M. Rubinstein, S. K. Kumar and D. Vlassopoulos, ACS Nano, 2021, 15, 16697–16708 CrossRef CAS PubMed.
- J. U. Kim and M. W. Matsen, Macromolecules, 2008, 41, 4435–4443 CrossRef CAS.
- S. Gupta, M. Camargo, J. Stellbrink, J. Allgaier, A. Radulescu, P. Lindner, E. Zaccarelli, C. N. Likos and D. Richter, Nanoscale, 2015, 7, 13924–13934 RSC.
- M. Kapnistos, D. Vlassopoulos, G. Fytas, K. Mortensen, G. Fleischer and J. Roovers, Phys. Rev. Lett., 2000, 85, 4072 CrossRef CAS PubMed.
- D. Vlassopoulos, G. Fytas, T. Pakula and J. Roovers, J. Phys.: Condens. Matter, 2001, 13, R855 CrossRef CAS.
- A. Scotti, M. F. Schulte, C. G. Lopez, J. J. Crassous, S. Bochenek and W. Richtering, Chem. Rev., 2022, 122, 11675–11700 CrossRef CAS PubMed.
- J. E. Houston, L. Fruhner, A. de la Cotte, J. Rojo González, A. V. Petrunin, U. Gasser, R. Schweins, J. Allgaier, W. Richtering and A. Fernandez-Nieves, et al. , Sci. Adv., 2022, 8, eabn6129 CrossRef CAS PubMed.
- M. Karg, A. Pich, T. Hellweg, T. Hoare, L. A. Lyon, J. Crassous, D. Suzuki, R. A. Gumerov, S. Schneider and I. I. Potemkin, et al. , Langmuir, 2019, 35, 6231–6255 CrossRef CAS PubMed.
- A. Scotti, U. Gasser, E. S. Herman, M. Pelaez-Fernandez, J. Han, A. Menzel, L. A. Lyon and A. Fernández-Nieves, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 5576–5581 CrossRef CAS PubMed.
- A. Scotti, A. R. Denton, M. Brugnoni, J. E. Houston, R. Schweins, I. I. Potemkin and W. Richtering, Macromolecules, 2019, 52, 3995–4007 CrossRef CAS.
- A. Scotti, J. Houston, M. Brugnoni, M. Schmidt, M. Schulte, S. Bochenek, R. Schweins, A. Feoktystov, A. Radulescu and W. Richtering, Phys. Rev. E, 2020, 102, 052602 CrossRef CAS PubMed.
- C. Pellet and M. Cloitre, Soft Matter, 2016, 12, 3710–3720 RSC.
- A.-M. Philippe, D. Truzzolillo, J. Galvan-Myoshi, P. Dieudonné-George, V. Trappe, L. Berthier and L. Cipelletti, Phys. Rev. E, 2018, 97, 040601 CrossRef CAS PubMed.
- T. Kureha, H. Minato, D. Suzuki, K. Urayama and M. Shibayama, Soft Matter, 2019, 15, 5390–5399 RSC.
- P. Van Der Scheer, T. Van De Laar, J. Van Der Gucht, D. Vlassopoulos and J. Sprakel, ACS Nano, 2017, 11, 6755–6763 CrossRef CAS PubMed.
- Y. Shi, B. Deng, O. Gulbiten, M. Bauchy, Q. Zhou, J. Neuefeind, S. R. Elliott, N. J. Smith and D. C. Allan, Nat. Commun., 2023, 14, 13 CrossRef CAS PubMed.
- L. Zha, Y. Zhang, W. Yang and S. Fu, Adv. Mater., 2002, 14, 1090–1092 CrossRef CAS.
- J. Dubbert, K. Nothdurft, M. Karg and W. Richtering, Macromol. Rapid Commun., 2015, 36, 159–164 CrossRef CAS PubMed.
- M. Brugnoni, A. Scotti, A. A. Rudov, A. P. Gelissen, T. Caumanns, A. Radulescu, T. Eckert, A. Pich, I. I. Potemkin and W. Richtering, Macromolecules, 2018, 51, 2662–2671 CrossRef CAS.
- J. Dubbert, T. Honold, J. S. Pedersen, A. Radulescu, M. Drechsler, M. Karg and W. Richtering, Macromolecules, 2014, 47, 8700–8708 CrossRef CAS.
- A. Scotti, A. Denton, M. Brugnoni, R. Schweins and W. Richtering, Phys. Rev. E, 2021, 103, 022612 CrossRef CAS PubMed.
- A. Scotti, U. Gasser, A. V. Petrunin, L. Fruhner, W. Richtering and J. E. Houston, Soft Matter, 2022, 18, 5750–5758 RSC.
- F. Hagemans, F. Camerin, N. Hazra, J. Lammertz, F. Dux, G. Del Monte, O.-V. Laukkanen, J. J. Crassous, E. Zaccarelli and W. Richtering, ACS nano, 2023, 17(8), 7257–7271 CrossRef CAS PubMed.
- K. Geisel, A. A. Rudov, I. I. Potemkin and W. Richtering, Langmuir, 2015, 31, 13145–13154 CrossRef CAS PubMed.
- J. Vialetto, F. Camerin, F. Grillo, S. N. Ramakrishna, L. Rovigatti, E. Zaccarelli and L. Isa, ACS Nano, 2021, 15, 13105–13117 CrossRef CAS PubMed.
- G. L. Hunter and E. R. Weeks, Rep. Prog. Phys., 2012, 75, 066501 CrossRef PubMed.
- R. Pelton and P. Chibante, Colloids Surf., 1986, 20, 247–256 CrossRef CAS.
- D. E. Koppel, J. Chem. Phys., 1972, 57, 4814–4820 CrossRef CAS.
- G. Batchelor, J. Fluid Mech., 1977, 83, 97–117 CrossRef.
- G. Romeo, L. Imperiali, J.-W. Kim, A. Fernández-Nieves and D. A. Weitz, J. Chem. Phys., 2012, 136, 124905 CrossRef PubMed.
- A. Scotti, U. Gasser, E. Herman, J. Han, A. Menzel, L. A. Lyon and A. Fernandez-Nieves, Phys. Rev. E, 2017, 96, 032609 CrossRef CAS PubMed.
- H. Senff and W. Richtering, J. Chem. Phys., 1999, 111, 1705–1711 CrossRef CAS.
- J. J. Crassous, M. Siebenbürger, M. Ballauff, M. Drechsler, O. Henrich and M. Fuchs, J. Chem. Phys., 2006, 125, 204906 CrossRef CAS PubMed.
- M. Pelaez-Fernandez, A. Souslov, L. Lyon, P. M. Goldbart and A. Fernandez-Nieves, Phys. Rev. Lett., 2015, 114, 098303 CrossRef CAS PubMed.
- M. M. Cross, J. Colloid Sci., 1965, 20, 417–437 CrossRef CAS.
- T. S. Plivelic, A. E. Terry, R. Appio, K. Theodor and K. Klementiev, AIP Conf. Proc., 2019, 030013 CrossRef.
- J. Filik, A. Ashton, P. Chang, P. Chater, S. Day, M. Drakopoulos, M. Gerring, M. Hart, O. Magdysyuk and S. Michalik, et al. , J. Appl. Crystallogr., 2017, 50, 959–966 CrossRef CAS PubMed.
- M. Stieger, J. S. Pedersen, P. Lindner and W. Richtering, Langmuir, 2004, 20, 7283–7292 CrossRef CAS PubMed.
- O. Virtanen, A. Mourran, P. Pinard and W. Richtering, Soft Matter, 2016, 12, 3919–3928 RSC.
- J. S. Pedersen, D. Posselt and K. Mortensen, J. Appl. Crystallogr., 1990, 23, 321–333 CrossRef.
- L. Rovigatti, N. Gnan, L. Tavagnacco, A. J. Moreno and E. Zaccarelli, Soft Matter, 2019, 15, 1108–1119 RSC.
- A. Martin-Molina and M. Quesada-Perez, J. Mol. Liq., 2019, 280, 374–381 CrossRef CAS.
- T. Höfken, C. Strauch, S. Schneider and A. Scotti, Nano Lett., 2022, 22, 2412–2418 CrossRef PubMed.
- K. Kremer and G. S. Grest, J. Chem. Phys., 1990, 92, 5057–5086 CrossRef CAS.
- I. Berndt, J. S. Pedersen and W. Richtering, J. Am. Chem. Soc., 2005, 127, 9372–9373 CrossRef CAS PubMed.
- N. Hazra, A. Ninarello, A. Scotti, J. E. Houston, P. Mota-Santiago, E. Zaccarelli and J. J. Crassous, Macromolecules, 2023, 57, 339–355 CrossRef.
- A. Scotti, Soft Matter, 2021, 17, 5548–5559 RSC.
- U. Gasser, J. Phys.: Condens. Matter, 2009, 21, 203101 CrossRef CAS PubMed.
- A. Scotti, M. Brugnoni, C. G. Lopez, S. Bochenek, J. J. Crassous and W. Richtering, Soft Matter, 2020, 16, 668–678 RSC.
- D. Quemada, Rheol. Acta, 1977, 16, 82–94 CrossRef.
- A. V. Petrunin, M. M. Schmidt, R. Schweins, J. E. Houston and A. Scotti, Langmuir, 2023, 39, 7530–7538 CrossRef CAS PubMed.
- J.-P. Hansen and L. Verlet, Phys. Rev., 1969, 184, 151 CrossRef CAS.
- M. Watzlawek, C. N. Likos and H. Löwen, Phys. Rev. Lett., 1999, 82, 5289 CrossRef CAS.
- U. Gasser, J.-J. Lietor-Santos, A. Scotti, O. Bunk, A. Menzel and A. Fernandez-Nieves, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 052308 CrossRef CAS PubMed.
- T. Höfken, U. Gasser, S. Schneider, A. V. Petrunin and A. Scotti, Macromol. Rapid Commun., 2024, 2400043 CrossRef PubMed.
- B. Roux, Comput. Phys. Commun., 1995, 91, 275–282 CrossRef CAS.
- M. J. Bergman, N. Gnan, M. Obiols-Rabasa, J.-M. Meijer, L. Rovigatti, E. Zaccarelli and P. Schurtenberger, Nat. Commun., 2018, 9, 5039 CrossRef PubMed.
- F. Dubreuil, N. Elsner and A. Fery, Eur. Phys. J. E: Soft Matter Biol. Phys., 2003, 12, 215–221 CrossRef CAS PubMed.
- H. Edelsbrunner and E. P. Mücke, ACM Transactions On Graphics (TOG), 1994, 13, 43–72 Search PubMed.
- F. Di Lorenzo and S. Seiffert, Colloid Polym. Sci., 2013, 291, 2927–2933 CrossRef CAS.
- W. Kob and H. C. Andersen, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 51, 4626 CrossRef CAS PubMed.
- S. Auer and D. Frenkel, Nature, 2001, 413, 711–713 CrossRef CAS PubMed.
- T. Sentjabrskaja, E. Babaliari, J. Hendricks, M. Laurati, G. Petekidis and S. U. Egelhaaf, Soft Matter, 2013, 9, 4524–4533 RSC.
- B. Sierra-Martin and A. Fernandez-Nieves, Soft Matter, 2012, 8, 4141–4150 RSC.
- F. Khabaz, T. Liu, M. Cloitre and R. T. Bonnecaze, Phys. Rev. Fluids, 2017, 2, 093301 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00862f |
| This journal is © The Royal Society of Chemistry 2024 |