Open Access Article
Open Access ArticleCore–shell nanogels: the effects of morphology, electro- and magnetostatic interactions†
Alla B.
Dobroserdova
 *a,
Elena S.
Minina
b,
Pedro A.
Sánchez
*a,
Elena S.
Minina
b,
Pedro A.
Sánchez
 b,
Christos N.
Likos
b,
Christos N.
Likos
 b and
Sofia S.
Kantorovich
b and
Sofia S.
Kantorovich
 b
b
aUral Federal University, Ekaterinburg, Russian Federation. E-mail: alla.dobroserdova@urfu.ru
bFaculty of Physics, University of Vienna, Vienna, Austria
First published on 3rd June 2024
Abstract
We study the influence of core–shell morphology on the structural characteristics of nanogels. Using computer simulations, we examine three different types of systems, distinguished by their intermonomer interactions: those with excluded volume only; those with charged monomers and excluded volume; and those with excluded volume combined with a certain number of magnetised nanoparticles incorporated within the nanogel. We observe that if the polymers in the shell are short and dense, they tend to penetrate the core. This effect of backfolding is enhanced in charged nanogels, regardless of whether all monomers are charged, or only the core or shell ones. The presence of an experimentally available amount of magnetic nanoparticles in a gel, on the one hand, does not lead to any significant morphological changes. On the other hand, the morphology of the nanogel with magnetic particles has an impact on its magnetic susceptibility. Particular growth of the magnetic response is observed if a long shell of a nanogel is functionalised.
1 Introduction
Nanogels or microgels are soft colloidal particles made of a permanently cross-linked network of polymers. The remarkable feature of nanogels is that these polymer particles are soluble and extremely sensitive to any changes in the environment, be that temperature or pH of the solvent, or an external electric field.1–6 In particular, these particles, whose typical size ranges from one hundred nanometres to several micrometres, can shrink and swell as a result of the polymeric structure with a several-fold change in size in response to external stimuli. This ability has led to an interest in nanogels as promising smart materials. Today, many applications are taking advantage of nanogel properties, e.g., drug delivery in medicine, oil recovery in the petroleum industry, in sensing and in coating technologies.4,7–12Nano- and microgels exhibit several unique properties that lay the foundation for their potential use as an effective platform for biological applications.13,14 These include the possibility of a high water content, excellent biocompatibility, suitable mechanical properties, physical and chemical structure, and the presence of an internal network for the packaging and encapsulation of payloads.15,16 Particularly useful for the encapsulation are the nanogels that possess a core–shell topology. The structure with a central core can be used to contain therapeutic agents, protected by an outer shell.17
The various uses of nanogels, in particular, can be attributed to the ability to control their dimensions, degradability, softness, porosity, amphiphilicity, and surface charge by adjusting the concentration of the cross-linking agent, monomer type, and ratio.18–21 An important feature of nanogels is that a decrease in their volume and size in response to external stimuli occurs in the nanosecond time range,22–24 stimulating their use in biological lubricants25 and drug carriers.26–33 For the remote control of drug release, one can use light or ultrasound, or functionalise nanogels with magnetic nanoparticles and apply external magnetic fields.34–47 Alternatively, the targeted delivery of biomaterials can be achieved through the use of particular ligands. This way, active transport of anticancer agents or more sensitive biological detection has been achieved.48–54 Due to their high water content and internal network capabilities, nanogels are also ideal for 3D cell culture applications.45,55 The ability to exchange solvent and solute between a nanogel of a core–shell topology and the environment due to changes in the size and shape of the nanogel itself makes nanogels ideal for the detection of small biomolecules.56 Nanogels can also be used as a biodetector for monitoring and diagnosis of diabetes.57,58
Anisotropy of physical properties and biological organisation is one of the main characteristics of most tissues in the human body. Due to the water-rich composition of hydrogels, their biocompatibility, and tunable properties, hydrogels have been taken as scaffold materials for the creation of artificial tissues. Because unmodified hydrogels are composed of randomly oriented polymer networks, resulting in homogeneous structures with isotropic properties that differ from those observed in biological systems, magnetic materials have been proposed as potential agents to promote anisotropy in hydrogels. This has enabled the use of hydrogels in tissue engineering.59,60 Magnetic nanomaterials have found excellent application in the diagnosis and treatment of cancerous tumour processes.61–63
In addition to conventional experimental approaches used to study nanogels directly in a laboratory where they are synthesised, nowadays we can also rely on computer simulations to study the properties of nanogels.6,64–74 Most of these works take as a basis a bead-spring model75 to model polymer chains. The most common approach to create a quasi-spherical nano- or microgel relies on the placement of the polymer chain in a lattice-like manner, where the lattice vertices serve as cross-linkers, like, e.g., in ref. 76. To avoid regular lattices, approaches based on Wertheim theory6 or distance proximity cross-linking77 have been proposed. In case the polymeric details of a nanogel can be neglected, coarser models based on the Hertzian potential are used.78,79 In the work reported in ref. 80, Yukawa-type electrostatic repulsion was also added. In general, not only have charged nanogels been theoretically studied,67,68,81,82 but also nanogels functionalised with magnetic particles.77,83 In the work reported in ref. 84, the deformations of two- and three-dimensional models of magnetic gels were studied. The polymer chains in gels are represented by entropic springs; deformation is the result of the interaction of magnetic particles. The combined use of the Yukawa potential, which promotes short-range repulsion, and the magnetic dipole–dipole interaction, which promotes long-range attraction, in systems of two-dimensional colloidal particles can be found in ref. 85. In this work, the authors calculated a bulk-phase diagram that contained gas, crystalline, liquid and supercritical liquid phases.
Ref. 86 provided detailed information on the mutual influence of temperature-dependent core–shell swelling for microgels in the form of a core–shell structure of two thermosensitive polymers with different lower critical solution temperatures with dual temperature sensitivity. In ref. 87 and 88, microgels of core–shell topology with a solid core were considered. Despite a plethora of studies on nanogel rheology, interactions, and structure, a detailed study of the core–shell morphology and the effects of the shell size and density on the structure of the nanogel has not been carried out yet. In order to fill this gap, in this paper, we investigate neutral, charged, and magnetic core–shell nanogels, varying the size, density, type, and cross-linker distribution in the shell.
The paper is organised as follows. In the next section, we describe simulation methods and models used to study nanogels. The results are split into three subsections according to the type of intermonomer interaction. The paper ends with a brief conclusion and an outlook.
2 Methods
2.1 General framework
We use coarse-grained molecular dynamics simulations. The latter is based on the numerical solution of Langevin equations of motion: | (1) |
 | (2) |
![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) i and
i and ![[small tau, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1ca.gif) i are the force and torque (pertaining to magnetic particles only) acting on the ith particle; Mi and Ii are the mass and inertia, respectively;
i are the force and torque (pertaining to magnetic particles only) acting on the ith particle; Mi and Ii are the mass and inertia, respectively; ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) i and
i and ![[small omega, Greek, vector]](https://www.rsc.org/images/entities/i_char_e13e.gif) i are the velocity and angular velocity of the ith particle, respectively; ΓT and ΓR are the translational and rotational friction coefficients, respectively; and
i are the velocity and angular velocity of the ith particle, respectively; ΓT and ΓR are the translational and rotational friction coefficients, respectively; and ![[small xi, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1cd.gif) Ti and
Ti and ![[small xi, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1cd.gif) Ri are the random force and torque, respectively, which have Gaussian distributions.
Ri are the random force and torque, respectively, which have Gaussian distributions.
The term ‘particle’ in our work is used for a coarse-grained Kuhn segment of a polymer, as well as for a magnetic point dipolar particle in the case of magnetic nanogels (MNGs). As long as we focus on the equilibrium properties, all particles are identical and have the same diameter σ and a unit mass, m. When magnetic nanogels are addressed, each magnetic particle also possesses a magnetic moment |![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) | = μ, fixed in magnitude and orientation within the particle body.
| = μ, fixed in magnitude and orientation within the particle body.
It is important to note that all variables used in the computer simulations are dimensionless: distance r* = r/σ, magnetic moment |![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) |2 = |
|2 = |![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) e|2/(ε/σ3), temperature T* = kBT/ε, and time t* = t(ε/(mσ2))1/2, where σ is a particle diameter, ε is the energy scale of the Lennard-Jones potential,89
e|2/(ε/σ3), temperature T* = kBT/ε, and time t* = t(ε/(mσ2))1/2, where σ is a particle diameter, ε is the energy scale of the Lennard-Jones potential,89![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) e is an experimentally measured magnetic moment, kB is the Boltzmann constant, and m is a particle mass.
e is an experimentally measured magnetic moment, kB is the Boltzmann constant, and m is a particle mass.
This routine is carried out in the molecular dynamics simulation package ESPResSo.90,91 To solve the equations of motion (1) and (2), we use a velocity Verlet algorithm92 with a fixed time step Δt = 0.01. To set up the simulations, we employ dimensionless units ε = σ = 1, which determine the energy, length, and mass scales. Since the values of the translational and rotational friction coefficients do not affect the equilibrium characteristics, in this work they are determined to be equal to unity (ΓT = ΓR = 1). The dimensionless temperature was kept constant at T* = 1 using a Langevin thermostat with a dimensionless friction coefficient equal to unity. After the equilibration, whose length is determined by the system and varied between 105 and 106 time steps, the statistics are collected during at least 108 time steps. Note that for each set of simulations throughout the paper and for each set of parameters, we always model 50 independent samples of nanogels and consider different configurations of each individual sample to ensure proper statistics.
2.2 Neutral core–shell nanogels
To model a nanogel core of a spherical shape, we use a recently developed approach77,93 that allows one to create a randomly cross-linked polymer network.We use six bead-spring polymer chains made of Mc = 100 monomers of diameter σ, whose excluded volume is modeled by the Weeks–Chandler–Andersen (WCA) potential94 being a truncated and shifted Lennard-Jones potential:89
 | (3) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ij is the vector connecting the centres of the ith and jth particles, and ε is the value of the Lennard-Jones term in |
ij is the vector connecting the centres of the ith and jth particles, and ε is the value of the Lennard-Jones term in |![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ij| = rcut.
ij| = rcut.
The monomers in the chains are bonded by FENE springs (finitely extensible nonlinear elastic model),95 defined by the following potential:
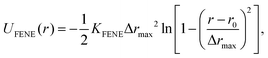 | (4) |
We place the polymer chains inside a spherical shell whose radius was comparable to that of the gyration radius of a single unconfined polymer chain. In such an approach, we model a polymer mixture in a good solvent.75 The system is equilibrated during the 106 time steps Δt = 0.01. Once equilibrium is reached, the polymers are in a mixed state due to the size of the spherical confinement96 chosen so that segregation is avoided.
Next, in order to create a nanogel, we cross-link Nclinks pairs of monomers that belong to different polymer chains and are at a distance closer than a given threshold by a harmonic bond:
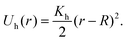 | (5) |
This potential has a minimum at particle distance r = R = σ, r is the elongation of the harmonic spring, and Kh = 10 is Hooke's spring constant that represents the rigidity of the matrix. These parameters, on the one hand, allow us to use a relatively large integration time step, obtaining sufficient statistics. On the other hand, they allow reproduction of experimentally observed structural properties.77
Finally, we delete the spherical confinement and equilibrate the obtained nanogel. Thus, the nanogel core is created. The properties of the nanogels were thoroughly investigated in ref. 93.
In order to create the shell, we choose Ksh outermost monomers of the core, i.e., the monomers that are the largest distance from the centre of mass of the core, and we attach a polymer chain consisting of Msh monomers using the FENE bond (4) to each outermost monomer. In order to study the influence of the shell on the nanogel size and shape, we used the same core for modelling, but we considered different shells by varying the number of polymers Ksh and the length of these polymers Msh comprising the shell. The values of the parameter Ksh are chosen so that when considering two core–shell nanogels with shell polymer lengths Msh = 10 and Msh = 20, the total number of monomers in the shell is the same. We investigated both cross-linked and non-cross-linked shells. To cross-link a shell, we use the same procedure as described above with the fraction of cross-linked monomers ψlinks = 2Nshlinks/Nsh, which is defined as a ratio of the number of cross-linked monomers in the shell to the total number of monomers Nsh = Msh·Ksh in the shell. Here, Nshlinks is the number of bonds between monomers in the shell that need to be created. The values of the parameters for the construction of the shell are summarised in Table 1.
| M sh | K sh | N sh | N shlinks | ψ links |
|---|---|---|---|---|
| 10 | 100 | 1000 | 10 | 0.02 |
| 20 | 50 | |||
| 10 | 100 | 1000 | 20 | 0.04 |
| 20 | 50 | |||
| 10 | 100 | 1000 | 30 | 0.06 |
| 20 | 50 | |||
| 10 | 100 | 1000 | 50 | 0.1 |
| 20 | 50 | |||
| 10 | 150 | 1500 | 10 | 0.013 |
| 20 | 75 | |||
| 10 | 150 | 1500 | 20 | 0.027 |
| 20 | 75 | |||
| 10 | 150 | 1500 | 30 | 0.04 |
| 20 | 75 | |||
| 10 | 150 | 1500 | 50 | 0.067 |
| 20 | 75 | |||
| 10 | 200 | 2000 | 10 | 0.01 |
| 20 | 100 | |||
| 10 | 200 | 2000 | 20 | 0.02 |
| 20 | 100 | |||
| 10 | 200 | 2000 | 30 | 0.03 |
| 20 | 100 | |||
| 10 | 200 | 2000 | 50 | 0.05 |
| 20 | 100 | |||
The procedure described above is shown schematically in Fig. 1. The core monomers are coloured blue, and the shell ones are coloured green. Black FENE springs indicate cross-linkers in the polymers. The centre of mass is indicated by a grey circle with an orange contour. The outermost monomers, circled blue in the diagram, lay on the surface of an orange sphere (here, a circle). To the latter monomers, the shell polymers are attached with yellow springs (classical harmonic potential). Cross-linking of core and shell polymers in this work is performed using the classical harmonic potential, which is represented in the diagram by magenta (for the core) and red (for the shell) springs.
2.3 Charged core–shell nanogel
In this work, along with good solvent conditions, we also study charged core–shell nanogels. In order to allow for weakly charged nanogels, we introduce the Yukawa potential:98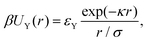 | (6) |
We consider three cases of charged nanogels with a core–shell morphology. First, when only the core of the nanogel is charged; second, when only the shell is charged; and the third case combines the first two ones, i.e., all particles in the nanogel are charged. It also turned out that if the shell is not cross-linked, the impact of electrostatics is rather weak, so we will present the data for nanogels with cross-linked shells only.
2.4 Magnetic core–shell nanogels
Finally, we consider two possible cases of filling the matrix with magnetic nanoparticles (MNPs). In the first case, a magnetic component is added only to the core. For that, we randomly replace 10% of the core monomers with magnetic ones. In the second case, along with the magnetic core, we consider the magnetic shell. Therefore, we additionally randomly replace 10% of the beads in the shell with magnetic ones.As mentioned above, magnetic particles have point dipoles at their centres, |![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) | = μ, and the pair of particles i and j interact via the magnetic dipole–dipole potential:
| = μ, and the pair of particles i and j interact via the magnetic dipole–dipole potential:
 | (7) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ij, as before, is the vector, connecting particle centres. This interaction can be characterised by the following parameter:
ij, as before, is the vector, connecting particle centres. This interaction can be characterised by the following parameter: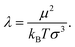 | (8) |
It shows the ratio between the magnetic energy of two dipoles in the “head-to-tail” configuration and the thermal energy. Long-range magnetostatic interactions are calculated with the dipolar P3M algorithm.99
It is worth noting that each nonmagnetic bead in the model represents a Kuhn segment, and, considering that the size of a polymer bead is the same as that of the magnetic nanoparticle, i.e., on the order of 20 nm, the characteristic size of the modelled nanogels is between 100 and 500 nm.
3 Main results
3.1 Neutral nanogels
Fig. 2 shows snapshots of core–shell nanogels with non-cross-linked shells and different shell lengths (Msh = 10 for Fig. 2(a), Msh = 20 for Fig. 2(b)). As can be seen, the obtained nanogels have a clear well-preserved core (blue particles) and a shell (green particles) around it. In Fig. 2(b), some long dangling shell chains can be seen that are not that apparent in Fig. 2(a). Otherwise, visual inspection reveals very minor differences.A quantitative analysis below, however, unveils a drastic impact of the shell polymer length on the structural characteristics of nanogels. Fig. 3 shows the asphericity, b = αz2 − (αx2 + αy2)/2 = (3αz2 − Rg2)/2 (where Rg is the gyration radius, and αx, αy, αz are the principal moments of the gyration tensor), of the core–shell nanogels in a good solvent with different fractions of cross-linked monomers ψlinks in the shell rescaled by the square of the gyration radius Rg2. Brown corresponds to nanogels with monomers Nsh = 1000 in the shell, purple is chosen for Nsh = 1500, and we use yellow for Nsh = 2000. In the figure, one can observe a slight increase in asphericity with an increase in the fraction of cross-linked particles.
Due to the fact that the core has no smooth spherical shape, the polymer chains used to model the shell were not uniformly distributed on the core surface. It leads to a slight shape deformation, especially if the shell has been built up by fewer polymers and these polymers were longer (compare Fig. 3(a) and (b)). Another interesting detail to mention is that the asphericity almost does not change with the number of cross-linkers in the shell. The largest difference in the asphericity observed of cross-linked and non-cross-linked nanogels does not exceed 1.5%. This confirms that the nanogel shape is mainly determined by its core and the grafting density of the shell polymers.
Similarly, a weak impact of ψlinks on the gyration radii can be observed in Fig. 3(c) and (d) showing the dependence of the ratio of the gyration radius of a cross-linked nanogel to the gyration radius of a non-cross-linked nanogel, Rlinksg/Rno_linksg, on the fraction of cross-linked shell monomers.
The curves decay slightly with growing ψlinks in the shell independently of the length Ksh. However, this difference between the gyration radii of the nanogel with the most cross-linked shell and the one with a non-cross-linked shell is small and does not reach even 1.5%, even in the case of the thicker shell (see Fig. 3(d)).
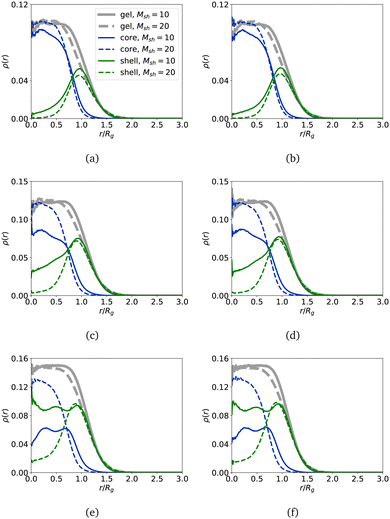
In order to verify that our core–shell nanogels preserve the structure meant by the model, we plot in Fig. 4 the density profiles, ρ(r), computed for the monomers comprising the core and the shell separately and compare them with the density profiles for the total structure where the core and shell monomers are not distinguished in the calculation. Here, r is the distance from the nanogel centre of mass and is normalised by Rg along the horizontal axis. The values of ρ for the shell composed of polymer chains of length Msh = 10 are plotted with solid curves and those of Msh = 20 with dashed ones. Here, in Fig. 4, grey represents all particles in the nanogel, blue represents particles in a core, and green represents particles in a shell. The first column corresponds to the results for nanogels with a non-cross-linked shell, and the second column is chosen for the cross-linked shell with parameter Nshlinks = 50. The shape of the density profile of the core resembles that of a regular nanogel with a plateau near the centre of mass and rapid decay toward the periphery. Regarding the density profile of the shell, it is convenient to look at the figures for Msh = 20 (dashed green curves) from top to bottom. This type of density profile in all figures has a pronounced peak at r ≈ Rg and smoothly decays toward both the centre of mass and the nanogel boundary. Moreover, the density of shell monomers near the centre of mass is around zero, and the density grows slightly for a larger number of polymers grafted to the core. This is a clear sign that a nanogel has a distinct shell around its core that is almost not penetrated by the shell. Indeed, the free volume available for a chain in the shell grows with the cube of the distance from the centre of mass. So, for a long chain, it is advantageous to loose some conformational entropy in the local vicinity of the core and extend further away, where it has enough space to assume equilibrium coiling. However, if the shell consists of shorter chains (Msh = 10, solid curves), one can note that for larger Ksh (the parameter Ksh increases when moving along the graphs from top to bottom), the density of the shell monomers continues to grow in the vicinity of the nanogel centre of mass. As mentioned above, the total number of monomers comprising the shell is equal regardless of the shell length Msh. Then, in the case of polymer chains of length Msh = 10, more polymers are used to build the shell on top of the core. The environment for short chains becomes very crowded, and the configurational entropy reduces significantly. Unlike long chains, short ones cannot extend out to gain free volume, so the more short polymers in the shell, the smaller the entropic gain for the polymers to stay outside of the core as the surrounding is crowded. With a change in its conformations, the core can accommodate a shell polymer chain inside, at least partially. Once the short chain enters the core, it remains there to avoid paying an entropic penalty to move cross the core boundary where the concentration of monomers and cross-linkers is the highest. This effect can be pushed to extremes: the density profile of the shell becomes higher than that of the core (see the blue and green solid curves in Fig. 4(e) and (f)). This is a clear sign that the polymers comprising the shell and the core are mixed, and the nanogel cannot be considered a core–shell nanogel anymore. Importantly, the density of cross-linkers in the shell should be very high to affect the density profiles, as the values used in this manuscript have basically no impact, not on the density profiles, nor on the gyration radii Fig. 3(d).
In Fig. 5, we plot how the core size changes, (Rcoreg − R0g)/R0g, with respect to the three parameters (Ksh, Msh and ψlinks) used to construct the shell on top of the original nanogel in a good solvent with gyration radius R0g.
In Fig. 5(a), for a shell with short polymer chains of length Msh = 10 and Ksh = 100, the core size decreases by 1%. However, the denser shells with Ksh = 150 and Ksh = 200 cause swelling of the core by 2% and 8%, respectively. Better cross-linked shells exhibit a lower swelling, but only by 1%. The swelling of the core in the case of short polymers in a shell is caused by the penetration of the shell monomers into the core.
In contrast, for core–shell nanogels with a shell composed of longer polymer chains (Fig. 5(b), Msh = 20), the construction of the shell causes significant core shrinkage, up to 11%. The density profiles confirm that the shell avoids penetrating the core. Cross-linking the shell facilitates shrinking by tightening the network around the core, but is not the primary factor. The key parameters are the polymer length in the shell and the number of these polymers attached to the core, resembling a shell grafting density, with caution due to the nonspherical core.
In summary, this section highlights that the most spherical shape is achieved with short chains and dense grafting. While cross-linking of the shell has a minimal impact, the morphology is significantly influenced by the density of the shell and the length of the chains. Short and dense shells benefit from entropy by blending into the core.
3.2 Charged nanogels
Fig. 6 shows nine snapshots of core–shell nanogels, εY = 4, eqn (6). We stick to the largest value of εY because the effects are more visible. As for the case of neutral nanogels, the core particles are blue and those of the shell are green. In the first row, all of the monomers are charged; in the second and third rows, respectively, the shell or the core remain charge neutral. Only in the last column is the shell cross-linked with Nshlinks = 50, otherwise, the gels with a non-cross-linked shell are shown. In the first column, the shell is made of long, Msh = 20, but not many, Ksh = 100 polymers. These snapshots (a), (d), and (f) can be compared with their counterparts (b), (e), and (h) where nanogels with shorter shell polymers, Msh = 10, but with the same grafting density are shown. In the last column, the cross-linked shell is made of rather dense and short polymers, Msh = 10, Ksh = 200. The same feature can be seen from all nine snapshots: the polymers with charged monomers tend to stretch significantly. For uniformly charged systems, both the core and the shell swell notably; if the shell is charge-neutral and the core is charged, the swelling of the core seems to free some space for the shell polymers to penetrate. Instead, the charge in the shell visually results in the decrease of the core size.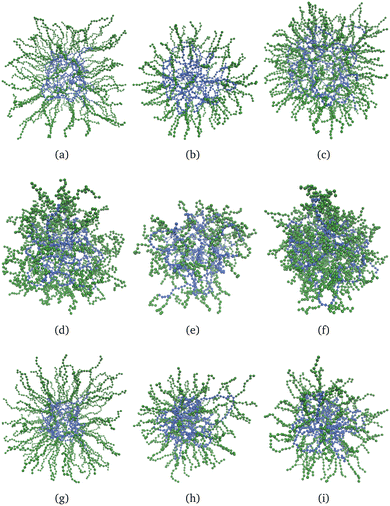 | ||
| Fig. 6 Snapshots of charged core–shell nanogels, εY = 4 in eqn (6); the core particles are blue, the shell – green: (a)–(c) all monomers in a nanogel are charged; (d)–(f) only the monomers in the core are charged; (g)–(i) only the monomers in the shell are charged. In the first two columns, (a), (d), (g), (b), (e) and (h), the nanogel shell is non-cross-linked, Nshlinks = 0. In the last column, (c), (f) and (i), Nshlinks = 50. In the first column, (a), (d) and (g), Msh = 20, Ksh = 100; in the second column, (b), (e) and (h), Msh = 10, Ksh = 100; in the third column, (c), (f) and (i), Msh = 10, Ksh = 200. | ||
In order to quantify the observations, in Fig. 7 we plot the density profiles of the monomers in different nanogels versus the distance from the nanogel centre of mass, normalised by Rg.
If the number of monomers in the shell is low, Nsh = 1000, and all or core-only monomers are charged, as shown in Fig. 7(a) and (c), respectively, the nanogel maintains its core–shell structure. The density profiles of the shell monomers, represented by green curves, are distinctly separate from the core monomers, depicted in blue. When all monomers are charged, as illustrated in Fig. 7(a), one can observe oscillations in the total (grey) and core (blue) density profiles within the core region. This behaviour indicates that the monomers in the core exhibit nearly periodic layering due to electrostatic repulsion. Similar oscillations in the profiles are visible in Fig. 7(b) for denser shells with Nsh = 2000. However, in this scenario, the distinction between core and shell monomers is less pronounced. Specifically, akin to uncharged nanogels, the core–shell structure almost disappears for short shell polymers, as evidenced by the green and blue solid lines, if comparing Fig. 7(d) to Fig. 7(c). Both subplots display density profiles for nanogels with charged cores and neutral shells. In cases where the shell is dense, it permeates the core. Notably, the comparison between charged and uncharged nanogels (Fig. 4(e) and 7(d)) indicates that the observed effects are primarily influenced by the size and concentration of the shell rather than the charges themselves. The presence of charges is evident in the profile oscillations, highlighting the more structured nature of charged nanogels compared to neutral ones. For Nsh = 1500, the qualitative effects remain the same, and the corresponding plots are included in the ESI.†
Fig. 7(e) and (f) illustrate the density profiles of nanogels featuring a charged shell. Among these profiles, only one nanogel stands out for maintaining a core–shell structure without exhibiting layering, which corresponds to the nanogel with the least amount (Ksh = 50) of long polymers (Msh = 20) in the shell (shown by the dashed curves in Fig. 7(e)). Nevertheless, unlike other cases, there is no plateau with a peak near the grafting surface; instead, the peak is noticeably shifted towards the nanogel's center of mass. Additionally, it is evident that the dashed blue and green curves intersect near this peak. The occurrence of layering while still maintaining the core–shell structure is observed in nanogels with Ksh = 100. Conversely, nanogels with Ksh = 200 short (Msh = 10) polymers in the shell completely lose their core–shell structure, as it becomes more favorable for the strongly repelling polymer chains to penetrate the core.
Since cross-linking of the shell does not lead to qualitative changes in the density profiles, below we focus exclusively on nanogels with a non-cross-linked shell. We also limit the results for the most dilute and dense cases, the data for Nsh = 1500 is plotted in the ESI.† Mixing of core and shell monomers is expected to cause relative changes in the gyration radii of the nanogel, RYukg, compared to the neutral counterparts, Rneutrg. In Fig. 8(a), (c) and (e), we analyse the relative changes in the gyration radius of the entire nanogel, (RYukg − Rneutrg)/Rneutrg (in percent), as a function of εY (plotted with filled symbols). In order to relate the total expansion of the nanogel to the extension of its core, in Fig. 8(b), (d) and (f), with open symbols, we plot the ratio (RYuk,cg − Rneutr,cg)/Rneutr,cg in percent, where RYuk,cg denotes the core gyration radius of a nanogel with at least some charged monomers, and Rneutr,cg is the radius of gyration of the core of a neutral nanogel with the same morphology. Here, in Fig. 8(a) and (b), the ratio is plotted for the nanogel, whose monomers are all charged; the plots in Fig. 8(c) and (d) are for nanogels with a charged core, and in Fig. 8(e) and (f) – for the nanogels with a charged shell. The yellow symbols are used for the Nsh = 2000 monomers in the shell, while the brown ones are for Nsh = 1000. With circles, we plotted the results for short polymers Msh = 10, and with squares – for Msh = 20. We plotted the eye-guiding lines for clarity and preserved the convention of Fig. 7, in which solid lines were used for Msh = 10, dashed lines – for Msh = 20, independently of the grafting density.
 | ||
| Fig. 8 (a), (c) and (e) Signed difference (RYukg − Rneutrg)/Rneutrgversus the charge repulsion strength εY; the gyration radii are calculated for the entire nanogels, filled symbols. (b), (d) and (f) Signed difference (RYuk,cg − Rneutr,cg)/Rneutr,cgversus the charge repulsion strength εY calculated for the gyration radii of the nanogel cores, open symbols. (a) and (b) All monomers in the nanogels are charged; (c) and (d) only monomers in the core are charged; (e) and (f) only monomers in the shell are charged. The colours help to distinguish the total number of monomers in the shell. Yellow colour: Nsh = 2000; brown colour: Nsh = 1000. The shape of the symbol is preserved for a fixed shell polymer length. Circles and solid lines: Msh = 10; squares and dashed lines: Msh = 20. The type of line (dashed or solid) is the same as in Fig. 7. | ||
As expected, for fully charged nanogels, we observe the strongest swelling with growing εY, Fig. 8(a) and (b). When comparing nanogels with the same Nsh, both the entire gel (Fig. 8(a)) and its core (Fig. 8(b)) show a stronger εY-dependent growth if the shell polymers are longer (squares are above circles of the corresponding colour). While the core swells more if the shell is denser (the yellow open symbols in Fig. 8(b), Nsh = 2000 are above the brown ones, Nsh = 1000), the relative increase in the gyration radius of the entire gel, whose low-density shell is made of long polymers, is slightly stronger than that of the nanogel with a denser shell, but shorter polymers (the brown squares, Nsh = 1000, Msh = 20, are above the yellow circles, Nsh = 2000, Msh = 10). This can be understood by looking at the density profiles plotted with dashed lines in Fig. 7(a) and solid lines in Fig. 7(b). In the first case, the shape of ρ(r) evidences a clear preservation of the morphology of the core and the shell, while the solid lines in Fig. 7(b) correspond to the penetration of the shell in the core with the highest density near the grafting surface. The latter peak causes a strong swelling of the core and offers extra space for the shell monomers. Instead, a preserved core–shell morphology allows the shell polymers to stretch more radially outward. This effect of Msh can be visually assessed when comparing the amount of green monomers inside the blue core in a characteristic conformation in Fig. 6(a), Msh = 20, to Fig. 6(b) and (c), Msh = 10.
The mixing between the core and the shell monomers for Nsh = 2000, Msh = 10, for the case of gels with a charged core only results in a smaller, but still very strong, εY-induced swelling, as seen in Fig. 8(c) and (d). Here, naturally, the core, Fig. 8(d), shows a stronger response to the growth of εY and can almost double its size compared to its neutral counterpart. Both Fig. 8(c) and (d) evidence that for the highest monomer density in the shell, the most structural change is expected from the gels with longer grafted polymers (yellow squares, Nsh = 2000, Msh = 20).
The same conclusion holds for Fig. 8(e) and (f), where we plot, respectively, the relative swelling of the entire nanogel and its core for the case of a neutral core and a charged shell. However, it is worth noting several unexpected findings. First, comparing the swelling of fully charged nanogels in Fig. 8(a) for the case of Nsh = 2000, Msh = 10 (yellow circles, solid lines), with the same results for the nanogel with a charged shell only, Fig. 8(e), we see almost no difference. For longer polymers and the same monomer density in the shell (yellow squares, dashed lines), the swelling is much higher if all monomers are charged. This means that for Nsh = 2000, Msh = 10, some of the shell monomers are seeking space in the core and because of electrostatic repulsion cause overall swelling. It is confirmed by appreciating the similarities between the relative swelling of the core for the nanogel with the charged shell (yellow open circles, solid line, Fig. 8(f)) and the analogous plot for a fully charged nanogel in Fig. 8(b). Longer chains in the shell, Nsh = 2000, Msh = 20, do not contribute much to the growth of RYuk,cg (yellow squares, Fig. 8(f)); instead, they stretch radially outward and lead to a significant growth of the total gyration radius of the nanogel. It is true even if the effects of εY on the core are minimal, as in the case of Nsh = 1000, Msh = 20 (brown open squares, dashed line, Fig. 8(f)): the overall Rg still grows significantly (brown filled squares, dashed line, Fig. 8(e)).
Summarising the findings of this part, we observe that charge-like repulsive interactions in a nanogel either between all monomers or selectively between monomers in the core or in the shell not only lead to an increase in the overall nanogel size but also facilitate the loss of the core–shell morphology, particularly if the shell polymers are short. The most pronounced mixing of the core and shell monomers occurs when only the core monomers are charged. Interestingly enough, even if only the shell monomers are charged, they partially penetrate into a neutral core and lead to its swelling with increasing repulsion strength. It is worth noting that the findings of this section are only applicable for weakly charged nanogels. The presence of explicit counterions in the case of highly charged polyelectrolyte nanogels could lead to a different swelling behaviour due to the modified osmotic equilibrium between the microgel and the surrounding solvent or particular recharging mechanisms,100–102 not reflected in our approach. Moreover, cross-linker connectivity affects swelling ratios. In particular, if connectivity is low, as in our work, only x-like cross-linking is possible, corresponding to connectivity four in the work,103 and a higher swelling is expected.
3.3 Magnetic nanogels
In Fig. 9 we present computer simulation snapshots of magnetic nanogels. There are two options: first, in Fig. 9, magnetic nanoparticles (MNPs), shown in red, can be found only in the core of a nanogel; second, see Fig. 9(b) and (d), MNPs are also in the shell and are coloured orange to distinguish them from the core MNPs.According to the results for neutral and charged gels described above, here we selected the most reliable core–shell-morphology-preserving candidates for computer simulations of magnetic nanogels. Therefore, for magnetic nanogels, we consider Msh = 10 and Msh = 20 with Ksh = 100.
As shown in Fig. 9, all MNGs do not exhibit special shape and/or stretching effects; instead they look similar to the neutral nanogels presented in Fig. 2. In order to verify whether the presence of MNPs alters the structure of a nanogel, in Fig. 10, density profiles ρ(r) are presented for different strengths of magnetic interactions. Here, we plot the results for Msh = 10 and Msh = 20 only for the case of MNPs being both in the core and in the shell, since the presence of particles in the shell did not affect the outcome, nor did the value of the magnetic interactions (for more information, check the ESI†).
Comparing Fig. 10(a) with the solid lines in Fig. 4(a), or Fig. 10(b) to the dashed lines in Fig. 4(e), we can conclude that density profiles are not affected at all by the presence of strongly interacting MNPs, at least at the concentration studied here.
Not only are the shape of a nanogel and the monomer distribution in it robust to the addition of MNPs, the size of the gel remains basically unchanged compared to its neutral counterparts, as evidenced in Table 2, where the difference between the gyration radii (Rmagng − Rneutrg)/Rneutrg is collected for systems with different shell polymer lengths, Msh, different locations of magnetic particles in the core–shell nanogel, and different values of the parameter λ. One can see that the difference is negative, but it barely exceeds one percent. In fact, without an applied magnetic field, even if magnetic particles aggregate and deform the polymer matrix locally, the effects are averaging out in contrast to the isotropically repulsive Yukawa case.
| M sh | Location of magnetic particles | λ = 3 | λ = 5 | λ = 6 |
|---|---|---|---|---|
| 10 | Core | −0.2 | −0.7 | −1.3 |
| Core and shell | −0.1 | −0.5 | −0.8 | |
| 20 | Core | −0.4 | −0.9 | −1.1 |
| Core and shell | −0.4 | −0.4 | −0.3 |
At this point, the question arises whether MNPs have any impact on the nanogels’ behaviour at all, or if the studied experimentally available concentration46,104 of MNPs is too low. In Table 3, we collect the values of the magnetic initial susceptibility, χ0, of the nanogels for different MNGs. The values were obtained by using the fluctuation–dissipation theorem:
 | (9) |
![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) tot is the total magnetic dipole moment of the system, 〈·〉av means averaging over all magnetic particles, and V is the MNG volume, calculated using the mean distance to the surface from the centre of mass as a radius. The initial susceptibility shows how strongly a MNG can respond to an applied magnetic field, i.e., the values of χ0 define the initial slopes of the system magnetisation curves. Here, the effects of the MNPs are evident. The initial susceptibility has a maximum, which occurs at the value of the dipole–dipole magnetic interaction parameter, λ = 5, independently of the MNG morphology.
tot is the total magnetic dipole moment of the system, 〈·〉av means averaging over all magnetic particles, and V is the MNG volume, calculated using the mean distance to the surface from the centre of mass as a radius. The initial susceptibility shows how strongly a MNG can respond to an applied magnetic field, i.e., the values of χ0 define the initial slopes of the system magnetisation curves. Here, the effects of the MNPs are evident. The initial susceptibility has a maximum, which occurs at the value of the dipole–dipole magnetic interaction parameter, λ = 5, independently of the MNG morphology.
| M sh | Location of magnetic particles | λ = 3 | λ = 5 | λ = 6 |
|---|---|---|---|---|
| 10 | Core | 0.04 | 0.06 | 0.04 |
| Core and shell | 0.06 | 0.13 | 0.05 | |
| 20 | Core | 0.06 | 0.06 | 0.04 |
| Core and shell | 0.12 | 0.14 | 0.03 |
Although the initial growth of χ0 with λ is related to the formation of highly magnetoresponsive chain-like clusters, the presence of a maximum is associated with the formation of rings or other magnetic-flux-closing structures with zero net magnetic moment. The presence of such aggregates in the system leads to an effective reduction in the magnetically active fraction of particles when the temperature and density of the magnetic particles are low.105 In terms of the coupling parameter, λ, in liquid carriers, one can roughly distinguish between homogeneous particle distribution for λ < 2, chaining for 2 < λ < 5, and clusters with magnetic flux closure for λ > 6, as shown by various studies.106–109
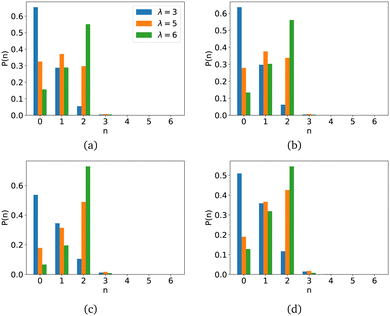
In order to verify that the polymer matrix does not fully block the formation of MNP clusters, we calculated the average probabilities for a MNP to have n magnetic neighbours, P(n). The results are presented in Fig. 11.
The blue colour in Fig. 11 corresponds to nanogels with parameter λ = 3, orange is selected for parameter λ = 5, and green is used for parameter λ = 6. The first row (Fig. 11(a) and (b)) of the figures corresponds to the shell polymer length Msh = 10, and the results for another length, Msh = 20, can be found in the figures in the second row (Fig. 11(c) and (d)). Figures in the first column (Fig. 11(a) and (c)) are constructed for nanogels with a magnetic core only, while those in the second column (Fig. 11(b) and (d)) are for nanogels with a magnetic core and shell. As can be seen, for systems with a weak magnetic interaction, cluster formation is unlikely, and most magnetic particles do not have magnetic neighbours; the highest values of P(n) are found for n = 0. With an increase in the intensity of magnetic interactions, an increase in the number of magnetic neighbours can be noted. These are orange and green. It can also be noted that an increase in the length of the polymers in the shell also promotes cluster formation, since the number of magnetic neighbours in the system increases. Note that for λ = 6, the highest probability is found at n = 2, namely, the particles are likely to have two neighbours, like those in rings, particularly considering that the number of particles having only one neighbour – a free end for λ = 6 – is smaller than for lower intensities of magnetic interaction.110
To summarise this section, one can say that for the MNPs to change the size of the MNGs, one needs a much higher concentration as studied here. In this case, magnetic dipole–dipole interactions between particles are expected to make MNGs more compact with respect to neutral nanogels.83 Our results also suggest that taking into account the magnetic dipole–dipole interaction does not lead to perturbations in the core–shell structure or in the monomer distribution. At the same time, even for the concentration of MNPs studied here, we observed the changes in the magnetic response. Moreover, a longer shell provides more possibilities for MNPs to rearrange into more energetically advantageous configurations, this way enhancing or impeding the magnetic response depending on λ.
4 Conclusions
We utilised molecular dynamics simulations to explore the influence of the core–shell morphology on the structural characteristics of nanogels. We examined three distinct types of nanogels, distinguished by their inter-monomer interactions: those with excluded volume only (neutral nanogels); those with charged monomers and excluded volume (charged nanogels); and those with excluded volume combined with a certain number of magnetic nanoparticles incorporated within the nanogel (magnetic nanogels). While keeping the core structure and size constant, we varied the length of the grafted polymers forming the shell, their density, and method of shell cross-linking.Our analysis of neutral nanogels revealed notable trends. In particular, we observed that nanogels with short chains and dense grafting exhibited the most spherical shape. Although the cross-linking of the shell had minimal influence, significant alterations in morphology were primarily driven by the density of the shell and the length of the chain. In particular, short, dense shells experienced entropic benefits from mingling into the core.
With respect to charged nanogels, repulsive interactions within the nanogel, whether among all monomers or selectively between core or shell constituents, not only enlarged the overall nanogel size but also instigated the loss of core–shell morphology, particularly evident with shorter shell polymers. Moreover, the most pronounced intermixing of core and shell monomers was observed when the core constituents were charged solely. Intriguingly, even if only the shell monomers possessed charges, they exhibited partial penetration into a neutral core, leading to its swelling with increasing repulsion strength.
In the realm of magnetic nanogels, our study illustrated that consideration of magnetic dipole–dipole interactions did not disrupt the core–shell architecture or monomer distribution, at least within the examined concentration range. Nevertheless, even a modest quantity of magnetic nanoparticles, particularly when encased within longer polymer shells, wielded significant influence over the nanogel magnetic response.
In general, the versatility and tunability demonstrated by nanogels in response to structural modifications pave the way for innovative solutions in drug delivery, tissue engineering, diagnostics, and beyond. Continued research in this area promises to unlock further potential and catalyse the development of novel nanogel-based technologies with diverse applications in biomedical and materials science domains. In particular, at the moment we are investigating how the morphology of a nanogel impacts its encapsulating and elastic properties.
List of notations
![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) i
i
| The force acting on the ith particle |
![[small tau, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1ca.gif) i
i
| The torque (pertaining to magnetic particles only) acting on the ith particle |
| M i | The mass of the ith particle |
| I i | The inertia of the ith particle |
![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) i
i
| The velocity of the ith particle |
![[small omega, Greek, vector]](https://www.rsc.org/images/entities/i_char_e13e.gif) i
i
| The angular velocity of the ith particle |
| Γ T | The translational friction coefficient |
| Γ R | The rotational friction coefficient |
![[small xi, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1cd.gif) T
i
T
i
| The random force acting on the ith particle |
![[small xi, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1cd.gif) R
i
R
i
| The random torque acting on the ith particle |
| σ | The particle diameter |
| m | The particle mass |
![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif)
| The particle magnetic moment vector |
| μ | The length of the particle magnetic moment vector |
| r | The distance |
| r* | The dimensionless distance in computer simulations |
![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) e
e
| The experimentally measured magnetic moment |
| ε | The energy scale of the Lennard-Jones potential |
| k B | The Boltzmann constant |
| T | The temperature |
| T* | The dimensionless temperature |
| t | The time |
| t* | The dimensionless time |
| Δt | The time step |
| M c | The number of monomers making up the polymers in the core |
| U WCA(i,j) | The Weeks–Chandler–Andersen (WCA) potential between ith and jth particles |
| r cut | The cutoff distance for the Weeks–Chandler–Andersen potential |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ij
ij
| The vector connecting the centres of ith and jth particles |
| U FENE(r) | The FENE (Finitely Extensible Nonlinear Elastic Model) potential |
| K FENE | The prefactor for the FENE potential |
| Δrmax | The maximal stretching for the FENE potential |
| r 0 | The equilibrium bond length for the FENE potential |
| N clinks | The number of cross-linked pairs of monomers in the core |
| U h(r) | The classical harmonic potential |
| K h | The Hooke's spring constant |
| R | The equilibrium bond length for the harmonic potential |
| K sh | The number of polymers in the shell |
| M sh | The length of polymers in the shell |
| ψ links | The fraction of cross-linked monomers in the shell |
| N shlinks | The number of bonds between monomers in the shell |
| N sh | The total number of monomers in the shell |
| U Y(r) | The Yukawa potential |
| κ | The inverse screening length for the Yukawa potential |
| ε Y | The strength of the Yukawa potential |
| U dd(i,j) | The magnetic dipole–dipole potential between ith and jth particles |
| λ | The magnetic dipole–dipole interaction parameter |
| R g | The gyration radius |
| b | The asphericity |
| α x , αy, αz | The principal moments of the gyration tensor |
| R linksg | The gyration radius of a core–shell nanogel with a cross-linked shell |
| R no_linksg | The gyration radius of a core–shell nanogel with a non-cross-linked shell |
| R coreg | The gyration radius of the core of a core–shell nanogel |
| R 0g | The gyration radius of the original nanogel |
| R neutrg | The gyration radius of a neutral core–shell nanogel |
| R Yukg | The gyration radius of a charged core–shell nanogel |
| R neutr,cg | The gyration radius of the core of a neutral core–shell nanogel |
| R Yuk,cg | The gyration radius of the core of a charged core–shell nanogel |
| R magng | The gyration radius of a magnetic core–shell nanogel |
| χ 0 | The magnetic initial susceptibility |
![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) tot
tot
| The total magnetic dipole moment of the system |
| 〈·〉av | Averaging over all magnetic particles |
| V | The magnetic nanogel volume |
| P(n) | The average probability for a magnetic nanoparticle to have n magnetic neighbours |
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The research was supported by the Russian Science Foundation (project 19-72-10033). Computer simulations were performed at the Vienna Scientific Cluster and the Ural Federal University cluster.Notes and references
- T. Hoare and R. Pelton, Macromolecules, 2004, 37, 2544–2550 CrossRef CAS.
- J. Yin, D. Dupin, J. Li, S. P. Armes and S. Liu, Langmuir, 2008, 24, 9334–9340 CrossRef CAS.
- K. Bayliss, J. S. van Duijneveldt, M. A. Faers and A. W. P. Vermeer, Soft Matter, 2011, 7, 10345–10352 RSC.
- A. Fernandez-Nieve, H. M. Wyss, J. Mattsson and D. A. Weitz, Microgels in Drug Delivery, Wiley-VCH Verlag GmbH & Co. KGaA, 2011 Search PubMed.
- T. Colla, C. N. Likos and Y. Levin, J. Chem. Phys., 2014, 141, 234902 CrossRef.
- N. Gnan, L. Rovigatti, M. Bergman and E. Zaccarelli, Macromolecules, 2017, 50, 8777–8786 CrossRef CAS.
- J. Retama, B. Lopez-Ruiz and E. Lopez-Cabarcos, Biomaterials, 2003, 24, 2965–2973 CrossRef CAS PubMed.
- Z. Guo, H. Sautereau and D. E. Kranbuehl, Macromolecules, 2005, 38, 7992–7999 CrossRef CAS.
- Y. Liu, Y.-M. Wang, S. Sedano, Q. Jiang, Y. Duan, W. Shen, J.-H. Jiang and W. Zhong, Chem. Commun., 2018, 54, 4329–4332 RSC.
- C. Wu, T. Chen, D. Han, M. You, L. Peng, S. Cansiz, G. Zhu, C. Li, X. Xiong, E. Jimenez, C. J. Yang and W. Tan, ACS Nano, 2013, 7, 5724–5731 CrossRef CAS PubMed.
- V. C. Lopez, J. Hadgraft and M. Snowden, Int. J. Pharm., 2005, 292, 137–147 CrossRef CAS PubMed.
- J. A. Bonham, M. A. Faers and J. S. van Duijneveldt, Soft Matter, 2014, 10, 9384–9398 RSC.
- M. Molina, M. Asadian-Birjand, J. Balach, J. Bergueiro, E. Miceli and M. Calderón, Chem. Soc. Rev., 2015, 44, 6161–6186 RSC.
- S. Seiffert, Angew. Chem., Int. Ed., 2013, 52, 11462–11468 CrossRef CAS PubMed.
- Y. Lu and M. Ballauff, Prog. Polym. Sci., 2011, 36, 767–792 CrossRef CAS.
- D. J. McClements, Adv. Colloid Interface Sci., 2017, 240, 31–59 CrossRef CAS.
- M. Zhalechin, S. M. Dehaghi, M. Najafi and A. Moghimi, Heliyon, 2021, 7(5), E06652 CrossRef CAS.
- Q. Yang, K. Wang, J. Nie, B. Du and G. Tang, Biomacromolecules, 2014, 15, 2285–2293 CrossRef CAS PubMed.
- E. M. Ahmed, J. Adv. Res., 2015, 6, 105–121 CrossRef CAS PubMed.
- Y. Gao, J. Xie, H. Chen, S. Gu, R. Zhao, J. Shao and L. Jia, Biotechnol. Adv., 2014, 32, 761–777 CrossRef CAS PubMed.
- M. Asadian-Birjand, A. Sousa-Herves, D. Steinhilber, J. C. Cuggino and M. Calderón, Curr. Med. Chem., 2012, 19, 5029–5043 CrossRef CAS.
- J. Wang, D. Gan, L. A. Lyon and M. A. El-Sayed, J. Am. Chem. Soc., 2001, 123, 11284–11289 CrossRef CAS PubMed.
- C. E. Reese, A. V. Mikhonin, M. Kamenjicki, A. Tikhonov and S. A. Asher, J. Am. Chem. Soc., 2004, 126, 1493–1496 CrossRef CAS.
- R. Pelton and P. Chibante, Colloids Surf., 1986, 20, 247–256 CrossRef CAS.
- G. Liu, X. Wang, F. Zhou and W. Liu, ACS Appl. Mater. Interfaces, 2013, 5, 10842–10852 CrossRef CAS PubMed.
- Z. Cao, X. Zhou and G. Wang, ACS Appl. Mater. Interfaces, 2016, 8, 28888–28896 CrossRef CAS.
- Y. Shao, W. Huang, C. Shi, S. T. Atkinson and J. Luo, Ther. Delivery, 2012, 3, 1409–1427 CrossRef CAS PubMed.
- H. Wei, R.-X. Zhuo and X.-Z. Zhang, Prog. Polym. Sci., 2013, 38, 503–535 CrossRef CAS.
- D. R. Lynch and S. H. Snyder, Annu. Rev. Biochem., 1986, 55, 773–799 CrossRef CAS PubMed.
- C. Coll, A. Bernardos, R. Martínez-Máñez and F. Sancenón, Acc. Chem. Res., 2013, 46, 339–349 CrossRef CAS.
- S. Ganta, H. Devalapally, A. Shahiwala and M. Amiji, J. Controlled Release, 2008, 126, 187–204 CrossRef CAS.
- A. Balaceanu, V. Mayorga, W. Lin, M.-P. Schürings, D. E. Demco, A. Böker, M. A. Winnik and A. Pich, Colloid Polym. Sci., 2013, 291, 21–31 CrossRef CAS.
- M. A. C. Stuart, W. T. S. Huck, J. Genzer, M. Müller, C. Ober, M. Stamm, G. B. Sukhorukov, I. Szleifer, V. V. Tsukruk, M. Urban, F. Winnik, S. Zauscher, I. Luzinov and S. Minko, Nat. Mater., 2010, 9, 101–113 CrossRef PubMed.
- A. Chan, R. P. Orme, R. A. Fricker and P. Roach, Adv. Drug Delivery Rev., 2013, 65, 497–514 CrossRef CAS PubMed.
- S. Lal, S. E. Clare and N. J. Halas, Acc. Chem. Res., 2008, 41, 1842–1851 CrossRef CAS.
- A. M. Alkilany, S. E. Lohse and C. J. Murphy, Acc. Chem. Res., 2013, 46, 650–661 CrossRef CAS.
- M. Marguet, C. Bonduelle and S. Lecommandoux, Chem. Soc. Rev., 2013, 42, 512–529 RSC.
- T.-Y. Liu, S.-H. Hu, D.-M. Liu, S.-Y. Chen and I.-W. Chen, Nano Today, 2009, 4, 52–65 CrossRef CAS.
- S. Mornet, S. Vasseur, F. Grasset, P. Veverka, G. Goglio, A. Demourgues, J. Portier, E. Pollert and E. Duguet, Prog. Solid State Chem., 2006, 34, 237–247 CrossRef CAS.
- Y. Wang, L. Wang, M. Yan, S. Dong and J. Hao, ACS Appl. Mater. Interfaces, 2017, 9, 28185–28194 CrossRef CAS PubMed.
- A. Schroeder, J. Kost and Y. Barenholz, Chem. Phys. Lipids, 2009, 162, 1–16 CrossRef CAS PubMed.
- Y.-Z. Zhao, L.-N. Du, C.-T. Lu, Y. Jin and S.-P. Ge, Int. J. Nanomed., 2013, 8, 1621–1633 Search PubMed.
- T.-Y. Liu, M.-Y. Wu, M.-H. Lin and F.-Y. Yang, Acta Biomater., 2013, 9, 5453–5463 CrossRef CAS.
- L. He, R. Zheng, J. Min, F. Lu, C. Wu, Y. Zhi, S. Shan and H. Su, J. Magn. Magn. Mater., 2021, 517, 167394 CrossRef CAS.
- C. A. Dreiss, Curr. Opin. Colloid Interface Sci., 2020, 48, 1–17 CrossRef CAS.
- M. U. Witt, S. Hinrichs, N. Möller, S. Backes, B. Fischer and R. V. Klitzing, J. Phys. Chem. B, 2019, 123, 2405–2413 CrossRef CAS PubMed.
- Y. Kim and X. Zhao, Chem. Rev., 2022, 122, 5317–5364 CrossRef CAS PubMed.
- A. D. Ellington and J. W. Szostak, Nature, 1990, 346, 818–822 CrossRef CAS.
- J. Liu, Z. Cao and Y. Lu, Chem. Rev., 2009, 109, 1948–1998 CrossRef CAS.
- Y. Wang, M. Yan, L. Xu, W. Zhao, X. Wang, S. Dong and J. Hao, J. Mater. Chem. B, 2016, 4, 5446–5454 RSC.
- C. Wu, D. Han, T. Chen, L. Peng, G. Zhu, M. You, L. Qiu, K. Sefah, X. Zhang and W. Tan, J. Am. Chem. Soc., 2013, 135, 18644–18650 CrossRef CAS PubMed.
- H. A. Kim, K. Nam and S. W. Kim, Biomaterials, 2014, 35, 7543–7552 CrossRef CAS PubMed.
- X. Zhang, S. Yao, C. Liu and Y. Jiang, Biomaterials, 2015, 39, 269–281 CrossRef CAS.
- N. Schleich, C. Po, D. Jacobs, B. Ucakar, B. Gallez, F. Danhier and V. Préat, J. Controlled Release, 2014, 194, 82–91 CrossRef CAS.
- J. C. Rose, D. B. Gehlen, T. Haraszti, J. Köhler, C. J. Licht and L. De Laporte, Biomaterials, 2018, 163, 128–141 CrossRef CAS.
- D. J. Kim, T. Y. Jeon, Y.-K. Baek, D.-H. K. Sung-Gyu Park and S.-H. Kim, Chem. Mater., 2016, 28, 1559–1565 CrossRef CAS.
- M. Zhou, J. Xie, S. Yan, X. Jiang, T. Ye and W. Wu, Macromolecules, 2014, 47, 6055–6066 CrossRef CAS.
- R. Ma and L. Shi, Polym. Chem., 2014, 5, 1503–1518 RSC.
- A. Pardo, M. Gómez-Florit, S. Barbosa, P. Taboada, R. M. A. Domingues and M. E. Gomes, ACS Nano, 2021, 15, 175–209 CrossRef CAS.
- B. Sung, M. H. Kim and L. Abelmann, Bioeng. Transl. Med., 2021, 6, e10190 CrossRef CAS PubMed.
- A. Seyfoori, S. A. Seyyed Ebrahimi, A. Yousefi and M. Akbari, Biomater. Sci., 2019, 7, 3359–3372 RSC.
- S. R. S. Veloso, E. Tiryaki, C. Spuch, L. Hilliou, C. O. Amorim, V. S. Amaral, P. J. G. Coutinho, P. M. T. Ferreira, V. Salgueiriño, M. A. Correa-Duarte and E. M. S. Castanheira, Nanoscale, 2022, 14, 5488–5500 RSC.
- A. Seyfoori, S. A. Seyyed Ebrahimi, M. Samandari, E. Samiei, E. Stefanek, C. Garnis and M. Akbari, Small, 2023, 19, e2205320 CrossRef.
- M. Quesada-Pérez and A. Martín-Molina, Soft Matter, 2013, 9, 7086–7094 RSC.
- A. Ghavami, H. Kobayashi and R. G. Winkler, J. Chem. Phys., 2016, 145, 244902 CrossRef.
- S. Ahualli, A. Martín-Molina, J. A. Maroto-Centeno and M. Quesada-Pérez, Macromolecules, 2017, 50, 2229–2238 CrossRef CAS.
- D. Sean, J. Landsgesell and C. Holm, Gels, 2018, 4(1), 2 CrossRef.
- M. Quesada-Pérez, J. A. Maroto-Centeno, A. Martín-Molina and A. Moncho-Jordá, Phys. Rev. E, 2018, 97, 042608 CrossRef.
- H. Kobayashi, R. Halver, G. Sutmann and R. G. Winkler, Polymers, 2017, 9(1), 15 CrossRef PubMed.
- L. Rovigatti, N. Gnan and E. Zaccarelli, J. Phys.: Condens. Matter, 2018, 30, 044001 CrossRef PubMed.
- C. Hofzumahaus, P. Hebbeker and S. Schneider, Soft Matter, 2018, 14(20), 4087–4100 RSC.
- A. Martín-Molina and M. Quesada-Pérez, J. Mol. Liq., 2019, 280, 374–381 CrossRef.
- M. Formanek and A. J. Moreno, Soft Matter, 2021, 17, 2223–2233 RSC.
- M. M. D. R. Veniero Lenzi and L. S. A. Marques, Mol. Simul., 2021, 47, 27–36 CrossRef.
- G. S. Grest and K. Kremer, Phys. Rev. A: At., Mol., Opt. Phys., 1986, 33, 3628–3631 CrossRef CAS.
- A. Chremos, J. F. Douglas, P. J. Basser and F. Horkay, Soft Matter, 2022, 18, 6278–6290 RSC.
- E. Minina, P. Sánchez, C. Likos and S. Kantorovich, J. Magn. Magn. Mater., 2018, 459, 226–230 CrossRef CAS.
- L. Rovigatti, N. Gnan, A. Ninarello and E. Zaccarelli, Macromolecules, 2019, 52, 4895–4906 CrossRef CAS.
- L. Athanasopoulou and P. Ziherl, Soft Matter, 2017, 13, 1463–1471 RSC.
- M. J. Bergman, S. Nöjd, P. S. Mohanty, N. Boon, J. N. Immink, J. J. E. Maris, J. Stenhammar and P. Schurtenberger, Soft Matter, 2021, 17, 10063–10072 RSC.
- G. Del Monte, F. Camerin, A. Ninarello, N. Gnan, L. Rovigatti and E. Zaccarelli, J. Phys.: Condens. Matter, 2021, 33, 084001 CrossRef CAS PubMed.
- L. Pérez-Mas, A. Martín-Molina and M. Quesada-Pérez, Soft Matter, 2020, 16, 3022–3028 RSC.
- I. S. Novikau, E. V. Novak, E. S. Pyanzina and S. S. Kantorovich, J. Mol. Liq., 2022, 346, 118056 CrossRef CAS.
- R. Weeber, P. Kreissl and C. Holm, Phys. Sci. Rev., 2023, 8, 1465–1486 Search PubMed.
- N. P. Kryuchkov, F. Smallenburg, A. V. Ivlev, S. O. Yurchenko and H. Löwen, J. Chem. Phys., 2019, 150, 104903 CrossRef PubMed.
- I. Berndt, J. S. Pedersen and W. Richtering, J. Am. Chem. Soc., 2005, 127, 9372–9373 CrossRef CAS PubMed.
- K. Geisel, A. Rudov, I. I. Potemkin and W. Richtering, Langmuir, 2015, 31, 13145–13154 CrossRef CAS PubMed.
- N. Barooah, J. Mohanty and A. Bhasikuttan, Langmuir, 2022, 38, 6249–6264 CrossRef CAS.
- J. E. Lennard-Jones, Proc. R. Soc. London, Ser. A, 1924, 106, 441–462 Search PubMed.
- H. J. Limbach, A. Arnold, B. A. Mann and C. Holm, Comput. Phys. Commun., 2006, 174, 704–727 CrossRef CAS.
- A. Arnold, O. Lenz, S. Kesselheim, R. Weeber, F. Fahrenberger, D. Roehm, P. Košovan and C. Holm, in Meshfree Methods for Partial Differential Equations VI, Springer, Berlin, Heidelberg, 2013, vol. 89, pp. 1–23 Search PubMed.
- W. C. Swope, H. C. Andersen, P. H. Berens and K. R. Wilson, J. Chem. Phys., 1982, 76, 637–649 CrossRef CAS.
- E. S. Minina, P. A. Sánchez, C. N. Likos and S. S. Kantorovich, J. Mol. Liq., 2019, 289, 111066 CrossRef.
- J. D. Weeks, D. Chandler and H. C. Andersen, J. Chem. Phys., 1971, 54, 5237–5247 CrossRef CAS.
- K. Kremer and G. S. Grest, J. Chem. Phys., 1990, 92, 5057–5086 CrossRef CAS.
- S. Jun, A. Arnold and B.-Y. Ha, Phys. Rev. Lett., 2007, 98, 128303 CrossRef.
- J.-C. An, A. Weaver, B. Kim, A. Barkatt, D. Poster, W. N. Vreeland, J. Silverman and M. Al-Sheikhly, Polymer, 2011, 52, 5746–5755 CrossRef CAS.
- H. Yukawa, Proc. Phys.-Math. Soc. Jpn., 1935, 17, 48–57 Search PubMed.
- J. J. Cerdà, V. Ballenegger, O. Lenz and C. Holm, J. Chem. Phys., 2008, 129, 234104 CrossRef.
- D. Jia and M. Muthukumar, Gels, 2021, 7, 49 CrossRef CAS.
- J. Landsgesell, D. Beyer, P. Hebbeker, P. Košovan and C. Holm, Macromolecules, 2022, 55, 3176–3188 CrossRef CAS.
- B. Zheng, Y. Avni, D. Andelman and R. Podgornik, Macromolecules, 2023, 56, 5217–5224 CrossRef CAS.
- L. G. Rizzi and Y. Levin, J. Chem. Phys., 2016, 144, 114903 CrossRef CAS PubMed.
- T. Kyrey, J. Witte, A. Feoktystov, V. Pipich, B. Wu, S. Pasini, A. Radulescu, M. U. Witt, M. Kruteva, R. von Klitzing, S. Wellert and O. Holderer, Soft Matter, 2019, 15, 6536–6546 RSC.
- S. Kantorovich, A. O. Ivanov, L. Rovigatti, J. M. Tavares and F. Sciortino, Phys. Rev. Lett., 2013, 110, 148306 CrossRef PubMed.
- R. van Roij, Phys. Rev. Lett., 1996, 76, 3348–3351 CrossRef CAS.
- Y. Levin, Phys. Rev. Lett., 1999, 83, 1159–1162 CrossRef CAS.
- Y. Levin, P. S. Kuhna and M. C. Barbosaa, Physica A, 2001, 292, 129–136 CrossRef CAS.
- S. S. Kantorovich, A. O. Ivanov, L. Rovigatti, J. M. Tavares and F. Sciortino, Phys. Chem. Chem. Phys., 2015, 17, 16601–16608 RSC.
- P. A. Sánchez, E. S. Pyanzina, E. V. Novak, J. J. Cerdà, T. Sintes and S. S. Kantorovich, Macromolecules, 2015, 48, 7658–7669 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00450g |
| This journal is © The Royal Society of Chemistry 2024 |