Tuning the optoelectronic properties of emerging solar absorbers through cation disorder engineering

Abstract

Chalcogenide solar absorbers, such as AgBiS₂ and kesterites, have gained a resurgence of interest recently, owing to their high stability compared to metal–halide compounds, as well as their rising efficiencies in photovoltaic devices. Although their optical and electronic properties are conventionally tuned through the composition and structure, cation disorder has increased in prominence as another important parameter that influences these properties. In this minireview, we define cation disorder as the occupation of a cation crystallographic site with different species, and the homogeneity of this cation disorder as how regular the alternation of species in this site is. We show that cation disorder is not necessarily detrimental, and can lead to increases in absorption coefficient and reductions in bandgap, enabling the development of ultrathin solar absorbers for lightweight photovoltaics. Focusing on kesterites and ABZ₂ materials (where A = monovalent cation, B = divalent cation, and Z is a chalcogenide anion), we discuss how the degree and homogeneity of cation disorder influences the optical properties, charge-carrier transport and photovoltaic performance of these materials, as well as how cation disorder could be tuned and quantified. We finish with our perspectives on the important questions moving forward in making use of cation disorder engineering as a route to achieve more efficient solar absorbers.

---

Yi-Teng Huang

Yi-Teng Huang is currently a postdoctoral researcher at Department of Chemistry of University of Oxford, under the supervision of Prof. Robert Hoye. He completed his PhD in Physics at University of Cambridge (2019–2023) before joining Prof. Robert Hoye's group at Oxford. His research interests include understanding the mechanism behind defect tolerance, cation disorder, charge-carrier phonon coupling, and developing optoelectronic devices based on novel semiconductors.

Robert L. Z. Hoye

Robert L. Z. Hoye is an Associate Professor at the University of Oxford. He completed his PhD at the University of Cambridge (2012–2014), followed by a postdoc at MIT (2015–2016), and two College Research Fellowships at the University of Cambridge (2016–2020). He began his independent academic career at the University of Cambridge with a Royal Academy of Engineering (RAEng) Research Fellowship (2018–2019), followed by a Lectureship (2020–2022) and Senior Lectureship (2022) at Imperial College London, before moving to the University of Oxford as Associate Professor (2022−present). He leads a group working on developing optoelectronic materials for energy harvesting and conversion, light emission and radiation detection.

---

1. Introduction

Discovering solar absorbers that are simultaneously efficient, cost-effective, stable, scalable, and comprised of nontoxic, earth-abundant elements, has long been the overarching goal of the thin film photovoltaics (PVs) community.^1–3 These emerging solar absorbers are important not only for single-junction outdoor PVs, but also as the bottom- or top-cell for multi-junction devices,^4,5 devices to harvest energy from indoor lighting to more sustainably power Internet of Things electronics,^6,7 as well as building-integrated PVs and agrivoltaics.⁸ As such, these materials have significant potential to fulfil energy harvesting requirements that are complementary to the capabilities of crystalline silicon PVs, and many of the compounds investigated are inorganic materials, including kesterites,^9–11 chalcopyrites,^12–14 chalcogenides,^15–17 chalcohalides^18–20 and metal–halide perovskites.^21–23 Historically, efforts at discovering these materials have focussed on the optical properties of the solar absorbers, namely bandgap and absorption coefficient.³ More recently, charge-carrier transport has taken on a much more prominent role in materials discovery than before, especially to account for the effects of defect states and carrier localization, which have limited the potential of many emerging materials.^24–27

A key property that influences these optoelectronic properties is cation disorder. Disorder has long been a prominent and common feature²⁸ in inorganic compounds. Although the links between the transport of charge-carriers and phonons with cation disorder has been widely studied in the thermoelectrics field,^29,30 such effects have either not been widely considered in emerging inorganic solar absorbers, or have typically been thought to be detrimental. Recent work on AgBiS₂ and related materials have shown that this is not necessarily the case, and processing the samples to achieve a homogeneous arrangement of cations occupying the same crystallographic lattice site can lead to improvements in the absorption coefficient,³¹ as well as reduce the degree of carrier localization, which enhances mobilities.³²

In this minireview, we discuss the effects of cation disorder on the optoelectronic properties and PV performance of inorganic solar absorbers. We define cation disorder as the occupation of a cation lattice site by a different cation species, and that homogeneous cation disorder is when there is perfect alternation between the cation species on the same lattice site, as displayed in Fig. 1(a) and (b). That is, we would define full cation order as when the cation species occupy different lattice sites (Fig. 1(a)). The degree of cation disorder can be further quantified by the “order parameter S”,^33,34 which is expressed as

S = 2(P^A_A − 0.5) (1)

with P^A_A the probability of finding the cation A at the A cation lattice site, and can also be described by its occupancy. This parameter will hence vary from 1 to 0 when cation distribution transforms from a fully ordered (P^A_A = 1) to fully disordered (P^A_A = 0.5) configuration. Usually, the transformation towards the cation disordered configuration is accompanied by a change of the space group for the crystal, since a higher degree of symmetry will be seen when different cations tend to randomly occupy the same crystallographic site.

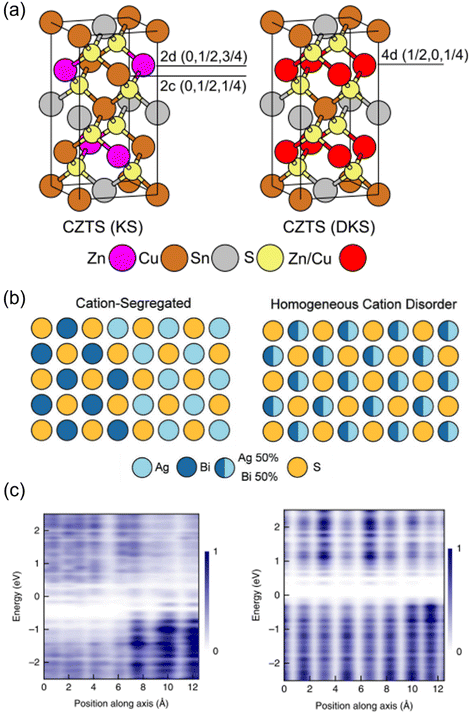Fig. 1 Cation disorder in different materials. (a) Unit cells of ordered (left) and disordered (right) Cu₂ZnSnS₄. During the order–disorder transition, the Wyckoff positions of Cu₂ZnSnS₄ will be changed from 2c and 2d to position 4d. The space group will also change from I4̄ to I4̄2m. Reprinted with permission from ref. 39. Copyright 2017 Elsevier. (b) Schematic of AgBiS₂ crystal structures with different degrees of cation disorder. In the homogeneous cation disorder configuration, Ag⁺ and Bi³⁺ cations can randomly occupy the same lattice sites. Reprinted with permission under the CC-BY-4.0 license from ref. 32. (c) The change on the planar-averaged local electronic density of states (DOS) for AgBiS₂ when changing from inhomogeneously (left) to homogeneously cation disordered. The color bar refers to the normalized 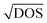. Reprinted with permission from ref. 31. Copyright 2022, Springer Nature.

In the following sections, we will discuss how the degree and homogeneity of cation disorder impacts several optoelectronic properties, and how it could be controlled or experimentally quantified. The materials focussed on in this minireview are kesterites and ABZ₂ materials, which have been the most studied solar absorbers from the perspective of cation disorder. It should be noted that although the concept of cation disorder discussed here mainly involves the interchange between two types of cations, it can be generalized to three or more cations if the cations involved have similar ionic radii and chemical properties, as has been reported in some mixed-cation ternary chalcogenides,³⁵ perovskites,³⁶ and high-entropy materials.^37,38 The discussion and points made in this minireview can hence be applied across the wider set of emerging inorganic solar absorbers, as well as provide insights into how cation disorder can be more consciously tuned as a design parameter to improve the optoelectronic properties of photovoltaic materials.

2. Impact of cation disorder

2.1 Optical properties

It has been experimentally and theoretically verified that cation disorder can change the bandgaps of several kesterites and AgBiS₂. Owing to the broadening of the density of states (DOS) at band edges, the bandgaps of these materials tend to decrease with increases in the degree of cation disorder. For example, in AgBiS₂, the bandgap was predicted (based on the hybrid functional HSE06) to decrease from over 1.5 eV in the fully ordered state (matildite phase) to 0 eV in the fully homogeneous Ag⁺–Bi³⁺ disordered state (cubic phase).⁴⁰ In other words, AgBiS₂ could be transformed from a semiconductor into a metal when cation ordering is reduced.

Interestingly, such a bandgap change is reversible in kesterites, and is highly associated with the order–disorder transition in these materials. Rey et al. have shown that the degree of cation disorder in Cu₂ZnSnSe₄ could be controlled by different post-synthesis annealing treatments.³³ As shown in Fig. 2(a), the bandgaps of Cu₂ZnSnSe₄ films determined by their Tauc plots could not only be reduced at higher annealing temperatures, but also be enlarged again at lower annealing temperatures, with a very minor hysteresis effect. This bandgap-temperature curve strongly indicates a second-order phase transition, where a continuous rather than an abrupt change with temperature was present. It could be also seen that the bandgap was more or less the same at temperatures above 200 °C, which could be understood if complete disorder on Cu⁺–Zn²⁺ has been reached, and 200 °C is therefore considered to be the critical temperature T_C for the order–disorder transition in Cu₂ZnSnSe₄.

Fig. 2 Impact of cation disorder on optoelectronic properties. (a) The change in the bandgap of Cu₂ZnSnS₄ with different degrees of cation disorder (controlled by different annealing temperatures). The inset shows the Tauc plots of Cu₂ZnSnSe₄ annealed at different temperatures. Reprinted with permission from ref. 33. Copyright 2014, AIP Publishing. (b) Absorption coefficient spectra of AgBiS₂ nanocrystals (NCs) annealed at different temperatures. Reprinted with permission from ref. 31. Copyright 2022, Springer Nature. (c) The Tauc plots and photoluminescence (PL) spectra of Cu₂ZnSnS₄ with different degrees of cation disorder. Reprinted with permission from ref. 41. Copyright 2017, John Wiley and Sons. (d) Charge density isosurfaces of a relaxed electron–hole pair in a cation-disordered NaBiS₂ supercell. Na, Bi, and S atoms are colored pink, blue and yellow, respectively. The translucent yellow and blue isosurfaces represent electron and hole densities, respectively. Reprinted under the CC-BY-4.0 license from ref. 45. (e) The normalized kinetics of NaBiS₂ NCs acquired from the short-time transient absorption (TA) and optical-pump-terahertz-probe (OPTP) measurements. Reprinted under the CC-BY-4.0 license from ref. 45. (f) Photoconductivity transients (Δσ) of Cu₂ZnSnSe₄ in different cation ordering configurations. Reprinted with permission from ref. 48. Copyright 2018, Elsevier.

Since the bandgap reduction in these cation-disordered materials has been attributed to band-edge broadening, it is intuitive to assume an enlarged Urbach energy E_U in a more disordered phase. Although some works did report a larger E_U in a more cation-disordered Cu₂ZnSnS₄ film,⁴¹ other works have also reported the opposite trend.⁴² Additionally, AgBiS₂ has exhibited a significant reduction in E_U from 173 meV to 26 meV when cation disorder became more homogeneous (i.e., closer to an arrangement where completely random Ag⁺ and Bi³⁺ cations are distributed in the octahedral holes in the rocksalt structure). On the one hand, a more disordered structure could cause bandgap or band edge fluctuations, raising the possibility of band tailing. But on the other side, the spread of the band-edge DOS might be decreased when the structure approaches the homogeneously cation-disordered phase, as displayed in Fig. 1(c). We hence note that the correlation between E_U values and cation disorder is not as straightforward as expected.

If the upper valence band (VB) and lower conduction band (CB) of a cation-disordered material are mainly composed of the orbitals from a specific species, then the band edge DOS of such a material will be significantly influenced by the degree of cation disorder. As an example, the band edge DOS of disordered rocksalt AgBiS₂ is shown in Fig. 1(c), where we can see that both the Ag-dominated VB maximum (VBM) and Bi-dominated CB minimum (CBM) are homogenized following an increase in the uniformity of the Ag⁺–Bi³⁺ distribution. The more homogeneous band-edge DOS then leads to enhanced transition dipole moments, and therefore higher absorption coefficients, as shown in Fig. 2(b), where a more homogeneous cation distribution in AgBiS₂ NCs could be reached with higher annealing temperatures. A similar enhancement in the absorption coefficients with increased cation homogeneity is also theoretically predicted in some ternary nitrides such as MgGeN₂,⁴³ although this is yet to be experimentally proven.

Finally, since cation disorder is basically a type of antisite defect (but can occur with much higher concentrations than typical point defects in the dilute limit), the non-radiative recombination rate might be also increased in materials with high degree of cation disorder, which would lead to reduced photoluminescence (PL) intensities or quantum yields. This detrimental effect of cation disorder on PL has been commonly observed in both Cu₂ZnSnS₄ and Cu₂ZnSnSe₄ films,^41,44 as displayed in Fig. 2(c). It should be noted that although the mechanism behind this effect is still unclear, the difference between the PL peak energy and the bandgap was almost constant, independent of the bandgap changes. Furthermore, similar to the bandgap, all the aforementioned PL properties showed high reversibility when kesterites experienced repeated order–disorder transitions.⁴² These results clearly indicate the great impact of cation disorder on PL properties, potentially via changing the corresponding defect densities.

2.2 Charge-carrier transport

It has been shown that cation disorder can significantly impact charge-carrier transport in some ABZ₂ materials, such as NaBiS₂ and AgBiS₂, which is also highly associated with the significant impact of cation disorder on the band-edge DOS of these materials. For example, Na⁺ cations do not contribute any orbitals to the band extrema in NaBiS₂, while Bi s orbitals make weak contributions to the upper VB, thus leading to a very flat VBM and hence large hole effective mass.⁴⁵ Moreover, S²⁻ anions coordinated by 5 or 6 Na⁺ cations (i.e., in Na⁺-rich clusters) tend to exhibit higher energy levels relative to the VBM due to the reduced Coulomb interaction from Na⁺ compared to Bi³⁺ cations. As a result, S p orbitals from these sulfur sites with high Na⁺ coordination form flat bands just above the VBM, which could tightly capture holes to form small polarons, with hole wavefunctions constrained to within approximately one unit cell. For electrons, a similar localization process takes place at Bi³⁺-rich clusters, albeit the electrons are less tightly bound, with their wavefunctions spreading over a slightly larger region compared to holes. Therefore, electrons and holes are spatially separated in cation-disordered NaBiS₂, and there is an ultrafast decay in the sum mobility after photo-excitation owing to the strong carrier localization, as shown in Fig. 2(d).

On the other hand, the VB of AgBiS₂ is composed of a large proportion of Ag d orbitals, leading to a more disperse VBM and hence a smaller hole effective mass. Nevertheless, since the VB and CB of AgBiS₂ are dominantly contributed by Ag d–S p orbitals and Bi p–S p orbitals, respectively, cation disorder can still lead to localized DOS in Ag⁺- and Bi³⁺-rich regions,^31,32 as shown in Fig. 1(c). It has been claimed that such a localized DOS will lead to a reduced dimensionality in the electronic structure of AgBiS₂ despite its 3D crystal structure, which can potentially limit the charge-carrier transport. In addition, according to Holstein-Anderson theory, even minimal disorder can also lead to the formation of small polarons.^46,47 As a result, significant charge-carrier localization could be still present in cation-disordered AgBiS₂.

Interestingly, for kesterite materials, such as Cu₂ZnSnSe₄, the degree of cation disorder barely affects the sum mobilities or carrier kinetics,⁴⁸ as shown in Fig. 2(e). A possible explanation can be seen from the electronic structure of Cu₂ZnSnSe₄, for which the upper VB and lower CB primarily consist of Cu d orbitals and Sn s–S p orbitals, respectively. Since calculations have predicted the Cu–Zn antisites to be the most favourable defects in Cu₂ZnSnSe₄, cation disorder in this material is expected to primarily affect the VB states and hole transport. Nevertheless, due to the fluctuating VB,⁴⁹ the hole mobility of Cu₂ZnSnSe₄ is lower than its electron mobility by over an order of magnitude, and therefore, the cation disorder will not significantly limit the charge-carrier transport, which is dominated by the much more mobile electrons, of this material. In terms of Cu₂ZnSnS₄, although direct experimental evidence is currently lacking, calculations have shown no signs of either small electron or hole polaron formation in its disordered phase.⁵⁰

2.3 PV performance

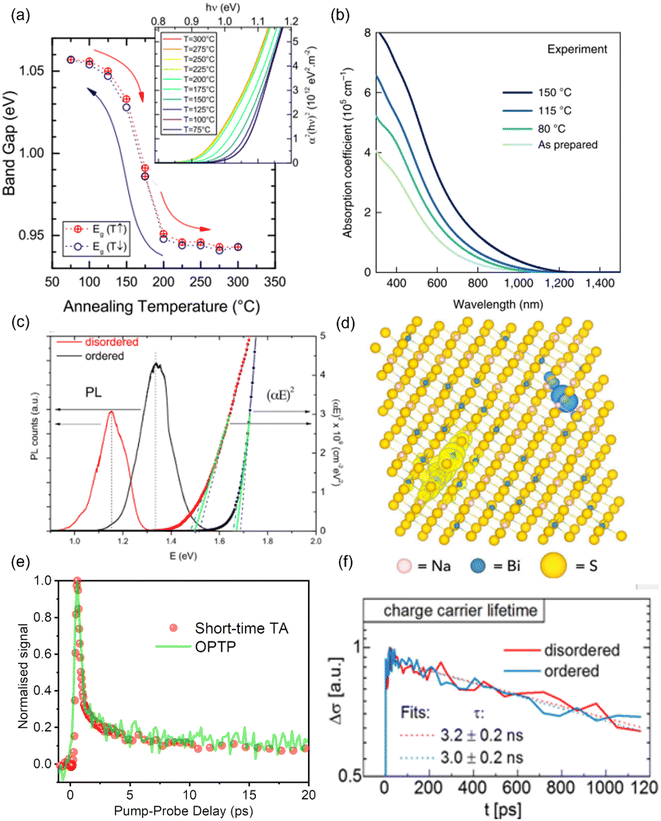
Given the significant impact of cation disorder on the optoelectronic properties of materials, it is not surprising to see different PV performance in solar cells fabricated based on materials with different degrees of cation disorder. It has been shown that AgBiS₂ nanocrystals (NCs) with more homogeneous cation disorder can exhibit stronger absorption and hence a higher spectroscopic limited maximum efficiency (SLME), as displayed in Fig. 3(a). Therefore, improving the homogeneity of cation disorder was critical for AgBiS₂ solar cells to reach its current certified record power conversion efficiency (PCE) of 8.85%, which is one of the highest values among all bismuth-based solar absorbers.

Fig. 3 Impact of cation disorder on photovoltaic performance. (a) The spectroscopic limited maximum efficiencies (SLMEs) of AgBiS₂ NC films as a function of thickness and annealing temperature, which changes the degree of cation disorder. Reprinted with permission from ref. 31. Copyright 2022, Springer Nature. (b) Open-circuit voltage deficit (V^def_OC) of solar cells fabricated based on Cu₂ZnSnSe₄ with different degree of cation disorder and hence different bandgaps E_g. Reprinted with permission from ref. 53. Copyright 2016, Elsevier. (c) A set of short-circuit current density (J_SC)-open-circuit voltage (V_OC) data points acquired from the same batch of Cu₂ZnSnSe₄ solar cells. PD and PO refer to highly cation disordered and relatively cation ordered Cu₂ZnSnSe₄, respectively. Reprinted with permission from ref. 42. Copyright 2016, John Wiley and Sons. (d) Current density–voltage curves of Cu₂ZnSnS₄ devices with different degrees of cation disorder. LT-PDA and HT-PDA refer to the post deposition annealing at low (160 °C) and high temperatures (300 °C), respectively. LT-PDA could lead to a higher degree of cation order, while HT-PDA tended to lower the degree of cation order. “dx” in the brackets refers to the x^th day after device fabrication. Reprinted with permission from ref. 41. Copyright 2017, John Wiley and Sons.

More studies on the role of cation disorder in kesterite solar cells have been reported. Earlier work used to regard cation disorder as the main cause of the large open-circuit voltage (V_OC) deficit^42,51–53 (i.e., difference between the experimental V_OC values and theoretical V_OC values, usually >380 meV), which was believed to be the culprit limiting the PCEs of kesterite solar cells. However, more recent studies have indicated that the V_OC deficit of kesterite solar cells was in fact not directly related to the degree of cation disorder in kesterites.⁵³ As shown in Fig. 3(b), the minimum V_OC deficit that could be achieved in Cu₂ZnSnSe₄ solar cells with different degrees of cation disorder was almost unchanged. Such a lack of a dependence of the V_OC on cation disorder has been rationalized by the shallow levels of Cu_Zn/Zn_Cu antisite defects, as well as the limited effect of these defects on the band edges.^50,54 However, it has been computationally predicted that the formation energies for deep-level Sn_Zn antisite defects and their defect complexes can be lowered when cation disorder is present, even at a relatively low degrees.⁵⁰ Since a fully ordered configuration can never be achieved at room temperature, the V_OC deficit in kesterite solar cells is most likely caused by the inevitable non-radiative recombination resulting from deep-level defects. Based on the Shockley-Read-Hall recombination model with these disorder-facilitated defects taken into account, the maximum PCE for Cu₂ZnSnS₄ solar cells has been estimated to drop from 25% to 14%,⁵⁰ which is close to the present record value.

At the same time, we can expect the V_OC values to increase in solar cells fabricated with more ordered kesterites, not necessarily because of reduced V_OC deficits, but rather the wider bandgaps compared to their disordered counterparts, which can lead to larger quasi-Fermi level splitting. However, this V_OC increase is usually accompanied by a decrease in short-circuit current density (J_SC) (Fig. 3(c)) because of the reduced absorption range. As a result, improved and reduced PCEs/external quantum efficiencies (EQEs) in solar cells with a more ordered configuration have been reported simultaneously in literature.^41,55 Therefore, compared to AgBiS₂ solar cells, it is still too early to conclude if cation disorder has a similarly positive impact on kesterite solar cells.

Apart from the main characteristics discussed above, some additional considerations that could affect the performance of kesterite solar cells were also reported recently. For the conventional Cu₂ZnSnS₄ solar cell architecture (glass/MoS₂/Cu₂ZnSnS₄/CdS/ZnO/ITO), a parasitic diode at the MoS₂/Cu₂ZnSnS₄ interface may block hole transport and lead to “S-shaped” J–V curves with very low fill factors (FFs), as displayed in Fig. 2(d). It has been shown that with more disordered Cu₂ZnSnS₄, such an S-shaped feature could be removed, leading to smoother J–V curves with improved FFs. The proposed explanation is that this phenomenon is caused by the shallower VBM in more disordered Cu₂ZnSnS₄, which could make a better energy level alignment between MoS₂/Cu₂ZnSnS₄ interface and Cu₂ZnSnS₄. Consequently, both the hole transport and FF were improved.⁴¹ In addition, from capacitance–voltage (C–V) measurements, a smaller charge-carrier density was observed in more ordered Cu₂ZnSnS_xSe_1−x solar cells, which could result in a wider space charge region and enhance charge-carrier collection efficiency.⁴² However, such a large space charge region might also lead to a more voltage-dependent photocurrent and reduce the FF. More analyses on devices will be hence needed to elucidate the actual impacts of a reduced charge-carrier density in kesterite solar cells.

3. Strategies to tune cation disorder

Since cation disorder originates from the similar ionic radii of the two cations, introducing a third type of cation with a much different size is an apparent strategy to mitigate cation disorder. For kesterites, substituting Ag⁺ for Cu⁺ or Ba²⁺ for Zn²⁺ have been found to be effective on tuning their degree of cation disorder. In both cases, the ionic radius of Ag⁺ (1.14 Å) and Ba²⁺ (1.56 Å) is significantly larger than that of Cu⁺ and Zn²⁺, which are both approximately 0.74 Å. Calculations have shown that the formation energies of Ag_Cu and Cu_Ba antisites and even their related defect complexes, such as Ag_Zn + Zn_Ag, are higher than the common antisite defects in conventional kesterites.^56,57 Particularly, the large charge difference between Ba²⁺ and Sn⁴⁺ also increases the formation energies of Sn-related defects,⁵⁷ which tend to have deep levels and are more detrimental to PV performance. As a result, both the degree of cation disorder and also the total defect concentrations of kesterites are predicted to decrease after Ag⁺- or Ba²⁺- substitution. It has been verified that (Cu,Ag)₂ZnSnSe₄ with different Ag compositions could show different bandgaps and low-temperature (10 K) PL peaks,⁵⁸ as shown in Fig. 4(a). These results provide further evidence that the degree of cation disorder varies with different Ag/(Ag + Cu) ratios. However, it should be noted that not all of the cations with a large size mismatch with Cu⁺ or Zn²⁺ could have similar effects on suppressing cation disorder. For example, Cd²⁺ was believed to be favorable for substituting Zn²⁺ because of its larger ionic radius (0.92 Å), while calculations have shown that the formation energy of Cu_Cd is still the lowest among all defects in Cu₂ZnSnS₄ and only slightly higher than that of Cu_Zn, indicating that the degree of cation disorder cannot be changed effectively via Cd²⁺ substitution.⁵⁶ Such an unexpected result originates from the narrow chemical potential region for stabilizing Cu₂CdSnS₄, which can only be formed when the chemical potential of Cd is below −0.9 eV. At such low chemical potentials, the formation energy for Cu_Cd is also low, and cation disorder due to the prevalence of these antisite defects will still occur.⁵⁹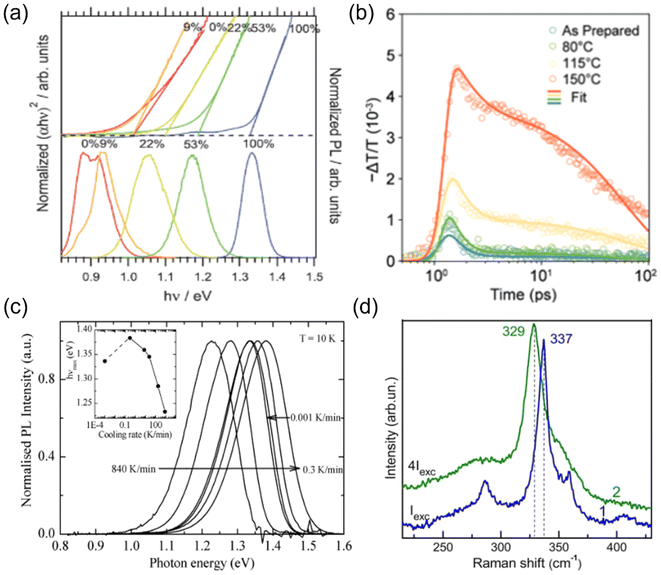

Fig. 4 Strategies to tune cation disorder. (a) Normalized Tauc plots (top) and normalized PL spectra (bottom) of (Cu,Ag)₂ZnSnSe₄. The labelled ratios correspond to Ag/(Ag + Cu) values. α and hν represent the absorption coefficient and photon energy, respectively. Reprinted with permission from ref. 58. Copyright 2016, John Wiley and Sons. (b) Photoconductivity (proportional to −ΔT/T) kinetics of AgBiS₂ NC films annealed (post-synthesis) at different temperatures for 10 min. Higher post-synthesis annealing temperatures can lead to higher degrees of cation disorder in AgBiS₂. Reprinted under the CC-BY-4.0 license from ref. 32. (c) Low-temperature (10 K) PL spectra of Cu₂ZnSnS₄ powders quenched from 573 K to 473 K at different cooling rates. The inset shows the PL peak positions (hν_max) for the samples quenched at different cooling rates. Reprinted with permission from ref. 61. Copyright 2014, Elsevier. (d) Raman spectra of a Cu-rich Cu₂ZnSnS₄ sample excited by a 514.5 nm wavelength laser at a low (blue line) and high (green line) power. Reprinted with permission ref. 64. Copyright 2013, John Wiley and Sons.

Additionally, another commonly used strategy to tune cation disorder is through annealing. Such a treatment can be conducted during or after synthesis. For the annealing treatment during synthesis, it has been shown that kesterite powders annealed at different temperatures followed by quenching could have different degrees of cation disorder, which was verified from the gradual change in bandgaps and lattice parameters.⁶⁰ This result suggests that the cation distribution configuration formed during synthesis could be fixed by swift quenching. Interestingly, the cooling rates were also found to lead to different degrees of cation disorder. As shown in Fig. 4(c), using lower cooling rates seemed to further mitigate the cation disorder in Cu₂ZnSnS₄ powders, leading to blue shifts of the bandgaps and corresponding PL peak positions.⁶¹

On the other hand, post-synthesis annealing treatment has been widely adopted in kesterites and ABZ₂ materials since it is the most convenient strategy to tune cation disorder in thin film samples, which could be potentially applied in PV devices. As indicated in Section 2.1 and Fig. 2(a), post-synthesis annealing could lead to a continuous transition of Cu₂ZnSnS₄ from a more ordered phase to a completely disordered phase when passing through the critical temperature T_C.³³ It should be noted that although most post-synthesis annealing treatments only required around 1 h to achieve the final disordered phases, a longer time (>20 h) was usually needed for the transformation into (relatively) ordered phases at temperatures below 150 °C. Such a long treatment time can then allow the slow diffusion process of cations to fully complete, and also enable the structure to reach thermal equilibrium. Similar phase transitions through a critical temperature T_C were also observed in AgBiS₂ and AgBiSe₂,^62,63 which exhibited a sudden drop in conductivity and thermopower (i.e., thermoelectric voltage divided by the temperature difference across the material) when a homogeneous disordered configuration was reached in these materials. Since the T_C for these ABZ₂ materials was usually above 300 °C, we might expect post-synthesis annealing at temperatures below 300 °C should mitigate the cation disorder of these materials, as observed in kesterites. However, the latest experimental results showed that for AgBiS₂ NC films, even post-synthesis annealing at temperatures below 150 °C seemed to be sufficient to increase the degree of cation disorder.^31,32 This clear difference between AgBiS₂ and kesterites is not yet explained until now.

Finally, apart from thermal energy discussed above, light energy or an applied electric field might also change the cation disorder of materials. Valakh et al. have shown that when a Cu₂ZnSnS₄ particle was excited by a high-power 514.5 nm wavelength laser, its Raman peaks shifted and broadened, indicating an increased degree of cation disorder.⁶⁴ In terms of the impact of an applied electric field on cation disorder, although a direct investigation has not yet been reported, significant ion migration has been observed in AgBiS₂ and NaBiS₂ devices under bias,^65,66 suggesting that the cations may be mobile. Nevertheless, more quantitative investigations will be needed to verify the effectiveness and reproducibility of these light- or electric field-induced changes in cation disorder.

4. Quantifying and comparing cation disorder

The most common technique for characterizing cation disorder is Raman spectroscopy.^67–69 As shown in Fig. 5(a), disordered Cu₂ZnSnS₄ powders (VF) showed clearly broadened Raman peaks compared to relatively ordered ones (VS) owing to a distribution of vibrational modes caused by different cation configurations.⁶⁷ The difference between the ordered and disordered samples can be further enhanced if resonance Raman spectroscopy is used^67,68 (lower part of Fig. 5(a), which used a 785 nm wavelength laser excitation). Scragg et al. also proposed that the order parameter S of a specific sample can be quantified by its “Q value”, which is defined as the ratio of the characteristic Raman m_2A peak to m_3A peak intensity.⁶⁷ The former peak corresponds to the main A-symmetry mode, while the latter is believed to highly associate with the Cu–Zn distribution. Both peaks have been found to be highly sensitive to cation disorder. Fig. 5(b) presents the Q values and full-width-at-half-maximum (FWHM) values of the main m_1A peaks for a series of Cu₂ZnSnS₄ films annealed at different temperatures, where we can deduce a critical temperature T_C for the order–disorder transition.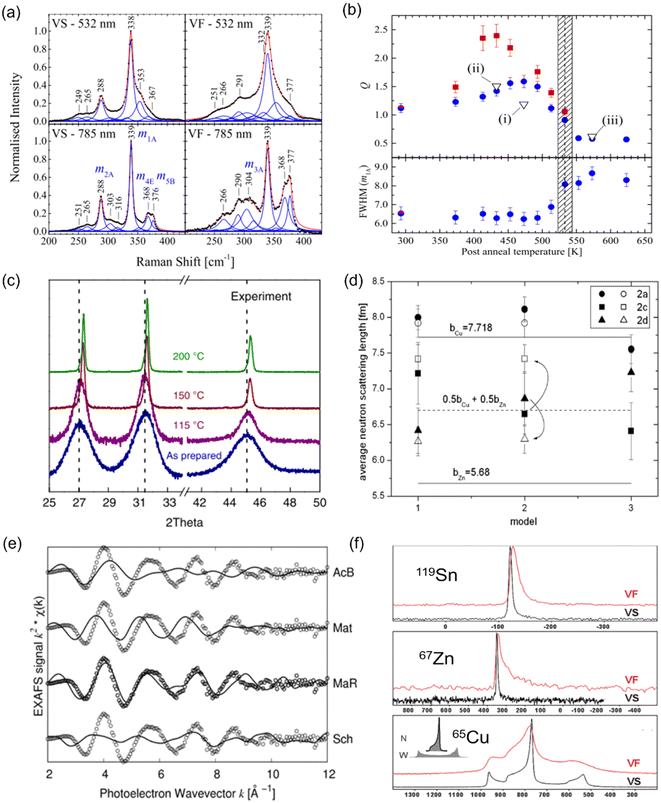

Fig. 5 Characterization techniques for understanding and quantifying cation disorder. (a) Normalized Raman spectra with peak fitting for disordered (VF) and relatively ordered (VS) Cu₂ZnSnS₄ powders. The spectra taken under 532 nm (non-resonance) and 785 nm (resonance) laser excitations were recorded for comparison. Reprinted with under the terms of the CC-BY-4.0 license from ref. 67. (b) Variation in the Q value, which is defined as the ratios of the Raman peak intensity on m_2A to m_3A modes (part Fig. (a)), for Cu₂ZnSnS₄ films annealed at different temperatures for 1 h (blue circles) and 24 h (red squares). The full-width-at-half-maximum (FWHM) values of the Raman peak on the m_1A mode for these samples are also displayed. The shaded area indicates the probable region of the critical temperature T_c for order–disorder transition. Reprinted under the terms of the CC-BY-4.0 license from ref. 67. (c) X-ray diffraction (XRD) patterns of pristine and AgBiS₂ NC films annealed at different temperatures. Reprinted with permission from ref. 31. Copyright 2022, Springer Nature. (d) Fitted average neutron scattering lengths in the Cu₂ZnSnS₄ powders using different structural models. Closed and open symbols refer to the disordered and relatively ordered samples, respectively. The two solid lines indicate the neutron scattering length for Cu⁺ and Zn²⁺ cations, and the dotted line refers to the average neutron scattering length of Cu⁺ and Zn²⁺ cations. Reprinted with permission from ref. 72. Copyright 2011, Elsevier. (e) Extended X-ray absorption fine structure (EXAFS) spectra of a AgBiS₂ NC film (open circles) along with the simulated curves (solid lines) based on 4 structures: acanthite (AcB), matildite (Mat), matildite with random cation occupation (MaR), and schapbachite (Sch). Reprinted under the terms of the CC-BY-4.0 license from ref. 73. (f) Solid-state nuclear magnetic resonance (NMR) spectra of ¹¹⁹Sn, ⁶⁷Zn, and ⁶⁵Cu for Cu₂ZnSnS₄ powders cooled down at different rates. The VF and VS samples are as indicated in Fig. (a). The unit of the horizontal axis (chemical shift) is in ppm. Reprinted with permission from ref. 74. Copyright 1999, Royal Society of Chemistry.

Additionally, different cation configurations can also slightly change the bond lengths and hence the corresponding X-ray diffraction (XRD) patterns. An example can be seen in AgBiS₂ NC films annealed at higher temperatures (Fig. 5(c)), which tended to have shorter Ag–S bonds when cation disorder became more homogeneous, causing a shift of the XRD peaks towards larger angles.³¹ Furthermore, if single-crystalline materials can be synthesized, single-crystal XRD can serve as another powerful tool for characterizing the degree of cation disorder since it can provide information on lattice parameters and cation occupancies at specific lattice sites.^70,71 Unfortunately, this technique cannot apply to the kesterites discussed in this review, due to the identical electron densities of Cu⁺ and Zn²⁺ cations. In this respect, neutron scattering measurements can be more suitable for studying cation disorder in kesterites because the neutron scattering length of Cu⁺ and Zn²⁺ cations is very different. By fitting the average neutron scattering lengths determined from neutron diffraction patterns, the cation occupancies at each lattice site can be precisely extracted. An example for Cu₂ZnSnS₄ is displayed in Fig. 5(d), where we can see that site 2a is almost exclusively occupied by Cu⁺ independent of the models used or degree of disorder, while site 2c and 2d can be occupied by both Cu⁺ and Zn²⁺ cations,⁷² leading to the fitted neutron scattering length closer to the average value of Cu⁺ and Zn²⁺.

Recently, X-ray absorption spectroscopy (XAS) and nuclear magnetic resonance (NMR) spectroscopy were also used to probe cation disorder in both ABZ₂ materials and kesterites. The extended X-ray absorption fine structure (EXAFS) spectra of materials include information on the bond lengths and coordination numbers of the target atoms, which can help to predict the level of cation segregation, as well as the crystal structure,⁷³ as displayed in Fig. 5(e). On the other hand, NMR spectroscopy is particularly sensitive to the local chemical environments of the target nuclei, and similar to Raman spectroscopy, its characteristic peak widths and shifts will be affected by changes in the cation configurations,^68,74 as seen from the example shown in Fig. 5(f) for Cu₂ZnSnS₄.

It can be seen that techniques commonly used to characterize cation disorder now mainly rely on the comparison between ordered and disordered samples, while a more direct way to probe cation arrangements is still lacking. Techniques such as high-resolution transmission electron microscopy (HRTEM) or atom probe tomography (APT),⁷⁵ which can visualize different atoms with sub-nanometer resolution, can be useful for more directly characterizing cation disorder. However, the critical challenge for these techniques will be to characterize the materials without altering them during sample preparation or during the measurement itself.

5. Conclusion and outlook

In conclusion, cation disorder, which is widely found in inorganic materials, has proven to not necessarily be detrimental to the performance of these materials as solar absorbers, but rather can be an important tuning parameter to optimize their efficiency in PV devices. The effect of the degree of cation disorder and its homogeneity on the properties of solar absorbers has mostly been studied thus far in kesterites (Cu₂ZnSnS₄ and Cu₂ZnSnSe₄) and AgBiS₂. Among these materials, it has been shown that cation disorder affects the bandgap, steepness of the absorption onset, absorption coefficient, and charge-carrier mobility, which all determine the ultimate efficiencies of these materials in solar cells. However, there is still much to be learned regarding how cation disorder affects these properties, and how cation disorder can be controlled and quantified. For example, whilst it has been shown that improving the homogeneity of cation disorder in AgBiS₂ flattens the energy landscape,³¹ which leads to reduced Urbach energies, Cu₂ZnSnS₄ has shown the opposite trend.⁴² Furthermore, it was previously believed that an increased degree of cation disorder in Cu₂ZnSnS₄ led to increased V_OC deficits, but more recently there has been debate about whether this is the case, and whether cation disorder influences V_OC through non-radiative recombination or simply through changes in the bandgap (and therefore the achievable quasi-Fermi level splitting).^41,42

As the field moves forward, it will be important to actively look for cation disorder in novel solar absorber materials and to establish its link with its optoelectronic properties. What makes this challenging at present is that there is no straightforward method to quantify the degree and homogeneity of cation disorder in materials. Current approaches are all indirect and rely firstly on establishing correlations between cation disorder and the signals measured. For example, EXAFS can probe the local environment around the target cations, but requires simulations in order to interpret the measured spectra. The same can be said for neutron scattering measurements or NMR. More direct methods of probing cation disorder would be beneficial, such as using HRTEM techniques. But at the same time, it will be important to ensure that the measurement conditions or sample preparation methods do not alter cation disorder in the materials. For example, materials that are ionic conductors may readily change the arrangement of cations when energy is input from the probing beam during imaging, or from the mechanical/thermal energy input when samples are crushed to finer powder to measure.

Being able to quantify cation disorder more accurately will be critical for developing more reliable methods to control the degree and homogeneity of cation disorder. Currently, cation disorder is mostly tuned by the ionic radii of the species present and post-annealing. However, it has been found that the ionic radius is only a proxy for how likely it is for two cations to occupy the same crystallographic lattice site, and it is important to evaluate this by directly calculating the energy for antisite defect formation.^56,57 Furthermore, whilst post-synthesis annealing at 115 °C has been effective for tuning the homogeneity of cation disorder in AgBiS₂,³¹ low-temperature annealing has not been found to have similar effects in NaBiS₂.⁴⁵ Efforts should therefore be made to uncover alternative strategies for tuning these parameters, for example through the application of light, electric field, or the use of ligands and dopants. Realizing these routes can potentially open up more opportunities to achieve efficient photovoltaics from emerging solar absorbers. Additionally, it is important to monitor the changes in cation disorder when solar cells are in operation. That is, either under bias or over the temperature range from −40 °C to +85 °C in standard thermal cycling stability tests.⁷⁶ Given the absence of such studies, we encourage more investigations into such in-operando measurements in the future, possibly through the use of in situ Raman spectroscopy or time-resolved XRD.

Author contributions

R. L. Z. H. conceived of the topic for this minireview. Y.-T. H. and R. L. Z. H. wrote the review and edited it together.

Conflicts of interest

The authors declare no conflicts of interest.

Acknowledgements

The authors would like financial support from the Engineering and Physical Sciences Research Council (no. EP/V014498/2).

References

1. L. Meng, J. You and Y. Yang, Nat. Commun., 2018, 9, 5265.
2. A. M. Ganose, D. O. Scanlon, A. Walsh and R. L. Z. Hoye, Nat. Commun., 2022, 13, 4715.
3. V. Steinmann, R. E. Brandt and T. Buonassisi, Nat. Photonics, 2015, 9, 355–357.
4. G. E. Eperon, M. T. Hörantner and H. J. Snaith, Nat. Rev. Chem., 2017, 1, 0095.
5. P. K. Nayak, S. Mahesh, H. J. Snaith and D. Cahen, Nat. Rev. Mater., 2019, 4, 269–285.
6. H. Michaels, M. Rinderle, I. Benesperi, R. Freitag, A. Gagliardi and M. Freitag, Chem. Sci., 2023, 14, 5350–5360.
7. V. Pecunia, L. G. Occhipinti and R. L. Z. Hoye, Adv. Energy Mater., 2021, 11, 2100698.
8. J. C. Blakesley, R. S. Bonilla, M. Freitag, A. M. Ganose, N. Gasparini, P. Kaienburg, G. Koutsourakis, J. D. Major, J. Nelson, N. K. Noel, B. Roose, J. S. Yun, S. Aliwell, P. P. Altermatt, T. Ameri, V. Andrei, A. Armin, D. Bagnis, J. Baker, H. Beath, M. Bellanger, P. Berrouard, J. Blumberger, S. A. Boden, H. Bronstein, M. J. Carnie, C. Case, F. A. Castro, Y.-M. Chang, E. Chao, T. M. Clarke, G. Cooke, P. Docampo, K. Durose, J. R. Durrant, M. R. Filip, R. H. Friend, J. M. Frost, E. A. Gibson, A. J. Gillett, P. Goddard, S. N. Habisreutinger, M. Heeney, A. D. Hendsbee, L. C. Hirst, M. S. Islam, K. D. G. I. Jayawardena, M. B. Johnston, M. Kauer, J. Kettle, J.-S. Kim, D. Lamb, D. Lidzey, J. Lim, R. MacKenzie, N. Mason, I. McCulloch, K. P. McKenna, S. B. Meier, P. Meredith, G. Morse, J. D. Murphy, C. Nicklin, P. Ortega-Arriaga, T. Osterberg, J. B. Patel, A. Peaker, M. Riede, M. Rush, J. W. Ryan, D. O. Scanlon, P. J. Skabara, F. So, H. J. Snaith, L. Steier, J. Thiesbrummel, A. Troisi, C. Underwood, K. Walzer, T. Watson, J. M. Walls, A. Walsh, L. D. Whalley, B. Winchester, S. D. Stranks and R. L. Z. Hoye, arXiv, 2023, preprint, arXiv:2310.19430,  DOI:10.48550/arXiv.2310.19430.
9. S. Chen, A. Walsh, X. G. Gong and S. H. Wei, Adv. Mater., 2013, 25, 1522–1539.
10. D. B. Mitzi, O. Gunawan, T. K. Todorov, K. Wang and S. Guha, Sol. Energy Mater. Sol. Cells, 2011, 95, 1421–1436.
11. T. K. Todorov, K. B. Reuter and D. B. Mitzi, Adv. Mater., 2010, 22, 156–159.
12. A. Chirilǎ, P. Reinhard, F. Pianezzi, P. Bloesch, A. R. Uhl, C. Fella, L. Kranz, D. Keller, C. Gretener, H. Hagendorfer, D. Jaeger, R. Erni, S. Nishiwaki, S. Buecheler and A. N. Tiwari, Nat. Mater., 2013, 12, 1107–1111.
13. U. Rau and H. W. Schock, Appl. Phys. A: Mater. Sci. Process., 1999, 69, 131–147.
14. D. A. R. Barkhouse, O. Gunawan, T. Gokmen, T. K. Todorov and D. B. Mitzi, Prog. Photovolt.: Res. Appl., 2015, 20, 6–11.
15. C. Shen, T. Li, Y. Zhang, R. Xie, T. Long, N. M. Fortunato, F. Liang, M. Dai, J. Shen, C. M. Wolverton and H. Zhang, J. Am. Chem. Soc., 2023, 145, 21925–21936.
16. S. A. Mcdonald, G. Konstantatos, S. Zhang, P. W. Cyr, E. J. D. Klem, L. Levina and E. H. Sargent, Nat. Mater., 2005, 4, 138–142.
17. J. Tang, K. W. Kemp, S. Hoogland, K. S. Jeong, H. Liu, L. Levina, M. Furukawa, X. Wang, R. Debnath, D. Cha, K. W. Chou, A. Fischer, A. Amassian, J. B. Asbury and E. H. Sargent, Nat. Mater., 2011, 10, 765–771.
18. H. Shi, W. Ming and M.-H. Du, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 93, 104108.
19. K. T. Butler, S. McKechnie, P. Azarhoosh, M. VanSchilfgaarde, D. O. Scanlon and A. Walsh, Appl. Phys. Lett., 2016, 108, 112103.
20. U. V. Ghorpade, M. P. Suryawanshi, M. A. Green, T. Wu, X. Hao and K. M. Ryan, Chem. Rev., 2023, 123, 327–378.
21. A. Swarnkar, A. R. Marshall, E. M. Sanehira, B. D. Chernomordik, D. T. Moore, J. A. Christians, T. Chakrabarti and J. M. Luther, Science, 2016, 354, 92–95.
22. G. E. Eperon, G. M. Paternò, R. J. Sutton, A. Zampetti, A. A. Haghighirad, F. Cacialli and H. J. Snaith, J. Mater. Chem. A, 2015, 3, 19688–19695.
23. A. K. Jena, A. Kulkarni and T. Miyasaka, Chem. Rev., 2019, 119, 3036–3103.
24. S. R. Rondiya, R. A. Jagt, J. L. Macmanus-Driscoll, A. Walsh and R. L. Z. Hoye, Appl. Phys. Lett., 2021, 119, 220501.
25. R. A. Jagt, I. Bravić, L. Eyre, K. Gałkowski, J. Borowiec, K. R. Dudipala, M. Baranowski, M. D. Yksik, T. W. J. van deGoor, T. Kreouzis, M. Xiao, A. Bevan, P. Płochocka, S. D. Stranks, F. Deschler, B. Monserrat, J. L. MacManus-Driscoll and R. L. Z. Hoye, Nat. Commun., 2023, 14, 2452.
26. L. R. V. Buizza and L. M. Herz, Adv. Mater., 2021, 33, 202007057.
27. A. Walsh and A. Zunger, Nat. Mater., 2017, 16, 964–967.
28. J. Leeman, Y. Liu, J. Stiles, S. B. Lee, P. Bhatt, L. M. Schoop and R. G. Palgrave, PRX Energy, 2024, 3, 011002.
29. V. Vijay, S. Harish, J. Archana and M. Navaneethan, CrystEngComm, 2021, 23, 5522–5530.
30. S. Roychowdhury, T. Ghosh, R. Arora, M. Samanta, L. Xie, N. K. Singh, A. Soni, J. He, U. V. Waghmare and K. Biswas, Science, 2021, 371, 722–727.
31. Y. Wang, S. R. Kavanagh, I. Burgués-Ceballos, A. Walsh, D. Scanlon and G. Konstantatos, Nat. Photonics, 2022, 16, 235–241.
32. M. Righetto, Y. Wang, K. A. Elmestekawy, C. Q. Xia, M. B. Johnston, G. Konstantatos and L. M. Herz, Adv. Mater., 2023, 35, 2305009.
33. G. Rey, A. Redinger, J. Sendler, T. P. Weiss, M. Thevenin, M. Guennou, B. ElAdib and S. Siebentritt, Appl. Phys. Lett., 2014, 105, 112106.
34. G. H. Vineyard, Phys. Rev., 1956, 102, 981–992.
35. A. Baqais, N. Tymińska, T. LeBahers and K. Takanabe, Chem. Mater., 2019, 31, 3211–3220.
36. S. Zeiske, O. J. Sandberg, N. Zarrabi, C. M. Wolff, M. Raoufi, F. Peña-Camargo, E. Gutierrez-Partida, P. Meredith, M. Stolterfoht and A. Armin, J. Phys. Chem. Lett., 2022, 13, 7280–7285.
37. M. C. Folgueras, Y. Jiang, J. Jin and P. Yang, Nature, 2023, 621, 282–288.
38. C. Y. He, Y. Li, Z. H. Zhou, B. H. Liu and X. H. Gao, Adv. Mater., 2024, 2400920, 1–36.
39. M. Quennet, A. Ritscher, M. Lerch and B. Paulus, J. Solid State Chem., 2017, 250, 140–144.
40. F. Viñes, G. Konstantatos and F. Illas, Phys. Chem. Chem. Phys., 2017, 19, 27940–27944.
41. C. Malerba, M. Valentini and A. Mittiga, Sol. RRL, 2017, 1, 1700101.
42. S. Bourdais, C. Choné, B. Delatouche, A. Jacob, G. Larramona, C. Moisan, A. Lafond, F. Donatini, G. Rey, S. Siebentritt, A. Walsh and G. Dennler, Adv. Energy Mater., 2016, 6, 1502276.
43. Q. Feng, Ceram. Int., 2023, 49, 19533–19536.
44. D. M. Bishop, B. McCandless, T. Gershon, M. A. Lloyd, R. Haight and R. Birkmire, J. Appl. Phys., 2017, 121, 065704–065701.
45. Y.-T. Huang, S. R. Kavanagh, M. Righetto, M. Rusu, I. Levine, T. Unold, S. J. Zelewski, A. J. Sneyd, K. Zhang, L. Dai, A. J. Britton, J. Ye, J. Julin, M. Napari, Z. Zhang, J. Xiao, M. Laitinen, L. Torrente-Murciano, S. D. Stranks, A. Rao, L. M. Herz, D. O. Scanlon, A. Walsh and R. L. Z. Hoye, Nat. Commun., 2022, 13, 4960.
46. F. X. Bronold, F. X. Bronold, H. Fehske and H. Fehske, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 731021–731024.
47. F. X. Bronold, A. Alvermann and H. Fehske, Philos. Mag., 2004, 84, 673–704.
48. H. Hempel, R. Eichberger, I. Repins and T. Unold, Thin Solid Films, 2018, 666, 40–43.
49. H. Hempel, C. J. Hages, R. Eichberger, I. Repins and T. Unold, Sci. Rep., 2018, 8, 14476.
50. W. Chen, D. Dahliah, G. M. Rignanese and G. Hautier, Energy Environ. Sci., 2021, 14, 3567–3578.
51. T. Gokmen, O. Gunawan, T. K. Todorov and D. B. Mitzi, Appl. Phys. Lett., 2013, 103, 103506.
52. J. J. S. Scragg, J. K. Larsen, M. Kumar, C. Persson, J. Sendler, S. Siebentritt and C. Platzer Björkman, Phys. Status Solidi B, 2016, 253, 247–254.
53. G. Rey, T. P. Weiss, J. Sendler, A. Finger, C. Spindler, F. Werner, M. Melchiorre, M. Hála, M. Guennou and S. Siebentritt, Sol. Energy Mater. Sol. Cells, 2016, 151, 131–138.
54. U. Rau and J. H. Werner, Appl. Phys. Lett., 2004, 84, 3735–3737.
55. M. Kauk-Kuusik, K. Timmo, M. Pilvet, K. Muska, M. Danilson, J. Krustok, R. Josepson, V. Mikli and M. Grossberg-Kuusk, J. Mater. Chem. A, 2023, 11, 23640–23652.
56. Z.-K. K. Yuan, S. Chen, H. Xiang, X.-G. G. Gong, A. Walsh, J.-S. S. Park, I. Repins and S.-H. H. Wei, Adv. Funct. Mater., 2015, 25, 6733–6743.
57. D. Shin, B. Saparov and D. B. Mitzi, Adv. Energy Mater., 2017, 7, 1602366.
58. T. Gershon, Y. S. Lee, P. Antunez, R. Mankad, S. Singh, D. Bishop, O. Gunawan, M. Hopstaken and R. Haight, Adv. Energy Mater., 2016, 6, 4–10.
59. Z. K. Yuan, S. Chen, H. Xiang, X. G. Gong, A. Walsh, J. S. Park, I. Repins and S. H. Wei, Adv. Funct. Mater., 2015, 25, 6733–6743.
60. A. Ritscher, M. Hoelzel and M. Lerch, J. Solid State Chem., 2016, 238, 68–73.
61. M. Grossberg, J. Krustok, T. Raadik, M. Kauk-Kuusik and J. Raudoja, Curr. Appl. Phys., 2014, 14, 1424–1427.
62. H. Jang, S. Abbey, W. H. Nam, B. Frimpong, C. V. Nguyen, S. J. Joo, H. S. Shin, J. Y. Song, E. N. Cho, M. Kim, Y. S. Jung and M. W. Oh, J. Mater. Chem. A, 2021, 9, 4648–4657.
63. S. N. Guin, S. Banerjee, D. Sanyal, S. K. Pati and K. Biswas, Inorg. Chem., 2016, 55, 6323–6331.
64. M. Y. Valakh, O. F. Kolomys, S. S. Ponomaryov, V. O. Yukhymchuk, I. S. Babichuk, V. Izquierdo-Roca, E. Saucedo, A. Perez-Rodriguez, J. R. Morante, S. Schorr and I. V. Bodnar, Phys. Status Solidi RRL, 2013, 7, 258–261.
65. Y. T. Huang, D. Nodari, F. Furlan, Y. Zhang, M. Rusu, L. Dai, Z. Andaji-Garmaroudi, D. Darvill, X. Guo, M. Rimmele, T. Unold, M. Heeney, S. D. Stranks, H. Sirringhaus, A. Rao, N. Gasparini and R. L. Z. Hoye, Small, 2023, 2310199.
66. Y. T. Huang, M. Schleuning, H. Hempel, Y. Zhang, M. Rusu, T. Unold, A. Musiienko, O. Karalis, N. Jung, S. J. Zelewski, A. J. Britton, N. Ngoh, W. Song, L. C. Hirst, H. Sirringhaus, S. D. Stranks, A. Rao, I. Levine and R. L. Z. Hoye, Adv. Funct. Mater., 2024, 2310283.
67. J. J. S. Scragg, L. Choubrac, A. Lafond, T. Ericson and C. Platzer-Björkman, Appl. Phys. Lett., 2014, 104, 041911.
68. M. Paris, L. Choubrac, A. Lafond, C. Guillot-Deudon and S. Jobic, Inorg. Chem., 2014, 53, 8646–8653.
69. X. Fontané, V. Izquierdo-Roca, E. Saucedo, S. Schorr, V. O. Yukhymchuk, M. Y. Valakh, A. Pérez-Rodríguez and J. R. Morante, J. Alloys Compd., 2012, 539, 190–194.
70. A. Zucchini, P. Comodi, A. Katerinopoulou, T. Balic-Zunic, C. McCammon and F. Frondini, Phys. Chem. Miner., 2012, 39, 319–328.
71. A. Nicolson, J. Breternitz, S. R. Kavanagh, Y. Tomm, K. Morita, A. G. Squires, M. Tovar, A. Walsh, S. Schorr and D. O. Scanlon, J. Am. Chem. Soc., 2023, 145, 12509–12517.
72. S. Schorr, Sol. Energy Mater. Sol. Cells, 2011, 95, 1482–1488.
73. J. K. Kesavan, F. D′acapito, P. Scardi, A. Stavrinadis, M. Z. Akgul, I. Burgués-Ceballos, G. Konstantatos and F. Boscherini, Nanomaterials, 2020, 10, 316.
74. L. Choubrac, M. Paris, A. Lafond, C. Guillot-Deudon, X. Rocquefelte and S. Jobic, Phys. Chem. Chem. Phys., 2013, 15, 10722–10725.
75. A. Sharma, A. H. Pandey, M. K. Jangid, V. Srihari, H. K. Poswal and A. Mukhopadhyay, ACS Appl. Mater. Interfaces, 2023, 15, 782–794.
76. M. V. Khenkin, E. A. Katz, A. Abate, G. Bardizza, J. J. Berry, C. Brabec, F. Brunetti, V. Bulović, Q. Burlingame, A. DiCarlo, R. Cheacharoen, Y. B. Cheng, A. Colsmann, S. Cros, K. Domanski, M. Dusza, C. J. Fell, S. R. Forrest, Y. Galagan, D. DiGirolamo, M. Grätzel, A. Hagfeldt, E. vonHauff, H. Hoppe, J. Kettle, H. Köbler, M. S. Leite, S. (Frank)Liu, Y. L. Loo, J. M. Luther, C. Q. Ma, M. Madsen, M. Manceau, M. Matheron, M. McGehee, R. Meitzner, M. K. Nazeeruddin, A. F. Nogueira, Ç. Odabaşı, A. Osherov, N. G. Park, M. O. Reese, F. DeRossi, M. Saliba, U. S. Schubert, H. J. Snaith, S. D. Stranks, W. Tress, P. A. Troshin, V. Turkovic, S. Veenstra, I. Visoly-Fisher, A. Walsh, T. Watson, H. Xie, R. Yıldırım, S. M. Zakeeruddin, K. Zhu and M. Lira-Cantu, Nat. Energy, 2020, 5, 35–49.

---