Time-resolved photoelectron diffraction imaging of methanol photodissociation involving molecular hydrogen ejection

Abstract

Imaging ultrafast atomic and molecular hydrogen motion with femtosecond time resolution is a challenge for ultrafast spectroscopy due to the low mass and small scattering cross section of the moving neutral hydrogen atoms and molecules. Here, we propose time- and momentum-resolved photoelectron diffraction (TMR-PED) as a way to overcome limitations of existing methodologies and illustrate its performance using a prototype molecular dissociation process involving the sequential ejection of a neutral hydrogen molecule and a proton from the methanol dication. By combining state-of-the-art molecular dynamics and electron-scattering methods, we show that TMR-PED allows for direct imaging of hydrogen atoms in action. More specifically, the fingerprint of hydrogen dynamics reflects the time evolution of polarization-averaged molecular-frame photoelectron angular distributions (PA-MFPADs) as would be recorded in X-ray pump/X-ray probe experiments with few-femtosecond resolution. We present the results of two precursor experiments that support the feasibility of this approach.

---

1 Introduction

X-ray free-electron lasers (XFELs) and ultrafast electron diffraction (UED) open new routes to visualize femtosecond-scale temporal variations of the structure of matter.¹ In this context, tracing the motion of hydrogen atoms or protons has become a topic of thorough investigation due to its importance in chemistry and chemical biology. X-ray and electron diffraction by XFELs and UED is, however, less sensitive to such hydrogen motions because of the low scattering cross sections of the hydrogen atom with X-rays and relativistic electrons, making the corresponding studies a true challenge.² For gas-phase isolated molecules, two alternative approaches have successfully been used to visualize the hydrogen motion that causes isomerization in, e.g., acetylene (HCCH), one of the most widely studied systems: Coulomb explosion imaging^3–7 and laser-induced electron diffraction.⁸ Both approaches use COLTRIMS reaction microscopes^9–11 that allow one to record the three-dimensional momenta of fragment ions and emitted electrons in coincidence. This experimental approach was initially limited to small molecules. But recently, employing an intense near-infrared laser as ionizing radiation and COLTRIMS as the detection technique, studies on the topic of this paper have been performed.^12,13 For example, Kling et al. observed Coulomb explosion of CH₃CH₂OH and identified the fragments H₂O⁺ and H₃O⁺, which can only be regarded as a result of single and double hydrogen migration, respectively.¹⁴ The theoretical studies reported in that paper suggested that these hydrogen migration processes take place in both molecular cations and dications. Yet, these hydrogen motions have so far not been visualized with femtosecond time resolution in any previous experiment.

In this work, we consider as a case study methanol, CH₃OH, the simplest alcohol. The fragmentation dynamics of doubly ionized methanol has been widely studied under different conditions. In a pioneering work conducted by Eland,¹⁵ the triatomic hydrogen ion H₃⁺ was found to be a primary fragment in the photoionization of several small molecules, including methanol. A photoelectron–photoion–photoion coincidence (PEPIPICO) scheme was used, which relies on the charge separation of the doubly charged parent ions for the detection of the corresponding reaction channels. Electron-impact-ionization experiments¹⁶ in combination with coincidence momentum-imaging techniques have also been employed to investigate the formation of di- and triatomic hydrogen molecular ions during the fragmentation of the methanol dication. From these experiments, a hydrogen atom migration mechanism, with the formation of an intermediate dicationic structure, was proposed. Formation of H₃⁺ in doubly ionized methanol has also been observed under the impact of 1.2 MeV Ar⁸⁺ projectiles¹⁷ and has been interpreted as the result of an intramolecular bond rearrangement of the methyl group. Experiments with the same projectile but at lower impact energies (120 keV) on deuterated methanol (both CD₃OH and CH₃OD) have shown the presence of tri-hydrogen ions after hydrogen migration, pointing out the different processes at different collision energies.¹⁸ Thus, two mechanisms for the formation of tri-hydrogen cations from doubly ionized methanol have been proposed: one solely involving the methyl side and the other one involving both the methyl and hydroxyl sides of the methanol parent. Optimization of intense femtosecond-laser pulses using pulse-shaping approaches on deuterated methanol CD₃OH¹⁹ has been used to manipulate the ratio of D₂H⁺ to D₃⁺ formation, thus favoring one mechanism vs. the other. Furthermore, single-photon double ionization of methanol leading to methanol dications in a singlet spin state has shown that H₃⁺ is abundantly produced.²⁰

With the advent of ultrafast techniques, time-resolved studies of the dynamics responsible for hydrogen migration processes have recently allowed for obtaining a temporal picture of these processes. Pioneering experiments on the two-body Coulomb explosion of doubly ionized methanol produced by an intense laser field using coincidence momentum imaging have shown that the lifetime of the ejection process of H₃⁺ should be longer than 1 ps.²¹ Subsequent experiments performed using strong laser fields and supporting ab initio molecular dynamics (MD) simulations have shown a much shorter time for the formation of H₃⁺: ∼100 fs.^22,23 Time-resolved extreme-ultraviolet pump/near-infrared probe experiments, combined with high-level nonadiabatic ab initio MD simulations, have suggested an even faster formation of H₃⁺, on a sub-100 fs time scale.²⁴ The time-resolved detection of H₃⁺ from the methanol dication induced by intense-field sequential ionization (few-cycle laser pulses)²⁵ has also been employed to investigate the vibrational dynamics of the methanol cation.

Earlier first-principles MD simulations performed on doubly ionized methanol²⁶ have shown that initially a vibrationally and rotationally excited neutral H₂ moiety is formed. This H₂ then moves around the remaining dicationic fragment for a few tens to hundreds of femtoseconds (hydrogen roaming) before triatomic hydrogen is formed and ejected. This picture is nowadays accepted, as well as the fact that H₃⁺ formation is an ultrafast process occurring from a few tens to hundreds of femtoseconds. However, despite all the above-mentioned efforts, experiments showing in real time the formation and roaming of H₂ and the subsequent H₃⁺ ejection from doubly charged methanol remain to be done. As the frontier of different experimental approaches is constantly pushed nowadays, in particular due to the above-mentioned XFEL technique, direct imaging of hydrogen migration processes with few-femtosecond temporal and angstrom spatial resolution has finally come into reach. In order to support and demonstrate the feasibility of such experiments, theoretical simulations of the time- and momentum-resolved photoelectron diffraction (TMR-PED) resulting from hydrogen migration in the methanol, ethanol, propanol, and isopropanol dications have been recently reported.^27,28

In this paper, we focus on the methanol dication for a more in-depth investigation of all possible dissociation channels (DCs). For this, we have performed global reaction route mapping (GRRM) calculations and more extensive MD simulations. Joining potential energy surface exploration with MD simulations has been successfully used to explain a variety of previous experiments (see, e.g., ref. 14 and 29–36). To demonstrate how to visualize the H motion in the methanol dication, polarization-averaged molecular-frame photoelectron angular distributions (PA-MFPADs), which are equivalent to TMR-PED, are computed for the major DC, CHO⁺ + H₂ + H⁺. The calculations show that hydrogen migration reflects the time evolution of the PA-MFPADs as they would be recorded in X-ray pump/X-ray probe experiments with few-femtosecond resolution. To support the feasibility of the proposed approach, we present the results of two precursor experiments, one performed at the European XFEL (Schenefeld, Germany) and the other one at the PETRA III synchrotron (Hamburg, Germany).

2 Theoretical modeling and choice of the relevant observables

To experimentally realize the TMR-PED measurements that probe hydrogen motions in doubly ionized methanol, CH₃OH²⁺, two ultrashort X-ray pulses are needed. The first pulse (pump) is used to ionize either the C 1s or O 1s core levels of neutral methanol and to produce dications via Auger decay. The second pulse (probe) is employed to generate the O 1s photoelectron for the PED measurement as a function of the pump–probe delay. We have picked O 1s ionization as a natural choice for the probe step because methanol contains a single oxygen atom and most migrating hydrogen atoms end up in the vicinity of it. Conceptually, however, photoelectron diffraction imaging does not rely on such distinct marker atoms to be present in a molecule. To measure the molecular-frame momentum of the electron ejected by the probe pulse, the 3D orientation of the molecule in space must be determined. For this, specific reaction channels must be selected from among all competing channels. To make this selection and identify the reaction plane (please see Section 4.3 for the definition of the reaction plane), we propose to employ Coulomb explosion imaging (CEI) triggered by the probe pulse and restrict the recorded data set to specific fragmentation channels. After interaction of doubly charged methanol with the X-ray probe pulse, the resulting triply charged methanol will further ionize as a result of Auger decay, thus leading to a quadruply charged species that will finally break up into various (mostly singly) charged fragments. In addition, to simplify the atomic assignment in the experiment, one could use isotope-labeled samples, such as, e.g., CH₃OD.^37,38 However, since the dynamics are significantly slower (and therefore computationally more expensive) for deuterated species than that for non-deuterated species, we will only use non-deuterated methanol in our simulations.

Our theoretical simulations rely on the combination of three different approaches to fully characterize the fragmentation dynamics of doubly charged methanol, the ionization by the probe pulse, and the subsequent electron diffraction. We have thoroughly explored the potential energy surfaces of doubly ionized methanol with singlet and triplet spin multiplicities using the GRRM methodology. Then, MD simulations are used to mimic the nuclear dynamics following ionization by the pump pulse. Finally, PA-MFPADs resulting from the probe step are computed along the different nuclear trajectories resulting from the MD simulations.

2.1 Exploration of the potential energy surfaces – isomerization and fragmentation paths

Stable equilibrium structures (EQs) of CH₃OH²⁺ with both singlet and triplet spin multiplicities were optimized from the geometry of the neutral EQ using the GRRM program^39–41 combined with the quantum chemistry program package Gaussian16.⁴² Then, an automated exploration of the isomerization followed by dissociation pathways for singlet/triplet dications CH₃OH²⁺ was started from the optimized EQs by using the scaled hypersphere search-anharmonic downward distortion following (SHS-ADDF) method, implemented in the GRRM program at the DFT-B3LYP/6-311G(2d,d,p)(=CBSB7) level of theory. All possible isomerization pathways were fully explored, and DCs were judged from interatomic distances using the DownDC and UpDC options in the GRRM program. When the distance between an atom A and another atom B exceeds 0.1 × DownDC × 2 × (R^A_b + R^B_b), they are recognized to be nonbonding. In those cases where the global reaction route mappings were carried out using an uphill walking method, the threshold in distance is given by 0.1 × UpDC × 2 × (R^A_b + R^B_b). The covalent radii R_b for each atom were taken from ref. 43. We adapted larger judging-parameter values than the default ones, using DownDC = 15 and UpDC = 20.

2.2 Molecular dynamics

Technical details of our ab initio MD simulations of CH₃OH²⁺ have been given in ref. 28 and so a brief description is presented here. The MD simulations of singlet and triplet CH₃OH²⁺ were performed at the same level of theory: B3LYP/CBSB7. We assume that inner-shell single ionization of the neutral molecule by the X-ray pulse occurs at the equilibrium geometry. We also assume that the subsequent Auger–Meitner relaxation to the electronic ground state of each spin multiplicity of CH₃OH²⁺ is almost instantaneous in comparison with the subsequent nuclear dynamics. As a consequence, the dication will be in a highly rovibrational state of the electronic ground state of CH₃OH²⁺, and all trajectories describing the nuclear dynamics will be initiated from that electronic ground state at the equilibrium geometry assuming some initial internal energy. In this work, we have chosen 5 eV. The corresponding initial velocities of each atom were randomly sampled using the MD software Newton-X.^44–46 The validity of this simple approximation has been demonstrated in many previous studies, e.g., in ref. 14 and 29–36. In ref. 28, we compared the MD results for hydrogen migration in dications of different alcohols and confirmed that 5 eV is a reasonable excess energy for methanol. The time evolution of classical nuclear trajectories after the initial time t = 0 was then computed on the fly using the atom-centered density matrix propagation (ADMP) method^47–49 implemented in Gaussian16⁴² with a time step of 0.1 fs. For both singlet and triplet CH₃OH²⁺, we ran 1000 trajectories.

2.3 Theory of polarization-averaged molecular-frame photoelectron angular distributions (PA-MFPADs)

PA-MFPADs, resulting at each time step of the trajectories obtained in the MD simulations described above, have been calculated by using a single-channel approximation, so that they are proportional to the square modulus of the electric-dipole matrix element between the core and continuum states. We have employed the multiple-scattering theory⁵⁰ to calculate the continuum states. The multiple-scattering theory uses a multi-center expansion in spherical harmonics together with a numerical solution of the local Schrödinger equation on each atomic site. The scattering potentials are approximated by the spherically symmetric ones, the so-called Muffin-tin approximation. To reduce computation time, we have used atomic non-SCF electron densities.⁵¹ We have checked the validity of this approximation by comparing at 0.1, 20, and 50 fs the resulting PA-MFPADs with those obtained by using the actual DFT electron density. The results are nearly indistinguishable. The real part of the Hedin–Lundqvist potential^52,53 is used as the optical potential. While the full multiple-scattering scheme has been used for a photoelectron energy of 100 eV, a single-scattering approximation has been used for 500 eV and 2.5 keV where its appropriateness was confirmed by a test calculation. The maximum values of the angular momentum, l_max, for the partial-wave expansion were 5, 5, and 4 for the 100 eV case, 9, 8, and 7 for the 500 eV case, and 17, 17, and 14 for the 2.5 keV case, for O, C, and H, respectively. These values were estimated using the formula l_max ∼ kR_s, where R_s is the Muffin-tin radius obtained using the Norman criterion⁵⁴ without overlapping for the starting structure at 0 fs. The Muffin-tin radii and l_max are fixed during the dynamics. To obtain the PA-MFPADs we took the sum of the three Cartesian components of the electric–dipole matrix elements divided by 3.⁵⁵ All the TMR-PED calculations have been performed by using the MsSpec code.⁵⁶

3 Supporting experiments

While this paper focuses on the theoretical description and prediction of the photodissociation process and the accompanying photoelectron diffraction, we have performed two precursor experiments in order to support the modeled findings. Firstly, we used a COLTRIMS reaction microscope^9,11 to investigate the oxygen K-shell ionization of methanol using circularly polarized light pulses from the PETRA III synchrotron source. This experiment mimics the pump step of the proposed TMR-PED study. These measurements yielded 3D molecular-frame photoelectron angular distributions of the emitted oxygen K-shell electrons (for a breakup of the molecule into CH₃⁺/OH⁺), which have been published elsewhere.⁵⁷ In addition, the measurements demonstrate the population of several different dicationic states after absorption of the pump photon. Secondly, we performed a Coulomb explosion imaging measurement at the European X-ray free-electron laser (EuXFEL) using the COLTRIMS reaction microscope located at the SQS instrument. In this study, we performed Coulomb explosion imaging of (deuterated) methanol molecules.

The COLTRIMS setup employed at the beamline P04 of the PETRA III synchrotron used two 80 mm diameter microchannel-plate detectors with hexagonal delay-line position readout⁵⁸ for the coincident detection of ions and electrons. The spectrometer, which guided ions and electrons generated by the photoreaction to the two detectors, consisted of an ion arm with a length of 7 cm and an electron arm with a length of 15 cm. The extraction field was chosen as 21.9 V cm⁻¹ and a superimposed homogeneous magnetic field (6.3 G) allowed for the detection of electrons with a kinetic energy of up to 30 eV with full solid-angle coverage. Methanol was introduced into the main chamber as vapor forming a supersonic gas jet by slightly heating a reservoir containing methanol to a temperature of 316 K (vapor pressure ∼400 mbar) and using a nozzle of 100 μm diameter. Further details of this experiment can be found in ref. 57.

For the experimental campaign performed at the EuXFEL, the total length of the ion spectrometer was 180 mm, which included a high-electric-field region with a length of 50 mm and a field-free drift region of 130 mm length. The extraction field at the interaction point of the XFEL light and the supersonic gas jet had a strength of approximately 325 V cm⁻¹. A hexagonal delay-line detector with an active area of 120 mm diameter was used for this measurement.

While we actually performed a two-color X-ray pump/X-ray probe experiment⁵⁹ at the EuXFEL, the full analysis of the time-resolved data set is still ongoing. We therefore present only results where we integrated over all pump–probe delays and merged the corresponding recorded data sets. We employed two different photon energies for the pump and the probe pulse, namely 550 eV and 660 eV, respectively. The pulse durations were approximately 10 fs for the pump pulse and approximately 20 fs for the probe pulse. These pulse durations were estimated using a grating spectrometer for spectral diagnostics of the FEL beam.^60,61 The total energy on the X-ray gas monitor (XGM⁶²) of the SQS instrument was about 110 μJ when both colors were used and about 100 μJ when only the pump pulse was used.

4 Results and discussion

4.1 Potential energy surfaces

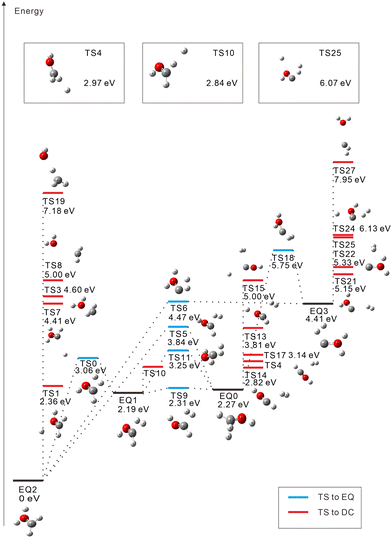
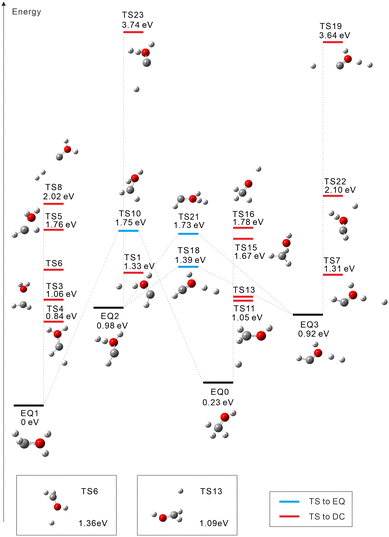
The starting points in the exploration of the potential energy surfaces (EQ0, CH₃–OH²⁺) were obtained by geometry optimization for the singlet and triplet spin multiplicities of the dication starting from the neutral geometry of CH₃OH (see Fig. 1 and 2, respectively). Relative energies were calculated including the zero-point vibrational-energy (ZPVE) correction for singlet and triplet states and referenced to the most stable structure found in each case. Four equilibrium geometries (EQi) were obtained in each surface: singlet and triplet states. The starting EQ0 was not the most stable stationary point. A hydrogen-transferred structure CH₂=OH₂²⁺ is more stable than EQ0: EQ2 for singlet and EQ1 for triplet states. In addition to B3LYP, we also performed ωB97X-D and MP2 geometry optimizations and then CCSD(T) single-point energy calculations on the MP2-optimized geometries of CH₃–OH²⁺ and CH₂=OH₂²⁺. The results confirm that the latter structure is more stable, which is consistent with previous studies.^63–66 In the case of the triplet state, the direct connection pathway from EQ0 and EQ1 to EQ2 and EQ3 was not obtained.

Fig. 1 Calculated isomerization and dissociation pathways for the singlet dication CH₃OH²⁺ (red: O, gray: C, and white: H). EQi, TSi: equilibrium geometry and transition state, respectively. The energy difference from the neutral ground state to the dication EQ0 is calculated to be +28.59 eV for the singlet state (including the ZPVE correction). Due to space limitations, three TSs are shown in boxes.

Fig. 2 Calculated isomerization and dissociation pathways for the triplet dication CH₃OH²⁺ (red: O, gray: C, and white: H). EQi, TSi: equilibrium geometry and transition state, respectively. The energy difference from the neutral ground state to the dication EQ0 is calculated to be +30.34 eV for the triplet state (including the ZPVE correction). Due to space limitations, two TSs are shown in boxes.

During the search for transition states (TSs), some of them (e.g., such as those connecting the same EQs or connecting DCs to each other) turned out not to be meaningful. These were discarded and are not included in Fig. 1 and 2. For the singlet state, 22 TSs are obtained: six of them are EQ-connecting TSs, and the other sixteen are connected to DCs. Several TSs are found to connect EQ structures with the COH₂⁺ + H₂⁺ DC; they are in an energy range of 5.15 eV to 2.27 eV with respect to EQ0. Proton-loss channels have also been found: the remaining fragment is CH₂OH⁺ (TSs 1, 4, and 10), CHOH₂⁺ (TS7), CHO⁺⋯H₂ (TS13), or COH⁺⋯H₂ (TSs 15, 24, and 25), where the ⋯ symbol represents a weakly bound complex. H₃⁺ dissociation pathways are connected to EQ0 via TS14 (2.82 eV) and TS17 (3.14 eV) and to EQ3 via TS22 (5.33 eV). Three C–O bond-breaking DCs (CH₃⁺ + OH⁺, CH₂⁺ + H₂O⁺, and CH⁺ + H₃O⁺) are connected to EQ2 (CH₂=OH₂²⁺) via TSs 3, 8, and 19, respectively. These channels imply energy barriers in a range of 2.27 eV to 4.60 eV from EQ0 and the isomerization to EQ2. The CH₂⁺ + H₂O⁺ dissociation path was also calculated to be connected directly to EQ3 through TS27 (7.95 eV).

For the triplet state, 17 TSs were obtained (Fig. 2). Three TSs are EQ-connecting TSs, and the other fourteen TSs are connected to DCs. Judging from the Mulliken charge for the dissociating systems, TSs 16 and 19 are connected to H⁺ dissociation producing CH₃O⁺ (TS16) or COH⁺⋯H₂ (TS19). Seven TSs formally lead to H^0.5+ ejection yielding CH₂OH^1.5+ (TSs 6, 11, and 13), CHOH₂^1.5+ (TSs 1, 4, and 7), or COH⁺⋯H₂^0.5+ (TS23). Five more TSs are connected to other DCs: COH₂⁺ + H₂⁺ (TS8 at 2.02 eV), CHO⁺⋯H + H₂⁺ (TS22 at 2.10 eV), CH₃⁺ + OH⁺ (TS15 at 1.67 eV), CH₂⁺ + H₂O⁺ (TS3 at 1.06 eV), and CH⁺ + H₃O⁺ (TS5 at 1.76 eV). In ref. 20, a photodissociation experiment of methanol dications combined with nonadiabatic ab initio MD simulations revealed that the production of H₃⁺ occurs exclusively in the singlet state. This is compatible with our finding that there is no dissociation pathway from EQ0 to H₃⁺ in the triplet state.

4.2 Molecular dynamics

Table 1 provides the branching ratios for the fragmentation channels of singlet and triplet CH₃OH²⁺, respectively, obtained from 1000 MD trajectories each. In the fragment assignment, we assumed that there is a bond between two atoms with an internuclear distance shorter than 4 Å. The long threshold distance of 4 Å was chosen to distinguish bond cleavage from large-amplitude vibrations induced by high kinetic energy. If a threshold of 3 Å is used, the branching ratios in Table 1 change by no more than a few percent. Note that fragment assignment was done at the end of each trajectory. Thus, trajectories exhibiting very-large-amplitude motions exceeding the 4 Å threshold, as in H₂ roaming, where internuclear distances can temporally reach up to 9 Å,²⁴ were not affected by the choice of this threshold. The integer charge of each fragment was determined in reference to the non-integer Mulliken charges of constituent atoms. The table also lists the branching ratios for subchannels where the H atom initially bonded to O is distinguished from those initially bonded to C and denoted by A. One can see that, for both singlet and triplet CH₃OH²⁺, hydrogen migration can occur not only from C to O but also from O to C, although the ratios for such subchannels with hydrogen migration are small. Note that more than two fragments can be generated by multiple fragmentation in MD trajectories, while the GRRM results in Fig. 1 and 2 focus on two-body DCs (single fragmentation).

Table 1 Branching ratios for the fragmentation channels of singlet and triplet CH₃OH²⁺ with an initial kinetic energy of 5 eV obtained from 1000 MD trajectories each. In addition, each fragmentation channel is divided into subchannels where the H atom initially bonded to O is denoted by A distinct from those initially bonded to C

Channel	% Ratio		Subchannel	% Ratio
	Singlet	Triplet		Singlet	Triplet
CH2OH^2+ + H		1.9	CH2OA^2+ + H		1.9
CH2OH^+ + H^+	33.6	22.1	CH2OA^+ + H^+	32.0	21.3
			CH2OH^+ + A^+	1.6	0.6
			CHAOH^+ + H^+		0.2
CHO^+ + H2+H^+	22.1		CHO^+ + H2 + A^+	20.0
			CHO^+ + HA + H^+	1.6
			CAO^+ + H2 + H^+	0.5
CHOH^2+ + H2	14.5	0.2	CHOA^2+ + H2	14.4	0.2
			CHOH^2+ + HA	0.1
CHOH^+ + H2^+	10.5	5.8	CHOA^+ + H2^+	10.4	5.7
			CHOH^+ + HA^+	0.1	0.1
COH^+ + H2^+ + H		0.7	COA^+ + H2^+ + H		0.7
COH^+ + H2 + H^+	4.8		COA^+ + H2 + H^+	4.8
CH3OH^2+	3.8	2.3	CH3OA^2+	3.8	2.3
CH2OH2^2+	3.6	0.4	CH2OHA^2+	3.6	0.4
CH3O^2+ + H		0.5	CH3O^2+ + A		0.4
			CH2AO^2+ + H		0.1
CH3O^+ + H^+	2.2	2.0	CH3O^+ + A^+	1.4	1.7
			CH2AO^+ + H^+	0.8	0.3
CHOH^+ + H^+ + H	2.2	24.4	CHOA^+ + H^+ + H	2.2	23.8
			CHOH^+ + H^+ + A		0.3
			CHOH^+ + A^+ + H		0.3
CHOH + H^+ + H^+		0.4	CHOA + H^+ + H^+		0.4
CHOH2^2+ + H		0.2	CHOHA^2+ + H		0.2
CHOH2^+ + H^+	0.5	0.8	CHOHA^+ + H^+	0.5	0.8
CH2O^+ + H2^+		1.0	CHAO^+ + H2^+		0.6
			CH2O^+ + HA^+		0.4
CH2O^+ + H^+ + H	0.5	27.1	CH2O^+ + H^+ + A	0.3	14.8
			CH2O^+ + A^+ + H		11.6
			CHAO^+ + H^+ + H	0.2	0.7
CH2O + H^+ + H^+		0.4	CH2O + H^+ + A^+		0.4
CHO^+ + H3^+	0.5		CAO^+ + H3^+	0.3
			CHO^+ + H2A^+	0.2
CHO^+ + H^+ + H + H	0.5	6.4	CHO^+ + A^+ + H + H	0.3	1.7
			CHO^+ + H^+ + H + A	0.2	4.7
COH^+ + H3^+	0.4		COA^+ + H3^+	0.4
COH^+ + H^+ + H + H		0.4	COA^+ + H^+ + H + H		0.4
CHO^+ + H2^+ + H	0.2	1.0	CHO^+ + H2^+ + A	0.2	0.7
			CHO^+ + HA^+ + H		0.2
			CAO^+ + H2^+ + H		0.1
CO + H2 + H^+ + H^+	0.1		CO + H2 + H^+ + A^+	0.1
CH3^2+ + OH		0.1	CH3^2+ + OA		0.1
CH3^+ + OH^+		1.4	CH3^+ + OA^+		1.4
CH2^+ + H2O^+		0.3	CH2^+ + HAO^+		0.3
CH2O^2+ + H2		0.1	CH2O^2+ + HA		0.1
COH2^+ + H2^+		0.1	COHA^+ + H2^+		0.1

---

In the singlet case, the C–O bond is unbroken in all trajectories. This is consistent with the fact that TSs 3, 8, 19, and 27 connected to the C–O breaking DCs in Fig. 1 are higher in energy on a relative scale. The most dominant channel is CH₂OH⁺ + H⁺ (33.6%) as expected from the corresponding TSs (1, 4, and 10), which are the first, third, and fourth lowest TSs leading to DCs. More than half (53.1%) of the 1000 trajectories generate molecular-hydrogen species H₂ (41.5%), H₂⁺ (10.7%), and H₃⁺ (0.9%). However, the third and fourth dominant channels, CHOH²⁺ + H₂ (14.5%) and CHOH⁺ + H₂⁺ (10.5%), are not predicted by GRRM. It is considered that the fourth arises from the third by “inverse harpooning”, i.e., a long-range electron transfer from H₂ to CHOH²⁺.⁶⁷ The emergence of these channels is attributed to a dynamical (kinetic energy) effect. The second dominant channel CHO⁺ + H₂ + H⁺ (22.1%) can be viewed mainly as a result of the further fragmentation of the third one CHOH²⁺ + H₂ → CHO⁺ + H⁺ + H₂ (i.e., H⁺ ejection from CHOH²⁺). There may be also minor contributions such as the dissociation of the weakly bound complex CHO⁺⋯H₂ (see TS13) and that of H₃⁺ resulting from CHO⁺ + H₃⁺ (see TS17). When the excess energy of CH₃OH²⁺ is doubled to 10 eV, CHO⁺ + H₂ + H⁺ becomes the dominant channel (27.4%), followed by the CH₂OH⁺ + H⁺ channel (18.1%), due to further fragmentation of the CH₂OH⁺ moiety. This indicates that the CHO⁺ + H₂ + H⁺ channel predominates over a wide range of excess energies. In Section 4.3, we present PA-MFPADs computed for the subchannel with H⁺ detached from O, i.e., CHO⁺ + H₂ + A⁺ (20.0%).

Almost all triplet TSs (except TSs 19 and 23) in Fig. 2 are very low-lying in energy compared to the singlet TSs in Fig. 1. This accounts for the wide variety of fragmentation channels of triplet CH₃OH²⁺ shown in Table 1; for instance, the C–O bond cleavage is observed in the triplet case (albeit only at 1.8%). The deviation from the DCs with half-integer charged fragments, e.g., CH₂OH^1.5+ + H^0.5+, due to high kinetic energy prefers the homolytic cleavage CH₂OH⁺ + H⁺ (22.1%) to the heterolytic one CH₂OH²⁺ + H (1.9%). Including these channels, a large number of trajectories (88.3%) produce atomic fragments H and/or H⁺ (most of them undergoing multiple fragmentation), while the yields of H₂ (0.3%) and H₂⁺ (8.6%) are quite low. The channel of particular interest, where H₂ and H⁺ are emitted from CH₃OH²⁺, is not found in the triplet case.

4.3 Polarization-averaged molecular-frame photoelectron angular distributions

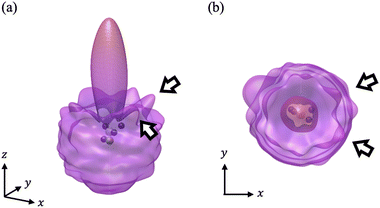
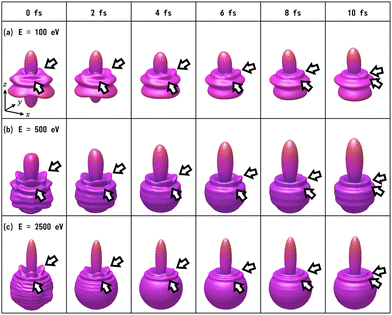
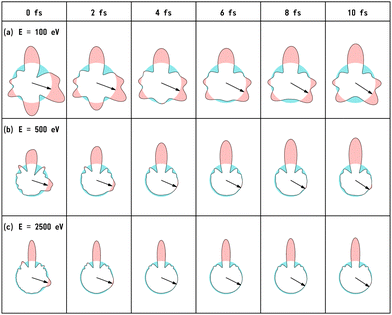
We have calculated the PA-MFPADs averaged over 200 trajectories of one of the main fragmentation channels, CHO⁺ + H₂ + A⁺, where the H motion in the dication CH₃OH²⁺ is significant. Fig. 3 shows a PA-MFPAD for an arbitrary single trajectory from different viewing directions at 6 fs after formation of a doubly charged methanol ion at 500 eV photoelectron energy. We see how the two H atoms come together. Snapshots of three arbitrarily chosen single-trajectory PA-MFPADs are given in the ESI† (for more detailed information, see Fig. S1–S3). Fig. 4 shows the temporal evolution of the PA-MFPADs for the H₂ ejection at photoelectron energies of (a) 100 eV, (b) 500 eV, and (c) 2.5 keV after the formation of the doubly charged methanol ion. In order to reproduce the actual experimental situation, the PA-MFPADs of the corresponding trajectories should be averaged in the reaction plane. In Fig. 4, we define the reaction plane as the plane containing the triangle whose vertices coincide with the C atom on the z axis (z > 0, i.e., upward direction), the O atom at the origin, and the center of gravity of the ejected H₂ in the zx plane (x > 0). In this figure, however, the z axis (molecular axis) is tilted by 20 degrees from the plane of the figure and the x axis is rotated by −30 degrees along the z axis to enable better visualization of the peak structure of the PA-MFPAD corresponding to the forward scattering of H₂. Snapshots of the PA-MFPADs from another viewing direction are given in the ESI† (see Fig. S4). As can be seen, diffraction of the O 1s photoelectron by the different atomic centers leads to pronounced lobes or depletions with respect to a perfectly isotropic (spherical) distribution. Therefore, for a fixed-in-space molecule with known orientation, one can unambiguously associate the motions of the hydrogen atoms or protons to a specific structural variation in the PA-MFPADs. The structural variation is more pronounced at low energy (100 eV) than at high energies (500 eV and 2.5 keV), since slower electrons are more sensitive to the details of the multi-centric molecular potential. The two arrows in each time frame indicate, as a guide to the eye, the position of the peak associated with the two hydrogen atoms that become H₂. The moving lobe is very well localized, especially at 2.5 keV, which makes the identification of the motion of the H atoms easier. However, as the H atoms move away from the O atom, it is difficult to track the ejected H atoms at high energies, especially if a certain amount of time has elapsed. The two H atoms become H₂ in about 10 fs. After that, the H₂ dissociates from the doubly charged methanol and the corresponding peak of the PA-MFPADs is no longer visible.

Fig. 3 A single-trajectory PA-MFPAD for H₂ ejection at 500 eV photoelectron energy at 6 fs upon formation of a doubly charged methanol ion. Color code for the atoms: oxygen – green, carbon – white, and hydrogen – blue. To guide the eye, two arrows indicate the position of the peaks connected to two hydrogen atoms, which ultimately become H₂. We put the O atom at the origin, the C atom at the z axis (z > 0), and the center of mass of the ejected H₂ at the zx plane (x > 0). (a) View in which the z axis is tilted 20 degrees from the figure plane and the x axis is rotated −30 degrees from the figure plane. (b) View from the positive z axis.

Fig. 4 Snapshots of PA-MFPADs averaged over 200 trajectories for the H₂ ejection at photoelectron energies (a) 100 eV, (b) 500 eV, and (c) 2.5 keV. To guide the eye, two arrows (in each time frame) indicate the position of the peaks associated with two hydrogen atoms, which ultimately become H₂. We set the O atom at the origin, the C atom on the z axis (z > 0), and the center of gravity of ejected H₂ on the zx plane (x > 0). In the figure, the z axis is tilted by 20 degrees off the plane of the figure and the x axis is rotated by −30 degrees off the plane of the figure, to make it easier to see the peak corresponding to the H₂ ejection.

One can see that, at a photoelectron energy of 2.5 keV, the two hydrogen peaks are almost invisible after a few femtoseconds, so they are unlikely to be observed in an experiment given the experimental noise. However, the peaks are more pronounced at photoelectron energies of 100 and 500 eV, indicating that this is the best choice for their experimental visualization.

We note that PA-MFPAD measurements can therefore be potentially used to infer H₂ roaming. In most previous experiments, H₂ roaming is identified indirectly using disruptive pump–probe techniques, with the detection of subsequent charged fragments, such as H₃⁺ after H⁺ abstraction by the H₂ roamer. In contrast, PAD measurements as those proposed in this work would allow one to characterize roaming of a neutral H₂ fragment by tracking its motion in time and space.

Finally, Fig. 5 shows the temporal evolution of the PA-MFPADs for the H⁺ ejection (i.e., in terms of the labeling employed above, the A⁺ ejection) at photoelectron energies of (a) 100 eV, (b) 500 eV, and (c) 2.5 keV. Please note that the temporal evolution is much more pronounced for low kinetic energies (similar to that shown in Fig. 4). We define the reaction plane as the plane of the figure, containing the triangle whose vertices coincide with the C atom on the z axis (z > 0), the O atom at the origin, and the H⁺ in the zx plane (x > 0). Please note that this is a different definition from that of Fig. 4. The arrows indicate the angles averaged over 200 trajectories for the position of the ejected H⁺ in each time frame. Up to about 4 fs, the peak position of the PA-MFPADs corresponds to the averaged angle, but the peak disappears with time, especially at high energies. Within 10 fs, there are many trajectories in which the H ion is bonded to the O atom, and the O–H distance averaged over 200 trajectories at 10 fs is slightly smaller than it is at 8 fs. However, the H⁺ ion starts moving at random angles soon after irradiation by the XFEL pump pulse. The rapidly smearing peak position of the PA-MFPADs for the H⁺ ions is due to the random H⁺ motion and not due to the increase of the O–H⁺ distance. The range of angles that the H⁺ ion can take in the zx plane at 10 fs is 115 degrees.

Fig. 5 Snapshots of PA-MFPADs averaged over 200 trajectories for the H⁺ ejection at photoelectron energies (a) 100 eV, (b) 500 eV, and (c) 2.5 keV. The arrows indicate the angles averaged over 200 trajectories for the position of H⁺ ejected in each time frame. We set the O atom at the origin, the C atom on the z axis (z > 0), and the ejected H⁺ on the zx plane, i.e., the plane of the figure (x > 0).

4.4 Results of our precursor experiments

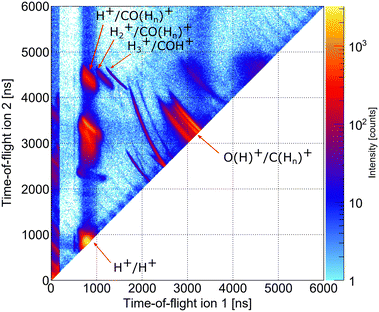
As indicated in Section 3, we performed two precursor experiments yielding information on the conceptual feasibility of the measurements proposed here. Two aspects are investigated: firstly, the synchrotron measurement provides information on the population of different dicationic states after the initial photoionization of the molecule using single photons with an energy higher than the O 1s threshold. The synchrotron measurement corresponds to the pump step of the current TMR-PED study. Secondly, the measurements performed at the European XFEL answer the question whether the molecular orientation at the instant of the emission of the probing electron (wave) can be determined from the coincident measurement of ionic molecular fragments (under experimental conditions suitable for coincident detection of the electrons).

By inspecting the ions measured in coincidence at the beamline P04 of the PETRA III synchrotron, using a photon energy of 550 eV, we observe different breakup channels of the methanol molecule. This measurement was performed using conventional methanol molecules (i.e., without deuteration). Fig. 6 shows a coincidence map of the flight times of the first two ions, which were detected after the oxygen K-shell photoionization (and subsequent Auger decay). Among several features, which stem from ionization of residual gases (e.g., N₂, O₂, and H₂O), distinct islands indicate the breakup of the methanol molecule into different fragments. In the upper left corner, three features are labeled, which correspond to a coincident detection of singly charged CO (or COH_n) fragments with protons, molecular hydrogen ions, and H₃⁺ ions. Accordingly, the left-most feature of the three may correspond to the dicationic breakup channel discussed in Section 4.3, i.e., the breakup channel CHO⁺ + H₂ + H⁺ (A⁺). However, as the experiment is insensitive to neutral particles, it cannot be ensured that the fragment, which was not detected, is indeed molecular hydrogen. In addition, we cannot determine from the experiment whether the measured proton belonged originally to the methyl side or the hydroxyl side of the molecule. The strongest feature in Fig. 6 (located in the bottom left corner) belongs to cases where two protons were detected in coincidence, which may result from a more violent fragmentation of the methanol molecule or from the fragmentation of water molecules (i.e., from the background). An almost symmetric breakup of the molecule can be found between the two lines, which are caused by residual nitrogen and oxygen molecules fragmenting into two singly charged atomic ions. The corresponding line is labeled as O(H)⁺/C(H_n)⁺. We provide the relative abundance of the detected fragmentation channels in Table 2. The values provided there are given relative to the absolute abundance of the H₃⁺/COH⁺ fragmentation channel.

Fig. 6 Photoion–photoion coincidence map depicting the dependence of the flight times of the first and second ions detected in our synchrotron measurement. Several features belonging to the breakup of methanol molecules are visible. See the text for details.

Table 2 Relative abundance of different breakup channels of the methanol molecule after ionization with photons of hν = 550 eV. The values provided are normalized to the measured abundance of the breakup channel H₃⁺/COH⁺, which is a particularly clean fragmentation channel in our measured data

Breakup channel	Relative abundance
CH3^+/OH^+	9.24
CH2^+/OH^+	5.39
H3^+/COH^+	1.0
H2^+/COH^+	2.45
H^+/COH^+	17.32

---

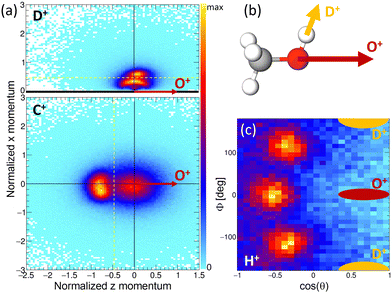
The results of the Coulomb explosion imaging experiment performed at the European XFEL on deuterated methanol, i.e., CH₃OD [see Fig. 7(b)], are shown in Fig. 7. Among several other breakup channels, we used the subset of measured data where we detected four ions in coincidence, namely H⁺ + D⁺ + C⁺ + O⁺, for the plots presented there. This coincidence channel is particularly interesting with respect to the modeled results presented in Section 4.3. If the absorption of the first X-ray photon generated the (fragmenting) dicationic state CHO⁺ + H₂ + D⁺ (labeled A⁺ above), the absorption of a second photon will increase by two the charge of the CHO⁺ fragment, resulting in CHO³⁺. A rapid fragmentation of this triply charged molecular ion into H⁺ + C⁺ + O⁺ is highly probable. Accordingly, this four-fold coincidence subset of the measured data is a prime candidate for the observation of the PA-MFPADs presented in Section 4.3. Fig. 7(a) shows the measured ion momenta in a molecular frame of reference. Contrary to Section 4.3, in this coordinate frame, the emission direction of the O⁺ ion defines the z axis. Together with the momentum of the D⁺ ion, the zx plane is spanned. This plane is defined such that the emission direction of the D⁺ is pointing towards positive values of x in all cases. We plot the measured momenta of the D⁺ and C⁺ ions in this molecular frame after normalizing the magnitude of all momenta such that the magnitude of the O⁺ equals 1. The corresponding momentum distribution of the D⁺ is shown in Fig. 7(a) in the top panel. It consists of two features, an arc-like distribution occurring at lower momenta and a more localized feature at p_x > 0.5 a.u. Circular (or arc-like) distributions are typically a sign of a rotation during (or prior to) the fragmentation process, i.e., a fingerprint of a slower breakup of the molecule. The other main feature, however, indicates an emission direction of the D⁺ ion relative to the emission direction of the O⁺, which fits the geometry of the methanol-OD molecule [compare to the sketch shown in Fig. 7(b)]. The lower panel of Fig. 7(a) shows the molecular-frame momentum distribution of the C⁺ ion. Two main features are visible here: firstly, a strong peak located at the left, which indicates a clear back-to-back emission of the C⁺ and the O⁺ ions. Secondly, the histogram has a less pronounced contribution centered around zero momentum. In order to visualize the momentum-space properties of the measured proton, we employ spherical coordinates and inspect their angular emission distribution in a different molecular frame. There, the azimuthal and polar angles of the proton emission direction are given with respect to the sum and difference momenta of the C and O ions. The proton's angular distribution is shown in Fig. 7(c). For reference, the approximate emission directions of the O⁺ and D⁺ in this coordinate frame are given by the red and yellow areas. The angular distributions show three main peaks, which correspond to the three possible sites the proton was initially emitted from. Please note that the data set shown in Fig. 7(c) is in addition restricted with respect to the momenta of the other ions. We have selected the D⁺ and C⁺ momenta such that the regions that indicate a slow(er) fragmentation of the molecule are excluded. That is, we have discarded the D⁺ momenta in panel (a) below the yellow dotted line (namely, the arc-like feature) and the C⁺ momenta located to the right of the yellow line. In case we employ the full data set, the proton angular distribution shown in Fig. 7(c) has less contrast, but the three main peaks are still visible (not shown). In combination, these measurements support the feasibility of the proposed study of time-resolved electron diffraction. It was shown that (i) the desired dicationic state is generated in an experiment and (ii) a Coulomb explosion imaging measurement, which provides indeed the information on the molecular orientation at the instant of the absorption of a second X-ray photon (i.e., at the instant of the probe step), can be performed. In particular, the Coulomb explosion imaging experiments performed at the EuXFEL were done at X-ray fluences that would still allow for measuring electrons in coincidence, just as has been shown in earlier experiments on O₂ molecules.^68–70 It should be noted, however, that such experiments are at the current frontier of what is technically achievable. Coincident measurement of multiple ions and electrons under typical XFEL conditions remains a very challenging task. The effective repetition rates available, for example, at the European XFEL are in the range of approximately 500 Hz, and (as indicated above) typically only subsets of the recorded data can be employed for the extraction of PA-MFPADs. This has strong implications on the statistics that needs to be recorded. In addition, to observe the features of the roaming particles these MFPADs need to be measured in three dimensions. In earlier work, it was sufficient to measure the electron emission angle relative to the molecular axis, which relaxed the requirements with respect to recorded statistics drastically.

Fig. 7 Left row: experimental ion momenta in the molecular frame defined by the emission direction of the O⁺ ion (defining the z axis) and the D⁺ ion (spanning together with the O⁺ the zx plane and defining the positive x direction), measured at SQS/EuXFEL. In the top panel, the momentum of the D⁺ ion is depicted in that frame, in the bottom panel the momentum of the C⁺ ion is shown. Right row: sketch of the breakup of the methanol-OD molecule (top panel). The bottom panel on the right shows the three-dimensional angular emission distribution of the measured protons in the coordinate frame spanned by the O⁺ and D⁺ ions [yellow lines in panels (a) and (b) indicate filters for the ion momenta used in panel (c), see the text for details].

5 Conclusions

We have presented a theoretical study of the fragmentation dynamics of doubly ionized methanol molecules in the gas phase, with emphasis on channels involving emission of atomic and molecular hydrogen. We have systematically explored the corresponding potential energy surfaces, performed molecular dynamics (MD) simulations, and described time- and momentum-resolved photoelectron diffraction (TMR-PED) as would be observed in (attosecond) X-ray pump/X-ray probe experiments. Due to the generation of two X-ray pulses of different photon energies and pulse durations on the order of several hundred attoseconds, as has been demonstrated recently at FEL facilities such as LCLS⁷¹ and EuXFEL,⁷² the realization of the suggested studies would be possible and the related experiments are expected to highlight the performances of this new operation mode of X-ray free-electron lasers. The calculated polarization-averaged molecular-frame photoelectron angular distributions (PA-MFPADs) exhibit the signature of hydrogen dynamics in the form of moving features that evolve in the few-femtosecond time scale and allow for a straightforward visualization in real space. The theoretical results are supported by two experiments, which confirm the conceptual feasibility of the proposed approach. Measuring TMR-PED has in principle become feasible by using X-ray free-electron laser pulses, which are now available with a sufficiently high repetition rate and ultrashort duration (a few femtoseconds down to sub-femtoseconds). Along these lines, the first electron–ion coincidence measurements have emerged recently,^68–70 which combined such XFEL-generated light pulses with multi-coincidence detection techniques (such as COLTRIMS). We therefore expect that TMR-PED will provide unprecedented insight into hydrogen migration processes in the very near future.

Author contributions

K. Y., M. K., H. X., N. K., S. G., F. O., Y. T., S. D.-T., F. M. K. H., and K. U. performed the theoretical modeling. K. Y., S. G., F. O., Y. T., and K. H. computed the PA-MFPADs. M. K. performed the molecular dynamics simulations. H. X. and N. K. computed the isomerization and dissociation pathways. F. T., K. F., L. K., J. S., D. T., M. S., R. D., and T. J. carried out the synchrotron experiments at PETRA III. F. T., R. B., B. E., T. Ma., T. Mu., D. E. R., P. S., S. U., M. M., E. W., D. R., A. R., E. K., and T. J. prepared and conducted the experiments at the European XFEL. T. J. analyzed the experimental data. M. K., N. K., F. T., T. J., S. D.-T., F. M., K. H., and K. U. wrote the manuscript.

Data availability

Source data are available for this paper. Data recorded for the experiment at the European XFEL are available at https://doi.org/10.22003/XFEL.EU-DATA-002902-00. The datasets used and/or analyzed during the current study are available upon reasonable request form the corresponding authors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was partially performed under the Cooperative Research Program of “Network Joint Research Center for Materials and Devices” and partially funded by the Spanish Ministry of Science and Innovation – Ministerio Español de Ciencia e Innovación MICINN – projects PID2022-138288NB-C31 and PID2022-138470NB-I00, the Severo Ochoa Programme for Centres of Excellence in R & D (CEX2020-001039-S) and the María de Maeztu Programme for Units of Excellence in R & D (CEX2023-001316-M). K. Y. acknowledges that this work was supported by JST, the establishment of university fellowships towards the creation of science technology innovation, Grant Number JPMJFS2115. N. K. and K. U. acknowledge research funding from the Institute for Quantum Chemical Exploration (IQCE). F. T. acknowledges funding from the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – Project 509471550, Emmy Noether Programme. E. W., D. R., and A. R. were supported by the US Department of Energy, Office of Science, Office of Basic Energy Sciences, under contract No. DE-FG02-86ER13491. K. H. acknowledges funding from JSPS KAKENHI under Grant No. 18K05027 and 17K04980. This article is based upon work from COST actions CA18212 – Molecular Dynamics in the GAS phase (MD-GAS) and CA18222 – Attosecond Chemistry (AttoChem), supported by COST (European Cooperation in Science and Technology). We acknowledge the generous allocation of computer time at the Centro de Computación Científica at the Universidad Autónoma de Madrid (CCC-UAM). We acknowledge DESY (Hamburg, Germany), a member of the Helmholtz Association HGF, for the provision of experimental facilities. Parts of this research were carried out at PETRA III and we would like to thank the P04 team for assistance in using the beamline. Beamtime was allocated for proposal I-20180746 EC. We acknowledge the European XFEL in Schenefeld, Germany, for the provision of XFEL beamtime at the SQS instrument and would like to thank the staff for their assistance. The experimental work was supported by the Cluster of Excellence “CUI: Advanced Imaging of Matter” of the Deutsche Forschungsgemeinschaft (DFG)-EXC 2056-project ID 390715994, by BMBF, and in part by the Deutsche Forschungsgemeinschaft (DFG) Project No. 328961117-SFB 1319 ELCH (extreme light for sensing and driving molecular chirality, subproject B1). Open Access funding provided by the Max Planck Society.

Notes and references

1. K. Amini, A. Rouzée and M. J. J. Vrakking, Structural Dynamics with X-ray and Electron Scattering, Royal Society of Chemistry, 2023.
2. E. G. Champenois, N. H. List, M. Ware, M. Britton, P. H. Bucksbaum, X. Cheng, M. Centurion, J. P. Cryan, R. Forbes, I. Gabalski, K. Hegazy, M. C. Hoffmann, A. J. Howard, F. Ji, M.-F. Lin, J. P. F. Nunes, X. Shen, J. Yang, X. Wang, T. J. Martinez and T. J. A. Wolf, Phys. Rev. Lett., 2023, 131, 143001.
3. Y. H. Jiang, A. Rudenko, O. Herrwerth, L. Foucar, M. Kurka, K. U. Kühnel, M. Lezius, M. F. Kling, J. van Tilborg, A. Belkacem, K. Ueda, S. Düsterer, R. Treusch, C. D. Schröter, R. Moshammer and J. Ullrich, Phys. Rev. Lett., 2010, 105, 263002.
4. C. E. Liekhus-Schmaltz, I. Tenney, T. Osipov, A. Sanchez-Gonzalez, N. Berrah, R. Boll, C. Bomme, C. Bostedt, J. D. Bozek, S. Carron, R. Coffee, J. Devin, B. Erk, K. R. Ferguson, R. W. Field, L. Foucar, L. J. Frasinski, J. M. Glownia, M. Gühr, A. Kamalov, J. Krzywinski, H. Li, J. P. Marangos, T. J. Martinez, B. K. McFarland, S. Miyabe, B. Murphy, A. Natan, D. Rolles, A. Rudenko, M. Siano, E. R. Simpson, L. Spector, M. Swiggers, D. Walke, S. Wang, T. Weber, P. H. Bucksbaum and V. S. Petrovic, Nat. Commun., 2015, 6, 8199.
5. M. Pitzer, G. Kastirke, M. Kunitski, T. Jahnke, T. Bauer, C. Goihl, F. Trinter, C. Schober, K. Henrichs, J. Becht, S. Zeller, H. Gassert, M. Waitz, A. Kuhlins, H. Sann, F. Sturm, F. Wiegandt, R. Wallauer, L. P. H. Schmidt, A. S. Johnson, M. Mazenauer, B. Spenger, S. Marquardt, S. Marquardt, H. Schmidt-Böcking, J. Stohner, R. Dörner, M. Schöffler and R. Berger, ChemPhysChem, 2016, 17, 2465–2472.
6. X. Li, et al. , Phys. Rev. Res., 2022, 4, 013029.
7. R. Boll, J. M. Schäfer, B. Richard, K. Fehre, G. Kastirke, Z. Jurek, M. S. Schöffler, M. M. Abdullah, N. Anders, T. M. Baumann, S. Eckart, B. Erk, A. De Fanis, R. Dörner, S. Grundmann, P. Grychtol, A. Hartung, M. Hofmann, M. Ilchen, L. Inhester, C. Janke, R. Jin, M. Kircher, K. Kubicek, M. Kunitski, X. Li, T. Mazza, S. Meister, N. Melzer, J. Montano, V. Music, G. Nalin, Y. Ovcharenko, C. Passow, A. Pier, N. Rennhack, J. Rist, D. E. Rivas, D. Rolles, I. Schlichting, L. P. H. Schmidt, P. Schmidt, J. Siebert, N. Strenger, D. Trabert, F. Trinter, I. Vela-Perez, R. Wagner, P. Walter, M. Weller, P. Ziolkowski, S.-K. Son, A. Rudenko, M. Meyer, R. Santra and T. Jahnke, Nat. Phys., 2022, 18, 423–428.
8. B. Wolter, M. G. Pullen, A.-T. Le, M. Baudisch, K. Doblhoff-Dier, A. Senftleben, M. Hemmer, C. D. Schröter, J. Ullrich, T. Pfeifer, R. Moshammer, S. Gräfe, O. Vendrell, C. D. Lin and J. Biegert, Science, 2016, 354, 308–312.
9. R. Dörner, V. Mergel, O. Jagutzki, L. Spielberger, J. Ullrich, R. Moshammer and H. Schmidt-Böcking, Phys. Rep., 2000, 330, 95–192.
10. J. Ullrich, R. Moshammer, A. Dorn, R. Dörner, L. P. H. Schmidt and H. Schmidt-Böcking, Rep. Prog. Phys., 2003, 66, 1463.
11. T. Jahnke, T. Weber, T. Osipov, A. L. Landers, O. Jagutzki, L. P. H. Schmidt, C. L. Cocke, M. H. Prior, H. Schmidt-Böcking and R. Dörner, J. Electron Spectrosc. Relat. Phenom., 2004, 141, 229–238.
12. E. Wang, N. G. Kling, A. C. LaForge, R. Obaid, S. Pathak, S. Bhattacharyya, S. Meister, F. Trost, H. Lindenblatt, P. Schoch, M. Kübel, T. Pfeifer, A. Rudenko, S. Díaz-Tendero, F. Martín, R. Moshammer, D. Rolles and N. Berrah, J. Phys. Chem. Lett., 2023, 14, 4372–4380.
13. T. Severt, E. Weckwerth, B. Kaderiya, P. Feizollah, B. Jochim, K. Borne, F. Ziaee, K. Raju P., K. D. Carnes, M. Dantus, D. Rolles, A. Rudenko, E. Wells and I. Ben-Itzhak, Nat. Commun., 2024, 15, 74.
14. N. G. Kling, S. Díaz-Tendero, R. Obaid, M. R. Disla, H. Xiong, M. Sundberg, S. D. Khosravi, M. Davino, P. Drach, A. M. Carroll, T. Osipov, F. Martín and N. Berrah, Nat. Commun., 2019, 10, 2813.
15. J. H. D. Eland, Rapid Commun. Mass Spectrom., 1996, 10, 1560–1562.
16. R. K. Kushawaha and B. Bapat, Chem. Phys. Lett., 2008, 463, 42–46.
17. S. De, J. Rajput, A. Roy, P. N. Ghosh and C. P. Safvan, Phys. Rev. Lett., 2006, 97, 213201.
18. K. Hayakawa, J. Mastumoto, H. Shiromaru and Y. Achiba, J. Phys. B: At., Mol. Opt. Phys., 2011, 44, 075207.
19. N. Iwamoto, C. J. Schwartz, B. Jochim, K. Raju P., P. Feizollah, J. L. Napierala, T. Severt, S. N. Tegegn, A. Solomon, S. Zhao, H. Lam, T. N. Wangjam, V. Kumarappan, K. D. Carnes, I. Ben-Itzhak and E. Wells, J. Chem. Phys., 2020, 152, 054302.
20. K. Gope, E. Livshits, D. M. Bittner, R. Baer and D. Strasser, J. Phys. Chem. Lett., 2020, 11, 8108–8113.
21. T. Okino, Y. Furukawa, P. Liu, T. Ichikawa, R. Itakura, K. Hoshina, K. Yamanouchi and H. Nakano, Chem. Phys. Lett., 2006, 419, 223–227.
22. N. Ekanayake, M. Nairat, B. Kaderiya, P. Feizollah, B. Jochim, T. Severt, B. Berry, K. R. Pandiri, K. D. Carnes, S. Pathak, D. Rolles, A. Rudenko, I. Ben-Itzhak, C. A. Mancuso, B. S. Fales, J. E. Jackson, B. G. Levine and M. Dantus, Sci. Rep., 2017, 7, 4703.
23. N. Ekanayake, T. Severt, M. Nairat, N. P. Weingartz, B. M. Farris, B. Kaderiya, P. Feizollah, B. Jochim, F. Ziaee, K. Borne, K. Raju P., K. D. Carnes, D. Rolles, A. Rudenko, B. G. Levine, J. E. Jackson, I. Ben-Itzhak and M. Dantus, Nat. Commun., 2018, 9, 5186.
24. E. Livshits, I. Luzon, K. Gope, R. Baer and D. Strasser, Commun. Chem., 2020, 3, 49.
25. T. Ando, A. Shimamoto, S. Miura, A. Iwasaki, K. Nakai and K. Yamanouchi, Commun. Chem., 2018, 1, 7.
26. K. Nakai, T. Kato, H. Kono and K. Yamanouchi, J. Chem. Phys., 2013, 139, 181103.
27. F. Ota, S. Abe, K. Hatada, K. Ueda, S. Díaz-Tendero and F. Martín, Phys. Chem. Chem. Phys., 2021, 23, 20174–20182.
28. T. Kuraoka, S. Goto, M. Kanno, S. Díaz-Tendero, J. Reino-González, F. Trinter, A. Pier, L. Sommerlad, N. Melzer, O. D. McGinnis, J. Kruse, T. Wenzel, T. Jahnke, H. Xue, N. Kishimoto, K. Yoshikawa, Y. Tamura, F. Ota, K. Hatada, K. Ueda and F. Martín, J. Phys. Chem. A, 2024, 128, 1241–1249.
29. S. Maclot, D. G. Piekarski, A. Domaracka, A. Méry, V. Vizcaino, L. Adoui, F. Martín, M. Alcamí, B. A. Huber, P. Rousseau and S. Díaz-Tendero, J. Phys. Chem. Lett., 2013, 4, 3903–3909.
30. D. G. Piekarski, R. Delaunay, S. Maclot, L. Adoui, F. Martín, M. Alcamí, B. A. Huber, P. Rousseau, A. Domaracka and S. Díaz-Tendero, Phys. Chem. Chem. Phys., 2015, 17, 16767–16778.
31. E. Erdmann, M. Łabuda, N. F. Aguirre, S. Díaz-Tendero and M. Alcamí, J. Phys. Chem. A, 2018, 122, 4153–4166.
32. M. McDonnell, A. C. LaForge, J. Reino-González, M. Disla, N. G. Kling, D. Mishra, R. Obaid, M. Sundberg, V. Svoboda, S. Díaz-Tendero, F. Martín and N. Berrah, J. Phys. Chem. Lett., 2020, 11, 6724–6729.
33. P. Rousseau, D. G. Piekarski, M. Capron, A. Domaracka, L. Adoui, F. Martín, M. Alcamí, S. Díaz-Tendero and B. A. Huber, Nat. Commun., 2020, 11, 3818.
34. D. Barreiro-Lage, P. Bolognesi, J. Chiarinelli, R. Richter, H. Zettergren, M. H. Stockett, L. Carlini, S. Díaz-Tendero and L. Avaldi, J. Phys. Chem. Lett., 2021, 12, 7379–7386.
35. D. Mishra, J. Reino-González, R. Obaid, A. C. LaForge, S. Díaz-Tendero, F. Martín and N. Berrah, Phys. Chem. Chem. Phys., 2022, 24, 433–443.
36. S. Ganguly, D. Barreiro-Lage, N. Walsh, B. Oostenrijk, S. L. Sorensen, S. Díaz-Tendero and M. Gisselbrecht, Commun. Chem., 2022, 5, 16.
37. K. Gope, E. Livshits, D. M. Bittner, R. Baer and D. Strasser, Nat. Sci., 2021, 1, e10022.
38. J. M. Farrar, Nat. Sci., 2022, 2, e20210090.
39. S. Maeda, K. Ohno and K. Morokuma, Phys. Chem. Chem. Phys., 2013, 15, 3683–3701.
40. K. Ohno and H. Satoh, Exploration on Quantum Chemical Potential Energy Surfaces: Towards the Discovery of New Chemistry, RSC, Theoretical and Computational Chemistry Series, 2022.
41. K. Ohno, Chem. Rec., 2016, 16, 2198–2218.
42. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016.
43. B. Cordero, V. Gómez, A. E. Platero-Prats, M. Revés, J. Echeverría, E. Cremades, F. Barragán and S. Alvarez, Dalton Trans., 2008, 2832–2838.
44. M. Barbatti, G. Granucci, M. Persico, M. Ruckenbauer, M. Vazdar, M. Eckert-Maksić and H. Lischka, J. Photochem. Photobiol., A, 2007, 190, 228–240.
45. M. Barbatti, M. Ruckenbauer, F. Plasser, J. Pittner, G. Granucci, M. Persico and H. Lischka, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 26–33.
46. M. Barbatti, M. Bondanza, R. Crespo-Otero, B. Demoulin, P. O. Dral, G. Granucci, F. Kossoki, H. Lischka, B. Mennucci, S. Mukherjee, M. Pederzoli, M. Persico, M. Pinheiro Jr, J. Pittner, F. Plasser, E. Sangiogo Gil and L. Stojanonic, J. Chem. Theory Comput., 2022, 18, 6851–6865.
47. H. B. Schlegel, J. M. Millam, S. S. Iyengar, G. A. Voth, A. D. Daniels, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 2001, 114, 9758–9763.
48. S. S. Iyengar, H. B. Schlegel, J. M. Millam, G. A. Voth, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 2001, 115, 10291–10302.
49. H. B. Schlegel, S. S. Iyengar, X. Li, J. M. Millam, G. A. Voth, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 2002, 117, 8694–8704.
50. C. R. Natoli, M. Benfatto, S. Della Longa and K. Hatada, J. Synchrotron Radiat., 2003, 10, 26–42.
51. J. P. Desclaux, Comput. Phys. Commun., 1975, 9, 31–45.
52. L. Hedin and S. Lundqvist, Solid State Phys., 1970, 23, 1–181.
53. L. Hedin and B. I. Lundqvist, J. Phys. C: Solid State Phys., 1971, 4, 2064.
54. J. G. Norman Jr., Mol. Phys., 1976, 31, 1191–1198.
55. F. Ota, K. Yamazaki, D. Sébilleau, K. Ueda and K. Hatada, J. Phys. B: At., Mol. Opt. Phys., 2021, 54, 024003.
56. D. Sébilleau, C. Natoli, G. M. Gavaza, H. Zhao, F. Da Pieve and K. Hatada, Comput. Phys. Commun., 2011, 182, 2567–2579.
57. L. Kaiser, K. Fehre, N. M. Novikovskiy, J. Stindl, D. Tsitsonis, G. Gopakumar, I. Unger, J. Söderström, O. Björneholm, M. Schöffler, T. Jahnke, R. Dörner, F. Trinter and P. V. Demekhin, J. Phys. B: At., Mol. Opt. Phys., 2020, 53, 194002.
58. O. Jagutzki, A. Cerezo, A. Czasch, R. Dörner, M. Hattaß, M. Huang, V. Mergel, U. Spillmann, K. Ullmann-Pfleger, T. Weber, H. Schmidt-Böcking and G. D. W. Smith, IEEE Trans. Nucl. Sci., 2002, 49, 2477–2483.
59. S. Serkez, W. Decking, L. Froehlich, N. Gerasimova, J. Grünert, M. Guetg, M. Huttula, S. Karabekyan, A. Koch, V. Kocharyan, Y. Kot, E. Kukk, J. Laksman, P. Lytaev, T. Maltezopoulos, T. Mazza, M. Meyer, E. Saldin, E. Schneidmiller, M. Scholz, S. Tomin, M. Vannoni, T. Wohlenberg, M. Yurkov, I. Zagorodnov and G. Geloni, Appl. Sci., 2020, 10, 2728.
60. A. Koch, J. Risch, W. Freund, T. Maltezopoulos, M. Planas and J. Grünert, J. Synchrotron Radiat., 2019, 26, 1489–1495.
61. N. Gerasimova, D. La Civita, L. Samoylova, M. Vannoni, R. Villanueva, D. Hickin, R. Carley, R. Gort, B. E. Van Kuiken, P. Miedema, L. Le Guyarder, L. Mercadier, G. Mercurio, J. Schlappa, M. Teichman, A. Yaroslavtsev, H. Sinn and A. Scherz, J. Synchrotron Radiat., 2022, 29, 1299–1308.
62. T. Maltezopoulos, F. Dietrich, W. Freund, U. F. Jastrow, A. Koch, J. Laksman, J. Liu, M. Planas, A. A. Sorokin, K. Tiedtke and J. Grünert, J. Synchrotron Radiat., 2019, 26, 1045–1051.
63. W. J. Bouma and L. Radom, J. Am. Chem. Soc., 1983, 105, 5484–5486.
64. B. F. Yates, W. J. Bouma and L. Radom, J. Am. Chem. Soc., 1986, 108, 6545–6554.
65. B. Thapa and H. B. Schlegel, J. Phys. Chem. A, 2014, 118, 1769–1776.
66. C. Li, C.-H. Chin, T. Zhu and J. Z. H. Zhang, J. Mol. Struct., 2020, 1217, 128410.
67. K. Gope, E. Livshits, D. M. Bittner, R. Baer and D. Strasser, Sci. Adv., 2022, 8, eabq8084.
68. G. Kastirke, et al. , Phys. Rev. X, 2020, 10, 021052.
69. G. Kastirke, et al. , Phys. Rev. Lett., 2020, 125, 163201.
70. G. Kastirke, F. Ota, D. V. Rezvan, M. S. Schöffler, M. Weller, J. Rist, R. Boll, N. Anders, T. M. Baumann, S. Eckart, B. Erk, A. De Fanis, F. Kehre, A. Gatton, S. Grundmann, P. Grychtol, A. Hartung, M. Hofmann, M. Ilchen, C. Janke, M. Kircher, M. Kunitski, X. Li, T. Mazza, N. Melzer, J. Montano, V. Music, G. Nalin, Y. Ovcharenko, A. Pier, N. Rennhack, D. E. Rivas, R. Dörner, D. Rolles, A. Rudenko, P. Schmidt, J. Siebert, N. Strenger, D. Trabert, I. Vela-Perez, R. Wagner, T. Weber, J. B. Williams, P. Ziolkowski, L. P. H. Schmidt, A. Czasch, Y. Tamura, N. Hara, K. Yamazaki, K. Hatada, F. Trinter, M. Meyer, K. Ueda, P. V. Demekhin and T. Jahnke, Phys. Chem. Chem. Phys., 2022, 24, 27121–27127.
71. J. Duris, S. Li, T. Driver, E. G. Champenois, J. P. MacArthur, A. A. Lutman, Z. Zhang, P. Rosenberger, J. W. Aldrich, R. Coffee, G. Coslovich, F.-J. Decker, J. M. Glownia, G. Hartmann, W. Helml, A. Kamalov, J. Knurr, J. Krzywinski, M.-F. Lin, J. P. Marangos, M. Nantel, A. Natan, J. T. O'Neal, N. Shivaram, P. Walter, A. L. Wang, J. J. Welch, T. J. A. Wolf, J. Z. Xu, M. F. Kling, P. H. Bucksbaum, A. Zholents, Z. Huang, J. P. Cryan and A. Marinelli, Nat. Photonics, 2020, 14, 30–36.
72. S. Serkez, et al., 2024, manuscript under preparation.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp01015a

---