Dy(OH)₃: a paramagnetic magnetocaloric material for hydrogen liquefaction

Abstract

The magnetic properties of a series of Ln(OH)₃ (where Ln = Gd–Er) coordination polymer materials have been examined to evaluate their potential as magnetocaloric materials. Dy(OH)₃ was found to exhibit an impressive magnetic entropy change of 33.4 J kg⁻¹ K⁻¹ at 12 K for a magnetic field change of 5-0 T, based on magnetisation measurements. Further magnetic heat capacity analysis indicated a maximum adiabatic temperature change of 8.4 K at 22.7 K. The favourable magnetocaloric parameters obtained for Dy(OH)₃ demonstrated its effectiveness to act as a magnetic cooling material for hydrogen liquefaction, since the boiling point of hydrogen aligns well with the temperature for peak magnetocaloric performance of Dy(OH)₃ for high field changes.

---

Introduction

Low temperature cooling capabilities are essential for a number of diverse applications such as quantum computing, spintronics and medical imaging techniques that require cooling to temperatures well below 80 K.^1–3 Underlying these applications is the dependence on liquid cryogens, particularly liquid helium, an expensive and finite resource.⁴ One specific application that requires cooling to these temperatures is hydrogen liquefaction, in which gaseous hydrogen is condensed to its liquid state by cooling to 20.15 K before the resulting liquid hydrogen is stored in pressurised, thermally insulated containers. This greatly increases the storage density of the fuel key to employing the hydrogen economy to decarbonise modern society, enabling more efficient hydrogen storage and transport.^5,6 Due to the very low boiling point of hydrogen, liquefaction processes typically require the use of cryogens and a series of heat exchangers to condense the gas to its liquid state, the end result being an extended and energy-intensive process.⁷

An alternative to cryogen-assisted hydrogen liquefaction is that of a magnetocaloric-based liquefaction system in which magnetic materials utilising the magnetocaloric effect cool the feed gas to below the boiling point of liquid hydrogen; this would involve either using a sequence of magnetocalorics to cool from 77 K to 20 K or combining magnetocalorics with a cryocooler, whose efficiencies increase significantly towards the higher part of this temperature range.^8–11 This avoids the need for using liquid helium for low-temperature cooling and is more efficient than using a purely cryocooler-based system. The magnetocaloric effect refers to low temperature cooling obtained by placing paramagnetic materials in a cycled magnetic field to facilitate an entropically driven solid-state cooling process.¹² The advantage of such magnetic refrigeration is the renewable and recyclable nature of the working material and elimination of the need for expensive and non-renewable helium as a refrigerant leading to much interest in magnetocaloric materials from both fundamental^13–15 and applied perspectives.^16,17 Previously reported magnetocaloric materials have attained 60% of the ideal (Carnot) efficiency,¹⁸ but further improvements are required in the design and development of magnetocaloric materials before they can be employed as a practical alternative to conventional cryogen-based cooling methods. In order to maximise cooling efficiency, magnetocaloric materials must satisfy a number of design parameters, namely a dense structure with a high concentration of magnetic cations and large increases in magnetisation at low applied fields.

One class of materials capable of satisfying these requirements are coordination polymer materials in which small inorganic ligands, such as carbonates¹⁹ or hydroxides,²⁰ or simple organic ligands such as formate²¹ or oxalate²² can be used to synthesise structurally dense materials with a high concentration of magnetic ions.^23,24 Gd-based materials are the most heavily studied among magnetocalorics due to their high S = 7/2 spin number that leads to large magnetic entropy changes with the predicted maximum change given by nR ln(2S + 1). Despite this, the majority of Gd-based magnetocalorics are optimised for operation at ∼2 K where, although magnetic entropy changes of 42.8–66.4 J kg⁻¹ K⁻¹ have been reported,^25–27 increases in temperature lead to rapid decreases in magnetocaloric efficiency. Recently however, a number of materials have been reported that retain promising magnetocaloric properties up to 10 K through exploiting magnetic frustration arising from 1D chains of Ising spins within the crystal structure.^14,28–35

Currently, materials that maintain favourable magnetocaloric properties at temperatures above 10 K are much less common. In most cases, magnetic entropy changes and hence, magnetocaloric performance, decrease with increasing temperature. Despite this, several examples of favourable magnetocaloric performance at higher temperatures have been reported, such as GdCrO₄ which shows a maximum magnetic entropy change of 29.0 J kg⁻¹ K⁻¹ at 22 K for a field change of 9-0 T (ref. 36 and 37) and GdCo₂B₂ which undergoes a maximum change of 21.5 J kg⁻¹ K⁻¹ at 25 K for a field change of 7-0 T,³⁸ while entropy changes of between 15 and 20 J kg⁻¹ K⁻¹ at ∼20 K have been observed for similarly large field changes in other materials.^39–42 Several classes of materials such as various high entropy transition metal alloys and intermetallic RECo₁₂B₆ (where RE = Ce, Pr, Nd) materials have also achieved more modest magnetic entropy changes at temperatures ranging from 210 to 420 K (ref. 43 and 44) and 50–200 K (ref. 45) respectively. Compared to the high performance achieved at lower temperatures using more modest applied fields, this still leaves great scope for new magnetocaloric materials development at higher temperatures.

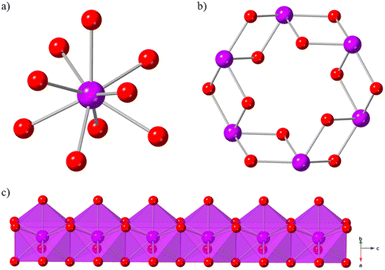
Ln(OH)₃ coordination polymer materials are ideal candidates for high temperature magnetocaloric studies. They form in well characterised 3D hexagonal structures,⁴⁶ in which simple hydroxide ligands enable high magnetic density, and they have magnetic properties^47–50 that are favourable to magnetocaloric performance at higher temperatures. The Ln(OH)₃ series is known to crystallise as dense, 3D structures with hexagonal 1D channels (Fig. 1b). The nine-coordinate Ln(III) ions (Fig. 1a) are bridged by μ₃-OH⁻ ligands to form chains of face-sharing polyhedra (Fig. 1c) along the c-axis that are connected in an edge-sharing fashion within the ab-plane.

Fig. 1 Crystal structure of Gd(OH)₃ showing (a) the nonacoordinate Gd(III) ion, (b) the hexagonal channels viewed down the c-axis and (c) 1D chains of Gd(III) face-sharing polyhedra. Atom labelling: Gd = purple and O = red. The hydrogen atoms have been omitted for clarity.

Ln–O bonds range from 2.437(8) and 2.452(14) Å in Gd(OH)₃ to 2.402(4) and 2.439(6) Å in Er(OH)₃ with the associated magnetic superexchange angles (Table S1†) similarly ranging from 95.4(4)° and 112.4(4)° in Gd(OH)₃ to 94.45(17)° and 111.94(11)° in Er(OH)₃, which gives the possibility of ferromagnetic coupling for the heavier lanthanides with Ising like-spins.⁴⁶ Consistent with this, while Gd(OH)₃ is known to order antiferromagnetically at 1.7 K (ref. 20) and Er(OH)₃ to remain paramagnetic down to 1.2 K,⁴⁷ the Tb, Dy and Ho analogues demonstrate ferromagnetic ordering with reported ordering temperatures of 3.7,⁴⁹ 3.5 and 2.5 K,⁵⁰ respectively. These previous studies have also described the Ising-like spin behaviour of the Tb, Dy and Ho materials in which the spins are aligned along the c-axis with dominant interactions between adjacent Ln chains, properties favourable to the design of magnetocaloric materials.

Here, we examine the magnetocaloric properties of the Ln(OH)₃ (Ln = Gd–Er) series of materials, using magnetisation and magnetic heat capacity methods to calculate the magnetic entropy and adiabatic temperature changes. Notably, while Tb(OH)₃ and Ho(OH)₃ maintain respectable performance over a 4–20 K temperature range, Dy(OH)₃ shows an even larger magnetic entropy change of 28.0 J kg⁻¹ K⁻¹ at 20 K for a 5-0 T field change. To the best of our knowledge, this material displays the largest entropy change reported for a magnetocaloric per weight at 20 K for this field change. The material also demonstrates an excellent adiabatic temperature change, −ΔT_ad, of 8.4 K at 22.7 K for a 5-0 T field change, which is higher than those reported for other magnetocaloric materials such as ErCo₂Ni_0.17Al_0.03 (ref. 51) and GdCrO₄.³⁷ Given its performance, Dy(OH)₃ is a viable magnetocaloric cooling material for cooling at the relatively high temperature of 20 K for use in applications such as the final stage of a magnetocaloric based hydrogen liquefaction system.

Results and discussion

Synthesis and structure

Polycrystalline samples of the five Ln(OH)₃ materials were synthesised using a hydrothermal reaction of the chosen Ln(NO)₃·xH₂O and 20 M NaOH solution which was heated at 200 °C in a sealed reaction vessel for 72 h. Powder X-ray diffraction analysis (Fig. S1–S5†) of the resulting solids confirmed the Gd, Tb, Dy, Ho and Er phases were all consistent with the previously reported hexagonal P6₃/m Ln(OH)₃ structures.⁴⁶

Magnetic susceptibility and magnetisation

The magnetic susceptibility properties of the Ln(OH)₃ series were characterised using SQUID magnetometry over a 1.8–300 K temperature range under an applied field 1000 Oe (see ESI† for experimental details). The magnetic susceptibility of the Gd and Er materials did not show any indications of long-range magnetic ordering down to 1.8 K while field cooled and zero field cooled susceptibility measurements of the Tb, Dy and Ho phases diverge at low temperatures, consistent with the ferromagnetic ordering previously reported for these materials (Fig. S6–S10†).^49,50 In order to identify the type of magnetic interactions present in these materials, the inverse susceptibility was fitted using the Curie–Weiss law (Fig. S11–S15†). The data was not fitted over the full 1.8–300 K temperature range, as the inverse susceptibility of the Tb–Er containing materials began to deviate from linearity at lower temperatures, likely in part due to crystal field effects. Instead, fits were carried out over both a high temperature range, where quenching of the orbital angular momentum by the weak crystal field of the lanthanides should not be significant, and a narrow low temperature range in which local linearity of the inverse susceptibility was maintained, which might be expected to give a better indication of the strength of magnetic interactions at these temperatures. The resulting Weiss temperatures, θ_CW, obtained from fitting the Curie–Weiss law (Table 1), indicated the presence of ferromagnetic interactions in the Tb(OH)₃ and Dy(OH)₃ materials while the Weiss temperature of Gd(OH)₃ was consistent with antiferromagnetic interactions; the results obtained for the Gd, Tb and Dy phases are consistent with their ordered states at low temperatures.^47–50 Surprisingly the θ_CW of Ho(OH)₃ is weakly negative over both temperature ranges, despite its ferromagnetic ordered state,⁵⁰ while the θ_CW of Er(OH)₃ changes from 3.67 K for the higher temperature fit to −8.95 K for the lower temperature fit. This may be a result of these materials having the highest orbital angular moments of the series and therefore being the most strongly influenced by crystal field effects.⁵²

Table 1 Magnetic properties of the Ln(OH)₃ series where high temperature Curie–Weiss fits were performed over a temperature range of 100–300 K

Ln	Expected μeff (μB)	High-T θCW (K)	High-T μeff (μB)	Low-T fit (K)	Low-T θCW (K)	Low-T μeff (μB)
Gd	7.94	−1.10	7.62	10–50	−1.83	7.63
Tb	9.72	20.15	9.51	10–50	0.97	10.75
Dy	10.65	19.60	10.62	10–50	5.08	11.33
Ho	10.60	−2.55	10.40	20–50	−1.69	10.26
Er	9.58	3.67	9.58	18–50	−8.95	10.32

---

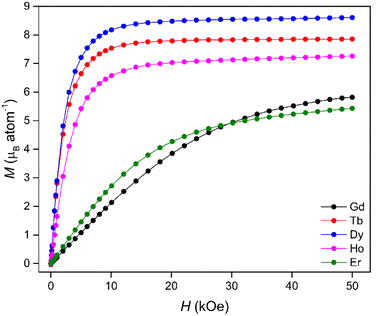
Isothermal magnetisation measurements at 4 K (Fig. 2) revealed that the Tb, Dy and Ho materials underwent rapid magnetisation at low fields with only minor increases in magnetisation observed beyond an applied field of 20 kOe. In contrast, the Gd and Er phases displayed much more gradual magnetisation behaviour with saturation unobserved even at the maximum applied field of 50 kOe, consistent with strong antiferromagnetic interactions. The rapid increases in the Tb(OH)₃, Dy(OH)₃ and Ho(OH)₃ magnetisation with magnetic field at low temperature (Fig. S16–S20†) were attributed to ferromagnetic interactions allowing easy alignment with the applied field. This is supported by the χ_MT data (Fig. S21–S25†) which all show sustained increases in χ_MT on cooling to near 4 K before decreasing below about 3 K. This indicates the onset of a ferromagnetic transition near 4 K, consistent with previous reports.^47,53 The influence of strong antiferromagnetic interactions contributing to the gradual magnetisation of the Gd(OH)₃ and Er(OH)₃ is also consistent with the temperature dependence of χ_MT, which decreases monotonically below 100 K in these materials.

Fig. 2 Isothermal magnetisation curves of the Ln(OH)₃ series at 4 K.

Previous single crystal studies of the magnetic properties of lanthanide hydroxide materials have characterised the magnetic interactions of the Tb, Dy and Ho phases as indicative of anisotropic Ising-type systems, with spins aligned parallel to the c-axis and the dominant interactions found between linear chains of Ln nearest-neighbours.^47,49,50 In comparison, the magnetic interactions of the Gd material are more consistent with a Heisenberg spin system characterised primarily by nearest-neighbour interactions within Gd chains and weak coupling between the chains, although non-trivial magnetic dipole interactions are also suggested to be present.⁴⁸

Using the Maxwell relation, ΔS_m(T) = ∫[∂M(T, B)/∂T]_BdB, the magnetocaloric properties of the Ln(OH)₃ series were evaluated by their magnetic entropy changes (Table 2) between 4 and 20 K and magnetic field changes of 1-0 and 5-0 T. The maximum entropy change, −ΔS^max_m of the series at 4 K for a 1-0 T field change (Fig. 3a) was 20.3 J kg⁻¹ K⁻¹ measured in Tb(OH)₃, while Gd(OH)₃ showed the smallest −ΔS^max_m of the series at 3.9 J kg⁻¹ K⁻¹. The magnetic entropy changes for the Tb, Dy and Ho materials were characterised by rapid decreases with increasing temperature, consistent with the loss of spin alignment with the applied field due to increasing thermal fluctuations. The magnetic entropy changes for a 2-0 T field change (Fig. S26, Table S2†) for Tb and Ho also began decreasing with increasing temperature after 4 K while the Dy phase only underwent an incremental increase of 0.7 J kg⁻¹ K⁻¹. Notably Dy(OH)₃ underwent a slight increase to reach a −ΔS^max_m of 23.8 J kg⁻¹ K⁻¹ at 7 K before reaching a minimum of 9.1 J kg⁻¹ K⁻¹ at 20 K, substantially higher than that observed at 20 K for ΔB = 1-0 T (cf. 2.7 J kg⁻¹ K⁻¹).

Table 2 Maximum entropy changes (−ΔS^max_m) and peak temperatures (T_max) of the Ln(OH)₃ series at different field changes

Ln	ΔB = 1-0 T			ΔB = 5-0 T
	T max (K)	−ΔS^maxm (J kg^−1 K^−1)	−ΔS^maxm (mJ cm^−3 K^−1)	T max (K)	−ΔS^maxm (J kg^−1 K^−1)	−ΔS^maxm (mJ cm^−3 K^−1)
Gd	4	3.9	21.1	4	43.7	239.9
Tb	4	20.3	113.4	5	26.8	150.0
Dy	4	19.4	112.4	12	33.4	193.4
Ho	4	17.5	103.8	9	28.7	170.5
Er	4	5.5	33.3	4	26.5	161.6

---

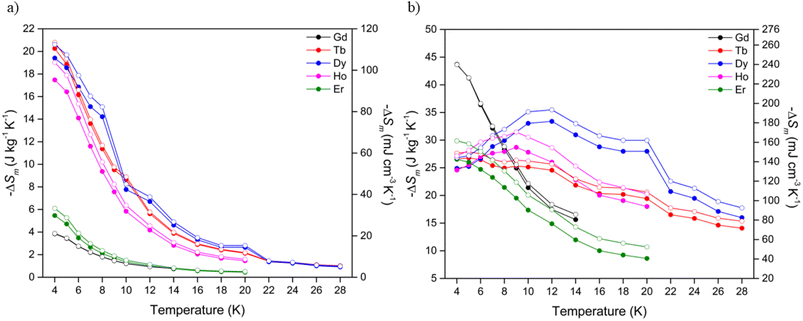Fig. 3 Magnetic entropy changes of the Ln(OH)₃ series for (a) ΔB = 1-0 T and (b) ΔB = 5-0 T. The filled and open symbols denote mass and volumetric entropy units respectively.

In contrast to the performance at low fields, at high fields (Fig. 3b) the Gd(OH)₃ material displayed the largest magnetic entropy change of the series, with a −ΔS^max_m of 43.7 J kg⁻¹ K⁻¹ at 4 K followed by sustained decreases with increasing temperature. This is consistent with previous studies that reported a maximum magnetic entropy change of 50.1 J kg⁻¹ K⁻¹ for the Gd(OH)₃ phase at 2 K and ΔB = 7-0 T.²⁰ The Er(OH)₃ material showed similar decreases with temperature in its magnetic entropy change with a maximum of 26.5 J kg⁻¹ K⁻¹ at 4 K followed by continued decreases with increasing temperature.

Unusually, the magnetic entropy changes for ΔB = 5-0 T of Dy(OH)₃ and Ho(OH)₃ initially rise with increasing temperature, reaching a maximum of 33.4 J kg⁻¹ K⁻¹ and 28.7 J kg⁻¹ K⁻¹ at 12 and 9 K respectively. Tb(OH)₃ also showed a gradual decrease in entropy change up to 20 K such that its values for 5-0 T field changes at this temperature are comparable to Dy(OH)₃ and Ho(OH)₃, with all of these above 20 J kg⁻¹ K⁻¹. We anticipate that this likely stems from the ferromagnetic correlations within the paramagnetic phase of these materials as previously established for the ferromagnetic Ising chains in A(HCO₂)₃ (A = Tb and Ho) and BOHCO₃ (B = Tb and Dy) with the higher temperature scale in these hydroxides resulting from the stronger magnetic interactions within them.^{14,21,33,47,49,50,54} Future studies of the hydroxides using modern neutron diffractometers to establish if they have magnetic diffuse scattering at these temperatures are needed to confirm this hypothesis.

Of the Ln(OH)₃ phases, Dy(OH)₃ has the most significant performance at temperatures that could be used for hydrogen liquefaction, retaining a value of 28.0 J kg⁻¹ K⁻¹ (162.0 mJ cm⁻³ K⁻¹) at 20 K. Additional measurements were made to higher temperatures, which showed that a magnetic entropy change of 16.0 J kg⁻¹ K⁻¹ was obtained even at 28 K. To the best of our knowledge, the highest performing magnetocaloric materials at around 20 K that have previously been reported are GdCrO₄ and GdCo₂B₂, which for a field change of 5-0 T have a −ΔS^max_m of 18.8 J kg⁻¹ K⁻¹ (101.0 mJ cm⁻³ K⁻¹)^36,37 and 17.1 J kg⁻¹ K⁻¹ (138.3 mJ cm⁻³ K⁻¹)³⁸ at 22 K and 25 K, respectively. In terms of volumetric entropy changes, the (Er_xR_1−x)Co₂ (R = Dy, Ho) series of materials⁵⁵ are also known to undergo large changes of >200 mJ cm⁻³ K⁻¹, the magnitude and temperature range (20–80 K) of which can be further tuned via transition metal doping.⁵¹ It should be noted, however, that while these materials have very large volumetric entropy changes due to their high densities, their mass entropy changes are considerably smaller than Dy(OH)₃ due to their much heavier formula unit.

Heat capacity and adiabatic temperature change

To investigate the entropy change of the Dy(OH)₃ material further, heat capacity measurements of the polycrystalline sample were obtained over an applied field range of 5-0 T (see ESI† for further details). At zero applied field, a large spike is observed in the specific heat capacity, C_p, at 3.41 K (Fig. 4a) which was attributed to a ferromagnetic phase transition in line with previously reported data.⁵⁰ Consistent with this, increases in applied field strength led to a broadening of the transition peak while the transition temperature remains approximately constant. Integration of the heat capacity data, combined with a direct magnetocaloric measurement performed at 3 K (see ESI†), allowed the derivation of the total entropy from the thermodynamic measurements (Fig. S27†) and the magnetic entropy changes up to ΔB = 5-0 T (Fig. 4b).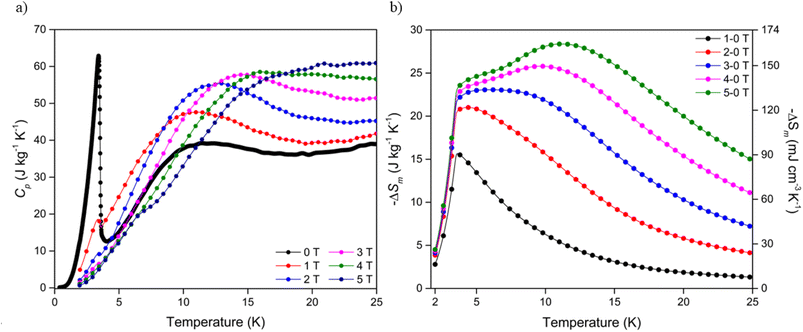

Fig. 4 (a) Specific heat capacity of Dy(OH)₃ at applied fields of between 0 and 5 T and (b) magnetic entropy changes determined from heat capacity data for field changes up to ΔB = 5-0 T.

The temperature dependence of the magnetic entropy change obtained directly from the thermodynamic measurements is in line with that calculated indirectly from the magnetisation data, such that the maximum entropy change is shifted to higher temperatures with increasing magnetic field strength (Table S3†). For ΔB = 1-0 T, a −ΔS^max_m of 15.6 J kg⁻¹ K⁻¹ (90.6 mJ cm⁻³ K⁻¹) was calculated at 3.6 K while, for ΔB = 5-0 T, a much higher −ΔS^max_m of 28.4 J kg⁻¹ K⁻¹ (164.3 mJ cm⁻³ K⁻¹) was obtained at 11.2 K. Despite the magnitude of the magnetic entropy changes calculated from both the magnetisation and heat capacity being consistent, a reduction of ∼15% was observed in entropy changes determined from the heat capacity measurements relative to those determined from the magnetisation data (28.4 vs. 33.4 J kg⁻¹ K⁻¹ respectively for ΔB = 5-0 T). This apparent discrepancy may be attributed to the crystallites of the heat capacity sample deviating from 100% alignment with the magnetic easy axis (the c-axis), thus leading to the observed decrease in magnetic entropy change due to the higher fields required to magnetise the crystallites that deviate from alignment with the easy axis. This assumption is not unreasonable given the polycrystalline nature of the sample and known magnetic anisotropy of Ln(OH)₃ materials. Correlations between magnetic entropy changes, sample alignment and applied magnetic field directions have previously been reported in materials with strong magnetic anisotropy.^56–58 Regardless of the field change applied −ΔS_m decreases rapidly below 3.5 K, as would be anticipated since the emergence of long range ferromagnetic order will greatly decrease the entropy change under applied fields.

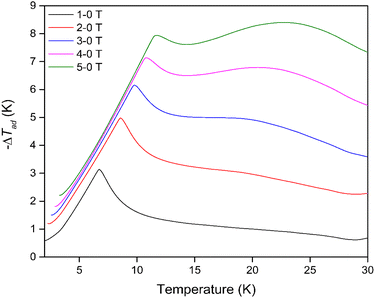
The thermodynamic data also allowed the adiabatic temperature change (−ΔT_ad) of Dy(OH)₃, the temperature change the material experiences when switching off the applied magnetic field under adiabatic conditions, to be calculated. This is determined directly from Fig. S27† as the temperature change at constant entropy between difference field curves. As with the magnetic entropy change, −ΔT_ad was found to have a strong magnetic field dependence (Fig. 5) with the maximum −ΔT_ad shifting to higher temperatures with increasing magnetic field strength (Table S4†). At a low field change of ΔB = 1-0 T, the maximum −ΔT_ad of 3.1 K was obtained at 6.8 K, while for a high field change of ΔB = 5-0 T, the maximum −ΔT_ad of 8.4 K was shifted to the far higher temperature of 22.7 K. In principle, this means that when held under a 5 T field at 22.7 K, removing the field will cause the material to cool by 8.4 K to 14.3 K. The −ΔT_ad of Dy(OH)₃ is particularly promising compared to other materials that exhibit high ΔT_ad near 20 K for a similar 5-0 T field change e.g. about 6.5 K for ErCo_1.8Ni_0.17Al_0.03,⁵¹ 7 K for GdCo₂B₂ (ref. 38) and 8 K for GdCrO₄,³⁷ amongst others (Table S5†).

Fig. 5 Adiabatic temperature changes of Dy(OH)₃ for magnetic field change up to ΔB = 5-0 T.

This result again demonstrates the potential for the Dy(OH)₃ material to act as a viable magnetocaloric at elevated temperatures, particularly for hydrogen liquefaction applications as both the Dy(OH)₃ −ΔT_ad and −ΔS^max_m parameters at high field changes show favourable performance near the boiling point of hydrogen.

Conclusions

This study has examined the magnetic and magnetocaloric properties of five Ln(OH)₃ materials (where Ln = Gd–Er) over a temperature range from 2 to 25 K. For low magnetic field changes, ΔB = 1-0 T, the magnetic entropy changes calculated from magnetisation measurements show Tb(OH)₃ and Dy(OH)₃ to be far superior than Gd(OH)₃ despite their fewer unpaired spins, with the −ΔS^max_m of 20.3 J kg⁻¹ K⁻¹ calculated for the Tb material at 4 K which is over five times greater than the −ΔS^max_m of 3.9 J kg⁻¹ K⁻¹ for Gd(OH)₃ at the same temperature. At high field changes, ΔB = 5-0 T, however, Dy(OH)₃ demonstrated superior performance over a much wider temperature range compared to the other members of the series with a −ΔS^max_m that first increases with increasing temperature from 24.9 J kg⁻¹ K⁻¹ at 4 K to 33.4 J kg⁻¹ K⁻¹ at 12 K then gradually decreases beyond this such that a −ΔS_m of 16.0 J kg⁻¹ K⁻¹ is retained at 28 K.

The magnetocaloric properties of the Dy(OH)₃ material were examined further using thermodynamic measurements with a high field −ΔS_m^max of 28.4 J kg⁻¹ K⁻¹ at 11.2 K recorded. The adiabatic temperature change was also determined from the heat capacity analysis with an −ΔT_ad of 8.4 K at 22.7 K determined for a ΔB = 5-0 T field change, significantly higher than the −ΔT_ad of 3.1 K obtained for a field change of ΔB = 1-0 T. This demonstrates Dy(OH)₃ as a promising magnetocaloric that can achieve a large temperature change around 20 K.

Given the favourable magnetocaloric properties, determined from both direct and indirect measurements, the potential for the Dy(OH)₃ material to be employed as a magnetic cooling material for moderate temperature applications has been demonstrated. One such application is in the hydrogen liquefaction process, as the boiling point of hydrogen (20.15 K) aligns well with the optimum magnetocaloric parameters determined for Dy(OH)₃ in this study making it very promising for the final stage of a magnetocaloric based liquefaction system.

Author contributions

The study was conceived by PJS in collaboration with FMG, with PJS and FMG responsible for funding acquisition and supervising the project team. Sample synthesis was performed by PWD who also collected and analysed the diffraction and magnetometry data. Heat capacity data were collected and analysed by JC and TG. PWD wrote the original draft of the manuscript with all authors reviewing and editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We would like to thank EPSRC for funding this research via grants EP/T027886/1 and EP/T028033/1.

References

1. T. D. Ladd, F. Jelezko, R. Laflamme, Y. Nakamura, C. Monroe and J. L. O'Brien, Nature, 2010, 464, 45–53.
2. A. Hirohata, K. Yamada, Y. Nakatani, I.-L. Prejbeanu, B. Diény, P. Pirro and B. Hillebrands, J. Magn. Magn. Mater., 2020, 509, 166711.
3. L. Gyongyosi and S. Imre, Comput. Sci. Rev., 2019, 31, 51–71.
4. A. Cho, Science, 2009, 326, 778–779.
5. A. M. Oliveira, R. R. Beswick and Y. Yan, Curr. Opin. Chem. Eng., 2021, 33, 100701.
6. M. van der Spek, C. Banet, C. Bauer, P. Gabrielli, W. Goldthorpe, M. Mazzotti, S. T. Munkejord, N. A. Røkke, N. Shah, N. Sunny, D. Sutter, J. M. Trusler and M. Gazzani, Energy Environ. Sci., 2022, 15, 1034–1077.
7. M. Aziz, Energies, 2021, 14, 5917.
8. T. Numazawa, K. Kamiya, T. Utaki and K. Matsumoto, Cryogenics, 2014, 62, 185–192.
9. I. Park and S. Jeong, Cryogenics, 2017, 88, 106–115.
10. I. Park and S. Jeong, IOP Conf. Ser.: Mater. Sci. Eng., 2015, 101, 012106.
11. T. Utaki, K. Kamiya, T. Nakagawa, T. A. Yamamoto and T. Numazawa, in Proceedings of the 14th Cryocooler Conference (ICC14), ed. S. D. Miller and R. G. Ross Jr, International Cryocooler Conference, Inc., Boulder, Colorado, 2007, pp. 645–653.
12. A. Smith, Eur. Phys. J. H, 2013, 38, 507–517.
13. M. Falsaperna and P. J. Saines, Dalton Trans., 2022, 51, 3394–3410.
14. R. J. C. Dixey and P. J. Saines, Inorg. Chem., 2018, 57, 12543–12551.
15. M. Wali, R. Skini, M. Khlifi, E. Dhahri and E. K. Hlil, Dalton Trans., 2015, 44, 12796–12803.
16. J. Lyubina, J. Phys. D: Appl. Phys., 2017, 50, 053002.
17. A. Kitanovski, Adv. Energy Mater., 2020, 10, 1903741.
18. V. Franco, J. S. Blázquez, B. Ingale and A. Conde, Annu. Rev. Mater. Res., 2012, 42, 305–342.
19. Y.-C. Chen, L. Qin, Z.-S. Meng, D.-F. Yang, C. Wu, Z. Fu, Y.-Z. Zheng, J.-L. Liu, R. Tarasenko, M. Orendáč, J. Prokleška, V. Sechovský and M.-L. Tong, J. Mater. Chem. A, 2014, 2, 9851–9858.
20. Y. Yang, Q.-C. Zhang, Y.-Y. Pan, L.-S. Long and L.-S. Zheng, Chem. Commun., 2015, 51, 7317–7320.
21. P. J. Saines, J. A. M. Paddison, P. M. M. Thygesen and M. G. Tucker, Mater. Horiz., 2015, 2, 528–535.
22. S.-D. Han, X.-H. Miao, S.-J. Liu and X.-H. Bu, Chem.–Asian J., 2014, 9, 3116–3120.
23. M. Kurmoo, Chem. Soc. Rev., 2009, 38, 1353–1379.
24. G. Mínguez Espallargas and E. Coronado, Chem. Soc. Rev., 2018, 47, 533–557.
25. Y.-C. Chen, F.-S. Guo, Y.-Z. Zheng, J.-L. Liu, J.-D. Leng, R. Tarasenko, M. Orendáč, J. Prokleška, V. Sechovský and M.-L. Tong, Chem.–Eur. J., 2013, 19, 13504–13510.
26. G. Lorusso, J. W. Sharples, E. Palacios, O. Roubeau, E. K. Brechin, R. Sessoli, A. Rossin, F. Tuna, E. J. L. McInnes, D. Collison and M. Evangelisti, Adv. Mater., 2013, 25, 4653–4656.
27. E. Palacios, J. A. Rodríguez-Velamazán, M. Evangelisti, G. J. McIntyre, G. Lorusso, D. Visser, L. J. de Jongh and L. A. Boatner, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 214423.
28. P. Mukherjee and S. E. Dutton, Adv. Funct. Mater., 2017, 27, 1701950.
29. N. D. Kelly, C. Liu and S. E. Dutton, J. Solid State Chem., 2020, 292, 121640.
30. P. W. Doheny, S. J. Cassidy and P. J. Saines, Inorg. Chem., 2022, 61, 4957–4964.
31. N. D. Kelly and S. E. Dutton, Inorg. Chem., 2020, 59, 9188–9195.
32. R. J. C. Dixey, F. Orlandi, P. Manuel, P. Mukherjee, S. E. Dutton and P. J. Saines, Philos. Trans. R. Soc., A, 2019, 377, 20190007.
33. R. J. C. Dixey, G. B. G. Stenning, P. Manuel, F. Orlandi and P. J. Saines, J. Mater. Chem. C, 2019, 7, 13111–13119.
34. P. Mukherjee, Y. Wu, G. I. Lampronti and S. E. Dutton, Mater. Res. Bull., 2018, 98, 173–179.
35. T. Numazawa, K. Kamiya, T. Okano and K. Matsumoto, Phys. B, 2003, 329–333, 1656–1657.
36. A. Midya, N. Khan, D. Bhoi and P. Mandal, J. Appl. Phys., 2014, 115, 17E114.
37. E. Palacios, C. Tomasi, R. Sáez-Puche, A. J. Dos santos-García, F. Fernández-Martínez and R. Burriel, Phys. Rev. B, 2016, 93, 064420.
38. L. Li, K. Nishimura and H. Yamane, Appl. Phys. Lett., 2009, 94, 102509.
39. J. Head, P. Manuel, F. Orlandi, M. Jeong, M. R. Lees, R. Li and C. Greaves, Chem. Mater., 2020, 32, 10184–10199.
40. R. Li, G. Li and C. Greaves, J. Mater. Chem. A, 2018, 6, 5260–5264.
41. S. Pakhira, C. Mazumdar and R. Ranganathan, J. Magn. Magn. Mater., 2019, 484, 456–461.
42. L. Li and M. Yan, J. Mater. Sci. Technol., 2023, 136, 1–12.
43. Y. Zhang, P. Xu, J. Zhu, S. Yan, J. Zhang and L. Li, Mater. Today Phys., 2023, 32, 101031.
44. Y. Zhang, W. Hao, C. Hu, X. Wang, X. Zhang and L. Li, Adv. Funct. Mater., 2023, 2310047.
45. Z. Ma, P. Xu, J. Ying, Y. Zhang and L. Li, Acta Mater., 2023, 247, 118757.
46. G. W. Beall, W. O. Milligan and H. A. Wolcott, J. Inorg. Nucl. Chem., 1977, 39, 65–70.
47. W. P. Wolf, H. Meissner and C. A. Catanese, J. Appl. Phys., 1968, 39, 1134–1136.
48. A. T. Skjeltorp, C. A. Catanese, H. E. Meissner and W. P. Wolf, Phys. Rev. B: Solid State, 1973, 7, 2062–2091.
49. C. A. Catanese, A. T. Skjeltorp, H. E. Meissner and W. P. Wolf, Phys. Rev. B: Solid State, 1973, 8, 4223–4246.
50. C. A. Catanese and H. E. Meissner, Phys. Rev. B: Solid State, 1973, 8, 2060–2074.
51. X. Tang, H. Sepehri-Amin, N. Terada, A. Martin-Cid, I. Kurniawan, S. Kobayashi, Y. Kotani, H. Takeya, J. Lai, Y. Matsushita, T. Ohkubo, Y. Miura, T. Nakamura and K. Hono, Nat. Commun., 2022, 13, 1817.
52. S. Cotton, Lanthanide and Actinide Chemistry, Wiley, Hoboken, 2006.
53. H. E. Meissner and W. P. Wolf, J. Appl. Phys., 1969, 40, 1038.
54. R. J. C. Dixey, P. Manuel, F. Orlandi, P. Mukherjee, S. E. Dutton, G. B. G. Stenning and P. J. Saines, J. Mater. Chem. C, 2020, 8, 12123–12132.
55. Y. Zhu, K. Asamoto, Y. Nishimura, T. Kouen, S. Abe, K. Matsumoto and T. Numazawa, Cryogenics, 2011, 51, 494–498.
56. H. Zhang, C. Xing, H. Zhou, X. Zheng, X. Miao, L. He, J. Chen, H. Lu, E. Liu, W. Han, H. Zhang, Y. Wang, Y. Long, L. van Eijk and E. Brück, Acta Mater., 2020, 193, 210–220.
57. N. Maraytta, J. Voigt, C. Salazar Mejía, K. Friese, Y. Skourski, J. Perßon, S. M. Salman and T. Brückel, J. Appl. Phys., 2020, 128, 103903.
58. P. Konieczny, D. Czernia and T. Kajiwara, Sci. Rep., 2022, 12, 16601.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ta05358j

---