Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Alkylated green fluorescent protein chromophores: dynamics in the gas phase and in aqueous solution†
Eleanor K.
Ashworth
 a,
Min-Hsien
Kao
a,
Cate S.
Anstöter‡
a,
Min-Hsien
Kao
a,
Cate S.
Anstöter‡
 b,
Gerard
Riesco-Llach
b,
Gerard
Riesco-Llach
 c,
Lluís
Blancafort
c,
Lluís
Blancafort
 c,
Kyril M.
Solntsev
c,
Kyril M.
Solntsev
 d,
Stephen R.
Meech
d,
Stephen R.
Meech
 a,
Jan R. R.
Verlet
a,
Jan R. R.
Verlet
 b and
James N.
Bull
b and
James N.
Bull
 *a
*a
aSchool of Chemistry, Norwich Research Park, University of East Anglia, Norwich, NR4 7TJ, UK. E-mail: james.bull@uea.ac.uk
bDepartment of Chemistry, Durham University, Durham, DH1 3LE, UK
cInstitut de Química Computacional i Catàlisi and Departament de Química, Universitat de Girona, C/M.A. Capmany 69, 17003 Girona, Spain
dSchool of Chemistry and Biochemistry, Georgia Institute of Technology, Atlanta, Georgia 30332, USA
First published on 21st August 2023
Abstract
Fluorescent labelling of macromolecular samples, including using the green fluorescent protein (GFP), has revolutionised the field of bioimaging. The ongoing development of fluorescent proteins require a detailed understanding of the photophysics of the biochromophore, and how chemical derivatisation influences the excited state dynamics. Here, we investigate the photophysical properties associated with the S1 state of three alkylated derivatives of the chromophore in GFP, in the gas phase using time-resolved photoelectron imaging, and in water using femtosecond fluorescence upconversion. The gas-phase lifetimes (1.6–10 ps), which are associated with the intrinsic (environment independent) dynamics, are substantially longer than the lifetimes in water (0.06–3 ps), attributed to stabilisation of both twisted intermediate structures and conical intersection seams in the condensed phase. In the gas phase, alkylation on the 3 and 5 positions of the phenyl ring slows the dynamics due to inertial effects, while a ‘pre-twist’ of the methine bridge through alkylation on the 2 and 6 positions significantly shortens the excited state lifetimes. Formation of a minor, long-lived (≫ 40 ps) excited state population in the gas phase is attributed to intersystem crossing to a triplet state, accessed because of a T1/S1 degeneracy in the so-called P-trap potential energy minimum associated with torsion of the single-bond in the bridging unit connecting to the phenoxide ring. A small amount of intersystem crossing is supported through TD-DFT molecular dynamics trajectories and MS-CASPT2 calculations. No such intersystem crossing occurs in water at T = 300 K or in ethanol at T ≈ 77 K, due to a significantly altered potential energy surface and P-trap geometry.
1. Introduction
The discovery of green fluorescent protein (GFP) from the Aequorea victoria jellyfish was a cornerstone in the ‘green revolution’ of biological fluorescence imaging and the visualisation of cellular processes.1–3 The optical absorption and emission properties of GFP are dictated by a chromophore based on the p-hydroxybenzylidene-2,3-dimethylimidazolinone anion (pHBDI−, Fig. 1) that is situated within the β -barrel structure of the protein.4 Although the Aequorea victoria jellyfish is an uncommon organism, the desirable optical properties of GFP and derivative fluorescent proteins, and the ease with which they can be deployed as optical markers in biochemical systems, has resulted in widespread adoption in photobiology,5,6 leading to the 2008 Nobel Prize in Chemistry.7 Since the discovery and first demonstrations of GFP in photobiology, significant efforts have been devoted to understanding the detailed photophysics of the chromophore,8 the role of the protein environment in the photophysics, and the influence of solvation on the chromophore's excited state dynamics.9,10 This understanding drives the development of improved fluorescent proteins and analytical toolkits for monitoring cellular processes.11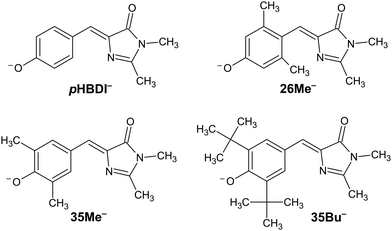 | ||
| Fig. 1 Structure of pHBDI− and three alkylated derivatives, 26Me−, 35Me−, and 35Bu−, (synthesis described in ref. 12). Chromophores are shown with the Z configuration of the bridging unit connecting the rings. Double-bond torsion causes imidazolinone ring twisting (I-torsion), while single-bond torsion causes phenoxide ring twisting (P-torsion). | ||
A notable feature of pHBDI− photophysics is that fluorescence in solution is very weak; pHBDI− has a fluorescence quantum yield of ≈10−4 in water at room temperature, compared with ≈0.8 in the protein.13,14 The low fluorescence quantum yield for the chromophore in solution is generally attributed to the facile internal rotation of the phenoxide ring and Z–E isomerisation, with both pathways leading to internal conversion.15,16 In the protein environment, these rotations are hindered by steric and non-covalent interactions from the photoreceptor binding pocket.17,18 Attempts to observe gas-phase fluorescence from pHBDI− at T ≈ 300 K and T ≈ 100 K using the LUNA2 instrument at Aarhus University, including by some of the present authors, have been unsuccessful.19,20 Synthetic modification of the pHBDI chromophore to explore structure–function relationships has resulted in numerous analogues offering altered spectral properties and excited state dynamics. These analogues include halogenation21–24 and/or alkylation12 on the phenyl ring, methylation of the hydroxyl group,25 replacement of the hydroxyl group with an amine group,26–28 and shifted hydroxyl group positions.29–31 In one investigation, Conyard et al.12 synthesised a series of alkylated pHBDI derivatives postulating that, in solution, the additional steric bulk should hinder both Z–E isomerisation of the methylene bond and internal rotation of the single bond. In principle, alkylation (weakly electron donating) should only perturb the electronic structure minimally and, thus, have little influence the intrinsic photophysics of the chromophore.
There have been a range of gas-phase studies on pHBDI−, mostly performed at T ≈ 300 K. The principal appeal of studies in the gas phase is to inform on intrinsic photochemical dynamics, which can be compared with theoretical simulations in a straightforward manner. Where deviations exist, the experimental data provides direction for theoreticians to refine their models. Gas-phase investigations include using action spectroscopy strategies such as photodissociation,32–38 photodetachment/photoelectron,24,39,40 and photoisomerisation.41 When taken together, these studies have characterised many of the fundamental photophysical properties of pHBDI−, including the underlying absorption spectrum, electron binding energies and autodetachment processes, propensity for reverse Z–E photoisomerisation, and the impact of microsolvation. Time-resolved photoelectron and photodissociation strategies have shown that the lifetime of the S1 state is several picoseconds at T ≈ 300 K.39,42–44
Computational studies seeking to understand specific photophysical properties have been applied to several pHBDI analogues, both in isolation and in solvated environments, with alterations including halogenation45–47 and alkylation37,48,49 on the phenyl ring. Notably, there have been numerous molecular dynamics and potential energy surface investigations on pHBDI− assuming gas-phase, solution, and protein environments (see ref. 44, 50 and 51 and references therein), with the goal of establishing a theoretical understanding of the intrinsic chromophore dynamics versus environmental influences. The recent, and most robust, simulations by Martínez and co-workers15,16 used ab initio molecular dynamics with multi-state CASSCF wavefunctions to propagate the excited state dynamics of pHBDI− in isolation and also in (explicit) water. These studies highlight the importance and interplay of two S1/S0 conical intersections, one associated with torsion of the phenoxide moiety (P-torsion) and the other, leading to Z–E isomerisation, associated with torsion of the imidazolone moiety (I-torsion). Both pathways contribute to deactivation of the excited state but have distinct lifetimes; in the gas phase ≈40% of excited molecules undergo internal conversion through P-torsion, while ≈60% do so through I-torsion. Time-resolved experiments are presumed to measure the combination of these pathways. Significantly, the simulations predicted that the excited-state lifetimes for pHBDI− in water are shorter than in the gas phase, due to both a stabilisation of twisted intermediate structures and a lowering in energy of the conical intersection seam for internal conversion. From a synthetic perspective, it is interesting to incorporate various functionalities onto the ring systems in order to ‘tune’ the conical intersection energies and topologies.52 Harnessing such synthetic control of conical intersection properties is key for the rational design of chromophores offering improved fluorescence and/or isomerisation quantum yield.
This paper details time-resolved measurements performed in the gas-phase and in water on the four chromophores shown in Fig. 1. The chromophores were probed in the gas phase using time-resolved photoelectron imaging, and in water using femtosecond fluorescence upconversion. Significantly, we found that alkylation on the 3 and 5 positions increases the excited-state lifetimes in both the gas phase and in aqueous solution compared with pHBDI−, with the gas-phase lifetimes being substantially longer than those in solution. The latter of these trends is at odds with many other organic chromophore systems, where the gas-phase excited state dynamics are more rapid than those in solution due to the absence of vibrational energy transfer to solvent. We present evidence for a weak intersystem crossing (ISC) pathway in the gas phase due to a S1/T1 degeneracy at the so-called P-trap on the excited-state potential energy surface; this degeneracy is lost in solution due to substantial changes to the potential energy surface associated with solvation.
2. Methods
2.1. Gas-phase photoelectron spectroscopy
Photoelectron spectroscopy (imaging) on the target anions was performed using an instrument that combines electrospray ionisation, ion trapping and thermalisation to T ≈ 300 K, time-of-flight m/z separation, and velocity-map imaging detection.53,54 Briefly, anions electrosprayed from methanol solution were accumulated in a radio frequency ring-electrode ion trap. The trapped anions were unloaded at a 333 Hz repetition rate into a set of colinear time-of-flight optics that accelerated the ions along a 1.3 m flight region toward a continuous-mode penetrating field velocity-mapping assembly.54 Laser light was timed to interact with the mass-selected ion packet at the centre of the velocity-map imaging stack. Ejected photoelectrons were velocity-mapped onto a dual (chevron) multichannel plate detector, followed by a P43 phosphor screen, which was monitored with a charge-coupled device camera. Velocity-map images were accumulated with a 500 ns gate pulse applied to the second multi-channel plate. The velocity-mapping resolution was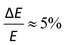 , and the electron kinetic energy (eKE) scale was calibrated from the spectrum of I−. Velocity-map image reconstructions used antialiasing and polar onion-peeling algorithms,55 providing the photoelectron spectra and associated photoelectron angular distributions, quantified by the conventional β2 anisotropy parameter.56 Values of β2 for atomic orbitals range between +2 and −1, with the limits corresponding to a cos2
, and the electron kinetic energy (eKE) scale was calibrated from the spectrum of I−. Velocity-map image reconstructions used antialiasing and polar onion-peeling algorithms,55 providing the photoelectron spectra and associated photoelectron angular distributions, quantified by the conventional β2 anisotropy parameter.56 Values of β2 for atomic orbitals range between +2 and −1, with the limits corresponding to a cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ (parallel) and a sin2
θ (parallel) and a sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ (perpendicular) ejected electron distribution relative to the incident laser polarisation vector, respectively. However, β2 values for electron ejection from molecular orbitals typically span a reduced range. Higher order β4 parameters were not statistically significant in this study.
θ (perpendicular) ejected electron distribution relative to the incident laser polarisation vector, respectively. However, β2 values for electron ejection from molecular orbitals typically span a reduced range. Higher order β4 parameters were not statistically significant in this study.
Single-colour photoelectron spectra to obtain electron detachment parameters were performed at hν = 3.44 eV (360 nm) using light from a Continuum Horizon OPO laser coupled with a Continuum Surelite Nd:YAG pump laser, ≈1 mJ pulse−1 (unfocussed). This photon energy was chosen based on earlier work demonstrating predominantly direct photodetachment (i.e. non-resonant) electron ejection in the spectral region between the S1 and S2 states.37,39
For the time-resolved experiments, femtosecond laser pulses were derived from a Spectra-Physics Ti:sapphire oscillator and regenerative amplifier. The hν = 2.50 eV (495 ± 5 nm, ≈20 μJ) pump pulses were produced by fourth-harmonic generation (two successive BBO crystals) of the idler output from an optical parametric amplifier (Light Conversion TOPAS-C). The photon energy of the pump pulse was chosen to be close to the maximum in the action spectra (i.e. vertical excitation energy) for the target anions.37 This choice of energy allows for direct comparison with the reference ab initio molecular dynamics studies,16 which assume trajectories from the vertical excitation geometry. The hν = 1.55 eV (800 nm, ≈100 μJ) probe pulse was the fundamental output of the femtosecond laser. Pump and probe pulses were delayed relative to each other (Δt) using a motorised delay line. The pump and probe pulses were combined colinearly using a dichroic mirror and were loosely focused into the interaction region using a curved metal mirror. The pump–probe cross correlation was ≈60 fs; the cross-correlation was measured in a non-linear crystal and is consistent with fits to the data.
It is worth noting that previous experiments on pHBDI− photophysics following excitation of the S1 state have been reported using the instrument described above,42 although these earlier experiments used an older ion trap that resulted in ion vibrational temperatures greater than 300 K (likely T = 400–500 K). Since publication of that study, the ion trap was upgraded to achieve thermalisation to T ≈ 300 K.57
2.2. Time-resolved fluorescence upconversion
Aqueous anionic solutions of the chromophores were prepared to a concentration corresponding to a maximum absorbance of ≈0.1 over the S1 ← S0 band. Deprotonation was achieved using a drop of 1 M NaOH, and the solution spectrum (pH ≈ 10) was confirmed to correspond to the anion by comparing neutral and anionic absorption spectra (there is a > 70 nm red-shift upon deprotonation).12Time-resolved fluorescence upconversion measurements on the target anions in water were performed using the instrument described in ref. 58. In brief, ≈800 nm light (≈20 fs pulses at 80 MHz) was generated using a continuous wave Nd:YVO4 laser driving a Kerr lens mode-locked Ti:sapphire oscillator. Focussing of the fundamental light (≈840 mW), using a 150 mm focal length concave mirror, into a 50 μm thickness barium borate crystal (BBO, type I) produced the second harmonic (400 nm, ≈11 mW). Separation of the 800 nm and 400 nm light was achieved with a dichroic mirror, and the delay between the pump and probe light pulses was adjusted using a computer-controlled motorised delay stage (0.1 μm resolution). Temporal broadening along the beam path was minimised using chirped mirrors. A concave mirror was used to focus the 400 nm pump pulse onto the sample, contained in a static 2 mm path length quartz cell. The resulting fluorescence was focussed by a reflective microscope objective (15× magnification) through a CG455 Schott filter and was frequency mixed (upconverted) with the 800 nm light in a 100 μm thickness BBO crystal (type I). The upconverted signal was passed through a UG11 Schott filter and monochromator (Photon Technology International Model 101, resolution 2 nm mm−1) prior to entering the low-noise photomultiplier (PMT, Hamamatsu R585). The PMT response was acquired by a computer-interfaced Stanford Research Systems photon counter (SR400). The instrument cross correlation was characterised at ≈45 fs through up-conversion of Raman scattering.
2.3. Computational details
Static electronic structure calculations were performed using the Gaussian 16.B01 and ORCA 5.0.3 software packages.59,60 Ground electronic state energies, optimised geometries and vibrational frequencies were computed at the ωB97X-D/aug-cc-pVTZ level of theory followed by single-point energy calculations at the DLPNO-CCSD(T)/aug-cc-pVTZ level.61–63 Optimised microsolvated geometries were computed at the MP2/aug-cc-pVDZ level of theory64 with five explicit water molecules combined with the SMD implicit solvation model.65 The initial microsolvated geometries were determined by placing water molecules around the chromophore in several configurations, followed by optimising the geometries of the waters with a PM6 semi-empirical Hamiltonian.66 Vertical excitation energies of the lowest energy solvated structures were computed at the DLPNO-STEOM-CCSD/aug-cc-pVDZ level of theory.67Molecular dynamics trajectories for pHBDI− were carried out with Newton-X68,69 coupled to Gaussian 16, using TD-DFT with the CAM-B3LYP functional and the 6-311G(d,p) basis set. The S1/T1 degeneracy and the spin–orbit coupling was analysed for a representative trajectory with a long residence time in the P-trap (see ESI†). Trajectories were propagated on the S1 state with a step size of 0.5 fs, and terminated when the S1/S0 gap was smaller than 0.15 eV. Initial conditions were obtained from Wigner sampling at T = 0 K and vertical excitation. MS-CASPT2 calculations were carried out with a (16,14) active space (16 π-electrons in 14 π-orbitals), and the ANO-S basis set (3s2p1d contraction for C, H, and N; 2s1p contraction for O) using Molcas 8.2.70,71 Three roots were calculated by state-averaging with equal weights. The default ionisation potential electron affinity (IPEA) correction of 0.25 au72 and an imaginary level shift73 of 0.1 au were applied. The singlet and triplet states were obtained in separate calculations. The spin–orbit coupling elements were obtained from the MS-CASPT2 perturbationally-modified complete active space configuration interaction (PM-CASCI) wavefunctions. Benchmarking has shown that the CASPT2 method combined with the IPEA shift can provide ππ* excitation energies and relative triplet and singlet energies to better than 0.14 eV (mean absolute energy).74
3. Results and discussion
3.1. Electron detachment parameters
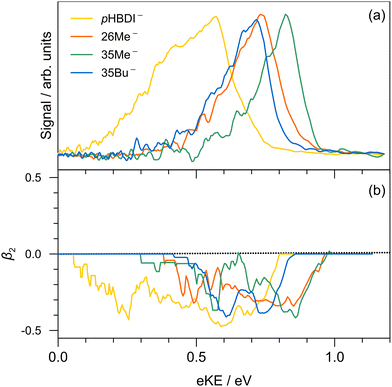
Single-colour photoelectron spectra recorded at hν = 3.44 eV (360 nm) for the four anions are shown in Fig. 2. The adiabatic (ADE) and vertical detachment energy (VDE), given in parentheses in Table 1, were determined from the spectral peak maximum and the high-kinetic-energy edge, respectively (by taking the difference between the excitation energy, 3.44 eV, and the respective maximum/edge values). The experimental values are consistent with the ADE and VDE values computed at the DLPNO-CCSD(T)/aug-cc-pVTZ level of theory as given in Table 1. Our experimental values for pHBDI− (ADE = 2.72 ± 0.05 eV, VDE = 2.87 eV) are in close accord with the T > 300 K photoelectron spectroscopy values determined by Horke et al.,75 and with a T ≈ 20 K detachment threshold measurement at 2.73 ± 0.01 eV.76 Measured β2 values over the photoelectron bands are negative (Fig. 2b), consistent with prompt detachment of a π-electron from a planar (or near planar) anion.For pHBDI−, it is known that the electron detachment threshold (2.72 ± 0.05 eV in this work) occurs over the S1 ← S0 absorption band (maximum at 2.56 ± 0.02 eV).37,40,77 While our photoelectron spectra for the alkylated chromophore anions reveal that the electron detachment parameters are lower in energy than for pHBDI−, the maximum in the absorption spectrum for each is 2.49 ± 0.02 eV,37 meaning that much of the absorption band (at T ≈ 300 K) is situated above the detachment threshold and has shape resonance character78 – this may have implications for the excited-state lifetimes.
3.2. Time-resolved photoelectron spectroscopy
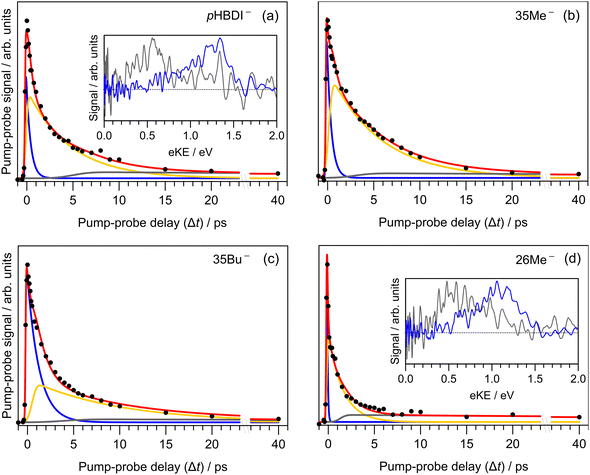
Results from the time-resolved photoelectron imaging experiments on the four target anions are shown in Fig. 3. The total pump–probe signal for each anion was fit with a three-component model: , where the fitted contributions from component 1 are blue, 2 are orange, and 3 are grey. Lifetime τ3 corresponds to loss of component 3. Inset in Fig. 3a and d are example time-resolved photoelectron spectra corresponding to Δt≈0 fs (associated with fit component 1, blue) and to Δt≈10 ps (containing signatures from components 2 and 3, grey); time-resolved spectra for pHBDI− are consistent with those reported by Mooney et al.42 Our fittings assumed an initial Gaussian cross-correlation function (≈60 fs) convoluted with exponential decay functions (and growth functions for τ2 and τ3). The extracted τ1 and τ2 lifetimes from the fits are summarised in Table 2, with both sets of lifetimes having the trend: 26Me− < pHBDI− < 35Me− < 35Bu−.
, where the fitted contributions from component 1 are blue, 2 are orange, and 3 are grey. Lifetime τ3 corresponds to loss of component 3. Inset in Fig. 3a and d are example time-resolved photoelectron spectra corresponding to Δt≈0 fs (associated with fit component 1, blue) and to Δt≈10 ps (containing signatures from components 2 and 3, grey); time-resolved spectra for pHBDI− are consistent with those reported by Mooney et al.42 Our fittings assumed an initial Gaussian cross-correlation function (≈60 fs) convoluted with exponential decay functions (and growth functions for τ2 and τ3). The extracted τ1 and τ2 lifetimes from the fits are summarised in Table 2, with both sets of lifetimes having the trend: 26Me− < pHBDI− < 35Me− < 35Bu−.
| Species | τ g1 | τ g2 | τ w1 | τ w2 | τ eth1 | τ eth2 |
|---|---|---|---|---|---|---|
| a 26Me− data could not be fit with a double exponential; τw1 is close to being limited by the laser cross-correlation. Uncertainties are given in the ESI. | ||||||
| pHBDI− | 0.46 | 4.64 | 0.29 | 1.19 | 0.25 | 0.87 |
| 26Me− | 0.07 | 1.58 | 0.06 | —a | 0.07 | 0.49 |
| 35Me− | 0.47 | 5.53 | 0.45 | 2.34 | 0.44 | 2.71 |
| 35Bu− | 1.28 | 9.72 | 0.61 | 3.19 | 0.59 | 2.97 |
We interpret the gas-phase excited-state lifetimes and dynamics in accord with the potential energy surface shown in Fig. 4a, which was adapted from ref. 16. Briefly, the potential energy surface involves two torsion coordinates, both of which lead to a conical intersection. The torsion coordinates correspond to twisting of either the single bond (P-torsion, phenoxide ring twisting) or the double bond (I-torsion, imidazolinone ring twisting) of the methine bridge. The P-torsion coordinate passes through a shallow S1 minimum, termed the P-trap, where some fraction of the excited-state population may be temporarily contained. The P-trap has a highly twisted geometry, with the single-bond methine bridge dihedral angle of ≈102°.16 Furthermore, the nearby conical intersection in this region has a ‘sloped’ (and uphill) topology, giving the tendency for excited state motions to undergo several crossings (and vibrations through the P-trap) before internal conversion. On the other hand, the I-torsion co-ordinate is associated with small barrier (e.g. several hundred cm−1) followed by a downhill conical intersection, leading to prompt internal conversion.79–81
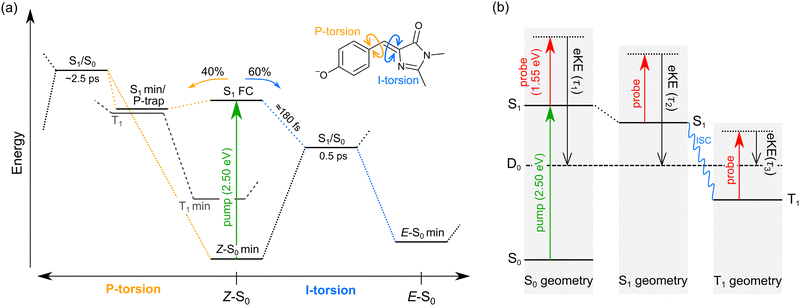 | ||
| Fig. 4 Summary of gas-phase pHBDI− photophysics (similar potential energy surfaces apply for the alkylated derivatives): (a) potential energy surface for pHBDI− based on molecular dynamics results adapted from ref. 16. P-torsion corresponds to rotation of the phenoxide group about the single bond on the methine bridge, and I-tosion represents rotation of the imidazolinone group about the double bond on the methine bridge. The simulations on pHBDI− by List and co-workers15,16 determined that ≈40% (≈34% in water) of the excited-state population passes through the S1 minimum to reach the P-torsion S1/S0 conical intersection, while ≈60% (≈66% in water) of the excited population passes through the I-torsion S1/S0 conical intersection. We propose that a small amount of intersystem crossing occurs in the S1 minimum along the P-torsion coordinate (the so-called P-trap, where the methine bridge dihedral angle is ≈102°). (b) Jablonski diagram assigning the origins of the three excited-state lifetimes extracted from the time-resolved photoelectron spectra. Anions are excited to S1 by a hν = 2.50 eV pump pulse, and the excited-state population is probed as a function of time (Δt) with 1.55 eV laser pulses. The excited-state lifetimes τ1, τ2, and τ3 reflect probing of the initial prompt relaxation from the Franck–Condon geometry (component 1), loss of relaxed S1 population (component 2), and loss of T1 population (component 3), respectively. Lifetimes τ1 and τ2 are on the order of femtoseconds to picoseconds, while τ3 is hundreds of picoseconds or longer because T1 is situated well below the detachment threshold and because of the electron reconfiguration required to achieve the electron configuration for the neutral D0 state. Note, in (b) the energy of the D0 state varies with geometry, but is shown as a straight line for simplicity. | ||
In our fits to the gas-phase time-resolved data, lifetime τ1 corresponds to rapid motion away from the Franck–Condon geometry (i.e. nuclear relaxation on S1 with a concerted change in probe/photodetachment cross-section), and lifetime τ2 represents the loss of this relaxed population through the combination of internal conversion (major) and autodetachment (minor) processes. τ3 will be further discussed in Section 3.3. The ratio of rate constants for deactivation of the excited state by internal conversion (IC) and autodetachment (AD) has been estimated at kAD/kIC ≈ 0.05 ± 0.01 (T > 300 K, invariant to pump photon energy in the 2.39–2.57 eV range),43 implying that internal conversion outcompetes autodetachment. Fluorescence is deemed a negligible deactivation channel because, as outlined in the introduction, all attempts at probing gas-phase fluorescence on the four target anions at T ≈ 300 K and T ≈ 100 K were unsuccessful. It is also worth noting that calculations of oscillator strengths indicate that the P-trap is essentially non-fluorescent in the gas phase due to substantial torsion, and is weakly fluorescent in solution due to a smaller torsion angle.15,16 The similarity in τg1 (where superscript g implies gas phase) for pHBDI− and 35Me− suggests that the additional methyl groups have little effect on the prompt dynamics, i.e. the initial twisting away from the Franck–Condon geometry is fast. Conversely, the ≈1 ps difference in lifetime τg2 between pHBDI− and 35Me− suggests passage through the conical intersections in 35Me− is more hindered, presumably due to inertial effects and the intramolecular vibrational energy redistribution required to access the conical intersections. The longest recorded lifetimes were for 35Bu−, with both τg1 and τg2 exhibiting a two-fold increase relative to pHBDI−, attributed to steric bulk and inertial effects from the tert-butyl groups (such inertial effects become quenched in solution). 26Me− has the shortest lifetimes, particularly τg1, which is limited by the laser cross-correlation. This result is consistent with the excited-state lifetimes recorded for 26Me− in ethanol solution,12 where the short lifetime was attributed to the non-planarity of the ground-state geometry, i.e. the geometry is already pre-twisted (P-twist angle ≈20° in the gas phase, see ESI†) and, thus, closer to the conical intersection geometry. This pre-twist is because of steric interaction between the methyl groups and close-lying H-atoms. A similar lifetime shortening was induced by methyl substitution at the pHBDI− central carbon, which also leads to a pre-twisted ground state.82
Previous photoelectron spectroscopy measurements of S1 excited-state lifetimes for pHBDI− (T > 300 K) were τ1 = 330 fs and τ2 = 1.4 ps.42 The present τg2 lifetime is roughly three-fold longer, which is attributed to some combination of: (a) differences in ion vibrational temperature between the experiments, and (b) that the earlier study assumed a bi-exponential fit of the data that did not account for the very long time component, τ3 (further discussed in Section 3.3). The time-resolved photoelectron spectroscopy experiment described in this work used an improved version of the instrument in ref. 42 incorporating a new ion trap in which ions are thermalised to T ≈ 300 K. Thus, we consider the present gas-phase lifetimes more reliable room temperature measurements. In a different time-resolved photodissociation study utilising an ion storage ring and pumping at 480 nm (2.58 eV compared with 2.50 eV in this work),44 reported lifetimes of τ1 = 1.3 ± 0.2 ps, τ2 = 11.5 ± 0.5 ps (T ≈ 300 K), and the longer lifetimes at T ≈ 100 K of τ1 = 4.6 ± 2.1 ps, τ2 = 27 ± 2 ps, and τ3 = 1.2 ± 0.1 ns assuming a tri-exponential model. No τ3 parameter was fitted to the T ≈ 300 K data, presumably because signal level was very low. The authors assigned the τ3 ≈ 1.2 ns lifetime at low temperature to a small fraction of the excited-state population becoming held in the P-trap (Fig. 4a), which slowly escapes through the I-torsion coordinate. In the present work, we were unable to measure the lifetime of the long-lived component at T ≈ 300 K due to experimental limitations, rather we give it as τ3 ≫ 40 ps. To our knowledge, there are no reports of long-lived excited-state lifetimes for any pHBDI− derivatives in solution (aside from hot ground state dynamics).
3.3. Intersystem crossing
The minor, long-lived excited-state lifetime (τ3) observed for all four of the pHBDI-based anions could originate from: (1) relaxation of a small amount of S1 population that becomes confined in the P-trap (i.e. insufficient energy to access any conical intersection), or (2) intersystem crossing (ISC) to a lower-lying triplet state (T1). We discuss these two possibilities below, referring to the Jablonski diagram shown in Fig. 4. Note that, although the Jablonski diagram in Fig. 4 is specific to gas-phase pHBDI−, the overall features apply to the alkylated derivatives.In the time-resolved photodissociation study by Andersen and co-workers,44 a long-lived excited-state component at T ≈ 100 K was ascribed to possibility (1), where population in the P-trap eventually either overcomes excited-state barriers to reach the double-bond torsion (I-torsion, Fig. 4) conical intersection, or undergoes fluorescence. The subsequent ab initio molecular dynamics study by List et al.16 highlighted the importance of the alternative, P-torsion conical intersection, close to the P-trap geometry, which ≈40% of population accessed at T ≈ 300 K. In terms of the present data that provide the extra dimension of time-resolved electron kinetic energy distributions, if we assume the P-trap interpretation for lifetime τ3, our calculations at the DLPNO-STEOM-CCSD/aug-cc-pVDZ level of theory (assuming the P-trap geometry from ref. 16), predict a time-resolved eKE maximum at ≈0.8 eV. This is somewhat higher in energy than the maximum in the eKE distribution shown in Fig. 3a (inset, grey trace). Furthermore, assuming the P-trap interpretation, it is unclear why we would observe such a long timescale component in our T ≈ 300 K experiment, considering that the internal energy exceeds the height of the barriers on the S1 potential energy surface and autodetachment is always an open channel because the total internal energy exceeds the detachment threshold.
The second interpretation involves intersystem crossing (ISC) to form the T1 (triplet) state, with lifetime τ3 corresponding to vibrational autodetachment from T1. We argue for this mechanism for several reasons. Qualitatively, P-torsion (Fig. 4a) from the S1 Franck–Condon geometry, leading to the S1 minimum (P-trap), effectively ‘decouples’ the phenoxide ring from the rest of the molecule. Once decoupled, the molecule can be thought of as two non-conjugated units, consisting of the negatively-charged phenoxide ring and the neutral imidazolinone. pHBDI− is well known to undergo a moderate degree of charge-transfer on excitation,37 which, in this decoupled form, results in a phenoxy radical and an imidazolinone radical anion. Therefore, the P-trap geometry is, in essence, a decoupled biradical (Fig. 5), and such forms tend to have degenerate singlet and triplet states.84–86 Thus, near degenerate singlet and triplet states are expected at the P-trap geometry. Quantitatively, the S1/T1 separation at the P-trap geometry, determined from MS-CASPT2 calculations at the TD-DFT optimised structure (see ESI† for details), is 0.01 eV, suggesting an ISC seam is accessible (or nearby). Furthermore, the energy profile from a molecular dynamics trajectory that stays for approximately 2 ps in the P-trap shows a small average S1/T1 energy gap (0.32 ± 0.25 eV) – see ESI.† The spin–orbit coupling (SOC) element, calculated at the MS-CASPT2 level of theory for 10 points of the trajectory with the smallest S1/T1 energy gap, is 0.15 ± 0.03 cm− 1. This non-negligible SOC is consistent with a small ISC probability (e.g. a few percent as suggested from the experimental relative signal intensities) for trajectories staying in the P-trap over a timescale of the observed τ2 lifetimes. While our hybrid strategy provides qualitative evidence for ISC, it would be desirable in future work to deploy an ab initio molecular dynamics method able to directly describe intersystem crossing and could thus determine an ISC quantum yield. We note that other molecular dynamics simulations on gas-phase pHBDI− derivatives (ref. 16, 50 and 51) did not consider the possibility of ISC.
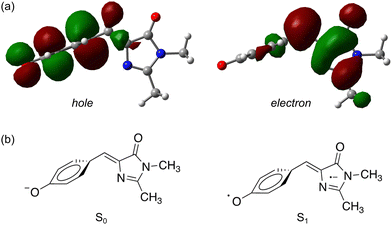 | ||
| Fig. 5 Natural transition orbitals83 for the S1 ← S0 transition in pHBDI−: (a) the P-trap minimum energy geometry, (b) schematic illustrations of the resulting ground and excited-state electronic configurations. | ||
Further evidence for the ISC interpretation comes from the time-resolved eKE distributions. The global minimum on the T1 surface has a planar geometry, and our DLPNO-STEOM-CCSD/aug-cc-pVTZ calculations predict that the time-resolved eKE distribution from the relaxed T1 state should give rise to a peak at 0.61 eV, which is in good agreement with the experimental data (Fig. 3a, inset, grey trace peaks at ≈0.6 eV). The T1 potential energy minimum (planar) was calculated to lie 1.9 eV above the S0 equilibrium geometry, and ≈0.4 eV below the P-trap geometry. It is worth noting that the probe (800 nm) photodetachment cross-sections from the S1 state (P-trap) and T1 state (planar equilibrium geometry) will likely differ, meaning that absolute quantification of the extent of ISC is difficult; we estimate the ISC contribution at ≈5%. However, the assigned ISC dynamics appear common to the four target chromophore anions, implying similar potential energy surfaces (Fig. 4).
3.4. Excited state lifetimes in water
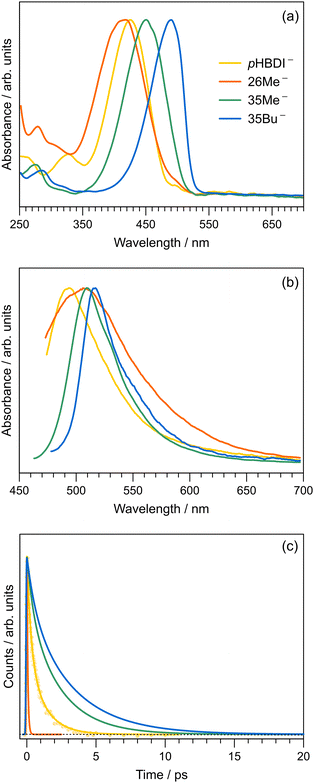
To compare our gas-phase excited-state lifetimes with those recorded in solution, we studied the target anions in water using time-resolved fluorescence upconversion pumping at ≈400 nm. Aqueous absorption spectra are shown in Fig. 6a, with each chromophore exhibiting strong absorption at the pump wavelength. The corresponding fluorescence spectra, when exciting at ≈400 nm, are shown in Fig. 6b. Spectra recorded at T ≈ 77 K in ethanol are given in the ESI,† and relevant spectral properties are summarised in Table 3. Fits of the upconverted fluorescence decay curves at T = 300 K, shown in Fig. 6c, involved a two-component exponential decay function (with the exception of 26Me−). The fitted lifetimes are given in Table 2, with the data for pHBDI− closely matching earlier upconversion data,87 while the other anions are similar to data recorded in ethanol12 – the fitted lifetimes in ethanol and water are within 0.05 ps (τ1) and 0.4 ps (τ2) of each other. We interpret lifetime τ1 as dominated by rapid nuclear motion away from the Franck–Condon geometry convoluted with prompt solvent reorganisation, and lifetime τ2 as linked to loss of S1 population. Because the fluorescence emission spectrum does not show any substantial variation with pump–probe delay, i.e. fluorescence lifetimes are independent of the up-converted wavelength over the emission spectrum, we interpret the fluorescence emission to occur from a broad range of geometries. This model is consistent with the idea that the P-trap potential energy minimum in solution is substantially less twisted from the Franck–Condon geometry compared with in the gas-phase and is a shallow minimum, with molecular dynamics simulations showing facile dihedral angle twisting.15 A less twisted P-trap geometry in water is associated with reduced biradical character and, consequently, the intersystem crossing seam will be shifted away from the P-trap geometry. The shorter τ2 lifetimes in solution compared with the gas phase infer that access to S1/S0 conical intersection(s) is more favourable in solution. While this trend was predicted for pHBDI− from ab initio molecular dynamics,15,16 the present work shows that same stabilisation of the twisted intermediate and conical intersections occurs for the alkylated derivatives. There is no evidence for any ISC in solution (at either T = 300 K or T ≈ 77 K, discussed below), which would manifest as phosphorescence in the emission spectra and a long-lifetime component (phosphorescence or delayed fluorescence) in the time-resolved measurements.| Water | Ethanol | ||||||
|---|---|---|---|---|---|---|---|
| λ abs | λ em | λ abs | λ ex | λ em | |||
| 300 K | 300 K | 300 K | 77 K | 300 K | 77 K | ||
| a The T = 300 K excitation spectrum could not be recorded for 26Me− due to low fluorescence quantum yield. | |||||||
| pHBDI− | 426 | 491 | 441 | 461 | 421 | 496 | 458 |
| 26Me− | 417 | 509 | 439 | —a | 425 | 520 | 513 |
| 35Me− | 450 | 510 | 473 | 490 | 458 | 505 | 475 |
| 35Bu− | 490 | 515 | 509 | 507 | 491 | 518 | 507 |
The short τ1 lifetime for 26Me− (limited by cross correlation) parallels the gas-phase results, and is linked with the pre-twisted Franck–Condon geometry along the P-torsion coordinate.12 Our calculations of the Franck–Condon geometry reveal a P-twist angle for 26Me− at ≈20° in the gas phase and ≈48° in water (see ESI†). Given that, for aqueous pHBDI−, the P-torsion conical intersection occurs at a P-twist angle of ≈73°,15 and assuming a similar case for 26Me−, the twisted Franck–Condon geometry for 26Me− (≈48°) means that little motion is required to reach the P-torsion conical intersection in 26Me−.
The fluorescence emission spectra for aqueous 35Me− and 35Bu− are red-shifted and slightly narrower compared with that for pHBDI−. The red-shifted emission is attributed to stabilisation of the S1 excited state, and a narrowing is presumably associated with restricted torsion of these alkylated molecules in their fluorescent state (consistent with longer excited-state lifetimes).29 The much broader emission spectrum for 26Me− is consistent with emission from a wider range of geometries and the shortest excited-state lifetime.
The fluorescence emission spectra for aqueous 35Me− and 35Bu− are red-shifted and slightly narrower compared with that for pHBDI−. The red-shifted emission is attributed to stabilisation of the S1 excited state, and a narrowing is presumably associated with restricted torsion of these alkylated molecules in their fluorescent state (consistent with longer excited-state lifetimes).29 The much broader emission spectrum for 26Me− is consistent with emission from a wider range of geometries and the shortest excited-state lifetime.
Finally, we can compare our fluorescence upconversion lifetimes with those recorded for pHBDI− in water using femtosecond stimulated Raman spectroscopy (FSRS).88 The τ1 component is similar in both cases, as it reflects initial relaxation away from the Franck–Condon geometry. On the other hand, the τ2 component is longer when measured using FSRS (τ2 ≈ 2.1 ± 0.1 ps) compared with that measured by upconversion (τ2 ≈ 1.19 ± 0.18 ps). Presumably, the longer FSRS lifetime, if real, is linked with some fraction of excited state population which does not access fluorescent geometries.
3.5. Cryogenic measurements
To explore the influence of temperature on the absorption and fluorescence emission spectra of the target anions, we recorded fluorescence excitation, emission, and lifetime data at T ≈ 77 K by immersing a cryogenic EPR tube containing an ethanolic solution in a liquid nitrogen bath. Cryogenic measurements in water are not possible due to volume expansion upon freezing and the formation of a poor quality glassy matrix. Wavelengths of maximum response from the fluorescence excitation (as proxies for absorption) and emission spectra are given in Table 3 (see ESI† for the T ≈ 77 K spectra). The Stokes shifts and fitted excited-state lifetimes from the cryogenic measurements are given in the ESI.† The Stokes shifts in water at T = 300 K are substantially larger than those in ethanol, particularly for 35Bu−, which we attribute to a combination of hydrogen-bonding stabilisation of the deprotonation site, which is more easily accessed in water due to the smaller molecular size of the solvent and reduced steric interaction with the alkyl groups, and because of the high dielectric constant effect from water.Excited-state lifetimes at T ≈ 77 K in ethanol are 2.7–3.1 ns. Significantly, there was no evidence for T1 state formation in either the time-resolved traces or the emission spectra. Considering all data together, we conclude that component 3 with lifetime τ3 in the gas-phase time-resolved spectra is most likely associated with the T1 state. A similar ISC process is absent in solution due to substantial changes in the potential energy surface with solvation15 perturbing the S1/T1 geometry in the P-trap. Future efforts might like to investigate pHBDI− derivatives including heavy atoms facilitating ISC, provided that the heavy atom functionality does not perturb the P-trap and T1 state degeneracy.
4. Conclusions
We have reported time-resolved experiments, in both the gas phase and in aqueous solution, on a series of anions linked to the chromophore found in green fluorescent protein. The gas-phase lifetimes for the S1 state span 1.6–10 ps, while those in aqueous solution are shorter at 0.06–0.3 ps. These anions present an intriguing case where the gas-phase dynamics are slowed compared to those in solution, a situation which contrasts with many other organic ions because, in the gas phase, nuclear motion is not hindered and there is no vibrational energy redistribution to the environment. The excited-state dynamics were interpreted in terms of a dual conical intersection potential energy surface possessing a shallow and twisted S1 potential energy minimum (P-trap). Significantly, through molecular dynamics simulations, we identified an intersystem crossing seam that is degenerate with the P-trap, facilitating a small amount of intersystem crossing (ISC), consistent with a minor, long-lived (≫40 ps) component in the gas phase measurements. No similar ISC was found in aqueous solution (or seen in any other solution-based study on pHBDI−); this absence was attributed to a significant geometry change and stabilisation of the P-trap and possibly conical intersections in solution.There are several avenues for future work. First, time-resolved photoelectron imaging measurements should be repeated at cryogenic temperatures, allowing increased spectral resolution of the electron kinetic energy distributions and also to prolong S1 lifetimes, e.g. by exciting on the red-edge of the absorption band. Efforts to increase the S1 excited state lifetime should result in an increase in the fraction of the population undergoing ISC. Second, the gas-phase Z–E photoisomerisation experiments on pHBDI−, reported by some of the current authors,41 should be extended to these alkylated anions, with efforts to quantify (relative) Z–E photoisomerisation quantum yields. When such measurements are interpreted in conjunction with ab initio molecular dynamics simulations similar to those performed by Martinez and co-workers,16 the fraction of the excited-state population passing through each conical intersection seam could be inferred. There is also the possibility to couple femtosecond pump–probe spectroscopy to such an ion mobility experiment, potentially allowing the lifetimes connected with isomerising and non-isomerising excited-state populations to be disentangled. Third, it would be interesting to perform synthetic modifications to the six-membered ring (e.g. through addition of heavy atoms) to increase ISC coupling strengths, allowing for clear investigation of the ISC dynamics.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.Author contributions
Photoelectron imaging experiments were performed by JNB and CAS in the laboratory of JRRN. Solution spectroscopy experiments were performed by EKA and MHK in the laboratory of SRM. Static electronic structure calculations were performed by EKA, and dynamical calculations were performed by GRL and LB. The alkylated molecules were originally synthesised by KS as part of an earlier study. The manuscript was prepared by EKA and JNB, and was discussed by all authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Funding was provided by a start-up grant at University of East Anglia and an EPSRC New Investigator Award (EP/W018691) to JNB. LB and GRL thank the Ministerio de Ciencia, Innovación y Universidades (Spain) for project PID-2019-104654GB-I00 and the Red Española de Supercomputación for computational time (project QSB-2018-1-0040). EKA acknowledges a University of East Anglia Doctoral Studentship. Electronic structure calculations were carried out on the High Performance Computing Cluster supported by the Research and Specialist Computing Support service at the University of East Anglia.Notes and references
- M. Chalfie, Y. Tu, G. Euskirchen, W. W. Ward and D. C. Prasher, Science, 1994, 263, 802–805 CrossRef CAS PubMed.
- R. Y. Tsien, Annu. Rev. Biochem., 1998, 67, 509–544 CrossRef CAS PubMed.
- C. L. Walker, K. A. Lukyanov, I. V. Yampolsky, A. S. Mishin, A. S. Bommarius, A. M. Duraj-Thatte, B. Azizi, L. M. Tolbert and K. M. Solntsev, Curr. Opin. Chem. Biol., 2015, 27, 64–74 CrossRef CAS PubMed.
- M. Ormö, A. B. Cubitt, K. Kallio, L. A. Gross, R. Y. Tsien and S. J. Remington, Science, 1996, 273, 1392–1395 CrossRef PubMed.
- N. C. Shaner, P. A. Steinbach and R. Y. Tsien, Nat. Methods, 2005, 2, 905–909 CrossRef CAS PubMed.
- A. S. Mishin, V. V. Belousov, K. M. Solntsev and K. A. Lukyanov, Curr. Opin. Chem. Biol., 2015, 27, 1–9 CrossRef CAS PubMed.
- P. S. Weiss, ACS Nano, 2008, 2, 1977 CrossRef CAS PubMed.
- K. Nienhaus and G. U. Nienhaus, J. Phys.: Condens. Matter, 2016, 28, 443001 CrossRef PubMed.
- S. R. Meech, Chem. Soc. Rev., 2009, 38, 2922–2934 RSC.
- A. Henley and H. H. Fielding, Int. Rev. Phys. Chem., 2019, 38, 1–34 Search PubMed.
- G. U. Nienhaus, Angew. Chem., Int. Ed., 2008, 47, 8992–8994 CrossRef CAS PubMed.
- J. Conyard, M. Kondo, I. A. Heisler, G. Jones, A. Baldridge, L. M. Tolbert, K. M. Solntsev and S. R. Meech, J. Phys. Chem. B, 2011, 115, 1571–1577 CrossRef CAS PubMed.
- H. Niwa, S. Inouye, T. Hirano, T. Matsuno, S. Kojima, M. Kubota, M. Ohashi and F. Tsuji, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 13617–13622 CrossRef CAS PubMed.
- A. Acharya, A. M. Bogdanov, B. L. Grigorenko, K. B. Bravaya, A. V. Nemukhin, K. A. Lukyanov and A. I. Krylov, Chem. Rev., 2016, 117, 758–795 CrossRef PubMed.
- C. M. Jones, N. H. List and T. J. Martínez, Chem. Sci., 2021, 12, 11347–11363 RSC.
- N. H. List, C. M. Jones and T. J. Martínez, Chem. Sci., 2022, 13, 373–385 RSC.
- M. E. Martin, F. Negri and M. Olivucci, J. Am. Chem. Soc., 2004, 126, 5452–5464 CrossRef CAS PubMed.
- M. G. Romei, C.-Y. Lin, I. I. Mathews and S. G. Boxer, Science, 2020, 367, 76–79 CrossRef CAS PubMed.
- C. Kjær, J. Langeland, T. T. Lindkvist, E. R. Sørensen, M. H. Stockett, H. G. Kjaergaard and S. B. Nielsen, Rev. Sci. Instrum., 2021, 92, 033105 CrossRef PubMed.
- E. K. Ashworth, J. Langeland, M. H. Stockett, T. T. Lindkvist, C. Kjær, J. N. Bull and S. B. Nielsen, J. Phys. Chem. A, 2022, 126, 9553–9563 CrossRef CAS PubMed.
- S. P. Laptenok, J. Conyard, P. C. B. Page, Y. Chan, M. You, S. R. Jaffrey and S. R. Meech, Chem. Sci., 2016, 7, 5747–5752 RSC.
- C. Chen, L. Zhu, S. A. Boulanger, N. S. Baleeva, I. N. Myasnyanko, M. S. Baranov and C. Fang, J. Chem. Phys., 2020, 152, 021101 CrossRef CAS PubMed.
- S. A. Boulanger, C. Chen, L. Tang, L. Zhu, N. S. Baleeva, I. N. Myasnyanko, M. S. Baranov and C. Fang, Phys. Chem. Chem. Phys., 2021, 23, 14636–14648 RSC.
- J. L. Woodhouse, A. Henley, R. Lewin, J. M. Ward, H. C. Hailes, A. V. Bochenkova and H. H. Fielding, Phys. Chem. Chem. Phys., 2021, 23, 19911–19922 RSC.
- T. Chatterjee, M. Mandal, A. Das, K. Bhattacharyya, A. Datta and P. K. Mandal, J. Phys. Chem. B, 2016, 120, 3503–3510 CrossRef CAS PubMed.
- S. Rafiq, B. K. Rajbongshi, N. N. Nair, P. Sen and G. Ramanathan, J. Phys. Chem. A, 2011, 115, 13733–13742 CrossRef CAS PubMed.
- C.-W. Cheng, G.-J. Huang, H.-Y. Hsu, C. Prabhakar, Y.-P. Lee, E. W.-G. Diau and J.-S. Yang, J. Phys. Chem. B, 2013, 117, 2705–2716 CrossRef CAS PubMed.
- G.-J. Huang, C.-W. Cheng, H.-Y. Hsu, C. Prabhakar, Y.-P. Lee, E. W.-G. Diau and J.-S. Yang, J. Phys. Chem. B, 2013, 117, 2695–2704 CrossRef CAS PubMed.
- J. Dong, K. M. Solntsev and L. M. Tolbert, J. Am. Chem. Soc., 2006, 128, 12038–12039 CrossRef CAS PubMed.
- K. M. Solntsev, O. Poizat, J. Dong, J. Rehault, Y. Lou, C. Burda and L. M. Tolbert, J. Phys. Chem. B, 2008, 112, 2700–2711 CrossRef CAS PubMed.
- C. McLaughlin, M. Assmann, M. A. Parkes, J. L. Woodhouse, R. Lewin, H. C. Hailes, G. A. Worth and H. H. Fielding, Chem. Sci., 2017, 8, 1621–1630 RSC.
- S. B. Nielsen, A. Lapierre, J. U. Andersen, U. V. Pedersen, S. Tomita and L. H. Andersen, Phys. Rev. Lett., 2001, 87, 228102 CrossRef CAS PubMed.
- M. W. Forbes and R. A. Jockusch, J. Am. Chem. Soc., 2009, 131, 17038–17039 CrossRef CAS PubMed.
- H. V. Kiefer, H. B. Pedersen, A. V. Bochenkova and L. H. Andersen, Phys. Rev. Lett., 2016, 117, 243004 CrossRef PubMed.
- J. Langeland, C. Kjær, L. H. Andersen and S. BrøndstedNielsen, ChemPhysChem, 2018, 19, 1686–1690 CrossRef CAS PubMed.
- W. Zagorec-Marks, M. M. Foreman, J. R. R. Verlet and J. M. Weber, J. Phys. Chem. Lett., 2020, 11, 1940–1946 CrossRef CAS PubMed.
- E. K. Ashworth, M. H. Stockett, C. Kjær, P. C. B. Page, S. R. Meech, S. B. Nielsen and J. N. Bull, J. Phys. Chem. A, 2022, 126, 1158–1167 CrossRef CAS PubMed.
- N. J. A. Coughlan, M. H. Stockett, C. Kjær, E. K. Ashworth, P. C. B. Page, S. R. Meech, S. B. Nielsen, L. Blancafort, W. S. Hopkins and J. N. Bull, J. Chem. Phys., 2021, 155, 124304 CrossRef CAS PubMed.
- C. W. West, J. N. Bull, A. S. Hudson, S. L. Cobb and J. R. R. Verlet, J. Phys. Chem. B, 2015, 119, 3982–3987 CrossRef CAS PubMed.
- W. Zagorec-Marks, M. M. Foreman, J. R. R. Verlet and J. M. Weber, J. Phys. Chem. Lett., 2019, 10, 7817–7822 CrossRef CAS PubMed.
- E. Carrascosa, J. N. Bull, M. S. Scholz, N. J. A. Coughlan, S. Olsen, U. Wille and E. J. Bieske, J. Phys. Chem. Lett., 2018, 9, 2647–2651 CrossRef CAS PubMed.
- C. R. S. Mooney, D. A. Horke, A. S. Chatterley, A. Simperler, H. H. Fielding and J. R. R. Verlet, Chem. Sci., 2013, 4, 921–927 RSC.
- C. W. West, A. S. Hudson, S. L. Cobb and J. R. R. Verlet, J. Chem. Phys., 2013, 139, 071104 CrossRef PubMed.
- A. Svendsen, H. V. Kiefer, H. B. Pedersen, A. V. Bochenkova and L. H. Andersen, J. Am. Chem. Soc., 2017, 139, 8766–8771 CrossRef CAS PubMed.
- X. Li, L. W. Chung and G. Li, J. Chem. Theory Comput., 2016, 12, 5453–5464 CrossRef CAS PubMed.
- S. Bose, S. Chakrabarty and D. Ghosh, J. Phys. Chem. B, 2016, 120, 4410–4420 CrossRef CAS PubMed.
- S. Bose, S. Chakrabarty and D. Ghosh, J. Phys. Chem. B, 2017, 121, 4790–4798 CrossRef CAS PubMed.
- M. D. Davari, F. J. A. Ferrer, D. Morozov, F. Santoro and G. Groenhof, ChemPhysChem, 2014, 15, 3236–3245 CrossRef CAS PubMed.
- F. J. A. Ferrer, M. D. Davari, D. Morozov, G. Groenhof and F. Santoro, ChemPhysChem, 2014, 15, 3246–3257 CrossRef PubMed.
- S. Olsen, K. Lamothe and T. J. Martínez, J. Am. Chem. Soc., 2010, 132, 1192–1193 CrossRef CAS PubMed.
- L. Zhao, P.-W. Zhou, B. Li, A.-H. Gao and K.-L. Han, J. Chem. Phys., 2014, 141, 235101 CrossRef PubMed.
- M. S. Schuurman and A. Stolow, Annu. Rev. Phys. Chem., 2018, 69, 427–450 CrossRef CAS PubMed.
- G. M. Roberts, J. Lecointre, D. A. Horke and J. R. R. Verlet, Phys. Chem. Chem. Phys., 2010, 12, 6226–6232 RSC.
- D. A. Horke, G. M. Roberts, J. Lecointre and J. R. R. Verlet, Rev. Sci. Instrum., 2012, 83, 063101 CrossRef PubMed.
- G. M. Roberts, J. L. Nixon, J. Lecointre, E. Wrede and J. R. R. Verlet, Rev. Sci. Instrum., 2009, 80, 053104 CrossRef CAS PubMed.
- R. N. Zare, Mol. Photochem., 1972, 4, 1–37 CAS.
- L. H. Stanley, C. S. Anstöter and J. R. R. Verlet, Chem. Sci., 2017, 8, 3054–3061 RSC.
- I. A. Heisler, M. Kondo and S. R. Meech, J. Phys. Chem. B, 2009, 113, 1623–1631 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 16 Revision B.01, Gaussian Inc. Wallingford CT, 2016 Search PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- J. T. H. Dunning, Jr., J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- C. Riplinger, B. Sandhoefer, A. Hansen and F. Neese, J. Chem. Phys., 2013, 139, 134101 CrossRef PubMed.
- M. J. Frisch, M. Head-Gordon and J. A. Pople, Chem. Phys. Lett., 1990, 166, 275–280 CrossRef CAS.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- J. J. P. Stewart, J. Mol. Model., 2007, 13, 1173–1213 CrossRef CAS PubMed.
- M. Nooijen and R. J. Bartlett, J. Chem. Phys., 1997, 107, 6812–6830 CrossRef CAS.
- M. Barbatti, M. Ruckenbauer, F. Plasser, J. Pittner, G. Granucci, M. Persico and H. Lischka, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 4, 26–33 Search PubMed.
- M. Barbatti, G. Granucci, M. Ruckenbauer, F. Plasser, R. Crespo-Otero, J. Pittner, M. Persico and H. Lischka, NEWTON-X: A package for Newtonian Dynamics Close to the Crossing Seam (v. 2.2), 2018, Available at www.newtonx.org.
- F. Aquilante, J. Autschbach, R. K. Carlson, L. F. Chibotaru, M. G. Delcey, L. D. Vico, I. F. Galván, N. Ferré, L. M. Frutos, L. Gagliardi, M. Garavelli, A. Giussani, C. E. Hoyer, G. L. Manni, H. Lischka, D. Ma, P. Å. Malmqvist, T. Müller, A. Nenov, M. Olivucci, T. B. Pedersen, D. Peng, F. Plasser, B. Pritchard, M. Reiher, I. Rivalta, I. Schapiro, J. Segarra-Martí, M. Stenrup, D. G. Truhlar, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, V. P. Vysotskiy, O. Weingart, F. Zapata and R. Lindh, J. Comput. Chem., 2015, 37, 506–541 CrossRef PubMed.
- F. Aquilante, J. Autschbach, A. Baiardi, S. Battaglia, V. A. Borin, L. F. Chibotaru, I. Conti, L. D. Vico, M. Delcey, I. F. Galván, N. Ferré, L. Freitag, M. Garavelli, X. Gong, S. Knecht, E. D. Larsson, R. Lindh, M. Lundberg, P. Å. Malmqvist, A. Nenov, J. Norell, M. Odelius, M. Olivucci, T. B. Pedersen, L. Pedraza-González, Q. M. Phung, K. Pierloot, M. Reiher, I. Schapiro, J. Segarra-Martí, F. Segatta, L. Seijo, S. Sen, D.-C. Sergentu, C. J. Stein, L. Ungur, M. Vacher, A. Valentini and V. Veryazov, J. Chem. Phys., 2020, 152, 214117 CrossRef CAS PubMed.
- G. Ghigo, B. O. Roos and P.-Å. Malmqvist, Chem. Phys. Lett., 2004, 396, 142–149 CrossRef CAS.
- N. Forsberg and P.-Å. Malmqvist, Chem. Phys. Lett., 1997, 274, 196–204 CrossRef CAS.
- R. Sarkar, P.-F. Loos, M. Boggio-Pasqua and D. Jacquemin, J. Chem. Theory Comput., 2022, 18, 2418–2436 CrossRef CAS PubMed.
- D. A. Horke and J. R. R. Verlet, Phys. Chem. Chem. Phys., 2012, 14, 8511–8515 RSC.
- S. H. M. Deng, X.-Y. Kong, G. Zhang, Y. Yang, W.-J. Zheng, Z.-R. Sun, D.-Q. Zhang and X.-B. Wang, J. Phys. Chem. Lett., 2014, 5, 2155–2159 CrossRef CAS PubMed.
- A. V. Bochenkova and L. H. Andersen, J. Phys. Chem. Lett., 2022, 13, 6683–6685 CrossRef CAS PubMed.
- K. D. Jordan and P. D. Burrow, Chem. Rev., 1987, 87, 557–588 CrossRef CAS.
- M. Ben-Nun, F. Molnar, K. Schulten and T. J. Martínez, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 1769–1773 CrossRef CAS PubMed.
- D. Asturiol, B. Lasorne, G. A. Worth, M. A. Robb and L. Blancafort, Phys. Chem. Chem. Phys., 2010, 12, 4949–4958 RSC.
- L. Blancafort, ChemPhysChem, 2014, 15, 3166–3181 CrossRef CAS PubMed.
- J. Conyard, I. A. Heisler, Y. Chan, P. C. B. Page, S. R. Meech and L. Blancafort, Chem. Sci., 2018, 9, 1803–1812 RSC.
- R. L. Martin, J. Chem. Phys., 2003, 118, 4775–4777 CrossRef CAS.
- L. Salem and C. Rowland, Angew. Chem., Int. Ed. Engl., 1972, 11, 92–111 CrossRef CAS.
- M. Abe, Chem. Rev., 2013, 113, 7011–7088 CrossRef CAS PubMed.
- T. Stuyver, B. Chen, T. Zeng, P. Geerlings, F. D. Proft and R. Hoffmann, Chem. Rev., 2019, 119, 11291–11351 CrossRef CAS PubMed.
- D. Mandal, T. Tahara and S. R. Meech, J. Phys. Chem. B, 2004, 108, 1102–1108 CrossRef CAS.
- M. A. Taylor, L. Zhu, N. D. Rozanov, K. T. Stout, C. Chen and C. Fang, Phys. Chem. Chem. Phys., 2019, 21, 9728–9739 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available: Molecular dynamics trajectory data; fluorescence spectroscopy; modelling microsolvation; dihedral angles; Cartesian coordinates of optimised geometries; optimised microsolvated geometries. See DOI: https://doi.org/10.1039/d3cp03250g |
| ‡ Current address: Department of Chemistry, University of York, Heslington, YO10 5DD, UK. |
| This journal is © the Owner Societies 2023 |