Dual-responsive zwitterion-modified nanopores: a mesoscopic simulation study†
Zhaohong
Miao
 ,
Zheng
Chen
,
Li
Wang
,
Lizhi
Zhang
,
Zheng
Chen
,
Li
Wang
,
Lizhi
Zhang
 and
Jian
Zhou
and
Jian
Zhou
 *
*
School of Chemistry and Chemical Engineering, Guangdong Provincial Key Lab for Green Chemical Product Technology, South China University of Technology, Guangzhou, Guangdong, 510640, P. R. China. E-mail: jianzhou@scut.edu.cn; Fax: +86 20 87114069; Tel: +86 20 87114069
First published on 9th March 2022
Abstract
In this work, dissipative particle dynamics simulation was carried out to investigate the intelligent switching effect of nanopores grafted by the zwitterionic polymer brushes poly(carboxybetaine) with excellent antifouling properties. The result shows that with different grafting densities and grafting lengths, zwitterionic polymer brushes show typical pH- and salt-responsiveness features. When the grafting density is greater than 0.2 accompanying a grafting length of 40, pH has a significant effect on the structure and pore size of the nanopores, that is, the pore remains open under neutral condition and exhibits a switching effect under acidic condition. Similarly, the size of the nanopore can be tuned by altering the grafting density and polymer chain length under salt-concentration-responsive conditions. Differently, compared with the pH effect, the salt concentration has an obvious impact on the switching effect, i.e., responsiveness emerges with a lower grafting density and length. This work provides molecular level mechanism and theoretical guidance for the design of smart nanopores modified by zwitterionic polymer brushes, as well as plays an important role in the construction of nanopores with antifouling and pH/salt-responsive properties.
Introduction
Anti-fouling is one of the most crucial requirements in biomaterials-related engineering fields.1–7 Three generations of anti-fouling polymer materials have been successively dug out and studied: 2-hydroxyethyl methacrylate (HEMA)-based polymers,8,9 PEGylated-based polymers10–12 and zwitterionic-based polymers.13,14 Although the first two generations of materials display good anti-fouling performance based on their hydrophilicity, their property is still limited under complex conditions, which leads to the reduction of their anti-fouling ability.15–18 Inspired by the cell membrane structure, zwitterionic-based polymers based on the natural bio-inert theory have been developed, which have equal positive and negative charges.13,14,19,20 Therefore, zwitterionic polymers exhibit their antifouling properties due to the strong electrostatic interactions with surrounding water molecules which facilitates the formation of a stronger hydration layer compared with the hydration layer formed by the H-bond interaction in (HEMA)-based and PEGylation-based polymers. Because of the bionic characteristics and outstanding anti-fouling properties, zwitterionic-based materials have been explored more and more deeply in the past decade, and have been proved as a preferred candidate for surface modification in biomedical and engineering applications as well as in membrane science of flow control, such as biomedical membranes, desalination membranes, and chemical sensor membranes.21–26 In more detail, Vinod et al. summarized a series of bio-inspired strategies for designing antifouling biomaterials. In their review, a list for comparison of various antifouling strategies had been presented; zwitterionic polymers, as a typical chemical modification material, possess prominent advantages, such as long-term antifouling characteristics and unique capability for ligand immobilization.27 As Banerjee et al. summarized in their review, to fabricate antifouling coating, zwitterionization is one of the best options for resisting proteins.1 Additionally, Fam et al. explored the efficient stealth coating of nanoparticles in drug delivery systems, in which the polyzwitterions with superior ionic solvation, created highly hydrophilic surfaces to reduce protein adsorption, and resolved the limitation of stability.28 Moreover, Sin et al. overviewed studies focused on hemocompatibility of zwitterionic interfaces and membranes. They illustrated the development of antifouling materials in detail, especially zwitterionic polymers; they further introduced the fabrication and applications of zwitterionic interfaces and membranes, which proved that zwitterionic polymers are promising materials in the biomedical field.29Additionally, porous membranes, with intelligent responsiveness that can respond to environmental factors such as pH, temperature, ionic strength, electric fields, etc., have been paid special attention in recent years.30–34 Chu and coworkers summarized the stimuli-responsive membranes and proved the important role of smart membranes in separation processes.35 Moreover, Liu et al. summarized the developments in various stimuli-responsive smart gating membranes, in which the zwitterionic material, as a typical polyelectrolyte material, plays a key role in the ion-strength-responsive gating.36 Palivan et al. introduced bioinspired polymer vesicles and membranes for biological and medical applications. In their work, it was shown that the intrinsic stimuli-responsiveness is the most important property of biological membranes which is also the subject of artificial membranes.37 In greater detail, the surface or pore characteristics and permeation properties (hydraulic permeability and diffusional permeability) of the stimuli-responsive membranes can be dramatically adjusted by the modification of functional materials which further realizes the flow control with an intelligent switching effect, especially in the field of micro/nano flow control.38–41 Consequently, it has become increasingly important for the intelligent stimuli-responsive modification of nanopores. As for the definition of a nanopore, as mentioned in the article, it is considered that both “nanopores” and “nanochannels” are in common mutual use. In terms of shape, a nanopore is defined simply as a pore having a diameter in the range of 1 to 100 nm, with the pore diameter larger than its depth.42 Nowadays, with the demand for the application of micro/nano flow control, based on the structure of the nanopore/nanochannel and the requirement of different properties, mass modifications of nanopore/nanochannel are being explored. For instance, Siwy et al. prepared a polyimide foil with a single asymmetric electro-responsiveness pore, namely, the effect of ion-current rectification can be strongly influenced by the surface charge of the pore, which can be regulated by the pH of the electrolyte.43 Alem et al. modified the nanopore walls of the PET membrane by N-isopropylacrylamide (NIPAM) brushes. They found that the temperature modulated permeability properties of this responsive polymeric system showed a pore-size dependent character. That is, for larger pores (Φ ∼ 330 nm), as the PNIPAM chain conformations expanded (T < LCST), the pore size as well as the permeabilities decreased compared to the collapsed conformation, while for narrower pores (Φ ∼ 80 nm), the expanded PNIPAM brushes (T < LCST) offered greater hydration ability, resulting in improved permeability compared to that of the collapsed conformation.44 Guo et al. fabricated a dual-functional nanofluidic device that integrated the ionic gate and the ionic rectifier within one solid-state nanopore which was realized by grafting temperature- and pH-responsive poly(-N-isopropyl acrylamide-co-acrylic acid) brushes onto the wall of a cone-shaped nanopore.31 Wang et al. constructed a poly(ethylene terephthalate) film modified by immobilizing zirconium(IV) ions with a single nanopore, which showed biomimetic ion-responsiveness and could be used as an ionic sensor.38
Although stimuli-responsive membranes have been studied broadly, membrane fouling still restricts their application. Combining the advantages of zwitterionic materials, porous membranes have been further explored, and some interesting results have been obtained.45 Nanopores in membranes modified with zwitterionic polymer brushes not only retain or even obtain more sensitive switching effects, but also display excellent anti-fouling performance, which is of great significance for the application.42 For example, Yameen et al. synthesized single conical nanopores displaying pH-tunable rectifying characteristics, in which the zwitterionic polymer brushes modified in the surface of nanopores played an important effect in manipulating ionic transport.46 Wang et al. fabricated a salt-responsive membrane with an ultrahigh gating ratio by grafting zwitterionic nanohydrogels onto a poly(acrylic acid)-grafting-poly(vinylidene fluoride) (PAA-g-PVDF) microporous membrane which realized highly sensitive responsiveness and anti-fouling simultaneously.30
Notwithstanding the progress achieved in the experimental study of stimuli-responsive nanopores modified by zwitterionic polymers, the molecular details of the structure and functions remain poorly understood, which further restricts their application in various fields, especially in microfluidic applications. Computer simulations can supplement the experimental work and facilitate the exploration of new achievements.47,48 Nevertheless, some computer simulation studies have been carried out to explore the nanopore properties, and the structure–activity relationship is not well understood49–51 for zwitterion-modified nanopores. Owing to the fact that physical phenomena observed at the macroscopic scale are essentially determined by the microstructure of matter, mesoscopic simulation actually serves as a bridge between molecular information and macroscopic properties. Dissipative particle dynamics (DPD) simulation which matches the temporal and spatial scale of polymer self-assembly behaviours has been proved to be one of the most effective methods to investigate polymer properties at the mesoscopic scale.52–55 In this study, DPD simulation was performed to study the switching effect of nanopores modified by zwitterionic polymer poly(carboxybetaine) (PCBMA)56,57 brushes, which is one of the most widely used technique and combines ultralow fouling and ease functionalization. The effects of chain length and grafting density of polymers on the smart switching of nanopores were studied under both neutral and highly acidic pH conditions, as well as different salt concentration conditions. The effects of pH and salt concentration on the nanopore switching and nanopore sizes were further compared. This study aims to explore the molecular mechanism of the switching effect of zwitterionic-polymer-modified nanopores and provides theoretical guidance for designing smart nanopores.
Experimental
Simulation method
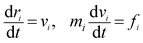 | (1) |
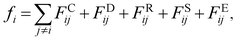 | (2) |
The interaction between the beads is determined by cutoff radius reduced unit rc, which is set to 1. The length unit rc can be converted to the real length unit by equation rc = (ρ × Nm × Vw)1/3. Specifically, the first three forces are determined by the positions and velocities of beads i and j, as given by eqn (3)–(5),
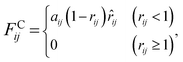 | (3) |
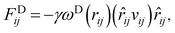 | (4) |
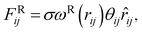 | (5) |
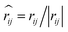 , and νij = vj − vi, aij is the maximum repulsion parameter between particle i and j, γ is the dissipation strength, σ denotes the noise amplitude; θij is a random number with zero mean and unit variance;
, and νij = vj − vi, aij is the maximum repulsion parameter between particle i and j, γ is the dissipation strength, σ denotes the noise amplitude; θij is a random number with zero mean and unit variance; 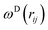 and
and 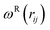 are r-dependent weight functions. According to the fluctuation–dissipation theorem, Español and Warren61 showed a relationship between the two weight functions, as eqn (6) and (7),
are r-dependent weight functions. According to the fluctuation–dissipation theorem, Español and Warren61 showed a relationship between the two weight functions, as eqn (6) and (7),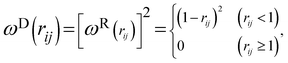 | (6) |
| σ2 = 2γkBT, | (7) |
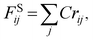 | (8) |
The electrostatic force FEij is calculated by a modified Ewald sum method according to González–Melchor et al.,62
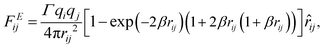 | (9) |
Models and simulation parameters
The studied system is composed of a zwitterionic polymer, nanopore and water. In this work, the diameter and the length of the pore system is set as 30 and 42 rc, respectively, which fits the definition of a nanopore. The CG models of the zwitterionic polymer and nanopore are shown in Fig. 1. The CG model of PCBMA contains three types of beads, B, N and C, which represent the backbone chain, the amino group and the carboxyl group, respectively (Fig. 1a). The zwitterionic polymers are grafted onto the nanopore via the fixed head beads (the fixed head bead is the B bead on the one end of PCBMA chain). The beads of the nanopore are denoted as P and the wall density of the nanopore is the same as that of the system with ρ = 3.63,64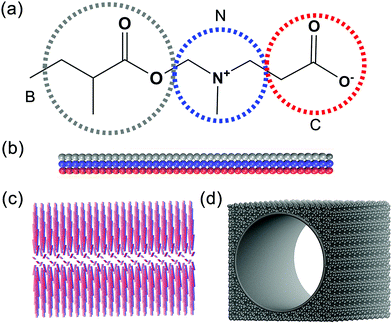 | ||
| Fig. 1 The molecular structure and coarse-grained models of the PCBMA monomer (a), polymer chain (b); polymer brush (c) and nanopore (d). | ||
Calculating the bead–bead repulsion parameter or DPD interaction parameter aij is the most important step in DPD simulations. The repulsion parameters were obtained according to the following equations,54,65
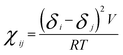 | (10) |
| aij = aii + 3.27χij | (11) |
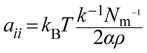 | (12) |
In eqn (10), χij is the Flory–Huggins parameter that represents the interaction parameters between beads i and j, V is the reference molar volume, R is the ideal gas constant, δi and δj are the solubility parameters for beads i and j, respectively, and T is the temperature of the system. In eqn (11), aii represents the repulsion parameter between beads of the same kind. In eqn (12), α is a constant with a value of 0.101 ± 0.001 and Nm is the number of water molecules represented by one DPD water bead. k−1 is dimensionless compressibility, and its value is about 15.98 at room temperature. ρDPD is the number density of the system, which is chosen as ρ = 3; kBT represents the energy unit in DPD simulations as the unit temperature kBT =1. Therefore, the repulsion parameter between the same bead aii is 25.00.
Table 1 shows the repulsion parameters aij between different beads at 298 K. In the experiment, the nanopore in the polystyrene (PS) membrane is hydrophobic.66 According to previous works,67,68 the repulsive parameter between P and other beads is set as 100.
| B | N | C | W | P | A+ | A− | |
|---|---|---|---|---|---|---|---|
| Note: W is the water bead; A+ and A−, containing one positive and negative unit charge, are counter ion beads, which are used to keep the system electrically neutral depending on the net charge of the simulation system. | |||||||
| B | 25.00 | ||||||
| N | 72.50 | 25.00 | |||||
| C | 27.00 | 89.42 | 25.00 | ||||
| W | 78.64 | 57.78 | 51.81 | 25.00 | |||
| P | 100.00 | 100.00 | 100.00 | 100.00 | 25.00 | ||
| A+ | 78.64 | 57.78 | 51.81 | 25.00 | 100.00 | 25.00 | 25.00 |
| A− | 78.64 | 57.78 | 51.81 | 25.00 | 100.00 | 25.00 | 25.00 |
Moreover, the pH-responsive behaviours of zwitterion-modified nanopore in aqueous buffers are explored under neutral and highly acidic conditions. Under highly acidic conditions, PCBMA is fully protonated and charged. Hence, the counterions A+ and A− are added to preserve the charge neutrality of the simulation systems. The repulsive parameters aij of the counterions are the same as that of water. In order to explore the salt concentration-responsiveness properties, NaCl is chosen, the molar concentrations of salt ions were calculated69 by 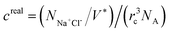 , where
, where 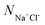 is the number of salt ion pairs and NA is the Avogadro number. The repulsive parameters of Na+ or Cl− beads are the same as those of counter ion A+ or A− beads.
is the number of salt ion pairs and NA is the Avogadro number. The repulsive parameters of Na+ or Cl− beads are the same as those of counter ion A+ or A− beads.
Simulation
In this work, DPD simulations are conducted using the DL_MESO 2.5 package.70 The system is a cubic box with a box length of 35 × 35 × 42 rc, where rc is the basic length unit in DPD simulations. The pore size is set to Φ = 30 rc with a length of 42 rc. To ensure that the final states of the systems reach equilibrium, a step size of Δt = 0.05 τ was employed, where τ = 1 is the reduced DPD time unit, the simulation steps are at least 4 × 105, the periodic boundary conditions were applied in all three directions. The Ewald sum approach was used in long-range electrostatic interactions, electrostatic cutoff releC = 3, real-space convergence parameter α = 0.975, and reciprocal space (k-vector) range kmax = (5, 5, 5).Results and discussion
PCBMA has side chains composed of cationic quaternary ammonium and anionic carboxylate functional groups, the latter can be easily converted into other functional groups. Due to its ultralow fouling, functionalizability, biomimetic, biocompatible and noncytotoxic characters, PCBMA has been widely studied as a functional zwitterionic polymer. In this work, PCBMA has been chosen as functional brushes for grafting onto the nanopores to reveal the mechanisms of antifouling and stimuli-responsiveness properties. The model is shown in Fig. 1. The switching effect of zwitterionic modified nanopores can be modulated by two major factors, pH value and salt concentration. In addition, the polymer grafting density and chain length also have impacts at different pH and salt concentration conditions.pH-Controlled pore opening/closure
As shown in Fig. 1, the PCBMA polymer is charge neutral under neutral conditions. Whereas it is positively charged under acidic conditions due to the protonation of the carboxylic acid group. This intrinsic property of surface charge responsive to pH allows the conformation changes of PCBMA polymers, which further tunes surface properties with selective permeability. In this work, aiming to explore the pH-responsiveness of the PCBMA-modified nanopores, the performances under neutral and highly acidic conditions were discussed and compared. Additionally, the grafting density in this work is defined as the number of grafting chains per membrane area, and the chain length (N) means the polymerization degree of PCBMA. All units in this work are DPD simulation reduced units.Effect of grafting density
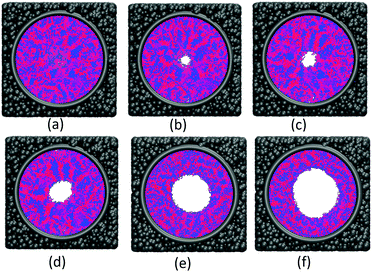
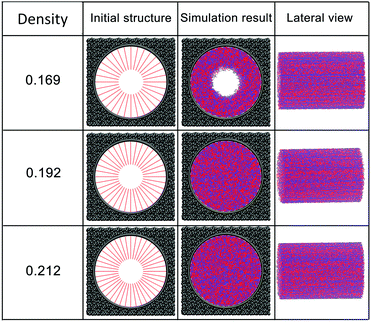
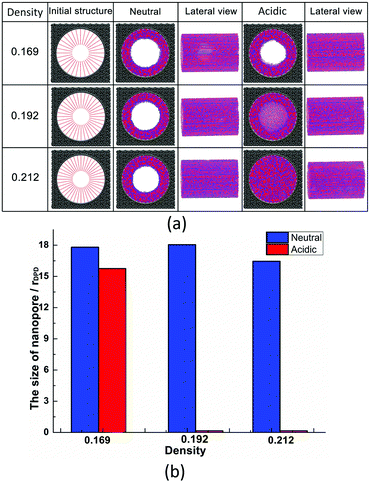
The effect of polymer grafting density on nanopores grafted PCBMA brushes as a smart switch is investigated with respect to the polymer chain length (the number of monomer unit) of 40. As shown in Fig. 2a, one can see that, under both neutral and acidic conditions, the nanopores maintain the open state at the lower polymer grafting density (0.169); however, from the lateral view of the nanopore, it clearly shows that zwitterionic polymers cannot cover the surface of the entire nanopore at lower grafting density under neutral conditions. As the grafting density increases to 0.192, the nanopore still remains open under neutral conditions. While under acidic conditions, the pore is partially open. As the grafting density further increases to 0.212, the state of the nanopore is distinct apparently: under neutral conditions, the pore size slightly reduces and still remains open; while the pore closes completely under acidic conditions. To discover the change of the nanopore sizes clearly, Poreblazer 3.0.2 package71 was adopted to quantitatively calculate the pore size. As observed in Fig. 2b, at the lower grafting density (0.169), the nanopore sizes decrease from 17.8 to 15.7 under neutral and acidic conditions. Differently, for systems with grafting densities of 0.196 and 0.212, the nanopore sizes are 18.0 and 16.5 under neutral conditions; while the nanopore sizes become zero under acidic conditions, which is consistent with the above simulation results.The main reason for these performances is that under the neutral conditions, the zwitterionic polymer is electroneutral and the PCBMA chains tend to collapse or contract by inter and/or intrachain associations, giving rise to the nanopore-opening; as the pH transforms to the highly acidic, PCBMA is fully protonated and carries a positive charge; thus, the electrostatic repulsion increases, accompanying the interaction of inter and/or intrachain forces, eventually resulting in the extension of the PCBMA chains and the pore-closure. The potential energies of systems under different conditions also prove the results. The potential energy under neutral conditions is 9.69, while that under acidic conditions is 8.66. Moreover, to display the switching-off process clearly, the trajectory snapshots of conformation changes for the system of length 40 and grafting density 0.212 under highly acidic conditions are shown in Fig. 3. The more direct animation of the switching process can be observed from the video S1 in the ESI.†
The simulation results are consistent with that of the previous work by Huo et al.72 They explored different deprotonation degrees of PCBMA and found that with the decrease of pH, the deprotonation degree decreases, and the PCBMA segments extend. This also proves the reliability of our simulation result.
In addition, PCBMA as a typical polyzwitterion has strong hydration capabilities. The tightly bound, structured water layer around the zwitterionic pendant groups is induced electrostatically, which plays an important role in fouling-resistance. Therefore, proper grafting density is important to obtain an antifouling water layer. Experimental results by Xiang et al.73 indicated that at the grafting densities larger than 20%, the nanopore exhibits antifouling properties. Furthermore, Wu et al.74 also proposed that modified membranes with high grafting density possess better antifouling characteristics. All these agree with our simulation results. Since nanopore exhibits improved antifouling properties when the grafting density of zwitterionic polymer is higher than 20%, in the following sections, the grafting density of zwitterionic polymer brushes is set to 0.212.
Effect of the chain length
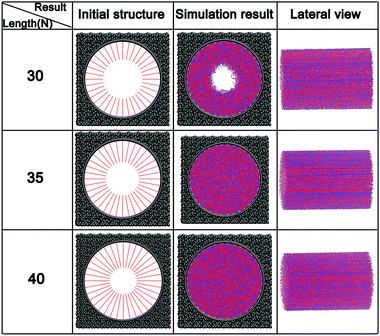
At a constant grafting density of 0.212, the effect of PCBMA chain length (polymerization degree) on the nanopore switching is investigated. The simulation results are shown in Fig. 4a. Obviously, when the polymerization degree of PCBMA is 35, the nanopores remain open under both neutral and acidic conditions. As chain length increases by 5, there are different states of nanopores, in which the pores remain open and completely close under neutral and acidic conditions, respectively. As the chain length increases up to 45, the nanopores are both “closed” under neutral or highly acidic conditions. Thus, the nanopore switching effect cannot be achieved for short or long chain lengths. Gratifyingly, the smart pH-responsiveness switching can be achieved at the intermediate length of 40.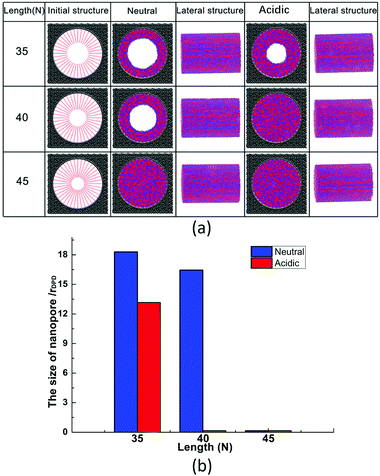 | ||
| Fig. 4 (a) Morphologies of PCBMA with different grafted lengths under neutral and acidic conditions; (b) the pore sizes of nanopores under neutral and acidic conditions. | ||
In addition, the pore sizes were calculated quantitatively. As depicted in Fig. 4b, at a length of 35, the nanopore under neutral conditions is 18.3, while under acidic conditions it is 13.2. The differences result from that under acidic conditions, zwitterion particles become charged, which leads to electrostatic repulsion between them; thus, the chains stretch. As the chain lengths increase under the neutral conditions, the nanopore sizes decrease from 18.3 to 16.5, and then to zero. While under the influence of protonation, under acidic conditions, the pore size becomes zero at a chain length of 40 and remains closed at a length of 45.
To verify the pH-responsive properties of the nanopore, taking the system of grafting density 0.212 as an example, the morphological changes of the nanopore have been observed from acidic conditions to the neutral conditions. The conformation changes are shown in Fig. 5 and the more detailed information can be observed from the video S1 in the ESI.† The size of the final nanopore is 16.3 which changes slightly compared with that (16.5) before switching-off. The result further confirmed that the zwitterionic polymer PCBMA modified nanopores achieve a reversible smart on–off character, which is consistent with previous experimental results.43,46
The results indicate that, considering the factor of pH, to achieve a smart switching effect and satisfactory antifouling performance, it is better to choose a grafting density of 0.212 and a PCBMA chain length of 40. Moreover, the properties of pH-responsiveness and antifouling of porous membranes are favourable in some industrial applications, such as oil exploitation, industrial wastewater treatment, and drug delivery in vivo. Our simulation results might provide some instructions for functional material exploration in these applications.
Salt concentration-controlled pore open/closure
Due to the presence of cationic quaternary ammonium and anionic carboxylate functional groups, the salt concentration may affect the electrostatic interaction of PCBMA, further affecting the brush performance in nanopores. Consequently, in this section, the effect of salt concentration on the switching of the nanopore was studied. As well as influences of grafting density and chain length were discussed.The experimental result of Wu et al. demonstrated that the flow control and antifouling performances were positively correlated with the grafting density and chain length.74 The simulation result in this work can give guidance for choosing certain grafting density and chain length to realize both antifouling and dual-responsiveness performance of the nanopore in the flow control field.
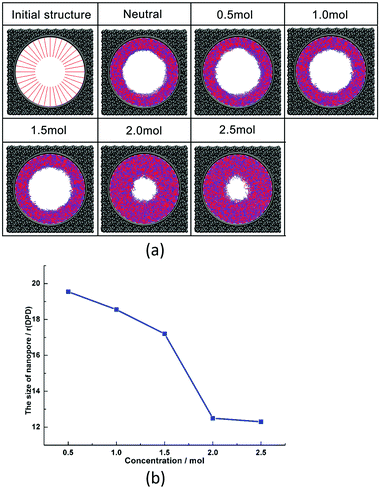 | ||
| Fig. 8 (a) Morphologies of nanopores under different salt concentrations; (b) pore sizes of nanopores under different salt concentrations. | ||
This phenomenon is related to the special structure of zwitterionic polymer PCBMA. When it is in a salt solution, the positive or negative ions of salt solution assemble at the cationic quaternary ammonium or anionic carboxylate groups due to the electrostatic interactions. It can weaken the self-association between cationic and anionic groups of PCBMA. Therefore, the zwitterionic polymer PCBMA shrinks at low salt concentrations due to the self-association between quaternary ammonium or carboxylate groups; as the salt concentrations increase, the self-association between cationic and anionic groups weakens and causes the polymer chain to gradually swell, which leads to nanopore shrinkage. Until the salt concentration continues to increase, the size of the nanopore changes slightly.
Liao et al.75 and Chen et al.47 explored the effect of ionic strength with NaCl salt on the underwater oleophobicity of a zwitterionic system. They found that the addition of salt weakened the self-association between zwitterion molecules, which led to the enhancement of hydration, which indicated the improvement of antifouling properties. Actually, these agree with the result in this work, and our work gives a clear morphology of PCBMA at different salt concentrations, which further contributes to understanding the mechanism of PCBMA conformation transition at different salt concentrations at the molecular level and provides guidance for experimental synthesis.
Conclusions
In summary, DPD simulations were performed to study the switching effect of zwitterionic polymer-brush-modified nanopores at the mesoscale level. Due to the intrinsic structure, nanopores modified by PCBMA brushes display pH and salt concentration dual-responsiveness. In addition, the grafting density and chain length of the zwitterionic polymer PCBMA have a significant effect on the switching of nanopores under different pH and salt concentration conditions.The simulation results show that nanopores modified by PCBMA brushes show obvious pH-responsiveness. In detail, the grafting density has a greater effect on the nanopore switching under different pH conditions. At lower grafting densities, the inner surface of the nanopore cannot be fully covered under any pH condition, so its antifouling performance is not ideal. When the grafting density is 0.212, zwitterionic polymers can cover the entire nanopore, and it can form completely closed nanopores under acidic conditions. Therefore, a relatively high grafting density should be chosen to prepare smart nanopores. Moreover, the effect of different chain lengths on the nanopore switching was also investigated. When the chain length is too short, closed nanopores cannot be formed under any pH condition, but when the chain length is too long, the nanopore is always closed. Therefore, the switching effect of nanopores can only be achieved with a relatively medium chain length of 40.
On the other hand, nanopores modified by PCBMA display salt-concentration-responsiveness which can affect the switching. It is found that the grafting density and chain length of zwitterionic polymers also play a certain role in nanopore switching at different salt concentrations. Compared with results under pH-responsive conditions, the switching effect of the nanopore can be achieved at a relatively lower grafting density of 0.192 and a relatively shorter chain length of 35, which means that the nanopore switching is more sensitive to the salt concentration. Finally, the influence of salt concentration on the nanopore size is explored. It is found that the pore size decreases at low salt concentrations (0.5 to 1.5 M), but when the salt concentration is increased to 2.0 M, the pore size decreases obviously. If the salt concentration continues to increase, the pore size shrinks little, and an even higher salt concentration is required to form a closed nanopore. By comparing the effects of salt concentration and pH on the switching of nanopores, it was found that the salt concentration has a relatively stronger effect on the switching.
These results can provide the molecular mechanism and theoretical guidance for designing smart nanopores modified by a zwitterionic polymer, and the smart nanopore will play an important role in anti-fouling and biomedical applications. Deeply, we hope that this work can supply some guidelines for the development of zwitterion-modified nanopores in smart nanoflow control devices.
Author contributions
Zhaohong Miao performed the experiments, data analysis, investigation, paper writing and original manuscript revision; Zheng Chen performed data analysis, investigation and original manuscript revision; Li Wang performed the experiments, data analysis and original manuscript revision; Lizhi Zhang performed the manuscript revision; Jian Zhou designed the concept, supervised the experiments and manuscript revision. All authors contributed to the general discussion.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. 51936005 and 21776093) and the GuangDong Basic and Applied Basic Research Foundation (2022A1515010876). We also thanks to the GPU hours provided by the SCUTGrid at the South China University of Technology.Notes and references
- I. Banerjee, R. C. Pangule and R. S. Kane, Adv. Mater., 2011, 23, 690–718 CrossRef CAS PubMed
.
- J. N. Shen, H. M. Ruan, L. G. Wu and C. J. Gao, Chem. Eng. J., 2011, 168, 1272–1278 CrossRef CAS
.
- M. P. Schultz, J. A. Bendick, E. R. Holm and W. M. Hertel, Biofouling, 2011, 27, 87–98 CrossRef CAS PubMed
.
- T. S. Wong, S. H. Kang, S. K. Y. Tang, E. J. Smythe, B. D. Hatton, A. Grinthal and J. Aizenberg, Nature, 2011, 477, 443–447 CrossRef CAS PubMed
.
- J. Yin and B. L. Deng, J. Membr. Sci., 2015, 479, 256–275 CrossRef CAS
.
- I. Amara, W. Miled, R. B. Slama and N. Ladhari, Environ. Toxicol. Pharmacol., 2018, 57, 115–130 CrossRef CAS PubMed
.
- W. Yang, H. S. Sundaram, J. R. Ella, N. He and S. Jiang, Acta Biomater., 2016, 40, 92–99 CrossRef CAS PubMed
.
- E. H. Leduc and S. J. Holt, J. Cell Biol., 1965, 26, 137–155 CrossRef CAS PubMed
.
- A. L. Lewis, Z. L. Cumming, H. H. Goreish, L. C. Kirkwood, L. A. Tolhurst and P. W. Stratford, Biomaterials, 2001, 22, 99–111 CrossRef CAS PubMed
.
- H. W. Ma, J. H. Hyun, P. Stiller and A. Chilkoti, Adv. Mater., 2004, 16, 338–341 CrossRef CAS
.
- J. Zheng, L. Y. Li, H. K. Tsao, Y. J. Sheng, S. F. Chen and S. Y. Jiang, Biophys. J., 2005, 89, 158–166 CrossRef CAS PubMed
.
- G. Mantovani, F. Lecolley, L. Tao, D. M. Haddleton, J. Clerx, J. J. L. M. Cornelissen and K. Velonia, J. Am. Chem. Soc., 2005, 127, 2966–2973 CrossRef CAS PubMed
.
- R. F. A. Zwaal and A. J. Schroit, Blood, 1997, 89, 1121–1132 CrossRef CAS PubMed
.
- S. F. Long, S. Clarke, M. C. Davies, A. L. Lewis, G. W. Hanlon and A. W. Lloyd, Biomaterials, 2003, 24, 4115–4121 CrossRef CAS PubMed
.
- B. Mrabet, M. N. Nguyen, A. Majbri, S. Mahouche, M. Turmine, A. Bakhrouf and M. M. Chehimi, Surf. Sci., 2009, 603, 2422–2429 CrossRef CAS
.
- C. Yoshikawa, A. Goto, Y. Tsujii, T. Fukuda, T. Kimura, K. Yamamoto and A. Kishida, Macromolecules, 2006, 39, 2284–2290 CrossRef CAS
.
- E. Ostuni, R. G. Chapman, R. E. Holmlin, S. Takayama and G. M. Whitesides, Langmuir, 2001, 17, 5605–5620 CrossRef CAS
.
- M. C. Shen, L. Martinson, M. S. Wagner, D. G. Castner, B. D. Ratner and T. A. Horbett, J. Biomater. Sci., Polym. Ed., 2002, 13, 367–390 CrossRef CAS PubMed
.
- Y. Kadoma, Egypt. J. Text. Polym. Sci. Technol., 1978, 35, 423–427 CAS
.
- K. Ishihara, T. Ueda and N. Nakabayashi, Polym. J., 1990, 22, 355–360 CrossRef CAS
.
- Y.-N. Chou, A. Venault, Y.-H. Wang, A. Chinnathambi, A. Higuchi and Y. Chang, J. Mater. Chem. B, 2018, 6, 4909–4919 RSC
.
- A. Venault, Y. W. Bai, G. V. Dizon, H. Y. E. Chou, H. C. Chiang, C. T. Lo, J. Zheng, P. Aimar and Y. Chang, J. Mater. Chem. B, 2019, 7, 7184–7194 RSC
.
- P. Liu, Q. Chen, L. Li, S. Lin and J. Shen, J. Mater. Chem. B, 2014, 2, 7222–7231 RSC
.
- Q. Shao and S. Y. Jiang, Adv. Mater., 2015, 27, 15–26 CrossRef CAS PubMed
.
- X. Peng, H. L. Liu, Q. Yin, J. C. Wu, P. Z. Chen, G. Z. Zhang, G. M. Liu, C. Z. Wu and Y. Xie, Nat. Commun., 2016, 7, 1–8 Search PubMed
.
- T. Chen, F. Wu, Z. Chen, J. Huo, Y. Zhao, L. Zhang and J. Zhou, J. Colloid Interface Sci., 2021, 587, 173–182 CrossRef CAS PubMed
.
- V. B. Damodaran and N. S. Murthy, Biomater. Res., 2016, 20, 18 CrossRef PubMed
.
- S. Y. Fam, C. F. Chee, C. Y. Yong, K. L. Ho, A. R. Mariatulqabtiah and W. S. Tan, Nanomaterials, 2020, 10, 787 CrossRef CAS PubMed
.
- M.-C. Sin, S.-H. Chen and Y. Chang, Polym. J., 2014, 46, 436–443 CrossRef CAS
.
- A. Q. Wang, W. X. Fang, J. Y. Zhang, S. J. Gao, Y. Z. Zhu and J. Jin, Small, 2020, 16, 1903925 CrossRef CAS PubMed
.
- W. Guo, H. Xia, L. Cao, F. Xia, S. Wang, G. Zhang, Y. Song, Y. Wang, L. Jiang and D. Zhu, Adv. Funct. Mater., 2010, 20, 3561–3567 CrossRef CAS
.
- Z. Chen, J. Huo, L. Hao and J. Zhou, Curr. Opin. Chem. Eng., 2019, 23, 21–33 CrossRef
.
- Q. Chen, J. Bai, J. Li, K. Huang, X. Li, B. Zhou and W. Cai, Chem. Eng. J., 2014, 252, 89–94 CrossRef CAS
.
- J. Peng, N. Zhao, S. Lin, W. Wang, M. J. Zhang, Y. Y. Su, R. Xie, X. J. Ju, Z. Liu and L. Y. Chu, Chem. Eng. J., 2021, 407, 127138 CrossRef CAS
.
- L. Chu, R. Xie and X. Ju, Chin. J. Chem. Eng., 2011, 19, 891–903 CrossRef CAS
.
- Z. Liu, W. Wang, R. Xie, X. J. Ju and L. Y. Chu, Chem. Soc. Rev., 2016, 45, 460–474 RSC
.
- C. G. Palivan, R. Goers, A. Najer, X. Zhang, A. Car and W. Meier, Chem. Soc. Rev., 2016, 45, 377–411 RSC
.
- S. Q. Zhang, T. Sun and J. H. Wang, Microchim. Acta, 2015, 182, 1387–1393 CrossRef CAS
.
- Y. Liu, D. Zhang, B. Ren, X. Gong, L. Xu, Z. Q. Feng, Y. Chang, Y. He and J. Zheng, J. Mater. Chem. B, 2020, 8, 3814–3828 RSC
.
- Y. Wang, J. Wu, D. Zhang, F. Chen, P. Fan, M. Zhong, S. Xiao, Y. Chang, X. Gong, J. Yang and J. Zheng, J. Mater. Chem. B, 2019, 7, 5762–5774 RSC
.
- C. Lavigueur, J. G. García, L. Hendriks, R. Hoogenboom, J. J. L. M. Cornelissen and R. J. M. Nolte, Polym. Chem., 2011, 2, 333–340 RSC
.
- X. Hou, W. Guo and L. Jiang, Chem. Soc. Rev., 2011, 40, 2385–2401 RSC
.
- Z. Siwy, D. Dobrev, R. Neumann, C. Trautmann and K. Voss, Appl. Phys. A: Mater. Sci. Process., 2003, 76, 781–785 CrossRef CAS
.
- H. Alem, A.-S. Duwez, P. Lussis, P. Lipnik, A. M. Jonas and S. Demoustier-Champagne, J. Membr. Sci., 2008, 308, 75–86 CrossRef CAS
.
- Z. Y. Jiang, L. Y. Chu, X. M. Wu, Z. Wang, X. B. Jiang, X. J. Ju, X. H. Ruan and G. H. He, Rev. Chem. Eng., 2020, 36, 67–105 Search PubMed
.
- B. Yameen, M. Ali, R. Neumann, W. Ensinger, W. Knoll and O. Azzaroni, J. Am. Chem. Soc., 2009, 131, 2070–2071 CrossRef CAS PubMed
.
- Z. Chen, M. R. Liao, L. Z. Zhang and J. Zhou, AIChE J., 2021, 67, e17103 CAS
.
- J. Huo, H. Jiang, Z. Chen and J. Zhou, Chem. Eng. Sci., 2018, 191, 490–499 CrossRef CAS
.
- M. Belkin, S. H. Chao, G. Giannetti and A. Aksimentiev, J. Comput. Electron., 2014, 13, 826–838 CrossRef CAS PubMed
.
- B. X. Xu, B. L. Wang, T. Park, Y. Qiao, Q. L. Zhou and X. Chen, J. Chem. Phys., 2012, 136, 184701 CrossRef PubMed
.
- E. Madai, M. Valisko and D. Boda, J. Mol. Liq., 2019, 283, 391–398 CrossRef CAS
.
- S. Zeng, X. Quan, H. Zhu, D. Sun, Z. Miao, L. Zhang and J. Zhou, Langmuir, 2021, 37, 1225–1234 CrossRef CAS PubMed
.
- P. Espanol and P. B. Warren, J. Chem. Phys., 2017, 146, 150901 CrossRef PubMed
.
- R. D. Groot and P. B. Warren, J. Chem. Phys., 1997, 107, 4423–4435 CrossRef CAS
.
- Z. Chen, L. Wang and J. Zhou, CIESC J., 2019, 70, 271–279 CAS
.
- A. Z. Niu, D. J. Liaw, H. C. Sang and C. Wu, Macromolecules, 2000, 33, 3492–3494 CrossRef CAS
.
- J. Ladd, Z. Zhang, S. Chen, J. C. Hower and S. Jiang, Biomacromolecules, 2008, 9, 1357–1361 CrossRef CAS PubMed
.
- P. J. Hoogerbrugge and J. M. V. A. Koelman, EPL, 1992, 19, 155–160 CrossRef
.
- R. D. Groot and K. L. Rabone, Biophys. J., 2001, 81, 725–736 CrossRef CAS PubMed
.
- R. D. Groot, J. Chem. Phys., 2003, 119, 10454 CrossRef CAS
.
- P. Espanol and P. Warren, EPL, 1995, 30, 191–196 CrossRef CAS
.
- M. Gonzalez-Melchor, E. Mayoral, M. E. Velazquez and J. Alejandre, J. Chem. Phys., 2006, 125, 224107 CrossRef PubMed
.
- Q. Q. Cao, C. C. Zuo, L. J. Li, Y. J. Li and Y. Yang, Biomicrofluidics, 2012, 6, 034101 CrossRef PubMed
.
- Q. Q. Cao, C. C. Zuo, L. J. Li, Y. H. Zhang and G. Yan, J. Polym. Sci., Part B: Polym. Phys., 2012, 50, 805–811 CrossRef CAS
.
- R. D. Groot and T. J. Madden, J. Chem. Phys., 1998, 108, 8713–8724 CrossRef CAS
.
- I. Velzeboer, C. Kwadijk and A. A. Koelmans, Environ. Sci. Technol., 2014, 48, 4869–4876 CrossRef CAS PubMed
.
- Z. Posel, Z. Limpouchová, K. Šindelka, M. Lísal and K. Procházka, Macromolecules, 2014, 47, 2503–2514 CrossRef CAS
.
- W. Li, W. Chu and Z. Jian, Chem. Res. Chin. Univ., 2018, 39, 85–94 Search PubMed
.
- E. Meneses-Juarez, C. Marquez-Beltran, J. F. Rivas-Silva, U. Pal and M. Gonzalez-Melchor, Soft Matter, 2015, 11, 5889–5897 RSC
.
- M. A. Seaton, R. L. Anderson, S. Metz and W. Smith, Mol. Simul., 2013, 39, 796–821 CrossRef CAS
.
- L. Sarkisov and A. Harrison, Mol. Simul., 2011, 37, 1248–1257 CrossRef CAS
.
- J. Huo, Z. Chen and J. Zhou, Langmuir, 2018, 35, 1973–1983 CrossRef PubMed
.
- T. Xiang, C. D. Luo, R. Wang, Z. Y. Han, S. D. Sun and C. S. Zhao, J. Membr. Sci., 2015, 476, 234–242 CrossRef CAS
.
- J. J. Wu, J. Zhou, J. Q. Rong, Y. Lu, H. Dong, H. Y. Yu and J. S. Gu, Chin. J. Polym. Sci., 2018, 36, 528–535 CrossRef CAS
.
- M. Liao, G. Cheng and J. Zhou, J. Phys. Chem. C, 2017, 121, 17390–17401 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1tb02416g |
| This journal is © The Royal Society of Chemistry 2022 |

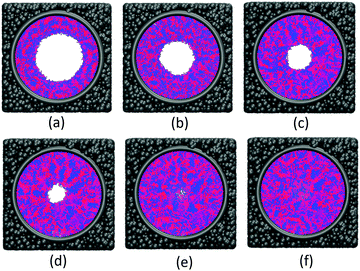
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000; (c) step 100
000; (c) step 100