Electronic spectroscopy of phthalocyanine in a supersonic jet revisited
Florian
Schlaghaufer
and
Alkwin
Slenczka
 *
*
Institute for Physical and Theoretical Chemistry, University of Regensburg, Regensburg, Germany. E-mail: alkwin.slenczka@ur.de
First published on 8th August 2022
Abstract
Spectroscopic investigation of phthalocyanine in the gas phase has tremendously profited from molecular beam spectroscopy. Isentropic expansion succeeds in reducing the population of rovibrational states to the vibrational ground state so that only low energy rotational states remain populated. However, with respect to UV-vis spectroscopy the pioneers of molecular beam spectroscopy came to the discouraging conclusion that the information contained in the rotational structure of a large molecule is minimal, and even if the rotational structure could be resolved with great effort, the results are unlikely to be worth the difficulty [Levy, Annu. Rev. Phys. Chem., 1980, 31 197–225]. Just over 4 decades later we would like to announce that the result is worth the effort, indeed. Even without full line resolution, the rotational structure at the electronic band origin of phthalocyanine provides deep insight into configurational details of phthalocyanine for both electronic states. These details serve as gas phase compliment to the investigation of microsolvation in superfluid helium droplets. To the best of our knowledge this is the largest molecule ever analyzed by means of its rotational degrees of freedom.
1 Introduction
The importance of porphyrins and phthalocyanines is unquestionable as outlined by others in two publications devoted exclusively to this class of organic molecules, namely, The Handbook of Porphyrin Science1 with in the meantime 46 volumes, and The Journal of Porphyrins and Phthalocyanines2 published since 1997. Besides all technological, biological, chemical, pharmaceutical, and medical aspects to which porphyrins and phthalocyanines contribute, they still serve as model species for electronic spectroscopy with interesting photophysical properties. A relatively large oscillator strength combined with a considerable fluorescence quantum yield warrants for brilliant fluorescence spectra of numerous such derivatives. Starting in the 1960s, the group of Martin Gouterman was devoted to the photophysical characterization of porphyrins and phthalocyanines by means of absorption and emission spectra (for phthalocyanines see e.g. ref. 3–6). One of the issues addressed in this seminal work is the splitting of the Q-band in the electronic excitation of free base phthalocyanines (Pc) and porphyrins and was resolved in hot vapor as well as in solution. Q-band splitting is a consequence of the D2h symmetry that stems from two inner hydrogen atoms (cf.Fig. 1). The lower energy band was assigned to the Qx-band while the band at higher energy was named the Qy-band, according to their polarization within the molecular frame of inertia along the a- and the b-axis, respectively. For Pc, the spectral gap between the Qx and Qy band origins amounts to roughly 1000 cm−1. Since Pc is a closed-shell aromatic compound the energetically excited states associated with the Qx- and the Qy-band are referred to as S1 and S2, respectively.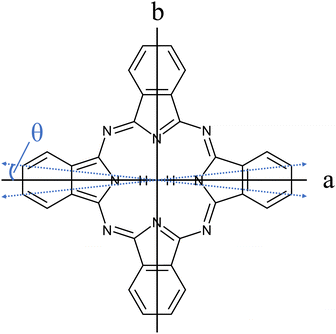 | ||
| Fig. 1 Structure of Pc (C32H18N8). The inertial axes in the Pc plane are denoted by a and b. The blue dashed double-arrows indicate the orientation of the electronic transition dipole moment as obtained from the spectroscopic experiment discussed below (cf.Fig. 7 and Table 1). Out of the 18 hydrogen atoms only the inner two that define the a-axis are shown. | ||
Great improvement in spectral resolution could be obtained by means of matrix isolation spectroscopy.7 There it was found that the Qx–Qy band gap depends on the matrix material. Before vibrationally resolved electronic spectra of matrix isolated Pc were reported,8 electronic spectroscopy in a molecular beam caused a quality change in spectral resolution. By means of a seeded supersonic molecular beam,9,10 Donald Levy presented the fully resolved vibrational structure of Pc in fluorescence excitation and dispersed emission spectra.11–14 In contrast to matrix isolation, molecules cooled via seeded beam expansion are entirely isolated and, thus, without any environmental perturbation. Fluorescence excitation spectra revealed insight into the vibrational energy levels of the electronically excited state while dispersed emission spectra recorded upon excitation at the electronic band origin provided the corresponding data for the electronic ground state. Remarkable similarity of vibrational frequencies and only weak Franck–Condon factors for vibronic transitions revealed almost identical structures and binding conditions in both electronic states, S0 and S1. In contrast, deviations in the vibrational structure starting about 1000 cm−1 beyond the electronic band origin in excitation compared to dispersed emission were due to the Herzberg–Teller coupling of the first two electronically excited states of Pc that are involved in the Qx and Qy bands, respectively. Despite spectral resolution of little less than 1 cm−1 the rotational structure of electronic and vibronic transitions remained hidden in this molecular beam experiment.
The interest in porphyrins and among those also Pc continued with the focus on both spectroscopic15–17 as well as theoretical analysis18–20 of those rather large organic compounds and their clusters with other small molecules such as H2O, CO2, MeOH and EtOH,21 and last but not least noble gases such as argon.22,23 As in the case of the first molecular beam spectra,11–14 none of these spectroscopic investigations in the gas phase ever passed the limit of spectral resolution to obtain a rotational structure. Moreover, one of the pioneers of electronic spectroscopy in molecular beams came to the conclusion that it is not worth the effort to promote experimental conditions to rotational resolution for large molecules such as Pc.24
Electronic spectroscopy and infrared- (IR-) and Raman-spectroscopy of matrix isolated free-base porphyrins have also continued to date among other objectives to clarify the Qx to Qy band gap.25–28 However, all these spectra suffer from a matrix induced spectral shift of electronic transition energies and, therefore, do not reveal the energetic conditions for the isolated Pc molecule. Equilibration among the two excited states of the Qx and Qy bands has also been reported for free base Pc derivatives in solution in ref. 29.
A new boost to high resolution electronic spectroscopy of porphyrins came from helium droplet spectroscopy.30 Thereby, superfluid helium droplets serve as a cryogenic matrix which incorporates closed shell organic molecules via pick up on the flight through a gas cell.31 The initially postulated gentleness and homogeneity attributed to a matrix exhibiting superfluidity with vanishing viscosity had to be revised. Not only the droplet size distribution as naturally present in a helium droplet beam32 but also the formation of solvation complexes consisting of the dopant species with some helium atoms rigidly attached33,34 is responsible for inhomogeneity which in many cases prevents rotational resolution in the electronic spectra of molecules in helium droplets.35,36 Moreover, rotational motion is not inhibited in a superfluid. This makes helium droplets a cryogenic host with unique properties as compared to solid matrices. However, with the exception of glyoxal as dopant species37 the rotational substructure in electronic spectra remains hidden under inhomogeneous line broadening. This is in contrast to the fully line resolved rotational structure recorded in the IR spectra of molecules and molecular compounds in superfluid helium nanodroplets.38,39
In order to obtain deeper insight into the structure of a molecule, the rotational structure is a most valuable source of information. The rotational structure resolved for the same molecule when doped into a superfluid helium droplet provides deep insight into the phenomenon of microsolvation in helium droplets. Therefore, however, one has to look behind the curtain of inhomogeneous line broadening. According to the line shape model described in ref. 35 and 36, one option would be an experiment under quasi bulk helium conditions as approached with large helium droplets (≥107 He atoms). Even though the substructure resolved for Pc in large helium droplets could be fitted by a rotor spectrum of a planar (and oblate) symmetric top,40 this particular rotor model was inappropriate since the Pc solvation complex is not planar. Alternatively, one may stay with smaller helium droplets and, thus, with a greatly improved signal to noise ratio, and record Stark spectra in order to look behind the curtain of inhomogeneous line broadening. The spectral variations induced by the change from a free rotor to a harmonic librator as accomplished by increasing the Stark field should be detectable despite inhomogeneous line broadening. However, for non-polar molecular species such as Pc which are insensitive to the first order Stark effect the latter is not an option. Therefore, we have taken the challenge to obtain rotational parameters of the isolated molecule from high resolution electronic spectra of Pc in a seeded supersonic beam as the first step. In a second step, these data can serve as a starting point for the transformation of the precise free rotor model into the helium solvated rotor by adding a helium solvation layer to the inertial ellipsoid of the isolated molecule in order to perform simulations of the electronic spectra of Pc in helium droplets for any kind of droplet size distribution as published recently.41 This paper covers the first of the two steps. A molecular beam experiment of Pc will be presented that allows resolving the rotational structure at the electronic band origin of Pc for the first time. By means of simple algorithms discussed below the rotational constants and, thus, the moments of inertia of Pc were deduced for the S0 and the S1 state with surprisingly high precision.
2 Experimental
The experimental setup is based on a vacuum machine and a single mode dye laser system described elsewhere.42 In order to obtain seeded molecular beams of Pc a homemade nozzle made of Pyrex tubing was mounted in the nozzle chamber. It was equipped with a heating device that features a copper cylinder wrapped by a thermocoax heating wire which allows for temperatures up to 550 °C. Thermal radiation of the heating unit was shielded by aluminum foil. At an appropriate temperature solid Pc inside the glass tubing was sublimated and seeded into a pressurized flow of rare gases. By isentropic expansion a supersonic jet was generated that passed a skimmer to enter the detection chamber. Notably, the experimental design allows in addition measurements without a skimmer, only a few mm downstream of the nozzle. The detection scheme has already been described in ref. 42.As mentioned by Levy,11 Pc like other organic compounds suffers thermal decomposition upon passage over hot metal surfaces, which renders the usage of standard nozzles useless. Therefore we fabricated nozzles from 6 × 1 Pyrex tubing by abrading or cutting which led to nozzle diameters (dNozzle) between 10 μm and 250 μm. The first are suitable for usage with helium as the carrier gas, the latter for argon. Stagnation pressures of up to 100 bar for helium and 250 mbar for argon were applied. Pc (29H,31H-phthalocyanine C32H18N8, purity: 98%, mol.-weight: 514.54 g mol−1) was purchased from Sigma Aldrich and used without further purification.
3 Results and discussion
3.1 Overview
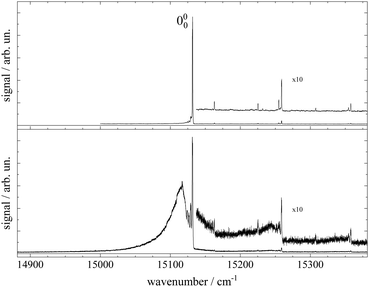
Fluorescence excitation spectra of Pc recorded from a molecular beam are shown in Fig. 2. The spectrum in the upper panel was recorded about 10 mm behind the nozzle and with helium as the carrier gas provided at a stagnation pressure of 25 bar. This experiment resembles the experimental approach from the literature.11–14,17,21,23 The laser was a cw dye laser that operated in a single mode which provides a much smaller bandwidth as compared to those experiments using pulsed dye lasers.17,21,23 In contrast, the spectrum in the lower panel in Fig. 2 was recorded from a skimmed molecular beam of Pc seeded into Ar gas at a stagnation pressure of only 180 mbar. This spectrum was recorded 150 mm downstream from the nozzle. The spectrum in the upper panel of Fig. 2 reproduces vibronic resonances reported already in ref. 13, 17, 21 and 23 and discussed there in great detail. In the lower panel the same sharp resonances are accompanied by broad and intense signals in the red.The measured spectral range of about 500 cm−1 is centered around an intense sharp peak at 15131.690(2) cm−1 with a FWHM of about 0.6 cm−1 when seeded into helium (upper panel) and 1 cm−1 when seeded into argon (lower panel), which is known as the electronic band origin of Pc.11,13 Furthermore there are very weak resonances to the blue of the electronic band origin representing vibronic transitions of Pc into the first excited singlet state (S1). The electronic band origin and the accompanying vibronic resonances have all been reported in the literature.13,21 However, the number of those resonances identified in the spectra shown in Fig. 2 was less compared to those reported by Fitch et al.13 and Menapace et al.21 This is due to the greatly reduced laser intensity in our experiment, which discriminates against resonances with low oscillator strength while avoiding saturation for those with high oscillator strengths. Following the discussion in ref. 13 and 14, weak vibronic progressions tantamount to negligible Franck–Condon factors for Δv > 0 are indicative of almost identical conditions concerning configurations and intramolecular binding energies in both electronic states (S0 and S1) of the Pc molecule.
Upon closer inspection, the electronic band origin as well as the most intense vibronic resonances are accompanied to the red by a series of peaks with frequency spacings of about 2.4 cm−1 as marked in Fig. 3. Upon seeding into argon (cf.Fig. 3, lower panel) this series is followed by an intense broad and unstructured signal extending further to the red. Moreover, on top of the broad signal and 15 cm−1 to the red of the electronic band origin there is a tiny peak. In general, signal contributions to the red of the electronic band origin in the excitation spectrum of a molecule are hot bands. If so, the different intensities of the red shifted signals in both panels of Fig. 2 and 3 reveal that cooling by means of seeded beam expansion is more efficient for the experimental conditions chosen in combination with helium as the carrier gas. Unfortunately, the high gas flux of helium needed to obtain efficient cooling in combination with the poor pumping efficiency for helium did not allow obtaining an intense skimmed molecular beam from our continuous nozzle expansion. And upon reducing the gas flux, adiabatic cooling was more efficient for argon than for helium as to be expected from the velocity slip.
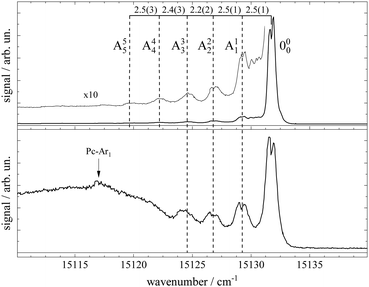 | ||
| Fig. 3 Spectral sections from the fluorescence excitation spectra of Pc shown in Fig. 2 including the electronic band origin as the most intense peak. Vertical dashed lines mark the frequency positions of a hot band progression revealing vibrational temperatures of THev ≈ 10 K (top panel) and TArv ≈ 40 K (bottom panel). Numbers in the top panel indicate the frequency gap between successive hot bands in units of cm−1. In the bottom panel, the signal of a Pc-Ar1 cluster (cf. ref. 23) is marked by a vertical arrow. | ||
Besides cooling, cluster formation is an issue of seeded beam expansion. As known from previous investigations23 the tiny peak at 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 116 cm−1 recorded for argon as the carrier gas represents a cluster consisting of Pc and one argon atom. The efficiency of cluster formation scales with the polarizability of the carrier noble gas which is larger for argon than for helium. In the case of argon as the carrier gas, cluster formation was a limiting factor and the stagnation pressure chosen for the spectrum shown in the lower panels of Fig. 2 and 3 was a compromise between optimized cooling and minimized cluster formation. The broad and unstructured signals upon which the cluster peak resides are hot bands of bare Pc as well as of larger clusters of Pc and argon. Similar observations were reported previously using helium as the carrier gas13,17,21 and in one case for helium with a minute admixture of argon.23 Besides the carrier gas, the major difference of these studies to the present experiment were a pulsed laser with high peak intensity and fluorescence detection from the unskimmed beam already a few mm behind the nozzle. Thus, spectral resolution was limited by laser band width, saturation broadening, and Doppler broadening which, finally, prevent rotational resolution.
116 cm−1 recorded for argon as the carrier gas represents a cluster consisting of Pc and one argon atom. The efficiency of cluster formation scales with the polarizability of the carrier noble gas which is larger for argon than for helium. In the case of argon as the carrier gas, cluster formation was a limiting factor and the stagnation pressure chosen for the spectrum shown in the lower panels of Fig. 2 and 3 was a compromise between optimized cooling and minimized cluster formation. The broad and unstructured signals upon which the cluster peak resides are hot bands of bare Pc as well as of larger clusters of Pc and argon. Similar observations were reported previously using helium as the carrier gas13,17,21 and in one case for helium with a minute admixture of argon.23 Besides the carrier gas, the major difference of these studies to the present experiment were a pulsed laser with high peak intensity and fluorescence detection from the unskimmed beam already a few mm behind the nozzle. Thus, spectral resolution was limited by laser band width, saturation broadening, and Doppler broadening which, finally, prevent rotational resolution.
Cooling by means of a seeded beam expansion leads to non-thermal population distributions among and within the internal degrees of freedom with a surplus of higher excited states compared to a Boltzmann distribution. These deviations from thermal equilibrium are a consequence of the correlation of the amount of energy to be dissipated with the number of collisions of the molecule and the carrier gas.9 The observation of a saturation behavior of the spectrally resolved hot band progression similar to that of the electronic band origin speaks for transitions with similar Franck–Condon factors and, thus, for transitions with Δv = 0. The shift to the red reveals the reduction of the mode frequencies for the electronically excited state which amounts to roughly 2.4(2) cm−1. Thus, the progression might represent hot bands of a particular vibrational mode, say mode A, exhibiting electronic transitions obeying Δv = 0 as marked in Fig. 3. The intensity profiles of the two spectra shown in this figure fit to a Boltzmann distribution with a T/ν0 ratio of 0.67 K cm and 2.5 K cm for helium (top panel) and argon (bottom panel) as carrier gases, respectively. Assigning the hot band progression to the lowest energy (15 cm−1) mode of Pc [cf.Table 1 in ref. 21], where isoindole rings on opposite sides perform a butterfly motion [see ref. 21] the Boltzmann fits reveal temperatures of 10 K and 40 K for helium and argon as carrier gases, respectively. These are reasonable temperatures for such a low energy mode as a result of the seeded beam expansion under the given stagnation conditions. Moreover, the reduction of the vibrational mode frequency in the electronically excited state by 16% is only expected for such low energy modes while higher energy modes were found to be unchanged for Pc (cf. ref. 14). A rather regular spacing of these signals speaks against an alternative assignment to individual vibrational modes for each peak.
A closer look at the spectra shown in Fig. 3 reveals a splitting of some of the peak signals, most clearly resolved for the electronic band origin but in addition for most of the peaks in the hot band progression and also for vibronic resonances to the blue of the electronic band origin. The spectral shape is indicative of a rotational band envelope which receives further evidence from its reproducibility. For further analysis of this substructure additional spectra were taken at the optimum of spectral resolution obtainable with our experimental setup.
3.2 High resolution measurements and simulation
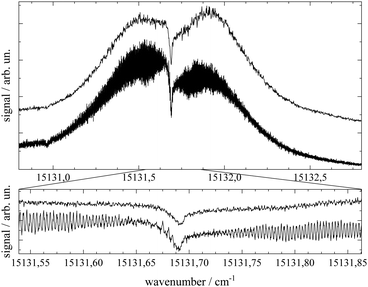
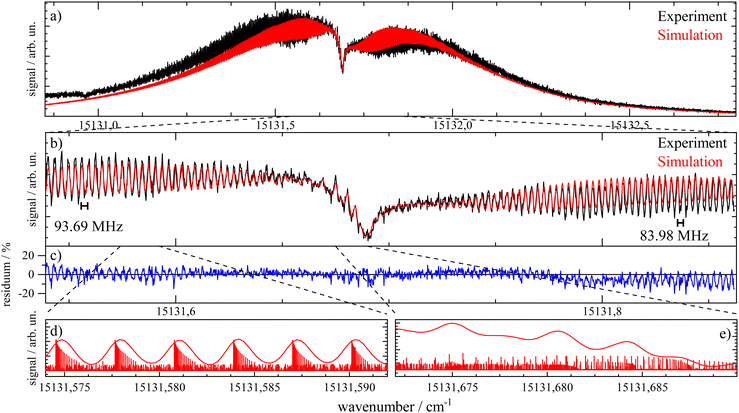
Important aspects to consider when optimizing spectral resolution in the gas-phase experiment are Doppler broadening and saturation broadening. Doppler broadening can significantly be reduced in a skimmed molecular beam. Moreover, since the Doppler width scales with the velocity of Pc molecules in the molecular beam the acceleration of Pc in the seeded beam expansion should be kept as small as possible. For both beam collimation by a skimmer and limited acceleration, argon is the favored carrier gas. Saturation broadening can readily be minimized by attenuation of the laser output power, however, under the limiting premise of a reasonable signal to noise ratio. Hence, appropriate experimental conditions for the optimized spectral resolution of the rotational structure in the electronic spectrum of Pc in the molecular beam were obtained using argon as the carrier gas applied at moderate stagnation pressure in the order of 0.1 bar despite significant contributions from vibrational hot bands (cf. lower panel of Fig. 2). Moreover, saturation broadening was eliminated by attenuating the laser output power to the range of μW which still allowed obtaining an acceptable signal level. As shown in Fig. 4 for the entire rotational band (upper panel) and in addition for the center section with the remarkable Q-branch dip (lower panel), for appropriate tuning of the laser frequency significant spectral substructures within the rotational bands could be resolved at the electronic band origin of Pc when using argon as the carrier gas (lower traces). The corresponding spectrum recorded with helium as the carrier gas shows only the band envelop superimposed by statistical noise (upper traces).Spectral resolution of the rotational structure spans from recording the rotational band envelop as the minimum to a fully line resolved rotational structure as the optimum. The first was obtained for the spectrum of Pc recorded with helium as the carrier gas. More details of the rotational structure could be obtained using argon as the carrier gas, however, the resulting structure is still far from line resolution. Instead, each of the peaks in the substructure represents a subband of the Pc rotor consisting of hundreds of rotational lines. The brilliance of the rotational structure is highly sensitive to the molecular beam expansion conditions which affect the population distribution of the corresponding rotational states and in addition the Doppler broadening via the beam velocity.
The spectral shape of the rotational structure of Pc groups into the P-, Q-, and R-branch according to the selection rules for rotational transitions. The Q-branch with ΔJ = 0 occupies the center while the P-branch with ΔJ = −1 and the R-branch with ΔJ = +1 dominate the red and the blue tail, respectively, of the rotational band. The highly brilliant rotational structures resolved for argon at the red and blue sides of the spectrum (cf. lower panel of Fig. 4) are sub-bands of the P- and R-branch, respectively, while the center part which exhibits a different substructure superimposed to a remarkable dip is an expression of the Q-branch. The substructure of the P- and R-branch shows rather regularly spaced peaks with a FWHM of about 42 MHz with a spacing in the P-branch of roughly 94 MHz and in the R-branch of 84 MHz. The difference in the spacing indicates a blue-shaded rotational band structure which gives a first hint at the change of moments of inertia upon electronic excitation. The remarkable dip reflects a split Q-branch whose structure is most pronounced at the red side of the dip. This first glance disproves the speculations on the rotational band spectral shape at the electronic band origin of Pc from ref. 13 stating that it should be dominated by an intense Q-branch feature.
In order to obtain the maximum of information on the structure of Pc in both electronic states the experimentally resolved rotational substructure needs to be simulated quantitatively. Therefore, several molecular and experimental parameters must be selected and optimized to perfectly reproduce the experimental spectrum. These parameters include in the first place for each electronic state of Pc as a slightly asymmetric rotor three rotational constants A, B, and C. The rotational state distribution is another fitted parameter which in an ideal case is determined by a single temperature of a Boltzmann distribution, however, in a more realistic scenario it is given by a non-thermal distribution which can be approximated by a linear combination of several Boltzmann distributions for different temperatures (see for example ref. 43). In combination with the rotational state distribution the range of rotational states considered for the simulation need to be chosen adequately in order to avoid spectral artifacts within the rotational band. Another important parameter is the purely electronic transition frequency which adjusts the rotational structure to absolute values of the frequency axis. Moreover, the orientation of the transition dipole moment within the molecular frame needs to be considered. For a perfect alignment along the a-axis (cf.Fig. 1) only a-type transitions need to be calculated while a tiny tilt of the transition dipole moment within the molecular plane requires a small contribution of b-type transitions. The a- and b-type transitions exhibit different spectral structures and are, thus, effective on the spectral pattern of the simulation. Finally, the line width of single rotational transitions needs to be considered which in the present case is given by a Voigt-profile which requires two line width parameters for the Gaussian and the Lorentzian contribution. Altogether, a number of 12 parameters need to be considered in the case of a thermal rotational state population. In a first approach centrifugal distortion was neglected which was justified by the well-known rigidity of Pc and finally confirmed by the obtained result of the simulated spectra.
Simulations were performed using the public domain program package PGOPHER.44 Since in the present case the experimental spectrum is an intermediate between the band resolved and line resolved rotational structures, some but not the maximum of information on the molecular rotor is on hand (for excellent reviews see for example ref. 45 and 46). This bears problems for the spectral analysis as previously mentioned in the literature.47,48 Consequently, the simulation of spectra could not rely on the fitting algorithms provided with PGOPHER but instead on correlation automated rotational fitting (CARF)49 as will be outlined in the following.
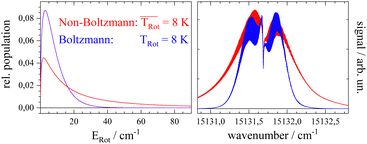
Before starting CARF one needs to choose reasonable starting values for the fitted parameters. These were found by manually optimizing a PGOPHER simulation of the experiment via consecutive variation of the parameters. The initial data set for the first manual fitting cycle took rotational constants for the electronic ground state A′′, B′′, and C′′ and a perfect a-type transition as provided by theoretical investigations reported in ref. 50 and also in ref. 51, respectively. The electronic band origin was initially located at the dip frequency of the Q-branch. The Gaussian FWHM of 0.0007 cm−1 (21 MHz) was estimated from the linewidth of a hyper fine resolved electronic spectrum of iodine in a molecular beam employing argon as the carrier gas recorded in the same machine. Since the velocity slip between Pc and argon is larger than for iodine and argon this value of 21 MHz for the Doppler broadening extracted from the iodine spectrum represents an upper limit for the Doppler broadening of Pc. In order to match the brilliance of the experimental rotational substructure a Voigt profile with an additional Lorentzian contribution exhibiting a FWHM of 0.0015 cm−1 was utilized for the simulation. These and the other parameters were optimized by trial and error. Thereby, one acquires experience of which section of the rotational structure is particularly sensitive to which of the parameters. For example, the simulation of the substructure superimposed to the dip in the Q-branch required a tiny but significant tilt of the transition dipole moment towards the b-axis which is implemented by adding a small contribution of b-type transitions to the main part of a-type transitions. This is visualized in panel (a) of Fig. 8 where the complete simulation (red) is plotted as a result of the sum of an a-type (green) and a b-type (blue) spectrum. While most of the parameters were optimized by fitting only the center part of the electronic band origin shown in the lower panel of Fig. 4, the rotational state distribution was optimized by fitting mainly the P- and R-branch in the red and blue wings shown in the upper panel of the same figure. The resulting non-Boltzmann distribution shown in red in the left panel of Fig. 5 is a weighted sum of several Boltzmann distributions with temperatures from 2 K to 200 K with an average temperature of 8 K. However, it deviates drastically from an 8 K Boltzmann distribution which was added in blue to the same panel. The non-Boltzmann distribution features a surplus of population in states with larger rotational energy, since the cooling efficiency decreases with increasing energy separation between neighbouring levels as mentioned above. In the right panel of Fig. 5 the simulated spectra for both rotational state distributions visualize the impact of the non-Boltzmann distribution (red) on the P- and R-branch in contrast to a thermal state distribution with the same average temperature (blue).
Besides a reasonable set of starting values, CARF as for any other automated fitting algorithms requires a quantitative criterion to evaluate the quality of a fit. A useful measure is the residuum of the simulation with respect to the experimental data. In order to implement a quality criterion (QC) a single number was calculated which was the inverse of the integral of the squared residuum along the frequency. Improvement of the simulation follows an increase of this number. According to the empirically obtained sensitivity with respect to the simulated rotational structure the CARF algorithm was applied to only 7 of the 12 parameters, namely, rotational constants A′′, B′′, and C′′, for S0 as well as A′, B′, and C′, for S1, and the fraction of the admixture of b-type transitions defined by a tilt angle of the dipole transition moment with respect to the a-axis of Pc. All the other parameters were kept as obtained by the manual fitting procedure. Within a reasonable range centered around the manually optimized set of 7 parameters the area for the fitting algorithm was defined. Thereby the range was kept to the following values:
| 0.00295 ≤ A′′, A′, B′′, B′ ≤ 0.00305 cm−1, |
| 0.00148 ≤ C′′, C′ ≤ 0.0015 cm−1, and |
| 0° ≤ θ ≤ 45°. |
Similar to those reported for other fitting procedures such as genetic algorithms1, within this 7-dimensional parameter space a number of 1000 sets of starting parameters were selected randomly but with the precondition of a QC of at least 10.
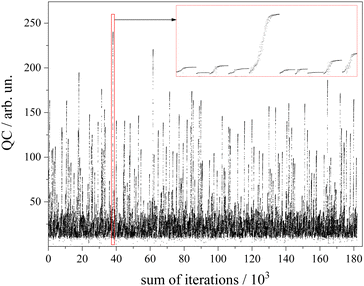
The algorithm for optimization of the simulation was a Downhill–Simplex-routine.52 For each of the abovementioned 1000 sets of starting parameters an optimization routine was executed. Altogether a number of 180.000 simulations were calculated (cf. 90.000–250.000 in GA routines45) which corresponds to an average number of 180 simulations to approach the convergence criterion. The development of the QC with the number of simulations for each of the 1000 cycles is depicted in Fig. 6. The intended offset of QC = 10 can be recognized. The red framed section is depicted in the inset with magnified scaling. It covers a number of 10 optimization cycles whose converged QC differs drastically. Since the QC does not consider spectral weighting according to the non-uniform sensitivity of the rotational structure, all results beyond a QC value of 200 were inspected by the eye in order to choose the one with appropriate fitting of both the Q-branch substructure and the undulations in the P- and R-branches.
The best result of the fit is shown as a red curve in panel (b) of Fig. 7 together with the experimental spectrum added in black. The residuum given in percent of the experimental intensity is plotted in panel (c). The parameters of this simulation are listed in Table 1. The corresponding errors for each of the parameters were deduced from the sensitivity of the QC factor on the variation of the corresponding parameter. The non-Boltzmann rotational state distribution shown in red in the left panel of Fig. 5 was obtained by manual fitting of the far wings of the P- and R-branch (cf. panel (a) of Fig. 7). Deviations of the simulation to the red tail of the P-branch are due to hot bands that spectrally overlap with the electronic band origin. In panels d and e two sections of the simulation are plotted with a magnified frequency axis which is the result of a convolution of the underlying stick spectrum with an appropriate Voigt line profile. Some notes will follow on the fitted parameters with particular focus on those 7 optimized by means of the CARF simulation. Moreover, the interpretation of the set of optimum parameters with respect to the structure of Pc will be outlined.
| Parameter | This work | Literature |
|---|---|---|
| a Molecular beam experiment.8 b Experiment in solution.53 c DFT-calculation.34 | ||
| ν 0/cm−1 | 15131.6891 | 15131.8a |
|
8 | |
| τ/ns | 3.5(5) | 6b |
| |θ|/° | 6.6(15) | |
| A′′/cm−1 | 0.0029903(12) | 0.0029907c |
| B′′/cm−1 | 0.0029758(10) | 0.0029826c |
| C′′/cm−1 | 0.0014930(2) | 0.0014933c |
| ΔI′′/amu Å2 | −11(6) | 0c |
| κ′′ | 0.981(3) | 0.989c |
| A′/cm−1 | 0.0029805(11) | |
| B′/cm−1 | 0.0029783(10) | |
| C′/cm−1 | 0.0014911(2) | |
| ΔI′/amu Å2 | −11(6) | |
| κ′ | 0.997(3) | |
| ΔA/cm−1 | −9.8(23) × 10−6 [−3.3(8) ‰] | |
| ΔB/cm−1 | +2.5(20) × 10−6 [+0.8(7) ‰] | |
| ΔC/cm−1 | −1.9(4) × 10−6 [−1.3(3) ‰] | |
3.3 Fitted parameters and the structure of phthalocyanine
The discussion of the fitted parameters follows as they are listed in Table 1. The electronic band origin was optimized manually and was found to coincide with the frequency position of the dip in the Q-branch. It represents the energy gap between the zero point energies of the electronic ground state and the S1 state of Pc. As mentioned before, which amounts to 8 K is an average value of a non-Boltzmann rotational state distribution. Compared to an 8 K Boltzmann distribution the population is shifted such that higher rotational states are favored. Even with this population shift to higher rotational states (cf.Fig. 5), cooling in this seeded beam expansion is quite efficient, although the stagnation pressure is only 250 mbar.
which amounts to 8 K is an average value of a non-Boltzmann rotational state distribution. Compared to an 8 K Boltzmann distribution the population is shifted such that higher rotational states are favored. Even with this population shift to higher rotational states (cf.Fig. 5), cooling in this seeded beam expansion is quite efficient, although the stagnation pressure is only 250 mbar.
The lifetime τ of the electronically excited state of Pc has been derived from the Lorentzian contribution of the line shape function whose linewidth of 0.0015(2) cm−1 corresponds to τ = 3.5(5) ns as part of a Voigt line shape discussed above. In solution the corresponding lifetime was measured to be about τ ≈ 6 ns.53 While in general the lifetime is expected to be reduced in solution due to energy dissipation into the solvent, the solvent may modify the intersystem crossing rate of Pc in such a way that the excited state lifetime is found to be increased compared to the gas phase.
The transition dipole moment was found to be tilted by roughly 7° from the a-axis within the molecular plane (cf.Fig. 1). It corresponds to a ratio of a-type to b-type transitions of 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. In particular the spectral structure within the center dip which is dominated by the Q-branch requires the addition of b-type transitions as can be recognized from the corresponding contributions plotted in green (a-type) and blue (b-type) in panel (a) of Fig. 8. In contrast, the quite regular undulations that dominate the P- and R-branch are very similar for the a-type and b-type. The admixture of b-type transitions could only be obtained from the rotational substructure that was resolved for the first time at the electronic band origin of Pc. This finding reveals the modification of the character of the electronic states of Pc. Thus, the transition assigned to a Qx band is in fact a mixture of 90% Qx and 10% Qy. Similarly, one can expect a minor admixture of a-type transitions to the Qy band.
1. In particular the spectral structure within the center dip which is dominated by the Q-branch requires the addition of b-type transitions as can be recognized from the corresponding contributions plotted in green (a-type) and blue (b-type) in panel (a) of Fig. 8. In contrast, the quite regular undulations that dominate the P- and R-branch are very similar for the a-type and b-type. The admixture of b-type transitions could only be obtained from the rotational substructure that was resolved for the first time at the electronic band origin of Pc. This finding reveals the modification of the character of the electronic states of Pc. Thus, the transition assigned to a Qx band is in fact a mixture of 90% Qx and 10% Qy. Similarly, one can expect a minor admixture of a-type transitions to the Qy band.
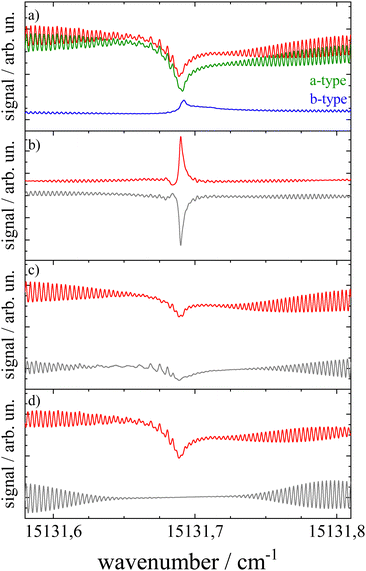 | ||
| Fig. 8 Simulations of the rotational structure resolved for Pc at the electronic band origin. Panel (a): red curve depicts the best fit shown already in Fig. 7 which is a sum of a-type (green) and b-type (blue) transitions. Panels (b–d) visualize the sensitivity of the simulation towards minute changes in rotational constants. The simulation was repeated, however, with ΔA = 0, indicating A′′ = A′ (panel (b)), ΔB = 0 (panel (c)), and ΔC = 0 (panel (d)). All other parameters are as listed in Table 1. The residuum to the best fit is added in grey. For further details see the text. | ||
Upon looking at the rotational constants obtained for both electronic states the very minute changes of all three values are striking. While electronic excitation is accompanied by a decrease in the A and C constant by 0.33% and 0.13%, respectively, the B constant increases by about 0.08%. The significance of such minute changes and the significance of the five digit numbers listed in Table 1 for all six rotational constants have been visualized in panels (b–d) of Fig. 8. Each panel shows the relevant spectral section simulated for the parameters as listed in Table 1, except for keeping A′ = A′′ (panel (b)), B′ = B′′ (panel (c)), and C′ = C′′ (panel (d)). The mismatch is depicted by the corresponding residuum added in grey which is most striking in panel (b). This particular simulation explains the note in ref. 13 on a rotational structure that was expected to be dominated by a sharp and intense Q-branch. This is only the case for the singularity of identical A-constants in both electronic states whereas for minute changes the sharply peaking Q-branch collapses into a spectrally broader double peak which merges into the P- and R-branch. However, the accurate conditions concerning the change of rotational constants as revealed by the rotational substructure do not speak against the rigidity of Pc upon excitation at the electronic band origin. In contrast, the marginal nevertheless significant changes of rotational constants upon excitation at the Qx band quantitatively confirm that the molecular structure of Pc is quite rigid, even with respect to electronic excitation. This is in line with the interpretation of the weak vibronic resonances of Pc outlined above. Further evidence for the rigidity of Pc is received by the rigid rotor model omitting centrifugal distortion in both electronic states.
Furthermore, the inertial defect defined as
| ΔI = IC − IA − IB | (1) |
Another quantity describing the shape of the Pc molecule as an asymmetric rotor is Ray's asymmetry parameter κ.58 This value is calculated for each electronic state from the rotational constants according to
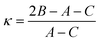 | (2) |
The value of Ray's asymmetry parameter varies from −1 to +1. The two limiting values represent a prolate symmetric top (−1) and an oblate symmetric top (+1) between which all variants of asymmetric top rotors are found. For the rotational constants listed in Table 1 one obtains κ′′ = 0.981(3) for the electronic ground state and κ′ = 0.997(3) for S1. Both values are pretty close to 1. However, the analysis clearly reveals the asymmetric top rotor character for Pc as expressed from Ray's asymmetry parameter whose deviation from a value of 1 is significant.
In summary, the analysis of the rotational structure resolved at the electronic band origin allows for a deep insight into the structural details of Pc in both electronic states for the first time. Besides the deviation from a pure a-type transition and the maintaining of planarity, the tiny changes in the rotational constants during electronic excitation result in an increase in the moment of inertia for the a-axis and a decrease for the b-axis (cf.Fig. 1). As can be read from the values of Ray's asymmetry parameter for S0 and S1, excitation at the electronic band origin shifts the Pc molecule closer towards a symmetric top rotor. Translated into a shift of masses, the changes in the moments of inertia reveal stretching along the b-axis and compression along the a-axis whereby both effects together lead to stretching perpendicular to the c-axis. Since there are 58 atoms involved in the shift of masses one cannot conclude on the corresponding change of intramolecular distances. The rotational constants deduced from the structure of Pc according to recent DFT-calculations54 are in fairly good agreement with the experimental ones obtained in the present study (cf.Table 1). However, the B-rotational constant differs significantly in such a way that the theoretical result does not match the asymmetry of the Pc rotor type quantitatively. This is also expressed by the kappa-parameter listed in Table 1. A possible explanation for this discrepancy might be an underestimation of the influence of the two central hydrogen atoms on the structure of the Pc molecule by the DFT-calculation. The experimental data listed in the left column of Table 1 serve as a benchmark for future quantum chemical calculations on the structure of Pc in S0 and S1 expressed by the moments of inertia as well as on the corresponding transition dipole moment. To our best knowledge, the rotational constants are the smallest ever deduced from fitting an experimentally resolved rotational structure of a molecule.
4 Conclusions
This work stays in the continuation of electronic spectroscopy of Pc. Thereby, with continuously improved spectral resolution, first, the electronic states4,5 and later an accompanying vibrational structure11–14,17,21,23 have been the subject of various experimental enterprises. With an additional improvement of spectral resolution and by means of electronic spectroscopy in a molecular beam we succeeded in resolving the rotational structure of such a large molecule for the first time. The molecular beam source consisted of a home-built heatable Pyrex glass nozzle used a long time ago.11–14 Reliable operation at temperatures as high as 775 K required tricky measures to finally generate a well collimated seeded supersonic jet. As a result, a deep insight into the rotational substructure at the electronic band origin of Pc could be obtained which, however, is still far from the line resolved spectra as generally obtained for much smaller molecular species in a molecular beam.Contrary to discouraging statements regarding the expected gain of information (cf. ref. 24), the analysis of the rotational structure has provided very precise details about Pc in two electronic states. Thus, Pc is a perfectly planar and only a slightly asymmetric top rotor in the electronic ground state and in the S1 state which exceeds the ground state energetically by 15131.69 cm−1. The corresponding transition dipole moment was found to be tilted by 7° in plane with respect to the molecular a-axis so that the electronic band origin is a hybrid consisting of 90% a-type and 10% b-type transitions. This is in contrast to a pure a-type transition, as reported from quantum chemical calculations.20 The tiny nevertheless significant change in the rotational constants upon electronic excitation reveals a tiny change in the molecular geometry which shifts Pc even closer to a symmetric top rotor. Thus, the inertial ellipsoid of Pc in the S1 state is more cylindrical around the c-axis than in the S0 state. These findings confirm the rigidity of Pc upon excitation at the electronic band origin11–14 since the changes in the rotational constants are only minute, nevertheless, with tremendous influence on the rotational structure. Evidence of rigidity of Pc upon excitation at the Qx band does not require the analysis of the rotational substructure, whereas the tiny details accompanying electronic excitation expressed by the parameters listed in Table 1 were only accessible via analysis of the spectrally resolved rotational structure.
With these molecular characteristics of Pc on hand, we plan to elucidate the microsolvation of large molecules in superfluid helium droplets. The experimental analysis of the inertial ellipsoid of Pc in the gas phase allows us to precisely dissect the helium induced contribution from the corresponding spectra recorded for Pc in helium droplets. It might be a promising ansatz to analyze the structure of a solvation complex of Pc in helium droplets. Furthermore, this analysis will be extended towards the high resolution spectra of other phthalocyanine-derivatives as well as van der Waals-clusters of these large molecules with smaller ones like for example water. All these activities will be accompanied by further improvement of the fitting procedure by focusing on spectral sections which are particularly sensitive to the fitted parameters.
Author contributions
This paper is part of the Doctoral Thesis of F. S. conducted under supervision of A. S.Conflicts of interest
None of the authors have any conflict of interest regarding this article.Acknowledgements
We are indebted to the Deutsche Forschungsgemeinschaft (DFG) for financial support through SPP 1807 “Control of London Dispersion Interactions in Molecular Chemistry”. We would also like to thank Matthias Kawalek for support in programming, Bernhard Dick for stimulating suggestions concerning the fit algorithm, and Johannes Fischer for fruitful discussions.References
-
Handbook of Porphyrin Science, ed. K. Kadish, K. Smith and R. Guilard, World Scientific Publishing Co., Singapore, 2010 Search PubMed
.
- The Journal of Porphyrins and Phthalocyanines, ed. K. Kadish, World Scientific Publishing Co., Singapore, 1997–2022 Search PubMed
.
-
The Porphyrins, vol. III, ed. M. Gouterman and D. Dolphin, Academic Press, New York, 1978 Search PubMed
.
- D. Eastwood, L. Edwards, M. Gouterman and J. Steinfeld, J. Mol. Spectrosc., 1966, 20, 381–390 CrossRef CAS
.
- L. Edwards, D. H. Dolphin and M. Gouterman, J. Mol. Spectrosc., 1970, 35, 90–109 CrossRef CAS
.
- L. Edwards and M. Gouterman, J. Mol. Spectrosc., 1970, 33, 292–310 CrossRef CAS
.
- L. Bajema, M. Gouterman and B. Meyer, J. Mol. Spectrosc., 1968, 27, 225–235 CrossRef CAS
.
- V. E. Bondybey and J. H. English, J. Am. Chem. Soc., 1979, 101, 3446–3450 CrossRef CAS
.
-
H. Pauly and G. Scoles, Atomic and molecular beam methods, Oxford University Press, New York, 1988, vol. 1 Search PubMed
.
-
H. Pauly and G. Scoles, Atomic and molecular beam methods, Oxford University Press, New York, 1992, vol. 2 Search PubMed
.
- P. S. Fitch, L. Wharton and D. H. Levy, J. Chem. Phys., 1978, 69, 3424–3426 CrossRef CAS
.
- P. S. Fitch, L. Wharton and D. H. Levy, J. Chem. Phys., 1979, 70, 2018–2019 CrossRef CAS
.
- P. S. Fitch, C. A. Haynam and D. H. Levy, J. Chem. Phys., 1980, 73, 1064–1072 CrossRef CAS
.
- P. S. Fitch, C. A. Haynam and D. H. Levy, J. Chem. Phys., 1981, 74, 6612–6620 CrossRef CAS
.
- U. Even, J. Magen, J. Jortner, J. Friedman and H. Levanon, J. Chem. Phys., 1982, 77, 4374–4383 CrossRef CAS
.
- U. Even and J. Jortner, J. Chem. Phys., 1982, 77, 4391–4399 CrossRef CAS
.
- F. L. Plows and A. C. Jones, J. Mol. Spectrosc., 1999, 194, 163–170 CrossRef CAS PubMed
.
- E. Ortí, R. Crespo, M. C. Piqueras and F. Toms, J. Mater. Chem., 1996, 6, 1751–1761 RSC
.
- P. Day, Z. Wang and R. Pachter, THEOCHEM, 1998, 455, 33–50 CrossRef CAS
.
- K. Toyota, J.-y Hasegawa and H. Nakatsuji, J. Phys. Chem. A, 1997, 101, 446–451 CrossRef CAS
.
- J. Menapace and E. Bernstein, J. Chem. Phys., 1987, 87, 6877–6889 CrossRef CAS
.
- U. Even, J. Jortner and Z. Berkovitch-Yellin, Can. J. Chem., 1985, 63, 2073–2080 CrossRef CAS
.
- S. H. Cho, M. Han Yoon and S. K. Kim, Chem. Phys. Lett., 2000, 326, 65–72 CrossRef CAS
.
- D. H. Levy, Annu. Rev. Phys. Chem., 1980, 31, 197–225 CrossRef CAS
.
- C. Crépin, N. Shafizadeh, W. Chin, J.-P. Galaup, J. G. McCaffrey and S. Arabei, Low Temp. Phys., 2010, 36, 451–457 CrossRef
.
- C. Murray, N. Dozova, J. G. McCaffrey, S. FitzGerald, N. Shafizadeh and C. Crépin, Phys. Chem. Chem. Phys., 2010, 12, 10406–10422 RSC
.
- C. Murray, N. Dozova, J. G. McCaffrey, N. Shafizadeh, W. Chin, M. Broquier and C. Crépin, Phys. Chem. Chem. Phys., 2011, 13, 17543–17554 RSC
.
- S. Arabei, J. G. McCaffrey, J.-P. Galaup, N. Shafizadeh and C. Crépin, Phys. Chem. Chem. Phys., 2015, 17, 14931–14942 RSC
.
- Y. Baeten, E. Fron, C. Ruzié, Y. H. Geerts and M. van der Auweraer, ChemPhysChem, 2015, 16, 3992–3996 CrossRef CAS PubMed
.
- J. P. Toennies and A. F. Vilesov, Angew. Chem., Int. Ed., 2004, 43, 2622–2648 CrossRef CAS PubMed
.
- M. Lewerenz, B. Schilling and J. P. Toennies, J. Chem. Phys., 1995, 102, 8191–8207 CrossRef CAS
.
- M. Lewerenz, B. Schilling and J. Toennies, Chem. Phys. Lett., 1993, 206, 381–387 CrossRef CAS
.
- M. Hartmann, A. Lindinger, J. P. Toennies and A. F. Vilesov, J. Phys. Chem. A, 2001, 105, 6369–6377 CrossRef CAS
.
- A. Lindinger, J. Peter Toennies and A. F. Vilesov, Phys. Chem. Chem. Phys., 2001, 3, 2581–2587 RSC
.
- B. Dick and A. Slenczka, J. Chem. Phys., 2001, 115, 10206–10213 CrossRef CAS
.
- A. Slenczka, B. Dick, M. Hartmann and J. Peter Toennies, J. Chem. Phys., 2001, 115, 10199–10205 CrossRef CAS
.
- N. Pörtner, J. P. Toennies and A. F. Vilesov, J. Chem. Phys., 2002, 117, 6054–6060 CrossRef
.
-
M. Hartmann, Hochauflösende Spektroskopie von Molekülen in 4 Helium- und 3 Helium-Clustern, 1997 Search PubMed
.
- M. Y. Choi, G. E. Douberly, T. M. Falconer, W. K. Lewis, C. M. Lindsay, J. M. Merritt, P. L. Stiles and R. E. Miller, Int. Rev. Phys. Chem., 2006, 25, 15–75 Search PubMed
.
- R. Lehnig, M. Slipchenko, S. Kuma, T. Momose, B. Sartakov and A. Vilesov, J. Chem. Phys., 2004, 121, 9396–9405 CrossRef CAS PubMed
.
- S. Fuchs, J. Fischer, A. Slenczka, M. Karra and B. Friedrich, J. Chem. Phys., 2018, 148, 144301 CrossRef CAS PubMed
.
- R. E. F. E. Riechers, PhD thesis, University of Regensburg, Germany, 2011.
- M. Schmitt, C. Ratzer, K. Kleinermanns and W. L. Meerts, Mol. Phys., 2004, 102, 1605–1614 CrossRef CAS
.
- C. M. Western, J. Quant. Spectrosc. Radiat. Transfer, 2017, 186, 221–242 CrossRef CAS
.
- W. L. Meerts and M. Schmitt, Int. Rev. Phys. Chem., 2006, 25, 353–406 Search PubMed
.
- D. W. Pratt, Annu. Rev. Phys. Chem., 1998, 49, 481–530 CrossRef CAS PubMed
.
- C. A. Haynam, D. V. Brumbaugh and D. H. Levy, J. Chem. Phys., 1984, 81, 2282–2294 CrossRef CAS
.
- L. A. Philips and D. H. Levy, J. Chem. Phys., 1986, 85, 1327–1332 CrossRef CAS
.
- R. Helm, H.-P. Vogel and H. Neusser, Chem. Phys. Lett., 1997, 270, 285–292 CrossRef CAS
.
- P. Day, Z. Wang and R. Pachter, THEOCHEM, 1998, 455, 33–50 CrossRef CAS
.
- V. A. Kuzmitsky, D. I. Volkovich, L. L. Gladkov and K. N. Solovyov, J. Appl. Spectrosc., 2018, 85, 829–839 CrossRef CAS
.
- J. A. Nelder and R. Mead, Comput. J., 1965, 7, 308–313 CrossRef
.
- H. Stadelmann, J. Lumin., 1972, 5, 171–186 CrossRef CAS
.
- Q. Zhou, Z.-F. Liu, T. J. Marks and P. Darancet, APL Mater., 2021, 9, 121112 CrossRef CAS
.
- D. R. Herschbach and V. W. Laurie, J. Chem. Phys., 1964, 40, 3142–3153 CrossRef CAS
.
- T. Oka, J. Mol. Struct., 1995, 352–353, 225–233 CrossRef
.
- J. K. G. Watson, J. Chem. Phys., 1993, 98, 5302–5309 CrossRef CAS
.
- B. S. Ray, Z. Phys., 1932, 78, 74–91 CrossRef CAS
.
| This journal is © the Owner Societies 2022 |