Elucidating the photoprotective properties of natural UV screening agents: ZEKE–PFI spectroscopy of methyl sinapate

Abstract

As a prominent derivative of a natural sunscreen, methyl sinapate is an ideal candidate to provide fundamental insight into strategies on how to come to a rational design of artificial sunscreen filters with improved photoprotective properties. Here, static and time-resolved Zero Kinetic Energy–Pulsed Field Ionization (ZEKE–PFI) photoelectron spectroscopy has been used to study the spectroscopy and decay pathways of its electronically excited states. We find that different conformers are subject to distinct structural changes upon electronic excitation, and trace the structural changes that occur upon excitation back to the character of the LUMO. Ionization efficiency spectra in combination with pump–probe ZEKE–PFI spectra are consistent with the conclusion that the long-lived electronically excited state observed in the decay of the lowest excited singlet state is the lowest excited triplet state. Concurrently with providing information on the electronically excited states, the studies allow for a detailed characterization of the spectroscopic properties of the ground state of the radical ion, which is important in the context of the use of cinnamates in nature as antioxidants. Our studies determine the adiabatic ionization energies of the syn/cis, anti/cis and anti/trans conformers as 60 291.1 ± 0.5, 60 366.9 ± 0.5 and 60 503.9 ± 1.0 cm⁻¹, respectively, and provide accurate vibrational fequencies of low-frequency modes of the molecular ion in its electronic ground state. Finally, the studies emphasize the important role of vibrational and electronic autoionization processes that start to dominate the ionization dynamics in non-rigid molecules of the present size.

---

1. Introduction

UV screening agents used in nature to protect plants and organisms from the harmful effects of UV radiation have attracted over the past decades considerable interest.^1–4 These filters have been optimized by evolution to provide protection against UV radiation while at the same time avoiding photochemical reactions of the filter itself that might give rise to harmful side reactions. They therefore form a source of inspiration for the development of novel artificial UV filters for applications in sunscreen formulations,^5–12 but also in photothermal applications in which the energy of the photon is converted into heat that is subsequently used for tailored purposes.^13–17 The basis for a rational design and potential optimization of the performance of novel filters – in nature, after all, also other requirements need to be met than merely an efficient absorption of the photon and the harmless dissipation of its energy – lies in a detailed understanding of what determines the absorption characteristics and decay pathways of the electronically excited state manifold of these filters. In view of the attention that nowadays is given to protection against solar radiation and the potential of photothermal materials, it is not surprising that over the years increasingly more studies have been reported that focus on these aspects. The development of spectroscopic techniques that enable such studies over a wide range of wavelengths, encompassing time scales ranging from femtoseconds to days and longer, and under a large variety of environmental conditions^18–27 in combination with advanced quantum chemical calculations^28–33 has from this point of view contributed significantly to the body of knowledge that is currently available.

Cinnamates and hydroxycinnamates^{18,19,22,23,27,34–49} are from the above point of view a class of compounds of particular interest. They are ubiquitously employed in plants and bacteria for UV-B protection, while hydroxycinnamates are at the same time also used in nature as potent antioxidants.^50–54 One of the prototypical sets of compounds that has been studied extensively over the past years both under isolated and solvent conditions and with various experimental and theoretical techniques, are sinapate esters^{10,37,41,43,47,48,55,56} with methyl sinapate (MS, Scheme 1), being the most simple representative of these esters, one of its protagonists. Recently, we have applied high-resolution Resonance Enhanced MultiPhoton Ionization (REMPI) spectroscopic techniques to study its spectroscopy and excited-state dynamics, and the influence of interactions with a solvent environment on these properties.⁵⁷ An important observation in these studies was the presence of a till then not observed decay pathway leading to a potentially detrimental long-lived electronically excited triplet state.

Scheme 1 Molecular structure of relevant conformers of methyl sinapate (MS) and employed atom numbering, syn/anti and cis/trans referring to the relative orientation of the O–H and C₇=C₈ bonds, and of the C₇=C₈ and C₉=O bonds, respectively.

Our studies and the pioneering high-resolution studies by Zwier et al.³⁷ on an extensive set of sinapate esters employed vibrational activity in the S₁ ← S₀ excitation spectrum to characterise the spectroscopic and dynamic properties of S₁. In the present study we aim to obtain further insight into these properties by projecting the excited-state wavefunction on the vibronic manifold of the ion using Zero Kinetic Energy–Pulsed Field Ionization (ZEKE–PFI) photoelectron spectroscopy.^58,59 The advantage of this technique is that it does not depend on the radiative properties of electronically excited states. As such, it is therefore not only a powerful alternative means to study S₁, but can also elucidate pathways involving ‘dark’ electronically excited states.

As mentioned previously, sinapate esters also attract considerable interest because of their use as antioxidants. Since these properties depend to a large extent on the ionization energy of a given compound,^50,60,61 an accurate determination of the ionization energy is key to establishing structure–activity relationships. For cinnamic acid and its derivatives such data are as yet, however, quite scarce.^62–64 ZEKE–PFI is from that point of view the method of choice as it allows ionization energies to be measured with an accuracy that is orders of magnitude better than possible with other techniques such as He(I) photoelectron spectroscopy. Apart from ionization energies, ZEKE–PFI studies also provide detailed information on the vibrational manifold of the ground state of the radical cation. As such, they are thus an excellent means to benchmark the results of quantum chemical calculations on ionic states.

In this work we report ZEKE–PFI spectra that have been obtained after excitation to the lowest electronically excited singlet state of various conformers of MS. From these spectra ionization energies and vibrational frequencies in the ground state of the radical cation are determined with sub-wavenumber resolution. Comparison with theoretically predicted vibrationally resolved excitation and ZEKE–PFI spectra provides a detailed view on the changes in molecular structure that occur upon excitation and ionization. Finally, we show that the results of wavelength dependent ionization efficiency studies and time-resolved ZEKE–PFI studies provide further support for the conclusion that intersystem crossing to the triplet manifold is one of the pathways along which internal conversion from the lowest excited singlet state takes place.

2. Methods

2.1 Experimental

Methyl sinapate was synthesized according to previously reported procedures.^57,65 R2PI, UV-depletion (UV-D), and ZEKE–PFI spectroscopy has been performed using a molecular beam setup described in detail before,^34,66 and therefore only details pertaining to the present experiments will be provided. Briefly, in the current study the sample was heated in a glass container to a temperature of 140 °C and seeded into a supersonic expansion of 1.5 bar neon using a General Valve pulsed nozzle with an orifice diameter of 0.5 mm that was kept 5 °C higher in temperature to avoid clogging. After passing through a 2 mm skimmer, the molecular beam entered the ionization chamber where either mass-resolved ion detection took place using a reflectron time-of-flight (R.M. Jordan Co.) or electron detection using a custom-built setup (R.M. Jordan Co.).

For recording two-color R2PI excitation spectra a frequency-doubled Sirah Cobra-Stretch dye laser operating on DCM or Rhodamine 101 and pumped by a Spectra Physics Lab 190 Nd:YAG laser was employed in combination with a Neweks PSX-501 ArF excimer laser (193 nm, 6.42 eV) with typical pulse energies of 10–50 μJ and 1 mJ, respectively. In the UV-D experiments, depletion of the ground state took place using a frequency-doubled Sirah Precision Scan dye laser operating on DCM and pumped by a Spectra Physics Lab 190 Nd:YAG laser with a typical pulse energy of 2 mJ. Both dye lasers have been calibrated using a HighFinesse WS5 wavelength meter. ZEKE–PFI spectroscopy has been performed using these two dye laser systems with typical pulse energies of ∼1 mJ for the pump laser and 2–4 mJ for the probe laser. In these experiments high-n Rydberg states were excited under field-free conditions and subsequently field-ionized by a pulsed electric field of ∼2 V cm⁻¹ that was applied 300 ns after the laser pulse, leading to a clear separation of prompt and PFI electrons in the time-of-flight spectrum of the electrons.

2.2 Theoretical

Geometry optimization of MS in the electronic ground state of the neutral molecule (S₀) and the cation (D₀) has been performed using Density Functional Theory (DFT) while Time Dependent DFT (TD-DFT) was employed to optimize the geometry of the molecule in its first electronically excited singlet state (S₁). At each optimized geometry harmonic force fields were calculated that were subsequently employed to perform Franck–Condon calculations of intensities in the vibronic spectra of the S₁ ← S₀ and D₀ ← S₁ transitions. Such calculations have been performed employing various functionals and basis sets (B3LYP/6-311G(d), PBE0/cc-pVDZ, CAM-B3LYP/cc-pVDZ, M06-2X/cc-pVDZ, M05-2X/6-31+G(d) and wB97XD/cc-pVDZ) in order to determine the sensitivity of predicted excitation and ionization energies as well as Franck–Condon spectra on the employed functional and basis set. Although S₁ excitation energies were found to depend significantly on whether range-separated functionals were used or not, this was much less the case for ionization energies and Franck–Condon spectra. Based on the comparison with experimentally determined energies and spectra, the M05-2X/6-31+g(d) calculations appear to give slightly better results, and we will in the following therefore use the results of those calculations. To facilitate comparison of experimental and predicted Franck–Condon spectra, calculated vibrational frequencies were scaled with a scaling factor of 0.936.⁶⁷ All calculations have been performed with the Gaussian 16, Rev. A.03 suite of programs.⁶⁸

3. Results and discussion

3.1 A ZEKE view on the spectroscopic properties of the S₁ and D₀ states of MS conformers

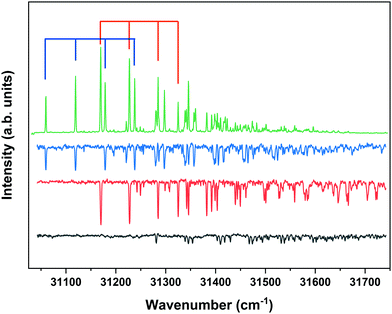
Although the present study primarily focusses on the ZEKE–PFI spectra of conformers of MS, we will repeatedly need to refer to their S₁ ← S₀ excitation spectra. Fig. 1 displays to this purpose the R2PI spectrum of MS as reported previously^37,57 together with UV-D spectra of the syn/cis, anti/cis and anti/trans conformations, the cis conformations being dominantly present while the trans conformation is only present in minor amounts. The latter spectra are strongly saturated but serve to indicate which band in the R2PI spectrum is associated with each particular conformer. For the further discussion it will also be useful to consider the Franck–Condon predictions for these spectra shown in Fig. 2. This Figure shows that for all conformations a dominant progression in the in-plane C₄–C₇=C₈ bending mode b is predicted with the b²₀ and b¹₀ transitions being the most intense ones for the syn and anti conformers, respectively. Interestingly – and important for the later discussion of Franck–Condon intensities in the ZEKE spectra – this is indeed observed in the experimental spectrum for the syn conformer, but not for the anti conformers for which the b⁰₀ transition is found to be the transition with the highest intensity.

Fig. 1 R2PI excitation spectrum of methyl sinapate (green) together with UV-D spectra of the syn/cis (blue), anti/cis (red) and anti/trans (black) conformers of MS obtained at depletion frequencies of 31 059.8, 31 170.1, and 31 353.9 cm⁻¹, respectively. Blue and red scales indicate bⁿ₀ progressions of the C₄–C₇=C₈ bending mode of corresponding conformer (see text).

Fig. 2 Predicted S₁ ← S₀ Franck–Condon spectra for the syn/cis (blue), anti/cis (red) and anti/trans (black) conformers of MS obtained at the M05-2X/6-31+G(d) level with vibrational frequencies scaled by 0.936. 0–0 transitions have been taken at excitation energies as observed experimentally.

In order to explore the ionization pathways of MS after excitation to S₁ two types of experiments have been performed. In the first, ion yields are monitored as a function of the energy of the photon used to ionize the molecule from S₁. In the second, the yield is monitored of zero-kinetic-energy electrons produced after pulsed field ionization of high-n Rydberg states excited from S₁. As a typical example of the first approach, Fig. 3 shows the ionization efficiency spectrum obtained after exciting the S₁ ← S₀ origin transition of the syn/cis conformer at 31 059.8 cm⁻¹. This spectrum shows a well-defined threshold at 60 155 ± 5 cm⁻¹ which is actually much sharper than often observed in ionization threshold measurements, indicating that ionization from S₁ is not accompanied by major geometry changes. The spectrum reported in Fig. 3 has been obtained under conditions in which the high-n Rydberg states experience a DC electric field of 516 V cm⁻¹. Extrapolation to zero electric field using a field-induced shift in cm⁻¹ of 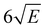with E the electric field in V cm^−1 69 then leads to an adiabatic ionization threshold of 60 291 ± 5 cm⁻¹ (7.475 eV). Compared with methyl-4-hydroxycinnamate for which an ionization threshold of 65 154 cm⁻¹ (8.078 eV) has been determined,¹⁸ this implies that the substitution with the two methoxy groups ortho to the hydroxyl group lowers the ionization potential by more than 0.6 eV. For p-coumaric acid and ferulic acid ionization thresholds have been determined of 65 200 and 63 560 cm⁻¹ (8.084 and 7.892 eV),⁷⁰ respectively. These thresholds suggest that substitution with one methoxy group leads to a lowering of the ionization potential by 1640 cm⁻¹ (0.203 eV). The observation that in MS the ionization potential is lowered by significantly more than 0.4 eV indicates that the two methoxy substituents cannot be considered separately, but reinforce each other's influence on the ionization potential.

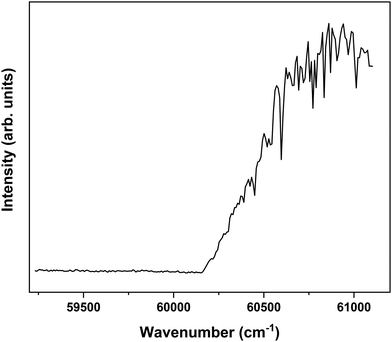Fig. 3 Ionization threshold spectrum obtained for excitation at the S₁ ← S₀ origin transition (31 059.8 cm⁻¹) of the syn/cis conformer of MS.

Interestingly, Fig. 3 shows at higher energies a series of sharp dips in the ion ionization yield. Comparison with dispersed emission spectra reported previously³⁷ leads to the conclusion that these dips are associated with transitions in which stimulated emission to the ground state occurs. The observation of stimulated S₁ → S₀ transitions is in line with the large oscillator strength predicted for transitions involving the V(ππ*) state and thereby provides further support for the conclusion that the initially excited singlet state is the V(ππ*) state.³⁷ At the same time, it opens up the possibility to further explore the higher-energy part of the potential energy surface of this state by recording excitation spectra obtained after populating specific vibrational levels in the ground state via stimulated emission. Such experiments are presently underway.

Fig. 4 displays the corresponding ZEKE spectrum for the syn/cis conformer, i.e., after exciting the S₁ ← S₀ origin transition at 31 059.8 cm⁻¹. This spectrum shows well-resolved bands with a FWHM of about 6 cm⁻¹ whose energies and assignments are reported in Table S1 (see ESI†). The lowest-energy band in this spectrum associated with ionization to the vibrationless level of D₀ is found at 60 285.8 cm⁻¹. In this case extrapolation to zero electric field using a pulsed-field induced shift of 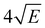⁶⁹ leads to an ionization energy of 60 291.1 ± 0.5 cm⁻¹ (7.4752 ± 0.0001 eV), which is in excellent agreement with the value found in the ion threshold measurements but significantly more accurate. Zero-point corrected calculations of the adiabatic ionization energy predict a value of 7.417 eV which compares impressively well with the experimental value.

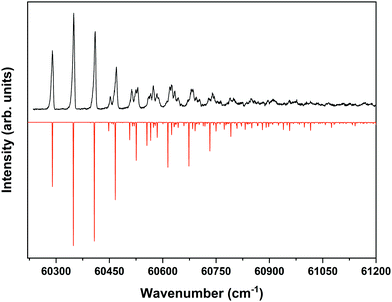Fig. 4 ZEKE–PFI spectrum obtained for excitation at the S₁ ← S₀ origin transition (31 059.8 cm⁻¹) of the syn/cis conformer of MS together with the corresponding Frank–Condon simulation (red).

The same figure displays the simulation of the Franck–Condon spectrum of transitions from the vibrationless level of S₁ to vibrational levels of D₀ based on the equilibrium geometries and harmonic force fields of the two states, which shows in general quite a satisfactory agreement. Similar to the vibrational activity in the S₁ ← S₀ excitation spectrum, the D₀ ← S₁ 0⁰ spectrum is dominated by a progression in the bending mode b whose frequency for all practical purposes does not change upon ionization. It is interesting to notice that the intensity distribution over the fundamental and overtones of this mode is nearly the same in the S₁ ← S₀ (Fig. 1) and the D₀ ← S₁ 0⁰ (Fig. 4) spectra. Inspection of the equilibrium geometries of the S₀, S₁, and D₀ states in combination with Franck–Condon simulations of the D₀ ← S₀ spectrum leads to the conclusion that the primary reason for this similarity is that the equilibrium geometry and harmonic force fields of the S₀ and D₀ states are quite comparable. S₁ and D₀ are essentially described by the HOMO → LUMO excitation and (HOMO)⁻¹ configuration, respectively. It can therefore be concluded that the activity of the bending mode in the S₁ ← S₀ excitation spectrum (and conversely in the D₀ ← S₁ ZEKE spectrum) is largely induced by the LUMO, which does not seem unreasonable as this orbital is characterized by a strong antibonding character between C₇ and C₈.

Table S1 (see ESI†) shows that apart from the bending mode b, also several other low-frequency modes are active in the D₀ ← S₁ 0⁰ ZEKE spectrum, thereby providing detailed insight in the lower vibrational manifold of the ground state of the ion. Importantly, these assignments show that the molecule remains planar upon ionization as no (v_i)¹₀ transitions of nontotally-symmetric modes are observed. Table 1 compares the frequencies of totally-symmetric modes in D₀ with their S₁ counterparts as determined from a more extensive analysis of the S₁ ← S₀ excitation spectrum than reported previously.^37,57 Inspection of these frequencies leads to the conclusion that only minor changes occur, a conclusion that is supported by the calculated harmonic force fields which moreover show that for these low-frequency modes Duschinsky mixing hardly occurs upon ionization. Above ∼500 cm⁻¹ vibrational energy the ZEKE spectrum becomes quite congested. Although some bands can still be identified with reasonable confidence, this congestion in combination with small predicted Franck–Condon activities precludes the identification of higher-frequency totally-symmetric modes other than the ones reported in Table 1.

Table 1 Experimental vibrational frequencies (cm⁻¹) for S₁ and D₀ states of syn/cis and anti/cis MS conformers

Mode^a	syn/cis		anti/cis		Description^c
a Standard labelling vibrational mode: a′(1–56), a′′(57–87) with decreasing frequencies. b Not possible to determine because of overlap with bands of other conformers or coincidence with combination bands predicted to have large intensity. c For atom numbering see Scheme 1 with atom labels as following logically from description with b = bending and s = scissoring.
	S1	D0	S1	D0
56	59.8	59.9	57.5	60.2	b(4,7,8); b(7,8,9)
55	161.4	162.8	154.8	163.3	s(7,8,9)
54			175.9	171.9	s(3,2,O)
53	226.8	235.1	228.1		b(5,6,O); b(4,7,8)
52	272.9	270.3	260.2	267.9	s(6,1,O); s(2,1,O)
51	327.0	321.7		319.7	s(6,1,O); s(2,1,O); s(O,9,O)
50				353.7	s((2,O,C)

---

The ZEKE spectrum recorded after excitation at 31 170.1 cm⁻¹ of the S₁ 0⁰ level of the anti/cis conformer is reported in Fig. 5 together with the Franck–Condon simulation of this spectrum, while the assignments of the bands in the experimental ZEKE spectrum are given in Table S2 (see ESI†). For the anti/cis conformer we find that ionization to the D₀ 0⁰ level occurs at 60 361.6 ± 0.5 cm⁻¹, which – extrapolated to zero electric field – leads to an adiabatic ionization energy of 60 366.9 ± 0.5 cm⁻¹ (7.4846 ± 0.0001 eV). Similar to the 0–0 excitation energies of the two conformers to the S₁ state for which the anti/cis is found to be higher than the syn/cis conformer by 110.3 cm⁻¹, the D₀ adiabatic ionization energy of the anti/cis conformer is also found to be higher than that of the syn/cis conformer, albeit slightly less (75.8 cm⁻¹ (9.4 meV)). This ordering is reproduced by our calculations that predict the D₀ zero-point level of the anti/cis conformer to be higher by 59 cm⁻¹.

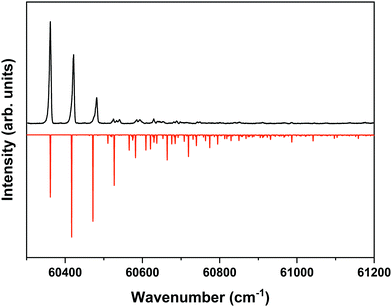Fig. 5 ZEKE–PFI spectrum obtained for excitation at the S₁ ← S₀ origin transition (31 170.1 cm⁻¹) of the anti/cis conformer of MS together with the corresponding Frank–Condon simulation (red).

Inspection of the vibrational activity in the D₀ ← S₁ 0⁰ spectrum leads to the conclusion that in general the same modes are active as found for the syn/cis conformer (see Table S2 in the ESI†) with once again the progression of the bending mode b dominating the spectrum. Similar to the syn/cis conformer several other low-frequency modes can be identified with frequencies that do not change appreciably upon ionization from S₁ (see Table 1). What in view of the good agreement between experiment and theory found for the syn/cis conformer in first instance would not have been expected is that the intensity distribution over the bⁿ₀ progression observed in the experimental spectrum differs considerably from the theoretical prediction. While at all levels of theory that have been explored, the calculations predict this progression to have the largest intensities for the b¹₀ and b²₀ transitions, experiment shows that this occurs for the b⁰₀ transition. Interestingly, the same observation was made for the activity of the bending mode in the S₁ ← S₀ excitation spectrum of the anti/cis conformer (vide supra). For the syn/cis conformer it was concluded that the activity of this mode in this excitation spectrum was essentially due to the occupation of the LUMO. Combining this observation with the conclusion from the calculations that also for the anti/cis conformer the equilibrium geometry and harmonic force fields of the S₀ and D₀ states are very similar, one rapidly comes to the conclusion that the differences between the experimental S₁ ← S₀ and D₀ ← S₁ 0⁰ spectra and their theoretical counterparts must be attributed to an equilibrium geometry of S₁ that is not calculated completely correctly.

Inspection of the equilibrium geometries of the ground and excited singlet states of the two conformers shows that for the syn/cis conformer the C₄–C₇=C₈ angle is reduced from 127.6° to 123.9°, while for the anti/cis conformer a reduction from 127.6° to 124.1° is predicted. To assess to what extent the equilibrium geometry of the anti/cis conformer in S₁ is calculated incorrectly, we have reconstructed the equilibrium geometry of the anti/cis conformer in S₁ using the experimentally observed intensities of the (v_i)¹₀ transitions of totally-symmetric vibrations in the S₁ ← S₀ excitation spectrum using the procedures by Doktorov.⁷¹ We then find an C₄–C₇=C₈ angle of 126.0°, a reduction of the change that was predicted in the original calculations by roughly half. Although the underlying electronic reasons for this difference between the two conformations still need to be explored further, it is clear that the present study provides an excellent example of the strengths of molecular beam spectroscopy as it is able to ‘translate’ subtle structural differences into quite distinct experimental observations.

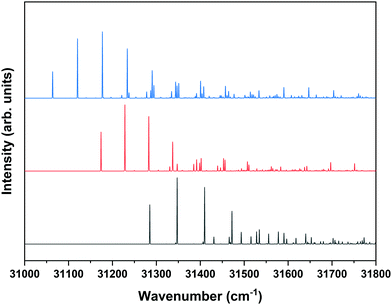
Fig. 1 shows that under the employed experimental conditions also the anti/trans conformer is present, albeit in a considerably lower amount than the other two conformers. Combined with the fact that the S₁ ← S₀ origin transition of this conformer occurs at a higher excitation energy than that of the other two, this leads to a situation in which it is quite difficult to identify bands in the REMPI spectrum that can uniquely be assigned to the anti/trans conformer. In the majority of the cases, potential anti/trans bands contain contributions of transitions belonging to the syn/cis and anti/cis conformers as well. Fig. 6 therefore reports ZEKE spectra recorded for excitation at 31 353.9 cm⁻¹ and 31 281.3 cm⁻¹. The first transition involves a band in the REMPI spectrum that is not (or only in the very shoulder of another band) observed in the depletion spectra of the syn/cis and anti/cis conformers while the second one is the first band that appears when recording a depletion spectrum using 31 353.9 cm⁻¹ to monitor the ion signal. Even then an unambiguous analysis of these ZEKE spectra remains difficult since inspection of these spectra leads to the conclusion that quite a number of bands are at energies that coincide with those of D₀ vibrational levels determined for the syn/cis and anti/cis conformers. It nevertheless appears that the band at 60 498.5 cm⁻¹ cannot be assigned to either of these two, and we therefore tentatively assign this band to the transition to the vibrationless level of the D₀ state of the anti/trans conformer. Extrapolated to zero electric field, this leads to an adiabatic ionization energy of 60 503.9 ± 1.0 cm⁻¹ (7.5016 ± 0.0001 eV). Zero-point corrected calculations find for this conformer an adiabatic ionization energy of 7.447 eV which compares well with the experimental value and nicely follows the experimental ordering IP(syn/cis) < IP(anti/cis) < IP(anti/trans). Once again we find that the difference in 0–0 excitation energy to S₁ with respect to the syn/cis and anti/cis conformers (228.5 and 118.2 cm⁻¹, respectively) is close to the difference in adiabatic ionization energies (208.9 and 138.2 cm⁻¹).

Fig. 6 ZEKE–PFI spectrum obtained for excitation at the tentatively assigned S₁ ← S₀ origin transition (31 281.3 cm⁻¹) of MS (bottom) and at 31 353.9 cm⁻¹ (top) where an unassigned S₁ vibrational level of the anti/trans conformer is excited.

An aspect that merits further consideration is the fact that Fig. 4–6 show limited vibrational activity for vibrational excess energies of about 500 cm⁻¹. This is at odds with our theoretical calculations that predict for all conformers appreciable intensity in the C=C stretch region. We surmise from this observation that at these energies the high-n Rydberg states converging upon D₀ vibrational levels that are excited in our experiments are subject to efficient vibrational autoionization. Such processes would deplete the reservoir of neutral states that otherwise would be ionized by the pulsed electric field and give rise to ‘zero kinetic energy’ electrons. Theoretically it should be possible to reduce these autoionization processes by exciting Rydberg states with even higher principal quantum numbers n and/or using different pulsed field schemes,⁷² but our experimental conditions precluded the observation of ZEKE signals using such conditions.

3.2 A ZEKE view on the S₁ excited-state dynamics of MS

In our previous studies⁵⁷ we have concluded (i) that the V(ππ*) state is vertically as well as adiabatically the lowest electronically excited singlet state, and (ii) that intersystem crossing to the triplet manifold is one of its decay pathways albeit that the efficiency of this pathway is significantly less than in coumarates because of the absence of an efficient ¹ππ* → ¹nπ* → ³ππ* route. In the present studies we have explored to what extent ZEKE spectroscopy could provide further insight on this intersystem crossing pathway and the triplet state from which the molecule subsequently decays back to the ground state.

Our calculations find that MS adopts a perpendicular geometry of the vinyl double bond in its lowest excited triplet state⁵⁷ – similar to the other cinnamates and hydroxycinnamates that have been studied so far^{23,43,46,49,70,73} – and predicts that this state has an adiabatic excitation energy of 2.47 eV at the M05-2X/6-31+G(d) level. This would imply an adiabatic ionization energy of T₁ of about 4.95 eV. Ideally, one would therefore expect to see an increase in the ZEKE signal in this energy region after exciting S₁. Extensive scans in the 230–260 nm region did, however, not show such an increase. On hindsight this is not so surprising because at these energies electronic and vibrational autoionization processes will undoubtedly dominate the ionization dynamics.

In order to find further support for the conclusion that the long-lived state observed in our ns pump–probe experiments⁵⁷ is associated with T₁, ionization efficiency scans have been performed in which the molecular ion yield is monitored after exciting S₁ and ionizing with photons in the 230–260 nm region. Fig. 7 displays such a scan after exciting the S₁ ← S₀ 0–0 transition of the syn/cis conformer. Starting from about 43 200 cm⁻¹ (5.36 eV) this spectrum shows a clear increase in ionization efficiency, which would imply that ionization takes place from a state with an excitation energy of ∼2.12 eV. This is somewhat lower than predicted by our calculations but in line with what would be expected on the basis of previously determined excitation energies of the lowest excited triplet state of p-coumaric acid (2.40 eV),⁷⁰ methyl-4-hydroxycinnamate, (2.36 eV)⁷³ and ferulic acid (2.20 eV).⁴⁸ We thus conclude that the lowest excited triplet state is indeed one of the pathways along which photon energy is dissipated after photon absorption by MS.

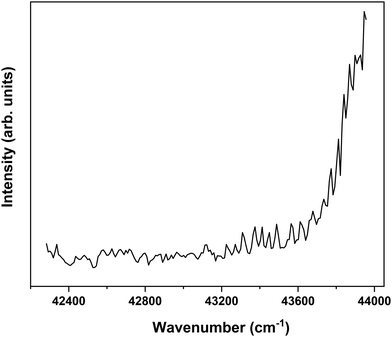Fig. 7 Ionization efficiency spectrum obtained after excitation at the S₁ ← S₀ origin transition (31 059.8 cm⁻¹) of the syn/cis conformer of MS and ionizing with photons in the 230–260 nm region.

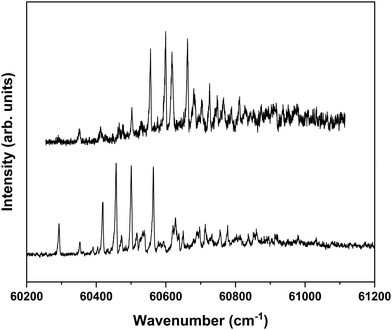
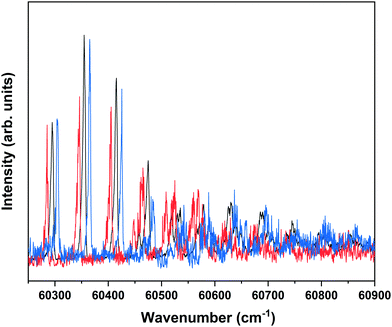
Nanosecond pump–probe REMPI experiments indicate that intersystem crossing from S₁ to the triplet manifold occurs with a time constant of 2–3 ns.⁵⁷ This suggests that time-resolved ZEKE experiments in which the time delay between excitation of S₁ and excitation of high-n Rydberg states is carefully tuned might provide further indications of this decay process. Fig. 8 shows to this purpose three ZEKE spectra in the 60 200–60 900 cm⁻¹ range obtained after excitation of the 0–0 transition to the S₁ state of the syn/cis conformer (ZEKE spectra over an extended range are provided in the ESI†). The red trace has been recorded for a pump–probe delay of −10 ns. Importantly, under such conditions the two lasers still overlap partly in time, the probe laser thus probing S₁ on a time scale as short as possible. The black and blue traces, on the other hand, have been recorded for conditions under which both lasers coincide or are delayed by +10 ns, respectively. Although the −10 and +10 ns traces have a lower signal-to-noise ratio than the 0 ns trace, there are suggestive differences between, in particular, the red trace, and the black and blue traces. While the latter two show a reasonably similar intensity distribution over the vibrational bands, the red trace clearly has higher intensities for bands in the lower-energy region than the other two. This is what indeed would be expected for a situation in which S₁ decays under energy-conserving conditions to the vibrational manifold of a lower-lying electronically excited state as this will shift the centre of gravity of vibrational progressions to higher vibrational levels. Although these time-resolved ZEKE experiments thus provide further means to obtain insight in the excited-state dynamics of S₁, they do not allow yet for detailed quantitative analyses. Similar studies performed with ps lasers are in that respect highly attractive as in such experiments one should be able to follow in much more detail the initial part of the decay. We hope that the present results will stimulate further research along these lines.

Fig. 8 Time-dependent ZEKE spectra obtained for excitation at the S₁ ← S₀ origin transition (31 059.8 cm⁻¹) of the syn/cis conformer of MS for a delay between excitation and ionization laser of −10 ns (red), 0 ns (black), and +10 ns (blue). For clarity traces have been displaced horizontally with respect to each other.

4. Conclusions

In the present experiments the spectroscopic and dynamic properties of the strongly-absorbing electronically excited singlet state of methyl sinapate – a prototypical example for a class of molecules responsible in nature for the photoprotection of plants – have been studied using high-resolution multiphoton ionization and photoelectron spectroscopic techniques. Together with quantum chemical predictions of Franck–Condon activity in S₁ ← S₀ and D₀ ← S₁ spectra our ZEKE–PFI studies have shown that the structural changes that occur upon excitation to S₁ should predominantly be attributed to the occupation and character of the LUMO, and not to the removal of an electron from the HOMO. It has been found that the – at first sight minor – differences in structure between syn and anti conformers result in remarkably distinct activities of the C₄–C₇=C₈ bending mode b that can be traced back to a change in the C₄–C₇=C₈ angle which is twice as large for the syn as for the anti conformer. In combination with a more complete assignment of bands in the S₁ ← S₀ excitation spectra of the syn/cis and anti/cis conformers than reported up till now, these spectra have provided detailed information on the vibrational manifold of the S₁ state, which is key to benchmark advanced quantum chemical calculations on these chromophores.

In our experiments it has been observed that ZEKE–PFI spectra in regions of the ionization manifold where activity would have been expected – either because of changes in structure upon ionization, or because of relaxation processes to high-lying vibrational levels of lower-lying electronically excited states – did not show such signals. We contend that this absence of ZEKE–PFI signals is due to fast vibrational and electronic autoionization processes in medium- to large-sized compounds. Since these energy regions often can provide valuable information on aspects ranging from the assignment of vibrational levels in the electronically excited state and relaxation processes in this state to mode frequencies in the ionic state, it would be worthwhile to perform experiments on such compounds in spectrometers that have been optimized in terms of stray fields and electric field pulse sequences to suppress autoionization processes as much as possible.

Further insight and support for proposed radiationless decay processes from S₁ involving the triplet manifold has been obtained in experiments in which the ionization efficiency from S₁ was monitored as a function of the ionization wavelength, and by time-resolved ZEKE–PFI experiments. The former experiments showed a step-like increase at wavelengths that are consistent with ionization from the first excited triplet state. The latter experiments showed that the intensity distribution over vibrational bands in the ZEKE–PFI spectrum shifts to higher vibrational energies, in line with what would be expected for a decay pathway to a lower-lying electronically excited state.

Concurrently with providing information on electronically excited states of the neutral molecule, the present studies have also allowed us to characterize in detail the spectroscopic properties of the ground state of the radical cation, a state that is key to understanding the role these compounds play as antioxidants but that so far has been difficult to study. Here, we have determined with sub-wavenumber resolution the adiabatic ionization energy of methyl-sinapate conformers and vibrational frequencies in D₀. As a side line, it is interesting to notice that the present data also give access to internal reorganization energies upon ionization, parameters that are important to know for charge-transfer processes. It is well known that methoxy substitution increases the antioxidative efficiency of phenolic acids.⁵⁰ The present study has now provided a quantitative measure of this increase in terms of ionization potential and its dependence on conformational structure. Such information is essential for assessing the influence of other factors that determine the antioxidant capability of these compounds.

Author contributions

J. F. and W. J. B. conceived the spectroscopy experiments and quantum chemical calculations. J. F. and L. F. acquired the REMPI and ZEKE–PFI data, and performed the quantum chemical calculations. J. F., L. F. and W. J. B. analysed the data. J. F. and W. J. B. wrote the manuscript with input of L. F.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Drs H. Sanders for the synthesis of methyl sinapate, and thanking Michiel Hilbers and Dr Wim Roeterdink for technical support. Jiayun Fan acknowledges a doctoral fellowship from the China Scholarship Council (No. 201808440365). This project has received funding from the European Union's Horizon 2020 research and innovation programme under the grant agreement No. 828753.

Notes and references

1. R. Jansen, U. Osterwalder, S. Q. Wang, M. Burnett and H. W. Lim, J. Am. Acad. Dermatol., 2013, 69, 867.e1-2.
2. C. L. Mitchelmore, E. E. Burns, A. Conway, A. Heyes and I. A. Davies, Environ. Toxicol. Chem., 2021, 40, 967–988.
3. D. Piccinino, E. Capecchi, E. Tomaino, S. Gabellone, V. Gigli, D. Avitabile and R. Saladino, Antioxidants, 2021, 10, 274.
4. N. Serpone, Photochem. Photobiol. Sci., 2021, 20, 189–244.
5. V. G. Stavros, Nat. Chem., 2014, 6, 955–956.
6. N. Saewan and A. Jimtaisong, J. Cosmet., Dermatol. Sci. Appl., 2015, 14, 47–63.
7. M. T. Ignasiak, C. Houée-Levin, G. Kciuk, B. Marciniak and T. Pedzinski, ChemPhysChem, 2015, 16, 628–633.
8. K. Glusac, Nat. Chem., 2016, 8, 734–735.
9. R. Losantos, I. Funes-Ardoiz, J. Aguilera, E. Herrera-Ceballos, C. García-Iriepa, P. J. Campos and D. Sampedro, Angew. Chem., Int. Ed., 2017, 56, 2632–2635.
10. M. D. Horbury, E. L. Holt, L. M. M. Mouterde, P. Balaguer, J. Cebrián, L. Blasco, F. Allais and V. G. Stavros, Nat. Commun., 2019, 10, 4748.
11. Y. C. Boo, Antioxidants, 2020, 9, 637.
12. J. Krutmann, T. Passeron, Y. Gilaberte, C. Granger, G. Leone, M. Narda, S. Schalka, C. Trullas, P. Masson and H. W. Lim, J. Eur. Acad. Dermatol. Venereol., 2020, 34, 447–454.
13. X. Huang, I. El-Sayed, W. Qian and M. El-Sayed, J. Am. Chem. Soc., 2006, 128, 2115–2120.
14. R. Li, L. Zhang and P. Wang, Nanoscale, 2015, 7, 17167–17194.
15. D. Zhi, T. Yang, J. O'Hagan, S. Zhang and R. F. Donnelly, J. Controlled Release, 2020, 325, 52–71.
16. X. Zhao, C. Huang, D. Xiao, P. Wang, X. Luo, W. Liu, S. Liu, J. Li, S. Li and Z. Chen, ACS Appl. Mater. Interfaces, 2021, 13, 7600–7607.
17. T. T. Abiola, B. Rioux, J. M. Toldo, J. Alarcan, J. M. Woolley, M. A. P. Turner, D. J. L. Coxon, M. Telles do Casal, C. Peyrot, M. M. Mention, W. J. Buma, M. N. R. Ashfold, A. Braeuning, M. Barbatti, V. G. Stavros and F. Allais, Chem. Sci., 2021, 12, 15239–15252.
18. E. M. M. Tan, S. Amirjalayer, S. Smolarek, A. Vdovin, A. M. Rijs and W. J. Buma, J. Phys. Chem. B, 2013, 117, 4798–4805.
19. E. M. M. Tan, S. Amirjalayer, B. H. Bakker and W. J. Buma, Faraday Discuss., 2013, 163, 321–340.
20. M. Yamaji and M. Kida, J. Phys. Chem. A, 2013, 117, 1946–1951.
21. M. Staniforth and V. G. Stavros, Proc. R. Soc. A, 2013, 469, 20130458.
22. Y. Peperstraete, M. Staniforth, L. A. Baker, N. D. N. Rodrigues, N. Cole-Filipiak, W. Quan and V. G. Stavros, Phys. Chem. Chem. Phys., 2016, 18, 28140–28149.
23. K. Yamazaki, Y. Miyazaki, Y. Harabuchi, T. Taketsugu, S. Maeda, Y. Inokuchi, S. Kinoshita, M. Sumida, Y. Onitsuka, H. Kohguchi, M. Ehara and T. Ebata, J. Phys. Chem. Lett., 2016, 7, 4001–4007.
24. E. L. Holt and V. G. Stavros, Int. Rev. Phys. Chem., 2019, 38, 243–285.
25. V. Balevičius Jr, T. Wei, D. Di Tommaso, D. Abramavicius, J. Hauer, T. Polívka and C. D. P. Duffy, Chem. Sci., 2019, 10, 4792–4804.
26. M. Kao, R. K. Venkatraman, M. Sneha, M. Wilton and A. Orr-Ewing, J. Phys. Chem. A, 2021, 125, 636–645.
27. S. Kinoshita, Y. Harabuchi, Y. Inokuchi, S. Maeda, M. Ehara, K. Yamazaki and T. Ebata, Phys. Chem. Chem. Phys., 2021, 23, 834–845.
28. T. N. V. Karsili, B. Marchetti, M. N. R. Ashfold and W. Domcke, J. Phys. Chem. A, 2014, 118, 11999–12010.
29. L. P. da Silva, P. J. O. Ferreira, M. S. Miranda and J. C. G. Esteves da Silva, Photochem. Photobiol. Sci., 2015, 14, 465–472.
30. J. M. Toldo, M. T. do Casal and M. Barbatti, J. Phys. Chem. A, 2021, 125, 5499–5508.
31. B. Xie, X. Tang, X. Liu, X. Chang and G. Cui, Phys. Chem. Chem. Phys., 2021, 23, 27124–27149.
32. T. T. Abiola, N. d. N. Rodrigues, C. Ho, D. J. L. Coxon, M. D. Horbury, J. M. Toldo, M. T. do Casal, B. Rioux, C. Peyrot, M. M. Mention, P. Balaguer, M. Barbatti, F. Allais and V. G. Stavros, J. Phys. Chem. Lett., 2021, 12, 337–344.
33. X. Chang, T. Zhang, Y. Fang and G. Cui, J. Phys. Chem. A, 2021, 125, 1880–1891.
34. S. Smolarek, A. Vdovin, E. M. M. Tan, M. de Groot and W. J. Buma, Phys. Chem. Chem. Phys., 2011, 13, 4393–4399.
35. E. M. M. Tan, M. Hilbers and W. J. Buma, J. Phys. Chem. Lett., 2014, 5, 2464–2468.
36. Y. Miyazaki, K. Yamamoto, J. Aoki, T. Ikeda, Y. Inokuchi, M. Ehara and T. Ebata, J. Chem. Phys., 2014, 141, 244313.
37. J. C. Dean, R. Kusaka, P. S. Walsh, F. Allais and T. S. Zwier, J. Am. Chem. Soc., 2014, 136, 14780–14795.
38. X. Chang, C. Li, B. Xie and G. Cui, J. Phys. Chem. A, 2015, 119, 11488–11497.
39. X. Xie, C. Li, Q. Fang and G. Cui, J. Phys. Chem. A, 2016, 120, 6014–6022.
40. N. D. N. Rodrigues, M. Staniforth, J. D. Young, Y. Peperstraete, N. Cole-Filipiak, J. R. Gord, P. S. Walsh, D. M. Hewett, T. S. Zwier and V. G. Stavros, Faraday Discuss., 2016, 194, 709–729.
41. L. A. Baker, M. D. Horbury, S. E. Greenough, F. Allais, P. S. Walsh, S. Habershon and V. G. Stavros, J. Phys. Chem. Lett., 2016, 7, 56–61.
42. M. D. Horbury, L. A. Baker, N. D. N. Rodrigues, W. Quan and V. G. Stavros, Chem. Phys. Lett., 2017, 673, 62–67.
43. S. Kenjo, Y. Iida, N. Chaki, S. Kinoshita, Y. Inokuchi, K. Yamazaki and T. Ebata, Chem. Phys., 2018, 515, 381–386.
44. J. Moon, H. Baek, J. S. Lim and J. Kim, Bull. Korean Chem. Soc., 2018, 39, 427–434.
45. B. Herzog, L. Amorós-Galicia, M. Sohn, M. Hofer, K. Quass and J. Giesinger, Photochem. Photobiol. Sci., 2019, 18, 1773–1781.
46. S. Kinoshita, Y. Inokuchi, Y. Onitsuka, H. Kohguchi, N. Akai, T. Shiraogawa, M. Ehara, K. Yamazaki, Y. Harabuchi, S. Maeda and T. Ebata, Phys. Chem. Chem. Phys., 2019, 21, 19755–19763.
47. X. Zhao, J. Luo, S. Yang and K. Han, J. Phys. Chem. Lett., 2019, 10, 4197–4202.
48. X. Zhao, J. Luo, Y. Liu, P. Pandey, S. Yang, D. Wei and K. Han, J. Phys. Chem. Lett., 2019, 10, 5244–5249.
49. S. Muramatsu, S. Nakayama, S. Kinoshita, Y. Onitsuka, H. Kohguchi, Y. Inokuchi, C. Zhu and T. Ebata, J. Phys. Chem. A, 2020, 124, 1272–1278.
50. C. A. Rice-Evans, N. J. Miller and G. Paganga, Free Radical Biol. Med., 1996, 20, 933–956.
51. L. Setti, C. Faulds and S. Giuliani, Sci. Technol., 2001, 83, 1–5.
52. B. Baderschneider and P. Winterhalter, J. Agric. Food Chem., 2001, 49, 2788–2798.
53. N. Nićiforović and H. Abramovič, Compr. Rev. Food Sci. Food Saf., 2014, 13, 34–51.
54. C. Peyrot, M. M. Mention, F. Brunissen and F. Allais, Antioxidants, 2020, 9, 782.
55. L. A. Baker, M. Staniforth, A. L. Flourat, F. Allais and V. G. Stavros, ChemPhotoChem, 2018, 2, 743–748.
56. Y. Liu, X. Zhao, J. Luo and S. Yang, J. Lumin., 2019, 206, 469–473.
57. J. Fan, W. Roeterdink and W. J. Buma, Mol. Phys., 2021, 119, e1825850.
58. K. Muller-Dethlefs and E. W. Schlag, Annu. Rev. Phys. Chem., 1991, 42, 109–136.
59. M. C. R. Cockett, Chem. Soc. Rev., 2005, 34, 935–948.
60. B. Yang, A. Kotani, K. Arai and F. Kusu, Anal. Sci., 2001, 17, 599–604.
61. A. Galano, G. Mazzone, R. Alvarez-Diduk, T. Marino, J. Alvarez-Idaboy and N. Russo, Annu. Rev. Food Sci. Technol., 2016, 7, 335–352.
62. I. Novak, L. Klasinc and S. P. McGlynn, Spectrochim. Acta, Part A, 2018, 189, 129–132.
63. L. Pasa Tolić, B. Kovač, L. Klasinc and S. M. Shevchenko, Croat. Chem. Acta, 1990, 63, 37–54.
64. D. Ajò, M. Casarin, G. Granozzi and G. Rizzardi, J. Mol. Struct., 1983, 101, 167–171.
65. F. Allais, S. Martinet and P. Ducrot, Synthesis, 2009, 3571–3578.
66. S. Smolarek, A. Vdovin, A. Rijs, C. A. van Walree, M. Z. Zgierski and W. J. Buma, J. Phys. Chem. A, 2011, 115, 9399–9410.
67. I. M. Alecu, J. Zheng, Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2010, 6, 2872–2887.
68. M. J. Frisch, G. W. Trucks, H. BSchlegel, et al., Revision A.03, Gaussian, Inc.,Wallingford, CT, 2016.
69. F. Merkt, Annu. Rev. Phys. Chem., 1997, 48, 675–709.
70. Y. Iida, S. Kinoshita, S. Kenjo, S. Muramatsu, Y. Inokuchi, C. Zhu and T. Ebata, J. Phys. Chem. A, 2020, 124, 5580–5589.
71. E. V. Doktorov, I. A. Malkin and V. I. Man'ko, J. Mol. Spectrosc., 1977, 64, 302–326.
72. U. Hollenstein, R. Seiler, H. Schmutz, M. Andrist and F. Merkt, J. Chem. Phys., 2001, 115, 5461–5469.
73. S. Kinoshita, Y. Miyazaki, M. Sumida, Y. Onitsuka, H. Kohguchi, Y. Inokuchi, N. Akai, T. Shiraogawa, M. Ehara, K. Yamazaki, Y. Harabuchi, S. Maeda, T. Taketsugu and T. Ebata, Phys. Chem. Chem. Phys., 2018, 20, 17583–17598.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp05958k

---