Batch analysis of microplastics in water using multi-angle static light scattering and chemometric methods

Abstract

Size and concentration are two important parameters for the analysis of microplastics (MPs) in water. The analytical tools reported so far extract this information in a single-particle analysis mode, dramatically increasing the analysis time. Here, we present a combination of multi-angle static light scattering technique, called “Goniophotometry”, with chemometric multivariate data processing for the batch analysis of size and concentration of MPs in water. Nine different sizes of polystyrene (PS) MPs with diameters between 500 nm and 20 μm are investigated in two different scenarios with uniform (monodisperse) and non-uniform (polydisperse) size distribution of MPs, respectively. It is shown that Principal Component Analysis (PCA) can reveal the existing relationship between the scattering data of mono- and polydisperse samples according to the size distribution of MPs in mixtures. Therefore, a Linear Discriminant Analysis (LDA) model is constructed based on the PCA of scattering data of PS monodisperse samples and is subsequently employed to classify the size of MPs not only in unknown mono- and polydisperse PS samples, but also for other types of MPs such as Polyethylene (PE) and Polymethylmethacrylate (PMMA). When the size of MPs is classified, their concentration is measured using a simple linear fit. Finally, a Linear Least Square (LLS) model is used to evaluate the reproducibility of the measurements.

---

Introduction

Microplastics (MP) have long been ingrained in our lives with multiple works reporting on the traces of microplastic particles in water,¹ in soil,² in the atmosphere,³ in living organisms,⁴ in food,⁵ and so on. A recent study showed that microplastic particles can exist in human placentas⁶ whilst another showed that infants up to 12 months-old can be exposed to the consumption of millions of microplastic particles per day when fed by milk in plastic bottles.⁷ The term “microplastic” was coined in 2004 by Richard Thompson et al.⁸ and refers, as the name suggests, to plastic particles sized on the micron scale. Although there is no unique consensus to the exact definition of this size range, the research community mostly specifies this range between 1 μm and 5 mm.⁹ Regardless of the appellation used to define the size range of the plastic particles, there is a crucial need for a reliable detection method to enrich our knowledge about this contamination source in the environment.

Different methods have been proposed for the detection of microplastics such as visual inspection/microscopy,¹⁰ Fourier-transform infrared spectroscopy (FTIR),¹¹ Raman spectroscopy,¹² scanning electron microscopy plus energy-dispersive X-ray spectroscopy (SEM/EDS),¹³ Pyrolysis-Gas Chromatography-Mass Spectrometry (Py-GC-MS),¹⁴ Thermal Extraction Desorption-Gas Chromatography-Mass Spectrometry (TED-GC-MS),¹⁵ and light scattering.¹⁶ Nevertheless, none of these methods can fully characterize in a non-destructive way MPs in terms of their size, number, mass, morphology, and type, which are some of the necessary information for developing a standardized protocol for the analysis of microplastics, currently lacking in the field.¹⁷ For example, Raman and FTIR are the most used spectroscopic techniques for identifying the types of the MPs, while it can be time consuming to characterize the size and number of the MPs by these methods. Besides, they do not provide any information about mass and morphology.¹⁸ In contrast, the thermo-analytical techniques such as Py-GC-MS and TED-GC-MS, are suitable for studying the type and mass of the MPs. Nonetheless, they are destructive and do not provide any information about the number and morphology of the MPs.¹⁹ To overcome this challenge, the combination of different analytical techniques was proposed as a practical solution for obtaining extensive information on microplastics in different matrices.²⁰ Therefore, there is a need to determine the most optimal technique for measuring a target parameter and as such to further explore the boundaries/limitations of existing techniques. In this regard, the applicability of light scattering as a promising approach for characterizing the size and concentration of microplastics in water is demonstrated in this paper.

Light scattering is a well-established technique having broad applications in different fields, especially in particle analysis.^21–23 Light scattering techniques are often divided into two broad categories being dynamic or static. In the former, the scattered light intensity is a function of time, while in the latter, the scattered light intensity is a function of angle.²⁴ It was recently demonstrated that light scattering can be used for detecting transparent and translucent MPs in freshwater and for studying their surface characteristics.^25,26 However, the authors mainly targeted large plastic particles in the order of millimeters which are easy to detect. In fact, the challenges arise when the scales shift towards the interface between the submicron and micron regime, where the analytical methods applicable to nanoscales reach their upper limits, and the applicable methods to microscales reach their lower limits of application.²⁷ Not surprisingly, the probability of detecting more plastic particles in these regimes is higher as demonstrated by Schymanski et al.²⁸ Hence, it is of high importance to develop either independent or combined analytical tools that are capable of analyzing MPs in the small regimes with particle sizes of less than 10 μm.^27,28 In the work performed by Caputo et al.,²⁷ the authors investigated the performance of nine different analytical methods to characterize the size and mass of Polystyrene (PS) particles. They concluded that the light scattering methods do not have the capability of resolving multiple populations of particles in polydisperse samples. While, Clementi et al.²⁹ estimated the particle size distribution of dilute latexes in a polydisperse sample through multiangle dynamic light scattering and an optimization strategy based on a Genetic Algorithm (GA). However, only two diameters of PS particles smaller than 1 μm were analyzed in the mentioned work. Huang et al.³⁰ proposed an integrated microfluidic chip composed of a preconcentration stage and an on-chip multi-angle laser scattering module for the detection of waterborne parasites. The authors applied Principal Component Analysis (PCA) to extract the Zernike moment features of scattering patterns and Linear Discriminant Analysis (LDA) algorithm for the classification of the patterns. They also demonstrated the applicability of their proposed technique for discriminating the diameter of PS particles between 2 and 10 μm. Nevertheless, the detection of particles was done one by one in a sheath-flow-based microfluidic chip that requires a long analysis time.

The present paper demonstrates the applicability of a multi-angle static light scattering analyzer, called goniophotometer, for the batch analysis of size and concentration of MPs in both mono- and polydisperse samples. A relatively broad range of diameters of PS MPs was chosen for the characterization of the proposed technique. PCA and LDA were used to discriminate between the size of the MPs in different monodisperse PS samples. An LDA algorithm was then trained using the PCA of PS monodisperse samples to classify the size of PS, PE and PMMA MPs in polydisperse mixtures. To verify the reproducibility of the proposed approach, two independent batches of measurements were conducted at two different times. The findings reported here shed light on a promising approach for the batch analysis of microplastics in water and revealed the significance of chemometric methods such as PCA and LDA.

Materials and methods

Microplastic samples

PS plastic particles were used as the reference MPs throughout this work. PS is commercially available in different size ranges and it is the third most frequently reported polymer type of microplastics in water after polyethylene (PE) and polypropylene (PP) in literature.¹⁷ Therefore, nine different sizes of the monodisperse PS microspheres packaged in a 2.5% solids (w/v) aqueous suspension with diameters of 0.5, 0.75, 1, 2, 3, 4.5, 6, 10, and 20 μm were purchased from Polysciences Europe GmbH and used as received unless further explained. Polydisperse PE (1–4, 3–16, and 20–27 μm) and PMMA (3–10 μm) microspheres were purchased from Cospheric LLC in the form of dry powder and were subsequently suspended in solution using Tween 20 surfactant (Thermo Fisher Scientific). Different concentrations of each size of MPs were prepared by mixing a certain amount of stock solutions in 3 mL of deionized (DI) water. The samples were shaken manually before each measurement to achieve an even distribution of the MPs in water. Ultraviolet (UV) fused quartz cuvettes suitable for the wavelength range between 190 nm to 2.5 μm were purchased from Thorlabs and used as the sample containers for the measurements. The cuvettes had a standard 12.5 mm square profile with four polished windows and a transmitted optical path length of 10 mm.

Goniophotometer

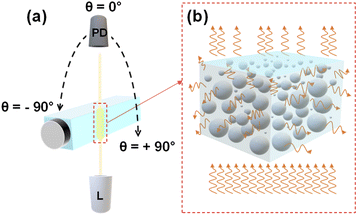
Light scattering measurements were performed using a REFLET-180S goniophotometer (Light Tec) which can work either in transmittance or reflectance mode. As the measured signal by the instrument was relative, thus the normalization of the machine via a standard sample with known reflectance or transmittance was needed for absolute measurements. Because the transmittance mode was employed throughout this work, so all the measurements were normalized relative to the signal of air in which the photodetector faced the light source directly. As depicted in Fig. 1(a), the optical design consists of two symmetric arms being the illumination and the detection parts which are focused at the same point on the sample. The collimated light from a 100 W Tungsten Halogen lamp with a beam diameter of 0.2 millimeter passes through the sample container at a fixed position and the photodetector detects the scattered light (Fig. 1(b)) by scanning from θ = −90° to +90° with an angular resolution of 0.1°. The total duration of one measurement was 30 s. The measurement was repeated three times for each concentration to evaluate the repeatability. Between measurements with various concentrations, the sample container was perfectly cleaned with water, ethanol, water, and dried by air pressure, respectively. The optical setup was placed inside a dark box to avoid interference from ambient lighting during the measurement and the whole process was automatically controlled via dedicated software (REFLET).

Fig. 1 The schematic of the multi-angle static light scattering measurement setup (a); “PD” and “L” stand for photodiode and light source, respectively. (b) Demonstrates the scattering of light by MPs.

Data analysis

The format of the output file was a two columns matrix consisting of the Bidirectional Transmittance Distribution Function (BTDF) versus the scattering angles which was defined using the following formula: BTDF (θd, φd, θi, φi) = L(θd, φd)/E(θi, φi); where, L(θd, φd) was the sample luminance in the direction (θd, φd), and E(θi, φi) was the illuminance on the sample surface in the direction (θi, φi). Further processing and analysis on the output data were performed using MATLAB and The Unscrambler (Aspen Technology).

The use of advanced data analysis methods in combination with different analytical techniques has proved to be a practical approach for the analysis of MPs in several studies.^20,31,32 The same approach was implemented in this work using PCA and LDA to analyze the measured scattering signals of MPs. PCA is known as an unsupervised chemometric method that can split between the groups of a dataset by identifying the existing patterns or trends among them with no prior knowledge.³³ Therefore, PCA was applied on the first derivative of the logarithmic scattering intensity patterns of the mono- and polydisperse samples to discriminate the size of the MPs. In contrast to the PCA which is an unsupervised learning method, LDA is one of the most popular supervised chemometric techniques that was used for pattern recognition.^33,34 To identify the unknown samples using LDA, a mathematical model was constructed based on the features of known samples. For this purpose, since the number of original variables was large, preliminary unsupervised data compression method was used to avoid overfitting.^33,34

Results and discussion

PS monodisperse samples

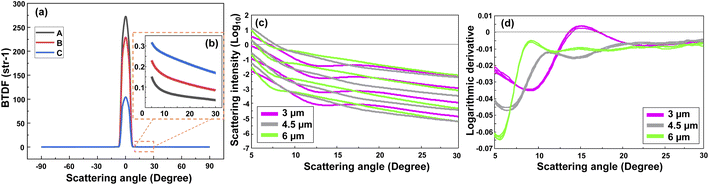
Fig. 2(a) represents the scattering intensity patterns of three different concentrations of PS MPs with a diameter of 0.5 μm. Similar patterns were obtained for the other MP sizes. As seen, the output signal had a symmetric shape between 0° and ±90° angular range, and the transmitted signal, i.e., the non-scattered light, was dominant between −5° and 5°. This can be better visualized from the peak of the intensity patterns at 0°, where the intensity of the sample with a lower concentration (“A”) was higher than the intensities of the other two samples with the higher concentrations (“B” and “C”). Nevertheless, the scattering signal became dominant above 5°, while it was noisy and featureless above 30°. Therefore, only the positive side of the scan in the angular range between 5° to 30° was considered for the analysis. Fig. 2(b) shows that the scattering intensity pattern moves downward between 5–30°. A rather similar behavior was observed in the scattering intensity patterns of other PS monodisperse samples with this difference that the scattering intensity of the larger MPs tended to drop faster at smaller scattering angles. This is due to the fact that the large particles scatter the light in a narrower angular range in comparison to the small particles which scatter the light more evenly in a wider angular range.²¹

Fig. 2 Scattering intensity patterns of 3 different concentrations (A < B < C) of PS MPs with a diameter of 0.5 μm (a), and the magnified scattering intensity patterns between 5° and 30° (b). Logarithmic scattering intensity patterns of three different sizes of PS MPs (MP diameters of 3, 4.5, and 6 μm) with different concentrations (c), and their corresponding first derivative that is calculated using a second-order, nine-point Savitsky–Golay filter (d).

Although one may calculate the concentration of the MPs using the scattering intensity plot and with an a priori knowledge about the MPs size and shape, this will be a hard task if nothing is known about the MPs. Thus, firstly it is necessary to discriminate between the size of the MPs in a sample. Fig. 2(c) demonstrates the scattering intensity plot related to the different sizes and concentrations of the PS MPs. Please note that the output logarithm was calculated to have a comparable contribution from the weak scattered signals at large angles. As seen, the plot contains rich information about the MPs concentration, however, it may be difficult to discriminate between the size of the MPs due to the large overlaps between the curves. The overlap would become higher if all the measured concentrations of different MP sizes were included (see Fig. S1(a)†). Therefore, the first derivative of the corresponding scattering intensity patterns was calculated using a second order, nine-point Savitsky-Golay filter that is demonstrated in Fig. 2(d). Consequently, most of the information about the concentration of MPs was removed. However, the difference between the shape of the scattering intensity patterns was significantly enhanced with respect to the size of the scatterers. Although only a few concentrations of the three measured sizes of PS MPs were selected here for a better demonstration, the same result was obtained for the other samples, as are shown in Fig. S1(a) and (b).† Again, the best results were obtained between the 5–30° angular range due to the aforementioned reasons. Accordingly, this data was used as the input for the PCA analysis of monodisperse samples that is explained in the following section.

PCA of PS monodisperse samples

PCA is a method for compressing the information and the Principal Components (PCs) are the uncorrelated mutually orthogonal axes resulting from linear combinations of original variables that maximize the variance of projections along each PC.³⁵Fig. 3(a) and (b) demonstrate the results of the first four PCs of the PCA analysis that explain 96% of the total variance. As it is clear from Fig. 3(a), the first two PCs accounting for more than 80% of the total variance, discriminated between the MPs larger than 1 μm. While PC3 and PC4 (Fig. 3(b)), albeit explaining a smaller portion of the total variance, split the MPs smaller than 1 μm. By looking at the loading plots shown in Fig. S2(a),† it becomes apparent that PC1 and PC2 have their loadings mainly at small scattering angles below 15°, confirming the fact that most of the variations are related to that region where the scattering intensity is higher. In fact, the large MPs are stronger scatterers than the small MPs, and they mainly scatter the light at small angular ranges as mentioned before.³⁶ As such, PC1 and PC2 explained a large portion of the total variance related to the scattering data of large MPs. In contrast, the loadings of PC3 and PC4 (Fig. S2(b)†) are weak and broadened to larger scattering angles, meaning that the contributions from these angles or small MPs are more included in the PC3 and PC4 axes. This is because the weak scattering signals of small MPs, that are more evenly distributed throughout the angular range, become comparable to that of large MPs at large angles.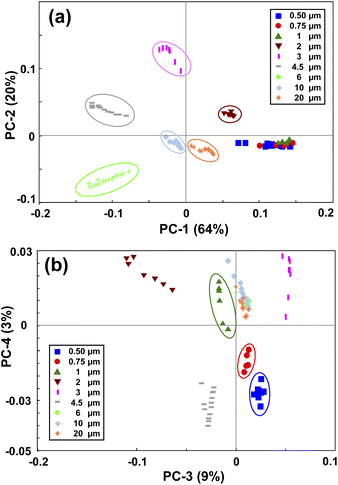

Fig. 3 Principal component analysis of the PS monodisperse samples. (a) shows the PC1 and PC2 map, and (b) shows the PC3 and PC4 map.

Therefore, by applying PCA on the first derivative of the logarithmic scattering intensity patterns of PS monodisperse samples, information about the size of the MPs can be extracted. However, four PCs were needed for discriminating the nine selected sizes of the PS MPs. In the next step, an LDA classifier was trained using the results of PCA analysis to recognize the scattering intensity patterns of unknown monodisperse samples.

Size discrimination of the PS monodisperse samples with LDA classifier

As mentioned before, the result of PCA analysis was used to build an LDA model. LDA calculated a membership probability for each object according to the object position in the PCA space and the hypothesis that all classes follow a multivariate normal distribution. To incorporate the experimental uncertainties in the model, two sets of measurements (187 scans in total) were conducted at two different times, 50% of each were then used to train the LDA algorithm. All the scans were normalized versus the scattering intensity pattern of pure water which was measured in both sets of measurements. To further alleviate the influence of noise, the analysis was confined between 5° to 20° angular range. After PCA analysis, an optimal number of five PCs explaining 99% of the total variance was chosen through cross-validation. The most important PCs were the first three ones explaining 94% of the total variance and the other two accounted for minor features (Fig. S3†). All five PCs were fed into the LDA classifier after being auto-scaled, i.e., divided by their standard deviation, for having equal importance. Eventually, the classification was carried on using a PCA-LDA model and the five auto-scaled PCs as predictors.

Fig. 4 demonstrates the classification results which are summarized in the form of a confusion matrix. As seen, all the MPs larger than 1 μm were correctly assigned to their relevant classes. Nonetheless, some incorrect predictions occurred which were mainly related to MPs smaller than 1 μm, and therefore, the overall accuracy of prediction became 90.3%. This revealed that the model had good accuracy in discriminating between the monodisperse samples of 1 μm and larger MPs, however, the accuracy deteriorated for resolving the samples composed of submicron-sized MPs. This was expected because the small MPs were separated using the PCs that explained a small portion of the total variance. Therefore, they also affected the accuracy of the LDA which was trained by them for classifying the size of the small MPs. Nevertheless, a clear division between the nanoscale and microscale monodisperse samples was feasible.

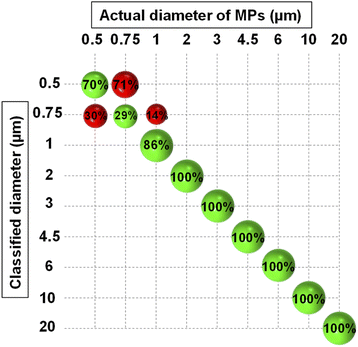Fig. 4 Confusion matrix resulting from the classification of PS monodisperse samples using PCA-LDA model. The green and red spheres show the correct and wrong classification rates, respectively.

Polydisperse samples

Microplastics do not exist in a single size in the environment. Mechanical stress, photo/thermal degradation, and other weathering processes lead to the continuous fragmentation of plastic particles.^18,37,38 This further increases the arduousness of MPs analysis, as each analytical technique is applicable to a certain size range as mentioned already. Although separation of MPs with different diameters is possible using metallic filters with small mesh sizes, this may not be a time- and cost-effective approach.^39,40 Therefore, it is desirable to eliminate the filtration steps where possible. This, however, is a challenging task and requires an analytical technique capable of classifying MPs in polydisperse mixtures. Accordingly, the approach proposed in this work has been tested for classifying the size and concentration of MPs in polydisperse samples.

The experiments were performed with three different groups of PS MPs based on their size, respectively, small (0.5, 0.75, and 1 μm), medium (2, 3, and 4.5 μm), and large (3, 6, and 10 μm) MPs. Then, two batches of PS polydisperse samples with different complexities were investigated. In the first batch, the concentration of MPs was kept constant at each group and only the compositions were changed. Labelling of the mixtures was also used for a better demonstration. For example, “111” is a sample relevant to either the small, medium, or large group with an equal concentration of each component from that group, and “110” describes a sample with an equal concentration of the first two components and zero concentration of the last component from a relevant group. The order of the components in a sample is based on the size of each component starting from the smaller towards the larger diameters. In the second batch, the composition of the MPs was always the same, but the concentration of each component was different. Labelling of the mixtures was used here as well. For example, “112” describes a sample relevant to either the small, medium, or large group in which the concentration of the third component is two times the concentrations of the first two components. Please note that these labels were used exclusively for each group of PS polydisperse MPs. Since PE and PMMA MPs were supplied as polydisperse samples in specific size ranges, they were more complex compared to the previous cases.

The same pre-processing as for monodisperse samples was applied on the scattering intensity patterns of the polydisperse samples before PCA analysis. Like before, the logarithm of the output intensity patterns (Fig. S4(a)†) yielded information about the concentration of the MPs and its derivative (Fig. S4(b)†) helped to discriminate between the sizes of the MPs. Therefore, the latter was used for the PCA analysis of the polydisperse samples explained in the next section.

PCA of polydisperse samples

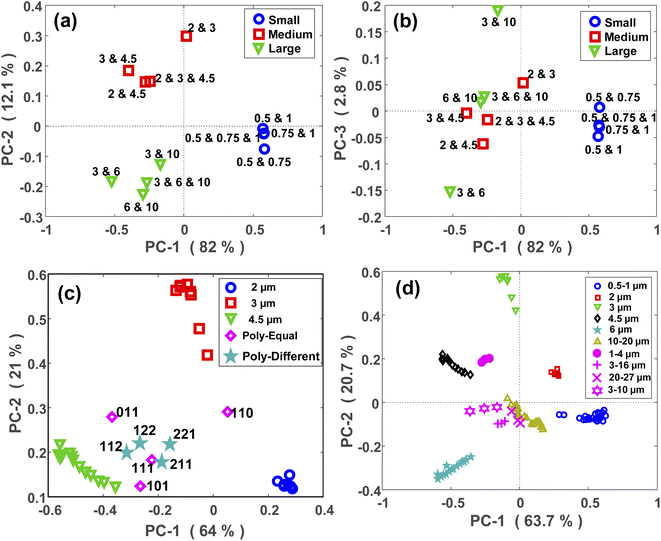
The PCA maps of PS polydisperse samples with equal concentrations are shown in Fig. 5(a) and (b). PC1 and PC2 (Fig. 5(a)) explained a large portion of the total variance through which the polydisperse mixtures were well split based on their corresponding size categories. By incorporating the PC3 in the model, a within-group split was achievable as demonstrated in Fig. 5(b). For example, the sample composed of 3 and 10 μm MPs was well separated from the other sample composed of 3 and 6 μm MPs, and both samples were related to the large group. However, it should be noted that PC3 explained a small portion of the total variance, thus it might not be as reliable as the first two PCs.

Fig. 5 PCA maps of PS polydisperse samples with equal concentrations; (a) shows the PC1-PC2 map and (b) shows the PC1-PC3 map (all sizes are in micrometer). (c) Shows the projection of the scattering intensity patterns of the polydisperse samples onto the PCA maps of their constituent MPs (monodisperse samples of 2, 3, and 4.5 μm MPs). The pink diamonds and the pale blue stars show the PCA maps of polydisperse samples with equal and unequal concentrations of each size, respectively. (d) Shows the projection of PCA maps of PE (pink circle, cross and plus symbols) and PMMA (pink stars) polydisperse samples onto the PCA maps of all the PS monodisperse samples.

In a next step, the scattering intensity patterns of all the polydisperse samples with either equal or unequal concentrations were projected onto the PCA model of monodisperse samples. A typical map of this projection is demonstrated for the medium-sized MPs (2, 3, and 4.5 μm) in Fig. 5(c). The aim was to see if any relationship exists between the maps of mono- and polydisperse samples on the PCA space. At first glance, it can be easily interpreted that the PCA location of a polydisperse sample falls in between the PCA locations of its constituent MPs. For example, since the sample “110” was a polydisperse sample composed of 2 and 3 μm MPs, its PCA location fell in between the PCA locations of the monodisperse samples of 2 and 3 μm MPs. The same argument is valid for the other points. Furthermore, it can be observed that the PCA location of the polydisperse samples diverged towards the PCA location of their largest constituent. This is clearly visible for the samples “011” and “101”, whose PCA locations diverged towards the PCA location of 4.5 μm MP which was their largest constituent. This is because the larger MPs are stronger scatterers and therefore, their scattering signal plays the main role within a polydisperse mixture. Due to the larger size difference between the constituent MPs of the sample “101” in comparison to the sample “011”, the divergence of the former was higher than that for the latter.

Fig. 5(c) also demonstrates the projection of scattering intensity patterns of polydisperse samples with unequal concentrations (star symbols) onto the PCA map of monodisperse samples. Unlike the previous case, there was no clear relationship between these two PCA maps, however, there were certain remarks to be noted. First, the PCA location of all four samples fell in between the PCA locations of their constituent MPs, i.e., the monodisperse samples. Second, the deviation of the points towards the PCA of their larger constituent existed here, as well. Finally, the PCA location of a polydisperse sample deviated towards the PCA location of the monodisperse sample whose concentration was higher in it. This was more distinct for the “112” and “221” samples. In fact, since the concentration of 4.5 μm was two times the concentration of 2 and 3 μm MPs in the “112” sample, its PCA shifted towards the PCA of 4.5 μm monodisperse sample. While, in the “221” sample, the concentration of 4.5 μm MP was half the concentration of 2 and 3 μm MPs, and therefore, its PCA located closer to the PCA of 2 and 3 μm MPs.

Relatively similar results were obtained for the PE, PMMA and large-sized PS MPs as shown in Fig. 5(d) and S5(b),† respectively. Nevertheless, the outcome was different for the polydisperse samples which were composed of the small PS MPs (Fig. S5(a)†). The only valuable result was that the samples containing 1 μm MPs had a different PCA location than the samples without it. This again confirms the capability of the proposed approach for discriminating between micron and sub-micron scale MPs.

Size discrimination of PS, PE and PMMA polydisperse samples with LDA classifier

Classification of PS, PE and PMMA polydisperse samples with either equal or different concentrations was performed using the LDA classifier trained by the PCA of the PS monodisperse samples. In this case, right or wrong classification was not explored because the PCA locations of unknown polydisperse samples had no coincidence with the PCA locations of other known monodisperse samples, except for one case in the small group. However, according to the outcome of PCA-LDA model, polydisperse samples were assigned to one of the three size categories, i.e., small, medium, or large, and the dominant size within each mixture was revealed. Note, that the result of the PCA analysis in the angular range between 5–25° was used here to train the LDA classifier. The new choice of angular range was for reducing the influence of noise, whereas most of the size-dependent information was also contained in this region.

Therefore, three classifiers were created using two, three, and four PCs, as predictors, all of which gave a 100% classification rate on the training set (known PS monodisperse samples). The classification of polydisperse samples was then performed through each of these classifiers. The results are summarized in Table S1.† As can be seen, all the polydisperse samples were correctly assigned to their relevant size categories and the results were similar using three classifiers, indicating that only two PCs were enough for a flawless classification. Almost in all cases, the PCA-LDA model classified the size of the polydisperse samples with respect to the largest constituent MP in the mixture. This revealed that the larger MPs which were the stronger scatterers, dominated the others even when they were in a lower concentration (at least for a factor of 2 in relative abundance). However, only in one case (3–6–10 μm (221)), the size of the sample was assigned to 6 μm using the PCA-LDA model trained by four PCs. Probably, the difference between the scattering efficiency of 6 and 10 μm MPs was not so strong to overcome the effect of the concentration. However, four PCs were needed to detect it. Another interesting result is the correct size classification of PE and PMMA polydisperse samples. This means the model is not only applicable to the PS MPs but can also be used for the size classification of other types of plastic particles.

Quantitative measurement of PS MPs concentration

After specifying the size of the MPs in a sample, their concentration can be determined using the scattering intensity at an arbitrary angle from the selected angular range (5–30°). Fig. 6(a) represents the decimal logarithms of MP concentration in 3 mL of DI water against the scattering intensity which was measured at 30° for all MP sizes. The corresponding RMSEC (Root Mean Square Error of Calibration) and R² coefficients for each plot are summarized in Fig. 6(b), as well. As seen, almost a linear relationship was obtained between the logarithms of scattering intensity and the concentration of MPs for all sizes. Therefore, a simple linear fit was enough for measuring the concentration of MPs in a sample, provided that the size of the MPs was known.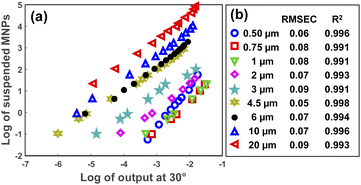

Fig. 6 The logarithm of MPs concentration in 3 mL of DI water versus the logarithm of scattering intensity at 30° (a). (b) Demonstrates the RMSEC and R² values for each concentration plot.

It was also tried to detect the concentration of MPs in the polydisperse samples using a Principal Component Regression (PCR) model that was created based on the PCA of monodisperse samples. According to the LDA classification results of polydisperse samples, the largest MP was considered as the reference size for each mixture for determining the concentrations of all the constituent MPs. However, as expected, a sensible underestimation of the MPs concentration occurred in most cases. This can be explained since LDA classified the size of the MPs based on the largest scatterer in a polydisperse sample, and therefore, the effect of smaller MPs was overlooked.

Reproducibility assessment

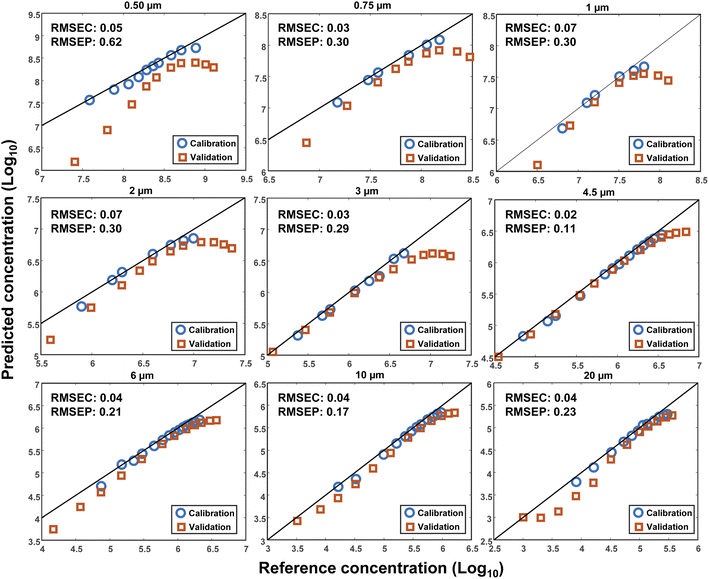
To investigate the reproducibility of the results, another set of measurements was conducted after the initial measurements at a different time. The volume of DI water was kept constant (3 mL), however, another cuvette with the same characteristics was used. A wider range of MPs concentrations was measured for each size to estimate the plateau of the output signal. Consequently, a Linear Least Square (LLS) model was used to investigate the reproducibility of the measurements. The first dataset was used as the calibration and the second as the validation. This time, the decimal logarithm of the scattering intensity at 10° was selected for the concentration plots, the results of which are demonstrated in Fig. 7 for all sizes together with their corresponding RMSEC and RMSEP (Root Mean Square Error of Prediction) values. As seen, an acceptable reproducibility was obtained for almost all sizes except for the particles with a diameter of 0.5 μm, where a remarkable systematic error was observed between the results. However, the error decreased by increasing the size of the particles, such that the best result was obtained for the particles with a diameter of 4.5 μm, for which the RMSEC and RMSEP were small, as well. It should be noted that the RMSEP was not only influenced by the systematic error but also bore the impact of nonlinearity at high concentrations. In other words, a better result was expected if the highest concentrations were removed from the validation dataset.

Fig. 7 The logarithm of the predicted concentrations of PS MPs versus their reference concentrations in 3 mL of DI water. The blue circles and red squares show the calibration and validation data points, respectively. The values of Root Mean Square Error of Calibration (RMSEC) and prediction (RMSEP) are demonstrated on each plot, as well.

The lack of perfect reproducibility can be attributed to various parameters. First, a possible mismatch between the optical and mechanical characteristics of the cuvettes that were used during each set of measurements. Second, the displacement of the cuvettes during the measurements. And third, the settling and/or sticking of the particles at the bottom or to the inner walls of the cuvettes. Finally, the limited precision of the pipettes that were used for making the different concentrations of the MPs. Although efforts were made to minimize the impact of each of these parameters, some uncertainties were still inevitable.

Conclusions

Despite being a well-known technique for the characterization of small particles, light scattering received less attention in comparison to other common techniques such as Raman spectroscopy and FTIR, for the analysis of microplastics. Neither Raman nor FTIR can characterize the size and concentration of multiple microplastic particles in a batch mode with a single-run measurement. Here, it was demonstrated that the combination of light scattering with chemometric pattern recognition algorithms, such as PCA and LDA, can bring valuable advantages for the batch analysis of the size and concentration of microplastics in water. Therefore, three kinds of MPs samples including monodisperse, equal- and unequal-concentration polydisperse with different levels of complexities were fully investigated. It was shown that PCA can reveal the relationship between the scattering intensity patterns of these samples. Moreover, a PCA-LDA model, created only based on the scattering data of PS monodisperse samples, was employed to classify the size of the PS, PE and PMMA MPs in polydisperse mixtures. This is particularly useful when the size of the MPs is completely unknown in a mixture. Finally, a simple linear fit was used to determine the concentration of MPs in water.

A further precise classification would have been feasible if the PCA-LDA model was trained using the different compositions of polydisperse samples. In that case, one might get an estimate about the size of each constituent MP instead of solely knowing the largest scatterer in a polydisperse sample. Undoubtedly, numerous data would also be required for the purpose of training. Alternatively, the use of machine learning approaches such as neural networks (NN) and genetic algorithms can be beneficial as well.

Overall, the results reported in this work may open a new perspective for the batch analysis of microplastics in water. Although artificial plastic particles were used throughout this work, the so-called real samples at this stage of microplastic detection undergo multiple filtrations and purification processes and end up being close to what we have tested. However, as a next step, it may be necessary to examine the possibilities of light scattering techniques for the characterization of different shapes of real microplastic samples in water. Nevertheless, it would be unavoidable to incorporate the spectroscopic techniques in the final scheme for a relatively complete analysis.

Author contributions

Mehrdad Lotfi Choobbari: conceptualization, methodology, investigation, writing – original draft, visualization; Leonardo Ciaccheri: formal analysis, data curation, validation, software; Tatevik Chalyan: supervision, validation, writing – review & editing; Barbara Adinolfi: writing – review & editing; Hugo Thienpont: funding acquisition, resources; Wendy Meulebroeck: supervision, validation, writing – review & editing; Heidi Ottevaere: supervision, project administration, funding acquisition, validation, resources, writing – review & editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the “MONPLAS” European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 860775. This work was also supported in part by the Methusalem and Hercules foundations and the OZR of the Vrije Universiteit Brussel (VUB).

References

1. D. Elkhatib and V. Oyanedel-Craver, Environ. Sci. Technol., 2020, 54, 7037–7049.
2. Z. Akdogan and B. Guven, Environ. Pollut., 2019, 254, 113011.
3. Y. Zhang, S. Kang, S. Allen, D. Allen, T. Gao and M. Sillanpää, Earth-Sci. Rev., 2020, 203, 103118.
4. C. F. Araujo, M. M. Nolasco, A. M. P. Ribeiro and P. J. A. Ribeiro-Claro, Water Res., 2018, 142, 426–440.
5. C. Vitali, R. Peters, H.-G. Janssen and M. W. F. Nielen, TrAC, Trends Anal. Chem., 2022, 116670.
6. A. Ragusa, A. Svelato, C. Santacroce, P. Catalano, V. Notarstefano, O. Carnevali, F. Papa, M. C. A. Rongioletti, F. Baiocco, S. Draghi, E. D'Amore, D. Rinaldo, M. Matta and E. Giorgini, Environ. Int., 2021, 146, 106274.
7. D. Li, Y. Shi, L. Yang, L. Xiao, D. K. Kehoe, Y. K. Gun'ko, J. J. Boland and J. J. Wang, Nat. Food, 2020, 1, 746–754.
8. R. C. Thompson, Y. Olsen, R. P. Mitchell, A. Davis, S. J. Rowland, A. W. G. John, D. McGonigle and A. E. Russell, Science, 2004, 304, 838.
9. C. Campanale, I. Savino, I. Pojar, C. Massarelli and V. F. Uricchio, Sustainability, 2020, 12, 6755.
10. T. M. Karlsson, A. Kärrman, A. Rotander and M. Hassellöv, Environ. Sci. Pollut. Res., 2020, 27, 5559–5571.
11. A. Käppler, D. Fischer, S. Oberbeckmann, G. Schernewski, M. Labrenz, K. J. Eichhorn and B. Voit, Anal. Bioanal. Chem., 2016, 408, 8377–8391.
12. Z. Sobhani, X. Zhang, C. Gibson, R. Naidu, M. Megharaj and C. Fang, Water Res., 2020, 174 DOI:10.1016/j.watres.2020.115658.
13. J. Wagner, Z. M. Wang, S. Ghosal, C. Rochman, M. Gassel and S. Wall, Anal. Methods, 2017, 9, 1479–1490.
14. B. EL Hayany, L. EL Fels, K. Quénéa, M. F. Dignac, C. Rumpel, V. K. Gupta and M. Hafidi, J. Environ. Manage., 2020, 275 DOI:10.1016/j.jenvman.2020.111249.
15. E. Dümichen, A.-K. Barthel, U. Braun, C. G. Bannick, K. Brand, M. Jekel and R. Senz, Water Res., 2015, 85, 451–457.
16. B. Kanyathare, B. O. Asamoah, U. Ishaq, J. Amoani, J. Räty and K. E. Peiponen, Chemosphere, 2020, 248 DOI:10.1016/j.chemosphere.2020.126071.
17. A. A. Koelmans, N. H. Mohamed Nor, E. Hermsen, M. Kooi, S. M. Mintenig and J. De France, Water Res., 2019, 155, 410–422.
18. C. F. Araujo, M. M. Nolasco, A. M. P. Ribeiro and P. J. A. Ribeiro-Claro, Water Res., 2018, 142, 426–440.
19. C. Schwaferts, R. Niessner, M. Elsner and N. P. Ivleva, TrAC, Trends Anal. Chem., 2019, 112, 52–65.
20. B. N. Vinay Kumar, L. A. Löschel, H. K. Imhof, M. G. J. Löder and C. Laforsch, Environ. Pollut., 2021, 269, 116147.
21. R. Xu, Particuology, 2015, 18, 11–21.
22. G. Balakrishnan, F. Lagarde, C. Chassenieux and T. Nicolai, Preprints, 2020, 2020030189, 1–27.
23. W. D. Dick, P. J. Ziemann and P. H. McMurry, Aerosol Sci. Technol., 2007, 41, 549–569.
24. R. J. W. Hodgson, J. Colloid Interface Sci., 2001, 240, 412–418.
25. B. O. Asamoah, B. Kanyathare, M. Roussey and K. E. Peiponen, Chemosphere, 2019, 231, 161–167.
26. B. O. Asamoah, M. Roussey and K. E. Peiponen, Chemosphere, 2020, 254, 126789.
27. F. Caputo, R. Vogel, J. Savage, G. Vella, A. Law, G. Della Camera, G. Hannon, B. Peacock, D. Mehn, J. Ponti, O. Geiss, D. Aubert, A. Prina-Mello and L. Calzolai, J. Colloid Interface Sci., 2021, 588, 401–417.
28. D. Schymanski, C. Goldbeck, H. U. Humpf and P. Fürst, Water Res., 2018, 129, 154–162.
29. L. A. Clementi, J. R. Vega and L. M. Gugliotta, Part. Part. Syst. Charact., 2010, 27, 146–157.
30. W. Huang, L. Yang, G. Yang and F. Li, Biomed. Opt. Express, 2018, 9, 1520.
31. H. de M. Back, E. C. Vargas Junior, O. E. Alarcon and D. Pottmaier, Chemosphere, 2022, 287, 131903.
32. C. Fang, Y. Luo, X. Zhang, H. Zhang, A. Nolan and R. Naidu, Chemosphere, 2022, 286, 131736.
33. M. Esteki, Z. Shahsavari and J. Simal-Gandara, Food Control, 2018, 91, 100–112.
34. A. G. Mignani, L. Ciaccheri, H. Ottevaere, H. Thienpont, L. Conte, M. Marega, A. Cichelli, C. Attilio and A. Cimato, Anal. Bioanal. Chem., 2011, 399, 1315–1324.
35. R. G. Brereton, J. Jansen, J. Lopes, F. Marini, A. Pomerantsev, O. Rodionova, J. M. Roger, B. Walczak and R. Tauler, Anal. Bioanal. Chem., 2017, 409, 5891–5899.
36. P. J. Lloyd, Chem. Eng., 1974, 81, 120–123.
37. M. Eriksen, L. C. M. Lebreton, H. S. Carson, M. Thiel, C. J. Moore, J. C. Borerro, F. Galgani, P. G. Ryan and J. Reisser, PLoS One, 2014, 9, 1–15.
38. D. M. Mitrano and W. Wohlleben, Nat. Commun., 2020, 11, 1–12.
39. W. Fu, J. Min, W. Jiang, Y. Li and W. Zhang, Sci. Total Environ., 2020, 721, 137561.
40. B. E. Oßmann, G. Sarau, S. W. Schmitt, H. Holtmannspötter, S. H. Christiansen and W. Dicke, Anal. Bioanal. Chem., 2017, 409, 4099–4109.

---

Footnote

† Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2ay01215d

---