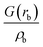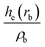Intermetallic species in the Negishi coupling and their involvement in inhibition pathways

Abstract

The formation of M–Zn-intermetallic species (M = Ni, Pd) in the course of the Negishi reaction in THF solvent and their potential impact on in situ catalyst inhibition were investigated by DFT calculations carried out at two levels of theory. The solvent coordination to the transition metal centers was explicitly accounted for in the calculations. Two model PR₃ ligands (PR₃ = PMe₃ and PPh₃), as well as a model NHC-type ligand (1,3-diisopropylimidazol-2-ylidene), were selected. The formation of the intermetallic species during the catalytic process effectively removes the key in-cycle cross-coupling intermediates M(0)L₂, cis-[L₂PhM(II)X], and trans-[L₂PhM(II)X] from the main Negishi catalytic cycle. The reaction between the ZnX₂ by-product of the cross-coupling and the M(0)L₂ species yields bi-metallic adducts with M–Zn dative bonds. The nature of these bonds in the resulting complexes was analyzed with QTAIM. ZnX₂ coordination to [L₂PhM(II)X] intermediates prevents the binding of alkylzinc halide (RZnX) reagents and blocks the cross-coupling process. Based on these findings, we consider LiX additives as agents that passivate the Lewis-acidic ZnX₂ by-product and therefore limit the product inhibition. This work highlights the profound effect of a system view on catalytic cross-coupling reactions, where interactions between components of catalytic systems are taken into account explicitly, and discourage the use of single-cycle-only models.

---

1. Introduction

Computational modeling has become indispensable in mechanistic studies of catalytic reactions by providing practical tools for generation of valuable insights into reaction mechanisms.^1–8 Designing new catalytic systems based on modeling data, however, is still challenging.^9–12 Catalytic processes in organic synthesis are often performed in the liquid phase, and conventional quantum chemical approaches to model kinetics and thermodynamics in solution sometimes cause significant inaccuracies or even give misleading results.¹³ The errors in computational modeling may be associated with the inherent limitations of the quantum chemical methods or may be caused by the incompleteness of considered mechanistic proposals.⁸ The inherent mechanistic complexity of cross-coupling reactions that cannot be captured with simplistic single-cycle catalytic models (as in Fig. 1a) is now well-recognized.^6,14–17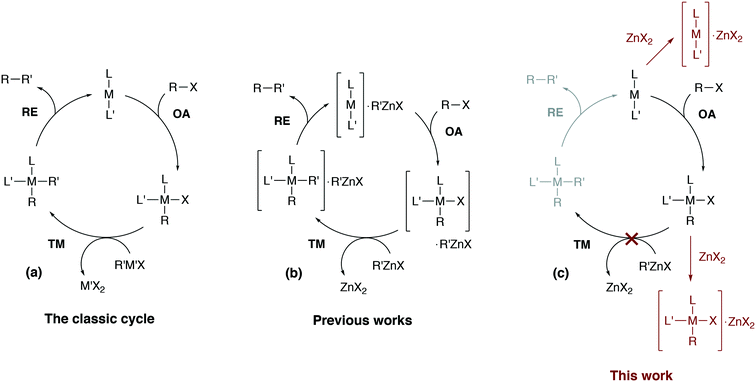

Fig. 1 (a) The simplified conventional cross-coupling catalytic cycle and (b) a model catalytic cycle in the Negishi reaction accounting for the formation of intermetallic species proposed in previous works (see ref. 24 for example), and (c) a model cycle accounting for the product inhibition proposed in this work. L′ = ligand, solvent, co-solvent, etc.

Catalytic cross-coupling reactions have become one of the cornerstones of organic synthesis. Among these, the Negishi reaction is a useful method for the cross-coupling of organo-(pseudo)halides RX with air- and moisture-sensitive organozinc reagents RZnX or R₂Zn. One of its key advantages is an extensive substrate scope (coupling of sp-, sp²-, and sp³-carbon moieties).^18–20 Zinc reagents rapidly undergo transmetalation and thus the Negishi reaction, unlike the Heck or Suzuki reactions, may proceed at temperatures well below the ambient temperature, e.g., at −45 or −55 °C, while, under optimized conditions, the TONs may reach ca. 10⁶.²¹ Thus, despite the air- and moisture-sensitivity of the employed reagents, Negishi cross-coupling has become a powerful synthetic methodology suitable for the synthesis of pharmaceuticals.²² This reaction is often selected in total synthesis, where the reaction efficiency is of paramount importance.^18,23

Divalent zinc compounds, such as ZnX₂, RZnX, and R₂Zn, are Lewis acids.²⁵ Nickel and palladium metal-complex catalysts are a common choice in Negishi cross-coupling and, at the same time, are Lewis bases. The possibility of Ni–Zn and Pd–Zn hetero-bimetallic Lewis pair formation is well recognized.²⁶ Indeed, organometallic Zn compounds can be ligands binding to Ni and Pd centers.²⁷ The involvement of RZnX–Pd intermetallic species in the Negishi reaction catalysis has been demonstrated both computationally and experimentally (Fig. 1b).^14,24 Considering computational and computational-experimental works only,^4,28–33 the Negishi cross-coupling is actively studied. However, the involvement of the reaction by-product ZnX₂ in the catalytic mechanism was modeled only in the case of the final reductive elimination stage.^24,34 An inhibiting effect of ZnX₂ accumulation in the course of the reaction was demonstrated experimentally as zinc halide additives slowed down Pd-catalyzed Negishi coupling reactions and even terminated the catalytic process entirely in some cases.^14,33,35

In this article, we consider how the formation of intermetallic M–Zn species can effectively remove the key intermediates M(0)L₂, cis-[L₂PhM(II)X] and trans-[L₂PhM(II)X] from the catalytic cycle in the Negishi reaction. A detailed DFT analysis was carried out on models of widely-used phosphine- and NHC-ligand-based Ni and Pd catalytic systems (Fig. 1c). Our results provide an alternative explanation for the role of salt additives, the importance of which has been highlighted earlier in a series of experimental studies.^15,35–37 The current work highlights the importance of a system view on a catalytic transformation, in which interactions between components of the catalytic system are explicitly accounted for, and illustrates how a single-cycle-only model of a catalytic process may be inadequate.

This article is organized as follows. It begins with section 2.1 which provides a brief description of the computational methods and modeling approaches that were selected here to compute the Gibbs free energies of key elementary reaction steps. Section 3.1 is devoted to the formulation of the catalytic model for the case of phosphine-based catalytic systems. This is followed by section 3.2, where possible transformations of [M(PR₃)₂] species (M = Ni, Pd) to catalytic and non-catalytic M(0)–Zn intermediates (Fig. 1c, the off-cycle transformation on the top) are discussed. This section also includes a detailed analysis of the electronic structure of the M(0)–Zn bond (M = Ni, Pd) in the framework of the quantum theory of atoms in molecules (QTAIM), and the effect of solvent (THF) coordination to transition metal centers. Sections 3.3 to 3.5 describe the proposed mechanism of product inhibition in phosphine- and NHC-based systems emerging from a competitive formation of pre-transmetalation intermediates and M–Zn off-cycle resting states (Fig. 1c, the bottom off-cycle transformation). Our findings and implications are summarized in section 4 of the manuscript.

2. Computational details

All DFT calculations were performed using the ORCA program package (ver 4.0.1).³⁸ Geometry optimizations and vibrational frequency calculations were performed at two levels of theory. First, the B97-3c method was used which is a combination of the re-parameterized B97 GGA functional, a specially modified Gaussian basis set of triple-ζ quality, an atom-pairwise correction for GGA functionals (accounts for artificial elongation of chemical bonds involving main-group elements), and the D3-dispersion correction.³⁹ The method was shown to be exceptionally reliable in the modeling of organometallic reactions.⁴⁰ Second, a combination of the TPSS functional⁴¹ and the def2-SVP basis set⁴² was used. In this case, we used the empirical D3(BJ) and gCP corrections (three-body dispersion terms were included).^39,43,44 It should be noted that the TPSS functional often performs well in transition metal chemistry benchmarks.^45–48 The RI-approximation was used throughout.^49–55 The Stuttgart–Dresden ECPs for Pd (ref. 56) and I (ref. 57) were used. The chosen levels of theory are designated as B97-3c and TPSS-D3/DZP. A detailed description of the chosen computational parameters is given in the ESI.†

The implicit solvent C-PCM model was used to model bulk solvent effects.⁵⁸ We added coordinated THF molecules to model transition metal species, where it was favorable, according to test geometry optimization runs. Explicit inclusion of solvent molecules along with the use of continuum solvent models is often referred to as the cluster-continuum approach. This approach often allows accurate modeling of computationally complex kinetic and mechanistic phenomena.^30,59–61

Free energies were calculated according to eqn (1):

G^A = E^A + ΔG^A_QRRHO + ΔG^A_solv + ΔG_conc, (1)

where G^A is the Gibbs free energy of species A and E^A is their total energy (includes total electron energy as well as the empirical D3(BJ) and gCP corrections); the term ΔG^A_QRRHO includes the thermochemical corrections according to the QRRHO approximation (see ESI† section 1 for details),⁶² computed at the same level of theory as the E^A term; the ΔG^A_solv term is the solvation free energy calculated with the C-PCM approach, including the charge-correction, dispersion, and cavitation terms.⁶³ A concentration correction, ΔG_conc equal to 1.69 kcal mol⁻¹, was used to account for the change of the system state from the ideal gas to the 1 M solution.^64–66 Therefore, the free energies, reported in this work, are the standard Gibbs free energies of the elementary chemical transformations except those involving THF solvent.

A solvent is commonly present in excess to reactants and intermediates. Therefore, according to Le Chatelier's principle, discoordination of solvent molecules from metal centers is expected to be less favorable compared to a hypothetical decoordination of the same solvent molecule when the former are in the 1 M standard state. Neglecting the solvent excess in cluster-continuum computations and using the conventional QRRHO approach offered a rather small mean absolute deviation of 2.2 kcal mol⁻¹ from AIMD calculation results in related systems.⁶⁷ We, however, found that accounting for the solvent excess may have a picture-change effect on calculation results. Specifically, the Gibbs free energies of some elementary transformations changed sign (see below) upon application of a THF concentration correction that was used in a previous computational study of the Negishi reaction:

ΔG^THF_exc = RT ln(12.33/1).

The ΔG^THF_exc term is equal to 1.49 kcal mol⁻¹, where 12.33 M is “the concentration of THF in pure THF.”³⁰ The Gibbs free energy of free (uncoordinated) THF species was calculated as:

G^THF = E^THF + ΔG^THF_QRRHO + ΔG^THF_solv + ΔG_conc + ΔG^THF_exc, (2)

Phosphine and N-heterocyclic carbene ligands are the most widely used in cross-coupling catalysis.⁶⁸ In sections 3.1–3.3, we modeled the Ni and Pd systems with the trimethylphosphine (PMe₃) and triphenylphosphine (PPh₃) ligands. While the former is a model ligand imposing moderate steric hindrance,⁶⁹ the latter is a widely-used ligand in cross-coupling chemistry.⁶⁸ We selected 1,3-diisopropylimidazol-2-ylidene (here, i-Pr-Im) as a model NHC-type ligand in section 3.4. While ligands such as 1,3-dimesitylimidazol-2-ylidene (IMes) and bis(2,6-bis(diisopropyl)phenyl)imidazol-2-ylidene (IPr) are widely used in cross-coupling catalysis, i-Pr-Im is used more rarely in the synthesis of transition metal complexes.^70,71 Using i-Pr-Im instead of IMes or IPr as a model ligand reduces computational time and, at the same time, accounts for the steric bulk of the side groups bound to the imidazolium core.

3. Results and discussion

3.1. Model of the catalytic reaction

We considered the formation of M–Zn intermetallic species in the course of a model AlkZnX–ArX cross-coupling process, catalyzed by Ni and Pd systems with phosphine ligands (Fig. 2). Ethylzinc halides EtZnX and phenyl halides PhX (X = Cl, Br, I) were chosen as model AlkZnX and ArX. Only bis-phosphine species 1 were considered because under ligand-free or ligand-deficient conditions, formation of nanoparticles and oligomeric species may take place (see, e.g., ref. 72 and 73 for original studies and ref. 17 and 74 for reviews). The catalytic role of such aggregates is beyond the scope of this study and has been discussed elsewhere.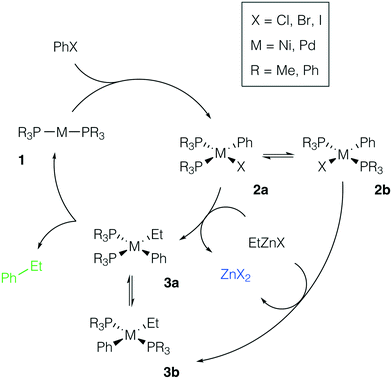

Fig. 2 Model catalytic cycle for Negishi coupling of PhX and EtZnX in d10-metal phosphine-based catalyst systems. The inset shows the functionalities varied in the model systems; see the ESI† for all obtained results.

Potential ligand dissociation may lead to the formation of dimers R₃P[PhM(μ₂-X)]₂PR₃ from 2a and 2b with the concomitant release of two phosphine molecules. Test calculations at the B97-3c and TPSS-D3/DZP levels for the case of X = Br indicated that this process is thermodynamically unfavorable (see Tables S15–S16 and S41–S42†). The dimerization was endergonic by at least +8.5 kcal mol⁻¹ in the Ni systems and by at least +12.5 kcal mol⁻¹ in the Pd systems at both levels of theory (L = PR₃ = PMe₃ or PPh₃). Alternatively, the degradation of phosphine ligands may lead to the formation of mono-ligated complexes, which are prone to dimerization. We assumed the degradation due to quaternization or oxidation of phosphine ligands to be negligible as this would require the presence of impurities (acids⁷⁵ or air,⁷⁶ respectively) in the reaction mixture.

There are two specific molecular-level phenomena that need to be explicitly mentioned when constructing the representative mechanistic models for the considered type of catalytic systems. First, solvent coordination to the transition metal centers should be explicitly accounted for. In THF solutions, zinc compounds ZnX₂ and RZnX exist as tetrahedral [(THF)₂ZnX₂] and [(THF)₂RZnX] species (see ref. 30 and 77). The feasibility of THF–Ni and THF–Pd coordination depends on the nature and oxidation state of the metal center and it will be discussed in more detail below. Secondly, Ni-catalyzed cross-coupling reactions may proceed via a mechanistic path different from the M(0)/M(II) catalytic cycle (the even-electron cycle, Fig. 2), operating in Pd-catalyzed cross-coupling reactions, including Pd-catalyzed Negishi Alk–Ar-coupling reactions.¹⁴ For example, an odd-electron Ni(I)/Ni(III) cycle may become operative in Ni systems.⁴ The odd-electron and even-electron cycles, however, are interconnected via comproportionation/disproportionation (the Ni(0) + Ni(II) ⇌ Ni(I) process),^78–80 while extensive evidence suggests that both cycles may be active under catalytic conditions.^78,81–83 We considered only the Ni(0)/Ni(II) cycle (Fig. 2, M = Ni) for the possibility of a direct comparison with the Pd case. One can straightforwardly extend the presented modeling to the case of the Ni(I)/Ni(III) cycle, which would be an interesting topic for further studies.

3.2. Modeling transformations of the [M(PR₃)₂] species

We modeled a set of possible elementary chemical transformations of 2-coordinated catalytic M(0) species 1 at the B97-3c and TPSS-D3/DZP levels (M = Ni, Pd, Fig. 3). Since 1 are formally the 14e⁻-species, one may expect these to be highly reactive. While in THF solutions the [Pd(PR₃)₂] species remain two-coordinated, the [Ni(PR₃)₂] species can bind THF molecules, forming a tetrahedral complex 1′. The formation of PMe₃-coordinated complex 1′ was endergonic (4.9 kcal mol⁻¹), and the formation of complex 1′ with PPh₃-ligands was exergonic by −1.8 kcal mol⁻¹, according to the calculations at the B97-3c level of theory. The TPSS-D3/DZP calculations predicted the formation of both PMe₃ and PPh₃ complexes to be exergonic by −6.5 and −9.4 kcal mol⁻¹, respectively (see Tables S1 and S2 in the ESI†). It should be noted that a conventional approach to the calculation of the Gibbs formation energies (with the 1 M standard states for 1 and THF, see eqn (1) of the Computational details section) of complexes 1′ gave endergonic values of 7.9 and 1.1 kcal mol⁻¹ for the PMe₃- and PPh₃-bound species at the B97-3c level of theory. At the same time, the formation of complexes 1′ remained exergonic when modeled at TPSS-D3/DZP without the THF concentration correction applied, see Tables S1 and S2.†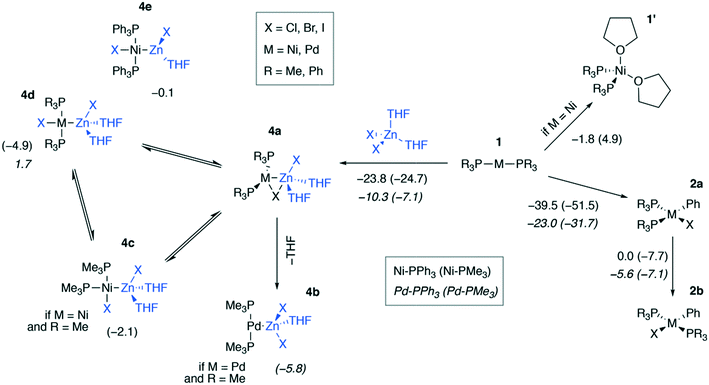

Fig. 3 Possible transformations of under-coordinated species [Ni(PR₃)₂] and [Pd(PR₃)₂] in THF involving ZnX₂ and PhX. The Gibbs free energies of the elementary transformations computed at the B97-3c level for the case of X = I are given under the corresponding arrows, and the Gibbs free energies of the 4a → 4b–e transformations are shown above the corresponding structures. Upper inset: Functionalities varied in the model systems, see the ESI† for X = Cl, I. Lower inset (used notation): ΔG values in Ni systems are given in regular typeface, and ΔG values in Pd systems are in italic typeface; PPh₃ and PMe₃ ligand systems – without and in parentheses, respectively.

The by-product of the Negishi reaction [(THF)₂ZnX₂] can bind to the catalytic species 1 to form intermediates 4a–e. The computed reaction Gibbs free energies for the 1 → 4a transformation are given in Fig. 3. The resulting intermediates 4a can isomerize to yield the intermetallic species 4b–e. Relaxed potential energy surface (PES) scans were performed at both chosen levels of theory with the C-PCM solvation model applied to estimate the kinetic favorability of the transformations (Fig. S1†). The estimated barriers were below ca. 7 kcal mol⁻¹ in all cases except one, namely, the 4c → 4d isomerization of [(THF)₂ZnCl][(PMe₃)₂PdCl], for which the estimated barrier at the TPSS-D3/DZ level was ∼15 kcal mol⁻¹. The relative stability of the intermediates 4a–e and the barriers depended on the structure of the species and the DFT method employed (see the ESI† for all PES scan results).

While Zn(II) species are known to be Lewis acids, and both Ni and Pd are known to be Lewis bases,²⁶ electronic structure analysis is desirable to assign intermetallic species 4a–e to the class of metal-only Lewis pairs. This was accomplished by carrying out a topological analysis of the electron density in complexes 4a, 4b, and 4c in the framework of QTAIM. Bond critical points (BCPs) corresponding to Zn–M bonding interactions were found in all three types of intermediates (see Fig. 4 for contour maps of the electron density gradient paths in three representative cases). The QTAIM analysis showed Ni–Zn and Pd–Zn bonds to be similar to the donor-acceptor type (see ref. 84 and 85 for the used classification), and the corresponding bond ellipticity (ε_b) values were close to zero, indicating σ-symmetry (see Table 1 for the selected cases and Table S57† for all obtained QTAIM data).

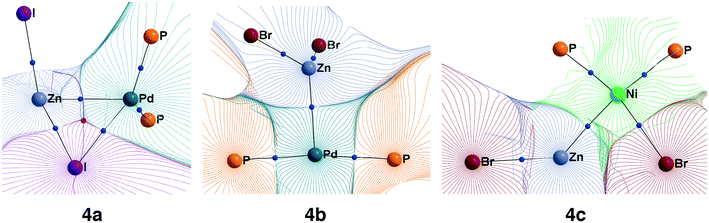Fig. 4 Basin gradient paths in representative M–Zn-species with PMe₃-ligands (see Fig. 3). Bond critical points are blue spheres, and ring critical points are red spheres.

Table 1 QTAIM parameters of the M–Zn-bonding interaction (M = Ni, Pd) in 4a–c

Intermediate	ρ b	∇^2ρb			δ(M,Zn)	ε b	q(M)^a	q(Zn)^a
ρ b is the electron density in the BCP, ∇^2ρb is the electron density Laplacian in the BCP, εb is the bond ellipticity, G(rb) is the positive definite kinetic energy density in the BCP, he(rb) is the electron energy density in the BCP, δ(M,Zn) is the QTAIM delocalization index of the M–Zn bond, and q(M) and q(Zn) are Ni (Pd) and Zn Bader charges, respectively.a Δq(A) values (the Bader charge increase or decrease upon the formation of the intermetallic species) are in parentheses.b Automatic choice of the integration algorithm (AIMAll default, see Computational details in the ESI).
L = PPh3
4a; M = Ni; X = Br^b	0.05	0.07	0.62	−0.24	0.49	0.06	0.07 (0.10)	1.02 (−0.09)
4a; M = Pd; X = Br^b	0.04	0.08	0.65	−0.17	0.36	0.12	−0.15 (0.08)	1.07 (−0.04)
L = PMe3
4c; M = Ni; X = Br	0.06	0.07	0.57	−0.26	0.65	0.05	0.07 (0.19)	0.85 (−0.26)
4b; M = Pd; X = Br	0.05	0.12	0.74	−0.18	0.57	0.01	−0.23 (0.04)	0.93 (−0.17)
4c; M = Ni; X = I	0.06	0.08	0.59	−0.26	0.65	0.03	0.01 (0.12)	0.79 (−0.17)
4a; M = Pd; X = I	0.05	0.10	0.71	−0.19	0.48	0.03	−0.22 (0.05)	0.93 (−0.03)

---

The formation of the intermediate 4c led to the oxidation of the Ni center, which we associate with the migration of X to Ni. On the other hand, no migration of X from Zn to Pd occurred upon 4b formation, and no oxidation of the Pd center was observed, accordingly. We observed the decrease of the positive charge on the Zn center. In 4b, we attribute this to the ligand migration and the associated metal–metal redox process, whereas in the case of 4b this effect is likely due to the detachment of the THF ligand. A cyclic M–Zn–X-moiety was found in 4a (see the corresponding ring BCP in Fig. 4), and the oxidation of Zn atoms upon 4a formation was much less pronounced than in the case of 4b and 4c (Table 1). To summarize, the formation of the intermetallic adducts upon the interaction of [(THF)₂Zn(II)X₂] with the complexes [Ni(0)(PR₃)₂] and [Pd(0)(PR₃)₂] is exergonic. Only the Pd–Zn complex 4b can strictly be ascribed to metal-only Lewis pairs. The formation of the other intermetallic complexes formally involves redox processes within the metal–metal moiety; therefore, they cannot be attributed to this class of compounds.

The results in Fig. 3 show that the oxidative addition (OA) of PhI (1 → 2a) in the Ni and Pd systems is more exergonic than the formation of intermetallic species 4a–e. Considering all modeled cases (including X = Cl, Br; see the ESI†), the 1 → 4a–e reactions are at least 19.0 kcal mol⁻¹ less exergonic than the competing OA processes 1 → 2a in all Ni systems, as modeled at the TPSS-D3/DZP level (varying L = PMe₃ and PPh₃, PhX = PhCl, PhBr, and PhI). The same 1 → 4a–e transformations are at least 19.0 kcal mol⁻¹ less exergonic than the 1 → 2a counterparts in the Pd systems (TPSS-D3/DZP, L = PMe₃ and PPh₃, PhX = PhCl, PhBr, and PhI). Comparing the exergonicity of the same processes, 1 → 4a–evs.1 → 2a, at the B97-3c level, the calculations predict the latter process to be more exergonic by 10.0 and 14.0 kcal mol⁻¹ in Ni and Pd systems, respectively.

The estimated activation barriers of the OA stage in the modeled systems did not exceed ∼12 kcal mol⁻¹ (see Fig. S2†). Therefore, species 2a and 2b can form readily. It should be noted that the estimated barriers of the 2a → 2b isomerization were as high as ca. 25 kcal mol⁻¹ (see the ESI†). Therefore, the formation of the unwanted 2b intermediate should be kinetically unfavorable in Pd systems. Generally, OA of aryl halides proceeds with moderate barriers that mostly do not exceed 25 kcal mol⁻¹ for Ni and Pd bis-phosphine complexes.^73,81 The OA step is often rate-determining in Pd-based cross-coupling systems.⁴ The rate determining role of OA was proposed in the case of the closely related Ar–Alk Negishi coupling, based on experimental data as well.¹⁴

3.3. Mechanism of product inhibition involving [(R₃P)₂ArM(II)X] species

The stability of intermediates 2a and 2b is well-known; in the case of M = Ni, these species are not only important intermediates in cross-coupling reactions but are also bench-stable (air-stable, in some cases) catalyst precursors.^78,86–882a and 2b were considered as the most stable among the intermediates in the cycle depicted in Fig. 1 (i.e. these species are viewed as the in-cycle catalyst resting states). Therefore, one may have an inhibiting effect in the case of formation of an off-cycle resting state from 2a and 2b. For example, in catalytic systems with a 1 : 1 metal to phosphine ratio, dimerization of [LArM(II)X] species or binding of water molecules leading to the formation of a resting state [LArMX]–H₂O may occur.^73,78 In the present work, we focus on catalytic systems with Ni and Pd bis-phosphine catalytic species, and the latter can form off-cycle resting states as well in Negishi cross-coupling, as we demonstrate below.

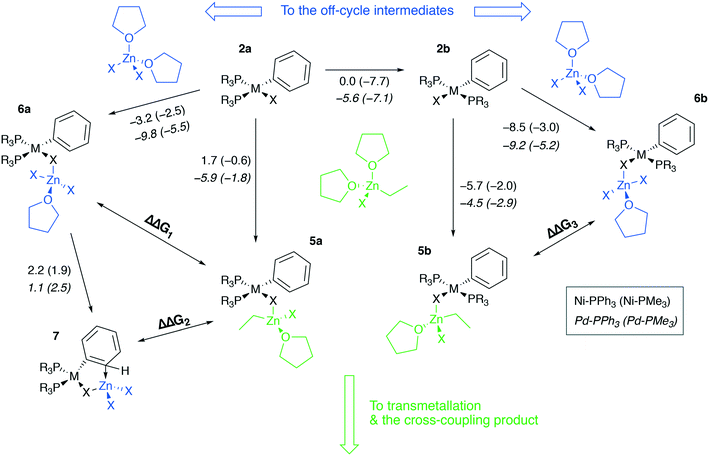
To proceed along the cross-coupling cycle, 2a and 2b react with a zinc reagent (here, [(THF)₂EtZnX], X = Cl, Br, I) in the transmetalation stage. This stage begins with the formation of a pre-transmetalation complex for which several possible structures of the complex were proposed in the computational studies. Here structures 5a and 5b were selected as representative models of a complex with bulky phosphine ligands, commonly employed in synthetic applications (Fig. 5). The same pre-transmetalation complexes were proposed in previous computational studies of the Negishi cross-coupling reaction involving Ni and Pd catalytic systems with bulky phosphine ligands.^31,81

Fig. 5 Competitive binding of [(THF)₂ZnX₂] and [(THF)₂EtZnX] to cis-[L₂PhM(II)X] and trans-[L₂PhM(II)X], M = Ni or Pd, L = PMe₃ or PPh₃. The elementary reaction free energies computed at the B97-3c level for the case of X = I are given under the corresponding arrows. Inset (used notation): ΔG values in Ni systems are given in regular typeface, and ΔG values in Pd systems are in italic typeface; PPh₃ and PMe₃ ligand systems – without and in parentheses, respectively.

Along with the formation of tetrahedral complexes [(THF)₂ZnX₂] and [(THF)₂RZnX] in THF solutions, zinc halides and organozinc halides form tetrahedral zincate species exchanging THF ligands to X⁻ anions. In the present case, 5a, 6a, 5b, 6b, and 7 may form, having the zincate-type moieties [(THF)EtZnX₂] and [(THF)ZnX₃], and releasing THF molecules. While 5a and 5b are the in-cycle intermediates, 6a and 6b are the off-cycle resting states competing with the former two counterparts. The thermodynamics of the 6a(b)vs.5a(b) competitive formation may be rationalized through the consideration of ΔΔG_1–3 values (Table 2, negative values indicate preferred formation of 6a(b) and 7).

Table 2 Computed ΔΔG values for the competitive formation of 6a(b) and 7vs.5a(b) in THF

	ΔΔG1: 2a → 6avs.2a → 5a		ΔΔG2: 2a → 7vs.2a → 5a		ΔΔG3: 2a → 6avs.2a → 5a
	M = Ni	M = Pd	M = Ni	M = Pd	M = Ni	M = Pd
a Without parentheses: computed at the B97-3c level. b In parentheses: computed at the TPSS-D3/DZP level. Negative values indicate that the 6a(b) and 7 formation is more exergonic than the formation of 5a(b).
X = Cl
L = PPh3	−3.2^a (−3.2)^b	−3.6 (−7.7)	−0.3 (−0.3)	−1.0 (−3.6)	−1.9 (−4.4)	−3.0 (−1.8)
L = PMe3	−2.6 (−3.1)	−2.1 (−3.8)	0.5 (0.4)	1.1 (1.1)	−1.4 (−3.6)	−2.7 (−4.5)
X = Br
L = PPh3	−4.2 (−1.9)	−4.3 (−6.2)	−2.8 (−2.9)	−1.7 (−5.5)	−3.1 (−6.5)	−3.8 (−7.2)
L = PMe3	−3.1 (−2.4)	−0.6 (−5.1)	0.5 (−2.0)	0.9 (−4.4)	−1.6 (−2.5)	−3.3 (−10.1)
X = I
L = PPh3	−4.9 (−0.7)	−3.9 (−1.3)	−2.7 (−1.2)	−2.7 (−2.1)	−2.8 (−2.9)	−4.7 (−1.6)
L = PMe3	−1.9 (1.1)	−3.7 (−0.3)	0.0 (−0.1)	−1.2 (−0.2)	−1.0 (0.3)	−2.3 (−0.2)

---

Table 2 shows that the formation of the off-cycle intermediates 6a(b) is systematically more favorable (exergonic) than that of the pre-transmetalation complexes 5a(b). The trans- complex 2b is thermodynamically preferred over the cis counterpart 2a; both 2a → 6a and 2b → 6b off-cycle processes are worth considering as the cis-intermediate 2a may represent a model case relevant to catalytic systems with bidentate phosphine ligands employed in cross-coupling catalysis.²¹ The Pd systems are somewhat more prone to the formation of the off-cycle resting states (columns 2 vs. 3, 7/12 cases; columns and 6 vs. 7, 10/12 cases). The complexes 7, having no THF molecules coordinated to the transition metal centers, are unstable in THF according to the computations at the B97-3c level (see the ESI†). Regarding the stability of 7 in THF, TPSS-D3/DZP calculations predict, on the contrary, the comparable stability of 2a and 7 in THF solution (the Gibbs free energies of the 2a → 7 transition ranged from −2.3 to −0.9 kcal mol⁻¹ for M = Ni and Pd, and X = Cl and Br, see the ESI†).

Another qualitative divergence between the B97-3c and TPSS-D3/DZP results was associated with the relative stability of the 5a, 6a, 5b, and 6b intermediates (see the ESI for the results). Particularly, the formation free energies of the intermediates increased in the order Cl < Br < I when calculated at the TPSS-D3/DZP level. Whereas for X = Cl, the formation of 5a and 6a from 2a, as well as of 5b and 6b from 2b, was exergonic in almost all cases, for X = I, the reactions 2a → 5a, 2a → 6a, 2b → 5b, and 2b → 6b were all endergonic. For X = Br, 2a → 6a and 2b → 6b were exergonic (0 to −3.2 kcal mol⁻¹, M = Ni and Pd, L = PMe₃ and PPh₃, TPSS-D3/DZP), while 2a → 5a and 2b → 5b were predicted to be endergonic (0.2 to 6.8 kcal mol⁻¹). The calculations at the B97-3c level did not reveal these stability trends for 5a, 6a, 5b, and 6b as a function of X.

The computed ΔΔG_1–3 values vary within several kcal mol⁻¹, suggesting that the cross-coupling kinetics may be affected by the 6a, 7, and 6b formation. If we consider an equilibrium of A + B = C + D, the reaction free energy of 2 kcal mol⁻¹ already leads to the ∼100 : 1 concentration ratio between the components.³⁰ In our systems, for example, the 5b ⇌ 6b equilibrium (M = Pd, L = PPh₃, X = I, B97-3c) is shifted towards the off-cycle intermediate 6b (in line with the computed ΔΔG₃ value of −4.7 kcal mol⁻¹) which translates to the equilibrium [5b] to [6b] concentration ratio of ca. 1 : 3000 under ambient conditions. In such a way, the reaction by-product [(THF)₂ZnX₂] passivates the post-oxidative addition intermediates 2a and 2b and suppresses the formation of 5b. The concentration of the latter intermediate determines the transmetalation rate v_TMvia the equation:

v_TM = −k[5b].

Therefore, even values of ΔΔG_1–3 in the range of −1 to −5 kcal mol⁻¹ may indicate the possibility of product inhibition.

Zinc reagents [(THF)₂RZnX] are in excess to the reaction by-product [(THF)₂ZnX₂] in the initial stage of the reaction. Furthermore, zinc reagents are usually added in a three- to four-fold stochiometric excess to an RX coupling partner.²¹ Therefore, at the beginning of the reaction, in-cycle species 5a(b) form preferentially; at this stage product inhibition due to an accumulation of 6a(b) and, possibly, 7 is negligible. This is in line with the experimental study by Koszinowski et al. who showed that the reaction rate significantly decreases after ca. 60 s, evidencing the bimodal kinetics in the Ar–Alk-type Negishi coupling with the Pd–S–Phos catalytic system.¹⁴ Besides, the transmetalation step in the Negishi coupling was shown to be reversible.³³ Therefore, the reaction 3a(b) ⇌ 2a(b) → 6a(b) can potentially play a detrimental role by transforming the post-transmetalation intermediates 3a(b) to the off-cycle species.

3.4. Relative stability of lithium zincates in THF

A critical role of LiX additives in the Negishi reaction is generally recognized; it was concluded that their reaction-promoting effect is determined by the X⁻ anion.¹⁵ Higher-order zincates were proposed to form when a sufficient amount (usually, 2–4 equivalents) of the salt was added to the system.^14,15,36 If no salt promotor was added, the Ar–Alk-type coupling stopped after ca. 120 s (<20% conversion) despite an observed high initial reaction rate.¹⁴ Given the above discussion on the competitive formation of 5a(b) and 6a(b) intermediates, we propose an alternative explanation for the promoting effect of LiX additives.

Zinc atoms in ZnX₂ are more Lewis-acidic than Zn centers in RZnX.²⁵ At the same time, they both can form tetrahedral mono- and dianionic zincate species via binding to X⁻ anions.^15,25,77 Therefore, we propose that, in the presence of LiX salt, the 2a(b) → 6a(b) and 2a → 7 side reactions are prevented by the preferential formation of anionic zincates [(THF)ZnX₃]⁻ and [ZnX₄]²⁻. For the same reason, the more acidic [(THF)₂ZnX₂] by-product preferably binds to the post-oxidative addition intermediates 2a and 2bvia a bridging X group to yield intermetallic species such as 6a(b) and 7.

We estimated the relative stability of zincate forms of PhZnBr, EtZnBr, and ZnBr₂ in THF by modeling these species as contact ionic pairs with LiBr (Fig. 6, see ESI† section 5 for total energy values). The modeling of the ionic pairs was performed using the dispersion-corrected TPSS functional and the diffuse ma-def2-SVP basis set, to account for ionic Li–X bonding (see ESI† section 1 for Computational details). Calculations identified several Li binding modes in the ion pairs considered here. Li binding to [(THF)RZnBr₂]⁻, [(THF)ZnBr₃]⁻, and [ZnBr₄]²⁻ yields four-member Li–Br–Zn–Br ring structures (Fig. 6). Three-fold coordination of Li is realized with the di-anionic [RZnBr₃]²⁻. The binding of Li to the di-anionic zincates can occur via three μ₂-X groups or two μ₂-X groups and Li–Ph (Li–Me, if R = Et) interaction. Considering the Li–Ph interaction in more detail, Li formed a close contact of 2.36 Å with the C-1 atom of the Ph group in [PhZnBr₃]²⁻. In the [EtZnBr₃]Li₂ zincate, the Li formed a close contact with Me group (the C–Li distance is equal to 2.39 Å, and the H–Li distances are equal to 2.08 Å). The calculations pointed to the increase of the stability of the zincates in the order PhZnX < EtZnX < ZnX₂. Notably, this stability trend is more pronounced in the di-anionic species, compared to their mono-anionic counterparts (Fig. 6). Therefore, the addition of about 2 equivalents (relative to PhX, in our case) of LiX to the catalytic system can indeed block the inhibition by ZnX₂via their transformation to Li₂[ZnX₄].

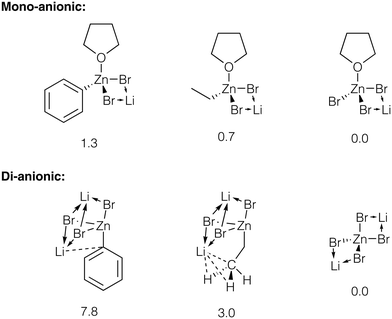Fig. 6 Strictures of the considered Li bromo-zincates. Relative energies are given under the structures, in kcal mol⁻¹, see ESI† sections 1 and 5 for details. Close contacts are shown with dotted lines, see text for discussion.

3.5. Mechanism of product inhibition in NHC-ligand catalytic systems

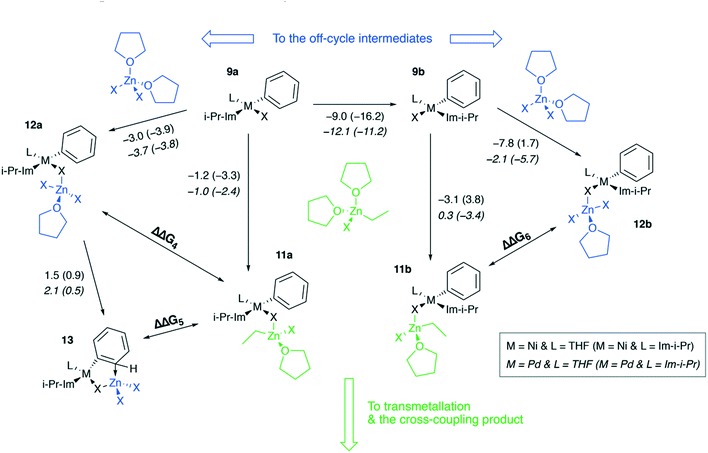
Ni and Pd catalytic systems with N-heterocyclic carbene (NHC) ligands are ubiquitous catalysts of the Negishi reaction.¹⁸ The formation of Zn–M(II)-intermetallic species can also take place in catalytic systems with NHC ligands (Fig. 7). Similarly, the 8 → 9a transformation is highly exergonic in mono-ligand Ni systems (TPSS-D3/DZP: −66.1 to −68.6 kcal mol⁻¹; B97-3c: −52.2 to −58.0 kcal mol⁻¹; X = Cl, Br, I; L = THF), as well as in their mono-ligand Pd counterparts (TPSS-D3/DZP: −35.2 to −39.6 kcal mol⁻¹; B97-3c: −27.1 to −34.6 kcal mol⁻¹; X = Cl, Br, I; L = THF), see the ESI.† The competing formation of the pre-transmetalation NHC complexes 11a(b) and the off-cycle intermetallic species 12a(b) and 13 can proceed (Fig. 8).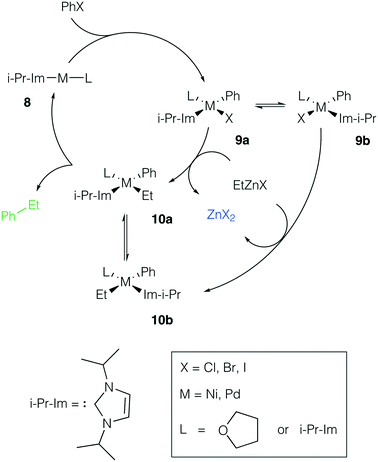

Fig. 7 Model catalytic cycle corresponding to the Negishi reaction between PhX and EtZnX in NHC-ligand systems. The inset shows the functionalities varied in the model systems, see the ESI† for all obtained results.

Fig. 8 Competitive binding of [(THF)₂ZnX₂] and [(THF)₂EtZnX] to cis-[L₂PhM(II)X] and trans-[L₂PhM(II)X], M = Ni, Pd, L = 1,3-diisopropylimidazol-2-ylidene or THF. The elementary reaction free energies, computed for the case of X = I at the B97-3c level, are given under the corresponding arrows. The inset shows the used notation.

The off-cycle resting states are more thermodynamically stable than the pre-transmetalation complexes, according to the computations at both B97-3c and TPSS-D3/DZP levels (Table S57†). This similarity between the M-NHC and M-PR₃ systems indicates that the proposed product inhibition mechanism is intrinsic to the Negishi cross-coupling reaction and does not depend on the metal or ligand choice. Therefore, we propose that LiX additives should play the same promoting role in the NHC-based catalytic systems. Namely, LiX reacts with the coupling by-product [(THF)₂ZnX₂] transforming it to non-inhibiting zincates [(THF)ZnX₃]⁻ and [ZnX₄]²⁻. Indeed, the importance of salt additives in NHC-based catalytic systems for the Negishi reaction was pointed out numerous times.^15,16,21,35

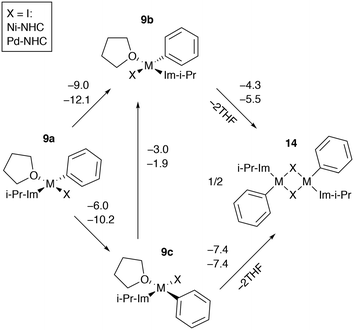
Dimerization of catalytic intermediates may proceed in mono-ligand M-NHC systems (Fig. 9). The species 9b and 9c, having X and THF ligands in the cis position, can undergo dimerization, releasing two weakly bound solvent molecules. While the process is exergonic in I-containing systems according to the B97-3c modeling results (Fig. 9), the formation of 14 from 9a–c is exergonic in almost all Ni and Pd systems with X = Cl or Br as well (modeled at the B97-3c and TPSS-D3/DZP levels, see Tables S7, S15–S17, S25, S33, S41–S43, S51†). Note that the B97-3c and TPSS-D3/DZP calculations gave qualitatively different results for Ni systems with X = I. Specifically, TPSS-D3/DZP predicted the formation of 14 from two equivalents of 9b to be endergonic by 2.1 kcal mol⁻¹ (Table S25†). Since 9b is the most stable intermediate among 9a–c, the endergonicity of the 9b → 14 transformation, modeled at TPSS-D3/DZP, may indicate that the dimerization cannot proceed in Ni-NHC systems with X = I so 9a and 9c preferably transform into 9b.

Fig. 9 Pathways of dimerization of mono-NHC species in THF. The elementary reaction free energies computed at the B97-3c level for the case of X = I are given above the corresponding arrows; the inset shows the used notation.

The formation of 14 in bis-ligated M-NHC systems would require the release of the second NHC from the transition metal centers. Such a dimerization process can be envisaged as a result of the NHC ligand degradation that has previously been reported by computational and experimental studies of Ni and Pd catalytic systems.^89–95 At the same time, a cross-coupling mechanism involving binuclear Ni complexes that resemble 14 was also proposed.⁹⁶ Further dedicated studies are necessary to clarify the role of 14 in the Negishi reaction, which is beyond the scope of this work.

4. Summary and conclusions

The presented computational results demonstrate the complexity of catalytic systems for the Negishi cross-coupling that emerges from the involvement of various Zn–Ni and Zn–Pd intermetallic species in the catalytic mechanism. Here possible associations of Ni and Pd catalytic intermediates with the reaction by-product ZnX₂ were investigated and the potential inhibiting role of the resulting bimetallic species was proposed. These reactions lead to the formation of off-cycle resting states in Ar–Alk coupling reactions. Oxidative addition of ArX (here modeled by PhX) to [M(0)L₂] is a highly exergonic process resulting in cis-[L₂PhM(II)X], which can further react with ZnX₂ to yield off-cycle Zn–M(II) intermetallic species. This transformation effectively hampers the necessary transmetalation step of the catalytic cycle.

The reaction by-product may also react with the [M(0)L₂] species, as we have shown for the case of the catalytic systems with PMe₃ and PPh₃ ligands. The PhX oxidative addition was significantly more exergonic than the reactions of ZnX₂ with [M(0)L₂] to form [(THF)₂ZnX][(PR₃)₂PdX]. Previous studies indicate that Zn reagents can inhibit the OA step of the cross-coupling catalytic cycle.²⁴ We hypothesize that in the Negishi reaction, in which oxidative addition is less exergonic (e.g., AlkX oxidative addition in the Alk–Alk coupling reactions), the formation of such intermetallic complexes [(THF)₂ZnX][(PR₃)₂PdX] may become thermodynamically favored over the catalytic OA path, thus invoking another product inhibition pathway. A detailed dedicated study of the associated oxidative addition paths over [(THF)₂ZnX][(PR₃)₂PdX] as well as the respective catalytic channels is desirable to establish a comprehensive mechanistic picture of the considered catalytic system.

In light of the proposed product inhibition mechanism, a promoting role of LiX additives in the Negishi coupling reaction can be clarified. The reaction by-product ZnX₂ is a Lewis acid having a high affinity towards the X⁻ anion of the additives. The conversion of the ZnX₂ by-product to coordinatively-saturated anionic halide complexes in excess of X⁻ can prevent the product inhibition in line with the experimental observations.¹⁴

To summarize, Negishi coupling is a well-established and efficient synthetic method; however, the understanding of its mechanism can still be improved. Targeted and rational design of catalytic systems would require knowing all significant mechanistic phenomena in a catalytic reaction such as interconversions of in-cycle intermediates, deactivation processes, and formation of catalyst's off-cycle resting states. Computational modeling enables us to predict new catalytic, as well as key non- and counter-catalytic, intermediates and deactivation paths. The off-cycle resting states in the present case are intermetallic electroneutral species bound with relatively weak coordination bonds. In this work, we studied the elementary transformations in the coordinating solvent THF and aimed to perform a mapping of possible elementary reactions. The formation of the intermetallic species involves solvent coordination/de-coordination, which can hardly be modeled without using explicit solvent models. In turn, this would require reaction path analysis using QM/MM MD or full AIMD modeling, which is prohibitively expensive, considering the hundreds of intermediates identified in this work. The mechanistic consideration of these intermetallic species requires the expansion of the mechanistic models beyond the simplified single-site/single-cycle catalytic models to allow for a more realistic catalytic model of the Negishi cross-coupling, which we believe to be a prerequisite for targeted catalyst design.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the Dutch Research Council for access to SurfSARA supercomputer facilities. Partial support from the Government of the Russian Federation (Grant 08-08) and the Ministry of Education and Science of Russian Federation (Project 11.1706.2017/4.6) is gratefully acknowledged. M. V. P. thanks Prof. Dr. Valentine Ananikov for useful discussions and mentorship.

References

1. V. Van Speybroeck, K. Hemelsoet, L. Joos, M. Waroquier, R. G. Bell and C. R. A. Catlow, Chem. Soc. Rev., 2015, 44, 7044.
2. T. Sperger, I. A. Sanhueza and F. Schoenebeck, Acc. Chem. Res., 2016, 49, 1311.
3. T. Sperger, H. C. Fisher and F. Schoenebeck, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2016, 6, 226.
4. T. Sperger, I. A. Sanhueza, I. Kalvet and F. Schoenebeck, Chem. Rev., 2015, 115, 9532.
5. Y. Lam, M. N. Grayson, M. C. Holland, A. Simon and K. N. Houk, Acc. Chem. Res., 2016, 49, 750.
6. D. Balcells and A. Nova, ACS Catal., 2018, 8, 3499.
7. Q. Peng, F. Duarte and R. S. Paton, Chem. Soc. Rev., 2016, 45, 6093.
8. E. A. Pidko, ACS Catal., 2017, 7, 4230–4234.
9. C. Poree and F. Schoenebeck, Acc. Chem. Res., 2017, 50, 605.
10. S. Hammes-Schiffer, Acc. Chem. Res., 2017, 50, 561.
11. D. J. Tantillo, Acc. Chem. Res., 2016, 49, 1079.
12. J. Jover and N. Fey, Chem. - Asian J., 2014, 9, 1714.
13. R. E. Plata and D. A. Singleton, J. Am. Chem. Soc., 2015, 137, 3811.
14. K. Böck, J. E. Feil, K. Karaghiosoff and K. Koszinowski, Chem. – Eur. J., 2015, 21, 5548.
15. H. N. Hunter, N. Hadei, V. Blagojevic, P. Patschinski, G. T. Achonduh, S. Avola, D. K. Bohme and M. G. Organ, Chem. – Eur. J., 2011, 17, 7845.
16. L. C. McCann, H. N. Hunter, J. A. C. Clyburne and M. G. Organ, Angew. Chem., Int. Ed., 2012, 51, 7024.
17. K. D. Vogiatzis, M. V. Polynski, J. K. Kirkland, J. Townsend, A. Hashemi, C. Liu and E. A. Pidko, Chem. Rev., 2019, 119, 2453.
18. D. Haas, J. M. Hammann, R. Greiner and P. Knochel, ACS Catal., 2016, 6, 1540.
19. E.-I. Negishi, X. Zeng, Z. Tan, M. Qian, Q. Hu and Z. Huang, in Metal-Catalyzed Cross-Coupling Reactions, Wiley-VCH Verlag GmbH, Weinheim, Germany, 2004, p. 815.
20. V. B. Phapale and D. J. Cárdenas, Chem. Soc. Rev., 2009, 38, 1598.
21. R. Jana, T. P. Pathak and M. S. Sigman, Chem. Rev., 2011, 111, 1417.
22. J. Magano and J. R. Dunetz, Chem. Rev., 2011, 111, 2177.
23. L. Kurti and B. Czako, Strategic Applications of Named Reactions in Organic Synthesis, Elsevier Science, 2005.
24. A. B. González-Pérez, R. Álvarez, O. N. Faza, Á. R. de Lera and J. M. Aurrecoechea, Organometallics, 2012, 31, 2053.
25. J. E. Fleckenstein and K. Koszinowski, Organometallics, 2011, 30, 5018.
26. J. Bauer, H. Braunschweig and R. D. Dewhurst, Chem. Rev., 2012, 112, 4329.
27. T. Bollermann, C. Gemel and R. A. Fischer, Coord. Chem. Rev., 2012, 256, 537.
28. M. García-Melchor, A. A. C. Braga, A. Lledós, G. Ujaque and F. Maseras, Acc. Chem. Res., 2013, 46, 2626.
29. K. J. Bonney and F. Schoenebeck, Chem. Soc. Rev., 2014, 43, 6609.
30. J. del Pozo, M. Pérez-Iglesias, R. Álvarez, A. Lledós, J. A. Casares and P. Espinet, ACS Catal., 2017, 7, 3575.
31. J. DelPozo, E. Gioria, J. A. Casares, R. Álvarez and P. Espinet, Organometallics, 2015, 34, 3120.
32. M. M. Hansmann, M. Pernpointner, R. Döpp and A. S. K. Hashmi, Chem. – Eur. J., 2013, 19, 15290.
33. B. Fuentes, M. García-Melchor, A. Lledós, F. Maseras, J. A. Casares, G. Ujaque and P. Espinet, Chem. – Eur. J., 2010, 16, 8596.
34. G. A. Chass, C. J. O'Brien, N. Hadei, E. A. B. Kantchev, W.-H. Mu, D.-C. Fang, A. C. Hopkinson, I. G. Csizmadia and M. G. Organ, Chem. – Eur. J., 2009, 15, 4281.
35. L. C. McCann and M. G. Organ, Angew. Chem., Int. Ed., 2014, 53, 4386.
36. G. T. Achonduh, N. Hadei, C. Valente, S. Avola, C. J. O'Brien and M. G. Organ, Chem. Commun., 2010, 46, 4109.
37. C. Valente, M. E. Belowich, N. Hadei and M. G. Organ, Eur. J. Org. Chem., 2010, 2010, 4343–4354.
38. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73.
39. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
40. J. G. Brandenburg, C. Bannwarth, A. Hansen and S. Grimme, J. Chem. Phys., 2018, 148, 064104.
41. J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401.
42. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297.
43. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456.
44. H. Kruse and S. Grimme, J. Chem. Phys., 2012, 136, 154101.
45. M. Chen, R. Craciun, N. Hoffman and D. A. Dixon, Inorg. Chem., 2012, 51, 13195.
46. M. Steinmetz and S. Grimme, ChemistryOpen, 2013, 2, 115.
47. T. Weymuth, E. P. A. Couzijn, P. Chen and M. Reiher, J. Chem. Theory Comput., 2014, 10, 3092.
48. S. Dohm, A. Hansen, M. Steinmetz, S. Grimme and M. P. Checinski, J. Chem. Theory Comput., 2018, 14, 2596.
49. E. J. Baerends, D. E. Ellis and P. Ros, Chem. Phys., 1973, 2, 41.
50. B. I. Dunlap, J. W. D. Connolly and J. R. Sabin, J. Chem. Phys., 1979, 71, 3396.
51. C. Van Alsenoy, J. Comput. Chem., 1988, 9, 620.
52. R. A. Kendall and H. A. Früchtl, Theor. Chim. Acta, 1997, 97, 158.
53. K. Eichkorn, F. Weigend, O. Treutler and R. Ahlrichs, Theor. Chim. Acta, 1997, 97, 119.
54. K. Eichkorn, O. Treutler, H. Öhm, M. Häser and R. Ahlrichs, Chem. Phys. Lett., 1995, 240, 283.
55. J. L. Whitten, J. Chem. Phys., 1973, 58, 4496.
56. D. Andrae, U. Häußermann, M. Dolg, H. Stoll and H. Preuß, Theor. Chim. Acta, 1990, 77, 123.
57. K. A. Peterson, J. Chem. Phys., 2003, 119, 11099.
58. V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995.
59. B. Wang and Z. Cao, J. Phys. Chem. A, 2010, 114, 12918.
60. R. B. Sunoj and M. Anand, Phys. Chem. Chem. Phys., 2012, 14, 12715.
61. L.-L. Han, S.-J. Li and D.-C. Fang, Phys. Chem. Chem. Phys., 2016, 18, 6182.
62. S. Grimme, Chem. – Eur. J., 2012, 18, 9955.
63. M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669.
64. J. N. Harvey, Faraday Discuss., 2010, 145, 487.
65. J. H. Jensen, Phys. Chem. Chem. Phys., 2015, 17, 12441.
66. R. E. Skyner, J. L. McDonagh, C. R. Groom, T. van Mourik and J. B. O. Mitchell, Phys. Chem. Chem. Phys., 2015, 17, 6174.
67. M. Besora, P. Vidossich, A. Lledós, G. Ujaque and F. Maseras, J. Phys. Chem. A, 2018, 122, 1392.
68. N. Hazari, P. R. Melvin and M. M. Beromi, Nat. Rev. Chem., 2017, 1, 0025.
69. C. A. Tolman, Chem. Rev., 1977, 77, 313.
70. A. Bittermann, D. Baskakov and W. A. Herrmann, Organometallics, 2009, 28, 5107.
71. C. L. Vélez, P. R. L. Markwick, R. L. Holland, A. G. DiPasquale, A. L. Rheingold and J. M. O'Connor, Organometallics, 2010, 29, 6695.
72. J. Li, L. Jin, C. Liu and A. Lei, Org. Chem. Front., 2014, 1, 50.
73. C. L. McMullin, N. Fey and J. N. Harvey, Dalton Trans., 2014, 43, 13545.
74. D. B. Eremin and V. P. Ananikov, Coord. Chem. Rev., 2017, 346, 2.
75. B. P. Carrow and J. F. Hartwig, J. Am. Chem. Soc., 2010, 132, 79.
76. R. H. Crabtree, Chem. Rev., 2015, 115, 127.
77. G. Zhang, J. Li, Y. Deng, J. T. Miller, A. J. Kropf, E. E. Bunel and A. Lei, Chem. Commun., 2014, 50, 8709.
78. M. Mohadjer Beromi, A. Nova, D. Balcells, A. M. Brasacchio, G. W. Brudvig, L. M. Guard, N. Hazari and D. J. Vinyard, J. Am. Chem. Soc., 2017, 139, 922.
79. S. Bajo, G. Laidlaw, A. R. Kennedy, S. Sproules and D. J. Nelson, Organometallics, 2017, 36, 1662.
80. D. D. Beattie, G. Lascoumettes, P. Kennepohl, J. A. Love and L. L. Schafer, Organometallics, 2018, 37, 1392.
81. E. Nicolas, A. Ohleier, F. D'Accriscio, A.-F. Pécharman, M. Demange, P. Ribagnac, J. Ballester, C. Gosmini and N. Mézailles, Chem. – Eur. J., 2015, 21, 7690.
82. C. M. Lavoie, R. McDonald, E. R. Johnson and M. Stradiotto, Adv. Synth. Catal., 2017, 359, 2972.
83. L. Iffland, A. Petuker, M. van Gastel and U.-P. Apfel, Inorganics, 2017, 5, 78.
84. P. Macchi, D. M. Proserpio and A. Sironi, J. Am. Chem. Soc., 1998, 120, 13429.
85. P. Macchi and A. Sironi, Coord. Chem. Rev., 2003, 238–239, 383.
86. E. A. Standley and T. F. Jamison, J. Am. Chem. Soc., 2013, 135, 1585.
87. J. D. Shields, E. E. Gray and A. G. Doyle, Org. Lett., 2015, 17, 2166.
88. J. Magano and S. Monfette, ACS Catal., 2015, 5, 3120.
89. A. V. Astakhov, O. V. Khazipov, E. S. Degtyareva, V. N. Khrustalev, V. M. Chernyshev and V. P. Ananikov, Organometallics, 2015, 34, 5759.
90. A. V. Astakhov, O. V. Khazipov, A. Y. Chernenko, D. V. Pasyukov, A. S. Kashin, E. G. Gordeev, V. N. Khrustalev, V. M. Chernyshev and V. P. Ananikov, Organometallics, 2017, 36, 1981.
91. O. V. Khazipov, M. A. Shevchenko, A. Y. Chernenko, A. V. Astakhov, D. V. Pasyukov, D. B. Eremin, Y. V. Zubavichus, V. N. Khrustalev, V. M. Chernyshev and V. P. Ananikov, Organometallics, 2018, 37, 1483.
92. E. G. Gordeev, D. B. Eremin, V. M. Chernyshev and V. P. Ananikov, Organometallics, 2018, 37, 787.
93. A. Y. Kostyukovich, A. M. Tsedilin, E. D. Sushchenko, D. B. Eremin, A. S. Kashin, M. A. Topchiy, A. F. Asachenko, M. S. Nechaev and V. P. Ananikov, Inorg. Chem. Front., 2019, 6, 482.
94. E. G. Gordeev and V. P. Ananikov, J. Comput. Chem., 2019, 40, 191.
95. V. M. Chernyshev, O. V. Khazipov, M. A. Shevchenko, A. Y. Chernenko, A. V. Astakhov, D. B. Eremin, D. V. Pasyukov, A. S. Kashin and V. P. Ananikov, Chem. Sci., 2018, 9, 5564.
96. K. Matsubara, H. Yamamoto, S. Miyazaki, T. Inatomi, K. Nonaka, Y. Koga, Y. Yamada, L. F. Veiros and K. Kirchner, Organometallics, 2017, 36, 255.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cy00752k

‡ Current address: Inorganic Systems Engineering Group, Department of Chemical Engineering, Delft University of Technology, Van der Maasweg 9, 2629 HZ Delft, The Netherlands.

---