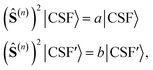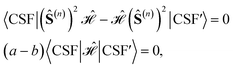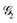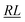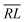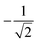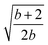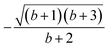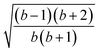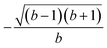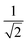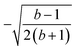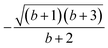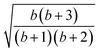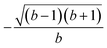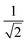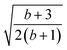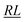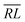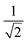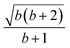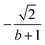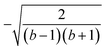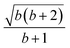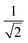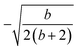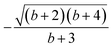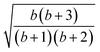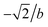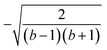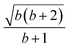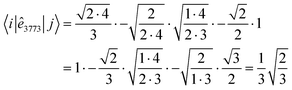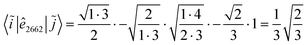Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Permutation symmetry in spin-adapted many-body wave functions†
Maru
Song
 a,
Ali
Alavi
ab and
Giovanni
Li Manni
a,
Ali
Alavi
ab and
Giovanni
Li Manni
 *a
*a
aElectronic Structure Theory Department, Max Planck Institute for Solid State Research, Heisenbergstraße 1, 70569 Stuttgart, Germany. E-mail: giovannilimanni@gmail.com; g.limanni@fkf.mpg.de
bYusuf Hamied Department of Chemistry, University of Cambridge, Lensfield Road, Cambridge CB2 1EW, UK
First published on 23rd April 2024
Abstract
In the domain of exchange-coupled polynuclear transition-metal (PNTM) clusters, local emergent symmetries exist which can be exploited to greatly increase the sparsity of the configuration interaction (CI) eigensolutions of such systems. Sparsity of the CI secular problem is revealed by exploring the site permutation space within spin-adapted many-body bases, and highly compressed wave functions may arise by finding optimal site orderings. However, the factorial cost of searching through the permutation space remains a bottleneck for clusters with a large number of metal centers. In this work, we explore ways to reduce the factorial scaling, by combining permutation and point group symmetry arguments, and using commutation relations between cumulative partial spin and the Hamiltonian operators, 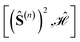 . Certain site orderings lead to commuting operators, from which more sparse wave functions arise. Two graphical strategies will be discussed, one to rapidly evaluate the commutators of interest, and one in the form of a tree search algorithm to predict how many and which distinct site permutations are to be analyzed, eliminating redundancies in the permutation space. Particularly interesting is the case of the singlet spin states for which an additional reversal symmetry can be utilized to further reduce the number of distinct site permutations.
. Certain site orderings lead to commuting operators, from which more sparse wave functions arise. Two graphical strategies will be discussed, one to rapidly evaluate the commutators of interest, and one in the form of a tree search algorithm to predict how many and which distinct site permutations are to be analyzed, eliminating redundancies in the permutation space. Particularly interesting is the case of the singlet spin states for which an additional reversal symmetry can be utilized to further reduce the number of distinct site permutations.
Understanding the ground- and excited-state electronic structures of polynuclear transition-metal (PNTM) clusters and their magnetic and catalytic properties represent important challenges in modern electronic structure theory.1
These compounds, abundant in nature, are the active sites of metalloproteins and make key enzymatic reactions possible. For example, FeS clusters are at the core of the nitrogenases, enzymes responsible for the nitrogen fixation process for the production of ammonia derivatives in soil and water;2–10 the oxygen evolving complex (OEC) in photosystem II consists of a CaMn3O4 cubane cluster, which is responsible for the water oxidation reaction within the more complex photosynthetic process.11–16 Biomimetic PNTM clusters also exist,17–20 such as the Co(II)3Er(III)(OR)4 cubane relevant in the context of the artificial water splitting process.21,22
PNTM clusters consist of transition-metal ions (lanthanide or actinide ions are also possible), at variable oxidation states, whose valence d (or f) orbitals are partially occupied. In general, the unpaired electrons at each magnetic site obey the first Hund's rule and feature parallel spins. However, strong ligand field effects may cause some of the valence electrons to pair, effectively reducing the formal local spin. Unusual spin structures may also exist, arising from the combination of a metal center with commutable spins with radical ligands, such that strong entanglement between the spin states at the metal center and the ligands is observed (spinmerism, proposed as an extension of mesomerism to the spin degree of freedom).23–25
The local spins couple across the magnetic sites, leading to a plethora of energetically low electronic states.26 In this context, electronic states can be distinguished into collinear states, with spins across the sites parallel or anti-parallel aligned, and non-collinear states, with spin across magnetic centers interacting at an angle (in the simple angular momentum vector model).
In principle, quantum chemical simulations represent a convenient tool to rationalize at the atomic scale chemical properties of PNTM systems, and could effectively contribute to the design of man-made compounds of desired magnetic and/or catalytic properties. Collinear states are often well described by (broken-symmetry, BS) single determinantal wave functions, at the core of Kohn–Sham DFT,7,27–46 upon an adequate choice of the exchange–correlation functional. However, in general single-determinantal strategies fail in describing the non-collinear interactions across the magnetic centers,47,48 albeit techniques exist, such as non-collinear DFT,49–55 and the extended BS-DFT,46 that have shown some success.
Multiconfigurational techniques based on the concept of active space,56,57 such as CASSCF,58–67 CASPT2,68–72 RASSCF and RASPT2,73–81 GASSCF and GASPT2,73,82–87 SplitGAS,87–89 and MC-PDFT,90–100 can describe on equal footings collinear and non-collinear electronic states with the minimal number of assumptions. However, the curse of dimensionality, i.e., the exponential growth of the many-body basis with the size of the active space, limits the applicability of these strategies to active spaces with at most 18 electrons and 18 electrons, CAS(18,18).101–103 The all-ferric Fe(III)4S4 cubane with 5 unpaired electrons per metal center, would already require a minimal CAS(20,20) for a qualitatively correct description of the spin coupling across the four sites for all low-energy spin states, which is prohibitively expensive with conventional approaches. Malrieu's difference-dedicated CI (DDCI)104–113 has been used with some success to predict spin multiplets; however, DDCI wave functions also suffer from an exponential scaling, and the computational limits are rapidly reached. Important electron correlation effects such as the superexchange mechanism,114–117 and metal-to-ligand (or ligand-to-metal) charge-transfer excited states can be described qualitatively correctly only at the price of even larger active spaces, which include orbitals and electrons from the bridging ligand atoms.118–120 These forms of electron correlation have been discussed in the literature.121 Larger PNTM clusters, such as the P-cluster and the FeMo-cofactor (FeMo-co) with their eight transition-metal centers, make theoretical predictions based on multiconfigurational approaches even harder.122–131
Methods that approximate full-CI wave functions in large active spaces, such as density matrix renormalization group (DMRG),1,132–143 selected configuration interaction (Selected-CI),144–156 and stochastic strategies based on full-CI quantum Monte-Carlo (FCIQMC)26,64,86,102,103,118,120,157–174 have been developed and applied with some success to problems requiring large active space wave functions. Yet, the ability of these schemes to solve the CI secular problem within a chosen active space strongly depends on the compression of the eigensolutions, for example by exploiting sparsity of the Hamiltonian and its eigenstates (FCIQMC), or correlated dependencies of the CI coefficients (DMRG). In turn the wave function compression is affected by the chosen one-electron basis.175 In general, dense wave functions require larger bond dimension values in DMRG (M > 1 × 104), and larger number of stochastic particles (walkers) in FCIQMC (Nwalkers > 1 × 1010) to converge, values that are computationally prohibitive for routine computations.
In the context of exchange-coupled PNTM complexes, including Fe(III)4S4 and Co(II)3Er(III)(OR)4, algorithms have been advised within DMRG to unitarily transform the active molecular orbitals (MO) into one-electron bases that are more conducive to fast convergence with respect to the M value.176,177 Similarly, within the spin-adapted FCIQMC algorithm based on the graphical unitary group approach (GUGA),118,178–184 MO transformations have been identified that increase the sparsity of the CI Hamiltonian and the corresponding ground- and excited-state eigenvectors, dramatically favoring the convergence of FCIQMC with respect to the walker numbers.26,86,118,119,170,185,186 It has numerically been shown that MO transformations that are optimal for DMRG differ from the ones that are optimal for GUGA-FCIQMC.185,186 In the case of FCIQMC, large active space calculations, correlating up to 44 electrons in 32 orbitals for the Fe(III)4S4 cubane, CAS(44,32),119,170 and up to 56 electrons in 56 orbitals for a Co(II)3Er(III)(OR)4 cubane, CAS(56,56),186 have been performed at a relatively lower walker number for specific orbital orderings.
Orbital (site) orderings can be identified that lead to sparse CI Hamiltonian matrices with a unique (quasi) block diagonal structure, when expressed in spin-adapted bases. Precisely this block diagonal structure minimizes the mixing of CSFs, from which the sparse wave functions arise. Also, in virtue of the blocking it has been possible to selectively target excited states.170
Using general model Heisenberg Hamiltonian operators187–192 for clusters of various dimensions, shapes, and local spin value at each magnetic site (in general Slocal > 1/2), Li Manni and co-workers193 have identified the rationale behind the wave function sparsity and the blocking of the CI Hamiltonian matrix in the commutation relations between cumulative partial spin operators,
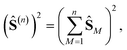 | (1) |
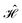 . The choice of the Heisenberg model Hamiltonian is two-fold. First, Heisenberg models describe the magnetic interactions in exchange-coupled PNTM clusters with a high degree of accuracy, and any valuable observation in terms of sparsity can be promptly transferred from the Heisenberg model to the full ab initio Hamiltonian.26,118,170,185,193 Moreover, site reordering is relevant only for open-shell electronic configurations, and its effects in terms of sparsity become more important as the number of unpaired electron (seniority) increases; from this point of view the Heisenberg model is most suited as the CI space consists exclusively of unpaired electrons.
. The choice of the Heisenberg model Hamiltonian is two-fold. First, Heisenberg models describe the magnetic interactions in exchange-coupled PNTM clusters with a high degree of accuracy, and any valuable observation in terms of sparsity can be promptly transferred from the Heisenberg model to the full ab initio Hamiltonian.26,118,170,185,193 Moreover, site reordering is relevant only for open-shell electronic configurations, and its effects in terms of sparsity become more important as the number of unpaired electron (seniority) increases; from this point of view the Heisenberg model is most suited as the CI space consists exclusively of unpaired electrons.
Specific site orderings may lead to vanishing commutators
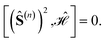 | (2) |
Considering that the smallest relevant partial spin operator is the one of a single site, (Ŝ(1))2, and that a CSF can be eigenfunction of such operator only if orbitals (and their electrons) residing on one magnetic center are adjacent, the grouping of orbitals on each site will always be assumed in the remainder of this document. Therefore, the permutation space to be investigated scales as N!, where N is the number of magnetic centers, and the search for optimal site orderings becomes rapidly computational demanding for clusters with an increasingly larger number of magnetic sites. Permutation and point group symmetries can be exploited to substantially reduce the search for site orderings that maximize wave function sparsity. This represents the main focus of the present work.
Site ordering not only affects the sparsity of the CI Hamiltonian matrix of exchange-coupled systems; in recent literature, its role has been discussed in the context of the Jordan–Wigner transformation for converting systems of spins into systems of fermions and vice versa; and in that context an extended Jordan–Wigner transformation has been proposed to circumvent this dependency.194,195
1 Commutators between partial spin and Hamiltonian operators
The connection between site ordering, partial spin operators, commutators and blocking of the CI Hamiltonian matrix in spin-adapted bases is quite remarkable, and it emerges from the well-known cumulative spin couplings of the GUGA method, which we briefly recall below.As in other genealogically constructed spin eigenfunctions,196 in GUGA, the spin of each individual electron is coupled to all previous ones in a cumulative manner; therefore, each CSF is by construction an eigensolution of any cumulative partial spin operator (not necessarily over magnetic sites). In the context of exchange-coupled PNTM clusters, it is reasonable to classify CSFs on the basis of their expectation values over the cumulative partial spin operators of the magnetic sites. The following CSFs
| |uuu,uud,ddd〉, |uuu,udu,ddd〉, |uuu,udd,udd〉, | (3) |
If we consider two CSFs with different eigenvalues (a ≠ b) over (Ŝ(n))2
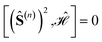 , we may write
, we may writeand since a ≠ b, it must be deduced that
 from which the block diagonal structure of the Hamiltonian matrix arises. In the example above, this well-known property of commuting operators197 would imply that CSFs with different (ŜAB)2 expectation values will not couple over
from which the block diagonal structure of the Hamiltonian matrix arises. In the example above, this well-known property of commuting operators197 would imply that CSFs with different (ŜAB)2 expectation values will not couple over 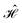 , and the CI Hamiltonian matrix will exhibit a blocked structure over the (ŜAB)2 expectation values. Thus, it is pivotal to establish commutation relations between cumulative partial spin and the Hamiltonian operators for different site orderings to understand and gain control over the structure and sparsity of the Hamiltonian matrix.
, and the CI Hamiltonian matrix will exhibit a blocked structure over the (ŜAB)2 expectation values. Thus, it is pivotal to establish commutation relations between cumulative partial spin and the Hamiltonian operators for different site orderings to understand and gain control over the structure and sparsity of the Hamiltonian matrix.
Considering that often magnetic interactions in exchange-coupled PNTM clusters are well described by Heisenberg models, and that for the Heisenberg model the evaluation of the above mentioned commutators is relatively easy, we will describe commutation relations and blocking on the basis of these models; and, in virtue of the correspondence between the two Hamiltonian operators, any insight gained over the simpler model can be transferred in first approximation to the more complex ab initio Hamiltonian. The strategy of transferring information from a simple model to a more complex one in the context of wave function compression has been already utilized in previous works.118,170,193 It is to be noted that, in general, exchange-coupled PNTM clusters exhibit local spin Slocal > 1/2, and the analysis below will deal with this general case, rather than specific examples with, say, S = 1/2 Heisenberg models.
Although Heisenberg models only approximately describe the full ab initio Hamiltonians of molecules, they are useful to understand the effect of orbital orderings on wave function compression. This is attributed to the fact that only u and d couplings are involved in wave function compression. Empty and doubly occupied orbitals are invariant under orbital orderings. This implies that CSFs with high seniority contribute more than low seniority CSFs to the wave function compression effects, as shown in Figure SI.1.† As an edge case, zero seniority CSFs are merely single Slater determinants, that are not affected by the ordering in which orbitals are coupled.
Thus, rather than focusing on ab initio Hamiltonians, we simplify the problem by restricting our analysis to Heisenberg models, which still hold the essential features of wave function compression via orbital orderings. As illustrated with a Co(II)3Er(III)(OR)4 cubane cluster in Section 5, our analysis on Heisenberg models can be easily extended to ab initio systems.
It is important to highlight that already Shavitt compared CI expansions based on different orbital transformations.198 Unfortunately, the orbital transformations he suggested and explored and the chemical systems investigated were not conducive to any major advantage in terms of compression, or reduced coupling (sparsity), and no other work followed. In contrast, in the case of exchange-coupled PNTM clusters the compression effects that follow localizations (in the case of ab initio models, based on molecular orbitals) and site reorderings are dramatic, with many orders of magnitude reduction of the non-vanishing coefficients in the CI expansion. This wave function compression is particularly appealing for methods that take advantage of the sparsity, including FCIQMC, and thus worth investigating.
In the following we summarize two approaches to calculate the 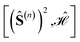 commutators, the conventional algebraic approach based on the Levi-Civita symbols, and a faster graphical approach.
commutators, the conventional algebraic approach based on the Levi-Civita symbols, and a faster graphical approach.
1.1 Levi-Civita approach
The commutator between a generalized Heisenberg Hamiltonian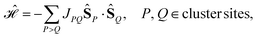 | (4) |
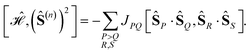 | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) j ∈ {x,y,z}),
j ∈ {x,y,z}),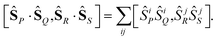 | (6) |
[Â![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) ,Ĉ ,Ĉ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) ] = ĈÂ[ ] = ĈÂ[![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) , ,![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) ] + Ĉ[Â, ] + Ĉ[Â,![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) ] ]![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) + Â[ + Â[![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) ,Ĉ] ,Ĉ]![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) + [Â,Ĉ] + [Â,Ĉ]![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) , , | (7) |
Considering commutation relations of local spin operators [ŜiP,ŜjQ] = iδPQεijkŜkP, from angular momentum theory,199eqn (7) suggests that non-vanishing commutators are of the form
| [ŜP·ŜQ,ŜR·ŜX], | (8) |
![[T with combining circumflex]](https://www.rsc.org/images/entities/b_char_0054_0302.gif) ABC,
ABC,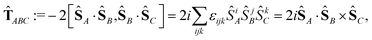 | (9) |
| (ŜA + ŜB)2 = (ŜA)2 + (ŜB)2 + 2(ŜA·ŜB). | (10) |
![[T with combining circumflex]](https://www.rsc.org/images/entities/b_char_0054_0302.gif) ABC is zero unless there are three different subscripts, (ABC). Changing the order of the subscripts results in a factor of (−1)p, where p is the number of pairwise swaps of the subscripts to recover the original (ABC) order. For example,
ABC is zero unless there are three different subscripts, (ABC). Changing the order of the subscripts results in a factor of (−1)p, where p is the number of pairwise swaps of the subscripts to recover the original (ABC) order. For example, ![[T with combining circumflex]](https://www.rsc.org/images/entities/b_char_0054_0302.gif) ABC =
ABC = ![[T with combining circumflex]](https://www.rsc.org/images/entities/b_char_0054_0302.gif) BCA = −
BCA = −![[T with combining circumflex]](https://www.rsc.org/images/entities/b_char_0054_0302.gif) BAC.
BAC.
We consider the Heisenberg Hamiltonian operator of an isosceles triangle as an example
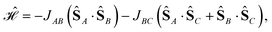 | (11) |
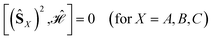 | (12) |
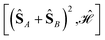 can be simplified, considering that (ŜA + ŜB)2 = (ŜA)2 + (ŜB)2 + 2(ŜA·ŜB) and that eqn (12) applies. Thus,
can be simplified, considering that (ŜA + ŜB)2 = (ŜA)2 + (ŜB)2 + 2(ŜA·ŜB) and that eqn (12) applies. Thus,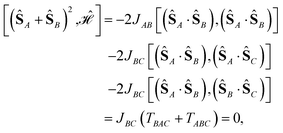 | (13) |
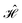 will be compressed.
will be compressed.
In the ACB ordering all CSFs will be eigenfunctions of the operator (ŜA + ŜC)2. The following commutator would be of interest
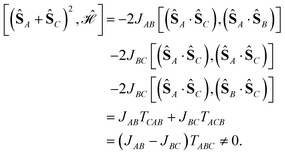 | (14) |
1.2 Graphical approach
The observations from Section 1.1 enable a convenient graphical strategy to evaluate commutators between cumulative partial spin and the Heisenberg Hamiltonian operators , by relying on the triangle rules summarized in Algorithm 1.
, by relying on the triangle rules summarized in Algorithm 1.For a given ordering of subscripts, say IJK in eqn (15), the coupling constant, JJK, between the site K in  and the site to its left in the subscripts (J in the case of IJK subscripts) has a positive sign, while the coupling constant JIK with the other site, I, has a negative sign.
and the site to its left in the subscripts (J in the case of IJK subscripts) has a positive sign, while the coupling constant JIK with the other site, I, has a negative sign.
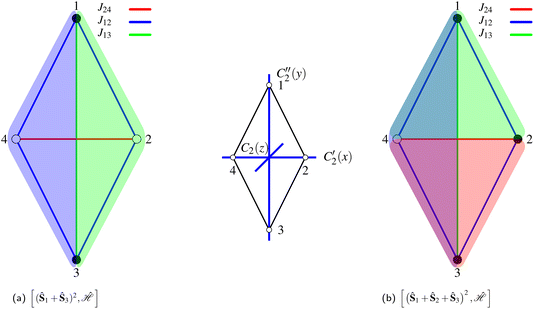
As an example of the applicability of the graphical method, a four-site rhombus cluster is considered (Fig. 1). In calculating 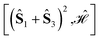 , following Algorithm 1 we identify two nodes belonging to
, following Algorithm 1 we identify two nodes belonging to 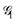 ({1,3}) and two nodes belonging to
({1,3}) and two nodes belonging to 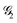 ({2,4}). From the two sets, two triangles can be formed, namely (132) and (134), which are marked in green and blue in Fig. 1a, respectively. The two triangles identify the entries in the summation in eqn (15) (see Algorithm 2). Similarly, in calculating
({2,4}). From the two sets, two triangles can be formed, namely (132) and (134), which are marked in green and blue in Fig. 1a, respectively. The two triangles identify the entries in the summation in eqn (15) (see Algorithm 2). Similarly, in calculating 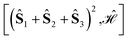 , the two groups
, the two groups 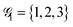 and
and 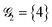 are identified, from which three triangles can be drawn, namely (124), (234) and (134) (different colors in Fig. 1b), corresponding to the three summands in Algorithm 3.
are identified, from which three triangles can be drawn, namely (124), (234) and (134) (different colors in Fig. 1b), corresponding to the three summands in Algorithm 3.
Eqn (15) shows that a source of (quasi) vanishing commutators is the cancellation of pairs of magnetic coupling constants with the same (or close) value, when an appropriate orbital/site ordering is chosen; thus, generally wave function compression can be achieved both for ferromagnetic and antiferromagnetic interactions, as long as an orbital/site ordering exists that leads to such cancellation.
2 Permutation symmetry within the Hamiltonian
While in the previous section a graphical procedure has been discussed to access the commutators between cumulative partial spin and the Hamiltonian operators, in this section the reduction of the dimensionality of the permutation space is discussed on the basis of the internal symmetries of the Hamiltonian operator. Two forms of Heisenberg Hamiltonian operators will be utilized, one in which the Hamiltonian operator commutes with all cumulative partial spin operator (Section 2.1), and a less strict one that commutes only with the first m cumulative spins (Section 2.2).2.1 Hamiltonian commuting with all cumulative partial spins
A general expression for a Heisenberg Hamiltonian that commutes with all cumulative partial spin operators follows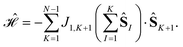 | (16) |
The Heisenberg Hamiltonian operator of the isosceles triangle and of the 4-site pyramidal structure (see Fig. 2) feature this form of Hamiltonian operator.
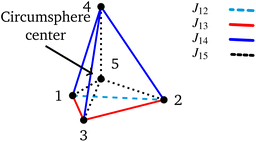 | ||
| Fig. 2 Pyramidal structure that fulfills eqn (16). Notice that the base of the pyramid is an isosceles triangle and the apex (vertex 4) is equally spaced from the vertices of the base (1, 2 and 3). In the middle of the pyramid the circumsphere center is also marked for a 5-site cluster that fulfills eqn (16). | ||
In order to obtain an isosceles triangle, given the first two sites, 1 and 2, the third site, 3, must reside in the plane dividing the base in two equal parts and perpendicular to the 12 direction (a two-dimensional degree of freedom). The 4-site polyhedron that corresponds to the Hamiltonian operator of eqn (16) is obtained by adding to the isosceles triangle a fourth point residing on the line passing from the triangle's circumcenter and perpendicular to the triangle plane (a one-dimensional degree of freedom). On the basis of geometrical criteria, a 5-site system featuring a Hamiltonian as given by eqn (16) is also possible; starting from the 4-site polyhedron of Fig. 2 the fifth site can only be uniquely located at the center of the circumsphere (no degree of freedom). It is clear that on the basis of geometrical considerations, a 6-site cluster that fulfills the conditions of the Hamiltonian operator of eqn (16) cannot exist, as a point in the three-dimensional space that is equally spaced from all previous 5 sites does not exists. In molecular clusters the magnetic coupling constants are not only dependent on the geometrical features of the cluster, but can also be affected by environmental effects, and ultimately magnetic symmetries may differ from the geometric ones. It is therefore relevant, for pure amusement, to investigate whether such a highly symmetric 6-site PNTM cluster could exist whose Hamiltonian features symmetries that go beyond the fundamental geometrical limits. Such a system would have an astonishingly sparse Hamiltonian matrix if expressed in a cumulatively spin-adapted basis.
For a 4-site pyramidal cluster (Fig. 2), eqn (16) reads as
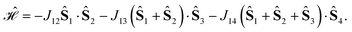 | (17) |
Are there site permutations equivalent to (1234) in terms of retaining vanishing commutation relations? From inspection of eqn (17), it emerges that upon (12) permutation, all cumulative partial spin operators still commute with the Hamiltonian operator, making the (2134) site ordering identical to (1234); this equivalence arises from the commutativity of dot products, i.e., Ŝi·Ŝj = Ŝj·Ŝi. Any other permutation would lead to one or more non-vanishing commutators, thus compromising the block structure of the corresponding Hamiltonian matrix and the sparsity of the corresponding eigensolutions.
2.2 Less constrained Hamiltonians
Model Hamiltonians may also exist that commute only with the first m cumulative partial spin operators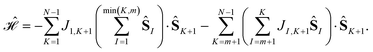 | (18) |
The 4-site square model Hamiltonian,
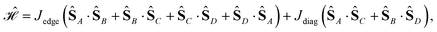 | (19) |
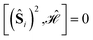 , may lead to important sparsity, in virtue of the separation of CSFs fulfilling and violating the first Hund's rule.
, may lead to important sparsity, in virtue of the separation of CSFs fulfilling and violating the first Hund's rule.
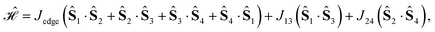 | (20) |
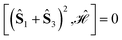 , for J12 = J23 and J34 = J14, and it is to be preferred over the (1234) ordering, which instead does not exhibit such a vanishing commutation relation.
, for J12 = J23 and J34 = J14, and it is to be preferred over the (1234) ordering, which instead does not exhibit such a vanishing commutation relation.
The permutation group of the rhombus is the D2dihedral group of order h = 4, which is made of the identity (E) and the three C2 rotations around the Cartesian axes (Fig. 1), and it is to be distinguished from the D2h point group symmetry the system belongs to. The list of N!/h = 6 symmetrically non-equivalent site permutations consists of the (1234), (2314), (2341), (1243), (1324) and (2413) orderings. These site orderings are listed in separate columns in Table 1, together with the symmetry equivalent site orderings that are obtained by applying the symmetry operations of the D2 dihedral group. In Table 1, an Sloc = 3/2 has been utilized (see Table SI.1 in the ESI† for Sloc = 1/2). The level of compression (measured by the L4-norm of the eigenvectors) as a function of different site orderings, for the energetically lowest states with total spin Stot = 0,1,3, are also reported in Table 1, for the geometry depicted in Fig. 1.
| Sym. elem. | Symmetry non-equivalent site orderings | |||||
|---|---|---|---|---|---|---|
| a The largest L4-norms are highlighted in bold and indicate the best site orderings. b We use J12 = J23 = J34 = J14 = −1.789, J13 = −1.000, and J24 = −2.000. | ||||||
| E | 1234 | 2314 | 2341 | 1243 | 1324 | 2413 |
| C 2(z) | 3412 | 4132 | 4123 | 3421 | 3142 | 4231 |
|
3214 | 2134 | 2143 | 3241 | 3124 | 2431 |
|
1432 | 4312 | 4321 | 1423 | 1342 | 4213 |
| L 4(Stot = 0) | 0.693 | 0.693 | 0.693 | 0.693 | 1.000 | 1.000 |
| L 4(Stot = 1) | 0.564 | 0.564 | 0.447 | 0.447 | 0.702 | 0.561 |
| L 4(Stot = 3) | 0.613 | 0.613 | 0.681 | 0.681 | 0.636 | 1.000 |
The L4-norm changes substantially as a function of the site ordering. For example, for Stot = 0, the ground-state wave function reaches its maximum compression, L4 = 1.00, for the (2413) and the (1324) orderings, indicating (within the cumulatively spin-adapted basis of CSFs) a single reference wave function. In contrast, the other four site orderings feature a less compact ground-state wave function with L4 = 0.69. This difference is to be attributed to the fact that for the (2413) ordering 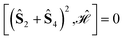 , while for any of the other site orderings, say (1243),
, while for any of the other site orderings, say (1243), 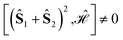 .
.
We also notice that while for (1324) and (2413) the commutators of the Hamiltonian operator with the 2-site partial spin operators vanish, i.e., 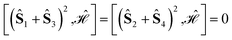 , the commutator with the three-site partial spin operator does not vanish, and it differs for the two site orderings, namely
, the commutator with the three-site partial spin operator does not vanish, and it differs for the two site orderings, namely 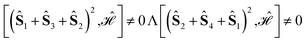 . It is precisely this difference that makes L4(1324) ≠ L4(2413) for Stot = 1,2. It is to be noted that there is no single site ordering that is best suited for all spin states. However, the (1324) and (2413) orderings are similarly best suited for all spin states, if we consider averaging the L4-norms over all spin states.
. It is precisely this difference that makes L4(1324) ≠ L4(2413) for Stot = 1,2. It is to be noted that there is no single site ordering that is best suited for all spin states. However, the (1324) and (2413) orderings are similarly best suited for all spin states, if we consider averaging the L4-norms over all spin states.
While identical eigenvectors are to be expected for point group symmetry equivalent site orderings, Table 1 shows that eigenvectors with identical L4-norm may also arise for symmetrically non-equivalent site orderings. For example, for the triplet spin state, Stot = 1, the six non-equivalent site orderings further group in four sets. This argument applies irrespective of the actual magnetic coupling constants considered. This is an interesting observation, indicating that additional symmetries exist that further reduce the number of non-equivalent site orderings. Thus, in the search for an optimal site ordering, instead of searching the entire permutation space (N! = 24) or in virtue of dihedral symmetry considerations, searching the reduced (N!/h = 6) space, it should be possible to further restrict the search over a yet smaller space. This space can be identified by a recursive procedure that relates permutations of tuples to the dihedral symmetry of the cluster and will be introduced in Section 3.
The dihedral group of the kite is D1 (h = 2), which is identical to C2 in non-standard orientation, where the 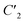 axis of the D1 group is chosen along the z and not the x direction. The symmetrically non-equivalent site permutations are thus N!/h = 12, as summarized in Table 2.
axis of the D1 group is chosen along the z and not the x direction. The symmetrically non-equivalent site permutations are thus N!/h = 12, as summarized in Table 2.
| Sym. elem. | Symmetry non-equivalent site orderings | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a L 4-norm calculated from the CI eigenvectors for each site ordering. b We use J12 = J14 = −1.638, J23 = J34 = −0.894, J13 = −0.741, and J24 = −1.000. | ||||||||||||
| E | 2314 | 3412 | 4132 | 1234 | 4123 | 1243 | 2341 | 3421 | 1324 | 3142 | 4231 | 2413 |
| C 2(z) | 4312 | 3214 | 2134 | 1432 | 2143 | 1423 | 4321 | 3241 | 1342 | 3124 | 2431 | 4213 |
| L 4(Stot = 0) | 0.693 | 0.693 | 0.693 | 0.693 | 0.693 | 0.693 | 0.693 | 0.693 | 1.000 | 1.000 | 1.000 | 1.000 |
| L 4(Stot = 1) | 0.420 | 0.420 | 0.549 | 0.549 | 0.554 | 0.554 | 0.507 | 0.507 | 0.676 | 0.676 | 0.661 | 0.799 |
| L 4(Stot = 3) | 0.650 | 0.650 | 0.672 | 0.672 | 0.682 | 0.682 | 0.821 | 0.821 | 0.409 | 0.409 | 0.822 | 0.984 |
The (2413) site ordering is the one that leads to maximum compression, because it is the only ordering for which the commutation relation 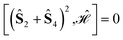 is fulfilled. This result is also graphically recognized (see Fig. 3) as the (24) pair splits the kite into two isosceles triangles, (241) and (243). As already observed for the rhombus case, symmetry non-equivalent site orderings further group on the basis of the L4-norm values, so that for example for the Stot = 1 and Stot = 3 states the 12 symmetry non-equivalent site orderings lead to only 7 groups on the basis of the L4-norm value. In Section 3, the further reduction of non-equivalent site permutations will be addressed and a recursive graphical procedure discussed.
is fulfilled. This result is also graphically recognized (see Fig. 3) as the (24) pair splits the kite into two isosceles triangles, (241) and (243). As already observed for the rhombus case, symmetry non-equivalent site orderings further group on the basis of the L4-norm values, so that for example for the Stot = 1 and Stot = 3 states the 12 symmetry non-equivalent site orderings lead to only 7 groups on the basis of the L4-norm value. In Section 3, the further reduction of non-equivalent site permutations will be addressed and a recursive graphical procedure discussed.
Moreover, in Tables 1 and 2 we also observe that the number of groups further reduces to only two for the Stot = 0 state. The further reduction of distinct site orderings for the singlet spin states is discussed in detail in Section 5.
3 Exploiting permutation symmetry via the tree search algorithm
In the previous sections it has been shown that different site orderings have an impact on the sparsity of the eigensolutions, as measured by the L4-norm of the many-body expansion, and that commutators between cumulative partial spin and the Hamiltonian operators can be used as descriptors of such sparsity. The number of non-equivalent site permutations can trivially be reduced by the order (h) of the point (or dihedral) group symmetry of the considered cluster (N!/h). However, it has been observed that site permutations not related by point group symmetry operations may still be grouped together under the metric of the L4-norm. Thus, it should be possible to further reduce the space of non-equivalent site permutations by exploiting additional internal symmetries of the Hamiltonian. A recursive graphical Tree Search Algorithm is presented, that is based on the commutators between cumulative partial spin and Hamiltonian operators, and that is relevant to identify the unique non-equivalent site orderings under the L4 metric, and thus to reduce the factorial scaling of the permutation space.A given site ordering, s, defines an array of commutators
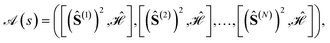 | (21) |
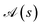 and
and 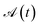 (where s and t define two site permutations), are considered equivalent if it is possible to establish equivalence between the commutators within the two arrays, otherwise numerically if the L4-norms (and thus the wave function structure) of the two site orderings, s and t, are identical. The size of the permutation space can then be reduced by excluding redundant site orderings leading to equivalent commutator arrays.
(where s and t define two site permutations), are considered equivalent if it is possible to establish equivalence between the commutators within the two arrays, otherwise numerically if the L4-norms (and thus the wave function structure) of the two site orderings, s and t, are identical. The size of the permutation space can then be reduced by excluding redundant site orderings leading to equivalent commutator arrays.
The effect of the point group symmetry on the array of commutators 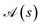 , as a whole, can be written as
, as a whole, can be written as
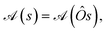 | (22) |
In order to establish the 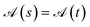 equivalence we proceed recursively by applying point group symmetry to the commutators
equivalence we proceed recursively by applying point group symmetry to the commutators 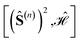 , for n values increasingly larger, n = 1, 2, 3, …, and so on. This is best done graphically, by means of a tree search algorithm. Fig. 4 shows the tree search algorithm applied to the kite cluster.
, for n values increasingly larger, n = 1, 2, 3, …, and so on. This is best done graphically, by means of a tree search algorithm. Fig. 4 shows the tree search algorithm applied to the kite cluster.
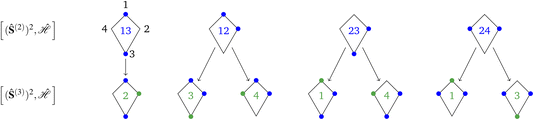 | ||
Fig. 4 Graphical representation (tree) of the cumulative partial spin operators and their commutation relation with  for a 4-site kite cluster. The seven nodes at the bottom correspond to the seven non-equivalent site orderings identified in Table 2 on the basis of the L4-norm. for a 4-site kite cluster. The seven nodes at the bottom correspond to the seven non-equivalent site orderings identified in Table 2 on the basis of the L4-norm. | ||
The tree is formed by nodes and in each node a subset of sites are marked with circles from which Ŝ(n) is built. For example, the top-left node of Fig. 4 represents the (Ŝ1 + Ŝ3)2 partial spin operator (nodes 1 and 3 are marked with blue circles), from which the 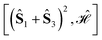 commutator is evaluated. Each row of the tree is characterized by a unique n value of the (Ŝ(n))2 partial spin operator, starting with n = 2 for the top row. Level-1 nodes are not considered as (Ŝ(1))2 always commutes with any Heisenberg Hamiltonian operators, implying that any choice of level-1 is equally good. We refer to the top row entries as level-2 nodes. Due to the commutativity of dot products, ŜA·ŜB = ŜB·ŜA, we do not need to consider the relative ordering of the first two sites, which are consequently marked in the same color.
commutator is evaluated. Each row of the tree is characterized by a unique n value of the (Ŝ(n))2 partial spin operator, starting with n = 2 for the top row. Level-1 nodes are not considered as (Ŝ(1))2 always commutes with any Heisenberg Hamiltonian operators, implying that any choice of level-1 is equally good. We refer to the top row entries as level-2 nodes. Due to the commutativity of dot products, ŜA·ŜB = ŜB·ŜA, we do not need to consider the relative ordering of the first two sites, which are consequently marked in the same color.
Each row collects all non-equivalent cumulative partial spin operators, on the basis of point-group symmetry considerations and commutativity of dot products. For example, in the top row of Fig. 4, the node labeled as (1–3) is identical to (3–1) for commutativity of the dot product Ŝ1·Ŝ3 = Ŝ3·Ŝ1, from which it also follows that 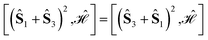 . Thus, only one between (1–3) and (3–1) is reported. Similarly, the (1–2) node is identical to (2–1) for commutativity, and identical to (1–4) and (4–1) for point-group symmetry considerations. The tree grows downwards to the next row (level 3). The (Ŝ(3))2 partial spin operators are derived from the level-2 by adding circles with level-specific colors (in Fig. 4 blue circles are utilized for level-2 and green circles are utilized for the newly introduced sites in level-3). Symmetry non-equivalent nodes lead to different branches of the tree. The tree grows until the last level is reached (level-N, for an N-site cluster). The level-N nodes span the permutation space of unique site orderings. In the case of the kite cluster (Fig. 4), there are four distinct nodes in level-2, and a total of seven distinct nodes in level-3. Branching from level-3 nodes to level-4 nodes is trivial and thus not shown in the figure. The seven distinct orderings obtained from the tree search algorithm match the ones identified in Table 2.
. Thus, only one between (1–3) and (3–1) is reported. Similarly, the (1–2) node is identical to (2–1) for commutativity, and identical to (1–4) and (4–1) for point-group symmetry considerations. The tree grows downwards to the next row (level 3). The (Ŝ(3))2 partial spin operators are derived from the level-2 by adding circles with level-specific colors (in Fig. 4 blue circles are utilized for level-2 and green circles are utilized for the newly introduced sites in level-3). Symmetry non-equivalent nodes lead to different branches of the tree. The tree grows until the last level is reached (level-N, for an N-site cluster). The level-N nodes span the permutation space of unique site orderings. In the case of the kite cluster (Fig. 4), there are four distinct nodes in level-2, and a total of seven distinct nodes in level-3. Branching from level-3 nodes to level-4 nodes is trivial and thus not shown in the figure. The seven distinct orderings obtained from the tree search algorithm match the ones identified in Table 2.
The further reduction of distinct site orderings for singlet spin states is explained in Section 5, and there its connection to the graphical tree search algorithm will also be made.
4 A hairy example: the six-site cluster
In this section the tree search algorithm is applied to a larger 6-site hexagonal cluster. The regular hexagon is in a D6 dihedral group (h = 12), and, in the absence of the tree search algorithm discussed in Section 3, it would be characterized by N!/h = 60 non-equivalent site permutations. By the application of the tree search algorithm we show that this number can further be reduced. The complete tree is shown in Fig. 5.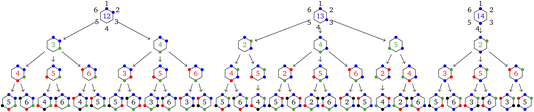 | ||
Fig. 5 Graphical representation (tree) of the cumulative partial spin operators and their commutation relation with  for a 6-site cluster in a regular hexagonal shape. The rows identify the levels corresponding to the for a 6-site cluster in a regular hexagonal shape. The rows identify the levels corresponding to the 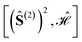 , , 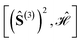 , , 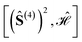 and and 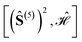 commutators. The 30 nodes at the bottom level correspond to the non-equivalent site orderings identified in Table SI.5† on the basis of the L4-norm. commutators. The 30 nodes at the bottom level correspond to the non-equivalent site orderings identified in Table SI.5† on the basis of the L4-norm. | ||
At the level-2 row we may identify 3 distinct pairs of sites, (12), (13) and (14). Any other pair is identical to the three above either for point group symmetry considerations or for the commutativity of the dot product. Thus, the three level-2 nodes indicate that there are only 3 non-equivalent commutators of the type 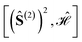 . Following the tree search algorithm recursively until level-5 reveals a total of 30 symmetry non-equivalent site orderings, which represents the number of distinct permutations under the L4-norm metric (see Table SI.5†). The tree search algorithm allows reduction of the permutation search from the initial 6! number of possible site orderings to only 30 distinct site permutations. The number of distinct site orderings reduces to only 12 when the permutation space of the singlet spin states is considered, a substantially smaller number. This further reduction will be discussed in detail in Section 5.
. Following the tree search algorithm recursively until level-5 reveals a total of 30 symmetry non-equivalent site orderings, which represents the number of distinct permutations under the L4-norm metric (see Table SI.5†). The tree search algorithm allows reduction of the permutation search from the initial 6! number of possible site orderings to only 30 distinct site permutations. The number of distinct site orderings reduces to only 12 when the permutation space of the singlet spin states is considered, a substantially smaller number. This further reduction will be discussed in detail in Section 5.
5 Higher reversal symmetry for singlet spin states
Table 1 (rhombus), Table 2 (kite) and Table SI.5† (regular hexagon) show that the number of distinct site orderings on the basis of the L4-norm values further reduces in the case of singlet spin states, Stot = 0, indicating that an additional symmetry exists that could easily be exploited.For singlet spin states, the Hamiltonian matrix elements for a given site ordering, s, are identical to the ones obtained when the reverse site ordering ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) is utilized
is utilized
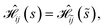 | (23) |
![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif) 〉 refer to the reversed CSFs of |i〉 and |j〉, respectively, in which the orbital ordering is reversed and u and d spin couplings flipped; for example, the reversed of |i〉 = |uduudd〉 is |i~〉 = |uuddud〉. A proof of eqn (23) is given in Section 5.1. Thus, the original and the reversed Hamiltonian matrices are identical, up to permutation of rows and columns, and so are their L4 norms. This symmetry is not present for spin states with Stot > 0, as it would lead to unphysical negative cumulative spins. Therefore, while the (1234) and (2314) site orderings in Table 1 have the same L4 norms for any spin state in virtue of eqn (21) and (22), for the singlet spin states also the (1234) and (4321) site orderings have the same L4 norms, precisely because they are the reverse orderings of each other. Similar arguments apply to the (1324) and (4231) site orderings for the rhombus, as well as all the equivalent orderings emerging for the singlet spin states of the kite example (Table 2) and the regular hexagon (Table SI.5†).
〉 refer to the reversed CSFs of |i〉 and |j〉, respectively, in which the orbital ordering is reversed and u and d spin couplings flipped; for example, the reversed of |i〉 = |uduudd〉 is |i~〉 = |uuddud〉. A proof of eqn (23) is given in Section 5.1. Thus, the original and the reversed Hamiltonian matrices are identical, up to permutation of rows and columns, and so are their L4 norms. This symmetry is not present for spin states with Stot > 0, as it would lead to unphysical negative cumulative spins. Therefore, while the (1234) and (2314) site orderings in Table 1 have the same L4 norms for any spin state in virtue of eqn (21) and (22), for the singlet spin states also the (1234) and (4321) site orderings have the same L4 norms, precisely because they are the reverse orderings of each other. Similar arguments apply to the (1324) and (4231) site orderings for the rhombus, as well as all the equivalent orderings emerging for the singlet spin states of the kite example (Table 2) and the regular hexagon (Table SI.5†).
The reversal symmetry for singlet spin states can also be identified graphically in the tree search algorithm, by following the tree from the bottom level to the top level and the ordering of the holes instead of the circles. For example, in the case of the kite (Fig. 4), the (2314) ordering arises from choosing the third node in level-2 and the fourth node in level-3. Reading this path in reverse ordering and following the holes (sites not marked by circles) we would obtain the (4132) ordering. These two site orderings will be in the same group on the basis of the L4 norm for the singlet spin states.
The equivalence between reverse site orderings identified for singlet spin states explains the number of distinct site orderings found for the Co(II)3Er(III)(OR)4 cubane cluster studied in ref. 186. For the Co(II)3Er(III)(OR)4 cubane an exhaustive site permutation search over all 4! site orderings for the lowest singlet spin state has revealed only 3 distinct site orderings on the basis of the weight of the dominant CSF (see Table 1 of ref. 186). The system is characterized by a C1 point group symmetry, and the magnetic interactions across the metal centers should in first approximation be described by a 6J-Heisenberg Hamiltonian; thus, no permutation symmetry can be exploited in the tree search algorithm, except the commutativity of the scalar products between the first two chosen sites, that reduces the number of non-equivalent site orderings to 4!/2. However, for the singlet spin states, site orderings and their reverse are equivalent (halving the distinct site orderings), and commutativity can also be applied to the reverse site orderings (another factor of 2 reduction). Thus, despite the low point group symmetry of the system, the permutation space is substantially reduced from 4! to only 3, on the ground of reversal symmetry and commutativity of the first two scalar products.
5.1 Proof of the reversal symmetry for singlet states
In the cases where Sloc > 1/2, we may assume that there are multiple parallel aligned electrons on each site (first Hund's rule). Thus, a general equation for the Heisenberg Hamiltonian operator reads as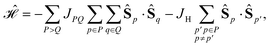 | (24) |
Heisenberg Hamiltonians can be expressed in terms of the exchange two-body spin-free excitation operators using the following relation185
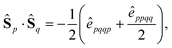 | (25) |
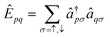 excites an electron of spin σ from the orbital q to the orbital p, and the operators
excites an electron of spin σ from the orbital q to the orbital p, and the operators 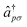 and âqσ are the electron creation and annihilation operators, respectively.
and âqσ are the electron creation and annihilation operators, respectively.
Inserting eqn (25) into eqn (24) we obtain
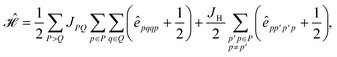 | (26) |
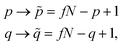 | (27) |
![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif)
![[Q with combining tilde]](https://www.rsc.org/images/entities/i_char_0051_0303.gif) in the reversed ordering. Therefore, the equality
in the reversed ordering. Therefore, the equality〈i|êpqqp|j〉 = 〈i~|ê![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) ![[q with combining tilde]](https://www.rsc.org/images/entities/i_char_0071_0303.gif) ![[q with combining tilde]](https://www.rsc.org/images/entities/i_char_0071_0303.gif) ![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) | |![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif) 〉, 〉, | (28) |
In GUGA, the matrix elements over exchange type two-body operators, êpqqp, are calculated as
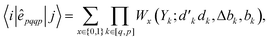 | (29) |
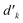 variable refers to the segment values of the bra CSF, |i〉;
variable refers to the segment values of the bra CSF, |i〉; 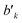 and bk are the cumulative spin values, 2Sk up to the k-level of the bra and ket functions, respectively; and Δbk refers to the
and bk are the cumulative spin values, 2Sk up to the k-level of the bra and ket functions, respectively; and Δbk refers to the 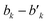 value.200 In eqn (29), all segment values,
value.200 In eqn (29), all segment values, 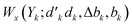 , over the k segments for the same x value are multiplied, and the resulting products over the two x values summed. For exchange type operators, êpqqp, only
, over the k segments for the same x value are multiplied, and the resulting products over the two x values summed. For exchange type operators, êpqqp, only 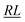 , RL, and
, RL, and 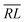 segment type symbols are to be considered out of all possible combinations (see Table VI of ref. 200). If k = q, the segment type is
segment type symbols are to be considered out of all possible combinations (see Table VI of ref. 200). If k = q, the segment type is 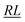 (tail node), if k = p, the segment type is
(tail node), if k = p, the segment type is 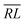 (head node), and the other internal segments are of the RL type.
(head node), and the other internal segments are of the RL type.
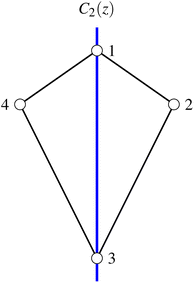
While within the GUGA framework, CSFs and their step vectors are generally represented graphically via Shavitt's graphs, for the special Heisenberg model case (where orbitals can only be singly occupied by u and d spins) a slightly modified version of the simpler genealogical branching diagrams can be utilized. In Fig. 6, two CSFs, |i〉 = |uududdud〉 and |j〉 = |uuuddudd〉, are graphically represented by a dashed and a solid line, respectively. The abscissa and the ordinate represent the k level and the corresponding cumulative bk value, respectively. In general, paths are followed from the left to the right (direct paths). One advantage of using genealogical branching diagrams over Shavitt graphs for CSFs with only unpaired electrons is that reading a CSF path from right to left (reverse path, follow the ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) levels in Fig. 6) is equivalent to reversing the CSF, with decreasing segments becoming increasing segments and vice versa. In any direct path, the node on the right of each segment indicates the cumulative bk value, while in any reverse path the node on the left of each segment represents the cumulative b
levels in Fig. 6) is equivalent to reversing the CSF, with decreasing segments becoming increasing segments and vice versa. In any direct path, the node on the right of each segment indicates the cumulative bk value, while in any reverse path the node on the left of each segment represents the cumulative b![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) .
.
When using the genealogical branching diagrams, the segments contributing to a direct coupling element, 〈i|êpqqp|j〉 are also the contributing segments to the inverse coupling element, 〈i~|ê![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif)
![[q with combining tilde]](https://www.rsc.org/images/entities/i_char_0071_0303.gif)
![[q with combining tilde]](https://www.rsc.org/images/entities/i_char_0071_0303.gif)
![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) |
|![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif) 〉. For example, in Fig. 6 the contributing segments of 〈i|ê7337|j〉 (filled in gray) are also the contributing segments of 〈i~|ê
〉. For example, in Fig. 6 the contributing segments of 〈i|ê7337|j〉 (filled in gray) are also the contributing segments of 〈i~|ê![[7 with combining tilde]](https://www.rsc.org/images/entities/char_0037_0303.gif)
![[3 with combining tilde]](https://www.rsc.org/images/entities/char_0033_0303.gif)
![[3 with combining tilde]](https://www.rsc.org/images/entities/char_0033_0303.gif)
![[7 with combining tilde]](https://www.rsc.org/images/entities/char_0037_0303.gif) |
|![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif) 〉 = 〈i~|ê2662|
〉 = 〈i~|ê2662|![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif) 〉 (eqn (27) has been used for the orbital label inversion). Although the same segments are used for the matrix element calculations of the original and the reversed two-body operators, the segment values
〉 (eqn (27) has been used for the orbital label inversion). Although the same segments are used for the matrix element calculations of the original and the reversed two-body operators, the segment values 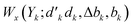 become
become 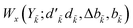 , which may not necessarily be the same as the segment values in the k indices. This behavior is shown with an example in Tables 5 and 6, where the 〈i|ê3773|j〉 and the 〈ĩ|ê2662|
, which may not necessarily be the same as the segment values in the k indices. This behavior is shown with an example in Tables 5 and 6, where the 〈i|ê3773|j〉 and the 〈ĩ|ê2662|![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif) 〉 are evaluated. The individual segment values for the direct and reversed matrix elements are in general not the same, however their products are and numerically prove eqn (28). A more general proof will be offered in the following.
〉 are evaluated. The individual segment values for the direct and reversed matrix elements are in general not the same, however their products are and numerically prove eqn (28). A more general proof will be offered in the following.
Instead of calculating the segment values using the original GUGA Table 3 with variables (b′, b, Δb, d′, d) of the reversed CSFs and the reversed generator, say ê2662, one could first convert Table 3 to a reversed table, where changes to the b′, b, Δb, d′, d are applied (Table 4), and then use the variables of the original CSFs and generator, say ê3773, with segment values collected from the reversed table. Table 4 is obtained by noting that if dk = 1 then d![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) = 2 (an up-spin in the direct branch is a down-spin in the reverse branch) and b
= 2 (an up-spin in the direct branch is a down-spin in the reverse branch) and b![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) = bk − 1; and vice versa, a dk = 2 is reversed to d
= bk − 1; and vice versa, a dk = 2 is reversed to d![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) = 1, and b
= 1, and b![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) = bk + 1. Moreover the
= bk + 1. Moreover the 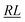 becomes
becomes 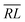 and vice versa. This strategy makes the evaluation of the Wx values convenient, as one can consistently use the
and vice versa. This strategy makes the evaluation of the Wx values convenient, as one can consistently use the 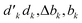 variables of the direct CSFs.
variables of the direct CSFs.
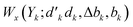 taken from ref. 200
taken from ref. 200

![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif) 〉 = 〈uduududd|ê2662|uuduuddd〉 Hamiltonian matrix element using tabulated value reported in Table 3. Segment values outside of the range [2,6] are not defined and are marked with —. W0 and V0 values are not reported as at least one of the contributing factors vanishes
〉 = 〈uduududd|ê2662|uuduuddd〉 Hamiltonian matrix element using tabulated value reported in Table 3. Segment values outside of the range [2,6] are not defined and are marked with —. W0 and V0 values are not reported as at least one of the contributing factors vanishes
Tables 3 and 4 show that the only difference in the contributions to W0 for x = 0 is the sign of 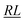 and
and 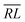 segment values; however, as any Hamiltonian matrix elements always contains only one
segment values; however, as any Hamiltonian matrix elements always contains only one 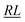 and one
and one 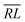 segment, the final products are always the same in sign and value for x = 0 terms. The tables also show coinciding segment values for (d′,d) = (1,1) and (d′,d) = (2,2) for the
segment, the final products are always the same in sign and value for x = 0 terms. The tables also show coinciding segment values for (d′,d) = (1,1) and (d′,d) = (2,2) for the 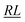 and
and 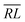 cases, as well as for the RL case with Δb = 0.
cases, as well as for the RL case with Δb = 0.
Next, we prove that
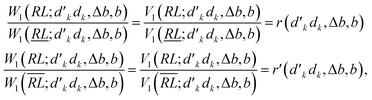 | (30) |
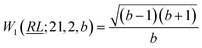 , and
, and 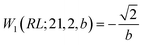 ; their ratio is
; their ratio is 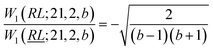 . The V1 counterpart of this ratio (from Table 4) is
. The V1 counterpart of this ratio (from Table 4) is 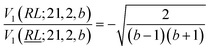 , which is the same as the ratio for W1. The equivalence of ratios holds for all d′d = 12 and d′d = 21, and both for
, which is the same as the ratio for W1. The equivalence of ratios holds for all d′d = 12 and d′d = 21, and both for 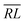 and
and 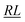 segment types (left as an exercise for the motivated reader).
segment types (left as an exercise for the motivated reader).
Thus, any 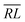 and
and 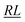 segments can always be expressed as
segments can always be expressed as
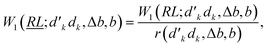 | (31) |
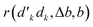 can be omitted, as it takes identical values for direct (W) and reversed (V) segment products.
can be omitted, as it takes identical values for direct (W) and reversed (V) segment products.
The details discussed above can be utilized to demonstrate eqn (28) by induction. The simplest possible loop types are considered as base case of the induction (see Fig. 7). In one case (Fig. 7a) a loop-opening segment of the type 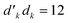 is immediately closed by the loop-closing
is immediately closed by the loop-closing 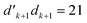 segment, and in another case (Fig. 7b) a loop-opening segment of the type
segment, and in another case (Fig. 7b) a loop-opening segment of the type 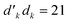 is followed by the loop-closing
is followed by the loop-closing 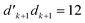 segment. The undulating lines outside the loops represent branches that are identical in the two coupled CSFs, 〈i|êpqqp|j〉, outside the range of the generator.
segment. The undulating lines outside the loops represent branches that are identical in the two coupled CSFs, 〈i|êpqqp|j〉, outside the range of the generator.
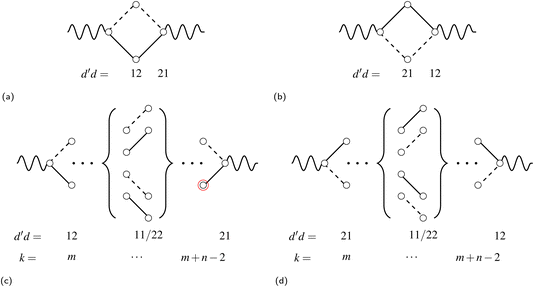 | ||
| Fig. 7 All possible loops that can appear in Heisenberg Hamiltonian matrices, represented via genealogical branching diagrams. The simplest loops are (a) for d′d = 12 and (b) for d′d = 21 loop openings. Arbitrary length-n loops are viewed as inserting n − 2 segments of d′d = 11 and/or d′d = 22 couplings in between the loop-opening and -closing segments: (c) a loop opened by d′d = 12 segments and (d) a loop opened by d′d = 21 segments. Indices of the loop-opening segment (m) and the one before the loop-closing segment (m + n − 2) are presented for (c) and (d). The b value of the node marked in red is β (see eqn (34)). Undulating lines denote any possible couplings before and after the opening and closing segments. | ||
The coupling element value of the loop in Fig. 7a, upon taking advantage of eqn (31) and omitting 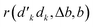 , is
, is
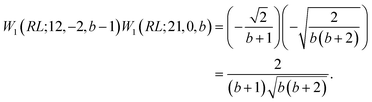 | (32) |
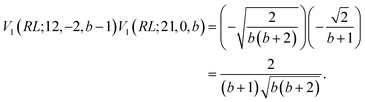 | (33) |
In the induction step, we insert a segment to the left of the closing segment; we may refer to the new segment as the n-segment, making the step vector of size n + 1 after insertion (see Fig. 7c and d). Only segment insertions of the d′d = 11 and d′d = 22 type will be considered, that retain the Δb value of the level prior to the insertion; other segment pairs lead either to closing loops which is invalid as the node of the inserted segment is not connected to the existing segment, or |Δb| > 2 which makes the coupling element zero, equally proving W1 ≡ V1 and thus eqn (28). As an example, we show the induction step for a generic loop with a W1(RL;12,−2,bm) loop-opening m segment (see Fig. 7c for reference). For a loop of length n, the b value of the loop-closing segment is bm+n−1, and the following equation
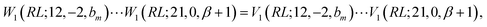 | (34) |
Inserting a d′d = 11 segment leads to the following change to the last factor of the left hand side of eqn (34)
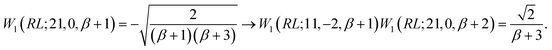 | (35) |
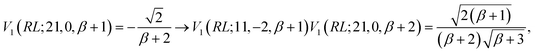 | (36) |
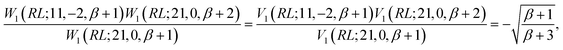 | (37) |
Equivalent conclusions are obtained by applying insertions to d′d = 21 loop-opening segments (Fig. 7d). Thus, the induction completely proves eqn (23) for any Heisenberg Hamiltonians within the singlet spin symmetry.
6 Conclusions
Within cumulatively spin-adapted many-body bases, site reorderings considerably impact the sparsity of the Hamiltonian matrix and its eigenfunctions, allowing methods that approximate the full CI solutions, including the spin-adapted FCIQMC algorithm, to converge rapidly to the exact solution for specific site orderings. Site permutations exist that lead to Hamiltonian matrices with a unique (quasi) block diagonal structure. Within each block, the spin-adapted functions (often referred to as configuration state functions, CSFs) have a common expectation value of the cumulative partial spin over the first n sites, 〈(Ŝ(n))2〉. The unique block structure is explained by the commutation relation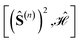 ; for some site orderings such commutator vanishes, allowing the Hamiltonian and the cumulative partial spin operators to share common eigensolutions (compatible observables). The sparsity that follows vanishing commutators is of broad impact. It applies to general systems with
; for some site orderings such commutator vanishes, allowing the Hamiltonian and the cumulative partial spin operators to share common eigensolutions (compatible observables). The sparsity that follows vanishing commutators is of broad impact. It applies to general systems with 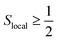 ; it equally applies to homonuclear and heteronuclear systems; it holds for PNTM clusters whose magnetic centers have the same or different local spins, as long as their interactions are dominantly of exchange type. For vanishing commutators the numerical values of the magnetic coupling constants do not have any impact on the sparsity of the Hamiltonian matrix, and sparsity persists whether Jpq > 0 or Jpq < 0.
; it equally applies to homonuclear and heteronuclear systems; it holds for PNTM clusters whose magnetic centers have the same or different local spins, as long as their interactions are dominantly of exchange type. For vanishing commutators the numerical values of the magnetic coupling constants do not have any impact on the sparsity of the Hamiltonian matrix, and sparsity persists whether Jpq > 0 or Jpq < 0.
Permutation and point group symmetries can be exploited such that the number of non-equivalent site orderings, on the basis of the L4-norm metric, is reduced as compared to the factorially growing (N!) permutation space. A tree search algorithm could be utilized to identify the distinct site orderings. The number of distinct site orderings is substantially reduced for the singlet spin states, on the basis of reversal symmetry and commutativity of scalar products. The importance of this strategy resides in its ability to reduce the space of distinct site orderings as compared to the factorial growth of the permutation space with the number of magnetic centers.
The equivalence between reverse site orderings for singlet spin states further reduces the number of distinct site orderings, as found, for example, for the Co(II)3Er(III)(OR)4 cubane cluster studied in ref. 186. In ref. 186, only three distinct site orderings have been identified upon searching the 4! permutation space of the singlet spin sector. The Co(II)3Er(III)(OR)4 system is characterized by a C1 point group symmetry; thus, in principle, no point-group symmetry arguments can be invoked to justify the reduction in distinct site orderings. In the present work, we demonstrated the reduction in distinct site orderings on the ground of the reversal symmetry and commutativity of the scalar products. Moreover, via the tree algorithm we have been able to predict what these three orderings are.
Author contributions
MS: data curation, formal analysis, investigation, software, validation, visualization, writing. AA: formal analysis, review & editing. GLM: conceptualization, data curation, formal analysis, investigation, methodology, software, supervision, validation, visualization, writing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Oskar Weser and Eline Welling for valuable discussions in the early stages of this project. Open Access funding provided by the Max Planck Society.References
- Y. Ma, S. Knecht, S. Keller and M. Reiher, J. Chem. Theory Comput., 2017, 13, 2533–2549 CrossRef CAS PubMed.
- R. H. Holm, P. Kennepohl and E. I. Solomon, Chem. Rev., 1996, 96, 2239–2314 CrossRef CAS PubMed.
- H. Beinert, R. H. Holm and E. Münck, Science, 1997, 277, 653–659 CrossRef CAS PubMed.
- R. Österberg, Nature, 1974, 249, 382–383 CrossRef PubMed.
- J. B. Howard and D. C. Rees, Chem. Rev., 1996, 96, 2965–2982 CrossRef CAS PubMed.
- S. J. Yoo, H. C. Angove, B. K. Burgess, M. P. Hendrich and E. Münk, J. Am. Chem. Soc., 1999, 121, 2534–2545 CrossRef CAS.
- M. Shoji, K. Koizumi, T. Taniguchi, Y. Kitagawa, S. Yamanaka, M. Okumura and K. Yamaguchi, Int. J. Quantum Chem., 2007, 107, 116–133 CrossRef CAS.
- M. Hans, W. Buckel and E. Bill, J. Biol. Inorg. Chem., 2008, 13, 563–574 CrossRef CAS PubMed.
- K. Miyagawa, M. Shoji, H. Isobe, S. Yamanaka, T. Kawakami, M. Okumura and K. Yamaguchi, Mol. Phys., 2020, 118(21–22), e1760388 CrossRef.
- C. Van Stappen, L. Decamps, G. E. Cutsail, R. Bjornsson, J. T. Henthorn, J. A. Birrell and S. DeBeer, Chem. Rev., 2020, 120, 5005–5081 CrossRef CAS PubMed.
- G. Renger, Angew. Chem., Int. Ed. Engl., 1987, 26, 643–660 CrossRef.
- S. Luber, I. Rivalta, Y. Umena, K. Kawakami, J.-R. Shen, N. Kamiya, G. W. Brudvig and V. S. Batista, Biochemistry, 2011, 50, 6308–6311 CrossRef CAS PubMed.
- H. Beinert, J. Biol. Inorg. Chem., 2000, 5, 2–15 CrossRef CAS PubMed.
- D. C. Johnson, D. R. Dean, A. D. Smith and M. K. Johnson, Annu. Rev. Biochem., 2005, 74, 247–281 CrossRef CAS PubMed.
- K. Yamaguchi, H. Isobe, M. Shoji, S. Yamanaka and M. Okumura, Mol. Phys., 2016, 114, 519–546 CAS.
- Y. Kurashige, G. K.-L. Chan and T. Yanai, Nat. Chem., 2013, 5, 660–666 CrossRef CAS PubMed.
- G. C. Papaefthymiou, E. J. Laskowski, S. Frota-Pessoa, R. B. Frankel and R. H. Holm, Inorg. Chem., 1982, 21, 1723–1728 CrossRef CAS.
- S. Mukhopadhyay, S. K. Mandal, S. Bhaduri and W. H. Armstrong, Chem. Rev., 2004, 104, 3981–4026 CrossRef CAS PubMed.
- T. A. Scott, C. P. Berlinguette, R. H. Holm and H.-C. Zhou, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 9741–9744 CrossRef CAS PubMed.
- G. Moula, T. Matsumoto, M. E. Miehlich, K. Meyer and K. Tatsumi, Angew. Chem., Int. Ed., 2018, 57, 11594–11597 CrossRef CAS PubMed.
- F. Evangelisti, R. Moré, F. Hodel, S. Luber and G. R. Patzke, J. Am. Chem. Soc., 2015, 137, 11076–11084 CrossRef CAS PubMed.
- M. Schilling, F. H. Hodel and S. Luber, ChemSusChem, 2017, 10, 4561–4569 CrossRef CAS PubMed.
- P. Roseiro, N. Ben Amor and V. Robert, ChemPhysChem, 2022, 23, e202100801 CrossRef CAS PubMed.
- P. Roseiro, L. Petit, V. Robert and S. Yalouz, ChemPhysChem, 2023, 24, e202200478 CrossRef CAS PubMed.
- P. Roseiro, S. Yalouz, D. J. R. Brook, N. Ben Amor and V. Robert, Inorg. Chem., 2023, 62, 5737–5743 CrossRef CAS PubMed.
- G. Li Manni, Phys. Chem. Chem. Phys., 2021, 23, 19766–19780 RSC.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- L. Noodleman, J. Chem. Phys., 1981, 74, 5737–5743 CrossRef CAS.
- W. Kohn, A. D. Becke and R. G. Parr, J. Phys. Chem., 1996, 100, 12974–12980 CrossRef CAS.
- L. Noodleman and E. J. Baerends, J. Am. Chem. Soc., 1984, 106, 2316–2327 CrossRef CAS.
- L. Noodleman and E. R. Davidson, Chem. Phys., 1986, 109, 131–143 CrossRef.
- L. Noodleman and D. Case, Adv. Inorg. Chem., 1992, 38, 423–470 CrossRef CAS.
- L. Noodleman, C. Peng, D. Case and J.-M. Mouesca, Coord. Chem. Rev., 1995, 144, 199–244 CrossRef CAS.
- F. Neese, Coord. Chem. Rev., 2009, 253, 526–563 CrossRef CAS.
- M. Shoji, K. Koizumi, Y. Kitagawa, T. Kawakami, S. Yamanaka, M. Okumura and K. Yamaguchi, Chem. Phys. Lett., 2006, 432, 343–347 CrossRef CAS.
- D. A. Pantazis, M. Orio, T. Petrenko, S. Zein, W. Lubitz, J. Messinger and F. Neese, Phys. Chem. Chem. Phys., 2009, 11, 6788–6798 RSC.
- D. Pantazis, M. Orio, T. Petrenko, S. Zein, E. Bill, W. Lubitz, J. Messinger and F. Neese, Chem. – Eur. J., 2009, 15, 5108–5123 CrossRef CAS PubMed.
- S. Schinzel, J. Schraut, A. Arbuznikov, P. Siegbahn and M. Kaupp, Chem. – Eur. J., 2010, 16, 10424–10438 CrossRef CAS PubMed.
- C. J. Cramer and D. G. Truhlar, Phys. Chem. Chem. Phys., 2009, 11, 10757–10816 RSC.
- E. Ruiz, J. Cano, S. Alvarez and P. Alemany, J. Comput. Chem., 1999, 20, 1391–1400 CrossRef CAS.
- E. Ruiz, A. Rodríguez-Fortea, J. Cano, S. Alvarez and P. Alemany, J. Comput. Chem., 2003, 24, 982–989 CrossRef CAS PubMed.
- O. Hübner and J. Sauer, Phys. Chem. Chem. Phys., 2002, 4, 5234–5243 RSC.
- O. Hübner and J. Sauer, J. Chem. Phys., 2002, 116, 617–628 CrossRef.
- L. Ding, X. Kuang and E. A. Shao, J. Mol. Model., 2013, 19, 1527–1536 CrossRef CAS PubMed.
- R. Bjornsson, F. Neese and S. DeBeer, Inorg. Chem., 2017, 56, 1470–1477 CrossRef CAS PubMed.
- F. Cappelluti, L. Bencivenni and L. Guidoni, Phys. Chem. Chem. Phys., 2020, 22, 16655–16664 RSC.
- A. Ghosh and P. R. Taylor, Curr. Opin. Chem. Biol., 2003, 7, 113–124 CrossRef CAS PubMed.
- P. R. Taylor, J. Inorg. Biochem., 2006, 100, 780–785 CrossRef CAS PubMed.
- T. Soda, Y. Kitagawa, T. Onishi, Y. Takano, Y. Shigeta, H. Nagao, Y. Yoshioka and K. Yamaguchi, Chem. Phys. Lett., 2000, 319, 223–230 CrossRef CAS.
- K. Yamaguchi, S. Yamanaka, M. Nishino, Y. Takano, Y. Kitagawa, H. Nagao and Y. Yoshioka, Theor. Chem. Acc., 1999, 102, 328–345 Search PubMed.
- Y. S, D. Yamaki, Y. Shigeta, H. Nagao and K. Yamaguchi, Int. J. Quantum Chem., 2001, 84, 670–676 CrossRef.
- P.-O. Löwdin and I. Mayer, Adv. Quantum Chem., 1992, 24, 79–114 CrossRef.
- S. Hammes-Schiffer and H. C. Andersen, J. Chem. Phys., 1993, 99, 1901–1913 CrossRef CAS.
- S. Luo, I. Rivalta, V. Batista and D. G. Truhlar, J. Phys. Chem. Lett., 2011, 2, 2629–2633 CrossRef CAS.
- X. Xu, K. R. Yang and D. G. Truhlar, J. Chem. Theory Comput., 2014, 10, 2070–2084 CrossRef CAS PubMed.
- T. Helgaker, P. Jørgensen and J. Olsen, Molecular Electronic Structure Theory, John Wiley & Sons, Ltd, Chichester, England, 2000 Search PubMed.
- G. Li Manni, K. Guther, D. Ma and W. Dobrautz, in Foundation of Multi-Configurational Quantum Chemistry, John Wiley & Sons, Ltd, 2020, ch. 6, pp. 133–203 Search PubMed.
- K. Ruedenberg and K. R. Sundberg, in MCSCF Studies of Chemical Reactions: Natural Reaction Orbitals and Localized Reaction Orbitals, ed. J.-L. Calais, O. Goscinski, J. Linderberg and Y. Öhrn, Springer US, Boston, MA, 1976, pp. 505–515 Search PubMed.
- B. O. Roos, P. R. Taylor and P. E. Sigbahn, Chem. Phys., 1980, 48, 157–173 CrossRef CAS.
- B. O. Roos, Int. J. Quantum Chem., 1980, 18, 175–189 CrossRef.
- B. O. Roos, P. R. Taylor and P. E. M. Siegbahn, Chem. Phys., 1980, 48, 157–173 CrossRef CAS.
- P. E. M. Siegbahn, J. Almlöf, A. Heiberg and B. O. Roos, J. Chem. Phys., 1981, 74, 2384–2396 CrossRef.
- B. O. Roos, in The Complete Active Space Self-Consistent Field Method and its Applications in Electronic Structure Calculations, John Wiley & Sons, Ltd, 1987, pp. 399–445 Search PubMed.
- G. Li Manni, S. D. Smart and A. Alavi, J. Chem. Theory Comput., 2016, 12, 1245–1258 CrossRef PubMed.
- D. A. Kreplin, P. J. Knowles and H.-J. Werner, J. Chem. Phys., 2019, 150, 194106 CrossRef PubMed.
- H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1985, 82, 5053–5063 CrossRef CAS.
- P. J. Knowles and H.-J. Werner, Chem. Phys. Lett., 1985, 115, 259–267 CrossRef CAS.
- K. Andersson and B. O. Roos, Chem. Phys. Lett., 1992, 191, 507–514 CrossRef CAS.
- K. Andersson, P.-Å. Malmqvist and B. O. Roos, J. Chem. Phys., 1992, 96, 1218–1226 CrossRef CAS.
- K. Andersson, Theor. Chim. Acta, 1995, 91, 31–46 CrossRef CAS.
- B. O. Roos, in The Complete Active Space Self-Consistent Field Method and Its Applications in Electronic Structure Calculations, John Wiley & Sons, Ltd, 2007, vol. 69, pp. 399–445 Search PubMed.
- A. A. Safari, R. J. Anderson and G. Li Manni, J. Phys. Chem. A, 2024, 128, 281–291 CrossRef CAS PubMed.
- J. Olsen, B. O. Roos, P. Jørgensen and H. J. A. Jensen, J. Chem. Phys., 1988, 89, 2185–2192 CrossRef CAS.
- P.-Å. Malmqvist, A. Rendell and B. O. Roos, J. Phys. Chem., 1990, 94, 5477–5482 CrossRef CAS.
- P.-Å. Malmqvist, B. O. Roos and B. Schimmelpfennig, Chem. Phys. Lett., 2002, 357, 230–240 CrossRef CAS.
- P.-Å. Malmqvist, K. Pierloot, A. R. M. Shahi, C. J. Cramer and L. Gagliardi, J. Chem. Phys., 2008, 128, 204109 CrossRef PubMed.
- P. Celani and H. J. Werner, J. Chem. Phys., 2000, 112, 5546–5557 CrossRef CAS.
- F. Ruipérez, F. Aquilante, J. M. Ugalde and I. Infante, J. Chem. Theory Comput., 2011, 7, 1640–1646 CrossRef PubMed.
- V. Sauri, L. Serrano-Andrés, A. R. M. Shahi, L. Gagliardi, S. Vancoillie and K. Pierloot, J. Chem. Theory Comput., 2011, 7, 153–168 CrossRef CAS PubMed.
- A. R. M. Shahi, C. J. Cramer and L. Gagliardi, Phys. Chem. Chem. Phys., 2009, 11, 10964–10972 RSC.
- S. Vancoillie, H. Zhao, V. T. Tran, M. F. A. Hendrickx and K. Pierloot, J. Chem. Theory Comput., 2011, 7, 3961–3977 CrossRef CAS PubMed.
- T. Fleig, J. Olsen and C. M. Marian, J. Chem. Phys., 2001, 114, 4775 CrossRef CAS.
- D. Ma, G. Li Manni and L. Gagliardi, J. Chem. Phys., 2011, 135, 044128 CrossRef PubMed.
- L. Roskop and M. S. Gordon, J. Chem. Phys., 2011, 135, 044101 CrossRef PubMed.
- D. Ma, G. Li Manni, J. Olsen and L. Gagliardi, J. Chem. Theory Comput., 2016, 12, 3208–3213 CrossRef CAS PubMed.
- O. Weser, K. Guther, K. Ghanem and G. Li Manni, J. Chem. Theory Comput., 2022, 18, 251–272 CrossRef CAS PubMed.
- G. L. Manni, PhD thesis, University of Geneva, 2013.
- G. Li Manni, F. Aquilante and L. Gagliardi, J. Chem. Phys., 2011, 134, 034114 CrossRef PubMed.
- G. Li Manni, D. Ma, F. Aquilante, J. Olsen and L. Gagliardi, J. Chem. Theory Comput., 2013, 9, 3375–3384 CrossRef CAS PubMed.
- G. Li Manni, R. K. Carlson, S. Luo, D. Ma, J. Olsen, D. G. Truhlar and L. Gagliardi, J. Chem. Theory Comput., 2014, 10, 3669–3680 CrossRef CAS PubMed.
- R. K. Carlson, G. Li Manni, A. L. Sonnenberger, D. G. Truhlar and L. Gagliardi, J. Chem. Theory Comput., 2015, 11, 82–90 CrossRef CAS PubMed.
- R. K. Carlson, D. G. Truhlar and L. Gagliardi, J. Chem. Theory Comput., 2015, 11, 4077–4085 CrossRef CAS PubMed.
- S. O. Odoh, G. Li Manni, R. K. Carlson, D. G. Truhlar and L. Gagliardi, Chem. Sci., 2016, 7, 2399–2413 RSC.
- L. Gagliardi, D. G. Truhlar, G. Li Manni, R. K. Carlson, C. E. Hoyer and J. L. Bao, Acc. Chem. Res., 2017, 50, 66–73 CrossRef CAS PubMed.
- L. Wilbraham, P. Verma, D. G. Truhlar, L. Gagliardi and I. Ciofini, J. Phys. Chem. Lett., 2017, 8, 2026–2030 CrossRef CAS PubMed.
- C. E. Hoyer, L. Gagliardi and D. G. Truhlar, J. Phys. Chem. Lett., 2015, 6, 4184–4188 CrossRef CAS PubMed.
- S. Ghosh, A. L. Sonnenberger, C. E. Hoyer, D. G. Truhlar and L. Gagliardi, J. Chem. Theory Comput., 2015, 11, 3643–3649 CrossRef CAS PubMed.
- C. E. Hoyer, S. Ghosh, D. G. Truhlar and L. Gagliardi, J. Phys. Chem. Lett., 2016, 7, 586–591 CrossRef CAS PubMed.
- S. Ghosh, C. J. Cramer, D. G. Truhlar and L. Gagliardi, Chem. Sci., 2017, 8, 2741–2750 RSC.
- D. Presti, S. J. Stoneburner, D. G. Truhlar and L. Gagliardi, J. Phys. Chem. C, 2019, 123, 11899–11907 CrossRef CAS.
- F. Aquilante, J. Autschbach, R. K. Carlson, L. F. Chibotaru, M. G. Delcey, L. De Vico, I. F. Galván, N. Ferré, L. M. Frutos, L. Gagliardi, M. Garavelli, A. Giussani, C. E. Hoyer, G. Li Manni, H. Lischka, D. Ma, P.-Å. Malmqvist, T. Müller, A. Nenov, M. Olivucci, T. B. Pedersen, D. Peng, F. Plasser, B. Pritchard, M. Reiher, I. Rivalta, I. Schapiro, J. Segarra-Martí, M. Stenrup, D. G. Truhlar, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, V. P. Vysotskiy, O. Weingart, F. Zapata and R. Lindh, J. Comput. Chem., 2016, 37, 506–541 CrossRef CAS PubMed.
- I. F. Galván, M. Vacher, A. Alavi, C. Angeli, F. Aquilante, J. Autschbach, J. J. Bao, S. I. Bokarev, N. A. Bogdanov, R. K. Carlson, L. F. Chibotaru, J. Creutzberg, N. Dattani, M. G. Delcey, S. S. Dong, A. Dreuw, L. Freitag, L. M. Frutos, L. Gagliardi, F. Gendron, A. Giussani, L. González, G. Grell, M. Guo, C. E. Hoyer, M. Johansson, S. Keller, S. Knecht, G. Kovačević, E. Källman, G. Li Manni, M. Lundberg, Y. Ma, S. Mai, J. P. Malhado, P. A. Malmqvist, P. Marquetand, S. A. Mewes, J. Norell, M. Olivucci, M. Oppel, Q. M. Phung, K. Pierloot, F. Plasser, M. Reiher, A. M. Sand, I. Schapiro, P. Sharma, C. J. Stein, L. K. Sørensen, D. G. Truhlar, M. Ugandi, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, O. Weser, T. A. Wesołowski, P.-O. Widmark, S. Wouters, A. Zech, J. P. Zobel and R. Lindh, J. Chem. Theory Comput., 2019, 15, 5925–5964 CrossRef PubMed.
- G. Li Manni, I. F. Galván, A. Alavi, F. Aleotti, F. Aquilante, J. Autschbach, D. Avagliano, A. Baiardi, J. J. Bao, S. Battaglia, L. Birnoschi, A. Blanco-González, S. I. Bokarev, R. Broer, R. Cacciari, P. B. Calio, R. K. Carlson, R. C. Couto, L. Cerdán, L. F. Chibotaru, N. F. Chilton, J. R. Church, I. Conti, S. Coriani, J. Cuéllar-Zuquin, R. E. Daoud, N. Dattani, P. Decleva, C. de Graaf, M. G. Delcey, L. D. Vico, W. Dobrautz, S. S. Dong, R. Feng, N. Ferré, M. Filatov(Gulak), L. Gagliardi, M. Garavelli, L. González, Y. Guan, M. Guo, M. R. Hennefarth, M. R. Hermes, C. E. Hoyer, M. Huix-Rotllant, V. K. Jaiswal, A. Kaiser, D. S. Kaliakin, M. Khamesian, D. S. King, V. Kochetov, M. Krośnicki, A. A. Kumaar, E. D. Larsson, S. Lehtola, M.-B. Lepetit, H. Lischka, P. L. Ríos, M. Lundberg, D. Ma, S. Mai, P. Marquetand, I. C. D. Merritt, F. Montorsi, M. Mörchen, A. Nenov, V. H. A. Nguyen, Y. Nishimoto, M. S. Oakley, M. Olivucci, M. Oppel and D. Pad, J. Chem. Theory Comput., 2023, 19, 6933–6991 CrossRef CAS PubMed.
- J. Miralles, O. Castell, R. Caballol and J.-P. Malrieu, Chem. Phys., 1993, 172, 33–43 CrossRef CAS.
- J. Miralles, J.-P. Daudey and R. Caballol, Chem. Phys. Lett., 1992, 198, 555–562 CrossRef CAS.
- V. García, O. Castell, R. Caballol and J. Malrieu, Chem. Phys. Lett., 1995, 238, 222–229 CrossRef.
- O. Castell, R. Caballol, V. M. García and K. Handrick, Inorg. Chem., 1996, 35, 1609–1615 CrossRef CAS PubMed.
- O. Castell and R. Caballol, Inorg. Chem., 1999, 38, 668–673 CrossRef CAS.
- I. d. P. R. Moreira, F. Illas, C. J. Calzado, J. F. Sanz, J.-P. Malrieu, N. B. Amor and D. Maynau, Phys. Rev. B, 1999, 59, R6593–R6596 CrossRef CAS.
- J. Cabrero, N. Ben Amor, C. de Graaf, F. Illas and R. Caballol, J. Phys. Chem. A, 2000, 104, 9983–9989 CrossRef CAS.
- C. J. Calzado, J. F. Sanz and J. P. Malrieu, J. Chem. Phys., 2000, 112, 5158–5167 CrossRef CAS.
- C. J. Calzado, J. Cabrero, J. P. Malrieu and R. Caballol, J. Chem. Phys., 2002, 116, 2728–2747 CrossRef CAS.
- C. J. Calzado, J. Cabrero, J. P. Malrieu and R. Caballol, J. Chem. Phys., 2002, 116, 3985–4000 CrossRef CAS.
- H. Kramers, Physica, 1934, 1, 182–192 CrossRef CAS.
- P. W. Anderson, Phys. Rev., 1950, 79, 350–356 CrossRef.
- J. B. Goodenough, Phys. Rev., 1955, 100, 564–573 CrossRef CAS.
- J. Kanamori, J. Phys. Chem. Solids, 1959, 10, 87–98 CrossRef CAS.
- G. Li Manni, W. Dobrautz and A. Alavi, J. Chem. Theory Comput., 2020, 16, 2202–2215 CrossRef CAS PubMed.
- W. Dobrautz, O. Weser, N. A. Bogdanov, A. Alavi and G. Li Manni, J. Chem. Theory Comput., 2021, 17, 5684–5703 CrossRef CAS PubMed.
- N. A. Bogdanov, G. Li Manni, S. Sharma, O. Gunnarsson and A. Alavi, Nat. Phys., 2022, 18, 190–195 Search PubMed.
- G. M. Arantes and P. R. Taylor, J. Chem. Theory Comput., 2010, 6, 1981–1989 CrossRef CAS PubMed.
- R. Bjornsson, F. A. Lima, T. Spatzal, T. Weyhermüller, P. Glatzel, E. Bill, O. Einsle, F. Neese and S. DeBeer, Chem. Sci., 2014, 5, 3096–3103 RSC.
- R. Bjornsson, M. U. Delgado-Jaime, F. A. Lima, D. Sippel, J. Schlesier, T. Weyhermüller, O. Einsle, F. Neese and S. DeBeer, Z. Anorg. Allg. Chem., 2015, 641, 65–71 CrossRef CAS PubMed.
- R. Bjornsson, F. Neese and S. DeBeer, Inorg. Chem., 2017, 56, 1470–1477 CrossRef CAS PubMed.
- M. K. Chan, J. Kim and D. C. Rees, Science, 1993, 260, 792–794 CrossRef CAS PubMed.
- J. T. Henthorn, R. J. Arias, S. Koroidov, T. Kroll, D. Sokaras, U. Bergmann, D. C. Rees and S. DeBeer, J. Am. Chem. Soc., 2019, 141, 13676–13688 CrossRef CAS PubMed.
- Z. Li, S. Guo, Q. Sun and G. K.-L. Chan, Nat. Chem., 2019, 11, 1026–1033 CrossRef CAS PubMed.
- Z. Li, J. Li, N. S. Dattani, C. J. Umrigar and G. K.-L. Chan, J. Chem. Phys., 2019, 150, 024302 CrossRef PubMed.
- T. Lovell, J. Li, T. Liu, D. A. Case and L. Noodleman, J. Am. Chem. Soc., 2001, 123, 12392–12410 CrossRef CAS PubMed.
- J. W. Peters, O. Einsle, D. R. Dean, S. DeBeer, B. M. Hoffman, P. L. Holland and L. C. Seefeldt, Science, 2021, 371, eabe5481 CrossRef CAS PubMed.
- C.-H. Wang and S. DeBeer, Chem. Soc. Rev., 2021, 50, 8743–8761 RSC.
- S. R. White, Phys. Rev. Lett., 1992, 69, 2863–2866 CrossRef PubMed.
- S. R. White, Phys. Rev. B, 1993, 48, 10345–10356 CrossRef CAS PubMed.
- U. Schollwöck, Ann. Phys., 2011, 326, 96–192 Search PubMed.
- U. Schollwöck, Rev. Mod. Phys., 2005, 77, 259–315 CrossRef.
- N. Nakatani and S. Guo, J. Chem. Phys., 2017, 146, 094102 CrossRef.
- D. Zgid and M. Nooijen, J. Chem. Phys., 2008, 128, 144116 CrossRef PubMed.
- D. Ghosh, J. Hachmann, T. Yanai and G. K.-L. Chan, J. Chem. Phys., 2008, 128, 144117 CrossRef PubMed.
- J. Brabec, J. Brandejs, K. Kowalski, S. Xantheas, O. Legeza and L. Veis, J. Comput. Chem., 2021, 42, 534–544 CrossRef CAS PubMed.
- G. K.-L. Chan and S. Sharma, Annu. Rev. Phys. Chem., 2011, 62, 465–481 CrossRef CAS PubMed.
- S. Sharma and G. K.-L. Chan, J. Chem. Phys., 2012, 136, 124121 CrossRef PubMed.
- K. H. Marti and M. Reiher, Z. Phys. Chem., 2010, 224, 583–599 CrossRef CAS.
- S. Keller, M. Dolfi, M. Troyer and M. Reiher, J. Chem. Phys., 2015, 143, 244118 CrossRef PubMed.
- B. Huron, J. P. Malrieu and P. Rancurel, J. Chem. Phys., 1973, 58, 5745–5759 CrossRef CAS.
- S. Evangelisti, J.-P. Daudey and J.-P. Malrieu, Chem. Phys., 1983, 75, 91–102 CrossRef CAS.
- Y. Garniron, A. Scemama, P.-F. Loos and M. Caffarel, J. Chem. Phys., 2017, 147, 034101 CrossRef PubMed.
- D. S. Levine, D. Hait, N. M. Tubman, S. Lehtola, K. B. Whaley and M. Head-Gordon, J. Chem. Theory Comput., 2020, 16, 2340–2354 CrossRef CAS PubMed.
- J. E. T. Smith, B. Mussard, A. A. Holmes and S. Sharma, J. Chem. Theory Comput., 2017, 13, 5468–5478 CrossRef CAS PubMed.
- S. Sharma, A. A. Holmes, G. Jeanmairet, A. Alavi and C. J. Umrigar, J. Chem. Theory Comput., 2017, 13, 1595–1604 CrossRef CAS PubMed.
- A. A. Holmes, N. M. Tubman and C. J. Umrigar, J. Chem. Theory Comput., 2016, 12, 3674–3680 CrossRef CAS PubMed.
- N. M. Tubman, C. D. Freeman, D. S. Levine, D. Hait, M. Head-Gordon and K. B. Whaley, J. Chem. Theory Comput., 2020, 16, 2139–2159 CrossRef CAS PubMed.
- N. M. Tubman, J. Lee, T. Y. Takeshita, M. Head-Gordon and K. B. Whaley, J. Chem. Phys., 2016, 145, 044112 CrossRef PubMed.
- Y. Garniron, A. Scemama, E. Giner, M. Caffarel and P.-F. Loos, J. Chem. Phys., 2018, 149, 064103 CrossRef PubMed.
- N. Zhang, W. Liu and M. R. Hoffmann, J. Chem. Theory Comput., 2020, 16, 2296–2316 CrossRef CAS PubMed.
- V. G. Chilkuri and F. Neese, J. Comput. Chem., 2021, 42, 982–1005 CrossRef CAS PubMed.
- V. G. Chilkuri and F. Neese, J. Chem. Theory Comput., 2021, 17, 2868–2885 CrossRef CAS PubMed.
- G. H. Booth, A. J. W. Thom and A. Alavi, J. Chem. Phys., 2009, 131, 054106 CrossRef PubMed.
- D. Cleland, G. H. Booth and A. Alavi, J. Chem. Phys., 2010, 132, 041103 CrossRef PubMed.
- D. Cleland, G. H. Booth and A. Alavi, J. Chem. Phys., 2011, 134, 024112 CrossRef CAS PubMed.
- C. Overy, G. H. Booth, N. S. Blunt, J. J. Shepherd, D. Cleland and A. Alavi, J. Chem. Phys., 2014, 141, 244117 CrossRef PubMed.
- N. S. Blunt, S. D. Smart, J. A.-F. Kersten, J. S. Spencer, G. H. Booth and A. Alavi, J. Chem. Phys., 2015, 142, 184107 CrossRef CAS PubMed.
- G. H. Booth, S. D. Smart and A. Alavi, Mol. Phys., 2014, 112, 1855–1869 CrossRef CAS.
- N. S. Blunt, A. Alavi and G. H. Booth, Phys. Rev. Lett., 2015, 115, 050603 CrossRef CAS PubMed.
- R. E. Thomas, Q. Sun, A. Alavi and G. H. Booth, J. Chem. Theory Comput., 2015, 11, 5316–5325 CrossRef CAS PubMed.
- K. Guther, R. J. Anderson, N. S. Blunt, N. A. Bogdanov, D. Cleland, N. Dattani, W. Dobrautz, K. Ghanem, P. Jeszenszki, N. Liebermann, G. Li Manni, A. Y. Lozovoi, H. Luo, D. Ma, F. Merz, C. Overy, M. Rampp, P. K. Samanta, L. R. Schwarz, J. J. Shepherd, S. D. Smart, E. Vitale, O. Weser, G. H. Booth and A. Alavi, J. Chem. Phys., 2020, 153, 034107 CrossRef CAS PubMed.
- G. H. Booth, S. D. Smart and A. Alavi, Mol. Phys., 2014, 112, 1855–1869 CrossRef CAS.
- G. Li Manni and A. Alavi, J. Phys. Chem. A, 2018, 122, 4935–4947 CrossRef CAS PubMed.
- O. Weser, L. Freitag, K. Guther, A. Alavi and G. Li Manni, Int. J. Quantum Chem., 2021, 121, e26454 CrossRef CAS.
- G. Li Manni, D. Kats, D. P. Tew and A. Alavi, J. Chem. Theory Comput., 2019, 15, 1492–1497 CrossRef CAS PubMed.
- G. Li Manni, W. Dobrautz, N. A. Bogdanov, K. Guther and A. Alavi, J. Phys. Chem. A, 2021, 125, 4727–4740 CrossRef CAS PubMed.
- O. Weser, N. Liebermann, D. Kats, A. Alavi and G. Li Manni, J. Phys. Chem. A, 2022, 126, 2050–2060 CrossRef CAS PubMed.
- O. Weser, A. Alavi and G. L. Manni, J. Chem. Theory Comput., 2023, 19, 9118–9135 CrossRef CAS PubMed.
- E. Vitale, A. Alavi and D. Kats, J. Chem. Theory Comput., 2020, 16, 5621–5634 CrossRef CAS PubMed.
- E. Vitale, G. Li Manni, A. Alavi and D. Kats, J. Chem. Theory Comput., 2022, 18, 3427–3437 CrossRef CAS PubMed.
- R. Izsák, A. V. Ivanov, N. S. Blunt, N. Holzmann and F. Neese, J. Chem. Theory Comput., 2023, 19, 2703–2720 CrossRef PubMed.
- G. Barcza, O. Legeza, K. H. Marti and M. Reiher, Phys. Rev. A, 2011, 83, 012508 CrossRef.
- G. Moritz, B. A. Hess and M. Reiher, J. Chem. Phys., 2005, 122, 024107 CrossRef PubMed.
- J. Paldus, J. Chem. Phys., 1974, 61, 5321 CrossRef CAS.
- J. Paldus, Int. J. Quantum Chem., 1975, 9, 165 CrossRef CAS.
- J. Paldus, Phys. Rev. A, 1976, 14, 1620 CrossRef CAS.
- J. Paldus, J. Math. Chem., 2021, 59, 37–71 CrossRef CAS.
- I. Shavitt, Int. J. Quantum Chem., 1977, 12, 131 CrossRef.
- I. Shavitt, Int. J. Quantum Chem., 1978, 14, S12–S32 Search PubMed.
- W. Dobrautz, S. D. Smart and A. Alavi, J. Chem. Phys., 2019, 151, 094104 CrossRef PubMed.
- W. Dobrautz, V. M. Katukuri, N. A. Bogdanov, D. Kats, G. Li Manni and A. Alavi, Phys. Rev. B, 2022, 105, 195123 CrossRef CAS.
- R. Han, S. Luber and G. Li Manni, J. Chem. Theory Comput., 2023, 19, 2811–2826 CrossRef CAS PubMed.
- P. A. M. Dirac, Proc. R. Soc. A, 1926, 112, 661–677 CAS.
- W. Heisenberg, Z. Phys., 1928, 49, 619–636 CrossRef CAS.
- C. Kittel, Phys. Rev., 1960, 120, 335–342 CrossRef CAS.
- P. W. Anderson, Phys. Rev., 1959, 115, 2–13 CrossRef CAS.
- Theoretical Foundations of Molecular Magnetism, ed. R. Boča, Elsevier, 1999, vol. 1, pp. 1–874 Search PubMed.
- C. de Graaf and R. Broer, Magnetic Interactions in Molecules and Solids, Springer International Publishing, Cham, 2016 Search PubMed.
- G. Li Manni, D. Kats and N. Liebermann, J. Chem. Theory Comput., 2023, 19, 1218–1230 CrossRef CAS PubMed.
- T. M. Henderson, G. P. Chen and G. E. Scuseria, J. Chem. Phys., 2022, 157, 194114 CrossRef CAS PubMed.
- T. M. Henderson, F. Gao and G. E. Scuseria, Mol. Phys., 2023, 122(7–8), e2254857 Search PubMed.
- R. Pauncz, Spin Eigenfunctions: Construction and Use, Springer, 1979 Search PubMed.
- C. Cohen-Tannoudji, B. Diu and F. Laloe, Quantum mechanics, Wiley, New York, 1977, vol. 1, p. 898 Search PubMed.
- I. Shavitt, B. J. Rosenberg and S. Palalikit, Int. J. Quantum Chem., 1976, 10, 33–46 CrossRef CAS.
- D. M. Brink and G. R. Satchler, Angular Momentum, Oxford University Press, 1994 Search PubMed.
- I. Shavitt, in The Unitary Group for the Evaluation of Electronic Energy Matrix Elements, ed. J. Hinze, Springer Berlin Heidelberg, Berlin, Heidelberg, 1981, pp. 51–99 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4fd00061g |
| This journal is © The Royal Society of Chemistry 2024 |