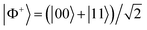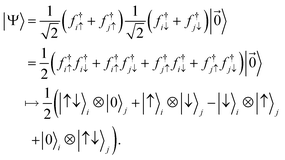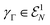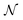Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
What can quantum information theory offer to quantum chemistry?
Damiano
Aliverti-Piuri
 ab,
Kaustav
Chatterjee
ab,
Lexin
Ding
ab,
Kaustav
Chatterjee
ab,
Lexin
Ding
 ab,
Ke
Liao
ab,
Ke
Liao
 ab,
Julia
Liebert
ab,
Julia
Liebert
 ab and
Christian
Schilling
ab and
Christian
Schilling
 *ab
*ab
aDepartment of Physics, Arnold Sommerfeld Center for Theoretical Physics, Ludwig-Maximilians-Universität München, Theresienstrasse 37, 80333 München, Germany. E-mail: c.schilling@physik.uni-muenchen.de
bMunich Center for Quantum Science and Technology (MCQST), Schellingstrasse 4, 80799 München, Germany
First published on 12th April 2024
Abstract
It is the ultimate goal of this work to foster synergy between quantum chemistry and the flourishing field of quantum information theory. For this, we first translate quantum information concepts, such as entanglement and correlation, into the context of quantum chemical systems. In particular, we establish two conceptually distinct perspectives on ‘electron correlation’, leading to a notion of orbital and particle correlation. We then demonstrate that particle correlation equals total orbital correlation minimized over all orbital bases. Accordingly, particle correlation resembles the minimal, thus intrinsic, complexity of many-electron wave functions, while orbital correlation quantifies their complexity relative to a basis. We illustrate these concepts of intrinsic and extrinsic correlation complexity in molecular systems, which also manifests the crucial link between the two correlation pictures. Our results provide theoretical justification for the long-favored natural orbitals for simplifying electronic structures, and open new pathways for developing more efficient approaches towards the electron correlation problem.
I. Introduction
Quantum chemistry (QChem) and its ability to accurately predict properties of molecules and materials is nowadays indispensable for a broad spectrum of modern quantum science. For instance, it deepens our understanding of chemical processes,1–6 as well as driving forward materials science.7–16 The success of QChem in recent years is owed to the significant progress made on the theoretical and algorithmic side, but also the increase of the computing power of hardware. In fact, almost all modern quantum chemical techniques rely on a compact representation (i.e., an effective storage) and efficient manipulation of the many-body wave function17–23 or the corresponding reduced density matrices.24–28 In particular, for weakly correlated systems, efficient and accurate solutions are now routinely obtained, even at large scales.29–32 In contrast, the problem of strong correlations remains a critical challenge. A promising direction to address and solve this problem might be offered by quantum computers as part of the ongoing second quantum revolution.33–35 However, the extent to which quantum computers can assist in solving the strong correlation problem is still under debate.36–39 To address the strong correlation problem, various heuristic schemes have been designed to compress the wave function20,40,41 or to reduce the original problem to a simpler one, e.g., through embedding techniques42–49 and effective Hamiltonian methods.50–60 In the meantime, measures have been developed that quantify the strong correlations from different perspectives61–64 in order to better understand the electron correlation problem and its complexity. Inspired by these works, we believe that a comprehensive understanding of the underlying correlation structure is imperative to facilitate the development of more efficient schemes for compressing and reducing the complexity of the correlation problem.At the same time, the concepts of correlation and complexity lie also at the heart of quantum information theory (QIT). With distinguishable parties as subsystems, concise and operationally meaningful characterization of various correlation types has long been established, the most famous one being entanglement.65–68 Together with the geometric picture of quantum states,69 different correlation types can be elegantly unified under the same theory.70 Such characterization of correlation is mathematically rigorous, thus offering precise assessment of the correlation in quantum systems. Crucially, it is also operationally meaningful, in that QIT quantifies correlation and entanglement as the exact amount of available resources in quantum systems for distinct information processing tasks, such as quantum teleportation71,72 and superdense coding.72,73 As we transition into the second quantum revolution, the practical aspects of quantum technologies also emerge as major challenges that cannot be tackled by the field of QIT alone. In particular, physical realization of qubits using molecular systems, and storing and manipulating quantum information therein, are all on-going interdisciplinary endeavors.
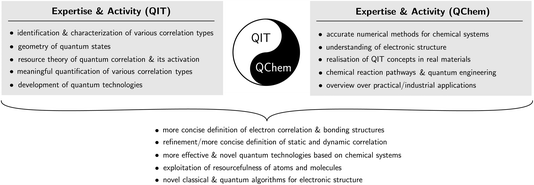
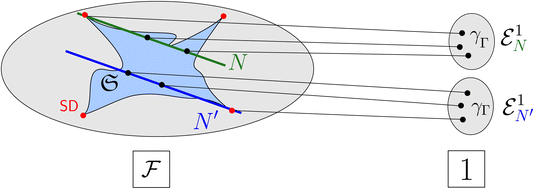
We illustrate and summarize the resulting interplay between QIT and QChem based on their different expertise and research activities in Fig. 1. Given the distinct strengths of both fields and their needs and long-term goals, the two fields can complement each other and form a powerful synergy. On one hand, QIT offers precise characterization of various aspects of electron correlation, which could simplify descriptions of correlated many-electron wave functions, refine our understanding of static and dynamic correlation, and even inspire new (classical or quantum) approaches towards the electron correlation problem.41,74–76 In order to achieve any of these, it is essential to adapt the correlation and entanglement theory from QIT, which was designed specifically for distinguishable systems, to systems of indistinguishable electrons. This is indeed a nontrivial task, as major theoretical considerations are involved regarding fermionic antisymmetry, superselection rules77,78 or the N-representability problem,79 amongst others. On the other hand, expertise from QChem is absolutely essential for the development of effective and novel quantum registers based on atoms and molecules, and for exploiting the resourcefulness of the entanglement therein.
It is therefore of great importance that the two communities join forces and open up a communication line for active discussions, which is exactly the purpose of this work. Our article focuses more on how quantum chemistry can benefit from QIT, and we structure it as follows. In Section II, we revisit the key concepts of the geometry of quantum states, as well as the entanglement and correlation in systems of distinguishable particles as studied in QIT. In Section III and IV, we explain how one can adapt these concepts to the setting of indistinguishable fermions, in both the orbital and particle picture, respectively. In Section V, we demonstrate several applications of using fermionic entanglement and correlation as tools for simplifying the structure of molecular ground states.
II. The quantum information paradigm
In this section we introduce some notation and recall basic aspects of quantum information theory. These are the crucial concepts of correlation and entanglement in composite quantum systems and the underlying paradigm of local operations and classical communication, discussed in the context of bipartite systems.A Quantum systems and quantum states
We start by considering a complex finite-dimensional Hilbert space of dimension d and denote the algebra of linear operators acting on
of dimension d and denote the algebra of linear operators acting on 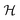 by
by 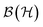 . Quantum states are then described by operators ρ on
. Quantum states are then described by operators ρ on 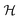 , which are Hermitian, positive semidefinite (i.e., all eigenvalues are nonnegative) and trace-normalized to unity. The corresponding set of all density operators,
, which are Hermitian, positive semidefinite (i.e., all eigenvalues are nonnegative) and trace-normalized to unity. The corresponding set of all density operators,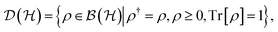 | (1) |
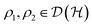 belongs to
belongs to 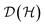 as well. In the following, provided there is no ambiguity, we will denote this set just with
as well. In the following, provided there is no ambiguity, we will denote this set just with 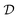 . The boundary of
. The boundary of 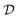 is given by those ρ that have at least one zero eigenvalue or, equivalently, that are not of full rank. Pure states are by definition the extremal points of the set
is given by those ρ that have at least one zero eigenvalue or, equivalently, that are not of full rank. Pure states are by definition the extremal points of the set 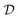 , i.e., those elements that cannot be expressed as a proper convex combination of other points. They are precisely those boundary points that are rank-one projectors, ρ = |ψ〉〈ψ|. We briefly illustrate all these aspects for the qubit, i.e., a quantum system with Hilbert space
, i.e., those elements that cannot be expressed as a proper convex combination of other points. They are precisely those boundary points that are rank-one projectors, ρ = |ψ〉〈ψ|. We briefly illustrate all these aspects for the qubit, i.e., a quantum system with Hilbert space 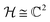 . Any qubit quantum state ρ can be parameterized as
. Any qubit quantum state ρ can be parameterized as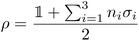 | (2) |
![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) := (n1, n2, n3) satisfying |
:= (n1, n2, n3) satisfying |![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) | ≤ 1 and {σi} being the set of Pauli matrices. In the three-dimensional
| ≤ 1 and {σi} being the set of Pauli matrices. In the three-dimensional ![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) -space, the set
-space, the set 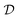 of quantum states takes the form of a ball centered around (0, 0, 0) (Bloch ball72). Its center corresponds to the maximally mixed state
of quantum states takes the form of a ball centered around (0, 0, 0) (Bloch ball72). Its center corresponds to the maximally mixed state 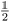 and the boundary of the ball, characterized by |
and the boundary of the ball, characterized by |![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) | = 1, contains only pure states. For systems with a Hilbert space of dimension larger than two,
| = 1, contains only pure states. For systems with a Hilbert space of dimension larger than two,  does not take the form of a ball anymore and most boundary points are not pure anymore (see, e.g., textbook ref. 69).
does not take the form of a ball anymore and most boundary points are not pure anymore (see, e.g., textbook ref. 69).
Equipped with a basic notion of quantum states, we can introduce expectation values of observables 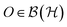 as 〈O〉ρ = Tr[Oρ]. It is instructive to interpret this as a complex linear functional,
as 〈O〉ρ = Tr[Oρ]. It is instructive to interpret this as a complex linear functional,
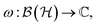 | (3) |
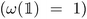 . Density operators
. Density operators 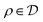 turn out to be in a one-to-one correspondence to such linear maps according to ωρ(O) = Tr[Oρ].80 As discussed below, this more abstract notion of quantum states in terms of complex linear maps has the advantage that it allows one to define, in composite systems, the concept of reduced states quite elegantly. In this approach, the notion of Hilbert spaces emerges only a posteriori from the Gelfand–Naimark–Segal (GNS) construction.80–82 Last but not least, the space
turn out to be in a one-to-one correspondence to such linear maps according to ωρ(O) = Tr[Oρ].80 As discussed below, this more abstract notion of quantum states in terms of complex linear maps has the advantage that it allows one to define, in composite systems, the concept of reduced states quite elegantly. In this approach, the notion of Hilbert spaces emerges only a posteriori from the Gelfand–Naimark–Segal (GNS) construction.80–82 Last but not least, the space 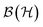 can be equipped with the Hilbert–Schmidt inner product 〈O1,O2〉 := Tr[O†1O2],
can be equipped with the Hilbert–Schmidt inner product 〈O1,O2〉 := Tr[O†1O2], 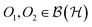 . This in turn induces a norm (Frobenius norm) that can then be used to quantify distances between linear operators in general and quantum states in particular, according to
. This in turn induces a norm (Frobenius norm) that can then be used to quantify distances between linear operators in general and quantum states in particular, according to 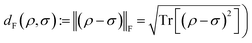 .
.
B Subsystems and reduced density operators
The concept of subsystems plays a pivotal role in the quantum sciences in general. For instance, conventional quantum computing exploits quantum effects in a multipartite system comprised of qubits. Also in physics and chemistry, it is often necessary to regard the system of interest just as a subsystem of a larger one, e.g., due to its interaction with an environment. Furthermore, the electrons and nuclei can be considered as subsystems of an atom, while atoms are subsystems of molecules. We now briefly recall the theory of bipartite systems made up of two subsystems that are distinguishable, such as the paradigmatic system of two distant labs A and B, or two particles of different species.The Hilbert space 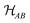 of such bipartite systems is given as the tensor product
of such bipartite systems is given as the tensor product
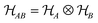 | (4) |
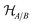 of ‘Alice and Bob’. At the level of operators, the compoundness of such systems translates to the relation
of ‘Alice and Bob’. At the level of operators, the compoundness of such systems translates to the relation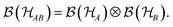 | (5) |
We first focus on one of the two subsystems only, say, Alice's one, and discuss in the next section the interplay between both subsystems. Resorting to the abstract and more elegant notion of quantum states (3), one identifies the joint system with the algebra 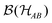 of operators and Alice's subsystem with its subalgebra
of operators and Alice's subsystem with its subalgebra
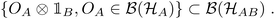 | (6) |
Indeed, the latter is closed under taking linear combinations, products and the adjoint. From a more fundamental point of view, it has actually been established by Zanardi83 that general subalgebras are precisely those mathematical objects that define subsystems.
Focusing on operators rather than on vectors in the Hilbert space has an immediate advantage when one defines reduced states of subsystems. For our setting, a given state 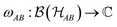 can be ‘reduced’ to a state
can be ‘reduced’ to a state 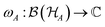 by restricting the action of ω to Alice's subalgebra, see eqn (6), i.e., to operators taking the form
by restricting the action of ω to Alice's subalgebra, see eqn (6), i.e., to operators taking the form 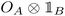 :
:
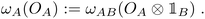 | (7) |
As stated in Section II A, one can then univocally associate to ωA a density operator 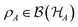 by requiring that the equality ωA(OA) = Tr[ρAOA] is valid
by requiring that the equality ωA(OA) = Tr[ρAOA] is valid 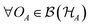 . If ρAB is the density operator corresponding to ωAB, the defining equality (7) then corresponds to
. If ρAB is the density operator corresponding to ωAB, the defining equality (7) then corresponds to
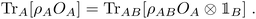 | (8) |
The reduced density operator ρA turns out to be the familiar partial trace (over the complementary subsystem B) of ρAB, i.e., ρA = TrB[ρAB].
C Independent subsystems and correlations
So far, we have revisited the mathematical framework for studying a single quantum system and introduced a notion of subsystems. If one is interested in the interplay of two or more subsystems, a few more tools are needed, which we are going to introduce in the following. This will then allow us in the subsequent section to define and quantify in rigorous terms the correlation and entanglement between subsystems.In analogy to Alice’s subsystem, Bob's subsystem B is associated with the subalgebra of operators 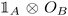 , where
, where 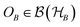 . An important remark is that any two ‘local’ operators
. An important remark is that any two ‘local’ operators 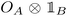 and
and 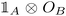 commute. This property of commutativity has been identified83 as the defining property of a general notion of independent subsystems: correlations between subsystems are understood as correlations between the outcomes of joint but independent measurements on subsystems A and B. The independence corresponds, on the mathematical level, to precisely the commutativity of the ‘local’ algebras of observables.
commute. This property of commutativity has been identified83 as the defining property of a general notion of independent subsystems: correlations between subsystems are understood as correlations between the outcomes of joint but independent measurements on subsystems A and B. The independence corresponds, on the mathematical level, to precisely the commutativity of the ‘local’ algebras of observables.
While correlations are conceptually rooted in the concept of (local) measurements and operators, they are encoded in terms of properties of the system's quantum states. Specifically, different types of correlations are related to different types of states (uncorrelated states, entangled states, etc.), while the amount of correlations can be assessed using correlation measures, i.e., functions M(ρ) of the density operator ρ.
D Hierarchy of states and correlation measures
The concise notion of correlation and entanglement is based on the notion of subsystems as discussed in Section II B and II C. As a motivation for the upcoming definition of uncorrelated states, we consider two local operators, and
and  , and their corresponding correlation function for a given state ρAB,
, and their corresponding correlation function for a given state ρAB,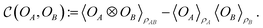 | (9) |
If for some pair of OA, OB the above function 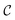 vanishes, it can still be non-zero for some other pair
vanishes, it can still be non-zero for some other pair 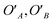 . This observation suggests that a state ρAB is uncorrelated if and only if its correlation function vanishes for any pair of local observables. The states for which this holds true are exactly those of the form ρAB = ρA ⊗ ρB, the so-called product states, forming the set
. This observation suggests that a state ρAB is uncorrelated if and only if its correlation function vanishes for any pair of local observables. The states for which this holds true are exactly those of the form ρAB = ρA ⊗ ρB, the so-called product states, forming the set
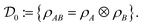 | (10) |
These states are precisely those that Alice and Bob can prepare through local operations. If Alice and Bob are in addition allowed to communicate classically, i.e., if we refer to the scheme of ‘local operations and classical communication’ (LOCC),65,84 they can create probabilistic mixtures of such uncorrelated states. These are the so-called ‘separable’ or ‘unentangled’ states, which form the set
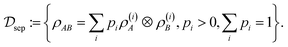 | (11) |
In fact, 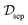 is the convex hull of the set
is the convex hull of the set 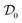 , with the extremal points given by the uncorrelated pure states |ψ〉A〈ψ|A ⊗ |ϕ〉B〈ϕ|B. In the following, we skip the subscript AB of ρAB whenever it is clear from the context that we refer to the joint quantum state.
, with the extremal points given by the uncorrelated pure states |ψ〉A〈ψ|A ⊗ |ϕ〉B〈ϕ|B. In the following, we skip the subscript AB of ρAB whenever it is clear from the context that we refer to the joint quantum state.
Based on the definition of uncorrelated and unentangled states one can now introduce measures of correlation and entanglement by quantifying, e.g., through the quantum relative entropy66,72,85
S(ρ‖σ) := Tr[ρ(log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ρ − log2 ρ − log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σ)], σ)], | (12) |
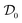 and
and 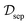 , respectively. The quantum relative entropy quantifies how difficult it is to distinguish ρ from σ86,87 and enjoys a number of useful properties, such as convexity in both arguments and unitary invariance, and it fulfills the ‘data processing’ inequality.88 This in turn leads to the following measures of correlation I† and entanglement E,
, respectively. The quantum relative entropy quantifies how difficult it is to distinguish ρ from σ86,87 and enjoys a number of useful properties, such as convexity in both arguments and unitary invariance, and it fulfills the ‘data processing’ inequality.88 This in turn leads to the following measures of correlation I† and entanglement E,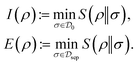 | (13) |
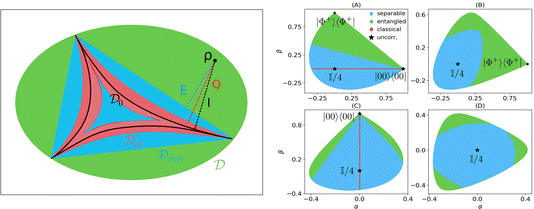
The geometrical nature of the measures in (13), as well as the different state manifolds, are graphically illustrated in Fig. 2.
One remarkable fact is that the minimization underlying I in (13) can be performed explicitly. Given a state ρAB, the minimizer is the product state ρA ⊗ ρB.70 This yields
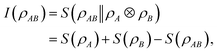 | (14) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log2
log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ρ] is the von Neumann entropy.
ρ] is the von Neumann entropy.
Another important aspect of the definition of I is that it universally bounds from above89–91 the correlation function of eqn (9) according to
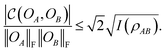 | (15) |
The bound (15) quantitatively confirms our intuition: whenever a state is close to 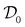 , then for any choice of local observables OA, OB the correlation function is small. In particular, when the correlation I is zero, then for all possible local operators the correlation function vanishes. A large value of correlation I is generally regarded unfavorable from a computation viewpoint, as such a state would require a larger amount of computational resources for preparing, storing and manipulating it. To the contrary, from the viewpoint of quantum information, such states are resourceful (see Section II E) and, thus, can be used to realize quantum information processing tasks, e.g., in quantum communication or quantum cryptography.92–94 Unlike for I, there does not exist a closed form for the (quantum relative entropy of) entanglement E(13). Nonetheless, it can be calculated for certain states that possess a large number of symmetries.95 In particular, for pure states |ψ〉 in
, then for any choice of local observables OA, OB the correlation function is small. In particular, when the correlation I is zero, then for all possible local operators the correlation function vanishes. A large value of correlation I is generally regarded unfavorable from a computation viewpoint, as such a state would require a larger amount of computational resources for preparing, storing and manipulating it. To the contrary, from the viewpoint of quantum information, such states are resourceful (see Section II E) and, thus, can be used to realize quantum information processing tasks, e.g., in quantum communication or quantum cryptography.92–94 Unlike for I, there does not exist a closed form for the (quantum relative entropy of) entanglement E(13). Nonetheless, it can be calculated for certain states that possess a large number of symmetries.95 In particular, for pure states |ψ〉 in 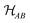 there exists a well-known closed form66
there exists a well-known closed form66
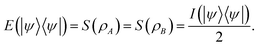 | (16) |
For general states, one of the crucial properties of E is that it does not increase under LOCC96 operations. This means when the parties A, B are restricted to LOCC, they can only degrade the entanglement content of their state. This relates nicely to the idea that entanglement is a resource that is useful for quantum information processing tasks.
Entanglement is not the only form of correlation that exists. Separable states can possess yet another type of correlation that is useful in quantum information protocols. Such correlations are called quantum correlations beyond entanglement. To be more specific, we first define the set of classical states,
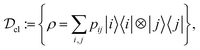 | (17) |
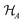 and
and 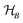 , respectively, and pij is some joint probability distribution, with pij ≥ 0 and
, respectively, and pij is some joint probability distribution, with pij ≥ 0 and 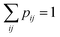 . In other words, a state χ is classical,
. In other words, a state χ is classical, 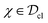 , if and only if it is diagonal in some product basis set {|i〉 ⊗ |j〉} for
, if and only if it is diagonal in some product basis set {|i〉 ⊗ |j〉} for 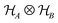 . These states are purely classical in the sense that their correlation structures can be understood on a purely classical level.70,97,98
. These states are purely classical in the sense that their correlation structures can be understood on a purely classical level.70,97,98
Given the set 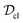 , we again use the quantum relative entropy to quantify the ‘distance’ of a given state ρ to that set. This leads to the following definition of quantum correlation:
, we again use the quantum relative entropy to quantify the ‘distance’ of a given state ρ to that set. This leads to the following definition of quantum correlation:
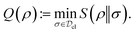 | (18) |
Similar to E(ρ), there is no closed formula for Q(ρ) in general. The quantity Q is sometimes regarded as symmetric discord or geometric discord and plays an important role for the realization of tasks such as quantum state merging99 or quantum key generation.100 Moreover, quantum correlation can be converted to entanglement, E, via distinct activation protocols.101
Note that any state of the form ρA ⊗ ρB can be written as 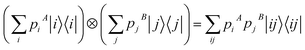 , which is of the form (17). Furthermore, it is clear by definition (17) that classical states are in particular separable. This leads to the following inclusion hierarchy
, which is of the form (17). Furthermore, it is clear by definition (17) that classical states are in particular separable. This leads to the following inclusion hierarchy
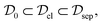 | (19) |
| I(ρ) ≥ Q(ρ) ≥ E(ρ). | (20) |
The hierarchy of the various sets of states and the geometric notion of the measures is presented in Fig. 2. Given the definition of quantum correlation contained in a state ρ, one can also quantify the amount of classical correlation contained in a state ρ. For this, one first finds the closest classical state 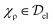 , which fulfills Q(ρ) = S(ρ‖χρ). Then the amount of classical correlation in ρ is defined as C(ρ) = I(χρ), i.e., the correlation contained in the state after all quantum correlation has been extracted.70
, which fulfills Q(ρ) = S(ρ‖χρ). Then the amount of classical correlation in ρ is defined as C(ρ) = I(χρ), i.e., the correlation contained in the state after all quantum correlation has been extracted.70
The above geometric ideas straightforwardly extend70 to systems composed of N > 2 distinguishable subsystems. Here the set of uncorrelated states contains density operators of form ρ = ⊗Ni=1ρi. The fully separable states are given by convex combination of uncorrelated states and classical states are given by 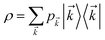 , where {|
, where {|![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) 〉 := ⊗Ni = 1|ki〉} is any product basis for
〉 := ⊗Ni = 1|ki〉} is any product basis for 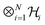 . As a generalization of eqn (14), the corresponding correlation I can be explicitly evaluated and follows as
. As a generalization of eqn (14), the corresponding correlation I can be explicitly evaluated and follows as
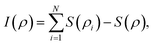 | (21) |
E Entanglement as a resource
To highlight in particular that entanglement plays the role of a key resource for quantum information processing tasks, we discuss two important protocols that form the building blocks of several other protocols in quantum information theory. The first protocol is that of quantum teleportation,71,72 which enables Alice to transmit an unknown quantum state |ψ〉a to Bob. It relies on the use of entanglement and LOCC. To explain this, suppose Alice and Bob are spatially separated and share a maximally entangled state of two electrons (or two qubits), given as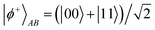 , where |0〉 refers to spin up and |1〉 refers to spin down. In addition, Alice possesses another electron in an unknown state |ψ〉a. Accordingly, the joint state of the three electrons can be written as
, where |0〉 refers to spin up and |1〉 refers to spin down. In addition, Alice possesses another electron in an unknown state |ψ〉a. Accordingly, the joint state of the three electrons can be written as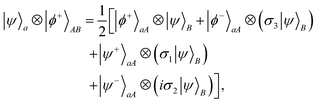 | (22) |
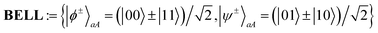 for
for 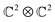 . From (22) it is apparent that the outcome of Alice's local measurement on a, A in the Bell basis identifies a distinctive unitary that Bob afterwards could apply in order to get the unknown state |ψ〉B of Alice. For example, if Alice measures |ϕ−〉aA, then Bob will need to apply the Pauli matrix σ3 on his system. This means that Bob is able to aptly recover Alice's unknown state after Alice has communicated classically her measurement outcome to him through two bits of information.
. From (22) it is apparent that the outcome of Alice's local measurement on a, A in the Bell basis identifies a distinctive unitary that Bob afterwards could apply in order to get the unknown state |ψ〉B of Alice. For example, if Alice measures |ϕ−〉aA, then Bob will need to apply the Pauli matrix σ3 on his system. This means that Bob is able to aptly recover Alice's unknown state after Alice has communicated classically her measurement outcome to him through two bits of information.
To discuss a second important protocol, we consider Alice and Bob being connected via a quantum communication channel. Alice holds a single electron that she can send to Bob in order to transmit information. Without additional resources, the best she can do is to encode the classical bit (0 or 1) onto the spin of the electron and pass it to Bob via the channel, who then measures the spin along the z-axis to determine the value of the classical bit. In this way, Alice can send one classical bit of information to Bob. However, if Alice and Bob share in addition an entangled state |ϕ+〉AB, then Alice can communicate two bits of information. To see this, notice that the set of states 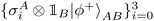 coincides with BELL up to phase factors and thus forms an orthonormal basis for
coincides with BELL up to phase factors and thus forms an orthonormal basis for 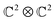 (here
(here  ). This means Alice can choose to apply one of the four unitary operators σi to her system and send her electron afterwards to Bob. Bob then performs a joint measurement on both electrons in the Bell basis to determine which of the four operators was applied by Alice. Accordingly, Alice could encode two classical bits using the four σi operators and Bob can decode by performing a Bell measurement. This protocol is called superdense coding.72,73
). This means Alice can choose to apply one of the four unitary operators σi to her system and send her electron afterwards to Bob. Bob then performs a joint measurement on both electrons in the Bell basis to determine which of the four operators was applied by Alice. Accordingly, Alice could encode two classical bits using the four σi operators and Bob can decode by performing a Bell measurement. This protocol is called superdense coding.72,73
If we denote a unit of entanglement (|ϕ+〉) with [qq], a quantum channel that transmits single qubits with [q → q] and a classical channel that transmits one bit with [c → c], then the above protocols can concisely be summarized as:
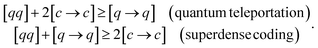 | (23) |
In these so-called resource inequalities,102 the sign ≥ emphasizes that the left hand side is at least as resourceful as the right hand side. To conclude, these two remarkable quantum protocols univocally demonstrate the necessity for a concise and operationally meaningful quantification of entanglement and various other correlation types.
III. The fermionic orbital picture
After having explained some basic concepts and tools from quantum information theory, we adapt them now to systems of identical fermions, and in particular electrons. In Section III B, we present the fermionic ‘orbital’ picture, which is based on the formalism of second quantization and accordingly regards atomic or molecular orbitals as subsystems. Since orbitals are distinguishable (as opposed to the fermions themselves), quantum information theoretical concepts can be applied in a straightforward manner, although the fermionic superselection rule requires some additional care (see Section III C). The ‘particle’ picture, which is based on 1st quantization, will be the subject of Section IV. It is rather delicate, since the antisymmetrization removes the mathematical feature that quantum information theory relies on, namely the tensor product structure of Hilbert spaces describing multipartite systems.A Notation and formalism
We consider a finite-dimensional one-particle Hilbert space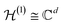 , which is spanned by the elements |1〉, |2〉, …, |d〉 of a reference orthonormal basis, also called ‘modes’. One can think of them as a basis of spin–orbitals given by |ϕi,σ〉 (which we sometimes abbreviate as |j〉), where |ϕi〉 represents a spatial orbital and σ ∈ {↑, ↓} is the spin variable. The corresponding Hilbert space for N ≤ d fermions is given as the antisymmetrized N-fold tensor product of
, which is spanned by the elements |1〉, |2〉, …, |d〉 of a reference orthonormal basis, also called ‘modes’. One can think of them as a basis of spin–orbitals given by |ϕi,σ〉 (which we sometimes abbreviate as |j〉), where |ϕi〉 represents a spatial orbital and σ ∈ {↑, ↓} is the spin variable. The corresponding Hilbert space for N ≤ d fermions is given as the antisymmetrized N-fold tensor product of 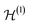 ,
,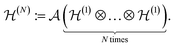 | (24) |
We also introduce the Fock space
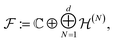 | (25) |
| {fi,f†j} = δij, {fi,fj} = {f†i,f†j} = 0, | (26) |
With the given reference basis {|i〉}, we can build an ‘occupation number’ basis for the Fock space 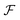 , composed of 2d Slater determinant state vectors
, composed of 2d Slater determinant state vectors
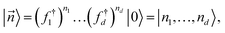 | (27) |
![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) ∈ {0,1}d. Here, |0〉 denotes the vacuum state. The occupation number basis indicates that there exists more than one potential tensor product structure within
∈ {0,1}d. Here, |0〉 denotes the vacuum state. The occupation number basis indicates that there exists more than one potential tensor product structure within 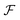 : Any partition of the reference basis into subsets induces a corresponding notion of subsystems. For instance, the partition into {|1〉, …, |d′〉} and {|d′ + 1〉, …, |d〉}, induces a respective unitary mapping from
: Any partition of the reference basis into subsets induces a corresponding notion of subsystems. For instance, the partition into {|1〉, …, |d′〉} and {|d′ + 1〉, …, |d〉}, induces a respective unitary mapping from 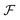 to the tensor product of the Fock space built on the first d′ modes and the Fock space built on the remaining modes:
to the tensor product of the Fock space built on the first d′ modes and the Fock space built on the remaining modes: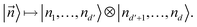 | (28) |
We remark that this mapping depends on the underlying reference basis of 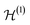 , or, at a more abstract level, on the choice of a subspace of
, or, at a more abstract level, on the choice of a subspace of 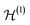 . Also, notice that some sign ambiguities in eqn (28) must be understood and resolved by means of the parity superselection rule (as explained in Section III C).
. Also, notice that some sign ambiguities in eqn (28) must be understood and resolved by means of the parity superselection rule (as explained in Section III C).
B Orbital correlation and entanglement
Based on mappings such as that of eqn (28), one can adapt the quantum information theoretical formalism discussed in Section II to the orbital picture of fermionic systems.We now discuss in more detail some instances of this formalism in the case of electron systems, where the spin degree of freedom comes into play as a factor 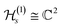 in the one-particle space,
in the one-particle space,
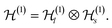 | (29) |
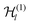 is spanned by a system-specific selection of d/2 spatial orbitals |ϕi〉. The corresponding reference basis of
is spanned by a system-specific selection of d/2 spatial orbitals |ϕi〉. The corresponding reference basis of 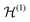 (see Section III A) is made up of the spin–orbitals |ϕi,σ〉. We now look at mappings of the form of eqn (28). These are useful for describing, e.g., a lattice of atoms that hosts electrons as a union of two half-lattices regarded as subsystems, a diatomic molecule as a system of two atoms, and the cloud of electrons around a nucleus as a union of a set of inner orbitals and a set of outer ones. One then often thinks of a partition of the d/2 orbitals spanning
(see Section III A) is made up of the spin–orbitals |ϕi,σ〉. We now look at mappings of the form of eqn (28). These are useful for describing, e.g., a lattice of atoms that hosts electrons as a union of two half-lattices regarded as subsystems, a diatomic molecule as a system of two atoms, and the cloud of electrons around a nucleus as a union of a set of inner orbitals and a set of outer ones. One then often thinks of a partition of the d/2 orbitals spanning 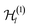 at first, e.g., into three subsets {|ϕ1〉, …, |ϕi1〉}, {|ϕi1+1〉, …, |ϕi2〉} and {|ϕi2+1〉, …, |ϕd/2〉}. This in turn induces a corresponding partition of the d spin orbitals spanning
at first, e.g., into three subsets {|ϕ1〉, …, |ϕi1〉}, {|ϕi1+1〉, …, |ϕi2〉} and {|ϕi2+1〉, …, |ϕd/2〉}. This in turn induces a corresponding partition of the d spin orbitals spanning 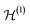 .
.
Particularly relevant partitions of the reference basis of the d spin–orbitals |ϕi,σ〉 are the following ones:
• Finest partition: each of the d spin–orbitals |ϕi,σ〉 constitutes a subsystem.
• Finest orbital partition: for i = 1, …, d/2 each pair {|ϕi,↑〉,|ϕi,↓〉} constitutes a subsystem, namely the one of the i-th spatial orbital.
• 1 vs. rest: one (spin-)orbital |ϕi〉 (|ϕi,σ〉) defines a two-mode (one-mode) subsystem; all other (spin-)orbitals form the second subsystem.
• 1 vs. 1 vs. rest: two (spin-)orbitals are identified as two subsystems; all other (spin-)orbitals form the third subsystem.
• Closed (doubly occupied) vs. active vs. virtual (empty) orbitals: this general tripartition underlies the idea of complete active spaces.
In particular, for valence bond theory the partition of choice is the one where two (orthonormalized) atomic orbitals i and j are singled out as subsystems, and all other orbitals constitute a third subsystem to be discarded.103 For |![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) 〉 = |n1↑,n1↓, …, nd/2,↑,nd/2,↓〉, eqn (28) is then adapted according to
〉 = |n1↑,n1↓, …, nd/2,↑,nd/2,↓〉, eqn (28) is then adapted according to
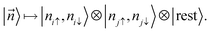 | (30) |
This mapping associates to each of the two orbitals of interest a ‘small’ Fock space spanned by just four state vectors characterized by spin occupancies: |0〉i/j, |↑〉i/j, |↓〉i/j, and |↑↓〉i/j. The idea of discarding orbitals |ϕk〉 with k ≠ i, j corresponds to a partial trace over all such orbitals, whose result is the reduced state ρij of the two orbitals.
The two-orbital reduced state ρij describes a bipartite system made up of two distinguishable subsystems, namely orbital |ϕi〉 and orbital |ϕj〉. By evaluating the correlation measures introduced in Section II D on ρij, one can quantify the correlations between the two orbitals. Such correlations in turn describe how bonded the orbitals |ϕi〉 and |ϕj〉 are. As an example, we consider a pure state ρij = |Ψ〉〈Ψ|, where |ϕi〉 and |ϕj〉 host two electrons with opposite spin in the ‘bonding’ orbital 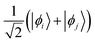 . Then, using eqn (30), we can identify |Ψ〉 with an element of the tensor product of the two Fock spaces of orbitals |ϕi〉 and |ϕj〉 mentioned above. We obtain
. Then, using eqn (30), we can identify |Ψ〉 with an element of the tensor product of the two Fock spaces of orbitals |ϕi〉 and |ϕj〉 mentioned above. We obtain
From a quantum information theoretical perspective, one notices that in this representation, |Ψ〉 looks like a maximally entangled state. Using eqn (16) and ignoring for the moment the role of superselection rules, the entanglement between the two orbitals evaluates to E(|Ψ〉) = log2(4) = 2.103
C Superselection rules
The discussions leading to eqn (28) in Section III A can be abstracted as follows. A bipartition of a reference basis of the one-particle space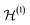 into two sets of modes A and B induces a splitting
into two sets of modes A and B induces a splitting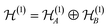 | (31) |
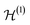 into two orthogonal subspaces. This splitting induces a tensor product structure in the Fock space,
into two orthogonal subspaces. This splitting induces a tensor product structure in the Fock space,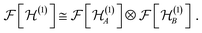 | (32) |
However, for A and B to qualify as valid subsystems, operators pertaining to modes in A should commute with those pertaining to modes in B, as per our discussion in Section II C. This is clearly not the case, given that the fermionic creation and annihilation operators associated with the modes in A anticommute with those relative to modes in B (see eqn (26)). This issue is overcome by imposing the so-called fermionic parity superselection rule (P-SSR),77,78 a fundamental rule of nature whose violation would actually make superluminal signalling (i.e., communication faster than the speed of light) possible.104,105 On the level of states, P-SSR ‘forbids’ coherent superpositions of even and odd fermion-number states. On the level of local operators,106–108 it dictates that physical local observables on modes in A/B must always commute with the local parity operator 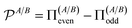 , where Π(A)τ is the projector onto the subspace of local particle number parity τ ∈ {even, odd}. Imposing such a commutation rule between the local observables and local parity operator selects out observables on A commuting with those on B. This leads to a proper description of A and B as subsystems. Operationally, such a rule has a drastic effect on the accessible entanglement and correlation contained in a state ρAB, as now the physically relevant state is given by the superselected version106,107ρPAB:
, where Π(A)τ is the projector onto the subspace of local particle number parity τ ∈ {even, odd}. Imposing such a commutation rule between the local observables and local parity operator selects out observables on A commuting with those on B. This leads to a proper description of A and B as subsystems. Operationally, such a rule has a drastic effect on the accessible entanglement and correlation contained in a state ρAB, as now the physically relevant state is given by the superselected version106,107ρPAB:
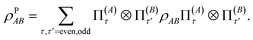 | (33) |
This implies that the various measures of correlations M = I, E, Q discussed in Section II D must be replaced by superselected versions of them, denoted by MP, where
| MP(ρAB) := M(ρPAB) | (34) |
IV. The fermionic particle picture
In Section III, the fermionic orbital picture has been introduced. We now turn our attention to the fermionic particle picture. It attempts to identify fermions themselves as subsystems and is therefore based on the formalism of first quantization. The antisymmetrization of state vectors prevents a straightforward application of the concepts developed in Section II and instead requires an adaption thereof.A Fermions as subsystems?
In Section II B, it was mentioned that, on an abstract level, subsystems are described by subalgebras of the operator algebra of the system under consideration. For a system of N fermions, we consider the algebra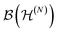 of operators on the N-fermion space. One may then wonder whether a single fermion constitutes a conventional subsystem. The underlying question can be made more precise: is there a subalgebra of
of operators on the N-fermion space. One may then wonder whether a single fermion constitutes a conventional subsystem. The underlying question can be made more precise: is there a subalgebra of 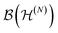 that describes a single fermion? It turns out110 that the answer to this critical question is unfortunately ‘no’. A particular promising candidate would have been the subset of ‘one-particle’ observables, i.e., operators of the form
that describes a single fermion? It turns out110 that the answer to this critical question is unfortunately ‘no’. A particular promising candidate would have been the subset of ‘one-particle’ observables, i.e., operators of the form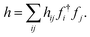 | (35) |
This subset, however, is not closed under multiplication. For instance, the product of f†ifi and f†jfj is the two-particle operator f†ifif†jfj = −f†if†jfifj. Therefore, this subset does not qualify as a proper physical subsystem.
The embedding of the N-fermion antisymmetric space 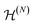 into the larger space
into the larger space 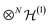 seemingly allows one to recover a tensor product structure. Yet, this approach is dubious and could easily lead to incorrect conclusions. This can be illustrated by considering two (spin-polarized) electrons that have never interacted and that occupy two orbitals |ϕ1〉, |ϕ2〉 localized in far-away regions. In fact, the corresponding Slater determinant state of the two electrons can be written as
seemingly allows one to recover a tensor product structure. Yet, this approach is dubious and could easily lead to incorrect conclusions. This can be illustrated by considering two (spin-polarized) electrons that have never interacted and that occupy two orbitals |ϕ1〉, |ϕ2〉 localized in far-away regions. In fact, the corresponding Slater determinant state of the two electrons can be written as
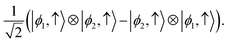 | (36) |
At first sight, this looks like an entangled state, in striking contrast to the fact that the two electrons have never interacted. Yet, this is merely an artefact of the misleading embedding into the Hilbert space of N = 2 distinguishable particles: the underlying algebra of observables is still the one of fermionic particles, rather than the one of distinguishable particles. Therefore these ‘exchange correlations’ are purely mathematical and do not exist in reality.
B Non-interacting states and nonfreeness
Since individual fermions do not qualify as subsystems, there does not exist a notion of correlation or entanglement between fermions in a strict quantum information theoretical sense. However, from the standpoint of quantum chemistry, one would like to address correlations as a consequence of interactions between particles. This suggests that if particles (electrons) are subjected to a non-interacting Hamiltonian h, see eqn (35), the corresponding eigenstates must be deemed as uncorrelated. These eigenstates are just Slater determinants. If one also considers mixed states, then there is actually a larger class of states which must be regarded as uncorrelated, namely the so-called free states.111–115 While Slater determinants are ground states of non-interacting Hamiltonians, free states are the thermal states of such Hamiltonians. The set of free states Γ on the Fock space is therefore defined as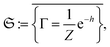 | (37) |
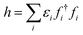 the corresponding free state can be represented in the Fock basis {|
the corresponding free state can be represented in the Fock basis {|![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) 〉} as
〉} as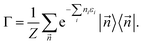 | (38) |
The outer summation in eqn (38) runs over all possible occupation vectors ![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) and the ‘partition function’ ensuring normalization reads
and the ‘partition function’ ensuring normalization reads 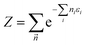 . States of the form given by eqn (38) are also sometimes referred to as number-conserving fermionic Gaussian states.116
. States of the form given by eqn (38) are also sometimes referred to as number-conserving fermionic Gaussian states.116
A fundamental property of free states, which in mathematical physics often serves as their actual definition, is that they satisfy a so-called generalized Wick theorem: every correlation function of a free state splits into a product of two-point correlation functions, which only involves the one-particle reduced density matrix (1RDM).111,113,117,118
The 1RDM of any state ρ on the Fock space follows via
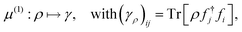 | (39) |
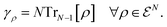 | (40) |
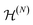 more conveniently with
more conveniently with 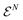 . The set of 1RDMs that are contained in the image of the set
. The set of 1RDMs that are contained in the image of the set 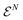 under the partial trace map in (40) are called ensemble N-representable and form the convex set
under the partial trace map in (40) are called ensemble N-representable and form the convex set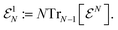 | (41) |
In general, 1RDMs do not have a unique preimage in the set 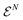 and thus also do not in the set of all states on the Fock space
and thus also do not in the set of all states on the Fock space 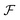 . This changes considerably if we restrict ourselves to the free states, since they are in a one-to-one correspondence with 1RDMs:113,115 for a free state Γ (38), the corresponding 1RDM reads
. This changes considerably if we restrict ourselves to the free states, since they are in a one-to-one correspondence with 1RDMs:113,115 for a free state Γ (38), the corresponding 1RDM reads
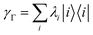 | (42) |
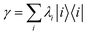 its corresponding free state follows as (see, e.g., 115)
its corresponding free state follows as (see, e.g., 115)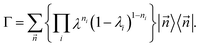 | (43) |
We illustrate this one-to-one relation between free states and their 1RDMs in Fig. 3. For different particle numbers N, N′, the free states mapping to 1RDMs in 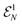 or
or 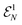 lie on hyperplanes of fixed average particle number 〈
lie on hyperplanes of fixed average particle number 〈![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) 〉Γ = N,N′.
〉Γ = N,N′.
Equipped with the definition of free states, one defines the so-called nonfreeness115,119
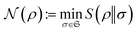 | (44) |
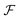 . Thus, the nonfreeness
. Thus, the nonfreeness 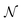 measures how far a state is from the set
measures how far a state is from the set 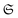 of free states and therefore quantifies the particle correlation in the spirit of quantum chemistry. Remarkably, the minimization in eqn (44) can be explicitly performed. Given a state ρ, the minimizer is the unique free state
of free states and therefore quantifies the particle correlation in the spirit of quantum chemistry. Remarkably, the minimization in eqn (44) can be explicitly performed. Given a state ρ, the minimizer is the unique free state 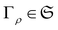 , which has the same 1RDM as ρ.115 As a result, the nonfreeness of ρ can be determined explicitly as115
, which has the same 1RDM as ρ.115 As a result, the nonfreeness of ρ can be determined explicitly as115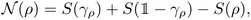 | (45) |
To make the connection between orbital correlations and nonfreeness/particle correlation precise, we now present a remarkable result that has not been properly acknowledged yet in quantum chemistry, despite its potential far-reaching implications. For this, we first consider the total orbital correlation in a state obeying the parity superselection rule (P-SSR, as per III C), i.e., we refer to the finest partition into single modes (associated with operators a(†)i) of the one-particle Hilbert space. This means we quantify correlation with respect to d subsystems given by the individual modes; see Section III B. Based on eqn (21), it means that we need to compute the entropy S(ρi) of every single mode reduced state ρi, obtained by tracing out all modes except the i-th one, that is ρi = Tric[ρ]. Given that our total state ρ is parity superselected, the reduced states take the form ρi = (1 − pi)|0〉〈0| + pi|1〉〈1|. Accordingly, the total orbital correlation follows as
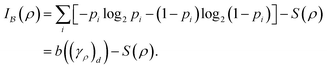 | (46) |
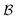 in (46) signifies that the value of the total orbital correlation depends on the choice of one-particle basis
in (46) signifies that the value of the total orbital correlation depends on the choice of one-particle basis 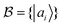 underlying the operators a(†)i. Moreover, in the second line, we have defined the binary entropy function b(x) = −x
underlying the operators a(†)i. Moreover, in the second line, we have defined the binary entropy function b(x) = −x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log2
log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) x − (1 − x) log2(1 − x) and (γρ)d denotes a diagonal matrix with entries equal to the diagonals of γρ in the particular basis {|ai〉}. Now, one may ask to which value this total correlation can be reduced by choosing a different reference basis. To answer this question, one must minimize
x − (1 − x) log2(1 − x) and (γρ)d denotes a diagonal matrix with entries equal to the diagonals of γρ in the particular basis {|ai〉}. Now, one may ask to which value this total correlation can be reduced by choosing a different reference basis. To answer this question, one must minimize 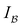 over all one-particle bases
over all one-particle bases 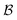 of
of 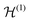 . This finally leads to the remarkable result120
. This finally leads to the remarkable result120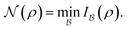 | (47) |
The proof of this equality uses tools from majorization theory121,122 to show that the minimising basis 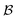 is simply the one of the natural modes/spin–orbitals. In words, relation (47) means nothing else than that the particle correlation measured through the nonfreeness is identical to the total orbital correlation minimized over all bases
is simply the one of the natural modes/spin–orbitals. In words, relation (47) means nothing else than that the particle correlation measured through the nonfreeness is identical to the total orbital correlation minimized over all bases 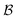 . Accordingly, particle correlation corresponds to the minimal, thus intrinsic, complexity of many-electron wave functions, while the orbital correlations quantify their complexity relative to a fixed basis. Hence, the relation (47) explains to what extent orbital optimization can reduce the computational complexity of an N-electron quantum state in quantum chemistry.
. Accordingly, particle correlation corresponds to the minimal, thus intrinsic, complexity of many-electron wave functions, while the orbital correlations quantify their complexity relative to a fixed basis. Hence, the relation (47) explains to what extent orbital optimization can reduce the computational complexity of an N-electron quantum state in quantum chemistry.
C Relation to Hartree–Fock theory
In this section, we first recall the Coulson challenge, which emphasizes the significance of the two-particle reduced density matrix (2RDM). Then, we present a remarkable connection between the 1RDM, 2RDM, free states and nonfreeness. This provides additional evidence for the crucial role all these quantities should play in quantum chemistry.Solving the ground-state problem for large systems is cursed by the exponential scaling of the dimension of the N-fermion Hilbert space 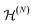 (24) with the system size. Most numerical methods to calculate the ground-state energy are based on the Rayleigh–Ritz variational principle, which corresponds to a minimization of the expectation value 〈Ψ|H|Ψ〉 over all
(24) with the system size. Most numerical methods to calculate the ground-state energy are based on the Rayleigh–Ritz variational principle, which corresponds to a minimization of the expectation value 〈Ψ|H|Ψ〉 over all 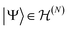 . This does not exploit, however, that most physical Hamiltonians include only pair-wise interactions. Based on this observation, Coulson formulated, in the closing speech at the 1959 Boulder conference in Colorado, the vision to replace the N-fermion wave function with the two-particle reduced density matrix (2RDM)
. This does not exploit, however, that most physical Hamiltonians include only pair-wise interactions. Based on this observation, Coulson formulated, in the closing speech at the 1959 Boulder conference in Colorado, the vision to replace the N-fermion wave function with the two-particle reduced density matrix (2RDM)
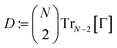 | (48) |
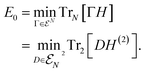 | (49) |
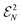 of ensemble N-representable 2RDMs, i.e.,
of ensemble N-representable 2RDMs, i.e., 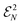 consists of exactly those 2RDMs D that are compatible with an ensemble N-fermion state.125–129 Moreover, we introduced the restriction H(2) of H onto the two-particle level. However, working on the two-particle level does not trivialize the ground-state problem: a significant part of the computational complexity of minimizing over an exponentially large N-fermion Hilbert space is shifted to the problem of finding an efficient description of the set
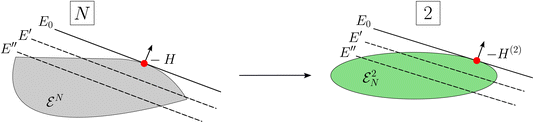
consists of exactly those 2RDMs D that are compatible with an ensemble N-fermion state.125–129 Moreover, we introduced the restriction H(2) of H onto the two-particle level. However, working on the two-particle level does not trivialize the ground-state problem: a significant part of the computational complexity of minimizing over an exponentially large N-fermion Hilbert space is shifted to the problem of finding an efficient description of the set 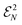 (Coulson challenge).126–129 We further illustrate eqn (49) in Fig. 4. Based on the Hilbert–Schmidt inner product, the expectation value TrN[ΓH] = 〈H,Γ〉N describes a linear functional on the space of linear operators on
(Coulson challenge).126–129 We further illustrate eqn (49) in Fig. 4. Based on the Hilbert–Schmidt inner product, the expectation value TrN[ΓH] = 〈H,Γ〉N describes a linear functional on the space of linear operators on 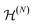 . Then, the ground-state energy E0 is obtained by shifting the corresponding hyperplane of constant value in the direction of −H until it touches the boundary (left side). Due to the linearity of the partial trace map, this linear structure immediately translates to the two-particle level illustrated in the right part of Fig. 4. This illustration of eqn (49) highlights the huge impact that the geometry of quantum states (recall also Section II D) and tools from convex analysis have in quantum chemistry. In particular, these concepts were so effective that their straightforward application led recently to more comprehensive foundations of functional theories.130–134
. Then, the ground-state energy E0 is obtained by shifting the corresponding hyperplane of constant value in the direction of −H until it touches the boundary (left side). Due to the linearity of the partial trace map, this linear structure immediately translates to the two-particle level illustrated in the right part of Fig. 4. This illustration of eqn (49) highlights the huge impact that the geometry of quantum states (recall also Section II D) and tools from convex analysis have in quantum chemistry. In particular, these concepts were so effective that their straightforward application led recently to more comprehensive foundations of functional theories.130–134
The minimization over N-fermion states in eqn (49) can be relaxed to states on the Fock space 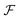 by introducing a chemical potential that fixes the total particle number N. For general states on
by introducing a chemical potential that fixes the total particle number N. For general states on 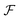 with indefinite particle number, their 2RDMs D can be defined in a similar fashion as in eqn (39) by introducing a map μ(2),
with indefinite particle number, their 2RDMs D can be defined in a similar fashion as in eqn (39) by introducing a map μ(2),
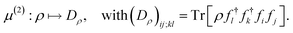 | (50) |
Moreover, the ground-state energy can be approximated by restricting the variational energy minimization to a submanifold of states. A quite crude but well-known example thereof is Hartree–Fock (HF) theory, where the minimization is restricted to the manifold of Slater determinants. Since the 1RDMs of Slater determinants are idempotent, γ2 = γ, their 2RDMs are given by
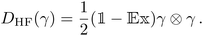 | (51) |
Thus, the HF energy EHF for a Hamiltonian H = h + W, where W denotes the two-body interaction, follows from minimizing the HF energy functional 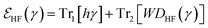 over all idempotent 1RDMs (we now skip the superscript (2) in the Hamiltonian denoting its restriction to the two-particle level). In his seminal work, Lieb showed that for positive semi-definite interactions W ≥ 0 this minimization can be relaxed to the set of all ensemble N-representable 1RDMs
over all idempotent 1RDMs (we now skip the superscript (2) in the Hamiltonian denoting its restriction to the two-particle level). In his seminal work, Lieb showed that for positive semi-definite interactions W ≥ 0 this minimization can be relaxed to the set of all ensemble N-representable 1RDMs 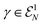 .135 By exploiting the one-to-one relation between 1RDMs and free states, it further follows that a relaxation from Slater determinant states on
.135 By exploiting the one-to-one relation between 1RDMs and free states, it further follows that a relaxation from Slater determinant states on 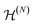 to free states on the Fock space does not alter the outcome of the energy minimization for W ≥ 0.113 This result exploits the remarkable fact that the 2RDM of any free state is given by precisely DHF, that is
to free states on the Fock space does not alter the outcome of the energy minimization for W ≥ 0.113 This result exploits the remarkable fact that the 2RDM of any free state is given by precisely DHF, that is
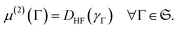 | (52) |
Thus, despite DHF(γ) being not ensemble N-representable for γ2 ≠ γ, it is indeed representable to a free state on the Fock space for all 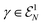 . Moreover, the corresponding free state is simply given by the free state (43) mapping to the 1RDM γ. In fact, the so-called Lieb variational principle133,135,136 and resulting HF functional FHF(γ) := Tr2[WDHF(γ)] provided the foundation for more sophisticated functional approximations in one-particle reduced density matrix functional theory.28,134,137–140
. Moreover, the corresponding free state is simply given by the free state (43) mapping to the 1RDM γ. In fact, the so-called Lieb variational principle133,135,136 and resulting HF functional FHF(γ) := Tr2[WDHF(γ)] provided the foundation for more sophisticated functional approximations in one-particle reduced density matrix functional theory.28,134,137–140
We illustrate the relation between free states and their 2RDMs and 1RDMs in Fig. 5. The set 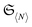 depicts the intersection of the set of free states
depicts the intersection of the set of free states 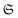 with the hyperplane of constant average particle number 〈
with the hyperplane of constant average particle number 〈![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) 〉Γ = N, as explained in Section IV B. This is meaningful, since also on the two- and one-particle level we refer to a fixed particle number in Fig. 5. The set of all states on the Fock space
〉Γ = N, as explained in Section IV B. This is meaningful, since also on the two- and one-particle level we refer to a fixed particle number in Fig. 5. The set of all states on the Fock space 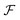 is illustrated in gray. In contrast to
is illustrated in gray. In contrast to 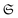 in Fig. 3, the intersection with a hyperplane might have the effect that not all extremal elements of
in Fig. 3, the intersection with a hyperplane might have the effect that not all extremal elements of 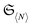 are Slater determinants (red dots) anymore. We then depict the image of the set
are Slater determinants (red dots) anymore. We then depict the image of the set 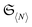 under the map μ(2) on the two-fermion level with the yellow set. As explained above, this set only intersects with the set
under the map μ(2) on the two-fermion level with the yellow set. As explained above, this set only intersects with the set 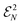 of ensemble N-representable 2RDMs at those 2RDMs whose preimage is a Slater determinant (illustrated by red dots on the right side). On the one-particle level, we compose the map μ(1) introduced above with the spectral map spec(·), which maps a 1RDM to its vector
of ensemble N-representable 2RDMs at those 2RDMs whose preimage is a Slater determinant (illustrated by red dots on the right side). On the one-particle level, we compose the map μ(1) introduced above with the spectral map spec(·), which maps a 1RDM to its vector  of eigenvalues λi. Due to the one-to-one relation between free states and 1RDMs
of eigenvalues λi. Due to the one-to-one relation between free states and 1RDMs  the image under this composed map is given by the Pauli hypercube (blue) whose vertices correspond to idempotent 1RDMs with eigenvalues λi ∈ {0, 1} (red dots).
the image under this composed map is given by the Pauli hypercube (blue) whose vertices correspond to idempotent 1RDMs with eigenvalues λi ∈ {0, 1} (red dots).
 | ||
Fig. 5 Illustration of the intersection of  with a hyperplane of fixed average particle number N (see also Fig. 3) denoted by with a hyperplane of fixed average particle number N (see also Fig. 3) denoted by 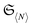 and its image under the maps μ(1/2) leading to the respective 1RDMs and 2RDMs. The red dots (left) illustrate the Slater determinants. The image of and its image under the maps μ(1/2) leading to the respective 1RDMs and 2RDMs. The red dots (left) illustrate the Slater determinants. The image of 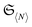 (light blue, left) under μ(2) (yellow set, right) only intersects with the set of ensemble N-representable 2RDMs (green) at those 2RDMs whose preimages are Slater determinants. On the one-particle level, we illustrate the Pauli hypercube (blue) of admissible natural occupation number vectors (light blue, left) under μ(2) (yellow set, right) only intersects with the set of ensemble N-representable 2RDMs (green) at those 2RDMs whose preimages are Slater determinants. On the one-particle level, we illustrate the Pauli hypercube (blue) of admissible natural occupation number vectors ![[small lambda, Greek, vector]](https://www.rsc.org/images/entities/i_char_e121.gif) (see text for more details). (see text for more details). | ||
V. Examples and illustrations
In the previous sections, we have established the notions of particle and orbital correlation. In particular, we presented a fundamental relation between them: the particle correlation measure of nonfreeness (44) equals the orbital-minimized total orbital correlation (see eqn (47)). In this section, we shall demonstrate this link between the orbital and particle picture, with both analytical and numerical examples. Moreover, we will relate these quantities with the so-called configuration interaction (CI) entropy of wave functions, a direct but computationally costly quantifier of the multireference character.A Analytical example
For two electrons in 2K modes (spin–orbitals that form an orthonormal basis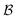 of
of 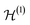 ), a general quantum state can be expanded in terms of Slater determinants,
), a general quantum state can be expanded in terms of Slater determinants,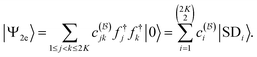 | (53) |
In the last equation of this configuration interaction (CI) expansion we collected the CI coefficients 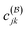 into a vector
into a vector 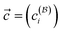 . In the natural orbital basis, |Ψ2e〉 admits a compact form containing at most K Slater determinants,141
. In the natural orbital basis, |Ψ2e〉 admits a compact form containing at most K Slater determinants,141
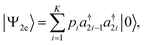 | (54) |
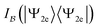 is at its minimum. In fact, the wave function |Ψ2e〉 is also expected to have the most compact form in the natural spin-orbital basis, where the compactness of the expansion is measured by the Shannon entropy
is at its minimum. In fact, the wave function |Ψ2e〉 is also expected to have the most compact form in the natural spin-orbital basis, where the compactness of the expansion is measured by the Shannon entropy 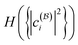 of the squared CIorthogonal matrices were sampled coefficients
of the squared CIorthogonal matrices were sampled coefficients 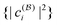 . We shall refer to it as the CI entropy. In other words, we conjecture for N = 2 fermions that the CI entropy in any basis
. We shall refer to it as the CI entropy. In other words, we conjecture for N = 2 fermions that the CI entropy in any basis  satisfies
satisfies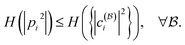 | (55) |
To verify this conjecture, we sampled various one-particle bases 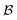 . To be more specific, for the case K = 2 (the first row in Fig. 6), 105 + 4 × 4 orthogonal matrices were sampled uniformly from the orthogonal group, which transform the natural orbitals to a target basis. For the case K = 3 (the second row in Fig. 6), 106 + 6 × 6 orthogonal matrices were sampled from the orthogonal group, and 106 additional ones are sampled around the identity. In Fig. 6, we present both quantities
. To be more specific, for the case K = 2 (the first row in Fig. 6), 105 + 4 × 4 orthogonal matrices were sampled uniformly from the orthogonal group, which transform the natural orbitals to a target basis. For the case K = 3 (the second row in Fig. 6), 106 + 6 × 6 orthogonal matrices were sampled from the orthogonal group, and 106 additional ones are sampled around the identity. In Fig. 6, we present both quantities 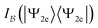 and
and 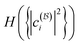 , for various states with different levels of intrinsic multireference character modulated by the choice of parameters pi in eqn (54) (i.e., the natural occupation numbers, up to a square). When only one |pi|2 is nonzero and therefore equal to 1, |Ψ2e〉 is a single Slater determinant. When various |pi|2's are fractional, |Ψ2e〉 always contains some multireference character in any orbital basis.
, for various states with different levels of intrinsic multireference character modulated by the choice of parameters pi in eqn (54) (i.e., the natural occupation numbers, up to a square). When only one |pi|2 is nonzero and therefore equal to 1, |Ψ2e〉 is a single Slater determinant. When various |pi|2's are fractional, |Ψ2e〉 always contains some multireference character in any orbital basis.
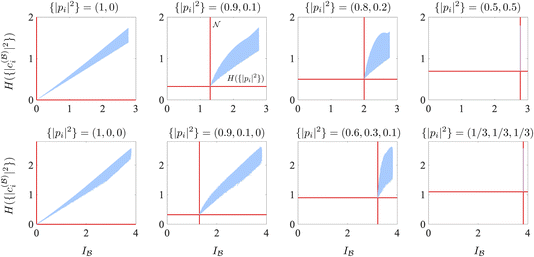 | ||
Fig. 6 Relation between total orbital correlation 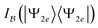 and Shannon entropy and Shannon entropy 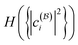 of the CI expansion coefficients of the two-electron quantum state (54) in 2K modes for numerous randomly sampled orbital reference bases of the CI expansion coefficients of the two-electron quantum state (54) in 2K modes for numerous randomly sampled orbital reference bases  . The horizontal and vertical red lines indicate the minima of the two quantities, given by H({|pi|2}) and . The horizontal and vertical red lines indicate the minima of the two quantities, given by H({|pi|2}) and 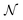 (nonfreeness), respectively. In the first row we set K = 2, and in the second row K = 3. Different plots in the same row correspond to different choices of the parameters {|pi|2}Ki=1 in (54) that uniquely determine the multireference structure of the state. (nonfreeness), respectively. In the first row we set K = 2, and in the second row K = 3. Different plots in the same row correspond to different choices of the parameters {|pi|2}Ki=1 in (54) that uniquely determine the multireference structure of the state. | ||
First, we observe that indeed, for each two-electron state |Ψ2e〉, the two correlation quantities 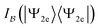 and
and 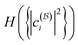 are simultaneously minimized, specifically by the natural spin-orbital basis. This provides the first evidence for our conjecture (55). In particular, when only two |pi|2's are nonzero (which is the general case if the number of modes is 2K = 4), the minima of the two quantities can be shown to be related by
are simultaneously minimized, specifically by the natural spin-orbital basis. This provides the first evidence for our conjecture (55). In particular, when only two |pi|2's are nonzero (which is the general case if the number of modes is 2K = 4), the minima of the two quantities can be shown to be related by
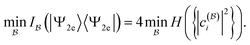 | (56) |
Second, it is clear from the plots that when 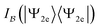 reduces, both the upper and lower bounds of
reduces, both the upper and lower bounds of 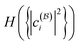 are also reduced. In particular, when
are also reduced. In particular, when 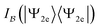 approaches its minimum, the gap between the two bounds of
approaches its minimum, the gap between the two bounds of 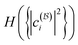 closes. Third, as the |pi|2's get close to each other and the intrinsic multireference character of the state thus increases, the range of the values of
closes. Third, as the |pi|2's get close to each other and the intrinsic multireference character of the state thus increases, the range of the values of 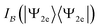 shrinks. This range collapses to a point when the natural occupation numbers become identical (which is evidenced by the line of blue dots sitting right on top of the vertical red line in the last column in Fig. 6). A similar effect is observed for
shrinks. This range collapses to a point when the natural occupation numbers become identical (which is evidenced by the line of blue dots sitting right on top of the vertical red line in the last column in Fig. 6). A similar effect is observed for 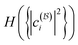 , but much less pronounced. Finally, if we focus on the natural spin-orbitals (represented by the data point at the intersection of the two red lines), we see that the CI entropy is monotonic with the total spin–orbital correlation.
, but much less pronounced. Finally, if we focus on the natural spin-orbitals (represented by the data point at the intersection of the two red lines), we see that the CI entropy is monotonic with the total spin–orbital correlation.
We remark that the conjectured inequality (55) can be proven analytically for any pure state of two fermions (N = 2). While a detailed proof goes beyond the scope of this article, in ref. 142 the interested reader can find the proof of a similar inequality that arises in the evaluation of the quantum correlation (eqn (18)) of any pure state of two distinguishable particles.
B Numerical illustrations
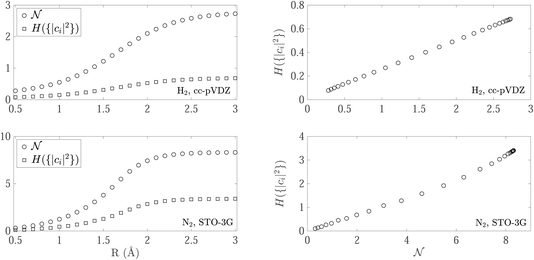
To elaborate on our observations from the two-electron examples, we now inspect the relation between the nonfreeness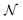 (44) and the CI entropy for the ground state of H2 (cc-pVDZ, 2 electrons in 10 orbitals) and N2 (STO-3G, 14 electrons in 10 orbitals) in the natural spin-orbital basis. For each molecule, we calculate first the full CI ground state based on the previously obtained HF orbitals. Then, we obtain the natural spin-orbitals by diagonalizing the 1RDM γ of the ground state. Lastly, we perform another full CI calculation based on the natural spin-orbitals, and acquire the CI coefficient vector
(44) and the CI entropy for the ground state of H2 (cc-pVDZ, 2 electrons in 10 orbitals) and N2 (STO-3G, 14 electrons in 10 orbitals) in the natural spin-orbital basis. For each molecule, we calculate first the full CI ground state based on the previously obtained HF orbitals. Then, we obtain the natural spin-orbitals by diagonalizing the 1RDM γ of the ground state. Lastly, we perform another full CI calculation based on the natural spin-orbitals, and acquire the CI coefficient vector ![[c with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0063_20d1.gif) in this basis. This procedure is carried out using the PySCF package,143 and is repeated for various internuclear distances of the molecules, ranging from 0.5 Å to 3 Å.
in this basis. This procedure is carried out using the PySCF package,143 and is repeated for various internuclear distances of the molecules, ranging from 0.5 Å to 3 Å.
We present the results in Fig. 7. For both molecules, as the internuclear distance R increases from below equilibrium, the multireference character of the ground states also increases. This can be directly seen in the left column, where both the nonfreeness  and the CI entropy
and the CI entropy 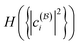 grow with the internuclear distances. Moreover, the relation between the nonfreeness
grow with the internuclear distances. Moreover, the relation between the nonfreeness 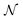 and the CI entropy
and the CI entropy 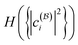 is monotonic (and even almost linear for H2), as the second column in Fig. 7 clearly demonstrates. This again highlights the high potential of the easily accessible nonfreeness as a universal tool for characterizing multireference wave functions, in place of the cumbersome, if not inaccessible, CI entropy
is monotonic (and even almost linear for H2), as the second column in Fig. 7 clearly demonstrates. This again highlights the high potential of the easily accessible nonfreeness as a universal tool for characterizing multireference wave functions, in place of the cumbersome, if not inaccessible, CI entropy  .
.
Our numerical results confirm that some of the insights from the analytical two-electron examples indeed extend to larger systems. Both the minimized total spin–orbital correlation, i.e., the nonfreeness 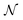 , and the CI entropy H({|ci|2}) in the natural basis are valid quantitative descriptors of the multireference character of the ground state. More importantly, the two descriptors are found to be monotonic functions of each other for both molecules. This suggests that the simple nonfreeness
, and the CI entropy H({|ci|2}) in the natural basis are valid quantitative descriptors of the multireference character of the ground state. More importantly, the two descriptors are found to be monotonic functions of each other for both molecules. This suggests that the simple nonfreeness  , which only involves the 1RDM γ, can reveal the high complexity of the wave function encoded in the CI expansion equally well as the CI entropy, which is difficult to calculate in practice.
, which only involves the 1RDM γ, can reveal the high complexity of the wave function encoded in the CI expansion equally well as the CI entropy, which is difficult to calculate in practice.
VI. Summary and conclusions
In order to foster synergy between quantum chemistry and quantum information theory, we translated the concepts of entanglement and correlation into the context of quantum chemical systems. By exploiting the formalism of first and second quantization, we established two conceptually distinct notions of correlation in fermion systems. To be more specific, we first recalled that subsets of orbitals define quantum subsystems in a precise way by referring to their respective algebras. This in turn allowed us to apply the common formalism of ‘local operations and classical communication’ (LOCC) to introduce a notion of orbital correlation and entanglement. In particular, to make it operationally meaningful, we elucidated why and how the fundamental number parity superselection rule needs to be taken into account. Moreover, to invite quantum chemists to join the ongoing second quantum revolution, we explained for which quantum information processing tasks the corresponding orbital entanglement could be used for. Quite to the contrary, electrons themselves do not obey the axioms of quantum subsystems and thus the paradigm of LOCC cannot be applied. Instead, we thus defined the ground and thermal states of noninteracting electron systems as the particle uncorrelated states. Measuring then the minimal distance of a quantum state ρ through the quantum relative entropy to the manifold of those ‘free states’, results directly in a measure of particle correlation.115,119 It is given by the particle-hole symmetrized von Neumann entropy S of the corresponding 1RDM γρ modified by the entropy of the total state, i.e.,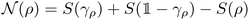 .
.
We then demonstrated that particle correlation equals total orbital correlation minimized with respect to all orbital reference bases. Accordingly, particle correlation equals the minimal, thus intrinsic, complexity of many-electron wave functions while orbital correlation quantifies their complexity relative to a basis. From a practical point of view, the particle correlation therefore defines the correlation threshold to which orbital optimization schemes can reduce the representational complexity of the many-electron wave function. Prime examples for methods with a particularly strong dependence on the orbital reference basis are the density matrix renormalization group (DMRG)-method, as well as variational quantum eigensolvers (VQE) in quantum computing. To further strengthen the connection between the particle and orbital picture, we presented an inherent relation between free states and Hartree–Fock theory: the states that were defined as particle uncorrelated from a quantum information perspective are precisely those that underlie the construction of the pivotal Hartree–Fock functional in one-particle reduced density matrix functional theory. Accordingly, it can be expected that the measure of particle correlation might be connected to the two-electron cumulant, which is discarded in Hartree–Fock theory.
We illustrated all these concepts and analytical findings in few-electron systems. With an analytic example of two-electron states and a numerical one concerning two concrete molecules, we made two instructive observations: (i) (at least for states of two electrons) both the total spin orbital correlation and the entropy of the CI coefficients are minimized in the natural orbital basis. (ii) The particle correlation, which is the minimized total spin orbital correlation, is a good approximation (up to a factor) to the complicated CI entropy relative to the natural orbitals, which measures directly the multireference character of the wave function expansion. At the same time, these results suggested a general guiding principle for simplifying the structure of the wave function: by reducing the total (spin) orbital correlation, one effectively trims away the excessive complexity in the wave function due to a sub-optimal orbital representation.
In summary, we believe that the fermion-compatible correlation and entanglement measures presented in this work facilitate a complete characterization and successful exploitation of the quantum resourcefulness of atoms and molecules for information processing tasks. In return, the profound connection between orbital and particle correlation, as well as their role in evaluating the multireference character of wave functions, could stimulate developments of novel and more efficient approaches to the electron correlation problem.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge financial support from the German Research Foundation (Grant SCHI 1476/1-1), the Munich Center for Quantum Science and Technology, and the Munich Quantum Valley, which is supported by the Bavarian state government with funds from the Hightech Agenda Bayern Plus. J. L. acknowledges funding from the International Max Planck Research School for Quantum Science and Technology (IMPRS-QST).References
- J. Almlöf, Ab initio calculations on porphin, Int. J. Quantum Chem., 1974, 8, 915 CrossRef.
- A. L. Dzubak, L.-C. Lin, J. Kim, J. A. Swisher, R. Poloni, S. N. Maximoff, B. Smit and L. Gagliardi, Ab initio carbon capture in open-site metal–organic frameworks, Nat. Chem., 2012, 4, 810 CrossRef CAS PubMed.
- Y. Kurashige, G. K.-L. Chan and T. Yanai, Entangled quantum electronic wavefunctions of the Mn4CaO5 cluster in photosystem II, Nat. Chem., 2013, 5, 660 CrossRef CAS PubMed.
- S. Sharma, K. Sivalingam, F. Neese and G. K.-L. Chan, Low-energy spectrum of iron–sulfur clusters directly from many-particle quantum mechanics, Nat. Chem., 2014, 6, 927 CrossRef CAS PubMed.
- G. Li Manni and A. Alavi, Understanding the mechanism stabilizing intermediate spin states in Fe(II)-Porphyrin, J. Phys. Chem. A, 2018, 122, 4935 CrossRef CAS PubMed.
- H. R. Larsson, H. Zhai, C. J. Umrigar and G. K.-L. Chan, The Chromium Dimer: Closing a Chapter of Quantum Chemistry, J. Am. Chem. Soc., 2022, 144, 15932 CrossRef CAS PubMed.
- T. Misawa and M. Imada, Superconductivity and its mechanism in an ab initio model for electron-doped LaFeAsO, Nat. Commun., 2014, 5, 5738 CrossRef CAS PubMed.
- L. Schimka, J. Harl, A. Stroppa, A. Grüneis, M. Marsman, F. Mittendorfer and G. Kresse, Accurate surface and adsorption energies from many-body perturbation theory, Nat. Mater., 2010, 9, 741 CrossRef CAS PubMed.
- G. H. Booth, A. Grüneis, G. Kresse and A. Alavi, Towards an exact description of electronic wavefunctions in real solids, Nature, 2013, 493, 365 CrossRef CAS PubMed.
- J. Yang, W. Hu, D. Usvyat, D. Matthews, M. Schütz and G. K.-L. Chan, Ab initio determination of the crystalline benzene lattice energy to sub-kilojoule/mole accuracy, Science, 2014, 345, 640 CrossRef CAS PubMed.
- T. Gruber, K. Liao, T. Tsatsoulis, F. Hummel and A. Grüneis, Applying the Coupled-Cluster Ansatz to Solids and Surfaces in the Thermodynamic Limit, Phys. Rev. X, 2018, 8, 21043 CAS.
- K. Liao, X.-Z. Li, A. Alavi and A. Grüneis, A comparative study using state-of-the-art electronic structure theories on solid hydrogen phases under high pressures, npj Comput. Mater., 2019, 5, 110 CrossRef CAS.
- I. Y. Zhang and A. Grüneis, Coupled Cluster Theory in Materials Science, Front. Mater. Sci., 2019, 6 DOI:10.3389/fmats.2019.00123.
- Z.-H. Cui, H. Zhai, X. Zhang and G. K.-L. Chan, Systematic electronic structure in the cuprate parent state from quantum many-body simulations, Science, 2022, 377, 1192 CrossRef CAS PubMed.
- N. A. Bogdanov, G. Li Manni, S. Sharma, O. Gunnarsson and A. Alavi, Enhancement of superexchange due to synergetic breathing and hopping in corner-sharing cuprates, Nat. Phys., 2022, 18, 190 Search PubMed.
- Z.-H. Cui, J. Yang, J. Tölle, H.-Z. Ye, H. Zhai, R. Kim, X. Zhang, L. Lin, T. C. Berkelbach, and G. K.-L. Chan, Ab initio quantum many-body description of superconducting trends in the cuprates, arXiv, 2023, preprint, arXiv:2306.16561 DOI:10.48550/arXiv.2306.16561.
- F. Coester, Bound states of a many-particle system, Nucl. Phys., 1958, 7, 421 CrossRef.
- F. Coester and H. Kümmel, Short-range correlations in nuclear wave functions, Nucl. Phys., 1960, 17, 477 CrossRef CAS.
- R. J. Bartlett and M. Musiał, Coupled-cluster theory in quantum chemistry, Rev. Mod. Phys., 2007, 79, 291 CrossRef CAS.
- S. R. White, Density matrix formulation for quantum renormalization groups, Phys. Rev. Lett., 1992, 69, 2863 CrossRef PubMed.
- S. Östlund and S. Rommer, Thermodynamic Limit of Density Matrix Renormalization, Phys. Rev. Lett., 1995, 75, 3537 CrossRef PubMed.
- G. H. Booth, A. J. Thom and A. Alavi, Fermion monte carlo without fixed nodes: A game of life, death, and annihilation in Slater determinant space, J. Chem. Phys., 2009, 131, 054106 CrossRef PubMed.
- A. A. Holmes, N. M. Tubman and C. J. Umrigar, Heat-Bath Configuration Interaction: An Efficient Selected Configuration Interaction Algorithm Inspired by Heat-Bath Sampling, J. Chem. Theory Comput., 2016, 12, 3674 CrossRef CAS PubMed.
- H. Nakatsuji, Equation for the direct determination of the density matrix, Phys. Rev. A: At., Mol., Opt. Phys., 1976, 14, 41 CrossRef CAS.
- D. A. Mazziotti, Contracted Schrödinger equation: Determining quantum energies and two-particle density matrices without wave functions, Phys. Rev. A: At., Mol., Opt. Phys., 1998, 57, 4219 CrossRef CAS.
- D. A. Mazziotti, Realization of Quantum Chemistry without Wave Functions through First-Order Semidefinite Programming, Phys. Rev. Lett., 2004, 93, 213001 CrossRef PubMed.
- M. Piris, Natural Orbital Functional Theory, in Reduced-Density-Matrix Mechanics: with Application to Many-Electron Atoms and Molecules, John Wiley & Sons, Ltd, 2007, ch. 14, pp. 385–427 Search PubMed.
- K. Pernal and K. J. H. Giesbertz, Reduced density matrix functional theory (RDMFT) and linear response time-dependent RDMFT (TD-RDMFT), in Density-Functional Methods for Excited States, ed. N. Ferré, M. Filatov, and M. Huix-Rotllant, Springer International Publishing, Cham, 2016, p. 125 Search PubMed.
- Z. Rolik and M. Kállay, A general-order local coupled-cluster method based on the cluster-in-molecule approach, J. Chem. Phys., 2011, 135, 104111 CrossRef PubMed.
- Z. Rolik, L. Szegedy, I. Ladjánszki, B. Ladóczki and M. Kállay, An efficient linear-scaling CCSD(T) method based on local natural orbitals, J. Chem. Phys., 2013, 139, 094105 CrossRef PubMed.
- Q. Ma, M. Schwilk, C. Köppl and H.-J. Werner, Scalable Electron Correlation Methods. 4. Parallel Explicitly Correlated Local Coupled Cluster with Pair Natural Orbitals (PNO-LCCSD-F12), J. Chem. Theory Comput., 2017, 13, 4871 CrossRef CAS PubMed.
- J. S. Kurian, H.-Z. Ye, A. Mahajan, T. C. Berkelbach and S. Sharma, Toward Linear Scaling Auxiliary-Field Quantum Monte Carlo with Local Natural Orbitals, J. Chem. Theory Comput., 2024, 20, 134 CrossRef CAS PubMed.
- J. P. Dowling and G. J. Milburn, Quantum technology: The second quantum revolution, Philos. Trans. R. Soc., A, 2003, 361, 1655 CrossRef PubMed.
- M. Atzori and R. Sessoli, The Second Quantum Revolution: Role and Challenges of Molecular Chemistry, J. Am. Chem. Soc., 2019, 141, 11339 CrossRef CAS PubMed.
- I. H. Deutsch, Harnessing the Power of the Second Quantum Revolution, PRX Quantum, 2020, 1, 020101 CrossRef.
- Y. Cao, J. Romero, J. P. Olson, M. Degroote, P. D. Johnson, M. Kieferová, I. D. Kivlichan, T. Menke, B. Peropadre, N. P. D. Sawaya, S. Sim, L. Veis and A. Aspuru-Guzik, Quantum chemistry in the age of quantum computing, Chem. Rev., 2019, 119, 10856 CrossRef CAS PubMed.
- A. J. McCaskey, Z. P. Parks, J. Jakowski, S. V. Moore, T. D. Morris, T. S. Humble and R. C. Pooser, Quantum chemistry as a benchmark for near-term quantum computers, npj Quantum Inf., 2019, 5, 99 CrossRef.
- S. McArdle, S. Endo, A. Aspuru-Guzik, S. C. Benjamin and X. Yuan, Quantum computational chemistry, Rev. Mod. Phys., 2020, 92, 015003 CrossRef CAS.
- S. Lee, J. Lee, H. Zhai, Y. Tong, A. M. Dalzell, A. Kumar, P. Helms, J. Gray, Z.-H. Cui, W. Liu, M. Kastoryano, R. Babbush, J. Preskill, D. R. Reichman, E. T. Campbell, E. F. Valeev, L. Lin and G. K.-L. Chan, Evaluating the evidence for exponentialquantum advantage in ground-state quantum chemistry, Nat. Commun., 2023, 14, 1952 CrossRef CAS PubMed.
- G. Li Manni, W. Dobrautz and A. Alavi, Compression of Spin-Adapted Multiconfigurational Wave Functions in Exchange-Coupled Polynuclear Spin Systems, J. Chem. Theory Comput., 2020, 16, 2202 CrossRef CAS PubMed.
- K. Liao, L. Ding, and C. Schilling, Unveiling Intrinsic Many-Body Complexity by Compressing Single-Body Triviality, arXiv, 2024, preprint, arXiv:2402.16841 DOI:10.48550/arXiv.2402.16841.
- A. Georges, G. Kotliar, W. Krauth and M. J. Rozenberg, Dynamical mean-field theory of strongly correlated fermion systems and the limit of infinite dimensions, Rev. Mod. Phys., 1996, 68, 13 CrossRef CAS.
- G. Knizia and G. K.-L. Chan, Density matrix embedding: A simple alternative to dynamical mean-field theory, Phys. Rev. Lett., 2012, 109, 186404 CrossRef PubMed.
- G. Knizia and G. K.-L. Chan, Density matrix embedding: A strong-coupling quantum embedding theory, J. Chem. Theory Comput., 2013, 9, 1428 CrossRef CAS PubMed.
- F. A. Wolf, A. Go, I. P. McCulloch, A. J. Millis and U. Schollwöck, Imaginary-Time Matrix Product State Impurity Solver for Dynamical Mean-Field Theory, Phys. Rev. X, 2015, 5, 041032 Search PubMed.
- Q. Sun and G. K.-L. Chan, Quantum embedding theories, Acc. Chem. Res., 2016, 49, 2705 CrossRef CAS PubMed.
- R. Schade and P. E. Blöchl, Adaptive cluster approximation for reduced density-matrix functional theory, Phys. Rev. B, 2018, 97, 245131 CrossRef CAS.
- D. Zgid and G. K.-L. Chan, Dynamical mean-field theory from a quantum chemical perspective, J. Chem. Phys., 2011, 134, 094115 CrossRef PubMed.
- S. Sekaran, M. Tsuchiizu, M. Saubanére and E. Fromager, Householder-transformed density matrix functional embedding theory, Phys. Rev. B, 2021, 104, 035121 CrossRef CAS.
- P.-O. Löwdin, Studies in perturbation theory: Part I. An elementary iteration-variation procedure for solving the Schrödinger equation by partitioning technique, J. Mol. Spectrosc., 1963, 10, 12 CrossRef.
- S. R. White, Numerical canonical transformation approach to quantum many-body problems, J. Chem. Phys., 2002, 117, 7472 CrossRef CAS.
- E. Neuscamman, T. Yanai and G. K.-L. Chan, A review of canonical transformation theory, Int. Rev. Phys. Chem., 2010, 29, 231 Search PubMed.
- F. A. Evangelista, A driven similarity renormalization group approach to quantum many-body problems, J. Chem. Phys., 2014, 141, 054109 CrossRef PubMed.
- M. Ochi, R. Arita and S. Tsuneyuki, Correlated Band Structure of a Transition Metal Oxide ZnO Obtained from a Many-Body Wave Function Theory, Phys. Rev. Lett., 2017, 118, 026402 CrossRef PubMed.
- H. Luo and A. Alavi, Combining the Transcorrelated Method with Full Configuration Interaction Quantum Monte Carlo: Application to the Homogeneous Electron Gas, J. Chem. Theory Comput., 2018, 14, 1403 CrossRef CAS PubMed.
- W. Dobrautz, H. Luo and A. Alavi, Compact numerical solutions to the two-dimensional repulsive Hubbard model obtained via nonunitary similarity transformations, Phys. Rev. B, 2019, 99, 075119 CrossRef CAS.
- K. Liao, T. Schraivogel, H. Luo, D. Kats and A. Alavi, Towards efficient and accurate ab initio solutions to periodic systems via transcorrelation and coupled cluster theory, Phys. Rev. Res., 2021, 3, 033072 CrossRef CAS.
- K. Liao, H. Zhai, E. M. Christlmaier, T. Schraivogel, P. L. Ríos, D. Kats and A. Alavi, Density Matrix Renormalization Group for Transcorrelated Hamiltonians: Ground and Excited States in Molecules, J. Chem. Theory Comput., 2023, 19, 1734 CrossRef CAS PubMed.
- N. P. Bauman, B. Peng, and K. Kowalski, Coupled cluster downfolding techniques: A review of existing applications in classical and quantum computing for chemical systems, arXiv, 2023, preprint, arXiv:2303.00087 DOI:10.48550/arXiv.2303.00087.
- K. Kowalski and N. P. Bauman, Quantum Flow Algorithms for Simulating Many-Body Systems on Quantum Computers, Phys. Rev. Lett., 2023, 131, 200601 CrossRef CAS PubMed.
- O. Tishchenko, J. Zheng and D. G. Truhlar, MultireferenceModel Chemistries for Thermochemical Kinetics, J. Chem. Theory Comput., 2008, 4, 1208 CrossRef CAS PubMed.
- T. J. Lee and P. R. Taylor, A diagnostic for determining the quality of single-reference electron correlation methods, Int. J. Quantum Chem., 1989, 36, 199 CrossRef.
- C. L. Janssen and I. M. B. Nielsen, New diagnostics for coupled-cluster and Møller–Plesset perturbation theory, Chem. Phys. Lett., 1998, 290, 423 CrossRef CAS.
- C. J. Stein and M. Reiher, Measuring multi-configurational character by orbital entanglement, Mol. Phys., 2017, 115, 2110 CrossRef CAS.
- R. F. Werner, Quantum states with Einstein-Podolsky-Rosen correlations admitting a hidden-variable model, Phys. Rev. A: At., Mol., Opt. Phys., 1989, 40, 4277 CrossRef PubMed.
- V. Vedral, M. B. Plenio, M. A. Rippin and P. L. Knight, Quantifying entanglement, Phys. Rev. Lett., 1997, 78, 2275 CrossRef CAS.
- L. Henderson and V. Vedral, Classical, quantum and total correlations, J. Phys. A, 2001, 34, 6899 CrossRef.
- B. Groisman, S. Popescu and A. Winter, Quantum, classical, and total amount of correlations in a quantum state, Phys. Rev. A: At., Mol., Opt. Phys., 2005, 72, 032317 CrossRef.
- I. Bengtsson and K. Życzkowski, Geometry of Quantum States: an Introduction to Quantum Entanglement, Cambridge University Press, Cambridge, 2nd edn, 2017 Search PubMed.
- K. Modi, T. Paterek, W. Son, V. Vedral and M. Williamson, Unified view of quantum and classical correlations, Phys. Rev. Lett., 2010, 104, 080501 CrossRef PubMed.
- C. H. Bennett, G. Brassard, C. Crépeau, R. Jozsa, A. Peres and W. K. Wootters, Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels, Phys. Rev. Lett., 1993, 70, 1895 CrossRef PubMed.
- M. A. Nielsen and I. L. Chuang, Quantum Computation and Quantum Information: 10th Anniversary Edition, Cambridge University Press, 2010 Search PubMed.
- C. H. Bennett and S. J. Wiesner, Communication via one- and two-particle operators on Einstein-Podolsky-Rosen states, Phys. Rev. Lett., 1992, 69, 2881 CrossRef PubMed.
- C. Krumnow, L. Veis, Ö. Legeza and J. Eisert, Fermionic orbital optimization in tensor network states, Phys. Rev. Lett., 2016, 117, 210402 CrossRef CAS PubMed.
- C. J. Stein and M. Reiher, Automated selection of active orbital spaces, J. Chem. Theory Comput., 2016, 12, 1760 CrossRef CAS PubMed.
- L. Ding, S. Knecht and C. Schilling, Quantum Information-Assisted Complete Active Space Optimization (QICAS), J. Phys. Chem. Lett., 2023, 14, 11022 CrossRef CAS PubMed.
- G.-C. Wick, A. S. Wightman and E. P. Wigner, Superselection rule for charge, Phys. Rev. D: Part. Fields, 1970, 1, 3267 CrossRef.
- G.-C. Wick, A. S. Wightman and E. P. Wigner, The intrinsic parity of elementary particles, Phys. Rev., 1952, 88, 101 CrossRef.
- V. Y. A. J. Coleman, Reduced Density Matrices. Coulson's Challenge, Springer-Verlag Berlin, 2000 Search PubMed.
- K. Landsman, Foundations of Quantum Theory, Springer Cham, 2017 Search PubMed.
- I. E. Segal, Irreducible representations of operator algebras, Bull. Amer. Math. Soc., 1947, 53, 73 CrossRef.
- I. Gelfand and M. Neumark, On the imbedding of normed rings into the ring of operators in Hilbert space, Recreat. Math., 1943, 54, 197 Search PubMed.
- P. Zanardi, Virtual quantum subsystems, Phys. Rev. Lett., 2001, 87, 077901 CrossRef CAS PubMed.
- E. Chitambar, D. Leung, L. Mančinska, M. Ozols and A. Winter, Everything you always wanted to know about LOCC (but were afraid to ask), Commun. Math. Phys., 2014, 328, 303 CrossRef.
- G. Lindblad, Expectations and entropy inequalities for finite quantum systems, Commun. Math. Phys., 1974, 39, 111 CrossRef.
- V. Vedral, The role of relative entropy in quantum information theory, Rev. Mod. Phys., 2002, 74, 197 CrossRef.
- F. Hiai and D. Petz, The proper formula for relative entropy and its asymptotics in quantum probability, Commun. Math. Phys., 1991, 143, 99 CrossRef.
- M. Tomamichel, Quantum Information Processing with Finite Resources, Springer International Publishing, 2016 Search PubMed.
- M. M. Wolf, F. Verstraete, M. B. Hastings and J. I. Cirac, Area laws in quantum systems: Mutual information and correlations, Phys. Rev. Lett., 2008, 100, 070502 CrossRef PubMed.
- J. Watrous, Lecture Notes on the “Theory of Quantum Information, 2011 Search PubMed.
- C. Schilling, Orbital Entanglement and Correlation, in Simulating Correlations with Computers, ed. E. Pavarini and E. Koch, Forschungszentrum Jülich GmbH Zentralbibliothek, Verlag, 2021, ch. 9, p. 261 Search PubMed.
- A. K. Ekert, Quantum cryptography based on Bell's theorem, Phys. Rev. Lett., 1991, 67, 661 CrossRef PubMed.
- H. Buhrman, R. Cleve, S. Massar and R. de Wolf, Nonlocality and communication complexity, Rev. Mod. Phys., 2010, 82, 665 CrossRef.
- E. Chitambar and G. Gour, Quantum resource theories, Rev. Mod. Phys., 2019, 91, 025001 CrossRef.
- K. G. H. Vollbrecht and R. F. Werner, Entanglement measures under symmetry, Phys. Rev. A: At., Mol., Opt. Phys., 2001, 64, 062307 CrossRef.
- M. B. Plenio and S. Virmani, An introduction to entanglement measures, arXiv, 2006, preprint, arXiv:quant-ph/0504163 DOI:10.48550/arXiv.quant-ph/0504163.
- J. Oppenheim, M. Horodecki, P. Horodecki and R. Horodecki, Thermodynamical approach to quantifying quantum correlations, Phys. Rev. Lett., 2002, 89, 180402 CrossRef PubMed.
- S. Luo, Using measurement-induced disturbance to characterize correlations as classical or quantum, Phys. Rev. A: At., Mol., Opt. Phys., 2008, 77, 022301 CrossRef.
- V. Madhok and A. Datta, Interpreting quantum discord through quantum state merging, Phys. Rev. A: At., Mol., Opt. Phys., 2011, 83, 032323 CrossRef.
- X. Wu and T. Zhou, Geometric discord: A resource for increments of quantum key generation through twirling, Sci. Rep., 2015, 5, 13365 CrossRef CAS PubMed.
- M. Piani, S. Gharibian, G. Adesso, J. Calsamiglia, P. Horodecki and A. Winter, All nonclassical correlations can be activated into distillable entanglement, Phys. Rev. Lett., 2011, 106, 220403 CrossRef PubMed.
- I. Devetak, A. W. Harrow and A. J. Winter, A resource framework for quantum shannon theory, IEEE Trans. Inf. Theory, 2008, 54, 4587 Search PubMed.
- L. Ding, S. Knecht, Z. Zimborás and C. Schilling, Quantum correlations in molecules: From quantum resourcing to chemical bonding, Quantum Sci. Technol., 2023, 8, 015015 CrossRef.
- M. Johansson, Comment on ‘Reasonable fermionic quantum information theories require relativity’, arXiv, 2016, preprint, arXiv:1610.00539 DOI:10.48550/arXiv:1610.00539.
- L. Ding, S. Mardazad, S. Das, S. Szalay, U. Schollwöck, Z. Zimborás and C. Schilling, Concept of orbital entanglement and correlation in quantum chemistry, J. Chem. Theory Comput., 2021, 17, 79 CrossRef CAS PubMed.
- H. M. Wiseman, S. D. Bartlett, and J. A. Vaccaro, Ferreting out the fluffy bunnies: Entanglement constrained by generalized superselection rules, in Laser Spect., World Scientific, 2004, pp. 307–314 Search PubMed.
- S. D. Bartlett and H. M. Wiseman, Entanglement constrained by superselection rules, Phys. Rev. Lett., 2003, 91, 097903 CrossRef PubMed.
- N. Schuch, F. Verstraete and J. I. Cirac, Quantum entanglement theory in the presence of superselection rules, Phys. Rev. A: At., Mol., Opt. Phys., 2004, 70, 042310 CrossRef.
- L. Ding, G. Dünnweber and C. Schilling, Physical entanglement between localized orbitals, Quantum Sci. Technol., 2024, 9, 015005 CrossRef.
- D. Aliverti, K. Chatterjee, J. Liebert, L. Ding, and C. Schilling, Single particles are not standard subsystems of a system of many identical particles, unpublished.
- H. Araki, On quasifree states of CAR and Bogoliubov automorphisms, Publ. Res. Inst. Math. Sci., 1970, 6, 385 Search PubMed.
- J. Blaizot and G. Ripka, Quantum Theory of Finite Systems, MIT Press, 1986 Search PubMed.
- V. Bach, E. Lieb and J. Solovej, Generalized Hartree-Fock theory and the Hubbard model, J. Stat. Phys., 1994, 76, 3 CrossRef.
- A. D. Gottlieb and N. J. Mauser, Properties of nonfreeness: An entropy measure of electron correlation, Int. J. Quantum Inf., 2007, 5, 815 CrossRef.
- A. Gottlieb and N. Mauser, Correlation in fermion or boson systems as the minimum of entropy relative to all free states, arXiv, 2014, preprint, arXiv:1403.7640 DOI:10.48550/arXiv.1403.7640.
- J. Surace and L. Tagliacozzo, Fermionic Gaussian states: An introduction to numerical approaches, SciPost Phys. Lect. Notes, 2022, 54 CrossRef.
- D. W. Robinson, A theorem concerning the positive metric, Commun. Math. Phys., 1965, 1, 89 CrossRef.
- V. Bach, Hartree-Fock theory, Lieb's variational principle, and their generalizations, arXiv, 2022, arXiv:2209.10189 DOI:10.48550/arXiv.2209.10189.
- A. D. Gottlieb and N. J. Mauser, New measure of electron correlation, Phys. Rev. Lett., 2005, 95 CrossRef CAS PubMed.
- N. Gigena and R. Rossignoli, Entanglement in fermion systems, Phys. Rev. A: At., Mol., Opt. Phys., 2015, 92, 042326 CrossRef.
- A. W. Marshall, I. Olkin, and B. C. Arnold, Inequalities: Theory of Majorization and its Application, Springer, New York, NY, 2010 Search PubMed.
- M. Nielsen and G. Vidal, Majorization and the interconversion of bipartite states, Quantum Inf. Comput., 2001, 1, 76 Search PubMed.
- C. A. Coulson, Present state of molecular structure calculations, Rev. Mod. Phys., 1960, 32, 170 CrossRef CAS.
- A. J. Coleman, Reduced density matrices—Then and now, Int. J. Quantum Chem., 2001, 85, 196 CrossRef CAS.
- A. J. Coleman, Structure of fermion density matrices, Rev. Mod. Phys., 1963, 35, 668 CrossRef.
- C. Garrod and J. K. Percus, Reduction of the N-Particle variational problem, J. Math. Phys., 1964, 5, 1756 CrossRef CAS.
- H. Kummer, N-representability problem for reduced density matrices, J. Math. Phys., 1967, 8, 2063 CrossRef.
- D. A. Mazziotti, Structure of fermionic density matrices: Complete N-Representability conditions, Phys. Rev. Lett., 2012, 108, 263002 CrossRef PubMed.
- D. A. Mazziotti, Quantum many-body theory from a solution of the N-Representability problem, Phys. Rev. Lett., 2023, 130, 153001 CrossRef CAS PubMed.
- C. Schilling, Communication: Relating the pure and ensemble density matrix functional, J. Chem. Phys., 2018, 149, 231102 CrossRef PubMed.
- J. Liebert, F. Castillo, J.-P. Labbé and C. Schilling, Foundation of one-particle reduced density matrix functional theory for excited states, J. Chem. Theory Comput., 2022, 18, 124 CrossRef CAS PubMed.
- M. Penz and R. van Leeuwen, Density-functional theory on graphs, J. Chem. Phys., 2021, 155, 244111 CrossRef CAS PubMed.
- T. Helgaker and A. M. Teale, Lieb variation principle in density-functional theory, arXiv, 2022, preprint, arXiv:2204.12216 DOI:10.48550/arXiv.2204.12216.
- J. Liebert, A. Y. Chaou and C. Schilling, Refining and relating fundamentals of functional theory, J. Chem. Phys., 2023, 158, 214108 CrossRef CAS PubMed.
- E. H. Lieb, Variational principle for many-fermion systems, Phys. Rev. Lett., 1981, 46, 457 CrossRef CAS.
- V. Bach, S. Breteaux, H. K. Knörr and E. Menge, Generalization of Lieb's variational principle to Bogoliubov–Hartree–Fock theory, J. Math. Phys., 2014, 55, 012101 CrossRef.
- A. Müller, Explicit approximate relation between reduced two- and one-particle density matrices, Phys. Lett. A, 1984, 105, 446 CrossRef.
- M. A. Buijse and E. J. Baerends, An approximate exchange-correlation hole density as a functional of the natural orbitals, Mol. Phys., 2002, 100, 401 CrossRef CAS.
- O. Gritsenko, K. Pernal and E. J. Baerends, An improved density matrix functional by physically motivated repulsive corrections, J. Chem. Phys., 2005, 122, 204102 CrossRef PubMed.
- M. Piris, Global natural orbital functional: Towards the complete description of the electron correlation, Phys. Rev. Lett., 2021, 127, 233001 CrossRef CAS PubMed.
- J. Schliemann, J. I. Cirac, M. Kuśś, M. Lewenstein and D. Loss, Quantum correlations in two-fermion systems, Phys. Rev. A: At., Mol., Opt. Phys., 2001, 64, 022303 CrossRef.
- V. Vedral and M. B. Plenio, Entanglement measures and purification procedures, Phys. Rev. A: At., Mol., Opt. Phys., 1998, 57, 1619 CrossRef CAS.
- Q. Sun, T. C. Berkelbach, N. S. Blunt, G. H. Booth, S. Guo, Z. Li, J. Liu, J. D. McClain, E. R. Sayfutyarova, S. Sharma, S. Wouters and G. K.-L. Chan, PySCF: The Python-based simulations of chemistry framework, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1340 Search PubMed.
Footnote |
| † Note that I is also sometimes referred to as ‘total correlation’ to highlight that it contains in general both classical and quantum correlations |
| This journal is © The Royal Society of Chemistry 2024 |