Machine learning-aided engineering of a cytochrome P450 for optimal bioconversion of lignin fragments

Abstract

Using machine learning, molecular dynamics simulations, and density functional theory calculations we gain insight into the selectivity patterns of substrate activation by the cytochromes P450. In nature, the reactions catalyzed by the P450s lead to the biodegradation of xenobiotics, but recent work has shown that fungi utilize P450s for the activation of lignin fragments, such as monomer and dimer units. These fragments often are the building blocks of valuable materials, including drug molecules and fragrances, hence a highly selective biocatalyst that can produce these compounds in good yield with high selectivity would be an important step in biotechnology. In this work a detailed computational study is reported on two reaction channels of two P450 isozymes, namely the O-deethylation of guaethol by CYP255A and the O-demethylation versus aromatic hydroxylation of p-anisic acid by CYP199A4. The studies show that the second-coordination sphere plays a major role in substrate binding and positioning, heme access, and in the selectivity patterns. Moreover, the local environment affects the kinetics of the reaction through lowering or raising barrier heights. Furthermore, we predict a site-selective mutation for highly specific reaction channels for CYP199A4.

---

Introduction

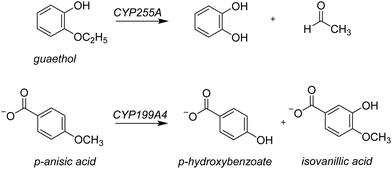
Lignin is one of the most common polymer structures in nature and is mainly present in the secondary cell wall of plants. The lignin structure mostly contains aromatic and phenolic constituents bridged by ether bonds. Its biodegradation by peroxides typically reduces these polymers to monomer and dimer units,¹ that in nature form the building blocks of natural products. In biotechnology, however, these lignin fragments have broad use for the biosynthesis of fragrances, resins, and drug molecules, to name just a few. As lignin is a sustainable compound from plants, harnessing the biotechnological potential of such lignin fragments is an attractive way to create a greener production line in many industrial settings. However, often natural enzymes produce a mixture of products making the reaction of limited interest for industrial applications. On the other hand, if through site-selective mutations the processes can be optimized to reduce waste-products and enhance the selectivity of specific products this will enhance their use. To gain insight into the renewable synthesis of valuable chemicals from lignin monomers, we performed a computational study targeting the activation of lignin fragments by cytochrome P450 enzymes and their product distributions.

Cytochromes P450s (CYPs) are highly efficient enzymes for the biosynthesis and biodegradation of chemicals in nature and are also found in various parts of the human body.² Particularly, in the liver there are a range of CYP450 isozymes involved in the biodegradation of xenobiotics while several other CYP450 isozymes take part in the biosynthesis of hormones. The CYPs typically act as mono-oxygenases and install one oxygen atom from O₂ into a substrate, usually through an aliphatic or aromatic hydroxylation reaction.² Although the CYPs are not known to activate lignin chains, there is evidence they react with lignin fragments, i.e. monomers, dimers, or trimers. To be specific, two lignin-degrading CYP isozymes have been identified recently, namely CYP255A, also known as GcoA, and CYP199A4. The former has been shown to take on a diversity of lignin monomers and react these through oxygen activation to the corresponding products arising from O-dealkylation and aromatic hydroxylation.³ Thus, CYP255A binds the lignin fragment guaethol and performs the oxidative O-deethylation to form catechol and acetaldehyde products,⁴ while the CYP199A4 isozyme reacts with the lignin fragment p-anisic acid to give p-hydroxybenzoate through O-demethylation.^4b,5 On the other hand, the Nocardia corallina bacterium produces a mixture of p-hydroxybenzoate and isovanillic acid products through CYP activation of p-anisic acid,⁶Scheme 1. Recent work on the CYP199A4 S244D mutant showed enhanced reactivity as compared to wildtype with alkyl hydroxylation as the dominant pathway in a reaction with p-alkylbenzoic acids as substrates.⁷ In CYP199A2 the engineering of active site Ser residues to an anionic amino acid led to a change in regioselectivity of p-cresol activation.⁸ More recently, Cong et al. engineered the H₂O₂ access channels in CYP199A4 and showed enhanced peroxygenase activity.⁹ Similarly, biomimetic nonheme iron complexes react p-anisic acid with H₂O₂ to form a mixture of products originating from O-demethylation and ortho-hydroxylation.¹⁰

Scheme 1 Guaethol and p-anisic acid activation by P450 enzymes.

In the past few years, several computational studies have been reported on lignin-fragment activation by CYP isozymes.^4,11 These studies report on the mechanistic features of the reaction between the active species of CYP isozymes, namely Compound I (CpdI or the iron(IV)-oxo heme cation radical species) and lignin fragments. In particular, the reaction mechanisms between CpdI and syringol and guaiacol as substrates for O-demethylation reactions were reported.^4a,11a,b The studies showed that hydrogen atom abstraction from a phenolic O–H group has low barriers and alternative pathways can only proceed when the phenol group of the substrate points away from the heme and/or forms hydrogen bonds with the protein. Furthermore, engineering cytochrome P450 substrate specificity can be a way of optimizing small compound production and creating environmentally friendly production lines of valuable materials. Computational modelling was shown to be useful to predict enzyme mutants and is regularly done alongside experiment.¹² For instance, computational guided protein engineering converted S-mandelate synthase into R-mandelate synthase.¹³ In this work, we combine machine learning, molecular dynamics, and quantum mechanics approaches to investigate product distributions of engineered protein structures and study the conversion of p-anisic acid and guaethol by various P450 variants.

Methods

MD simulations

The guaethol-bound CYP255A and p-anisic acid-bound CYP199A4 structures were taken from Protein Data Bank (5OMS and 4DO1 PDB IDs, respectively).^4a,5b,14 The two structures were cleaned of solvent molecules and two enzymatic structures were created for the CYP199A4 system, namely one where the substrate was retained in the crystal structure coordinates and one where the substrate was removed and then docked back into the structure with Autodock Vina.¹⁵ These two models for the CYP199A4 system had the substrate in a similar orientation and resulted in enzyme folds that were very close (ESI,† Fig. S5). Hydrogen atoms were added to each of the structures using the H++ webserver, considering pH 7 conditions.¹⁶ All protonation states of titratable residues were further manually inspected, and all carboxylate groups were in their deprotonated forms, while all Arg and Lys side chains were protonated. The histidine amino acid side chains in the enzyme structures were all taken as singly protonated on either the N_δ or N_ε atom. The heme was manually converted into a Compound I (CpdI) structure by adding an oxygen atom to the heme at a distance of 1.686 Å above the iron atom and the heme forcefield parameters were determined with the MCPB.py routine available in Amber 2018.^17,18 Subsequently, the LEaP module as available in Amber 2018 was used to solvate each structure with TIP3P water molecules in rectangular box with a 10 Å of padding in all directions, while sodium and chloride ions were added to create a simulation box with net charge zero.¹⁹ The protein and substrate atoms were described by the ff14SB force field,²⁰ and each system was subjected to 10 000 steps of energy minimization, that is 5000 of steepest descent followed by 5000 of conjugate gradient. The energy-minimized structures were then heated to 300 K and equilibrated in three consecutive steps at constant pressure for 40 picoseconds, in steps of 2 fs. An MD production run without geometric constraints was performed for 750 ns for CYP255A and 1000 ns for its mutants.

DFT cluster model calculations

In this work we use QM cluster models, where we take the oxidant, substrate and a second-coordination sphere region that determines the shape and size of the substrate binding pocket and helps with positioning the substrate and oxidant in the enzyme. These cluster models have been used extensively to gain insight into enzymatic reaction mechanisms, the electronic and spectroscopic properties of short-lived intermediates of catalytic cycles and predict product distributions of wildtype and mutant structures.²¹ In particular, in recent studies on caffeine activation by CYP1A2 cluster models of about 300 atoms were shown to reproduce the experimental product distributions quite well even though the absolute barriers differed by less than 4 kcal mol⁻¹.²² Furthermore, using QM cluster calculations on hydrogen atom abstraction from taurine by the nonheme iron(IV)-oxo species of taurine/α-ketoglutarate-dependent dioxygenase reproduced the experimentally obtained free energy of activation to within 1 kcal mol⁻¹.²³ As such, these cluster models of larger than 200 atoms should give an accurate representation of enzymatic reactivity.

The snapshot selection from the MD runs to create cluster models was based on two variables, namely the number of hydrogen bonds between the substrate and the protein and the root-mean-square-deviation (RMSD) of protein residues with respect to their average structure. Thus, the MD trajectory for each system was analysed and the structure (snapshot) that was geometrically the closest to the average structure of that MD was selected. Scheme 2 shows the wildtype QM cluster models of CYP255A with guaethol bound and CYP199A4 with p-anisic acid bound. Thus, the CYP199A4 cluster model was composed by 255 atoms and included a truncated heme with all side chains replaced by hydrogen atoms, the iron atom with its distal oxo and axial thiolate ligands, the p-anisic acid molecule, two water molecules, and the side chains of the residues Arg₉₂, Ser₉₅, Leu₉₆, Glu₉₉, Phe₁₈₂, Val₁₈₁, Phe₁₈₅, Arg₂₄₃, Ser₂₄₄, Ser₂₄₇, Ala₂₄₈, Gly₂₄₉, Thr₂₅₂ and Phe₂₉₈. The CYP255A cluster model was composed of 306 atoms and involved the truncated heme group, the iron atom, the distal oxo group and the axial Cys residue abbreviated as methylthiolate. In addition, the model contained the guaethol substrate, two water molecules, and the side chains of the residues Phe₇₅, Ile₈₀, Ile₈₁, Phe₁₆₉, the chain Val₂₄₁-Tyr₂₄₂-Leu₂₄₃-Leu₂₄₄-Gly₂₄₅-Ala₂₄₆-Met₂₄₇-Gln₂₄₈-Glu₂₄₉, Ile₂₉₂, the dimer Ala₂₉₅-Thr₂₉₆ and Phe₃₉₅. The net charge of the CYP255A QM cluster model was −1, whereas that of CYP199A4 was zero. All cluster model calculations were run without geometric constraints as the use of constraints often leads to a string of small imaginary frequencies that affects the accuracy of the free energy values. However, the absence of constraints in the structure and a comparison of the optimized geometries with the crystal structure coordinates and the MD simulation results show little changes in the position of the protein chains.

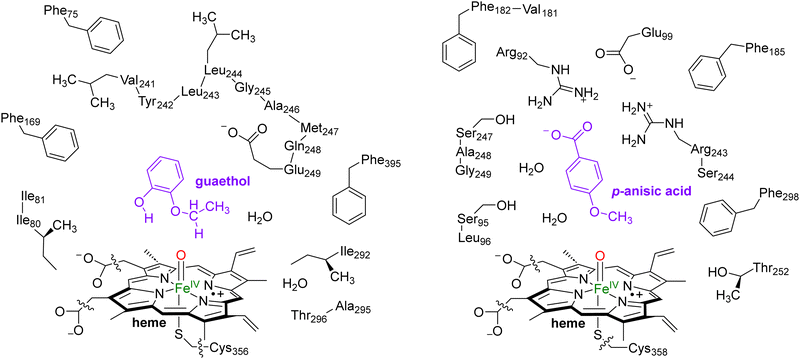Scheme 2 QM Cluster models of CYP255A with guaethol bound (left) and CYP199A4 with p-anisic acid bound (right) studied for wildtype protein reactivities.

Geometry optimizations, analytical frequencies and constraint geometry scans were carried out in Gaussian-09 using the unrestricted hybrid density functional method UB3LYP with the LANL2DZ basis set with effective core potential on iron, and the 6-31G* basis set for the C, H, N, O, and S atoms (basis set BS1).^24–26 Full geometry optimizations for the transition state structures were performed and their outcome was confirmed by a frequency calculation. A single imaginary frequency confirmed the correct vibrational distortion of the structure to be a transition state, while local minima were confirmed by finding real frequencies only. Single-point calculations were done with a continuum polarized conductor model with a dielectric constant mimicking chlorobenzene (ε = 5.7),²⁷ and an enlarged basis set consisting of 6-311+G* basis set on H, C, N, O, and S atoms and LACV3P+ basis set with core potential on iron (basis set BS2). Free energies were calculated at a temperature of 298 K. These methods have been validated against experimental free energies of activation for biomimetic oxygen atom transfer reactions and reproduced experimental data within 3 kcal mol⁻¹.²⁸ In addition, using large cluster models the selectivity patterns of substrate activation could be predicted and gave the correct trends compared to experimental product distributions.²⁹

Results and discussion

Wildtype MD simulations for CYP255A and CYP199A4

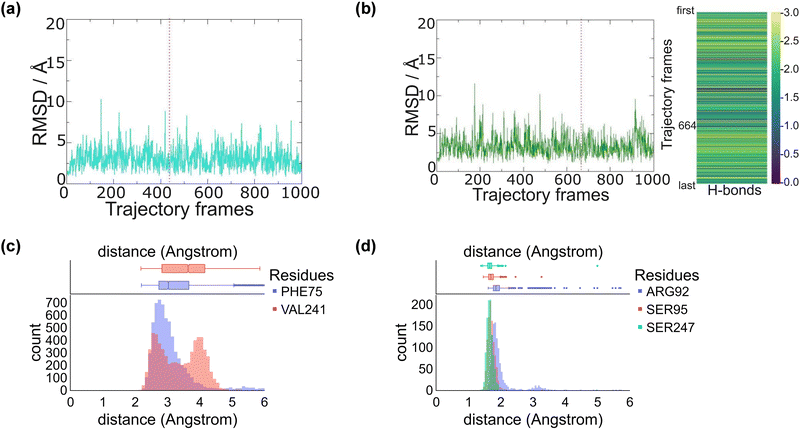
We started the work from the crystal structure coordinates for CYP255A from the protein databank file (pdb) 5OMS, while we used the 4DO1 pdb for CYP199A4.^4a,5b,14 We then manually created a CpdI active site in each structure by addition of an oxo group to the sixth ligand position of iron from the heme to form the iron(IV)-oxo heme cation radical species. Substrates – guaethol and p-anisic acid – were either kept as they were in the crystal structures or re-docked onto the binding pocket (ESI,† Fig. S4–S6). Thereafter, an all-atom NPT molecular dynamics (MD) simulation was performed for each system, see ESI,† Fig. S7–S20. The all-atoms root-mean-square-deviation (RMSD) for each MD trajectory stabilizes within 20–30 ns (see ESI,† Fig. S7 and S14) for the protein, substrate and heme atoms. We then plotted the RMSD values with respect to the average structure and show these plots for CYP255A and CYP199A4 in Fig. 1. As can be seen the structures are highly stable with minimal changes along the MD run that preserve the overall fold of the protein.

Fig. 1 Snapshot selection and average substrate–protein distances as obtained from the MD simulations. RMSD is plotted with respect to the average structure from the MD simulation. (a) RMSD of CYP255A with the selected snapshot highlighted with a dashed line. (b) RMSD of CYP199A4 with the selected snapshot highlighted with a dashed line and the number of hydrogen bonds between substrate and active site residues for each snapshot on the right. (c) Substrate–protein distances during the MD simulation on CYP255A. (d) Substrate–protein distances during the MD simulation on CYP199A4.

We also analysed the position of the substrate in the binding pocket along the MD simulations on CYP255A and CYP199A4, see Fig. 1(c) and (d). Thus, in CYP199A4 substrate p-anisic acid is bound tightly through its carboxylate in a salt bridge interaction with the side chain of Arg₉₂ at a distance well below 2 Å. In addition, there are short hydrogen bonding interactions between the substrate and the alcohol groups of Ser₉₅ and Ser₂₄₇. In CYP255A, by contrast, substrate guaethol has no carboxylate group and only an ether and phenol group available for hydrogen bonding interactions with the protein. As such it is substantially weaker bound than p-anisic acid in the CYP450 active site. An analysis of nearby protein residues (Fig. 1(d)) gives the shortest interactions with the peptide chains of Phe₇₅ and Val₂₄₁.

Wildtype CpdI calculations for CYP255A and CYP199A4

The most representative frame from each trajectory (dashed lines in Fig. 1(a) and (b)) were used to create QM cluster models of the active site with substrate, oxidant, and second coordination sphere included. Scheme 2 above summarizes the wildtype structures and which residues of the second coordination sphere were included. These cluster models have been shown to reproduce experimentally determined product distributions and rate constants accurately and are good mimics for enzyme reactivity.^22,23 Model I is based on the CYP255A protein structure and had 306 atoms, whereas Model II is based on CYP199A4 and had 255 atoms, in both cases with their respective substrates in the same configuration as in their crystal structures. We conducted DFT calculations for the individual systems and optimized all structures in the gas phase without constraints, considering both doublet (S = 1/2) and quartet (S = 3/2) spin states, see Fig. 2. Previous calculations on CYP reactivity showed CpdI to react via multistate reactivity patterns on competing doublet and quartet spin state surfaces and consequently we started the calculations from a CpdI system with nearby substrate, i.e. the reactants complex RC.³⁰ Moreover, experimental work of Green et al. identified CpdI as the active species that reacts with substrate.³¹ The two spin states are close in energy (within 1 kcal mol⁻¹) for the two isozymes and similar first coordination sphere bonding patterns are seen (Fig. 2). In particular, the Fe–O distance falls within a small window of 1.633–1.645 Å, while the Fe–S distance ranges from 2.506–2.584 Å. These optimized geometries match previously obtained calculations with QM cluster models or QM/MM well.³⁰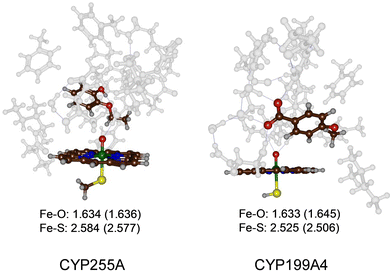

Fig. 2 UB3LYP/BS1 optimized geometries of the reactant CpdI cluster models of CYP255A and CYP199A4 WT with substrate bound. Bond lengths are in Å. Quartet spin data in parenthesis.

Reaction of CYP255A with guaethol

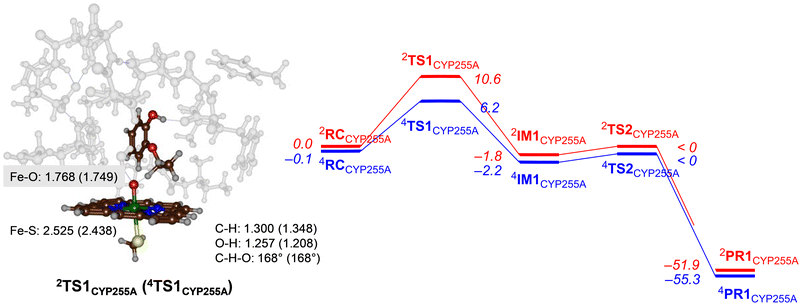
Next, we explored potential reaction mechanisms for the cluster models and for CYP255A we studied ethoxy group hydroxylation as a precursor to the O-deethylation reaction. The results for guaethol activation by a DFT cluster model of CpdI of CYP255A is shown in Fig. 3. The reaction starts with a hydrogen atom abstraction from the secondary C–H bond of the ethoxy group of guaethol via a transition state TS1_CYP255A to form a radical intermediate IM1_CYP255A. Thereafter a radical rebound via transition state TS2_CYP255A leads to the alcohol products complexes PR1_CYP255A. Constraint geometry scans for the radical rebound pathways on either spin state, however, find very small barriers of less than 2 kcal mol⁻¹ and hence are identified in Fig. 3 as “< 0 kcal mol⁻¹”. This is not unusual as often the radical rebound is very small in P450 calculated reaction mechanisms.³² The rate-determining step for guaethol activation by P450 CpdI is the initial hydrogen atom abstraction and has a free energy of activation of ΔG^‡ = 6.2 kcal mol⁻¹ on the quartet spin state surface and ΔG^‡ = 10.6 kcal mol⁻¹ on the doublet spin state surface. These barriers are very small and hence the reaction will proceed rapidly to form the alcohol product complexes with high exergonicity.

Fig. 3 UB3LYP calculated pathways for ethoxy group hydroxylation of guaethol by CYP255A wildtype model. Free energies (ΔG in kcal mol⁻¹) are with energies at BS2 level of theory and with ZPE, thermal and entropic corrections included at 298 K. Also shown are optimized geometries of the rate-determining transition states with distances in Å and angles in degrees.

The hydrogen atom abstraction transition states are shown on the right-hand-side of Fig. 3. Both structures bind the phenol group through a hydrogen bonding interaction with the peptide chain between Val₂₄₁–Tyr₂₄₂ and thereby position the ethoxy group in the direction of the heme. In the transition state structures the O–H distance is shorter than the C–H distance, which implicates a product-type geometry, where the structure is closer to the IM1 than the RC configuration. In particular, the O–H distance is 1.257 Å in ²TS1_CYP255A and 1.208 Å in ⁴TS1_CYP255A, while the C–H distance is 1.300 Å in ²TS1_CYP255A and 1.348 Å in ⁴TS1_CYP255A. Both transition states are characterized by a large imaginary frequency for the O–H–C stretch vibration. The structure and imaginary frequency of the calculated transition states matches previous calculations on transition states for hydrogen atom abstraction reactions reported previously.³³

Reaction of CYP199A4 with p-anisic acid

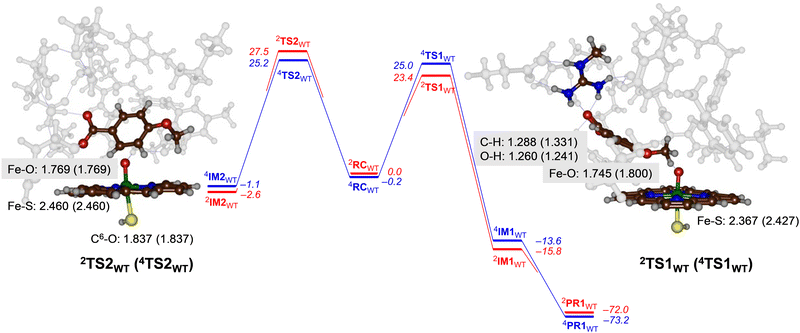
For CYP199A4 the activation of p-anisic acid was studied for aromatic hydroxylation of the C₃-position of the substrate as well as O-demethylation of the methoxy group. Thus, O-demethylation starts with a hydrogen atom abstraction transition state (TS1) to form a radical intermediate (IM1), which after OH rebound leads to the alcohol product complexes PR1. We ran extensive geometry scans for the OH rebound steps for the various models in all spin states and in all cases the OH rebound was facile and led to the formation of the alcohol product complexes with negligible barrier. This alcohol product PR1 is expected to release the alcohol product that in solution or with the help of a proton leads to formaldehyde release.³⁴ The alternative pathway tested from reactants was aromatic hydroxylation, which starts with an electrophilic transition state TS2 for C–O bond formation leading to an electrophilic intermediate IM2. In aromatic hydroxylation, the pathway was shown to proceed with proton transfer from the ipso-position to the heme followed by a shuttle to the oxygen atom to form phenol products.³⁵ In the calculations reported here the transition states for proton shuttle were small and negligible and the electrophilic transition state is rate-determining.

The transition state geometries were fully optimized and confirmed by frequency calculations. Reaction pathways for O-dealkylation were calculated for both CYP255A and CYP199A4, while aromatic hydroxylation was also explored for CYP199A4. The full set of DFT results are provided in the (ESI†). Fig. 4 shows the calculated free energy landscape and rate-determining transition states for aromatic hydroxylation and O-demethylation of p-anisic acid activation by CYP199A4. For both pathways, the initial transition state, TS1 or TS2, is rate-determining, while subsequent barriers are small and lead to a highly exothermic pathway to form products. The wildtype hydrogen atom abstraction barriers are ΔG = 23.4 kcal mol⁻¹ on the doublet spin surface and ΔG = 25.0 kcal mol⁻¹ on the quartet spin state. By contrast, the aromatic pathway has free energies of activation of ΔG = 27.5 kcal mol⁻¹ on the low-spin and ΔG = 25.2 kcal mol⁻¹ in the high-spin for the wildtype structure. A difference in free energy between the lowest free energy barrier for aliphatic hydrogen atom abstraction and electrophilic addition transition state is ΔG = 1.8 kcal mol⁻¹. Using transition state theory, this free energy difference would correspond to a product ratio of 95 : 5 for O-demethylation versus aromatic hydroxylation. Indeed, experimental work detected products originating from O-demethylation only.⁵

Fig. 4 UB3LYP calculated pathways for aromatic hydroxylation (from RC to the left) and methoxy group hydroxylation (from RC to the right) for CYP199A4 wildtype model. Free energies (ΔG in kcal mol⁻¹) are with energies at BS2 level of theory and with ZPE, thermal and entropic corrections included at 298 K. Also shown are optimized geometries of the rate-determining transition states with distances in Å.

Geometrically, the ^4,2TS1_WT structures are relatively central with similar C–H and O–H distances. They also are characterized with a large imaginary frequency (of i1323 cm⁻¹ for ⁴TS1_WT and i1834 cm⁻¹ for ²TS1_WT) representative of a hydrogen atom transfer that will incur a significant amount of quantum chemical tunnelling.³⁶ Structurally, the Fe−O and Fe−S distances in the transition state structures in Fig. 4 match those in Fig. 3 for CYP255A. Electronically the two models give the same electron transfer pathways that lead to Fe–O elongation due to more antibonding character along this bond. The hydrogen atom abstraction barriers for CYP199A4 are very central with C–H and O–H distances of 1.288 (1.331) and 1.260 (1.241) Å in the doublet (quartet) spin state, respectively. These distances match previous calculations on hydrogen atom abstraction transition states reported for CYP450 reaction mechanisms.^30,37

The aromatic hydroxylation transition states have a long C–O bond of 1.837 Å for both spin states and also lead to Fe–O elongation. These structures match aromatic hydroxylation transition states reported previously.^35,38

Unsupervised learning for selecting the best CYP199A4 mutant

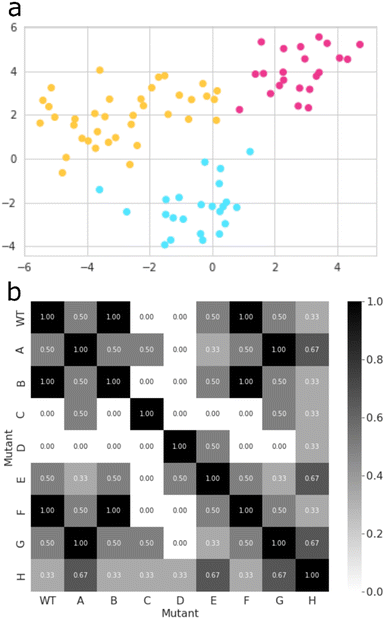
Thereafter, we searched for mutants that affect the regioselectivity of the reaction. Close inspection of the wildtype CYP199A4 crystal structure and its MD trajectory has led us to note the importance of the side chains of specific amino acid residues in the substrate-binding pocket. Intermolecular salt-bridges and/or hydrogen bonding interactions between substrate and protein inside the substrate binding pocket lock the substrate into a specific orientation that guides catalysis. Thus, mutating such residues and moving the position of these salt-bridges would alter the catalysis and lead to different product distributions. We carried out a machine learning approach combined with MD simulations to obtain a matrix of key mutant outcomes, as shown in Fig. 5. A set of eight CYP199A4 mutants (ESI,† Table S1 and Fig. S4) was submitted to 1 μs MD simulations under NPT conditions. The trajectory of each system was divided into separate windows of 100 ns, and each window, alongside with wildtype trajectories, became a datapoint of a dataset with each column/feature referring to specific geometrical or energetic descriptors of that trajectory bin (ESI,† Fig. S6, S14–S28). Our initial dataset features focused on (a) the Euclidean distances between the distal oxo ligand and atoms C3, C7, and C8 of the substrate, as well as the Euclidean distance between the latter and all four porphyrin nitrogen atoms; (b) the substrate RMSD; (c) the root-mean-square-structural-fluctuation (RMSF) of the active site residues, in combination with the Coulomb and van der Waals interactions between the substrate and these residues; (d) the angle Fe–O3_SUB–C1_SUB; and (e) dihedral S_AXIAL–Fe–O_DISTAL–C4_SUB. All features were decorrelated by means of principal component analysis (PCA),³⁹ and a new dataset containing only the principal components that explained a relevant share of variance (higher than 0.01) was created (ESI,† Fig. S29). Then, the best clustering of this new dataset was explored based on the Calinski–Harabasz index, the inertia, the silhouette coefficient, and the Davies–Bouldin index,⁴⁰ which all converged to the same result (ESI,† Fig. S30).

Fig. 5 CYP199A4 mutant clustering and selection: (a) a t-SNE plot that illustrates how all datapoints of the PCA-transformed dataset are grouped in three distinct clusters; (b) a heatmap derived from the similarity matrix based on the pairwise Jaccard similarity between all CYP199A4 variations, according to the cluster labels of each datapoint – values range from 0.00 (completely different) to 1.00 (completely identical).

Thus, the inertia measures how compact the clusters are and its metric is calculated from the sum of the squared distances between each datapoint and its nearest cluster centre. Thereafter, the best value of the inertia metric is assessed by the elbow method, which indicates the number of clusters at which it starts to level off.^40a The Calinski–Harabasz index was also used and evaluates the ratio of between-cluster dispersion and within-cluster dispersion. It is calculated as the ratio of the sum of between-cluster dispersion and within-cluster dispersion – higher values indicate better-defined clusters.^40b We also looked into the silhouette coefficient, which measures how similar a datapoint is to its own cluster compared to other clusters. The silhouette coefficient has a value that ranges from −1 to 1, whereby a high silhouette score indicates that the datapoint is well matched to its own cluster and poorly matched to neighbouring clusters.^40c Lastly, the Davies–Bouldin index was calculated and measures the average similarity between each cluster and its most similar cluster by taking into account both the within-cluster and between-cluster distances. In particular, lower values indicate better clustering, and a value of 0 indicates perfect clustering.^40d Finally, the K-means algorithm as implemented in Scikit-learn package was used to group all datapoints into three clusters (Fig. 5(a)).⁴¹

The best mutant was chosen based on Jaccard Similarity scores,⁴² by comparing each CYP199A4 variation (wildtype and mutants). The reason for this is that variations clustered together tend to behave similarly and lead to similar products distributions. The aim of this machine learning strategy was to find a mutant that does not cluster with any wildtype datapoint, and, therefore, gives a unique structure with a potentially unique product distribution. To this end, we searched for mutants whose data show no resemblance to wildtype, and, based on the grid shown in Fig. 5(b), mutants C and D were identified as the most suitable structures. While variant D contains mutation Arg92Leu/Leu396Arg, the C variant has mutation Ser244Ala/Ala248Thr. As such, in variant D the position of the active site Arg residue is moved in the protein and, as this side chain forms a salt-bridge with the carboxylate group of the substrate, it may position the substrate differently in the active site and thereby produce alternative products. The double mutation in D does not change the lipophilicity of the active site and just moves an Ala and Arg residue within the binding pocket. On the other hand, in mutant C the Ala residue is moved, but the Ser residue is replaced by Thr which may have an impact on the protein lipophilicity of the substrate binding pocket.⁴³ To further test the effect of the mutations we applied the evolutionary scale model⁴⁴ and compared the structures of wildtype with the eight mutants, see Fig. S31 (ESI†). In general, the differences are minor and not expected to give major changes in structure and activity. By contrast, in mutant C a hydroxyl group in the active site is moved and its effect may be more subtle on catalysis. Therefore, we reasoned that mutant D has the largest potential to cause changes in catalysis and selectivity in the enzyme and we decided to proceed with mutant D only. Moreover, the MD simulation for mutant D shows the highest dissimilarity to all other variations (Fig. 5(b)), and, hence, has the higher potential for unique product distributions.

Computationally predicted mutants and their reactivity

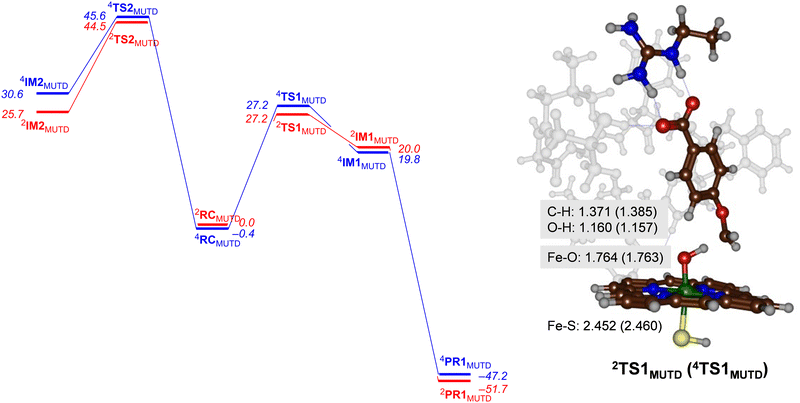
Next, we performed calculations on the mutant and highlight the difference of the transition state structure with particular emphasis on the position of the Arg residue in the substrate binding pocket that forms a salt bridge with the substrate carboxylate. We calculated the aromatic hydroxylation of the C₃-position (viaTS2_MUTD) and hydrogen atom abstraction from the methoxy group (viaTS1_MUTD), see Fig. 6. Both pathways are followed by either barrierless rebound or small proton shuttle barriers and give products with high exothermicity. As such the TS1_MUTD and TS2_MUTD transition states are the rate-determining steps for aliphatic and aromatic hydroxylation. The optimized hydrogen atom abstraction transition states are shown in Fig. 6. They have a product-type geometry with short O–H and long C–H distances. To be specific, the O–H distances are only 1.160 and 1.157 Å, whereas a typical O–H distance in an iron-hydroxo complex is 1.0 Å. The C–H distances have elongated to 1.371 Å (doublet) and 1.385 Å (quartet) in the transition state structures.

Fig. 6 UB3LYP calculated pathways for aromatic hydroxylation (from RC to the left) and methoxy group hydroxylation (from RC to the right) for CYP199A4 Mutant D. Free energies (ΔG in kcal mol⁻¹) are with energies at BS2 level of theory and with ZPE, thermal and entropic corrections included at 298 K. Also shown are optimized geometries of the rate-determining transition states with distances in Å.

As can be seen from Fig. 6 the mutant exhibits high aromatic hydroxylation barriers (TS2_MUTD), well over ΔG > 40 kcal mol⁻¹, while the hydrogen atom abstraction barriers (TS1_MUTD) are ΔG = 27.2 kcal mol⁻¹ for both spin states, which will render hydroxylation unlikely to proceed at room temperature conditions. Also, a Boltzmann distribution over the barrier heights for the mutant reaction predicts >99% O-demethylation and little aromatic hydroxylation. Our results, therefore, show that mutant D indeed reacts with p-anisic acid to give highly selective O-demethylation reactions and should do this reaction with even higher selectivity than wildtype. However, as the experimental work on wildtype gives mostly O-demethylation products, the machine learning process itself did not lead to a major shift in the product distributions. Nevertheless, the results clearly show that substrate is positioned tightly with its aromatic C–H bonds pointing away from the heme at large distances. As such it is better positioned for selective hydroxylation of the methoxy group and may be more suitable for industrial applications than wildtype protein. In particular, our variant favours the production of 4-hydroxybenzoate appreciably, and no other product should be expected from CYP199A4-mediated catalysis.

An analysis of the optimized geometries highlights the differences with wildtype structures. In particular, the structural differences between mutant D and WT CYP199A4 induces a substrate “tilting” in the active site of the former. Thus, the substrate in mutant D is positioned more upright, while in the wildtype is more sideways positioned (cf.Fig. 4 and 6). The strong polar interaction between the active site Arg residue and the carboxylate of the substrate moves the substrate in a different orientation. Interestingly, the distance analysis of the MD trajectory for the mutant as compared to wildtype gave the C₃-atom of substrate closer to Cpd I than the methoxy C–H group, and therefore implicated favourable aromatic hydroxylation for the mutant. Consequently, although the MD trajectory predicts dominant aromatic hydroxylation over O-demethylation for mutant D, this is contradicted by high level quantum chemical calculations that show that the aromatic hydroxylation channel incurs high energy barriers. Consequently, MD simulations alone may give incomplete suggestions on product distributions and reaction channels. A similar conclusion was obtained when we ran extensive MD simulations on caffeine binding to CYP1A1 enzymes, where the distance distributions obtained from long MD simulations predicted the wrong product distributions as compared to experiment.²² DFT cluster calculations, however, gave the correct product distributions despite the fact the starting distance for the favourable channel were longer than for the lesser favourable channel.

This “tilting” of the substrate likely stems from the repositioning of Arg₇₆, which creates a strong salt-bridge with the carboxylate group of the substrate. Leu₃₈₀, in its turn, is likely to interact with the methoxy group. Empirical observations like these helped choose the mutations that were explored in this work. Moreover, our DFT results on mutant D show that engineering CYP199A4 will change the ideal substrate-binding orientation and can lead to a more selective reaction process and the complete elimination of aromatic hydroxylation by-products in the process. Furthermore, the barriers and structures obtained for O-deethylation of guaethol by CYP255A CpdI are comparable to those obtained in previous studies that involved this enzyme and other lignin fragments.⁴ Clearly, the second coordination sphere in the substrate binding pocket hamper the aromatic hydroxylation pathway and prevent ideal approach of the substrate to CpdI. These results provide further insight into how lignin monomers are transformed into valuable chemicals through P450 catalysis.

Conclusions

In summary, the machine learning-aided strategy presented here for CYP199A4 mutant selection is a unique way to select the desired species amongst many variations: if one has a reference, either a positive or negative control, and a means to calculate the similarity between all variations and this reference – in our case, the molecular dynamics behaviour-, then it should be simple to find the species which is closest (or farthest) from the reference. In our specific case, we believe that future enzyme-engineering strategies can greatly benefit from this methodology if there is access to mutant molecular dynamics data or any other type of data that represents the behaviour of interest. In a case-to-case scenario, it is safe to assume that the critical stage of such protocol is the choice of collective variables that will describe the event of interest.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

A. H. S. D. and M. S. S. acknowledge support from the São Paulo Research Foundation (FAPESP) via grants 2021/10472-3 and 2013/08293-7, respectively.

Notes and references

1. (a) M. Ahmad, J. N. Roberts, E. M. Hardiman, R. Singh, L. D. Eltis and T. D. H. Bugg, Biochemistry, 2011, 50, 5096; (b) A. O. Falade, U. U. Nwodo, B. C. Iweriebor, E. Green, L. V. Mabinya and A. I. Oko, Microbiol. Open, 2017, 6, e00394; (c) M. E. Brown and M. C. Y. Chang, Curr. Opin. Chem. Biol., 2014, 19, 1; (d) X. Li and Y. Zheng, Biotechnol. Prog., 2020, 36, e2922; (e) R. Zhuo and F. Fan, Sci. Total Environ., 2021, 778, 146132; (f) B. Venkatesagowda and R. F. H. Dekker, Enzyme Microb. Technol., 2021, 147, 109780; (g) T. D. H. Bugg, Chem. Commun., 2024, 60, 804.
2. (a) M. Sono, M. P. Roach, E. D. Coulter and J. H. Dawson, Chem. Rev., 1996, 96, 2841; (b) I. G. Denisov, T. M. Makris, S. G. Sligar and I. Schlichting, Chem. Rev., 2005, 105, 2253; (c) P. R. Ortiz de Montellano, Chem. Rev., 2010, 110, 932; (d) Handbook of Porphyrin Science, ed. K. M. Kadish, K. M. Smith and R. Guilard, World Scientific Publishing Co., New Jersey, USA, 2010; (e) Iron-containing enzymes: Versatile catalysts of hydroxylation reaction in nature, ed. S. P. de Visser and D. Kumar, RSC Publishing, Cambridge, UK, 2011; (f) X. Huang and J. T. Groves, Chem. Rev., 2018, 118, 2491; (g) F. P. Guengerich, ACS Catal., 2018, 8, 10964; (h) N. P. Dunham and F. H. Arnold, ACS Catal., 2020, 10, 12239; (i) T. L. Poulos and A. H. Follmer, Acc. Chem. Res., 2022, 55, 373.
3. (a) M. M. Machovina, S. J. B. Mallinson, B. C. Knott, A. W. Meyers, M. Garcia-Borràs, L. Bu, J. E. Gado, A. Oliver, G. P. Schmidt, D. J. Hinchen, C. F. Crowley, C. W. Johnson, E. L. Neidle, C. M. Payne, K. N. Houk, G. T. Beckham, J. E. McGeehan and J. L. DuBois, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 13970; (b) A. C. Harlington, K. E. Shearwin, S. G. Bell and F. Whelan, Chem. Commun., 2022, 58, 13321.
4. (a) S. J. B. Mallinson, M. M. Machovina, R. L. Silveira, M. Garcia-Borràs, N. Gallup, C. W. Johnson, M. D. Allen, M. S. Skaf, M. F. Crowley, E. L. Neidle, K. N. Houk, G. T. Beckham, J. L. DuBois and J. E. McGeehan, Nat. Commun., 2018, 9, 2487; (b) M. E. Wolf, D. J. Hinchen, J. L. DuBois, J. E. McGeehan and L. D. Eltis, Curr. Opin. Biotechnol., 2022, 73, 43.
5. (a) S. G. Bell, A. B. H. Tan, E. O. D. Johnson and L.-L. Wong, Mol. BioSyst., 2010, 6, 206; (b) S. G. Bell, W. Yang, A. B. H. Tan, R. Zhou, E. O. D. Johnson, A. Zhang, W. Zhou, Z. Rao and L.-L. Wong, Dalton Trans., 2012, 41, 8703; (c) T. Coleman, R. R. Chao, J. B. Bruning, J. J. De Voss and S. G. Bell, RSC Adv., 2015, 5, 52007; (d) J. M. Klenk, J. Ertl, L. Rapp, M.-P. Fischer and B. Hauer, Mol. Catal., 2020, 484, 110739.
6. R. L. Crawford, E. McCoy, J. M. Harkin, T. K. Kirk and J. R. Obst, Appl. Microbiol., 1973, 26, 176.
7. R. R. Chao, I. C.-K. Lau, T. Coleman, L. R. Churchman, S. A. Child, J. H. Z. Lee, J. B. Bruning, J. J. De Voss and S. G. Bell, Chem. – Eur. J., 2021, 27, 14765.
8. T. Furuya, Y. Shitashima and K. Kino, J. Biosci. Bioeng., 2015, 119, 47.
9. P. Zhao, F. Kong, Y. Jiang, X. Qin, X. Tian and Z. Cong, J. Am. Chem. Soc., 2023, 145, 5506.
10. O. V. Makhlynets, P. Das, S. Taktak, M. Flook, R. Mas-Ballesté, E. V. Rybak-Akimova and L. Que Jr, Chem. – Eur. J., 2009, 15, 13171.
11. (a) H. S. Ali, R. H. Henchman and S. P. de Visser, Chem. – Eur. J., 2020, 26, 13093; (b) Q. Cheng and N. J. DeYonker, J. Phys. Chem. B, 2021, 125, 3296; (c) W. Singh, S. F. G. Santos, P. James, G. W. Black, M. Huang and K. D. Dubey, ACS Omega, 2022, 7, 21109.
12. (a) A. Hernández-Ortega, M. G. Quesne, S. Bui, D. J. Heyes, R. A. Steiner, N. S. Scrutton and S. P. de Visser, J. Am. Chem. Soc., 2015, 137, 7474; (b) H. Eom, Y. Cao, H. Kim, S. P. de Visser and W. J. Song, J. Am. Chem. Soc., 2023, 145, 5880.
13. S. M. Pratter, C. Konstantinovics, C. L. M. DiGiuro, E. Leitner, D. Kumar, S. P. de Visser, G. Grogan and G. D. Straganz, Angew. Chem., Int. Ed., 2013, 52, 9677.
14. H. M. Berman, J. Westbrook, Z. Feng, G. Gilliland, T. N. Bhat, H. Weissig, I. N. Shindyalov and P. E. Bourne, Nucleic Acids Res., 2000, 28, 235.
15. O. Trott and A. J. Olson, J. Comput. Chem., 2010, 31, 455.
16. R. Anandakrishnan, B. Aguilar and A. V. Onufriev, Nucleic Acids Res., 2012, 40, 537.
17. P. Li and K. M. Merz, J. Chem. Inf. Model., 2016, 56, 599.
18. D. A. Case, I. Y. Ben-Shalom, S. R. Brozell, D. S. Cerutti, T. E. Cheatham, III, V. W. D. Cruzeiro, T. A. Darden, R. E. Duke, D. Ghoreishi, M. K. Gilson, H. Gohlke, A. W. Goetz, D. Greene, R. Harris, N. Homeyer, Y. Huang, S. Izadi, A. Kovalenko, T. Kurtzman, T. S. Lee, S. LeGrand, P. Li, C. Lin, J. Liu, T. Luchko, R. Luo, D. J. Mermelstein, K. M. Merz, Y. Miao, G. Monard, C. Nguyen, H. Nguyen, I. Omelyan, A. Onufriev, F. Pan, R. Qi, D. R. Roe, A. Roitberg, C. Sagui, S. Schott-Verdugo, J. Shen, C. L. Simmerling, J. Smith, R. Salomon-Ferrer, J. Swails, R. C. Walker, J. Wang, H. Wei, R. M. Wolf, X. Wu, L. Xiao, D. M. York and P. A. Kollman, AMBER-2018, University of California, San Francisco, 2018.
19. P. Mark and L. Nilsson, J. Phys. Chem. A, 2001, 43, 9954.
20. J. A. Maier, C. Martinez, K. Kasavajhala, L. Wickstrom, K. E. Hauser and C. Simmerling, J. Chem. Theory Comput., 2015, 11, 3696.
21. (a) S. Shaik, D. Kumar, S. P. de Visser, A. Altun and W. Thiel, Chem. Rev., 2005, 105, 2279; (b) D. Li, Y. Wang and K. Han, Coord. Chem. Rev., 2012, 256, 1137; (c) M. R. A. Blomberg, T. Borowski, F. Himo, R.-Z. Liao and P. E. M. Siegbahn, Chem. Rev., 2014, 114, 3601; (d) F. Himo, J. Am. Chem. Soc., 2017, 139, 6780; (e) F. Himo and S. P. de Visser, Commun. Chem., 2022, 5, 29.
22. T. Mokkawes and S. P. de Visser, Chem. – Eur. J., 2023, 29, e202203875.
23. H. S. Ali and S. P. de Visser, Chem. – Eur. J., 2022, 28, e202104167.
24. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Gaussian, Inc., Wallingford CT, 2009.
25. (a) A. D. Becke, J. Chem. Phys., 1993, 98, 5648; (b) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785.
26. (a) P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270; (b) M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. DeFrees and J. A. Pople, J. Chem. Phys., 1982, 77, 3654.
27. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999.
28. (a) P. Barman, P. Upadhyay, A. S. Faponle, J. Kumar, S. S. Nag, D. Kumar, C. V. Sastri and S. P. de Visser, Angew. Chem., Int. Ed., 2016, 55, 11091; (b) F. G. Cantú Reinhard, P. Barman, G. Mukherjee, J. Kumar, D. Kumar, D. Kumar, C. V. Sastri and S. P. de Visser, J. Am. Chem. Soc., 2017, 139, 18328; (c) P. Barman, F. G. Cantú Reinhard, U. K. Bagha, D. Kumar, C. V. Sastri and S. P. de Visser, Angew. Chem., Int. Ed., 2019, 58, 10639.
29. (a) F. G. Hardy, H. P. H. Wong and S. P. de Visser, Chem. – Eur. J., 2024, 30, e202400019; (b) Y. Cao, S. Hay and S. P. de Visser, J. Am. Chem. Soc., 2024, 146, 11726.
30. (a) F. Ogliaro, S. Cohen, S. P. de Visser and S. Shaik, J. Am. Chem. Soc., 2000, 122, 12892; (b) J. C. Schöneboom, H. Lin, N. Reuter, W. Thiel, S. Cohen, F. Ogliaro and S. Shaik, J. Am. Chem. Soc., 2002, 124, 8142; (c) C. M. Bathelt, J. Zurek, A. J. Mulholland and J. N. Harvey, J. Am. Chem. Soc., 2005, 127, 12900; (d) M. Radoń, E. Broclawik and K. Pierloot, J. Chem. Theory Comput., 2011, 7, 898; (e) R. Lonsdale, J. Oláh, A. J. Mulholland and J. N. Harvey, J. Am. Chem. Soc., 2011, 133, 15464; (f) Ü. İsci, A. S. Faponle, P. Afanasiev, F. Albrieux, V. Briois, V. Ahsen, F. Dumoulin, A. B. Sorokin and S. P. de Visser, Chem. Sci., 2015, 6, 5063; (g) A. Hermano Sampaio Dias, R. Yadav, T. Mokkawes, A. Kumar, M. S. Skaf, C. V. Sastri, D. Kumar and S. P. de Visser, Inorg. Chem., 2023, 62, 2244.
31. M. J. Field, P. H. Oyala and M. T. Green, J. Am. Chem. Soc., 2022, 144, 19272.
32. (a) S. Shaik, S. Cohen, S. P. de Visser, P. K. Sharma, D. Kumar, S. Kozuch, F. Ogliaro and D. Danovich, Eur. J. Inorg. Chem., 2004, 207; (b) E. F. Gérard, V. Yadav, D. P. Goldberg and S. P. de Visser, J. Am. Chem. Soc., 2022, 144, 10752.
33. (a) F. Ogliaro, N. Harris, S. Cohen, M. Filatov, S. P. de Visser and S. Shaik, J. Am. Chem. Soc., 2000, 122, 8977; (b) T. Kamachi and K. Yoshizawa, J. Am. Chem. Soc., 2003, 125, 4652; (c) J. S. Schöneboom, S. Cohen, H. Lin, S. Shaik and W. Thiel, J. Am. Chem. Soc., 2004, 126, 4017; (d) D. Kumar, S. P. de Visser and S. Shaik, J. Am. Chem. Soc., 2004, 126, 5072; (e) S. P. de Visser and L. S. Tan, J. Am. Chem. Soc., 2008, 130, 12961; (f) S. Shaik, W. Lai, H. Chen and Y. Wang, Acc. Chem. Res., 2010, 43, 1154; (g) H. Isobe, K. Yamaguchi, M. Okumura and J. Shimada, J. Phys. Chem. B, 2012, 116, 4713; (h) H. Hirao, Z. H. Cheong and X. Wang, J. Phys. Chem. B, 2012, 116, 7787; (i) H. Hirao, P. Chuanprasit, Y. Y. Cheong and X. Wang, Chem. – Eur. J., 2013, 19, 7361; (j) R. Lonsdale, K. T. Houghton, J. Żurek, C. M. Bathelt, N. Foloppe, M. J. de Groot, J. N. Harvey and A. J. Mulholland, J. Am. Chem. Soc., 2013, 135, 8001; (k) R. Lai and H. Li, J. Phys. Chem. B, 2016, 120, 12312; (l) A. S. Faponle, M. G. Quesne and S. P. de Visser, Chem. – Eur. J., 2016, 22, 5478.
34. (a) P. Schyman, D. Usharani, Y. Wang and S. Shaik, J. Phys. Chem. B, 2010, 114, 7078; (b) T. Mokkawes, Z. Q. Lim and S. P. de Visser, J. Phys. Chem. B, 2022, 126, 9591.
35. (a) S. P. de Visser and S. Shaik, J. Am. Chem. Soc., 2003, 125, 7413; (b) C. M. Bathelt, A. J. Mulholland and J. N. Harvey, J. Phys. Chem. A, 2008, 112, 13149; (c) S. Shaik, P. Milko, P. Schyman, D. Usharani and H. Chen, J. Chem. Theory Comput., 2011, 7, 327; (d) D. Kumar, G. N. Sastry and S. P. de Visser, J. Phys. Chem. B, 2012, 116, 718; (e) C. Colomban, A. H. Tobing, G. Mukherjee, C. V. Sastri, A. B. Sorokin and S. P. de Visser, Chem. – Eur. J., 2019, 25, 14320; (f) S. Louka, S. M. Barry, D. J. Heyes, M. Q. E. Mubarak, H. S. Ali, L. M. Alkhalaf, A. W. Munro, N. S. Scrutton, G. L. Challis and S. P. de Visser, J. Am. Chem. Soc., 2020, 142, 15764.
36. (a) M. Pickl, S. Kurakin, F. G. Cantú Reinhard, P. Schmid, A. Pöcheim, C. K. Winkler, W. Kroutil, S. P. de Visser and K. Faber, ACS Catal., 2019, 9, 565; (b) H. Chen, A. Zhou, D. Sun, Y. Zhao and Y. Wang, J. Phys. Chem. B, 2021, 125, 8419; (c) Z. Wang, W. Diao, P. Wu, J. Li, Y. Fu, Z. Guo, Z. Cao, S. Shaik and B. Wang, J. Am. Chem. Soc., 2023, 145, 7252.
37. (a) D. Kumar, L. Tahsini, S. P. de Visser, H. Y. Kang, S. J. Kim and W. Nam, J. Phys. Chem. A, 2009, 113, 11713; (b) X.-X. Li, V. Postils, W. Sun, A. S. Faponle, M. Solà, Y. Wang, W. Nam and S. P. de Visser, Chem. – Eur. J., 2017, 23, 6406.
38. (a) A. S. Faponle, M. G. Quesne, C. V. Sastri, F. Banse and S. P. de Visser, Chem. – Eur. J., 2015, 21, 1221; (b) F. G. Cantú Reinhard, M. A. Sainna, P. Upadhyay, G. A. Balan, D. Kumar, S. Fornarini, M. E. Crestoni and S. P. de Visser, Chem. – Eur. J., 2016, 22, 18608; (c) Y. Zhang, T. Mokkawes and S. P. de Visser, Angew. Chem., Int. Ed., 2023, 62, e202310785.
39. R. Bennett, IEEE Trans. Inform. Theory, 1969, 15, 517.
40. (a) M. Chavent, Pattern Recogn. Lett., 1998, 19, 989; (b) T. Calinski and J. Harabasz, Commun. Stat., 1974, 3, 1; (c) P. J. Rousseeuw, J. Comput. Appl. Math., 1987, 1, 20; (d) D. L. Davies and D. W. Bouldin, IEEE Trans. Pattern Anal. Mach. Intell., 1979, 2, 224.
41. (a) F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825; (b) L. van der Maaten and G. Hinton, J. Mach. Learn. Res., 2008, 9, 11.
42. P. Jaccard, New Phytol., 1912, 11, 37.
43. W. J. Zamora, J. M. Campanera and F. J. Luque, J. Phys. Chem. Lett., 2019, 10, 883.
44. A. Rives, J. Meier, T. Sercu, S. Goyal, Z. Lin, J. Liu, D. Guo, M. Ott, C. L. Zitnick, J. Ma and R. Fergus, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2016239118.

---

Footnote

† Electronic supplementary information (ESI) available: Tables with energies, group spin densities, group charges and Cartesian coordinates of optimized structures as well as details of molecular dynamics and machine learning studies. See DOI: https://doi.org/10.1039/d4cp01282h

---