Coincidence mass spectrometry study of double ionization of pyrene by 70 eV electron impact

Abstract

We have performed coincidence mass spectrometry of fragmentation of pyrene molecules by 70 eV electron impact. Ionized fragments have been mass selected using a reflectron time-of-flight mass spectrometer, and a field programmable gate array has been used for the timing of the electron and ion extraction pulses and for the event-by-event detection of the ions. Double ionization results in a number of prominent fragmentations producing two singly-ionized fragments with kinetic energies of up to a few eV. A number of fragmentations produce ions with four or more carbon atoms, which can only be formed by the breaking of at least three C–C bonds.

---

1 Introduction

Polycyclic aromatic hydrocarbons (PAHs) have been the focus of many studies in recent years, because of their occurrence in the Earth's atmosphere and in the interstellar medium. PAHs and soot particles are abundantly produced in combustion processes and are considered to be hazardous to the environment and to health.^1,2 The infrared emission bands observed for many objects in the interstellar medium are widely attributed to the presence of PAHs.^3–5 These molecules have been the focus of many laboratory studies to understand their role in the chemistry of the interstellar medium and in astrophysical objects.^6–10 In these environments pyrene and other PAHs can be excited and fragmented by photon absorption and in collisions with ions, electrons, and atoms. Low-energy secondary electrons in inelastic collisions with molecules are considered to be the driving force behind a wide variety of astrochemical processes. Chemical reactions in the ice mantles of interstellar dust grains are induced by UV light and cosmic rays, and by the secondary electrons produced by these irradiations.^11,12 In planetary atmospheres, secondary electrons are produced by solar radiation and by cosmic rays.¹³

The purpose of this paper is to study the formation of doubly-charged pyrene by 70 eV electron impact and provide new insights into the fragmentations producing two singly-charged fragments.

Many collision studies of PAH molecules have shown clear evidence for the formation of multiply-charged molecular ions and coincidence techniques have been used to investigate the decay of these ions. Because of the availability of a wide range of photon energies, many of these studies have used synchrotron radiation and more recently FEL radiation for double photoionization of hydrocarbons and aromatic molecules.¹⁴ We briefly summarise recent research specific to pyrene.

Pyrene and other PAHs have been the subject of a number of VUV-photodissociation and photoelectron spectroscopy experiments.^15–19 Photoionization using time-of-flight mass spectrometry has been applied by Wehlitz and Hartman²⁰ and Johansson et al.²¹ Monfredini et al.²² have measured mass spectra produced by X-ray photodissociation of pyrene and other PAHs. Marciniak et al.²³ and Lee et al.²⁴ have investigated the dissociation and ionization dynamics of pyrene and other PAHs in ultrafast time-resolved XUV-IR pump–probe experiments. Lee et al.²⁵ have applied recoil-frame covariance map imaging to study dication and trication dissociation of fluorene, phenanthrene and pyrene.

Noble et al.²⁶ have studied ultrafast electronic relaxations from the S₃ state of pyrene in an fs pump–probe experiment. A number of recent experiments have been performed on pyrene cations^27–30 and on hydrogenated pyrene.^31,32 Lietard and Verlet³³ have applied photoelectron spectroscopy to study microhydration of pyrene anions.

A number of groups have investigated the formation of doubly charged PAHs in ion–molecule collisions.⁹ Ławicki et al.³⁴ and Seitz et al.³⁵ have measured mass spectra showing multiple ionization and fragmentation of pyrene molecules and other PAHs in collision with multiply-charged ions. Ji et al.³⁶ have measured absolute double differential cross-sections for electron emission from pyrene molecules in interaction with keV protons. Chen et al.³⁷ have investigated the formation of molecular hydrogen from pyrene, anthracene and coronene molecules that are internally heated by collisions with keV ions, a process that may be of relevance for H₂ formation in astrophysical environments.

Several authors have published mass spectra for pyrene.^38–40 Tobita et al.⁴¹ have determined single and double ionization energies in experiments involving electron and photon impact. Keller et al.⁴² have measured electron energy loss spectra from threshold to 30 eV.

Kingston et al.⁴³ have identified preferred charge separation fragmentations for doubly- and triply-charged pyrene molecules formed by charge stripping of singly- and doubly-charged pyrene molecules passing through a collision cell containing nitrogen gas.

A number of studies have been published involving collisions of helium atoms with PAH cations, including pyrene and hydrogenated pyrene.^44–48 Yamakita et al.⁴⁹ have measured penning ionization electron spectra of pyrene, chrysene, and coronene in collision with metastable helium atoms. Several groups have researched the fragmentation of pyrene clusters and solvated pyrene molecules in collisions with photons^50–52 and with ions.^35,53,54 The photochemistry of pyrene in water ice has also been studied.^55,56

Pyrene and other PAHs have been the subject of many theoretical studies. Singh et al.⁵⁷ have performed R-matrix calculations to obtain electron scattering cross sections for anthracene and pyrene in the range 0.1–15 eV. Simon et al.^58,59 have performed molecular dynamics calculations on the dissociation of pyrene and other PAH cations. Theoretical calculations have also been reported in a number of experimental papers.^{25,29–31,35–37,46–48,50}

The purpose of this paper is to examine the fragmentations of pyrene into two singly-charged fragments after double ionization by electron impact. Coincidence mass spectrometry has been used to measure the coincidence map for pyrene, and to the best of our knowledge this is the first coincidence map published for pyrene. Coincidence mass spectrometry involves the event by event detection of ions using a single time-of-flight mass spectrometer, and the application of covariance analysis techniques to extract the coincidence map.^60,61

New detailed insights into the fragmentation dynamics of doubly-charged pyrene are important for benchmarking theory and modelling, and for the understanding of reaction mechanisms that are of relevance in astrophysical environments and the interstellar medium. If two or more electrons are rapidly removed from a molecule in a collision process, the resulting multiply-charged molecular cation rapidly fragments into cationic fragments due to internal electrostatic repulsion, a process that is called Coulomb explosion.⁶² Whereas ions produced by single ionisation of a molecule have thermal energies, singly-charged ions produced by double ionisation can have energies up to about a few eV, and therefore can induce reactions in the interstellar medium that thermal ions cannot.

Pyrene is the smallest PAH in which the aromatic rings are ortho- and peri-fused to the others. In a perifused PAH at least one carbon atom is a member of three aromatic rings; in pyrene this involves two atoms. Contrary to anthracene, which has been the subject of our earlier study,⁶³ singly-charged fragments of pyrene with four or more carbon atoms can only be formed by the breaking of at least three C–C bonds.

2 Experiment

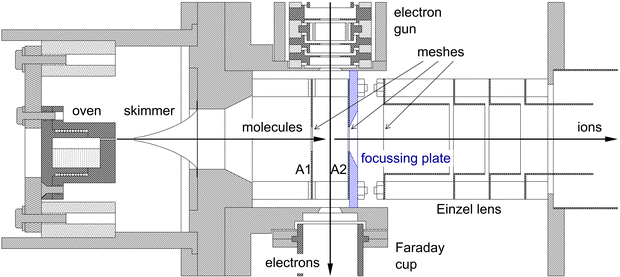
The experimental set-up consists of a molecular beam of pyrene, a pulsed electron beam, and a reflectron time-of-flight mass spectrometer, contained in three inter-connected and differentially pumped vacuum chambers. The set-up has been used before to study single ionization of anthracene⁶⁴ and phenanthrene⁶⁵ and double ionization of anthracene.⁶³ A schematic overview of the experiment can be found in Fig. 2 of ref. 66. The pulsed valve in⁶⁶ was replaced by the oven containing pyrene. Fig. 1 shows the current lay-out of the interaction region.

Fig. 1 Overview of the interaction region showing the oven containing pyrene, the skimmer, the electron gun, and the Einzel lens at the entrance to the reflectron time-of-flight mass spectrometer. The electron gun and the Faraday cup are only partially shown. The focussing plate has been added to enhance the collection of singly-charged ions from double ionisations (see discussion in the text).

The beam of pyrene molecules is generated by resistively heating pyrene powder (99% purity from Sigma Aldrich) contained in a small oven to a temperature of 120 °C. Molecules are effusing from a capillary (0.5 mm diameter and 4.5 mm length) in the oven and pass through a skimmer (1.2 mm diameter) into the collision chamber where they are collided with electrons.

The electron gun is pulsed at a rate of 13.26 kHz with a 0.20 μs pulse width. The energy resolution of the electron beam is about 0.8 eV FWHM. The electron gun consists of a Wehnelt cylinder with a tungsten hairpin filament, 5 cylindrical lens elements with apertures, and a set of deflection plates. All elements are machined out of single pieces of molybdenum. To enhance the stability of the electron beam the gun is surrounded by a resistively heated cylinder kept at a temperature of 60 °C.

The electrons are passing between two plates A1 and A2 in Fig. 1, and positively charged fragments are extracted into the mass spectrometer 0.04 μs after the electron pulse by applying a short pulse of −100 V to plate A1, with plate A2 kept at ground. The ions are detected by a microchannel plate detector which has two microchannel plates stacked in chevron configuration and an active area of 40 mm diameter. The pulses from the detector are discriminated by an Ortec 9327 1-GHz Amplifier and Timing Discriminator. The NIM output pulses from the discriminator are converted to LVTTL and input into a National Instruments 9402 digital input/output module connected to a cRIO9075 field programmable gate array (FPGA).

The FPGA is used to time the pulsing of the electron gun and the ion extraction voltage, and to record the mass-resolved detection of singly-charged ions on an event-by-event basis. The average event rate is 0.24 ions per electron pulse.

A detailed model of the coincidence data acquisition was used to process the event-by-event data, to correct for detector dead time and for random coincidences, and to obtain the map of true coincidences. More details are provided in ref. 63.

Compared to⁶³ we have made two improvements to the experiment. To enhance the collection of singly-charged ions produced by double ionization, we have placed a 3.1 mm thick plate containing a 9.6 mm diameter aperture with a 26.6° bevelled edge directly after and against the first mesh that the ions pass through in the reflectron mass spectrometer, as illustrated in Fig. 1. This plate produces a small amount of focusing in the second acceleration stage for ions with initial velocities away from the main axis of the mass spectrometer.

We have also reduced the effective detector dead-time by reducing the width of the LVTTL pulses produced by the NIM to TTL converter mentioned above. The dead-time is now about 140 ns, limited by the pulse processing on the FPGA and its 9402 digital input/output module.

3 Results and discussions

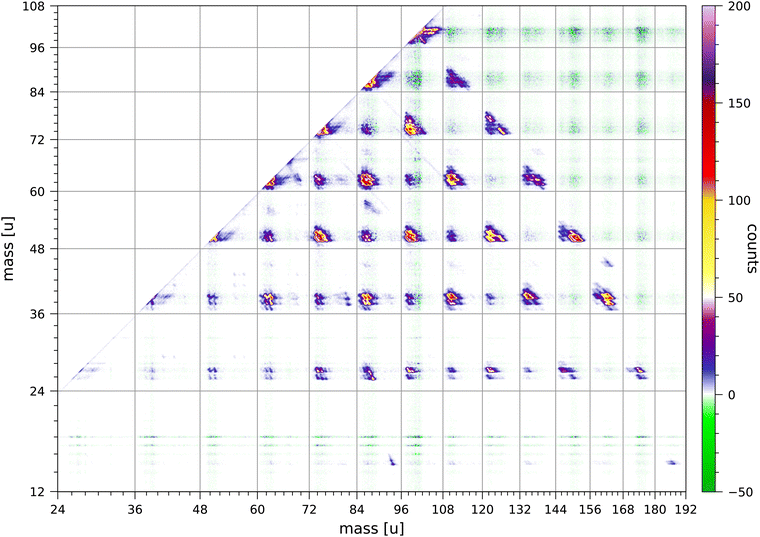
The data set used in this paper was accumulated over 235 hours and comprises 1.12 × 10¹⁰ sweeps. We have used an electron energy of 70 eV, because this energy is most often used in mass spectrometry. It would be of interest to measure a coincidence map for pyrene at an electron energy closer to the threshold for double ionisation, however, the much lower rate of coincident production of singly-charged ions from double ionisation would result in a much longer data acquisition time.

Fig. 2 shows the relevant section of the full coincidence map extracted from the data set. The mass scales are plotted such that the scales are linear in flight time. The colour scale is in counts with strong fragmentations in yellow, red and pink colours and weak fragmentations in shades of blue. Negative counts are in green and arise from the correction for random coincidences. Negative counts are due to the statistical uncertainties in the rates of true and random coincidences.

Fig. 2 The relevant section of the full map of true coincidences for singly-charged ions produced by double ionisation of pyrene by 70 eV electron impact. Both scales are linear in ion time of flight and the mass scales are adjusted accordingly. The colour scale shows the content of individual bins.

Double ionization processes can be written as

e⁻ + C₁₆H₁₀ → C₁₆H₁₀⁺⁺ + 3e⁻ →

C_aH_m⁺ + C_bH_n⁺ + 3e⁻ + neutral fragments (1)

In the following discussions we indicate the coincidence groups as (a, b) where a and b are the number of carbon atoms in each of the fragments. The Coulomb repulsion of the two ions produced in each fragmentation results in an elongated distribution aligned approximately along the counter diagonal through the point (m₁, m₂), in which the masses of the two ions are m₁ = (12a + m) u and m₂ = (12b + n) u.

In order to qualitatively understand the shapes of these distributions, we have done Monte–Carlo trajectory calculations for one of the most prominent fragmentations:

C₁₆H₁₀⁺⁺ → C₄H₂⁺ + C₁₂H₆⁺ + 2H (2)

Fig. 3 shows the simulated and measured sections of the coincidence map for this fragmentation. The simulated map is obtained from trajectory calculations for 340 000 ion pairs. Details on the calculations are given in the appendix of ref. 63. The focussing plate mentioned above was included in these calculations. Because of this focussing plate the distributions we observe for pyrene are less bimodal than the distributions for anthracene in ref. 63.†

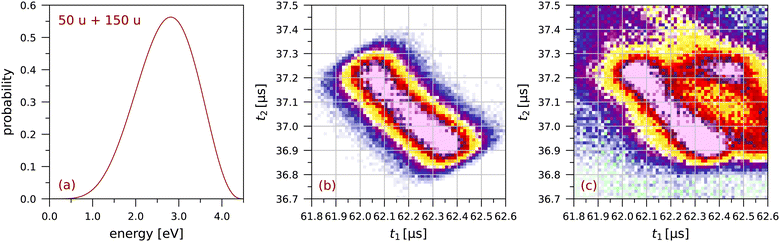Fig. 3 The fragmentation C₄H₂⁺ + C₁₂H₆⁺: (a) the probability distribution for the total fragmentation energy used in the simulation, (b) the simulated coincidence map using Monte Carlo trajectory calculations (see⁶³), and (c) a small section of the measured coincidence map (64 × 64 bins). The colour scales are the same as in Fig. 2.

The extent of each distribution along the counter diagonal is a measure of the fragmentation energy available in the dissociation producing the two singly-charged ions. In the simulation in Fig. 3 we have chosen the maximum energy so as to match the extent of the measured distribution. For each randomly chosen value of the fragmentation energy, this energy is divided between the two fragment ions assuming a total momentum of zero. The width of the distribution along the diagonal is due to the finite size of the interaction region, taken to be 0.6 mm FWHM in the simulation.

Several calculations have been made for different shapes of the probability distribution in Fig. 3(a) until a good overall agreement was obtained between the simulated and measured sections of the coincidence map in Fig. 3(b) and (c), respectively. This shows that singly-charged ions with kinetic energies of a few eV are produced in these fragmentations.

Lee et al.²⁵ have determined a total kinetic energy release of 2.49 ± 0.07 eV for the C₄H_x⁺ + C₁₂H_y⁺ fragmentation of doubly charged pyrene (see their Table 1). The maximum in Fig. 3 is at a slightly higher energy of 2.8 eV, possibly related to the higher electron impact energy of 70 eV as compared to the 40.9 eV photon energy used by Lee et al.²⁵ We note that we have had to use the extended probability distribution in Fig. 3(a) to obtain a good agreement between Fig. 3(b) and (c). The minimum in the distribution along the counter diagonal is directly related to the shape of the low-energy tail of the probability distribution.

A number of overall observations can be made from the coincidence map Fig. 2. Fragmentations for which the total number of carbon atoms in both fragments is even are generally significantly stronger than fragmentations for which the total is odd. Strong fragmentations are observed for groups (a, b) with a + b = 8, 10, 12, 14 and 16, and weaker fragmentations are observed for a + b = 7, 9, 11 and 13. No fragmentations are observed for groups with a + b = 15. Most of the fragments have 2 or 3 hydrogen atoms, but in the groups (a, b) with b ≥ 9 the larger fragment can have 5, 6, 7 or 8 hydrogen atoms. Fragments with only one hydrogen atom are sparsely produced and mostly in groups (a, b) with a = 3 or 5. Fragments with only one carbon atom are only minimally produced; the least weak of these fragmentations is CH₃⁺ + C₁₅H₇⁺. Ionised fragments with only carbon atoms are not observed.

The coincidence map of singly-charged fragments produced by electron impact and by ion impact on anthracene^63,67 also show that fragmentations for which the total number of carbon atoms in both fragments is even are preferred. The coincidence map of naphthalene⁶⁸ shows very weak fragmentations of groups (a, b) with a + b = 9. The fragmentation of doubly-charged fluorene, phenanthrene, and pyrene molecules produced by 40.9 eV XUV laser pulses favours reaction pathways involving two-body breakup with loss of neutral fragments totalling an even number of carbon atoms.²⁴

Fig. 4 and 5 show a number of coincident groups in more detail. Fig. 4 shows six groups in which the sum of the carbon atoms is equal to 16, the number of carbon atoms in the parent molecule. The two strongest fragmentations in Fig. 4 are in group (4, 12):

C₁₆H₁₀⁺⁺ → C₄H₂⁺ + C₁₂H₆⁺ + 2H (3)

C₁₆H₁₀⁺⁺ → C₄H₂⁺ + C₁₂H₈⁺ (4)

Clearly these fragmentations can only be formed by the breakage of three C–C bonds accompanied by the loss of two H atoms (in (3)) or the rearrangement of one H atom (in (4)).

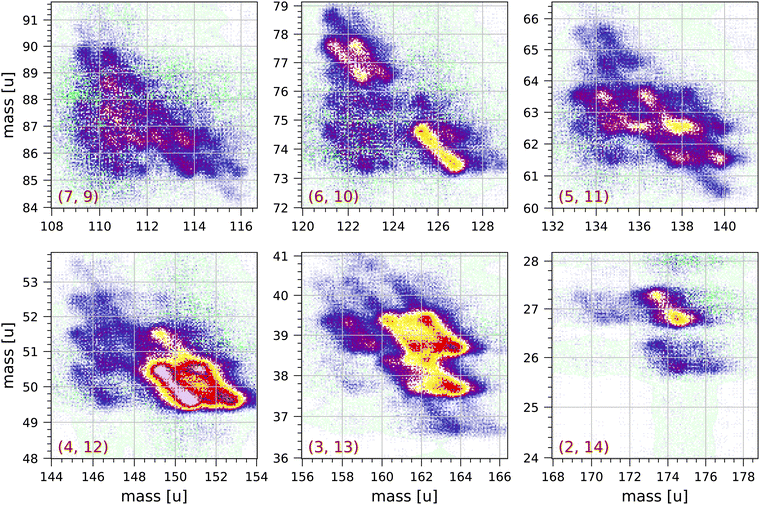Fig. 4 Sections of the measured coincidence map for the six coincidence groups (a, b) with a + b = 16, where a and b are the number of carbon atoms in both fragments. Each section contains 160 × 160 bins and corresponds to 2 × 2 μs in ion flight time. The mass scales are adjusted accordingly. The colour scales are the same as in Fig. 2.

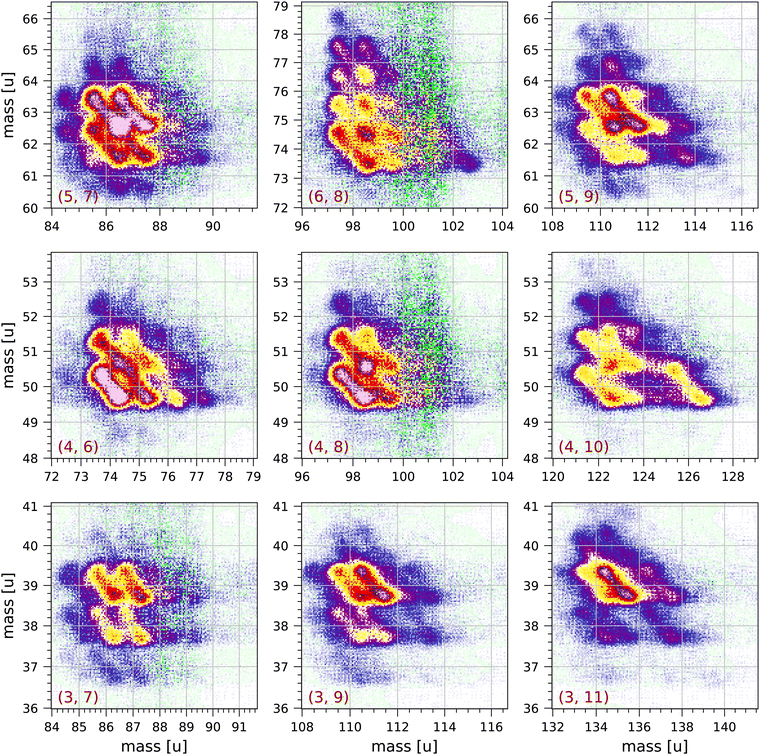Fig. 5 Sections of the measured coincidence map for a selection of nine coincidence groups (a, b) with a + b < 16, where a and b are the number of carbon atoms in both fragments. Each section contains 160 × 160 bins and corresponds to 2 × 2 μs in ion flight time. The mass scales are adjusted accordingly. The colour scales are the same as in Fig. 2.

Group (3, 13) shows several prominent fragmentations producing C₃H₃⁺ and C₃H₂⁺. The most significant fragmentation is:

C₁₆H₁₀⁺⁺ → C₃H₃⁺ + C₁₃H₇⁺ (5)

which is possible by the breakage of two C–C bonds.

The other fragmentations are accompanied by the loss of one or more hydrogen atoms.

Group (2, 14) shows one significant fragmentation:

C₁₆H₁₀⁺⁺ → C₂H₃⁺ + C₁₄H₆⁺ + H (6)

which involves the breakage of two C–C bonds, accompanied by the transfer of one H atom and the loss of one H atom.

In group (5, 11) the four strongest fragmentations all result in an odd number of H atoms in the largest fragment. All fragmentations in this group must involve the breakage of (at least) three C–C bonds. A number of weaker fragmentations are also present, but notably there is only one fragmentation producing a fragment with only one H atom: C₁₆H₁₀⁺⁺ → C₅H⁺ + C₁₁H₇⁺ + 2H. The fragmentation C₁₆H₁₀⁺⁺ → C₅H₂⁺ + C₁₁H₄⁺ + 4H does not occur.

In group (6, 10) the most distinct fragmentations are:

C₁₆H₁₀⁺⁺ → C₆H₂⁺ + C₁₀H₆⁺ + 2H (7)

C₁₆H₁₀⁺⁺ → C₆H₅⁺ + C₁₀H_2,3⁺ + (3,2)H (8)

both involving the breakage of (at least) three C–C bonds. Fragmentation (7) may be characteristic for pyrene, and we note that a possibly similar fragmentation is observed in group (4, 10), see fragmentation (9) below.

Group (7, 9) shows a number of possible fragmentations, none of which are very prominent, all involving the breakage of (at least) three C–C bonds, and all involving the loss of at least one H atom. Notably, the fragmentation C₁₆H₁₀⁺⁺ → C₇H₂⁺ + C₉H₄⁺ + 4H does not occur.

Fig. 5 shows a selection of nine groups with a + b < 16. Most of the fragments produced in these groups have two or three hydrogen atoms. Also in the groups near the diagonal in Fig. 2 (groups (a, b) with a = b) the most abundantly produced fragments have two or three hydrogen atoms. The strongest fragmentations are observed in groups (5, 7), (5, 9), (4, 6) and (4, 8). Only a few fragmentations produce fragments with more than 3 hydrogen atoms. Fragments with only one hydrogen atom are sparsely produced and mostly in groups (5, 7), (5, 9), (3, 7) and (3, 9).

In group (4, 10) a significant fragmentation is

C₁₆H₁₀⁺⁺ → C₄H₂⁺ + C₁₀H₆⁺ + neutral fragment(s) (9)

This fragmentation appears to be similar to fragmentation (7) with possibly the release of a single C₂H₂ neutral fragment.

In groups (3, 7) and (4, 6) some of the distributions clearly have angles that deviate from the counter diagonal, which may be caused by the loss of one or more neutral fragments from one of the charged fragments as it is travelling through the mass spectrometer.

In groups (4, 8) and (6, 8) the most prominent fragmentations are those in which the larger fragment has 2 or 3 hydrogen atoms. The large scatter observed in these groups at 100 u and 101 u is due to the relatively large correction for random coincidences: apart from the parent peak at 202 u, 100 u and 101 u are the largest peaks in the non-coincident mass spectrum. This is also observed in the other groups (a, b) with b = 8 in Fig. 2. We conclude that 101 u is not or very sparsely produced as a singly-ionised fragment after double ionisation. This implies that the 101 u peak in the non-coincident mass spectrum can only be either C₈H₅⁺ produced by single ionisation and fragmentation or C₁₆H₁₀⁺⁺ produced by double ionisation, or a combination of both.

By fitting with Gaussians, we find that the ratios of the peak areas for 203 u/202 u and for 101.5 u/101 u are both equal to 0.20 ± 0.01, which is slightly larger than the isotope ratio 0.179. Because 101.5 u can only be due to C₁₅¹³CH₁₀⁺⁺ we conclude that 101 u is almost entirely due to the doubly-charged parent molecule. This also implies that 100 u is mostly C₁₆H₈⁺⁺. A similar conclusion has been drawn for the 89 u peak in the mass spectrum of anthracene, see discussion in.⁶³

The patterns of pyrene fragmentations observed in the groups (a = 2, 3, b), where the smaller fragment has 2 or 3 carbon atoms, are similar in overall appearance to the patterns of anthracene fragmentations observed in the groups (a = 2,3, b − 2) in.⁶³ This is to be expected assuming that the formation of C_2,3H_2,3⁺ involves breakage of a C–C bond breakage in one of the terminal carbon rings, followed by charge separation and the breakage of a second C–C bond, see Scheme 1 proposed by Kingston et al.⁴³

Kingston et al.⁴³ have studied the preferred fragmentation routes of doubly-charged pyrene ions produced by charge stripping of singly-charged pyrene molecules passing through nitrogen gas. They note that the preferred fragmentation routes lead to the singly-charged fragments C₃H₃⁺ and C₄H₂⁺ but not to CH₃⁺ and C₂H₂⁺ (see their Table 2). In Fig. 1 many of the fragmentations produce 39, 40 u and 50, 51 u, however 26, 27 u are also produced, although in somewhat lesser abundance.

We observe clear but unexpected structures near the diagonal of the full coincidence map. The largest of these structures are observed near 101 u and near 202 u, and these are shown in Fig. 6. These structures cannot be due to ringing, because they extend over 1.4 μs, which is much longer than expected for our fast pulse-counting electronics. The structures show clear clumps at integer masses, but there are no extended distributions characteristic of Coulomb explosion (with the exception of the fragmentation C₈H₂⁺ + C₈H₆⁺ + 2H observed in the (8, 8) group). Pyrene dimers are not produced by our effusive source.

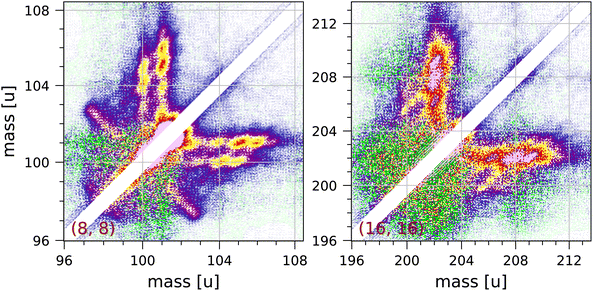Fig. 6 Two symmetrised sections of the measured coincidence map near the diagonal showing structures attributed to collective effects (see discussion in the text). Each section contains 240 × 240 bins and corresponds to 3 × 3 μs in ion flight time. The mass scales are adjusted accordingly. The colour scales are the same as in Fig. 2.

We suspect that these structures may be due to a collective effect. In order to obtain adequate statistics for the coincidence map for pyrene we have used fairly high electron and molecular beam intensities. The structures observed indicate the coincident detection of a singly or doubly charged pyrene ion and a pyrene ion with up to 4 or 5 hydrogen atoms attached to it. Hydrogen attachment to PAHs has been studied by a number of groups.^{31,47,48,69,70} A pyrene ion may be able to pick up hydrogen atoms produced by fragmentation of other molecules and lingering in the interaction region, but we do not understand what mechanism would then produce coincidences with another pyrene ion without extra hydrogen atoms attached.

In five locations in the coincidence map very weak fragmentations are observed with one fragment of half-integer m/q. These fragmentations must be due to triple ionisation. The least weak of these fragmentations is

C₁₆H₁₀⁺⁺⁺ → C₂H₂⁺ + C₁₄H₈⁺⁺ (10)

and the other fragmentations are

C₁₆H₁₀⁺⁺⁺ → CH₃⁺ + C₁₅H₇⁺⁺ (11)

C₁₆H₁₀⁺⁺⁺ → C₃H_2,3⁺ + C₁₃H₇⁺⁺ (+H) (12)

C₁₆H₁₀⁺⁺⁺ → C₅H₃⁺ + C₁₁H_6,7⁺⁺ (+H) (13)

C₁₆H₁₀⁺⁺⁺ → C₇H₃⁺ + C₉H_6,7⁺⁺ (+H) (14)

All these fragmentations involve a break-up of the molecule into two fragments, in some of the cases accompanied by the loss of a single hydrogen atom. Subsequent fragmentation of the doubly-charged fragments may provide a minor contribution to the coincidence groups discussed.

Kingston et al.⁴³ have measured the singly-charged fragments produced by triple ionisation of pyrene and other PAHs. The singly-charged ions we observe in fragmentations (10)–(14) correspond to the ions Kingston et al.⁴³ list in their Table 3. In our measurements any C₄H₂⁺ fragments produced by triple ionisation are masked by the strong production of C₄H₂,₃⁺ following double ionisation.

4 Conclusions

Double ionization of pyrene by electron impact results in a number of prominent fragmentations producing two singly-ionized fragments. Fragmentations for which the total number of carbon atoms in both fragments are more likely than fragmentations for which the total is odd. No fragmentations are observed for groups in which the sum of the carbon atoms is 15. Most of the fragments have 2 or 3 hydrogen atoms, but the larger fragment can have 5, 6, 7 or 8 hydrogen atoms if it has 9 or more carbon atoms. Fragments with only carbon atoms and no hydrogen atoms are not present, and we observe fragments with only one hydrogen atom in only a few places. Several fragmentations produce singly-charged fragments with four or more carbon atoms, which can only be formed by the breaking of at least three C–C bonds.

Our measurements indicate that ions with kinetic energies of a few eV can be produced, sufficient to induce reactions in astrophysical environments that cannot be induced by thermal ions produced by single ionization.

Author contributions

The application of the field programmable gate array for the recording of mass spectra on an event-by-event basis and the associated programming was done by MG. The model of the coincidence data acquisition used for the extraction of the map of true coincidences was developed and implemented by MG. The measurements and the trajectory simulations were done by PvdB. PvdB wrote most of the paper, and MG contributed to the discussion of the results.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This article is based on research done in relation to COST Action CA18212—Molecular Dynamics in the GAS phase (MD-GAS), supported by COST (European Cooperation in Science and Technology).

Notes and references

1. A. B. Patel, S. Shaikh, K. R. Jain, C. Desai and D. Madamwar, Front. Microbiol., 2020, 11, 562813.
2. N. Premnath, K. Mohanrasu, R. Guru Raj Rao, G. H. Dinesh, G. Siva Prakash, V. Ananthi, K. Ponnuchamy, G. Muthusamy and A. Arun, Chemosphere, 2021, 280, 130608.
3. A. G. G. M. Tielens, Rev. Mod. Phys., 2013, 85, 1021.
4. S. A. Sandford, M. Nuevo, P. P. Bera and T. J. Lee, Chem. Rev., 2020, 120, 4616.
5. A. G. G. M. Tielens, Molecular Astrophysics, Cambridge University Press, Cambridge, 2021.
6. V. M. Bierbaum, V. Le Page and T. P. Snow, EAS Publ. Ser., 2011, 46, 427.
7. D. K. Böhme, Phys. Chem. Chem. Phys., 2011, 13, 18253.
8. M. Larsson, W. D. Geppert and G. Nyman, Rep. Prog. Phys., 2012, 75, 066901.
9. M. Gatchell and H. Zettergren, J. Phys. B: At., Mol. Opt. Phys., 2016, 49, 162001.
10. G. Wenzel, C. Joblin, A. Giuliani, S. Rodriguez Castillo, G. Mulas, M. Ji, H. Sabbah, S. Quiroga, D. Pena and L. Nahon, Astron. Astrophys., 2020, 641, 98.
11. N. J. Mason, B. Nair, S. Jheeta and E. Szymańska, Faraday Discuss., 2014, 168, 235.
12. M. C. Boyer, N. Rivas, A. A. Tranb, C. A. Verish and C. R. Arumainayagam, Surf. Sci., 2016, 652, 26.
13. L. Campbell and M. J. Brunger, Int. Rev. Phys. Chem., 2016, 35, 297.
14. R. Wehlitz, J. Phys. B: At., Mol. Opt. Phys., 2016, 49, 222004.
15. D. A. Hagan and J. H. D. Eland, Rapid Commun. Mass Spectrom., 1991, 5, 512.
16. Y. Ling, Y. Gotkis and C. Lifshitz, Eur. J. Mass Spectrom., 1995, 1, 41.
17. H. W. Jochims, H. Baumgärtel and S. Leach, Astrophys. J., 1999, 512, 500.
18. P. M. Mayer, V. Blanchet and C. Joblin, J. Chem. Phys., 2011, 134, 244312.
19. P. M. Mishra, L. Avaldi, P. Bolognesi, K. C. Prince, R. Richter and U. R. Kadhane, J. Phys. Chem. A, 2014, 118, 3128.
20. R. Wehlitz and T. Hartman, J. Phys.: Conf. Ser., 2014, 488, 012013.
21. K. O. Johansson, M. F. Campbell, P. Elvati, P. E. Schrader, J. Zádor, N. K. Richards-Henderson, K. R. Wilson, A. Violi and H. A. Michelsen, J. Phys. Chem. A, 2017, 121, 4447.
22. T. Monfredini, H. M. Quitián-Lara, F. Fantuzzi, W. Wolff, E. Mendoza, A. F. Lago, D. A. Sales, M. G. Pastoriza and H. M. Boechat-Roberty, Mon. Not. R. Astron. Soc., 2019, 488, 451.
23. A. Marciniak, V. Despré, T. Barillot, A. Rouzée, M. C. E. Galbraith, J. Klei, C.-H. Yang, C. T. L. Smeenk, V. Loriot, S. Nagaprasad Reddy, A. G. G. M. Tielens, S. Mahapatra, A. I. Kuleff, M. J. J. Vrakking and F. Lépine, Nat. Commun., 2015, 6, 7909.
24. J. W. L. Lee, D. S. Tikhonov, P. Chopra, S. Maclot, A. L. Steber, S. Gruet, F. Allum, R. Boll, X. Cheng, S. Düsterer, B. Erk, D. Garg, L. He, D. Heathcote, M. Johny, M. M. Kazemi, H. Köckert, J. Lahl, A. K. Lemmens, D. Loru, R. Mason, E. Müller, T. Mullins, P. Olshin, C. Passow, J. Peschel, D. Ramm, D. Rompotis, N. Schirmel, S. Trippel, J. Wiese, F. Ziaee, S. Bari, M. Burt, J. Küpper, A. M. Rijs, D. Rolles, S. Techert, P. Eng-Johnsson, M. Brouard, C. Vallance, B. Manschwetus and M. Schnell, Nat. Commun., 2021, 12, 6107.
25. J. W. L. Lee, D. S. Tikhonov, F. Allum, R. Boll, P. Chopra, B. Erk, S. Gruet, L. He, D. Heathcote, M. M. Kazemi, J. Lahl, A. K. Lemmens, D. Loru, S. Maclot, R. Mason, E. Müller, T. Mullins, C. Passow, J. Peschel, D. Ramm, A. L. Steber, S. Bari, M. Brouard, M. Burt, J. Küpper, P. Eng-Johnsson, A. M. Rijs, D. Rolles, C. Vallance, B. Manschwetus and M. Schnell, Phys. Chem. Chem. Phys., 2022, 24, 23096.
26. J. A. Noble, C. Aupetit, D. Descamps, S. Petit, A. Simon, J. Mascetti, N. Ben Amor and V. Blanchet, Phys. Chem. Chem. Phys., 2019, 21, 14111.
27. M. Wolf, H. V. Kiefer, J. Langeland, L. H. Andersen, H. Zettergren and H. T. Schmidt, Astrophys. J., 2016, 832, 24.
28. J. Zhen, S. Rodriguez Castillo, C. Joblin, G. Mulas, H. Sabbah, A. Giuliani, L. Nahon, S. Martin, J.-P. Champeaux and P. M. Mayer, Astrophys. J., 2016, 822, 113.
29. B. West, F. Useli-Bacchitta, H. Sabbah, V. Blanchet, A. Bodi, P. M. Mayer and C. Joblin, J. Phys. Chem. A, 2014, 118, 7824.
30. B. West, S. Rodriguez Castillo, A. Sit, S. Mohamad, B. We, C. Joblin, A. Bodi and P. M. Mayer, Phys. Chem. Chem. Phys., 2018, 20, 7195.
31. M. H. Stockett, L. Avaldi, P. Bolognesi, J. N. Bull, L. Carlini, E. Carrascosa, J. Chiarinelli, R. Richter and H. Zettergren, Astrophys. J., 2021, 913, 46.
32. Y. Huo, M. K. Espinoza Cangahuala, V. Zamudio-Bayer, M. Goulart, M. Kubin, M. Timm, J. T. Lau, B. von Issendorff, R. Hoekstra, S. Faraji and T. Schlathölter, Mon. Not. R. Astron. Soc., 2023, 523, 865.
33. A. Lietard and J. R. R. Verlet, J. Phys. Chem. Lett., 2022, 13, 3529.
34. A. Ławicki, A. I. S. Holm, P. Rousseau, M. Capron, R. Maisonny, S. Maclot, F. Seitz, H. A. B. Johansson, S. Rosén, H. T. Schmidt, H. Zettergren, B. Manil, L. Adoui, H. Cederquist and B. A. Huber, Phys. Rev. A: At., Mol., Opt. Phys., 2011, 83, 022704.
35. F. Seitz, A. I. S. Holm, H. Zettergren, H. A. B. Johansson, S. Rosén, H. T. Schmidt, A. Ławicki, J. Rangama, P. Rousseau, M. Capron, R. Maisonny, A. Domaracka, L. Adoui, A. Méry, B. Manil, B. A. Huber and H. Cederquist, J. Chem. Phys., 2011, 135, 064302.
36. M.-C. Ji, J.-P. Champeaux, P. Moretto-Capelle, J. Renoud, L. Polizzi, S. Faure, M. Sence and P. Cafarelli, J. Phys. B: At., Mol. Opt. Phys., 2020, 53, 225207.
37. T. Chen, M. Gatchell, M. H. Stockett, R. Delaunay, A. Domaracka, E. R. Micelotta, A. G. G. M. Tielens, P. Rousseau, L. Adoui, B. A. Huber, H. T. Schmidt, H. Cederquist and H. Zettergren, J. Chem. Phys., 2015, 142, 144305.
38. M. E. Wacks, J. Chem. Phys., 1964, 41, 1661.
39. B. Shushan and R. K. Boyd, Org. Mass Spectrom, 1980, 15, 445.
40. B. P. Mathur, E. M. Burgess, D. E. Bosfwick and T. F. Moran, Org. Mass Spectrom, 1981, 16, 92.
41. S. Tobita, S. Leach, H. W. Jochims, E. Rühl, E. Illenberger and H. Baumgärtel, Can. J. Phys., 1994, 72, 1060.
42. J. W. Keller, M. A. Coplan and R. Goruganthu, Astrophys. J., 1992, 391, 872.
43. R. G. Kingston, M. Guilhaus, A. G. Brenton and J. H. Beynon, Org. Mass Spectrom, 1985, 20, 406.
44. M. H. Stockett, H. Zettergren, L. Adoui, J. D. Alexander, U. Bērziņš, T. Chen, M. Gatchell, N. Haag, B. A. Huber, P. Hvelplund, A. Johansson, H. A. B. Johansson, K. Kulyk, S. Rosén, P. Rousseau, K. Støchkel, H. T. Schmidt and H. Cederquist, Phys. Rev. A: At., Mol., Opt. Phys., 2014, 89, 032701.
45. M. H. Stockett, M. Gatchella, N. de Ruettea, L. Giacomozzia, T. Chena, P. Rousseauc, S. Maclot, J.-Y. Chesnel, L. Adouic, B. A. Huber, U. Bērziņš, H. T. Schmidt, H. Zettergren and H. Cederquista, Int. J. Mass Spectrom., 2015, 392, 58.
46. M. H. Stockett, M. Gatchell, T. Chen, N. de Ruette, L. Giacomozzi, M. Wolf, H. T. Schmidt, H. Zettergren and H. Cederquist, J. Phys. Chem. Lett., 2015, 6, 4504.
47. M. Gatchell, M. H. Stockett, N. de Ruette, T. Chen, L. Giacomozzi, R. F. Nascimento, M. Wolf, E. K. Anderson, R. Delaunay, V. Vizcaino, P. Rousseau, L. Adoui, B. A. Huber, H. T. Schmidt, H. Zettergren and H. Cederquist, Phys. Rev. A: At., Mol., Opt. Phys., 2015, 92, 050702.
48. M. Wolf, L. Giacomozzi, M. Gatchell, N. de Ruette, M. H. Stockett, H. T. Schmidt, H. Cederquist and H. Zettergren, Eur. Phys. J. D, 2016, 70, 85.
49. Y. Yamakita, M. Yamauchi and K. Ohno, J. Chem. Phys., 2009, 130, 024306.
50. C. Joblin, L. Dontot, G. A. Garcia, F. Spiegelman, M. Rapacioli, L. Nahon, P. Parneix, T. Pino and P. Bréchignac, J. Phys. Chem. Lett., 2017, 8, 3697.
51. J. Zhen, T. Chen and A. G. G. M. Tielens, Astrophys. J., 2018, 863, 128.
52. G. A. Garcia, L. Dontot, M. Rapacioli, F. Spiegelman, P. Bréchignac, L. Nahon and C. Joblin, Phys. Chem. Chem. Phys., 2023, 25, 4501.
53. R. Delaunay, M. Gatchell, P. Rousseau, A. Domaracka, S. Maclot, Y. Wang, M. H. Stockett, T. Chen, L. Adoui, M. Alcamí, F. Martín, H. Zettergren, H. Cederquist and B. A. Huber, J. Phys. Chem. Lett., 2015, 6, 1536.
54. R. Delaunay, A. Mika, A. Domaracka, B. A. Huber and P. Rousseau, Eur. Phys. J. D, 2018, 72, 149.
55. J. Bouwman, H. M. Cuppen, A. Bakker, L. J. Allamandola and H. Linnartz, Astron. Astrophys., 2010, 511, A33.
56. A. Lignell, L. I. Tenelanda-Osorio and M. S. Gudipati, Chem. Phys. Lett., 2021, 778, 138814.
57. S. Singh, D. Gupta, B. Antony, M. Tudorovskaya and J. Tennyson, J. Phys. Chem. A, 2020, 124, 7088.
58. A. Simon, M. Rapacioli, G. Rouaut, G. Trinquier and F. X. Gadéa, Philos. Trans. R. Soc., A, 2017, 375, 20160195.
59. A. Simon, J. P. Champeaux, M. Rapacioli, P. Moretto Capelle, F. X. Gadéa and M. Sence, Theor. Chem. Acc., 2018, 137, 106.
60. L. J. Frasinski, J. Phys. B: At., Mol. Opt. Phys., 2016, 49, 152004.
61. C. Vallance, D. Heathcote and J. W. L. Lee, J. Phys. Chem. A, 2021, 125, 1117.
62. T. Yatsuhashi and N. Nakashima, J. Photochem. Photobiol., C, 2018, 34, 52.
63. P. J. M. van der Burgt and M. L. Gradziel, Eur. Phys. J. D, 2022, 76, 60.
64. P. J. M. van der Burgt, M. Dunne and M. L. Gradziel, Eur. Phys. J. D, 2018, 72, 31.
65. P. J. M. van der Burgt, M. Dunne and M. L. Gradziel, J. Phys.: Conf. Ser., 2019, 1289, 012008.
66. G. Barrett and P. J. M. van der Burgt, J. Phys.: Conf. Ser., 2008, 101, 012008.
67. G. Reitsma, H. Zettergren, S. Martin, R. Brédy, L. Chen, J. Bernard, R. Hoekstra and T. Schlathölter, J. Phys. B: At., Mol. Opt. Phys., 2012, 45, 215201.
68. G. Reitsma, H. Zettergren, L. Boschman, E. Bodewits, R. Hoekstra and T. Schlathölter, J. Phys. B: At., Mol. Opt. Phys., 2013, 46, 245201.
69. V. Le Page, T. P. Snow and V. M. Bierbaum, Astrophys. J., 2009, 704, 274.
70. J. A. Rasmussen, J. Phys. Chem. A, 2013, 117, 4279.

---

Footnote

† Trajectory calculations for the 39 u + 139 u fragmentation in anthracene⁶² indicate that the use of the focussing plate would increase the probability that both ions hit the detector from about 12% to about 25%. In the simulation in Fig. 2(b) 42% of the ions are detected.

---