Open Access Article
Open Access ArticleThe stochastic wave function method for diffusion of alkali atoms on metallic surfaces
E. E.
Torres-Miyares
 *a,
D. J.
Ward
*a,
D. J.
Ward
 b,
G.
Rojas-Lorenzo
b,
G.
Rojas-Lorenzo
 c,
J.
Rubayo-Soneira
c,
J.
Rubayo-Soneira
 cd,
W.
Allison
b and
S.
Miret-Artés
cd,
W.
Allison
b and
S.
Miret-Artés
 ad
ad
aInstituto de Física Fundamental, Consejo Superior de Investigaciones Científicas, Serrano 123, 28006, Madrid, Spain. E-mail: elena.torres@iff.csic.es; s.miret@iff.csic.es
bSMF Cavendish Laboratory, JJ Thomson Avenue, Cambridge, UK. E-mail: djw77@cam.ac.uk; wa14@cam.ac.uk
cInstituto Superior de Tecnologías y Ciencias Aplicadas (InSTEC),Universidad de La Habana, Avenida Allende No. 1110, Plaza, La Habana 10400, Cuba. E-mail: grojas37@gmail.com; jrubayo@gmail.com
dDonostia International Physics Center (DIPC), Paseo Manuel de Lardizabal, 4, 20018, Donostia-San Sebastian, Spain
First published on 3rd February 2023
Abstract
The stochastic wave function method is proposed to study the diffusion regimes of alkali atoms on metallic surfaces. The Lindblad approach, based on the microscopic Hamiltonian information in the Caldeira–Leggett model, is presented and numerical calculations of the dynamics are carried out to characterize surface diffusion for two different systems: Na–Cu(111) and Li–Cu(111). Calculations of the intermediate scattering function for an isolated adsorbate are compared, in the Brownian limit, with results deduced from helium spin-echo (HeSE) experiments after reducing them to single adsorbate dynamics. To illustrate the method we present the dependence on momentum transfer and the temperature dependency. Results show that the experiment can be described at a quantitative level by the 1-D quantum model (reduced dimensionality).
1 Introduction
The adsorption of alkali metal on metallic surfaces has technological impact on industrial catalytic processes.1 For example, the presence of controlled quantities of alkali metals influences a variety of heterogeneous catalytic processes2,3 and the complexity of the behaviour observed4,5 is surprising given the relatively simple electronic structure in the alkali metal adsorption. Alkali metals tend to chemisorb at high symmetry sites without disturbing the underlying substrate4 and, at low coverages, the valence charge of the alkali metal is shifted towards the substrate due to the difference in electron affinity leading to a dipole moment whereas, at high coverage, the alkali layer takes on a metallic character.6,7 The adsorption site, itself, can depend on the coverage.8Recent studies of the diffusion of alkali atoms on Cu(001) and Cu(111) surfaces include Na–Cu(111),9 Na–Cu(001),10–13 K–Cu(001)14 and Li–Cu(001).7 In addition to experiment, calculations15,16 provide knowledge of both the adsorbate–substrate interaction and the inter-adsorbate forces giving information relevant to phenomena such as adsorption, desorption, dissociation and recombination.17
A description of the force fields (adsorbate–adsorbate and adsorbate–substrate interactions) is necessary to formulate the molecular dynamics of alkali metal on metallic surfaces. The Langevin formalism18 provides a classical description that is sufficient in many situations.19 Adsorbate–adsorbate interactions can be included explicitly20 or treated approximately with an additional white shot noise.21 Here, we treat the problem quantum-mechanically in one dimension (reduced dimensionality), using a new theoretical method that has been proposed by some of the present authors22,23 in this context. We apply the method in the diffusive limit to discuss two systems for which new experimental data exist: Na–Cu(111) and Li–Cu(111). In the context of surface diffusion, the model has never been used and represents an alternative to the classical, Langevin formalism.
The work focuses on an interpretation of the dynamical behaviour in the limit of long-times, where the motion is primarily diffusive. In that limit, the dynamics are determined predominantly by the energy landscape and are insensitive to the spectrum of thermal excitations.24 We extract the behaviour, at long-times, from the intermediate scattering function in both experiment and calculation before comparing the two. In addition, and where relevant, we eliminate the effect of adsorbate–adsorbate interactions from the experimental data through an effective incoherent intermediate scattering function in the neutron scattering context, using methods that have been described previously.20
Our primary aim, here, is to demonstrate that a fully quantum approach to diffusive dynamics is now a practical proposition for the analysis of experiment. Most previous work has assumed classical behaviour, except in systems, such as the diffusion of atomic hydrogen at low temperatures, where quantum effects are expected to dominate. By demonstrating that the quantum calculations can represent experiments for light adsorbates, such as Li, as well as heavier adsorbates, such as Na, our work covers the regime where the validity of classical methods may be open to question.
The paper is organized as follows. In Section 2, the Caldeira–Leggett model, Lindblad theory and stochastic wave function method are presented as a theoretical model for the surface diffusion processes. In Section 3, new numerical and experimental results for two different systems, Na–Cu(111) and Li–Cu(111), are presented and compared with previous analytic results. Finally, in Section 4, the main conclusions of this work are summarized and future perspectives are presented.
2 The stochastic wave function method
The pioneering Caldeira–Leggett (CL) formalism is used to describe the motion of a quantum Brownian particle linearly coupled to an Ohmic environment in the weak-coupling and high-temperature limits.25,26 Assuming short environmental correlation times and tracing out the environment degrees of freedom, a Markovian quantum master equation for the reduced density matrix is written for a one dimensional problem as27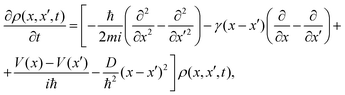 | (1) |
| D = 2mγkBT, | (2) |
However this formalism has a few drawbacks, the determinant of the generator of the CL master equation is negative and is only valid for high temperatures. Different attempts to obtain a master equation from microscopic Hamiltonians preserving the density positivity have been made.28,29 Several works limited to the weak-coupling30,31 or high-temperature regime32 are found in the literature. A new approach using the quantum dynamical semigroups by Lindblad29 and Kossakowski et al.33 arrived to a generator of a completely positive map. Unlike closed systems where the dynamics can be described by the unitary time evolution, finding an appropriate equation of motion for the density matrix is the main goal. An open system can be represented as a system-plus-environment scheme. In this case, the dissipative evolution of the reduced density matrix depends on the Liouville functional 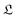
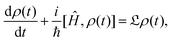 | (3) |
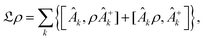 | (4) |
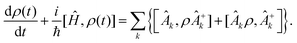 | (5) |
The structure of the operators Âk is unknown but it can be found based on the microscopic Hamiltonian information coming from the CL formalism.
The minimal invasive modification to the CL master eqn (1) can be carried out by just adding an additional term of the form γ[![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) , [
, [![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) , ρ]]/8mkBT, which is small in the high temperature limit,
, ρ]]/8mkBT, which is small in the high temperature limit,
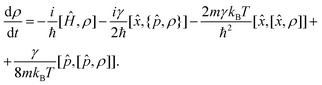 | (6) |
From eqn (6), the CL master equation can be brought into Lindblad form (5) for one Lindblad operator Âk given by a linear combination of the position ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) and momentum
and momentum ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) operators,
operators,
 = μ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) + iν + iν![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) , Â+ = μ , Â+ = μ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) − iν − iν![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) | (7) |
Replacing the operators (7) in the Lindblad eqn (5), the corresponding Markovian master equation is
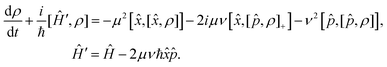 | (8) |
In the coordinate space, this equation takes the following expression
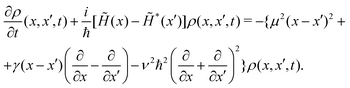 | (9) |
A simplest way to solve the master eqn (9) is using a set of stochastic wave functions {|ψ〉}, where each function obeys the following differential equation
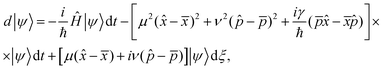 | (10) |
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) = 〈ψ|
= 〈ψ|![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) |ψ〉,
|ψ〉, ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) = 〈ψ|
= 〈ψ|![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) |ψ〉 and dξ are complex stochastic variables fulfilling the properties of a Wiener process dξ (the mean and variance of fluctuations are zero and dt1/2, respectively):
|ψ〉 and dξ are complex stochastic variables fulfilling the properties of a Wiener process dξ (the mean and variance of fluctuations are zero and dt1/2, respectively): 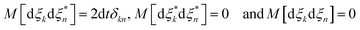 , where M stands for a mean over fluctuations due to the stochastic process.34Eqn (10) is known as the Îto stochastic differential equation.
, where M stands for a mean over fluctuations due to the stochastic process.34Eqn (10) is known as the Îto stochastic differential equation.
Previously, the Îto stochastic differential equation has only been applied to a limited number of adsorbate systems. The idealised vibrational relaxation and desorption of O2–Pt(111) have been discussed by Gao,28 while some of the present authors have studied Xe–Pt(111).22,23 Here, we apply a similar method to the dynamics of sodium and lithium atoms, in the diffusive regime on a copper surface in order to compare them directly with information extracted from new and recent helium spin-echo experiments.
3 Experiment and numerical results
3.1 Experiment
Experimental data for both Na/Cu(111) and Li/Cu(111) are obtained from helium spin-echo (HeSE) measurements using an incident energy Ei ≃ 8 meV, and at a surface coverage of θ ≃ 0.025 ML. Surface temperatures for the data presented here were Ts = 155 K for the Na case and Ts = 140 K for the Li case. Measurements for Na/Cu(111) have been described previously.9,20 The Li/Cu(111) data are obtained and analysed in a similar manner. Specifically, the experiment generates a normalised intermediate scattering function (ISF) corresponding to coherent scattering from all features on the surface. Static features, such as surface steps or point defects, give a constant, time-independent contribution to the ISF which is removed by fitting a constant background. Features due to inelastic scattering, such as those generated by single-phonon scattering add a periodic contribution that can be removed effectively by Fourier filtering in the energy-domain.9 The remaining features are attributed to quasi-elastic scattering from the ballistic and diffusive motion of the adsorbates. The mean rate of energy transfer, γ, between an adsorbate and the heat-bath of the substrate acts to distinguish between ballistic motion, which dominates at short times, t ≪ 1/γ, and diffusive motion, which is predominant at long times, t ≫ 1/γ. In the present work, we are concerned with diffusive motion and thus extract the necessary information from the long-time behaviour of the ISFs. The procedure used to analyse diffusive motion is described in detail in Rittmeyer et al.,9 and, for Na/Cu(111), we obtain the characteristic decay rates of the diffusive correlations by excluding data for t < 18 ps. In all of the data below, we assume an exponential time dependence of the form I(ΔK, t) ∼ exp(−α(ΔK)t), where the dephasing rate, α, is presented as a function of ΔK.In the case of Na/Cu(111), one further step of analysis is necessary before the experiment can be compared with the calculations. The numerical method describes correlations in the motion of a single diffusing entity whereas the experiment necessarily involves many adsorbates. Spatial correlations observed in the experiment include a self-part, which tracks the correlation of an individual particle, and a distinct-part, which tracks the pairwise correlations with other particles.35 For Na/Cu(111), the inter-adsorbate forces are significant and we extract the self-correlations assuming pairwise forces and a power-law form-factor,20 before comparison with the calculations.
3.2 Numerical results
In order to solve the Îto stochastic differential eqn (10) we have used the split operator method described in ref. 36. As seen in previous works,37 the Lindblad operators coefficients have been taken as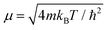 and
and 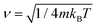 . In this way, the temperature has been incorporated in the system description. Position
. In this way, the temperature has been incorporated in the system description. Position ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) and momentum
and momentum ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) operators are propagated in the coordinate and momentum space, respectively. The numerical code was developed to solve, N times, the stochastic differential eqn (10). In order to obtain the observables average values, the number of realizations N is chosen to be large enough to reach the numerical stability and convergence.
operators are propagated in the coordinate and momentum space, respectively. The numerical code was developed to solve, N times, the stochastic differential eqn (10). In order to obtain the observables average values, the number of realizations N is chosen to be large enough to reach the numerical stability and convergence.
The discrete wave function ψ(x, t) is evaluated, at each time t, in equally spaced points belonging to the interval [x1,xNs], Ns being the number of points a power of 2 (in this way the fast Fourier transform can be used when necessary)
| ψ(x, t) ≡{ψ(x1, t); ψ(x2, t); ψ(x3, t);⋯; ψ(xNs, t)} | (11) |
The wave function normalization is calculated as
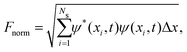 | (12) |
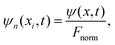 | (13) |
![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) for the N realizations can be expressed as
for the N realizations can be expressed as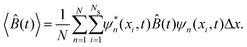 | (14) |
The ISF is a key quantity in the surface diffusion context and, for a single adsorbate, the ISF can be written as.
I(ΔK, t) = 〈e−iΔK·![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) (0)eiΔK· (0)eiΔK·![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) (t)〉 (t)〉 | (15) |
For our problem, ΔK = ΔK is the wave vector transfer parallel to the surface, ![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) (t) =
(t) = ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) (t) and
(t) and ![[R with combining circumflex]](https://www.rsc.org/images/entities/b_char_0052_0302.gif) (0) =
(0) = ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) (0) are the position operators of the adatom/adsorbate at time t and t = 0, respectively. The x-dimension is considered as one of the symmetry directions of the surface, where the projection on the wave vector transfer is carried out. Now, from eqn (15) we have that
(0) are the position operators of the adatom/adsorbate at time t and t = 0, respectively. The x-dimension is considered as one of the symmetry directions of the surface, where the projection on the wave vector transfer is carried out. Now, from eqn (15) we have that
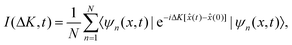 | (16) |
![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) (t)−
(t)−![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) (0)] and
(0)] and ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) can be obtained from eqn (14). Thus, the ISF I(ΔK, t) is then calculated according to
can be obtained from eqn (14). Thus, the ISF I(ΔK, t) is then calculated according to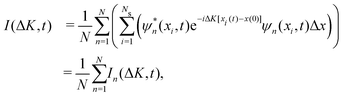 | (17) |
The unidimensional space is chosen to be x ∈ [−80, 80] Å, with a number of points Ns = 4096 and a number of realizations N = 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. The increment Δx, given by Δx = (xf − xi)/Ns, for these parameters, is Δx = 0.04 Å. The initial wave function is considered to be a Gaussian wafunction given by
000. The increment Δx, given by Δx = (xf − xi)/Ns, for these parameters, is Δx = 0.04 Å. The initial wave function is considered to be a Gaussian wafunction given by
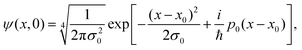 | (18) |
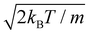 at a temperature T and the adsorbate with mass m. The time integration step chosen is Δt = 66.1462 a.u. = 1.6 fs in order to reach numerical convergence for the ISF.
at a temperature T and the adsorbate with mass m. The time integration step chosen is Δt = 66.1462 a.u. = 1.6 fs in order to reach numerical convergence for the ISF.
3.3 Diffusion of Na on Cu(111)
In the stochastic wave function calculations, a potential with a single Fourier component and the periodicity of the substrate is assumed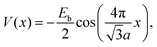 | (19) |
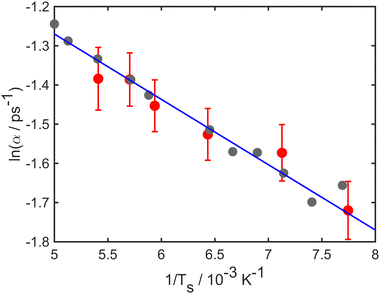
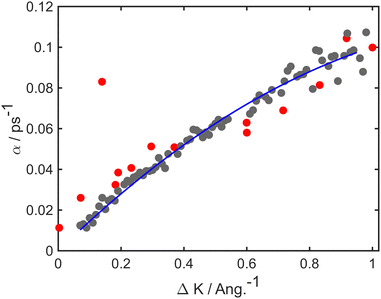
At long times t ≫ γ−1 (say ten times γ−1), the ISF is expected to decay as an exponential function I(t) ∼ exp(−αt), where the dependence of α on the scattering momentum-transfer, ΔK, provides information about the rate and nature of the diffusive motion. Fig. 1 shows decay rates α(ΔK) from the stochastic wave function formalism (grey points) in comparison with experimental results (red points). The blue curve in Fig. 1 corresponds to the analytic result for single hops obtained using the Chudley–Elliott model,39 which has the form
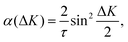 | (20) |
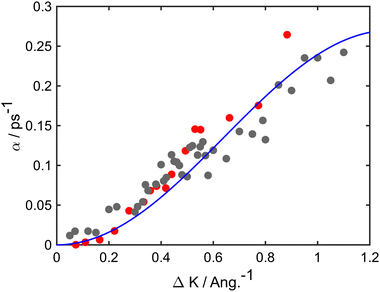 | ||
| Fig. 1 Decay rate α of the Brownian component in the ISF, as a function of momentum transfer ΔK for Na adsorbates on Cu(111) surface at Ts = 155 K. Numerical calculations (grey points) are shown for simulations up to 50 ps using a friction γ = 0.20 ps−1 and an energy barrier Eb = 55 meV. Experimental data (red points) are for dephasing rates of single adsorbate dynamics.20 The solid blue curve corresponds to idealised single-jumps (see text) and illustrates that the long-time dynamics of the system is described well by the classical Chudley–Elliott model. | ||
Stochastic wave function calculations also reproduce the temperature dependence observed in experiment, which over a limited temperature range is well represented by an Arrhenius law
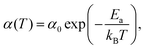 | (21) |
3.4 Diffusion of Li on Cu(111)
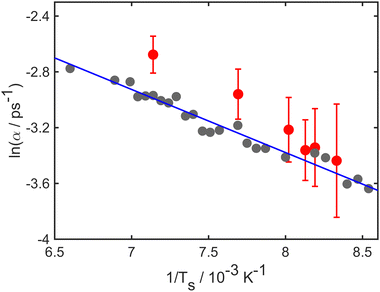
Simulations and experiment for the case of Li diffusion are analysed in a similar manner to those for Na. In the case of the experiment, there is little evidence for collective motion and so we compare the experimental α(ΔK) directly with values derived from the numerical simulations. Both experiment and simulations correspond to T = 140 K, and, in the simulations, the energy barrier is Eb = 45 meV, the friction coefficient is γ = 1.20 ps−1 and the values of α extracted from data up to 20 ps.Fig. 3 shows a comparison of the simulations and experiment, which are shown, respectively, as grey and red data-points. The solid blue line is a guide to the eye and is included to facilitate comparison of the two data-sets. Simulations follow the experimental trend closely, and show somewhat less scatter than the experiment. Notice that the trends in both simulation and experiment, as represented by the solid line, are quite different to those in the case of Na/Cu(111), above. We conclude that the motion of the lithium atoms is not in the same “classical” regime of single-hops that was evident for Na and, therefore, some aspects of the dynamics are in a “quantum” regime. The close agreement of simulation and experiment, seen in Fig. 3 as well as Fig. 1, demonstrates the ability of the simulations to reproduce trends in both quantum and classical regimes.
 | ||
| Fig. 3 Decay rate, α, as a function of momentum transfer, ΔK, for Li adsorbates on Cu(111); numerical results (grey points), experimental results (red points). The solid blue curve is included as a guide for the eye to facilitate comparison of simulation and experiment. The overall trend of the line does not follow a conventional dynamical signature such as that illustrated by the example of Na/Cu(111) in Fig. 1. In the simulations an energy barrier of Eb = 45 meV with friction γ = 1.20 ps−1 was used. Numerical results up to 20 ps are considered to extract the Brownian component of the motion. | ||
The temperature dependence of the diffusive motion is illustrated in Fig. 4, which shows an Arrhenius plot for the temperature dependence of the decay rate. Log(α), is plotted against the inverse temperature 1/T. Numerical results (grey points) and experimental results (red points) both have linear trends as expected from the Arrhenius law. The solid blue line shows a fit to the simulations data and corresponds to an effective activation energy of 41 meV. Notice, however, that the trend in the experiment suggests a somewhat steeper slope than that used to reproduce the simulations.
4 Conclusions
The stochastic wave function method has been used to analyze the surface diffusion of alkali atoms on a metallic surface. Both Na/Cu(111) and Li/Cu(111) have been studied and the results of simulations compared directly with experiment. In particular, we have obtained the time dependency of the intermediate scattering function in the Brownian regime, i.e. for times t ≫ 1/γ, where γ is the mean rate of energy transfer. In both systems, agreement is evident in the ΔK dependence of the correlation decay-rate, α, as well as its temperature dependence. Na/Cu(111) is confirmed as a high friction system where the α(ΔK) dependence follows the expectation for a classical atom performing single-hops between nearest-neighbour sites. In the case of Li/Cu(111), the α(ΔK) dependence does not follow any simple analytic model (for example, the Chudley–Elliott model), indicating that the diffusion cannot be explained simply in terms of the behaviour of a classical particle. The precise effects responsible for such an α(ΔK) dependence are not obvious; however, they are reproduced well by the quantum calculations. Thus, we have demonstrated the stochastic wave function method can represent a “classical” regime as well as the quantum one, though clearly our future understanding could be improved given a larger experimental and computational data-set.In our calculations we use a 1D potential, to represent the dynamics. The adsorbate, however, moves in 2D so the question of higher dimensionality is significant. Clearly, quantum motion along a reaction coordinate will be affected by the form of the potential in an orthogonal direction and the effect may be significant. A prominent example is that of inverse isotope effects in H/D motion,40,41 where a constricted transition state can increase the local zero-point energy to the extent that lighter adsorbates have a lower transition rate than a heavier isotope. Even in such extreme cases it is still viable to describe the motion within a 1D potential, but with an effective barrier that is mass dependent. For this reason, the calculated potentials we use to describe the data should be regarded as effective potentials rather than the true adiabatic potential energy.
Furthermore, the success of our numerical approach suggests its extension further into the 2D quantum regime, where very light adsorbates, such as atomic hydrogen, are known to tunnel through the diffusion barrier. Work in this direction is now in progress.
Author contributions
All authors have contributed equally to this work.Conflicts of interest
There are no conflicts to declare.Acknowledgements
E. E. T.-M. and S. M. A. would like to thank Fundación Humanismo y Ciencia for financial support. G. R.-L. and J. R.-S. would also thank the Advanced Computational Team at Higher Institute for Technologies and Applied Sciences (Havana University) for the support provided during the realization of this work and to Project NA223LH-INSTEC-003. The authors acknowledge use of and support by the Cambridge Atom Scattering Facility (https://atomscattering.phy.cam.ac.uk) and EPSRC award EP/T00634X/1.References
- W. D. Mross, Alkali doping in heterogeneous catalysis, Catal. Rev.: Sci. Eng., 1983, 25(4), 591–637 CrossRef CAS.
- I. Waluyo, K. Mudiyanselage, F. Xu, W. An, P. Liu, J. A. Boscoboinik, J. A. Rodriguez and D. J. Stacchiola, Potassium-promoted reduction of Cu2O/Cu (111) by CO, J. Phys. Chem. C, 2019, 123, 8057–8066 CrossRef CAS.
- R. Qin, L. Zhou, P. Liu, Y. Gong, K. Liu, C. Xu, Y. Zhao, L. Gu, G. Fu and N. Zheng, Alkali ions secure hydrides for catalytic hydrogenation, Nat. Catal., 2020, 3, 703–709 CrossRef CAS.
- R. D. Diehl and R. McGrath, Structural studies of alkali metal adsorption and coadsorption on metal surfaces, Surf. Sci. Rep., 1996, 23, 43–171 CrossRef CAS.
- R. D. Diehl and R. McGrath, Current progress in understanding alkali metal adsorption on metal surfaces, J. Phys.: Condens. Matter, 1997, 9, 951–968 CrossRef CAS.
- P. Fouquet and G. Witte, Observation of metallization transition of 2D alkali metal films, Phys. Rev. Lett., 1999, 83, 360–363 CrossRef CAS.
- D. A. MacLaren, W. Luo, G. P. Brivio, C. Huang, G. Fratesi and W. Allison, Charge redistribution in the formation of one-dimensional lithium wires on Cu(001), Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82(8), 081413 CrossRef.
- A. Spreinat, D. J. Ward, W. Allison, J. Ellis, A. P. Jardine, M. Sacchi, A. Raghavan, L. Slocombe and N. Avidor, Alkali metal adsorption on metal surfaces: new insights from new tools, Phys. Chem. Chem. Phys., 2021, 23, 7822–7829 RSC.
- S. P. Rittmeyer, D. J. Ward, P. Gütlein, J. Ellis, W. Allison and K. Reuter, Energy dissipation during diffusion at metal surfaces: Disentangling the role of phonons versus electron-hole pairs, Phys. Rev. Lett., 2016, 117, 196001 CrossRef PubMed.
- J. P. Toennies, L. Y. Chen, A. P. Graham, F. Hofmann and S. C. Ying, Determination of the Na/Cu(001) potential energy surface from helium scattering studies of the surface dynamics, Phys. Rev. Lett., 1997, 78(20), 3900 CrossRef.
- H. Hedgeland, W. Allison, G. Alexandrowicz, A. P. Jardine and J. Ellis, Onset of 3D collective surface diffusion in the presence of lateral interactions: Na/Cu(001), Phys. Rev. Lett., 2006, 97(15), 156103 CrossRef PubMed.
- A. S. Sanz, R. Martínez-Casado, J. L. Vega and S. Miret-Artés, Line shape broadening in surface diffusion of interacting adsorbates with quasielastic He atom scattering, Phys. Rev. Lett., 2007, 98(21), 216102 CrossRef PubMed.
- M. I. Trioni, G. P. Brivio, G. Fratesi, G. Alexandrowicz and W. Allison, Crucial electronic contributions to measures of surface diffusion by he atom scattering, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 235444 CrossRef.
- H. R. Davies, A. P. Jardine, G. Alexandrowicz, W. Allison, J. Ellis, G. Fratesi, H. Hedgeland, P. R. Kole and G. P. Brivio, Surface dynamics and friction of K/Cu(001) characterized by helium-3 spin-echo and density functional theory, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80(12), 125426 CrossRef.
- A. Toro-Labbé and L. Padilla-Campos, Theoretical study of the diffusion of alkali metals on a Cu(111) surface, J. Mol. Struct.: THEOCHEM, 1997, 390(1–3), 183–192 Search PubMed.
- G. Fratesi, Potential energy surface of alkali atoms adsorbed on Cu(001), Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80(045422), 8 Search PubMed.
- N. H. March, V. Bortolani and M. P. Tosi, Interaction of atoms and molecules with solid surfaces, Springer Science & Business Media, 2013 Search PubMed.
- J. Ellis and A. P. Graham, The use of quasielastic helium atom scattering to study correlated motion in adsorbate overlayers, Surf. Sci., 1997, 377–379, 833–842 CrossRef CAS.
- R. Ferrando, M. Diamant, S. Rahav and G. Alexandrowicz, Interpretation of surface diffusion data with Langevin simulations: a quantitative assessment, J. Phys.: Condens. Matter, 2015, 27, 125008 CrossRef PubMed.
- A. Tamtögl, A. P. Jardine, E. Bahn, J. Ellis, S. Miret-Artés, D. J. Ward, A. Raghavan and W. Allison, Inter-adsorbate forces and coherent scattering in helium spin-echo experiments, Phys. Chem. Chem. Phys., 2021, 23, 7799 RSC.
- A. S. Sanz, R. Martínez-Casado, J. L. Vega and S. Miret-Artés, Surface diffusion and low vibrational motion with interacting adsorbates: A shot noise description, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 051128 CrossRef PubMed.
- E. E. Torres-Miyares, G. Rojas-Lorenzo, J. Rubayo-Soneira and S. Miret-Artés, Surface diffusion by means of stochastic wave functions. the ballistic regime, Mathematics, 2021, 9(4), 362 CrossRef.
- E. E. Torres-Miyares, G. Rojas-Lorenzo, J. Rubayo-Soneira and S. Miret-Artés, Surface diffusion within the Caldeira-Leggett formalism, Phys. Chem. Chem. Phys., 2022, 24(26), 15871–15890 RSC.
- P. Hänggi and P. Jung, Colored noise in dynamical systems, Adv. Chem. Phys., 2007, 89, 239–326 CrossRef.
- R. Feynman and R. B. Leighton, The Brownian movement, Feynman lectures of physics, 1964, vol. 1, p. 41 Search PubMed.
- U. Weiss, Quantum Dissipative Systems, World Scientific Publishing, Singapore, 2nd edn, 1999 Search PubMed.
- A. O. Caldeira and A. J. Leggett, Quantum tunnelling in a dissipative system, Ann. Phys., 1983, 149(2), 374–456 Search PubMed.
- S. Gao, Lindblad approach to quantum dynamics of open systems, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57(8), 4509 CrossRef CAS.
- G. Lindblad, On the generators of quantum dynamical semigroups, Commun. Math. Phys., 1976, 48(2), 119–130 CrossRef.
- S. Gao, Quantum kinetic theory of vibrational heating and bond breaking by hot electrons, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55(3), 1876 CrossRef CAS.
- A. Tameshtit and J. E. Sipe, Positive quantum brownian evolution, Phys. Rev. Lett., 1996, 77(13), 2600 CrossRef CAS PubMed.
- L. Diósi, On high-temperature Markovian equation for quantum Brownian motion, EPL, 1993, 22(1), 1 CrossRef.
- A. Kossakowski, On quantum statistical mechanics of non-Hamiltonian systems, Rep. Math. Phys., 1972, 3, 247 CrossRef.
- R. Durrett, Probability: theory and examples, Cambridge University Press, 2019, vol. 49 Search PubMed.
- L. Van Hove, Correlations in space and time and Born approximation scattering in systems of interacting particles, Phys. Rev., 1954, 95(1), 249 CrossRef CAS.
- J. Halliwell and A. Zoupas, Quantum state diffusion, density matrix diagonalization, and decoherent histories: A model, Phys. Rev. D: Part. Fields, 1995, 52(12), 7294 CrossRef CAS PubMed.
- H. P. Breuer and F. Petruccione, The theory of open quantum systems, Oxford University Press on Demand, 2002 Search PubMed.
- D. J. Ward, Spin-echo lineshapes in helium atom scattering from adsorbates, PhD thesis, Cambridge University, 2013 Search PubMed.
- C. T. Chudley and R. J. Elliott, Neutron scattering from a liquid on a jump diffusion model, Proc. Phys. Soc., 1961, 77(2), 353 CrossRef.
- S. W. Rick, D. L. Lynch and J. D. Doll, The quantum dynamics of hydrogen and deuterium on the Pd(111) surface: A path integral transition state theory study, J. Chem. Phys., 1993, 99, 8183 CrossRef CAS.
- T. Miyake, K. Kusakabe and S. Tsuneyuki, Inverse isotope effects in the surface diffusion of atoms, Surf. Sci., 1996, 363, 403–408 CrossRef CAS.
| This journal is © the Owner Societies 2023 |