Population balance models for polymer upcycling: signatures of the mechanism in the molecular weight evolution
Ryan
Yappert
 a and
Baron
Peters
a and
Baron
Peters
 *ab
*ab
aChemical and Biomolecular Engineering, University of Illinois at Urbana-Champaign, 61801, USA. E-mail: baronp@illinois.edu
bChemistry and Biochemistry, University of Illinois at Urbana-Champaign, 61801, USA
First published on 3rd November 2022
Abstract
Chemical and catalytic upcycling processes could help realize a circular plastics economy, but current models for testing mechanistic hypotheses and designing catalysts remain primitive. This work shows how proposed catalytic mechanisms can be incorporated into population balance models to predict the time evolution of molecular weight distributions. We develop models for homogeneous and heterogeneous catalysts, including catalysts that cut at chain ends and catalysts that cut at random locations. For heterogeneous catalysts, we illustrate the effect of adsorption constants that depend on polymer chain length. We discuss ongoing efforts and challenges in measuring and modeling the time evolving molecular weight distributions in polymer upcycling processes.
1. Introduction
Millions of tons of plastic are produced each year. Most is discarded in landfills, lost to the natural environment, or incinerated.1 Polymer upcycling efforts aim to transform plastics into value-added products.2 In its broadest definition, polymer upcycling includes a variety of strategies: producing novel composites,3 use of functionalization4 and compatibilizers,5 conversion to carbon materials (nanosheets, nanotubes, etc.),6 and selective degradation to fuels, lubricants, etc.7 For this work, we focus primarily on upcycling via selective catalytic degradation.Before polymer upcycling technologies can be implemented, challenges in plastics collection and sorting, process design, and catalyst development must be addressed.6,8–11 Catalyst development for polymer upcycling is complicated by some particularly unique challenges.12–16 First, the starting reactants in polymer upcycling are a jumble of polymers with many different molecular weights. Second, the process involves thousands of intermediates all being consumed and generated en route to products. Third, if things go badly, the process may yield multiphase mixtures containing hundreds or thousands of different products.
Because so many species are involved, we cannot use the familiar “initial rates” or “integrated rate law” analyses for small molecule reactions.17 Moreover, experiments cannot monitor the rates at which each product is formed. They can monitor time-evolving molecular weight distributions (MWDs) by sampling reactions at various time points, e.g. with chromatographic or spectrographic methods.13,18–20
Many experimental studies have reported the number average and/or weight-average molecular weight. Across multiple studies, with entirely different catalysts, polymers, and reaction conditions, the results show a fast initial drop in molecular weight with slower and slower decreases in molecular weight at long times.7,12,17,21 These results could be due to catalyst deactivation or to length-dependent selectivity.21 Zhang et al. provided a quantitative model to help explain these results.12 In brief, cleavage of long polymers at early times results in a massive reduction of molecular weight, but as depolymerization proceeds there are more chains to cut and each cut results in a smaller reduction of molecular weight. In the model of Zhang et al., the rate of cutting was also affected by product inhibition.12
Here we further simplify the model from Zhang et al.12 Let N0 be the initial number of molecules and let r(t) be the rate of cleavage events per unit time. Each cleavage event increases the number of molecules by one, and so the total mass is gradually distributed across an increasing number of molecules. Using only the definitions of the average molecular weight MN, with no further assumptions, it can be shown that the number average molecular weight declines with time (t) as22
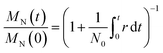 | (1) |
Eqn (1) holds regardless of how, which, or where polymers are cleaved. The result is always an MN(t) vs. t curve with approximately the same shape, whether chains are cut by hydrogenolysis12,21,23,24 or tandem metathesis/chain isomerization,7,18 longest chains first or shortest chains first,25 at the chain ends26,27 or at random locations along the chain,28–30etc. It also applies to linear or branched polymers. In this sense, eqn (1) is a universal feature of depolymerization. Eqn (1) also provides a simple way to extract a cleavage rate (cuts per time) from data, and (given the amount of catalyst) to obtain a quantitative catalyst activity, for example from r(t) divided by the number of catalyst sites. Because of its generality, it enables activity comparisons across different catalysts and different polymer chemistries.
Despite the utility of eqn (1), the fact that all catalysts, mechanisms, and polymers lead to a similar MNvs. t curve limits its value as a tool for identifying the underlying mechanism. Additional information, like weight-average molecular weight vs. time data can be used to construct the polydispersity as a function of time, but this has a similarly mechanism-agnostic shape for similar reasons. Moreover, MW primarily reflects the longest chains and thus provides limited information about small reaction products. Mechanistic studies require more detailed models that can predict both the product distribution and the entire MWD as a function of time.
The widely-used bottom-up strategy for modeling catalytic processes starts from molecular mechanistic hypotheses, ab initio calculations, microkinetic modeling, and ultimately predicts the product formation kinetics, reaction orders, activation parameters, etc.31–33 Bottom-up models have successfully predicted kinetics and MWDs in some polymerizations, and the bottom-up strategy may also be successful for polymer upcycling.34–36 However, polymer upcycling by a heterogeneous catalyst involves polymer adsorption at sites, surfaces, or pores, in conjunction with multistep reactions involving many rate constants. With so many parameters to compute, errors in the quantum chemistry, force fields, or adsorption models may impair the predictions even if the hypothesized upcycling mechanisms are correct.
An alternative approach is to construct phenomenological kinetic models based on specific mechanistic hypotheses and test them against experimental data.37–40 This can be done with deterministic rate equations or kinetic Monte Carlo,41cf. studies of long-chain vs. short-chain selectivity and product distributions from selectivity for different cleavage locations.21,42–45 Note that, even at the lab scale, experiments begin with upwards of billions of chains. Therefore the stochastic simulation results (if converged) should match the predictions of the corresponding deterministic rate laws46 and (when they can be solved) the deterministic models are more easily fitted to quantitatively extract rate parameters from experimental data.47
What types of deterministic kinetic models can predict MWDs for depolymerization? Kinetic lumping models48,49 predict the rates at which groups or “lumps” are consumed and generated, e.g. the reactants and products may be lumped into gases, liquids, and wax fractions. Recent work by Wu et al.25 takes this direction.
Population balance equations (PBEs) go a step further, predicting the entire evolving MWD.39 This work shows how, without specifying the mechanism at the most detailed level of elementary steps, we can already categorize upcycling mechanisms into a few “motifs” and construct the appropriate PBE. For constructing population balance models, most catalytic depolymerization processes will fit into one of sixteen categories.
• A catalyst may be homogeneous or heterogeneous.21,50
• It may operate processively or non-processively.51,52
• It may cleave chains near their ends or at random locations along the chain.13,21
• The polymers themselves may be dissolved in a solvent or a liquid melt with no solvent.44,45
Each category gives a different population balance model, different solutions for the molecular weight evolution in time, and a different interpretation for the kinetic parameters. Each upcycling strategy implies a specific type of PBE with solutions that predict characteristic “signatures” of the mechanistic motif. Our goal is to discover easily identified signatures that can help to identify the underlying mechanism.
In constructing the population balance model, note that polymer fillers and even chemically inert particles in a composite may add new scission pathways. For example, they may change the importance of mass transfer and/or increase levels of shear induced mechanical chain scission. In some cases, the observed behavior is a combination of multiple mechanisms. Some processes employ “tandem” catalysts to combine advantages of the individual catalyst mechanism categories.7,18,45,53 We restrict ourselves here to ideal cases with single mechanisms.
In the following sections, we illustrate the predicted molecular weight evolution for the proposed mechanisms in several upcycling strategies. Each calculation starts from a lognormal MWD with MN(0) = 3.0 kDa and MW(0) = 3.3 kDa. First, in Section 2, we define a dimensionless time scale that helps to place the molecular weight evolution on a commensurate time scale regardless of the mechanism, the rate parameters, and their absolute sizes.
2. Activity comparisons
The mechanisms we discuss in this work span a range of conditions, catalyst concentrations, and reaction orders. Accordingly, the absolute time t is often inconvenient for comparing them. As previously noted by Helfferich, there is no universal way to nondimensionalize the rate equations that emerge from different mechanisms.54 To allow comparison between mechanisms after a similar number of cleavage events, we invoke a dimensionless “cut time” τ. τ is the equivalent of the integral in eqn (1), and may be alternatively written based on the number of newly created molecules in the population: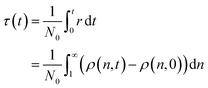 | (2) |
3. Homogeneous mechanisms
We begin our discussion of mechanistic motifs for homogeneous reactions (catalytic or not) of the form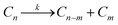 | (3) |
3.1. Random cleavage
Random cleavage usually refers to any process in which all bonds are equally likely to be cut, although nonuniform cases have also been studied.60 An schematic of random cleavage for a single starting chain is shown in Fig. 1. Examples of polymer upcycling strategies based on this method include an aminolysis process for polyesters61 and homogeneous cross alkane metathesis schemes based on work of Goldman and Brookhart.62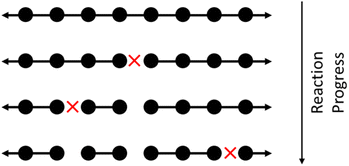 | ||
| Fig. 1 Illustrating homogeneous random cleavage. Circles represent monomers in a large polymer. Long chains are repeatedly broken into smaller chains, with each cleavage site marked with a red X. | ||
A kinetic model may be constructed by considering polymer length as a discrete or continuous quantity. Discrete models are (in principle) more accurate because the number of monomers is countable. However, continuous models tend to be more mathematically convenient for large chains, so we focus on models with a continuous chain length here.63 We borrow the continuous formulation of Staggs to account for cleavage steps:64
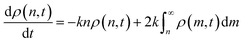 | (4) |
Eqn (4) describes the change in ρ(n,t), i.e. the population of chains of length n at time t, as n-mers are cut to form smaller species and as larger chains are cut to form n-mers. As an n-mer possesses approximately n bonds that can break independently, the first term is weighted by that length. The integrand is likewise weighted by m, but the probability of cutting an m-mer to an n-mer is 2m−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) dm. The overall timescale of the process is determined by k, which in this case is an effective first order rate constant with units of cuts per time per bond.
dm. The overall timescale of the process is determined by k, which in this case is an effective first order rate constant with units of cuts per time per bond.
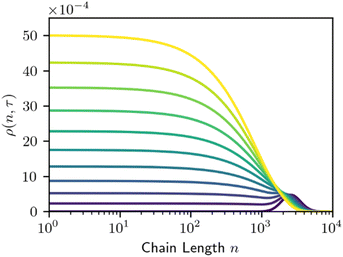
The simplicity of this model makes it amenable to analytic and numerical solutions, and we direct the reader to the existing literature for a more detailed discussion of those solutions.29,30,65,66 The time evolution for homogeneous random cleavage is shown below in Fig. 2.
Homogeneous random cleavage manifests as a rising plateau, particularly among small species that are not present in the initial distribution. As depolymerization proceeds, the plateau grows narrower due to the preferential cutting of the longest chains, and taller, as further cuts increase the number of small fragments.
Homogeneous random cleavage quickly generates all possible chain lengths, from monomer to the largest initial chain. This rapid accumulation of small chain lengths can cause a rapid initial increase in the dispersity of the population, as shown in Fig. 3.
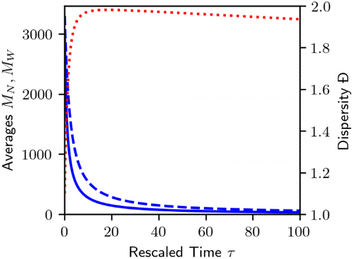 | ||
| Fig. 3 Plot of number average chain length (MN, solid blue), weight average chain length (MW, dashed blue), and dispersity (Đ = MW/MN, dotted red) for homogeneous random cleavage as shown in Fig. 2. | ||
As random cleavage quickly generates lengths that were not part of the initial MWD, dispersity will rapidly increase. At later stages, long chains will be depleted, and the dispersity will eventually decrease again. In principle, at infinite time, all bonds will be cleaved, and all polymers will be transformed to monomer, with MN = MW = Đ = 1. An analysis of the moments of the MWD for homogeneous random cleavage processes has been given by McCoy and Madras.60
3.2. Non-processive chain-end scission
These mechanisms remove a fixed-size oligomer or monomer from an end of a polymer chain. Such behavior is common in biological systems, e.g. β-amylase depolymerizes large, polymeric starches (blood sugar) into glucose by hydrolyzing glucosidic linkages.67 An example upcycling process based on this mechanism is the tandem chain migration + olefin metathesis scheme proposed by Guironnet and Peters.18 An illustration of this mechanistic motif is shown in Fig. 4.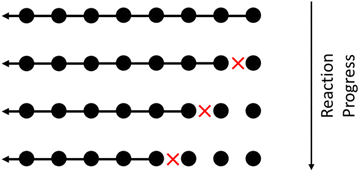 | ||
| Fig. 4 Illustration of a chain-end cleavage process. Circles represent monomers in a large polymer. With each cleavage reaction, marked by a red X, a monomer is removed from the end of the chain. | ||
The discrete nature of the cuts make fully continuous formulations difficult, and in most cases the smallest species must be explicitly modeled.63,68 Zeman and Amundson developed tools to model chain length as a continuous variable, with a simple pseudo-elementary rate constant k, and with the monomer concentration separately determined by conservation of mass.18,69 The balance equation at the continuum population level for chain-end cleavage in homogeneous solution is:26
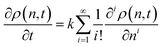 | (5) |
The required number of terms for the continuous treatment to be valid depends on the smoothness and broadness of the polymer distribution. Typically, the second derivative term (i = 2) is sufficient.26 Because cuts are always made at the end of a chain, the rate constant k is first order in chains rather than bonds. Guironnet and Peters have shown how the appropriate pseudo-elementary rate constant k can be derived from more detailed kinetic schemes.18 The monomers and long chain populations must both be considered when computing the number and weight averages. The time evolution for a chain-end scission process is shown in Fig. 5.
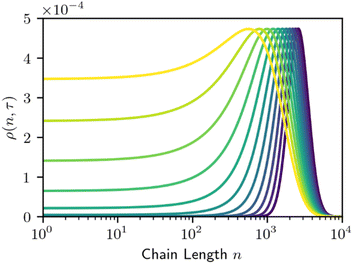 | ||
| Fig. 5 Time evolution the MWD by homogeneous chain-end cleavage. Monomer concentration is not shown to prevent distortion of the vertical axis. Lines are evenly spaced in τ, with Δτ = 200. | ||
Chain-end scission results in a gradual broadening and translation of the MWD towards lower chain lengths. The rate of this broadening and translation depends on the initial width of the MWD and the size of the fragment removed. Systems that cleave variable length oligomers will give faster broadening than systems that cleave the same fragment each time.18 When viewed on a log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n scale, this broadening does result in a rising plateau like that of homogeneous random scission (Fig. 2). However, the initial MWD gradually shifts leftward from chain-end scission, while the initial MWD is decimated after orders of magnitude fewer random cleavage steps. In this sense, random cleavage is more efficient at rapidly altering the MWD than chain-end cleavage.
n scale, this broadening does result in a rising plateau like that of homogeneous random scission (Fig. 2). However, the initial MWD gradually shifts leftward from chain-end scission, while the initial MWD is decimated after orders of magnitude fewer random cleavage steps. In this sense, random cleavage is more efficient at rapidly altering the MWD than chain-end cleavage.
Unlike random cleavage, there is typically a clear demarcation between volatile and nonvolatile products in chain-end cleavage, particularly when the initial distribution is primarily long polymer chains.70 An easy separation between products and long polymers may have practical reaction engineering advantages at the process design stage. However, it can create difficulties for data analysis in bench-scale experiments. Discarding the small molecule products when characterizing the MWD will affect the results.70 Procedures that include vs. exclude the very small fragments produced by chain-end scission can give very different trends in MN, MW, and Đ, as shown in Fig. 6.
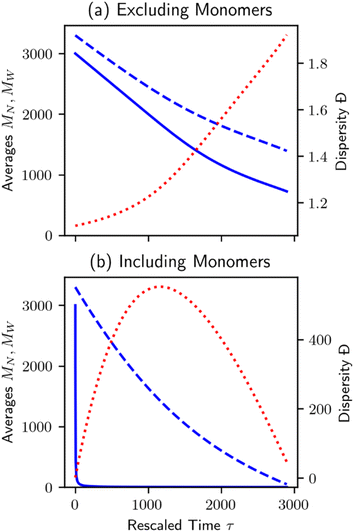 | ||
| Fig. 6 Plot of number average chain length (MN, solid blue), weight average chain length (MW, dashed blue), and dispersity (Đ = MW/MN, dotted red) for the population evolution in Fig. 2. Note the large difference in dispersity scale between plots. (a) Small molecule products are not counted, and (b) small molecule products are counted when calculating averages and dispersity. | ||
With the simplest cases of random and chain-end scission discussed, it is important to note that many processes are in fact combinations of the two.30,38,56,68,71–73 For example, in the polysaccharide/amylase system, there are three classes of enzymes that work together to depolymerize starches: α-amylase catalyzes random cleavage, while β- and γ-amylase catalyze chain-end cleavage.74–76 The relative concentration and activity of these amylases can dramatically alter the evolution of the MWD.77,78 A single catalyst that targets bonds at random may also have a significant chain-end scission preference due to different chemistries at chain ends.40
4. Heterogeneous mechanisms
We now focus on models for polymer upcycling by heterogeneous catalysts. Heterogeneous catalytic mechanisms introduce additional theoretical difficulties. In particular, one must consider the bulk MWD and the distribution of molecular weights for adsorbed polymers.47 Long chains and short chains compete for adsorption sites on the surface, with preferential adsorption determined by the loss of entropy upon adsorption and enthalpic interactions that (in some cases) favor adsorption.79,80 We address two regimes in this work: a polymer melt in which a polymer in the bulk is surrounded by like polymers, and a dilute solution in which the polymer in the bulk primarily interacts with a solvent. In both cases, we utilize quasi-equilibrium adsorption models. The models will be inaccurate if the reaction is too fast for polymer conformations in the interfacial layer to relax to a local conformational equilibrium, or if boundary layer transport (where applicable) is too slow to maintain an equilibrium with the bulk.4.1. Random cleavage at melt-catalyst interface
In this section we consider a polymer melt in contact with a heterogeneous catalyst that cleaves chains at random locations. A schematic for this case is shown in Fig. 7. Examples of catalysts that likely work via this mechanism include hydrogenolysis by Ru/C43 and Ru/TiO2,42 tandem hydrogenolysis and aromatization on Pt/γ-Al2O3,12 and melt hydroconversion by Pt/WO3/ZrO2.81In a melt, the entire catalyst surface is in contact with polymers, but the contacts may be segments from chains with different lengths. Therefore, we define a surface coverage such that the fraction of all catalytic sites occupied by segments of an n-mer is given by θ(n). Because the surface must be covered entirely, ∫θ(n)dn = 1. The MWD of the adsorbed chains may deviate from the MWD of chains in the bulk. We may account for this nonideality by writing
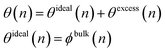 | (6) |
| θexcess(n)/ϕbulk(n) = A(1 − n/MW) | (7) |
If we assume quasi-equilibrated coverages, then the fraction of the surface covered by n-mers is
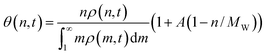 | (8) |
In formulating eqn (8) we have ignored excess mixing volumes by assuming that, for each n, nρ(n,t) is proportional to the bulk volume fraction ϕbulk(n). Now the bulk MWD changes in response to the equilibrium adsorption and kinetics of scission as
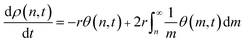 | (9) |
Eqn (9) parallels the result for homogeneous random scission, eqn (4), except the surface coverage θ allows the dependence on chain length to be more complex. In homogeneous random scission, the polymer reactivity is proportional to the number of bonds in the chain (eqn (4)). Non-zero values of parameter A lead to length-dependent adsorption and to a length-dependent cleavage selectivity that deviates from the bulk volume fractions. For example, when A < 0, long chains are favored to adsorb and cleave. When A > 0, short chains are favored. The preferential adsorption relative to the bulk populations is shown in Fig. 8 for a series of different A values.
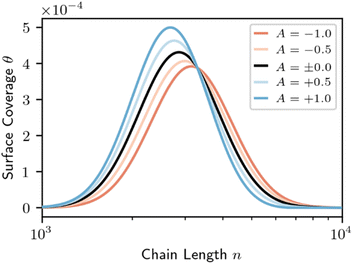 | ||
| Fig. 8 Surface coverage (eqn (8)) for varying surface segregation parameter A, for the initial distribution shown in Fig. 2. Red denotes a long-chain favored surface; blue denotes a short-chain favored surface. The bulk mass fraction for all cases is equal to the surface coverage for the non-interacting surface (black). | ||
If products of an intermediate molecular weight are desired, e.g. in hydrogenolysis of polyethylene, the catalyst should be designed such that A < 0 if possible. If A > 0 instead, then long chains will be excluded from the surface, causing the short chains to be repeatedly cut and resulting in a mixture with large fractions of over-hydrogenolysis products (like methane) and uncut chains. Fig. 9 shows that, according to eqn (8) and (9), the MWD evolves in a manner like that for homogeneous random scission. Fig. 9 shows the dependence on parameter A by plotting solutions for A = −1.0 and A = +1.0.
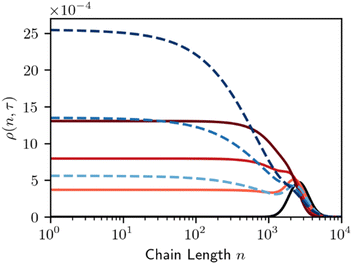 | ||
| Fig. 9 Time evolution of the MWD for random-cleavage at a melt-catalyst interface. Black line denotes initial polymer population. Red denotes a long chain favoring surface (A = −1), dashed blue denotes a short chain favoring surface (A = +1), per Fig. 8. Lines are evenly spaced in τ, with Δτ = 0.5. | ||
As in Section 3, we may also consider the dispersity of the resulting polymer. This is demonstrated in Fig. 10. Surfaces that favor the adsorption of longer species (A < 0) result in a less disperse polymer product relative to the homogeneous case shown in Fig. 3. Short chain favoring surfaces (A > 0) do exactly the opposite, with an increase in dispersity.
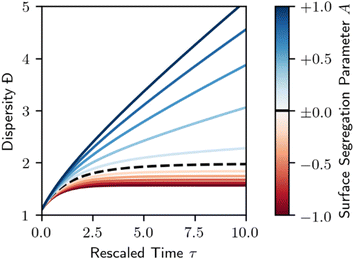 | ||
| Fig. 10 Dispersity for melt-surface random scission. Dashed black line denotes the homogeneous case (A = 0, Fig. 3). Red denotes a long chain favoring surface (A < 0), blue denotes a short chain favoring surface (A > 0), per Fig. 8. Lines are evenly spaced in A, with ΔA = 0.2. | ||
In the melt, where enthalpic driving forces largely cancel with those of other chemically similar chains, the value of A will be largely determined by entropic factors. Long chains lose more conformational entropy upon adsorption to a flat surface than short chains, so catalysts that present a flat interface to the melt may lead to the situation with A > 0.42–45,83 It may be possible to tune the value of A (and the product distribution) by altering the chemistry of the chain ends to disfavor the surface or to design special pore geometries that favor adsorption of long chains as done by Tennakoon et al. and Wu et al.13,25
Note that the surface segregation model of van der Gucht et al. breaks down for very large polymers in highly polydisperse melts. For positive A, i.e. a surface that preferentially adsorbs smaller polymers, there may even be chains for which 1 + A(1 − n/MW) is negative. According to this linear relationship, these extremely long chains are entirely unreactive, kept away from the surface by the abundance of shorter chains. These chains will not become reactive with the passage of time, as depolymerization can only decrease the average chain length. The possibility of a nonreactive set of very large chains must be considered when using these equations with very large maximum chain lengths nmax, or very small average chain lengths MW. When generating Fig. 9 and 10, we replaced any negative values of θ(n,t) < 0 with θ(n,t) = 0. Further development of preferential adsorption models would be a useful direction. Note that the ideal and excess coverages in eqn (6) are additive, in contrast to activity models where non-ideality is included via a multiplicative activity coefficient. It would be useful in future work to develop models which automatically satisfy the proper asymptotes in the long chain and dilute limits, like regular solution models84 and Margules models.85
4.2. Solute-surface random scission
Now we consider heterogeneous catalytic cleavage of polymers that are dissolved in solution. In this case, the surface is no longer guaranteed contact with polymers, and this necessitates a more complicated handling of the surface-polymer interactions and adsorption.86–89 We assume that polymer chains adsorb to a reactive surface from solution and proceed to either desorb back to the bulk or react, as shown in Fig. 11. As an examples of this type of system, Ellis et al. considered a SnPt/γ-Al2O3 and Re2O7/γ-Al2O3 system with n-pentane solvent.45Again, we assume well-mixed conditions where coverages are quasi-equilibrated with the bulk polymer concentrations. Note that this assumption may be lifted using standard techniques for treating exterior transport limitations. Namely, one would replace the bulk populations in the models below with unknown populations near the catalyst surface and equate the resulting rates to the rate of chain transport from the bulk through a boundary layer to the surface. External mass transport models are currently under development.
To build the PBE, we again consider the fractional surface coverage θ(n) representing the fraction of sites in contact with segments from an n-mer. The bulk MWD evolves as in the melt-surface case, by the same PBE as that in eqn (9). The difference lies in the isotherms for the bulk-surface coverage relationship. To determine θ(n) in this case, we invoke a common multi-site generalization of the Langmuir isotherm:90
| snKnρ(n,t) = θ(n,t)/θ0(t)sn | (10) |
Kn = ke![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−ΔHadssn + TΔSads] exp[−ΔHadssn + TΔSads] | (11) |
Multiplying both sides of eqn (11) by θ0(t)sn, and integrating both sides from n = 1 to ∞ yields a single equation for the fraction of empty sites:
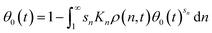 | (12) |
At the initial time step, the fraction of empty sites may be solved to a tight error tolerance for the initial coverages of adsorbed polymers, and then included in the system of differential equations to compute changes in coverage over the integration period. Differentiation of eqn (12) and rearrangement yields
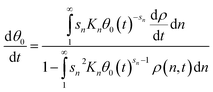 | (13) |
Unlike previous models discussed in this work, eqn (10)–(13) depend on the total concentration N0. As the total concentration of chains rises, the surface becomes more occupied. While this effect does impact the evolving MWD, the contribution is minor relative to that of the adsorption energetics. We focus here on the convenient case where keN0 = 1.
When integrating forward in time, only one nonlinear solution needs to be computed at the first step. From the computed fraction of empty sites, the individual species coverages may be estimated and interpolated by eqn (10). The change in the population for the current timestep follows from eqn (9), and (13) then also predicts the revised fraction of empty sites.
Solute-surface adsorption behavior can cause drastic departures from the prior cases. The form of eqn (10) reveals that the primary factor controlling a species surface coverage is the number of sites it demands. Polymer adsorption theories suggest that the preferred number of contacts between a polymer and a surface scales roughly as n1/2.91–94 Based on this, and the fact that an adsorbed monomer should have one contact with the surface, (s1 = 1) we perform calculations for such that a monomer occupies one site. Then, the adsorption energetics may be varied. We initially consider the surface coverage in quasi-equilibrium with the initial polymer population, relative to the bulk population, by analogy to Fig. 8, in Fig. 12.
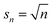 | (14) |
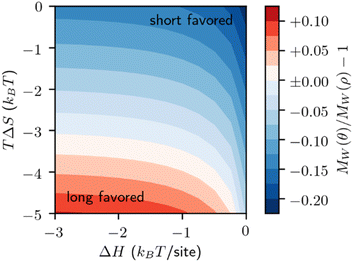
Fig. 12 reveals that this model, like the melt-surface case, may prefer either long or short chains depending on the energetics of adsorption. This preference is primarily driven by the constant entropic penalty for adsorption. When this penalty is strong, large chains are preferred, as they adsorb to multiple sites and thus have a greater enthalpy of adsorption. When this penalty is weak, small chains are preferred, as they demand fewer sites each to adsorb and do not require a large enthalpy to offset the entropic penalty.
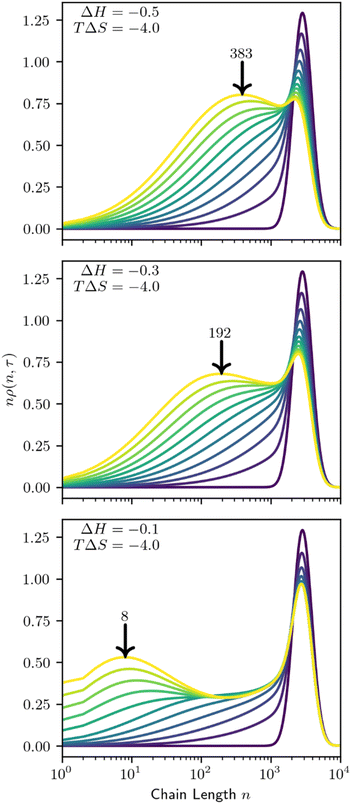
Preferential adsorption strongly impacts the evolving MWD as cleavage proceeds. Minor differences in the behavior of the initial distribution may be magnified as polymers are cleaved and the MWD evolves. We demonstrate this in Fig. 13, as small adjustments to the adsorption enthalpy drive significant changes in the product distribution. According to the model, solute-surface random scission creates significant amounts of small products (n = 1–100). Therefore, we show the mass-weighted MWD, nρ(n,t), to highlight the differences between distributions.
As the system evolves, it develops a new peak in the mass-weighted MWD that represents the primary product size by mass. The size of the primary product is associated with both the site-dependent ΔH and site-independent TΔS parameters. At fixed conversion, smaller values of ΔH and/or TΔS cause the primary product size to decrease, approximately correlated with the initial preference shown in Fig. 12. Increased conversion will also decrease the primary product size.
When adsorption strongly favors small species a bimodal distribution may arise, with the primary product coexisting with the initial distribution, even at high conversion (Fig. 13, bottom). After the first few catalytic turnovers, the products of cleaving the initial, large polymers preferentially adsorb. The products of their cleavage in turn are preferentially adsorbed, and so on, creating an abundance of small molecular weight products.
5. Conclusions
Population balance models have long been a powerful tool to predict product distributions for both polymerization and depolymerization processes, but most research has focused on the simplest of problems for which analytical solutions exist. Here we have demonstrated the beginnings of a framework to translate specific mechanistic proposals into population balance models. The population balance models then yield specific predictions about the molecular weight evolution. We have developed models for a variety of processes and mechanisms. Each mechanism and its corresponding population balance model predicts “fingerprints” in the molecular weight evolution by which an observed behavior may be matched to an appropriate underlying mechanism. Efforts are underway to fit these models to experimental data as a quantitative way of mechanism identification.Conflicts of interest
There are no conflicts to declare for this work.Acknowledgements
This work was supported by the Institute for Cooperative Upcycling of Plastics (iCOUP), an Energy Frontier Research Center funded by the U.S. Department of Energy (DOE), Office of Basic Energy Sciences, Division of Chemical Sciences, Geosciences, and Biosciences, via subcontract from Award DE-AC-02-07CH11358 at Ames Laboratory. We thank all members of the iCOUP team for helpful discussions.References
- R. Geyer, J. R. Jambeck and K. L. Law, Production, use, and fate of all plastics ever made, Sci. Adv., 2017, 3, e1700782 CrossRef PubMed.
- L. J. Broadbelt, Catalytic resource recovery from waste polymers, in Catalysis, The Royal Society of Chemistry, 1999, vol. 14, pp. 110–147 Search PubMed.
- N. A. Rorrer, S. Nicholson, A. Carpenter, M. J. Biddy, N. J. Grundl and G. T. Beckham, Combining Reclaimed PET with Bio-based Monomers Enables Plastics Upcycling, Joule, 2019, 3, 1006–1027 CrossRef CAS.
- C. Jehanno, J. Demarteau, D. Mantione, M. C. Arno, F. Ruiperez, J. L. Hedrick, A. P. Dove and H. Sardon, Synthesis of Functionalized Cyclic Carbonates through Commodity Polymer Upcycling, ACS Macro Lett., 2020, 9, 443–447 CrossRef CAS PubMed.
- X. Tang, C. Liu, J. Keum, J. Chen, B. E. Dial, Y. Wang, W. Y. Tsai, W. Bras, T. Saito and C. C. Bowland, et al., Upcycling of semicrystalline polymers by compatibilization: mechanism and location of compatibilizers, RSC Adv., 2022, 12, 10886–10894 RSC.
- C. Zhuo and Y. A. Levendis, Upcycling waste plastics into carbon nanomaterials: A review, J. Appl. Polym. Sci., 2014, 131, 39931 CrossRef.
- X. Jia, C. Qin, T. Friedberger, Z. Guan and Z. Huang, Efficient and selective degradation of polyethylenes into liquid fuels and waxes under mild conditions, Sci. Adv., 2016, 2, e1501591 CrossRef PubMed.
- E. B. Mejia, S. Al-Maqdi, M. Alkaabi, A. Alhammadi, M. Alkaabi, N. Cherupurakal and A. I. Mourad, Upcycling of HDPE Waste using Additive Manufacturing: Feasibility and Challenges, in 2020 Advances in Science and Engineering Technology International Conferences (ASET), 4 Feb–9 April 2020, 2020, pp. 1–6, DOI:10.1109/ASET48392.2020.9118269.
- X. Liu, M. Hong, L. Falivene, L. Cavallo and E. Y. X. Chen, Closed-Loop Polymer Upcycling by Installing Property-Enhancing Comonomer Sequences and Recyclability, Macromolecules, 2019, 52, 4570–4578 CrossRef CAS.
- F. P. La Mantia, Polymer Mechanical Recycling: Downcycling or Upcycling?, Prog. Rubber, Plast. Recycl. Technol., 2004, 20, 11–24 CrossRef CAS.
- A. Rahimi and J. M. García, Chemical recycling of waste plastics for new materials production, Nat. Rev. Chem., 2017, 1, 0046 CrossRef.
- F. Zhang, M. Zeng, R. D. Yappert, J. Sun, Y. H. Lee, A. M. LaPointe, B. Peters, M. M. Abu-Omar and S. L. Scott, Polyethylene upcycling to long-chain alkylaromatics by tandem hydrogenolysis/aromatization, Science, 2020, 370, 437–441 CrossRef CAS PubMed.
- A. Tennakoon, X. Wu, A. L. Paterson, S. Patnaik, Y. Pei, A. M. LaPointe, S. C. Ammal, R. A. Hackler, A. Heyden and I. I. Slowing, et al., Catalytic upcycling of high-density polyethylene via a processive mechanism, Nat. Catal., 2020, 3, 893–901 CrossRef CAS.
- J. M. García, Catalyst: design challenges for the future of plastics recycling, Chem, 2016, 1, 813–815 Search PubMed.
- M. Chu, W. Tu, S. Yang, C. Zhang, Q. Li, Q. Zhang and J. Chen, Sustainable chemical upcycling of waste polyolefins by heterogeneous catalysis, SusMat, 2022, 2, 161–185 CrossRef.
- M. Chu, Y. Liu, X. Lou, Q. Zhang and J. Chen, Rational Design of Chemical Catalysis for Plastic Recycling, ACS Catal., 2022, 12, 4659–4679 CrossRef CAS.
- P. A. Kots, B. C. Vance and D. G. Vlachos, Polyolefin plastic waste hydroconversion to fuels, lubricants, and waxes: a comparative study, React. Chem. Eng., 2022, 7, 41–54 RSC.
- D. Guironnet and B. Peters, Tandem Catalysts for Polyethylene Upcycling: A Simple Kinetic Model, J. Phys. Chem. A, 2020, 124, 3935–3942 CrossRef CAS PubMed.
- T. Gruendling, M. Guilhaus and C. Barner-Kowollik, Quantitative LC-MS of polymers: determining accurate molecular weight distributions by combined size exclusion chromatography and electrospray mass spectrometry with maximum entropy data processing, Anal. Chem., 2008, 80, 6915–6927 CrossRef CAS PubMed.
- M. Dey, J. A. Castoro and C. L. Wilkins, Determination of molecular weight distributions of polymers by MALDI-FTMS, Anal. Chem., 2002, 67, 1575–1579 CrossRef.
- G. Celik, R. M. Kennedy, R. A. Hackler, M. Ferrandon, A. Tennakoon, S. Patnaik, A. M. LaPointe, S. C. Ammal, A. Heyden and F. A. Perras, et al., Upcycling Single-Use Polyethylene into High-Quality Liquid Products, ACS Cent. Sci., 2019, 5, 1795–1803 CrossRef CAS PubMed.
- S. L. Malhotra, Ultrasonic Solution Degradations of Poly(Alkyl Methacrylates), J. Macromol. Sci., Part A: Pure Appl.Chem., 1986, 23, 729–748 CrossRef.
- L. Yao, J. King, D. Wu, S. S. C. Chuang and Z. Peng, Non-thermal plasma-assisted hydrogenolysis of polyethylene to light hydrocarbons, Catal. Commun., 2021, 150 Search PubMed.
- S. P. Ertem, C. E. Onuoha, H. Wang, M. A. Hillmyer, T. M. Reineke, T. P. Lodge and F. S. Bates, Hydrogenolysis of Linear Low-Density Polyethylene during Heterogeneous Catalytic Hydrogen–Deuterium Exchange, Macromolecules, 2020, 53, 6043–6055 CrossRef CAS.
- X. Wu, A. Tennakoon, R. Yappert, M. Esveld, M. S. Ferrandon, R. A. Hackler, A. M. LaPointe, A. Heyden, M. Delferro and B. Peters, et al., Size-Controlled Nanoparticles Embedded in a Mesoporous Architecture Leading to Efficient and Selective Hydrogenolysis of Polyolefins, J. Am. Chem. Soc., 2022, 144, 5323–5334 CrossRef CAS PubMed.
- M. Kostoglou, Mathematical analysis of polymer degradation with chain-end scission, Chem. Eng. Sci., 2000, 55, 2507–2513 CrossRef CAS.
- Y. K. Ho, P. Doshi, H. K. Yeoh and G. C. Ngoh, Modeling chain-end scission using the Fixed Pivot technique, Chem. Eng. Sci., 2014, 116, 601–610 CrossRef CAS.
- V. J. Triacca, P. E. Gloor, S. Zhu, A. N. Hrymak and A. E. Hamielec, Free radical degradation of polypropylene: random chain scission, Polym. Eng. Sci., 1993, 33, 445–454 CrossRef CAS.
- J. E. J. Staggs, Modelling random scission of linear polymers, Polym. Degrad. Stab., 2002, 76, 37–44 CrossRef CAS.
- B. J. McCoy, Polymer thermogravimetric analysis: effects of chain-end and reversible random scission, Chem. Eng. Sci., 2001, 56, 1525–1529 CrossRef CAS.
- M. Neurock and R. A. van Santen, Molecular Heterogeneous Catalysis: A Conceptual and Computational Approach, Wiley-VCH, 2006, p. 488 Search PubMed.
- R. D. Cortright, S. A. Goddard, J. E. Rekoske and J. A. Dumesic, Kinetic study of ethylene hydrogenation, J. Catal., 1991, 127, 342–353 CrossRef CAS.
- J. K. Nørskov, F. Studt, F. Abild-Pedersen and T. Bligaard, Fundamental Concepts in Heterogeneous Catalysis, Wiley, 2014 Search PubMed.
- D. Moscatelli, C. Cavallotti and M. Morbidelli, Prediction of molecular weight distributions based on ab initio calculations: application to the high temperature styrene polymerization, Macromolecules, 2006, 39, 9641–9653 CrossRef CAS.
- K. Min, H. Gao and K. Matyjaszewski, Development of an ab initio emulsion atom transfer radical polymerization: from microemulsion to emulsion, J. Am. Chem. Soc., 2006, 128, 10521–10526 CrossRef CAS PubMed.
- C. Y. Lin, M. L. Coote, A. Gennaro and K. Matyjaszewski, Ab initio evaluation of the thermodynamic and electrochemical properties of alkyl halides and radicals and their mechanistic implications for atom transfer radical polymerization, J. Am. Chem. Soc., 2008, 130, 12762–12774 CrossRef CAS PubMed.
- I. Kryven and P. D. Iedema, A Novel Approach to Population Balance Modeling of Reactive Polymer Modification Leading to Branching, Macromol. Theory Simul., 2013, 22, 89–106 CrossRef CAS.
- S. Lin, W. Yu, X. Wang and C. Zhou, Study on the Thermal Degradation Kinetics of Biodegradable Poly(propylene carbonate) during Melt Processing by Population Balance Model and Rheology, Ind. Eng. Chem. Res., 2014, 53, 18411–18419 CrossRef CAS.
- D. Ramkrishna and M. R. Singh, Population balance modeling: current status and future prospects, Annu. Rev. Chem. Biomol. Eng., 2014, 5, 123–146 CrossRef CAS PubMed.
- J. E. J. Staggs, Population balance models for the thermal degradation of PMMA, Polymer, 2007, 48, 3868–3876 CrossRef CAS.
- A. B. Bortz, M. H. Kalos and J. L. Lebowitz, A new algorithm for Monte Carlo simulation of Ising spin systems, J. Comput. Phys., 1975, 17, 10–18 CrossRef.
- P. A. Kots, S. Liu, B. C. Vance, C. Wang, J. D. Sheehan and D. G. Vlachos, Polypropylene Plastic Waste Conversion to Lubricants over Ru/TiO2 Catalysts, ACS Catal., 2021, 11, 8104–8115 CrossRef CAS.
- J. E. Rorrer, C. Troyano-Valls, G. T. Beckham and Y. Román-Leshkov, Hydrogenolysis of Polypropylene and Mixed Polyolefin Plastic Waste over Ru/C to Produce Liquid Alkanes, ACS Sustainable Chem. Eng., 2021, 9, 11661–11666 CrossRef CAS.
- J. E. Rorrer, G. T. Beckham and Y. Roman-Leshkov, Conversion of Polyolefin Waste to Liquid Alkanes with Ru-Based Catalysts under Mild Conditions, JACS Au, 2021, 1, 8–12 CrossRef CAS PubMed.
- L. D. Ellis, S. V. Orski, G. A. Kenlaw, A. G. Norman, K. L. Beers, Y. Román-Leshkov and G. T. Beckham, Tandem Heterogeneous Catalysis for Polyethylene Depolymerization via an Olefin-Intermediate Process, ACS Sustainable Chem. Eng., 2021, 9, 623–628 CrossRef CAS.
- B. Peters, Reaction Rate Theory and Rare Events, Elsevier, 2017 Search PubMed.
- R. Yappert and B. Peters, A population balance model for processive depolymerization catalysts: chemistry’s version of the “while” loop, ACS Catal., 2022, 12(16), 10353–10360 CrossRef CAS.
- H. Huang, M. Fairweather, J. F. Griffiths, A. S. Tomlin and R. B. Brad, A systematic lumping approach for the reduction of comprehensive kinetic models, Proc. Combust. Inst., 2005, 30, 1309–1316 CrossRef.
- E. Ranzi, M. Dente, A. Goldaniga, G. Bozzano and T. Faravelli, Lumping procedures in detailed kinetic modeling of gasification, pyrolysis, partial oxidation and combustion of hydrocarbon mixtures, Prog. Energy Combust. Sci., 2001, 27, 99–139 CrossRef CAS.
- L. Monsigny, J.-C. Berthet and T. Cantat, Depolymerization of Waste Plastics to Monomers and Chemicals Using a Hydrosilylation Strategy Facilitated by Brookhart's Iridium(III) Catalyst, ACS Sustainable Chem. Eng., 2018, 6, 10481–10488 CrossRef CAS.
- A. B. Deutman, S. Cantekin, J. A. Elemans, A. E. Rowan and R. J. Nolte, Designing processive catalytic systems. Threading polymers through a flexible macrocycle ring, J. Am. Chem. Soc., 2014, 136, 9165–9172 CrossRef CAS PubMed.
- S. J. Horn, P. Sikorski, J. B. Cederkvist, G. Vaaje-Kolstad, M. Sorlie, B. Synstad, G. Vriend, K. M. Varum and V. G. Eijsink, Costs and benefits of processivity in enzymatic degradation of recalcitrant polysaccharides, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 18089–18094 CrossRef CAS PubMed.
- P. Kaur, G. Singh and S. K. Arya, Tandem catalytic approaches for lignin depolymerization: a review, Biomass Convers. Biorefin., 2022 DOI:10.1007/s13399-022-02980-6.
- F. G. Helfferich, Kinetics of Multistep Reactions, Elsevier Science, 2004 Search PubMed.
- Y. Kodera and B. J. McCoy, Distribution kinetics of radical mechanisms: Reversible polymer decomposition, AIChE J., 1997, 43, 3205–3214 CrossRef CAS.
- T. Ueno, E. Nakashima and K. Takeda, Quantitative analysis of random scission and chain-end scission in the thermal degradation of polyethylene, Polym. Degrad. Stab., 2010, 95, 1862–1869 CrossRef CAS.
- B. W. Yates and D. M. Shinozaki, Radiation degradation of poly(methyl methacrylate) in the soft x-ray region, J. Polym. Sci., Part B: Polym. Phys., 1993, 31, 1779–1784 CrossRef CAS.
- Z. Kabátek, B. Gaš and J. Vohlídal, Gel permeation chromatography of polymers degrading randomly in the column Theoretical treatment and practical aspects, J. Chromatogr. A, 1997, 786, 209–218 CrossRef.
- J. Vohlídal, Polymer degradation: a short review, Chem. Teacher Int., 2021, 3, 213–220 CrossRef.
- B. J. McCoy and G. Madras, Degradation kinetics of polymers in solution: Dynamics of molecular weight distributions, AIChE J., 1997, 43, 802–810 CrossRef CAS.
- J. Demarteau, K. E. O'Harra, J. E. Bara and H. Sardon, Valorization of Plastic Wastes for the Synthesis of Imidazolium-Based Self-Supported Elastomeric Ionenes, ChemSusChem, 2020, 13, 3122–3126 CrossRef CAS PubMed.
- M. C. Haibach, S. Kundu, M. Brookhart and A. S. Goldman, Alkane metathesis by tandem alkane-dehydrogenation-olefin-metathesis catalysis and related chemistry, Acc. Chem. Res., 2012, 45, 947–958 CrossRef CAS PubMed.
- B. J. McCoy and G. Madras, Discrete and continuous models for polymerization and depolymerization, Chem. Eng. Sci., 2001, 56, 2831–2836 CrossRef CAS.
- J. E. J. Staggs, A continuous model for vapourisation of linear polymers by random scission and recombination, Fire Saf. J., 2005, 40, 610–627 CrossRef CAS.
- R. Simha and L. A. Wall, Kinetics of Chain Depolymerization, J. Phys. Chem., 1952, 56, 707–715 CrossRef CAS.
- P. E. Sánchez-Jiménez, L. A. Pérez-Maqueda, A. Perejón and J. M. Criado, A new model for the kinetic analysis of thermal degradation of polymers driven by random scission, Polym. Degrad. Stab., 2010, 95, 733–739 CrossRef.
- A. Bijttebier, H. Goesaert and J. Delcour, Amylase action pattern on starch polymers, Biologia, 2008, 63, 989–999 CrossRef CAS.
- J. E. J. Staggs, Discrete bond-weighted random scission of linear polymers, Polymer, 2006, 47, 897–906 CrossRef CAS.
- R. J. Zeman and N. R. Amundson, Continuous polymerization models—I, Chem. Eng. Sci., 1965, 20, 331–361 CrossRef CAS.
- J. E. J. Staggs, Modelling end-chain scission and recombination of linear polymers, Polym. Degrad. Stab., 2004, 85, 759–767 CrossRef CAS.
- Y. K. Ho, P. Doshi and H. K. Yeoh, Modelling simultaneous chain-end and random scissions using the fixed pivot technique, Can. J. Chem. Eng., 2018, 96, 800–814 CrossRef CAS.
- A. Gleadall, J. Pan, M. A. Kruft and M. Kellomaki, Degradation mechanisms of bioresorbable polyesters. Part 1. Effects of random scission, end scission and autocatalysis, Acta Biomater., 2014, 10, 2223–2232 CrossRef CAS PubMed.
- Y. Kodera and B. J. McCoy, Distribution kinetics of polymer thermogravimetric analysis: a model for chain-end and random scission, Energy Fuels, 2002, 16, 119–126 CrossRef CAS.
- A. Bijttebier, H. Goesaert and J. A. Delcour, Amylase action pattern on starch polymers, Biologia, 2008, 63, 989–999 CrossRef CAS.
- W. Banks and C. T. Greenwood, Mathematical models for the action of alpha-amylase on amylose, Carbohydr. Res., 1977, 57, 301–315 CrossRef CAS PubMed.
- Y. K. Ho, P. Doshi, H. K. Yeoh and G. C. Ngoh, Interlinked population balance and cybernetic models for the simultaneous saccharification and fermentation of natural polymers, Biotechnol. Bioeng., 2015, 112, 2084–2105 CrossRef CAS PubMed.
- D. E. Evans, C. Li and J. K. Eglinton, Improved prediction of malt fermentability by measurement of the diastatic power enzymes β-Amylase, α-Amylase, and limit dextrinase: I. survey of the levels of diastatic power enzymes in commercial malts, J. Am. Soc. Brew. Chem., 2018, 66, 223–232 CrossRef.
- E. Evans, B. van Wegen, Y. Ma and J. Eglinton, The impact of the thermostability of α-Amylase, β-Amylase, and limit dextrinase on potential wort fermentability, J. Am. Soc. Brew. Chem., 2018, 61, 210–218 CrossRef.
- I. A. Bitsanis and G. ten Brinke, A lattice Monte Carlo study of long chain conformations at solid-polymer melt interfaces, J. Chem. Phys., 1993, 99, 3100–3111 CrossRef CAS.
- A. Silberberg, Distribution of conformations and chain ends near the surface of a melt of linear flexible macromolecules, J. Colloid Interface Sci., 1982, 90, 86–91 CrossRef CAS.
- S. Liu, P. A. Kots, B. C. Vance, A. Danielson and D. G. Vlachos, Plastic waste to fuels by hydrocracking at mild conditions, Sci. Adv., 2021, 7, eabf8283 CrossRef CAS PubMed.
- J. van der Gucht, N. A. M. Besseling and G. J. Fleer, Surface Segregation in Polydisperse Polymer Melts, Macromolecules, 2002, 35, 6732–6738 CrossRef CAS.
- B. C. Vance, P. A. Kots, C. Wang, Z. R. Hinton, C. M. Quinn, T. H. Epps, L. T. J. Korley and D. G. Vlachos, Single pot catalyst strategy to branched products via adhesive isomerization and hydrocracking of polyethylene over platinum tungstated zirconia, Appl. Catal., B, 2021, 299 Search PubMed.
- K. A. Dill and S. Bromberg, Molecular Driving Forces: Statistical Thermodynamics in Biology, Chemistry, Physics, and Nanoscience, Garland Science, 2003 Search PubMed.
- J. M. Smith, H. C. Van Ness, M. M. Abbott and M. T. Swihart, Introduction to Chemical Engineering Thermodynamics, McGraw-Hill Education, 2018 Search PubMed.
- G. J. Fleer, J. van Male and A. Johner, Analytical approximation to the Scheutjens–Fleer theory for polymer adsorption from dilute solution. 1. trains, loops, and tails in terms of two parameters: the proximal and distal lengths, Macromolecules, 1999, 32, 825–844 CrossRef CAS.
- S. P. F. M. Roefs, J. M. H. M. Scheutjens and F. A. M. Leermakers, Adsorption Theory for Polydisperse Polymers, Macromolecules, 1994, 27, 4810–4816 CrossRef CAS.
- J. M. H. M. Scheutjens and G. J. Fleer, Statistical theory of the adsorption of interacting chain molecules. 1. Partition function, segment density distribution, and adsorption isotherms, J. Phys. Chem., 1979, 83, 1619–1635 CrossRef CAS.
- M. A. C. Stuart, J. M. H. M. Scheutjens and G. J. Fleer, Polydispersity effects and the interpretation of polymer adsorption isotherms, J. Polym. Sci., Polym. Phys. Ed., 1980, 18, 559–573 CrossRef.
- T. Nitta, M. Kuro-Oka and T. Katayama, An adsorption isotherm of multi-site occupancy model for heterogeneous surface, J. Chem. Eng. Jpn., 1984, 17, 45–52 CrossRef CAS.
- A. Milchev, V. Rostiashvili, S. Bhattacharya and T. Vilgis, Polymer chain adsorption on a solid surface: scaling arguments and computer simulations. in Nanophenomena at Surfaces, ed. Michailov M., Springer Series in Surface Sciences, Springer Berlin Heidelberg, 2011, pp. 185–204 Search PubMed.
- S. Metzger, M. Müller, K. Binder and J. Baschnagel, Adsorption transition of a polymer chain at a weakly attractive surface: Monte Carlo simulation of off-lattice models, Macromol. Theory Simul., 2002, 11, 985–995 CrossRef CAS.
- P. Grassberger, Simulations of grafted polymers in a good solvent, J. Phys. A: Math. Gen., 2005, 38, 323–331 CrossRef CAS.
- E. Eisenriegler, K. Kremer and K. Binder, Adsorption of polymer chains at surfaces: Scaling and Monte Carlo analyses, J. Chem. Phys., 1982, 77, 6296–6320 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2022 |