Structural and electronic insight into the effect of indium doping on the photocatalytic performance of TiO2 for CO2 conversion†
Patricia
Reñones
 a,
Fernando
Fresno
*a,
Freddy E.
Oropeza
a,
Fernando
Fresno
*a,
Freddy E.
Oropeza
 a,
Giulio
Gorni
a,
Giulio
Gorni
 b and
Víctor A.
de la Peña O'Shea
b and
Víctor A.
de la Peña O'Shea
 *a
*a
aPhotoactivated Processes Unit, IMDEA Energy, Avda. Ramón de la Sagra 3, 28935, Móstoles, Madrid, Spain. E-mail: fernando.fresno@imdea.org; victor.delapenya@imdea.org
bCELLS-ALBA Synchrotron, Carrer de la Llum 2-26, 08290 Cerdanyola del Valles, Barcelona, Spain
First published on 4th November 2021
Abstract
The photocatalytic conversion of CO2 to fuels and useful chemicals is a valuable artificial photosynthesis approach that simultaneously addresses the valorization of CO2 emissions and the storage of solar energy. In this work, we show how indium doping influences the activity and selectivity of TiO2 as a CO2 reduction photocatalyst using water as the electron donor, and how silver nanoparticles deposited on the semiconductor surface reinforce these effects, leading to promising photocatalytic systems with enhanced performance. For that purpose, catalysts with different indium contents have been synthesized by a simple wet chemical method starting from anatase TiO2, and a selected In-doped sample has been further modified by silver decoration following an impregnation method. The catalysts have been thoroughly characterized using different physicochemical techniques and tested for UV photocatalytic CO2 conversion in a laboratory-made, continuous flow gas-phase reaction system. Characterization results point at a substitutional doping of indium into the anatase crystal structure, as inferred from the absence of additional phases visible by X-ray diffraction as well as Raman and UV-vis spectroscopy, and further supported by an expansion of the unit cell volume calculated from XRD profile refinement and ratified by DFT calculations, and the absence of In–In scattering in EXAFS spectra. This substitution does not modify the optical band gap of the synthesized catalysts but, according to XPS, theoretical calculation and fluorescence spectra, induces electronic modifications that reduce the n-type character and the electron–hole recombination rate. In-doped catalysts show an increased selectivity towards the highly reduced product CH4 in photocatalytic CO2 reduction tests, whereas the main product attained with undoped titania is CO. Silver decoration, which leads to the initial formation of silver oxides that are reduced to metallic Ag nanoparticles under the UV light used in the reactions, dramatically reduces electron–hole recombination and further enhances the selectivity to methane and ethane in CO2 photocatalytic conversion.
Introduction
Nowadays there is a large consensus in the scientific community about the need for a great deal of effort into the search for clean fuels, in order to reduce the CO2 emissions to the atmosphere and escape from the current linear, fossil-based energy system into a circular, renewable-based one.1 One of the cornerstones for this transition lies in the development of robust technologies to achieve the efficient conversion of small, low-energy molecules like H2O, N2 and CO2 into fuels and chemicals using only renewable energy sources, solar par excellence.2,3 In this respect, a promising pathway to convert CO2 into renewable fuels is artificial photosynthesis using semiconductor photocatalysts, based on the red-ox reactivity of electron–hole pairs created upon irradiation with light of photon energy equal to or greater than the semiconductor band gap.4 Compared to other CO2 recycling technologies like electrochemical reduction or thermo-catalytic hydrogenation, photocatalytic and photoelectrochemical routes are today in a lower state of development, though they offer a promising potential in the medium term for direct solar-into-chemical energy conversion.5–7 However, for this technology to become reality and be transferred into the energy industry chain, a significant enhancement of the process in terms of efficiency and selectivity control is still needed.8–10The most studied catalyst for this reaction, as in the rest of photocatalysis applications, is TiO2 because of a unique combination of properties that include comparatively high photonic efficiency, (photo)chemical stability, low cost and non-toxicity.11 However, it presents some disadvantages that can be summarized in two, namely, being active only under UV light, which covers ca. 5% of the solar spectrum in energy terms;12 and the fact that, even if its photoactivity is higher than in many other semiconductors, it is still limited by a fast electron–hole recombination. Considering this, two general strategies arise to improve solar light utilization with titania: modifying it in order to extend the absorption towards the visible region, either by doping, heterostructuring or sensitizing;13,14 or improving its activity under UV for making the best possible use of this high-energy part of the solar spectrum. Indeed, solar-activated artificial photosynthesis for hydrogen production using TiO2-based photocatalysts has been demonstrated at a pilot-plant scale, with significant activity.15 UV enhancement of titania photocatalysts can be reached following different pathways of materials modification,8 among which doping with metal cations and surface decoration with nanosized metal co-catalysts play a significant role.10,16–18 Cation doping offers a remarkable synthetic versatility since it can be used to modify the structural, electronic and/or surface characteristics of the titania host, depending on the nature of the guest cation. For example, Ce-doping has been reported to modify the chemical potential of photoinduced electrons and holes,19,20 and to inhibit electron–hole recombination,21 resulting in higher activity for CO2 reduction. The latter effect, which leads to improved inner charge transport and hence higher photoconductivity, has also been reported for Cu-doped TiO2 photocatalysts for CO2 conversion,22 and a similar outcome has been described for Mo-doped titania nanotubes.23 Bi3+-doped TiO2 photocatalysts, in turn, have been reported to show enhanced charge separation accompanied by higher CO2 adsorption capacity with respect to pure titania,24 while cobalt doping also modifies the surface chemistry of TiO2 by inducing the formation of oxygen vacancies, resulting in modified product selectivity.25 In3+ is an interesting cation to be used as TiO2 dopant since it has been theoretically proven to induce the formation of electronic states related to oxygen vacancies that may decrease the electron–hole recombination rate and hence improve photocatalytic activity.26 Furthermore, it can induce a stronger s-orbital character in the conduction band arising from the overlap of In 5s and O 2p orbitals, which is correlated with low electronic effective masses, unlike large d-orbital character bands which have much larger electronic effective masses.27 This is a critical factor to improve the electronic mobility. In addition, it can form solid solutions with TiO2 in a wide compositional range.28,29 Thus, In-doped TiO2 photocatalysts have been explored for different photocatalytic reactions, where the electronic and surface modifications induced by In3+ have led to improved activities for the degradation of pollutants in water30–32 or air33 and for hydrogen production by photoreforming of alcohols.26,34 Regarding CO2 reduction, few works have explored the potential of indium doped titania for obtaining solar fuels or chemicals in this way. To the best of the authors' knowledge, only Tahir et al. have reported in several papers the activity of this kind of materials for such reaction. Thus, they showed an enhancement of one order of magnitude in the production of (mainly) carbon monoxide, with respect to unmodified TiO2, in a monolithic reactor fed by CO2 and H2O and irradiated with a Hg lamp with a maximum emission at 252 nm. The authors related the improvement to a segregated In2O3 phase forming an heterojunction with titania rather than doping.35 The presence of metallic indium acting as electron mediator for the same reaction under 365 nm light was in turn invoked to account for the enhancement of titania activity upon indium incorporation through a sol–gel synthesis followed by calcination at 500 °C.36 The activity of indium-doped titania for photocatalytic CO2 hydrogenation to obtain hydrocarbons in a monolithic reactor, irradiated at λmax = 252 nm, was further improved by copper co-doping37 or decoration with gold nanoparticles.38 However, in spite of these relatively numerous works, we believe the structural and electronic modifications induced by indium doping and their effect on photocatalytic CO2 conversion activity and selectivity have not, been investigated deeply enough. In this work, we approach these interesting doped systems from a theoretical and experimental point of view. We discuss the photocatalytic observations in terms of the structural and electronic modifications induced in TiO2 by indium doping.
Furthermore, the presence of metallic co-catalysts has been reported to largely influence both photocatalytic activity and reaction selectivity. Indeed, the latter can be tailor-modified not only by the surface decoration with the nanoparticles, but also by tuning their size or shape.17 Several metals like copper, gold, platinum or silver, have indeed been described to modify the selectivity toward highly electron-demanding products like methanol or methane,39–44 which can be traced back to the metal properties as an electron mediator,45,46 as well as to metal-induced modifications of the surface chemistry.47,48 In this respect, silver can be a remarkable example because of a comparatively low price and interesting photophysical and catalytic properties that enable it to act both as co-catalyst and electron mediator,45,49 as well as to display surface plasmon resonance characteristics with direct effect on the light harvesting efficiency of the photocatalytic system.40,42 In this work, we show how silver nanoparticles deposited on the semiconductor surface reinforce the effect of indium doping on the activity and selectivity of TiO2 as a CO2 reduction photocatalyst using water as electron donor, leading to promising photocatalytic systems with enhanced light utilization properties.
Considering the above-mentioned, catalysts with different indium contents have been synthesized by a simple wet chemical method starting from anatase TiO2, and a selected In-doped sample has been further modified by silver decoration following an impregnation method. All the catalysts have been thoroughly characterized using different physicochemical techniques and tested for UV photocatalytic CO2 conversion in a laboratory-made, continuous flow gas-phase reaction system. We found that In-doped catalysts show an increased selectivity towards the highly reduced product CH4 in photocatalytic CO2 reduction tests, whereas the main product attained with bare TIO2 is CO. Silver decoration dramatically reduces electron–hole recombination and further enhances the selectivity to methane and ethane in CO2 photocatalytic conversion. We discuss these photocatalytic observations in terms of the structural and electronic modifications induced in TiO2 by indium doping and by further decoration with Ag nanoparticles.
Experimental
Preparation of catalysts
In all cases the TiO2 employed is a commercial anatase-type titanium dioxide (TiO2, PC500) supplied by CristalACTIV™. For the synthesis of In-doped TiO2, the appropriate amount of In(NO3)3 (Sigma-Aldrich) was dissolved in 70 mL of a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (v/v) ethanol–water mixture, after which the TiO2 powder was added to the solution and dispersed in an ultrasonic bath for 1 h. The solvent was then removed in a rotatory evaporator (60 °C, 200 mbar, 80 rpm). The resulting powders were dried at 100 °C overnight, ground in an agate mortar, calcined in air at 400 °C for 4 h with a 10 °C min−1 heating ramp, and ground again. By this procedure, samples with different nominal indium amounts (1, 5 and 10 wt%) were obtained, hereafter named as In–TiO2-1, In–TiO2-5 and In–TiO2-10, respectively.
1 (v/v) ethanol–water mixture, after which the TiO2 powder was added to the solution and dispersed in an ultrasonic bath for 1 h. The solvent was then removed in a rotatory evaporator (60 °C, 200 mbar, 80 rpm). The resulting powders were dried at 100 °C overnight, ground in an agate mortar, calcined in air at 400 °C for 4 h with a 10 °C min−1 heating ramp, and ground again. By this procedure, samples with different nominal indium amounts (1, 5 and 10 wt%) were obtained, hereafter named as In–TiO2-1, In–TiO2-5 and In–TiO2-10, respectively.
For silver decoration, a selected In-doped TiO2 catalyst was suspended in 25 mL of an aqueous solution of the appropriate amount of AgNO3 (Sigma-Aldrich) for a final amount of metallic silver of 1 wt%. Water was then removed in a rotatory evaporator and the resulting powder was dried overnight at 100 °C, ground in an agate mortar, calcined in air at 400 °C for 4 h with a temperature ramp of 5 °C min−1, and ground again. The so-obtained sample is hereafter named as Ag/In–TiO2-1.
Catalyst characterization
Indium contents were determined by ICP-OES using a PerkinElmer Optima3300 DV instrument, while total content of carbon, hydrogen and nitrogen were determined using a THERMO SCIENTIFIC elementary analyzer Flash 2000 model. X-ray diffraction (XRD) was measured on a Panalytical EMPYREAN X-ray diffractometer using Cu Kα radiation (λ = 1.54178 Å) at a scanning rate of 0.01° s−1. From XRD patterns, average crystal sizes were calculated by applying Scherrer's formula to the most intense peak, and Pawley refinements were realized with FullProf software.50 Raman spectra were recorded at room temperature using a JASCO NRS-5000/7000 series Raman spectrometer with an excitation wavelength of 532 nm. TEM images were obtained using a JEOL 2100F microscope operated at 200 kV and equipped with an EDX detector (Oxford Instruments). The specific surface areas of the photocatalysts were measured from N2 adsorption isotherms at 77 K recorded on a QUADRASORB device from Quantachrome Instruments. Before the measurement the samples were degassed under N2 atmosphere at 105 °C for 20 h. The optoelectronic properties were studied by UV-vis diffuse reflectance spectroscopy using a Lambda 1050 PerkinElmer instrument in the range of 250–800 nm, with BaSO4 as reference. Band gaps were determined from Tauc plots.51 The fluorescence spectra were measured on a PerkinElmer LS55 spectrometer, using 300 nm as excitation wavelength and a cut-off filter at 350 nm. Fluorescence lifetimes were measured by time-correlated single photon counting (TCSPC) in a Mini-τ equipment from Edinburgh Instruments, with a laser diode of 372.2 nm wavelength and a pulse width of 61.2 ps at a repetition rate of 1 MHz and using an emission band pass filter at 400 ± 25 nm. Decay data were fitted to monoexponential curves.X-ray photoelectron spectra (XPS) were recorded with a lab-based spectrometer (SPECS GmbH) using a monochromated Al Kα source (hν = 1486.6 eV) operated at 50 W. Data were recorded with a PHOIBOS 150 NAP 1D-DLD analyser in fixed analyser transmission (FAT) mode. The pass energy was set to 40 eV for survey scans and 20 eV for high-resolution regions. The binding energy scale was calibrated using Au 4f7/2 (84.01 eV) and Ag 3d5/2 (368.20 eV). Recorded spectra were additionally calibrated against the C 1s internal reference. Data interpretation was done with Casa XPS software. Shirley or two-point linear background were used depending on the spectrum shape. Surface chemical analysis was done based on the peak area of high-resolution spectra and the CasaXPS sensitivity factors (where RSF of C 1s = 1.000).
Indium K-edge XAS spectra were measured at the CLÆSS beamline of the ALBA synchrotron using a Si(311) monochromator. The samples were prepared as 5 mm pellets mixing proper amount of powder with cellulose. The spectra were recorded in transmission mode at room temperature in the energy range 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800–28
800–28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 eV and the incident and transmitted intensities were detected with two ionization chambers. In2O3 was used as reference and the spectrum of In-foil was taken from the Farrel-Lytle database.52 The analysis of XANES and EXAFS data was performed using ATHENA and ARTEMIS software of the DEMETER package.53
000 eV and the incident and transmitted intensities were detected with two ionization chambers. In2O3 was used as reference and the spectrum of In-foil was taken from the Farrel-Lytle database.52 The analysis of XANES and EXAFS data was performed using ATHENA and ARTEMIS software of the DEMETER package.53
Computational methods
DFT calculations were carried out using the VASP5.4.4 code54,55 with projector-augmented wave (PAW) potentials56,57 to account for the core−valence interaction. Indium (In) was substitutionally doped onto two Ti sites in a (2 × 2 × 1) anatase supercell leading to a dopant concentration of 12.5 atom%. The total energies corresponding to the optimized geometries of all samples were calculated using the spin polarized version of the Perdew–Burke–Ernzerhof (PBE).58 The Heyd–Scuseria–Enzerhof hybrid functional (HSE06)59,60 was used, with the exchange contribution set at 25% and the screening parameter set to 0.2 A−1. k-Point sampling used a (4 × 4 × 4) Monkhorst–Pack sampling grid for the bulk unit cell. No symmetry constraints were applied to the doped structures. For oxygen vacancy compensation one oxygen atom was removed in the structure with two dopants.Photocatalytic reactions
The performance of the synthesized catalysts in photocatalytic CO2 reduction with water in gas phase was tested in continuous mode in a stainless steel photoreactor with a volume of 280 mL with a borosilicate window for irradiation (Fig. S1 in ESI†). The powder catalysts were deposited on glass microfibre filters, using a suspension of 100 mg of catalyst in ultrapure (Milli-Q) water. Pure carbon dioxide (99.9999%, Praxair) and ultrapure water were fed into the reaction system with a CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O molar ratio of 7.25 by means of a Controlled Evaporation and Mixing (CEM) unit. The reaction was carried out at 2 bar and 50 °C, and irradiation was provided by 4 fluorescent UV lamps (λmax = 365 nm) of 6 W each. In a typical procedure, the reactor is outgassed and flushed with argon (99.9999%, Praxair) for 1 hour to remove any residual compounds weakly adsorbed on the catalyst surface. Then a mixture of CO2/H2O is fed to the reactor for 1 h to establish the adsorption–desorption balance at the reaction temperature. Then, the reactor is pressurized and after 1 h irradiation is started. The reaction products are analyzed in line every 22 min over a period of 15 hours by means of an Agilent GC 7890A gas chromatograph equipped with three columns (QPLOT, Molesieve 5A and CP-Sil5B), one thermal conductivity detector (TCD), two flame ionization detectors (FID) and a mechanizer.
H2O molar ratio of 7.25 by means of a Controlled Evaporation and Mixing (CEM) unit. The reaction was carried out at 2 bar and 50 °C, and irradiation was provided by 4 fluorescent UV lamps (λmax = 365 nm) of 6 W each. In a typical procedure, the reactor is outgassed and flushed with argon (99.9999%, Praxair) for 1 hour to remove any residual compounds weakly adsorbed on the catalyst surface. Then a mixture of CO2/H2O is fed to the reactor for 1 h to establish the adsorption–desorption balance at the reaction temperature. Then, the reactor is pressurized and after 1 h irradiation is started. The reaction products are analyzed in line every 22 min over a period of 15 hours by means of an Agilent GC 7890A gas chromatograph equipped with three columns (QPLOT, Molesieve 5A and CP-Sil5B), one thermal conductivity detector (TCD), two flame ionization detectors (FID) and a mechanizer.
Results and discussion
Physico-chemical characterization of the photocatalysts
Table 1 collects the chemical analysis results obtained from ICP-OES and XPS for the In-doped TiO2 samples. The bulk In content obtained from ICP-OES essentially matches the nominal one, with slightly higher In incorporation yield with higher nominal content. The surface chemical compositions obtained from XPS reveal a significant positive deviation of the surface In concentration with respect to the bulk one, which indicates a preferential occupancy of In atoms in the material surface. This behaviour could be expected considering the employed doping method, and has been reported for other TiO2 systems doped with post-transition metals, including Sn and Sb.61–63| Sample | In content (wt%) | Cell parameter (Å) | Crystallite size (nm) | BET specific surface area (m2 g−1) | Band gap (eV) | |||
|---|---|---|---|---|---|---|---|---|
| Nominal | ICP-OES | XPS | a = b | c | ||||
| a With respect to TiO2. | ||||||||
| TiO2 | — | — | — | 3.7864 | 9.5133 | 16.4 | 104 | 3.14 |
| In–TiO2-1 | 1 | 0.66 ± 0.03 | 2.0 ± 0.3 | 3.7866 | 9.5143 | 15.7 | 106 | 3.12 |
| In–TiO2-5 | 5 | 4.9 ± 0.2 | 8.0 ± 0.7 | 3.7935 | 9.5397 | 12.4 | 121 | 3.14 |
| In–TiO2-10 | 10 | 10.2 ± 0.5 | 18 ± 2 | 3.7987 | 9.5400 | 8.9 | 141 | 3.15 |
| Ag/In–TiO2-1 | 1 | 0.66 ± 0.03a | 2.0 ± 0.3 | 3.7866 | 9.5143 | 15.8 | 93 | 3.14 |
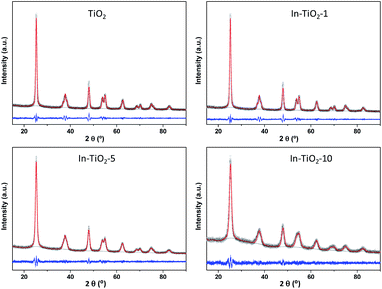
X-ray diffractograms and their Pawley refinements are shown in Fig. 1. In all cases, only reflections corresponding to the anatase phase of TiO2 are observed, without the appearance of any peaks related to indium oxides in the In-containing samples. The increase of In loading leads to a decreased crystallinity which is clearly observed in the shape of the peak and in the pattern background determined by the profile fitting. The crystal cell parameters provided by Pawley refinements (Table 1) show a quasi linear increase in the a and c cell axes, but reaching a plateau in the latter with In contents higher than 5 wt%. Given that In3+ has a larger ionic radius (0.80 Å) than Ti4+ (0.61 Å),64 this structural expansion would agree with a substitutional doping of In3+ for Ti4+ in the anatase lattice, suggesting that In3+ cations are able to diffuse from the surface into the anatase crystalline lattice. In addition, values calculated from the Scherrer formula (Table 1) reveal that crystal size decreases with indium content, revealing an effect of indium on TiO2 that has been previously related to In-doping,30,32,33,36 even in pre-crystallized commercial TiO2 samples31 as is the case of the present study. In the case of the silver-decorated catalyst, no additional reflections corresponding to metallic silver or any silver oxide are present either, and the diffractogram (Fig. S2†) matches the one of the corresponding In-doped TiO2 sample without silver, indicating that, differently from the indium incorporation procedure, the one for silver does not introduce further changes in TiO2 at the long-range structural level.42,45
As in the case of X-ray diffraction, the Raman spectra of undoped and In-doped TiO2 (Fig. S3†) show only the peaks corresponding to anatase, i.e., ca. 144 (Eg), 196 (Eg), 393 (B1g), 514 (A1g + B1g) and 635 (Eg) cm−1.65 No additional peaks attributable to In2O3, with the most intense band at ca. 308 cm−1,66 are observed in doped samples, nor is any silver-related band67 in the case of the Ag/In–TiO2-1 sample, the spectrum of which (not shown) essentially matches the In–TiO2-1 one. For a position and width analysis of the most intense Eg mode of anatase at ca. 144 cm−1, the band was fitted in every case to an asymmetric variation of the pseudo-Voigt profile.68 Fig. S4 and S5 in ESI† show the Raman shifts and the full widths at half maximum (FWHM) obtained from these fittings against the reciprocal of crystal size and the indium content, respectively. The band width behaves approximately as predicted by the phonon confinement model, i.e., FWHM increases as the crystal size decreases.69,70 However, opposed effects seem to occur in the case of the Raman shift, with a red displacement with respect to TiO2 at low indium content and a blue one at higher contents. Both phonon confinement due to crystal size69,70 and cell expansion due to doping26,71 would cause a higher Raman shift in In-doped samples with respect to TiO2, and this effect seems to dominate the spectra of samples with In wt% ≥5. However, assuming that In is replacing Ti in the crystal structure as suggested by the determined cell parameters, at similar crystal sizes as it is the case of TiO2 and In–TiO2-1, the considerably larger atomic mass of indium could shift this vibration mode to lower energy, since this mode involves displacements of both Ti and O atoms in anatase.72 Therefore, considering the effect of doping in crystal size, unit cell size and vibration frequencies, the observations made in Raman spectra would agree with a substitutional doping of In into TiO2, in line with XRD results. The Raman spectrum of In–TiO2-1 shows no modifications upon silver-decoration, which confirms that deposition of silver does not affect the structural features of the In-doped anatase.
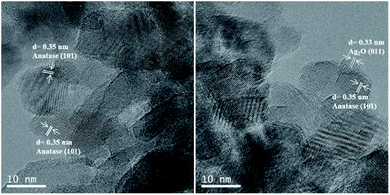
HR-TEM micrographs of both In–TiO2-1 and Ag/In–TiO2-1 catalysts (Fig. 2) display a relatively homogeneous distribution of particles with sizes between 7 and 18 nm, without significant morphological changes upon silver decoration. The structure analysis shows the lattice fringes corresponding to TiO2 (101) plane in an antase crystal phase and Ag2O (011) plane. EDX analyses reveal an average indium contents in both samples in accordance with the bulk ones obtained from ICP-OES, with values between 0.4 and 1.9 wt% In in different areas, and confirms the presence of 0.7–0.8 wt% Ag in Ag/In–TiO2-1, with particles of ca. 4–7 nm initially ascribed to Ag2O (marked in the figure), although it was noticed that the Ag oxides species tend to reduce to Ag0 and get charged under the electron beam.
Textural properties were evaluated by N2 adsorption–desorption isotherms, and the resulting BET surface areas are included in Table 1. In agreement with crystal size variations, In-doped samples show higher areas than bare titania, more notably with higher indium contents where the decrease in crystal size is more marked. On the other hand, silver incorporation decreases the surface area, which is probably related to the partial blocking by the Ag/Ag2O nanoparticles of TiO2 interparticle voids, largely responsible for the surface area in these samples.42,45
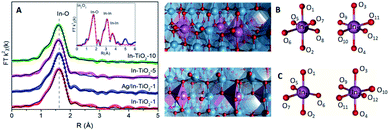
In order to gain deeper insight into the structural properties, EXAFS studies were performed in all samples in a reduced R-range from 1.0 to 2.2 Å. The In K-edge FT-k2χ(k) spectra of In-doped TiO2 samples (Fig. 3A) show only a first shell due to In–O single scattering while, in contrast, for In2O3 intense second and third shells are observed and associated to In–In single scattering paths. The coordination number of In–TiO2-x samples was fixed to six after checking that, leaving the coordination number as a free parameter, no relevant improvements of the fit were obtained and the fitted value was consistent with six. This result indicates that In3+ cations are hexacoordinated by oxygen ions, while the absence of In–In scattering suggests a high dispersion of In3+, with no clusters formed, strongly suggesting that indium exists as a dopant in the anatase structure and discarding the occurrence of an amorphous or even an extremely dispersed In2O3 phase. Moreover, a slight decrease (less than 2%) of the In–O bond distance is observed with respect to In2O3 reference, indicating a stronger In–O bond in In–TiO2-x samples (see Table S1 in ESI†).
DFT calculations were performed to complete these structural studies with the determination of the bonding interactions, energy cost and electronic properties of In–TiO2 doped systems. Taking into account the EXAFS data, the inclusion of a trivalent dopant (In3+) substituting for a Ti4+ atom can lead to two main possibilities, either the formation of an oxygen hole (O− polaron state), or other compensation mechanisms, such as the formation of an oxygen vacancy for every 2 In3+ dopants. Firstly, to determine the relative stability of In doped TiO2, the substitution energy (Es) and vacancy formation energy (Ev) were calculated, considering that two Ti atoms are replaced (Fig. 3B), using use eqn (1):
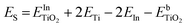 | (1) |
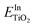 and
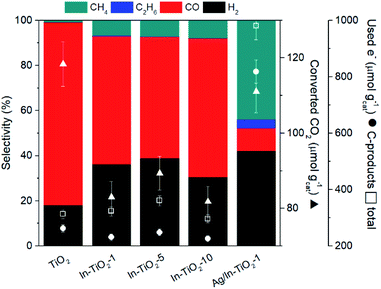
and 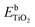 are the total energies of the doped system and bare TiO2, respectively, while ETi and EIn are energies per atom for metal Ti and In. This substitution energy is positive (Es = 19.14 eV), indicating that this is a metastable state, thermodynamically less stable than bare TiO2, in agreement with other authors.73 To determine intrinsic thermodynamic stability of doped TiO2, the formation energy of InxTi1−xO2 was calculated through eqn (2):
are the total energies of the doped system and bare TiO2, respectively, while ETi and EIn are energies per atom for metal Ti and In. This substitution energy is positive (Es = 19.14 eV), indicating that this is a metastable state, thermodynamically less stable than bare TiO2, in agreement with other authors.73 To determine intrinsic thermodynamic stability of doped TiO2, the formation energy of InxTi1−xO2 was calculated through eqn (2):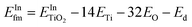 | (2) |
On the other hand, the oxygen vacancy formation energy (EVac) was also computed following eqn (3):
| EVac = EInxTi1−xO2−y +1/2EO − EInxTi1−xO2 | (3) |
The In–O bond distances in the structures with and without vacancies (Fig. 3C) are summarized in Table S2.† In the case of the stoichiometric structure, the In–O bonds are equal in the whole system. On the other hand, for the O-vacancy structure, a decrease in the bond length is observed in the apical (by 0.15–0.10 Å) and equatorial positions (0.030 Å), except for the case of In–O opposite to the vacancy, which is increased by 0.02 Å. The Ti–In distance closer to the vacancy is increased by 0.08 Å. This tendency leads to an increase in the cell parameters with the presence of In, consistently with XRD results. Previous studies have shown that the presence of oxygen vacancies can favour the photocatalytic activity, insofar as they can decrease the electron–hole recombination rate and enhance charge transfer.25,26
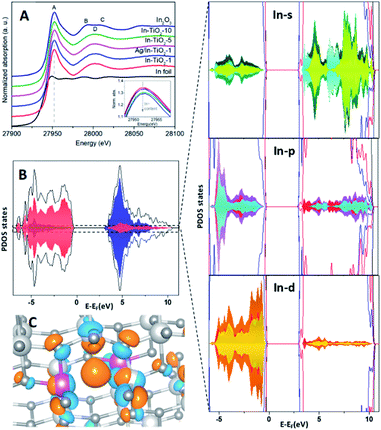
Fig. 4A shows the In K-edge XANES spectra of samples and references. A whiteline (feature A) centred at 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 952 eV, transition associated to excitations of 1s electrons to unoccupied 5p states, is observed in all In–TiO2-x samples and In2O3 reference. However, for In2O3 there are two clear continuum resonances at 27
952 eV, transition associated to excitations of 1s electrons to unoccupied 5p states, is observed in all In–TiO2-x samples and In2O3 reference. However, for In2O3 there are two clear continuum resonances at 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 992 (B) and 28
992 (B) and 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 011 eV (C) while in the In-doped TiO2 samples only one appears centred between (B) and (C) at ca. 28
011 eV (C) while in the In-doped TiO2 samples only one appears centred between (B) and (C) at ca. 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 002 eV (D). The edge position, taken as the first maximum of the first derivative spectra, is at 27
002 eV (D). The edge position, taken as the first maximum of the first derivative spectra, is at 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 940 eV for In foil and at 27
940 eV for In foil and at 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 946 eV for In–TiO2-x and In2O3 samples, as shown in Fig. S6.† This indicates the presence of In3+ in all In doped samples. A slight decrease of the whiteline is observed when increasing the doping level, as displayed in the inset of Fig. 4A. To quantify these changes, a peak fitting was performed using an arctan function to model the main edge step and a pseudo-Voigt function (PVF) was used to fit the whiteline intensity. The results of the fit (see Fig. S7 and Table S3†) indicate a variation of the peak area of about 5% when increasing the In doping from 1 to 10 wt%, while the In2O3 reference has the smallest whiteline intensity. Such variation is associated to a decrease of the unoccupied density of 5p states and could suggest a slight increase of covalence. In fact, a higher covalence produces a less localized density of states and lower white line intensities are expected.75
946 eV for In–TiO2-x and In2O3 samples, as shown in Fig. S6.† This indicates the presence of In3+ in all In doped samples. A slight decrease of the whiteline is observed when increasing the doping level, as displayed in the inset of Fig. 4A. To quantify these changes, a peak fitting was performed using an arctan function to model the main edge step and a pseudo-Voigt function (PVF) was used to fit the whiteline intensity. The results of the fit (see Fig. S7 and Table S3†) indicate a variation of the peak area of about 5% when increasing the In doping from 1 to 10 wt%, while the In2O3 reference has the smallest whiteline intensity. Such variation is associated to a decrease of the unoccupied density of 5p states and could suggest a slight increase of covalence. In fact, a higher covalence produces a less localized density of states and lower white line intensities are expected.75
To further study the effect of In doping in the electronic structure, partial density of states (PDOS) analyses were carried in In-substituted TiO2 both with (InxTi1−xO2−y) and without (InxTi1−xO2) oxygen vacancies (Fig. 4B and S8,† respectively). In all cases, the valence band (VB) is mainly formed by the overlapping between Opσ and Ti 3d(eg) orbitals to form the bonding σ states, being the valence band maximum (VBM) composed by non-bonding O pπ states, while the conduction band minimum (CBM) is mainly formed by Ti 3d orbitals. This evidences a covalent interaction of the Ti–O bonds that is also observed in In–O bonds. The presence of indium leads to a different behaviour of the systems with and without vacancies. In the case of InxTi1−XO2, PDOS exhibits a contribution whose energy levels are distributed in a wide range of energies above and below the Fermi level (EF), known as band tail,76,77 which is composed by the hybridization of O 2p with Ti 4d and In 5d orbitals. These states could indicate the presence of a polaron.74 In addition, the CBM exhibits a new state at 3.15 eV from Ti 4d with a slight contribution of In 5d. At higher energy, the antibonding state yielded by the In 5s–O 2p interactions, together with empty In-5p states, are observed, corroborating XANES results. The presence of this hybridization favours the charge transport once extra carriers fill the band.78 Furthermore, both indium atoms show similar contributions to the DOS, meaning that they are equivalent and that the excess of charge is homogeneously distributed between their environments. This is also corroborated by the examination of nearest neighbour (NN) indium atoms, where bands located above EF are mainly contributed for apical oxygen (Fig. S9A and B†). On the other hand, the presence of oxygen vacancies (VO) also leads to a noticeable hybridization in the VBM of O 2p with Ti 4d and In 5d orbitals, without the presence of states above EF. The CBM also shows a new state at 3.19 eV arising from Ti 4d, with the presence of antibonding states formed by In 5s–O 2p interactions, together with In 5p states. A more specific study of In atoms shows that, in the case of VBM, both indium atoms show a similar contribution for the 4d and 5s bands but with a decrease in the density of states for the indium atom close to the oxygen vacancy (see Fig. S8C and D†). In addition, the presence of the VO leads to a higher contribution to the bottom of the CB from In p/d orbitals and their NN (see Fig. S9C and D†). Thus, the presence of these vacancies as charge carriers results in an increase of carrier concentration and therefore in an enhancement in conductivity, which was experimentally reported by Zhao et al.79
The band gaps obtained for In-doped systems are 2.8 eV and 2.9 eV for stoichiometric and OV cases respectively, which is decreased in comparison with the value for the undoped system (3.3 eV), as was also confirmed by previous studies.73,74 This reduction in the band gap is due to the contribution of 5s5p orbitals to the Ti 3d conduction band. In turn, Bader charges show an increase in the charge of the indium and titanium atoms closer to the oxygen vacancy of 0.05 and 0.06 electrons, respectively, in comparison with the EInxTi1−xO2 structure. In addition, an excess of Bader charge (0.17 electrons) is localized on the apical oxygen site neighbouring each In-dopant. Fig. 4C shows the excess spin density plots where charge is localized in the oxygen vacancy site, comparable to an F-centre, and with some distribution onto neighbouring In and Ti sites.
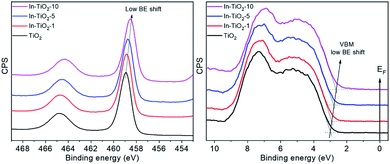
Fig. 5 shows the XPS of all In-doped TiO2 samples in the Ti2p and valence band regions. A clear and continuous shift towards low binding energies can be observed as the In concentration increases. This observation may be interpreted as an energy shift of the Fermi level (EF) of TiO2 towards the centre of the band gap. This may result from the suppression of the formation of Ti3+ defects that pin the EF to the bottom of the CB and are responsible of the TiO2 n-type semi-conductivity. Indeed, the DFT calculations described above suggest that In-doping introduces empty energy levels below the CBM of TiO2, which may indeed act as electron acceptors, leading to a lower concentration of n-type carriers in the anatase CB. Optoelectronic properties were further studied by means of UV-vis as well as static and time-resolved fluorescence spectroscopies. Regarding the former (Fig. 6A), the spectra of all samples are characterized by the sharp absorption onset at ca. 390 nm corresponding to the indirect band gap transition of anatase TiO2.80 No additional absorption edge exists in the visible region that can be ascribed to the In2O3 phase (Eg 2.7 eV),81 and no significant displacement of the onset with respect to TiO2 is observed in doped samples.
In this respect, a red shift of the band gap has been predicted for In-doped anatase with 12.5 at% of dopant,26 which is considerably larger than the indium content of the present samples (7.5 at% maximum). Experimentally, it has not been clearly reported whether In doping modifies the band gap of TiO2 or not, with authors indicating very large31 or slight30,32,34 red shifts with similar dopant contents, or reflecting essentially unchanged absorption spectra,35,38 or even slight blue shifts33 with respect to undoped titania.
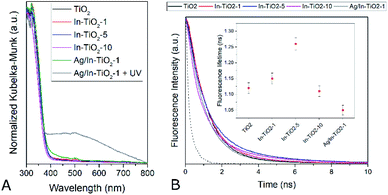
Experimentally, it has not been clearly reported whether In doping modifies the band gap of TiO2 or not, with authors indicating very large31 or slight30,32,34 red shifts with similar dopant contents, or reflecting essentially unchanged absorption spectra,35,38 or even slight blue shifts33 with respect to undoped titania. The band gap values estimated for the present samples by means of Tauc plots for indirect semiconductors are listed in Table 1 and, in any case, confirm that the catalysts studied here do not show a significant optical band gap modification as far as the accuracy of the graphical method allows to discern, in spite of the trend shown by theoretical calculations and XPS. Regarding the silver-modified catalyst, a shoulder in the visible region appears that cannot be ascribed to a band gap modification but is likely to arise from the presence of silver oxide(s) in a too small amount to be detected by XRD, as already suggested by TEM.42,82 After this sample has been exposed to UV radiation, however, a broad band centred at ca. 500 nm appears, which can be ascribed to the surface plasmon resonance absorption of silver nanoparticles,83,84 confirming that, as had been previously observed, metallic silver nanoparticles form on the surface of the catalyst only when it is irradiated with UV light and the original silver oxide is photoreduced to the metallic state, meaning that the actual co-catalyst is formed in situ during the photocatalytic reactions described below.42,45,82
Fluorescence spectra (Fig. S10†), in turn, show the typical radiative de-excitation events for nanosized titania photocatalysts, with an intense band centred at ca. 430 nm corresponding to the band-to-band recombination and additional weaker contributions at longer wavelengths usually assigned to excitonic photoluminescence resulting from surface defects and oxygen vacancies.85 Modified titania samples show the same positions of fluorescence bands, with only changes in intensity. Thus, upon In doping, the intensity of photoluminescence intensity decreases, which can be traced back to partially suppressed recombination and/or a higher contribution of non-radiative de-excitation events.26,85 The presence of silver further reduces the spectrum intensity to approximately half the one observed for the silver-free doped counterpart. Time-resolved fluorescence measurements taken at the maximum emission wavelength (Fig. 6B), and the corresponding intensity decay curve fittings, show that fluorescence lifetime (inset in Fig. 6B) increases with indium doping up to 5 wt%. In the absence of a second phase, as deduced from all the structural data discussed above, this can be ascribed to a longer lifetime of conduction band electrons in doped anatase.86 Therefore, fluorescence lifetimes suggest that indium doping actually decreases the electron–hole recombination in titania, as indicated by DFT calculations, and hence increases the lifetime of charge carriers available for photocatalytic reactions. This effect, however, is lost at the highest doping level, suggesting, as has been frequently discussed,36 that doping cations may become recombination centres when introduced in excessive amounts.
The situation is reversed with silver decoration and, as seen in Fig. 6B inset, anatase fluorescence lifetime decreases in the silver-modified In-doped sample. When a metal and a semiconductor phases coexist as in this case, this observation can be directly related to a lower electron population in the conduction band of the photoexcited semiconductor due to the extraction of electrons by the metal, provided that the relative electronics are favourable,17 which is the case for the Ag/TiO2 system, in which this transfer has been proved to strongly influence the photocatalytic behaviour.45
Photocatalytic CO2 reduction
Fig. 7 shows the cumulative productions of the four main reaction products in the photocatalytic conversion of CO2 with the different synthesized catalysts. In all cases, these products are carbon monoxide, methane and considerably smaller amounts of ethane, as CO2 conversion products, together with hydrogen arising from the water reduction reaction that competes with CO2 reduction for conduction band electrons. Traces of methanol were also obtained with all catalysts. As previously reported,42,43,45,87 TiO2 leads to CO as the main carbon product, together with hydrogen, which means that the product of the CO2 + H2O photocatalytic transformation is syngas, of well-known synthetic interest,88 with small amounts of hydrocarbons like methane and ethane. Indium doping, however, modifies this product distribution in such a way that carbon monoxide production decreases notably and the evolution of methane is somewhat enhanced, as is slightly that of ethane. In other words, indium doping increases the selectivity of the reaction towards hydrocarbons, essentially methane, which may have greater interest than CO because of their direct use as fuels, and this increase becomes larger as the dopant content increases, as depicted in Fig. 8. The shift in selectivity towards higher electron-demanding products has been previously related to an increased availability of conduction band electrons in the photoexcited catalyst as a result of enhanced electron–hole pair lifetime,9,45,82 and in the present case this can be related to indium doping insofar as the fluorescence lifetimes displayed above have shown a reduced recombination rate in doped systems up to 5 wt% In doping, with which electron utilization is maximum.26,30 This comes, however, by an increased production of hydrogen, which in principle is not the target reaction product. In this respect, large efforts are still needed to selectively use photogenerated electrons for CO2 reduction rather that H+ reduction if CO2 conversion with water as electron donor is chosen as the paradigmatic process for solar fuels production.7,8 Therefore, the results shown here with indium doping of TiO2 mean a step in the direction of controlling the selectivity of CO2 reduction towards hydrocarbons and especially methane, but, as seen in Fig. 8, this occurs at the expense of conversion. In turn, the total electron utilization, when the different number of electrons needed to convert CO2 into the different products is considered, is enhanced to a limited extent, as also included in Fig. 8.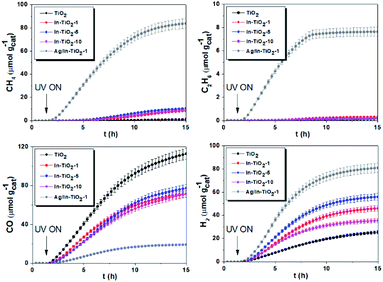 | ||
| Fig. 7 Cumulative production of the main products of photocatalytic CO2 reduction with the different synthesized catalysts. | ||
 | ||
| Fig. 8 Coloured bars: product selectivities obtained with the different catalysts. Symbols: CO2 conversions (triangles) and electron use (circles: in C-products; squares: in total products). | ||
When silver nanoparticles are further introduced into the catalytic system, however, the positive effect of driving the reaction towards highly reduced products is greatly enhanced, achieving a selectivity towards hydrocarbons (methane and ethane) of nearly 50% as a result of the dramatic increase of these products with respect to undecorated catalysts observed in Fig. 8.
In the same line of the discussion above, this can be traced back to extensive electron–hole recombination suppression, reinforced by the ability of metallic nanoparticles to act as electron transfer centres between the photoexcited semiconductor and the adsorbed reactant molecules, as inferred from Fig. 6B.8,17,45,82,89 With the silver-decorated In-doped catalyst, the utilization of electrons, both total and carbon-selective (Fig. 8), is therefore greatly enhanced with respect to the original pristine TiO2 sample. Additional effort is again required to suppress hydrogen production, which in this last case accounts for ca. 40% of reaction products, and is slightly enhanced with respect to undecorated systems.
Conclusions
In this work, we have shown that indium doping influences the activity and selectivity of TiO2 as a CO2 reduction photocatalyst using water as electron donor, and that silver nanoparticles deposited on the semiconductor surface reinforce these effects, leading to promising photocatalytic systems with enhanced light utilization properties. Characterization results point at a substitutional doping of indium into the anatase crystal structure, as inferred from the absence of additional phases visible by X-ray diffraction as well as Raman and UV-vis spectroscopy, and further supported by an expansion of the unit cell volume calculated from XRD profile refinement and ratified by DFT calculations, and the absence of In–In scattering in EXAFS spectra. This substitution does not modify the optical band gap of the synthesized catalysts but, according to XPS, theoretical calculations and time-resolved fluorescence spectra, induces electronic modifications that reduce the n-type character and the electron–hole recombination rate. In-doped catalysts show an increased selectivity towards the highly reduced product CH4 in photocatalytic CO2 reduction tests, in contrast with the main formation of CO attained with undoped titania. Silver decoration, which leads to the initial formation of silver oxides that are reduced to metallic Ag nanoparticles under the UV light used in the reactions, dramatically reduces electron–hole recombination by extracting photoexcited electrons from the conduction band of titania and acting as electron transfer centres, further enhancing the selectivity to methane and ethane in CO2 photocatalytic conversion.Author contributions
P. R.: conceptualization, formal analysis, investigation, methodology, visualization, writing – original draft. F. F.: conceptualization, formal analysis, investigation, visualization, writing – review and editing, supervision. F. E. O.: formal analysis, investigation, visualization, writing – original draft. G. G.: formal analysis, investigation, visualization, writing – original draft. V. A. P. O.: conceptualization, formal analysis, investigation, visualization, writing – review and editing, supervision.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Spanish AEI (PID2019-106315RB-I00). Authors also wish to thank Comunidad de Madrid and European Structural Funds for their financial support for FotoArt-CM project (S2018/NMT-4367) and Fundación Ramón Areces. The authors also thank ALBA Cells Synchrotron (Barcelona, Spain) and CSUC supercomputing centre for funded access to their facilities.Notes and references
- M. Aresta, Greenhouse Gases: Sci. Technol., 2019, 9, 610–612 CrossRef.
- R. Schlögl, Angew. Chem., Int. Ed., 2019, 58, 343–348 CrossRef.
- R. Shi, X. Zhang, G. I. N. N. Waterhouse, Y. Zhao and T. Zhang, Adv. Energy Mater., 2020, 10, 1–10 Search PubMed.
- U. Diebold, Surf. Sci. Rep., 2003, 48, 53–229 CrossRef CAS.
- O. S. Bushuyev, P. De Luna, C. T. Dinh, L. Tao, G. Saur, J. van de Lagemaat, S. O. Kelley and E. H. Sargent, Joule, 2018, 2, 825–832 CrossRef CAS.
- F. M. Mota and D. H. Kim, Chem. Soc. Rev., 2019, 48, 205–259 RSC.
- M. T. Spitler, M. A. Modestino, T. G. Deutsch, C. X. Xiang, J. R. Durrant, D. V. Esposito, S. Haussener, S. Maldonado, I. D. Sharp, B. A. Parkinson, D. S. Ginley, F. A. Houle, T. Hannappel, N. R. Neale, D. G. Nocera and P. C. McIntyre, Sustainable Energy Fuels, 2020, 4, 985–995 RSC.
- F. Fresno, I. J. Villar-García, L. Collado, E. Alfonso-González, P. Renones, M. Barawi and V. A. De La Pena O'Shea, J. Phys. Chem. Lett., 2018, 9, 7192–7204 CrossRef CAS.
- J. Fu, K. Jiang, X. Qiu, J. Yu and M. Liu, Mater. Today, 2020, 32, 222–243 CrossRef CAS.
- S. Sorcar, S. Yoriya, H. Lee, C. A. Grimes and S. P. Feng, Mater. Today Chem., 2020, 16, 100264 CrossRef CAS.
- X. Chen and S. S. Mao, Chem. Rev., 2007, 107, 2891–2959 CrossRef CAS.
- B. Ohtani, J. Photochem. Photobiol., C, 2010, 11, 157–178 CrossRef CAS.
- M. Pelaez, N. T. Nolan, S. C. Pillai, M. K. Seery, P. Falaras, A. G. Kontos, P. S. M. Dunlop, J. W. J. Hamilton, J. A. Byrne, K. O'Shea, M. H. Entezari and D. D. Dionysiou, Appl. Catal., B, 2012, 125, 331–349 CrossRef CAS.
- K. Perović, F. M. dela Rosa, M. Kovačić, H. Kušić, U. L. Štangar, F. Fresno, D. D. Dionysiou and A. L. Bozic, Materials, 2020, 13, 1338 CrossRef.
- S. Y. Arzate Salgado, R. M. Ramírez Zamora, R. Zanella, J. Peral, S. Malato and M. I. Maldonado, Int. J. Hydrogen Energy, 2016, 41, 11933–11940 CrossRef CAS.
- Z. Fu, Q. Yang, Z. Liu, F. Chen, F. Yao, T. Xie, Y. Zhong, D. Wang, J. Li, X. Li and G. Zeng, J. CO2 Util., 2019, 34, 63–73 CrossRef CAS.
- J. Ran, M. Jaroniec and S. Qiao, Adv. Mater., 2018, 30, 1704649 CrossRef.
- A. Meng, L. Zhang, B. Cheng and J. Yu, Adv. Mater., 2019, 31, 1–31 Search PubMed.
- L. Matějová, K. Kočí, M. Reli, L. Čapek, A. Hospodková, P. Peikertová, Z. Matěj, L. Obalová, A. Wach, P. Kuśtrowski and A. Kotarba, Appl. Catal., B, 2014, 152–153, 172–183 CrossRef.
- K. Kočí, L. Matějová, N. Ambrožová, M. Šihor, I. Troppová, L. Čapek, A. Kotarba, P. Kustrowski, A. Hospodková and L. Obalová, J. Sol-Gel Sci. Technol., 2016, 78, 550–558 CrossRef.
- Z. Xiong, Y. Zhao, J. Zhang and C. Zheng, Fuel Process. Technol., 2015, 135, 6–13 CrossRef CAS.
- H. She, Z. Zhao, W. Bai, J. Huang, L. Wang and Q. Wang, Mater. Res. Bull., 2020, 124, 110758 CrossRef CAS.
- N. H. Nguyen, H. Y. Wu and H. Bai, Chem. Eng. J., 2015, 269, 60–66 CrossRef CAS.
- J. H. Lee, H. Lee and M. Kang, Mater. Lett., 2016, 178, 316–319 CrossRef CAS.
- T. Wang, X. Meng, G. Liu, K. Chang, P. Li, Q. Kang, L. Liu, M. Li, S. Ouyang and J. Ye, J. Mater. Chem. A, 2015, 3, 9491–9501 RSC.
- V. Kumaravel, S. Rhatigan, S. Mathew, J. Bartlett, M. Nolan, S. J. Hinder, P. K. Sharma, A. Singh, J. A. Byrne, J. Harrison and S. C. Pillai, J. Phys. Chem. C, 2019, 123, 21083–21096 CrossRef CAS.
- G. Hautier, A. Miglio, D. Waroquiers, G.-M. Rignanese and X. Gonze, Chem. Mater., 2014, 26, 5447–5458 CrossRef CAS.
- A. J. Atanacio, T. Bak, J. Nowotny and K. E. Prince, J. Am. Ceram. Soc., 2013, 96, 1366–1371 CrossRef CAS.
- F. Brown, M. J. R. Flores, N. Kimizuka, Y. Michiue, M. Onoda, T. Mohri, M. Nakamura and N. Ishizawa, J. Solid State Chem., 1999, 144, 91–99 CrossRef CAS.
- E. Wang, W. Yang and Y. Cao, J. Phys. Chem. C, 2009, 113, 20912–20917 CrossRef CAS.
- Z. Jin, W. Duan, W. Duan, B. Liu, X. Chen, F. Yang and J. Guo, Appl. Catal., A, 2016, 517, 129–140 CrossRef CAS.
- M. B. Suwarnkar, G. V. Khade, S. B. Babar and K. M. Garadkar, J. Mater. Sci.: Mater. Electron., 2017, 28, 17140–17147 CrossRef CAS.
- M. Hinojosa-Reyes, S. Arriaga, L. A. Diaz-Torres and V. Rodríguez-González, Chem. Eng. J., 2013, 224, 106–113 CrossRef CAS.
- R. Sasikala, A. R. Shirole, V. Sudarsan, Jagannath, C. Sudakar, R. Naik, R. Rao and S. R. Bharadwaj, Appl. Catal., A, 2010, 377, 47–54 CrossRef CAS.
- M. Tahir and N. S. Amin, Appl. Catal., A, 2013, 467, 483–496 CrossRef CAS.
- M. Tahir and N. A. S. Amin, Appl. Catal., B, 2015, 162, 98–109 CrossRef CAS.
- M. Tahir and N. S. Amin, Appl. Catal., A, 2015, 493, 90–102 CrossRef CAS.
- B. Tahir, M. Tahir and N. S. Amin, Appl. Surf. Sci., 2015, 338, 1–14 CrossRef CAS.
- T. Ohno, T. Higo, N. Murakami, H. Saito, Q. Zhang, Y. Yang and T. Tsubota, Appl. Catal., B, 2014, 152–153, 309–316 CrossRef CAS.
- P. Pathak, M. J. Meziani, L. Castillo and Y. P. Sun, Green Chem., 2005, 7, 667–670 RSC.
- J.-Y. Liu, B. Garg and Y.-C. Ling, Green Chem., 2011, 13, 2029–2031 RSC.
- L. Collado, P. Jana, B. Sierra, J. M. Coronado, P. Pizarro, D. P. Serrano and V. A. de la Peña O'Shea, Chem. Eng. J., 2013, 224, 128–135 CrossRef CAS.
- L. Collado, A. Reynal, J. M. Coronado, D. P. Serrano, J. R. Durrant and V. A. De la Peña O'Shea, Appl. Catal., B, 2015, 178, 177–185 CrossRef CAS.
- Y. Wang, J. Zhao, Y. Li and C. Wang, Appl. Catal., B, 2018, 226, 544–553 CrossRef CAS.
- L. Collado, A. Reynal, F. Fresno, M. Barawi, C. Escudero, V. Perez-Dieste, J. M. Coronado, D. P. Serrano, J. R. Durrant and V. A. de la Peña O'Shea, Nat. Commun., 2018, 9, 4986 CrossRef.
- K. C. Christoforidis and P. Fornasiero, ChemCatChem, 2019, 11, 368–382 CrossRef CAS.
- M. Tasbihi, F. Fresno, U. Simon, I. J. Villar-García, V. Pérez-Dieste, C. Escudero and V. A. de la Peña O'Shea, Appl. Catal., B, 2018, 239, 68–76 CrossRef CAS.
- L. Lu, S. Wang, C. Zhou, Z. Shi, H. Zhu, Z. Xin, X. Wang, S. Yan and Z. Zou, J. Mater. Chem. A, 2018, 6, 14838–14846 RSC.
- K. Li, T. Peng, Z. Ying, S. Song and J. Zhang, Appl. Catal., B, 2016, 180, 130–138 CrossRef CAS.
- J. Rodríguez-Carvajal, Phys. B, 1993, 192, 55–69 CrossRef.
- J. Tauc, Mater. Res. Bull., 1968, 3, 37–46 CrossRef CAS.
- http://ixs.iit.edu/database/data/Farrel_Lytle_data/ .
- B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–541 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- B. G. Janesko, T. M. Henderson and G. E. Scuseria, Phys. Chem. Chem. Phys., 2009, 11, 443–454 RSC.
- T. M. Henderson, J. Paier and G. E. Scuseria, Phys. Status Solidi, 2011, 248, 767–774 CrossRef CAS.
- F. E. Oropeza, B. Davies, R. G. Palgrave and R. G. Egdell, Phys. Chem. Chem. Phys., 2011, 13, 7882–7891 RSC.
- F. E. Oropeza and R. G. Egdell, Chem. Phys. Lett., 2011, 515, 249–253 CrossRef CAS.
- F. E. Oropeza, K. H. L. Zhang, R. G. Palgrave, A. Regoutz, R. G. Egdell, J. P. Allen, N. M. Galea and G. W. Watson, J. Phys. Chem. C, 2013, 117, 15221–15228 CrossRef CAS.
- CRC Handbook of Chemistry and Physics, ed. D. R. Lide, CRC Press, 2005 Search PubMed.
- J. Zhang, M. Li, Z. Feng, J. Chen and C. Li, J. Phys. Chem. B, 2005, 110, 927–935 CrossRef PubMed.
- W. B. White and V. G. Keramidas, Spectrochim. Acta, Part A, 1972, 28, 501–509 CrossRef CAS.
- R. S. Zeferino, M. B. Flores and U. Pal, J. Appl. Phys., 2011, 109, 14308 CrossRef.
- A. L. Stancik and E. B. Brauns, Vib. Spectrosc., 2008, 47, 66–69 CrossRef CAS.
- S. Kelly, F. H. Pollak and M. Tomkiewicz, J. Phys. Chem. B, 1997, 101, 2730–2734 CrossRef CAS.
- W. F. Zhang, Y. L. He, M. S. Zhang, Z. Yin and Q. Chen, J. Phys. D: Appl. Phys., 2000, 33, 912–916 CrossRef CAS.
- M. A. Debeila, R. P. K. Wells and J. A. Anderson, J. Catal., 2006, 239, 162–172 CrossRef CAS.
- P. Mazzolini, V. Russo, C. S. Casari, T. Hitosugi, S. Nakao, T. Hasegawa and A. Li Bassi, J. Phys. Chem. C, 2016, 120, 18878–18886 CrossRef CAS.
- J. Liu, M. Weng, S. Li, X. Chen, J. Cen, J. Jie, W. Xiao, J. Zheng and F. Pan, Phys. Chem. Chem. Phys., 2020, 22, 39–53 RSC.
- A. Iwaszuk and M. Nolan, J. Phys.: Condens. Matter, 2011, 23, 334207 CrossRef PubMed.
- R. Sarangi, Coord. Chem. Rev., 2013, 257, 459–472 CrossRef CAS.
- X. Chen, L. Liu, P. Y. Yu and S. S. Mao, Science, 2011, 331, 746–750 CrossRef CAS PubMed.
- L. Collado, I. Jansson, A. E. Platero-Prats, V. Perez-Dieste, C. Escudero, E. Molins, L. Casas I Doucastela, B. Sánchez, J. M. Coronado, D. P. Serrano, S. Suarez and V. A. De La Peña-O’Shea, ACS Catal., 2017, 7, 1646–1654 CrossRef CAS.
- Y.-B. Lu, T. L. Yang, Z. C. Ling, W.-Y. Cong, P. Zhang, Y. H. Li and Y. Q. Xin, J. Mater. Chem. C, 2015, 3, 7727–7737 RSC.
- W. Zhao, W. Wang, X. Feng, L. He, Q. Cao, C. Luan and J. Ma, Ceram. Int., 2017, 43, 8391–8395 CrossRef CAS.
- O. Carp, C. L. Huisman and A. Reller, Prog. Solid State Chem., 2004, 32, 33–177 CrossRef CAS.
- S. K. Poznyak, D. V. Talapin and A. I. Kulak, J. Phys. Chem. B, 2001, 105, 4816–4823 CrossRef CAS.
- F. Fresno, S. Galdón, M. Barawi, E. Alfonso-González, C. Escudero, V. Pérez-Dieste, C. Huck-Iriart and V. A. de la Peña O'Shea, Catal. Today, 2021, 361, 85–93 CrossRef CAS.
- T. Hirakawa and P. V. Kamat, J. Am. Chem. Soc., 2005, 127, 3928–3934 CrossRef CAS.
- H. Li, W. Lu, J. Tian, Y. Luo, A. M. Asiri, A. O. Al-Youbi and X. Sun, Chem.–Eur. J., 2012, 18, 8508–8514 CrossRef CAS.
- J. Liqiang, Q. Yichun, W. Baiqi, L. Shudan, J. Baojiang, Y. Libin, F. Wei, F. Honggang and S. Jiazhong, Sol. Energy Mater. Sol. Cells, 2006, 90, 1773–1787 CrossRef.
- U. Noomnarm and R. M. Clegg, Photosynth. Res., 2009, 101, 181–194 CrossRef CAS.
- F. Fresno, P. Reñones, E. Alfonso, C. Guillén, J. F. Trigo, J. Herrero, L. Collado and V. A. de la Peña O'Shea, Appl. Catal., B, 2018, 224, 912–918 CrossRef CAS.
- R. M. Navarro, M. A. Peña and J. L. G. Fierro, Chem. Rev., 2007, 107, 3952–3991 CrossRef CAS.
- Q. Wang, P. Dong, Z. Huang and X. Zhang, Chem. Phys. Lett., 2015, 639, 11–16 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Additional figures and tables. See DOI: 10.1039/d1ta08347c |
| This journal is © The Royal Society of Chemistry 2022 |