Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Experimental investigations and model-based optimization of CZZ/H-FER 20 bed compositions for the direct synthesis of DME from CO2-rich syngas†
Stefan
Wild
 a,
Bruno
Lacerda de Oliveira Campos
a,
Bruno
Lacerda de Oliveira Campos
 a,
Thomas A.
Zevaco
a,
Thomas A.
Zevaco
 a,
David
Guse
a,
David
Guse
 b,
Matthias
Kind
b,
Stephan
Pitter
b,
Matthias
Kind
b,
Stephan
Pitter
 a,
Karla
Herrera Delgado
a,
Karla
Herrera Delgado
 *a and
Jörg
Sauer
*a and
Jörg
Sauer
 a
a
aIKFT – Institute of Catalysis Research and Technology, Karlsruhe Institute of Technology, Hermann-von-Helmholtz-Platz 1, D-76344 Eggenstein-Leopoldshafen, Germany. E-mail: karla.herrera@kit.edu
bTVT – Institute of Thermal Process Engineering, Karlsruhe Institute of Technology, Kaiserstraße 12, D-76131 Karlsruhe, Germany
First published on 2nd January 2022
Abstract
Experimental kinetics studies and model-based optimization were performed for the direct synthesis of dimethyl ether (DME) in a wide range of process conditions, including various CuO/ZnO/ZrO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H-FER 20 bed compositions. Thus, in order to improve the DME productivity using fluctuating CO/CO2 gas feeds such as those that could be used in power-to-fuel technologies, a series of experiments was carried out at 30 bar by varying the CO2/COx inlet ratio (0.4–0.9), temperature (483–513 K), gas hourly space velocity (2.78, 3.57 s−1), and the weight ratio of the catalyst components CuO/ZnO/ZrO2 and H-FER 20 (from 1 to 70.4). A lumped kinetic model for the methanol synthesis from the literature was extended for the direct DME synthesis. With only eight fitted parameters, the model adequately simulates an extensive array of data points measured with a six-fold parallel reactor setup. The resulting model was applied to optimize the CuO/ZnO/ZrO2
H-FER 20 bed compositions. Thus, in order to improve the DME productivity using fluctuating CO/CO2 gas feeds such as those that could be used in power-to-fuel technologies, a series of experiments was carried out at 30 bar by varying the CO2/COx inlet ratio (0.4–0.9), temperature (483–513 K), gas hourly space velocity (2.78, 3.57 s−1), and the weight ratio of the catalyst components CuO/ZnO/ZrO2 and H-FER 20 (from 1 to 70.4). A lumped kinetic model for the methanol synthesis from the literature was extended for the direct DME synthesis. With only eight fitted parameters, the model adequately simulates an extensive array of data points measured with a six-fold parallel reactor setup. The resulting model was applied to optimize the CuO/ZnO/ZrO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H-FER 20 ratio and the obtained optimization results were validated experimentally, confirming the simulated performance enhancement. For a CO2-rich feed (CO2/COx = 0.9), the optimum volumetric CuO/ZnO/ZrO2
H-FER 20 ratio and the obtained optimization results were validated experimentally, confirming the simulated performance enhancement. For a CO2-rich feed (CO2/COx = 0.9), the optimum volumetric CuO/ZnO/ZrO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H-FER 20 ratio under kinetic operating conditions is 91.5/8.5 vol%. Extrapolation based on the new model for industrially relevant operating cases show an optimal H-FER 20 volume fraction below 5 vol%, resulting in a COx conversion of 47% at a DME selectivity of 88%.
H-FER 20 ratio under kinetic operating conditions is 91.5/8.5 vol%. Extrapolation based on the new model for industrially relevant operating cases show an optimal H-FER 20 volume fraction below 5 vol%, resulting in a COx conversion of 47% at a DME selectivity of 88%.
Introduction
A future with a CO2-neutral carbon economy necessitates the development of mature power-to-fuel technologies.1,2 Synthetic fuels and chemicals produced from sustainable and economically viable hydrogen production can compensate for fluctuating and over-potential power generation from renewable energy sources.3 In addition, adapted synthesis routes can be used to recycle CO2 yielding CO2-neutral or even CO2-consuming fuels and chemicals.4 One of the most promising options for a flexible and carbon neutral production of chemical energy carriers is the use of CO2-rich syngas and its further conversion using efficient and long-term stable catalysts. Besides other synthetic hydrocarbons, dimethyl ether (DME) is a particularly interesting product due to its promising physical and chemical properties.5 DME is the simplest ether, has no C–C bonds and contains oxygen. Therefore, the exhaust gas after the combustion of DME contains less carbon monoxide, unburned hydrocarbons and soot than, for example, during the combustion of butane or diesel.6 In addition, DME is an attractive intermediate for the chemical industry, e.g. for the production of alkyl aromatics, dimethyl sulfate, methyl acetate or light olefins.7–11The industrially applied two-step synthesis requires two individual reactors, one for methanol (MeOH) production, where CO and CO2 are hydrogenated to MeOH ((R1) and (R2)), linked by the WGS reaction (R3).
CO hydrogenation to MeOH
| CO + 2H2 ⇌ CH3OH ΔH°298 K = −90.4 kJ mol−1 | (R1) |
| CO2 + 3H2 ⇌ CH3OH + H2O ΔH°298 K = −49.4 kJ mol−1 | (R2) |
| CO + H2O ⇌ CO2 + H2 ΔH°298 K = −41.0 kJ mol−1 | (R3) |
MeOH dehydration
| 2CH3OH ⇌ CH3OCH3 + H2O ΔH°298 K = −23.5 kJ mol−1 | (R4) |
New possible applications of DME in the alternative fuel sectors have not only led to an increase in DME production, but also to numerous research activities in the field of process development9 to maximize the process efficiency. Particularly for the direct DME synthesis, the effectiveness of the available reactor volume can be improved by optimizing the DME yield as a function of the ratio of MeOH-catalyst/dehydration-agent. The findings, gained through an isochoric optimization of the DME yield, could generally be applied in existing plants with an appropriate reactor concept, without the need for a new reactor design, and thus additional necessary investments. Alternatively, in new plant designs, an optimized catalyst bed ratio enables more compact reactors, thus reducing investment costs. In addition, an optimized catalyst bed composition also represents an opportunity with regard to a possibly improved CO2 conversion.
The widely studied CuO/ZnO/Al2O3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ-Al2O3 (CZA/γ-Al2O3) catalyst system has been investigated in CO-rich syngas from the viewpoint of bed composition (Table 1). For a bed variation of CZA/γ-Al2O3, Peláez et al.17 reported that the DME yield is increased up to a CZA/γ-Al2O3 mass ratio of 12.3 (in H2/CO = 1.5 − CO2/COx = 0). Guang-xin et al.18 used a slurry autoclave reactor with a fixed CZA catalyst mass and a successively increasing γ-Al2O3 mass. They demonstrated that for a pure CO-syngas (H2/CO = 1.0 − CO2/COx = 0), the maximum CO conversion is found at a CZA
γ-Al2O3 (CZA/γ-Al2O3) catalyst system has been investigated in CO-rich syngas from the viewpoint of bed composition (Table 1). For a bed variation of CZA/γ-Al2O3, Peláez et al.17 reported that the DME yield is increased up to a CZA/γ-Al2O3 mass ratio of 12.3 (in H2/CO = 1.5 − CO2/COx = 0). Guang-xin et al.18 used a slurry autoclave reactor with a fixed CZA catalyst mass and a successively increasing γ-Al2O3 mass. They demonstrated that for a pure CO-syngas (H2/CO = 1.0 − CO2/COx = 0), the maximum CO conversion is found at a CZA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ-Al2O3 weight ratio of 20. A further mass increase of γ-Al2O3 leads to a decrease in CO conversion. The DME selectivity reaches a nearly constant value at a CZA/γ-Al2O3 mass ratio of 8, whereas a minor loading of γ-Al2O3 showed a significant decrease in DME selectivity.
γ-Al2O3 weight ratio of 20. A further mass increase of γ-Al2O3 leads to a decrease in CO conversion. The DME selectivity reaches a nearly constant value at a CZA/γ-Al2O3 mass ratio of 8, whereas a minor loading of γ-Al2O3 showed a significant decrease in DME selectivity.
| MeOH catalyst | Dehydr. catalyst | Optimala,b MeOH/Dehydr. catalyst mass ratio | CO2/COx | Ref. |
|---|---|---|---|---|
| a Based on DME yields. b Based on COx conversion. | ||||
| CZA | γ-Al2O3 | 12.3a | 0.0 | Peláez et al.17 |
| CZA | γ-Al2O3 | 20b | 0.0 | Jia et al.25 |
| CZA | γ-Al2O3 | 9b | 0.66 | Peinado et al.19 |
| CZA | γ-Al2O3 | 5b | 0.34 | Bae et al.20 |
| CZA | γ-Al2O3 | 2b | 0.2/0.4/0.6/0.8 | Delgado Otalvaro et al.21 |
| CZA | H-ZSM-5 | 9a | 0.12 | García-Trenco et al.23 |
| CZA | H-ZSM-5 | 5a | 1.0 | Ren et al.24 |
A catalyst bed variation using CO2-rich syngas was studied by Peinado et al.19 with CZA/γ-Al2O3 (CO/CO2/H2: 1/1.9/7.7 − CO2/COx = 0.66) showing increased COx conversions (up to 24 mol%) for a CZA/γ-Al2O3 weight ratio of 9. However, DME was only converted from COx with a selectivity of 1%. Increasing the amount of γ-Al2O3 in the bed improved the DME selectivity, but at the expense of COx conversion. Bae et al.20 also investigated a bed variation of the CZA/γ-Al2O3 catalyst system for a CO/CO2 syngas mixture of CO/CO2/H2: 41/21/38 − CO2/COx = 0.34. Here, CO conversion (29.3 mol%) is increasing up to a CZA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ-Al2O3 weight ratio of 5, however, accompanied by a decrease in DME selectivity (7.9 mol%). In a recent study, Delgado Otalvaro et al.21 found similar results with a variable CO2/COx feed, where an increasing CZA/γ-Al2O3 ratio promotes COx conversion and a DME yield at a low CO2 content in the feed; however, a high CO2 feed content significantly reduces DME selectivity.
γ-Al2O3 weight ratio of 5, however, accompanied by a decrease in DME selectivity (7.9 mol%). In a recent study, Delgado Otalvaro et al.21 found similar results with a variable CO2/COx feed, where an increasing CZA/γ-Al2O3 ratio promotes COx conversion and a DME yield at a low CO2 content in the feed; however, a high CO2 feed content significantly reduces DME selectivity.
Catalyst systems involving zeolites (Table 1) as dehydrating agents have also been investigated for CO-rich syngas compositions. Abu-Dahrieh et al.22 investigated a combination of CZA/HZSM-5 (Si/Al = 80) and found an increased DME yield for a CZA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HZSM-5 mass ratio of 3 at 533 K, 20 bar (H2/CO/CO2/Ar: 62/31/4/3 − CO2/COx = 0.11). García-Trenco et al.23 investigated a variation of a hybrid catalyst system consisting of CZA/H-ZSM-5 (Si/Al = 40) under similar conditions (H2/CO/CO2: 66/30/4 − CO2/COx = 0.12, 40 bar and 533 K) and found that even at a CZA
HZSM-5 mass ratio of 3 at 533 K, 20 bar (H2/CO/CO2/Ar: 62/31/4/3 − CO2/COx = 0.11). García-Trenco et al.23 investigated a variation of a hybrid catalyst system consisting of CZA/H-ZSM-5 (Si/Al = 40) under similar conditions (H2/CO/CO2: 66/30/4 − CO2/COx = 0.12, 40 bar and 533 K) and found that even at a CZA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H-ZSM-5 mass ratio of 9, no significant decrease in the DME yield takes place.
H-ZSM-5 mass ratio of 9, no significant decrease in the DME yield takes place.
A catalyst bed variation of H-ZSM5 in combination with a fixed CZA catalyst mass24 in a pure CO2 syngas feed (CO2/COx = 1.0) revealed a nearly stable CO2 conversion (26 mol%) while DME selectivity remained constant up to a CZA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HZSM-5 mass ratio of 5.
HZSM-5 mass ratio of 5.
Arena et al.26 reported the advantages of CZZ compared to CZA systems in the scope of CO2 hydrogenation. Extensive studies of a CuO/ZnO/ZrO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H-FER 20 (CZZ/FER) catalyst system revealed that the catalyst system showed promising activity for flexible conversion of both CO-rich and CO2-rich syngas to DME, as well as superior activity compared to a commercial CZA system,27,28 confirming the aforementioned favorable activity of Zr-promoted Cu/ZnO systems in CO2-rich environments. A comparison of the dehydration properties of γ-Al2O3 and FER at different CO2/COx syngas ratios shows that DME selectivity is less affected for both in CO-rich and CO2-rich syngas when FER is used,27,29 suggesting that even at higher CZZ ratios, better COx conversion and thus higher DME yields are possible. Based on the current state of knowledge, a detailed understanding of the dependency of the process variable conversion and selectivity at large CZZ/FER ratios is of great interest. Besides, the dependence on the syngas composition is important as both CO and CO2 can be converted27 and the transition from WGS (R3) to the rWGS reaction is observable to reveal the respective correlations between the catalyst bed composition and CO/CO2 hydrogenation ((R1) and (R2)).
H-FER 20 (CZZ/FER) catalyst system revealed that the catalyst system showed promising activity for flexible conversion of both CO-rich and CO2-rich syngas to DME, as well as superior activity compared to a commercial CZA system,27,28 confirming the aforementioned favorable activity of Zr-promoted Cu/ZnO systems in CO2-rich environments. A comparison of the dehydration properties of γ-Al2O3 and FER at different CO2/COx syngas ratios shows that DME selectivity is less affected for both in CO-rich and CO2-rich syngas when FER is used,27,29 suggesting that even at higher CZZ ratios, better COx conversion and thus higher DME yields are possible. Based on the current state of knowledge, a detailed understanding of the dependency of the process variable conversion and selectivity at large CZZ/FER ratios is of great interest. Besides, the dependence on the syngas composition is important as both CO and CO2 can be converted27 and the transition from WGS (R3) to the rWGS reaction is observable to reveal the respective correlations between the catalyst bed composition and CO/CO2 hydrogenation ((R1) and (R2)).
To the best of our knowledge, such a broad range of operating conditions has not been studied or modeled yet. Our hypothesis is that important impulses for further process development will be derived from the knowledge of syngas composition dependencies. Herein, we investigate the catalyst bed composition of the system CZZ/FER at different process parameters, i.e. the CO2 content in the synthesis gas, temperature and space time. To describe and simulate a wide operating range, a kinetic model was developed to calculate an optimized CZZ/FER ratio within the studied operating conditions. The model is also applied for predicting the process performance at industrially relevant operating cases.
For CO2 hydrogenation to DME, Ren et al.24 showed that the mixing method of the catalyst components (CZA/HZSM-5) has a minor impact on conversion and the DME yield but significantly influences catalyst stability. Similarly, in a CO-rich environment as reported by García-Trenco et al.,23 slightly increased conversion is observed with a physically mixed bed compared to a hybrid mixed bed configuration. It has also been reported30,31 that due to closer contact within a hybrid catalyst, Cu and even Zn ion migration from the MeOH-forming catalyst into the dehydration component may occur, reducing both acidity and the available Cu and Cu/Zn surface areas. Also, increased Cu migration into the zeolite pores was found by Fierro et al.32 at elevated water vapour concentrations. Accordingly, a higher CO2 feed content should increase Cu migration due to enhanced water production via the rWGS reaction (R3). In order to reduce these transport effects, the catalytic components used in this work were separately pressed, sieved and subsequently physically mixed, as described afterwards.
Experimental
Catalyst preparation
The CZZ catalyst was prepared by a continuous co-precipitation method from metal nitrate and sodium bicarbonate solutions resulting in pH 7 using a micro jet mixer.28 The suspension was then aged at 313 K for 2 h. The solids were filtered, dried at 383 K for 16 h and calcined at 623 K with 3 K min−1 for 4 h. Characterization techniques used were described in a previous work.28 A commercial ferrierite-type zeolite H-FER 20 (FER) from Zeolyst International with a Si/Al ratio of 20 was used as a dehydration catalyst. Before use, FER was calcined at 823 K for 4 h in air.Catalyst characterization
Selected chemical and physical data of the CZZ catalyst are shown in Table 4. The XRD analysis of the CZZ catalyst precursor and the calcined pre-catalyst can be found in chapter S9.† Physico-chemical properties of FER are taken from a study by Kim et al.33 and shown in Table 5.Catalytic activity study
Each catalyst component was finely powdered, pressed and sieved into fractions of 250–500 μm, followed by physical mixing of the components in the required mass ratio. The studied catalytic bed configurations are summarized in Table 2. Within this sieve fraction, the bulk density amounts to 882.5 kg m−3 for CZZ and to 415.0 kg m−3 for FER.| Catalyst bed no. [—] | CZZ [wt%] | FER [wt%] | CZZ [vol%] | FER [vol%] |
|---|---|---|---|---|
| CB 1 | 50.0 | 50.0 | 32.0 | 68.0 |
| CB 2 | 81.2 | 18.8 | 67.0 | 33.0 |
| CB 3 | 89.5 | 10.5 | 80.0 | 20.0 |
| CB 4 | 95.0 | 5.0 | 90.0 | 10.0 |
| CB 5 | 98.6 | 1.4 | 97.0 | 3.0 |
The catalyst beds were 100 ± 1 mm in length. The physical mixtures were diluted with silicon carbide (SiC, Hausen Mineraliengroßhandel GmbH) of the same grain size as the catalyst components for isothermal operation. To ensure an adequate grain distribution of the catalytic components CZZ, FER and SiC, the beds were filled as five-fold stacks. The catalyst bed volume was constant at 4.20 ml. At the top and bottom of the beds, additional SiC layers were placed.
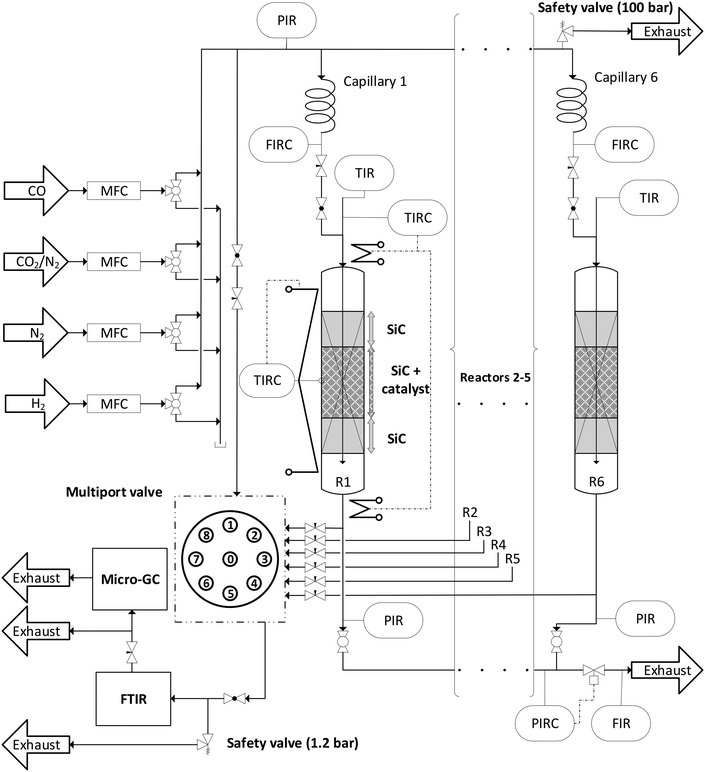
Direct DME synthesis was performed in a self-constructed parallel reactor system “MURSS” (multi-reactor-screening-system, see Fig. 1 and S2†) with stainless steel fixed bed reactors (inner diameter: 17.4 mm; length: 600 mm). Each reactor can be independently heated with heating cartridges and brass jaws over a length of 400 mm. A catalyst bed temperature profile is measured using axial thermocouples. Gas supply is controlled using mass flow controllers (Bronkhorst Hi-Tec). Feed gases, carbon monoxide (CO, 99.97 vol%), nitrogen (N2, 99.9999 vol%), hydrogen (H2, 99.9999 vol%) and a mixture carbon of CO2/N2 (50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 ± 1.0 vol%), were supplied by Air Liquid Germany GmbH. The total inlet gas flow is distributed via a capillary system, with fine flow adjustment by flow meters before each reactor. A volume fraction of approx. 5 vol% of the reactor outlet gas flows and the bypass flow is directed to a multi-position valve (Valco), which is connected to a FTIR CX4000 (Gasmet Technologies Oy) equipped with a micro gas chromatograph (Inficon Micro GC Fusion). The GC is equipped with two thermal conductivity (TCD) detectors connected to RT-Molsieve 5A, 0.25 mm (10 m) and RT-Q-Bond, 0.25 mm (12 m) columns. Each operating point was held for 200 min and the catalyst beds were measured consecutively. After finishing the variation loops of CO2/COx values for each temperature, the reactor was purged with N2 for one hour (the general sequence of the process parameters is shown in Fig. S1†).
50 ± 1.0 vol%), were supplied by Air Liquid Germany GmbH. The total inlet gas flow is distributed via a capillary system, with fine flow adjustment by flow meters before each reactor. A volume fraction of approx. 5 vol% of the reactor outlet gas flows and the bypass flow is directed to a multi-position valve (Valco), which is connected to a FTIR CX4000 (Gasmet Technologies Oy) equipped with a micro gas chromatograph (Inficon Micro GC Fusion). The GC is equipped with two thermal conductivity (TCD) detectors connected to RT-Molsieve 5A, 0.25 mm (10 m) and RT-Q-Bond, 0.25 mm (12 m) columns. Each operating point was held for 200 min and the catalyst beds were measured consecutively. After finishing the variation loops of CO2/COx values for each temperature, the reactor was purged with N2 for one hour (the general sequence of the process parameters is shown in Fig. S1†).
Reduction of the CZZ catalyst volume fraction was performed at 2 bar with 5 vol% H2 diluted in N2, while temperature was increased from 373 K to 473 K with a ramp of 10 K h−1, followed by further heating to a final reduction temperature of 493 K with 50/50 vol% H2/N2 at a rate of 10 K h−1. After another 60 min, the reactor was purged with N2, cooled to 483 K and, subsequently the pressure increased to 30 bar. The feed gas composition was H2/COx/N2 = 45/20/35 vol%, and the considered CO and CO2 feed concentrations respectively CO2/COx inlet ratios are shown in Table 3. Before kinetic measurements, the catalyst beds were exposed to a run-in period of 75 h time on stream (ToS) by varying the temperature (493, 503, and 513 K), CO2/COx inlet ratio (0.4, 0.7, and 0.9) and gas hourly space velocity (GHSV) (2.78 and 3.57 s−1) at 30 bar. These measurements were used for the validation of the optimized catalyst bed ratio. The kinetic measurements were performed at each feed gas composition shown in Table 3, with temperatures between 483 and 513 K and two GHSV values of 2.78 and 3.57 s−1 with regard to the catalyst volume.
| CO2/COx | CO/vol% | CO2/vol% |
|---|---|---|
| 0.40 | 12.0 | 8.0 |
| 0.60 | 8.0 | 12.0 |
| 0.70 | 6.0 | 14.0 |
| 0.75 | 5.0 | 15.0 |
| 0.80 | 4.0 | 16.0 |
| 0.90 | 2.0 | 18.0 |
Experimental error analysis
Before starting the kinetic investigations, the experimental error of the novel system (Fig. 1) was estimated to verify that the data quality in parallel operation is in a similar range to when using a single PFR system. The error caused by an unequal flow distribution via the capillary system is in the range of ±1.2–1.5%. The complete error analysis and the error estimation can be found in S3.†Performance indicators
In all experiments, the carbon balance (eqn (S1)†) presented a maximum deviation of ±3%. The COx conversion is calculated as follows (eqn (1)):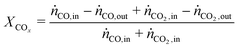 | (1) |
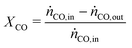 | (2) |
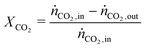 | (3) |
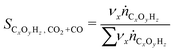 | (4) |
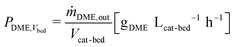 | (5) |
 | (6) |
Kinetic model development
Kinetic description of the direct DME synthesis is based on the six-parameter model for the MeOH synthesis from Lacerda de Oliveira Campos et al.,34 which has been extended to include the MeOH dehydration step.In the MeOH synthesis model, only CO2 hydrogenation (eqn (7)) and the rWGS reaction (eqn (8)) are considered, as theoretical studies suggest that direct CO hydrogenation is not significant at a moderate or high CO2 content.35,36 The reaction rates of CO2 hydrogenation (rCO2 mol s−1) and rWGS (rrWGS mol s−1) are shown as follows:
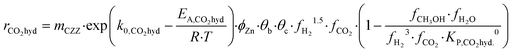 | (7) |
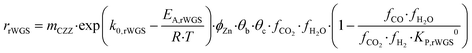 | (8) |
The fugacity coefficients are calculated with the Peng–Robinson equation, using binary interaction parameters and other parameters from the literature.40,41 The free sites θb and θc are calculated as follows:
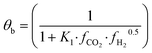 | (9) |
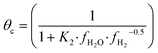 | (10) |
| Z–H + CH3OH(g) ⇄ Z–H–CH3OH | (11) |
| Z–H–CH3OH + CH3OH(g) ⇄ CH3OCH3(g) + H2O(g) + Z–H | (12) |
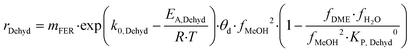 | (13) |
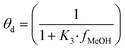 | (14) |
The estimation of the kinetic parameters is done by solving an optimization problem, where the objective function is the minimization of the normalized squared errors of the prediction (ŷiout,j) of the carbonaceous compounds (CO, CO2, MeOH and DME), the so-called chi-squared (χ2) regression method. The normalization with experimental yiout,i squared values is performed to prevent overweighting of high conversion points and underweighting of low conversion points.
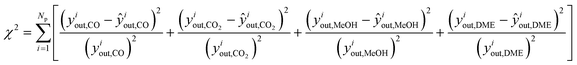 | (15) |
In order to figure out the best parameter set and to calculate the confidence intervals, a 5-fold cross validation (CV) method was used.43,44 The 240 experimental points were randomly divided into five groups of 48 points each, and the optimization problem was solved five times, each one with four of the five groups as a training set, resulting in five sets of parameters. The group of parameters with which the model has the lowest χ2 value for the total 240 points is chosen as the best one. The confidence interval (CI) of each parameter is derived by calculating the standard deviation of each parameter considering the five parameter sets and multiplying by the t-student factor (0.05 two-tail significance and 232 degrees of freedom). The optimization problems are solved with the Matlab function fminsearch (varying the starting values).
The 5-fold cross validation (CV(5)) value is a mean value of the χ2 five different parameter sets (eqn (16)). The closer it is to the χ2 value of the best fit, the better the model should simulate experiments outside the training set.
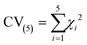 | (16) |
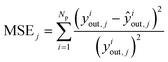 | (17) |
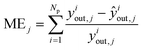 | (18) |
Results and discussion
Model validation
The group of parameters with the best fit and the respective CI are shown in Table 6, with all eight parameters being statistically significant. The statistical evaluation of the chosen parameter set is shown in Table 7, with a total χ2 of 3.406 for the best fit and a CV(5) of 3.439. The CV(5) value is close to the best χ2, which suggests that the model can adequately simulate experiments outside the training set.The MSE and ME of all optimized species are significantly low, with MeOH and DME showing mean errors of only 7% and 5%, respectively. The MSE and ME values of the training and the validation sets are significantly close, which also points to the good performance of the model outside the training region.
In Fig. 2, parity plots are shown correlating the experiments and simulated results using the best-fit parameter set shown in Table 6.
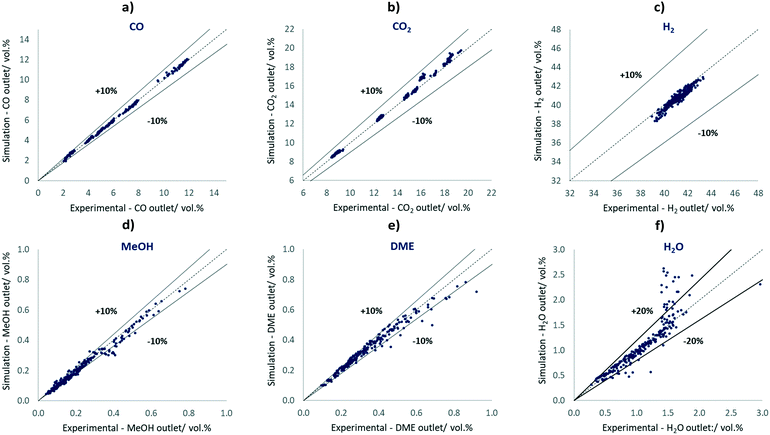 | ||
| Fig. 2 Parity plots of CO, CO2, H2, MeOH, DME and H2O comparing the 240 simulated results with the respective experimental results. | ||
The simulated concentrations are mostly located inside the ±10% lines of the experimental values, including all H2 points, all CO points, all CO2 points, 74% of the MeOH points, and 87% of the DME points. In the parity plot of H2O, 86% of the points are within ±20% lines. The experiments seem to be affected by H2O concentrations above 1.5 vol% as a result of condensation effects, most likely due to the pressure-affected analysis stage as well as dead volumes or cold spots. Therefore, condensation of mainly water, but also of MeOH at higher product concentrations may occur. In our study, however, only 12.5% of all points are within this concentration range.
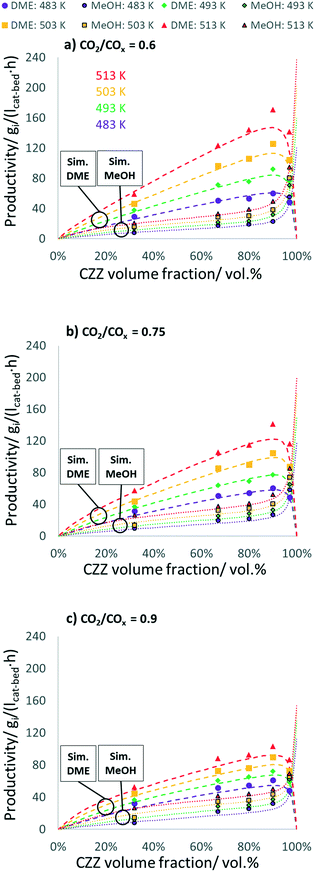
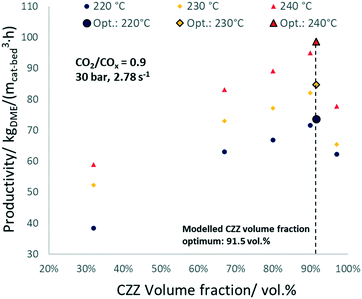
In Fig. 3, experimental and simulated DME and MeOH productivities are shown as a function of CZZ volume fraction (ζCZZ) for the following operating conditions: CO2/COx inlet ratios of 0.6 (a), 0.75 (b) and 0.9 (c) at 30 bar, 2.78 s−1 and 483–513 K in steps of 10 K in between (further CO2/COx inlet ratios are shown in the ESI†).
The dashed lines correspond to the simulated values and the dots correspond to the experimentally measured productivities for MeOH (framed dots) and DME (unframed dots), respectively. The model simulates the trends adequately, with slight underestimations of the DME productivity at 513 K. Here, non-isothermal bed temperature can be excluded from axial temperature measurements with maximum ΔT values of 1.1 K (Fig. S13†).
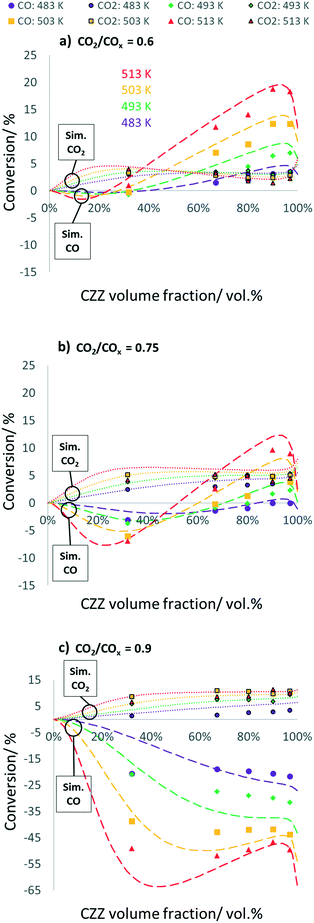
In Fig. 4, CO and CO2 conversions are shown, each as a function of ζCZZ for the following operating conditions: CO2/COx inlet ratios of 0.6 (a), 0.75 (b) and 0.9 (c) at 30 bar, 2.78 s−1, and 483–513 K (further CO2/COx inlet ratios are shown in Fig. S7†). The CO and CO2 conversions are adequately predicted by the kinetic model. At a CO2/COx feed of 0.90, there are some deviations from the experimentally measured CO conversion, probably due to the fact that the initial CO concentration is low, which leads to an amplification of the small deviations in the final CO concentration when calculating the corresponding CO conversion.
DME productivity vs. CZZ/FER variation
From the results shown in Fig. 3, it can be observed that an increase in temperature leads to a largely uniform increase in the productivity of DME and MeOH, indicating a strong kinetically controlled operating regime, additionally evidenced by the wide gap from the thermodynamic equilibrium (Fig. S10†). With a ζCZZ of 0 vol%, no MeOH is formed and the subsequent MeOH dehydration cannot take place and, as a result, no DME is produced. With increasing ζCZZ, both MeOH and consequently DME are formed. Further increasing ζCZZ up to ca. 90 vol% enhances MeOH and DME productivities, whereby different temperatures or CO2/COx inlet ratios slightly shift the optimum towards more or less CZZ content (see Fig. 7). This indicates that, for ζCZZ up to ca. 90 vol%, FER is in excess, which means that the MeOH dehydration is running close to equilibrium. In this operating region, the rate of the reaction system is controlled only by the MeOH synthesis (over CZZ). A further increase of ζCZZ leads to a marked decrease in DME productivity and, accordingly, to a sharp increase in non-dehydrated MeOH. This suggests that FER is not in excess anymore, which means that neither the MeOH synthesis nor the MeOH dehydration are in equilibrium, and the rates of the reaction system are determined by both CZZ and FER masses.High MeOH dehydration activity, as shown here with a FER catalyst component, was similarly reported by Peláez et al.17 with a variation of the CZA/γ-Al2O3 catalyst system. In their study, a highest DME yield was achieved with a CO2-free syngas at a CZA/γ-Al2O3 ratio of 92.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7.5 wt%, being close to the experimental CZZ/FER optimum of 95
7.5 wt%, being close to the experimental CZZ/FER optimum of 95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 wt% reported in this work. In this context, it should be noted that changing the COx source from CO to CO2 increases water production (R3) typically leading to a rapid decrease in dehydration performance when γ-Al2O3 is used.19,21,27,29 In comparison, when the dehydration of MeOH takes place over a solid acid component with fewer Lewis acid sites (known to adsorb water) such as FER,15,27 HZSM5 (ref. 45–47) or SAPO,48 high DME productivity can be maintained even at an increased CO2 content in syngas or in the presence of increased water content. In our study, increasing the CO2 feed content leads to decreased DME productivity (Fig. 3a–c), being more evident at higher temperatures. Since the thermodynamic influence can be largely ruled out in this operating range (Fig. S10†), it is a kinetically controlled phenomenon. A temperature-controlled decrease in DME and MeOH productivities by increasing the CO2 content is explained by Sahibzada et al.49 arguing that the lower concentrations of products under differential conditions (low conversion) are less inhibiting MeOH production from CO2.
5 wt% reported in this work. In this context, it should be noted that changing the COx source from CO to CO2 increases water production (R3) typically leading to a rapid decrease in dehydration performance when γ-Al2O3 is used.19,21,27,29 In comparison, when the dehydration of MeOH takes place over a solid acid component with fewer Lewis acid sites (known to adsorb water) such as FER,15,27 HZSM5 (ref. 45–47) or SAPO,48 high DME productivity can be maintained even at an increased CO2 content in syngas or in the presence of increased water content. In our study, increasing the CO2 feed content leads to decreased DME productivity (Fig. 3a–c), being more evident at higher temperatures. Since the thermodynamic influence can be largely ruled out in this operating range (Fig. S10†), it is a kinetically controlled phenomenon. A temperature-controlled decrease in DME and MeOH productivities by increasing the CO2 content is explained by Sahibzada et al.49 arguing that the lower concentrations of products under differential conditions (low conversion) are less inhibiting MeOH production from CO2.
CO and CO2 conversion vs. CZZ/FER variation
For a CO2/COx inlet ratio of 0.6 (Fig. 4a), an increase in ζCZZ leads to an increase in CO2 conversion up to a ζCZZ of approx. 30 vol%. At ζCZZ values below 32 vol%, the CO2 conversion is higher than the CO conversion. Below a ζCZZ of approx. 23 vol%, CO is produced in small amounts. A further increase of ζCZZ has a beneficial effect on CO conversion up to a ζCZZ value of about 95 vol%. Analogously, the CO2 conversion decreases slightly. This effect is mainly caused by the fact that the increased MeOH formation leads to increased MeOH dehydration (R4) and thus water formation. The produced water allows higher CO conversion via the accelerated WGS reaction (R3) to CO2 and H2, partially regenerating the consumed CO2. At ζCZZ above approx. 95 vol%, less DME and consequently water are formed, resulting in a reduced WGS reaction rate and thus decreasing CO conversion, leading to a slightly increased CO2 conversion.An increase in the CO2/COx inlet ratio to 0.75 shows a similar pattern for CO and CO2 conversion (Fig. 4b) with shifts toward more CO formation at lower ζCZZ values and less CO conversion at higher ζCZZ values, these effects being even more pronounced at higher reaction temperatures. At ζCZZ values above ca. 35%, the CO2 conversion shows almost constant values at the respective measured temperatures, showing that the WGS reaction rate is lowered by less CO in the syngas feed (R3).
Further increasing the CO2/COx inlet ratio to 0.9 (Fig. 4c) leads to a pattern where CO is unexceptionally formed over the entire CZZ/FER variation range via the rWGS reaction (R3). The CO2 conversion is favoured by an increased ζCZZ value, but to a smaller extent than the CO conversions at lower CO2/COx inlet ratios (Fig. 4a and b). A further potential increase in CO2 conversion with an optimized CZZ/FER ratio is probably limited by increased water formation from the rWGS reaction occupying the active sites (Cu/Zn) at the CZZ catalyst.35,36
In summary, the increase of CO2 conversion with optimized ζCZZ is limited due to water formation by CO2 hydrogenation and MeOH dehydration, accelerating the WGS reaction and preventing the enhancement of CO2 conversion, whereby this effect being more pronounced at increased temperature. An increase of CO2 conversion at higher ζCZZ values should be possible by in situ water removal, e.g. with a membrane reactor system50,51 or by doping the CZZ catalyst aiming at stronger binding of formate to the Cu sites, which could inhibit the rWGS reaction and thus accelerate CO2 hydrogenation on the Cu/Zn sites.36
MeOH and DME selectivity vs. CZZ/FER variation
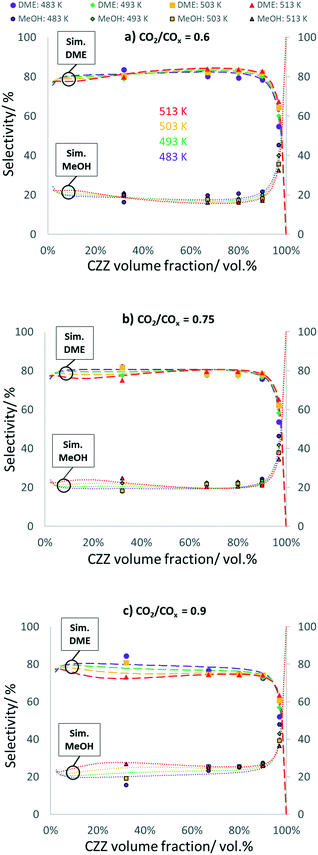
In Fig. 5, DME and MeOH selectivities are shown as a function of ζCZZ for the following operating conditions: CO2/COx inlet ratios of 0.6 (a), 0.75 (b) and 0.9 (c) at 30 bar, 2.78 s−1, and 483–513 K, (further CO2/COx inlet ratios are shown in Fig. 8). A similar pattern can be seen for each CO2/COx inlet ratio investigated: high and constant DME selectivities for ζCZZ up to ca. 90 vol% and a sharp decrease of DME when ζCZZ is increased above 90 vol%.A higher CO2 content in the feed slightly decreases DME selectivity, e.g. for ζCZZ = 90 vol%: from 82% (CO2/COx = 0.6) to 75% (CO2/COx = 0.9). The temperature influence on selectivity is not very pronounced. However, for ca. ζCZZ < 25 vol% at CO2/COx = 0.6, for ca. ζCZZ < 50 vol% at CO2/COx = 0.75, and for ca. ζCZZ < 90 vol% at CO2/COx = 0.9, temperature negatively affects DME selectivity. Since for ca. ζCZZ < 90 vol% MeOH dehydration is in equilibrium, the selectivities of MeOH and DME will be affected when this equilibrium is disturbed.
As MeOH dehydration is slightly exothermic (R4), an increase in temperature should directly decrease DME selectivity. Nevertheless, increased temperature is affecting DME selectivity in a more pronounced way by influencing the rWGS reaction (R3) and CO2 hydrogenation (R2) and thus the water concentration/selectivity (see Fig. S9†). The patterns of the respective water selectivities (eqn (S15)†) clearly display that the changes of DME selectivities follow the inverse trend of the water selectivities.
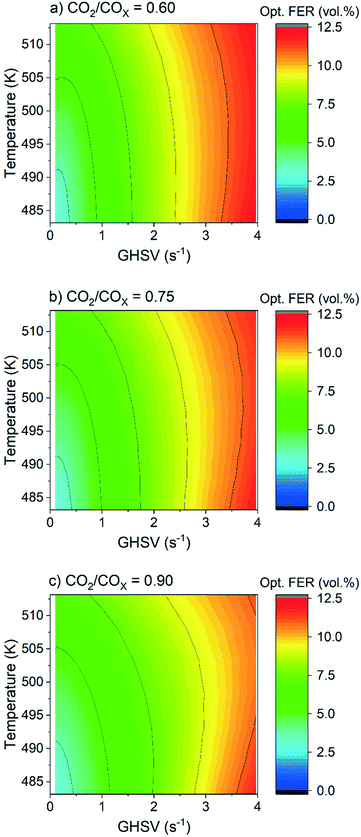
Optimized CZZ/FER ratio
The validated kinetic model was used to find the optimum FER amount with respect to the highest DME productivity. For a CO2-rich feed (CO2/COx = 0.9), 30 bar, and 2.78 s−1, an optimal ζCZZ value of 91.5 vol% was found, with a temperature variation (493–513 K) having only marginal influence under these operating conditions (see Fig. 7c). This simulated optimum ζCZZ value was experimentally validated, following the same run-in period as the catalyst beds in Table 2. Fig. 6 shows the DME productivities of the run-in period (unframed dots) and the experimental validation of the model-based optimized catalyst bed (framed dots).Compared to the catalyst bed with the highest experimental DME productivity (ζCZZ = 90 vol%), the simulated optimal value (ζCZZ = 91.5 vol%) achieved a slight relative increase in DME productivity at all measured temperatures: 493 K (2.9%), 503 K (3.2%), and 513 K (3.8%). Since the present model adequately simulated the experiments, it is applied to investigate the optimum FER volume fraction (ζFER) within a broader GHSV range, including industrially relevant operating conditions. In Fig. 7, the optimized FER amounts are shown at 30 bar and CO2/COx inlet ratios of 0.6 (a), 0.75 (b) and 0.9 (c) and under a variation of temperature and GHSV. The FER optimum value is mostly affected by the GHSV, with less FER being necessary for lower GHSV (achieving ζFER values lower than 5 vol%). Increasing the temperature slightly increases the FER optimum amount, while increasing the CO2 content in the feed marginally decreases the FER optimum amount. Since lower GHSV leads to increased COx conversion and thus enhanced DME production, higher water accumulation is expected. The lower FER amount required for an optimized DME productivity at lower GHSV is therefore a hint that the activity of FER is less affected by water accumulation than the activity of CZZ. This hypothesis is supported by the fact that the optimum FER amount is slightly lower for higher CO2/COx inlet ratios (cf.Fig. 7a–c), which also increase water formation.
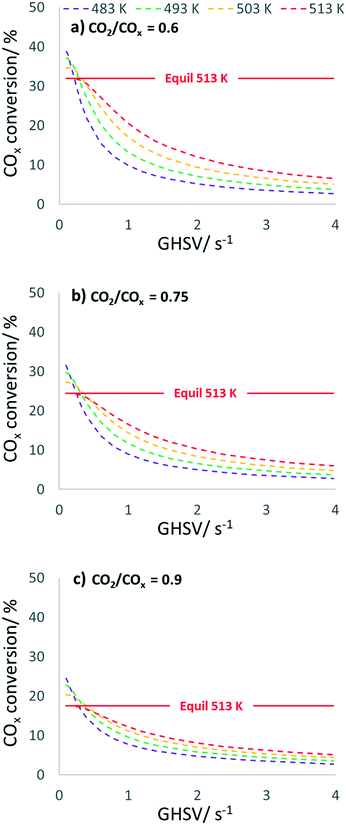
In Fig. 8, COx conversion is plotted against the GHSV under the same conditions considered in Fig. 7. The GHSV variation shows a clearly kinetically dominated range between 1 and 4 s−1, while an increase in the thermodynamic control is expected as GHSV decreases, with COx conversion achieving its equilibrium at 513 K.
By using process parameters of 513 K and a CO2/COx inlet ratio of 0.6, a GHSV of 0.4 s−1 leads to 95.8% of the thermodynamically possible COx conversion (XCOx,equil = 31.9%) at a DME selectivity of 90.1%, while CO2/COx = 0.75 affords 95.4% of the possible conversion (XCOx,equil = 24.4%) at a DME selectivity of 87.4%, and CO2/COx = 0.9 affords 94.8% of the possible conversion (XCOx,equil = 17.6%) at a DME selectivity of 83.4%. A GHSV of 0.4 s−1 corresponds to a seven times lower volume flow, chosen in the kinetic measurements presented here. Further simulations were performed at 60 bar and without N2 dilution (H2/CO/CO2 in the feed = 70/12/18 vol%), i.e. closer to industrial conditions. Although this requires a greater extrapolation of our model, the preliminary and interesting finding is that in this case probably even lower amounts of FER (less than 3 vol%) already ensure efficient DME production. From simulation at 513 K, such an optimized CZZ/FER bed ratio enables a COx conversion of more than 47% at a GHSV below 0.4 s−1 (Fig. S11 and S12†), which corresponds to 90.3% of the thermodynamically possible COx conversion (XCOx,equil = 52.2%) at a DME selectivity of 88.9%. Further experimental validation in this operating range would be valuable to back up these promising simulated results.
Other CZZ catalysts with different properties (cf.Table 4) as well as ferrierites (cf.Table 5) with other Si/Al ratios would require a refit of the parameter set (Table 6) and possibly a new evaluation of the result interpretation.
| Catalyst | Cu/wt% | Zn/wt% | Zr/wt% | S BET/m2 g−1 | S Cu/m2 g−1 | d CuO/nm calcined catalyst |
|---|---|---|---|---|---|---|
| d CuO: CuO crystallite size (XRD). SCu: specific copper surface area (N2O-RFC). SBET: Brunauer–Emmett–Teller (BET) surface area. | ||||||
| CZZ | 62 | 31 | 7 | 98 | 36 | 7 |
| Catalyst | S BET/m2 g−1 | NH3-TPD peak positon/K | Acid amount/mmol NH3 per gcat | |||
|---|---|---|---|---|---|---|
| LT region | HT region | Total acidity | LT region | HT region | ||
| FER | 390 | 481 | 656 | 0.70 | 0.31 | 0.39 |
Conclusions
Kinetic experiments for direct DME synthesis were carried out under various operating conditions, with particular emphasis on the CZZ/FER bed composition. A new kinetic model was developed and validated with a vast array of experimental data. It was applied in model-based optimization to determine the optimal FER volume fraction with respect to DME productivity under the variation of temperature, GHSV and CO2/COx inlet ratios. An optimum CZZ/FER catalyst bed ratio (91.5/8.5 vol%) for a CO2-rich feed was calculated with the model and then validated experimentally verifying that the results obtained from the optimization are accurate. Extrapolations of the model to process conditions closer to industrially relevant conditions showed that the optimal FER volume fraction actually decreases at lower GHSV. From these findings, the necessity for additional validation beyond the scope of the present study is derived, which is the subject of current investigations. Our experiments, together with the results from modelling also underline that water formation from MeOH dehydration accelerates the WGS reaction regenerating CO2. This at first prevents a significant increase of CO2 conversion with an optimized catalyst bed, which is why alternative reactor concepts where water can be separated in situ, e.g. membrane reactors, appear promising. In the outlook for a further possibility to increase CO2 conversion, a catalyst modification (e.g., with promoters) could be purposeful, which strengthens binding of the intermediate formate to the Cu sites, which otherwise inhibit the rWGS reaction and thus accelerate CO2 hydrogenation over Cu/Zn. We believe that the model presented here is particularly well suited to describe and predict the reaction kinetics and to support the search for an optimal reactor and/or process design for direct DME synthesis due to its broad range of validity.| k 0,CO2 | k 0,rWGS | k 0,DME | E A,CO2 | E A,rWGS | K 1 | K 2 | K 3 | |
|---|---|---|---|---|---|---|---|---|
| [—] | [—] | [—] | kJ mol−1 | kJ mol−1 | Bar−1.5 | Bar−0.5 | Bar−1 | |
| Best-fit | 9.57 | 26.23 | 3.08 | 75.53 | 119.71 | 0.38 | 8.28 | 52.92 |
| CI± | 0.44 | 2.43 | 0.54 | 2.29 | 9.44 | 0.14 | 0.90 | 30.14 |
| Statistics | All points | Training | Validation |
|---|---|---|---|
| χ 2 | 3.406 | 2.954 | 0.452 |
| MSE – CO | 5.02 × 10−4 | 4.81 × 10−4 | 5.87 × 10−4 |
| MSE – CO2 | 4.57 × 10−4 | 3.80 × 10−4 | 7.64 × 10−4 |
| MSE – MeOH | 8.89 × 10−3 | 9.78 × 10−3 | 5.33 × 10−3 |
| MSE – DME | 4.34 × 10−3 | 4.74 × 10−3 | 2.74 × 10−3 |
| ME – CO | 0.0154 | 0.0149 | 0.0171 |
| ME – CO2 | 0.0144 | 0.0130 | 0.0199 |
| ME – MeOH | 0.0689 | 0.0726 | 0.0541 |
| ME – DME | 0.0502 | 0.0527 | 0.0404 |
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the Helmholtz Association for funding this research (Research Programme “Storage and Cross-linked Infrastructures”, Topic “Synthetic Hydrocarbons”). We thank the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES) for financing the PhD scholarship of Bruno Lacerda de Oliveira Campos (Process Number: 88881.174609/2018-01). We kindly acknowledge the support of TVT-KIT group, analytics and chemical laboratory colleagues and especially Sabrina Polierer and Lucas Warmuth from IKFT-KIT for their support in characterization.References
- N. Dahmen, U. Arnold, N. Djordjevic, T. Henrich, T. Kolb, H. Leibold and J. Sauer, J. Supercrit. Fluids, 2015, 96, 124–132 CrossRef CAS.
- A. Varone and M. Ferrari, Renewable Sustainable Energy Rev., 2015, 45, 207–218 CrossRef.
- A. Buttler and H. Spliethoff, Renewable Sustainable Energy Rev., 2018, 82, 2440–2454 CrossRef CAS.
- G. A. Olah, A. Goeppert and G. S. Prakash, J. Org. Chem., 2009, 74, 487–498 CrossRef CAS PubMed.
- E. Catizzone, G. Bonura, M. Migliori, F. Frusteri and G. Giordano, Molecules, 2018, 23, 1–31 Search PubMed.
- B. V. Ga and P. Q. Thai, Appl. Sci., 2020, 10, 3416–3434 CrossRef.
- M. R. Gogate, Pet. Sci. Technol., 2018, 36, 562–568 CrossRef CAS.
- Z. Azizi, M. Rezaeimanesh, T. Tohidian and M. R. Rahimpour, Chem. Eng. Process., 2014, 82, 150–172 CrossRef CAS.
- V. Dieterich, A. Buttler, A. Hanel, H. Spliethoff and S. Fendt, Energy Environ. Sci., 2020, 13, 3207–3252 RSC.
- S. Ahlgren, A. Baky, S. Bernesson, Å. Nordberg, O. Norén and P. A. Hansson, Biosyst. Eng., 2008, 99, 145–155 CrossRef.
- J. Ereña, I. Sierra, A. T. Aguayo, A. Ateka, M. Olazar and J. Bilbao, Chem. Eng. J., 2011, 174, 660–667 CrossRef.
- Y. Wang, H. Liu, H. Zhang and W. Ying, React. Kinet., Mech. Catal., 2016, 119, 585–594 CrossRef CAS.
- S. M. K. Aboul-Fotouh, L. I. Ali, M. A. Naghmash and N. A. K. Aboul-Gheit, J. Fuel Chem. Technol., 2017, 45, 581–588 CrossRef CAS.
- M. Sánchez-Contador, A. Ateka, P. Rodriguez-Vega, J. Bilbao and A. T. Aguayo, Ind. Eng. Chem. Res., 2018, 57, 1169–1178 CrossRef.
- F. Frusteri, M. Migliori, C. Cannilla, L. Frusteri, E. Catizzone, A. Aloise, G. Giordano and G. Bonura, J. CO2 Util., 2017, 18, 353–361 CrossRef CAS.
- R. Ahmad, D. Schrempp, S. Behrens, J. Sauer, M. Döring and U. Arnold, Fuel Process. Technol., 2014, 121, 38–46 CrossRef CAS.
- R. Peláez, P. Marín and S. Ordóñez, Fuel Process. Technol., 2017, 168, 40–49 CrossRef.
- J. Guang-xin, M. Hong-bin, T. Yi-sheng and H. Yi-zhuo, Ind. Eng. Chem. Res., 2005, 44, 2011–2015 CrossRef.
- C. Peinado, D. Liuzzi, M. Retuerto, J. Boon, M. A. Peña and S. Rojas, Chemical Engineering Journal Advances, 2020, 4, 100039–100047 CrossRef.
- J.-W. Bae, H. S. Potdar, S.-H. Kang and K.-W. Jun, Energy Fuels, 2008, 22, 223–230 CrossRef CAS.
- N. Delgado Otalvaro, G. Sogne, K. Herrera Delgado, S. Wild, S. Pitter and J. Sauer, RSC Adv., 2021, 11, 24556–24569 RSC.
- J. Abu-Dahrieh, D. Rooney, A. Goguet and Y. Saih, Chem. Eng. J., 2012, 203, 201–211 CrossRef CAS.
- A. García-Trenco, A. Vidal-Moya and A. Martínez, Catal. Today, 2012, 179, 43–51 CrossRef.
- S. Ren, S. Li, N. Klinghoffer, M. Yu and X. Liang, Carbon Resour. Convers., 2019, 2, 85–94 CrossRef CAS.
- G. Jia, Y. Tan and Y. Han, Ind. Eng. Chem. Res., 2006, 45, 1152–1159 CrossRef CAS.
- F. Arena, K. Barbera, G. Italiano, G. Bonura, L. Spadaro and F. Frusteri, J. Catal., 2007, 249, 185–194 CrossRef CAS.
- S. Wild, S. Polierer, T. A. Zevaco, D. Guse, M. Kind, S. Pitter, K. Herrera Delgado and J. Sauer, RSC Adv., 2021, 11, 2556–2564 RSC.
- S. Polierer, D. Guse, S. Wild, K. Herrera Delgado, T. N. Otto, T. A. Zevaco, M. Kind, J. Sauer, F. Studt and S. Pitter, Catalysts, 2020, 10, 816–833 CrossRef CAS.
- E. Catizzone, M. Migliori, A. Purita and G. Giordano, J. Energy Chem., 2019, 30, 162–169 CrossRef.
- B. Voss, A. Katerinopoulou, R. Montesano and J. Sehested, Chem. Eng. J., 2019, 377, 121940 CrossRef CAS.
- S. Guffanti, C. G. Visconti and G. Groppi, Ind. Eng. Chem. Res., 2020, 59, 14252–14266 CrossRef CAS.
- G. Fierro, G. Ferraris and G. Moretti, Appl. Catal., B, 2009, 91, 499–506 CrossRef CAS.
- Y. T. Kim, K.-D. Jung and E. D. Park, Microporous Mesoporous Mater., 2010, 131, 28–36 CrossRef CAS.
- B. Lacerda de Oliveira Campos, K. Herrera Delgado, S. Pitter and J. R. Sauer, Ind. Eng. Chem. Res., 2021, 60, 15074–15086 CrossRef CAS.
- F. Studt, M. Behrens, E. L. Kunkes, N. Thomas, S. Zander, A. Tarasov, J. Schumann, E. Frei, J. B. Varley, F. Abild-Pedersen, J. K. Nørskov and R. Schlögl, ChemCatChem, 2015, 7, 1105–1111 CrossRef CAS.
- B. Lacerda de Oliveira Campos, K. Herrera Delgado, S. Wild, F. Studt, S. Pitter and J. Sauer, React. Chem. Eng., 2021, 6, 868–887 RSC.
- J. D. Grunwaldt, A. M. Molenbroek, N. Y. Topsøe, H. Topsøe and B. S. Clausen, J. Catal., 2000, 194, 452–460 CrossRef CAS.
- S. Kuld, M. Thorhauge, H. Falsig, C. F. Elkjær, S. Helveg, I. Chorkendorff and J. Sehested, Science, 2016, 352, 969–974 CrossRef CAS PubMed.
- C. Ovesen, B. Clausen, J. Schiøtz, P. Stoltze, H. Topsøe and J. K. Nørskov, J. Catal., 1997, 168, 133–142 CrossRef CAS.
- L. Meng and Y.-Y. Duan, Fluid Phase Equilib., 2005, 238, 229–238 CrossRef CAS.
- L. Meng, Y.-Y. Duan and X.-D. Wang, Fluid Phase Equilib., 2007, 260, 354–358 CrossRef CAS.
- A. A. Arvidsson, P. N. Plessow, F. Studt and A. Hellman, J. Phys. Chem. C, 2020, 124, 14658–14663 CrossRef CAS.
- J. Gareth, W. Daniela, H. Trevor and T. Robert, An introduction to statistical learning: with applications in R, Spinger, 2013 Search PubMed.
- Y. Slotboom, M. J. Bos, J. Pieper, V. Vrieswijk, B. Likozar, S. R. A. Kersten and D. W. F. Brilman, Chem. Eng. J., 2020, 389, 124181–124196 CrossRef CAS.
- G. Bonura, M. Cordaro, L. Spadaro, C. Cannilla, F. Arena and F. Frusteri, Appl. Catal., B, 2013, 140–141, 16–24 CrossRef CAS.
- J. Ereña, R. Garoña, J. M. Arandes, A. T. Aguayo and J. Bilbao, Catal. Today, 2005, 107–108, 467–473 CrossRef.
- Y. Zhang, Y. Zhang, F. Ding, K. Wang, W. Xiaolei, B. Ren and J. Wu, Chem. Ind. Chem. Eng. Q., 2017, 23, 49–56 CrossRef CAS.
- A. Ateka, J. Ereña, P. Pérez-Uriarte, A. T. Aguayo and J. Bilbao, Int. J. Hydrogen Energy, 2017, 42, 27130–27138 CrossRef CAS.
- M. Sahibzada, I. S. Metcalfe and D. Chadwick, J. Catal., 1998, 174, 111–118 CrossRef CAS.
- N. Diban, A. M. Urtiaga, I. Ortiz, J. Ereña, J. Bilbao and A. T. Aguayo, Chem. Eng. J., 2013, 234, 140–148 CrossRef CAS.
- S. Poto, F. Gallucci and M. Fernanda Neira d'Angelo, Fuel, 2021, 302, 121080–121093 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1re00470k |
| This journal is © The Royal Society of Chemistry 2022 |