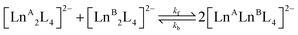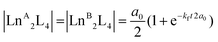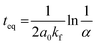DOI:
10.1039/D2QI00641C
(Research Article)
Inorg. Chem. Front., 2022,
9, 4495-4505
Dynamic lanthanide exchange between quadruple-stranded cages: the effect of ionic radius differences on kinetics and thermodynamics†
Received
28th March 2022
, Accepted 19th June 2022
First published on 20th June 2022
Abstract
Seven different [Ln2L4]2− (Ln = La, Nd, Eu, Tb, Er, Tm and Lu) lanthanide-based quadruple-stranded helicates are here reported and transmetalation among the pre-assembled cages is studied. Combining two homonuclear helicates, [LnA2L4]2− and [LnB2L4]2−, leads to the formation of a mixture of homo- and heteronuclear systems due to ion exchange. This dynamic behaviour is studied by electrospray ionization mass spectrometry (ESI-MS) both qualitatively and quantitatively, allowing one to gain information on the thermodynamics and on the kinetics of the process. The rate of the Ln ion exchange is strongly correlated with the difference in the lanthanide effective ionic radius (ΔEIR). Upon increasing the ΔEIR, the kinetic constants grow exponentially: from the minimum to the maximum value of the ΔEIR, the kinetic constants of the forward and backward reactions increase by three orders of magnitude. In contrast, the equilibrium constant is the same for all the [LnA2L4]2−/[LnB2L4]2− couples, showing that the transmetalation is mainly entropy driven towards a statistical mixture and not affected by the ΔEIR.
Introduction
Among metallo-supramolecular systems, lanthanide (Ln)-based architectures are attracting increasing attention due to their remarkable optical and magnetic properties. However, with Ln3+ ions, the design and control of the final supramolecule can be challenging. This is a direct consequence of the inner nature of the 4f orbitals: the ligand-field effects are small, and the coordination chemistry of these ions is similar across the entire series with the coordination number and geometry very variable and basically dependent on the steric properties of the ligand. There is, however, a steady variation of the effective ionic radius (EIR) across the series, which is the so-called “lanthanide contraction”. Although the radius difference (ΔEIR) is quite small (ca. 0.20 Å between La3+ and Lu3+ and ca. 0.02 Å between two consecutive lanthanides), it can have important chemical consequences on the nature and features of supramolecular complexes. For instance, the ΔEIR coupled to the use of multicompartmental ligands has been used to control the self-assembly of heterobimetallic helicates,1,2 while the ΔEIR effect has been shown to lead to lanthanide-selective self-assembly through multivalency and cooperativity.3,4 Furthermore, ΔEIR effects were proved to strongly affect the formation of the more stable thermodynamic product and the final metallo-supramolecular structure5–11 as well as the rate of conversion between different aggregates.11 More subtle effects have also been reported, such as variation of the twist angles in pseudo-helical Ln tripodal complexes12 and fine-tuning of the helicity and the helical winding in oligo(salamo)-based metal LZn3Ln helicates.13
In the past few decades, advances in the coordination chemistry of multinuclear compounds have been exploited to drive the self-assembly of many new discrete supramolecular motifs. Due to the nature of the metal–ligand interactions, many of these systems have a dynamic character with reversible association and dissociation able to generate complex mixtures. To unveil such dynamic behaviours, it is necessary to fully understand, control and design their functional properties. Mass spectrometry (MS) is a powerful tool to study such supramolecules14–16 for determining both the ensembles’ structure in terms of composition, shape, and size, and their dynamic behaviour and formation pathways.17–25 However, only a relatively small number of studies report MS quantitative analyses for metallo-supramolecular complexes.17–19,23–27 Among the dynamic processes displayed by supramolecular complexes, post-synthetic ion exchange is particularly important since it provides new pathways to synthesize heterometallic systems or species that cannot be achieved by direct metal–ligand coordination.20,21,24–36 Despite the importance of this synthesis strategy, little rigorous works have been reported on the kinetics33 and the thermodynamics29,30 of the ion exchange process for supramolecular complexes.
Oligo-β-diketones are versatile ligands for the preparation of metallo-supramolecular architectures37,38 ranging from metallocycles, cages and MOFs,39–43 to triple- and quadruple-stranded helicates44–53 and even to interlocked structures.54–57 Recently, we reported two [Ln2L4]2− quadruple-stranded helicates (Ln = La, Eu and Gd) that show dynamic and adaptive helicity reorganization due to a guest-to-host chirality transfer.44 Herein, by using a closely related bis-β-diketone ligand, we report a larger series of seven [Ln2L4]2− quadruple-stranded helicates (Ln = La, Nd, Eu, Tb, Er, Tm and Lu), Fig. 1, that once assembled undergo transmetalation. The thermodynamics and kinetics of the dynamic ion exchange have been studied and the role of the Ln3+ ΔEIR has been evaluated. The process has been qualitatively and quantitatively characterized by time-dependent electrospray ionization mass spectrometry (ESI-MS). Mixing a series of two homonuclear [LnA2L4]2− and [LnB2L4]2− with increasing Ln3+ ΔEIR always leads to the formation of a statistical mixture of homo- and heteronuclear helicates due to the Ln exchange. All the studied systems have an equilibrium constant close to K = 4. The Ln3+ ΔEIR, hence, does not affect the thermodynamics of the process that is mainly governed by statistical factors and entropy driven. On the other hand, we demonstrate that the rate of the dynamic ion exchange is Ln3+ radii dependent, Fig. 1b. The kinetic constants of the forward and backward reactions revealed an exponential trend correlated with the Ln3+ ΔEIR of the two homonuclear pre-assembled cages, Fig. 1c. This fundamental study provides new tools and guidelines to investigate dynamic processes in metallo-supramolecular ensembles, and for the precise preparation and control of lanthanide-based mixed coordination-driven systems.
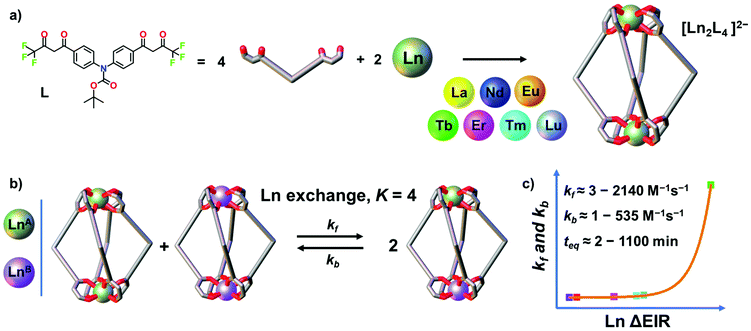 |
| | Fig. 1 (a) Self-assembly of seven [Ln2L4]2− cages (Ln = La, Nd, Eu, Tb, Er, Tm and Lu). (b) Dynamic Ln3+ ion exchange equilibrium between two pre-assembled cages and (c) exponential trend of the kinetic constants depending on the Ln ΔEIR. | |
Results and discussion
[Ln2L4]2− cage synthesis and characterization
The bis-β-diketone ligand was synthesized using a two-step protocol: (i) Ulmann coupling followed by (ii) Claisen condensation, and characterized as described in the ESI† (NMR Fig. S1–S4† and single crystal XRD Fig. S6†). The lantern-like cages with the general formula [Ln2L4]2− were prepared by adding an ethanol solution of the deprotonated ligand to an ethanol solution of a Ln3+ salt. Seven different Ln3+ ions were used to self-assemble [Ln2L4]2− cages where Ln = La, Nd, Eu, Tb, Er, Tm and Lu. Two bases, tetraethylammoniun hydroxide and dicyclohexylamine, were employed. Cages with countercation NEt4+ were used for ESI-MS and XRD analyses, while cages with the DCHA+ (dicyclohexylammonium) countercation were used for NMR studies due to their higher solubility. A metal![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ligand molar ratio of 1
ligand molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.5 leads to the formation of the pure compound in a good yield (Table S1†). All the cages show very clean ESI-MS spectra with only one signal ascribed to the [Ln2L4]2− double-negative charged species. The experimental isotopic pattern of each species is in good agreement with the calculated one, Fig. 2. The systems were also characterized by 1H-NMR and Fig. 3a shows the ligand (H2L, L2−) and [La2L4]2− cage spectra. Upon deprotonation, all the ligand signals undergo upfield shifting. The strongest effect is observed for the proton H1, in the α position of the β-diketonate moiety, shifting from ca. 7.1 to ca. 5.9 ppm, while the tert-butyl protons (H4) are barely perturbated. After La3+ coordination, the cage shows only a single set of signals with a total of four resonances, in agreement with the ligand C2 symmetry and the mean C4 symmetry of the quadruple-stranded [La2L4]2− architecture. H1, the H atom closer to the metal center, is downfield shifted to ca. 6.2 ppm. Diffusion-ordered NMR spectroscopy (DOSY) was performed to provide dimensional information. Two distinct bands were observed and ascribed to the cage and to the DCHA+ cation. The calculated hydrodynamic diameter for [La2L4]2− is 23.5 Å. The NMR spectra for the Eu and Lu systems (Fig. S5†) are also reported in the ESI†, while the Nd, Tb, Er and Tm analogue spectra showed very poor resolution due to these metals’ high magnetic moments.
2.5 leads to the formation of the pure compound in a good yield (Table S1†). All the cages show very clean ESI-MS spectra with only one signal ascribed to the [Ln2L4]2− double-negative charged species. The experimental isotopic pattern of each species is in good agreement with the calculated one, Fig. 2. The systems were also characterized by 1H-NMR and Fig. 3a shows the ligand (H2L, L2−) and [La2L4]2− cage spectra. Upon deprotonation, all the ligand signals undergo upfield shifting. The strongest effect is observed for the proton H1, in the α position of the β-diketonate moiety, shifting from ca. 7.1 to ca. 5.9 ppm, while the tert-butyl protons (H4) are barely perturbated. After La3+ coordination, the cage shows only a single set of signals with a total of four resonances, in agreement with the ligand C2 symmetry and the mean C4 symmetry of the quadruple-stranded [La2L4]2− architecture. H1, the H atom closer to the metal center, is downfield shifted to ca. 6.2 ppm. Diffusion-ordered NMR spectroscopy (DOSY) was performed to provide dimensional information. Two distinct bands were observed and ascribed to the cage and to the DCHA+ cation. The calculated hydrodynamic diameter for [La2L4]2− is 23.5 Å. The NMR spectra for the Eu and Lu systems (Fig. S5†) are also reported in the ESI†, while the Nd, Tb, Er and Tm analogue spectra showed very poor resolution due to these metals’ high magnetic moments.
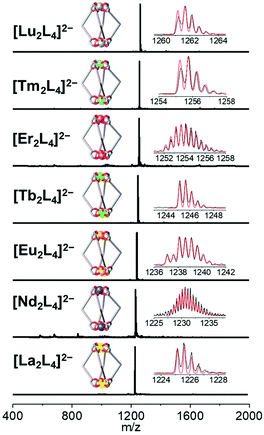 |
| | Fig. 2 ESI-MS spectra of the seven {[Ln2L4](NEt4)2} cages (Ln = La, Nd, Eu, Tb, Er, Tm and Lu). Insets: experimental (black) and simulated (red) isotopic patterns. | |
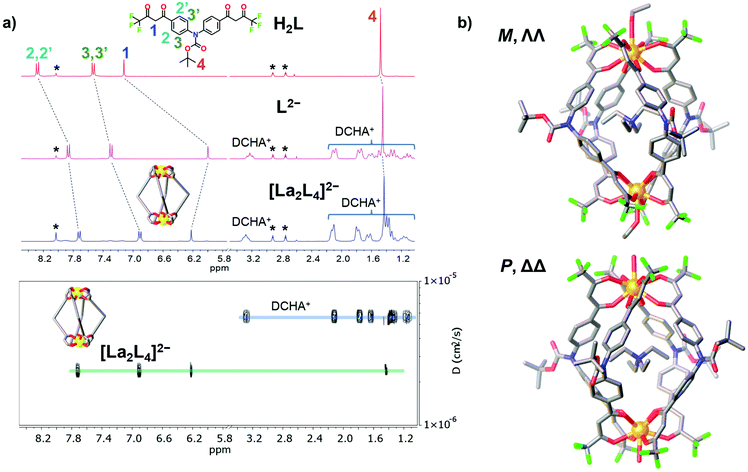 |
| | Fig. 3 (a) 1H-NMR spectra (25 °C, 300 MHz, DMF-d7) of ligand H2L, deprotonated ligand L2− and the cage [La2L4]2−. DOSY of [La2L4]2−. * = DMF. (b) Crystal structure of the Eu helicate, M and P forms in the asymmetric unit. H atoms and external NEt4+ ions omitted for clarity. Color code: C, grey; O, red; N, blue; F, green; Eu, orange. | |
For the Eu cage, it was possible to obtain single crystals suitable for XRD from the slow evaporation of mother liquors (ethanol). Structural determination ultimately confirmed the cage assembly and the formation of helicate systems (Fig. 3b). Both the right-handed (P, ΔΔ) and left-handed (M, ΛΛ) helicates are present in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio as an enantiomeric pair in the asymmetric unit (Fig. S7 and S8†), likewise to what was previously observed for a similar quadruple-stranded helicate.44 Each helicate hosts a NEt4+ counterion in its cavity. The Eu–O distances are in the range of 2.486–2.639 Å and the Eu⋯Eu distances are 12.054 Å and 12.199 Å for the two crystallographic independent helicates, respectively. The H⋯H distances of the tert-butyl groups of opposite ligands are close to 23 Å. This value is in good agreement with the hydrodynamic diameter calculated from the DOSY experiment (23.5 Å) for the lanthanum cage. Conversely to previous findings,44 the Eu ions do not display an octa-coordination mode since they are nona-coordinated. The Eu ions are tetrakis-chelated by four β-diketonato groups and the ninth site is occupied by a water or ethanol molecule. In particular, with the space group being centrosymmetric, the unit cell contains four helicates: two are ethanol coordinated (one M and one P helicate), the other two are water coordinated (one M and one P helicate), Fig. S7b.† The nona-coordination can be a consequence of the crystallization environment in the presence of good coordinating solvents such as ethanol and water. ESI-MS analysis did not show any adduct with water or ethanol. DFT studies were performed both on octa- and nona-coordinated La cages. The comparison of the X-ray nona-coordinated Eu helicate and the DFT-optimized octa-coordinated La helicate shows that the ligand arrangement in the two systems is very similar as highlighted by the overlay of the two structures (Fig. S10†). Moreover, the solvent molecule binding energy has also been determined: −7.4 and −8.5 kcal mol−1 for water and ethanol, respectively (see the ESI for details, Table S3†). This suggests that these molecules can be easily lost, as for instance during electro-spray ionization.
1 ratio as an enantiomeric pair in the asymmetric unit (Fig. S7 and S8†), likewise to what was previously observed for a similar quadruple-stranded helicate.44 Each helicate hosts a NEt4+ counterion in its cavity. The Eu–O distances are in the range of 2.486–2.639 Å and the Eu⋯Eu distances are 12.054 Å and 12.199 Å for the two crystallographic independent helicates, respectively. The H⋯H distances of the tert-butyl groups of opposite ligands are close to 23 Å. This value is in good agreement with the hydrodynamic diameter calculated from the DOSY experiment (23.5 Å) for the lanthanum cage. Conversely to previous findings,44 the Eu ions do not display an octa-coordination mode since they are nona-coordinated. The Eu ions are tetrakis-chelated by four β-diketonato groups and the ninth site is occupied by a water or ethanol molecule. In particular, with the space group being centrosymmetric, the unit cell contains four helicates: two are ethanol coordinated (one M and one P helicate), the other two are water coordinated (one M and one P helicate), Fig. S7b.† The nona-coordination can be a consequence of the crystallization environment in the presence of good coordinating solvents such as ethanol and water. ESI-MS analysis did not show any adduct with water or ethanol. DFT studies were performed both on octa- and nona-coordinated La cages. The comparison of the X-ray nona-coordinated Eu helicate and the DFT-optimized octa-coordinated La helicate shows that the ligand arrangement in the two systems is very similar as highlighted by the overlay of the two structures (Fig. S10†). Moreover, the solvent molecule binding energy has also been determined: −7.4 and −8.5 kcal mol−1 for water and ethanol, respectively (see the ESI for details, Table S3†). This suggests that these molecules can be easily lost, as for instance during electro-spray ionization.
Qualitative and quantitative ESI-MS of the Ln3+ ion dynamic exchange
Time-dependent ESI-MS analysis was used to study both qualitatively and quantitatively possible dynamic processes between two pre-assembled cages, [LnA2L4]2− and [LnB2L4]2−. Preliminary experiments were performed by mixing two equimolar solutions of the [Eu2L4]2− and [Tb2L4]2− cages in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio in a sealed vial at 50 °C, and monitoring their ESI-MS spectra at increasing time, Fig. 4b. At time zero, only the patterns ascribed to the two homometallic cages are present. After 60 minutes, the isotopic pattern of the heterometallic cage [EuTbL4]2− appears, as confirmed by comparison with the calculated one (Fig. S19†), showing that the two homometallic cages undergo ion exchange, forming a mixture of heteronuclear and homonuclear systems. The intensity of the Ln-mixed cage increases over time to the detriment of the homometallic ones. In order to apply ESI-MS to monitor the concentration of the different species at different times, we hypothesized that the [Ln2L4]2− species have comparable ionization efficiencies. To confirm this hypothesis, the ESI-MS spectrum of a solution containing equimolar amounts of the two homometallic cages [Eu2L4]2− and [Tb2L4]2− was repetitively measured just after mixing. If the hypothesis is correct, the two cages must exhibit MS spectra that indicate an equal relative amount. The relative amount was deduced according to eqn (1). Then, eqn (2) can be easily used to derive the molarity of the species (see the ESI† for details).
1 ratio in a sealed vial at 50 °C, and monitoring their ESI-MS spectra at increasing time, Fig. 4b. At time zero, only the patterns ascribed to the two homometallic cages are present. After 60 minutes, the isotopic pattern of the heterometallic cage [EuTbL4]2− appears, as confirmed by comparison with the calculated one (Fig. S19†), showing that the two homometallic cages undergo ion exchange, forming a mixture of heteronuclear and homonuclear systems. The intensity of the Ln-mixed cage increases over time to the detriment of the homometallic ones. In order to apply ESI-MS to monitor the concentration of the different species at different times, we hypothesized that the [Ln2L4]2− species have comparable ionization efficiencies. To confirm this hypothesis, the ESI-MS spectrum of a solution containing equimolar amounts of the two homometallic cages [Eu2L4]2− and [Tb2L4]2− was repetitively measured just after mixing. If the hypothesis is correct, the two cages must exhibit MS spectra that indicate an equal relative amount. The relative amount was deduced according to eqn (1). Then, eqn (2) can be easily used to derive the molarity of the species (see the ESI† for details).| | 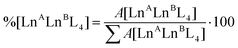 | (1) |
| | 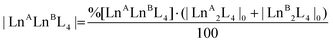 | (2) |
where %[LnALnBL4] is the relative amount of the cage, A[LnALnBL4] is the integrated area of the species isotopic pattern, and |LnALnBL4| is the molarity of the homonuclear cage if LnA = LnB, and the heteronuclear cage if LnA ≠ LnB. |LnA2L4|0 and |LnB2L4|0 are the initial molar concentrations of the homometallic species, respectively. Application of eqn (1) always gave values of about 50% for the relative amounts of the [Eu2L4]2− and [Tb2L4]2− cages (Table S4†), as expected for an equimolar mixture of the two cages, confirming that they have similar ionization efficiencies.
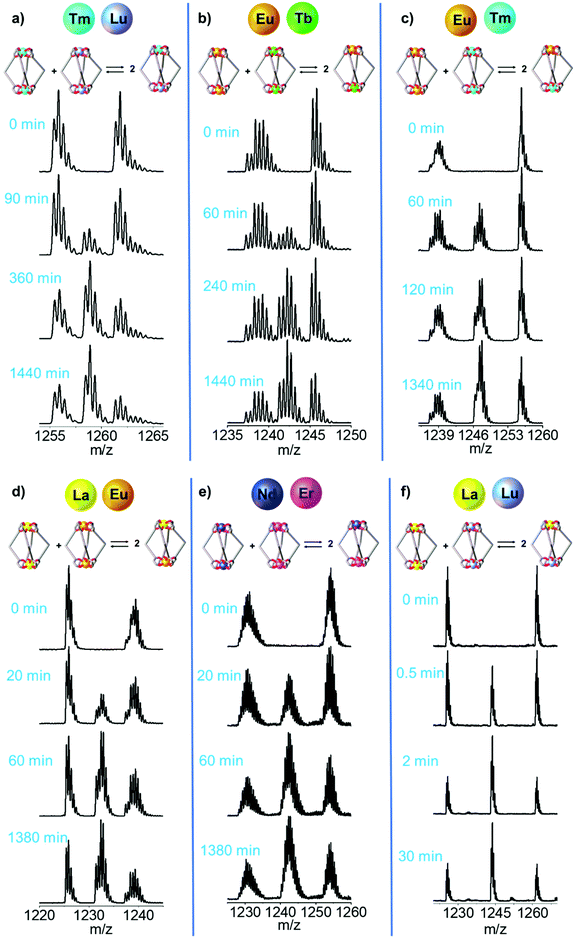 |
| | Fig. 4 Time-dependent ESI-MS spectra of an equimolar solution of [LnA2L4]2− and [LnB2L4]2−. Dynamic Ln3+ ion exchange between the couples with increasing ionic radius difference (ΔEIR): (a) [Tm2L4]2−/[Lu2L4]2−, (b) [Eu2L4]2−/[Tb2L4]2−, (c) [Eu2L4]2−/[Tm2L4]2−, (d) [La2L4]2−/[Eu2L4]2−, (e) [Nd2L4]2−/[Er2L4]2− and (f) [La2L4]2−/[Lu2L4]2−. The ESI† reports more spectra and simulated isotopic patterns (Fig. S13, S14, S18, S19, S23, S24, S28, S29, S33, S34, S38 and S39†). | |
The ESI-MS spectra of Fig. 4b and Fig. S18† were used to derive the relative amount and concentration of the different cages during the ion exchange. At equilibrium, a statistical mixture of homometallic (25%) and heterometallic (50%) cages is obtained, Fig. 5b and Table S6.† Then, the same approach was applied to study the ion exchange with other [LnA2L4]2−/[LnB2L4]2− couples, namely [Tm2L4]2−/[Lu2L4]2−, [Eu2L4]2−/[Tm2L4]2−, [La2L4]2−/[Eu2L4]2−, [Nd2L4]2−/[Er2L4]2− and [La2L4]2−/[Lu2L4]2−. Homonuclear cages bearing different Ln3+ ions were chosen in order to have Ln3+ ions spread across the lanthanide series, providing a range of effective ionic radii (EIR) and ionic radius differences (ΔEIR), as detailed in Table 1. The couples were also chosen in order to give similar values of ΔEIR but the Ln3+ ions were combined across the lanthanide series, such as [Tm2L4]2−/[Lu2L4]2− and [Eu2L4]2−/[Tb2L4]2− (ΔEIR 0.02 and 0.03 Å, respectively) or [La2L4]2−/[Eu2L4]2− and [Nd2L4]2−/[Er2L4]2− (ΔEIR 0.11 and 0.12 Å, respectively). The use of ESI-MS allows one to investigate also [LnA2L4]2−/[LnB2L4]2− couples that cannot be analyzed using NMR due to poor resolution. The only important constraint in the choice of the [LnA2L4]2−/[LnB2L4]2− couple is that there must be no significant overlaps between the isotopic patterns of the homonuclear and heteronuclear cages. The same protocol used for the couple [Eu2L4]2−/[Tb2L4]2− was applied. First, the two homonuclear cages were tested to verify whether they possess the same ionization efficiencies (Table S6, and Fig. S11†) in order to draw quantitative information from ESI-MS. Second, time-dependent analyses were performed to follow the dynamic ion exchange (Fig. 5, Tables S5–S10†). Fig. 5 clearly shows that all the [LnA2L4]2−/[LnB2L4]2− couples give a statistical mixture of homonuclear and heteronuclear cages, but the times to reach it are different.
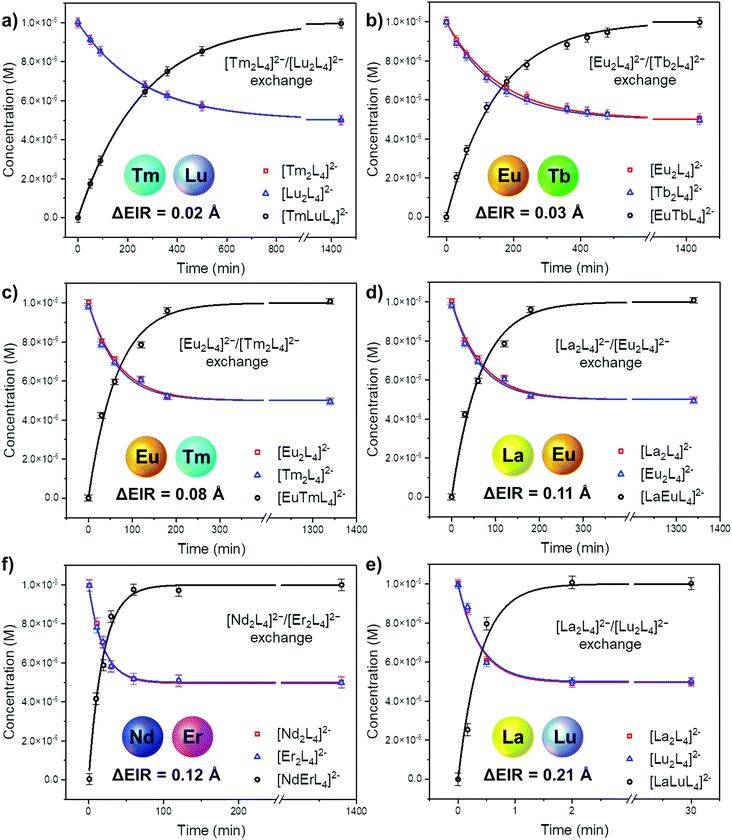 |
| | Fig. 5 Concentration over time during the Ln3+ ion exchange reaction as obtained by time-dependent ESI-MS of equimolar [LnA2L4]2−/[LnB2L4]2− mixtures. Kinetic profiles according to eqn (4) for the homometallic cages (red and blue lines) and eqn (5) for the heterometallic cages (black lines). Fitting details are reported in Fig. S15–S17, S20–S22, S25–S27, S30–S32, S35–37, and S40–S42. | |
Table 1 Ln3+ ion EIR and ΔEIR for the couples [LnA2L4]2−/[LnB2L4]2−and K, kf, kb and teq for the Ln3+ ion exchange reactions
| |
La3+ |
Nd3+ |
Eu3+ |
Tb3+ |
Er3+ |
Tm3+ |
Lu3+ |
| Ln3+ EIRa (Å) |
1.18 |
1.12 |
1.07 |
1.04 |
1.00 |
0.99 |
0.97 |
| [LnA2L4]2−/[LnB2L4]2− |
ΔEIR (Å) |
K
|
k
f (M−1 s−1) |
k
b (M−1 s−1) |
t
eq (min) |
|
For octa-coordinated Ln3+ ions.58
|
| [Tm2L4]2−/[Lu2L4]2− |
0.02 |
3.97 ± 0.35 |
3.20 ± 0.01 |
0.8 ± 0.01 |
1199.3 ± 4.7 |
| [Eu2L4]2−/[Tb2L4]2− |
0.03 |
4.05 ± 0.26 |
5.49 ± 0.07 |
1.37 ± 0.02 |
700.2 ± 9.3 |
| [Eu2L4]2−/[Tm2L4]2− |
0.08 |
3.98 ± 0.29 |
12.78 ± 0.46 |
3.20 ± 0.11 |
300.9 ± 10.8 |
| [La2L4]2−/[Eu2L4]2− |
0.11 |
3.98 ± 0.29 |
30.09 ± 1.02 |
7.52 ± 0.25 |
127.7 ± 4.3 |
| [Nd2L4]2−/[Er2L4]2− |
0.12 |
4.00 ± 0.40 |
42.77 ± 1.46 |
10.69 ± 0.36 |
89.8 ± 3.1 |
| [La2L4]2−/[Lu2L4]2− |
0.21 |
4.02 ± 0.35 |
2140.31 ± 166.50 |
535.08 ± 41.63 |
1.8 ± 0.1 |
Thermodynamics and kinetics analysis of the Ln3+ ion dynamic exchange
Starting from two homometallic cages with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio, two homometallic and one heterometallic cages with a ratio 1
1 ratio, two homometallic and one heterometallic cages with a ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 are obtained, eqn (3). Based on a statistical analysis,59 we can anticipate that the equilibrium constant will be K = 4. Indeed, at equilibrium, the experimental concentrations are all very close to the following values: |LnA2L4| = |LnB2L4| = 5 × 10−6 M and |LnALnBL4| = 1 × 10−5 M. All the Ln3+ ion exchange reactions, hence, have the same equilibrium constant (Table 1). This suggests that the ion exchange process is essentially entropy driven and hence governed by statistical factors. If the enthalpic contribution is negligible, we can infer that the different homometallic and heterometallic cages have similar stabilities across the lanthanide series.
2 are obtained, eqn (3). Based on a statistical analysis,59 we can anticipate that the equilibrium constant will be K = 4. Indeed, at equilibrium, the experimental concentrations are all very close to the following values: |LnA2L4| = |LnB2L4| = 5 × 10−6 M and |LnALnBL4| = 1 × 10−5 M. All the Ln3+ ion exchange reactions, hence, have the same equilibrium constant (Table 1). This suggests that the ion exchange process is essentially entropy driven and hence governed by statistical factors. If the enthalpic contribution is negligible, we can infer that the different homometallic and heterometallic cages have similar stabilities across the lanthanide series.| | 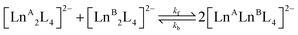 | (3) |
In contrast, the kinetics of the Ln3+ ion exchange reaction are very different. Fig. 5 highlights that by increasing the ionic radius difference (ΔEIR) between the involved Ln3+ ions, the time to reach the statistical mixture decreases. Some previous works17–19 treated the kinetics of dynamic ligand exchange between pre-assembled metallo-supramolecular architectures as first- or second-order direct reactions without considering the reversible nature of the equilibrium. This simplification can be adopted only under specific conditions (see below), otherwise it can lead to misleading results (see the ESI, Fig. S12†). As a matter of fact, the dynamic exchange reaction (ion or ligand) is a reversible reaction and its kinetics must be treated as a pair of forward and backward reactions (kinetic constants kf and kb, respectively). These two reactions occur simultaneously and are related to the equilibrium constant by K = kf/kb. Only if kf ≫ kb (high value for K), the reverse reaction can be neglected, and the kinetics analysis simplifies to a rate law for a direct reaction. However, in the cases here discussed K = 4 and kb will be one quarter of kf: the backward reaction cannot be neglected. The kinetics of the dynamic Ln3+ ion exchange has been treated as two opposing second-order reactions (see the ESI† for the detailed treatment). This leads to eqn (4) and (5) that give the concentrations of the homometallic and heterometallic species over time, respectively.
| | 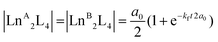 | (4) |
| | | |LnALnBL4| = a0(1 − e−kft2a0) | (5) |
where
a0 is the initial concentration of the homometallic cages,
kf is the kinetic constant of the forward reaction, and
t is the time. Moreover, the performed kinetic analysis allows one to estimate
teq, the time to reach the equilibrium,
i.e. the statistical mixture,
eqn (6) (see the ESI
† for details).
| | 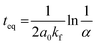 | (6) |
where
α is an arbitrary small number (see the ESI
† for details). For calculations of
teq, we assumed
α = 0.01, which corresponds to a homometallic cage concentration that is 1% higher than the equilibrium concentration.
Fitting the experimental data with eqn (4) and (5), Fig. 5, allowed us to determine kf and then kb for the different [LnA2L4]2−/[LnB2L4]2− couples involved in the ion dynamic exchange reaction. Table 1 summarizes the obtained results as the average of the values for the two homometallic cages and the heterometallic one (Table S9†). The more the ΔEIR between the two Ln3+ ions increases, the more kf (and kb) increases and consequently teq decreases. For instance, kf is 3.20 ± 0.01 M−1 s−1 (teq 1199.3 ± 4.7 min) for the couple [Tm2L4]2−/[Lu2L4]2− with the minimum ΔEIR = 0.02 Å. For the exchange reaction [Eu2L4]2−/[Tb2L4]2−, ΔEIR = 0.03 Å and kf is 5.49 ± 0.07 M−1 s−1 (teq 700.2 ± 9.2 min), for [Eu2L4]2−/[Tm2L4]2−, ΔEIR = 0.08 Å and kf is 12.78 ± 0.46 M−1 s−1 (teq 300.9 ± 10.8 min), for [La2L4]2−/[Eu2L4]2−, ΔEIR = 0.11 Å and kf is 30.09 ± 1.02 M−1 s−1 (teq 127.7 ± 4.3 min), and for [Nd2L4]2−/[Er2L4]2−, ΔEIR = 0.12 Å and kf is 42.77 ± 1.46 M−1 s−1 (teq 89.8 ± 3.1 min). The couple [La2L4]2−/[Lu2L4]2− with the highest ΔEIR = 0.21 Å shows a dramatic increase of kf (2140.31 ± 166.50 M−1 s−1) with a teq value of only 1.8 ± 0.1 minutes.
Two considerations deserve to be mentioned. First, mononuclear Ln β-diketonate complexes are known to be kinetically labile and to easily undergo ligand exchange.60–63 For instance, Eu β-diketonate solutions were found to give a mixture of the tetrakis [EuL4]−, tris [EuL3], bis [EuL2]+, and mono [EuL]2+ β-diketonate systems depending on the solvent and concentration.64 Second, among Ln metallosupramolecular systems, it has been previously demonstrated that Ln tetrahedra architectures display fast conversion to helicates when using large ions, the middle Ln ones give moderate conversion while the smaller ones show slow conversion rates.11 Hence, based on these considerations, it can be hypothesized that the Ln transmetalation may involve the partial dissociation of the two homometallic [Ln2L4]2− helicates to allow the ion exchange and that the overall kinetics may be governed by the homometallic helicate with the slower rate of dissociation even if we did not observe any undissociated species by either NMR or ESI-MS analyses. However, the experimental data do not evidence a clear relationship between the exchange rate and the effective ionic radius of one of the two Ln3+ ions of the [LnA2L4]2−/[LnB2L4]2− couple in terms of more or less labile homometallic systems and hence faster or slower dissociation. Indeed, one may argue that if the exchange kinetics was governed by the dissociation rate of the helicate with the smaller ion, the expected kf trend should be: [La2L4]2−/[Lu2L4]2− ≈ [Tm2L4]2−/[Lu2L4]2− > [Eu2L4]2−/[Tm2L4]2− > [Nd2L4]2−/[Er2L4]2− > [Eu2L4]2−/[Tb2L4]2− > [La2L4]2−/[Eu2L4]2−. On the other hand, an overall kinetic governed by the dissociation rate of the helicate with the bigger ion should give the following order: [La2L4]2−/[Lu2L4]2− ≈ [La2L4]2−/[Eu2L4]2− > [Nd2L4]2−/[Er2L4]2− > [Eu2L4]2−/[Tb2L4]2− ≈ [Eu2L4]2−/[Tm2L4]2− > [Tm2L4]2−/[Lu2L4]2−. Neither a more complex lability pattern like that displayed by hydrated Ln3+ ions for water dissociation rates showing a maximum for the central ions and lower values at the beginning and end of the Ln series65 allows one to rationalize the exchange rates here observed. Indeed, experimental data show the following kinetic constant order: [La2L4]2−/[Lu2L4]2− ≫ [Nd2L4]2−/[Er2L4]2− > [La2L4]2−/[Eu2L4]2− > [Eu2L4]2−/[Tm2L4]2− > [Eu2L4]2−/[Tb2L4]2− > [Tm2L4]2−/[Lu2L4]2−, suggesting a more complex mechanism that possibly involves both the homometallic helicates as suggested by the second-order kinetics.
As a matter of fact, plotting kf and kbversus the ΔEIR, Fig. 6a, reveals an exponential dependence of the kinetic constant's values related to the Ln3+ ionic radius difference of the two homonuclear cages participating in the ion exchange. An exponential relationship was also found by plotting teqversus ΔEIR, Fig. 6b. The collected data allow one to span across the entire Ln series, studying the exchange reaction with [LnA2L4]2−/[LnB2L4]2− couples having different or very close values of ΔEIR (for instance: [La2L4]2−/[Eu2L4]2− and [Nd2L4]2−/[Er2L4]2− or [Tm2L4]2−/[Lu2L4]2− and [Eu2L4]2−/[Tb2L4]2−), choosing Ln3+ ions from the beginning, the middle, and the end of the Ln series. The analyzed combinations show that the values of ΔEIR between LnA and LnB can be used as an empirical parameter to predict the exchange reaction rate. This means that based on the ΔEIR it is possible to know the exchange rate and that, on working with small and intermediate values of ΔEIR (slow/moderate Ln exchange rates), it is experimentally possible to precisely control the homometallic/heterometallic mixture composition by simply tuning the mixing time and then stopping the reaction by evaporating the solvent or embedding the system in some polymers to prepare a solid solution. This fine control is particularly appealing for the preparation of mixed Ln systems to exploit their luminescence properties (for instance Eu/Tb systems).
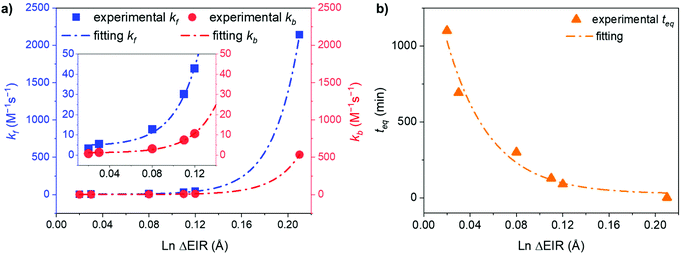 |
| | Fig. 6 Exponential trends of (a) kf and kb, and (b) teq for the Ln3+ ion exchange kinetics correlated with the Ln ΔEIR. Inset: magnification of the 0.01–0.14 Å ΔEIR region. Fitting details are reported in Fig. S43.† | |
Conclusions
In summary, a series of quadruple-stranded dinuclear helicates [Ln2L4]2− were prepared using a bis-β-diketone ligand and seven different Ln3+ ions (Ln = La, Nd, Eu, Tb, Er, Tm and Lu) and fully characterized by NMR, ESI-MS, DFT and single crystal XRD. The dynamic behavior of these systems was studied qualitatively and quantitatively by ESI-MS, providing information on how fast the ion exchange process between two pre-assembled homonuclear cages is completed, leading to a statistical mixture of homonuclear and heteronuclear cages. The thermodynamics of the transmetalation reaction is not affected by the Ln3+ ionic radius difference (ΔEIR) of the two homonuclear pre-assembled cages participating in the ion exchange. This suggests that the process is mainly entropy driven and that both the homometallic and heterometallic cages have similar stabilities across the Ln series. In contrast, the rate of Ln3+ ion exchange is strongly correlated with the ΔEIR, which can be used as an empirical parameter to know the exchange rate. The more the ΔEIR increases, the more the exchange rate increases. Both the forward and the backward kinetic constants (kf and kb) and the equilibration time (teq) show an exponential trend related to the Ln3+ ΔEIR. We envisage that this fundamental study will advance the supramolecular chemistry of Ln coordination-driven cages in terms of the synthesis, properties, and applications, in particular, of Ln-mixed systems where the control of the composition is paramount for the final functional properties such as magnetism and luminescence. In fact, rigorous knowledge of the ion exchange kinetics will allow the preparation of Ln-mixed systems with precise control over their composition in terms of homonuclear and heteronuclear systems by simply tailoring the mixing time of different pre-assembled cages.
Author contributions
M.R.a conceptualization and supervision. M.R.a, M.R.b, A.C., L.B., R.S., S.C. and J.T. investigation. M.R.a and S.C formal analysis. L.A. and G.H.C funding acquisition. M.R.a writing – original draft. All authors writing – review & editing.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The authors thank Prof. S. Santi of the University of Padova for helpful discussions. This work was funded by the National Research Council (CNR) with grant PROGETTI@CNR P@CNR_01_TerMoSmart, by the University of Padova with grant P-DiSC#01BIRD2021-UNIPD and P-DiSC#09BIRD2020-UNIPD and by the Deutsche Forschungsgemeinschaft DFG through GRK2376 “Confinement-controlled Chemistry”— project 331085229.
References
- N. André, R. Scopelliti, G. Hopfgartner, C. Piguet and J.-C. G. Bünzli, Discriminating between lanthanide ions: self-assembly of heterodimetallic triple-stranded helicates, Chem. Commun., 2002, 214–215 RSC.
- N. André, T. B. Jensen, R. Scopelliti, D. Imbert, M. Elhabiri, G. Hopfgartner, C. Piguet and J. C. G. Bünzli, Supramolecular recognition of heteropairs of lanthanide ions: A step toward self-assembled bifunctional probes, Inorg. Chem., 2004, 43, 515–529 CrossRef PubMed.
- A. M. Johnson, M. C. Young, X. Zhang, R. R. Julian and R. J. Hooley, Cooperative thermodynamic control of selectivity in the self-assembly of rare earth metal–ligand helices, J. Am. Chem. Soc., 2013, 135, 17723–17726 CrossRef CAS PubMed.
- X.-Z. Li, L.-P. Zhou, L.-L. Yan, Y.-M. Dong, Z.-L. Bai, X.-Q. Sun, J. Diwu, S. Wang, J.-C. Bünzli and Q.-F. Sun, A supramolecular lanthanide separation approach based on multivalent cooperative enhancement of metal ion selectivity, Nat. Commun., 2018, 9, 547 CrossRef.
- Y. Wu, S. Morton, X. Kong, G. S. Nichol and Z. Zheng, Hydrolytic synthesis and structural characterization of lanthanide-acetylacetonato/hydroxo cluster complexes – A systematic study, Dalton Trans., 2011, 40, 1041–1046 RSC.
- S. Zebret, C. Besnard, G. Bernardinelli and J. Hamacek, Thermodynamic discrimination in the formation of tetranuclear lanthanide helicates, Eur. J. Inorg. Chem., 2012, 2012, 2409–2417 CrossRef CAS.
- K. P. Carter, K. E. Thomas, S. J. A. Pope, R. J. Holmberg, R. J. Butcher, M. Murugesu and C. L. Cahill, Supramolecular assembly of molecular rare-earth–3,5-dichlorobenzoic acid–2,2′:6′,2′′-terpyridine materials: Structural systematics, luminescence properties, and magnetic Behavior, Inorg. Chem., 2016, 55, 6902–6915 CrossRef CAS.
- A. Vuillamy, S. Zebret, C. Besnard, V. Placide, S. Petoud and J. Hamacek, Functionalized triptycene-derived tripodal ligands: Privileged formation of tetranuclear cage assemblies with larger Ln(III), Inorg. Chem., 2017, 56, 2742–2749 CrossRef CAS PubMed.
- H.-Y. Wong, W. T. K. Chan and G.-L. Law, Assembly of lanthanide(III) cubanes and dimers with single-molecule magnetism and photoluminescence, Inorg. Chem., 2018, 57, 6893–6902 CrossRef CAS.
- C. Chen and A. Zhang, Radii-dependent self-assembly polynuclear lanthanide complexes as catalysts for CO2 transformation into cyclic carbonates, New J. Chem., 2021, 45, 20155–20163 RSC.
- K. H. Yim, C. T. Yeung, M. R. Probert, W. T. K. Chan, L. E. Mackenzie, R. Pal, W. T. Wong and G. L. Law, Helicate-to-tetrahedron transformation of chiral lanthanide supramolecular complexes induced by ionic radii effect and linker length, Commun. Chem., 2021, 4(116), 1–10 Search PubMed.
- S. Mizukami, H. Houjou, M. Kanesato and K. Hiratani, Adjustment of twist angles in pseudo-helical lanthanide complexes by the size of metal ions, Chem. – Eur. J., 2003, 9, 1521–1528 CrossRef CAS PubMed.
- S. Sairenji, S. Akine and T. Nabeshima, Lanthanide contraction for helicity fine-tuning and helix-winding control of single-helical metal complexes, Dalton Trans., 2016, 45, 14902–14906 RSC.
- H. Wang, C. Guo and X. Li, Multidimensional mass spectrometry assisted metallo-supramolecular chemistry, CCS Chem., 2021, 3161–3184 Search PubMed.
- Z. Qi, T. Heinrich, S. Moorthy and C. A. Schalley, Gas-phase chemistry of molecular containers, Chem. Soc. Rev., 2014, 44, 515–531 RSC.
- E. Kalenius, M. Groessl and K. Rissanen, Ion mobility–mass spectrometry of supramolecular complexes and assemblies, Nat. Rev. Chem., 2019, 3, 4–14 CrossRef CAS.
- Y.-R. Zheng and P. J. Stang, Direct and quantitative characterization of dynamic ligand exchange between coordination-driven self-assembled supramolecular polygons, J. Am. Chem. Soc., 2009, 131, 3487–3489 CrossRef CAS.
- S. Sato, Y. Ishido and M. Fujita, Remarkable stabilization of M 12 L 24 spherical frameworks through the cooperation of 48 Pd(II)−pyridine interactions, J. Am. Chem. Soc., 2009, 131, 6064–6065 CrossRef CAS.
- L. Wang, B. Song, S. Khalife, Y. Li, L.-J. Ming, S. Bai, Y. Xu, H. Yu, M. Wang, H. Wang and X. Li, Introducing seven transition metal ions into terpyridine-based supramolecules: self-assembly and dynamic ligand exchange study, J. Am. Chem. Soc., 2020, 142, 1811–1821 CrossRef CAS PubMed.
- M. Rancan, J. Tessarolo, P. L. Zanonato, R. Seraglia, S. Quici and L. Armelao, Self-assembly of a constitutional dynamic library of Cu(II) coordination polygons and reversible sorting by crystallization, Dalton Trans., 2013, 42, 7534–7538 RSC.
- B. Akhuli, L. Cera, B. Jana, S. Saha, C. A. Schalley and P. Ghosh, Formation and transmetalation mechanisms of homo- and heterometallic (Fe/Zn) trinuclear triple-stranded side-by-side helicates, Inorg. Chem., 2015, 54, 4231–4242 CrossRef CAS PubMed.
- B. Jana, L. Cera, B. Akhuli, S. Naskar, C. A. Schalley and P. Ghosh, Competitive transmetalation of first-row transition-metal ions between trinuclear triple-stranded side-by-side helicates, Inorg. Chem., 2017, 56, 12505–12513 CrossRef CAS PubMed.
- E. O. Bobylev, D. A. Poole, B. de Bruin and J. N. H. Reek, Selective formation of Pt12L24 nanospheres by ligand design, Chem. Sci., 2021, 12, 7696–7705 RSC.
- E. O. Bobylev, B. de Bruin and J. N. H. Reek, Catalytic formation of coordination-based self-assemblies by halide impurities, Inorg. Chem., 2021, 60, 12498–12505 CrossRef CAS.
- E. O. Bobylev, D. A. Poole, B. de Bruin and J. N. H. Reek, How to prepare kinetically stable self-assembled Pt12L24 nanocages while circumventing kinetic traps, Chem. – Eur. J., 2021, 27, 12667–12674 CrossRef CAS PubMed.
- F. J. Rizzuto, M. Kieffer and J. R. Nitschke, Quantified structural speciation in self-sorted CoII6L4 cage systems, Chem. Sci., 2018, 9, 1925–1930 RSC.
- C. Bravin, A. Guidetti, G. Licini and C. Zonta, Supramolecular cages as differential sensors for dicarboxylate anions: Guest length sensing using principal component analysis of ESI-MS and 1H-NMR raw data, Chem. Sci., 2019, 10, 3523–3528 RSC.
- X. Z. Li, L. P. Zhou, S. J. Hu, L. X. Cai, X. Q. Guo, Z. Wang and Q. F. Sun, Metal ion adaptive self-assembly of photoactive lanthanide-based supramolecular hosts, Chem. Commun., 2020, 56, 4416–4419 RSC.
- S. Akine, T. Taniguchi, T. Saiki and T. Nabeshima, Ca2+- and Ba2+-selective receptors based on site-selective transmetalation of multinuclear polyoxime−zinc(II) complexes, J. Am. Chem. Soc., 2005, 127, 540–541 CrossRef CAS PubMed.
- S. Akine, T. Taniguchi and T. Nabeshima, Helical metallohost−guest complexes via site-selective transmetalation of homotrinuclear complexes, J. Am. Chem. Soc., 2006, 128, 15765–15774 CrossRef CAS PubMed.
- Y.-B. Dong, P. Wang, J.-P. Ma, X.-X. Zhao, H.-Y. Wang, B. Tang and R.-Q. Huang, Coordination-driven nanosized lanthanide “molecular lantern” with tunable luminescent properties, J. Am. Chem. Soc., 2007, 129, 4872–4873 CrossRef CAS PubMed.
- M. E. Carnes, M. S. Collins and D. W. Johnson, Transmetalation of self-assembled, supramolecular complexes, Chem. Soc. Rev., 2014, 43, 1825–1834 RSC.
- D. Zare, Y. Suffren, H. Nozary, A. Hauser, C. Piguet, D. Zare, D. Nozary, P. rof DrC. Piguet, D. Suffren and D. Hauser, Controlling lanthanide exchange in triple-stranded helicates: A way to optimize molecular light-upconversion, Angew. Chem., Int. Ed., 2017, 56, 14612–14617 CrossRef CAS PubMed.
- J. R. Shakirova, E. V. Grachova, V. V. Gurzhiy, S. K. Thangaraj, J. Jänis, A. S. Melnikov, A. J. Karttunen, S. P. Tunik and I. O. Koshevoy, Heterometallic cluster-capped tetrahedral assemblies with postsynthetic modification of the metal cores, Angew. Chem., Int. Ed., 2018, 57, 14154–14158 CrossRef CAS PubMed.
- H. Ube, K. Endo, H. Sato and M. Shionoya, Synthesis of hetero-multinuclear metal complexes by site-selective redox switching and transmetalation on a homo-multinuclear complex, J. Am. Chem. Soc., 2019, 141, 10384–10389 CrossRef CAS PubMed.
- X. Hu, J. Chai, C. Zhang, J. Lang, S. P. Kelley, S. Feng, B. Liu, D. A. Atwood and J. L. Atwood, Biomimetic self-assembly of Co II-seamed hexameric metal–organic nanocapsules, J. Am. Chem. Soc., 2019, 141, 9151–9154 CrossRef PubMed.
- J. K. Clegg, F. Li and L. F. Lindoy, Oligo-β-diketones as versatile ligands for use in metallo-supramolecular chemistry: Recent progress and perspectives, Coord. Chem. Rev., 2022, 455, 214355 CrossRef CAS.
- R. W. Saalfrank, H. Maid and A. Scheurer, Supramolecular coordination chemistry: The synergistic effect of serendipity and rational design, Angew. Chem., Int. Ed., 2008, 47, 8794–8824 CrossRef CAS PubMed.
- J. K. Clegg, K. Gloe, M. J. Hayter, O. Kataeva, L. F. Lindoy, B. Moubaraki, J. C. McMurtrie, K. S. Murray and D. Schilter, New discrete and polymeric supramolecular architectures derived from dinuclear (bis-β-diketonato)copper(II) metallocycles, Dalton Trans., 2006, 3977–3984 RSC.
- J. K. Clegg, S. S. Iremonger, M. J. Hayter, P. D. Southon, R. B. Macquart, M. B. Duriska, P. Jensen, P. Turner, K. A. Jolliffe, C. J. Kepert, G. V. Meehan and L. F. Lindoy, Hierarchical self-assembly of a chiral metal–organic framework displaying pronounced porosity, Angew. Chem., Int. Ed., 2010, 49, 1075–1078 CrossRef CAS PubMed.
- M. Rancan, A. Dolmella, R. Seraglia, S. Orlandi, S. Quici and L. Armelao, A templating guest sorts out a molecular triangle from a dimer–trimer constitutional dynamic library, Chem. Commun., 2012, 48, 3115–3117 RSC.
- J. K. Clegg, F. Li, K. A. Jolliffe, L. F. Lindoy, G. V. Meehan, S. Parsons, P. A. Tasker and F. J. White, Hierarchical assembly of discrete copper(II) metallo-structures from pre-assembled dinuclear (bis-β-diketonato)metallocycles and flexible difunctional co-ligands, Dalton Trans., 2013, 42, 14315–14323 RSC.
- M. Rancan, J. Tessarolo, M. Casarin, P. L. Zanonato, S. Quici and L. Armelao, Double level selection in a constitutional dynamic library of coordination driven supramolecular polygons, Inorg. Chem., 2014, 53, 7276–7287 CrossRef CAS PubMed.
- M. Rancan, J. Tessarolo, A. Carlotto, S. Carlotto, M. Rando, L. Barchi, E. Bolognesi, R. Seraglia, G. Bottaro, M. Casarin, G. H. Clever and L. Armelao, Adaptive helicity and chiral recognition in bright europium quadruple-stranded helicates induced by host–guest interaction, Cell Rep. Phys. Sci., 2022, 3, 100692 CrossRef CAS.
- G. Han, Y. Zhou, Y. Yao, Z. Cheng, T. Gao, H. Li and P. Yan, Preorganized helical chirality controlled homochiral self-assembly and circularly polarized luminescence of a quadruple-stranded Eu2L4 helicate, Dalton Trans., 2020, 49, 3312–3320 RSC.
- Y. B. Tan, Y. Okayasu, S. Katao, Y. Nishikawa, F. Asanoma, M. Yamada, J. Yuasa and T. Kawai, Visible circularly polarized luminescence of octanuclear circular Eu(III) helicate, J. Am. Chem. Soc., 2020, 142, 17653–17661 CrossRef CAS PubMed.
- N. Suko, H. Itamoto, Y. Okayasu, N. Okura and J. Yuasa, Helix-mediated over 1 nm-range chirality recognition by ligand-to-ligand interactions of dinuclear helicates, Chem. Sci., 2021, 12, 8746–8754 RSC.
- A. P. Bassett, S. W. Magennis, P. B. Glover, D. J. Lewis, N. Spencer, S. Parsons, R. M. Williams, L. De Cola and Z. Pikramenou, Highly luminescent, triple- and quadruple-stranded, dinuclear Eu, Nd, and Sm(III) lanthanide complexes based on bis-diketonate ligands, J. Am. Chem. Soc., 2004, 126, 9413–9424 CrossRef CAS PubMed.
- A. J. Brock, I. M. Etchells, E. G. Moore and J. K. Clegg, Dinuclear triple stranded phenyl-spaced 1,3-bis-β-diketonato lanthanide(III) complexes: synthesis, structures and spectroscopy, Dalton Trans., 2021, 50, 4874–4879 RSC.
- R. Chen, Q. Q. Yan, S. J. Hu, X. Q. Guo, L. X. Cai, D. N. Yan, L. P. Zhou and Q. F. Sun, Dinuclear helicate or mononuclear pincer lanthanide complexes from one ligand: stereo-controlled assembly and catalysis, Org. Chem. Front., 2021, 8, 2576–2582 RSC.
- X. Gao, H. Li, P. Chen, W. Sun and P. Yan, A series of triple-stranded lanthanide(III) helicates: Syntheses, structures and single molecular magnets, Polyhedron, 2017, 126, 1–7 CrossRef CAS.
- P. Chen, H. Li, W. Sun, J. Tang, L. Zhang and P. Yan, Crystallization of triple- and quadruple-stranded dinuclear bis-β-diketonate-Dy(III) helicates: Single molecule magnetic behavior, CrystEngComm, 2015, 17, 7227–7232 RSC.
- H. Li, P. Chen, W. Sun, L. Zhang and P. Yan, Solvent triggered structural diversity of triple-stranded helicates: Single molecular magnets, Dalton Trans., 2016, 45, 3175–3181 RSC.
- H. Ju, J. K. Clegg, K.-M. Park, L. F. Lindoy and S. S. Lee, Formation of a dicopper platform based polyrotaxane whose “string” and “bead” are constructed from the same components, J. Am. Chem. Soc., 2015, 137, 9535–9538 CrossRef CAS PubMed.
- G. Truccolo, Z. Tessari, J. Tessarolo, S. Quici, L. Armelao and M. Rancan, A Cu(II) metallocycle for the reversible self-assembly of coordination-driven polyrotaxane-like architectures, Dalton Trans., 2018, 47, 12079–12084 RSC.
- M. Rancan, G. Truccolo, A. Carlotto, S. Quici and L. Armelao, A Zn(II) metallocycle as platform to assemble a 1D+1D → 1D polyrotaxane via π⋯π stacking of an ancillary ligand, Inorganics, 2019, 7, 137 CrossRef CAS.
- F. Li, J. K. Clegg, L. F. Lindoy, R. B. MacQuart and G. V. Meehan, Metallosupramolecular self-assembly of a universal 3-ravel, Nat. Commun., 2011, 2, 1–5 Search PubMed.
-
CRC Handbook of Chemistry and Physics, ed. W. M. Haynes, D. R. Lide and T. J. Bruno, CRC Press, 97th edn, 2016 Search PubMed.
- G. Ercolani, C. Piguet, M. Borkovec and J. Hamacek, Symmetry numbers and statistical factors in self-assembly and multivalency, J. Phys. Chem. B, 2007, 111, 12195–12203 CrossRef CAS PubMed.
- M. L. Bhaumik, Exchange of rare-earth ions in chelate solutions, J. Inorg. Nucl. Chem., 1965, 27, 243–244 CrossRef CAS.
- N. Serpone and R. Ishayek, Ligand-exchange equilibrium studies of some octacoordinate yttrium(III)-β-diketonate complexes by hydrogen-1 nuclear magnetic resonance spectroscopy, Inorg. Chem., 1971, 10, 2650–2656 CrossRef CAS.
- F. A. Cotton, P. Legzdins and S. J. Lippard, Nuclear magnetic resonance studies of eight-coordinate β-diketonate complexes related to laser chelates, J. Chem. Phys., 1966, 45, 3461–3462 CrossRef CAS.
- K. Binnemans, Rare-earth beta-diketonates, Handb. Phys. Chem. Rare Earths, 2005, 35, 107–272 Search PubMed.
- H. Samelson, C. Brecher and A. Lempicki, Spectroscopy and coordination chemistry of europium chelate solutions: Concentration and solvent effects, J. Mol. Spectrosc., 1966, 19, 349–371 CrossRef CAS.
- D. P. Fay, D. Litchinsky and N. Purdie, Ultrasonic absorption in aqueous salts of the lanthanides, J. Phys. Chem., 1969, 73, 544–552 CrossRef CAS.
|
| This journal is © the Partner Organisations 2022 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Maria
Rando
*a,
Maria
Rando
 b,
Luigi
Bosi
b,
Alice
Carlotto
b,
Luigi
Bosi
b,
Alice
Carlotto
 b,
Roberta
Seraglia
b,
Roberta
Seraglia
 c,
Jacopo
Tessarolo
c,
Jacopo
Tessarolo
 d,
Silvia
Carlotto
d,
Silvia
Carlotto
 ab,
Guido H.
Clever
ab,
Guido H.
Clever
 d and
Lidia
Armelao
d and
Lidia
Armelao
 be
be
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ligand molar ratio of 1
ligand molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.5 leads to the formation of the pure compound in a good yield (Table S1†). All the cages show very clean ESI-MS spectra with only one signal ascribed to the [Ln2L4]2− double-negative charged species. The experimental isotopic pattern of each species is in good agreement with the calculated one, Fig. 2. The systems were also characterized by 1H-NMR and Fig. 3a shows the ligand (H2L, L2−) and [La2L4]2− cage spectra. Upon deprotonation, all the ligand signals undergo upfield shifting. The strongest effect is observed for the proton H1, in the α position of the β-diketonate moiety, shifting from ca. 7.1 to ca. 5.9 ppm, while the tert-butyl protons (H4) are barely perturbated. After La3+ coordination, the cage shows only a single set of signals with a total of four resonances, in agreement with the ligand C2 symmetry and the mean C4 symmetry of the quadruple-stranded [La2L4]2− architecture. H1, the H atom closer to the metal center, is downfield shifted to ca. 6.2 ppm. Diffusion-ordered NMR spectroscopy (DOSY) was performed to provide dimensional information. Two distinct bands were observed and ascribed to the cage and to the DCHA+ cation. The calculated hydrodynamic diameter for [La2L4]2− is 23.5 Å. The NMR spectra for the Eu and Lu systems (Fig. S5†) are also reported in the ESI†, while the Nd, Tb, Er and Tm analogue spectra showed very poor resolution due to these metals’ high magnetic moments.
2.5 leads to the formation of the pure compound in a good yield (Table S1†). All the cages show very clean ESI-MS spectra with only one signal ascribed to the [Ln2L4]2− double-negative charged species. The experimental isotopic pattern of each species is in good agreement with the calculated one, Fig. 2. The systems were also characterized by 1H-NMR and Fig. 3a shows the ligand (H2L, L2−) and [La2L4]2− cage spectra. Upon deprotonation, all the ligand signals undergo upfield shifting. The strongest effect is observed for the proton H1, in the α position of the β-diketonate moiety, shifting from ca. 7.1 to ca. 5.9 ppm, while the tert-butyl protons (H4) are barely perturbated. After La3+ coordination, the cage shows only a single set of signals with a total of four resonances, in agreement with the ligand C2 symmetry and the mean C4 symmetry of the quadruple-stranded [La2L4]2− architecture. H1, the H atom closer to the metal center, is downfield shifted to ca. 6.2 ppm. Diffusion-ordered NMR spectroscopy (DOSY) was performed to provide dimensional information. Two distinct bands were observed and ascribed to the cage and to the DCHA+ cation. The calculated hydrodynamic diameter for [La2L4]2− is 23.5 Å. The NMR spectra for the Eu and Lu systems (Fig. S5†) are also reported in the ESI†, while the Nd, Tb, Er and Tm analogue spectra showed very poor resolution due to these metals’ high magnetic moments.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio as an enantiomeric pair in the asymmetric unit (Fig. S7 and S8†), likewise to what was previously observed for a similar quadruple-stranded helicate.44 Each helicate hosts a NEt4+ counterion in its cavity. The Eu–O distances are in the range of 2.486–2.639 Å and the Eu⋯Eu distances are 12.054 Å and 12.199 Å for the two crystallographic independent helicates, respectively. The H⋯H distances of the tert-butyl groups of opposite ligands are close to 23 Å. This value is in good agreement with the hydrodynamic diameter calculated from the DOSY experiment (23.5 Å) for the lanthanum cage. Conversely to previous findings,44 the Eu ions do not display an octa-coordination mode since they are nona-coordinated. The Eu ions are tetrakis-chelated by four β-diketonato groups and the ninth site is occupied by a water or ethanol molecule. In particular, with the space group being centrosymmetric, the unit cell contains four helicates: two are ethanol coordinated (one M and one P helicate), the other two are water coordinated (one M and one P helicate), Fig. S7b.† The nona-coordination can be a consequence of the crystallization environment in the presence of good coordinating solvents such as ethanol and water. ESI-MS analysis did not show any adduct with water or ethanol. DFT studies were performed both on octa- and nona-coordinated La cages. The comparison of the X-ray nona-coordinated Eu helicate and the DFT-optimized octa-coordinated La helicate shows that the ligand arrangement in the two systems is very similar as highlighted by the overlay of the two structures (Fig. S10†). Moreover, the solvent molecule binding energy has also been determined: −7.4 and −8.5 kcal mol−1 for water and ethanol, respectively (see the ESI for details, Table S3†). This suggests that these molecules can be easily lost, as for instance during electro-spray ionization.
1 ratio as an enantiomeric pair in the asymmetric unit (Fig. S7 and S8†), likewise to what was previously observed for a similar quadruple-stranded helicate.44 Each helicate hosts a NEt4+ counterion in its cavity. The Eu–O distances are in the range of 2.486–2.639 Å and the Eu⋯Eu distances are 12.054 Å and 12.199 Å for the two crystallographic independent helicates, respectively. The H⋯H distances of the tert-butyl groups of opposite ligands are close to 23 Å. This value is in good agreement with the hydrodynamic diameter calculated from the DOSY experiment (23.5 Å) for the lanthanum cage. Conversely to previous findings,44 the Eu ions do not display an octa-coordination mode since they are nona-coordinated. The Eu ions are tetrakis-chelated by four β-diketonato groups and the ninth site is occupied by a water or ethanol molecule. In particular, with the space group being centrosymmetric, the unit cell contains four helicates: two are ethanol coordinated (one M and one P helicate), the other two are water coordinated (one M and one P helicate), Fig. S7b.† The nona-coordination can be a consequence of the crystallization environment in the presence of good coordinating solvents such as ethanol and water. ESI-MS analysis did not show any adduct with water or ethanol. DFT studies were performed both on octa- and nona-coordinated La cages. The comparison of the X-ray nona-coordinated Eu helicate and the DFT-optimized octa-coordinated La helicate shows that the ligand arrangement in the two systems is very similar as highlighted by the overlay of the two structures (Fig. S10†). Moreover, the solvent molecule binding energy has also been determined: −7.4 and −8.5 kcal mol−1 for water and ethanol, respectively (see the ESI for details, Table S3†). This suggests that these molecules can be easily lost, as for instance during electro-spray ionization.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio in a sealed vial at 50 °C, and monitoring their ESI-MS spectra at increasing time, Fig. 4b. At time zero, only the patterns ascribed to the two homometallic cages are present. After 60 minutes, the isotopic pattern of the heterometallic cage [EuTbL4]2− appears, as confirmed by comparison with the calculated one (Fig. S19†), showing that the two homometallic cages undergo ion exchange, forming a mixture of heteronuclear and homonuclear systems. The intensity of the Ln-mixed cage increases over time to the detriment of the homometallic ones. In order to apply ESI-MS to monitor the concentration of the different species at different times, we hypothesized that the [Ln2L4]2− species have comparable ionization efficiencies. To confirm this hypothesis, the ESI-MS spectrum of a solution containing equimolar amounts of the two homometallic cages [Eu2L4]2− and [Tb2L4]2− was repetitively measured just after mixing. If the hypothesis is correct, the two cages must exhibit MS spectra that indicate an equal relative amount. The relative amount was deduced according to eqn (1). Then, eqn (2) can be easily used to derive the molarity of the species (see the ESI† for details).
1 ratio in a sealed vial at 50 °C, and monitoring their ESI-MS spectra at increasing time, Fig. 4b. At time zero, only the patterns ascribed to the two homometallic cages are present. After 60 minutes, the isotopic pattern of the heterometallic cage [EuTbL4]2− appears, as confirmed by comparison with the calculated one (Fig. S19†), showing that the two homometallic cages undergo ion exchange, forming a mixture of heteronuclear and homonuclear systems. The intensity of the Ln-mixed cage increases over time to the detriment of the homometallic ones. In order to apply ESI-MS to monitor the concentration of the different species at different times, we hypothesized that the [Ln2L4]2− species have comparable ionization efficiencies. To confirm this hypothesis, the ESI-MS spectrum of a solution containing equimolar amounts of the two homometallic cages [Eu2L4]2− and [Tb2L4]2− was repetitively measured just after mixing. If the hypothesis is correct, the two cages must exhibit MS spectra that indicate an equal relative amount. The relative amount was deduced according to eqn (1). Then, eqn (2) can be easily used to derive the molarity of the species (see the ESI† for details).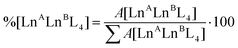
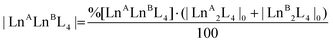


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio, two homometallic and one heterometallic cages with a ratio 1
1 ratio, two homometallic and one heterometallic cages with a ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 are obtained, eqn (3). Based on a statistical analysis,59 we can anticipate that the equilibrium constant will be K = 4. Indeed, at equilibrium, the experimental concentrations are all very close to the following values: |LnA2L4| = |LnB2L4| = 5 × 10−6 M and |LnALnBL4| = 1 × 10−5 M. All the Ln3+ ion exchange reactions, hence, have the same equilibrium constant (Table 1). This suggests that the ion exchange process is essentially entropy driven and hence governed by statistical factors. If the enthalpic contribution is negligible, we can infer that the different homometallic and heterometallic cages have similar stabilities across the lanthanide series.
2 are obtained, eqn (3). Based on a statistical analysis,59 we can anticipate that the equilibrium constant will be K = 4. Indeed, at equilibrium, the experimental concentrations are all very close to the following values: |LnA2L4| = |LnB2L4| = 5 × 10−6 M and |LnALnBL4| = 1 × 10−5 M. All the Ln3+ ion exchange reactions, hence, have the same equilibrium constant (Table 1). This suggests that the ion exchange process is essentially entropy driven and hence governed by statistical factors. If the enthalpic contribution is negligible, we can infer that the different homometallic and heterometallic cages have similar stabilities across the lanthanide series.