Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Analysis of measured high-resolution doublet rovibronic spectra and related line lists of 12CH and 16OH†
Tibor
Furtenbacher
 a,
Samuel T.
Hegedus
b,
Jonathan
Tennyson
a,
Samuel T.
Hegedus
b,
Jonathan
Tennyson
 *b and
Attila G.
Császár
*b and
Attila G.
Császár
 *ac
*ac
aMTA-ELTE Complex Chemical Systems Research Group, Pázmány Péter sétány 1/A, H-1117 Budapest, Hungary. E-mail: attila.csaszar@ttk.elte.hu
bDepartment of Physics and Astronomy, University College London, Gower Street, London WC1E 6BT, UK. E-mail: j.tennyson@ucl.ac.uk
cLaboratory of Molecular Structure and Dynamics, Institute of Chemistry, ELTE Eötvös Loránd University and MTA-ELTE Complex Chemical Systems Research Group, Pázmány Péter sétány 1/A, H-1117 Budapest, Hungary
First published on 25th July 2022
Abstract
Detailed understanding of the energy-level structure of the quantum states as well as of the rovibronic spectra of the ethylidyne (CH) and the hydroxyl (OH) radicals is mandatory for a multitude of modelling efforts within multiple chemical, combustion, astrophysical, and atmospheric environments. Accurate empirical rovibronic energy levels, with associated uncertainties, are reported for the low-lying doublet electronic states of 12CH and 16OH, using the Measured Active Rotational-Vibrational Energy Levels (MARVEL) algorithm. For 12CH, a total of 1521 empirical energy levels are determined in the primary spectroscopic network (SN) of the radical, corresponding to the following seven electronic states: X 2Π, A 2Δ, B 2Σ−, C2 Σ+, D 2Π, E 2Σ+, and F 2Σ+. The energy levels are derived from 6348 experimentally measured and validated transitions, collected from 29 sources. For 16OH, the lowest four doublet electronic states, X 2Π, A 2Σ+, B 2Σ+, and C 2Σ+, are considered, and a careful analysis and validation of 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 938 rovibronic transitions, collected from 45 sources, results in 1624 empirical rovibronic energy levels. The large set of spectroscopic data presented should facilitate the refinement of line lists for the 12CH and 16OH radicals. For both molecules hyperfine-resolved experimental transitions have also been considered, forming SNs independent from the primary SNs.
938 rovibronic transitions, collected from 45 sources, results in 1624 empirical rovibronic energy levels. The large set of spectroscopic data presented should facilitate the refinement of line lists for the 12CH and 16OH radicals. For both molecules hyperfine-resolved experimental transitions have also been considered, forming SNs independent from the primary SNs.
1 Introduction
The free radicals methylidyne (CH) and hydroxyl (OH) play central roles in multiple chemical, combustion, astronomical, and atmospheric environments exhibiting a wide range of thermochemical properties. Therefore, their rovibronic spectra have been studied in considerable detail by methods of high-resolution molecular spectroscopy. Here we collect and analyze these data using the Measured Active Rotational-Vibrational Energy Levels (MARVEL) procedure.1–5The CH radical has played a fundamental role in the furtherance of our scientific understanding during the last century. The radical's spectrum was identified in 1918.6 In 1937,7 methylidyne became the first molecule detected in interstellar space, prior to the proliferation of radio spectroscopy in the post-WWII period. The assignment of the broad 429.5–431.5 nm band, the so-called G-band of Fraunhofer, containing transitions corresponding to 12CH, was made 26 years before 16OH was detected using radio astronomy.8 Beyond its original discovery in the interstellar medium, CH has been detected in stellar atmospheres,9 including the Sun,10,11 in comets,12 in protostellar accretion disks,13 in planetary nebula,14 and in extragalactic sources.15 CH is used as a tracer for molecular hydrogen in the interstellar medium due to its origin being predominantly from the radiative association and recombination of C+ and H.16 It is also used as part of the classification of carbon giants.17,18 CH is important in further chemical and physical environments. For example, during combustion of hydrocarbons it is an important intermediate giving the flame its characteristic blue color.19 The ubiquity of CH across multiple environments, with a broad range of thermodynamic conditions, is why CH is one of the spectroscopically most studied diatomic molecules. Furthermore, this is why the proposed analysis of the rovibronic spectra of CH is so pertinent and broadly beneficial for future studies, both in helping to interpret observations and to improve astronomical, chemical, and physical models. Note in this respect that several hyperfine transitions of 12CH have been measured with an accuracy of a few Hz, providing a convenient way to put limits on the possible variation of the fine-structure constant and the electron-proton mass ratio with respect to time and local densities.20
OH is arguably the most important free radical in the Earth's atmosphere,21,22 governing atmospheric chemistry during the day. The OH radical is responsible for airglow23,24 and it is, together with HO2, one of the most dominant oxidizing agents of organic molecules in the troposphere.25 The hydroxyl radical is highly relevant for chemists as it has a significant role in the reactions characterizing combustion systems and flames26,27 and even in heterogeneous catalysis.28 OH is also of significant astrophysical interest, since it can be found in comets,29 stellar atmospheres,30 including the solar photosphere31 and sunspots,32 interstellar clouds,33 exoplanets,27 and planetary atmospheres.34–36 Accordingly, a large number of transitions of OH have been detected, the assigned spectra extend from resolved Λ-doubling and hyperfine transitions37 in the microwave (MW) to rotation (the “pure rotation” and the “spin-flip” branches), vibration–rotation, and rovibronic transitions.
Both OH and CH have key transitions at THz frequencies which have been studied from space using observatories such as the Kuiper Airborne Observatory,38 the ISO (Infrared Space Observatory),39 and Herschel,40–42 provoking dedicated laboratory studies.43 More recently, similar studies have been performed with the airborne SOFIA (Stratospheric Observatory for Far-Infrared Astronomy) observatory.44–47 These studies often investigate hyperfine-resolved transitions.
Spectroscopic parameters and line lists have been published for both radicals. There are no CH data reported in the spectroscopic database and information system HITRAN,48 while 16OH is molecule #13 in there and HITRAN202049 lists altogether 55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 698 lines in the range of 0–43
698 lines in the range of 0–43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 408 cm−1 for 16OH. The GEISA-2020 database50 is based on effective Hamiltonian (EH) calculations and contains a large number of data for OH. The most recent line list9 among those available,9,51 created for 12CH and 13CH, covers rovibronic transitions X–X, A–X, B–X, and C–X. As for OH, the available CH line lists cover transitions within the ground state52 as well as A–X electronic transitions.53 The ground-state transitions form the so-called Meinel bands,54 used, for example, to estimate OH rotational temperatures. The line lists of ref. 9, 52 and 53 were created as part of the MoLLIST project.55 The Jet Propulsion Laboratory (JPL) catalog56 contains data for both CH and OH.
408 cm−1 for 16OH. The GEISA-2020 database50 is based on effective Hamiltonian (EH) calculations and contains a large number of data for OH. The most recent line list9 among those available,9,51 created for 12CH and 13CH, covers rovibronic transitions X–X, A–X, B–X, and C–X. As for OH, the available CH line lists cover transitions within the ground state52 as well as A–X electronic transitions.53 The ground-state transitions form the so-called Meinel bands,54 used, for example, to estimate OH rotational temperatures. The line lists of ref. 9, 52 and 53 were created as part of the MoLLIST project.55 The Jet Propulsion Laboratory (JPL) catalog56 contains data for both CH and OH.
A motivation for performing MARVEL analyses of high-resolution spectra is the construction of high-accuracy line lists. Given that first-principles theoretical procedures can predict transition intensities with an accuracy competitive with state-of-the-art experiments,57,58 use of empirical energy levels, such as those determined by the MARVEL procedure, to determine transition frequencies provides a route to constructing line lists of experimental quality. This is a major current objective of the ExoMol project.59 Note that similar MARVEL-based studies have already been performed on second-row hydride radicals, like9 BeH,60 a radical important for fusion studies, and 14NH.61
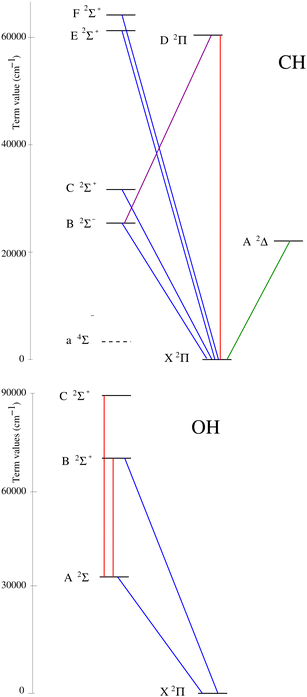
In this paper we undertake MARVEL studies for the lowest seven doublet electronic states of CH and the lowest four doublet electronic states of OH (see Fig. 1 for the states covered in this study). To do this we analyze the experimental spectroscopic data available for the parent 12CH6,9–15,20,40,51,62–105 and 16OH8,21,31,38,41,43–47,52,53,106–158 isotopologues, using the Hamiltonian-free MARVEL procedure,1–5 and obtain high-accuracy empirical rovibronic energy levels with well-defined uncertainties. The empirical energy levels obtained allow the critical assessment of line lists9,51–53 created previously for the two radicals. The principal aim of this study is to provide a set of validated experimental rovibronic transitions as well as a large number of empirical rovibronic energy levels, facilitating the construction of the next generation of line lists for 12CH and 16OH.
2 Methodological details
2.1 MARVEL
The MARVEL approach1–5 converts a set of assigned experimental transitions into empirical energy levels with associated uncertainties that are propagated from the input transitions to the output energy levels. This conversion relies on the construction of a spectroscopic network (SN),3,159–161 built upon the measured and assigned transitions.2.2 Quantum numbers
MARVEL requires that all transitions are assigned with a unique set of descriptors, usually quantum numbers, which are self-consistent across the entire dataset. A brief discussion of the labels we use is especially important as over time spectroscopists adopted different rules to assign the spectral lines of CH and OH, causing considerable confusion and making a global spectroscopic analysis error prone.The electronic ground state of CH, X 2Π, has the following electron configuration: (1σ)2 (2σ)2 (3σ)2 (1π)1. The four lowest-energy electronic states of CH (see the top panel of Fig. 1), a 4Σ− (Te = 6024.40 cm−1), A 2Δ (Te = 23148.7375 cm−1), B 2Σ− (Te = 24642.425 cm−1), and C 2Σ+ (Te = 31809.6428 cm−1), all arise from a 1π ← 3σ excitation. In this list Te is the electronic term and all Te values are taken from ref. 9. During the present SN-based study, we only consider doublet states. There are three more doublet states of 12CH besides X, A, B, and C, all above 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, which we considered: D 2Π, E 2Σ+, and F 2Σ+ (see the top panel of Fig. 1). In the literature, there has been some valid debate about the designation of the higher-lying Σ and Π electronic states of CH.66,84,162,163 While technically this may not be correct, we keep the traditional spectroscopic designation of the electronic states of CH, and, for example, denote the second 2Π state as D 2Π, with clear consequences for the designation of the higher 2Σ+ states.
000 cm−1, which we considered: D 2Π, E 2Σ+, and F 2Σ+ (see the top panel of Fig. 1). In the literature, there has been some valid debate about the designation of the higher-lying Σ and Π electronic states of CH.66,84,162,163 While technically this may not be correct, we keep the traditional spectroscopic designation of the electronic states of CH, and, for example, denote the second 2Π state as D 2Π, with clear consequences for the designation of the higher 2Σ+ states.
It is most appropriate to treat the high-resolution spectra of 12CH as a diatomic having Hund's case (b) coupling.37 This means that Ω (= Λ + Σ) is not a good quantum number (Λ and Σ are the quantum numbers for the projection of the electronic orbital angular momentum L and the electron spin angular momentum S onto the internuclear axis, respectively). Furthermore, L is coupled to the overall rotational angular momentum R to form N, and N is then coupled to S to form the angular momentum J (N = L + R and J = N + S). Thus, to label the rovibronic states of 12CH within MARVEL we use the following descriptors: the electronic state called state, e.g., X2Pi, the vibrational quantum number (v), the total angular momentum quantum number (J), the rotationless parity (e/f),164 and values of F1 and F2 to label the spin components. We denote the F1 and F2 spin components by 1 and 2 in the MARVEL transition file, respectively. Many CH spectra are assigned using the quantum number N, this can be used to give the spin components J = N + 1/2 and J = N − 1/2 corresponding to F1 and F2, respectively.51
The electronic ground state of OH, X 2Π, corresponds to the following electron configuration: (1σ)2 (2σ)2 (3σ)2 (1π)3. In this study, the rovibronic energy levels of the following four doublet states are considered: X 2Π, A 2Σ+, B 2Σ+, and C 2Σ+ (see the bottom panel of Fig. 1). The lower levels of 16OH are well represented by a Hund's case (a) coupling.37 The following descriptors were employed to label the rovibronic states of 16OH: state, Ω, v, J, and the rotationless parity164 (e/f). State designates the electronic state, Ω is the projection of the total angular momentum along the internuclear axis, and J is the total angular momentum quantum number without the nuclear spin. Regarding these descriptors we need to note the following: (1) in the case of 16OH, Ω can be either 1/2 or 3/2. The ground electronic state of 16OH is inverted (the spin-rotation constant of OH is negative); thus, the 2Π3/2 (F1) component lies below the 2Π1/2 (F2) component. (2) We follow the e/f scheme advocated in 78BrKaKeMi.165 This means that in the case of 2Π1/2 the order of parity (e/f) changes when J > 7/2. (3) In the case of 2Σ+ electronic states the Ω = 1/2 energy levels belong to the f parity (F1) and the Ω = 3/2 levels have e parity (F2).
3 Compilation of experimental sources
Our intention was to consider and analyse all literature sources of experimentally measured and assigned high-resolution 12CH and 16OH spectra. How far this was achieved is discussed separately for the two radicals.3.1 12CH
The structure of the CH band system treated in this study is displayed in Fig. 1 (see the top panel). The seven electronic states considered, X 2Π, A 2Δ, B 2Σ−, C 2Σ+, D 2Π, E 2Σ+, and F 2Σ+, are linked by a series of transitions, part of high-resolution, rotationally-resolved spectra. The lowest quartet state is the a 4Σ− state, whose term value is only about Te = 6024 cm−1.9,163 Nelis et al.86 recorded a far-infrared laser magnetic resonance spectrum containing 558 transitions within this state. Unfortunately, there are no reported intercombination transitions for CH linking the doublet and quartet manifolds. Thus, here we are concentrating on the SN formed by the seven doublet electronic states.The full list of data sources employed in the final MARVEL analysis9,10,20,62,63,66,73,74,76–79,81,83,84,87,89–97,99,101,102,105 of 12CH is given in Table 1, which also provides details of the range of wavenumbers and the number of transitions measured and validated for each vibronic band, with some statistical analysis of the uncertainties characterizing the source segments. After careful analysis, altogether 29 sources could be utilized, covering a total of 6348 transitions.
| Taga | Range | A/V | Avg. unc. | Max. unc. |
|---|---|---|---|---|
| a Tags denote experimental data-source segments employed during this study. The column ‘Range’ indicates the range (in cm−1) corresponding to validated wavenumber entries within the experimental transitions list. ‘A/V’ is an ordered pair, where A and V are the number of assigned and validated transitions related to a given source segment, respectively, obtained at the end of the MARVEL analysis. | ||||
| 13TrHeHiTa102 | 0.02–0.11 | 2/2 | 2.96 × 10−9 | 4.92 × 10−9 |
| 06McMoBrTh99 | 0.11–0.49 | 3/3 | 7.04 × 10−7 | 1.00 × 10−6 |
| 85StWoBr79 | 0.11–0.11 | 1/1 | 1.69 × 10−4 | 1.69 × 10−4 |
| 83BrBr74 | 0.16–0.81 | 4/4 | 2.01 × 10−4 | 5.98 × 10−4 |
| 84BrBr76 | 0.24–23529.83 | 82/81 | 5.59 × 10−3 | 2.80 × 10−2 |
| 83BoDeDe73 | 1.46–2.54 | 5/5 | 9.34 × 10−6 | 1.33 × 10−5 |
| 95Zachwiej_C91 | 14.27–15781.09 | 138/138 | 5.58 × 10−3 | 1.58 × 10−2 |
| 00Amano96 | 17.77–17.91 | 2/2 | 8.56 × 10−5 | 1.50 × 10−4 |
| 13TrHeToLe20 | 17.77–17.91 | 2/1 | 3.50 × 10−7 | 3.50 × 10−7 |
| 01DaEvBr97 | 67.07–141.78 | 8/8 | 5.78 × 10−5 | 1.33 × 10−4 |
| 10CoBe101 | 2093.93–3036.75 | 205/204 | 2.04 × 10−2 | 5.26 × 10−2 |
| 91BeBrOlHa89 | 2162.60–27561.99 | 572/570 | 9.84 × 10−3 | 7.36 × 10−2 |
| 87Bernath83 | 2309.84–2953.36 | 183/183 | 5.52 × 10−3 | 1.46 × 10−2 |
| 89MeGrSaFa10 | 2332.12–3037.34 | 378/378 | 5.38 × 10−3 | 3.50 × 10−2 |
| 84LuAm77 | 2580.65–2937.06 | 54/54 | 1.15 × 10−3 | 3.28 × 10−3 |
| 96KePaRyZa92 | 20202.55–27562.00 | 231/228 | 1.73 × 10−2 | 1.33 × 10−1 |
| 95Zachwiej91 | 20232.36–24007.21 | 1015/974 | 1.36 × 10−2 | 2.80 × 10−1 |
| 14MaPlVaCo9 | 21842.11–31628.30 | 679/535 | 5.11 × 10−1 | 2.04 |
| 41Gero63 | 22372.25–27561.60 | 1108/1091 | 1.29 × 10−1 | 1.59 |
| 90BeKePaRy87 | 23037.98–23878.85 | 557/498 | 6.14 × 10−2 | 4.58 × 10−1 |
| 98KuHsHuLe94 | 24475.90–27548.20 | 111/93 | 2.23 × 10−1 | 5.78 × 10−1 |
| 91Para90 | 25348.38–25823.34 | 59/50 | 8.45 × 10−3 | 2.28 × 10−2 |
| 99LiKuHsLe95 | 30980.42–32048.74 | 124/116 | 2.00 × 10−1 | 2.00 × 10−1 |
| 19MeLiUb105 | 31002.32–32269.09 | 213/212 | 6.85 × 10−2 | 5.00 × 10−1 |
| 32Heimer62 | 31049.00–32388.47 | 159/133 | 2.00 × 10−1 | 2.00 × 10−1 |
| 69HeJo66 | 31226.14–64621.60 | 150/115 | 3.78 × 10−1 | 4.14 |
| 97BeKeRy93 | 31387.80–32202.22 | 63/50 | 3.55 × 10−2 | 8.50 × 10−2 |
| 86UbMeTeDy81 | 31677.57–31908.06 | 35/32 | 3.17 × 10−3 | 8.25 × 10−3 |
| 85ChChCo78 | 63685.00–64155.00 | 48/46 | 4.568 | 8.87 |
| 87ChPaChCo84 | 63686.10–69110.30 | 157/149 | 2.04 | 7.99 |
Some of the available sources had to be excluded from our final MARVEL analysis. Table 2 lists these sources and gives a brief explanation for their exclusion. In a number of cases, like 65BlNi,65 the exclusion is due to the fact that the transitions reported are simply not available in the source. Other sources claimed to have measured highly-accurate and well-resolved transitions, but the accuracy of the transition data provided is not even close to the claimed uncertainty. Another case is the example of 88LyWo,85 who report successful measurement of the A 2Δ–X 2Π R1(5.5) transition with an uncertainty of 0.0002 cm−1 but with no actual transition wavenumber given.
| Source | Reason for exclusion |
|---|---|
| 00Amano96 | Criticised by 13TrHeHiTa102 as having large systematic errors. |
| 08JaZiMcPe100 | No extractable data; focuses on magnetic resonance. |
| 14TrHeToHi103 | Data provided by 13TrHeToLe.20 |
| 19MaRoBrMu104 | Modelling/experimental study with no extractable data. |
| 56KiBr64 | Data are superceded with those from more accurate sources. |
| 65BlNi65 | No extractable data available from this source. |
| 71BaBr67 | Data are superceded with those from more accurate sources. |
| 74RyElIrSu69 | Astronomical measurement of lower accuracy than laboratory determinations. |
| 78HoMuHeEv70 | Data are superceded with those from more accurate sources. |
| 83BrEv75 | Only Hamiltonian parameters are provided. |
| 83BrBr74 | Calculated data only. |
| 88LyWo85 | No transitions data provided. |
| 88NeBrEv86 | Only Hamiltonian parameters are provided. |
| 90NeBrEv88 | Only Hamiltonian parameters are provided. |
| 91GrLaSaVa11 | No transitions data provided. |
In addition to the observed sources provided in Table 1, additional ground-state transitions were incorporated into the final input transitions file, calculated from the effective Hamiltonian (EH) term values provided by Zachwieja.91 In the input transitions file, these lines are tagged as 95Zachwiej_C.xx and they are useful for two reasons. First, they help to fix the values of the ground-state energies, which is particularly important for 12CH, as it lacks a substantial list of MW transitions. An accurate set of ground-state energies helps determining whether a rovibronic transition is an outlier and therefore improves the self-consistency of the SN. Second, use of EH values allows two or more components of the SN to be unified, as they provide linking transitions that are otherwise not present among the observed ones. Utilization of EH energies does, however, have a drawback: we do not know the accuracy of the individual energy levels. In general, the energies of lower-J states are more accurately determined by the EH method than those of states with higher J values. When experimental results conflicted with an EH value, the effective Hamiltonian value was deleted. Our final list of transitions contains 138 transitions determined using the EH approach. It is the duty of future accurate measurements to replace as many of these artificial transitions as feasible.
3.2 16OH
The full list of 16OH data sources used in the final MARVEL analysis,21,31,43,52,53,116,121,131,133,137–141,143–145,147,150,151,154 along with some characteristics, is given in Table 3. Although we aim to process all experimentally measured transitions, sometimes the earlier experimental studies are just too inaccurate to justify their inclusion into the MARVEL input transitions file. For example, in the case of the A2Σ+–X2Π band, the average uncertainty of the 9200 lines of 18YoBeHoMa53 is about 5 × 10−4 cm−1, while the accuracy of earlier works, for example, 34TaKo166 and 62DiCr,167 is significantly worse, only about 0.01−0.1 cm−1. Consequently, we decided to exclude these sources from our analysis. For similar reasons, we excluded the airglow168–171 and night-sky23,54,172,173 spectra of 16OH from our analysis, as well. Some papers recorded spectra but do not provide any line positions.114,174| Source tag | Range/cm−1 | A/V | Avg. unc. | Max. unc. |
|---|---|---|---|---|
| 09BeCo_C154 | 0.06–36721.34 | 197/197 | 3.07 × 10−3 | 2.63 × 10−2 |
| 79KeCl21 | 51.40–147.85 | 41/41 | 9.45 × 10−2 | 2.10 × 10−1 |
| 11MaPiBaBr43 | 101.28–942.57 | 215/215 | 5.16 × 10−4 | 5.00 × 10−3 |
| 91HaWh140 | 101.30–330.30 | 28/28 | 2.96 × 10−2 | 7.00 × 10−2 |
| 95MeSaGrFa145 | 361.05–3407.62 | 620/620 | 3.61 × 10−3 | 6.20 × 10−2 |
| 97PoZoViTe147 | 396.57–563.87 | 19/19 | 5.00 × 10−3 | 5.00 × 10−3 |
| 09BeCo154 | 640.95–791.94 | 31/31 | 2.00 × 10−3 | 2.00 × 10−3 |
| 83GoMuLaDo31 | 814.32–961.66 | 31/31 | 8.55 × 10−3 | 1.05 × 10−1 |
| 85LeBoDe133 | 918.81–1095.03 | 38/38 | 2.66 × 10−3 | 3.05 × 10−2 |
| 94AbDaRaEn143 | 2066.66–8666.48 | 1925/1912 | 2.31 × 10−3 | 3.01 × 10−1 |
| 90AbDaRaEn137 | 2211.70–3922.00 | 295/286 | 5.00 × 10−3 | 5.11 × 10−2 |
| 76MaChMa121 | 2696.00–10358.28 | 1117/1057 | 1.05 × 10−2 | 1.13 × 10−1 |
| 84Amano131 | 3280.04–3767.76 | 38/38 | 5.55 × 10−3 | 1.50 × 10−2 |
| 01NiHaNe150 | 3558.07–3855.04 | 23/23 | 1.27 × 10−2 | 4.14 × 10−2 |
| 16BrBeWeSn52 | 4308.76–7154.83 | 351/351 | 8.00 × 10−4 | 2.61 × 10−3 |
| 02TeBeZoSh151 | 5540.67–6866.25 | 300/289 | 6.25 × 10−3 | 4.39 × 10−2 |
| 90SaCo138 | 7657.31–36730.42 | 75/65 | 2.93 × 10−1 | 4.00 × 10−1 |
| 18YoBeHoMa53 | 15702.77–43408.75 | 9257/9257 | 8.01 × 10−4 | 2.10 × 10−2 |
| 91CoSaCo139 | 17898.38–39286.60 | 328/320 | 4.79 × 10−1 | 5.50 × 10−1 |
| 94StBrAb144 | 29998.33–33059.25 | 562/562 | 1.42 × 10−2 | 7.00 × 10−2 |
| 72Engleman116 | 32122.39–35560.02 | 107/107 | 1.02 × 10−1 | 3.00 × 10−1 |
| 93CoChCo141 | 34993.51–46930.92 | 340/340 | 1.55 × 10−2 | 2.55 × 10−1 |
For a successful MARVEL analysis of transitions data one needs to construct a well-connected SN. It is essential to know the rotational energy levels of the vibrational ground state. Since there are no high-accuracy pure rotational measurements for 16OH, we had to rely on calculated energy levels, based on the EH results of 09BeCo.154 The calculated lines included are denoted by ‘_C’ in the database.
4 MARVEL results
4.1 12CH
A total of 6348 assigned transitions from 29 distinct data sources were included in our final MARVEL analysis of the measured spectra of 12CH. From these transitions 5906 lines belong to the principal component, determining 1521 empirical (MARVEL) energy levels. Our database contains 49 floating transitions (transitions which could not be linked to the principal component), as well, linking 82 rovibronic energy levels. These floating transitions are retained in the dataset as they might be linked easily to the principal component when new experimental data become available.After the necessary reassignments, only 393 transitions had to be removed from the dataset considered by the final MARVEL analysis, as they are not consistent with the validated transitions. These transitions are retained in the final list of transitions but are given as negative wavenumber entries. Table 4 gives a brief summary of the characteristics of the MARVEL results obtained for the seven doublet electronic states studied. The transitions file and the energy levels are given in the ESI.†
| State | v range | Levels | Unc. range | Avg. unc. | Range of energy levels |
|---|---|---|---|---|---|
| X2Π | 0–5 | 711 | 0.0000–1.3510 | 0.0252 | 0.0000–21277.3362 |
| A2Δ | 0–5 | 514 | 0.0051–1.0013 | 0.1910 | 23260.1771–39244.0815 |
| B2Σ− | 0–1 | 109 | 0.0071–0.5001 | 0.1026 | 25712.5053–31474.7352 |
| C2Σ+ | 0–2 | 141 | 0.0054–0.5001 | 0.0736 | 31791.6558–43701.3123 |
| D2Π | 0–2 | 58 | 0.1000–4.1430 | 0.7270 | 58999.2647–65867.9341 |
| E2Σ+ | 2–2 | 25 | 0.5000–2.7250 | 0.9777 | 68793.1355–70652.4969 |
| F2Σ+ | 0–0 | 15 | 0.5000–1.0000 | 0.7539 | 64531.9000–64793.2681 |
4.2 16OH
Employing 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 938 measured transitions, we could determine 1624 empirical rovibronic energy levels for 16OH. The detailed validation process resulted in the deletion of 119 transitions. The present MARVEL database contains 72 floating transitions including 81 rovibronic energy levels. Future high-resolution studies may connect these floating components to the principal one.
938 measured transitions, we could determine 1624 empirical rovibronic energy levels for 16OH. The detailed validation process resulted in the deletion of 119 transitions. The present MARVEL database contains 72 floating transitions including 81 rovibronic energy levels. Future high-resolution studies may connect these floating components to the principal one.
Table 5 provides information about four experimentally measured electronic states. It is interesting to note that there are more A 2Σ+–X 2Π than X 2Π–X 2Π transitions measured (not seen in Table 5). This is solely due to the source 18YoBeHoMa,53 in which more than 9200 assigned A 2Σ+–X 2Π lines are given. The transitions file and the energy levels of this study are available in the ESI.†
| State | v Range | Levels | Unc. range | Avg. unc. | Range of energy levels |
|---|---|---|---|---|---|
| X2Π | 0–13 | 1204 | 0.0000–0.3005 | 0.0035 | 0.0000–36721.3447 |
| A2Σ | 0–9 | 350 | 0.0011–0.5000 | 0.1209 | 32440.5786–52482.2452 |
| B2Σ+ | 0–1 | 40 | 0.0051–0.7071 | 0.0527 | 68406.2992–69409.1102 |
| C2Σ+ | 0–1 | 30 | 0.6103–0.7071 | 0.6845 | 88261.1865–89690.2761 |
5 Comparison with existing datasets
The Cologne Database for Molecular Spectroscopy (CDMS),175 one of the standard spectroscopic databases, contains data neither for CH nor for OH. There are, however, several other spectroscopic datasets assembled for CH and/or OH. Comparisons of these literature datasets with the results of the present study are given next.The source 96JoLaIwYu51 supposedly contains 112![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 821 calculated lines for 12CH, involving the lowest four doublet electronic states. At the time of the writing of this paper, these data are simply unavailable; thus, no comparison could be performed.
821 calculated lines for 12CH, involving the lowest four doublet electronic states. At the time of the writing of this paper, these data are simply unavailable; thus, no comparison could be performed.
5.1 MoLLIST55 for 12CH
We used the term values of the CH dataset of 14MaPlVaCo,9 downloaded from the VizieR website,176 to compare with our final empirical (MARVEL) energy levels. Fig. 2 shows the differences between the empirical energy levels of this study and the results of 14MaPlVaCo9 for the X 2Π, A 2Δ, and B 2Σ− electronic states.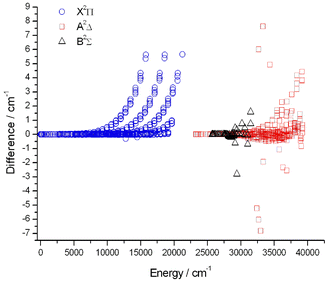 | ||
| Fig. 2 Differences between the MARVEL energy levels of this study and the empirical results of 14MaPlVaCo,9 concerning the X2Π, A2Σ+, and B2Σ− electronic states of the 12CH radical. | ||
Unfortunately, we found several conflicts between the positions of newly identified lines, Tables A.2–A.4 of ref. 9, and the official ESI of that study (and the latest version of this database downloaded from the VizieR website176). There are conflicts, for example, concerning the labels. To wit, according to Table A.2 of ref. 9, the transition at 22440.19 cm−1 is P22ff(17.5), but in the ESI it is designated as P22ee(17.5), i.e., there is a conflict in the rotationless parity. We found several similar cases and we used the labels found in the ESI during this analysis. Furthermore, Table A.3 of ref. 9 contains several non-existent rovibrational energy levels in the B 2Σ− state. For example, this table contains P22ff transitions, but in the 2Σ− state the parity of an F = 2 level is ‘e’.
As seen in Fig. 2, there are a few energies where the deviations are larger than 1 cm−1. The reason for these large differences is also the conflict between the 14MaPlVaCo article and its ESI. For example, the difference between the MARVEL and the 14MaPlVaCo values for the (A2Delta 3 11.5 e 2) level is more than 6.0 cm−1. In Table A.2 of ref. 9, the wavenumber of the P22ee(12.5) line is 22606.47 cm−1, but the wavenumber of this line in the ESI is 22612.49 cm−1.
5.2 MoLLIST55 for 16OH
We used the term values of the MoLLIST55 OH dataset downloaded from the ExoMol website,177,178 to compare with our final empirical energy levels. Fig. 3 shows the deviations between the empirical energy levels of this study and the results of the MoLLIST OH dataset for the X 2Π and A 2Σ+ electronic states.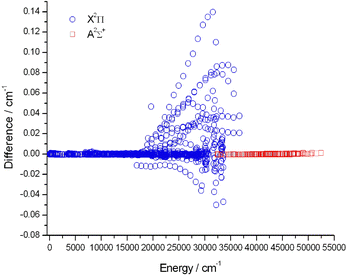 | ||
| Fig. 3 Differences between the MARVEL energy levels of this study and the empirical results of MoLLIST,55 concerning the X2Π and A2Σ+ electronic states of the 16OH radical. | ||
Fig. 3 shows that between 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and 40
000 and 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 there are several energies where the deviations are larger than 0.01 cm−1. It seems that there are conflicts between the measured transitions of 94AbDaRaEn143 and 95MeSaGrFa145 and the fitted MoLLIST55 results.
000 cm−1 there are several energies where the deviations are larger than 0.01 cm−1. It seems that there are conflicts between the measured transitions of 94AbDaRaEn143 and 95MeSaGrFa145 and the fitted MoLLIST55 results.
Furthermore, we compared the term values of 09BeCo154 to the MARVEL energy levels of the B 2Σ+ electronic state. Fig. 4 shows the deviations between the MARVEL energy levels and the results of 09BeCo154 for the B 2Σ+ electronic state. The MARVEL energy levels are determined by the measured transitions of 91CoSaCo139 and it is important to note that the authors of 91CoSaCo excluded from the fitting the last two transitions (clear outliers in Fig. 4). This explains why the differences between the MARVEL and the 09BeCo154 results are much larger in the case of the last two energy levels.
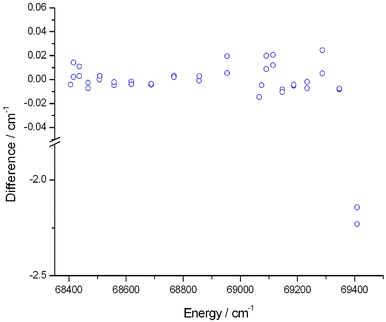 | ||
| Fig. 4 Differences between the MARVEL energy levels and the earlier results of 09BeCo154 concerning the B2Σ+ state of the 16OH radical. | ||
5.3 HITRAN and GEISA databases of 16OH
The canonical spectroscopic database and information system HITRAN202049 contains 55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 698 rovibronic transitions for the 16OH radical, involving the X 2Π and A 2Σ+ electronic states and the transitions go all the way up to 43408.75 cm−1. Therefore, it can be used to check the completeness of our empirical MARVEL dataset. Most of the line positions of the X 2Π–X 2Π and A 2Σ+–X 2Π bands have been updated in HITRAN2020, using the calculated parameters of 16BrBeWeSn.52
698 rovibronic transitions for the 16OH radical, involving the X 2Π and A 2Σ+ electronic states and the transitions go all the way up to 43408.75 cm−1. Therefore, it can be used to check the completeness of our empirical MARVEL dataset. Most of the line positions of the X 2Π–X 2Π and A 2Σ+–X 2Π bands have been updated in HITRAN2020, using the calculated parameters of 16BrBeWeSn.52
Since the line positions of HITRAN2020 are based on effective Hamiltonian calculations, it is not surprising that there are about 43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 lines that are not available in our MARVEL database, which contains almost exclusively experimental information. Of the transitions common to both HITRAN and MARVEL, we could reproduce about 13
000 lines that are not available in our MARVEL database, which contains almost exclusively experimental information. Of the transitions common to both HITRAN and MARVEL, we could reproduce about 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 lines within 0.05 cm−1. There are 370 HITRAN transitions where the differences between the HITRAN and the MARVEL lines are larger than 0.05 cm−1.
000 lines within 0.05 cm−1. There are 370 HITRAN transitions where the differences between the HITRAN and the MARVEL lines are larger than 0.05 cm−1.
Similar to the HITRAN2020 database, the recent version of GEISA-202050 is based on EH calculations. This database contains 42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 866 rovibronic transitions in the X 2Π–X 2Π and A 2Σ+–X 2Π band systems up to 35877.03 cm−1. The GEISA-2020 database also contains about 25
866 rovibronic transitions in the X 2Π–X 2Π and A 2Σ+–X 2Π band systems up to 35877.03 cm−1. The GEISA-2020 database also contains about 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 lines that are not part of our experimental database. Since the GEISA database does not contain exact information about the e/f parity, we could not perform a line-by-line comparison.
000 lines that are not part of our experimental database. Since the GEISA database does not contain exact information about the e/f parity, we could not perform a line-by-line comparison.
6 Hyperfine transitions
Although MARVEL has been used for the analysis of the spectra of a number of two- to five-atomic species, thus far networks of hyperfine-resolved transitions have not been considered. In those cases where hyperfine-resolved measured lines were available, only their average was utilized.61,179 For the radicals 12CH and 16OH, we decided to retain at least some of the experimental information about the hyperfine lines in the MARVEL transitions input file. Most of the published measured transitions are given in MHz; therefore, we keep this unit in our MARVEL database.Note that there are several outstanding papers which report highly accurate spin-rotation splittings within the A and C states of 12CH81,82 and the A 2Σ+ state of 16OH.71,72,122,127,130,136 For example, 86MeUbDy136 contains hyperfine-resolved transitions between e/f doublets in the v = 0 vibrational state, 83MeMaMeDy130 contains similar data for both the v = 0 and v = 1 vibrational states of 16OH, and 18FaFuMe157 provides 12 highly accurate hyperfine-resolved transitions connecting the X and A states of 16OH.
None of the hyperfine lines discussed here were employed during the MARVEL analysis of the large amount of hyperfine-unresolved data. The issue of how to combine a mixture of hyperfine resolved and unresolved transitions within a MARVEL procedure is a subject of active study180 and one we plan to address elsewhere.
6.1 12CH
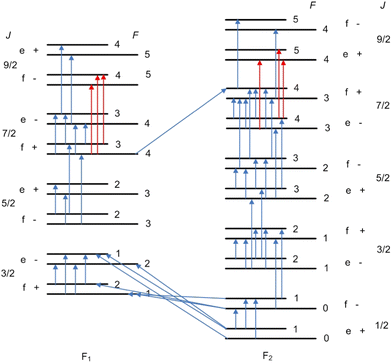
To construct the spectroscopic network of the hyperfine-resolved transitions for the 12CH radical we collected all available measured transitions belonging to the ground (v = 0) vibrational state. The full list of data sources employed in the final hyperfine MARVEL analysis of 12CH is given in Table 6, which also provides details on the range of frequencies and the number of transitions measured and validated, along with some statistical data about the uncertainties of the sources. This table also shows that we collected 73 transitions from 9 sources. In order to get a complete energy value set up to J = 9/2, we had to add 6 calculated lines (published in 01DaEvBr97) to the database.| Source tag | Range/MHz | A/V | Avg. unc./MHz | Max. unc./MHz |
|---|---|---|---|---|
| 85ZiTu80 | 701.68–724.79 | 2/2 | 1.00 × 10−2 | 1.00 × 10−2 |
| 13TrHeToLe20 | 701.68–3349.19 | 7/7 | 9.71 × 10−6 | 2.10 × 10−5 |
| 73RyElIr68 | 3263.79–3349.19 | 3/3 | 3.00 × 10−3 | 3.00 × 10−3 |
| 06CaMoBrTh98 | 3263.80–14778.96 | 9/9 | 2.00 × 10−3 | 3.00 × 10−3 |
| 83BrBr74 | 4847.84–24482.10 | 14/14 | 4.61 × 10−1 | 1.00 × 10−0 |
| 84BrBr76 | 7274.78–7398.38 | 4/4 | 2.63 × 10−1 | 4.50 × 10−1 |
| 00Amano96 | 532721.33–536795.68 | 6/6 | 2.90 × 10−1 | 8.50 × 10−1 |
| 13TrHeHiTa102 | 532721.59–536795.57 | 6/6 | 6.00 × 10−4 | 6.00 × 10−4 |
| 01DaEvBr97 | 2010810.46–4250352.95 | 16/15 | 1.53 × 10−1 | 6.50 × 10−1 |
| 01DaEvBr_C97 | 3376791.22–4238488.08 | 6/6 | 1.37 × 10−1 | 1.60 × 10−1 |
Fig. 5 shows the SN of the hyperfine transitions measured for the 12CH radical. As also seen there, we cannot reach the f and e levels of J = 9/2 energy states of F1 and F2, respectively, without the calculated transitions (red lines). Since this MARVEL database contains only the hyperfine transitions of the ground (v = 0) vibrational and electronic state, the following four descriptors were employed to label the rotational levels: Ω (1 for the F1 and 2 for the F2 component), J, the rotationless parity (e/f), and the total angular momentum F. Table 7 contains the first 36 MARVEL -determined hyperfine energy levels up to J = 9/2. As seen there, there are three hyperfine energy levels within the F2 component which are known with an outstanding accuracy of just a few (3–6) Hz.
| J | F1 | F2 | ||||||
|---|---|---|---|---|---|---|---|---|
| Parity | F | Energy/MHz | Unc./MHz | Parity | F | Energy/MHz | Unc./MHz | |
| 1/2 | e | 0 | 0.000 | 0.000 | ||||
| 1/2 | e | 1 | 13.713200 | 4.24 × 10−6 | ||||
| 1/2 | f | 0 | 3277.506647 | 5.20 × 10−6 | ||||
| 1/2 | f | 1 | 3349.192556 | 3.00 × 10−6 | ||||
| 3/2 | f | 1 | 536070.7812 | 6.00 × 10−4 | e | 1 | 2006762.629 | 2.00 × 10−1 |
| 3/2 | f | 2 | 536073.0819 | 6.00 × 10−4 | e | 2 | 2006812.83 | 2.00 × 10−1 |
| 3/2 | e | 2 | 536774.7595 | 6.00 × 10−4 | f | 1 | 2014087.83 | 2.00 × 10−1 |
| 3/2 | e | 1 | 536795.5695 | 6.00 × 10−4 | f | 2 | 2014161.25 | 2.00 × 10−1 |
| 5/2 | f | 3 | 2193034.61 | 4.58 × 10−1 | e | 2 | 4592650.00 | 2.24 × 10−1 |
| 5/2 | f | 2 | 2193043.82 | 4.96 × 10−1 | e | 3 | 4592693.00 | 2.24 × 10−1 |
| 5/2 | e | 2 | 2197913.93 | 6.38 × 10−1 | f | 2 | 4607406.67 | 2.24 × 10−1 |
| 5/2 | e | 3 | 2197882.44 | 6.08 × 10−1 | f | 3 | 4607471.96 | 2.24 × 10−1 |
| 7/2 | f | 4 | 4718557.56 | 4.47 × 10−1 | e | 3 | 7999837.21 | 2.69 × 10−1 |
| 7/2 | f | 3 | 4718571.82 | 4.86 × 10−1 | e | 4 | 7999876.51 | 2.45 × 10−1 |
| 7/2 | e | 4 | 4729822.75 | 3.32 × 10−1 | f | 3 | 8024257.39 | 2.45 × 10−1 |
| 7/2 | e | 3 | 4729858.84 | 5.71 × 10−1 | f | 4 | 8024319.08 | 2.45 × 10−1 |
| 9/2 | f | 5 | 8095348.78 | 4.66 × 10−1 | e | 4 | 12238325.35 | 2.93 × 10−1 |
| 9/2 | f | 4 | 8095365.91 | 4.69 × 10−1 | e | 5 | 12238362.39 | 2.77 × 10−1 |
| 9/2 | e | 5 | 8115282.26 | 3.46 × 10−1 | f | 4 | 12274610.34 | 2.65 × 10−1 |
| 9/2 | e | 4 | 8115321.04 | 5.80 × 10−1 | f | 5 | 12274669.61 | 3.32 × 10−1 |
6.2 16OH
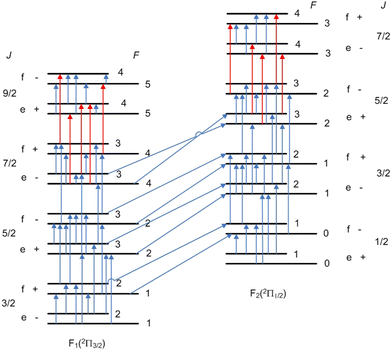
The SN of hyperfine-resolved transitions of 16OH is considerably larger than that of 12CH, containing more than 200 experimentally-measured hyperfine transitions, collected from 27 sources. MARVEL can only determine the absolute energy of a quantum state if, within the SN, there is a path leading from the given level to the lowest energy level. There are no hyperfine-resolved transitions connecting the different vibrational states of 16OH; thus, only the ground (v = 0) vibrational state is investigated here.We used the same four descriptors to label the rotational levels of 16OH hyperfine energies as in the case of 12CH: Ω (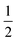 for the F2 and
for the F2 and 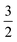 for the F1 component), J, the rotationless parity (e/f), and the total angular momentum F. As mentioned earlier, we followed the e/f scheme and the order of the F numbers advocated in 78BrKaKeMi (see Fig. 3 of 78BrKaKeMi165). This means that in the 2Π3/2 component the order of the quantum number F inverts above
for the F1 component), J, the rotationless parity (e/f), and the total angular momentum F. As mentioned earlier, we followed the e/f scheme and the order of the F numbers advocated in 78BrKaKeMi (see Fig. 3 of 78BrKaKeMi165). This means that in the 2Π3/2 component the order of the quantum number F inverts above 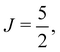 with larger F values belonging to lower energies. For the 2Π1/2 case the order of (e/f) parity components swaps for
with larger F values belonging to lower energies. For the 2Π1/2 case the order of (e/f) parity components swaps for 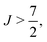 with the f states lying at lower energy. The full list of data sources employed in the final MARVEL analysis of the hyperfine lines of 16OH is given in Table 8. This table also provides details on the range of frequencies and the number of transitions measured and validated, along with some statistical data about the uncertainties of the sources.
with the f states lying at lower energy. The full list of data sources employed in the final MARVEL analysis of the hyperfine lines of 16OH is given in Table 8. This table also provides details on the range of frequencies and the number of transitions measured and validated, along with some statistical data about the uncertainties of the sources.
| Source tag | Range/MHz | A/V | Avg. unc./MHz | Max. unc./MHz |
|---|---|---|---|---|
| 75DeMa119 | 7.43–23838.93 | 11/11 | 2.50 × 10−2 | 5.23 × 10−2 |
| 75MeDy120 | 88.95–23826.62 | 17/17 | 5.88 × 10−3 | 1.00 × 10−2 |
| 73MeDy118 | 88.95–193.00 | 4/4 | 5.00 × 10−4 | 5.00 × 10−4 |
| 76MeMeMiDy122 | 1171.49–13441.42 | 11/11 | 1.82 × 10−3 | 5.00 × 10−3 |
| 06LeMeHuSa153 | 1612.23–1720.53 | 2/2 | 4.75 × 10−5 | 8.50 × 10−5 |
| 64Radford109 | 1612.23–1720.53 | 4/4 | 2.33 × 10−3 | 3.30 × 10−3 |
| 72MeDy117 | 1612.23–1720.53 | 4/4 | 1.25 × 10−4 | 2.00 × 10−4 |
| 79CoSaAuLe125 | 1612.23–66133.35 | 12/12 | 2.55 × 10−2 | 5.00 × 10−2 |
| 06HuLeSaYe152 | 1665.40–1667.36 | 2/2 | 8.00 × 10−6 | 1.20 × 10−5 |
| 59EhToSt108 | 1665.46–1667.34 | 2/2 | 6.50 × 10−2 | 1.00 × 10−1 |
| 68Goss111 | 1720.53–1720.53 | 1/1 | 3.00 × 10−3 | 3.00 × 10−3 |
| 68Radford113 | 4660.24–6049.08 | 7/7 | 6.56 × 10−3 | 1.10 × 10−2 |
| 70BaDiGoRa115 | 7749.91–7831.96 | 4/4 | 5.00 × 10−3 | 5.00 × 10−3 |
| 55DoSaTo107 | 7760.36–36994.43 | 12/12 | 6.31 | 35.75 |
| 77DeMaBaBr123 | 8534.86–70858.93 | 20/20 | 3.11 × 10−2 | 1.20 × 10−1 |
| 80SaVa128 | 13433.96–13442.13 | 4/4 | 2.64 × 10−2 | 5.35 × 10−2 |
| 99ThWuSpMe148 | 13434.00–13442.08 | 4/4 | 9.92 × 10−3 | 2.47 × 10−2 |
| 68PoBe112 | 13434.62–36994.43 | 8/8 | 1.15 × 10−1 | 4.78 × 10−1 |
| 96WuSpMeAn146 | 13434.64–13441.42 | 2/2 | 5.00 × 10−4 | 5.00 × 10−4 |
| 65PoLi110 | 13434.65–13441.41 | 2/2 | 2.00 × 10−2 | 2.00 × 10−2 |
| 53SaScDoTo106 | 23818.16–36994.43 | 4/4 | 3.01 × 10−1 | 5.99 × 10−1 |
| 81KoZoLe129 | 66094.85–70887.99 | 6/6 | 3.33 × 10−2 | 5.00 × 10−2 |
| 93VaEv_C142 | 1834735.02–4602881.87 | 35/35 | 7.90 × 10−2 | 1.56 × 10−1 |
| 13Drouin156 | 1834735.06–2603427.29 | 17/17 | 5.34 × 10−1 | 2.37 |
| 86BlFaPi134 | 1834735.51–3036645.05 | 17/17 | 9.37 × 10−1 | 2.47 |
| 86BrZiJeEv135 | 1837816.39–3789214.99 | 22/22 | 7.79 × 10−1 | 4.74 |
| 93VaEv142 | 1837816.39–4209632.49 | 13/13 | 1.20 × 10−1 | 4.00 × 10−1 |
| 85FaBlPi132 | 2509935.44–2509988.61 | 3/3 | 8.04 × 10−1 | 8.08 × 10−1 |
Fig. 6 shows the SN representation of the hyperfine transitions of the 16OH radical on its ground electronic and vibrational state. As seen there, we can reach the J = 9/2 and 7/2 energy levels of the F2 and F1 components, respectively, if we use the calculated hyperfine transitions of 93VaEv142 (red lines).
Table 9 contains the first 32 MARVEL-determined hyperfine energy levels. It is interesting to note that the most accurate transition, provided by 06HuLeSaYe,152 is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 667
667![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 358
358![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 996 ± 4 Hz; therefore, the uncertainty of the (X2Pi 1.5 0 1.5 e 2) level is an outstanding 10−10 cm−1 (i.e., better than 10−5 MHz, see Table 9). There are three hyperfine energy levels in the F1 component which have remarkable, about 10 Hz accuracy.
996 ± 4 Hz; therefore, the uncertainty of the (X2Pi 1.5 0 1.5 e 2) level is an outstanding 10−10 cm−1 (i.e., better than 10−5 MHz, see Table 9). There are three hyperfine energy levels in the F1 component which have remarkable, about 10 Hz accuracy.
| J | F1 | F2 | ||||||
|---|---|---|---|---|---|---|---|---|
| Parity | F | Energy/MHz | Unc./MHz | Parity | F | Energy/MHz | Unc./MHz | |
| 1/2 | e | 0 | 3786170.1 | 1.56 × 10−1 | ||||
| 1/2 | e | 1 | 3786185.0 | 1.56 × 10−1 | ||||
| 1/2 | f | 0 | 3790845.3 | 1.56 × 10−1 | ||||
| 1/2 | f | 1 | 3790935.7 | 1.56 × 10−1 | ||||
| 3/2 | e | 1 | 0.000 | 0.000 | e | 1 | 5620920.0 | 1.56 × 10−1 |
| 3/2 | e | 2 | 53.170893 | 1.08 × 10−5 | e | 2 | 5620931.9 | 1.56 × 10−1 |
| 3/2 | f | 1 | 1665.40180 | 1.20 × 10−5 | f | 1 | 5628681.8 | 1.56 × 10−1 |
| 3/2 | f | 2 | 1720.52989 | 1.00 × 10−5 | f | 2 | 5628752.0 | 1.56 × 10−1 |
| 5/2 | e | 2 | 2509987.83 | 2.84 × 10−2 | e | 2 | 8657190.1 | 1.57 × 10−1 |
| 5/2 | e | 3 | 2510001.83 | 2.80 × 10−2 | e | 3 | 8657207.9 | 1.57 × 10−1 |
| 5/2 | f | 2 | 2516018.58 | 2.84 × 10−2 | f | 2 | 8665326.0 | 1.57 × 10−1 |
| 5/2 | f | 3 | 2516036.92 | 2.80 × 10−2 | f | 3 | 8665397.5 | 1.57 × 10−1 |
| 7/2 | e | 4 | 6053780.92 | 3.21 × 10−2 | e | 3 | 12869482.9 | 1.89 × 10−1 |
| 7/2 | e | 3 | 6053788.36 | 3.17 × 10−2 | e | 4 | 12869506.5 | 1.89 × 10−1 |
| 7/2 | f | 4 | 6067222.34 | 3.21 × 10−2 | f | 3 | 12874956.0 | 1.89 × 10−1 |
| 7/2 | f | 3 | 6067223.00 | 3.17 × 10−2 | f | 4 | 12875030.0 | 1.89 × 10−1 |
| 9/2 | e | 5 | 10646265.25 | 8.34 × 10−2 | f | 4 | ||
| 9/2 | e | 4 | 10646286.57 | 8.33 × 10−2 | f | 5 | ||
| 9/2 | f | 5 | 10670091.87 | 8.34 × 10−2 | e | 4 | ||
| 9/2 | f | 4 | 10670104.18 | 8.33 × 10−2 | e | 5 | ||
6.3 Comparison with the JPL catalog for 12CH and 16OH
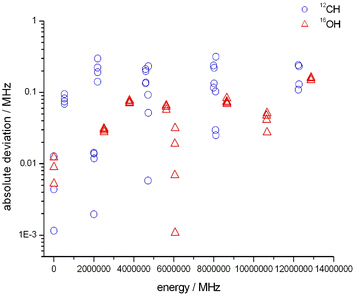
The Jet Propulsion Laboratory (JPL) catalog56 contains submillimeter, millimeter, and microwave spectral lines in the frequency range between 0 and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 GHz for more than 300 atomic and molecular species. Since the JPL catalog contains both calculated and experimental lines, with the corresponding ‘experimental’ energy levels, it was an obvious choice to use this database to check the quality of the empirical (MARVEL) results of this study. Fig. 7 shows the differences between the MARVEL and the JPL energy levels, both for 12CH and 16OH.
000 GHz for more than 300 atomic and molecular species. Since the JPL catalog contains both calculated and experimental lines, with the corresponding ‘experimental’ energy levels, it was an obvious choice to use this database to check the quality of the empirical (MARVEL) results of this study. Fig. 7 shows the differences between the MARVEL and the JPL energy levels, both for 12CH and 16OH.
 | ||
| Fig. 7 Comparison of the empirical (MARVEL) energy levels of this study with those of the JPL dataset for 12CH (blue circles) and 16OH (red triangles). | ||
For 12CH, the JPL catalog lists 58 experimentally measured hyperfine transitions and this dataset was extended with 67 lines of FT-IR measurements,83 which are not hyperfine resolved. The accuracy of the lines in the emission spectrum of 87Bernath83 is significantly worse than that of the hyperfine measurements; therefore, we decided to consider only the 58 hyperfine lines during the comparison. As Fig. 7 shows (see the empty blue circles), most of the differences between the empirical energy levels of this study and those of the JPL database are less than 200 kHz.
For the OH radical, the JPL catalog lists 3153 experimentally measured transitions, which belong to six isotopologues. From the transitions listed, 739 lines belong to the vibrational ground state of 16OH. It is important to note that the JPL database contains results from a far-infrared spectrum (11MaPiBaBr,43 with 0.0002 cm−1 average uncertainty), an IR spectrum (85LeBoDe,133 with 0.001 cm−1 average uncertainty), and a solar spectrum (95MeSaGrFa,145 with 0.001 cm−1 average uncertainty). As seen in Fig. 7, the differences between the MARVEL and the JPL energy levels (red triangles) are less than 200 kHz, mutually confirming the data contained.
7 Conclusions
Accurate empirical rovibronic energy levels, with dependable, statistically significant, individual uncertainties, are reported for the following seven and four doublet electronic states of 12CH and 16OH: (X 2Π, A 2Δ, B 2Σ−, C 2Σ+, D 2Π, E 2Σ+, and F 2Σ+) and (X 2Π, A 2Σ+, B 2Σ+, and C 2Σ+), respectively. For 12CH, a total of 1521 rovibronic energy levels are determined in the principal component of its measured spectroscopic network (SN), utilizing 6348 experimentally measured and validated transitions. For 16OH, after a careful analysis and validation of 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 938 rovibronic transitions, collected from 45 sources, 1624 empirical rovibronic energy levels are determined. Determination of the empirical energy levels is based on the Measured Active Rotational-Vibrational Energy Levels (MARVEL) algorithm.
938 rovibronic transitions, collected from 45 sources, 1624 empirical rovibronic energy levels are determined. Determination of the empirical energy levels is based on the Measured Active Rotational-Vibrational Energy Levels (MARVEL) algorithm.
The hyperfine lines measured for the two radicals are included in the MARVEL analysis. These accurately measured transitions form floating components within the SN; thus, at the moment, they do not contribute toward improving the overall accuracy of the experimental SNs of 12CH and 16OH. Nevertheless, in the near future it might become possible to connect the hyperfine-resolved and-unresolved components, see, for example, Bowesman et al.180 The most accurate line is provided by 06HuLeSaYe152 at 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 667
667![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 358
358![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 996 ± 4 Hz which allows the (X2Pi 1.5 0 1.5 e 2) level to be determined with an uncertainty of only 10−10 cm−1.
996 ± 4 Hz which allows the (X2Pi 1.5 0 1.5 e 2) level to be determined with an uncertainty of only 10−10 cm−1.
The present database of 12CH and 16OH transitions and energy levels are compared to several line lists, including the HITRAN2020,49 GEISA,50 MoLLIST,9 and JPL56 datasets. This comparison shows an overall satisfactory agreement and also points toward the inaccuracy of a small subset of effective Hamiltonian energies.
The large set of data presented should serve as a starting point to refine the line lists of these radicals. Such attempts have been made by us before, see the case of 12C2.181 We note that the determination of accurate energy levels will allow a large number of new transitions to be predicted with experimental accuracy; in the case of our recent study of formaldehyde (H2CO) this gearing led to a more than a twenty-fold increase in the number of predicted transitions relative to the number of unique measured transitions.182
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The work performed in London was supported by the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme through Advance Grant number 883830, and STFC grant ST/R000476/1. The work executed in Budapest received support from NKFIH (grant no. K138233). The authors are grateful to Thomas Masseron, Brian J. Drouin, Iouli E. Gordon, Peter F. Bernath, and Uffe Gråe Jørgensen for helpful discussions.Notes and references
- A. G. Császár, G. Czakó, T. Furtenbacher and E. Mátyus, Annu. Rep. Comput. Chem., 2007, 3, 155–176 CrossRef.
- T. Furtenbacher, A. G. Császár and J. Tennyson, J. Mol. Spectrosc., 2007, 245, 115–125 CrossRef CAS.
- T. Furtenbacher and A. G. Császár, J. Quant. Spectrosc. Radiat. Transfer, 2012, 113, 929–935 CrossRef CAS.
- A. G. Császár, T. Furtenbacher and P. Árendás, J. Phys. Chem. A, 2016, 120, 8949–8969 CrossRef PubMed.
- R. Tóbiás, T. Furtenbacher, J. Tennyson and A. G. Császár, Phys. Chem. Chem. Phys., 2019, 21, 3473–3495 RSC.
- T. Heurlinger, PhD thesis, 1918 Search PubMed.
- P. Swings and L. Rosenfeld, Astrophys. J., 1937, 86, 483–486 CrossRef CAS.
- S. Weinreb, A. H. Barrett, M. L. Meeks and J. C. Henry, Nature, 1963, 200, 829–831 CrossRef CAS.
- T. Masseron, B. Plez, S. Van Eck, R. Colin, I. Daoutidis, M. Godefroid, P.-F. Coheur, P. Bernath, A. Jorissen and N. Christlieb, Astron. Astrophys., 2014, 571, A47 CrossRef.
- F. Mélen, N. Grevesse, A. J. Sauval, C. B. Farmer, R. H. Norton, H. Bredohl and I. Dubois, J. Mol. Spectrosc., 1989, 134, 305–313 CrossRef.
- N. Grevesse, D. L. Lambert, A. J. Sauval, E. F. van Dishoeck, C. B. Farmer and R. H. Norton, Astron. Astrophys., 1991, 242, 488–495 CAS.
- R. Meier, D. Wellnitz, S. J. Kim and M. F. A'Hearn, Icarus, 1998, 136, 268–279 CrossRef CAS.
- S. Bottinelli, V. Wakelam, E. Caux, C. Vastel, Y. Aikawa and C. Ceccarelli, Mon. Not. R. Astron. Soc., 2014, 441, 1964–1973 CrossRef CAS.
- N. K. Rao, D. L. Lambert, A. B. S. Reddy, D. A. Garca-Hernández, A. Manchado and J. Daz-Luis, Publ. Astron. Soc. Pac., 2020, 132, 074201 CrossRef.
- J. B. Whiteoak, F. F. Gardner and B. Höglund, Mon. Not. R. Astron. Soc., 1980, 190, 17–22 CrossRef.
- M. Gerin, D. A. Neufeld and J. R. Goicoechea, Annu. Rev. Astron. Astrophys., 2016, 54, 181–225 CrossRef CAS.
- H. E. Bond, Astrophys. J., 1974, 194, 95–107 CrossRef CAS.
- A. Goswami, Mon. Not. R. Astron. Soc., 2005, 359, 531–544 CrossRef CAS.
- P. Versailles, G. M. Watson, A. C. Lipardi and J. M. Bergthorson, Combust. Flame, 2016, 165, 109–124 CrossRef CAS.
- S. Truppe, R. J. Hendricks, S. K. Tokunaga, H. J. Lewandowski, M. G. Kozlov, C. Henkel, E. A. Hinds and M. R. Tarbutt, Nat. Commun., 2013, 4, 2600 CrossRef CAS.
- D. Kendall and T. Clark, J. Quant. Spectrosc. Radiat. Transfer, 1979, 21, 511–526 CrossRef CAS.
- S. Gligorovski, R. Strekowski, S. Barbati and D. Vione, Chem. Rev., 2015, 115, 13051–13092 CrossRef CAS PubMed.
- D. E. Osterbrock, J. P. Fulbright, A. R. Martel, M. J. Keane, S. C. Trager and G. Basri, Publ. Astron. Soc. Pac., 1996, 108, 277 CrossRef.
- C. Franzen, P. J. Espy, N. Hofmann, R. E. Hibbins and A. A. Djupvik, Atmosphere, 2019, 10, 637 CrossRef CAS.
- O. Garmash, M. P. Rissanen, I. Pullinen, S. Schmitt, O. Kausiala, R. Tillmann, D. Zhao, C. Percival, T. J. Bannan, M. Priestley, A. M. Hallquist, E. Kleist, A. Kiendler-Scharr, M. Hallquist, T. Berndt, G. McFiggans, J. Wildt, T. Mentel and M. Ehn, Atmos. Chem. Phys., 2020, 20, 515–537 CrossRef CAS.
- M. Blocquet, C. Schoemaecker, D. Amedro, O. Herbinet, F. Battin-Leclerc and C. Fittschen, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 20014–20017 CrossRef CAS PubMed.
- S. K. Nugroho, H. Kawahara, N. P. Gibson, E. J. W. de Mooij, T. Hirano, T. Kotani, Y. Kawashima, K. Masuda, M. Brogi and J. L. Birkby, et al. , Astrophys. J., Lett., 2021, 910, L9 CrossRef CAS.
- K. Takanabe, A. M. Khan, Y. Tang, L. Nguyen, A. Ziani, B. W. Jacobs, A. M. Elbaz, S. M. Sarathy and F. F. Tao, Angew. Chem., Int. Ed., 2017, 56, 10403–10407 CrossRef CAS PubMed.
- Z. Wang, X. Chen, F. Gao, S. Zhang, X.-W. Zheng, W.-H. Ip, N. Wang, X. Liu, X.-T. Zuo, W. Gou and S.-Q. Chang, Astron. J., 2017, 154, 249 CrossRef.
- J. Melendez, B. Barbuy and F. Spite, Astrophys. J., 2001, 556, 858–871 CrossRef CAS.
- A. Goldman, D. G. Murcray, D. L. Lambert and J. F. Dominy, Mon. Not. R. Astron. Soc., 1983, 203, 767–776 CrossRef CAS.
- S. V. Berdyugina and S. K. Solanki, Astron. Astrophys., 2001, 380, L5–L8 CrossRef CAS.
- N. Tang, D. Li, N. Yue, P. Zuo, T. Liu, G. Luo, L. Chen, S.-L. Qin, Y. Wu and C. Heiles, Astrophys. J., Suppl., 2021, 252, 1 CrossRef CAS.
- G. Piccioni, P. Drossart, L. Zasova, A. Migliorini, J. C. Gerard, F. P. Mills, A. Shakun, A. G. Munoz, N. Ignatiev, D. Grassi, V. Cottini, F. W. Taylor, S. Erard and V.-V. E. T. Team, Astron. Astrophys., 2008, 483, L29–L33 CrossRef CAS.
- R. T. Clancy, B. J. Sandor, A. Garcia-Munoz, F. Lefevre, M. D. Smith, M. J. Wolff, F. Montmessin, S. L. Murchie and H. Nair, Icarus, 2013, 226, 272–281 CrossRef.
- N. Schoerghofer, M. Benna, A. A. Berezhnoy, B. Greenhagen, B. M. Jones, S. Li, T. M. Orlando, P. Prem, O. J. Tucker and C. Woehler, Space Sci. Rev., 2021, 217, 74 CrossRef.
- J. M. Brown and A. Carrington, Rotational Spectroscopy of Diatomic Molecules, Cambridge University Press, 2010 Search PubMed.
- J. Storey, D. Watson and C. Townes, Astron. Astrophys., 1981, 244, L27–L30 CAS.
- X.-W. Liu, M. J. Barlow, A. Dalgarno, J. Tennyson, T. Lim, B. M. Swinyard, J. Cernicharo, P. Cox, J.-P. Baluteau, D. Pequignot, Nguyen-Q-Rieu, R. J. Emery and P. E. Clegg, Mon. Not. R. Astron. Soc., 1997, 290, L71–L75 CrossRef CAS.
- S.-L. Qin, P. Schilke, C. Comito, T. Möller, R. Rolffs, H. S. P. Müller, A. Belloche, K. M. Menten, D. C. Lis, T. G. Phillips, E. A. Bergin, T. A. Bell, N. R. Crockett, G. A. Blake, S. Cabrit, E. Caux, C. Ceccarelli, J. Cernicharo, F. Daniel, M.-L. Dubernet, M. Emprechtinger, P. Encrenaz, E. Falgarone, M. Gerin, T. F. Giesen, J. R. Goicoechea, P. F. Goldsmith, H. Gupta, E. Herbst, C. Joblin, D. Johnstone, W. D. Langer, S. D. Lord, S. Maret, P. G. Martin, G. J. Melnick, P. Morris, J. A. Murphy, D. A. Neufeld, V. Ossenkopf, L. Pagani, J. C. Pearson, M. Pérault, R. Plume, M. Salez, S. Schlemmer, J. Stutzki, N. Trappe, F. F. S. van der Tak, C. Vastel, S. Wang, H. W. Yorke, S. Yu, J. Zmuidzinas, A. Boogert, R. Güsten, P. Hartogh, N. Honingh, A. Karpov, J. Kooi, J.-M. Krieg, R. Schieder, M. C. Diez-Gonzalez, R. Bachiller, J. Martin-Pintado, W. Baechtold, M. Olberg, L. H. Nordh, J. L. Gill and G. Chattopadhyay, Astron. Astrophys., 2010, 521, L14 CrossRef.
- S. F. Wampfler, G. J. Herczeg, S. Bruderer, A. O. Benz, E. F. van Dishoeck, L. E. Kristensen, R. Visser, S. D. Doty, M. Melchior, T. A. van Kempen, U. A. Yldz, C. Dedes, J. R. Goicoechea, A. Baudry, G. Melnick, R. Bachiller, M. Benedettini, E. Bergin, P. Bjerkeli, G. A. Blake, S. Bontemps, J. Braine, P. Caselli, J. Cernicharo, C. Codella, F. Daniel, A. M. di Giorgio, C. Dominik, P. Encrenaz, M. Fich, A. Fuente, T. Giannini, T. de Graauw, F. Helmich, F. Herpin, M. R. Hogerheijde, T. Jacq, D. Johnstone, J. K. Jørgensen, B. Larsson, D. Lis, R. Liseau, M. Marseille, C. M. Coey, D. Neufeld, B. Nisini, M. Olberg, B. Parise, J. C. Pearson, R. Plume, C. Risacher, J. Santiago-García, P. Saraceno, R. Shipman, M. Tafalla, F. F. S. van der Tak, F. Wyrowski, P. Roelfsema, W. Jellema, P. Dieleman, E. Caux and J. Stutzki, Astron. Astrophys., 2010, 521, L36 CrossRef.
- T. R. Gull, P. W. Morris, J. H. Black, K. E. Nielsen, M. J. Barlow, P. Royer and B. M. Swinyard, Mon. Not. R. Astron. Soc., 2020, 499, 5269–5301 CrossRef CAS.
- M. A. Martin-Drumel, O. Pirali, D. Balcon, P. Bréchignac, P. Roy and M. Vervloet, Rev. Sci. Instrum., 2011, 82, 113106 CrossRef CAS PubMed.
- H. Wiesemeyer, R. Güsten, S. Heyminck, K. Jacobs, K. M. Menten, D. A. Neufeld, M. A. Requena-Torres and J. Stutzki, Astron. Astrophys., 2012, 542, L7 CrossRef.
- T. Csengeri, K. M. Menten, F. Wyrowski, M. A. Requena-Torres, R. Güsten, H. Wiesemeyer, H.-W. Hübers, P. Hartogh and K. Jacobs, Astron. Astrophys., 2012, 542, L8 CrossRef.
- A. M. Jacob, K. M. Menten, H. Wiesemeyer, M.-Y. Lee, R. Guesten and C. A. Duran, Astron. Astrophys., 2019, 632, A60 CrossRef CAS.
- T. Csengeri, F. Wyrowski, K. M. Menten, H. Wiesemeyer, R. Güsten, J. Stutzki, S. Heyminck and Y. Okada, Astron. Astrophys., 2022, 658, A193 CrossRef CAS.
- L. S. Rothman, Nat. Rev. Phys., 2021, 3, 302–304 CrossRef.
- I. E. Gordon, L. S. Rothman, R. J. Hargreaves, R. Hashemi, E. V. Karlovets, F. M. Skinner, E. K. Conway, C. Hill, R. V. Kochanov, Y. Tan, P. Wcisło, A. A. Finenko, K. Nelson, P. F. Bernath, M. Birk, V. Boudon, A. Campargue, K. V. Chance, A. Coustenis, B. J. Drouin, J.-M. Flaud, R. R. Gamache, J. T. Hodges, D. Jacquemart, E. J. Mlawer, A. V. Nikitin, V. I. Perevalov, M. Rotger, J. Tennyson, G. C. Toon, H. Tran, V. G. Tyuterev, E. M. Adkins, A. Baker, A. Barbe, E. Canè, A. G. Császár, A. Dudaryonok, O. Egorov, A. J. Fleisher, H. Fleurbaey, A. Foltynowicz, T. Furtenbacher, J. J. Harrison, J.-M. Hartmann, V.-M. Horneman, X. Huang, T. Karman, J. Karns, S. Kassi, I. Kleiner, V. Kofman, F. Kwabia-Tchana, N. N. Lavrentieva, T. J. Lee, D. A. Long, A. A. Lukashevskaya, O. M. Lyulin, V. Y. Makhnev, W. Matt, S. T. Massie, M. Melosso, S. N. Mikhailenko, D. Mondelain, H. S. P. Müller, O. V. Naumenko, A. Perrin, O. L. Polyansky, E. Raddaoui, P. L. Raston, Z. D. Reed, M. Rey, C. Richard, R. Tóbiás, I. Sadiek, D. W. Schwenke, E. Starikova, K. Sung, F. Tamassia, S. A. Tashkun, J. V. Auwera, I. A. Vasilenko, A. A. Vigasin, G. L. Villanueva, B. Vispoel, G. Wagner, A. Yachmenev and S. N. Yurchenko, J. Quant. Spectrosc. Radiat. Transfer, 2022, 277, 107949 CrossRef CAS.
- T. Delahaye, R. Armante, N. Scott, N. Jacquinet-Husson, A. Chédin, L. Crépeau, C. Crevoisier, V. Douet, A. Perrin, A. Barbe, V. Boudon, A. Campargue, L. Coudert, V. Ebert, J.-M. Flaud, R. Gamache, D. Jacquemart, A. Jolly, F. K. Tchana, A. Kyuberis, G. Li, O. Lyulin, L. Manceron, S. Mikhailenko, N. Moazzen-Ahmadi, H. Müller, O. Naumenko, A. Nikitin, V. Perevalov, C. Richard, E. Starikova, S. Tashkun, V. Tyuterev, J. V. Auwera, B. Vispoel, A. Yachmenev and S. Yurchenko, J. Mol. Spectrosc., 2021, 380, 111510 CrossRef CAS.
- U. G. Jorgensen, M. Larsson, A. Iwamae and B. Yu, Astron. Astrophys., 1996, 315, 204–211 Search PubMed.
- J. S. Brooke, P. F. Bernath, C. M. Western, C. Sneden, M. Afsar, G. Li and I. E. Gordon, J. Quant. Spectrosc. Radiat. Transfer, 2016, 168, 142–157 CrossRef CAS.
- M. Yousefi, P. F. Bernath, J. Hodges and T. Masseron, J. Quant. Spectrosc. Radiat. Transfer, 2018, 217, 416–424 CrossRef CAS.
- A. B. Meinel, Astrophys. J., 1950, 111, 555 CrossRef.
- P. F. Bernath, J. Quant. Spectrosc. Radiat. Transfer, 2020, 240, 106687 CrossRef CAS.
- Jet Propulsion Laboratory, https://spec.jpl.nasa.gov/, Accessed: 2022-04-02.
- O. L. Polyansky, K. Bielska, M. Ghysels, L. Lodi, N. F. Zobov, J. T. Hodges and J. Tennyson, Phys. Rev. Lett., 2015, 114, 243001 CrossRef PubMed.
- K. Bielska, A. A. Kyuberis, Z. D. Reed, G. Li, A. Cygan, R. Ciuryło, D. Lisak, E. M. Adkins, L. Lodi, J. T. Hodges, V. Ebert, N. F. Zobov, J. Tennyson and O. L. Polyansky, Phys. Rev. Lett., 2022, 129, 043002 CrossRef.
- J. Tennyson, S. N. Yurchenko, A. F. Al-Refaie, V. H. J. Clark, K. L. Chubb, E. K. Conway, A. Dewan, M. N. Gorman, C. Hill, A. E. Lynas-Gray, T. Mellor, L. K. McKemmish, A. Owens, O. L. Polyansky, M. Semenov, W. Somogyi, G. Tinetti, A. Upadhyay, I. Waldmann, Y. Wang, S. Wright and O. P. Yurchenko, J. Quant. Spectrosc. Radiat. Transfer, 2020, 255, 107228 CrossRef CAS.
- D. Darby-Lewis, J. Tennyson, K. D. Lawson, S. N. Yurchenko, M. F. Stamp, A. Shaw, S. Brezinsek and JET Contributor, J. Phys. B: At., Mol. Opt. Phys., 2018, 51, 185701 CrossRef.
- D. Darby-Lewis, H. Shah, D. Joshi, F. Khan, M. Kauwo, N. Sethi, P. F. Bernath, T. Furtenbacher, R. Tóbiás, A. G. Császár and J. Tennyson, J. Mol. Spectrosc., 2019, 362, 69–76 CrossRef CAS.
- T. Heimer, Z. Phys., 1932, 78, 771–780 CrossRef CAS.
- L. Gerö, Z. Phys., 1941, 118, 27–36 CrossRef.
- N. H. Kiess and H. P. Broida, Astrophys. J., 1956, 123, 166–171 CrossRef CAS.
- R. Bleekrode and W. C. Nieuwpoort, J. Chem. Phys., 1965, 43, 3680–3687 CrossRef CAS.
- G. Herzberg and J. W. C. Johns, Astrophys. J., 1969, 158, 399–418 CrossRef CAS.
- K. M. Baird and H. Bredohl, Astrophys. J., 1971, 169, L83 CrossRef CAS.
- O. E. H. Rydbeck, J. Elldér and W. M. Irvine, Nature, 1973, 246, 466–468 CrossRef CAS.
- O. E. H. Rydbeck, J. Elldér, W. M. Irvine, A. Sume and A. Hjalmarson, Astron. Astrophys., 1974, 34, 479–482 CAS.
- J. T. Hougen, J. A. Mucha, D. A. Jennings and K. M. Evenson, J. Mol. Spectrosc., 1978, 72, 463–483 CrossRef CAS.
- J. J. ter Meulen, G. W. M. van Mierlo and A. Dymanus, Phys. Rev. Lett., 1979, 43, 29–32 CrossRef CAS.
- F. Raab, T. Bergeman, D. Lieberman and H. Metcalf, Phys. Rev. A: At., Mol., Opt. Phys., 1981, 24, 3120–3135 CrossRef CAS.
- M. Bogey, C. Demuynck and J. L. Destombes, Chem. Phys. Lett., 1983, 100, 105–109 CrossRef CAS.
- J. M. Brown and K. M. Evenson, Astrophys. J., 1983, 268, L51–L56 CrossRef CAS.
- J. M. Brown and K. M. Evenson, J. Mol. Spectrosc., 1983, 98, 392–403 CrossRef CAS.
- C. R. Brazier and J. M. Brown, Can. J. Phys., 1984, 62, 1563–1578 CrossRef CAS.
- K. G. Lubic and T. Amano, Can. J. Phys., 1984, 62, 1886–1888 CrossRef CAS.
- P. Chen, W. A. Chupka and S. D. Colson, Chem. Phys. Lett., 1985, 121, 405–407 CrossRef CAS.
- T. C. Steimle, D. R. Woodward and J. M. Brown, Astrophys. J., 1985, 294, L59–L62 CrossRef CAS.
- L. M. Ziurys and B. E. Turner, Astrophys. J., 1985, 292, L25 CrossRef CAS.
- W. Ubachs, G. Meyer, J. J. ter Meulen and A. Dymanus, J. Chem. Phys., 1986, 84, 3032–3041 CrossRef CAS.
- W. Ubachs, W. M. Van Herpen, J. J. Ter Meulen and A. Dymanus, J. Chem. Phys., 1986, 84, 6575–6580 CrossRef CAS.
- P. F. Bernath, J. Chem. Phys., 1987, 86, 4838–4842 CrossRef CAS.
- P. Chen, J. B. Pallix, W. A. Chupka and S. D. Colson, J. Chem. Phys., 1987, 86, 516–520 CrossRef CAS.
- L. Lynds and B. A. Woody, Appl. Opt., 1988, 27, 1225–1227 CrossRef CAS PubMed.
- T. Nelis, J. M. Brown and K. M. Evenson, J. Chem. Phys., 1988, 88, 2087–2088 CrossRef CAS.
- Z. Bembenek, R. Kepa, A. Para, M. Rytel, M. Zachwieja, J. Janjić and E. Marx, J. Mol. Spectrosc., 1990, 139, 1–10 CrossRef CAS.
- T. Nelis, J. M. Brown and K. M. Evenson, J. Chem. Phys., 1990, 92, 4067–4076 CrossRef CAS.
- P. F. Bernath, C. R. Brazier, T. Olsen, R. Hailey, W. T. M. L. Fernando, C. Woods and J. L. Hardwick, J. Mol. Spectrosc., 1991, 147, 16–26 CrossRef CAS.
- A. Para, J. Phys. B: At., Mol. Opt. Phys., 1991, 24, 3179 CrossRef CAS.
- M. Zachwieja, J. Mol. Spectrosc., 1995, 170, 285–309 CrossRef CAS.
- R. Kepa, A. Para, M. Rytel and M. Zachwieja, J. Mol. Spectrosc., 1996, 178, 189–193 CrossRef CAS.
- Z. Bembenek, R. Ke and M. Rytel, J. Mol. Spectrosc., 1997, 183, 1–5 CrossRef CAS.
- A. Kumar, C.-C. Hsiao, W.-C. Hung and Y.-P. Lee, J. Chem. Phys., 1998, 109, 3824–3830 CrossRef CAS.
- X. Li, A. Kumar, C.-C. Hsiao and Y.-P. Lee, J. Phys. Chem. A, 1999, 103, 6162–6166 CrossRef CAS.
- T. Amano, Astrophys. J., 2000, 531, L161 CrossRef PubMed.
- S. A. Davidson, K. M. Evenson and J. M. Brown, Astrophys. J., 2001, 546, 330–337 CrossRef CAS.
- M. C. McCarthy, S. Mohamed, J. M. Brown and P. Thaddeus, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 12263–12268 CrossRef CAS PubMed.
- M. C. McCarthy, S. Mohamed, J. M. Brown and P. Thaddeus, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 12263–12268 CrossRef CAS PubMed.
- M. Jackson, L. R. Zink, M. C. McCarthy, L. Perez and J. M. Brown, J. Mol. Spectrosc., 2008, 247, 128–139 CrossRef CAS.
- R. Colin and P. F. Bernath, J. Mol. Spectrosc., 2010, 263, 120–122 CrossRef CAS.
- S. Truppe, R. J. Hendricks, E. A. Hinds and M. R. Tarbutt, Astrophys. J., 2013, 780, 71 CrossRef.
- S. Truppe, R. J. Hendricks, S. K. Tokunaga, E. A. Hinds and M. R. Tarbutt, J. Mol. Spectrosc., 2014, 300, 70–78 CrossRef CAS.
- E. J. D. Mahoney, B. J. Rodriguez, S. Mushtaq, B. S. Truscott, M. N. R. Ashfold and Y. A. Mankelevich, J. Phys. Chem. A, 2019, 123, 9966–9977 CrossRef CAS PubMed.
- C. Medcraft, H. Linnartz and W. Ubachs, J. Mol. Spectrosc., 2019, 360, 15–23 CrossRef CAS.
- T. M. Sanders, A. L. Schawlow, G. C. Dousmanis and C. H. Townes, Phys. Rev., 1953, 89, 1158–1159 CrossRef CAS.
- G. C. Dousmanis, T. M. Sanders and C. H. Townes, Phys. Rev., 1955, 100, 1735–1754 CrossRef CAS.
- G. Ehrenstein, C. H. Townes and M. J. Stevenson, Phys. Rev. Lett., 1959, 3, 40–41 CrossRef CAS.
- H. E. Radford, Phys. Rev. Lett., 1964, 13, 534–535 CrossRef CAS.
- F. X. Powell and D. R. Lide, J. Chem. Phys., 1965, 42, 4201–4202 CrossRef CAS.
- W. M. Goss, Astrophys. J., Suppl. Ser., 1968, 15, 131 CrossRef.
- R. L. Poynter and R. A. Beaudet, Phys. Rev. Lett., 1968, 21, 305–308 CrossRef CAS.
- H. E. Radford, Rev. Sci. Instrum., 1968, 39, 1687–1691 CrossRef CAS.
- K. R. German and R. N. Zare, Phys. Rev., 1969, 186, 9–13 CrossRef CAS.
- J. A. Ball, D. F. Dickinson, C. A. Gottlieb and H. E. Radford, Astron. J., 1970, 75, 762 CrossRef CAS.
- R. Engleman, J. Quant. Spectrosc. Radiat. Transfer, 1972, 12, 1347–1350 CrossRef CAS.
- J. J. ter Meulen and A. Dymanus, Astrophys. J., 1972, 172, L21 CrossRef CAS.
- W. L. Meerts and A. Dymanus, Chem. Phys. Lett., 1973, 23, 45–47 CrossRef CAS.
- J. Destombes and C. Marlière, Chem. Phys. Lett., 1975, 34, 532–536 CrossRef CAS.
- W. L. Meerts and A. Dymanus, Can. J. Phys., 1975, 53, 2123–2141 CrossRef CAS.
- J. Maillard, J. Chauville and A. Mantz, J. Mol. Spectrosc., 1976, 63, 120–141 CrossRef CAS.
- J. J. ter Meulen, W. L. Meerts, G. W. M. van Mierlo and A. Dymanus, Phys. Rev. Lett., 1976, 36, 1031–1034 CrossRef CAS.
- J. L. Destombes, C. Marliere, A. Baudry and J. Brillet, Astron. Astrophys., 1977, 60, 55–60 CAS.
- R. A. Beaudet and R. L. Poynter, J. Phys. Chem. Ref. Data, 1978, 7, 311–362 CrossRef CAS.
- J. A. Coxon, K. V. L. N. Sastry, J. A. Austin and D. H. Levy, Can. J. Phys., 1979, 57, 619–634 CrossRef CAS.
- J. Destombes, B. Lemoine and C. Marlière-Demuynck, Chem. Phys. Lett., 1979, 60, 493–495 CrossRef CAS.
- F. Raab, T. Bergeman, D. Lieberman and H. Metcalf, Opt. Lett., 1980, 5, 427–429 CrossRef CAS PubMed.
- K. Sastry and J. Vanderlinde, J. Mol. Spectrosc., 1980, 83, 332–338 CrossRef CAS.
- W. F. Kolbe, W.-D. Zollner and B. Leskovar, Rev. Sci. Instrum., 1981, 52, 523–532 CrossRef CAS.
- J. J. ter Meulen, W. A. Majewski, W. L. Meerts and A. Dymanus, Chem. Phys. Lett., 1983, 94, 25–28 CrossRef CAS.
- T. Amano, J. Mol. Spectrosc., 1984, 103, 436–454 CrossRef CAS.
- J. Farhoomand, H. M. Pickett and G. A. Blake, Astrophys. J., 1985, 291, L19 CrossRef CAS.
- B. Lemoine, M. Bogey and J. Destombes, Chem. Phys. Lett., 1985, 117, 532–538 CrossRef CAS.
- G. A. Blake, J. Farhoomand and H. M. Pickett, J. Mol. Spectrosc., 1986, 115, 226–228 CrossRef CAS.
- J. M. Brown, L. R. Zink, D. A. Jennings, K. M. Evenson and A. Hinz, Astrophys. J., 1986, 307, 410 CrossRef CAS.
- J. J. ter Meulen, W. Ubachs and A. Dymanus, Chem. Phys. Lett., 1986, 129, 533–537 CrossRef CAS.
- M. C. Abrams, S. P. Davis, M. L. P. Rao and J. E. Rolf, Astrophys. J., 1990, 363, 326 CrossRef CAS.
- A. D. Sappey and R. A. Copeland, J. Mol. Spectrosc., 1990, 143, 160–168 CrossRef CAS.
- J. A. Coxon, A. D. Sappey and R. A. Copeland, J. Mol. Spectrosc., 1991, 145, 41–55 CrossRef CAS.
- J. Hardwick and G. C. Whipple, J. Mol. Spectrosc., 1991, 147, 267–273 CrossRef CAS.
- R. Copeland, B. Chalamala and J. Coxon, J. Mol. Spectrosc., 1993, 161, 243–252 CrossRef CAS.
- T. Varberg and K. Evenson, J. Mol. Spectrosc., 1993, 157, 55–67 CrossRef CAS.
- M. C. Abrams, S. P. Davis, M. L. P. Rao, J. E. Rolf and J. W. Brault, Astrophys. J., Suppl. Ser., 1994, 93, 351 CrossRef CAS.
- G. Stark, J. W. Brault and M. C. Abrams, J. Opt. Soc. Am. B, 1994, 11, 3 CrossRef CAS.
- F. Mélen, A. Sauval, N. Grevesse, C. Farmer, C. Servais, L. Delbouille and G. Roland, J. Mol. Spectrosc., 1995, 174, 490–509 CrossRef.
- H. Wurps, H. Spiecker, J. J. ter Meulen and P. Andresen, J. Chem. Phys., 1996, 105, 2654–2659 CrossRef CAS.
- O. L. Polyansky, N. F. Zobov, S. Viti, J. Tennyson, P. F. Bernath and L. Wallace, J. Mol. Spectrosc., 1997, 186, 422–447 CrossRef CAS PubMed.
- T. Thissen, H. Wurps, H. Spiecker, J. ter Meulen and P. Andresen, Astron. Astrophys., Suppl. Ser., 1999, 139, 625–628 CrossRef CAS.
- P. Andresen, T. Thissen, H. Spiecker and P. Andresen, J. Mol. Spectrosc., 2000, 200, 277–279 CrossRef CAS PubMed.
- S. A. Nizkorodov, W. W. Harper and D. J. Nesbitt, Chem. Phys. Lett., 2001, 341, 107–114 CrossRef CAS.
- K. Tereszchuk, P. F. Bernath, N. F. Zobov, S. V. Shirin, O. L. Polyansky, N. I. Libeskind, J. Tennyson and L. Wallace, Astrophys. J., 2002, 577, 496–500 CrossRef CAS.
- E. R. Hudson, H. J. Lewandowski, B. C. Sawyer and J. Ye, Phys. Rev. Lett., 2006, 96, 143004 CrossRef PubMed.
- B. L. Lev, E. R. Meyer, E. R. Hudson, B. C. Sawyer, J. L. Bohn and J. Ye, Phys. Rev. A: At., Mol., Opt. Phys., 2006, 74, 061402(R) CrossRef.
- P. F. Bernath and R. Colin, J. Mol. Spectrosc., 2009, 257, 20–23 CrossRef CAS.
- M. A. Martin-Drumel, S. Eliet, O. Pirali, M. Guinet, F. Hindle, G. Mouret and A. Cuisset, Chem. Phys. Lett., 2012, 550, 8–14 CrossRef CAS.
- B. J. Drouin, J. Phys. Chem. A, 2013, 117, 10076–10091 CrossRef CAS PubMed.
- A. Fast, J. E. Furneaus and S. A. Meek, Phys. Rev. A, 2018, 98, 052511 CrossRef CAS.
- J. Quan, Y. Chang, Z. Li, Y. Zhao, Z. Luo, Y. Wu, S. Zhang, Z. Chen, J. Yang, K. Yuan, X. Yang, B. C. Krüger, D. Schwarzer, A. M. Wodtke and G. B. Park, J. Mol. Spectrosc., 2021, 380, 111509 CrossRef CAS.
- A. G. Császár and T. Furtenbacher, J. Mol. Spectrosc., 2011, 266, 99–103 CrossRef.
- T. Furtenbacher, P. Árendás, G. Mellau and A. G. Császár, Sci. Rep., 2014, 4, 4654 CrossRef PubMed.
- P. Árendás, T. Furtenbacher and A. G. Császár, J. Math. Chem., 2016, 54, 806–822 CrossRef.
- A. Kalemos, A. Mavridis and A. Metropoulos, J. Chem. Phys., 1999, 111, 9536–9548 CrossRef CAS.
- G. J. Vázquez, J. M. Amero, H. P. Liebermann, R. J. Buenker and H. Lefebvre-Brion, J. Chem. Phys., 2007, 126, 164302 CrossRef PubMed.
- J. M. Brown, J. T. Hougen, K. P. Huber, J. W. C. Johns, I. Kopp, H. Lefebvre-Brion, A. J. Merer, D. A. Ramsay, J. Rostas and R. N. Zare, J. Mol. Spectrosc., 1975, 55, 500–503 CrossRef CAS.
- J. M. Brown, M. Kaise, C. M. L. Kerr and D. J. Milton, Mol. Phys., 1978, 36, 553–582 CrossRef CAS.
- T. Tanaka and Z. Koana, Proc. Phys.-Math. Soc. Jpn., 1934, 16, 365–400 Search PubMed.
- G. Dieke and H. Crosswhite, J. Quant. Spectrosc. Radiat. Transfer, 1962, 2, 97–199 CrossRef CAS.
- J. W. Chamberlain and F. L. Roesler, Astrophys. J., 1955, 121, 541 CrossRef CAS.
- L. Wallace, Astrophys. J., 1960, 132, 894 CrossRef CAS.
- P. Rousselot, C. Lidman, J.-G. Cuby, G. Moreels and G. Monnet, Astron. Astrophys., 2000, 354, 1134–1150 CAS.
- Y. Elsworth, J. J. Lopez-Moreno and J. F. James, J. Atmos. Sol.-Terr. Phys., 1997, 59, 117–124 CrossRef CAS.
- A. B. Meinel, Astrophys. J., 1950, 112, 120 CrossRef CAS.
- T. Maihara, F. Iwamuro, T. Yamashita, D. N. B. Hall, L. L. Cowie, A. T. Tokunaga and A. Pickles, Publ. Astron. Soc. Pac., 1993, 105, 940 CrossRef.
- F. L. Bettens, R. P. A. Bettens, R. D. Brown and P. D. Godfrey, J. Am. Chem. Soc., 2000, 122, 5856–5860 CrossRef CAS.
- C. P. Endres, S. Schlemmer, P. Schilke, J. Stutzki and H. S. Müller, J. Mol. Spectrosc., 2016, 327, 95–104 CrossRef CAS.
- https://vizier.u-strasbg.fr/viz-bin/VizieR?-source=J/A+A/571/A47-to=3 .
- Y. Wang, J. Tennyson and S. N. Yurchenko, Atoms, 2020, 8, 7 CrossRef.
- https://exomol.com/ .
- J. Tennyson, P. F. Bernath, L. R. Brown, A. Campargue, A. G. Császár, L. Daumont, R. R. Gamache, J. T. Hodges, O. V. Naumenko, O. L. Polyansky, L. S. Rothman, R. A. Toth, A. C. Vandaele, N. F. Zobov, S. Fally, A. Z. Fazliev, T. Furtenbacher, I. E. Gordon, S.-M. Hu, S. N. Mikhailenko and B. A. Voronin, J. Quant. Spectrosc. Radiat. Transfer, 2010, 111, 2160–2184 CrossRef CAS.
- C. A. Bowesman, H. Akbari, S. Hopkins, S. N. Yurchenko and J. Tennyson, J. Quant. Spectrosc. Radiat. Transfer, 2022, 289, 108295 CrossRef CAS.
- L. K. McKemmish, A.-M. Syme, J. Borsovszky, S. N. Yurchenko, J. Tennyson, T. Furtenbacher and A. G. Császár, Mon. Not. R. Astron. Soc., 2020, 497, 1081–1097 CrossRef CAS.
- A. R. Al-Derzi, S. N. Yurchenko, J. Tennyson, M. Melosso, N. Jiang, C. Puzzarini, L. Dore, T. Furtenbacher, R. Tobias and A. G. Császár, J. Quant. Spectrosc. Radiat. Transfer, 2021, 266, 107563 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp02240k |
| This journal is © the Owner Societies 2022 |