Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Excellent kinetics of single-phase Gd-doped ceria fuel electrodes in solid oxide cells†
Andreas
Nenning‡
 *,
Manuel
Holzmann‡
,
Jürgen
Fleig
and
Alexander K.
Opitz
*,
Manuel
Holzmann‡
,
Jürgen
Fleig
and
Alexander K.
Opitz
 *
*
TU Wien, Insitute of Chemical Technologies and Analytics, Getreidemarkt 9, A-1060 Vienna, Austria. E-mail: andreas.nenning@tuwien.ac.at; alexander.opitz@tuwien.ac.at
First published on 9th July 2021
Abstract
Ceria containing electrodes offer several advantages compared to state-of-the art nickel-yttria-stabilized zirconia (Ni-YSZ) cermets, such as higher ionic and electronic conductivities, and a high activity for oxygen exchange reactions on the oxide surface. They may also solve current issues like long-term degradation due to microstructural changes and carbon deposition, especially when they are used in dry hydrocarbon fuel, or CO2 electrolysis mode. For application, compatibility with existing powder-based fabrication methods is of high technological interest. These are the main reasons why ceria containing fuel electrodes can significantly improve cell performance, thus being especially interesting for intermediate temperature and metal-supported cells. In almost all studies so far, the relatively low electron conductivity of ceria-based materials was compensated by addition of a percolating Ni metal phase. Here, we show that anodes with a single phase gadolinia doped ceria (GDC) functional layer perform even better than cermets. The drawback of lower electronic conductivity results in an increased ohmic resistance, which is minimized by a thin functional layer and a current collecting layer on top. By temperature, thickness and atmosphere variations, we can divide the polarization resistance of the GDC anode into an ohmic, electrochemical and gas diffusion contribution. At 800 °C, the electrode arc diameter shrinks to extremely low ∼0.012 Ω cm2, even at low H2 and H2O pressures and with a significant contribution of gas phase diffusion kinetics.
Introduction
In solid oxide fuel cell (SOFC) technology, morphological degradation, coking and moderate kinetics are known issues of state of the art Ni-YSZ cermet anodes.1–3 Mixed ionic and electronic conductors are a promising alternative materials class for application in SOFC anodes, due to the increased number of electrochemically active sites and enhanced coking resistance. Perovskite-type materials as well as ceria-based electrodes deliver very promising results in terms of power density4–6 and stability.7,8 In most studies, a major difference between ceria and perovskite-type anodes is that perovskite-type materials are often used in a single phase functional layer,9–11 while ceria-based anodes are usually used as a cermet with Ni to compensate the relatively low electronic conductivity.5,12–17Noteworthy, in reducing conditions the electronic conductivity of many perovskites, such as SrTi0.3Fe0.7O3−δ18 is quite similar to that of Gd-doped ceria (GDC).19–21 By studying literature, it appears that most authors decide to use cermets or work with single phase mixed conductors based on the “classical” use of these materials. Perovskite-type anodes are usually based on the fabrication principles of perovskite-type cathodes, such as (La,Sr)(Co,Fe)O3−δ or (La,Sr)MnO3, which exhibit rather high electron conductivity in air (>100 S cm−1) and are therefore used as single phase materials. In contrast, ceria containing anodes are usually an adaption of the classical Ni-YSZ cermets, in which YSZ is replaced by GDC or Sm-doped CeO2 (SDC).
In this paper, we focus on electrochemical impedance testing and electrochemical modelling of single-phase porous GDC anodes. The 3D porous GDC electrodes were fabricated similarly to Ni-GDC cermets used in earlier studies.15 Those were used in metal-supported SOFCs allowing an exceptionally high power density of 1.2 W cm−2 at 0.9 V and 700 °C.22 Although the Ni-GDC anodes proved to be excellent in terms of kinetics, redox cycling stability,8 and stable operation for 1000 hours,22 their morphological stability for long-term (>10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 hours) operation is still an issue, especially when aiming at an application as solid oxide electrolysis cell (SOEC) cathode. There, in contrast to Ni-YSZ cermets where only depletion or agglomeration of nickel is the main issue,23–25 both Ni and GDC are mobile during operation of Ni-GDC cermets, especially in high humidity conditions,26,27 due to a strong metal support interaction (SMSI). These effects are not expected in electrodes with Ni free functional layers.
000 hours) operation is still an issue, especially when aiming at an application as solid oxide electrolysis cell (SOEC) cathode. There, in contrast to Ni-YSZ cermets where only depletion or agglomeration of nickel is the main issue,23–25 both Ni and GDC are mobile during operation of Ni-GDC cermets, especially in high humidity conditions,26,27 due to a strong metal support interaction (SMSI). These effects are not expected in electrodes with Ni free functional layers.
The major disadvantage of a pure GDC anode active layer lies in its moderate electronic conductivity. Here, we predict the impact of reduced electron conductivity on the anode ASR of ceria based fuel electrodes by circuit modelling and impedance measurements in varying H2:H2O gas mixing ratios. When the GDC functional layer is sufficiently thin (3 μm thickness), and has a current collecting layer on top, this adverse effect is minimized. Moreover, a thin GDC functional layer also minimizes potentially detrimental effects due to the relatively high chemical expansion coefficient of the material,28–30 since the occurring mechanical forces decrease with reduced film thickness.
When looking at the basic electrochemical properties of GDC, a single-phase functional layer has several advantages over Ni-GDC cermets, which are specifically:
(1) Larger specific electrochemically active GDC surface area.
(2) Higher effective ionic conductivity.
(3) Improved ionic contact between electrode and electrolyte.
(4) Enhanced coking resistance.
(5) Minimized morphological degradation.
(6) Excellent redox cycling stability.
There, points 1–3 are direct consequences of the higher volume fraction of GDC in the porous electrode, whereas the coking resistance is due to the adsorption properties of C1 species on ceria. In contrast to Ni, carbon preferentially adsorbs in form of carbonates,31 which leads to slow graphite growth kinetics, and enables dry CO2 electrolysis with outlet CO fractions exceeding the Boudouard equilibrium.32 Morphological degradation of SOFC/SOEC fuel electrodes happens primarily due to de-wetting of nickel and strong metal support interaction, especially in electrolysis mode.25,33 Therefore, degradation due to microstructure evolution – including redox cycling damage – can be very efficiently minimized when Ni is not present in the active layer. Despite these promising properties, experimental data on anodes with pure GDC active layers is scarce. One study of sol–gel derived nano-porous anodes shows promising results,34 whereas anodes with micrometre sized GDC particles exhibited much higher polarization resistance.35 In this paper, we show that also powder-based anodes with pure GDC functional layers exhibit excellent kinetics, and present a new easy to apply methodology to experimentally quantify the contributions of electron conduction, electrochemical reactions and gas diffusion kinetics to the overall polarization resistance.
Impedance simulation of porous GDC-based anodes
Physically justified models of the impedance of porous SOFC/SOEC electrodes are based on a transmission line equivalent circuit. This circuit contains elements representing resistances for electronic and ionic conduction, electrochemical reactions and ion transfer through the electrode electrolyte interface. If the electrode contains a mixed conducting material, a chemical capacitance (Cchem) in parallel to the electrochemical reaction resistance is added, which is the case for GDC-based fuel electrodes. This circuit model was first described by Adler et al. for SOFC cathodes,36 but is also applicable for Ni-YSZ and Ni-GDC anodes15,37–39 and other porous composite electrodes.3,40–42 Here, we take the impedance model for a mixed conducting SOFC anode with finite electron and ion conductivity, which we presented previously,15,43 and apply it to compare Ni-GDC cermet anodes with single phase GDC anodes. In both cases, the GDC surface is the active site for H2 oxidation or water splitting.15,44,45 The main difference between pure GDC and cermets lies in the effective electron conduction mechanism. In cermets, long-range electron transport primarily happens in the highly conductive Ni particle network, so they have a high effective electron conductivity. In pure GDC functional layers, the much longer electron transport path within the GDC phase may cause a significant contribution to the ASR. This is sketched in Fig. 1a. For impedance modelling, several microstructural parameters are needed such as specific surface area, tortuosity, volume fractions (GDC, Ni, pore), as well as materials parameters for specific electron and ion conductivity, and surface-specific oxygen exchange resistance. The mathematical derivation of the impedance function for these parameters is given in ref. 15. Numerical values of the microstructural parameters for the simulation are summarized in Table 1. With these, we simulate the impedance spectra of a 15 μm thick Ni-GDC cermet and pure GDC electrodes with different functional layer thicknesses. For the Ni phase, the tortuosity factor is unknown, but for any reasonable value below 30 and εNi ≈ 0.3, the electron conduction resistance is negligible.43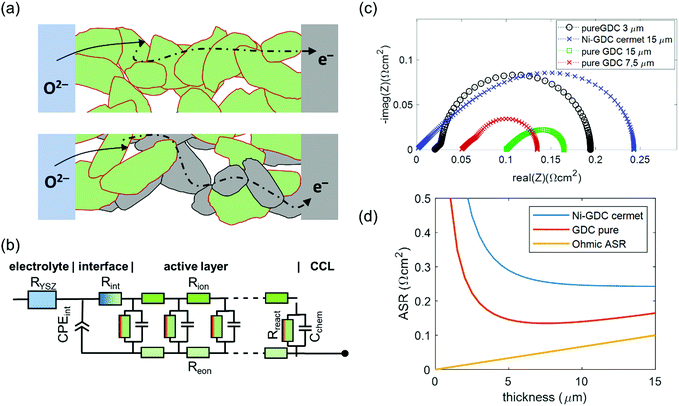 | ||
| Fig. 1 (a) Sketch of electrochemical reactions and charge transport in pure GDC and Ni-GDC cermet anodes (CCL = current collection layer). (b) Equivalent circuit for impedance simulation, adapted from ref. 15. (c) Simulated impedance spectra at 600 °C with parameter values taken from Table 1. (d) Plot of ASR vs. active layer thickness for Ni-GDC cermet and pure GDC anodes. | ||
| Parameter | Value, pure GDC | Value, Ni-GDC cermet | Ref. |
|---|---|---|---|
| GDC phase ion conductivity | 0.015 S cm−1 | 0.015 S cm−1 | Dense polycrystal19 |
| GDC/Ni phase electron conductivity | 0.022 S cm−1 (GDC) | 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 S cm−1 (Ni) 000 S cm−1 (Ni) |
Dense polycrystal20 |
| GDC phase volume fraction, εGDC | 0.6 | 0.3 | Porosity estimate from SEM cross-sections |
| GDC phase tortuosity, τGDC | 1.5 | 2.7 | Typical values from literature |
| Effective ion conductivity | 0.006 S cm−1 | 0.0017 S cm−1 |
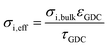
|
| Effective electron conductivity | 0.009 S cm−1 | >1000 S cm−1 |
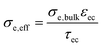
|
| Effective reaction resistance | 5 × 10−5 Ω cm3 | 10−4 Ω cm3 | Ref. 15 |
| Specific GDC surface area | 10 μm2 μm−3 | 5 μm2 μm−3 | Ref. 15 |
| Interfacial resistance Rint | 0 Ω cm2 | 0 Ω cm2 | Assumption for simulation |
The results of impedance modelling are summarized in Fig. 1. The circuit model from Fig. 1b was used for impedance simulation, with parameters taken from Table 1. In Fig. 1c, impedance spectra for pure GDC and Ni-GDC cermet anodes are plotted. Clearly visible, the electrode arc for pure GDC anodes is much smaller than for Ni-GDC cermet. This is due to the higher specific GDC surface area, on which the H2 oxidation reaction happens, and higher effective ionic conductivity due to higher GDC volume fraction and lower tortuosity in a single phase anode. The increased resistance due to electron conduction is visible as the high frequency real axis intercept, which grows with electrode thickness. The effect of thickness on the electrode area specific resistance (ASR) is plotted in Fig. 1d. Due to its high electron conductivity, the ASR of a Ni-GDC cermet decreases monotonically with thickness. In contrast, the pure GDC anode exhibits a minimum at 7.5 μm, due to the electron conduction resistance, which increases linearly with the GDC layer thickness (see ohmic ASR in Fig. 1d). An important outcome of this impedance simulation is that the size of the electrode arc is slightly smaller than the true ASR of the anode. Experimentally, determination of the ohmic ASR of the anode is not trivial, because it overlaps with the electrolyte resistance in measured impedance spectra. We will determine its value by variation of the GDC electron conductivity in different gas mixtures. The effects of gas diffusion and the resistance associated to ion transfer through the GDC–YSZ interface (Rint and CPEint) depend strongly on processing details and measurement conditions. Therefore, we omitted these in the simulation. From experimental Ni-GDC anode impedance studies,15 however, we expect at least some contribution from these processes in real electrodes.
Experimental
Symmetric cell fabrication
Symmetrical, electrolyte-supported cells based on 150 μm thick 8YSZ-electrolyte sheets (11 × 11 × 0.15 mm, Kerafol GmbH, Germany) were fabricated as follows:A paste was prepared by mixing GDC powder with a d50 of 270 nm (10 mol% Gd, manufacturer: Treibacher AG, Austria) in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 weight ratio with ink vehicle (FuelCellMaterials, USA). For homogenisation and de-agglomeration of GDC, the paste was treated for 15 minutes in a planetary ball mill (Pulverisette, Fritsch, Germany) using zirconia beakers and beads.
1 weight ratio with ink vehicle (FuelCellMaterials, USA). For homogenisation and de-agglomeration of GDC, the paste was treated for 15 minutes in a planetary ball mill (Pulverisette, Fritsch, Germany) using zirconia beakers and beads.
On four electrolytes, 14 μm thick GDC layers were brushed on both sides of the polycrystalline 8YSZ-electrolyte sheets. On three electrolytes, 3 μm thick GDC paste layers were spin-coated at 6000 rpm for 60 seconds. After a 5 minutes drying step at 120 °C, a current collection layer consisting of Pt-GDC cermet and finally a layer of Pt paste were brushed onto the pure GDC functional layer with a drying step in between.
In order to test the catalytic activity of the Pt-GDC|Pt current collecting layers, three cells with electrodes consisting just of the Pt-GDC|Pt current collection layers were fabricated as well.
After application of the electrode layers, the symmetrical cells were sintered at 1150 °C in air for 3 h.
In order to optimize the GDC–YSZ interface on one cell, an additional dense GDC layer was deposited on the 8YSZ substrates by pulsed laser deposition (PLD) prior to application of the electrode paste. This was done to improve the quality of the interface and to increase the adherence of the porous electrode on the YSZ electrolyte substrate. The target used for ablation was made of the same powder as the electrodes by cold-isostatic pressing and sintering. PLD deposition conditions were: 600 °C substrate temperature, laser energy 100 mJ per pulse (on the target), substrate target distance 7 cm, 5 Hz laser frequency and 30 minutes deposition time. The resulting layers were about 450 nm thick (see electron microscopy images below).
Impedance spectroscopy and equivalent circuit fitting
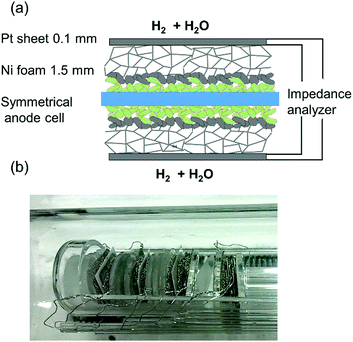
Impedance measurements were carried out in a single chamber setup consisting of fused silica, which allows simultaneous characterisation of four symmetrical model cells by using an electronic multiplexer. This setup was homogeneously heated in a foldable tube furnace (Carbolite-Gero, Germany). The chamber and cell holders consist entirely of fused silica, Pt wires and Ni foam for electrode contacting, as shown in Fig. 2. In order to minimise the gas diffusion impedance, several optimisations were made: a highly porous Ni foam (95% open porosity, 1.5–2 mm thickness) was used for contacting of electrodes. To maximize the diffusion coefficient of H2 and H2O molecules in the gas phase, the electrochemical tests were carried out at a reduced total pressure of ca. 60 mbar (25 mbar H2O plus 35 mbar H2). Please note that since the feed gas line was kept at room temperature, the humidification level could not exceed the water vapour pressure of 25 mbar. The pressure was regulated by continuously pumping the chamber at an inlet flow rate of 10–20 sccm. As recently reported in more detail, these measures allow significant reduction of the gas diffusion resistance. Binary gas diffusion within the Ni contacting foams and stagnant gas layer plays the most important role, and Knudsen diffusion within the small pores of the anode functional layer is less important, due to the thin, highly porous functional layer.15Impedance spectra were measured in 4-wire mode with a phase sensitive multimeter PSM 1753 with IAI interface (both: Newton's Fourth Ltd, UK) in a frequency range of 105–0.1 Hz and with an AC voltage of 20 mV root-mean-square (RMS). The experimental temperature range was 500–800 °C. The spectra were fitted with the software Zview.
Experimental results and discussion
Microstructural characterization
Fractured cross-sections of cells after electrochemical testing were investigated by scanning electron microscopy (SEM) imaging in secondary electron contrast mode, shown in Fig. 3. The electrodes exhibit homogeneous, isotropic microstructure with relatively uniform particle size of 200–300 nm, which is in line with the manufacturer's (Treibacher) statement of d50 = 270 nm. Therefore, no significant coarsening happened during sintering. For the spin-coated layers, a uniform thickness of 3 μm is achieved – see Fig. 3b – and the adhesion of the Pt current collector is good, due to the three-layer GDC|PtGDC|Pt architecture. In Fig. 3c, the 450 nm thick dense PLD layer between YSZ and electrode is visible. Also visible in the pictures, the mechanical stress during cleaving of the cells partly delaminated the current collecting layers (Fig. 3c), or introduced cracks in the electrolyte (Fig. 3c). These defects were not present before sample cleaving.Overall, the microstructure exhibits a large GDC surface area and a reasonable compromise between porosity, GDC volume fraction, and tortuosity in order to achieve both high electro-catalytic activity and high effective ion conductivity. This shows that the sintering temperature of 1150 °C is well suited. Higher sintering temperatures lead to loss of surface area and porosity, whereas lower sintering temperature weakens the mechanical stability and connectivity of GDC particles.
Temperature dependence of the electrode arc
Impedance spectra of GDC anodes at 600 and 800 °C are plotted in Fig. 4a and b. For better comparability, the ohmic resistance was subtracted. In contrast to the simulations, in which the (ASR) of ion transfer across the GDC–YSZ interface was neglected to demonstrate the effect of the electron transport in the GDC pase, the measured impedance spectra appear rather simple and most spectra exhibit only one slightly asymmetric arc. This difference is most likely caused by a large resistive interfacial contribution of the real electrodes, as we will discuss in more detail in the following. Consequently, our discussion will focus on the electrode arc diameter and summit frequency. Equivalent circuit fitting results and distribution of relaxation times (DRT) analysis are given in the ESI† and support the interpretation of the results presented in the main text.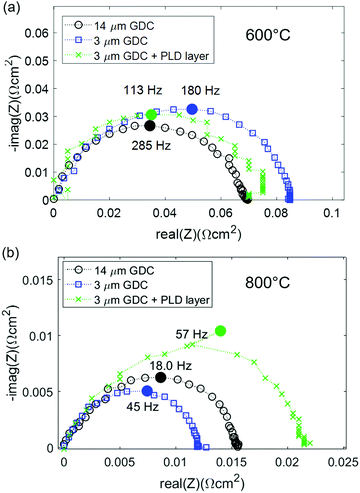 | ||
| Fig. 4 (a) Impedance spectra of different GDC anodes at (a) 600 °C and (b) 800 °C. The high frequency offset was subtracted from all spectra for the sake of easier comparability. | ||
At 600 °C, the arc diameter is slightly below 0.1 Ω cm2 and therefore similar to that expected from impedance modelling in Fig. 1 and decreases to ∼0.015 Ω cm2 at 800 °C. The lower summit frequency at higher temperatures indicates that the main contribution to the ASR switches to a process with slower characteristic time scale. This slower process is most likely gas diffusion, as shown in the following.
In order to relate the size of the electrode arc measured here to other studies found in literature, the temperature dependent ASR of the GDC anodes is plotted in Fig. 5a, and compared with a selection of other anodes with various materials that are found in literature. For our comparison, we only considered highest performing anodes with very low polarization resistance that were used in cells that deliver current densities >2 A cm−2 at 0.7 V. The value for Ni-YSZ46 anodes was taken from the high performance anode supported SOFCs from FZ Jülich. The Ni-GDC15 cermets contain the same GDC powder as our single phase anodes, and were used in metal-supported SOFCs with high power densities.22,47 The perovskite-type Sr0.95(Ti0.3Fe0.63Ni0.07)O3−δ48 anodes form metallic Ni–Fe alloy exsolutions, and are used in cells supported on La0.8Sr0.2Ga0.8Mg0.2O3−δ (LSGM) electrolytes. Furthermore, two examples of nanostructured anodes for intermediate-temperature SOFCs are given: infiltrated Ni-LSGM42 cermets used in anode supported cells with LSGM electrolyte, and sol–gel derived nano-GDC anodes with Pt current collector34 on symmetrical model cells. These studies were selected because they represent the lowest reported polarisation resistance values so far for different materials combinations that are known to the authors.
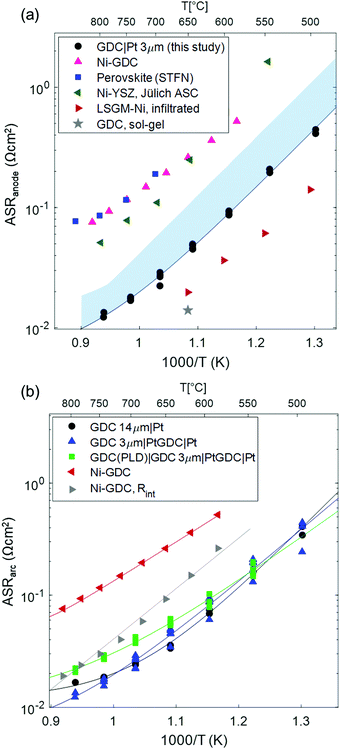 | ||
| Fig. 5 (a) Arrhenius plot of the polarization resistance of different anodes used in high power density SOFCs, compared to the GDC anodes of this study (black circles). The shaded blue area gives an estimate of the true ASR of the GDC anodes, including the ohmic contribution. Data sources were: Ni-GDC: ref. 15 (used in metal supported cells with sputtered YSZ electrolyte); perovskite (STFN = Sr0.95Ti0.63Ni0.07O3−δ): ref. 48 (used in electrolyte supported cell with LSGM electrolyte), Ni-YSZ, Jülich ASC: ref. 46 (anode supported cell with thin YSZ electrolyte); LSGM-Ni, infiltrated: ref. 42 (anode supported cell with LSGM electrolyte); GDC, sol–gel: ref. 34 (no cell data available). (b) Comparison of single phase GDC compared to Ni-GDC cermet anodes, and the GDC–YSZ interface resistance in Ni-GDC cermets. The solid lines in the Arrhenius plots represent the fit by eqn (1). | ||
Clearly visible, the anodes reported here have a lower polarization resistance than the powder-based Ni-YSZ, Ni-GDC and STFN anodes. Only infiltrated Ni-LSGM and nanostructured sol–gel derived GDC films exhibit even lower polarization resistances. However, LSGM and Nickel are known to react at high temperature, and sol–gel derived nanoporous electrodes that were calcined at only 800 °C34 most likely exhibit lower morphological stability than the GDC electrodes used in this study that were sintered at 1150 °C.
The true ASR of the anodes presented in this study is, however, larger than the measured electrode arc diameter, due to an ohmic contribution to the electrode ASR, as shown in the simulations. The shaded area in Fig. 5a represents the estimated true ASR, including the additional ohmic offset.
The effect of temperature on the electrode arc diameter (ASRarc) of different GDC based electrodes is plotted in Fig. 5b. The ASR follows an Arrhenius-like behaviour up to ca. 700 °C, and the slopes flatten at higher temperatures. This flattening is most likely due to an increasing importance of gas diffusion, which also explains the unusual decrease of the summit frequency at higher temperatures observed in Fig. 4. The flattening of the Arrhenius slopes was treated by fitting the data to a model in which the electrode arc diameter (ASRarc) has a thermally activated electrochemical and a temperature independent contribution from gas diffusion (Rdiff), expressed by eqn (1).
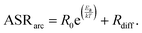 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O mixing ratio close to 1
H2O mixing ratio close to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 help to optimize this parameter.
1 help to optimize this parameter.
| Electrode type | R 0 (Ω cm2) | E a (eV) | R diff (Ω cm2) |
|---|---|---|---|
| GDC 14 μm|PtGDC|Pt | 2 × 10−8 | 1.11 | 0.012 |
| GDC 3 μm|PtGDC|Pt | 2.7 × 10−7 | 0.94 | 0.007 |
| GDC(PLD)|GDC 3 μm|PtGDC|Pt | 1.8 × 10−6 | 0.8 | 0.010 |
| Ni-GDC | 2.3 × 10−5 | 0.74 | 0.014 |
| Ni-GDC, Rint | 9.3 × 10−7 | 0.93 | n/a |
For comparison, also the polarization resistance of similarly prepared Ni-GDC cermets, taken from ref. 15 is plotted. For these, it was possible to determine the ASR of ion transfer across the YSZ|Ni-GDC interface (data row Ni-GDC, Rint) by equivalent circuit fitting. The polarization resistance of PtGDC|Pt cermet electrodes was also measured (Fig. S4, ESI†), and is very large (ca. 30 Ω cm2 at 600 °C). The very high polarization resistance of the Pt-GDC cermet proofs that a possible catalytic effect of the Pt current collector is definitely not responsible for the low polarization resistance of the pure GDC electrodes.
Interestingly, the activation energy of the pure GDC electrodes, especially without the PLD interlayer, is significantly higher than that of Ni-GDC cermets (0.95–1.1 vs. 0.7 eV, see Table 2). Surprisingly, the addition of a PLD-grown GDC layer at the electrode/electrolyte interface lowers the activation energy, but has even a slightly detrimental effect on the total ASR. Moreover, the activation energy of the ASR of electrodes without dense interlayer matches that of ion transfer across the GDC–YSZ interface observed on Ni-GDC cermet anodes,15 visible in Fig. 5b. This indicates that a significant part of the total ASR is likely caused by ion conduction through the interface (Rint in the circuit in Fig. 1b). The fact that the total ASR of pure GDC anodes is even lower than the GDC–YSZ interface feature in Ni-GDC cermets is reasonable, due to the higher density of GDC–YSZ sintering necks. With this in mind, we can compare the arc diameter of the 3 and 14 μm thick anodes. Interestingly, these diameters are almost identical, although the impedance modelling shown in Fig. 1 predicts a smaller arc for the thicker anode.
This behaviour leads to the conclusion that the electrochemically active zone of the GDC anode is even thinner than predicted from numerical modelling, and most likely less than 3 μm. This, in turn, suggests that the surface-specific electrochemical activity of GDC close to the interface is significantly higher than expected from model studies on thin films. Possibly, the solid solution of YSZ and GDC forming by inter-diffusion of the cations at the interface upon sintering has a strongly promoting effect on electro-catalytic activity. It has already been reported that co-doping of GDC with Zr increases its reducibility leading to an enhanced Ce3+ concentration in the material.49–51 The question how far an increased Ce3+ concentration is beneficial for the electro-catalytic activity of the inter-diffusion region of a porous GDC electrode on a YSZ electrolyte is, however, not unambiguously clarified yet.
The significant contribution of an electrode/electrolyte interface and gas diffusion resistance is also the reason why we did not straightforwardly fit the impedance results with the circuit from Fig. 1b. Due to the poor separation of the transmission line feature from the interfacial arc, it was not possible to obtain a uniquely converging fit with many free parameters.
The ohmic anode resistance revealed by atmosphere variation
Despite the excellent redox kinetics expressed by the small electrode arc diameter, the impedance modelling shows that such results may be misleading because the ohmic resistance, which is usually caused by the electrolyte alone, is to a noteworthy part also caused by an electron transport limitation within the electrode. As a consequence, the ohmic offset scales with the electron conductivity and thickness of the GDC phase, which can be tuned by varying the H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O mixing ratio. Impedance spectra were recorded at H2 partial pressures between 5 and 900 mbar, while keeping the H2O partial pressure constant at 25 mbar. Thereby, the equivalent p(O2) was varied by 5 orders of magnitude. Impedance spectra recorded at different p(H2) are plotted in Fig. 6a. Clearly visible, the ohmic high frequency offset resistance (denoted R1) decreases with increasing p(H2), as predicted by the simulation results (cf.Fig. 1c). When the H2
H2O mixing ratio. Impedance spectra were recorded at H2 partial pressures between 5 and 900 mbar, while keeping the H2O partial pressure constant at 25 mbar. Thereby, the equivalent p(O2) was varied by 5 orders of magnitude. Impedance spectra recorded at different p(H2) are plotted in Fig. 6a. Clearly visible, the ohmic high frequency offset resistance (denoted R1) decreases with increasing p(H2), as predicted by the simulation results (cf.Fig. 1c). When the H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O mixing ratio strongly deviates from unity, the gas diffusion resistance increases strongly.15 When the H2 partial pressure is high, the H2O diffusion coefficient decreases due to gas phase collisions, whereas at low p(H2) the diffusion resistance increases due to a lack of H2 molecules. Due to this, the electrode arcs at 5 and 960 mbar H2 exhibit two features at ≫100 Hz (electrode polarization) and one at 9 Hz (gas diffusion). Qualitatively, the high frequency electrode arc appears to shrink with increasing H2 partial pressure – as expected for an electrode process. However, the weak separation of the features does not allow a trustworthy equivalent circuit fit that can precisely quantify the individual gas diffusion and electrode kinetic resistances. Therefore, our quantitative discussion will focus on the effect of finite electron conductivity on the ohmic offset resistance. In the high frequency limit, all capacitors in the circuit model in Fig. 1b can be approximated as short circuits. Therefore, the ohmic offset resistance corresponds to a parallel connection of electron and ion conduction resistance. Hence, the difference of true electrolyte resistance (RYSZ) and measured high frequency offset (R1) is inversely proportional to the total conductivity of the GDC layer. In good approximation, at 600 °C the ion conductivity of GDC is independent of p(O2), whereas the electron conductivity scales with p(O2)−0.25.19–21 Therefore, the area specific ohmic resistance of the electrode (R1 − RYSZ) is expressed as
H2O mixing ratio strongly deviates from unity, the gas diffusion resistance increases strongly.15 When the H2 partial pressure is high, the H2O diffusion coefficient decreases due to gas phase collisions, whereas at low p(H2) the diffusion resistance increases due to a lack of H2 molecules. Due to this, the electrode arcs at 5 and 960 mbar H2 exhibit two features at ≫100 Hz (electrode polarization) and one at 9 Hz (gas diffusion). Qualitatively, the high frequency electrode arc appears to shrink with increasing H2 partial pressure – as expected for an electrode process. However, the weak separation of the features does not allow a trustworthy equivalent circuit fit that can precisely quantify the individual gas diffusion and electrode kinetic resistances. Therefore, our quantitative discussion will focus on the effect of finite electron conductivity on the ohmic offset resistance. In the high frequency limit, all capacitors in the circuit model in Fig. 1b can be approximated as short circuits. Therefore, the ohmic offset resistance corresponds to a parallel connection of electron and ion conduction resistance. Hence, the difference of true electrolyte resistance (RYSZ) and measured high frequency offset (R1) is inversely proportional to the total conductivity of the GDC layer. In good approximation, at 600 °C the ion conductivity of GDC is independent of p(O2), whereas the electron conductivity scales with p(O2)−0.25.19–21 Therefore, the area specific ohmic resistance of the electrode (R1 − RYSZ) is expressed as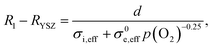 | (2) |
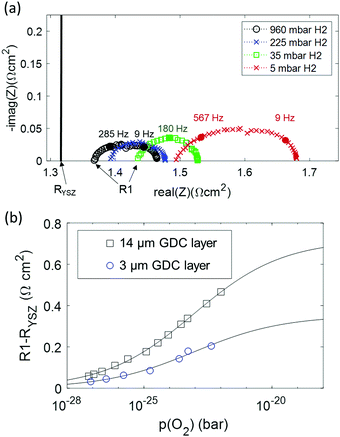 | ||
| Fig. 6 (a) Impedance spectra of a symmetrical GDC 3 μm |PtGDC|Pt cell at 600 °C in 25 mbar H2O, and varying H2 partial pressures. The black vertical line in part (a) represents the “real” electrolyte resistance RYSZ. (b) Difference of offset resistance (R1) and real electrolyte resistance (RYSZ) as a function of p(O2). The solid line represents the fit according to eqn (2). | ||
In summary, this analysis of the p(H2) dependence points out that at typical SOFC operating conditions with 50% humidification, about half of the ASR of a single-phase mixed conducting ceria anode is “hidden” in the ohmic offset due to its moderate electron conductivity. This offset increases with thickness, so a very thin active layer represents the optimum, although the electrode arc diameter is almost independent of the active layer thickness. Compared to Ni-GDC cermet electrodes that were used in high performance metal supported cells,22 we find that the total ASR of pure GDC fuel electrodes is about 2–3 times lower, even when the additional high frequency ohmic effect is considered as well.
At 600 °C in 35 mbar H2 + 25 mbar H2O, the 3 μm thick GDC anode has a total polarization resistance of 0.205 Ω cm2. This value can be divided into an arc diameter of 0.085 Ω cm2, of which 0.007 Ω cm2 are due to gas diffusion kinetics, and a “hidden” ohmic ASR of 0.12 Ω cm2 which is only revealed by the p(O2) dependence of R1.
The p(O2) dependence of the ohmic ASR identifies our novel single-phase GDC fuel electrode as a highly promising option especially for SOECs, in which the electronic conductivity increases upon cathodic polarization.
Increase of electrochemically active thickness in CO/CO2 mixtures
Another advantage of a pure GDC functional layer in the fuel electrode is its intrinsically high coking resistance.32 This is further facilitated by the absence of nickel that catalyses the deposition of carbon, which makes GDC a promising materials candidate for use with dry hydrocarbons or for CO2 electrolysis. To test the performance of our GDC based electrodes in a carbon-containing atmosphere, electrochemical characterization was carried out in CO/CO2 mixtures with 7% CO fraction. The obtained impedance results are plotted in Fig. 7. Clearly observable, the ASR is significantly larger than in H2/H2O atmospheres. In contrast to the measurements in H2 + H2O mixtures, the cell with thicker GDC layer performs much better. This is in line with the transmission-line type equivalent circuit model: due to the lower surface catalytic activity in CO/CO2 atmosphere, the electrochemically active thickness becomes significantly larger than 3 μm, in line with impedance modelling.15,43 Therefore, the thicker GDC layer has more surface available for electrochemical reactions, resulting in a lower ASR.15,43 Interestingly, the activation energy of 1.1 eV is similar to that in H2 + H2O atmosphere, but for a different reason: due to the significantly higher ASR, ion conduction across the GDC–YSZ interface (which is independent of the gas phase) cannot be rate limiting. Rather, the surface reaction mechanism is different in CO + CO2 mixtures, and exhibits a larger activation energy and slower specific kinetics. Due to the slower binary gas diffusion in CO + CO2 mixtures, also the gas diffusion resistance is significantly larger. This is shown in Fig. S2 (ESI†), where a temperature-independent feature with 0.09–0.11 Ω cm2 is observed in the spectra for the 14 μm electrode, consistent with the fit of the Arrhenius plot using eqn (1), which also gives an Rdiff value of 0.11 Ω cm2.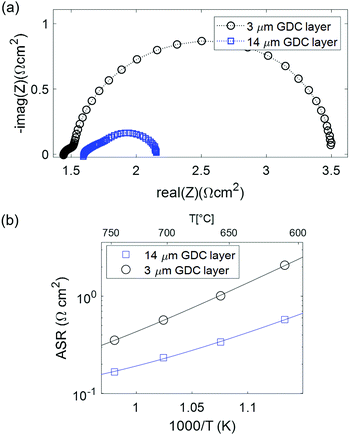 | ||
| Fig. 7 (a) Impedance spectra of symmetrical cells with 3 and 14 μm GDC layer thickness tested at 600 °C in 7% CO in CO2 atmosphere. (b) Arrhenius plot of the ASR. | ||
Conclusions and outlook
The impedance of symmetrical solid oxide model cells with pure GDC as anode functional layer was investigated in different gas phase and temperature conditions. Experimental results were compared to impedance modelling of pure GDC anodes and Ni-GDC cermets, which are in line with the predictions that best performance is achieved for pure GDC functional layers. The electrode arc of cells with 3 and 14 μm thick GDC layers is almost the same at 600 °C, which indicates that the electrochemically active thickness is less than 3 μm. Moreover, the activation energy (1–1.1 eV) is slightly higher than the value found in Ni-GDC cermets, and is most likely due to rate limiting ion transfer across the GDC–YSZ interface, where some interdiffusion and thus locally lowered ion conductivity is expected due to the 1150 °C sintering temperature. The gas diffusion resistance, which is about 0.01 Ω cm2, is the dominant part of the measured ASR at 800 °C. Also in CO/CO2 atmospheres, the ASR is reasonably low, but larger than in H2/H2O.To the author's best knowledge, the measured ASR of the pure GDC anodes is the lowest reported value for electrodes prepared by standard powder based processing routes, especially when considering that the test was performed at reduced pressure. Due to the much higher melting point of GDC compared to Nickel, the morphological stability – especially regarding redox cycling, sintering or dewetting behaviour – is expected to be significantly higher, compared to cermets. Due to the relatively low electron conductivity of the functional layer, it is important to fabricate a thin layer (ca. 3 μm), which was experimentally verified.
These results have the potential for substantial improvements in solid oxide cell (SOC) technology, especially for electrolysis cells. A nickel-free GDC functional layer may solve several problems, such as morphological degradation, redox cycling stability and carbon deposition, and is thus especially well-suited for dry CO2 electrolysis.
Author contributions
Investigation: MH, AN, writing – original draft: AN, writing, review & editing: MH, AN, AO, JF, methodology: AN, AO, supervision; AN, AO, JF, formal analysis: AN, MH.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the Christian Doppler Forschungsgesellschaft for financial support and Joseph Ring for providing the SEM images, which were recorded using facilities at the University Service Centre for Transmission Electron Microscopy (USTEM), TU Wien, Austria.References
- B. Shri Prakash, S. Senthil Kumar and S. T. Aruna, Renewable Sustainable Energy Rev., 2014, 36, 149–179 CrossRef CAS.
- N. Mahato, A. Banerjee, A. Gupta, S. Omar and K. Balani, Prog. Mater. Sci., 2015, 72, 141–337 CrossRef CAS.
- Z. Gao, L. V. Mogni, E. C. Miller, J. G. Railsback and S. A. Barnett, Energy Environ. Sci., 2016, 9, 1602–1644 RSC.
- F. Thaler, A. Nenning, C. Bischof, D. Udomsilp, L. G. J. de Haart, A. K. Opitz and M. Bram, ECS Trans., 2019, 91, 887–900 CrossRef CAS.
- C. Bischof, A. Nenning, A. Malleier, L. Martetschläger, A. Gladbach, W. Schafbauer, A. K. Opitz and M. Bram, Int. J. Hydrogen Energy, 2019, 44, 31475–31487 CrossRef CAS.
- M. C. Tucker, Energy Technol., 2017, 5, 2175–2181 CrossRef CAS.
- M. D. Gross, K. M. Carver, M. A. Deighan, A. Schenkel, B. M. Smith and A. Z. Yee, J. Electrochem. Soc., 2009, 156, B540–B545 CrossRef CAS.
- F. Thaler, D. Udomsilp, W. Schafbauer, C. Bischof, Y. Fukuyama, Y. Miura, M. Kawabuchi, S. Taniguchi, S. Takemiya, A. Nenning, A. K. Opitz and M. Bram, J. Power Sources, 2019, 434, 226751 CrossRef CAS.
- S. Tao and J. T. S. Irvine, J. Electrochem. Soc., 2004, 151, A252–A259 CrossRef CAS.
- T. Zhu, H. Troiani, L. V. Mogni, M. Santaya, M. Han and S. A. Barnett, J. Power Sources, 2019, 439, 227077 CrossRef CAS.
- D. E. Fowler, J. M. Haag, C. Boland, D. M. Bierschenk, S. A. Barnett and K. R. Poeppelmeier, Chem. Mater., 2014, 26, 3113–3120 CrossRef CAS.
- V. Rojek, D. Roehrens, M. Brandner, N. H. Menzler, O. Guillon, A. K. Opitz and M. Bram, ECS Trans., 2015, 68, 1297–1307 CrossRef CAS.
- U. P. Muecke, K. Akiba, A. Infortuna, T. Salkus, N. V. Stus and L. J. Gauckler, Solid State Ionics, 2008, 178, 1762–1768 CrossRef CAS.
- S. Zha, W. Rauch and M. Liu, Solid State Ionics, 2004, 166, 241–250 CrossRef CAS.
- A. Nenning, C. Bischof, J. Fleig, M. Bram and A. K. Opitz, Energies, 2020, 13, 987 CrossRef CAS.
- C. Xia and M. Liu, Solid State Ionics, 2001, 144, 249–255 CrossRef CAS.
- Y. Liu, S. Zha and M. Liu, Chem. Mater., 2004, 16, 3502–3506 CrossRef CAS.
- A. Nenning, L. Volgger, E. Miller, L. V. Mogni, S. Barnett and J. Fleig, J. Electrochem. Soc., 2017, 164, F364–F371 CrossRef CAS.
- S. R. Wang, T. Kobayashi, M. Dokiya and T. Hashimoto, J. Electrochem. Soc., 2000, 147, 3606–3609 CrossRef CAS.
- W. C. Chueh, W. Lai and S. M. Haile, Solid State Ionics, 2008, 179, 1036–1041 CrossRef CAS.
- W. Lai and S. M. Haile, J. Am. Ceram. Soc., 2005, 88, 2979–2997 CrossRef CAS.
- D. Udomsilp, J. Rechberger, R. Neubauer, C. Bischof, F. Thaler, W. Schafbauer, N. H. Menzler, L. G. J. de Haart, A. Nenning, A. K. Opitz, O. Guillon and M. Bram, Cell Rep. Phys. Sci., 2020, 100072 CrossRef.
- A. Zekri, K. Herbrig, M. Knipper, J. Parisi and T. Plaggenborg, Fuel Cells, 2017, 17, 359–366 CrossRef CAS.
- C. E. Frey, Q. Fang, D. Sebold, L. Blum and N. H. Menzler, J. Electrochem. Soc., 2018, 165, F357–F364 CrossRef CAS.
- M. Trini, A. Hauch, S. De Angelis, X. Tong, P. V. Hendriksen and M. Chen, J. Power Sources, 2020, 450, 227599 CrossRef CAS.
- A. Sciazko, Y. Komatsu, T. Shimura and N. Shikazono, J. Power Sources, 2020, 478, 228710 CrossRef CAS.
- A. Zekri, M. Knipper, J. Parisi and T. Plaggenborg, Phys. Chem. Chem. Phys., 2017, 19, 13767–13777 RSC.
- D. Marrocchelli, S. R. Bishop and J. Kilner, J. Mater. Chem. A, 2013, 1, 7673–7680 RSC.
- D. Marrocchelli, S. R. Bishop, H. L. Tuller and B. Yildiz, Adv. Funct. Mater., 2012, 22, 1958–1965 CrossRef CAS.
- S. R. Bishop, D. Marrocchelli, C. Chatzichristodoulou, N. H. Perry, M. B. Mogensen, H. L. Tuller and E. D. Wachsman, Annu. Rev. Mater. Res., 2014, 44, 205–239 CrossRef CAS.
- Z. L. A. Feng, M. L. Machala and W. C. Chueh, Phys. Chem. Chem. Phys., 2015, 17, 12273–12281 RSC.
- T. L. Skafte, Z. Guan, M. L. Machala, C. B. Gopal, M. Monti, L. Martinez, E. Stamate, S. Sanna, J. A. G. Torres, E. J. Crumlin, M. García-Melchor, M. Bajdich, W. C. Chueh and C. Graves, Nat. Energy, 2019, 4, 846–855 CrossRef CAS.
- M. P. Hoerlein, M. Riegraf, R. Costa, G. Schiller and K. A. Friedrich, Electrochim. Acta, 2018, 276, 162–175 CrossRef CAS.
- C. Graves, L. Martinez and B. R. Sudireddy, ECS Trans., 2016, 72, 183–192 CrossRef CAS.
- T. Nakamura, K. Yashiro, A. Kaimai, T. Otake, K. Sato, T. Kawada and J. Mizusaki, J. Electrochem. Soc., 2008, 155, B1244–B1250 CrossRef CAS.
- S. B. Adler, J. A. Lane and B. C. H. Steele, J. Electrochem. Soc., 1996, 143, 3554–3564 CrossRef CAS.
- A. Utz, J. Joos, A. Weber and E. Ivers-Tiffée, ECS Trans., 2011, 35, 1669 CrossRef CAS.
- V. Sonn, A. Leonide and E. Ivers-Tiffée, J. Electrochem. Soc., 2008, 155, B675 CrossRef CAS.
- S. Dierickx, T. Mundloch, A. Weber and E. Ivers-Tiffée, J. Power Sources, 2019, 415, 69–82 CrossRef CAS.
- J. Nielsen, T. Jacobsen and M. Wandel, Electrochim. Acta, 2011, 56, 7963–7974 CrossRef CAS.
- J. Nielsen and J. Hjelm, Electrochim. Acta, 2014, 115, 31–45 CrossRef CAS.
- Z. Gao, H. Wang, E. Miller, Q. Liu, D. Senn and S. Barnett, ACS Appl. Mater. Interfaces, 2017, 9, 7115–7124 CrossRef CAS.
- A. Opitz, M. Gerstl and M. Bram, Fuel Cells, 2019, 19, 417–428 CrossRef CAS.
- W. C. Chueh, Y. Hao, W. Jung and S. M. Haile, Nat. Mater., 2012, 11, 155–161 CrossRef CAS.
- M. Gerstl, A. Hutterer, J. Fleig, M. Bram and A. K. Opitz, Solid State Ionics, 2016, 298, 1–8 CrossRef CAS.
- F. Han, R. Mücke, T. Van Gestel, A. Leonide, N. H. Menzler, H. P. Buchkremer and D. Stöver, J. Power Sources, 2012, 218, 157–162 CrossRef CAS.
- D. Udomsilp, D. Roehrens, N. H. Menzler, C. Bischof, L. G. J. de Haart, A. K. Opitz, O. Guillon and M. Bram, J. Electrochem. Soc., 2017, 164, F1375–F1384 CrossRef CAS.
- T. Zhu, H. E. Troiani, L. V. Mogni, M. Han and S. A. Barnett, Joule, 2018, 2, 478–496 CrossRef CAS.
- W. Yuan, Q. Ma, Y. Liang, C. Sun, K. V. L. V. Narayanachari, M. J. Bedzyk, I. Takeuchi and S. M. Haile, J. Mater. Chem. A, 2020, 8, 9850–9858 RSC.
- S. R. Bishop, D. Marrocchelli, W. Fang, K. Amezawa, K. Yashiro and G. W. Watson, Energy Environ. Sci., 2013, 6, 1142–1146 RSC.
- H. C. Yao and Y. Y. Yao, J. Catal., 1984, 86, 254–265 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ma00202c |
| ‡ These authors contributed equally to the work. |
| This journal is © The Royal Society of Chemistry 2021 |