Heterogeneity of cell membrane structure studied by single molecule tracking

Abstract

Heterogeneity in cell membrane structure, typified by microdomains with different biophysical and biochemical properties, is thought to impact on a variety of cell functions. Integral membrane proteins act as nanometre-sized probes of the lipid environment and their thermally-driven movements can be used to report local variations in membrane properties. In the current study, we have used total internal reflection fluorescence microscopy (TIRFM) combined with super-resolution tracking of multiple individual molecules, in order to create high-resolution maps of local membrane viscosity. We used a quadrat sampling method and show how statistical tests for membrane heterogeneity can be conducted by analysing the paths of many molecules that pass through the same unit area of membrane. We describe experiments performed on cultured primary cells, stable cell lines and ex vivo tissue slices using a variety of membrane proteins, under different imaging conditions. In some cell types, we find no evidence for heterogeneity in mobility across the plasma membrane, but in others we find statistically significant differences with some regions of membrane showing significantly higher viscosity than others.

---

Introduction

It is now thought that structural heterogeneity of the plasma membrane plays a critical role in a variety of cell functions.^1–2 This contrasts with our classical view of the plasma membrane as a fluid mosaic bilayer of phospholipids and other amphipathic molecules within which proteins can diffuse in an unhindered manner.³ The path taken by a diffusing transmembrane protein should follow a random Brownian walk and a plot of its mean-squared displacement against time interval (MSD vs. dT) should be linear,⁴ with a gradient determined by D_lat, the lateral diffusion coefficient. D_lat should be a linear function of membrane viscosity and thickness but should have only a weak dependence (i.e. log-function) on protein radius and viscosity of the bounding aqueous media (i.e. cytosol and extra cellular fluid).^5,6 Recently a revised picture of the plasma membrane has emerged in which it is thought to have a more heterogenous structure compared to the classical fluid mosaic model, and there is biochemical and biophysical evidence for submicron, phase-separated, domains⁷ that are enriched with particular lipid species⁸ (“lipid rafts”) and regions of protein crowding or clustering. In addition, interaction of membrane proteins with the cortical cytoskeleton⁹ or extracellular matrix can lead to obstructions to free-diffusion¹⁰ (“picket-fences”). Together these features contribute to anomalous diffusive behaviour^11,12 whereby MSD vs. dT plots are non-linear and show distinct downward curvature. The features that contribute to membrane heterogeneity are thought to be transient in nature and to extend over a length scale <200 nm, making them notoriously difficult to study in live cells. However, the advent of super-resolution, single molecule imaging methods^2,13 allows “rafts”, “picket fences”, protein clustering and other heterogeneous properties to be studied in live cells and tissue slices in real-time.^14,15 An advantage of single molecule studies is that they eliminate problems of bulk averaging that can mask short-lived, sub-resolution structural heterogeneities. Individual transmembrane proteins have been used as probes of membrane structure because they are of uniform size, can be labelled with high-specificity and known stoichiometry, they target to known membrane compartments and genetic manipulation allows structural alterations. However, tracking of single fluorophores in live cells is technically challenging because the spatial resolution and temporal precision of tracking is limited by photon emission rate and photobleaching of the fluorescent moiety. A useful figure of merit for a given fluorophore is the average number of photons emitted before photobleaching, giving rise to the idea of a “photon budget”.¹⁶ For a given experiment, best use of the photon budget requires a compromise to be made between tracking precision and measurement bandwidth. To measure small-scale, rapid movements, high laser power is required so that single fluorophores are bright and can be tracked with high-precision at fast video frame rate, but the cost is they soon photobleach. At low laser power, fluorophores can be tracked for longer but tracking resolution is reduced because fewer photons are emitted per second. It is also important to consider fluorophore density across the sample field of view (see ESI of ref. 14†) because at high density, fluorophore tracking becomes difficult as paths overlap, whereas at low density fewer molecules pass through a given region of interest making it difficult to accumulate sufficient data for statistical analysis. In general, fluorescent fusion proteins (like eGFP) photobleach faster than synthetic organic fluorophores (like rhodamine or Cy-dyes) and offer a lower photon budget.

The aim of the current study has been to test whether live mammalian cell membranes exhibit heterogeneity in viscosity on the micron length-scale. We have explored whether heterogeneity in protein mobility is evident in immortalised cell lines, primary cell culture and live tissue samples using different protein probes. Total internal reflection fluorescence microscopy (TIRFM)¹⁷ was used to image membrane proteins labelled with single fluorophores and studied their diffusive behaviour to infer local membrane properties. We used a quadrat sampling method that enables statistical tests to be performed on data obtained from different regions of the cell. Trajectories were segmented and diffusion coefficients computed from ≥10 data points (∼0.5 second) sections of each trajectory. The image of the cell was then sub-divided into a checkerboard pattern of sample quadrats (∼1–4 μm² area each), and local statistics were calculated for trajectory segments that resided within each quadrat so statistical tests could be performed across different regions of the cell membrane. For most of the specimens tested, protein mobility was homogenous across the cell surface but in some cells we found evidence for spatial heterogeneity. We conclude that lipid rafts (if they exist) are evenly distributed across the plasma membrane of most cells, but in some cell types, they might show heterogeneity in density forming a “raft of rafts”.

Experimental

All chemicals were obtained from Sigma-Aldrich, UK, unless stated otherwise.

Cultured cell transfection and tissue labelling

All of the cells and tissue materials were imaged using a custom-made imaging chamber described previously.¹⁸ Human umbilical vein endothelial cells (HUVECs) (PromoCell GmbH, Heidelberg, Germany) derived from a pooled, primary cell culture were transfected with M₂-eGFP muscarinic receptor fusion protein (kind gift of Prof. J. W. Wells, University of Toronto, Canada) using nucleofection according to the manufacturer’s instructions (Amaxa GMBH). CHO-K1 cells were transfected with cDNAs encoding the mouse α1, β1, and δ nicotinic receptor subunits subcloned within vector pRBG4 (kind gift of S. M. Sine, Mayo Clinic, MN, USA). The mouse γ-subunit was tagged with eGFP inserted into the cytoplasmic loop between transmembrane helices M3 and M4 and subcloned in pRK5 plasmid (kind gift of V. Witzemann, Max-Plank-Institute, Heidelberg, Germany). Primary cardiomyocytes were prepared as described previously¹⁴ and allowed to settle on to the imaging coverslip before labelling with Cy3B-telenzepine (10 nM for 1 h at 23 °C). The HL1 cardiomyocyte cell-line was cultured for 24 h before labelling with Cy3B-telenzepine (1 nM for 3.5 h at 23 °C). Zebrafish heart was removed and washed in room temperature PBS (pH 7.2) (Thermo Fisher Scientific, UK) solution supplemented with 10 U ml⁻¹ heparin and 100 U ml⁻¹ penicillin–streptomycin for 5 min. After washing, the heart was moved into an ice-cold “relaxing solution” consisting of PBS supplemented with; 1 mM EDTA, 2.5 mM KOH, and 3 mM MgCl₂ for 5 min. A cutting block, with a 2 mm diameter cavity, and a single cutting-slot was used to bisect the heart along the ventricle axis.¹⁵ Mouse embryonic heart slices were prepared using procedures described previously.¹⁴ The prepared tissue slices were placed in relaxing PBS solution containing 10 nM of Cy3B-telenzepine for 1 h at 4 °C. This procedure labelled >95% of M₂ muscarinic receptors with the tight-binding fluorescent ligand. The tissue slice was fixed against the coverslip with a fine nylon mesh grid (∼0.5 × 0.5 mm²) stretched in a stainless-steel tambour. The chamber was filled with Hank’s Balanced-Salt solution supplemented with 20 mM HEPES (pH 7.4). All imaging was performed at 23 °C.

TIRF imaging

A custom-built TIRF microscope was used, as described previously.¹⁹ Briefly, the beam from a 100 mW, 488 nm laser or 150 mW, 561 nm laser (Light HUB-6, Omicron, Germany) was expanded using a Galilean beam expander and focused at the back focal-plane of a high numerical aperture, oil-immersion, objective lens (PlanApo, 100×, NA 1.45, Olympus, Japan) using a small, aluminium-coated mirror (3 mm diameter, Comar Optics, UK) placed at the edge of the back-aperture of the objective lens. The average laser power at the specimen plane was adjusted to ∼0.5 μW μm⁻² and the incident laser beam angle was adjusted to ∼63° to create the evanescent field at the glass–aqueous medium interface. A second small mirror was placed at the opposite edge of the objective lens back-aperture to remove the returning (internally-reflected) laser beam from the microscope and a narrow band-pass emission filter FF01-525/50 or FF01-593/40 (Semrock, Rochester, NY) was used to block the scattered 488/561 nm laser light and other unwanted light. An EMCCD camera (iXon897BV, Andor, UK) captured video sequences at a rate of 20–50 fps, and the data were stored on a computer hard drive for analysis.

Video data analysis

Video image sequences were analysed using GMimPro software (http://www.mashanov.uk), which employs an automatic single particle tracking algorithm (described previously²⁰) to detect and track individual fluorophores. The position of each fluorescent spot was localised with sub-pixel resolution using a Gaussian fitting method and systematic drift was corrected via cross-correlation. Individual particle trajectories were output as a table of x,y coordinates measured at each video frame (i.e. each time point) for every fluorophore detected in the sample. From the tabulated data, the mean-squared displacement (MSD) of each fluorophore was computed over all possible time intervals (dT) (e.g. 1,2,3…n frames). MSD vs. dT plots were then generated to examine the particle motion; a linear-relationship is expected for simple Brownian motion, but curvature indicates anomalous diffusion (discussed later). To extract statistically meaningful mobility data from the trajectory analysis, we analysed trajectories where single fluorescent spots could be tracked for at least 10 consecutive frames with a permitted spot displacement of ≤0.7 μm between frames.²⁰

Single molecule mobility maps

We created a map to depict the lateral diffusion coefficient of our labelled protein probes by taking sequential 10-frame time windows (∼400 ms) along each single molecule trajectory and estimating the local D_lat value from the gradient of the MSD vs. dT plot. For display purposes, tracks were dilated to be 5 pixels wide (0.5 μm) and coded to produce a pseudo-colour heat map of membrane viscosity. At positions where trajectories overlapped, the pixel intensity was averaged. This approach is similar, but not identical, to single particle velocimetry.

Measuring the local heterogeneity of cell membrane

We divided the image of each cell into a checkerboard pattern of sample quadrats and selected segments of single molecule trajectories that resided within each quadrat region. The local trajectory segments (at least 5 trajectories, ≥10 data points each per segment) were used to build an average MSD vs. dT plot. The initial slope of the plot was used to estimate the local D_lat (i.e. slope/4, for 2-dimensional diffusion). Local D_lat estimates were binned and histogrammed to build a global mobility map across the cell surface. The distribution of D_lat values of individual trajectories is described by a Gamma distribution due to the limited number of data points in each trajectory, but, according to the central limit theorem, the distribution of mean D_lat values measured at each quadrat sample should be normally distributed (i.e. Gaussian). We tested for heterogeneity across the checkerboard pattern of quadrat samples against an expectation based on the global distribution. The normality of the distributions was checked using the Kolmogorov–Smirnov (KS) test. The pairwise comparisons were done using Student’s t-test when both distributions were normal, and Mann–Whitney U (MW) test when at least one distribution was not normal.²¹ Calculations were performed using open-source R software.²²

Results

Comparison of membrane viscosity in HL1 cell-line vs. primary cardiomyocytes

We first imaged HL1 cells, a cardiac muscle cell-line, that natively-express M₂ muscarinic acetylcholine receptors (Fig. 1A and Movie 1†). Receptors were labelled using the tight-binding fluorescent ligand Cy3B-telenzepine¹⁴ under conditions that gave an optimal density of labelled receptors (∼0.8 receptors per μm²) for single molecule imaging and tracking purposes. Under the conditions used here, the Cy3B photobleaching rate was 0.19 s⁻¹, (Fig. S1A†) which allowed us to track individual molecules for around 5 s. Many trajectories were prematurely truncated because fluorophores overlapped during a single frame. This caused one track to terminate and a new track to be generated when the fluorophores separated. A small number of, non-specifically, surface-bound Cy3B-telenzepine molecules were completely immobile throughout the video recording and these objects were removed from the dataset. The projected image of all single molecule trajectories shows the degree of coverage across the cell surface (Fig. 1A(ii) and S2†). The cell periphery has a higher track density because fresh (unbleached) fluorophores diffuse into this region from the apical cell surface which is beyond the evanescent field.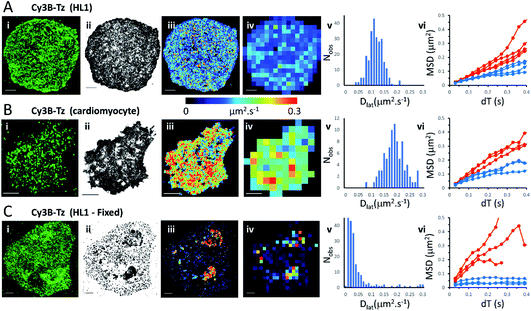

Fig. 1 M₂ muscarinic acetylcholine receptor diffusion on the plasma membrane of HL1 cells and primary cardiomyocytes. (A(i)) First video frame showing an HL1 cell-line with Cy3B-telenzepine labelled M₂ receptors. (ii) A projection of all single molecule trajectory paths. (iii) Heat-map showing locally averaged D_lat values; mean D_lat = 0.12 μm² s⁻¹, n = 7526 trajectories. (iv) Heat map of the quadrat-sampled (2 × 2 μm²) D_lat values. (v) Distribution of D_lat measured in each quadrat region across the cell: 250 compartments, overall mean (of the local mean values) D_lat = 0.112 ± 0.028 μm² s⁻¹ (±SD). (vi) MSD vs. dT plots for typical fast (where D_lat > mean +1.5 × SD; red) and slow (where D_lat < mean −1.5 × SD; blue) quadrat regions. Video was recorded at 33 fps. (B) Panels as for A except: (i) primary cardiomyocyte. (iii) Mean D_lat = 0.203 μm² s⁻¹, n = 3133 trajectories. (v) Quadrats: 86 (2 × 2 μm²); mean D_lat = 0.188 ± 0.043 μm² s⁻¹. (vi) See panel A. (C) Panels as for A except: (i) HL1 cell chemically fixed with 1% paraformaldehyde. (ii) Trajectory paths show that most molecules have very restricted motion following fixation. Some regions show receptor diffusion (dark areas where molecular trajectories greatly overlap). (iii) Most M₂ receptors are fixed, but some isolated regions show rapid receptor diffusion; average D_lat = 0.132 μm² s⁻¹, n = 6673 trajectories. (iv) Quadrats: 327 (2 × 2 μm²). (v) Distribution of D_lat values with overall mean D_lat = 0.029 ± 0.05 μm² s⁻¹. Fixed regions indicate the tracking noise floor (see main text and Fig. S1 C and D†). (vi) See panel A.

Analysis of individual trajectories (see methods) leads to estimates of D_lat for each molecule tracked and these values can be plotted as a pseudo-colour map (Fig. 1A(iii)) indicating M₂ receptor mobility at different regions across the cell surface. To test for homogeneity, the mobility map is divided into a checker-board pattern of sample quadrats (Fig. 1A(iv)). Each quadrat is then colour-coded to represent the average D_lat value within that region. According to the central limit theorem the distribution of mean D_lat values should be Gaussian (Fig. 1A(v)), and in the following text “mean D_lat” refers to the “mean of the quadrat means”. To investigate whether the diffusion of molecules in quadrats with extreme low or high D_lat values was anomalous we plotted MSD vs. dT diagrams from those, selected, quadrats (Fig. 1A(vi), S3A, B† and Table 1).

Table 1 Kolmogorov–Smirnov analysis of the local viscosity distributions^a

Figure	Sample	Mean (μm^2 s^−1)	SD	n	K–S D-statistic	p-Value	Conclusion
a Significance testing against normal distribution: *p-value < 0.05 (e.g. >95% confidence); **p-value < 0.01 ***p-value < 0.001.
Fig. 1	M2-Cy3B HL1	0.112	0.028	250	0.045	0.704	Normal
	M2-Cy3B primary myocyte	0.188	0.043	86	0.073	0.747	Normal
	M 2 -Cy3B HL1 fixed	0.029	0.050	327	0.283	<0.0001	Not-normal***
	M2-Cy3B inter-cell HL1	0.129	0.015	29	0.121	0.793	Normal
Fig. 2	M 2 -eGFP-HUVEC	0.204	0.086	150	0.178	0.0002	Not-normal***
Fig. 3	M2-Cy3B zebrafish cell 1 and cell 2	0.224	0.116	49	0.185	0.069	Normal
	Zebrafish cell 1	0.291	0.144	20	0.198	0.367	Normal
	Zebrafish cell 2	0.179	0.056	29	0.131	0.699	Normal
	M 2 -Cy3B mouse slice (all cells)	0.427	0.457	79	0.294	<0.0001	Not-normal***
	Mouse slice cell 1	0.533	0.518	27	0.253	0.052	Normal
	Mouse slice cell 2	0.534	0.590	18	0.370	0.010	Not-normal**
	Mouse slice cell 3	0.285	0.228	34	0.260	0.020	Not-normal*
Fig. 4	Nicotinic-eGFP-CHO	0.114	0.078	181	0.191	<0.0001	Not-normal***
Fig. 5A	Model	0.188	0.034	227	0.046	0.721	Normal
Fig. 5B	Model (both regions)	0.111	0.080	226	0.192	<0.0001	Not-normal***
	Model (non-raft)	0.188	0.030	120	0.056	0.847	Normal
	Model (raft region)	0.031	0.021	116	0.160	0.005	Not-normal**

---

We next imaged M₂ receptors in primary cultured mouse cardiomyocytes that had been labelled the same way as the HL1 cells (Fig. 1B and Movie 2†). We found receptor diffusion was significantly faster (D_lat = 0.2 μm² s⁻¹) compared to the HL1 cell-line (t-test with unequal variances (p < 0.0001), t(111) = −15.4, p < 2.2 × 10⁻¹⁶), implying membrane viscosity was lower in the primary cultured cells. The molecular tracks were analysed as before and binned to give a checkerboard pattern of quadrat samples across the cell (Fig. 1B(i–vi) and Table 1).

In order to measure localisation and tracking errors (i.e. the “noise floor” of our measurements), we imaged HL1 cells that had been chemically fixed using 1% paraformaldehyde. Interestingly, after several minutes treatment with fixative, many cells still had isolated regions, or “islands”, of membrane that appeared sealed off from the fixative and where the Cy3B-telenzepine-labelled receptors continued to diffuse (Fig. 1C and Movie 3†). This fixation artefact gave the opportunity to generate diffusion maps in cells that showed extreme heterogeneity in receptor mobility due to incomplete fixation. Cell regions where chemical fixation was effective allowed individual molecules to be selected and tracked in order to give an estimate of the localisation and tracking error measured under our imaging conditions. The sum of all noise sources gave 33 nm root mean squared deviation (rms) (i.e. MSD = 1 × 10⁻³ μm²) (Fig. S1C and D).† However, the quadrat sampling method gave a three-fold higher estimate of the noise floor: rms ∼100 nm (MSD = 1 × 10⁻² μm²) (Fig. 1C(v)). This difference arose because mobile molecules were often present within a given quadrat region. The quadrat mapping of D_lat values showed a heterogeneous distribution of values which is readily explained by the incomplete fixation, whereby some islands of plasma membrane seemed to be isolated and protected from the paraformaldehyde treatment. The mean D_lat values determined for each of the quadrat sample regions were histogrammed as before. The D_lat values showed an exponential distribution (Fig. 1C(iv)). Typical slow-moving quadrat regions (blue lines in Fig. 1C(vi)) exhibited MSD vs. dT plots that were highly anomalous, consistent with the molecules being either totally immobile or trapped in a confined area. The faster moving, outlier, D_lat values were from unfixed regions of membrane and MSD vs. dT plots (red lines in Fig. 1C(vi)) showed a variety of behaviours, with some quadrat regions showing a relatively linear slope of MSD vs. dT plots and others showing a distinct downward curvature consistent with anomalous diffusive behaviour (Table 1).

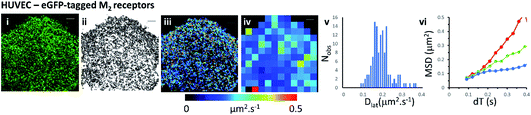
Mapping membrane viscosity using eGFP-tagged M₂ receptors

We next examined the mobility of a C-terminally-tagged M₂-receptor eGFP-fusion protein where the fluorophore is positioned on the intracellular-side of the molecule in contrast to the extrinsic, synthetic labelling with Cy3B-telenzepine used in the previous experiments. HUVECs were transiently transfected with a recombinant M₂-eGFP fusion construct in a mammalian cell expression vector and cells were then selected for imaging based on their receptor expression level (target level ∼0.8 receptors per μm²). The eGFP-tagged receptors moved rapidly and in a seemingly unhindered fashion across the plasma membrane (Fig. 2 and Movie 4†). The photobleaching rate of the eGFP fluorophore was 0.4 s⁻¹ (Fig. S1B†) which is twice as fast as the Cy3B fluorophore. In addition to that, fluorophores could only be tracked for ∼0.5 s, because the eGFP signal-to-noise intensity ratio is lower than for Cy3B and this leads to premature track termination (i.e. tracking can fail before the fluorophore bleaches). Individual static molecules were selected and tracked in order to give an estimate of the localisation and tracking error measured under our imaging conditions. The sum of all noise sources gave 26 nm root mean squared deviation (rms) (i.e. MSD = 1 × 10⁻³ μm²) (Fig. S1C and D†), similar precision to Cy3B. The average rate of receptor diffusion (D_lat = 0.2 μm² s⁻¹) was similar to the primary cardiomyocytes (MW, U = 6265, p = 0.715) but the trajectories appear more compact (Fig. 2(ii)vs.Fig. 1A and B panel (ii)) simply because they are of shorter duration. The short tracks mean that there is less coverage (i.e. fewer unique tracks per unit area) when membrane viscosity maps are generated using a 4 × 4 μm² quadrat size (Table 1).

Fig. 2 eGFP-tagged M₂ muscarinic acetylcholine receptor diffusing at the plasma membrane of HUVECs. (i) Single image from the beginning of the record shows individual eGFP-tagged M₂ receptors at the plasma membrane. (ii) Trajectory map; 5031 trajectories. (iii) Heat-map of D_lat; mean D_lat = 0.197 μm² s⁻¹. (iv) D_lat quadrat map; 129; 4 × 4 μm² quadrats (black indicates <5 trajectories, removed from later analysis). (v) Distribution of D_lat values; D_lat = 0.204 ± 0.086 μm² s⁻¹ (mean ± SD). (vi) MSD vs. dT plots for typical fast (where D_lat > mean +1.5 × SD; red), intermediate (where D_lat ≈ mean; green) and slow (where D_lat < mean −1.5 × SD; blue) quadrat regions. Video was recorded at 33 fps.

Comparison of Cy3B-telenzepine labelled M₂ receptors in zebrafish tissue slice vs. mouse tissue slice

We investigated the M₂ muscarinic receptor mobility in live tissue slices using two model cardiac systems (zebrafish and mouse), using Cy3B-telenzepine to fluorescently label the proteins. An initial observation was that the spread-area of the cells was noticeably smaller than for isolated primary cardiomyocytes and the HL1 cell-line; presumably because cells are held within the tissue and are less able to spread across the coverslip surface. Receptor density was similar in the tissue slices compared to the isolated cultured cells (∼1 receptor per μm²) (Fig. 3A, B and Movie 5† for comparison), but, the rate of diffusion was significantly faster in mouse tissue slices (mean D_lat = 0.43 μm² s⁻¹) compared to primary myocytes (MW, U = 1683, p = 2.3 × 10⁻⁸) and HL1 cell-line (MW, U = 2135, p < 2.2 × 10⁻¹⁶) and was similarly fast in the zebrafish tissue (mean D_lat = 0.33 μm² s⁻¹), but the median values were significantly different (MW, U = 1261, p = 0.001). Rapid receptor movement in both specimens produced a dense network of single molecule tracks so a small quadrat size (1 × 1 μm²) could be used and this gave a higher-resolution map of membrane viscosity (Fig. 3(iv)). A histogram of mean D_lat values derived from each quadrat sample was normally distributed (Fig. 3(v)). MSD vs. dT plots for three of the “slower” quadrat samples compared to 3 of the “faster” regions showed that MSD increased linearly with dT for both fast and slow samples and did not show substantial curvature (that would indicate anomalous diffusion) (Fig. 3(vi)).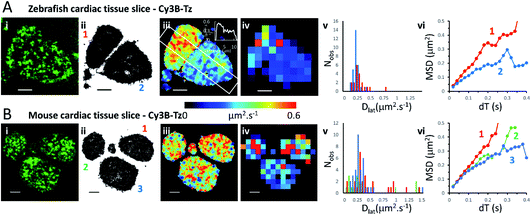

Fig. 3 Cy3B-telenzepine labelled M₂ muscarinic receptors in zebrafish and mouse cardiac tissue slices. (A(i)) First video frame showing individual Cy3B-telenzepine labelled M₂ receptors on the plasma membrane of zebrafish cardiomyocytes in a tissue slice. (ii) Map showing the trajectory paths of individual molecules (see Movie 3).† (iii) Pseudo-colour heat-map showing locally averaged M₂ receptor D_lat values. The overall mean D_lat = 0.33 μm² s⁻¹, 2518 trajectories. White rectangle shows profile plotted on the insert in the right-top corner. (iv) Heat map of the quadrat-sampled D_lat values; 49 quadrats (1 × 1 μm²) (black indicates <5 trajectories, removed from later analysis). (v) Distribution of D_lat measured in each quadrat region (red = “cell 1”, blue = “cell 2”): overall mean D_lat = 0.224 ± 0.116 μm² s⁻¹ (±SD): “cell 1” D_lat = 0.291 ± 0.144 μm² s⁻¹, “cell 2” D_lat = 0.179 ± 0.056 μm² s⁻¹. (vi) MSD vs. dT plots for typical “cell 1” (red), “cell 2” (blue) quadrat regions. (B) As for Panel A except: (i) mouse cardiomyocytes in a tissue slice. (iii) Mean D_lat = 0.428 μm² s⁻¹, 2336 trajectories. (iv) D_lat map: 83 quadrats (1 × 1 μm²). (v) Distribution of D_lat (“cell 1”(red); “cell 2” (green); “cell 3” (blue): mean D_lat = 0.427 ± 0.457 μm² s⁻¹). (vi) MSD vs. dT plots for typical quadrat regions (where D_lat ≈ global mean D_lat); within “cell 1” (red); “cell 2” (green); “cell 3” (blue).

Although the global average D_lat was significantly faster in tissue slices (D_lat = 0.33 μm² s⁻¹) than isolated cultured cells, the difference was smaller in the D_lat maps because faster trajectories were underrepresented and the mean D_lat value fell to 0.22 μm² s⁻¹ for the zebrafish tissue slices. Consistent with this, when quadrat size was increased to 2 × 2 μm², the mean D_lat value increased to 0.27 μm² s⁻¹. Interestingly, we found significant differences in mobility between neighbouring cells (Fig. 3(iii)), implying that there are significant differences in membrane composition between cardiomyocytes within a given tissue sample. In the example shown here, one cell gave D_lat = 0.29 μm² s⁻¹ the other, D_lat = 0.18 μm² s⁻¹ (t-test with unequal variances, t(23) = 3.224, p = 0.004).

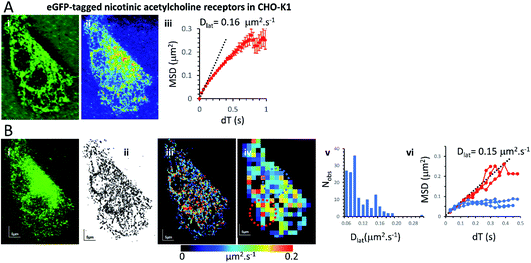
Mapping membrane viscosity using nicotinic acetylcholine ion channels

Our expectation was that the nicotinic acetylcholine receptor, which is a hetero-pentameric ion channel, should exhibit unrestricted diffusive motion at the plasma membrane. However, we found it did not localise strongly to the plasma membrane and most molecules were retained in the endoplasmic reticulum (ER) following transfection. This might arise because of its hetero-pentameric nature, comprising four different polypeptides; β1, δ, γ and two α1 subunits, that must assemble correctly following co-transfection of the α1, β1, and δ subunits, together with the eGFP-γ-subunit. It is likely that a fraction of eGFP-γ subunits failed to assemble correctly into the heteromeric complex and are retained in the ER. So, we see a mixture of fluorophores at the ER network and also at the plasma membrane. Receptors that had localised correctly to the plasma membrane were most evident beneath the cell nucleus where the ER was excluded. We tracked all fluorophores as before and generated mobility maps to investigate mobility across the cell (Fig. 4). Our data show, perhaps unsurprisingly, that the histogram of D_lat values derived from the quadrat maps is not normally distributed, and while MSD vs. dT plots produced from “fast-moving” quadrat regions (plasma membrane) are consistent with an unconstrained Brownian walk, “slow-moving” regions show anomalous diffusive behaviour (MSD vs. dT plots show a distinct downward curvature) because γ subunits are confined to the ER membrane network.

Fig. 4 Nicotinic acetylcholine receptors were present at the plasma membrane and the ER of CHO-K1 cells: diffusion of nicotinic receptors was highly anomalous because the eGFP tagged γ-subunit only partially targeted the plasma membrane and the majority was found in the ER. (A(i)) Average projection of the video stack. (ii) Standard-deviation projection shows the reticulated network and also darker regions (presumably below the nucleus) where the ER was excluded and receptors could be seen moving at the plasma membrane. (iii) The overall MSD vs. dT plot showed evidence of anomalous diffusion with initial gradient (determined by least-squares’ linear regression) indicating D_lat = 0.16 μm² s⁻¹. (B(i)) First video frame showing single fluorophores. (ii) Projection of all the single fluorophore trajectories. (iii) D_lat map from trajectory segments. (iv) D_lat quadrat map (black indicates <5 trajectories, removed from later analysis). (v) Distribution of quadrat D_lat means (note that the histogram is not normally distributed). (vi) MSD vs. dT for fast (where D_lat > mean +1.5 × SD; red) and slow (where D_lat < mean −1.5 × SD; blue) regions. The fast-moving regions were located under the cell nucleus where receptors diffused freely at the plasma membrane (MSD vs. dT plots were linear with initial gradient (determined as in A) giving D_lat = 0.15 μm² s⁻¹). The slow-moving regions were from the network (ER) regions where receptors showed anomalous diffusion (note distinct downward curvature).

Monte Carlo simulation of membrane protein random walks

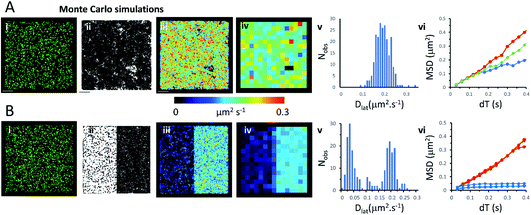
We used an object-based, Monte Carlo stochastic model²³ to generate sequences of simulated TIRFM videos (Fig. 5 and Movie 6†). The random movement of single molecules were realistically reproduced with known intensity levels, stochastic shot-noise, background noise and photobleaching behaviour consistent with our experimental TIRFM imaging modality. The simulated video data sets were analysed with the same image processing software used for our real data sets. We first checked that our localisation and tracking software gave consistent results over a wide range of simulated D_lat values (see ESI Fig. S5†). The example simulation in Fig. 5A shows trajectories detected in a sequence of images simulating molecules moving at D_lat = 0.2 μm² s⁻¹. The D_lat map (Fig. 5A(iii)) appears similar to our cell imaging data (Fig. 1A, B, 2 and 3). The local D_lat map calculated for a 2 × 2 μm² quadrat size showed a normal distribution of diffusion coefficients (Fig. 5A(v)). Note here, that any superficial appearance of heterogeneous behaviour is simply due to statistical variation across sample quadrats, and demonstrates the necessity for statistical tests of heterogeneity. In fact, there is no deviation from normality (Table 1).The MSD vs. dT plots (Fig. 5A(vi)) were linear for the “fast”, “intermediate” and “slow” quadrat samples (note: we define “fast” as D_lat > mean +1.5 × SD, “slow” D_lat < mean −1.5 × SD and “intermediate” as D_lat ≈ mean). We also simulated the presence of lipid raft regions 300 × 300 nm², dispersed randomly across the membrane (Fig. 5B, on the left-hand side of the modelled membrane) in which molecules were confined (D_lat = 0.02 μm² s⁻¹) and these regions adjoined others where molecules diffused freely with D_lat = 0.2 μm² s⁻¹ (on the right-hand side of the membrane). Now, the distribution of quadrat mean D_lat values were no longer normally distributed (Fig. 5B(v)). “Slow” regions showed anomalous diffusion with downward curvature, because molecules were confined within the modelled “lipid rafts”, whereas “fast” regions had linear MSD vs. dT plots.

Fig. 5 Monte Carlo simulation of single, fluorescently-tagged molecules moving at the plasma. (A(i)) Single image from the beginning of the simulated video recording shows individual fluorescent molecules (initial density 0.8 molecules per μm²). The simulated molecules are free to move in an unrestricted manner. (ii) Trajectory map consisting of 4434 trajectories. Fluorophore intensity, noise levels and photobleaching rate (0.2 s⁻¹) were chosen to closely mimic our real data sets. (iii) D_lat map. (iv) Quadrat sampled D_lat map, 227 quadrats; 2 × 2 μm², black squares contain <5 trajectories rejected from further analysis. (v) Histogram of quadrat D_lat values, is normally distributed and consistent with a single population. (vi) MSD vs. dT plots for typical fast (where D_lat > mean +1.5 × SD; red), intermediate (where D_lat ≈ mean; green) and slow (where D_lat < mean −1.5 × SD; blue) quadrat regions. (B) As for Panel A except: (i) the left-hand side of the simulation molecules are confined to lipid rafts; right-hand side molecules are free to move in an unrestricted manner, (ii) trajectory map, (iii) D_lat map, comprises two distinct regions. (iv) Quadrat sampled D_lat map. (v) Histogram of quadrat D_lat values, is now clearly bi-modal and not consistent with a single population. (vi) MSD vs. dT plots for typical fast (where D_lat > mean +1.5 × SD; red) and slow (where D_lat < mean −1.5 × SD; blue) quadrat regions. The “slow” (blue curves) regions show anomalous diffusive behaviour because molecules are trapped within modelled rafts of 300 × 300 nm² area.

Discussion

In the spirit of Faraday meetings our intention is to provoke discussion on the structure of biological membranes: the classical view of the plasma membrane is that it comprises a fluid-mosaic of lipids, proteins and other amphipathic molecules.³ This view has been challenged and it is now proposed that there is structural heterogeneity arising from lipid de-mixing and phase-separation which results in the formation of sub-micron sized microdomains or “lipid rafts”, enriched with saturated lipids, sphingolipids and cholesterol.²⁴ Our view of the plasma membrane has therefore changed from a fully-mixed fluid-mosaic sheet to a cholesterol- and protein-stabilised, oil-in-oil, emulsion that resembles a two-dimensional “mayonnaise”. The small-size and short-lived, nature of lipid microdomains has led to controversy^25–27 and as technologies have improved, microdomain size has fallen from 1 micrometre to as small as 10 nm diameter. Although phase separation has been demonstrated in model lipid systems^7,28 there are few, direct observations of heterogeneity in live mammalian cells at physiological temperature.^29,30 In a previous study, we found the mobility of M₂ receptors in HL1, CHO-K1 and primary cardiomyocytes showed no evidence of a phase transition over a −5 °C to +45 °C temperature range.¹⁴ Stability of lipid microdomains may be impacted by in-plane, protein–protein and protein–lipid interactions and there may be additional interactions that extend out of the membrane plane onto the intracellular cytoskeleton and/or extracellular matrix. These interactions may act to stabilise raft structures and corral or otherwise interfere with the free diffusion of membrane proteins¹⁰ which may either partition into the raft or the surrounding isotropic lipid, or may “hop” between the two regions.³¹

Notwithstanding the controversy surrounding the existence of lipid rafts and membrane microdomains, their proposed presence is thought to affect both the distribution and mobility of transmembrane proteins, with important consequences in neurobiology, virology, immunology and membrane–peptide interactions. One manifestation of membrane heterogeneity is that diffusive motion of transmembrane proteins becomes anomalous and MSD vs. dT plots are non-linear and show distinct downward inflection, indicating that molecules diffuse rapidly over short time and length scales, but more slowly over longer time intervals and distances.^12,28,32 A significant problem with use of MSD vs. dT plots is that raw data derived from single molecule imaging experiments rarely enables meaningful analysis to be made on a single molecular trajectory.^11,33 In earlier work, we found that muscarinic acetylcholine receptors (a class of membrane-spanning, 7-helix, G-protein coupled receptor) undergoes unrestricted diffusion at the plasma membrane.³⁴ So, we chose this protein as a prototype probe of membrane viscosity and structural heterogeneity. Here, we have investigated whether molecules diffuse at different speeds in different regions of the plasma membrane and whether in regions where molecules appear to move more slowly they also exhibit anomalous diffusive behaviour. We divided the cell membrane into 1 × 1 μm² or 2 × 2 μm² quadrats and analysed (≥5) independent molecular trajectories in each quadrat region so we could test for significant variation between cell membrane regions. We also tested if the mean D_lat values estimated at each quadrat were homogeneous and normally distributed, as expected by the central-limit theorem. We then specifically compared MSD vs. dT plots from “slow” and “fast” moving regions to see if the plots were linear or showed evidence of anomalous diffusive behaviour.

Measurement precision to some extent depends on imaging conditions, including the type of cell, choice of membrane protein and the fluorescent tag that has been employed. The density of single molecule trajectories (or “tracks”) and the spatial resolution of local D_lat maps, depends on the lateral diffusion (D_lat) and track duration; which are limited mainly by the fluorophore photobleaching rate. To generate a local D_lat estimate we constructed MSD vs. dT plots from single particle tracks that extended for ≥10 consecutive video frames.³⁵ Excitation laser power and imaging rate were optimised to allow molecules to be unambiguously tracked with high spatial and temporal resolution over a sufficient number of video frames. The density of unique single molecule trajectories that were accumulated over the entire imaging period (∼1 min) varied between samples even though the starting fluorophore density was similar (∼1 molecule per μm²). For most specimens a quadrat size of 2 × 2 μm² was used, but some (with high track density) allowed the use of a smaller quadrat size (1 × 1 μm²). For randomly moving molecules (free diffusion), a histogram of D_lat values obtained by fitting all of the individual single molecule MSD vs. dT plots over the entire cell surface is best described by a gamma distribution.^11,36 However, we show here that a histogram of mean D_lat values, obtained by averaging individual tracks within each quadrat sample area, obeys the central limit theorem and shows a normal distribution. Departure from normality implies heterogeneity in the data set at the level of the quadrat sample size; this can be assessed by Kolmogorov–Smirnov analysis (summarised in Table 1).

We found that the diffusive motion of M₂ receptors at the plasma membrane of HL1 cells, primary cardiomyocytes and zebrafish cardiac tissue slices all gave pooled MSD vs. dT plots (i.e. taking all molecular trajectories) that were linear (Fig. S4†), with no obvious evidence of anomalous diffusion. When trajectories were segmented and subdivided into checkerboards of quadrat samples, the histograms of mean D_lat values were found to be normally distributed. Thus, there was also no evidence for heterogeneity in receptor mobility across the plasma membrane of these specimens. When we further analysed the data by examining MSD vs. dT plots on quadrat sample trajectories drawn from seemingly “fast” and “slow” moving regions we found the plots have no obvious downward curvature. Together these findings are consistent with variation in individual D_lat values, being the result of random sampling of a homogeneous population. So, in these cases, lipid rafts must not cause anomalous diffusive motion and/or must be monodisperse and evenly distributed across the plasma membrane (see Table 1 and Fig. 1–3).

We found three specimens that convincingly exhibited D_lat histograms that were not normally distributed; implying that the quadrat samples were not drawn from a simple homogeneous population. We were interested to compare our findings for nicotinic acetylcholine receptors with another recent study³⁷ in which ion channel motion was tracked in frog embryonic muscle fibres using quantum dot labels and where MSD vs. dT plots were essentially linear once immobile objects were removed from the data sets and MSD vs. dT plots were essentially linear. However, an increasing deviation from unity gradient for log(MSD) vs. log(dT) plots at shorter times and smaller distances, indicated the receptors were diffusing in an anomalous manner that was best fit by an exponential distribution of diffusion coefficients. The authors point out that a distribution of diffusion coefficients is inconsistent both with simple lipid raft or cytoskeletal picket fence model. The same type of effect was seen in another high-resolution, quantum-dot tracking study.³⁸

In the current study, we found downward curvature of the MSD vs. dT plots when we analysed data collected across the whole CHO-K1 cells transfected with the eGFP-tagged γ-subunit and all other component polypeptides of the nicotinic receptor. This indicates a highly anomalous diffusive behaviour of the ion channel. However, the explanation for our finding is rather simple because a standard-deviation projection of the video data revealed that many of the eGFP-tagged subunits were associated with the ER, and when regions that were rich in ER were examined separately (using our quadrat sampling method), diffusion was slow and highly anomalous. However, regions of the cell where the ER was excluded (e.g. beneath the nucleus) the ion channels moved rapidly and exhibited linear MSD vs. dT plots. The rate of diffusion in the fast-moving regions was 10× greater than values reported in the earlier study using frog muscle cells.³⁷

We show that data averaging between the cells should be applied with caution, or avoided altogether, because variation in viscosity between the cells can be higher than variations within a single cell (see the viscosity map profile values on Fig. 3A(iii)). The D_lat quadrat distributions found between two neighbouring myocytes have very different K–S test scores when considered either separately or together (Fig. 3A(iv) and Table 1). Also, membrane heterogeneity within an individual endothelial cell expressing eGFP-tagged M₂ receptors was evidenced by the “non-normal” distribution of local viscosity values (Fig. 2(v) and Table 1). Visual inspection of the quadrat map (Fig. 2(iv)) revealed that mobility in the lower-left region of the cell was significantly lower than for the rest of the cell.

Conclusion

We have presented a method to analyse single fluorophore tracking data, which employs a quadrat sampling technique to partition data into localized maps of transmembrane protein mobility. We have shown that, in many cases, the plasma membrane has a uniform viscosity and homogeneous structure, and quadrat mean values are normally distributed as expected by the central limit theorem. However, and perhaps as expected, proteins that localised to two different membrane systems (nicotinic receptors found at the ER and plasma membrane or CHO-K1 cells) or following incomplete chemical fixation (M₂ receptors in HL1 cell) showed distinct heterogeneity. In one specimen, M₂ receptors in an endothelial cell, we found spatial variation in membrane viscosity across an individual cell, and while the bulk MSD vs. dT plot was perfectly linear (Fig. S3B†) the quadrat mean D_lat values were not normally distributed (Table 1). Closer inspection of the MSD vs. dT plots for “fast” and “slow” diffusing regions showed the difference in mobility was not due to anomalous diffusion (i.e. microscopic variation in structure) but more likely to a bulk variation in membrane viscosity (a “raft of rafts”) that impacts the macroscopic D_lat value but has minimal effect on microscopic, anomalous diffusive motion of individual M₂ receptors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Mr Alan Ling (Mechanical Engineering Workshop, Francis Crick Institute) for manufacturing some of the equipment used in this study, and Dr Qiling Xu (Neural Development Laboratory, Francis Crick Institute) for providing advice on zebrafish preparation. This work was supported by the Francis Crick Institute which receives its core funding from Cancer Research UK (FC001119), the UK Medical Research Council (FC001119), and the Wellcome Trust (FC001119). For the purpose of Open Access, the author has applied a CC BY public copyright licence to any Author Accepted Manuscript version arising from this submission. RL and LC were supported by Leverhulme Trust, project grant RPG-2016-407.

References

1. K. Jacobson, O. G. Mouritsen and R. G. W. Anderson, Nat. Cell Biol., 2007, 9, 7–14.
2. E. Sezgin, I. Levental, S. Mayor and C. Eggeling, Nat. Rev. Mol. Cell Biol., 2017, 18, 361–374.
3. S. J. Singer and G. L. Nicolson, Science, 1972, 175, 720–731.
4. H. C. Berg, Random walks in biology, Princeton University Press, Chichester, 1993.
5. P. G. Saffman and M. Delbruck, Proc. Natl. Acad. Sci. U. S. A., 1975, 72, 3111–3113.
6. Y. Gambin, R. Lopez-Esparza, M. Reffay, E. Sierecki, N. S. Gov, M. Genest, R. S. Hodges and W. Urbach, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 2098–2102.
7. T. Baumgart, A. T. Hammond, P. Sengupta, S. T. Hess, D. A. Holowka, B. A. Baird and W. W. Webb, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 3165–3170.
8. K. Simons and E. Ikonen, Nature, 1997, 387, 569–572.
9. M. Edinin, S. C. Kuo and M. P. Sheetz, Science, 1991, 254, 1379–1382.
10. A. Kusumi, C. Nakada, K. Ritchie, K. Murase, K. Suzuki, H. Murakoshi, R. S. Kasai, J. Kondo and T. Fujiwara, Annu. Rev. Biophys. Biomol. Struct., 2005, 34, 351–378.
11. H. Qian, M. P. Sheetz and E. L. Elson, Biophys. J., 1991, 60, 910–921.
12. M. J. Saxton and K. Jacobson, Annu. Rev. Biophys. Biomol. Struct., 1997, 26, 373–399.
13. D. M. Owen, A. Magenau, D. Williamson and K. Gaus, BioEssays, 2012, 34, 739–747.
14. T. A. Nenasheva, M. Neary, G. I. Mashanov, N. J. M. Birdsall, R. A. Breckenridge and J. E. Molloy, J. Mol. Cell. Cardiol., 2013, 57, 129–136.
15. G. I. Mashanov, T. A. Nenasheva, T. Mashanova, C. Maclachlan, N. J. M. Birdsall and J. E. Molloy, J. Gen. Physiol., 2020, 153, e202012657.
16. S. Shashkova and M. C. Leake, Biosci. Rep., 2017, 37(4), BSR20170031.
17. D. Axelrod, Methods Cell Biol., 1989, 30, 245–270.
18. T. A. Nenasheva, T. Carter and G. I. Mashanov, J. Microsc., 2012, 246, 83–88.
19. G. I. Mashanov, D. Tacon, A. E. Knight, M. Peckham and J. E. Molloy, Methods, 2003, 29, 142–152.
20. G. I. Mashanov and J. E. Molloy, Biophys. J., 2007, 92, 2199–2211.
21. M. J. Crawley, Statistics: An Introduction Using R, John Wiley & Sons, Chichester, 2nd edn, 2015.
22. R_Core_Team, R: A language and environment for statistical computing, http://www.R-project.org/.
23. G. I. Mashanov, J. R. Soc. Interface, 2014, 11, 20140442.
24. D. Lingwood and K. Simons, Science, 2010, 327, 46–50.
25. S. Munro, Cell, 2003, 115, 377–388.
26. J. F. Hancock, Nat. Rev. Mol. Cell Biol., 2006, 7, 456–462.
27. B. Nichols, Nature, 2005, 436, 638–639.
28. R. Metzler, J. H. Jeon and A. G. Cherstvy, Biochim. Biophys. Acta, 2016, 1858, 2451–2467.
29. C. Eggeling, C. Ringemann, R. Medda, G. Schwarzmann, K. Sandhoff, S. Polyakova, V. N. Belov, B. Hein, C. von Middendorff, A. Schonle and S. W. Hell, Nature, 2009, 457, 1159–1162.
30. D. M. Owen, D. J. Williamson, A. Magenau and K. Gaus, Nat. Commun., 2012, 3, 1256.
31. K. Suzuki, K. Ritchie, E. Kajikawa, T. Fujiwara and A. Kusumi, Biophys. J., 2005, 88, 3659–3680.
32. K. Ritchie, X. Y. Shan, J. Kondo, K. Iwasawa, T. Fujiwara and A. Kusumi, Biophys. J., 2005, 88, 2266–2277.
33. M. J. Saxton, Biophys. J., 1993, 64, 1766–1780.
34. J. A. Hern, A. H. Baig, G. I. Mashanov, B. Birdsall, J. E. T. Corrie, S. Lazareno, J. E. Molloy and N. J. M. Birdsall, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 2693–2698.
35. X. Michalet, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 041914.
36. M. J. Saxton, Biophys. J., 1997, 72, 1744–1753.
37. W. He, H. Song, Y. Su, L. Geng, B. J. Ackerson, H. B. Peng and P. Tong, Nat. Commun., 2016, 7, 11701.
38. A. V. Weigel, B. Simon, M. M. Tamkun and D. Krapf, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 6438–6443.

---

Footnotes

† Electronic supplementary information (ESI) available: Movie 1: M₂ muscarinic receptors labelled with Cy3B-telenzepine moving on the plasma membrane of cultured HL1 cardiomyocyte and imaged at 33 fps (23 °C). Real time movie, Movie 2: M₂ muscarinic receptors labelled with Cy3B-telenzepine moving on the plasma membrane of primary, cultured, cardiomyocyte extracted from embryonic mouse heart and imaged at 33 fps (23 °C). Movie 3: M₂ muscarinic receptors labelled with Cy3B-telenzepine on the plasma membrane of cultured HL1 cardiomyocyte treated with 1% of paraformaldehyde and imaged at 20 fps (23 °C). Some patches of plasma membrane adjacent to the substrate were sealed off by PFA and retained low viscosity allowing individual molecules to move freely inside these patches. Movie 4: M₂ muscarinic receptors tagged with eGFP transfected into a HUVEC and imaged at 33 fps (23 °C). Real time movie. Movie 5: tracking individual muscarinic receptors on the surface of a heart slice from the zebrafish reveals the fine viscosity map of the plasma membranes when imaged at 50 fps (23 °C). The trajectory map is inserted at the end of Movie 1 to show all the trajectories detected in this record (×0.5 real time). Movie 6: model simulating the random movements (D_lat = 0.2 μm² s⁻¹) of fluorescent molecules on the surface of a rectangular cell (30 × 30 × 5 μm³. TIRFM illumination mode). A trajectory map is inserted at the end of Movie 1 to show all the trajectories detected in this record (×0.5 real time). See DOI: 10.1039/d1fd00035g

‡ Current address: MRC LMB, Francis Crick Avenue, Cambridge, CB2 0QH, UK.

---