Evaluation of ultrasmall coinage metal M13(dppe)6 M = Cu, Ag, and Au clusters. Bonding, structural and optical properties from relativistic DFT calculations†
Peter L.
Rodríguez-Kessler
,
Macarena
Rojas-Poblete
and
Alvaro
Muñoz-Castro
 *
*
Laboratorio de Química Inorgánica y Materiales Moleculares, Facultad de Ingeniería, Universidad Autonoma de Chile, El Llano Subercaseaux 2801, Santiago, Chile. E-mail: alvaro.munoz@uautonoma.cl
First published on 20th July 2021
Abstract
Ultrasmall ligand-protected clusters are prototypical species for evaluating the variation at the bottom of the nanoscale range. Here we explored the ultrasmall gold–phosphine M13(dppe)6 cluster, as a prototypical framework to gain insights into the fundamental similarities and differences between Au, Ag, and Cu, in the 1–3 nm size range, via relativistic DFT calculations. Different charge states involving 8- and 10-cluster electron (ce) species with a 1S21P6 and 1S21P61D2 configuration, leading to structural modification in the Au species between Au13(dppm)65+ and Au13(dppm)63+, respectively. Furthermore, this structural distortion of the M13 core is found to occur to a lower degree for the calculated Ag and Cu counterparts. Interestingly, optical properties exhibit similar main patterns along with the series, inducing a blue-shift for silver and copper, in comparison to the gold parent cluster. For 10-ce species, the main features of 8-ce are retained with the appearance of several weak transitions in the range. The ligand–core interaction is enhanced for gold counterparts and decreased for lighter counterparts resulting in the Au > Cu > Ag trend for the interaction stabilization. Hence, the Ag and Cu counterparts of the Au13(dppm)6 cluster appear as useful alternatives, which can be further explored towards different cluster alternatives for building blocks for nanostructured materials.
Introduction
Atomically precise gold clusters have attracted increased interest due to their unique properties relative to the bulk material,1–9 enabling further elucidation of the nonscalable properties of ultrasmall nanoparticles.10–12 In the last few decades, several synthetic breakthroughs13–24 led the characterization of ligand passivated clusters in the 1–3 nm range with both structural and electronic features ascribed to the nature of the metallic core,25–30 usually rationalized via the divide-and-protect approach.31,32Among the different stabilizing groups, thiolates and phosphine ligands are widespread in the literature,25–28,33,34 ensuring strong gold–gold and gold–ligand bonds in stable structures against degradation.35–42 Au25(SR)18− (R = ligand) is one of the most noticeable ligand-protected gold clusters, composed of an atom-centered icosahedral core surrounded by six staple units, Au2(SR)3,35,43–45 featuring eight cluster electrons (8-ce)25,46 in a 1S21P6 electronic configuration. This fact accounts for its particular stability47 in analogy to closed-shell atoms, which are coined as superatoms with the central Au135+ core48 as a recursive motif in small and ultrasmall nanoparticles.49 It is noteworthy that Au25(SR)18− possesses a silver isoelectronic and isostructural analog, Ag25(SR)18−,50,51 suggesting that the Au135+ core features can also be observed in other lighter coinage metals31 such as Ag135+,50,52 and Cu135+.53
Recently, ultrasmall Au13(dppm)6 has been the focus of renewed interest since its early structural characterization in 1981,13 depicting a fully phosphine-protected Au13 core. Independently, Sun and Zhu groups showed full characterization of UV/vis and cyclic-voltammetry patterns and synthetic advantages, denoting the stability of such a cluster in several charge states, with structural rearrangements between the +5 and +3 charge states.54,55 The electronic structure of Au13(dppm)65+ is based on a closed-shell 1S21P6 configuration, similarly to Au25(SR)18−, providing a 1D character of low-lying unoccupied levels, with a variable structure in Au13(dppm)63+ denoting a distorted 10-ce Au13 core in a 1S21P61D2 configuration.
Such species provide useful templates to further evaluate the bonding and electronic characteristics, denoting the role of the ligand–shell in the stabilization and the relation between the core–structure and optical properties. Herein, we set to evaluate the plausible formation of lighter coinage-metal group counterparts to gain more insights into the century-old concern of fundamental similarities and differences between Au, Ag, and Cu, in terms of the structure and related properties, involving different charge states. In this contribution, we provide information on the overall ligand–core interaction, and optical and structural properties, for the ultrasmall M13(dppm)6 series, by using relativistic DFT methods, as a prototypical case of ligand-protected clusters.
Computational details
Computations were carried out at the relative density functional level of theory56 by using the ADF code,57 incorporating scalar corrections via the ZORA Hamiltonian.58 The triple-ξ Slater basis set, plus two polarization functions (STO-TZ2P) for valence electrons, were employed within the generalized gradient approximation (GGA) according to the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional.59,60 Dispersion corrections to DFT were taken into account via the pairwise Grimme3 approach.61,62 The use of the PBE-GGA functional provides accurate results for both the structure and optical properties of gold nanoclusters with minimal ligand simplifications,44,63–67 at an affordable computational cost, as denoted by Muniz-Miranda and coworkers.68 Optical properties were simulated by using the Van Leeuwen and Baerends functional (LB94),69 denoting a good performance in the study of excitation in ligand-protected clusters.70–74 Solvation effects were taken into account via a continuum solvation scheme given by the ‘COnductor-like Screening Model’ (COSMO) module from ADF, to describe the screening effects from solvation by using dichloromethane.75The frozen core approximation was applied to the [1s2–4f14] shells for Au, [1s2] for C, and [2s2] for P, leaving the remaining electrons to be treated variationally. Geometry optimizations were performed without any symmetry restraint via the analytical energy gradient method implemented by Versluis and Ziegler.76 An energy convergence criterion of 10−4 Hartree, gradient convergence criteria of 10−3 Hartree Å−1, and radial convergence criteria of 10−2 Å were employed for the evaluation of the relaxed structures.
Results and discussion
The characterized fully phosphine-protected Au13 core in its +5 charge state,55 exhibits a distorted atom-centered icosahedron passivated with six dppm units (Fig. 1), as the structure features two groups of distances found for the central atom and icosahedral cage (Aucent–Auico) length of 2.702 and 2.925 Å, respectively. Similarly, two groups of Auico–P distances are obtained of 2.282 and 2.346 Å, respectively, owing to a slight icosahedron ↔ cuboctahedron distortion with an elongation of certain distances (Table S1, ESI†). In its +3 charge state counterpart, the distortion of the icosahedron is increased54 leading to several Aucent–Auico distances (Tables S1 and S2, ESI†) in roughly six groups, which average to 2.819 Å, slightly shorter than 2.832 Å obtained for [Au13(dppm)6]5+, denoting a decrease of the cage radius upon addition of two electrons.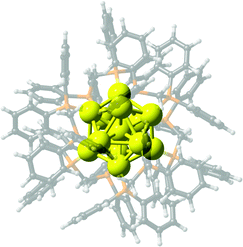 | ||
| Fig. 1 Schematic structures for M13(dppm)6 clusters. Color code: Au, Ag, Cu, yellow; C: black; P: orange; H: white. | ||
The calculated Aucent–Auico distances for [Au13(dppm)6]5+ (1), are averaged in two groups of 2.817 and 2.921 Å, respectively, leading to an average of 2.869 Å (Table 1), in good agreement to experimental values (2.832 Å), as also obtained for Auico–P separations (2.327 and 2.341 Å). For the +3 charge state (2), similar values to experimental data are obtained, with an averaged Aucent–Auico bond distance of 2.321 Å (experimental 2.314 Å).54
| M | Mcent–Mico | CShM | Mico–P | H–L gap |
|---|---|---|---|---|
| a Experimental data from ref. 55 (q = +5) and ref. 54 (q = +3). | ||||
| q = +5 | ||||
| Au | 2.869 | 0.315 | 2.334 | 1.431 |
| Au (Exp.)a | 2.832 | 0.568 | 2.314 | |
| Ag | 2.881 | 0.178 | 2.502 | 1.375 |
| Cu | 2.537 | 0.144 | 2.312 | 1.440 |
| q = +3 | ||||
| Au | 2.872 | 17.472 | 2.321 | 1.502 |
| Au (Exp.)a | 2.819 | 17.352 | 2.314 | |
| Ag | 2.889 | 0.217 | 2.503 | 0.183 |
| Cu | 2.483 | 0.058 | 2.279 | 0.323 |
In order to account for structural deviations from an ideal atom-centered icosahedron (Ih), we evaluated the continuous-shape-measure (CShM) developed by the group of Alvarez and coworkers.77–79 The resulting CShM values are close to zero for structures fully coincident with the reference icosahedron and increasing values accounting for the distortion degree. For the X-ray structure of [Au13(dppm)6]5+ (1), the Au13 core exhibits a CShM value of 0.568 (Calculated, 0.315), denoting the distortion of the cage given by the different groups of Aucent–Auico distances (vide intra). Moreover, for [Au13(dppm)6]3+ (2), the CShM value increases consequently to 17.352 (calc. 17.472) owing to the different types of Aucent–Auico distances.
The comparison between a perfect icosahedral structure, obtained by constraining equal Auico–Auico distances previous to relax the protecting ligand shell, and the fully optimized structure for [Au13(dppm)6]5+ (1), reveals a small energy difference of 6.0 kcal mol−1, in agreement with the small deviation accounted by the CShM value. In contrast, the larger distortion observed for [Au13(dppm)6]3+ (2) leads to a larger energy difference of 171.5 kcal mol−1 in comparison with the relaxed and perfect icosahedral Au13 core structure, denoting the preference for a high distortion of the core in the latter charge state.
The electronic structure for [Au13(dppm)6]5+ (1) is evaluated in terms of the superatom approach,25,46,80–82 denoting an 8 cluster electron (ce) count for the Au135+ core, fulfilling a 1S21P6 configuration (Fig. 2).25,46 The 1P shell remains the highest occupied molecular orbital (HOMO), in an almost three-fold degenerate level, whereas the low-lying unoccupied MO is a split of the 1D shell into three- and two-fold levels (Fig. 2), leading to a sizable HOMO–LUMO gap of 1.534 eV, in the range of the determined by electrochemical and UV-vis data (1.66 and 1.68 eV, respectively).55 Interestingly, for 2, the extra two-electrons reside at the 1Dz2 level, which in turn leads to a high stabilization of this shell. Now the HOMO–LUMO gap amounts to 1.502 eV, suggesting that the observed structural distortion of the Au133+ core enables a sizable HOMO–LUMO gap in a 10-ce 1S21P61D2z2 configuration. Isosurfaces for relevant shells are given at the ESI† (Fig. S1).
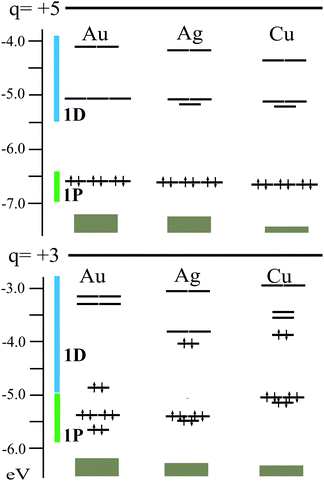 | ||
| Fig. 2 Electronic structure for M13(dppm)6 at +5 and +3 charge states. M = Au, Ag, and Cu 1P and 1D superatomic shells are denoted by green and blue. | ||
Furthermore, driven by the full characterization of Ag25(SR)18− with a central Ag135+ core,50,51 and similarities between Au135+ and Cu135+ cores,31 here we evaluate the hypothetical Ag and Cu counterparts of [Au13(dppm)6]5+. Interestingly, similar electronic features are found with calculated HOMO–LUMO gaps of 1.375 and 1.440 eV, for Ag and Cu species, respectively, denoting 1P and 1D based frontier orbitals. The relaxed structures show similar averaged Mcent–Mico distances for Ag (2.881 Å) and the Au parent (2.869 Å), with contraction to 2.537 Å for Cu species, denoting deviations from a perfect icosahedron core as given by the CShM values of 0.178 and 0.144, respectively, where values >0.1 are considered as distorted icosahedral cores.34 Moreover, this small distortion from the icosahedron led to a decreased energy difference between an ideal Ih-M13 core situation and the fully relaxed structures, of 6.1 for Ag (6.1 kcal mol−1) and for Cu (4.0 kcal mol−1) counterparts, which are similar to the observed for [Au13(dppm)6]5+ (1) (6.0 kcal mol−1).
However, the +3 charge state exhibits larger differences along with the series where the 10-ce 1S21P61D2z2 configuration exhibits a decreased HOMO–LUMO gap of 0.183 and 0.323 eV for Ag and Cu, respectively (Fig. 2). The relaxed structures for [Ag13(dppm)6]3+ and [Cu13(dppm)6]3+, are slightly distorted from a perfect icosahedron with CShM values of 0.217 and 0.058, respectively, in comparison to the Au parent (CShM = 17.472). Such a result denotes that the capabilities of coinage metal clusters to enable a structural rearrangement to maximize the HOMO–LUMO gap in 10-ce clusters, are different along with the triad, which is mostly enabled in gold species, whereas lighter silver and copper counterparts suggest lower structural flexibility upon 8- to 10-ce shift. Thus, such results suggest gold clusters to be more prone to reaccommodate structurally rather than Ag and Cu counterparts, resulting in a small HOMO–LUMO gap for the latter hypothetical species suggesting a lower kinetic and chemical stability. Hence, for 10-ce counterparts Ag and Cu clusters are less favored than the parent gold system, in contrast to 8-ce species which are expected to have a similar in magnitude HOMO–LUMO gap along the coinage metal group.
In order to gain more insights into the favorable stabilization given by the protecting layer of dppm ligands, the M135+-dppm interaction energy is evaluated (ΔEint, Table 2). A more favorable situation is obtained for the Au case, amounting to −1168.2 kcal mol−1, which decreases to −856.9 kcal mol−1 for Ag, and −1038.0 kcal mol−1 for Cu. Thus, the favorable bonding situation evolves along with the triad according to Au > Cu > Ag, as depicted for PPh3 and other ligands.83 In addition, for [Au13(dppm)6]3+ (2), the ΔEint amounts to −787.8 kcal mol−1 as a result of the two-extra electrons in the Au13 core denoting a sizable decrease in the core–ligand stabilization, which is similarly found for Ag and Cu, to −507.7 and −628.3 kcal mol−1, respectively. The preference for electronegative ligands for silver protected clusters observed in the literature over electroneutral ligands,34 account for the calculated less favorable core–ligand interaction along with the series, suggesting that electronegative ligands provide stronger interaction. However, the core–ligand interaction energy (ΔEint) for silver counterpart suggest a decreased but still sizable interaction, which in addition to the sizable HOMO–LUMO gap, provides the basis for further conceivable characterization.
| Charge +5 | Au | Ag | Cu | |||
|---|---|---|---|---|---|---|
| ΔEPauli | 1917.6 | 876.8 | 878.2 | |||
| ΔEelstat | −1722.1 | 55.8% | −901.6 | 52.0% | −917.9 | 47.9% |
| ΔEorb | −1254.3 | 40.6% | −745.5 | 43.0% | −902.1 | 47.1% |
| ΔEdisp | −109.4 | 3.5% | −86.6 | 5.0% | −96.2 | 5.0% |
| ΔEint | −1168.2 | −856.9 | −1038.0 | |||
| Charge +3 | Au | Ag | Cu | |||
|---|---|---|---|---|---|---|
| ΔEPauli | 2178.7 | 1037.3 | 1097.3 | |||
| ΔEelstat | −1854.3 | 62.5% | −914.5 | 59.2% | −985.3 | 57.1% |
| ΔEorb | −990.0 | 33.4% | −546.1 | 35.3% | −636.4 | 36.9% |
| ΔEdisp | −122.2 | 4.1% | −84.4 | 5.5% | −103.8 | 6.0% |
| ΔEint | −787.8 | −507.7 | −628.3 | |||
Moreover, the nature of the core–ligand interaction is accounted by the energy decomposition analysis (EDA) within the Morokuma–Ziegler scheme,84–86 dissecting the ΔEint quantity into different chemically meaningful terms, as85,87,88
| ΔEint = ΔEPauli + ΔEelstat + ΔEorb + ΔEdisp |
In this framework, the stabilizing ΔEelstat and ΔEorb terms are related to the electrostatic and covalent character of the interaction, respectively.88 The ΔEPauli term is given by the repulsive four-electron two-orbital interactions between occupied orbitals of the different fragments. In addition, the pairwise correction of Grimme62 (DFT-D3) accounts for London dispersion interactions (ΔEdisp) of stabilizing character. To overcome the basis set superposition error (BSSE) in the fragment interaction analysis of ΔEorb, the counterpoise method was employed.
For [Au13(dppm)6]5+ (1), the interaction is given by a 55.8% of electrostatic character (ΔEelstat), and 40.6% from covalent contributions (ΔEorb), and a small addition from ΔEdisp. Thus, the core–ligand interaction is of the main electrostatic character with a sizable bonding contribution. Upon addition of two electrons, in the 10-ce [Au13(dppm)6]3+ (2) species, the interaction is similarly of electrostatic character, denoting a sizable decrease in the bonding contribution (ΔEorb) from −1254.3 in 1 to −990.0 kcal mol−1 in 2, and an increase in the Pauli repulsion term, owing to the shorter Auico–P distance required to maximize the bonding stabilization in the latter.
For silver and copper counterparts, the nature of the core–ligand interaction is similar in nature to gold species, which denotes a decrease in the contributing terms. Interestingly, by comparing Ag and Cu species, the different energetic terms remain similar, with the exception of the covalent character, which increases sizably for Cu counterparts, resulting in the Au > Cu > Ag trend for the interaction stabilization.
Moreover, the covalent character (ΔEorb) can be further decomposed through the Natural Orbitals for Chemical Valence89–91 extension of EDA (EDA-NOCV).91 As a result, the identification of different individual orbital contributions given by their deformation densities accounts for individual charge-transfer channels between the core and the ligand layer.92,93 The obtained results exhibit a σ-donation from the phosphine ligands towards the core, as the main source of the bonding interaction in the Au13(dppm)6 formation (Fig. S2, ESI†).
The cyclic voltammetry (CV) results for [Au13(dppm)6]5+ (1),55 exhibit reversible redox couples for both first oxidation (+5 → +6) and reduction (+5 → +4). In addition, a redox couple above the solvent window (>−2.20 V vs. Ag/Ag+) is expected from calculations, suggesting the plausible formation of [Au13(dppm)6]3+ (2) by electrochemical methods. The calculations for the different charge states observed from CV experiments of 1, and by the +3 state in 2, allows us to evaluate the evolution from +3 to +6 species. The structures for [Au13(dppm)6]q from q = +3 to +6 (Table S1, ESI†), suggest similar averaged Aucent–Auico distances, accounting for a similar Au13 radius along with the redox processes. For silver, the averaged Agcent–Agico tend to decrease slightly from 2.889 to 2.872 Å, suggesting a small compression of the Ag13 cage, which contrasts with that found for the copper case, where averaged Cucent–Cuico distance increases from 2.483 to 2.634 Å. Such results suggest a variation of the M13 radii along with different charge states, depicted as a decrease in Ag, a lesser variation for Au, and in contrast, increasing for Cu species, according to the electron count from 10- to 7-ce. In comparison, for Au25(PET)18 species with charge states from −1 to +1, denoting 8- to 5-ce, the averaged Aucent–Auico distances taken from X-ray structures,35,94 show an increase as 2.774 < 2.783 < 2.808 Å (Table S3, ESI†), denoting that the ligand shell environment is relevant in a further relaxation of the core upon different charge states.
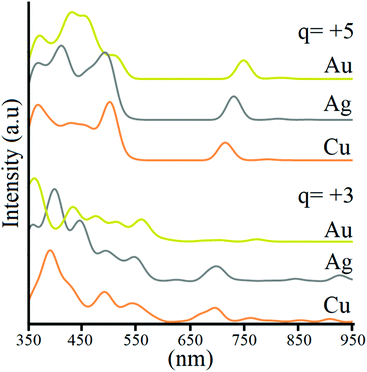
Lastly, optical properties were evaluated to account for the possible variation of the optical transition in the coinage metal triad. For [Au13(dppm)6]5+ (1),55 the optical spectrum is dominated by an absorption band at 440 nm, and weak transitions between 500 and 750 nm, which are ascribed to the main 1P → 1D transition via time-dependent DFT calculations, which are located mainly at the Au135+ core (ESI†). Our calculations are in agreement with the previous analysis for Au13, with the absorption maxima at 437 nm involving a wide 1P → Ligand, and 5d-Au block → 1D character manifold, denoting lower energy transitions between 1P-HOMO and 1D-LUMO as a small peak at 747 nm, and very weak lower energy transitions (Fig. 3). At 515 nm, a small shoulder is found, contributed by 71% of 1P → 1D, and 29% from Ligand → 1D transitions. Interestingly, for Ag and Cu counterparts, the same features of the absorption spectrum remain with a slight hypsochromic (blue-) shift of all the signals, with a small peak located at 728 and 713 nm, for Ag and Cu, respectively, showing an increase in the intensity of the Ligand → 1D shoulder, now located at 490 and 499 nm, respectively. The main transition is shifted to 409 and 366 nm, for Ag and Cu, denoting a similar pattern expected for the UV/vis spectrum, with a blue-shift of main peaks. At the +3 charge state, the spectrum retains the features shown for the +5 species, with the addition of several lower energy transitions of weak intensity owing to the appearance of 1D2dz2 → 1D0 excitations, allowed by structural distortions within the M13 core. Hence the main features of the UV-vis spectrum are preserved with the addition of weak lower energy peaks for the 10-ce clusters.
Conclusions
The ultrasmall Au13(dppm)6 cluster was studied in its +5 and +3 charge states, denoting structural, bonding, and optical property variations, ascribed to the respective 8- and 10-cluster electron counts. For Au13(dppm)65+, the Au13 core deviates from the ideal icosahedral structure, which is increased upon the addition of two electrons at Au13(dppm)63+, but retaining a similar averaged Aucore–Auico bond distance, accounting for the core radius. For Ag and Cu, the distortion from a perfect icosahedron is to a lesser extent, resulting in a reduced HOMO–LUMO gap for 10-ce (+3 charge state) species, in contrast to the sizable gap in 8-ce. Interestingly, the more significant distortion in Au13(dppm)63+ enables a further stabilization of the 1Dz2 shell, retaining a sizable HOMO–LUMO gap, despite the intermediate electron count. Thus, Cu13(dppm)63+ and Ag13(dppm)63+ species are expected to be less stable owing to the decreased HOMO–LUMO gap.Ligand–core interactions are larger for gold, followed by Cu, and lastly, Ag species, in agreement with the Au > Cu > Ag bonding energy trend observed for other ligands in monometallic complexes. From 8- to 10-ce, the ligand–core bonding decreases, owing to the two extra electrons in the M13 core, for all the species.
Optical properties reveal common features with a small blue-shift of the relevant peaks for lighter coinage metals, which are retained between 8- and 10-ce species, where the latter includes weak low-energy transition owing to 1Dz2 → 1D transitions slightly allowed by the deviations from a perfect icosahedron core. Hence, lighter coinage metal counterparts of the parent Au13(dppm)6 appear as feasible targets for further exploratory synthesis efforts, resulting in similar properties towards alternative ligand-protected clusters as building blocks for nanostructured materials.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by FONDECYT/ANID 1180683. Support from FONDECYT/ANID postdoctoral fellowship grants was involved in the current work. M. R-P. acknowledges Fondecyt postdoctorado 3190335. P. L. R.-K. acknowledges Fondecyt postdoctorado 3190329.References
- C. N. R. Rao, A. Müller and A. K. Cheetham, The Chemistry of Nanomaterials, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, FRG, 2004 Search PubMed.
- Y. Sun, Shape-Controlled Synthesis of Gold and Silver Nanoparticles, Science, 2002, 298, 2176–2179 CrossRef CAS PubMed.
- Y. Yin and D. Talapin, The chemistry of functional nanomaterials, Chem. Soc. Rev., 2013, 42, 2484 RSC.
- R. Jin, C. Zeng, M. Zhou and Y. Chen, Atomically Precise Colloidal Metal Nanoclusters and Nanoparticles: Fundamentals and Opportunities, Chem. Rev., 2016, 116, 10346–10413 CrossRef CAS PubMed.
- W. Kurashige, Y. Niihori, S. Sharma and Y. Negishi, Precise synthesis, functionalization and application of thiolate-protected gold clusters, Coord. Chem. Rev., 2016, 320–321, 238–250 CrossRef CAS.
- A. Fernando, K. L. D. M. Weerawardene, N. V. Karimova and C. M. Aikens, Quantum Mechanical Studies of Large Metal, Metal Oxide, and Metal Chalcogenide Nanoparticles and Clusters, Chem. Rev., 2015, 115, 6112–6216 CrossRef CAS PubMed.
- T. Stoll, E. Sgrò, J. W. Jarrett, J. Réhault, A. Oriana, L. Sala, F. Branchi, G. Cerullo and K. L. Knappenberger, Superatom State-Resolved Dynamics of the Au25(SC8H9)18− Cluster from Two-Dimensional Electronic Spectroscopy, J. Am. Chem. Soc., 2016, 138, 1788–1791 CrossRef CAS PubMed.
- R. Costi, A. E. Saunders and U. Banin, Colloidal Hybrid Nanostructures: A New Type of Functional Materials, Angew. Chem., Int. Ed., 2010, 49, 4878–4897 CrossRef CAS PubMed.
- I. Chakraborty and T. Pradeep, Atomically Precise Clusters of Noble Metals: Emerging Link between Atoms and Nanoparticles, Chem. Rev., 2017, 117, 8208–8271 CrossRef CAS PubMed.
- X. Jiang, B. Du, Y. Huang and J. Zheng, Ultrasmall noble metal nanoparticles: breakthroughs and biomedical implications, Nano Today, 2018, 21, 106–125 CrossRef CAS PubMed.
- B. H. Kim, M. J. Hackett, J. Park and T. Hyeon, Synthesis, Characterization, and Application of Ultrasmall Nanoparticles, Chem. Mater., 2014, 26, 59–71 CrossRef CAS.
- K. Zarschler, L. Rocks, N. Licciardello, L. Boselli, E. Polo, K. P. Garcia, L. De Cola, H. Stephan and K. A. Dawson, Ultrasmall inorganic nanoparticles: state-of-the-art and perspectives for biomedical applications, Nanomed. Nanotechnol., Biol. Med., 2016, 12, 1663–1701 CrossRef CAS PubMed.
- J. W. A. van der Velden, F. A. Vollenbroek, J. J. Bour, P. T. Beurskens, J. M. M. Smits and W. P. Bosnian, Gold clusters containing bidentate phosphine ligands. Preparation and X-Ray structure investigation of [Au5(dppmH)3(dppm)](NO3)2 and [Au13(dppmH)6](NO3)n, Recl. des Trav. Chim. des Pays-Bas, 1981, 100, 148–152 CrossRef CAS.
- B. K. Teo and H. Zhang, Cluster of clusters. Structure of a new cluster [(p-Tol3P)10Au13Ag12Cl7](SbF6)2 containing a nearly staggered-eclipsed-staggered metal configuration and five doubly-bridging ligands, Inorg. Chem., 1991, 30, 3115–3116 CrossRef CAS.
- C. E. Briant, B. R. C. Theobald, J. W. White, L. K. Bell, D. M. P. Mingos and A. J. Welch, Synthesis and X-ray structural characterization of the centred icosahedral gold cluster compound [Au13(PMe2Ph)10Cl2](PF6)3; the realization of a theoretical prediction, J. Chem. Soc., Chem. Commun., 1981, 201–202 RSC.
- A. Ghosh, O. F. Mohammed and O. M. Bakr, Atomic-Level Doping of Metal Clusters, Acc. Chem. Res., 2018, 51, 3094–3103 CrossRef CAS PubMed.
- Z. Lei, J. Li, Z. Nan, Z. Jiang and Q. Wang, Cluster From Cluster: A Quantitative Approach to Magic Gold Nanoclusters [Au25(SR)18]−, Angew. Chem., Int. Ed., 2021, 60, 14415–14419 CrossRef CAS PubMed.
- W. Wang and R. W. Murray, Reaction of Triphenylphosphine with Phenylethanethiolate-Protected Au38 Nanoparticles, Langmuir, 2005, 21, 7015–7022 CrossRef CAS PubMed.
- L. C. McKenzie, T. O. Zaikova and J. E. Hutchison, Structurally Similar Triphenylphosphine-Stabilized Undecagolds, Au11(PPh3)7Cl3 and [Au11(PPh3)8Cl2]Cl, Exhibit Distinct Ligand Exchange Pathways with Glutathione, J. Am. Chem. Soc., 2014, 136, 13426–13435 CrossRef CAS PubMed.
- D. M. P. Mingos, H. R. Powell and T. L. Stolberg, Synthesis and structural characterization of the tetrahedral cluster [Au4(PPh3)4(μ2-SnCl3)2], Trans. Met. Chem., 1992, 17, 334–337 CrossRef CAS.
- Y.-Z. Li, R. Ganguly, K. Y. Hong, Y. Li, M. E. Tessensohn, R. Webster and W. K. Leong, Stibine-protected Au13 nanoclusters: syntheses, properties and facile conversion to GSH-protected Au25 nanocluster, Chem. Sci., 2018, 9, 8723–8730 RSC.
- H. Ube, Q. Zhang and M. Shionoya, A Carbon-Centered Hexagold(I) Cluster Supported by N-Heterocyclic Carbene Ligands, Organometallics, 2018, 37, 2007–2009 CrossRef CAS.
- M. R. Narouz, S. Takano, P. A. Lummis, T. I. Levchenko, A. Nazemi, S. Kaappa, S. Malola, G. Yousefalizadeh, L. A. Calhoun, K. G. Stamplecoskie, H. Häkkinen, T. Tsukuda and C. M. Crudden, Robust, Highly Luminescent Au13 Superatoms Protected by N-Heterocyclic Carbenes, J. Am. Chem. Soc., 2019, 141, 14997–15002 CrossRef CAS PubMed.
- H. Shen, S. Xiang, Z. Xu, C. Liu, X. Li, C. Sun, S. Lin, B. K. Teo and N. Zheng, Superatomic Au13 clusters ligated by different N-heterocyclic carbenes and their ligand-dependent catalysis, photoluminescence, and proton sensitivity, Nano Res., 2020, 13, 1908–1911 CrossRef CAS.
- M. Walter, J. Akola, O. Lopez-Acevedo, P. D. Jadzinsky, G. Calero, C. J. Ackerson, R. L. Whetten, H. Grönbeck and H. Häkkinen, A unified view of ligand-protected gold clusters as superatom complexes, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 9157–9162 CrossRef CAS PubMed.
- A. W. Castleman and S. N. Khanna, Clusters, Superatoms, and Building Blocks of New Materials, J. Phys. Chem. C, 2009, 113, 2664–2675 CrossRef CAS.
- P. D. Jadzinsky, G. Calero, C. J. Ackerson, D. A. Bushnell and R. D. Kornberg, Structure of a Thiol Monolayer-Protected Gold Nanoparticle at 1.1 Å Resolution, Science, 2007, 318, 430–433 CrossRef CAS PubMed.
- S. A. Claridge, A. W. Castleman, S. N. Khanna, C. B. Murray, A. Sen and P. S. Weiss, Cluster-assembled materials, ACS Nano, 2009, 3, 244–255 CrossRef CAS PubMed.
- T. Bürgi, Properties of the gold-sulphur interface: from self-assembled monolayers to clusters, Nanoscale, 2015, 7, 15553–15567 RSC.
- T. Fehlner, J.-F. Halet and J.-Y. Saillard, Molecular Clusters. A Bridge to Solid State Chemistry, Cambridge Univ. Press. Cambridge, UK, 2007 Search PubMed.
- F. Gam, D. Paez-Hernandez, R. Arratia-Perez, C. W. W. Liu, S. Kahlal, J.-Y. J.-Y. Saillard and A. Muñoz-Castro, Coinage Metal Superatomic Cores: Insights into Their Intrinsic Stability and Optical Properties from Relativistic DFT Calculations, Chem. – Eur. J., 2017, 23, 11330–11337 CrossRef CAS PubMed.
- T. Tsukuda and H. Häkkinen, Protected Metal Clusters: From Fundamentals to Applications, Elsevier, 2015 Search PubMed.
- M. I. Bruce, J.-F. Halet, B. Le Guennic, B. W. Skelton, A. N. Sobolev, C. J. Sumby and A. H. White, Structural systematics of some trinuclear alkynyl and diynyl Group 11 complexes containing dppm [dppm = CH2(PPh2)2], Coord. Chem. Rev., 2018, 375, 2–12 CrossRef CAS.
- S. Takano and T. Tsukuda, Chemically Modified Gold/Silver Superatoms as Artificial Elements at Nanoscale: Design Principles and Synthesis Challenges, J. Am. Chem. Soc., 2021, 143, 1683–1698 CrossRef CAS PubMed.
- M. W. Heaven, A. Dass, P. S. White, K. M. Holt and R. W. Murray, Crystal structure of the gold nanoparticle [N(C8H17)4][Au25(SCH2CH2Ph)18], J. Am. Chem. Soc., 2008, 130, 3754–3755 CrossRef CAS PubMed.
- O. Toikkanen, V. Ruiz, G. Rönnholm, N. Kalkkinen, P. Liljeroth and B. M. Quinn, Synthesis and Stability of Monolayer-Protected Au38 Clusters, J. Am. Chem. Soc., 2008, 130, 11049–11055 CrossRef CAS PubMed.
- H. Qian, C. Liu and R. Jin, Controlled growth of molecularly pure Au25(SR)18 and Au38(SR)24 nanoclusters from the same polydispersed crude product, Sci. China: Chem., 2012, 55, 2359–2365 CrossRef CAS.
- P. Maity, S. Xie, M. Yamauchi and T. Tsukuda, Stabilized gold clusters: from isolation toward controlled synthesis, Nanoscale, 2012, 4, 4027–4037 RSC.
- H. Häkkinen, The gold–sulfur interface at the nanoscale, Nat. Chem., 2012, 4, 443–455 CrossRef PubMed.
- G. Schmid, The relevance of shape and size of Au55 clusters, Chem. Soc. Rev., 2008, 37, 1909 RSC.
- L. Srisombat, A. C. Jamison and T. R. Lee, Stability: a key issue for self-assembled monolayers on gold as thin-film coatings and nanoparticle protectants, Colloids Surf., A, 2011, 390, 1–19 CrossRef CAS.
- R. Juarez-Mosqueda, S. Malola and H. Häkkinen, Stability, electronic structure, and optical properties of protected gold-doped silver Ag29−xAux (x = 0–5) nanoclusters, Phys. Chem. Chem. Phys., 2017, 19, 13868–13874 RSC.
- X. Kang, H. Chong and M. Zhu, Au25(SR)18: the captain of the great nanocluster ship, Nanoscale, 2018, 10, 10758–10834 RSC.
- J. Akola, M. Walter, R. L. Whetten, H. Häkkinen and H. Grönbeck, On the structure of thiolate-protected Au25, J. Am. Chem. Soc., 2008, 130, 3756–3757 CrossRef CAS PubMed.
- T. Dainese, S. Antonello, J. A. Gascón, F. Pan, N. V. Perera, M. Ruzzi, A. Venzo, A. Zoleo, K. Rissanen and F. Maran, Au25(SEt)18, a Nearly Naked Thiolate-Protected Au25 Cluster: Structural Analysis by Single Crystal X-ray Crystallography and Electron Nuclear Double Resonance, ACS Nano, 2014, 8, 3904–3912 CrossRef CAS PubMed.
- H. Häkkinen, Atomic and electronic structure of gold clusters: understanding flakes, cages and superatoms from simple concepts, Chem. Soc. Rev., 2008, 37, 1847–1859 RSC.
- D. Jiang and S. Dai, From Superatomic Au25(SR)18− to Superatomic M@Au24 (SR)18q Core–Shell Clusters, Inorg. Chem., 2009, 48, 2720–2722 CrossRef CAS PubMed.
- F. K. Sheong, J.-X. Zhang and Z. Lin, An [Au13]5+ Approach to the Study of Gold Nanoclusters, Inorg. Chem., 2016, 55, 11348–11353 CrossRef CAS PubMed.
- S. Jin, S. Wang and M. Zhu, Insight into the Geometric and Electronic Structures of Gold/Silver Superatomic Clusters Based on Icosahedron M13 Units and Their Alloys, Chem. – Asian J., 2019, 14, 3222–3231 CrossRef CAS PubMed.
- C. P. Joshi, M. S. Bootharaju, M. J. Alhilaly and O. M. Bakr, [Ag25(SR)18]−: The “Golden” Silver Nanoparticle, J. Am. Chem. Soc., 2015, 137, 11578–11581 CrossRef CAS PubMed.
- H. Hirai, S. Ito, S. Takano, K. Koyasu and T. Tsukuda, Ligand-protected gold/silver superatoms: current status and emerging trends, Chem. Sci., 2020, 11, 12233–12248 RSC.
- L. G. AbdulHalim, M. S. Bootharaju, Q. Tang, S. Del Gobbo, R. G. AbdulHalim, M. Eddaoudi, D. Jiang and O. M. Bakr, Ag29(BDT)12(TPP)4: A Tetravalent Nanocluster, J. Am. Chem. Soc., 2015, 137, 11970–11975 CrossRef CAS PubMed.
- A. Baghdasaryan and T. Bürgi, Copper nanoclusters: designed synthesis, structural diversity, and multiplatform applications, Nanoscale, 2021, 13, 6283–6340 RSC.
- S. Jin, W. Du, S. Wang, X. Kang, M. Chen, D. Hu, S. Chen, X. Zou, G. Sun and M. Zhu, Thiol-Induced Synthesis of Phosphine-Protected Gold Nanoclusters with Atomic Precision and Controlling the Structure by Ligand/Metal Engineering, Inorg. Chem., 2017, 56, 11151–11159 CrossRef CAS PubMed.
- S.-S. Zhang, L. Feng, R. D. Senanayake, C. M. Aikens, X.-P. Wang, Q.-Q. Zhao, C.-H. Tung and D. Sun, Diphosphine-protected ultrasmall gold nanoclusters: opened icosahedral Au13 and heart-shaped Au8 clusters, Chem. Sci., 2018, 9, 1251–1258 RSC.
- K. G. Dyall and K. Fægri, Introduction to Relativistic Quantum Chemistry, Oxford University Press, New York, 2007 Search PubMed.
- Amsterdam Density Functional (ADF), 2019Code, Vrije Universiteit: Amsterdam, The Netherlands. Available at: http://www.scm.com Search PubMed.
- E. van Lenthe, E.-J. J. Baerends and J. G. Snijders, Relativistic total energy using regular approximations, J. Chem. Phys., 1994, 101, 9783 CrossRef CAS.
- J. P. Perdew, K. Burke and Y. Wang, Generalized gradient approximation for the exchange-correlation hole of a many-electron system, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 16533–16539 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- S. Ehrlich, J. Moellmann and S. Grimme, Dispersion-Corrected Density Functional Theory for Aromatic Interactions in Complex Systems, Acc. Chem. Res., 2013, 46, 916–926 CrossRef CAS PubMed.
- S. Grimme, Density functional theory with London dispersion corrections, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 211–228 CAS.
- O. Lopez-Acevedo, J. Akola, R. L. Whetten, H. Grönbeck and H. Häkkinen, Structure and Bonding in the Ubiquitous Icosahedral Metallic Gold Cluster Au144(SR)60, J. Phys. Chem. C, 2009, 113, 5035–5038 CrossRef CAS.
- D. Jiang, The expanding universe of thiolated gold nanoclusters and beyond, Nanoscale, 2013, 5, 7149–7160 RSC.
- J. Akola, K. A. Kacprzak, O. Lopez-Acevedo, M. Walter, H. Grönbeck and H. Häkkinen, Thiolate-Protected Au25 Superatoms as Building Blocks: Dimers and Crystals, J. Phys. Chem. C, 2010, 114, 15986–15994 CrossRef CAS.
- D. Jiang, M. Kühn, Q. Tang and F. Weigend, Superatomic Orbitals under Spin-Orbit Coupling, J. Phys. Chem. Lett., 2014, 5, 3286–3289 CrossRef CAS PubMed.
- M. Zhou, Z. Lei, Q. Guo, Q.-M. Wang and A. Xia, Solvent Dependent Excited State Behaviors of Luminescent Gold(I)–Silver(I) Cluster with Hypercoordinated Carbon, J. Phys. Chem. C, 2015, 119, 14980–14988 CrossRef CAS.
- F. Muniz-Miranda, M. C. Menziani and A. Pedone, Assessment of Exchange-Correlation Functionals in Reproducing the Structure and Optical Gap of Organic-Protected Gold Nanoclusters, J. Phys. Chem. C, 2014, 118, 7532–7544 CrossRef CAS.
- R. van Leeuwen and E. J. Baerends, Exchange-correlation potential with correct asymptotic behavior, Phys. Rev. A, 1994, 49, 2421–2431 CrossRef CAS PubMed.
- C. M. Aikens, Effects of Core Distances, Solvent, Ligand, and Level of Theory on the TDDFT Optical Absorption Spectrum of the Thiolate-Protected Au25 Nanoparticle, J. Phys. Chem. A, 2009, 113, 10811–10817 CrossRef CAS PubMed.
- E. B. Guidez and C. M. Aikens, Quantum mechanical origin of the plasmon: from molecular systems to nanoparticles, Nanoscale, 2014, 6, 11512–11527 RSC.
- N. Durante, A. Fortunelli, M. Broyer and M. Stener, Optical Properties of Au Nanoclusters from TD-DFT Calculations, J. Phys. Chem. C, 2011, 115, 6277–6282 CrossRef CAS.
- G.-T. Bae and C. M. Aikens, Time-Dependent Density Functional Theory Studies of Optical Properties of Au Nanoparticles: Octahedra, Truncated Octahedra, and Icosahedra, J. Phys. Chem. C, 2015, 119, 23127–23137 CrossRef CAS.
- P. Ai, M. Mauro, A. A. Danopoulos, A. Muñoz-Castro and P. Braunstein, Dual Emission of a Cyclic Hexanuclear Gold(I) Complex. Interplay between Au3 and Au2 Ligand-Supported Luminophores, J. Phys. Chem. C, 2019, 123, 915–921 CrossRef CAS.
- A. Klamt and V. Jonas, Treatment of the outlying charge in continuum solvation models, J. Chem. Phys., 1996, 105, 9972 CrossRef CAS.
- L. Versluis and T. Ziegler, The determination of molecular structures by density functional theory. The evaluation of analytical energy gradients by numerical integration, J. Chem. Phys., 1988, 88, 322–328 CrossRef CAS.
- A. Ruiz-Martínez, D. Casanova and S. Alvarez, Polyhedral Structures with an Odd Number of Vertices: Nine-Coordinate Metal Compounds, Chem. – Eur. J., 2008, 14, 1291–1303 CrossRef PubMed.
- S. Alvarez, P. Alemany, D. Casanova, J. Cirera, M. Llunell and D. Avnir, Shape maps and polyhedral interconversion paths in transition metal chemistry, Coord. Chem. Rev., 2005, 249, 1693–1708 CrossRef CAS.
- J. Cirera, E. Ruiz and S. Alvarez, Continuous Shape Measures as a Stereochemical Tool in Organometallic Chemistry, Organometallics, 2005, 24, 1556–1562 CrossRef CAS.
- S. Khanna and P. Jena, Assembling crystals from clusters, Phys. Rev. Lett., 1992, 69, 1664–1667 CrossRef CAS PubMed.
- J. U. Reveles, S. N. Khanna, P. J. Roach and A. W. Castleman, Multiple valence superatoms, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 18405–18410 CrossRef CAS PubMed.
- A. Muñoz-Castro, sp3-hybridization in superatomic clusters. Analogues to simple molecules involving the Au6 core, Chem. Sci., 2014, 5, 4749–4754 RSC.
- A. Muñoz-Castro, D. MacLeod Carey and R. Arratia-Perez, Relativistic effects on dative carbon-coinage metal bond. Evaluation of NHC-MCl (M = Cu, Ag, Au) from relativistic DFT, Polyhedron, 2021, 197, 115020 CrossRef.
- K. Morokuma, Molecular Orbital Studies of Hydrogen Bonds. III. C
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯H–O Hydrogen Bond in H2CO⋯H2O and H2CO⋯2H2O, J. Chem. Phys., 1971, 55, 1236–1244 CrossRef CAS.
O⋯H–O Hydrogen Bond in H2CO⋯H2O and H2CO⋯2H2O, J. Chem. Phys., 1971, 55, 1236–1244 CrossRef CAS. - G. Te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders, T. Ziegler, G. T. E. Velde, C. F. Guerra and S. J. A. Gisbergen, Chemistry with ADF, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- T. Ziegler and A. Rauk, On the calculation of bonding energies by the Hartree Fock Slater method, Theor. Chim. Acta, 1977, 46, 1–10 CrossRef CAS.
- M. von Hopffgarten and G. Frenking, Energy decomposition analysis, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 43–62 CAS.
- G. Frenking, M. Bickelhaupt and F. Matthias Bickelhaupt, The Chemical Bond, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2014, pp. 121–157 Search PubMed.
- R. F. Nalewajski, J. Mrozek and A. Michalak, Two-electron valence indices from the Kohn-Sham orbitals, Int. J. Quantum Chem., 1997, 61, 589–601 CrossRef CAS.
- A. Michalak, R. L. DeKock and T. Ziegler, Bond multiplicity in transition-metal complexes: applications of two-electron valence indices, J. Phys. Chem. A, 2008, 112, 7256–7263 CrossRef CAS PubMed.
- in The Chemical Bond: Fundamental Aspects of Chemical Bonding, ed. G. Frenking and S. Shaik, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2014 Search PubMed.
- A. Michalak, M. Mitoraj and T. Ziegler, Bond orbitals from chemical valence theory, J. Phys. Chem. A, 2008, 112, 1933–1939 CrossRef CAS PubMed.
- M. P. Mitoraj, A. Michalak and T. Ziegler, A combined charge and energy decomposition scheme for bond analysis, J. Chem. Theory Comput., 2009, 5, 962–975 CrossRef CAS PubMed.
- M. A. Tofanelli, K. Salorinne, T. W. Ni, S. Malola, B. Newell, B. Phillips, H. Häkkinen and C. J. Ackerson, Jahn-Teller effects in Au25(SR)18, Chem. Sci., 2016, 7, 1882–1890 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp02451e |
| This journal is © the Owner Societies 2021 |