Open Access Article
Open Access ArticleChiral optical scattering from helical and twisted silica nanoribbons†
Peizhao
Liu
 ab,
Yann
Battie
ab,
Yann
Battie
 c,
Yutaka
Okazaki
c,
Yutaka
Okazaki
 b,
Naoya
Ryu
b,
Naoya
Ryu
 d,
Emilie
Pouget
d,
Emilie
Pouget
 a,
Sylvain
Nlate
a,
Sylvain
Nlate
 a,
Takashi
Sagawa
a,
Takashi
Sagawa
 *b and
Reiko
Oda
*b and
Reiko
Oda
 *a
*a
aUniv. Bordeaux, CNRS, Bordeaux INP, CBMN, UMR 5248, F-33600 Pessac, France. E-mail: reiko.oda@u-bordeaux.fr
bGraduate School of Energy Science, Kyoto University, 606-8501, Kyoto, Japan. E-mail: sagawa.takashi.6n@kyoto-u.ac.jp
cUniversité de Lorraine, Laboratoire de Chimie et Physique – Approche Multi-échelles des Milieux Complexes, (LCP-A2MC), 1 Boulevard Arago, 57078 Metz, France
dMaterials Development Department, Kumamoto Industrial Research Institute, 3-11-38 Higashimachi, Higashi-ku, Kumamoto 862-0901, Japan
First published on 29th October 2021
Abstract
Helical and twisted silica nanoribbons, deposited in an in-plane direction and with a random orientation, on a quartz substrate showed chiral optical scattering, and the helical nanoribbons had a g-factor of the order of 10−2 below 250 nm. Their signs depend on the handedness of the nanohelices. The effect of the morphology and the orientation of the helices on the chiral optical scattering were investigated with simulations via the boundary element method.
The investigation of the chirality of solid materials has been the focus of intensive studies. While these studies have been performed mainly on crystalline and/or periodic structures,1 non-crystalline (non-ordered and non-periodic structures) materials also have the potential to show promising chiral properties.2 An interesting example is that of amorphous (non-crystalline) chiral silica synthesized via the sol–gel condensation of silica alkoxide with chiral organic molecular assemblies as templates. Numerous helical (morphologically chiral) nano-materials have been synthesized.3
In general, the optical activity (OA) observed from solid materials can be classified into three contributions: (i) absorption- and emission-based OA,1f,4 (ii) refraction-based OA5 and (iii) elastic scattering or non-elastic Raman scattering-based OA.6 Absorption- and emission-based OA are the difference in the absorption or emission of left-handed (LH) and right-handed (RH) circularly polarized (CP) light. Absorption-based OA (circular dichroism (CD)) has been widely studied for electronic-transition OA and vibrational OA. Emission-based OA corresponds to circularly polarized luminescence (CPL). Refraction-based OA (circular birefringence) comes from the difference in the velocities of LH-CP light and RH-CP light that pass through the OA medium, which is determined by the different refractive indices of the material for the RH- and LH-CP light. In contrast to electron transitions such as light absorption and emission, light scattering from nanometric or submicrometric materials shows interesting optical properties such as fadeless coloring in the UV-vis region7 based on the elastic light scattering. Scattering based OA comes from the scattering at the surfaces having different refractive indices from the surrounding media and having chiral structure. Due to the no-energy loss process, elastic scattering can lead to a number of promising applications. Meanwhile, the scattering-based OA observed from solid particles, which typically have high refractive indices, is often mixed with absorbance-based OA; therefore, the contributions of the two need to be separated. Indeed, in the transmission mode of UV-vis and CD spectrometers, the variation of the photon number through absorbance or scattering mechanisms is difficult to distinguish.
We have previously shown that silica nanohelices can be obtained via the sol–gel reaction of tetraethoxysilane (TEOS) using molecular assemblies of the chiral surfactant (C2H4-1,2-((CH3)2N+C16H33)2 with a tartrate counterion) as the organic template8 (Fig. S1, ESI†). With L- or D-tartrate as the counterion, RH- or LH-nanohelices are obtained, respectively. These silica nanohelices show strong vibrational circular dichroism (VCD) signals at the Si–O–Si asymmetric stretching vibrational band,3f but due to the transparency of silica in the UV-vis range, no electronic CD is expected. However, when dried on a substrate, these chiral silica nanoribbons show strong scattering in the UV range, which dominates the extinction and the absorption-based CD signals due to the high refractive index of silica. Therefore, when measuring the electronic CD signals it is very important to understand how the scattering affects the chiroptical signals with respect to the absorption-based signals. In this manuscript, we investigate and compare the optically active absorbance and scattering of helical/twisted silica nanoribbons using a CD spectrometer with or without an integration sphere and compare with the results obtained via simulation.
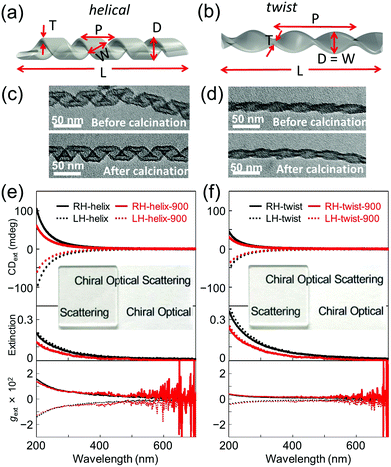
In order to investigate the effect of the scattering and absorbance of individualized silica nanohelices, their suspension was subjected to ultrasonication to create a homogeneous suspension of short nanohelices in ethanol.8b The suspension was drop-casted onto a 2 × 2 cm2 quartz substrate. These silica helices were then calcined at 900 °C directly on the quartz plate for 2 hours. As we have previously reported,3f the silica nanohelices shrink after calcination and the dimensions measured from TEM images are compared on 200 points as shown in Table S1 (ESI†). In Fig. 1a and b, the schematic images show the various dimensions for the helical and twisted ribbons: the pitch (P), width (W), diameter (D), length (L), and thickness (T) of the ribbons are shown.
The signals of absorbance and CD measured using the CD apparatus in transmission mode are based on the extinction, which includes both scattering and absorbance contributions, which we will call extinction and CDext, respectively, hereafter. When the silica nanohelices are dispersed in ethanol, the extinction increases in the UV range below 300 nm; meanwhile, no CDext is observed (Fig. S2, ESI†). When they are drop-casted onto the quartz substrates, the obtained transparent films showed strong extinction and CDext signals in the UV range. In Fig. 1c and d, we show the TEM images of RH-helical and -twisted nanoribbons before and after calcination. In Fig. 1e and f, the extinction and CDext observed from helical and twisted silica nanoribbons are shown for both the RH- and LH-ribbons before and after calcination at 900 °C. The extinction tails towards the wavelength up to 600 nm. Mirror-image CDext signals were observed for RH- (positive) and LH-nanohelices (negative). All the CDext signals of the films were obtained from the mean data of the CDext measured at two angles of 0° and 90° and the linear dichroism (LD) signals (less than 5 × 10−4) were measured in parallel (Fig. S3 and S4, ESI†). Both extinction and CDext signals decrease upon calcination. The CDext signals of the helical nanoribbons are higher than those of the twisted ribbon.
In order to quantify the contribution of the (chiral) scattering and absorbance from the silica nanohelices separately, CDabs measurements of drop-casted silica helix films were performed in diffuse reflection CD (DRCD) mode with various setups (ESI†) for which the scattered light is collected using the integration sphere on the CD apparatus. The results of DRCD and absorbance (or extinction) of the RH- and LH-helical and -twisted silica nanoribbons are shown in Fig. S5, S13 and S14 (ESI†), respectively.9 Very small CDabs signals (∼2 mdeg) were observed at around 200–250 nm compared to ∼100 mdeg for CDext signals, which correspond to impurities (e.g., OH or dissolved O2 molecules) and nonstoichiometric vacancies (e.g., oxygen).10 The amplitudes of the absorbance and CDabs intensities in the UV range are much smaller (∼1/10 and ∼1/33, respectively, at ∼200 nm) than that of the extinction and CDext, indicating that the scattering and the chiral optical scattering (COS) signals are the dominant origin of the extinction and CDext. Again, upon calcination at 900 °C, both the absorbance and CDabs decreased.
Hereafter, we focus on the scattering intensity and the COS. As seen from Table S1 (ESI†), both the helical and twisted nanoribbons shrink after calcination in all dimensions (the pitch, the diameter and the length). This is directly reflected in the decrease of the scattering intensity. In order to investigate how this shrinking affects the COS, we compared the g-factors, which correspond to the normalization of the CDext by the extinction. For both helical and twist ribbons, the g-factors before and after calcination are shown in Fig. 1e and f. No significant modification was observed both for the helical and twisted ribbons after calcination. For both morphologies, they showed a continuous decrease with increasing wavelength, showing a g-factor of ∼0.015 (at 200 nm) for the helical ribbons and ∼0.0035 (at 200 nm) for the twisted ribbons.
We then simulated the extinction and CDext values as well as the scattering cross-section and CDscat values (Fig. 2 and Fig. S7, ESI†) of the individual helical and twisted silica ribbons before and after calcination using the measured values shown in Table S1 (ESI†), using the boundary element method (BEM), as described in the ESI†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 11 using the dielectric function of silica given by Palik12 while ambient air is used as the medium. The simulations are performed by considering that the light beam is perpendicular to the helical/twisted ribbon (in-plane with the substrate). CDext and extinction cross-section values are very close to the CDscat and scattering cross-section values, respectively (Fig S7, ESI†), while the contribution of absorbance and CDabs is negligible, in good agreement with the experimental results. Thus, in the following discussion, CDext is assimilated to CDscat. Interestingly, the CDscat and the g-factors for helical ribbons are higher than those for twisted ribbons, also in good agreement with the experimental observations. In Fig S8 (ESI†), we show the simulation of the two structures in which we compare how the vectors perpendicular to the surface are arranged along the ribbons. These results show that the vectors at the surface of a twisted ribbon rotate with the highest angle only at the center of the ribbon, whereas those of a helical ribbon rotate all together with the same highest angle.
11 using the dielectric function of silica given by Palik12 while ambient air is used as the medium. The simulations are performed by considering that the light beam is perpendicular to the helical/twisted ribbon (in-plane with the substrate). CDext and extinction cross-section values are very close to the CDscat and scattering cross-section values, respectively (Fig S7, ESI†), while the contribution of absorbance and CDabs is negligible, in good agreement with the experimental results. Thus, in the following discussion, CDext is assimilated to CDscat. Interestingly, the CDscat and the g-factors for helical ribbons are higher than those for twisted ribbons, also in good agreement with the experimental observations. In Fig S8 (ESI†), we show the simulation of the two structures in which we compare how the vectors perpendicular to the surface are arranged along the ribbons. These results show that the vectors at the surface of a twisted ribbon rotate with the highest angle only at the center of the ribbon, whereas those of a helical ribbon rotate all together with the same highest angle.
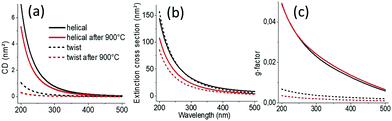 | ||
| Fig. 2 (a) Simulated extinction cross-section, (b) CDext, and (c) g-factors of helical and twisted silica nanoribbons. | ||
We then investigated how modification of the pitch and length of the ribbons affects the scattering intensities, the CDext values and the g-factors. Fig. S9 (ESI†) shows the simulations of how the g-factor at a wavelength of 200 nm evolves with the length (at a fixed pitch and diameter) and pitch (at a fixed length and diameter), respectively, of a single helical or twisted ribbon. The corresponding extinction and CDext values are shown in Fig. S10 (ESI†). The incident light is perpendicular to the axis of the helix. We observe clearly that for pitches and lengths in the range of the helical and twisted ribbons observed for the present system (P, 25–150 nm; L, 200–500 nm), the g-factors of the COS signals do not vary much as both the cross-section and CDscat decrease for the calcined helices with decreased dimension. As shown in Fig. S10 (ESI†), when the size of the ribbon decreases during the calcination, both CDext and extinction vary in the same direction (CDext ↑ and extinction ↑ for increasing L, whereas both CDext ↓ and extinction ↓ for increasing P) compensating the variation in each other.
Globally, these simulated data are in very good agreement with the experimental data. A slight difference is likely due to the fact that the simulation is done on one helix whereas the measurements are done on the ensemble of helices with large size polydispersities (Fig. 3), leading to inter-helix scattering. Also, the variation in the refractive index of silica before and after calcination is not taken into account in the simulation. Indeed, the refractive index should depend on the density of the helices.
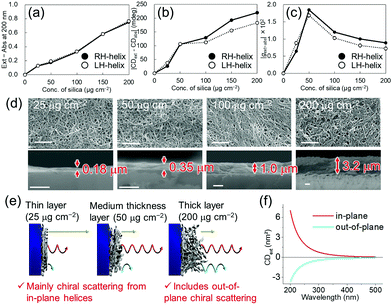 | ||
| Fig. 3 Thickness dependence of the silica nanohelix films on (a) the scattering (Ext – Abs) at 200 nm, (b) COS (|CDext – CDabs|), and (c) g-factor of the COS (|gext–abs|). The original spectra are shown in Fig. S11 (ESI†). (d) SEM images of the surface (top) and cross-section (bottom) of helical silica nanoribbon films with different thicknesses. Scale bars, 1 μm. (e) Proposed mechanisms of COS from nanohelix films. Yellow, red, and blue arrows are non-chiral scattered light from the quartz substrate, COS from in-plane helices, and opposite-handed COS from the out-of-plane helices respectively. (f) Simulated CDext of a helical nanoribbon oriented in-plane (red line) and out-of-plane (blue line) (Fig. S17, ESI†). | ||
Finally, we compared the effect of the quantity of silica nanoribbons on the substrates. As shown in Fig. 3, various thicknesses of silica nanoribbon films were prepared on the 2 × 2 cm2 quartz substrates and the extinction and CDext values were measured. While the intensity of the extinction increased linearly with the quantity of silica nanoribbons (Fig. 3a), CDext intensity increased much more slowly beyond 50 μg cm−2 of silica nanohelices (Fig. 3b), and the g-factor over this range decreased (Fig. 3c) with the concentration of helices. Scanning electron microscope (SEM) images confirmed that 25 μg cm−2 of silica nanoribbons was enough to homogeneously cover the quartz surface of the substrate (Fig. 3d). In order to understand the decrease in the COS signal (g-factor) for the larger quantities of silica helices, we investigated the effect of the orientation (in-plane or out-of-plane of a helix on the COS signal by simulation. As shown in Fig. 3f and Fig. S17 (ESI†), the out-of-plane helix showed an opposite simulated CDext signal from that of the in-plane helix.13 Although a similar coverage of the surfaces was observed for the top views of all the films, the cross-section SEM images of these films clearly showed the difference in their thicknesses. For the 25 and 50 μg cm−2 films, the silica layer thicknesses (0.18 μm and 0.35 μm, respectively), are thinner than the average length of the silica nanohelices. On the other hand, in the case of the 200 μg cm−2 film, the silica layer (3.2 μm) is thicker than the average length of the silica nanohelices. These results indicate that in the thinner layer (<50 μg cm−2), only in-plane orientation is allowed, whilst in the thicker layers (>100 μg cm−2), in-plane and out-of-plane orientations of silica nanohelices (Fig. 3e) can co-exist. Also, electromagnetic interaction between helices in the thicker layers of helices and the multiple scattering can perturb the polarization of the scattered light. These results can be compared with the drop-casted films of cut and non-cut nanoribbons (Fig. S12, ESI†). Non-cut silica nanoribbons show a smaller COS. In both cases, either for the highly concentrated drop-cast film or the non-cut film, silica nanohelices are strongly aggregated in 3D directions with a high proportion of out-of-plane helices.
We investigated the chiral optical scattering from helical and twisted silica nanoribbons deposited on substrates parallel to the surface with random in-plane orientation. Using a CD spectrometer in both transmission and diffuse reflection mode, we demonstrated that the contribution of the absorbance and absorbance-based CD is present but negligible compared with the scattering and COS. Helical ribbons show larger COS and g-factors compared with twisted ribbons. For both morphologies, the variation of g-factor was negligible after calcination. All these results are in good agreement with the simulation performed on a single helix oriented perpendicular to the incoming light. The simulation of the COS on a helix oriented parallel to the incoming light shows the opposite signal from that of the helix oriented perpendicularly, which is probably the origin of the decrease in COS for the aggregated helices which contain the helices oriented out of plane. The g-factors observed for helical ribbons are of the order of 10−2, which is surprisingly high for materials made from silica alone. Thus, the strategy shown here represents an original and promising method to create fadeless circular polarizers while keeping good transparency in the visible range, with one of the most abundant inorganic atoms, Si, and O by simple coating of silica nanohelices on transparent films.
This work was supported by the CNRS and Université de Bordeaux and the Kyoto University Strategic Partnership Program in the context of the France–Japan International Associated Laboratory, LIA-CNPA and by the Special Grants from the Ministry of Education, Culture, Sports, Science and Technology (MEXT) 2018–2021 (Development of International Liaison Laboratory in International Advanced Energy Science Research and Education Center (IAESREC) at Graduate School of Energy Science, Kyoto University). Y. O. thanks the Japan Society for the Promotion of Science KAKENHI (19K15376) and the Supporting Program for Interaction-based Initiative Team Studies (SPIRITS) of Kyoto University. P. L. thanks the support of the Chinese Scholarship Council (CSC).
Conflicts of interest
There are no conflicts to declare.Notes and references
- (a) C. W. Bunn and E. R. Howells, Nature, 1954, 174, 549–551 CrossRef CAS; (b) T. Matsuura and H. Koshima, J. Photochem. Photobiol., C, 2005, 6, 7–24 CrossRef CAS; (c) O. Vogl, J. Polym. Sci., Part A: Polym. Chem., 2011, 49, 1299–1308 CrossRef CAS; (d) K. Akagi, Science, 1998, 282, 1683–1686 CrossRef CAS PubMed; (e) C. Gautier and T. Burgi, J. Am. Chem. Soc., 2008, 130, 7077–7084 CrossRef CAS PubMed; (f) W. Ma, L. Xu, A. F. de Moura, X. Wu, H. Kuang, C. Xu and N. A. Kotov, Chem. Rev., 2017, 117, 8041–8093 CrossRef CAS PubMed; (g) M. V. Mukhina, V. G. Maslov, A. V. Baranov, A. V. Fedorov, A. O. Orlova, F. Purcell-Milton, J. Govan and Y. K. Gun'ko, Nano Lett., 2015, 15, 2844–2851 CrossRef CAS PubMed; (h) A. ben-Moshe, D. Szwarcman and G. Markovich, ACS Nano, 2011, 5, 9034–9043 CrossRef CAS PubMed; (i) A. Ben-Moshe, S. G. Wolf, M. Bar Sadan, L. Houben, Z. Fan, A. O. Govorov and G. Markovich, Nat. Commun., 2014, 5, 4302 CrossRef CAS PubMed; (j) H. E. Lee, H. Y. Ahn, J. Mun, Y. Y. Lee, M. Kim, N. H. Cho, K. Chang, W. S. Kim, J. Rho and K. T. Nam, Nature, 2018, 556, 360–365 CrossRef CAS PubMed.
- M. Simonyi, Z. Bikádi, F. Zsila and J. Deli, Chirality, 2003, 15, 680–698 CrossRef CAS PubMed.
- (a) Y. Ono, K. Nakashima, M. Sano, Y. Kanekiyo, K. Inoue, S. Shinkai, M. Sano and J. Hojo, Chem. Commun., 1998, 1477–1478, 10.1039/a802829j; (b) S. Marx and D. Avnir, Acc. Chem. Res., 2007, 40, 768–776 CrossRef CAS PubMed; (c) H. Qiu and S. Che, Chem. Soc. Rev., 2011, 40, 1259–1268 RSC; (d) K. J. C. van Bommel, A. Friggeri and S. Shinkai, Angew. Chem., Int. Ed., 2003, 42, 980–999 CrossRef CAS PubMed; (e) J. A. Kelly, M. Giese, K. E. Shopsowitz, W. Y. Hamad and M. J. MacLachlan, Acc. Chem. Res., 2014, 47, 1088–1096 CrossRef CAS PubMed; (f) Y. Okazaki, T. Buffeteau, E. Siurdyban, D. Talaga, N. Ryu, R. Yagi, E. Pouget, M. Takafuji, H. Ihara and R. Oda, Nano Lett., 2016, 16, 6411–6415 CrossRef CAS PubMed.
- (a) X. Gao, B. Han, X. Yang and Z. Tang, J. Am. Chem. Soc., 2019, 141, 13700–13707 CrossRef CAS PubMed; (b) H. Tanaka, Y. Inoue and T. Mori, ChemPhotoChem, 2018, 2, 386–402 CrossRef CAS; (c) J. Yan, W. Feng, J.-Y. Kim, J. Lu, P. Kumar, Z. Mu, X. Wu, X. Mao and N. A. Kotov, Chem. Mater., 2019, 32, 476–488 CrossRef.
- J. R. L. Moxon, A. R. Renshaw and I. J. Tebbutt, J. Phys. D: Appl. Phys., 1991, 24, 1187–1192 CrossRef CAS.
- (a) C. Bustamante, I. Tinoco, Jr. and M. F. Maestre, Proc. Natl. Acad. Sci. U. S. A., 1983, 80, 3568–3572 CrossRef CAS PubMed; (b) C. A. Ottaway and D. B. Wetlaufer, Arch. Biochem. Biophys., 1970, 139, 257–264 CrossRef CAS PubMed; (c) J. A. Schellman, Chem. Rev., 1975, 75, 323–331 CrossRef CAS; (d) T. Wu, G. Li, J. Kapitán, J. Kessler, Y. Xu and P. Bouř, Angew. Chem., Int. Ed., 2020, 59, 21895–21898 CrossRef CAS PubMed; (e) G. Li, J. Kessler, J. Cheramy, T. Wu, M. R. Poopari, P. Bouř and Y. Xu, Angew. Chem., Int. Ed., 2019, 58, 16495–16498 CrossRef CAS PubMed; (f) C. F. Bohren, Chem. Phys. Lett., 1974, 29, 458–462 CrossRef CAS; (g) Z. A. Awan and D. Seetharamdoo, Appl. Opt., 2020, 59, 5670–5679 CrossRef CAS PubMed; (h) J. Crassous, A. Amon and J. Crassous, Phys. Rev. A: At., Mol., Opt. Phys., 2012, 85, 023806 CrossRef.
- (a) T. Hu and J. Hong, ACS Appl. Mater. Interfaces, 2015, 7, 23489–23495 CrossRef CAS PubMed; (b) M. Iwata, M. Teshima, T. Seki, S. Yoshioka and Y. Takeoka, Adv. Mater., 2017, 29, 1605050 CrossRef PubMed; (c) Y. Takeoka, S. Yoshioka, A. Takano, S. Arai, K. Nueangnoraj, H. Nishihara, M. Teshima, Y. Ohtsuka and T. Seki, Angew. Chem., Int. Ed., 2013, 52, 7261–7265 CrossRef CAS PubMed.
- (a) T. Delclos, C. Aimé, E. Pouget, A. Brizard, I. Huc, M.-H. Delville and R. Oda, Nano Lett., 2008, 8, 1929–1935 CrossRef CAS PubMed; (b) Y. Okazaki, J. Cheng, D. Dedovets, G. Kemper, M.-H. Delville, M.-C. Durrieu, H. Ihara, M. Takafuji, E. Pouget and R. Oda, ACS Nano, 2014, 8, 6863–6872 CrossRef CAS PubMed; (c) K. Sugiyasu, S.-i. Tamaru, M. Takeuchi, D. Berthier, I. Huc, R. Oda and S. Shinkai, Chem. Commun., 2002, 1212–1213, 10.1039/B202799M.
- (a) Z. Liu, J. Ai, P. Kumar, E. You, X. Zhou, X. Liu, Z. Tian, P. Bouř, Y. Duan, L. Han, N. A. Kotov, S. Ding and S. Che, Angew. Chem., Int. Ed., 2020, 59, 15226–15231 CrossRef CAS PubMed; (b) M. Vybornyi, Y. Vyborna and R. Häner, ChemistryOpen, 2017, 6, 488–491 CrossRef CAS PubMed.
- D. L. Griscom, J. Ceram. Soc. Jpn., 1991, 99(10), 923–942 CrossRef CAS.
- U. Hohenester and A. Trügler, Comput. Phys. Commun., 2012, 183, 370–381 CrossRef CAS.
- E. D. Palik, Handbook of Optical Constants of Solids, 1985 Search PubMed.
- A. Kuzyk, R. Schreiber, Z. Fan, G. Pardatscher, E.-M. Roller, A. Högele, F. C. Simmel, A. O. Govorov and T. Liedl, Nature, 2012, 483, 311–314 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cc04200a |
| This journal is © The Royal Society of Chemistry 2021 |