Open Access Article
Open Access ArticleDesigning refractive index fluids using the Kramers–Kronig relations†
Tianqi
Sai
ab,
Matthias
Saba
 a,
Eric R.
Dufresne
a,
Eric R.
Dufresne
 b,
Ullrich
Steiner
b,
Ullrich
Steiner
 *a and
Bodo D.
Wilts
*a and
Bodo D.
Wilts
 *a
*a
aAdolphe Merkle Institute, University of Fribourg, Chemin des Verdiers 4, CH-1700 Fribourg, Switzerland. E-mail: ullrich.steiner@unifr.ch; bodo.wilts@unifr.ch
bDepartment of Materials, ETH Zürich, Vladimir-Prelog-Weg 5, CH-8093 Zürich, Switzerland
First published on 22nd April 2020
Abstract
For a number of optical applications, it is advantageous to precisely tune the refractive index of a liquid. Here, we harness a well-established concept in optics for this purpose. The Kramers–Kronig relation provides a physical connection between the spectral variation of the (real) refractive index and the absorption coefficient. In particular, a sharp spectral variation of the absorption coefficient gives rise to either an enhancement or reduction of the refractive index in the spectral vicinity of this variation. By using bright commodity dyes that fulfil this absorption requirement, we demonstrate the use of the Kramers–Kronig relation to predictively obtain refractive index values in water solutions that are otherwise only attained with toxic specialised liquids.
1 Introduction
The refractive index of a dielectric optical medium is typically considered to be an intrinsic property that is closely linked to the dipole moments of the atoms and molecules that constitute the optical medium.1 The tuning of optical substances – liquid as well as solid – by either doping the optical medium with high dipole-strength substances or by designing the chemical nature of the medium is commonplace. The latter is for example exploited in the manufacture of liquids with high refractive indices that are used to increase the resolution in photo-lithography. Commercial immersion liquids with refractive indices beyond 1.60 are usually composed of methylene iodide, arsenic tribromide, arsenic disulfide, sulfur and selenium.2–6 While widely used in industrial applications, these immersion liquids are toxic and the rational design of novel liquids based on non-toxic materials would be useful. This is particularly relevant for biological and medical high-resolution imaging, such as total internal reflection fluorescence microscopy,7 where high-index optics based on sapphire lenses facilitate super-resolution.8To this end, it is useful to consider the fundamental theories of the propagation of light. Based on the finite speed of the propagation of light, the consequences of causality for mathematical relationships of optical constants were considered nearly 100 years ago: for the scattering of light from an object, causality requires that “no scattered wave can exist before the incident wave has reached the scattering center”.9 Based on this consideration, Kramers10 showed that the refractive index of a medium can be calculated from its absorption spectrum. Combined with Kronig’s11 argument that a “dispersion relation is a sufficient and a necessary condition for strict causality to hold”, this establishes the well-known Kramers–Kronig relations, which constitute the connection between the in- and out-of-phase responses of a system to sinusoidal perturbations. Mathematically, the Kramers–Kronig relations connect the real and imaginary parts of any complex function that is analytic in the upper half-plane and vanishes sufficiently fast for large arguments.9,12 Physically, such a function corresponds to an analytical linear response function of finite width in the time domain.
For an optical system with a complex refractive index n = n + iκ, with n(ω) the ‘real’ refractive index and κ(ω) the extinction coefficient, both of which vary with the angular frequency of the electromagnetic field ω, the Kramers–Kronig relation can be written as9
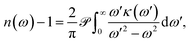 | (1) |
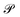 denotes the Cauchy principal value of the integral.
denotes the Cauchy principal value of the integral.
When used in spectroscopy, it is useful to write eqn (1) in terms of the optical wavelength λ = 2πc/ω, where c is the speed of light. A substitution of the integration variable yields
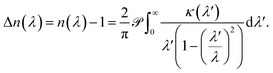 | (2) |
An additional requirement of the Kramers–Kronig relation is the superconvergence theorem,9 leading to
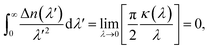 | (3) |
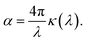 | (4) |
The use of the Kramers–Kronig relation in optics is extremely well established.9,13–15 It is often used to determine the spectral variation n(λ) of an analyte from a measured absorption spectrum, and vice versa.
While identical in terms of the underlying physics, this work explores an alternative approach to creating new high refractive index liquids with a designed optical response, by exploring the Kramers–Kronig relation. This concept was illustrated by the refractive index dispersion of pigments in biological samples,14,15 the oxygen saturation levels of human blood,13 and the high refractive index materials in the wing scales of pierid butterflies.16
2 Results and discussion
2.1 Conceptualisation of the Kramers–Kronig approach
Our concept is illustrated in Fig. 1. To explore the physical limits of the Kramers–Kronig effect, i.e. the relation between absorption and refractive index change, we assume a hypothetical pigment with a sharply defined boxcar-shaped absorption band with κ = 2.5 in the 100–400 nm wavelength range (Fig. 1a). Fig. 1b shows that in this hypothetical case, Δn is very strongly enhanced: Δn(400 nm) ≈ 7; Δn(400 nm) − Δn(∞) ≈ 4.8. A characteristic spectral feature of Δn is the long-wavelength decay, the region of “normal” dispersion, which can be approximated by the Cauchy equation17| nC = A + B/λ2, | (5) |
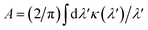 and
and 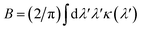 can be used as fitting parameters. Note that each spectral feature in the absorption spectrum gives rise to a long-wavelength Cauchy decay, and these are additive,9 ultimately determining the overall refractive index variation of a given material in each transparent wavelength window.
can be used as fitting parameters. Note that each spectral feature in the absorption spectrum gives rise to a long-wavelength Cauchy decay, and these are additive,9 ultimately determining the overall refractive index variation of a given material in each transparent wavelength window.
 | ||
| Fig. 1 Refractive index spectra, calculated by numerically solving eqn (2). (a) Hypothetical extinction spectrum confined to the 100–400 nm band. (b) Refractive index change Δn corresponding to (a). (c) Alternative hypothetical extinction spectrum and (d) corresponding Δn spectrum. Similar plots with extinction spectra given by single Lorentzian peaks are shown in Fig. S3.† | ||
While perhaps somewhat unrealistic, Fig. 1a and b illustrate the scope of our approach. Importantly, the enhancement of Δn extends to wavelengths where the absorption coefficient is practically zero. The strong enhancement close to, but above, the absorption band makes this idea particularly attractive in applications where only narrow-band illumination is required, e.g. telecommunication18 or lenses for immersion lithography.19 By carefully selecting a short-wavelength absorber, a high refractive index can be obtained in a controlled fashion.
Fig. 1c and d show a prediction which is closer to physical parameters that can be achieved for liquids: an extinction coefficient κ = 0.52 which corresponds to α ≈ 10.3 μm−1 at λ = 630 nm for a 0.6 M Brilliant Blue solution in water (see below). In this simulation, the absorption edge was smeared out over ca. 35 nm. Here, an overall refractive index enhancement of ≈1 is expected at 400 nm compared to the dye-free solution and a value of Δn ≈ 0.8 is expected at 430 nm, where the dye absorption has decayed to just a few percent of its maximal value. While perhaps not as impressive as the hypothetical case in Fig. 1b, this concept has the potential to enhance the refractive index of common liquids into the range commonly reserved for specialised toxic liquids.3
2.2 Food dyes for water-based refractive index fluids
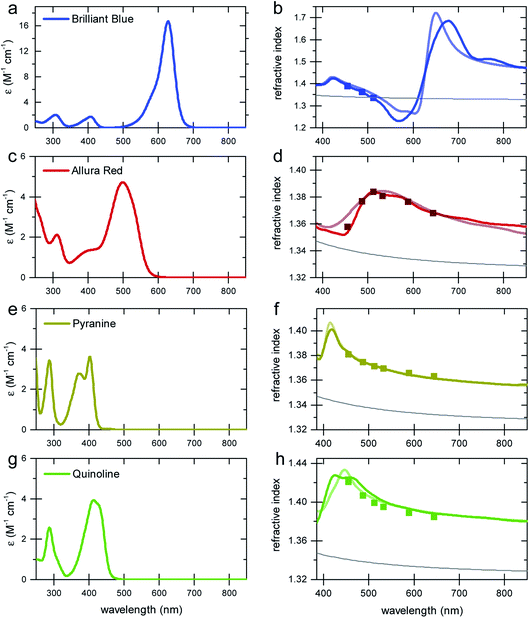
To demonstrate the concept of refractive index tuning through the selection of an appropriate absorber, four commonly used non-toxic, water-soluble dyes were investigated: the triarylmethane dye “Brilliant Blue”, the azo dye “Allura Red”, the sulfonated “Quinoline Yellow”, and the arylsulfonate “Pyranine”. The chemical structures and IUPAC names are given in Fig. S1 in the ESI.† The first three dyes are common food colorants,20 while the last is a fluorescent coloring agent used in hair dye and text markers. All four are water-soluble, non-toxic commodity compounds.To start our investigation, UV-Vis transmission spectra of all four dyes were acquired. Water solutions of the four dyes were prepared with a series of concentrations cd up to the solubility limit of the dyes (between 300 mM and 600 mM). The spectral absorption coefficients were then determined according to the Beer–Lambert law, as shown in Fig. 2. The absorption spectrum of Allura Red shows rather broad spectral peaks with a broad decay toward long wavelengths and an absorption peak at about 500 nm. In contrast, Brilliant Blue, Quinoline Yellow, and Pyranine show sharper spectral decays towards long wavelengths at 630 nm, 412 nm, and 428 nm, respectively, which combine the prerequisite for a strong Δn enhancement at these wavelengths according to eqn (2), with the possibility to achieve significant Δn enhancement in the spectral domain where light absorption is insignificant (see Fig. 1). In particular, Brilliant Blue is an excellent candidate dye with a molar absorbance of 17.25 ± 0.04 cm−1 at 630 nm.
Spectroscopic ellipsometry was employed to measure the spectral variation n(λ) of the various dye solutions, according to the protocol of Synowicki et al.21 In this method, dye solution drops are placed onto a rough glass substrate. The rough glass substrate enables the spreading of the water–dye solutions to provide a planar liquid surface and it suppresses the specular back reflection of the incident light beam from the liquid–substrate interface. Since only the phase relationship of the light reflected from the liquid–air surface is analysed, the ellipsometry data analysis is not very sensitive to the imaginary part of the refractive index κ. Therefore, only the real part of the refractive index n(λ) was extracted from the ellipsometric data. To test the reliability of this approach, the variation of the refractive index of water was determined in the 400–1000 nm wavelength range and an agreement with literature data of better than 0.5% was found (Fig. S2 in the ESI†). As a further test of the measurement protocol, a 6-wavelength (455–655 nm) Abbe refractometer was also used, with a measurement accuracy for refractive index of 4 × 10−4.
The results of the ellipsometry and refractometry measurements for the highest concentrations of the four dyes in water are shown in Fig. 2. A comparison with the spectral variation of the absorption curves bears out the qualitative variation of Δn in Fig. 1, i.e. all curves exhibit the signature predicted by the Kramers–Kronig relations.
To calculate the variation of n(λ) from the absorption curves in Fig. 2, the limitations of the integration of eqn (2) have to be discussed. The prediction of the Kramers–Kronig relation is only precise if the variation of the extinction coefficient κ is known for the entire spectral wavelength range (0 → ∞). Since this is generally impossible, we exploit the limiting properties of eqn (2) given by the Cauchy equation (eqn (5)).
Considering, for example, an absorption spectrum with two distinct spectral features (Fig. S3 in the ESI†), the integral in eqn (2) can be decomposed into two separate integrations, the results of which are then added to yield the overall spectral response n(λ).9 In the range of the long-wavelength absorption peak, the Δn contribution of the short-wavelength absorption peak can be approximated by eqn (5), which can be added to the result of eqn (2).
In the absence of spectral information below λ = 250 nm, which strongly affects the long-wavelength variation of Δn, the following approach was therefore adopted.
(1) Calculation of κ(λ) from the absorption curves in Fig. 2 using eqn (4), setting κ = 0 for λ < 250 nm and λ > 1000 nm.
(2) Integration of eqn (2) to obtain Δn(λ).
(3) Approximation of the refractive index variation of water nCw (Fig. S2 in the ESI†) by eqn (5).
(4) Calculation of nKK(λ) = Δn(λ) + nCw(λ) + nCd(λ), with another Cauchy-type refractive index contribution of the dye, nCd(λ), as given by eqn (5). The coefficients A and B were fitted so that nKK overlaps with the ellipsometry results in the short and long wavelength ranges far from the oscillatory feature in Δn (Table S1 in the ESI†).
The motivation for the fitting procedure resulting in nCd stems from the fact that κ(λ) of the dye is unknown for λ < 250 nm, the presence of which will give rise to a Cauchy-type decay for λ > 250 nm. Using this approach, an excellent agreement between calculated and measured refractive index spectra in the visible wavelength range was found (Fig. 2b, d, f and h).
2.3 Refractive index tuning
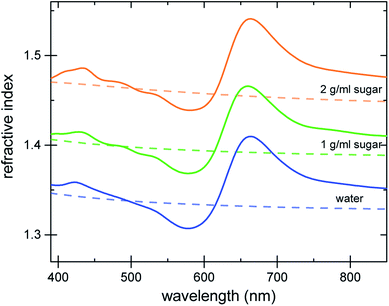
The refractive index of the liquid can be further tuned by changing the concentration of the dye. Fig. 3a demonstrates that is it possible to precisely obtain a desired refractive index at a target wavelength, by adjusting the concentration of the Brilliant Blue dye. Fig. 3b clearly demonstrates that Δn enhancements of up to ≈0.35 can be achieved in spectral regions where the absorption coefficient is close to zero. Further, the concentration series in Fig. 3a gives evidence for the presence of a finite nCd in the visible range. With increasing dye concentration, not only does the oscillatory feature of the refractive index become increasingly pronounced, stemming from the single absorption peak at 630 nm, the “baseline” at 380–400 nm also increases with dye concentration. Fig. 1 illustrates that Δn → 0 for shorter wavelengths compared to the absorption peak. Therefore, the baseline variation indicates the presence of a Cauchy term, eqn (5), stemming from dye absorption peaks below 380 nm.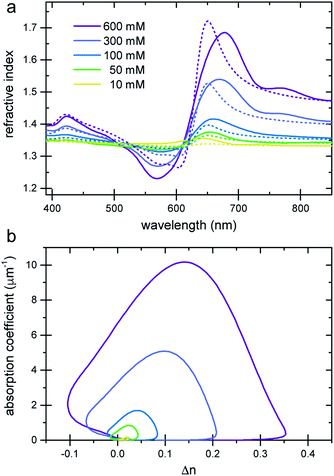 | ||
| Fig. 3 Refractive index variation of Brilliant Blue solutions in water as a function of dye concentration. (a) Ellipsometry measurements (solid lines) are compared to nKK(λ) calculated using the Kramers–Kronig relation (eqn (2), dashed lines). Note the increase in the refractive index at short wavelengths, which is indicative of additional dye absorption peaks below 250 nm (see text).22 (b) A plot of the absorption coefficient vs. Δn clearly reveals a substantial Δn enhancement in spectral regions where the absorption coefficient is practically zero. | ||
The comparison of the calculated nKK with the measured ellipsometry spectra is very good, given the fact that spectral information outside the 250–1000 nm wavelength window is missing and Cauchy approximations were employed instead. Note also that while the fit determining nCd(λ) improves the Kramers–Kronig description of the experimental data, the predictive quality of nKK even in the absence of any fitting (i.e. setting nCd = 0) is very good, showing the strength of this approach (Fig. S4 in the ESI†).
A further way to control the refractive index of a liquid at a given wavelength is the combination of the “traditional” method, the addition of a transparent additive, with the present Kramers–Kronig approach. Fig. 4 shows the measured refractive index spectra of 0.1 M Brilliant Blue dissolved in two sugar solutions. The combination of raising the Cauchy background (eqn (5)) with the Kramers–Kronig response of the dye provides a versatile way to control the refractive index of the solution across large parts of the optical spectrum.
3 Conclusions
In summary, we have harnessed a nearly 100 year old concept in optics for the design of refractive indices in liquids. When employing narrow bandwidth illumination, as e.g. provided by lasers, the well-established Kramers–Kronig relations that link the refractive index with the absorption coefficient provide an approach to specifically obtain a target refractive index in any narrow wavelength band. Using common food dyes, refractive indices close to 1.7 were obtained. It should be possible to further enhance the refractive index variation by developing dyes that optimise the Kramers–Kronig effect, featuring high absorption coefficients with a sharp long-wavelength decay. Alternatively, it might be possible to suspend organic or inorganic nanoparticles in solution to harness the high extinction coefficients of crystalline materials.16,23 Finally, while the refractive index enhancement at long wavelengths is larger than the refractive index reduction of the Kramers–Kronig oscillation caused by a well-defined absorption peak at shorter wavelengths, this effect can also be employed for targeted refractive index reduction, e.g. to index match or produce narrow-band anti-reflective coatings.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was partially funded by the ERC Advanced Grant (H2020-Prismoid, to US) and through the Swiss National Science Foundation through the NCCR Bio-inspired Materials (to TS, ERD, US, BDW) and the Ambizione Programme (168223, to BDW).Notes and references
- E. Hecht, Optics, Pearson, 2016 Search PubMed.
- R. D. Butler, Am. Mineral., 1933, 18, 386–401 CAS.
- J. J. Cargille, Immersion oil and the microscope, NY Microscop. Soc., Yearbook, 2008, vol. 9 Search PubMed.
- R. L. Darneal, Am. Mineral., 1948, 33, 346–352 CAS.
- R. Meyrowitz and E. S. Larsen Jr, Am. Mineral., 1951, 36, 746–750 CAS.
- C. West, Am. Mineral., 1936, 21, 245–249 CAS.
- M. Guo, P. Chandris, J. P. Giannini, A. J. Trexler, R. Fischer, J. Chen, H. D. Vishwasrao, I. Rey-Suarez, Y. Wu, X. Wu, C. M. Waterman, G. H. Patterson, A. Upadhyaya, J. W. Taraska and H. Shroff, Nat. Methods, 2018, 15, 425–428 CrossRef CAS PubMed.
- J. M. Laskar, P. S. Kumar, S. Herminghaus, K. E. Daniels and M. Schröter, Appl. Opt., 2016, 55, 3165 CrossRef CAS PubMed.
- V. Lucarini, J. J. Saarinen, K.-E. Peiponen and E. M. Vartiainen, Kramers–Kronig relations in optical materials research, Springer Science & Business Media, 2005, vol. 110 Search PubMed.
- H. A. Kramers, Atti Cong. Intern. Fisica (Transactions of Volta Centenary Congress) Como, 1927, vol. 2, pp. 545–557 Search PubMed.
- R. d. L. Kronig, J. Opt. Soc. Am., 1926, 12, 547–557 CrossRef CAS.
- H. M. Nussenzveig, Causality and dispersion relations, Academic Press, 1972 Search PubMed.
- D. J. Faber, M. C. Aalders, E. G. Mik, B. A. Hooper, M. J. van Gemert and T. G. van Leeuwen, Phys. Rev. Lett., 2004, 93, 028102 CrossRef PubMed.
- D. G. Stavenga, H. L. Leertouwer and B. D. Wilts, Light: Sci. Appl., 2013, 2, e100 CrossRef.
- D. G. Stavenga and B. D. Wilts, Philos. Trans. R. Soc., B, 2014, 369, 20130041 CrossRef PubMed.
- B. D. Wilts, B. Wijnen, H. L. Leertouwer, U. Steiner and D. G. Stavenga, Adv. Opt. Mater., 2017, 5, 1600879 CrossRef.
- F. Jenkins, Fundamentals of Optics, McGraw-Hill, New York, 1976 Search PubMed.
- G. P. Agrawal, Nonlinear Science at the Dawn of the 21st Century, Springer, 2000, pp. 195–211 Search PubMed.
- S. Owa and H. Nagasaka, J. Micro/Nanolithogr., MEMS, MOEMS, 2004, 3, 97–104 CrossRef CAS.
- N. Martins, C. L. Roriz, P. Morales, L. Barros and I. C. Ferreira, Trends Food Sci. Technol., 2016, 52, 1–15 CrossRef CAS.
- R. Synowicki, G. K. Pribil, G. Cooney, C. M. Herzinger, S. E. Green, R. H. French, M. K. Yang, J. H. Burnett and S. Kaplan, J. Vac. Sci. Technol., B: Microelectron. Nanometer Struct.--Process., Meas., Phenom., 2004, 22, 3450–3453 CrossRef CAS.
- Compared to the trend exhibited by the lower dye concentrations, the experimental curve of the 600 mM Brilliant Blue solution has a lower than expected refractive index maximum. Since this concentration is close to the solubility limit, a small fraction of the dye may have separated from the solution, resulting in an effective solution concentration below 600 mM. By extrapolation, the probable solution concentration of this data set was 540 mM.
- B. A. Palmer, V. J. Yallapragada, N. Schiffmann, E. M. Wormser, N. Elad, E. D. Aflalo, A. Sagi, S. Weiner, L. Addadi and D. Oron, Nat. Nanotechnol., 2020, 1–7 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Materials and methods, Table S1 and Fig. S1–S4. See DOI: 10.1039/d0fd00027b |
| This journal is © The Royal Society of Chemistry 2020 |