Open Access Article
Open Access ArticleCan solvated intermediates inform us about nucleation pathways? The case of β-pABA†
A. J.
Cruz-Cabeza
 a,
E.
Taylor
a,
I. J.
Sugden
a,
E.
Taylor
a,
I. J.
Sugden
 b,
D. H.
Bowskill
b,
D. H.
Bowskill
 b,
S. E.
Wright
a,
H.
Abdullahi
a,
D.
Tulegenov
a,
G.
Sadiq
c and
R. J.
Davey
b,
S. E.
Wright
a,
H.
Abdullahi
a,
D.
Tulegenov
a,
G.
Sadiq
c and
R. J.
Davey
 *a
*a
aDepartment of Chemical Engineering and Analytical Sciences, University of Manchester, M13PL, UK. E-mail: roger.davey@manchester.ac.uk
bMolecular Systems Engineering Group, Centre for Process Systems Engineering, Department of Chemical Engineering, Imperial College London, London SW7 2AZ, UK
cCambridge Crystallographic Data Centre, 12 Union Road, Cambridge CB2 1EZ, UK
First published on 4th August 2020
Abstract
Classical nucleation theory teaches the idea that molecular clusters form and grow in solution and that depending on prevailing conditions there is a chance for some to grow large enough to overcome the interfacial energy penalty and become mature crystals. However, from such a kinetic analysis, nothing is learnt of the nature of the composition or the molecular packing in such clusters. As a means of addressing this shortcoming consideration has, in the past, been given to the idea that in certain systems crystallography may offer additional, structural, insights. From this approach the notions of ‘nucleation pathway’ or ‘nucleation transition state’ have become useful concepts around which to formulate hypotheses as to how clusters may yield specific molecular packing, resulting for example, in the observation of crystal polymorphs. Here we offer an in-depth crystallographic analysis related to the nucleation of the α and β polymorphs of para-aminobenzoic acid in an attempt to reveal the pathways leading to the two forms. Using a combination of CSD analyses, crystal structure prediction and targeted crystallizations we explore plausible solution pathways to these polymorphs and discuss our results in the light of known kinetic data for the nucleation and growth of this material.
Introduction
In recent years significant advances have been made in our ability to measure and interpret the nucleation rates of organic molecules from solutions.1–3 The use of crystallographic data in the context of kinetic processes goes back to the work of Burgi et al.4 who demonstrated its utility in mapping the reaction co-ordinate during amine-carbonyl nucleophilic addition reactions. Their conclusions were based on the idea ‘that each example can be regarded as a case where the addition reaction has proceeded to a greater or lesser extent but has been frozen in at a certain stage by the intra- or intermolecular constraints imposed by the crystal environment’. A number of attempts have been made to utilise a similar idea in order to explore structural aspects of crystal nucleation. Thus in his 20035 paper concerning structures with high Z′ values, Steed commented that ‘the observed structure may readily be viewed as a fossil relic of the fastest growing crystal nucleus rather than a thermodynamic minimum structure’. In 20056 Banerjee et al. took this idea further in reporting the structure of sodium saccharinate where packing disorder was considered to reflect the nature of the nucleus: ‘there is enough in the structure that is unusual for us to believe that it represents a good approximation of what a crystal nucleus looks like’. Similar conclusions have been drawn from the structure of pentafluorophenol polymorphs.7 In 2014,8 Steed and Steed reviewed much available data and offered a balanced comment on the idea that metastable crystal forms may be viewed as fossil relics of kinetically determined initial nuclei. They concluded that this is indeed a difficult leap to make. In the case of solvates, however, one might anticipate more success. In 1999 Nangia and Desiraju9 reflected on the occurrence of solvates in the CSD and announced that in the context of a crystallisation pathway from solution to unsolvated crystal ‘the formation of a solvated crystal may be likened to an interruption of the sequence of events that accompany the ‘normal’ crystallisation’. This idea was taken up by Banerjee et al.10 in a study of an anthracenediol in which they compare the structure of the non-solvated form with that of five solvates and again return to the idea of the solvent as a kinetic mitigator of packing difficulties. Overall, this collection of studies all attempt to offer structural interpretations of processes whose outcomes rely significantly on kinetics. Often even the relative stability of the solid forms under consideration is not known or discussed. As far as we are aware the only report that makes any attempt to utilise crystallographic information to track the real-time transient nature of nucleation and growth concerns the crystallisation of trimesic acid from DMSO.11 This work provided structural characterisation of both the solution and the short-lived metastable solvate to demonstrate that molecules are able to make the jump from solution to the first nucleated solid phase with no change in their solvated coordination. The application of crystallographic data in furthering our understanding of nucleation is thus far from straightforward and fraught with difficulties as expected when using static data to interpret a kinetic process.Here we have returned to this problem as part of our examination of the nucleation of benzoic acids.12 We have been particularly concerned with p-aminobenzoic acid which crystallises from solution in one of two commonly observed polymorphs.13 The α form is based on the carboxylic acid dimer and the β structure utilises COOH⋯NH2 interactions, creating tetramer units linked by H-bonded chains.14 Crystallisation of the former is dominated by growth along the b-axis which involves infinite stacks related by translation while in the latter stacked molecules are limited to isolated dimers whose molecules are related by a centre of symmetry. Since the nucleation and growth of α is apparently ubiquitous from all solvents and at all temperatures15 some investigations have sought to probe the origin of the motif found in the β structure.16 It has been noted and confirmed in various studies that β is most reliably crystallised from aqueous solutions at low supersaturations.16,17 Hence, the question has arisen as to whether water plays some central role in the nucleation pathway to the β structure and indeed, in our earlier paper, we showed computationally how water might stabilise the centrosymmetric pABA dimer held by aromatic stacks.18 We give further consideration to this question here using a combination of methodologies and invoking the aid of crystallography – CSD analysis, crystal structure prediction (CSP), targeted crystallisation experiments and crystal structure determination. We consider the rarity of the β structure, the potential for various solvent mediated transition states to enable its formation and the possibility that the isolation of new solvated structures will inform our understanding.
Methods
Experimental methods
Experimental PXRD patterns of isolated solids were compared to those calculated from XRD structures for form identification. Additionally optical microscopy (Zeiss Axioplan) and single crystal XRD, where available, were necessary.
CSD searches
All searches were performed on the CSD best R-factor subset (2020 release) using ConQuest.19 This subset does not contain structure redeterminations. Conquest searches were carried out with the following filters: crystal structures must have 3D coordinates, no disorder, no errors, they must not be polymeric or contain ions and only organic molecular crystals were searched.| Form | Primary HBs | Secondary HBs | Aromatic stacks | ||
|---|---|---|---|---|---|
| α | β | α and β | α | β | |
| Interaction | COOH⋯COOH | COOH⋯NH2 | NH2⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C |
Translated | Inverted |
| CSD stats (102 hits) | 46% | 3% | 36% | 38% | 62% |
| HB propensity | 0.30 | 0.04 | 0.53 | — | — |
| Aromatic analyser score | — | — | — | 9.7 (strong) | 9.2 (strong) |
| CSP stats | 98% | 2% | — | 52% | 5% |
These searches were limited to single component crystal structures whereby the compound contained both an amino (NH2) and carboxylic (COOH) acid functional groups. Compounds containing primary amides of the type CONH2 were not considered since those NH2 groups behave significantly differently to amino groups. This search returned 102 hits.
| Compound/form | CSD refcode | Z′ | SG | Primary HB (donor–acceptor) | Secondary HB (donor–acceptor) | Stacking |
|---|---|---|---|---|---|---|
| a LC = complex long chain; t = translation; i = inversion; g = glide plane. Continuous interactions are given an infinity sign in brackets. See ESI† section 1 for CSD deposition numbers of the new structures. | ||||||
| pABA forms | ||||||
| α-pABA | AMBNAC07 | 2 | P21/n | Acid–acid | Amino–O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C |
t [∞] |
| γ-pABA | AMBNAC09 | 2 | Pna21 | Acid–acid | Amino–O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C |
t [∞] |
| β-pABA | AMBNAC12 | 1 | P21/n | Acid-amino | Amino–O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C |
i |
| δ-pABA | AMBNAC16 | 1 | Pn | Acid-amino | Amino–O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C |
t [∞] |
| pABA derivatives with α similarities | ||||||
| 3-Br | HOLTAE | 2 | Pna21 | Acid–acid | Amino–O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C |
t [∞] |
| 3-iProp | JISGAW | 1 | P21/c | Acid–acid | Amino–O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C |
t [∞] |
| 3-LCa | DUMYIV | 1 | P21/n | Acid–acid | Amino–O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C |
t [∞] |
| 3,5-diF | YOZFIE | 1 | Pmna | Acid–acid | Amino–O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C |
t [∞] |
| 3,5-diBr | BRABZA01 | 1 | Pman | Acid–acid | Amino–O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C |
t [∞] |
| 3,5-diI | YOZFUQ01 | 1 | Pmna | Acid–acid | Amino–O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C |
t [∞] |
| 2-F | This study | 4 | C2/c | Acid–acid | Amino–amino | t [∞] |
| 2-Cl | AYOSOX | 2 | P21 | Acid–acid | Amino–amino | t [∞] |
| 2-OH | AMSALA02 | 1 | P21/n | Acid–acid | Other | t [∞] |
| 3-Cl | This study | 1 | P21/c | Acid–acid | Other | t [∞] |
| 3-NO2 | PUQFUD | 1 | P21/n | Acid–acid | Other | i [∞] |
| 2-Me | This study | 2 | P212121 | Acid–acid | Amino-amino | Other |
| 3-Me | This study | 2 | P21/c | Acid–acid | Amino–O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C |
t |
| pF (2,3,5,6-tetraF) | This study | 1 | P21/c | Acid–acid | Amino–O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C |
t [∞] |
| pABA derivatives with β similarities | ||||||
| 3-OH | This study | 1 | Pbca | Acid–amino | Amino–O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C |
Other [∞] |
| Other pABA derivatives | ||||||
| 2-OMe | This study | 1 | P21/c | Other intra | Amino–O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C |
Other [∞] |
| 2-OMe-5-Cl | This study | 1 | P21/c | Other intra | Amino–O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C |
Other [∞] |
| 2-OEt-5-Cl | This study | 1 |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
Other intra | Amino–O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C |
g [∞] |
The CSD was searched for the pABA substructure whereby no specific substituents were placed in positions 2, 3, 5 and 6. Searches were limited to single component crystals. This search returned 9 structures.
| Substructurea | CSD Refcode | Componentsa | Primary HB | HB tetramer | Aromatic stacking | |
|---|---|---|---|---|---|---|
| a uc = uncharged; z = zwitterionic. b X = complex substituent. | ||||||
| Anhydrous | oABA-z | AMBACO07 | oABA-z oABA-uc | NH3+⋯COO− | No | Other |
| mABA-z | AMBNZA02 | mABA-z | NH3+⋯COO− | Yes | t [∞] | |
| mABA-z | SAQJAC01 | 6-OH-mABA-z | NH3+⋯COO− | Yes | t [∞] | |
| mABA-z | DOBPAO | 2-NH2-mABA-z 2-NH2-mABA-uc | NH3+⋯COO− | No | i | |
| mABA-z | VODWIU | 4-NH2-mABA-z | NH3+⋯COO− | Yes | t [∞] | |
| mABA-z | EQICOY | 2-OH-mABA-z | NH3+⋯COO− | Yes | t [∞] | |
| pABA-z | PEJYEJ | 3-Xb-pABA-z | NH3+⋯COO− | Yes, variation | Other | |
| Hydrates | mABA-z | POVGUC02 | 5-COOH-mABA-z water | NH3+⋯COO− | No | 21 [∞] |
| mABA-z | SOYPOM | 4-OH-mABA-z water | NH3+⋯COO− | No | i | |
The CSD was searched for zwitterionic pABA, mABA and oABA substructures with no specified substituents on positions 2, 3, 5 and 6 and 16 structures were retrieved.
| Conquest search query | N | Hydrogen bonds | Aromatic stacks | |||
|---|---|---|---|---|---|---|
| (COOH⋯COOH) s, 0.5 s, usa | (NH2⋯NH2) s, 0.5 s, usa | (COOH⋯NH2) s, 0.5 s, usa | s-S[t] | s-S[i] | ||
| a s = solvated dimer with two water molecules; 0.5 s = half solvated dimer with one water molecule; us = unsolvated dimer. Thus, for the acid⋯acid dimer, the fully solvated motif contains 2 molecules of water and 2 molecules of acid, the half solvated motif contains 1 molecule of water and 2 molecules of acid and the unsolvated motif is the typical unsolvated and R22(8) dimer. | ||||||
Benzoic acid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water water |
179 | 14%, 9%, 18% | — | — | 33% | 35% |
Aniline![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water water |
120 | — | 8%, 0%, 2% | — | 28% | 32% |
Amine-X-acid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water water |
60 | 3%, 0%, 7% | 0%, 0%, 0% | 0%, 0%, 13% | — | — |
The CSD was searched for hydrates of compounds (two components only, the hydrate and the main component) with no charges and containing the following substructures: i) benzoic acid (179 hits), ii) aniline (120 hits) and compounds containing both an amine and an acid group (amine-X-acid, 60 hits). There was no significant overlap between these searches.
CSD materials calculations
The following calculations were all performed with the CSD Materials Mercury (2020).20Molecular simulations
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water 1
water 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio, (4) pABA
1 ratio, (4) pABA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water 1
water 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio) were carried out using the code CrystalPredictor24 (version 2.4.3). Flexibility was determined using gas phase finite difference perturbations around degrees of freedom indicated as potentially flexible by second derivatives at the gas phase minimum; this meant the carboxylic acid group torsion. The level of theory used was B3LYP, with the Aug-CC-pVTZ basis set, in Gaussian 09. A uniform local approximate model (LAM) grid was set up for pABA, with LAMs evaluated at 0.0 and 180.0 degrees; a pass of the adaptive LAM algorithm25 indicated that this was sufficient to accurately describe the flexibility within the molecules. The potential parameters for C, H–C (hydrogen attached to carbon), N, O, and H-n (hydrogen attached to a polar atom) from the work of Williams and co-workers were used to describe the exchange-repulsion and dispersion interactions.26 The structure generation stage sampled the 59 most common space groups. 500 k and 1 million structural minimisations were run for the Z′ = 1 (1a, 2, 3, 4 and 5) and 2 (1b) searches respectively, using the smoothed intramolecular potential algorithm.27–29 After the CrystalPredictor calculations were complete, a final clustering of generated structures was carried out with the COMPACK algorithm. In order to refine the calculated lattice energies, the generated structures were minimised with an improved energy model for electrostatics consisting of atomic multipoles, with extended flexibility (amine hydrogen angles, and all angles within the carboxylic acid group), together with the same FIT potential, using CrystalOptimizer.30 The same level of theory (B3LYP/Aug-CC-pVTZ) was employed (see also ESI† section 3.1).
2 ratio) were carried out using the code CrystalPredictor24 (version 2.4.3). Flexibility was determined using gas phase finite difference perturbations around degrees of freedom indicated as potentially flexible by second derivatives at the gas phase minimum; this meant the carboxylic acid group torsion. The level of theory used was B3LYP, with the Aug-CC-pVTZ basis set, in Gaussian 09. A uniform local approximate model (LAM) grid was set up for pABA, with LAMs evaluated at 0.0 and 180.0 degrees; a pass of the adaptive LAM algorithm25 indicated that this was sufficient to accurately describe the flexibility within the molecules. The potential parameters for C, H–C (hydrogen attached to carbon), N, O, and H-n (hydrogen attached to a polar atom) from the work of Williams and co-workers were used to describe the exchange-repulsion and dispersion interactions.26 The structure generation stage sampled the 59 most common space groups. 500 k and 1 million structural minimisations were run for the Z′ = 1 (1a, 2, 3, 4 and 5) and 2 (1b) searches respectively, using the smoothed intramolecular potential algorithm.27–29 After the CrystalPredictor calculations were complete, a final clustering of generated structures was carried out with the COMPACK algorithm. In order to refine the calculated lattice energies, the generated structures were minimised with an improved energy model for electrostatics consisting of atomic multipoles, with extended flexibility (amine hydrogen angles, and all angles within the carboxylic acid group), together with the same FIT potential, using CrystalOptimizer.30 The same level of theory (B3LYP/Aug-CC-pVTZ) was employed (see also ESI† section 3.1).
Results
On the rarity of the β-pABA structural motifs
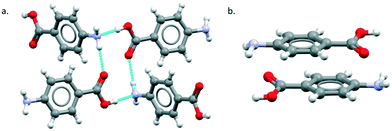
The major objective of this section is the use of the CSD searches to explore the rarity or otherwise of the β pABA structural motifs. Fig. 1 provides images of the two key motifs that constitute the β structure. The first motif (Fig. 1a) is a hydrogen bonded R44(12) tetramer constituted by two COOH⋯NH2 primary hydrogen bonds and two NH2⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C secondary hydrogen bonds (primary and secondary are used to underline the fact that NH2⋯O
C secondary hydrogen bonds (primary and secondary are used to underline the fact that NH2⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C is expected to be weaker and less directing that the COOH⋯NH2) the second motif (Fig. 1b) is the aromatic stacking interaction in which molecules are related by inversion symmetry. As mentioned earlier these differ significantly from the R22(8) HB dimer and translated aromatic stacks found in the α polymorph.
C is expected to be weaker and less directing that the COOH⋯NH2) the second motif (Fig. 1b) is the aromatic stacking interaction in which molecules are related by inversion symmetry. As mentioned earlier these differ significantly from the R22(8) HB dimer and translated aromatic stacks found in the α polymorph.
Table 1 provides a summary of the search results and related data for crystal structures of compounds containing both an amino (NH2) and carboxylic (COOH) acid functional groups, indicating the overall occurrence of the relevant motifs as found in the α and β structures.
In terms of the HB, in searches of a total of 102 structures the R22(8) carboxylic acid dimer motif is the most common (46%) followed by the secondary NH2⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) interactions (36%) and the COOH⋯NH2 primary hydrogen bond (3%). In fact, only three crystal structures were observed to have the COOH⋯NH2 hydrogen bond, two of which were the β and the δ pABA polymorphs. These overall statistics marry well with the HBP analysis which predicts the secondary NH2⋯O
interactions (36%) and the COOH⋯NH2 primary hydrogen bond (3%). In fact, only three crystal structures were observed to have the COOH⋯NH2 hydrogen bond, two of which were the β and the δ pABA polymorphs. These overall statistics marry well with the HBP analysis which predicts the secondary NH2⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C interaction as having the highest propensity followed by the R22(8) carboxylic acid dimers. The propensity for the COOH⋯NH2 interaction to form is very low (0.04) confirming the rarity of this motif. Turning to the aromatic interactions, the CSD statistics and aromatic analyser shows that stacks related by both translation and inversion are common and that the geometries of such stacks in α and β pABA lead to strong aromatic interactions.
C interaction as having the highest propensity followed by the R22(8) carboxylic acid dimers. The propensity for the COOH⋯NH2 interaction to form is very low (0.04) confirming the rarity of this motif. Turning to the aromatic interactions, the CSD statistics and aromatic analyser shows that stacks related by both translation and inversion are common and that the geometries of such stacks in α and β pABA lead to strong aromatic interactions.
Finally, an analysis of HB and aromatic stacking motifs in the CSP landscape for pABA generated in previous work (structures within 10 kJ mol−1 of the global minimum) reveals that, both the COOH⋯NH2 and the inverted aromatic stacks as found in the β-pABA forms are rare.13
p-Aminobenzoic acid derivatives
Beyond the overall statistics (Table 1) for compounds with amino and a carboxylic acid groups we also explored the specific motifs found in crystal structures of p-aminobenzoic acid derivatives. The CSD search returned 13 hits: the four known polymorphs of pABA plus nine derivatives. A search of the same substructure in Sigma Aldrich returned a number of pABA derivatives which were not available in the CSD. Nine of those (chosen based on affordability) were purchased, single crystal structures determined and their solubilities measured in water (see Methods and ESI† section 2). Overall, this combined search and experimentation yielded 18 structures of pABA derivatives. Table 2 provides a summary of the crystallographic data including Z′ values, space groups and the major motifs. Here the relative rarity of the β motifs is again evident. Of the of 18 derivatives, 12 show carboxylic acid R22(8) dimers together with infinite stacking of the aromatic rings via translation. This reflects our previous conclusions for pABA and other para substitute aromatic acids, of the importance of infinite (one dimensional) aromatic stacking in controlling the kinetics of nucleation and growth since the zero-dimensional carboxylic acid dimers cannot, alone, enable extension of the crystal structure.12 Two other derivatives (2-Me and 3-Me pABA) are also based on carboxylic acid R22(8) dimers but their continuous interactions which drive growth comprise a more complex mixture of stacks and CH⋯aromatic contacts. A further three derivatives (2-OMe, 2-OMe-5-Cl, 2-OEt-5-Cl) have either a methoxide or an ethoxide substituent on carbon 2 which results in the carboxylic acid geometry being anti rather than syn so as to form an intramolecular COOH⋯OMe/OEt hydrogen bond. The dominant interactions in these structures are the aromatic stacks, which are all strong and continuous, adopting different symmetries. Only one of the pABA derivatives (4-amino-3-hydroxyl-benzoic acid, 3-OH-pABA) was found to have a COOH⋯NH2 interaction similar to that found in the β form. This acid–amine interaction, however, does not assemble into the β HB tetramer (Fig. 1a). Instead, through involvement of the hydroxyl group, the structure displays a different kind of infinite hydrogen bonding arrangement as seen in Fig. 2.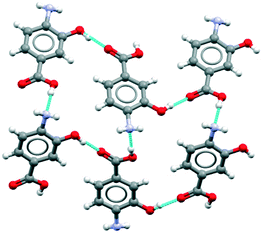 | ||
| Fig. 2 Hydrogen bonding observed in the crystal structure of 4-amino-3-hydroxyl-benzoicacid (3-OH-pABA). | ||
Thus, as with compounds containing both an amino (NH2) and carboxylic (COOH) acid functional groups, this family of substituted pABA structures confirm that the β pABA motifs are essentially unique. Because earlier work reported that β could only be reproducibly obtained from aqueous solution at very specific, low, supersaturations we also crystallised pF-pABA, 2F-pABA, 2Cl-pABA and 3Cl-pABA at a range of supersaturations (see Methods) and temperatures (10 °C and 25 °C) to check the outcome. In all cases, the forms obtained corresponded to those crystallised by slow evaporation from acetone/methanol and thus were analogous to the α-pABA structure. There was thus no evidence at either temperature or at low supersaturations, of a β-like structure.
In summary, the acid–amine interaction, hydrogen bonded tetramer and inverted stacking motifs found in the β-pABA structure are rare, both within the group of substituted p-aminobenzoic acids and within the CSD as a whole. This conclusion leads us, in the next section, to speculate on possible specific assembly pathways that may underpin the appearance of the β structure, particularly from aqueous solutions.
Potential molecular self-assembly pathways leading to the various pABA motifs
In an attempt to understand the difficulty of crystallisation of β pABA from solution, we hypothesise and discuss here a number of possible self-assembly pathways (Fig. 3).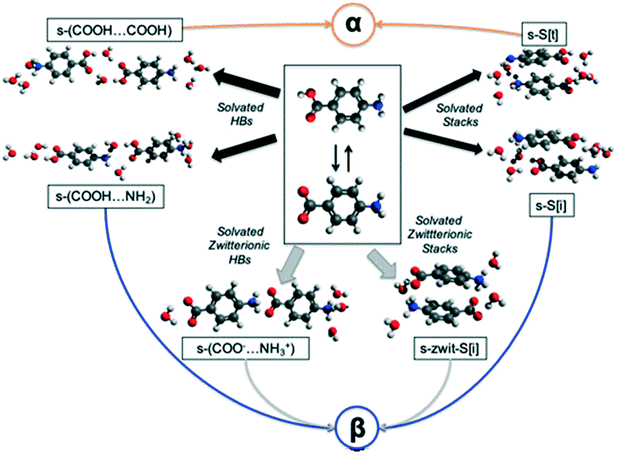 | ||
| Fig. 3 Plausible pathways for the solution assembly of the α and β motifs in pABA. Blue, orange, black and grey indicate β, α, hydrated and zwitterionic pathways respectively. | ||
First, in solution, the neutral pABA molecule is in equilibrium with its zwitterionic form (Fig. 3 central box) which may assemble via coulombic (COO−⋯NH3+) interactions followed by desolvation leading to the β form. Clearly, like charges would preclude such a route to the HB acid dimer. Such assembly may occur via direct head to tail interactions yielding s-(COO−⋯NH3+) species two of which would make the HB tetramer and/or through aromatic stacking forming s-zwit-S[i] species, where s refers to solvation and S to stacks. Once these species form, conversion to the β pABA motifs only requires direct proton transfer. This is referred to as the zwitterionic pathway.
Second, we explore the possibility that some solvent mediated molecular assemblies may be relatively stable as intermediate states. Since both α and β forms can be obtained from water (albeit at different supersaturations) the possibility that water plays a key role in creating a transient, hydrated, intermediate seems worth exploring. This possibility has been discussed previously18 and Fig. 3 shows two pathways from hydrated intermediates to either the β or the α polymorph. These two different routes involve the formation of stable solvated aromatic stacks (related by translation for α and inversion for β) and the formation of solvated carboxylic acid dimers for the α form and solvated acid⋯amine dimers for the β form. Such an assembly would then transform to either the α or the β structure by simple dehydration or concerted dehydration and insertion of amine groups or acid groups.
To explore the reality of these two pathways, we used a combination of CSD searches for appropriate zwitterionic and hydrated motifs, crystallisation conditions aimed at exploiting both hypothetical zwitterionic and hydrate routes and CSP calculations searching for potential hydrated structures.
The zwitterionic pathway
These data show that the NH3+⋯COO− dimer, a potential primary building block for the β tetramer, is present in all of the zwitterionic structures. However, analysis of the aromatic stacking also shows that the zwitterionic forms, like the uncharged species, prefer to form infinite stacks via translation (as found in α-pABA) rather than the centrosymmetric stacks typical of the β form. Most interestingly perhaps, the tetramer is not present in hydrates because of direct hydration of this zwitterionic motif.
Fig. 4 illustrates examples of these effects as seen in the mABA hydrate, showing the HB and stacking motifs. Thus in Fig. 4a the hypothesized zwitterionic tetramer of Fig. 3 is indeed evident but in combination with the translated stacks of Fig. 4b. We note from Table 3 that there are plenty of examples of zwitterionic oABA and mABA structures. In fact, these compounds are known to be able to crystallise in both the zwitterionic and uncharged forms (being rare examples of zwitterionic polymorphs). The only pABA derivative being zwitterionic, however, has an extra amino group in the meta position, thus, it can also be described as a mABA derivative.
Notwithstanding the small number of observations, we may conclude that this analysis fails to give any clear support to the zwitterionic pathway or to reveal why water may play a key role in the appearance of β.
| NH3+C6H6COO− ⇄ NH2C6H6COOH | (1) |
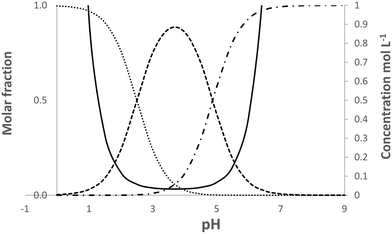 | ||
| Fig. 5 Calculated speciation and solubility at 25 °C for pABA in water in the pH range 0 to 9. Solid line solubility, …protonated species, -.-.-.deprotonated species, ------neutral species. | ||
Despite this situation in which no direct test of the mechanism is possible we do note two related features. Firstly, van de Graaf et al.32 not only reported Kz for pABA in pure aqueous solution but also in ethanol/water mixtures (50 and 75% ethanol). The percentage of zwitterions was estimated as 17% in pure water, falling to 0.27 and 0.015% with increasing alcohol content. Such decreasing percentages of zwitterion with increasing alcohol content does appear to be consistent with a zwitterion route since the β form is never crystallised from ethanol, irrespective of supersaturation.17 Further to this we note that, in aqueous solutions of mABA and oABA the proportion of zwitterions is significantly higher than in pABA with 73 and 80% respectively of neutral molecules being in the zwitterionic state.34,35 As mentioned above, both of these compounds crystallise in zwitterionic forms (Table 3, AMBNZA02, AMBACO07).
Our overall conclusions with regards the role of zwitterions are thus mixed. On the one hand, consideration of the CSD indicates little evidence for the zwitterionic tetramer in the solid forms of aminobenzoic acids and that when it is present it is not combined with inversion stacking. At the same time, the combination of speciation and solubility conspire to make a direct experimental test of this mechanism impossible. However, the appearance of zwitterionic structures and the difficulty in crystallising the β form of pABA do appear to show tentative links to the proportion of zwitterions in solution.
The hydrated pathway
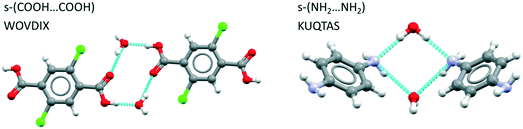
Examining first the hydrogen bond motifs we see that for hydrates of benzoic acid derivatives, the acid–acid dimer interaction is common, being found completely unsolvated in 18% of structures, solvated through one molecule of water only in 9% and solvated through two water molecules in 14%. The latter yields the desired tetramer, an example of which is displayed in Fig. 6(left) for WOVDIX. For aniline derivatives, the unsolvated amine–amine interaction is found in only 2% of structures (i.e. it is considerably less common than the acid dimer) while the fully hydrated tetramer is found in 8% as illustrated in Fig. 6 (right) for KUQTAS (p-phenylenediamine dihydrate). For hydrates of compounds with a carboxylic acid and an amine group (amine-X-acid), we found that the most common interaction is the unsolvated acid⋯amine dimer (13%), followed by the unsolvated acid⋯acid dimer (7%) and the solvated acid⋯acid tetramer (3%) similar to Fig. 6 (left).
As an adjunct to identifying the hydrated H-bonding motifs we further analysed the benzoic acid and aniline hydrate search results for aromatic stacks. 60–68% of these structures had aromatic stacking related by either translation or inversion. Remarkably, the aromatic stacking related by inversion comprised over 50% of the data in both groups. This is an important observation since stacks related by inversion are rare in unsolvated crystals of aminobenzoic acids as seen in Tables 2 and 3.
The overall conclusion from these CSD searches is that for hydrated structures aromatic interactions, both the inverted and translated stacks, are common whereas for the hydrogen bonds, the α pABA acid dimers are vastly more common than the acid–amine interactions. This hints at the stability of hydrated inverted stacks making them plausible precursors of the β-form of pABA as per the scheme of Fig. 3.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 pABA
2 pABA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water hydrates (see ESI† section 4 for structural landscapes). Analysis of motifs was done using the CSD motif analyser and searches were performed for both the characteristic α and β pABA motifs and water–pABA interactions. The results of these are summarised in Table 5. For the pABA motifs, the R22(8) acid dimer typical of α pABA is considerably more common (68 and 31% in 1
water hydrates (see ESI† section 4 for structural landscapes). Analysis of motifs was done using the CSD motif analyser and searches were performed for both the characteristic α and β pABA motifs and water–pABA interactions. The results of these are summarised in Table 5. For the pABA motifs, the R22(8) acid dimer typical of α pABA is considerably more common (68 and 31% in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 hydrate landscapes respectively) than the COOH⋯NH2 motif typical of β pABA (9 and 1% for the 1
2 hydrate landscapes respectively) than the COOH⋯NH2 motif typical of β pABA (9 and 1% for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 respectively). The α pABA aromatic stacking is also more common than the β pABA stacking (31 and 16% for 1
2 respectively). The α pABA aromatic stacking is also more common than the β pABA stacking (31 and 16% for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 versus 2 and 3%).
2 versus 2 and 3%).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 water
2 water![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pABA. HB motifs are always given as donor⋯acceptor
pABA. HB motifs are always given as donor⋯acceptor
| CSP structures | |||
|---|---|---|---|
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 pABA 1 pABA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water water |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 pABA 2 pABA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water water |
||
| Lowest Elatt (kJ mol−1) | −177.8 | −233.8 | |
| N structures within 20 kJ mol−1 from global minimum | 299 | 205 | |
| Alpha motifs | COOH⋯COOH dimer | 68% | 31% |
| Alpha stack | 31% | 16% | |
| Beta motifs | COOH⋯NH2 dimer | 9% | 1% |
| Inverted stack | 2% | 3% | |
| Alpha and beta | NH2⋯COOH (O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ) ) |
22% | 1% |
| Other hydrated interactions | COOH⋯w | 30% | 71% |
| NH2⋯w | 92% | 93% | |
| w⋯NH2 | 74% | 89% | |
w⋯COOH(O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ) ) |
63% | 96% | |
Overall, the results show that both the aromatic stacking with translation symmetry and the unsolvated acid–acid dimer are present as motifs in the majority of the most stable predictions. These motifs are characteristic of the α form. The water mostly hydrates the amino groups in the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 hydrates by forming amino–amino hydrated tetramers and in the 1
1 hydrates by forming amino–amino hydrated tetramers and in the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 hydrates by forming more complex water ring motifs (Fig. 7).
2 hydrates by forming more complex water ring motifs (Fig. 7).
Analysis of the water⋯pABA interactions show that one of the most abundant of those is the NH2(donor)⋯water(acceptor) interaction in all 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 solvates. This is perhaps unsurprising since in all pABA polymorphs there is always one –NH group which remains unable to hydrogen bond. Interestingly, the proportion of acid (donor)⋯water (acceptor) interactions decreases dramatically from 71% to 30% in going from the 1
2 solvates. This is perhaps unsurprising since in all pABA polymorphs there is always one –NH group which remains unable to hydrogen bond. Interestingly, the proportion of acid (donor)⋯water (acceptor) interactions decreases dramatically from 71% to 30% in going from the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 to 1
2 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 structures.
1 structures.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 pABA
2 pABA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water hydrates, it was possible to calculate the free energy of hydrate formation for pABA using the solvation model recently developed by Cruz-Cabeza et al.36 The model requires the computation of lattice energies using DFT-d, together with estimates of the entropy penalty of hydration using the enthalpy of fusion of ice. For the latter, sophisticated DFT-d methods37,38 were used. Table 6 summarises the free energy results, showing that formation of these hydrates will not occur spontaneously, the calculated ΔG being positive.
water hydrates, it was possible to calculate the free energy of hydrate formation for pABA using the solvation model recently developed by Cruz-Cabeza et al.36 The model requires the computation of lattice energies using DFT-d, together with estimates of the entropy penalty of hydration using the enthalpy of fusion of ice. For the latter, sophisticated DFT-d methods37,38 were used. Table 6 summarises the free energy results, showing that formation of these hydrates will not occur spontaneously, the calculated ΔG being positive.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 pABA
2 pABA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water
water
| ΔG hydrate formation (kJ mol−1 of hydrate) | |
|---|---|
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 pABA 1 pABA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water water |
7.3 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 pABA 2 pABA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water water |
15.1 |
Interestingly, application of the solvate prediction tool to further explore the likelihood of hydrate formation (based on the CSD) confirms this result, predicting that the formation of a pABA hydrate is highly unlikely with a hydrate prediction probability score of 0.094.
Overall, we are left to conclude that the existence of a pABA hydrate is very unlikely. If this is the case then, taken together with the discussion concerning zwitterions, it seems that neither scheme of Fig. 3 is amenable to experimental verification. Notwithstanding this, the next section considers the more general potential for the experimental isolation of pABA hydrates and solvates in order to see what further insights might be obtained.
The experimental search for solvated forms of p-aminocarboxylic acids
In the case of our experimental search for hydrates of pABA or one of its derivatives we describe here how the CSD was used to inform our choice of target solutes and solvents.The fluorination trick
During the many CSD searches performed over the course of this work, we made an intriguing observation that fluorinated analogues of carboxylic acids crystallise as hydrates more often than non-fluorinated analogues. Thus, Table 7 summarises such data for acetic, succinic and terephthalic acid analogues. Given this finding, we decided to use 4-amino-2,3,5,6-tetrafluorobenzoic acid (pF-pABA) alongside pABA in an experimental quest for hydrates.| Analogues | R | Anhydrous | Hydrates | Hydrate stoichiometry |
|---|---|---|---|---|
| Acetic acid analogues | CH3 | ACETAC | — | — |
| CH2F | FACETC | — | — | |
| CH2Cl | CLACET | — | — | |
| CH2Br | BRMACA | — | — | |
| CHCl2 | YIQGAH | — | — | |
| CHFBr | BARBAX | — | — | |
| CFClBr | OHIJAR | — | — | |
| CBr3 | WADFIR | — | — | |
| CCl3 | TCACAD | — | — | |
| CFCl2 | NAGVUM | RABBUN | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5 0.5 |
|
| CF2Cl | NAGWAT | RABCAU, RABCEY | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1 1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 4 |
|
| CF3 | TFACET | BULMAW10 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
|
| Succinic acid analogues | CH2–CH2 | SUCACB | — | — |
| CHCl–CH2 | CLSUCC | — | — | |
| CHBr–CH2 | WANEE | — | — | |
| CHBr–CHBr (trans) | SAZSES | — | — | |
| CHBr–CHBr (syn) | WOCHIF | — | — | |
| CHF–CHF (syn) | VEVSIZ | — | — | |
| CHF–CHF (trans) | — | VEVSUL | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
|
| CF2–CF2 | — | ZESZUS01 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
|
| Terephthalic acid analogues | H, H, H, H | TEPHTH | — | — |
| Cl, Cl, Cl, Cl | CIPZIL | — | — | |
| H, Br, Br, H | — | POFROS | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
|
| F, F, F, F | BITCEM | YABHOA | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
Choice of solvent
In an attempt to make the best choice of crystallisation solvents for isolating hydrates, we turned again to our CSD search of carboxylic acids (Table 4) crystallising either as hydrates or anhydrous forms. Analysis of structures for which information on the crystallisation solvent was available (Table 8) showed that acetone![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water (35%), ethanol
water (35%), ethanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water (31%) and methanol
water (31%) and methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water (21%) were most likely to result in hydrates. However, the data set is rather small (especially for the acetone
water (21%) were most likely to result in hydrates. However, the data set is rather small (especially for the acetone![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water data) and hence the results are of limited statistical significance. We notice that the probability of crystallising a hydrate is higher in the mixed solvents than in water, although this is most likely due to the organic component being added to increase the solubility of the target material. Accordingly we decided to use ethanol
water data) and hence the results are of limited statistical significance. We notice that the probability of crystallising a hydrate is higher in the mixed solvents than in water, although this is most likely due to the organic component being added to increase the solubility of the target material. Accordingly we decided to use ethanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water, methanol
water, methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water and acetone
water and acetone![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water as our solvent mixtures, together with dioxane
water as our solvent mixtures, together with dioxane![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water since previous literature reports suggest an as yet uncharacterised pABA form obtained from dioxane39 additionally high-pressure crystallisations were performed for pABA in water.13
water since previous literature reports suggest an as yet uncharacterised pABA form obtained from dioxane39 additionally high-pressure crystallisations were performed for pABA in water.13
| Crystallisation solvent | Crystallisation outcome | Hydrate crystallisation probability | ||
|---|---|---|---|---|
| Anhydrous acids | Hydrated acids | Total | Hydrates/total (%) | |
| Methanol | 211 | 24 | 235 | 10 |
| Ethanol | 230 | 18 | 248 | 7 |
| Water | 108 | 14 | 122 | 12 |
| Acetone | 120 | 2 | 122 | 2 |
| Ethyl acetate | 105 | 9 | 114 | 2 |
| Ethanol/water | 77 | 35 | 112 | 31 |
| Hexane/ethyl acetate | 63 | 2 | 65 | 3 |
| Methanol/water | 43 | 12 | 55 | 22 |
| Chloroform | 48 | 2 | 50 | 4 |
| Diethyl ether | 40 | 2 | 42 | 5 |
| Chloroform/methanol | 19 | 2 | 21 | 10 |
| Toluene | 16 | 3 | 19 | 16 |
| Methanol/dichloromethane | 14 | 3 | 17 | 18 |
| Acetone/water | 11 | 6 | 17 | 35 |
Crystallisation outcomes
As predicted, none of these experiments, including the high pressure, yielded a hydrate. However, four new solvates were obtained: a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 pABA
1 pABA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acetone, a 1.5
acetone, a 1.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 pABA
1 pABA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) dioxane, 1
dioxane, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 pF-pABA
2 pF-pABA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acetone and a 1
acetone and a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 pF-pABA
2 pF-pABA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) dioxane.
dioxane.
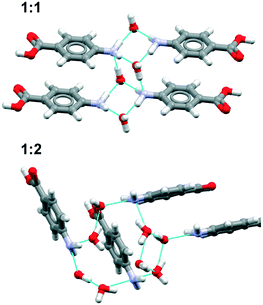
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) (acetone) interaction whereas in pF-pABA, all pF-pABA molecules are solvated with two NH⋯O
(acetone) interaction whereas in pF-pABA, all pF-pABA molecules are solvated with two NH⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) (acetone) interactions per molecule. These acetone solvates show similar interactions to a pABA
(acetone) interactions per molecule. These acetone solvates show similar interactions to a pABA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) nitromethane solvate reported previously (XECTOR).40
nitromethane solvate reported previously (XECTOR).40
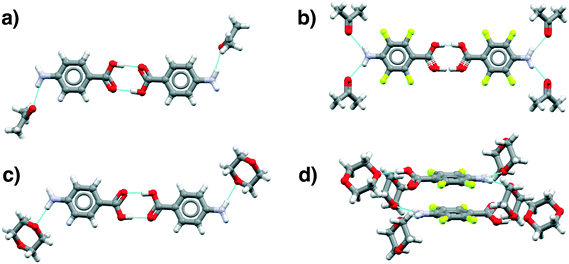 | ||
| Fig. 8 Main motifs found in the pABA (a and c) and pF-pABA (b and d) solvates with acetone (a and b) and dioxane (c and d). See ESI† section 1 for CSD deposition numbers of these structures. | ||
The dioxane solvates (Fig. 8c and d) show significant differences. pABA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) dioxane is similar to the pABA
dioxane is similar to the pABA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acetone and pABA
acetone and pABA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) nitromethane solvates with the carboxylic acid dimers and the dioxane solvating the amino group through one NH⋯O(dioxane) interaction. However, in these dioxane solvates, all pABA molecules are solvated unlike the acetonates where it is only half of them. For pF-pABA
nitromethane solvates with the carboxylic acid dimers and the dioxane solvating the amino group through one NH⋯O(dioxane) interaction. However, in these dioxane solvates, all pABA molecules are solvated unlike the acetonates where it is only half of them. For pF-pABA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) dioxane 1
dioxane 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 solvate, the higher proportion of solvent to pF-pABA molecules results in a full solvation of pF-pABA not only around the amino group but also the carboxylic acid group. Most intriguingly, the only remaining interaction between pF-pABA molecules in this structure is a stacked dimer in which the molecules are related by a centre of inversion (Fig. 8d).
2 solvate, the higher proportion of solvent to pF-pABA molecules results in a full solvation of pF-pABA not only around the amino group but also the carboxylic acid group. Most intriguingly, the only remaining interaction between pF-pABA molecules in this structure is a stacked dimer in which the molecules are related by a centre of inversion (Fig. 8d).
Thus, our experiments confirm the predictions that a hydrate form of pABA is highly unlikely. Further, they show that when pABA is solvated that the acid dimer remains intact with solvation favoured at the amino moiety. Only in pF-pABA is the solvent able to break the dimer with consequent formation of stacks related by inversion.
Discussion and conclusions
Extensive use of the CSD together with CSP and significant numbers of targeted crystallisation experiments have failed to produce evidence for any form of solution phase molecular assembly, involving solute and/or solvent, that might be considered as a transition state in the nucleation of β pABA. The study has confirmed that the motifs found in β pABA are rare in the CSD, in the new structures of pABA derivatives reported in this paper and in CSP of both pABA reported previously and pABA hydrates reported here. In fact, to create a crystal packing free from the acid dimer is indeed extremely difficult – 5 out of 6 of our new solvated structures are dimer based. However, the β motif is found in zwitterionic mABA and oABA structures and there is some tentative suggestion that a link may exist between the proportion of zwitterions in solution and the appearance of β but this cannot be confirmed experimentally. In terms of a solvated pathway, stable hydrates were not predicted and, indeed, we were unable to isolate a hydrated form. The dioxane solvate is alone in reflecting any element of the β structure, having no acid dimers and with phenyl rings related by inversion. This marries well with the fact that inverted stacks are more commonly observed in hydrates of benzoic acids than in anhydrous forms. This evidence supports the view that aromatic stacking is the first self-assembled interaction leading to the creation of molecular clusters and eventually crystal nuclei.12 The subsequent formation of the acid dimers may then be solvent dependant, related to the extent of pre-dimersation in solution. Finally, desolvation of the amino group takes place. Of course this aromatic stacking may lead to molecules and hence dimers either related by inversion or by translation. Dimers related by translation are in the correct geometry to further assemble through the acid–acid interaction resulting in α pABA. Dimers related by inversion would either need to re-arrange before forming the α structure (pF-pABA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) dioxane desolvates directly to the structure of pF-α pABA suggesting that this may be facile) or they could develop directly into the β polymorph. However, β appears only under very specific sets of conditions of low supersaturations and in aqueous solution so we may assume that it is here that dimers related by inversion can successfully compete. Of course, under most conditions of solvent and supersaturation a cluster comprising stacked acid dimers related by translation wins out (giving the α polymorph), growing much faster than a cluster of molecules related by inversion, which will need to grow via COOH⋯NH2 chains. This conclusion is supported by our measurement of the relative rates of growth of α and β crystals, which show that α wins out by about 2 orders of magnitude.18 A corollary to this is our previous demonstration that only by disrupting the translated stacks with an additive it is possible to inhibit their growth and thus prevent nucleation of the α structure. This enables β to appear consistently.41 Of course this line of argument parallels the assumptions made in the significant work of Weissbuch et al.42 that ‘…our approach rests on a working hypothesis that in supersaturated solutions the molecules assemble to form coexisting clusters adopting a variety of shapes and arrangements, some of which resemble the structure of the macroscopic crystals into which they eventually develop.’. In the case of pABA the outcome of the development of these clusters leads to the appearance of the α polymorph with the exception of its crystallisation from water where β can appear at low supersaturations. We may now confirm that the role of water here is not to provide a solution mediated pathway to β. Instead, it is the unusually high value of the pABA/water interfacial tension (4.83 mJ m−2 compared to 1–2 8 mJ m−2 in organic solvents), that creates a nucleation and growth dead zone, at low supersaturations, where α clusters cannot grow thus giving time for β to appear.18,43
dioxane desolvates directly to the structure of pF-α pABA suggesting that this may be facile) or they could develop directly into the β polymorph. However, β appears only under very specific sets of conditions of low supersaturations and in aqueous solution so we may assume that it is here that dimers related by inversion can successfully compete. Of course, under most conditions of solvent and supersaturation a cluster comprising stacked acid dimers related by translation wins out (giving the α polymorph), growing much faster than a cluster of molecules related by inversion, which will need to grow via COOH⋯NH2 chains. This conclusion is supported by our measurement of the relative rates of growth of α and β crystals, which show that α wins out by about 2 orders of magnitude.18 A corollary to this is our previous demonstration that only by disrupting the translated stacks with an additive it is possible to inhibit their growth and thus prevent nucleation of the α structure. This enables β to appear consistently.41 Of course this line of argument parallels the assumptions made in the significant work of Weissbuch et al.42 that ‘…our approach rests on a working hypothesis that in supersaturated solutions the molecules assemble to form coexisting clusters adopting a variety of shapes and arrangements, some of which resemble the structure of the macroscopic crystals into which they eventually develop.’. In the case of pABA the outcome of the development of these clusters leads to the appearance of the α polymorph with the exception of its crystallisation from water where β can appear at low supersaturations. We may now confirm that the role of water here is not to provide a solution mediated pathway to β. Instead, it is the unusually high value of the pABA/water interfacial tension (4.83 mJ m−2 compared to 1–2 8 mJ m−2 in organic solvents), that creates a nucleation and growth dead zone, at low supersaturations, where α clusters cannot grow thus giving time for β to appear.18,43
Conflicts of interest
There are no conflicts to declare.Acknowledgements
IJS acknowledges funding for this research via: Engineering and Physical Sciences Research Council grant No. EP/J014958/1, EP/J003840/1, EP/P022561/1 and EP/P020194. SEW thanks CCDC for financial support. For the DFT-d calculations, we are grateful for computational support from the UK Materials and Molecular Modelling Hub, which is partially funded by EPSRC (EP/P020194), for which access was obtained via the UKCP consortium and funded by EPSRC grant EP/P022561/1. For global search and refinement calculations, we would like to acknowledge the Imperial College Research Computing Service, DOI: 10.14469/hpc/2232. We gratefully acknowledge the use of the DMACRYS software, from the group of Professor Sally Price at University College London and discussions with A. Y. Tagwai, University of Manchester.References
- R. J. Davey, S. M. L. Schroeder and J. H. ter Horst, Angew. Chem., Int. Ed., 2013, 52, 2166–2179 CrossRef CAS PubMed.
- R. J. Davey, K. R. Back and R. A. Sullivan, Faraday Discuss., 2015, 179, 9–26 RSC.
- P. G. Vekilov, Cryst. Growth Des., 2010, 10, 5007–5019 CrossRef CAS PubMed.
- B. Burgi, J. D. Dunitz and E. Shefter, J. Am. Chem. Soc., 1973, 95, 5065–5067 CrossRef.
- J. W. Steed, CrystEngComm, 2003, 5, 169–179 RSC.
- R. Banerjee, P. M. Bhatt, M. T. Kirchner and G. R. Desiraju, Angew. Chem., Int. Ed., 2005, 44, 2515–2520 CrossRef CAS PubMed.
- D. Das, R. Banerjee, A. R. Mondal, J. A. K. Howard, R. Boesec and G. R. Desiraju, Chem. Commun., 2006, 555–557 RSC.
- K. M. Steed and J. W. Steed, Chem. Rev., 2015, 115, 2895–2933 CrossRef CAS PubMed.
- A. Nangia and G. R. Desiraju, Chem. Commun., 1999, 605–606 RSC.
- R. Banerjee, G. R. Desiraju, R. Mondal, A. S. Batsanovb, C. K. Broder and J. A. K. Howard, Helv. Chim. Acta, 2003, 83, 1339–1351 CrossRef.
- R. J. Davey, M. Brychczynska, G. Sadiq, G. Dent and R. G. Pritchard, CrystEngComm, 2013, 15, 856–859 RSC.
- A. J. Cruz-Cabeza, R. J. Davey, S. Salim Sachithananthan, R. Smith, S. K. Tang, T. Vetter and Y. Xiao, Chem. Commun., 2017, 53, 7905–7908 RSC.
- A. J. Cruz-Cabeza, R. J. Davey, I. D. H. Oswald, M. R. Ward and I. J. Sugden, CrystEngComm, 2019, 21, 2034–2042 RSC.
- S. Gracin and A. Fischer, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2005, 61, o1242–o1244 CrossRef CAS.
- M. Svard, F. L. Nordstrom, E. Hoffmann, B. Aziza and Å. C. Rasmuson, CrystEngComm, 2013, 15, 5020–5031 RSC.
- S. Gracin and Å. C. Rasmuson, Cryst. Growth Des., 2004, 4, 1013–1023 CrossRef CAS.
- J. F. B. Black, R. J. Davey, R. J. Gowers and A. Yeoh, CrystEngComm, 2015, 17, 5139–5142 RSC.
- J. F. B. Black, P. T. Cardew, A. J. Cruz-Cabeza, R. J. Davey, S. E. Gilks and R. A. Sullivan, CrystEngComm, 2018, 20, 768–776 RSC.
- I. J. Bruno, J. C. Cole, P. R. Edgington, M. Kessler, C. F. Macrae, P. McCabe, J. Pearson and R. Taylor, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 389–397 CrossRef PubMed.
- C. F. Macrae, I. Sovago, S. J. Cottrell, P. T. A. Galek, P. McCabe, E. Pidcock, M. Platings, G. P. Shields, J. S. Stevens, M. Towler and P. A. Wood, J. Appl. Crystallogr., 2020, 53, 226–235 CrossRef CAS PubMed.
- P. T. A. Galek, F. H. Allen, L. Fábián and N. Feeder, CrystEngComm, 2009, 11, 2634–2639 RSC.
- P. T. A. Galek, J. A. Chisholm, E. Pidcock and P. A. Wood, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2014, 70, 91–105 CrossRef CAS PubMed.
- This software forms part of CCDC's Crystal Form Consortium. Manuscript in preparation.
- M. Habgood, I. J. Sugden, A. V. Kazantsev, C. S. Adjiman and C. C. Pantelides, J. Chem. Theory Comput., 2015, 11, 1957–1969 CrossRef CAS PubMed.
- I. Sugden, C. S. Adjiman and C. C. Pantelides, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 864–874 CrossRef CAS PubMed.
- D. E. Williams and S. R. Cox, Acta Crystallogr., Sect. B: Struct. Sci., 1984, 40, 404–417 CrossRef.
- I. J. Sugden, C. S. Adjiman and C. C. Pantelides, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2019, 75, 423–433 CrossRef CAS.
- T. Beyer and S. L. Price, J. Phys. Chem. B, 2000, 104, 2647–2655 CrossRef CAS.
- S. R. Cox, L.-Y. Hsu and D. E. Williams, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1981, 37, 293–301 CrossRef.
- A. V. Kazantsev, P. G. Karamertzanis, C. S. Adjiman and C. C. Pantelides, J. Chem. Theory Comput., 2011, 7, 1998–2016 CrossRef CAS PubMed.
- R. A. Robinson and A. I. Biggs, Aust. J. Chem., 1957, 10, 128–134 CrossRef CAS.
- B. van de Graaf, A. J. Hoefnagel and B. M. Wepster, J. Org. Chem., 1981, 46, 653–657 CrossRef CAS.
- H.-C. Tseng, C.-Y. Lee, W.-L. Weng and I.-M. Shiah, Fluid Phase Equilib., 2009, 285, 90–95 CrossRef CAS.
- E. P. Sergeant, Aust. J. Chem., 1969, 22, 1189–1192 CrossRef.
- L. Zapała, J. Kalembkiewicz and E. Sitarz-palcza, Biophys. Chem., 2009, 140, 91–98 CrossRef PubMed.
- A. J. Cruz-Cabeza, S. E. Wright and A. Bacchi, Chem. Commun., 2020, 5127–5130 RSC.
- J. Moellmann and S. Grimme, J. Phys. Chem. C, 2014, 118, 7615–7621 CrossRef CAS.
- J. G. Brandenburg and S. Grimme, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 502–513 CrossRef CAS PubMed.
- M. Kuhnert-Brandstatter and H. Grimm, Microchim. Acta, 1969, 1208–1209 CrossRef.
- I. Rosbottom, C. Y. Ma, T. D. Turner, R. A. O'Connell, J. Loughrey, G. Sadiq, R. J. Davey and K. J. Roberts, Cryst. Growth Des., 2017, 17, 4151–4161 CrossRef CAS.
- J. F. B. Black, A. J. Cruz-Cabeza, R. J. Davey, R. D. Willacy and A. Yeoh, Cryst. Growth Des., 2018, 18, 7518–7525 CrossRef CAS.
- I. Weissbuch, M. Lahav and L. Leiserowitz, Cryst. Growth Des., 2003, 3, 125–150 CrossRef CAS.
- R. A. Sullivan, R. J. Davey, G. Sadiq, G. Dent, K. R. Back, J. H. ter Horst, D. Toroz and R. B. Hammond, Cryst. Growth Des., 2014, 14, 2689–2696 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2009891–2009903. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0ce00970a |
| This journal is © The Royal Society of Chemistry 2020 |