Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Storage time dependent photodissociation action spectroscopy of polycyclic aromatic hydrocarbon cations in the cryogenic electrostatic storage ring DESIREE
Mark H.
Stockett
 *,
Mikael
Björkhage
,
Henrik
Cederquist
,
Henning T.
Schmidt
and
Henning
Zettergren
*,
Mikael
Björkhage
,
Henrik
Cederquist
,
Henning T.
Schmidt
and
Henning
Zettergren
Stockholm University, Department of Physics, Stockholm, Sweden. E-mail: Mark.Stockett@fysik.su.se
First published on 21st November 2018
Abstract
The multi-photon photodissociation action spectrum of the coronene cation (C24H12+) has been measured in the cryogenic electrostatic storage ring DESIREE (Double ElectroStatic Ion Ring ExpEriment) as a function of storage time. These measurements reveal not only the intrinsic absorption profile of isolated coronene cations, but also the rate at which hot-band absorptions are quenched by radiative cooling. Just after injection, the action spectrum is severely reddened by hot-band absorptions. These hot bands fade with a time constant of 200 ms, which is consistent with radiative cooling via infrared emission from vibrational transitions. A comparison of the present results to those obtained in cryogenic ion trap experiments is discussed at length.
1 Introduction
The spectroscopy and photophysics of gas-phase Polycyclic Aromatic Hydrocarbon (PAH) ions such as coronene C12H24+ is motivated by their ubiquity in the Interstellar Medium (ISM).1 While it has become widely accepted that PAHs are responsible for the infrared emission observed throughout the ISM,1 other attributions of astronomical phenomena to PAHs remain unconfirmed or disputed. These include the ubiquitous Diffuse Interstellar Bands (DIBs),2 the blue luminescence seen from the Red Rectangle nebula,3 and the elevated abundance of H2 (purported to be catalytically formed by PAHs4–6) in photodissociation regions.7For direct comparison to astronomical observations, various experimental techniques (e.g. supersonic expansion,8 buffer gas cooling,9 and noble gas tagging10) have been employed to cool gas-phase PAH ions to internal temperatures similar to those predominant in the ISM i.e. <100 K. Despite its status at the prototypical PAH, only two previous action spectroscopy experiments have been reported for the coronene cation. The first, by Joblin and co-workers, recorded multi-photon photodissociation (MPD) action spectra of coronene ions inside a cryogenically cooled (35 K) Fourier Transform Ion Cyclotron Resonance (FTICR) mass spectrometer.11 More recently, Maier and coworkers reported the photodissociation action spectrum of C12H24+–He complexes at approximately 10 K.12 In the present experiments, which also employ MPD, isolated PAH ions relax at their intrinsic rates via infrared (IR) radiative cooling in the cryogenic (∼13 K), collision free environment of the Double ElectroStatic Ion Ring ExpEriment (DESIREE).13 The purpose of this contribution is to compare the results of these three very different implementations of cold ion action spectroscopy.
2 Experimental methods
Coronene powder (97%) was purchased from Sigma Aldrich. Hot coronene cations were produced using a Nielsen-type plasma ion source equipped with a temperature-controlled oven. The ions were accelerated to 15 keV and those with mass-to-charge ratio m/z = 300 were selected using a bending magnet. These ions were injected into the so-called “symmetric ring” (one of the two DESIREE storage rings13) and stored for up to one minute. The experiment is shown schematically in Fig. 1. Stored ions were excited at a 10 Hz repetition rate in one of the straight sections of the ring in a crossed-beam geometry using a tunable wavelength OPO laser system (EKSPLA). Neutral fragments (presumed to be H atoms) formed in this section are unaffected by the electrostatic steering fields and fly straight into a micro-channel plate (MCP) detector, labeled ‘Imaging Detector’ in Fig. 1. The detector signal is gated with a 1 μs width and a delay after the laser firing time corresponding to the flight time from the interaction region to the detector. This eliminates the counting of scattered laser light and strongly suppresses the counting of detector dark noise and background fragmentation events due to collisions between stored ions and residual gas in the ring. The excitation wavelength is stepped in between ion injections, creating a two-dimensional photodissociation action spectrum time series.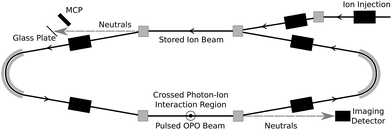 | ||
| Fig. 1 The DESIREE symmetric storage ring. Stored C12H12+ ions are irradiated in a crossed-beam geometry in the lower straight section. | ||
Photo-excited ions may in principle undergo delayed fragmentation up to several tens of milliseconds after irradiation, corresponding to several hundred revolutions around the storage ring (the revolution time is about 88 μs). Delayed fragmentation occurring in the same straight section as photo-excitation will be witnessed by the same MCP as the main prompt signal, while neutrals formed in the opposite straight section will fly to a different MCP equipped with a secondary electron emissive glass plate. In the present experiments, very little delayed fragmentation was observed, amounting to less than 1% of the prompt signal. Only the prompt signal is analyzed here.
Although the data presented here were recorded using injection cycles of up to 60 s, the actual beam storage lifetime (limited by collisions with residual background gas) is considerably longer.14,15 Measurements performed at the end of the cycle, when the beam was dumped into a Faraday cup, found a C24H12+ storage lifetime of about 400 s.
3 Results and discussion
3.1 Pulse energy dependence
The dependence of the photodissociation signal rate on the OPO laser pulse energy is shown in Fig. 2. The laser power was varied using neutral density filters. The photodissociation yield Γ is well represented by a power law Γ = E3. The dependence on the third power of the pulse energy E indicates that the absorption of three photons is required to induce the observed signal. There is no sign of saturation of the process at high pulse energies.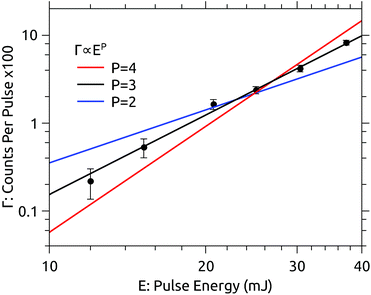 | ||
| Fig. 2 Dependence of the prompt dissociation signal rate Γ on the laser pulse energy E recorded at 450 nm. The yield follows a power law Γ ∝ E3. | ||
The lowest adiabatic dissociation energies of C24H12+ are about 5 eV for H-loss and 7 eV for C2H2-loss.16,17 The energy deposited by three 450 nm photons is 8.3 eV. Neutral fragments contributing to the measured prompt signal are formed within the first few μs after excitation. For larger molecules such as coronene, excitation energies considerably in excess of the dissociation energies are usually required to observe significant fragmentation on such timescales.18–20 Bearing in mind that the ions retain some internal energy prior to excitation, it seems most probable that H-loss is the dominant dissociation channel observed here. This is also the same channel observed by Joblin and coworkers.11
The pulse energy dependence in the present experiment is rather straightforward to interpret, which may be regarded as an advantage relative to ion trap experiments. In Joblin’s experiments, for example, the photodissociation yield is highly saturated, and is modeled with a Monte Carlo simulation which requires quantitative details of the photophysics of coronene as inputs. Complexities in modeling those experiments include the strongly varying spatial distribution of photon flux (due to the Gaussian laser beam profile) and the high shot-to-shot variation in the overlap between the laser beam and the ion cloud. The OPO laser system used in the present experiments has a relatively flat “top-hat” profile, and the stored ion beam fills the acceptance of the storage ring (at least after the first few ms) providing a more consistent target. Furthermore, only prompt dissociation occurring while the excited ions are still in the straight section of the storage ring (<5 μs after irradiation) is recorded here. This reduces the contribution of ions dissociating after the absorption of fewer than three photons, which would occur on much longer time scales (although for coronene such ions would probably not dissociate at all).
3.2 Action spectra – 1 s storage
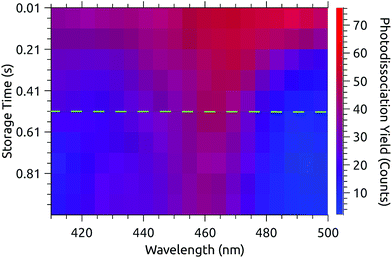
Fig. 3 shows a data set recorded with 1 s injection cycles presented as MPD action spectra for different laser firing times separated by the 100 ms repetition period of the laser. The first laser shot is 0.01 s after injection. These data are the sum of over 5500 cycles (nearly 300 per excitation wavelength). The number of counts at each wavelength–time point has been divided by the laser pulse energy (which was very nearly constant in this spectral range). The action spectrum at the earliest times (0.01 s, top of map) after injection is nearly flat, and over the course of the first second the spectrum collapses to a band centered at around 465 nm. The photodissociation signal at wavelengths longer than the band maximum, corresponding to hot-band absorptions, fades over the first few hundred milliseconds.The action spectrum appears to have converged to a steady state after 0.51 s (dashed line in Fig. 3). The average of the last five spectra in this series (i.e. those recorded after 0.51 s) is plotted as the solid line in the upper panel of Fig. 4. By subtracting this ‘cold spectrum’ from each action spectrum in the time series, one obtains the time-dependent contribution to the action spectrum of the vibrationally excited ions. The time-average of this hot-band contribution is shown as the dashed line in the upper panel of Fig. 4. This is perhaps not so interesting in itself, but the relative intensity of the hot-band contribution over time gives an indication of the timescale on which these vibrational excitations relax. Contributions from different excited vibrational states will of course relax with different rates, with this procedure giving a gross average. The normalized relative intensity of the hot-band contribution is shown in Fig. 5. These data are fit with a single exponential decay giving a cooling time constant of 0.205 ± 0.018 s. This is in line with expected values for cooling rates of PAHs by infrared emission.21,22
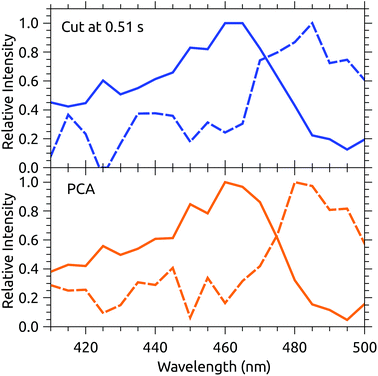 | ||
| Fig. 4 Upper panel: The solid line is the average of the action spectra recorded from 0.51–0.91 s. The dashed line is the average hot-band contribution found by subtracting the cold spectrum from the raw data. Lower panel: The dashed line is the first principal component (PC1) of the data from Fig. 3. The solid line is the cold spectrum found by subtracting PC1 from the raw data, with appropriate weighting (see text). | ||
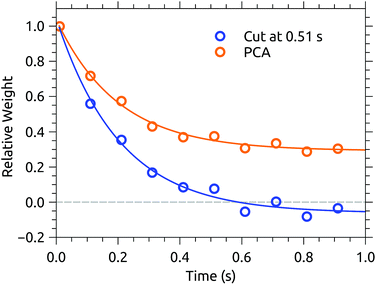 | ||
| Fig. 5 Time dependence of the relative intensity of the hot-band contribution to the action spectra from Fig. 3, and of the projection of the data on PC1. | ||
Cutting the action spectrum time series in half and declaring the second half cold may seem somewhat crude and arbitrary. Inspired by Støchkel and Andersen,23 a simple Principal Component Analysis (PCA) has also been carried out. PCA is a standard statistical procedure (here implemented using the PCA Python routine provided by the open-source scikit-learn library24) typically used to reduce high-dimensionality data sets by finding the orthogonal linear combinations of the variables which best account for the variability in the data. When applied to the present action spectrum time series, an m × n data matrix X consisting of the m time series (as row vectors) recorded at n different wavelengths, the procedure amounts to an eigenvalue decomposition of the covariance matrix XTX. The resulting vectors may be thought of as the eigenspectra which describe the variation in the action spectrum over time, with the eigenvalues indicating how much of the variation is captured by each PC. In the case of the data presented in Fig. 3, the vector with the largest eigenvalue, called the first principal component or PC1, explains over 75% of the variation, with the remaining components containing only statistical fluctuations. It is likely that a more granular data set would exhibit multiple significant PCs, reflective of the energy-dependence of the cooling rate. PC1 is shown in the lower panel of Fig. 4 (dashed line) and closely resembles the hot-band contribution obtained using the 0.51 s cut (upper panel, dashed line). The projection of the data onto PC1 gives its relative weight over time. As shown in Fig. 5, the relative weight of PC1 decays on the same time scale (0.200 ± 0.015 s) as the hot-band contribution. A cold spectrum is obtained by subtracting PC1 from each action spectrum in the time series (Fig. 3), weighted by its projection (Fig. 5), and taking an average. This is shown in the lower panel of Fig. 4 (solid line). Again, the cold spectrum obtained by arbitrarily cutting the data after 0.51 s is well reproduced by this method. The PCA approach has the advantage that one is not required to choose a fixed time cut a priori, and uses the entire data set to construct the cold spectrum, rather than just the data after the cut. While the results of the two methods are very similar in this case, the PCA approach could be valuable in cases where the cooling time is comparable to or longer than the measurement time.
3.3 Action spectra – 60 s storage
At DESIREE, very long storage and hence measurement times are available. Fig. 6 shows two slices of an action spectrum time series recorded over 60 seconds of storage time. Note that this measurement covers a narrower spectral region than those in Fig. 3.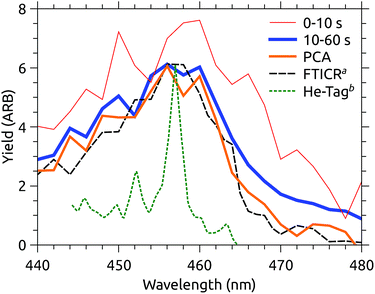 | ||
| Fig. 6 Action spectra recorded over different time intervals after injection into DESIREE, and extracted using PCA. aFTICR data from Joblin and coworkers.11bAction spectrum of He–C24H12+ complexes from Maier and coworkers.12 | ||
Also shown in Fig. 6 is the MPD action spectrum recorded by Joblin and coworkers (dashed black line).11 This spectrum closely resembles that recorded in the present experiments after the ions have relaxed for 10 s (blue line). Both spectra are presented with constant laser pulse energy, though the vertical scaling is arbitrary.
In Joblin’s experiments, C24H12+ ions were stored in the PIRENEA FTICR mass spectrometer cell cooled to 35 K and were cooled through collisions with He buffer gas. Evidently, the final vibrational distribution reached by the ions is similar in the two experiments, however, the photo-fragment yield in the PIRENEA experiment is somewhat lower above 465 nm. Caution should be exercised when interpreting small differences in action spectra recorded using such different techniques. A variety of technical considerations, e.g. differences in background subtraction, the number of photons absorbed, kinetic shifts, etc. could easily explain such a discrepancy. Temporarily suspending this skepticism, one may ask why it might be that the ions in PIRENEA appear colder than those in DESIREE, despite the fact that the nominal temperature inside DESIREE is significantly colder (13 K).
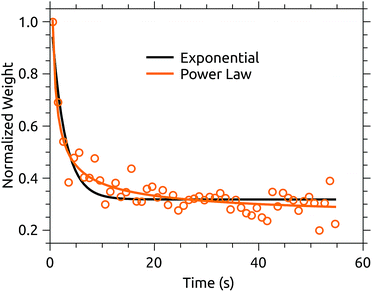
A plausible explanation is that buffer gas mediated cooling is simply more effective than spontaneous IR cooling. The former is limited by the coupling of translational motion in the trap to vibrational excitation.11 IR emission, on the other hand, slows dramatically as the degree of excitation of IR-active modes decreases.21 We can see a hint of this by examining the projection of the action spectrum time series on its first principal component, shown in Fig. 7. This cooling curve is not well represented by a single exponential decay, with a better fit obtained using a power law. Power law decays are a hallmark of isolated ensembles of particles with an initially broad energy distribution, such as molecular ions prepared with a plasma ion source like that used here.25–28Fig. 7 indicates that relaxation is not fully complete after the disappearance of obvious hot-band absorptions. If the power law fit to the PCA cooling curve in Fig. 7 is used to extract a cold spectrum, better agreement with the PIRENEA results is obtained as shown in Fig. 6. While the reader is again cautioned against over-interpreting small differences in action spectra, this result suggests that a principal component analysis can be used to analyze variations in action spectra occurring over timescales which are long compared to the measurement time. This is a significant advantage over arbitrarily cutting of the action spectrum time series at a time when the variation may not yet have ended.
Comparing the two MPD experiments (DESIREE and PIRENA), the take-away is that the action spectra are essentially the same within the margin of inter-lab variability. In contrast, Maier’s action spectrum of He-tagged C24H12+ complexes (also included in Fig. 6) is qualitatively sharper,12 although the band maximum at 457 nm is the same within the uncertainty of the MPD measurements.
3.4 Multi-photon effects
In comparing their action spectra of He-tagged C24H12+ to the earlier MPD results, Maier and co-workers offer two different explanations for the broadness of the bands in the latter. They write that the MPD “process leads to broadening effects of the bands due to the heating of the ion ensemble” and later that “widths of the bands in the MPD experiment are broader owing to the higher internal temperature of the ion”.12 The first issue is a common critique of photodissociation action spectroscopy generally: that such spectra do not accurately reflect the ion’s true absorption cross section. The second explanation, that the He-tagged ions are colder, is indisputable. The question addressed in this section is whether the broadness of the MPD spectra is due only to the higher initial temperature, or if additional broadening is induced by the MPD process.In MPD experiments using nanosecond pulsed lasers, it is generally assumed that the ions absorb photons sequentially, i.e. returning to a hot ground electronic state via ultrafast internal conversion and intramolecular vibrational redistribution in between absorption events. In this case, the photodissociation yield ΓPD at a wavelength λ is proportional to the probability of absorbing the number of photons N required to induce photodissociation on the time scale sampled by the experiment:
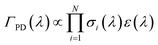 | (1) |
Measurements of rhodamine ions by the Roithová group, which have higher spectral resolution, show a clear blue-shift in the MPD action spectrum with decreasing trap temperature as hot-band absorptions become inactive.30 This confirms that at least some information about the initial low temperature absorption cross section is preserved in the MPD action spectrum. Roithová also gives action spectra of He-tagged rhodamine ions.30,31 Compared to these data, the MPD spectrum recorded at a 50 K trap temperature (the lowest reported by Roithová) is slightly (∼2 nm) redshifted and broadening is observed to both sides of the band maximum. The widths of the bands in the He-tagging spectra however are limited by the bandwidth of the excitation source, making it difficult to quantitatively compare them with the MPD spectra. Rhodamine dye cations are of course highly fluorescent, and the number of photons required to dissociate them is notably high.29,30 If most of the excitation energy is re-emitted optically, it may be reasoned that σi>1(λ) does not differ significantly from σ1(λ). It should also be noted that both Jockusch and Roithová use quasi-cw laser excitation sources, meaning that significant time (up to tens of milliseconds) may elapse in between excitation events during which the hot ions may relax by IR emission or collisions with trapping gas.
PAH cations are generally non-fluorescent and are instead characterized by very short excited state lifetimes. Maier estimates the excited state lifetime of C24H12+ to be 50 fs.12 Thus the full excitation energy (around 2.7 eV at 465 nm) is converted into vibrations. Reddening of σi>1(λ) relative to σ1(λ) might be expected due to enhancement of hot-band absorptions. This, however, would lead to a red-shift of the multi-photon spectra relative to Maier’s 1-photon spectrum, while instead a more symmetric broadening is seen in Fig. 6. Looking back at Fig. 3, we see that 10 ms after injection the action spectrum is nearly flat. Recall that this is itself a multi-photon action spectrum, and that the internal energy at 10 ms may be much higher than 2.7 eV, which corresponds roughly to room temperature. Still, the symmetric broadening of the MPD spectrum is consistent with σi>1(λ) = const. This is further supported by the similarity of the present 3-photon action spectrum to that from PIRENEA, which was modeled as arising from the absorption of more than 4 photons.11 The width of the MPD spectra can thus reasonably be assumed to be broadened relative to the He-tagged spectrum only by the higher initial temperature of the ions without invoking any additional broadening from the MPD process itself.
4 Conclusions
Multi-photon photodissociation action spectra of coronene cations have been recorded as a function of storage time in the cryogenic electrostatic ion storage ring DESIREE. Contributions from hot-band absorptions dissipate on a timescale consistent with IR radiative cooling from vibrational transitions. Spectra recorded more than 10 s after injection closely resemble those recorded in an ion trap mass spectrometer cooled to 35 K. Extrapolation of the cooling characteristic obtained by principal component analysis further increases this agreement. Considering the rather different experimental conditions, it has been argued that the MPD action spectra are proportional to the absorption cross section of the initial cold ion. Due to the higher internal temperature prior to excitation, the MPD spectra are symmetrically broadened relative to the one-photon photodissociation spectrum of C24H12+–He complexes, with no significant difference in the band maximum.In the present experiments, isolated C24H12+ ions cool via their intrinsic radiative transitions, exactly as they would in the ISM where collisional cooling is slow. Such a preparation might be considered to be a more realistic reproduction of interstellar conditions than cooling by interactions with buffer or carrier gases. Action spectra of He-tagged complexes provide accurate center wavelengths useful for the identification of interstellar absorption bands.32 The internal temperature of He-tagged complexes, however, is considerably lower than the prevailing conditions in interstellar clouds, where temperatures of non-polar molecules range from 30–80 K.33,34 Temperature controlled ion trap measurements, such as those carried out by the Joblin and Roithová groups, as well as time-dependent measurements on isolated, freely radiating ions possible in cryogenic electrostatic storage devices, are thus needed to asses the widths of optical transitions of purported interstellar ions. For example, a species whose He-tagged action spectrum shows a transition coincident with a diffuse interstellar band, but with an incommensurate band width at the temperature of interstellar clouds, is unlikely to be the carrier of that DIB. Further development of single-photon action spectroscopies of bare ions such as laser-induced fluorescence29,35,36 or laser-induced vibrational emission37 is needed to reduce any ambiguity associated with multi-photon processes like photodissociation.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The author thanks the operators and technical staff at DESIREE for their support. This work was supported by the Swedish Research Council (grants 2016-03675, 621-2015-04990, 621-2014-4501, and 621-2016-04181). The DESIREE infrastructure receives funding through the Swedish Research Council under the grant number 2017-00621.References
- A. G. G. M. Tielens, Annu. Rev. Astron. Astrophys., 2008, 46, 289–337 CrossRef CAS.
- M. Steglich, J. Bouwman, F. Huisken and T. Henning, Astrophys. J., 2011, 742, 2 CrossRef.
- U. P. Vijh, A. N. Witt and K. D. Gordon, Astrophys. J., Lett., 2004, 606, L65 CrossRef CAS.
- V. Mennella, L. Hornekær, J. Thrower and M. Accolla, Astrophys. J., Lett., 2012, 745, L2 CrossRef.
- G. Reitsma, L. Boschman, M. J. Deuzeman, O. González-Magaña, S. Hoekstra, S. Cazaux, R. Hoekstra and T. Schlathölter, Phys. Rev. Lett., 2014, 113, 53002 CrossRef CAS PubMed.
- M. Gatchell, M. H. Stockett, N. de Ruette, T. Chen, L. Giacomozzi, R. F. Nascimento, M. Wolf, E. K. Anderson, R. Delaunay, V. Vizcaino, P. Rousseau, L. Adoui, B. A. Huber, H. T. Schmidt, H. Zettergren and H. Cederquist, Phys. Rev. A, 2015, 92, 050702 CrossRef.
- E. Habart, F. Boulanger, L. Verstraete, G. P. des Forêts, E. Falgarone and A. Abergel, Astron. Astrophys., 2003, 397, 623–634 CrossRef CAS.
- D. Romanini, L. Biennier, F. Salama, A. Kachanov, L. Allamandola and F. Stoeckel, Chem. Phys. Lett., 1999, 303, 165–170 CrossRef CAS.
- J. Noble, C. Dedonder and C. Jouvet, Astron. Astrophys., 2015, 577, A79 CrossRef.
- T. Pino, N. Boudin and P. Bréchignac, J. Chem. Phys., 1999, 111, 7337–7347 CrossRef CAS.
- F. Useli-Bacchitta, A. Bonnamy, G. Mulas, G. Malloci, D. Toublanc and C. Joblin, Chem. Phys., 2010, 371, 16–23 CrossRef CAS.
- F.-X. Hardy, C. A. Rice and J. P. Maier, Astrophys. J., 2017, 836, 37 CrossRef.
- R. D. Thomas, H. T. Schmidt, G. Andler, M. Björkhage, M. Blom, L. Brännholm, E. Bäckström, H. Danared, S. Das, N. Haag, P. Halldén, F. Hellberg, A. I. S. Holm, H. A. B. Johansson, A. Källberg, G. Källersjö, M. Larsson, S. Leontein, L. Liljeby, P. Löfgren, B. Malm, S. Mannervik, M. Masuda, D. Misra, A. Orbán, A. Paál, P. Reinhed, K.-G. Rensfelt, S. Rosén, K. Schmidt, F. Seitz, A. Simonsson, J. Weimer, H. Zettergren and H. Cederquist, Rev. Sci. Instrum., 2011, 82, 065112 CrossRef CAS PubMed.
- H. T. Schmidt, R. D. Thomas, M. Gatchell, S. Rosén, P. Reinhed, P. Löfgren, L. Brännholm, M. Blom, M. Björkhage, E. Bäckström, J. D. Alexander, S. Leontein, D. Hanstorp, H. Zettergren, L. Liljeby, A. Källberg, A. Simonsson, F. Hellberg, S. Mannervik, M. Larsson, W. D. Geppert, K. G. Rensfelt, H. Danared, A. Paál, M. Masuda, P. Halldén, G. Andler, M. H. Stockett, T. Chen, G. Källersjö, J. Weimer, K. Hansen, H. Hartman and H. Cederquist, Rev. Sci. Instrum., 2013, 84, 055115 CrossRef CAS PubMed.
- E. Bäckström, D. Hanstorp, O. M. Hole, M. Kaminska, R. F. Nascimento, M. Blom, M. Björkhage, A. Källberg, P. Löfgren, P. Reinhed, S. Rosén, A. Simonsson, R. D. Thomas, S. Mannervik, H. T. Schmidt and H. Cederquist, Phys. Rev. Lett., 2015, 114, 143003 CrossRef PubMed.
- A. I. S. Holm, H. A. B. Johansson, H. Cederquist and H. Zettergren, J. Chem. Phys., 2011, 134, 044301 CrossRef CAS PubMed.
- M. H. Stockett, H. Zettergren, L. Adoui, J. D. Alexander, U. Bērziņš, T. Chen, M. Gatchell, N. Haag, B. A. Huber, P. Hvelplund, A. Johansson, H. A. B. Johansson, K. Kulyk, S. Rosén, P. Rousseau, K. Støchkel, H. T. Schmidt and H. Cederquist, Phys. Rev. A, 2014, 89, 032701 CrossRef.
- L. Chen, S. Martin, J. Bernard and R. Brédy, Phys. Rev. Lett., 2007, 98, 193401 CrossRef CAS PubMed.
- S. Martin, L. Chen, R. Brédy, G. Montagne, C. Ortega, T. Schlathölter, G. Reitsma and J. Bernard, Phys. Rev. A, 2012, 85, 052715 CrossRef.
- M. Wolf, H. V. Kiefer, J. Langeland, L. H. Andersen, H. Zettergren, H. T. Schmidt, H. Cederquist and M. H. Stockett, Astrophys. J., 2016, 832, 24 CrossRef.
- P. Boissel, P. de Parseval, P. Marty and G. Lefèvre, J. Chem. Phys., 1997, 106, 4973–4984 CrossRef CAS.
- J. Montillaud, C. Joblin and D. Toublanc, Astron. Astrophys., 2013, 552, A15 CrossRef.
- K. Støchkel and J. U. Andersen, J. Chem. Phys., 2013, 139, 164304 CrossRef PubMed.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- K. Hansen, J. U. Andersen, P. Hvelplund, S. P. Møller, U. V. Pedersen and V. V. Petrunin, Phys. Rev. Lett., 2001, 87, 123401 CrossRef CAS PubMed.
- J. U. Andersen, H. Cederquist, J. Forster, B. Huber, P. Hvelplund, J. Jensen, B. Liu, B. Manil, L. Maunoury and S. B. Nielsen, et al. , Eur. Phys. J. D, 2003, 25, 139–148 CrossRef CAS.
- S. Martin, J. Bernard, R. Brédy, B. Concina, C. Joblin, M. Ji, C. Ortega and L. Chen, Phys. Rev. Lett., 2013, 110, 063003 CrossRef CAS PubMed.
- K. Hansen, M. H. Stockett, M. Kaminska, R. F. Nascimento, E. K. Anderson, M. Gatchell, K. C. Chartkunchand, G. Eklund, H. Zettergren, H. T. Schmidt and H. Cederquist, Phys. Rev. A, 2017, 95, 022511 CrossRef.
- S. M. Wellman and R. A. Jockusch, J. Phys. Chem. A, 2015, 119, 6333–6338 CrossRef CAS PubMed.
- R. Navrátil, J. Jašík and J. Roithová, J. Mol. Spectrosc., 2017, 332, 52–58 CrossRef.
- J. Jašík, R. Navrátil, I. Němec and J. Roithová, J. Phys. Chem. A, 2015, 119, 12648–12655 CrossRef PubMed.
- E. K. Campbell, M. Holz, D. Gerlich and J. P. Maier, Nature, 2015, 523, 322–323 CrossRef CAS PubMed.
- J. P. Maier, N. M. Lakin, G. A. Walker and D. A. Bohlender, Astrophys. J., 2001, 553, 267 CrossRef CAS.
- N. Indriolo, T. R. Geballe, T. Oka and B. J. McCall, Astrophys. J., 2007, 671, 1736 CrossRef CAS.
- M. H. Stockett, J. Houmøller, K. Støchkel, A. Svendsen and S. Brøndsted Nielsen, Rev. Sci. Instrum., 2016, 87, 053103 CrossRef PubMed.
- M. H. Stockett, J. Houmøller and S. Brøndsted Nielsen, J. Chem. Phys., 2016, 145, 104303 CrossRef CAS PubMed.
- S. S. Kumar, P. Bizenberger, K. Blaum, C. Breitenfeldt, J. Göck, U. Grözinger, T. Henning, J. Karthein, B. Kern and C. Meyer, et al. , J. Phys.: Conf. Ser., 2015, 112072 CrossRef.
| This journal is © The Royal Society of Chemistry 2019 |