Prediction on the origin of selectivities of NHC-catalyzed asymmetric dearomatization (CADA) reactions

Abstract

Prediction of the regioselectivities (i.e., the active sites) of dearomatization reactions has been and continues to be one of the most challenging issues in the modern synthesis field. In this work, we provide a valuable case for predicting the origin of the chemoselectivity for organocatalyst-catalyzed asymmetric dearomatization (CADA) reactions. Herein, the possible mechanisms and the origin of selectivities of NHC-catalyzed asymmetric dearomatization reaction of isoquinoline have been systematically investigated using density functional theory (DFT) for the first time. Computational results show that the intermolecular Mannich-type transformation was both the stereoselectivity- and chemoselectivity-determining step. The NCI analysis reveals that C–H⋯Br and π⋯π interactions contribute significantly to the control of the stereoselectivity. Furthermore, the origin of regioselectivities on NHC-catalyzed asymmetric dearomatization reactions of other aromatic rings has been accurately predicted by performing the local reactivity index analysis. This work would provide valuable clues for predicting the origin of the selectivities and designing more effective organocatalysts for these kinds of reactions with high and special selectivities.

---

Introduction

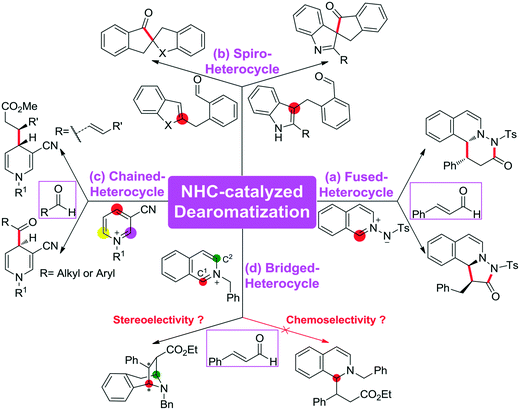
The C–C bond is one of the most fundamental bonds involved in organic compounds. The catalytic enantioselective construction of C–C bonds is one of the hottest topics in organic chemistry to rapidly access stereoenriched skeletons. In particular, catalytic asymmetric dearomatization (CADA) reactions are important transformations of aromatic compounds leading to a variety of ring systems through C–C bond construction. Recently, the CADA reactions, which have emerged as powerful organic transformation for the construction of complex molecules from the wide availability of cheap and versatile aromatic compounds, have gained increasing attention.¹ During the dearomatization reaction, the formation of quaternary carbon centers would facilitate the construction of three-dimensional spiro or bridged heterocyclic compounds.² Despite the high potential of this strategy, the main challenge of such an approach is the low reactivity of substrates and the difficult control of the chemo-, regio-, and stereoselectivities in the formation of the desired products.

For the CADA reactions, transition-metal catalytic strategies have been extensively applied for highly stereoselective dearomatization of aromatic compounds,³ while the utilization of organocatalytic approaches remains underdeveloped. Recently, the use of organocatalysis has opened up various kinds of new and exciting opportunities for providing different reactive modes. Pioneered by MacMillan, Jørgensen, and Jacobsen, the dearomatization reaction of (iso)quinolines, indoles, and pyridines catalyzed by organocatalysts has already attracted considerable attention in experiment.⁴ Noteworthily, N-heterocyclic carbene (NHC), which has an increasing number of applications as a nucleophilic organocatalyst to access an impressive set of reactions,⁵ such as the annulation reaction,⁶ cross-coupling reaction,⁷ and Stetter reaction⁸ as well as the C–X (X = C, F, Br, H, etc.) bond activation reaction,⁹ was widely employed to promote the CADA reactions of (hetero)aromatic compounds to construct various types of heterocycles.

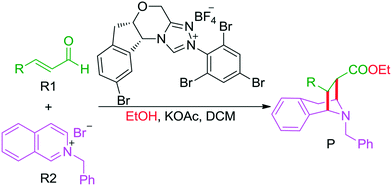
Scheme 1 summarizes some of the recently reported examples of NHC-catalyzed CADA reactions of (hetero)aromatic compounds. Glorius and co-workers reported that the dearomatization reaction of aromatic azomethine imines can be achieved for the construction of fused-heterocycles (Scheme 1a).¹⁰ Later on, Glorius¹¹ and Studer¹² developed the intramolecular dearomatization of benzofurans/benzothiophenes by hydroacylation and of indoles by oxidative NHC catalysis to afford spiro-heterocycles (Scheme 1b). In 2017, Rovis¹³ and Massi¹⁴ groups independently described the enantio- and diastereoselective addition of enals to N-alkylpyridinium salts to generate chained 1,4-dihydropyridines (DHPs) with good regioselectivity under NHC catalysis (Scheme 1c). Furthermore, Tan and co-workers reported an example of an NHC organocatalytic route for the construction of a bridged tropane framework with special chemoselectivity and high stereoselectivity through the CADA reaction (Scheme 1d),¹⁵ in which the isoquinoline provided two reactive sites for a double Mannich-type transformation. In these reactions, one can find that the regioselective sites (i.e., the ortho- or para-position of the aromatic ring) would participate in those CADA reactions, thus it should be important to identify and predict the potential active sites of the aromatic rings in theory for rational design. To the best of our knowledge, computational investigation on the detailed mechanism and origin of selectivities of NHC-catalyzed dearomatization reactions has remained hitherto unreported.

Scheme 1 Catalytic asymmetric dearomatization reactions enabled by NHC organocatalyst ((a) dearomatization of aromatic azomethine, (b) dearomatization of benzofurans/benzothiophenes, (c) dearomatization of N-alkylpyridinium, and (d) dearomatization of isoquinoline).

To shed light on the general mechanism and predict the origin of the selectivities of these kinds of reactions, we selected Tan's experimental work¹⁵ as a computational model (Scheme 1d) to perform a theoretical investigation, and we aimed to pursue the exact pictures of the reaction mechanism and disclose the origin of selectivities. This computational work would provide valuable clues for the rational design of the organocatalytic CADA reactions with controllable chemoselectivities and excellent stereoselectivities. The density functional theory (DFT) method, which has become one of the most powerful and efficient tools for clarifying the reaction mechanism and predicting the selectivities in NHC catalyzed reactions^16,17 as well as other asymmetric reactions,¹⁸ was employed to perform the theoretical simulations.

Results and discussion

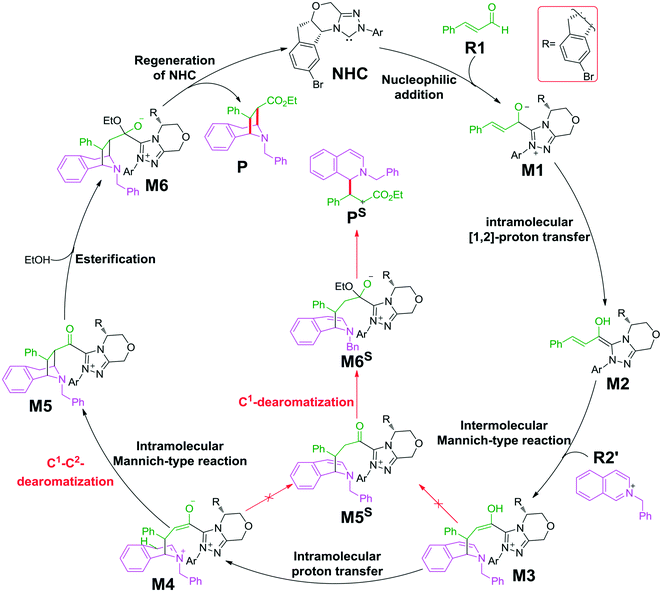
As shown in Scheme 2, the possible catalytic pathways for the NHC-catalyzed CADA reaction of isoquinoline, including C¹–C²-dearomatization and C¹-dearomatization pathways, have been suggested. The C¹–C²-dearomatization pathway mainly contains three stages, i.e., formation of the Breslow intermediate (stage 1), Mannich-type transformations (stage 2), and regeneration of NHC (stage 3). Alternatively, the C¹-dearomatization reaction may proceed via another active intermediate M5^S, in which the α-carbon is protonated from intermediate M3 or M4.

Scheme 2 The key mechanistic steps involved in the NHC-catalyzed dearomatization reaction.

Reaction mechanism of C¹–C²-dearomatization

Stage 1: formation of the Breslow intermediate. As shown in Scheme 2, stage 1 contains two steps, i.e., nucleophilic addition of NHC to R1 and [1,2]-proton transfer. Initially, the nucleophilic attack of the NHC catalyst on the carbonyl carbon of R1 triggers the reaction. Because of the existence of prochiral faces in reactant R1, the NHC can either attack on the Re face or Si face to generate the zwitterionic intermediate Re/Si-M1via transition state Re/Si-TS1. As shown in Fig. 1, the energy barriers of the Re and Si addition processes are 19.0 and 23.3 kcal mol⁻¹, and the relative Gibbs free energies of Re-M1 and Si-M1 are 15.8 and 13.7 kcal mol⁻¹, respectively.

Fig. 1 The energy profiles involved in stage 1 (the superscripts “A” and “E” represent AcOH- and EtOH-assisted proton transfer processes, respectively. The superscripts “a”, “b”, and “c” represent addition of the free energies of R2′, R2′ + AcOH, and R2′ + EtOH, separately).

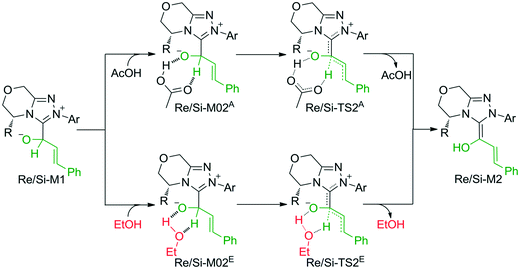
The second step is the [1,2]-proton transfer to give the well-known Breslow intermediate M2. The traditional direct proton transfer mechanism is difficult to occur under mild experimental conditions because the proton transfer process associated with a three-membered ring transition state requires an extremely high energy (Fig. S1 of the ESI†), which has been reported by various computational studies.¹⁹ Thus, the protic media-assisted proton transfer mechanism should be invoked to lower the energy barrier of the proton transfer process. Based on the details of Tan's experiment,¹⁵ ethanol (EtOH) is included in the reaction conditions, which should be viewed as a proton transfer medium. Moreover, the additive base NaOAc would be transformed to its conjugate acid AcOH by means of deprotonation of the triazolium salt, and the AcOH can also work as a protic medium to assist the proton transfer. As shown in Scheme 3, two possible protic media-assisted proton transfer pathways have been suggested for the formation of the Breslow intermediate, i.e., AcOH-assisted and EtOH-assisted proton transfer pathways.

Scheme 3 The possible pathways for the formation of the Breslow intermediate.

As depicted in Fig. 1, the energy barriers of AcOH-assisted proton transfer pathways are 12.4/14.7 kcal mol⁻¹, respectively, and those of EtOH-assisted proton transfer processes are 35.6/33.9 kcal mol⁻¹, which are much lower than those of the direct proton transfer pathways (ΔG^≠ = 55.6/58.1 kcal mol⁻¹, Fig. S1 of the ESI†). Comparing the three proton transfer pathways, the high energy barrier involved in the direct proton transfer pathway is mainly due to the large strain of the three-membered ring structure of the transition state. Meanwhile for the media-assisted proton transfer pathways, the energy barrier of the AcOH-assisted proton transfer pathway (12.4/14.7 kcal mol⁻¹, Fig. 1) is obviously lower than that of the EtOH-assisted proton transfer pathway (35.6/33.9 kcal mol⁻¹, Fig. 1), since the acidity of AcOH (pK_a = 5.0) is much stronger than that of EtOH (pK_a = 16.0). Moreover, the reaction pathway associated with the Re face addition (Re-TS1 → Re-M1 → Re-TS2^A → Re-M2) is calculated to be more energetically favorable than that associated with the Si face addition (Si-TS1 → Si-M1 → Si-TS2^A → Si-M2). Thus, it is reasonable to exclude the Si face addition pathway in the following sections.

Stage 2: Mannich-type transformation. In this stage, there are three steps, i.e., intermolecular Mannich-type transformation, intramolecular proton transfer, and intramolecular Mannich-type transformation.

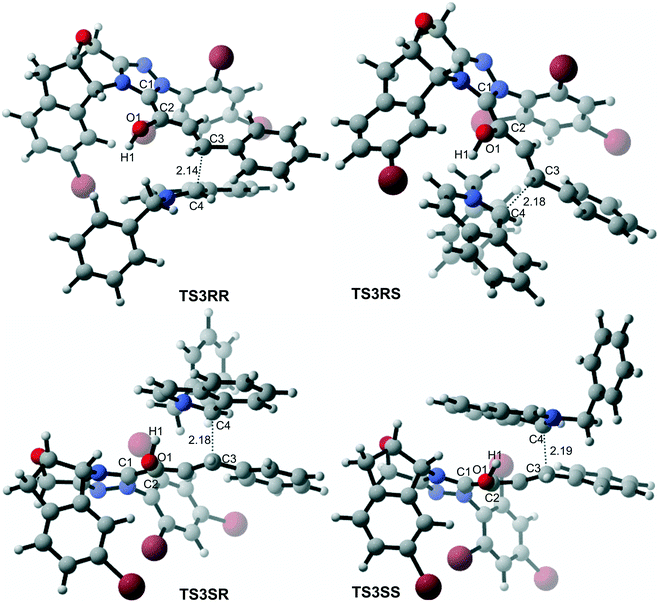
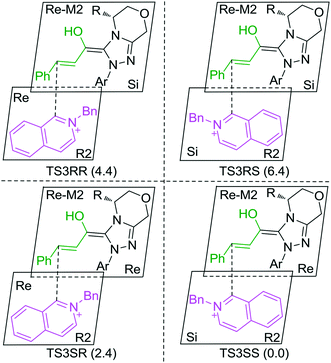
In the intermolecular Mannich-type transformation, two continuous chiral centers are formed in intermediate M3via transition state TS3. During the formation of C–C bonds, reactant R2′ can attack on either the Re or Si face of Re-M2 by Re or Si face addition to give four diastereoselective intermediates M3RR/RS/SR/SS through transition states TS3RR/RS/SR/SS, respectively. As an important note, the first letter after TS3 represents the chirality of the C3 atom, and the second letter represents the chirality of the C4 atom (Fig. 2). The energy barriers viaTS3RR/RS/SR/SS, as depicted in Fig. 3, are 13.9, 15.9, 11.9, and 9.5 kcal mol⁻¹, respectively. From Fig. 3, one can conclude that the reaction pathway associated with SS-configuration is more energetically favorable than the other three pathways, thus, we only take the SS-configurational pathway as reference for discussion in the following sections.

Fig. 2 3D-structures of the key transition states of the C–C bond formation step (distance in Å).

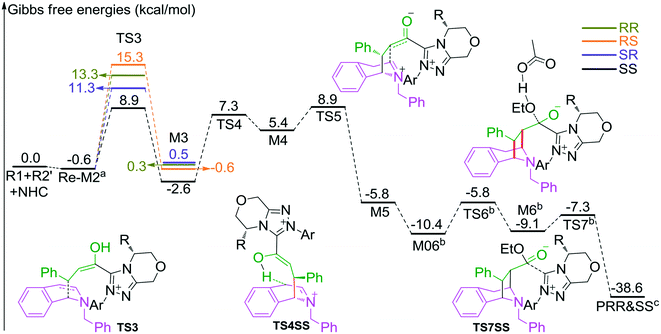Fig. 3 The most energetically favorable pathway involved in stages 2 and 3 of the NHC-catalyzed asymmetric dearomatization reaction of isoquinolines (the superscripts “a”, “b”, and “c” represent addition of the free energies of R2′, AcO⁻–EtOH, and NHC, respectively. The whole energy profile is provided in Fig. S2 of the ESI†).

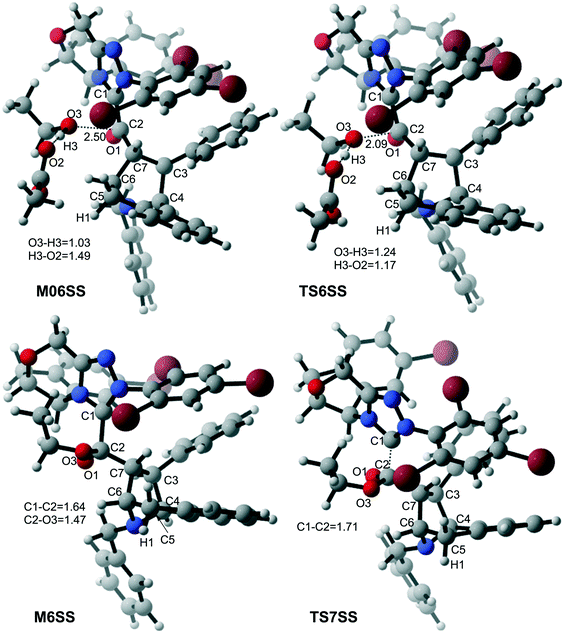
The next step is the proton transfer process for the formation of intermediate M4via transition state TS4. The energy barrier of this step is only 9.9 kcal mol⁻¹ (Fig. 3), indicating that this step can occur smoothly under experimental conditions.

Subsequently, the intramolecular Mannich-type transformation occurs via transition state TS5 for the formation of intermediate M5. The energy barrier of this step is only 3.5 kcal mol⁻¹ (Fig. 3), showing that this step is also a facile process.

Stage 3: esterification and regeneration of the catalyst. Two steps, including esterification reaction by the addition of ethanol and regeneration of the NHC catalyst, are involved in this stage.

With the aid of AcO⁻, the oxygen atom of ethanol nucleophilically attacks on the carbonyl carbon atom, which is coupled with the abstraction of the hydrogen atom of ethanol by the oxygen atom of AcO⁻ to afford the ester M6 (Fig. 4). The energy barrier of this step is 4.6 kcal mol⁻¹ (Fig. 3), which can be easily overcome under the experimental conditions. The last step of this reaction is the dissociation of the catalyst with the final product via transition state TS7, and the energy barrier of this step is only 1.8 kcal mol⁻¹ (Fig. 3), implying that the NHC catalyst can easily regenerate.

Fig. 4 3D-structures of the key transition states involved in stage 3 (distance in Å).

Chemoselective C¹-dearomatization

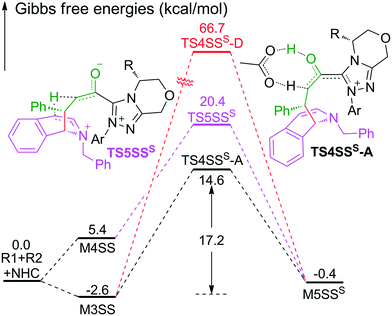
As shown in Scheme 2, the intermediate M3 can undergo an alternative type of dearomatization reaction to give intermediate M5^S, in which the protonation of the α-carbon of R1 is involved. Moreover, the intermediate M4 can also transform to M5^S. This is because the main catalytic reaction and the C¹-dearomatization share the same formation process of M3 or M4 and diverge afterward. On the other hand, the SS-configurational pathway has been revealed to be the most energy favorable. Thus, we only studied the process of C¹-dearomatization following from M3 or M4 associated with the SS-configurational pathway. During the protonation of the α-carbon, the direct proton transfer pathway associated with four-membered ring transition state TS4SS^S-D requires an energy barrier of 69.3 kcal mol⁻¹ (Fig. 5), which is too high for the pathway to occur under the experimental conditions. Meanwhile the energy barrier of the AcOH-assisted proton transfer pathway associated with transition state TS4SS^S-A is 17.2 kcal mol⁻¹ (Fig. 5). In addition, the energy barrier viaTS5SS^S is 20.4 kcal mol⁻¹ (Fig. 5). Obviously, the AcOH-assisted proton transfer pathway is the most energy favorable for the formation of intermediate M5SS^S (ΔG = −0.4 kcal mol⁻¹, Fig. 5). Compared with the reaction pathways associated with TS5SS and TS4SS^S-A, the C¹–C²-dearomatization reaction pathway viaTS5SS (ΔG^≠ = 11.5 kcal mol⁻¹, Fig. 3) is more energy favorable than the C¹-dearomatization reaction pathway associated with TS4SS^S-A (ΔG^≠ = 17.2 kcal mol⁻¹, Fig. 5), and the intermediate M5SS (ΔG = −5.8 kcal mol⁻¹, Fig. 3) is more stable than M5SS^S (ΔG = −0.4 kcal mol⁻¹, Fig. 5). Thus, it is unnecessary to further explore the subsequent process involved in the C¹-dearomatization.

Fig. 5 The energy profile of key steps involved in the C¹-dearomatization reaction (the superscript “S” represents the C¹-dearomatization and “D” and “A” represent the direct and AcOH-assisted proton transfer processes, respectively).

Origin of stereoselectivity

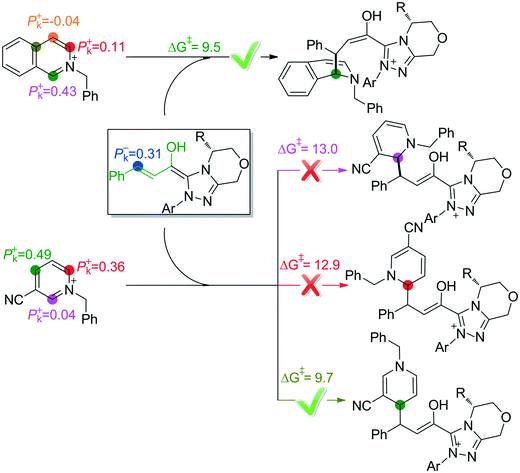
As discussed above, the intermolecular Mannich-type transformation was calculated to be the stereoselectivity-determining step, which was further confirmed by the benchmark calculations (more details are provided in Table S1 of the ESI†). The addition to different prochiral faces of Re-M2 by different faces of R2′ will lead to four diastereomeric intermediates, and concurrently, the chiralities of C3 and C4 atoms appear during the C3–C4 bond formation process. As shown in Scheme 4, the addition of the Re face of R2′ to the Re or Si face of Re-M2 results in the formation of M3SR and M3RRvia transition states TS3SR and TS3RR, respectively. Correspondingly, the addition of the Si face of R2′ to the Re or Si face of Re-M2 leads to the formation of M3SS and M3RS associated with transition states TS3SS and TS3RS, separately. The computational results show that the addition of the Re-face of Re-M2 to the Si-face of the R2′ is the most preferred mode for C–C bond formation. Moreover, the Re–Si transition state TS3SS is the most energetically favorable, and its energy barrier is 4.4 kcal mol⁻¹ lower than that via the Si–Re transition state TS3RR. Based on the Boltzmann distribution analysis, this value corresponds to an enantiomeric excess of 99.9%, which aligns well with the experimentally reported ee value of 93%.¹⁷

Scheme 4 Stereochemical possibilities for the C¹–C²-dearomatization reaction.

Having identified the most preferred stereochemical modes of the approach between the reactant and intermediates on the basis of the energies of the corresponding transition states, we then turned our attention toward discovering the origin of the stereoselectivity by using the non-covalent interaction (NCI) analysis. In the NCI pictures, the regions of attractive non-covalent interactions appear as green colored regions, while red regions represent repulsive interactions.

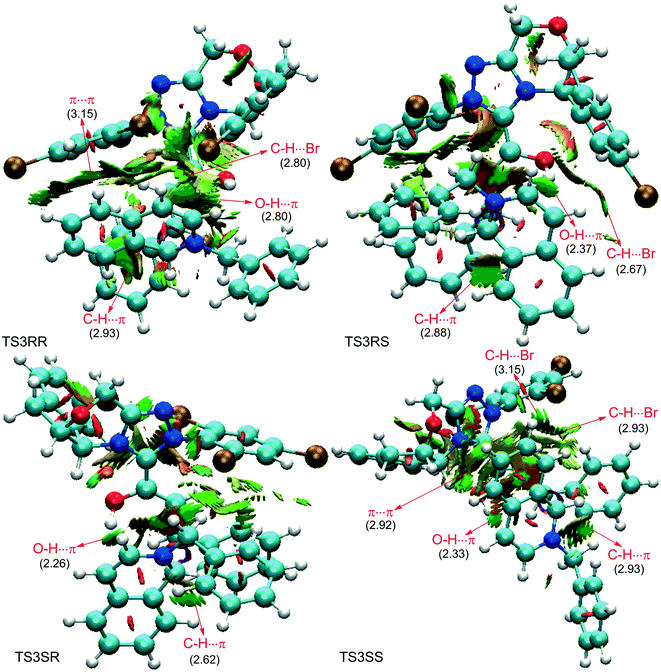
As depicted in Fig. 6, the NCI plots of the stereocontrolling transition states show that the non-covalent interactions are more preferred in the lowest energy barrier transition state TS3SS. There are more C–H⋯Br interactions in TS3SS than in the other three transition states (i.e., TS3RR, TS3RS, and TS3SS). Moreover, the π⋯π interaction is found to be stronger in TS3SS than in its enantioselective transition state TS3RR (the distances between two aryl groups are 2.92 and 3.15 Å in TS3SS and TS3RR, respectively), and is absent in transition states TS3RS and TS3SR. As an important note, other kinds of interactions such as O–H⋯π and C–H⋯π exist in the four transition states and have little difference between these transition states. As mentioned above, the more effective C–H⋯Br and π⋯π interactions stabilize the transition state TS3SS.

Fig. 6 The NCI analysis of the stereo-controlling transition states TS3RR, TS3RS, TS3SR, and TS3SS. Brown, cyan, red, blue, and white balls represent Br, C, O, N, and H atoms, respectively. Values in parentheses represent the distance between two attractive regions (values are in Å representing the distance between hydrogen and heavy atoms of two attractive regions).

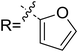
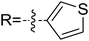
In order to further verify the reliability of the above predictions on the stereocontrolling transition states, we have investigated other three kinds of enals with R = 4-MePh, furan, and thiopene groups (Table 1). The computational results show that the selectivities of the reaction associated with different groups are in good agreement with the experimental observations, which indicates that the computational models would be reliable to predict the stereoselectivity for this kind of reaction. Moreover, NCI analysis has also been studied (the NCI pictures of the transition states with different substrates are provided in Fig. S3–S5 of the ESI†). According to the non-covalent interaction analysis, we can find that the π⋯π interaction is responsible for the origin of stereoselectivity.

Table 1 Verification of computational models

	TS3RR	TS3RS	TS3SR	TS3SS	ee%
					Exp.	Calc.
R = Me	5.0	7.9	2.5	0.0	96	99
	5.5	8.9	3.5	0.0	96	99
	2.4	5.4	1.6	0.0	91	96.6

---

Global reactivity index and Parr function analyses

Global reactivity index analysis. Disclosing the role of catalysts in an asymmetric reaction is valuable for researchers to rationally design more efficient organocatalysts and high stereoselectivity reactions. The use of global reactivity index (GRI) analysis has been identified to be a powerful method to uncover the role of organocatalysts,²⁰ especially for the NHC catalyst,^20d–f in which two characters (i.e., electrophilicity index and nucleophilicity index) are defined to illustrate the electrophilicity and nucleophilicity of a molecule.²¹

As shown in Table 2, the GRI analysis shows that the electrophilicity of intermediates Re-M1 and Re-M2 is decreased after complexation of NHC and [1,2]-proton transfer, while the nucleophilicity of Re-M1 and Re-M2 is increased. This phenomenon reveals that the addition of the NHC catalyst strengthens the nucleophilicity of the substrate R1, which can facilitate the addition of another reactant R2′. After the formation of M3SS and M4SS, the electrophilicity values of the intermediates M3SS and M4SS are enhanced and the nucleophilicity values of M3SS and M4SS are slightly weakened. This result indicates that the intermediates M3SS and M4SS are hard to protonate via transition states TS4SS^S-A and TS5SS^S.

Table 2 Energies of the HOMO (E_H, a.u.), LUMO (E_L, a.u.), electronic chemical potential (μ, a.u.), chemical hardness (η, a.u.), global electrophilicity (ω, eV), and global nucleophilicity (N, eV) of R1, R2′, Re-M1, Re-M2, M3SS, and M4SS

	E H	E L	μ	η	ω	N
a E (TCNE)HOMO = −0.37826 a.u. (HOMO energy is calculated at the M06-2X/6-31G(d, p)//IEF-PCMDCM level).
R1	−0.29	−0.04	−0.17	0.25	1.57	2.45
R2′	−0.32	−0.08	−0.20	0.24	2.27	1.63
Re-M1	−0.25	−0.02	−0.14	0.23	1.16	3.54
Re-M2	−0.21	−0.02	−0.12	0.19	1.03	4.63
M3SS	−0.26	−0.06	−0.16	0.20	1.74	3.27
M4SS	−0.25	−0.05	−0.15	0.20	1.53	3.54

---

Parr function analysis

The above discussions show that the protonation of α-carbon is less favorable than the intramolecular Mannich reaction (17.2 kcal mol⁻¹vs. 9.9 kcal mol⁻¹). Herein, we intended to carry out the Parr function analysis²² to disclose the origin of chemoselectivity and the role of NHC by analyzing the local electrophilicity and nucleophilicity of active sites.

Table 3 and Fig. S6 summarize the electrophilic and nucleophilic Parr functions of R1, R2′, Re-M1, Re-M2, M3SS, and M4SS. As can be seen in Table 3, one can find that the electrophilic Parr function (P_k⁺) of the C4 atom in R2′ is 0.43 and the nucleophilic Parr function (P_k⁻) of the C3 atom in Re-M2 is 0.31, which is in line with the GRI analysis. In intermediate M3SS, the nucleophilic Parr function (P_k⁻) of C5, C6, and C7 atoms is 0.36, −0.03, and 0.00 respectively, indicating that the nucleophilicity of the C5 atom is stronger than that of the C6 and C7 atoms. This phenomenon shows that the C5 atom accepts the proton more easily than the C6 and C7 atoms. In intermediate M4SS, the nucleophilic Parr function (P_k⁻) of the C7 atom is 0.65, which seems that the C7 atom has stronger proton accepting ability. Meanwhile the electrophilic Parr function (P_k⁺) of C5 (or hydrogen located on the C5 atom) and C6 atoms in M4SS is 0.00 and 0.74, respectively, revealing that the C6 atom should be more reactive than the C5 atom and can easily react with the C7 atom to occur the intramolecular Mannich reaction.

Table 3 The electrophilic and nucleophilic Parr functions (P_k⁺ and P_k⁻) at the key atoms of reactants R1 and R2′ and intermediates Re-M2, M3SS, and M4SS

		R1	R2′	Re-M1	Re-M2	M3SS	M4SS
a Values in parentheses refer to the local nucleophilic Pk^− and electrophilic Pk^+ Parr functions of hydrogen located on the C5 atom.
C2	P k ^+	0.13	—	0.00	−0.10	−0.05	0.01
	P k ^−	−0.09	—	0.02	0.40	0.00	−0.11
C3	P k ^+	0.28	—	0.03	0.10	−0.02	0.02
	P k ^−	−0.11	—	0.02	0.31	0.07	−0.06
C4	P k ^+	—	0.43	—	—	0.02	−0.01
	P k ^−	—	0.07	—	—	−0.03	0.04
C5	P k ^+	—	0.11	—	—	0.00	0.00 (0.00)
	P k ^−	—	0.06	—	—	0.36	0.00 (0.00)
C6	P k ^+	—	−0.04	—	—	0.00	0.74
	P k ^−	—	0.18	—	—	−0.03	0.01
C7	P k ^+	0.10	—	−0.01	0.20	0.29	−0.01
	P k ^−	0.41	—	0.07	−0.13	0.00	0.65

---

As mentioned above, the C¹-dearomatization is impossible to occur, mainly because the C7 atom in M3SS is less reactive in accepting a proton and the C5 atom is deactivated after protonation. Additionally, the possible reactive sites have also been predicted by using the Parr function on the basis of Rovis'¹³ and Tan's¹⁵ work. As shown in Fig. 7, the active site is the C4 atom when the isoquinoline is used as the substrate, while the para-carbon is the most active when the pyridine is used as the substrate. The predictions are in good accordance with Rovis' and Tan's experimental results, respectively.

Fig. 7 Prediction of the active sites by using the Parr function.

Conclusions

In summary, the possible reaction mechanisms and selectivities of NHC-catalyzed dearomatization reaction have been systematically investigated. The computational results suggest that the main catalytic mechanism consists of three major stages: (1) formation of the Breslow intermediate, (2) two sequential Mannich-type reactions (C¹–C²-dearomatization) for forming a tropane-skeleton intermediate, and (3) dissociation of the catalyst. The intermolecular Mannich-type reaction step is identified to be both the stereoselectivity- and regioselectivity-determining steps, in which the Re–Si addition leading to SS-configured products is predominant. The NCI analysis shows that the more effective C–H⋯Br and π⋯π interactions are the key factors that govern the stereoselectivity. Furthermore, the C¹-dearomatization is calculated to be less favorable, which is mainly due to the less reactivity in accepting the proton of β-carbon by using the Parr function analysis. Thus, one can predict the possible reactive sites through local reactivity analysis to provide valuable insights into rational design of potential catalysts in organocatalytic dearomatization reaction with excellent selectivities.

Computational details

All the calculations involved in the reaction were performed by using the density functional theory (DFT) method with the Gaussian 09 (ref. 23) suite of programs, which has been identified to be a powerful and widely used method for exploring the mechanisms of organic reactions.²⁴ The solution-phase structure optimization of all the stationary points was carried out at the M06-2X²⁵/6-31G(d, p)²⁶ level in DCM solvent using the integral equation formalism polarizable continuum model (IEF-PCM).²⁷ The energies discussed in this work were obtained by the addition of the thermal correction at the M06-2X/6-31G(d, p)//IEF-PCM_DCM level to the corresponding single-point energy at the M06-2X-D3/6-31++G (2df, 2pd)//IEF-PCM_DCM level. Non-covalent interaction (NCI) analysis was plotted by using Multiwfn (version 3.3.8)²⁸ and the computed 3D-structures were rendered using the CYLView software.²⁹

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The work described in this paper was supported by the National Natural Science Foundation of China (No. 21773214), the Outstanding Young Talent Research Fund of Zhengzhou University (No. 1521316001), the China Postdoctoral Science Foundation (No. 2015T80776), and the Startup Fund of Zhengzhou University of Light Industry (No. 13501050070).

References

1. For related reviews: (a) W.-T. Wu, L. M. Zhang and S.-L. You, Chem. Soc. Rev., 2016, 45, 1570–1580; (b) Z.-P. Yang, Q.-F. Wu, W. Shang and S.-L. You, J. Am. Chem. Soc., 2015, 137, 15899–15906; (c) X.-W. Liang, C. Zheng and S.-L. You, Chem. – Eur. J., 2016, 22, 1–17; (d) Q. P. Ding, X. L. Zhou and R. H. Fan, Org. Biomol. Chem., 2014, 12, 4807–4815; (e) J. A. Bull, J. J. Mousseau, G. Pelletier and A. B. Charette, Chem. Rev., 2012, 112, 2642–2713; (f) W. C. Wertjes, E. H. Southgate and D. Sarlah, Chem. Soc. Rev., 2018, 47, 7996–8017; (g) W. S. Sun, G. F. Li, L. Hong and R. Wang, Org. Biomol. Chem., 2016, 14, 2164–2176; (h) M. Zhang, W. S. Sun, G. M. Zhu, G. J. Bao, B. Z. Zhang, L. Hong, M. Li and R. Wang, ACS Catal., 2016, 6, 5290–5294.
2. C.-X. Zhuo, W. Zhang and S.-L. You, Angew. Chem., Int. Ed., 2012, 51, 12662–12686.
3. For selected reviews: (a) C. Zheng and S.-L. You, Chem, 2016, 1, 830–857; (b) A. R. Pape, K. P. Kaliappan and E. P. Kündig, Chem. Rev., 2000, 100, 2917–2940; (c) C.-X. Zhuo, C. Zheng and S.-L. You, Acc. Chem. Res., 2014, 47, 2558–2573.
4. (a) S. P. Brown, N. C. Goodwin and D. W. C. MacMillan, J. Am. Chem. Soc., 2003, 125, 1192–1194; (b) K. Frisch, A. Landa, S. Saaby and K. A. Jørgensen, Angew. Chem., Int. Ed., 2005, 44, 6058–6063; (c) M. S. Taylor, N. Tokunaga and E. N. Jacobsen, Angew. Chem., Int. Ed., 2005, 44, 6700–6704.
5. For some related reviews: (a) A. Grossmann and D. Enders, Angew. Chem., Int. Ed., 2011, 51, 314–325; (b) S. J. Ryan, L. Candish and D. W. Lupton, Chem. Soc. Rev., 2013, 42, 4906–4917; (c) M. N. Hopkinson, C. Richter, M. Schedler and F. Glorius, Nature, 2014, 510, 485–496; (d) R. S. Menon, A. T. Biju and V. Nair, Chem. Soc. Rev., 2015, 44, 5040–5052; (e) D. M. Flanigan, F. Romanov-Michailidis, N. A. White and T. Rovis, Chem. Rev., 2015, 115, 9307–9387; (f) X.-Y. Chen, Q. Liu, P. Chauhan and D. Enders, Angew. Chem., Int. Ed., 2017, 57, 3862–3873; (g) Y. Wang, D. H. Wei and W. J. Zhang, ChemCatChem, 2018, 10, 338–360; (h) K. J. R. Murauski, A. A. Jaworski and K. A. Scheidt, Chem. Soc. Rev., 2018, 47, 1773–1782.
6. For selected articles: (a) J. Izquierdo, A. Orue and K. A. Scheidt, J. Am. Chem. Soc., 2013, 135, 10634–10637; (b) Z. Q. Fu, H. Sun, S. J. Chen, B. Tiwari, G. H. Li and Y. R. Chi, Chem. Commun., 2013, 49, 261–263; (c) P. C. Chiang, J. Kaeobamrung and J. W. Bode, J. Am. Chem. Soc., 2007, 129, 3520–3521; (d) B. Cardinal-David, D. E. A. Raup and K. A. Scheidt, J. Am. Chem. Soc., 2010, 132, 5345–5347.
7. For selected articles: (a) J. F. Xu, C. L. Mou, T. S. Zhu, B. A. Song and Y. R. Chi, Org. Lett., 2014, 16, 3272–3275; (b) P. Haghshenas, J. W. Quail and M. Gravel, J. Org. Chem., 2016, 81, 12075–12083; (c) P. Haghshenas and M. Gravel, Org. Lett., 2016, 18, 4518–4521; (d) S. M. Langdon, C. Y. Legault and M. Gravel, J. Org. Chem., 2015, 80, 3597–3610.
8. For selected articles: (a) X. Q. Fang, X. K. Chen, H. Lv and Y. R. Chi, Angew. Chem., Int. Ed., 2011, 50, 11782–11785; (b) D. A. DiRocco and T. Rovis, J. Am. Chem. Soc., 2011, 133, 10402–10405; (c) T. Jousseaume, N. E. Wurz and F. Glorius, Angew. Chem., Int. Ed., 2011, 50, 1410–1414.
9. (a) B. S. Li, Y. H. Wang, Z. C. Jin, P. C. Zheng, R. Ganguly and Y. R. Chi, Nat. Commun., 2015, 6, 6207–6211; (b) Y. Wang, B. H. Wu, H. Y. Zhang, D. H. Wei and M. S. Tang, Phys. Chem. Chem. Phys., 2016, 18, 19933–19943; (c) Z. Q. Fu, J. F. Xu, T. S. Zhu, W. W. Y. Leong and Y. R. Chi, Nat. Chem., 2013, 5, 835–839; (d) Z. C. Jin, S. J. Chen, Y. H. Wang, P. C. Zheng, S. Yang and Y. R. Chi, Angew. Chem., Int. Ed., 2014, 53, 13506–13509; (e) L. Hao, S. J. Chen, J. F. Xu, B. Tiwari, Z. Q. Fu, T. Li, J. Lim and Y. R. Chi, Org. Lett., 2013, 15, 4956–4959; (f) Y. Y. Wang, D. H. Wei, Y. Wang, W. J. Zhang and M. S. Tang, ACS Catal., 2016, 6, 279–289; (g) J. Yan, K. X. Shi, C. T. Zhao, L. Y. Ding, S. S. Jiang, L. M. Yang and G. F. Zhong, Chem. Commun., 2018, 54, 1567–1570; (h) Z. X. Xiao, C. X. Yu, T. J. Li, X.-S. Wang and C. S. Yao, Org. Lett., 2014, 16, 3632–3635; (i) Q. Q. Shi, Y. Wang, Y. Y. Wang, L.-B. Qu, Y. Qiao and D. H. Wei, Org. Chem. Front., 2018, 5, 2739–2748.
10. C. Guo, M. Fleige, D. Janssen-Müller, C. G. Daniliuc and F. Glorius, Nat. Chem., 2015, 7, 842–847.
11. D. Janssen-Müller, M. Fleige, D. Schlüns, M. Wollenburg, C. G. Daniliuc, J. Neugebauer and F. Glorius, ACS Catal., 2016, 6, 5735–5739.
12. S. Bera, C. G. Daniliuc and A. Studer, Angew. Chem., Int. Ed., 2017, 56, 7402–7406.
13. D. M. Flanigan and T. Rovis, Chem. Sci., 2017, 8, 6566–6569.
14. G. D. Carmine, D. Ragno, O. Bortolini, P. P. Giovannini, A. Mazzanti, A. Massi and M. Fogagnolo, J. Org. Chem., 2018, 83, 2050–2057.
15. J. H. Xu, S. C. Zheng, J. W. Zhang, X. Y. Liu and B. Tan, Angew. Chem., Int. Ed., 2016, 55, 11834–11839.
16. For selected articles: (a) Y. Wang, D. H. Wei and M. S. Tang, J. Org. Chem., 2017, 82, 13043–13050; (b) Y. Wang, Y. Qiao, D. H. Wei and M. S. Tang, Org. Chem. Front., 2017, 4, 1987–1998; (c) Y. Wang, S.-R. Zhang, Y. Y. Wang, L.-B. Qu and D. H. Wei, Org. Chem. Front., 2018, 5, 2065–2072; (d) Y. Wang, L. J. Zheng, D. H. Wei and M. S. Tang, Org. Chem. Front., 2015, 2, 874–884; (e) Y. Wang, Y. Y. Wang, X. H. Wang, X. Li, L.-B. Qu and D. H. Wei, Catal. Sci. Technol., 2018, 8, 4229–4240.
17. (a) X. X. Wei, R. Fang and L. Z. Yang, Catal. Sci. Technol., 2015, 5, 3352–3362; (b) P.-C. Tu, L. Zhou, A. M. Kirillov, R. Fang and L. Z. Yang, Org. Chem. Front., 2018, 5, 1356–1365; (c) Y. Reddi and R. B. Sunoj, ACS Catal., 2017, 7, 530–537; (d) Y. Qiao, D. H. Wei and J. B. Chang, J. Org. Chem., 2015, 80, 8619–8630.
18. (a) C.-X. Yan, F. Yang, X. Yang, D.-G. Zhou and P.-P. Zhou, J. Org. Chem., 2017, 82, 3046–3061; (b) Q. Q. Shi, W. Zhang, Y. Wang, L.-B. Qu and D. H. Wei, Org. Biomol. Chem., 2018, 16, 2301–2311; (c) L. J. Zheng, M. S. Tang, Y. Wang, X. K. Guo, D. H. Wei and Y. Qiao, Org. Biomol. Chem., 2016, 14, 3130–3141.
19. (a) Y. Z. Xia, Y. Liang, Y. Y. Chen, M. Wang, L. Jiao, F. Huang, S. Liu, Y. H. Li and Z.-X. Yu, J. Am. Chem. Soc., 2007, 129, 3470–3471; (b) Y. Wang and Z.-X. Yu, J. Org. Chem., 2018, 83, 5384–5391; (c) Y. Wang, B. H. Wu, L. J. Zheng, D. H. Wei and M. S. Tang, Org. Chem. Front., 2016, 3, 190–203; (d) Y. Wang, M. S. Tang, Y. Y. Wang and D. H. Wei, J. Org. Chem., 2016, 81, 5370–5380.
20. (a) Y. Wang, X. K. Guo, M. S. Tang and D. H. Wei, J. Phys. Chem. A, 2015, 119, 8422–8431; (b) Y. Wang, D. H. Wei, Z. Y. Li, Y. Y. Zhu and M. S. Tang, J. Phys. Chem. A, 2014, 118, 4288–4300; (c) C. X. Yan, P.-P. Zhou, F.-L. Yang, R.-Z. Wu, X. Yang, F. Yang and X. F. Shao, Org. Chem. Front., 2018, 5, 2692–2709; (d) X. Li, Y. Y. Wang, Y. Wang, M. S. Tang, L.-B. Qu, Z. J. Li and D. H. Wei, J. Org. Chem., 2018, 83, 8543–8555; (e) X. Li, M. S. Tang, Y. Y. Wang, Y. Wang, Z. J. Li, L.-B. Qu and D. H. Wei, Chem. – Asian J., 2018, 13, 1710–1718; (f) W. Zhang, Y. Wang, D. H. Wei, M. S. Tang and X. J. Zhu, Org. Biomol. Chem., 2016, 14, 6577–6590.
21. (a) L. R. Domingo, J. A. Sáez, J. A. Joule, L. Rhyman and P. Ramasami, J. Org. Chem., 2013, 78, 1621–1629; (b) L. R. Domingo, M. Ríos-Gutiérrez and P. Pérez, J. Org. Chem., 2018, 83, 2182–2197.
22. (a) L. R. Domingo, P. Pérez and J. A. Sáez, RSC Adv., 2013, 3, 1486–1494; (b) L. J. Zheng, Y. Wang, D. H. Wei and Y. Qiao, Chem. – Asian J., 2016, 11, 3046–3054.
23. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision C.01, Gaussian Inc., Wallingford, CT, 2010.
24. (a) Y. Wang, C. Du, Y. Y. Wang, X. K. Guo, L. Fang, M.-P. Song, J.-L. Niu and D. H. Wei, Adv. Synth. Catal., 2018, 360, 2668–2677; (b) X. K. Guo, L.-B. Zhang, D. H. Wei and J.-L. Niu, Chem. Sci., 2015, 6, 7059–7071; (c) Y. Z. Lv, A. A. Ogunlana, H. L. Li, D. F. Gao, C. L. Wang and X. G. Bao, Catal. Sci. Technol., 2018, 8, 3379–3386; (d) Z. Y. Yu, X. T. Qi, Y. Z. Li, S. Liu and Y. Lan, Org. Chem. Front., 2016, 3, 209–216; (e) J. Y. Zhang, J. S. Lin, Y. W. Li, Y. X. Shao, X. Huang, C. Y. Zhao and Z. F. Ke, Catal. Sci. Technol., 2017, 7, 4866–4878; (f) X. Y. Lv, Y.-B. Wu and G. Lu, Catal. Sci. Technol., 2017, 7, 5049–5054.
25. (a) Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241; (b) Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157–167.
26. (a) W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261; (b) W. Sang-Aroon and V. Ruangpornvisuti, Int. J. Quantum Chem., 2007, 108, 1181–1188.
27. (a) B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 106, 5151–5158; (b) V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001.
28. T. Lu and F. W. Chen, J. Comput. Chem., 2011, 33, 580–592.
29. C. Y. Legault, CYLview, 1.0b, Universit'e de Sherbrooke, 2009, http://www.cylview.org.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8cy02238k

---