Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Ball size or ball mass – what matters in organic mechanochemical synthesis?
Adam A. L.
Michalchuk†
 *ab,
Ivan A.
Tumanov
*ab,
Ivan A.
Tumanov
 *ac and
Elena V.
Boldyreva
*ac and
Elena V.
Boldyreva
 *ac
*ac
aNovosibirsk State University, Pirogova Str. 2, Novosibirsk, 630090, Russian Federation. E-mail: i.tumanov.ssc@mail.ru; eboldyreva@catalysis.ru
bEaStCHEM School of Chemistry, University of Edinburgh, Joseph Black Building, David Brewster Rd., Edinburgh, UK. E-mail: adam.michalchuk@ed.ac.uk
cBoreskov Institute of Catalysis, Siberian Branch of the Russian Academy of Sciences, pr. Lavrentieva, 5, Novosibirsk 630090, Russian Federation
First published on 16th January 2019
Abstract
Ball mass is an important parameter that is known to have an influence on the outcome of a mechanochemical reaction induced by ball-milling. A standard way of modifying the ball mass is to change the size of the ball made of the same material. In this case, however, a change in mass is accompanied by a simulatneous change in the ball size. It is therefore not possible to disentangle the effects of mass and surface area in these cases. In the present work we report the results of experiments with specially designed and manufactured balls in which (1) milling ball mass is held constant, but their size differs, and (2) the ball mass is altered, with the diameter of the milling ball being held constant. Using the cocrystallisation of theophylline + nicotinamide as a case study it was found that both diameter and ball mass play crucial roles in determining the rate of a mechanochemical reaction. For comparison, we have also used milling balls with the same size (different mass), and others with the same mass (different size) made of different materials, as would be “traditional”. It was found that, despite having the same size, the lightest milling ball (nylon) was the most efficient in initiating the co-crystallisation, presumably due to the sorption of EtOH. Hence, the results of this manuscript also demonstrate how milling ball material can in fact be the most influential parameter, and potentially counterintuitive to classical mechanics.
Introduction
Ball-milling of solid mixtures has proved to be an efficient approach to the synthesis of organic and coordination compounds, ranging from multi-component crystals to poly-peptides.1–10 In particular, it is becoming increasingly important for obtaining pharmaceutical solids. Mechanochemical methods are attractive as environmentally benign techniques, and often permit rapid and high yield transformations. Despite their potential, the scale-up of mechanochemical reactions remains a great challenge. Unlike solution-phase chemistry, the sample in a mechanochemical reactor is not under equilibrium conditions, with transformations occurring as a result of stochastic, dynamic mechanical perturbation. Consequently, a transformation induced by mechanical treatment depends on many parameters, including the type, intensity and duration of treatment, the presence of fluid and solid additives, the ratio of the reactant particle size, and any preliminary mixing of the components.11–15 Any physicochemical transformation is driven by the relaxation of excess energy. In mechanochemistry, this excess energy is a function of mechanical impact, and is intimately connected to the mass and velocity of the impacting milling ball through the classical mechanical equations of motion.16–24Generally, reports which discuss the effects of the ball mass on mechanochemical transformations involve variation of the milling ball size (and hence mass).19,25 Alternatively, authors have varied the quantity of sample powder and thus the ball to sample mass ratio.20 Both methods lead to a change in the energy inserted into the sample, although only the former increases the total maximum energy input. Ball mass can influence mechanochemical transformations in a variety of ways. The primary effect can be associated to the increased energy of an accelerated body with larger mass. Reactions that require a critical minimum initiation energy will be strongly dependent on the mass of the milling ball. Mechanochemical reactions that are instead limited by the number of heterogeneous particle-particle contacts depend on ball mass through its influence on particle comminution and mixing.
Importantly, heavier milling balls tend in practice to be larger, and thus characterized by a larger surface area, increasing contact area with the sample. Unlike solution-phase chemistry, reaction zones in solid + solid mechanochemistry are limited to regions of the sample that are mechanically excited by the milling ball. Hence, an increase in milling ball surface area increases the proportion of sample being activated at each impact. One can liken this effect to milling experiments in which multiple milling balls are used. In such cases, an increase in reaction rate is not the result of increasing the energy of a single impact. It instead results from increasing the probability of striking the sample.
All physical and chemical transformations are limited in some way by collisions. This includes collisions between reacting molecules or particles to form a reactive contact, and between this reactive contact and an energy source (photon, electron, phonon, milling ball, etc.). These conditions must be simultaneously satisfied for a reaction to occur. This is particularly common in organic mechanochemistry, where sufficient thermal energy is often present in a system to facilitate a reaction. In such cases, the formation of reactive contacts (i.e. mixing) is limiting and the mechanochemical reaction can even take place in the absence of milling balls.26 In other cases, neither condition is initially met, and milling is required to achieve both. Thus it becomes very difficult to determine the mechanism by which a larger milling ball enhances reaction rate.
Quantitative analysis of a single-phase transformation suggested that increasing the size of a milling ball was more intimately related to an increase in its surface area, rather than the mass itself.19 That said, this previous study was also restricted by simultaneous variation in ball mass and surface area. It was therefore not possible to distinguish unambiguously between the two effects without specially designed experiments.
In this communication we report the results of a model study with specially designed and manufactured balls that differ in mass, but not in size. In addition, a series of milling balls were also manufactured that differ in size, but not in mass. Thus in this way, it may be possible to distinguish between the two potential modes of action of a milling ball. An easy way to produce such balls is to prepare them from different materials with different densities. However, this introduces an additional variable: the influence of material properties on mechanochemical reactions. While this effect is not expected to be universal, it has been documented in a number of organic and organometallic reactions.27–33
To exclude this effect, we have therefore also prepared “composite” milling balls, whose outer layers (i.e. those in contact with the sample) are composed of the same material (nylon and polyurethane), with the internal layer composed of varying quantities of lead. For comparison, we have also used balls having the same size (different mass), and of the same mass (different size) made of different materials.
As a case study, we investigate the ball-milling of a stoichiometric mixture of powdered theophylline + nicotinamide, Fig. 1. This system was chosen as the cocrystal is known to form readily upon mechanochemical treatment.34–38 Furthermore, this multi-component system represents the large majority of mechanochemical cocrystallistaion experiments that are currently reported in literature. Theophylline–nicotinamide mixtures are also known to cocrystallise during storage in high-humidity environments.39 The contacts between component particles can thus be expected to be critically important for this cocrystallisation, as has been observed in other moisture-mediated mechanochemical reactions.40
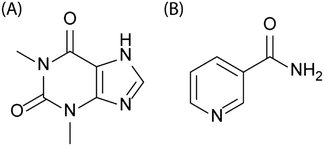 | ||
| Fig. 1 Schematic representation of the molecular structures of (A) theophylline and (B) nicotinamide. | ||
Experimental
Materials
Theophylline (Sigma-Aldrich, anhydrous, >99%) and nicotinamide (Fluka, 98.5%) were used as supplied, without further purification. Liquid assisted grinding (LAG) was performed using ethanol (distilled, 96%). X-ray powder diffraction of the pure components verified these solid phases to be orthorhombic theophylline (P21/n; form II) and nicotinamide.Ball milling
Ball milling was performed at room temperature in a Retsch Cryomill equipped with 5 ml milling jars (internal diameter 12 mm, internal length 44.6 mm), at vibration frequency of 25 Hz. The variety of milling balls used in this study is summarized in Table 1. The composite balls (CB) were generated from polyurethane or nylon balls, loaded with lead cores. All samples contained 180 mg of theophylline and 122 mg of nicotinamide (1 mmol of each reactant), a droplet of ca. 10 μL of ethanol was added to each reaction mixture before milling. Each experiment was performed in duplicate, on different days (once in summer and once in autumn), to ensure qualitative reproducibility. Seemingly anomalous experiments with nylon milling balls were performed in triplicate.| Material | Mass/g | Diameter/mm | |
|---|---|---|---|
| B1 | Brass | 0.50 | 4.7 |
| B2 | Brass | 1.13 | 6.4 |
| B3 | Brass | 3.80 | 9.5 |
| B4 | Aluminium | 0.13 | 4.7 |
| B5 | Aluminium | 0.36 | 6.4 |
| B6 | Aluminium | 0.72 | 8.0 |
| B7 | PTFE | 0.12 | 4.7 |
| B8 | PTFE | 0.30 | 6.4 |
| B9 | PTFE | 1.00 | 9.5 |
| B10 | Nylon | 0.06 | 4.7 |
| B11 | Nylon | 0.15 | 6.4 |
| B12 | Nylon | 0.50 | 9.5 |
| B13 | PU | 0.20 | 6.8 |
| CB1 | PU | 0.40 | 6.8 |
| CB2 | Nylon | 0.50 | 6.4 |
Characterisation
All solid samples were characterised by X-ray powder diffraction (XRPD) using a STOE-MP diffractometer. The diffractometer was equipped with a Cu anode (Kα1 = 1.54056 Å) and a bent Ge(111) monochromator.Results and discussion
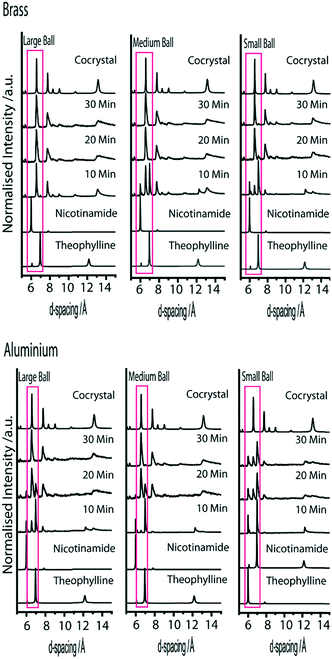
Same material, different size/mass
We begin discussion by exemplifying the standard approach used in mechanochemical literature.19,25 That is, we monitor ex situ the evolution of mechanochemical co-crystallisation using milling balls composed of the same material, but having different diameter and mass. In the ordering of decreasing mass, the selected milling balls are composed of brass, aluminium, polytetrafluoroethylene (PTFE), and nylon.Formation of the cocrystal can be qualitatively monitored by considering the major peaks associated with the reactant and product phases between d-spacings of 6–10 Å, Fig. 2. The product phase exhibits dominant reflections at 6.57 Å, corresponding to the (022) and (013) Bragg planes, as well as the (021) plane at a d-spacing 7.75 Å. The reactant phases instead exhibit their dominant reflections at d-spacings of 5.99 Å (nicotinamide (120) plane) and 6.96 Å (theophylline (201) plane).
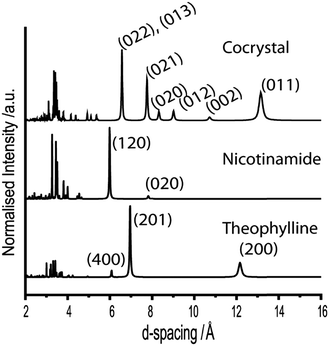 | ||
| Fig. 2 Simulated X-ray powder diffraction patterns for the three crystalline phases under investigation. The Bragg plane miller indices are indicated for the well resolved reflections in each phase. | ||
When milling is performed with the heaviest milling balls (brass, B1–B3), the reaction appears to go to completion within 30 min, regardless of which ball is chosen, Fig. 3. In fact, experiments with B3 were found to be complete in approximately 10 min (only trace quantities of reactant remain). In contrast, experiments with B2 contain large quantities of residual reactant after 10 min treatment, but reach completion within 20 min milling. Experiments with B1 contain only small quantities of product after 10 minutes, and reach completion within approximately 30 min milling. However, trace quantities of reactant remain after 30 min milling with B1. However, notable rheological changes were observed. Samples milled with B1 consisted mostly of freely-flowing powder, with small pellets having formed at both ends of the milling jar and on the surface of the milling ball. As the milling ball diameter was increased, the amount of free-flowing powder decreased. Samples milled with B3 were almost fully pelleted within the milling jar and over the surface of the milling ball. While this does not appear to adversely affect the reaction in the present case, the presence of tabletting and changes in powder rheology have been known to affect mechanochemical reactions in other systems.12,41,42
Despite having the same diameter as the brass milling balls, experiments conducted with lighter aluminium milling balls (B4–B6) did noticeably slow the reaction. In contrast to B3, experiments with B6 induced only slight conversion to the cocrystal in 10 min, with completion not seen until approximately 30 min milling. The conversion to cocrystal after 10 min milling with B5 is qualitatively less than with B6, but again reaches apparent completion within 30 min milling, Fig. 3. In drastic contrast is the profile obtained using the smallest milling ball. Only trace quantities of the product phase are visible after 10 min, with limited conversion to the product phase obtained after 30 minutes of milling. Further work is required to determine whether the small ball is capable of driving the reaction to completion given sufficient time, or if the energy imparted by this milling ball is below the critical threshold required to ensure mixing of reactant throughout the entire process.
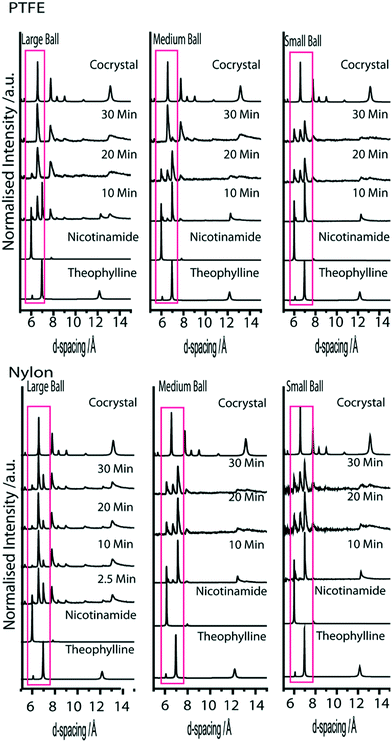
Milling balls constructed from synthetic polymer, PTFE, have approximately the same mass as the aluminium. We first note that the largest PTFE ball available (B9) was slightly larger than the large aluminium milling ball (B6), and hence weighed slightly more. It is therefore not surprising to find that a qualitative comparison of the reaction rate suggests the PTFE-induced cocrystallisation to occur slightly more quickly than the aluminium experiments, Fig. 4. However, B8 and B7 are effectively the same as the corresponding aluminium balls B5 and B4, respectively. Overall, B7–8 are found to behave in a similar manner to B4–5, suggesting that the material choice has little consequence in this case.
The case of nylon balls seems anomalous with respect to the trend observed across the other three systems, Fig. 4. Despite being notably lighter than all other milling balls tested, the nylon-induced reaction appears to proceed much faster than the aluminium and PTFE examples. This anomalous effect is not yet understood. Both PTFE and nylon are known to develop static charges (although opposite charges) when sheared, and thus this is unlikely to be the dominating effect, unless the reaction is sensitive to a particular charge. Instead, we suggest the enhanced effect of nylon may be due to its sorption of EtOH.43 Hence, impact of reactant powder with the nylon ball would introduce EtOH at every impact. While further work is required to elucidate this obscurity, it is clear that the choice of milling ball material can have an apparently drastic consequence on the rate of the reaction.
Experiments conducted with B1, B5, B8 and B12 are all performed with milling balls with effectively identical mass. However, while B5 (aluminium) and B8 (PTFE) both have diameter 6.4 mm, B1 (brass) has diameter 4.7 mm and B12 (nylon) has a diameter of 9.5 mm. If the XRPD patterns are compared after only 10 min milling, the lightest ball, B12, appears to have the largest amount of product phase present in the mixture. However, we stress that nylon appears to be anomalous in its ability to facilitate the LAG process reported here. As the experiment progresses to 30 min milling, the heaviest balls, B1 and B5, contain the largest amount of product phase. In fact, despite leading to the most rapid initial reaction rate, the milling reaction performed with B12 is least complete after 30 minutes.
Independent variation of milling ball parameters: size or mass
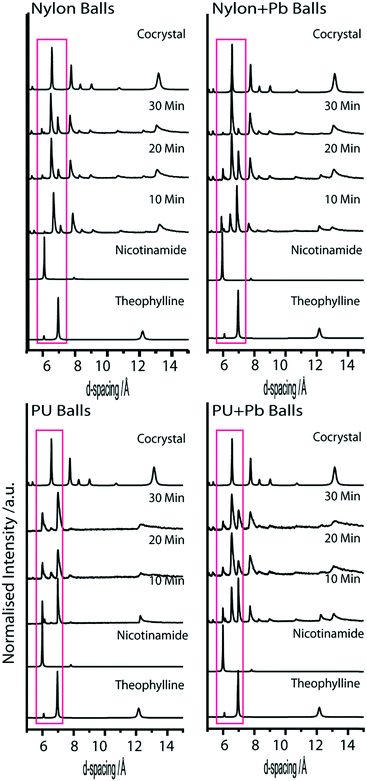
In an attempt to eliminate the effects of milling ball material on reaction rate, two further experiments were conducted using composite milling balls. Unfortunately, the composition of these milling balls was restricted to machinability. A lead core was added to a nylon milling ball of size B11, increasing its mass from 0.15 g to 0.50 g (i.e. the same mass as B12). Hence, comparison of experiments conducted with B11 and CB2 offers a means to investigate the relative effect of two milling balls with the same size and material, but different mass. Milling experiments conducted with CB2 (i.e. B11 with incorporated Pb weight) does lead to a more rapid conversion than the unaltered B11 experiments (see Fig. 5 compared to Fig. 4). Importantly, however, despite having the same mass, CB2 induced mechanochemical transformation substantially slower than B12 (i.e. the largest diameter nylon milling ball). This thus demonstrates that the impact mass is not the only factor that must be considered when investigating mechanochemical experiments. The explanation for this is rather straightforward, although it is often overlooked. As with any chemical or physical transformation, excess energy is required. In mechanochemical experiments, this excitation energy is pulsed, and occurs at the site of impact between reactant and milling ball. Hence, larger milling balls activate a larger quantity of powder at any given impact.In a second study, a milling ball was constructed from polyurethane (CB1), and compared to a pure polyurethane ball (B13). These were constructed so as to produce two milling balls composed of the same material, with the same diameter, but with different mass. As expected from the previous discussion, the larger impact energy does indeed lead to a considerably faster reaction rate than the lighter PU ball, Fig. 5. An interpretation for this phenomenon is somewhat less trivial than that offered for larger milling ball diameter. However, an explanation likely rests in a description for the depth of activation of the powder or heat generation (and hence quantity of powder activated). Both of these phenomena depend on the kinetic energy of the milling ball, and hence upon its mass.
Conclusions
The ‘excitation energy’ involved in mechanochemical experiments is pulsed, and distributed unequally across the sample as a function of time. This stems from the stochasticity of milling ball motion within a milling jar. Attempts at correlating milling ball characteristics with reaction rate have often been ascribed to fluid phase concepts, correlating only the excitation energy (i.e. milling ball kinetic energy) to reaction rate. In the present study, we present a qualitative investigation of the relative rates of mechano-cocrystallisation of theophylline + nicotinamide under LAG conditions. The reaction was followed using milling balls made from four different materials, namely brass, aluminium, PTFE and nylon. Each milling ball was available in three sizes, differing simultaneously in diameter and mass. As expected from literature, the larger (and simultaneously heavier) milling balls led to more rapid transformation. The only exception was nylon which, despite being the lightest, exhibited the second highest reaction rate. This clearly demonstrates that, in addition to physical dimensions of the milling ball, its material composition can also be important. To separate ball diameter and ball mass, composite milling balls were constructed. By analysing the relative rate of reaction induced by two nylon balls, each with the same mass but different diameter, it was clearly observed that the larger milling ball led to much faster reaction rate. This is likely due to the increased quantity of powder that is activated upon each impact. A second set of composite balls composed of polyurethane were also investigated. These milling balls had the same diameter, but different mass. The heavier of the two milling balls led to faster reaction rate in this case. The interpretation for this effect is less trivial, but likely stems from deeper penetration into the powder sample, or generation of larger quantities of heat upon impact. Both of these factors depend on the kinetic energy and hence mass of the milling ball.It is therefore evident that both diameter and ball mass play a crucial role in determining the rate of a mechanochemical reaction. Both factors must be considered when designing and interpreting mechanochemical reactions.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
IAT acknowledges the support by a grant from Russian Foundation for Basic Research (RFBR), research project No. 16-33-60086 mol_a_dk for IAT. EVB acknowledges support from the Russian Ministry and Science and Education.Notes and references
- D. Tan and T. Friščić, Eur. J. Org. Chem., 2018, 2018, 18–33 CrossRef CAS.
- H. Kulla, S. Haferkamp, I. Akhmetova, M. Rçllig, C. Maierhofer, K. Rademann and F. Emmerling, Angew. Chem., Int. Ed., 2018, 5930–5933 CrossRef CAS PubMed.
- E. Boldyreva, Chem. Soc. Rev., 2013, 42, 7719–7738 RSC.
- N. Kamali, K. Gniado, P. McArdle and A. Erxleben, Org. Process Res. Dev., 2018, 22, 796–802 CrossRef CAS.
- D. E. Crawford, C. K. G. Miskimmin, A. B. Albadarin, G. Walker and S. L. James, Green Chem., 2017, 19, 1507–1518 RSC.
- L. Tröbs and F. Emmerling, Faraday Discuss., 2014, 170, 109–119 RSC.
- M. P. Szymański, H. Jȩdrzejewska, M. Wierzbicki and A. Szumna, Phys. Chem. Chem. Phys., 2017, 19, 15676–15680 RSC.
- M. Glavinović, F. Qi, A. D. Katsenis, T. Friščić and J. P. Lumb, Chem. Sci., 2015, 7, 707–712 RSC.
- F. Fischer, M. Joester, K. Rademann and F. Emmerling, Chem. – Eur. J., 2015, 21, 14969–14974 CrossRef CAS PubMed.
- V. Declerck, P. Nun, J. Martinez and F. Lamaty, Angew. Chem., Int. Ed., 2009, 48, 9318–9321 CrossRef CAS PubMed.
- A. M. Belenguer, G. I. Lampronti, A. J. Cruz-Cabeza, C. A. Hunter and J. K. M. Sanders, Chem. Sci., 2016, 7, 6617–6627 RSC.
- A. A. L. Michalchuk, I. A. Tumanov and E. V. Boldyreva, CrystEngComm, 2013, 15, 6403–6412 RSC.
- A. A. L. Michalchuk, I. A. Tumanov, V. A. Drebushchak and E. V. Boldyreva, Faraday Discuss., 2014, 170, 311–335 RSC.
- N. Bouvart, R.-M. Palix, S. Arkhipov, I. A. Tumanov, A. A. L. Michalchuk and E. Boldyreva, CrystEngComm, 2018, 20, 1797–1803 RSC.
- E. A. Losev and E. V. Boldyreva, CrystEngComm, 2014, 16, 3857 RSC.
- M. Abdellaoui and E. Gaffet, J. Alloys Compd., 1994, 209, 351–361 CrossRef CAS.
- Y. Chen, M. Bibole, R. Le Hazif and G. Martin, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 14–21 CrossRef CAS.
- L. Takacs, Prog. Mater. Sci., 2002, 47, 355–414 CrossRef CAS.
- A. A. L. Michalchuk, I. A. Tumanov and E. V. Boldyreva, J. Mater. Sci., 2018, 53, 13380–13389 CrossRef CAS.
- H. Kulla, F. Fischer, S. Benemann, K. Rademann and F. Emmerling, CrystEngComm, 2017, 19, 3902–3907 RSC.
- J. Ding, T. Tsuzuki and P. G. McCormick, J. Alloys Compd., 1996, 234, 15–17 CrossRef.
- G. B. Schaffer and J. S. Forrester, J. Mater. Sci., 1997, 32, 3157–3162 CrossRef CAS.
- E. V. Shelekhov, V. V. Tcherdyntsev, L. Y. Pustov, S. D. Kaloshkin and I. A. Tomilin, Mater. Sci. Forum, 2000, 343–346, 603–608 CAS.
- A. Wagih, A. Fathy and A. M. Kabeel, Adv. Powder Technol., 2018, 29, 2527–2537 CrossRef CAS.
- F. Fischer, N. Fendel, S. Greiser, K. Rademann and F. Emmerling, Org. Process Res. Dev., 2017, 21, 655–659 CrossRef CAS.
- A. A. L. Michalchuk, K. S. Hope, S. R. Kennedy, M. V. Blanco, E. V. Boldyreva and C. R. Pulham, Chem. Commun., 2018, 54, 4033–4036 RSC.
- A. Stolle, T. Szuppa, S. E. S. Leonhardt and B. Ondruschka, Chem. Soc. Rev., 2011, 40, 2317–2329 RSC.
- J. G. Hernández and T. Friščić, Tetrahedron Lett., 2015, 56, 4253–4265 CrossRef.
- T. L. Cook, J. A. Walker and J. Mack, Green Chem., 2013, 15, 617–619 RSC.
- J. G. Hernández and C. Bolm, J. Org. Chem., 2017, 82, 4007–4019 CrossRef PubMed.
- J. L. Do, D. Tan and T. Friščić, Angew. Chem., Int. Ed., 2018, 57, 2667–2671 CrossRef CAS PubMed.
- Y. Sawama, N. Yasukawa, K. Ban, R. Goto, M. Niikawa, Y. Monguchi, M. Itoh and H. Sajiki, Org. Lett., 2018, 20, 2892–2896 CrossRef CAS PubMed.
- L. Chen, M. O. Bovee, B. E. Lemma, K. S. M. Keithley, S. L. Pilson, M. G. Coleman and J. Mack, Angew. Chem., Int. Ed., 2015, 54, 11084–11087 CrossRef CAS PubMed.
- D. Tan, L. Loots and T. Friščić, Chem. Commun., 2016, 52, 7760–7781 RSC.
- J. Lu and S. Rohani, Org. Process Res. Dev., 2009, 13, 1269–1275 CrossRef CAS.
- M. Karimi-Jafari, L. Padrela, G. M. Walker and D. M. Croker, Cryst. Growth Des., 2018, 18(10), 6370–6387 CrossRef CAS.
- A. Paradkar, R. S. Dhumal, A. L. Kelly, P. York and P. D. Coates, Pharm. Res., 2010, 27, 2725–2733 CrossRef PubMed.
- S. Patil, P. Agarwal, S. Rojatkar and K. Mahadik, Anal. Chem. Lett., 2018, 8, 321–330 CrossRef CAS.
- K. Izutsu, T. Koide, N. Takata, Y. Ikeda, M. Ono, M. Inoue, T. Fukami and E. Yonemochi, Chem. Pharm. Bull., 2016, 64, 1421–1430 CrossRef CAS PubMed.
- I. A. Tumanov, A. A. L. Michalchuk, A. A. Politov, E. V. Boldyreva and V. V. Boldyrev, CrystEngComm, 2017, 19, 2830–2835 RSC.
- A. A. L. Michalchuk, I. A. Tumanov, S. Konar, S. A. J. Kimber, C. R. Pulham and E. V. Boldyreva, Adv. Sci., 2017, 4, 1700132 CrossRef PubMed.
- B. P. Hutchings, D. E. Crawford, L. Gao, P. Hu and S. L. James, Angew. Chem., Int. Ed., 2017, 1–6 Search PubMed.
- M. P. McCourt, G. M. McNally and A. C. Ruddy, Dev. Chem. Eng. Miner. Process., 2004, 12, 159–168 CrossRef.
Footnote |
| † Current address: BAM Federal Institute for Materials Research and Testing, Richard-Willstätter-Straße 11, 12489 Berlin, Germany. |
| This journal is © The Royal Society of Chemistry 2019 |