Three-dimensional depth profiling of prostate tissue by micro ATR-FTIR spectroscopic imaging with variable angles of incidence†
Cai Li
Song
and
Sergei G.
Kazarian
 *
*
Department of Chemical Engineering, Imperial College London, South Kensington Campus, London SW7 2AZ, UK. E-mail: s.kazarian@imperial.ac.uk
First published on 29th January 2019
Abstract
The depth of penetration and effective thickness in ATR-FTIR spectroscopic imaging are dependent on the wavelength and angle of incidence of the incoming light beam. We have demonstrated, for the first time, that variable angle micro ATR-FTIR, which is created via the insertion of circular apertures, is intrinsic at examining embedded components within a prostate tissue specimen. This is done by constructing a 3D model from the stacks of 2D chemical images obtained, each of which represents the spatial distribution of a chosen spectral band assigned to the component of interest at a different probing depth. ATR-FTIR imaging is also shown to have the ability to resolve subcellular components of cells such as organelles. For differentiation of diseased and non-diseased tissues, statistical tests are employed to analyse the spectral datasets obtained. When the second derivative of the spectral datasets was subjected to t-test analysis, the spectral differences between both samples in the fingerprint region are shown to be more significant at a shallow depth of penetration, with the greatest variance at the spectral band of 1235 cm−1 (vasPO2−), depicted by plotting the scores of PCA on its first two PCs. Overall, this paper demonstrates a non-destructive, label-free approach for examining heterogeneous biological samples in the z-direction to construct a 3D model using micro ATR-FTIR imaging, in a qualitative and semi-quantitative manner.
Introduction
Fourier transform infrared (FTIR) spectroscopic imaging is a label-free vibrational spectroscopic technique that allows the study of biological materials to be carried out without the need for staining.1 FTIR spectroscopy has been widely used to study diseases.2 Its chemical specificity gives insights into the differentiation of diseases based on their chemical content. The most common modes of measurements in FTIR imaging are transmission and attenuated total reflection (ATR). The principles of the ATR-FTIR spectroscopic technique are as follows: when the incoming infrared (IR) light beam reaches the internal reflection element (IRE) of a high refractive index at an angle greater than its critical angle, total internal reflection takes place. At the interface between the sample and the crystal, an evanescent wave penetrates the sample in the range of a few micrometers. The measured absorption comes from the interaction of the evanescent wave with the sample. Typical IREs used for the study of biological specimens are zinc selenide (ZnSe), diamond and germanium (Ge) crystals.3 The ATR-FTIR imaging technique has its advantages and limitations. When coupled with a focal plane array (FPA) detector, it allows simultaneous acquisition of thousands of spectra, thereby saving time to record spectra from a large field of view (FOV) compared to a single element detector and enabling more accurate and quicker disease diagnostics. In addition, chemical images taken with an ATR crystal exhibit a higher spatial resolution compared to images obtained via the transmission mode.4 This is particularly advantageous for the investigation of small regions of interest in the sample. In the case of a biological specimen, the cellular and sub-cellular components could be explored in detail. ATR-FTIR imaging has also been deemed suitable to study live cells in an aqueous environment5 due to its shallow probing depth and thus the reduced interference of water spectra, which will result in the ‘dilution’ of the characteristic bands of the cells if this interference is not minimized. Besides, the Mie scattering phenomenon that causes peak shifts and spectral distortions, and consequently leads to misinterpretation of the results is avoided in ATR-FTIR spectroscopy. This eliminates the need for resolving Mie scattering issues with a complicated and tedious correction algorithm.6,7 In ATR-FTIR measurements, however, the sample needs to be in good contact with the crystal and with tissue samples, and due to their soft nature, the impression left by the crystal might cause damage.The approach of acquiring 3-dimensional (3D) imaging information by using a variable angle macro-ATR accessory for depth profiling has been demonstrated,8 but similar application with micro ATR-FTIR imaging in both qualitative and quantitative manners is very limited. The only paper describing variable angle micro ATR was that by Wrobel et al.;9 however, that work was on the investigation of homogeneous samples, i.e. PS, PMMA, and PDMS polymer films only. Importantly, those results give insight into the potentiality to extend this work to study the structure and morphology of tissues which may be employed for disease identification. This paper focuses on the use of the variable angle micro ATR-FTIR spectroscopic imaging technique to study the variability of the chemical content of prostate tissues across various probing depths. It should be realised that the methodology used in this paper is not the same as constructing a 3D model from the stacks of 2-dimensional (2D) slices of the images of the microtomed thin layers of samples in transmission mode, as it was done by varying the angle of incidence alone and multiple microtoming was not required.
Experimental methods
Attenuated total reflection microscopy
The experiments were carried out with a Cary 620 FTIR microscope coupled to an Agilent Varian 670 spectrometer (Agilent Technologies, Inc.). The microscope was equipped with a slide-on ATR accessory attached to the 15×-Cassegrain objective of the microscope, which enables different apertures to be introduced for the study of controlled angles of incidence. The internal reflection element (IRE) for ATR in this study is a germanium (Ge) crystal with a refractive index of 4. A liquid nitrogen cooled 64 × 64-pixel focal plane array (FPA), which has a field of view of 70 × 70 μm2, was used for simultaneous acquisition of IR spectral data. All measurements were taken in the mid IR range from 3900 cm−1 to 900 cm−1, at 8 cm−1 spectral resolution and with 256 coadded scans. The data obtained were processed and constructed into 2D- and 3D-chemical models with Matlab R2017b (The MathWorks, Inc.). To warrant the accuracy of the image obtained at different probing depths, a 0.01 g precision digital scale was placed beneath the sample to ensure that a uniform contact pressure was applied throughout the study at 5.00 ± 0.05 g. A reproducible pressure control was identified to be crucial for ATR-FTIR sampling experiments.10Sample preparation
The biological samples used in this study were prostate biopsy tissues. The tissues were microtomed from a paraffin-embedded specimen block at 3 μm thickness, after which they were mounted onto a 2 mm thick CaF2 window (Crystran Ltd). Two different tissues from the same patient were examined under ATR-FTIR imaging, one of which is a healthy section and the other is a malignant tissue. A Gleason score of 3 + 3 was assigned to the area of malignancy identified within the malignant tissue. The H & E images of the biopsy section were shown in a previous publication.4 All biopsy samples were de-paraffinized before subjecting to the measurement. The standard protocol was used for de-paraffinization as follows: the tissues were washed with hexane (HPLC grade) for 5 min, followed by 100, 95, 70, and 50 (v/v %) ethanol (HPLC grade), each for 2 min before being air-dried for 1 hour under ambient conditions.4 The tissues were kept in a desiccator at room temperature when no measurement was taken throughout the study.Design of the apertures
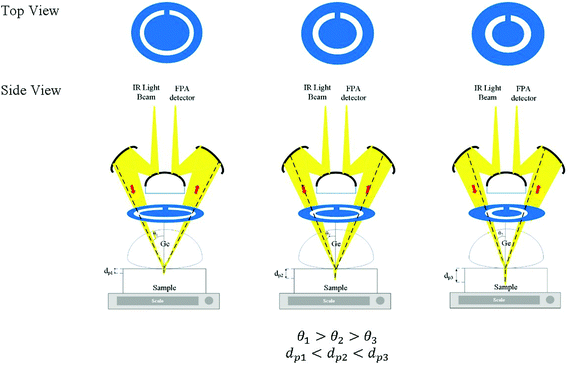
Laser-cut full circle apertures, with the circular slit width remaining consistent at 3 mm, were used to introduce multiple depths of penetration into the sample probed in this study. The light beam was circular and hence a circular slit within the aperture enables the maximum amount of light to pass through at the selected angle and be collected by micro ATR. The apertures were created with varying distances from the centre. The set-up of the aperture is shown in Fig. 1 below. The material used as the aperture was a black opaque acrylic with a thickness of 2 mm. Seven apertures (A1–7) were created in addition to the measurement without an aperture (A0), covering various incident angles of the IR beam, summarized in Table 1.| Aperture | Estimated θ | Estimated de@900 cm−1/μm (n2 = 1.45) | Estimated de@4000 cm−1/μm (n2 = 1.45) |
|---|---|---|---|
| A1 | 30.7 | 1.494 | 0.336 |
| A2 | 32.0 | 1.340 | 0.301 |
| A3 | 33.0 | 1.242 | 0.279 |
| A4 | 34.6 | 1.112 | 0.250 |
| A5 | 36.5 | 0.975 | 0.222 |
| A0 | 38.3 | 0.893 | 0.201 |
| A6 | 41.3 | 0.766 | 0.173 |
| A7 | 41.8 | 0.747 | 0.172 |
Calibration of the angles of incidence from the measured effective thickness
The concept of effective thickness, de, was applied to estimate the angles of incidence of the IR light beam with apertures. This quantity is dependent on the polarization of the light beam, angle of incidence and the refractive indices of IRE and the sample. de represents the thickness of a sample that would result in the same absorbance in a hypothetical transmission experiment, given by Harrick in eqn (1) and (2).11,12 It enables the straightforward application of Beer–Lambert's law on the spectral data obtained by ATR measurements, which states that the absorbance of a spectral band is directly proportional to de.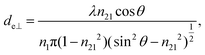 | (1) |
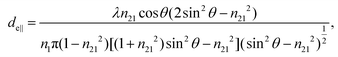 | (2) |
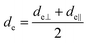 | (3) |
Although eqn (1)–(3) become the standard for the calculation of de in ATR measurement, they fail to account for the effect of anomalous dispersion on n2, that is prevalent for strongly absorbing samples. Because of this assumption that n2 remains constant, Harrick's equations have limitations on its applicability for non-absorbing or weakly absorbing bands only.13 Further methods to improve the accuracy of Harrick's equations were suggested and the inclusion of the optical constant method to the calculation was found to be the best for strongly absorbing media in their study. Nonetheless, the above less cumbersome formalism was used for the approximate determination of the incident angle in this experiment; as pointed out,14 when the spectral band of the bending mode of water was investigated, the deviation between the actual and approximate calculation fell within the experimental error, i.e. less than 3%.
On the other hand, the penetration depth, dp, is the normal distance from the interface between the IRE and sample where the intensity of the electric field of the evanescent wave decays to 1/e of its maximum value at the IRE surface.3dp is essentially different from de by definition, given by the following expression:
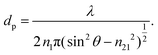 | (4) |
The value of dp approaches that of de when 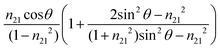 closes to 1, independent of the wavelength of the illumination beam. Both quantities of depths are in the order of micron in micro-ATR FTIR measurement. de and dp from the samples of different refractive indices were compared. For water, these values converge at ≈40°; whilst for the tissue specimen, this occurs at ≈35°, thus in our study where the angle falls between 35° and 40°, both eqn (3) and (4) are similarly applicable. The angle where de and dp are equal decreases when n2 increases, shown in the ESI (Fig. S1–S3†).
closes to 1, independent of the wavelength of the illumination beam. Both quantities of depths are in the order of micron in micro-ATR FTIR measurement. de and dp from the samples of different refractive indices were compared. For water, these values converge at ≈40°; whilst for the tissue specimen, this occurs at ≈35°, thus in our study where the angle falls between 35° and 40°, both eqn (3) and (4) are similarly applicable. The angle where de and dp are equal decreases when n2 increases, shown in the ESI (Fig. S1–S3†).
Results and discussion
Calibration of the apertures with liquid water
The infrared absorption of liquid water has been thoroughly investigated through theories and experiments to date. The correlation between its absorption and structures, as well as its dynamics, was well studied.15–17 Due to the extensive library of information available on the infrared spectrum of water, it was chosen as a reliable calibrating sample in this study. The incident angles were estimated from the peak absorbance of water from the baseline at a spectral band of 1643 cm−1 (assigned to the vibrational bending mode of water), Awater(1643), with known εwater = 21.8 M−1 cm−1 (ref. 18) and cwater = 55.5 M. From Beer–Lambert's law, de was calculated from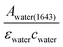 , which was then substituted into eqn (1)–(3) for the calculation of θ. The spectra of water obtained are shown in the ESI (Fig. S4 and S5†).
, which was then substituted into eqn (1)–(3) for the calculation of θ. The spectra of water obtained are shown in the ESI (Fig. S4 and S5†).
θ were found to be 30.7°, 32.0°, 33.0°, 34.6°, 36.5°, 41.3°, and 41.8° for A1–7, respectively, while A0 was 38.3°. The latter value is consistent with the manufacturer's specification of the 15× objective used, given NA = 0.62 (in transmission) and half angle of the light cone, 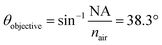 . Aperture A7 has the largest radius, hence allowing light to reach the sample at the greatest angle, probing the sample at its outermost (shallowest) layer closest to the surface. The radius of the aperture decreases from A7 to A1, measuring the sample at an increasing de.
. Aperture A7 has the largest radius, hence allowing light to reach the sample at the greatest angle, probing the sample at its outermost (shallowest) layer closest to the surface. The radius of the aperture decreases from A7 to A1, measuring the sample at an increasing de.
Chemical images at different penetration depths using apertures
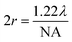 .19 In ATR measurement, the light passes through Ge IRE with a refractive index of 4, thus increasing the NA of the system by 4 times. In practice, the actual spatial resolution was found to be between 5 and 20 μm for mid-IR,20 lower than the value obtained from the Rayleigh criterion. Measurement of the prostate tissue at variable angles of incidence resulted in a non-uniformity of the spatial resolution of the 2D chemical images obtained in the x- and y-directions, as expected in the ATR-FTIR imaging with the microscope used in this study. A similar observation was noted for macro ATR-FTIR imaging with the diamond reflection accessory from the change in the aspect ratio of the imaging areas.21,22 The actual vertical and horizontal spatial resolution of the images in this work was estimated to be 5.3 μm and 4.2 μm, respectively, with the edge response method by measuring along a line across a sharp polyurethane/PMMA interface at 1600 cm−1 (6.25 μm in wavelength), shown in the ESI (Fig. S6–S9 and Table S1†), compared to 3.07 μm obtained when calculated with the Rayleigh criterion at the same wavelength. The observed disparity in the vertical and horizontal spatial resolution arises from the non-uniform illumination of the objective, since only half of the objective is used to illuminate the sample while the other half allows light to be collected in the setting of an IR microscope.3,21
.19 In ATR measurement, the light passes through Ge IRE with a refractive index of 4, thus increasing the NA of the system by 4 times. In practice, the actual spatial resolution was found to be between 5 and 20 μm for mid-IR,20 lower than the value obtained from the Rayleigh criterion. Measurement of the prostate tissue at variable angles of incidence resulted in a non-uniformity of the spatial resolution of the 2D chemical images obtained in the x- and y-directions, as expected in the ATR-FTIR imaging with the microscope used in this study. A similar observation was noted for macro ATR-FTIR imaging with the diamond reflection accessory from the change in the aspect ratio of the imaging areas.21,22 The actual vertical and horizontal spatial resolution of the images in this work was estimated to be 5.3 μm and 4.2 μm, respectively, with the edge response method by measuring along a line across a sharp polyurethane/PMMA interface at 1600 cm−1 (6.25 μm in wavelength), shown in the ESI (Fig. S6–S9 and Table S1†), compared to 3.07 μm obtained when calculated with the Rayleigh criterion at the same wavelength. The observed disparity in the vertical and horizontal spatial resolution arises from the non-uniform illumination of the objective, since only half of the objective is used to illuminate the sample while the other half allows light to be collected in the setting of an IR microscope.3,21
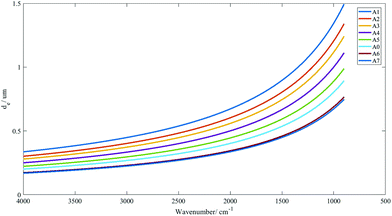
The range of penetration depths covered between 900 cm−1 and 4000 cm−1 with various apertures created is shown in Fig. 2, with the assumption that the tissue has a uniform refractive index of 1.45 (taking the mean of the refractive indices of a biological tissue, which was typically reported to lie between 1.35 and 1.55 (ref. 23)), albeit observations in previous studies that inhomogeneity in the optical properties of diseased and non-diseased tissue exists.24,25
Imaging of prostate tissues
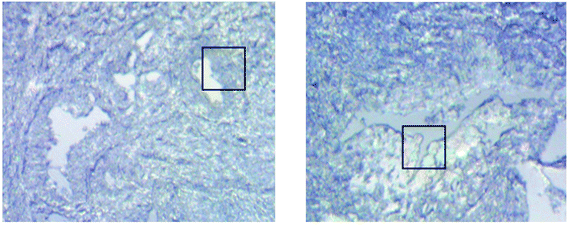
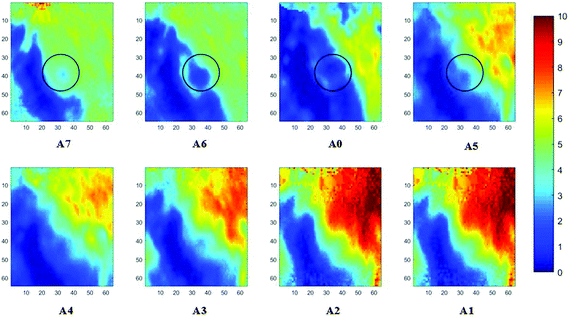
Measurements of the prostate biopsy with variable angles of incidence have been performed with the Ge crystal in contact with the sample at a constant pressure (described in Experimental methods). The areas of measurement are outlined in the visible images obtained under a 15× light microscope (Fig. 3). The distributions of the integrated absorbance at 1643 cm−1, assigned to the amide I band (mostly attributed to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching mode), have been constructed as chemical images and are shown in Fig. 5 (healthy tissue) and Fig. 4 (cancerous tissue), respectively. The area of strong amide I absorbance was associated with the cytoplasm of the cells which contains a high amount of proteins. At a greater penetration depth, the absorbance of the amide I band increases, creating an image of good contrast between the tissue and lumen (areas of weak absorbance). This observation is expected as the absorbance is dependent on the sample thickness, which increases with a greater probing depth. The mean absorbance spectra of 3 × 3 binned tissue areas of strong amide I absorbance with each aperture are plotted in the ESI (Fig. S10†). The variation in the morphology of the tissue along the z-axis has also been successfully captured in the images obtained from different penetration depths. In Fig. 5, a lumen that was embedded within the tissue appeared at the centre of the image for A6 and A0, which were not captured in either A7 or A5; whilst in Fig. 4, cells that are deep within the tissue layers were detected by depth-profiling of the tissue block. These areas were circled in the figures for clarity.
O stretching mode), have been constructed as chemical images and are shown in Fig. 5 (healthy tissue) and Fig. 4 (cancerous tissue), respectively. The area of strong amide I absorbance was associated with the cytoplasm of the cells which contains a high amount of proteins. At a greater penetration depth, the absorbance of the amide I band increases, creating an image of good contrast between the tissue and lumen (areas of weak absorbance). This observation is expected as the absorbance is dependent on the sample thickness, which increases with a greater probing depth. The mean absorbance spectra of 3 × 3 binned tissue areas of strong amide I absorbance with each aperture are plotted in the ESI (Fig. S10†). The variation in the morphology of the tissue along the z-axis has also been successfully captured in the images obtained from different penetration depths. In Fig. 5, a lumen that was embedded within the tissue appeared at the centre of the image for A6 and A0, which were not captured in either A7 or A5; whilst in Fig. 4, cells that are deep within the tissue layers were detected by depth-profiling of the tissue block. These areas were circled in the figures for clarity.
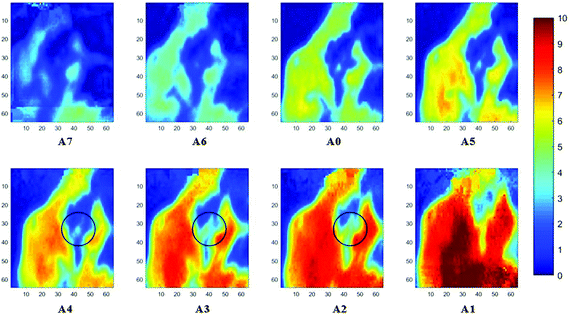
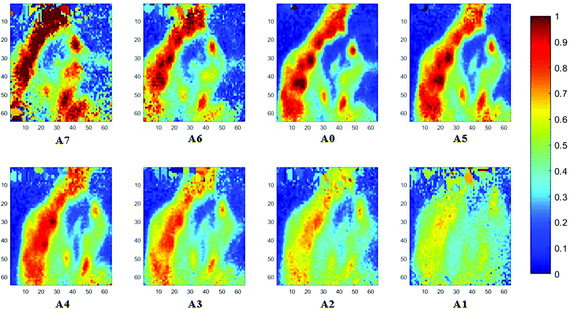
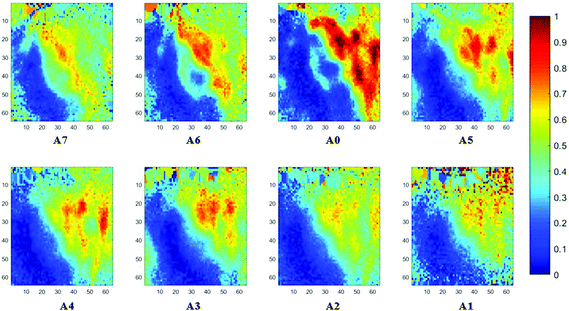
The spectral band at 1235 cm−1 is attributed to the vibrational mode of nucleic acids, i.e. DNA and RNA (vasPO2−).26 The distributions of the integrated absorbance at this wavenumber are constructed in Fig. 6 and 7 after normalisation of the amide I band across various angles, for healthy and cancerous tissue, respectively. Chemical images collected with aperture A1 and A7 suffer from poor resolution. These apertures allowed the incoming infrared beam at the edges, which carried fewer photons than the beam at the centre. Fewer photons that reached the detector resulted in the spectra of a low signal-to-noise ratio.
Examination of tissue morphology by constructing a 3D model from 2D chemical images
In our study, as the depth of penetration increases, the absorbance of the spectral band of nucleic acid was expected to decrease after normalisation of the amide I band which increases with the increasing depth of penetration; however, in contrast to the images based on the amide I band, the absorbance at the nucleic acid band showed a maximum at middle layers (A6, A0, and A5) and decreases further within the tissue (Fig. 7). This can be explained by looking at a single nucleus in a square tissue block. By varying the angle of the incoming light beam, the samples can be imaged not only along the x and y directions, but also along the z-direction, allowing a 3D model to be constructed from the slices of 2D images obtained at different thicknesses by interpolating between the slices. The subcellular localization and distribution of molecular components in onion cells was successfully examined through a 3D model in previous work.27 The 3D model of healthy prostate tissue sections is illustrated in Fig. 8. The tissue sections were microtomed at an approximate distance of 1/4 from the top of the nucleus. This is supported by plotting the absorbance of the phosphate band (which is proportional to the concentration of DNA) and the amide I spectral bands of an approximate single cell (area within the box in Fig. 8) versus the penetration depth on the same graph, shown in the ESI (Fig. S11†). The two lines exhibited an opposite trend. When the absorbance of the phosphate band reaches the maximum, that of amide I (before normalisation for the area within the box) falls to a minimum. This is because within the same imaging area, when more of the space was occupied by the nucleus, less cytoplasm was observed. This is less obvious for the healthy tissue section observed (a slight increase in the integrated absorbance within the nucleic acid band for A0 from A6 is not obvious from the chemical images of healthy tissue), but the chemical images of prostate cancer tissue clearly reveal a stark difference in the integrated absorbance to the decreasing trend that is expected, particularly the one for A0.With micro ATR-FTIR imaging, cells in the tissue, including the location and distribution of the nucleus, were closely examined. It is demonstrated here that this technique can resolve the sub-cellular organelle, the nucleus. Unlimited to just amide and DNA bands, construction of a 3D model at any wavenumber is feasible by using this variable angle micro ATR-FTIR imaging technique.
Differentiation of cancer from benign tissue
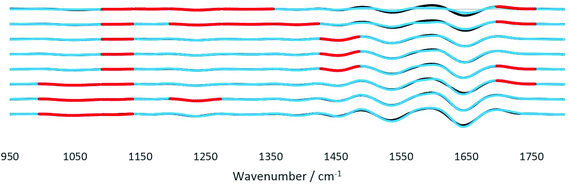
FTIR spectra of healthy and cancerous tissues were recorded for each angle of incidence with A0 to A7. The spectra were subjected to a S/N quality test whereby only spectra with a good S/N ratio were retained. This pre-processing step eliminated non-tissue spectra from interfering with the final spectra analysed, after taking the mean of all pixels representing tissue only. The signal is the peak absorbance at 1643 cm−1 (amide I) while the noise is the standard deviation of data between 2700 cm−1 and 2600 cm−1. Spectra which passed the quality test set at a threshold of 1% of the maximum S/N ratio were then differentiated twice, to correct for the baseline shift for accurate comparison of the spectra. As noise was inevitably enhanced when the second derivatives were taken, the Savitzky–Golay smoothing algorithm with 13 smoothing points was implemented to obtain smoothed second derivative spectra. The raw spectra and derived data for both tissue samples from the imaging datasets are presented in the ESI (Fig. S12–S17†). The complexity of the spectra presented is typical of a biological sample.28 From the FTIR spectra, vibrational modes and the corresponding biological components were assigned to the main spectral bands for interpretation of the results from comparing diseased and non-diseased tissues. In general, the fingerprint region ∼1340–950 cm−1 contains a series of complicated absorptions of multiple spectral bands, mostly assigned to the functional groups in nucleic acids; ∼1700–1500 cm−1 to amides or proteins, whereas, the vibrational modes of lipid molecules (or alkyl chains) manifest themselves in the spectral bands that lie in the region of ∼3000–2800 cm−1. The spectral interpretation was taken from ref. 26.The analysis protocol performed for the differentiation of datasets of different samples is similar to previous work on cell identification.29 To assess the significance of the statistical difference between the second derivatives of the spectra of the two tissues, Student's t-test was performed at each wavenumber from 1800 to 950 cm−1. Prior to t-test analysis, the data were found to be normally distributed using the Jarque–Bera normality test at the 5% significance level (Matlab R2017b).30 The paired t-test was suitable for the data of tissues of the same origin, i.e. from the same patient where the only difference is the diseased state. Fig. 9 depicts the results obtained by the statistical test. The wavenumbers where the null hypothesis is rejected at the 1% significance level (α < 0.01) were highlighted in red. The results from the t-test analysis for the whole range of wavenumbers are presented in the ESI (Table S2†). From the results, major differences are found to be in the fingerprint region (1500–1000 cm−1) where spectral biomarkers for the identification of prostate cancer have been identified.31 The components at different probing depths vary from one another, thus the difference between each layer also varied accordingly. For instance, between 35° (A4) and 42° (A7) good discrimination of the spectral bands at 1087 cm−1–995 cm−1 between the tissues was observed; however, decreasing the angle to between 31° (A1) and 33° (A3), the difference becomes significantly important. A mixture of overlapping bands of phospholipids, glycogen, and nucleic acids contributed to this difference.26 In contrast, at 1235 cm−1 and 1328 cm−1, the significance of the dissimilarity diminishes as the penetration depth increases with the decreasing angle. Both wavenumbers are assigned to amide III and the nucleic acid band, which are present at great quantities at the surface of the tissue because of the way the tissue was microtomed and measured, as explained in Fig. 8. Probing the shallow layers at the surface of the tissue via the insertion of apertures has provided the opportunity to measure the distinction between the samples in the fingerprint region, as compared to the data obtained without the aperture (A0), where the deviation in the amount of nucleic acids was not picked up at the set significance level mentioned before. Apart from this, disparity in other components was also observed. The lipid band at 1736 cm−1 was found to vary significantly between cancer and healthy tissues with an intermittent thickness. Lipids such as fatty acids and sterols are stored in droplets in cells, which are particularly widespread in the cytosol,32 hence the difference presumably originates from the randomness of the amount of these particles found at each layer. As for the spectral band at 1450 cm−1 (assigned to small carbon particles), the difference was picked up in the middle layers. Like lipid droplets, they are randomly distributed across the tissue. This spectral band has not been identified as a potentially useful spectral biomarker for the detection of prostate cancer. No statistically significant difference was observed for the amide I and II bands for the whole range of penetration depths. In short, probing the shallow layers at the surface of the tissues was more efficient at distinguishing between the two tissues based on the results of the t-test.
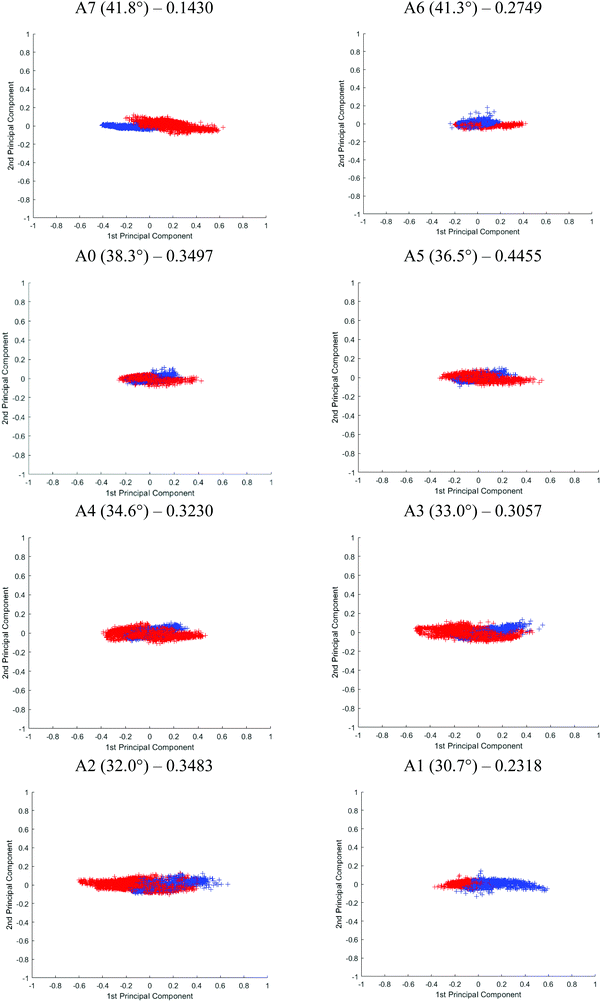
Although Student's t-test is useful in providing a preliminary picture of the statistically significant bands and gives insight into the effect of probing at different penetration depths, the variables (i.e. spectral bands) are in fact not completely independent of one another. PCA was used on top of the t-test to illustrate an overall discrepancy between the tissue specimens in the fingerprint and amide regions (between 1800 and 900 cm−1). The PCA score plot of each angle is shown in Fig. 10. The first 2 principal components (PCs) explain ∼96% of the total variance of the data. When the plot is projected on 2D space along the PC1 and PC2, the data spreads out along PC1. The variance explained by PC1 for different apertures is as follows: PC1A7 = 95%, PC1A6 = 92%, PC1A0 = 91%, PC1A5 = 91%, PC1A4 = 97%, PC1A3 = 91%, PC1A2 = 91%, and PC1A1 = 88%. Between 30°(A1) and 35°(A4), this PC is aligned along the spectral band between 1080 and 1053 cm−1 with minor contribution from the spectral band at 1235 cm−1. The former is attributed to the symmetric vibration (vs) of PO2−, while the latter to the asymmetric vibration (vas) of the same molecule. Beyond 35°, the trend is reversed, 1235 cm−1 becomes the dominating spectral band responsible for the variance observed in the first PC, as depicted in the ESI (Fig. S18†) when the percentage variance of the contribution to the PC was plotted at each wavenumber investigated. As the probing depth increases, the distribution of data that discriminate cancer from benign tissue shifts from vsPO2− to vasPO2−. This observation is consistent with the t-test analysis.
The effect of the penetration depth on the discrimination of the spectra obtained from the cancerous tissue from that of the healthy prostate tissue in micro ATR-FTIR measurement is studied. The best separation is obtained when probing at the surface of the tissue where vasPO2− is the dominating factor in PC1. At 41.8° (A7), the two clusters of data, plotted in different colours, are distinguishable from each other. A reasonably good separation is obtained at 30° (A1) with slight overlapping of the data; however, superposition is mainly observed when measurements were taken with other apertures. Following PCA, the classification of the data of the first 2 PCs is further evaluated by fitting them to the linear discriminant analysis (LDA) classifier in Matlab – a supervised classification model with a 10-fold cross validation.33 The predictive performance of the model is assessed through classification loss, which is the mean squared error between the predicted value and the true response, in this case, the diseased and non-diseased tissue. The cross-validation loss for each aperture is reported in Fig. 10. The lower the value of the loss, the more accurate the LDA model, in other words, the better the separation of the data. The results show that A7 has the lowest loss at 0.1430, followed by A1 at 0.2318 and A6 at 0.2749. The results from LDA correspond well to the visual observation of the degree of separation of the PCA. Therefore, we postulate that vasPO2− is a better spectral biomarker for distinguishing cancer tissue than vsPO2−.
Our findings, that probing tissues at a greater angle of incidence offers a more reliable differentiation between benign and cancerous tissue compared to probing thicker layers of the sample, are significant. At the same time, we recognise the limitations of this study such as the limited number of samples available and the observations for different types of tissues may not be the same. The results may also differ based on the way the tissue is microtomed or the configuration of the components within the tissue. However, this work demonstrates the feasibility of assessment of the tissue across various effective thicknesses, hence offering a higher possibility of recognising an embedded component or detecting spectral differences which might not be significant when probing at just one depth.
Conclusions
The identification of prostate cancer aggression with FTIR spectroscopy has been well documented; however, to our knowledge, this is the first time the discriminant between cancer and non-cancer prostate tissues has been shown to vary as a function of penetration depths using micro ATR-FTIR imaging. In this study, introducing specially designed apertures into the micro ATR-FTIR imaging system fitted with a slide-on Ge crystal allows the experiment to be conducted to investigate the variation of tissue components in the z-direction, i.e. as a function of depth. The penetration depth or effective thickness was physically altered by changing the angle of incidence between 30.7° and 41.8°. The improved design of laser cut apertures at a high precision allows the angle to be varied at a difference of ∼2°. With this variable angle micro-ATR spectroscopic technique, the image obtained at each different depth has a high spatial resolution and is free from optical aberrations. Significantly, this experiment has highlighted the importance of probing at the surface of the tissue, consolidated by statistical testing. Although limited by its shallow penetration depth on the μm scale, this work has demonstrated its applicability to non-destructive imaging of heterogeneous biological samples, allowing a 3D model to be constructed to study the components embedded within the tissue sample. This work opens up the possibility to investigate multi-layer heterogeneous samples without the need to microtome them to obtain stacks of 2D chemical images at different probing depths.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Dr Archana Kothari at the Department of Pathology, Kingston Hospital (London, UK) for providing the tissue samples.Notes and references
- J. A. Kimber and S. G. Kazarian, Spectroscopic imaging of biomaterials and biological systems with FTIR microscopy or with quantum cascade lasers, Anal. Bioanal. Chem., 2017, 409(25), 5813–5820 CrossRef CAS PubMed.
- M. J. Baker, H. J. Byrne and J. Chalmers, et al., Clinical applications of infrared and Raman spectroscopy: state of play and future challenges, Analyst, 2018, 143(8), 1735–1757 RSC.
- S. G. Kazarian and K. L. A. Chan, Micro- and macro-attenuated total reflection Fourier transform infrared spectroscopic imaging, Appl. Spectrosc., 2010, 64(5), 135A–152A CrossRef CAS PubMed.
- C. L. Song, M. Ryu, J. Morikawa, A. Kothari and S. G. Kazarian, Thermal effect on dispersive infrared spectroscopic imaging of prostate cancer tissue, J. Biophotonics, 2018, 11(12), e201800187 CrossRef PubMed.
- H. Shinzawa, B. Turner, J. Mizukado and S. G. Kazarian, Protein hydration in living cells probed by Fourier transform infrared (FT-IR) spectroscopic imaging, Analyst, 2017, 142(13), 2475–2483 RSC.
- W. J. Wiscombe, Improved Mie scattering algorithms, Appl. Opt., 1980, 19(9), 1505–1509 CrossRef CAS PubMed.
- P. Bassan, A. Kohler and H. Martens, et al., Resonant Mie scattering (RMieS) correction of infrared spectra from highly scattering biological samples, Analyst, 2010, 135(2), 268–277 RSC.
- K. L. A. Chan and S. G. Kazarian, Attenuated total reflection Fourier transform infrared imaging with variable angles of incidence: a three-dimensional profiling of heterogeneous materials, Appl. Spectrosc., 2007, 61(1), 48–54 CrossRef CAS PubMed.
- T. P. Wrobel, A. Vichi, M. Baranska and S. G. Kazarian, Micro-Attenuated Total Reflection Fourier Transform Infrared (Micro ATR FT-IR) Spectroscopic Imaging with Variable Angles of Incidence, Appl. Spectrosc., 2015, 69(10), 1170–1174 CrossRef CAS PubMed.
- Z. Lu, B. M. Cassidy, S. A. DeJong, R. G. Belliveau, M. L. Myrick and S. L. Morgan, Attenuated Total Reflection (ATR) Sampling in Infrared Spectroscopy of Heterogeneous Materials Requires Reproducible Pressure Control, Appl. Spectrosc., 2017, 71(1), 97–104 CrossRef CAS PubMed.
- N. J. Harrick, du Pre FK, Effective thickness of bulk materials and of thin films for internal reflection spectroscopy, Appl. Opt., 1966, 5(11), 1739–1743 CrossRef CAS PubMed.
- N. J. Harrick and A. I. Carlson, Internal reflection spectroscopy: validity of effective thickness equations, Appl. Opt., 1971, 10(1), 19–23 CrossRef CAS PubMed.
- L. A. Averett, P. R. Griffiths and K. Nishikida, Effective path length in attenuated total reflection spectroscopy, Anal. Chem., 2008, 80(8), 3045–3049 CrossRef CAS PubMed.
- U. P. Fringelli, ATR and Reflectance IR Spectroscopy, Applications, in Encyclopedia of spectroscopy and spectrometry, ed. J.C Lindon, G.E Tranter and J.L Holmes, Academic Press, United Kingdom, 2000, vol. 1, pp. 58–75 Search PubMed.
- C. W. Robertson and D. Williams, Lambert Absorption Coefficients of Water in the Infrared*, J. Opt. Soc. Am., 1971, 61(10), 1316 CrossRef CAS.
- H. D. Downing and D. Williams, Optical constants of water in the infrared, J. Geophys. Res., 1975, 80(12), 1656–1661 CrossRef CAS.
- L. W. Pinkley, P. P. Sethna and D. Williams, Optical constants of water in the infrared: Influence of temperature*, J. Opt. Soc. Am., 1977, 67(4), 494 CrossRef CAS.
- S. Y. Venyaminov and F. G. Prendergast, Water (H2O and D2O) Molar Absorptivity in the 1000–4000 cm−1Range and Quantitative Infrared Spectroscopy of Aqueous Solutions, Anal. Biochem., 1997, 248(2), 234–245 CrossRef CAS PubMed.
- L. Rayleigh, XXXI. Investigations in optics, with special reference to the spectroscope, London, Edinburgh Dublin Philos. Mag. J. Sci., 2009, 8(49), 261–274 CrossRef.
- J. A. Bailey, R. B. Dyer, D. K. Graff and J. R. Schoonover, High Spatial Resolution for IR Imaging Using an IR Diode Laser, Appl. Spectrosc., 2016, 54(2), 159–163 CrossRef.
- K. L. A. Chan and S. G. Kazarian, New opportunities in micro- and macro-attenuated total reflection infrared spectroscopic imaging: spatial resolution and sampling versatility, Appl. Spectrosc., 2003, 57(4), 381–389 CrossRef CAS PubMed.
- A. Nakamura, T. Koga and M. Fujimaki, et al., Application of Infrared Attenuated Total Reflection Spectroscopy to In Situ Analysis of Atheromatous Plaques in Aorta, Jpn. J. Appl. Phys., 2000, 39(Part 2, No. 6A), L490–L492 CrossRef CAS.
- F. P. Bolin, L. E. Preuss, R. C. Taylor and R. J. Ference, Refractive index of some mammalian tissues using a fiber optic cladding method, Appl. Opt., 1989, 28(12), 2297–2303 CrossRef CAS PubMed.
- T. Svensson, S. Andersson-Engels, M. Einarsdottir and K. Svanberg, In vivo optical characterization of human prostate tissue using near-infrared time-resolved spectroscopy, J. Biomed. Opt., 2007, 12(1), 014022 CrossRef PubMed.
- Z. Wang, K. Tangella, A. Balla and G. Popescu, Tissue refractive index as marker of disease, J. Biomed. Opt., 2011, 16(11), 116017 CrossRef PubMed.
- Z. Movasaghi, S. Rehman and D. I. Ur Rehman, Fourier Transform Infrared (FTIR) Spectroscopy of Biological Tissues, Appl. Spectrosc. Rev., 2008, 43(2), 134–179 CrossRef CAS.
- L. Quaroni, M. Obst, M. Nowak and F. Zobi, Three-dimensional mid-infrared tomographic imaging of endogenous and exogenous molecules in a single intact cell with subcellular resolution, Angew. Chem., Int. Ed., 2015, 54(1), 318–322 CrossRef CAS PubMed.
- M. J. German, A. Hammiche and N. Ragavan, et al., Infrared spectroscopy with multivariate analysis potentially facilitates the segregation of different types of prostate cell, Biophys. J., 2006, 90(10), 3783–3795 CrossRef CAS PubMed.
- A. Gaigneaux and E. Goormaghtigh, A new dimension for cell identification by FTIR spectroscopy: depth profiling in attenuated total reflection, Analyst, 2013, 138(14), 4070–4075 RSC.
- A. Ghasemi and S. Zahediasl, Normality tests for statistical analysis: a guide for non-statisticians, Int. J. Endocrinol. Metab., 2012, 10(2), 486–489 CrossRef PubMed.
- M. J. Baker, E. Gazi, M. D. Brown, J. H. Shanks, P. Gardner and N. W. Clarke, FTIR-based spectroscopic analysis in the identification of clinically aggressive prostate cancer, Br. J. Cancer, 2008, 99(11), 1859–1866 CrossRef CAS PubMed.
- A. R. Thiam, R. V. Farese Jr. and T. C. Walther, The biophysics and cell biology of lipid droplets, Nat. Rev. Mol. Cell Biol., 2013, 14(12), 775–786 CrossRef CAS PubMed.
- MathWorks. Discriminant Analysis. 2019; https://uk.mathworks.com/help/stats/classification-discriminant-analysis.html. Accessed 21 Jan, 2019.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8an01929k |
| This journal is © The Royal Society of Chemistry 2019 |