Open Access Article
Open Access ArticleOxidation potentials of phenols and anilines: correlation analysis of electrochemical and theoretical values†
Ania S.
Pavitt
 a,
Eric J.
Bylaska
b and
Paul G.
Tratnyek
a,
Eric J.
Bylaska
b and
Paul G.
Tratnyek
 *a
*a
aInstitute of Environmental Health, Oregon Health & Science University, 3181 SW Sam Jackson Park Road, Portland, OR 97239, USA. E-mail: tratnyek@ohsu.edu; Tel: +1-503-346-3431
bWilliam R. Wiley Environmental Molecular Sciences Laboratory, Pacific Northwest National Laboratory, P.O. Box 999, Richland, WA 99352, USA
First published on 10th February 2017
Abstract
Phenols and anilines have been studied extensively as reductants of environmental oxidants (such as manganese dioxide) and as reductates (e.g., model contaminants) that are transformed by environmental oxidants (ozone, triple organic matter, etc.). The thermodynamics and kinetics of these reactions have been interpreted using oxidation potentials for substituted phenols and anilines, often using a legacy experimental dataset that is of uncertain quality. Although there are many alternative oxidation potential data, there has been little systematic analysis of the relevance, reliability, and consistency of the data obtained by different methods. We have done this through an extensive correlation analysis of kinetic data for phenol or aniline oxidation by manganese oxide—compiled from multiple sources—and oxidation potentials obtained from (i) electrochemical measurements using cyclic and square wave voltammetry and (ii) theoretical calculations using density functional theory. Measured peak potentials (Ep) from different sources and experimental conditions correlate very strongly, with minimal root mean squared error (RMSE), slopes ≈ 1, and intercepts indicative of consistent absolute differences of 50–150 mV; whereas, one-electron oxidation potentials (E1) from different sources and theoretical conditions exhibit large RMSE, slopes, and intercepts vs. measured oxidation potentials. Calibration of calculated E1 data vs. measured Ep data gave corrected values of E1 with improved accuracy. For oxidation by manganese dioxide, normalization of rate constants (to the 4-chloro congener) allowed correlation of phenol and aniline data from multiple sources to give one, unified quantitative structure–activity relationship (QSAR). Comparison among these QSARs illustrates the principle of matching the observational vs. mechanistic character of the response and descriptor variables.
Environmental impactThe oxidation of substituted phenols, anilines, and various related electron shuttle compounds (ranging from biogenic dihydroxybenzenes to natural organic matter) is a major determinant of their environmental fate and effects. Describing the kinetics of these reactions with QSARs is useful for explaining the relative reactivity of important congener families (e.g. precursors to disinfection byproducts), or predicting oxidation rates for chemicals of emerging concern (e.g. metabolites of insensitive munitions compounds). Applications of our QSARs for oxidation by manganese oxide, or further development of QSARs for other environmental oxidants (ozone, triplet natural organic matter, etc.) will be improved by the new measured and calculated oxidation potentials presented here. |
Introduction
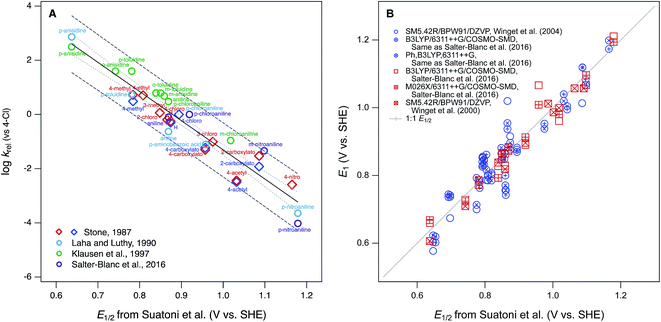
Phenol and aniline moieties are ubiquitous in the environment, biology, and commerce. They are characteristic components of many important organic compounds—including pesticides, pharmaceuticals, antioxidants, and various natural products—as well as polymeric materials, such as natural organic matter (NOM), lignin, and some resins and plastics. The most significant pathway for transformation of these compounds is often the oxidation of the phenol or aniline moieties, so this chemistry has been studied extensively. Many of these studies compare the reactivity of multiple substituted phenols and/or anilines, which has made them prototypical families of congeners for analysis of correlations between chemical structure and reactivity. The resulting abundance of data, and quantitative structure–activity relationships (QSARs) for correlations among these data, has led to a variety of cross-correlation and meta analyses and reviews thereof.1–3 This large body of work makes phenols and anilines good systems for illustrating or exploring general concepts regarding the development and application of correlation analysis.With respect to the oxidation of phenols and/or anilines, most correlation analyses are structured as relations between rate constants for oxidation of multiple substituted phenols/anilines (by a single oxidant) and one or more descriptor variables that are either measured from electrochemical experiments or calculated from molecular structure theory. Other work has emphasized the development of theoretical methods for calculation of phenol/aniline redox properties, in part using correlations to experimental data for validation and/or calibration. In both cases, the most commonly used experimental descriptor data is the set of electrochemically-measured half-wave oxidation potentials (E1/2) reported by Suatoni et al. in 1961.4 This dataset is attractive for correlation analysis because it is accessible and relatively large (including 41 phenols and 32 anilines), was obtained under a consistent set of conditions that are compatible with biological and environmental science, and has accumulated a legacy as a useful descriptor dataset in studies of reactivity of various environmental oxidants.
The first studies to make prominent use of the E1/2 data from Suatoni et al. in correlation analysis were focused on oxidation by manganese dioxide (MnO2). These studies reported that measured rates (or rate constants) for oxidation by MnO2 correlate well with E1/2 for mono substituted phenols5 and anilines.6,7 Klausen et al.7 showed that these correlations become superimposable when based on relative rate constants (krel), obtained by normalizing measured rate constants (usually kobs) to rate constants for a common reference compound (they used the 4-Cl congener). In a recent study, we showed that correlations based on krel for aniline oxidation by MnO2 were sufficiently comparable to justify fitting QSARs using kinetic data from multiple sources.8 In Fig. 1A, all of these data—including both phenols and anilines—are summarized, showing that the combined dataset for krel correlate sufficiently well to E1/2 from Suatoni et al. to fit a single QSAR. As a meta statistical analysis, the correlation in Fig. 1A is remarkably successful, but its theoretical interpretability is limited by the heterogeneous nature of the oxidant. Other correlation analyses that utilize E1/2 from Suatoni et al. involve oxidation of phenols by homogeneous solution-phase oxidants (singlet oxygen,2,9,10 chlorine dioxide,1,2,10,11 persulfate,10 and chromate10). Among these oxidants, chlorine dioxide is the most likely to produce kinetics controlled by simple outer-sphere one-electron transfer, and this made it possible to describe the kinetics using a model based on Marcus theory.11 For that analysis, free energies of oxidation for phenols by chlorine dioxide were calculated using the E1/2 data from Suatoni et al., assuming—and then supporting—their claim that these E1/2's are the one-electron oxidation potentials for phenols. The data by Suatoni et al. also are included in a compilation by Meites and Zuman,12 which has been cited as the source of oxidation potentials for correlation analysis of rate constants for anilines with carbonate radical13 and borate radical.14
The other most significant use of the E1/2 dataset from Suatoni et al.—in the development of theoretical methods for calculation of phenol/aniline redox properties—assumes that the accuracy of the measured potentials is sufficient for them to be useful in validation of redox potentials calculated from chemical structure theory.15,16 The primary example of this is work by Winget et al. where they found that their calculated one-electron oxidation potentials (E1) for anilines17,18 and phenols19 differed significantly from Suatoni's measured values of E1/2 and these differences vary significantly with the level of theory used in the calculations. They discussed various possible sources of “error” in the theoretical calculations, and suggested that some of this error could be corrected by using the expected value of E1 (here E1c, for corrected by calibration), calculated from a regression of E1 on E1/2. The results of this calculation are shown in Fig. 1B for selected sets of E1 calculated by Winget et al.17–19 and Salter-Blanc et al.8 A linear regression (not shown) performed on all the data in this correlation does not differ significantly from the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 line included in the figure, but the residuals are highly variable, within as well as between compounds, and therefore hard to rationalize as due to any one particular source of error.
1 line included in the figure, but the residuals are highly variable, within as well as between compounds, and therefore hard to rationalize as due to any one particular source of error.
The results in Fig. 1B illustrate some of the general concerns that arise from the use of correlation analysis with computational electrochemistry. The first is that the absolute precision and accuracy required to make modeling results statistically satisfactory becomes relatively less severe as the calibration and application range of the model increases. This is evident in the contrast between Fig. 1B, which suggests significant need for improvement in the residuals, versus studies such as Moens et al.20 that aim to model a much wider range of compound structures—with a much wider range of potentials—and therefore find that the residuals that arise from utilizing E1/2 data from Suatoni to be insignificant. Another general issue is that the overall fitness of correlation models increases when the variables included are consistent with each other—and with the intended applications of the model—with respect to their observational vs. mechanistic character. In this respect, a correlation such as in Fig. 1A, which is between two properties measured in solution for one class of reactions, is a favorable formulation for describing the observed kinetics of phenol/aniline oxidation. In contrast, a calibration such as in Fig. 1B is less favorable because it is based on correlation between two less consistent (less well “matched”) variables: one that is a property measured in solution and another that is calculated from theory assuming an elementary reaction step that may, or may not, dominate the solution chemistry.
From a fundamental, mechanistic perspective, the mismatch implicit in calibrating theoretically calculated E1's by correlation to electrochemically measured potentials, as in Fig. 1B, should have significant disadvantages.21,22 This has led recent studies to calibrate E1's using potentials measured by methods such as pulse radiolysis,22–26 which should provide a more accurate estimate of potentials for reversible, one-electron oxidation of phenols/anilines.27 However, these data are less common, more complex to measure, and not necessarily more closely matched to the processes that are controlling solution-phase oxidation kinetics. Therefore, they may not provide the most useful, or even the most accurate, structure–activity relationships for oxidation reactions of environmental interest. To explore this hypothesis, a correlation analysis was performed with new and previously published data for kinetics of phenol/aniline oxidation by MnO2, oxidation peak potentials measured electrochemically, and one-electron oxidation potentials calculated theoretically. Overall, the results show that correlations between these three properties are statistically similar, so the main factors that distinguish the results are (i) a small number and variable mixture of compounds that are significant outliers, usually of uncertain origin, and (ii) the breadth of structures and potentials covered, which is greater for the calculated and measured potentials reported here than was available previously.
Experimental
Chemical reagents
All of the substituted phenols and anilines used in experiments are summarized in ESI (Tables S1 and S2†) with source and purity data. 2-Propanol (isopropyl alcohol, IPA), sodium acetate, and acetic acid were from Fisher Scientific. All chemicals were obtained analytical grade or higher and used as received.Stock solutions of the phenols and anilines were dissolved in IPA and stored in amber bottles for a maximum of three days. The buffer–electrolyte was made with 0.5 M acetic acid and 0.5 M sodium acetate (pKa = 4.54). Before use, the buffer–electrolyte was diluted with IPA in varying amounts, usually to 25% or 50% IPA (v/v) to buffer.
Electrochemical methods
All square wave voltammograms (SWV) were acquired with an Autolab PGSTAT30. SWV were acquired at varying amplitudes of 50, 75, 100, and 125 mV, and varying scan rates of 30, 60, 120, 180, and 240 mV s−1. Staircase cyclic voltammograms (SCV) were acquired with a Pine AFCBP1 Bipotentiostat, or an Autolab PGSTAT30. SCV were acquired at varying scan rates of 25, 75, 125, 175, and 225 mV s−1. The step size was 2 mV for all runs. Most runs were performed in duplicate. The SCV and SWV peaks were fit using the peak search function in Nova 2.02 for the Autolab and Aftermath 1.4.7760 for the Pine instrument. The three-electrode cell consisted of a Pine Research Instrumentation low profile 3 mm glassy carbon working electrode, an Ag/AgCl 3 M KCl reference electrode (BASi), and a 0.5 mm diameter platinum wire (Alfa Aesar) counter electrode. All potentials measured in this work are corrected from the Ag/AgCl reference electrode to standard hydrogen electrode (SHE) by adding 209 mV.28 Note that the potentials measured by Suatoni et al. were reported vs. the saturated calomel electrode, so those data were converted to SHE by adding 241 mV![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 28 for use in this study.
28 for use in this study.
Before each set of electrochemical measurements, the working electrode was polished using a 0.05 μm MicroPolish Alumina (Buehler), washed with 1% Micro90 (International Products Corp.) and water, rinsed several times with DI water, sonicated for 5 min, and rinsed again with DI water. The electrochemical cell was prepared by adding 10 mL of buffer–electrolyte–IPA solution and purging for 10 min with N2 (ultra-high purity). After deaeration a background scan was performed, subsequently the solution was spiked with 1 mL of the compound of interest and purged for 2 min with N2. A layer of N2 was kept over the solution for the duration of the experiment. The initial concentration of all phenols and anilines in the cell was 2.5 × 10−4 M. The pH of the solution was measured using a glass combination electrode calibrated at pH 4.00 and 7.00. The measured pH (pHmeas) was 5.1 and 5.6 for 25% IPA and 50% IPA respectively.
Computational methods
In previous work,8 we compared the performance of several electronic structure methods (functionals, basis sets, and solvation models) for computation of one-electron oxidation potentials for aromatic amines (E1) from chemical structure theory, and a selection of those methods was used in this study, with minor modifications. Only oxidation of the neutral form of the parent compounds was considered (ArOH ⇌ ArOH+ + e− and ArNH2 ⇌ ArNH2+ + e−). The electronic structure calculations were carried out using density functional theory (DFT) calculations18 using the 6-311++G(2d,2p) basis set18,20 and the B3LYP21,22 and M06-2X23 exchange correlation functionals. Solvation energies for the parent and oxidized compounds were approximated using both the COSMO and COSMO-SMD methods. Other recent studies have performed similar calculations,17,18,20,22–26 and the calculations here, which make use of large triple zeta basis sets, are expected to be well converged. All of the calculations were done using NWChem.28 Additional details regarding the computation methods are given in ESI.†Results and discussion
Electrochemical method optimization and validation
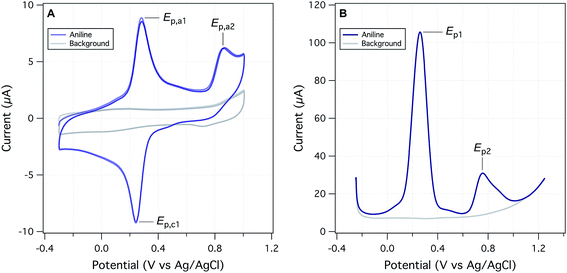
The objectives of this study include reevaluating the E1/2 dataset from Suatoni et al., but also establishing a new, expanded dataset of measured potentials using updated and refined methods. Therefore, we attempted to replicate Suatoni's methods as much as possible during preliminary investigation of operational variables that were likely to be significant, and only made changes where a substantial benefit was expected. Based on considerations presented in the ESI,† we chose solution chemical conditions that were nearly identical to those in Suatoni et al. (C0 = 2.5 × 10−4 M phenols or anilines, 0.5 M NaAc/HAc buffer in 50/50 v/v% isopropanol/water (pHmeas = 5.6), ambient temperature = 23 ± 2 °C). The only notable difference in solution conditions is that the experiments by Suatoni et al. were aerobic and ours were purged with N2 to remove O2. For our working electrode, we chose a commercial glassy carbon electrode, rather than trying to replicate the custom wax-impregnated electrode used by Suatoni et al. Preliminary experiments were performed on both a pyrolytic graphite edge electrode and a wax impregnated graphite electrode was used to simulate Suatoni et al. There was no difference in potentials between electrodes and since better results were obtained with the glassy carbon electrode only those results are presented.Suatoni et al. performed anodic voltammetry by polarography, apparently measuring only linear, anodic potential sweeps (in duplicate). They reported half-wave potentials (E1/2), but no raw data were shown, so the robustness of their calculations cannot be evaluated. In polarography, E1/2 is obtained from the potential of half the peak current,29 and these potentials are directly related to the formal reduction potentials used in the Nernst equation.30E1/2 can also be related to the half-peak potentials (Ep/2) obtained from cyclic voltammetry, because Ep/2 = E1/2 ± 28.0 mV per n (subtract for oxidation).29 To acquire Ep/2 from CVs such as obtained in this study, we could use the mean value of the cathodic and anodic peak potentials, or the potential that corresponds to the current at half height. Because the majority of our data were irreversible voltammograms, we did not use E1/2, or Ep/2, but instead we usually report peak potentials (Ep) obtained directly from the SCV data (exemplified with aniline in Fig. 2A). For two compounds (dopamine and 4-aminophenol), Ep was calculated from SCV data using (Epa + Epc)/2 because these compounds were reversible.31
We also performed square-wave voltammetry (SWV) using the same solution conditions and working electrode as in SCV and obtained peak potentials from these data as illustrated in Fig. 2B. In general, the SWV peaks are better resolved than those from SCV (because it uses the difference in current sampled at the end of the forward potential pulse and the end of the reverse potential pulse, thereby eliminating most of the non-faradaic current), but the resulting peak potentials are not expected to differ from those determined by SCV.31 Whether obtained by SWV or SCV, Ep should be related to Ep/2 by |Ep − Ep/2| = 56.5 mV per n for reversible and 47.7/αn for irreversible reactions (where α is the transfer coefficient, and n is the number electrons).29 Preliminary calculations suggest that this is approximately true for our data, but the results are not shown.
The shapes, and peak properties, of the SCVs and SWVs varied with the substituents on the various phenols and anilines, but also with experimental factors such as the scan rate and pH. Suatoni et al. measured only one scan, starting at 150 mV before the anodic peak and scanning at 2.4 mV s−1, whereas we performed SCVs with a variety of switching potentials and a range of scan rates. In most experiments, we used 0 to +1 V, but varied the scan rate from 25 to 225 mV s−1. The effect of scan rate on peak current or potential are among the criteria used to assess the reversibility of electrode reactions.31 With SWV, we varied the scan rate, as well as the potential step amplitude, because varying both of these parameters can provide insights into the electrode kinetics. The results and conclusions from varying these parameters, in both SCV and SWV, are discussed in the ESI.†
Despite differences due to experimental conditions, the SCVs for the various phenols and anilines have similar features, so they can be classified into four types. Most types (all except for type IV), exhibited an irreversible anodic peak, which is due to initial electron transfer from the parent phenol or aniline.32 The Ep data from these peaks are compared to Suatoni's E1/2 data below. For type I SCVs, the primary anodic peak height (ip,a) decreased slightly (some decreased significantly) with repeated scans. After the first scan, these compounds developed a reversible or quasi-reversible set of secondary peaks shifted to less positive potentials. This secondary peak appears with almost all anilines (e.g., Fig. 2A) and almost half of the phenols, seventeen in total. Secondary peaks were reported in Suatoni et al., for p-toluidine, p-ethylaniline, and 2,4-dimethylaniline, but our experimental data for p-toluidine showed one peak with a shoulder in both the SCV and SWV. Secondary peaks have been described and discussed in many, more recent electrochemical studies of phenols and anilines.32 The main cause for these peaks is that radicals formed by the oxidation of anilines and some phenols couple to form dimers, which are still electro-active but at lower oxidation potentials.33 For this study, the secondary peak formation was not considered further, although it may have implications for the redox properties of natural organic matter during diagenesis.34
Type II SCVs exhibit the primary oxidation peak, but no secondary peaks. The primary peak current decreases substantially with subsequent scans, resulting in no peaks by the fifth scan. This behavior is seen with fourteen phenols and two anilines. The disappearance of all peaks after multiple scans suggests passivation of the electrode, most likely due to adsorption. It has been previously documented that oxidation of phenols generates phenoxy radicals which dimerize and form a passivating film on solid electrodes.35 Type III CVs show the primary irreversible anodic peak whose current increases with the scan rate. Current is expected to increase with faster scan rate because slow scan rates allow the diffusion layer to grow further from the electrode, thereby decreasing the flux to the electrode. As the scan rate speeds up, the diffusion layer is smaller and the flux to the electrode is faster resulting in higher current. This behavior is seen with several phenols and 4-methyl-3-nitroaniline. Type IV CVs show one set of reversible or quasi-reversible peaks, as seen with 4-aminophenol and dopamine. For 4-aminophenol the peak separation by 60 mV suggests a one electron transfer reaction (based on the Nernst equation). The ratio of the peak currents averaged over five different scan rates is 1.075, which is also consistent with single electron transfer. The peak potentials shift 3–5 mV with the change in scan rate, but this small effect could be due to variations in peak selection.
Quantitative comparison of peak potentials
The primary data for Ep obtained with each substituted phenol or aniline, over the range of conditions tested, are summarized in ESI, Fig. S5.† The expected trends with respect to wave form, scan rate, etc. are evident in the figure, but the overall conclusion is that the range in primary potentials for individual compounds is about 100–200 mV. To select a representative value, we considered two options: the results from the first scan (for SCV this was 25 mV s−1 scan rate for SWV 30 mV s−1 scan rate, 50 mV amplitude and a step size of 2 mV) or the average of all scans (including measurements with varying scan rates and replicates). The main rationale for the former is that the first scan will be least affected by sorption and/or product formation during electrooxidation of the test compound; whereas the latter leverages more individual measurements and may be more representative of the range of conditions that are included in (meta) correlation analysis. The resulting four sets of Ep data (E1stpa and EAvgpa from SCV; E1stp1 and EAvgp1 from SWV) are summarized in Tables S4 and S5† for all of the phenols and anilines used in the experimental part of this study.The data in Tables S4 and S5† are the experimentally measured values, adjusted to SHE, but not corrected for any factors that require more complex justifications. One such factor is pH, which affects the oxidation potential of phenols and anilines mainly through (de)protonation of their hydroxyl or amino moieties. Assuming appropriate values for their pKa's, and a Nernstian relationship between potential and speciation of the hydroxyl or amino moieties, a variety of pH adjustments have been made (e.g., pH 5.6 to 0,11 pH 7 to 0,26). For reversible reactions with Nernstian electrode response, a pH adjustment can be made by decreasing the oxidation potentials 59 mV per unit increase in pH.27 However, for this study, we decided not to make pH adjustments to our measured Ep data because (i) our buffer and pH conditions were identical to those used by Suatoni et al.; (ii) using the estimated pKa's in Tables S2 and S3† and pH's that we measured before each set of electrochemical measurements (pHapp = 5.4–5.6) showed that variation in degree of protonation had negligible effect on Ep for the anilines and was <30 (usually <15) mV for the phenols; and (iii) there are numerous potential secondary effects that would be difficult to fully evaluate. One such secondary effect might be the influence of IPA on the pKa's on phenols, anilines, and water and another might be the influence of buffer speciation on electrode kinetics.36
Another factor that could merit corrections is the irreversibility of the primary anodic peaks used to obtain our Ep data. Recall from the discussion of SCV types (above and in ESI†) that many of the phenols and anilines studied did not give ideal reversible electrochemical peaks. Ep data can be adjusted to approximate (theoretical) reversible potentials as has been done for SCV of phenols.37 However, for this study, we decided not apply this correction to our Ep data because (i) Suatoni et al. did not do it, (ii) SCV peak type did not correlate in any way with the Ep data, and (iii) this correction involves assumptions that were unnecessary to make (e.g., regarding the kinetics of individual electrode reactions37).
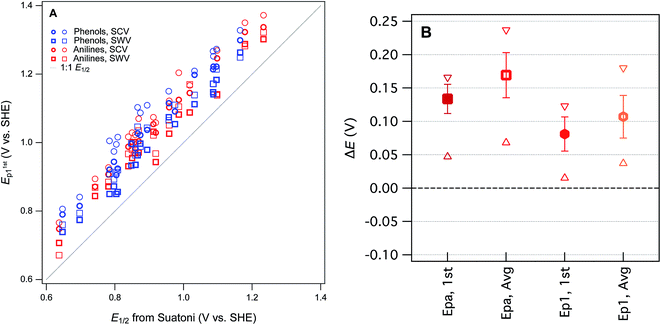
Our four sets of Ep data (from Tables S4 and S5†) are summarized by phenol or aniline in Fig. S6,† together with the E1/2 data from Suatoni et al. and electrochemical oxidation potentials from three other studies of complementary scope. In general, the variability among the datasets appears to be smaller than the variability between the phenols/anilines, which can be seen more clearly in the correlation between all of our Ep and Suatoni's E1/2, data, which is shown in Fig. 3. All of our Ep datasets appear to correlate with the same slope and intercept, so they can be fitted globally, which give 0.99 ± 0.02 and 0.13 ± 0.03, respectively (r2 = 0.92). The slope of 1 indicates all the measured Ep's have the same sensitivity to phenol/aniline structure, but the intercept suggests a well defined “offset” of about 130 mV (which is discussed further below).
To prioritize among the four sets of measured potentials, we considered three criteria: accuracy, precision, and relevance. Since our experiments were designed to match most of the conditions in the work by Suatoni et al., we calculated the difference between our values and Suatoni's (ΔE) and used this as one indicator of accuracy. Values of ΔE for each phenol or aniline are summarized in Fig. S6.† And the average, standard deviation, maximum, and minimum of these values are summarized in Fig. 3B. Based on the results in Fig. 3B, and the general considerations regarding the electrochemistry of phenols/anilines presented above, we chose to emphasize E1stp1 (the potential of the first anodic peak from the first scan obtained by SWV) in most of the correlation analysis that follows.
One overall implication of the results summarized in Fig. 3 and S6† is that the new experimental data presented here are 100–150 mV more positive than those reported in Suatoni et al. Two contributors to this offset are certain: (i) in cyclic voltammetry E1/2 should be ∼28 mV less than Ep for peaks with typical shape,29 and (ii) the difference between Suatoni's scan rate (2.4 mV s−1) and ours (25–240 mV s−1), should make their potentials about 50–150 mV higher than their E1/2's (based on results in ESI, Fig. S5†). This reduces the unexplained difference in potentials (ΔE) to a range of −75 mV to +25 mV. One possible contributor to the remaining ΔE is differences in cell design (Suatoni's cell volume and working electrode diameter were 2.5- and 2-fold greater than ours, respectively), which can influence electrode potential measurements in various ways, such as differences in iR drop, non-faradaic current, etc.30 Another possible effect of electrode kinetics is that the slow scan rate used by Suatoni et al. could have resulted in conditions at the electrode boundary layer that were influenced by convection as well as diffusion, which would influence Ep by unpredictably affecting the current response.28 Finally, it is possible that Suatoni's electrode potentials were affected by the presence of dissolved oxygen in their system, which can generate reactive oxygen species during anodic voltammetry, and these species can react directly with the electrode or with the test compounds.30 Taken together, these considerations are sufficient to rationalize the roughly 100–150 mV offset between E1/2 from Suatoni and E1stp1 from this study, and suggest that the absolute accuracy is likely greater for our E1stp1 dataset.
Computational method optimization and validation
For this study, the theoretical calculations of E1 were performed to serve three general purposes. First, to obtain a dataset with maximum overlap with the phenols and anilines for which there are electrochemical potentials from Suatoni et al. and/or the newly-measured values reported in this study, we included most of the phenols and anilines in Tables S2 and S3.† Second, to represent the putative initial oxidation step for phenols and anilines38–40 at the pH of Suatoni's work, E1 was calculated for simple electron transfer from the neutral form of the phenols and anilines to the corresponding phenoxy or aryl amino radicals (i.e., PhOH ⇌ PhOH+ + e− and ArNH2 ⇌ ArNH2+ + e−) assuming no atom transfers. Third, to provide an avenue for extending the coverage of substituent combinations in future work, we chose moderately-high, but accessible levels of theory, so calculations could be done for many compounds without special accommodations (such as for the larger or more flexible compounds). The range of computational conditions used was chosen to include those that proved most useful in our recent work,8 included one basis set (6-311++G(2d,2p)), two functionals (B3LYP and M062S) and two solvation models (COSMO and COSMO-SMD). The newly calculated values of E1 are given in Table S6† (phenols) and Table S7† (anilines).The newly calculated values of E1 are summarized for each phenol in Fig. S7† and each aniline in Fig. S8.† For comparison, we have included in the plots: literature values of E1 from prior studies that used Suatoni's E1/2 for validation,8,19 the E1/2 data from Suatoni et al., and the Ep data from this study (Tables S4 and S5†). It is evident from these figures that most of the range in E's is due to relatively consistent differences (i.e., offsets) between the E1 datasets (∼2–4 V), while the offset among the measured Ep's is much less (<0.5 V), and that the variability among the phenols and anilines within each dataset is intermediate in size (∼1 V). The relatively large offsets between sets of calculated and measured oxidation potentials is an issue that has been addressed in prior work by using the expected values of E1 (E1c) calculated from regression of E1 on experimental data.15 This approach has been used specifically with substituted phenols and/or anilines,18,26 but the results and implications have not been fully explored.
For validation and calibration of the E1 data obtained in this study, we compared our four sets of E1's vs. two sets of measured potentials, E1/2 from Suatoni et al. and Ep from this study. The direct plots and linear fits of each combination are shown in Fig. S9,† the fitting coefficients and goodness-of-fit statistics are given in Table S8,† and a subset of these results is summarized in Fig. 4A. The major features of the calibration fitting results are (i) the slopes are similar in most cases, but (ii) the intercepts differ considerably, and (iii) the residual variance about the fitted lines is greater for phenols than anilines. To examine the residuals for trends or outliers, we calculated E1c for combinations of E1's and measured potentials (Tables S9 and S10†) and plotted them versus the measured potential used for calibration in Fig. S10.† The most relevant subset of these results are shown in Fig. 4B. By factoring out the differences in slope and intercept between the calibrations, Fig. 4B shows that the residual variance in E1c for anilines is small and appears random. In contrast, the phenols exhibit significant scatter and clustering among the outliers that suggests systematic effects.
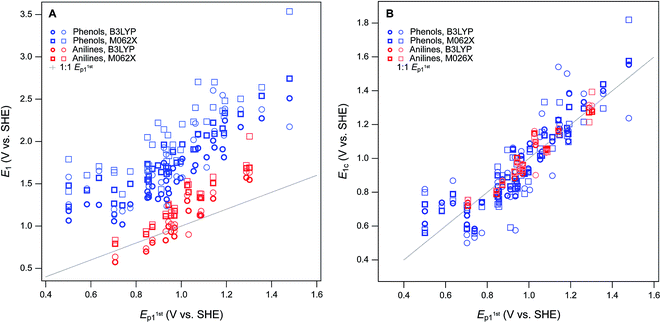 | ||
| Fig. 4 Comparisons between measured E1 (without calibration) and E1stp1 for phenols and anilines. (A) Direct comparison between measured potentials, (B) statistical analysis of the calibration equations from regression of E1 and E1stp1 (shown in Fig. S6†). In (A) and (B), phenols and anilines are distinguished, not combined. | ||
Overall, the two functionals used (B3LYP and M062X) performed equally well, so we emphasize M062X in the remaining discussion only because it was slightly preferred in our previous work.8 All of the most severe outliers in Fig. 4B fit two criteria. The most general is the SMD solvated E1's (lighter markers in Fig. 4B), which account for all of the more extreme values of E1c for each compound. Since the COSMO-SMD model has been extensively parameterized for compounds similar to the parent compounds in this study, these differences suggest that the parameterization of COSMO radii in the SMD model may need to be adjusted for the oxidized forms. The other notable group of outliers includes the three phenols with the lowest values of Ep1 (2-hydroxyl, 4-hydroxyl, and 2,6-dimethoxy), which plot about 100 mV high relative the trends in Fig. 4A and B. The absolute and relative values of Ep1 for these compounds are quite consistent with previous electrochemical studies,41 which suggests that the calculated values of E1 are too high. This anomaly might be rationalized in terms of their strongly electron donating substituents, and these differences might be corrected by using higher levels of electronic structure theory, such as CCSD(T) with large basis sets. However, these higher level calculations are very expensive and would only be accessible to researchers with access to very high performance computers, and would be inconsistent with our overall approach of favoring lumping over splitting where ever possible.
Structure–activity relationships
The ultimate goal of the cross-correlation analysis of oxidation potentials presented above is to validate them for use as descriptor variables in relationships between phenol/aniline structure and reactivity (i.e., QSARs). However, that analysis suggests that most of the differences between the four major sets of oxidation potentials (E1/2 from Suatoni et al. and Ep, E1, and E1c from this work) are due to compound-specific effects that may be dependent on operational factors. For example, the dissociation or migration of protons in association with hydroxyl groups could be affected by the cosolvent (IPA) used in the electrochemical measurements, or the basis set used in the modeling calculations. This complexity means that the four sets of oxidation potentials may have complementary value as descriptors in correlation analysis with kinetic data. This complementarity is apparent when the correlation presented in Fig. 1A—between log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) krel for phenol/aniline oxidation by MnO2 and E1/2 from Suatoni et al.—is compared with the correlations in Fig. 5, obtained using Ep and E1 as alternative descriptor variables.
krel for phenol/aniline oxidation by MnO2 and E1/2 from Suatoni et al.—is compared with the correlations in Fig. 5, obtained using Ep and E1 as alternative descriptor variables.
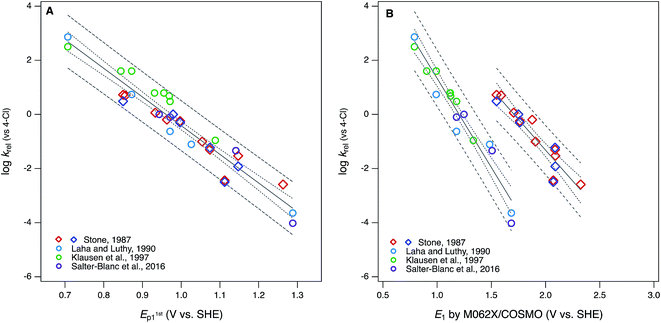 | ||
Fig. 5 Correlations of rate constants for oxidation by manganese oxides (krel) and oxidation potentials of phenols and anilines: (A) log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) krel from compiled sources (Table S1†) vs. E1stp1 from this study (Tables S4 and S5†); (B) log krel from compiled sources (Table S1†) vs. E1stp1 from this study (Tables S4 and S5†); (B) log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) krelvs. E1 without calibration, from this study (Tables S6 and S7†). Diamonds represent phenols and circles represent anilines. krelvs. E1 without calibration, from this study (Tables S6 and S7†). Diamonds represent phenols and circles represent anilines. | ||
The differences between the correlations to E1/2 (Fig. 1A) and E1stp1 (Fig. 5A) are subtle: mainly there is a slightly different distribution of residuals, resulting in slightly better overall regression statistics with E1stp1 (Table S13†). Since the two sets of electrochemical oxidation potentials are strongly covariant (Fig. 3A), the residuals in Fig. 1A and 5A are likely to arise from the same source. Certainly, one source could be experimental error in the original krel data, but another possibility is that it reflects compound-specific effects that influence the response and descriptor variables differently. In this case, a likely contributor to such effects is that the surface properties of MnO2 and graphitic carbon (the working electrode material) are very different, which could result in significantly different surface interactions with the phenols/anilines with different combinations of substituents.
Compared with the correlations between log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) krel and electrochemically determined oxidation potentials, the correlations to calculated E1's gave more diverse results. Using uncalibrated E1's (Fig. 5B) produces separate correlations for the phenols and anilines, both of which are statistically satisfactory, but the differences in slope and intercept are not consistent with the experimental potential data. Because of the latter, this appears to be a case where splitting the data into subsets leads to less chemically meaningful results. Calibration of E1's to the experimental potentials (E1/2 or E1stp1) normalizes the phenols and anilines to the same slope and intercept, so correlations between log
krel and electrochemically determined oxidation potentials, the correlations to calculated E1's gave more diverse results. Using uncalibrated E1's (Fig. 5B) produces separate correlations for the phenols and anilines, both of which are statistically satisfactory, but the differences in slope and intercept are not consistent with the experimental potential data. Because of the latter, this appears to be a case where splitting the data into subsets leads to less chemically meaningful results. Calibration of E1's to the experimental potentials (E1/2 or E1stp1) normalizes the phenols and anilines to the same slope and intercept, so correlations between log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) krel and E1c can be fit to one QSAR for all compounds (Fig. 6). The fitting statistics for these correlations are very good and similar to those obtained with experimentally measured potentials (Table S13†). Values of E1c obtained using the B3LYP functional produce nearly identical correlations to log
krel and E1c can be fit to one QSAR for all compounds (Fig. 6). The fitting statistics for these correlations are very good and similar to those obtained with experimentally measured potentials (Table S13†). Values of E1c obtained using the B3LYP functional produce nearly identical correlations to log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) krel (not shown).
krel (not shown).
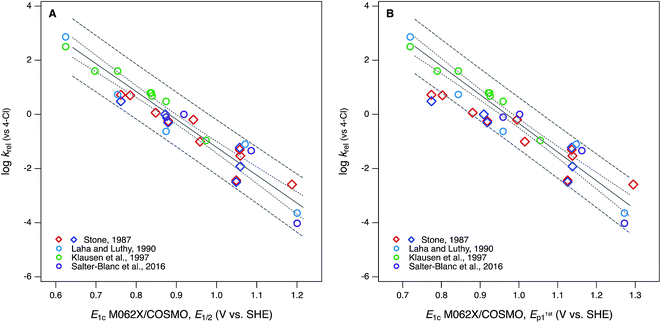 | ||
Fig. 6 Correlations of rate constants for oxidation by manganese oxides (krel) and oxidation potentials of phenols and anilines: (A) log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) krel from compiled sources (Table S1†) vs. E1 with calibration using data for E1/2; (B) log krel from compiled sources (Table S1†) vs. E1 with calibration using data for E1/2; (B) log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) krel from compiled sources vs. E1 with calibration using data for E1stp1 (Tables S9 and S10†). Diamonds represent phenols and circles represent anilines. krel from compiled sources vs. E1 with calibration using data for E1stp1 (Tables S9 and S10†). Diamonds represent phenols and circles represent anilines. | ||
In Fig. 6B, the three points that fall outside the prediction interval are 2-hydroxy, 4-hydroxy, and 2,6-dimethoxy phenol. The substituents on these compounds are likely to cause effects that require compound-specific modeling; e.g., a shift from one- to two-electron oxidation potentials corresponding to the formation of quinonoid products.42 In fact, these compounds are responsible for the three sets of anomalously high E1's in the lower-left corner of their calibrations to E1stp1 (Fig. S9B and S10B†), and it is the leverage that these points exert on the calibration regression that causes these compounds to appear as outliers in Fig. 6B. The E1/2 dataset from Suatoni et al. does not extend to phenols with such low potentials, so the corresponding E1's do not appear in Fig. S9A or S10A† and therefore do not have any effect on the correlation using E1c calibrated to E1/2 (Fig. 6A).
Comparing the statistical quality of all the QSARs derived here with log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) krel (Fig. 1A, 5A, 6, and Table S13†) shows little difference between the descriptors E1/2, Ep1, and E1c. However, other, subjective differences are important. For example, while the original experimental dataset of E1/2 by Suatoni et al. is large, it contains few compounds with challenging substituents. The new set of Ep's reported here includes more ionizable and polar functional groups, more substituents that are likely to cause proximity effects, more compounds with two or more substituents, and more complex phenols and anilines of biological or environmental interest (e.g., dopamine and triclosan). These complications favor net substituent effects that are not easily modelled, which can contribute to greater residuals in correlation analysis. These residuals can be useful, however, such as for diagnosing specific substituent effects, selection among descriptor variable datasets, and identification of the limits of applicability of a QSAR model.
krel (Fig. 1A, 5A, 6, and Table S13†) shows little difference between the descriptors E1/2, Ep1, and E1c. However, other, subjective differences are important. For example, while the original experimental dataset of E1/2 by Suatoni et al. is large, it contains few compounds with challenging substituents. The new set of Ep's reported here includes more ionizable and polar functional groups, more substituents that are likely to cause proximity effects, more compounds with two or more substituents, and more complex phenols and anilines of biological or environmental interest (e.g., dopamine and triclosan). These complications favor net substituent effects that are not easily modelled, which can contribute to greater residuals in correlation analysis. These residuals can be useful, however, such as for diagnosing specific substituent effects, selection among descriptor variable datasets, and identification of the limits of applicability of a QSAR model.
In addition to the diversity of substituents included, another subjective difference that distinguishes the QSARs obtained here using E1/2, Ep1, and E1c as descriptor variables is their suitability for use in prediction. For new phenols and anilines, Suatoni et al. concluded that values of E1/2 can be estimated by assuming additivity of substituent effects or a Hammett correlation between E1/2 and σ, and these approximations have proven useful in several subsequent studies.9,11 However, they are likely to break down with more complex compounds. The new datasets of experimental Ep1's reported in this study have the advantage of being extendable with new measurements using the modern methods documented and validated here. Interpolation of additional Ep1's without new measurements should be possible using the same additivity and Hammett correlation approaches used by Suatoni et al., but this was not verified as part of this work.
In contrast to experimental or empirical approaches to obtaining descriptor data for new phenols or anilines, purely in silico calculation of E1's from molecular structure theory could be very efficient (because the calculations can be programmed to run in batches). As demonstrated in this study, however, E1 must be calibrated to experimental data to ensure the absolute and relative accuracy of the results. Even after calibration, values of E1c for some compounds may not fully reflect the processes controlling oxidation in solution, which can cause unnecessary outliers when applied in QSARs (e.g., Fig. 6B). Such outliers could be avoided with sufficiently detailed modeling calculations, but this would obviate the efficiency of the modeling approach to populating new descriptor data. Overall, the balance of considerations (statistical and subjective) favor the experimental and empirical approach to obtaining descriptor data for predictive applications of QSARs.
In the end, the main advantage of correlation analysis performed using E1 from molecular structure theory is clarity and precision regarding the mechanisms that are represented by the descriptor. This complements the relative ambiguity of krel, E1/2, Ep regarding the mechanisms controlling these properties measured in solution. Correlation analysis between the two types of properties (empirical vs. theoretical) can provide insights into either, or both, as exemplified in this study for oxidation of phenols and anilines. Selection of one type of descriptor over another should be done with consideration of the principle of matching the observational vs. mechanistic character of descriptor variables. So, for the purpose of developing QSARs to predict rates of oxidation by MnO2, the most effective descriptors will be those that reflect similar interfacial redox processes (e.g., E1/2, Ep). For the purposes of testing hypotheses regarding the mechanism of electron transfer involving MnO2 (or other oxidants), there may be greater diagnostic value to correlation analysis with descriptors that are calculated from molecular structure theory (e.g., E1) and therefore mechanistically less ambiguous.
The complementary advantages of measured and calculated descriptors are somewhat obscured by the calibration of calculated descriptors with measured descriptors, as was done to obtain E1c in this study. We did this partly for the practical reasons that (i) we were interested in validating our newly measured values of Ep and (ii) experimental values of E1 are much less abundant, or easily obtained. However, the results of this decision also serves to illustrate the overall theme of this work, that lumping works best when the response and descriptor variables are matched with respect to observational vs. mechanistic character.
Acknowledgements
This work was supported by the U.S. National Science Foundation, Environmental Chemical Sciences Program (NSF Grant # 1506744) and the U.S. Department of Defense, Strategic Environmental Research and Development Program (SERDP Grant #ER-1735). Some of the electrochemistry was performed by David Panfilov, while on an internship funded by the NSF Center for Coastal Margin Observation and Research. The modeling portion of this research was performed using the Institutional Computing facility (PIC) at the Pacific Northwest National Laboratory (PNNL) and the Chinook, Barracuda, and Cascade computing resources at the Environmental Molecular Sciences Laboratory (EMSL). PNNL is operated by Battelle Memorial Institute for the U.S. Department of Energy (DOE). EMSL is a national scientific user facility, located at PNNL, and sponsored by the DOE's Office of Biological and Environmental Research (DE-AC06-76RLO 1830). We also acknowledge EMSL for supporting the development of NWChem. Structure database management and some property prediction was performed using Instant JChem (Instant JChem 16.12.5.0) ChemAxon [http://www.chemaxon.com]. This report has not been subject to review by any of the sponsors and therefore does not necessarily reflect their views and no official endorsement should be inferred.References
- S. Canonica and P. G. Tratnyek, Environ. Toxicol. Chem., 2003, 22, 1743–1754 CrossRef CAS PubMed.
- P. G. Tratnyek, in Perspectives in Environmental Chemistry, ed. D. L. Macalady, Oxford, New York, 1998, pp. 167–194 Search PubMed.
- Y. Lee and U. von Gunten, Water Res., 2012, 46, 6177–6195 CrossRef CAS PubMed.
- J. C. Suatoni, R. E. Snyder and R. O. Clark, Anal. Chem., 1961, 33, 1894–1897 CrossRef CAS.
- A. T. Stone, Environ. Sci. Technol., 1987, 21, 979–988 CrossRef CAS PubMed.
- S. Laha and R. G. Luthy, Environ. Sci. Technol., 1990, 24, 363–373 CrossRef CAS.
- J. Klausen, S. B. Haderlein and R. P. Schwarzenbach, Environ. Sci. Technol., 1997, 31, 2642–2649 CrossRef CAS.
- A. J. Salter-Blanc, E. J. Bylaska, M. A. Lyon, S. Ness and P. G. Tratnyek, Environ. Sci. Technol., 2016, 50, 5094–5102 CrossRef CAS PubMed.
- P. G. Tratnyek and J. Hoigné, Environ. Sci. Technol., 1991, 25, 1596–1604 CrossRef CAS.
- E. Rorije and J. G. M. Peijnenburg, J. Chemom., 1996, 10, 79–93 CrossRef CAS.
- P. G. Tratnyek and J. Hoigné, Water Res., 1994, 28, 57–66 CrossRef CAS.
- L. Meites and P. Zuman, CRC Handbook Series in Organic Electrochemistry, CRC, Cleveland, OH, 1979 Search PubMed.
- R. A. Larson and R. G. Zepp, Environ. Toxicol. Chem., 1988, 7, 265–274 CrossRef CAS.
- S. Padmaja, J. Rajaram and V. Ramakrishnan, Indian J. Chem., Sect. A: Inorg., Phys., Theor. Anal., 1990, 29, 422–424 Search PubMed.
- A. V. Marenich, J. Ho, M. L. Coote, C. J. Cramer and D. G. Truhlar, Phys. Chem. Chem. Phys., 2014, 16, 15068–15106 RSC.
- J. Ho, M. L. Coote, C. J. Cramer and D. G. Truhlar, in Organic Electrochemistry, ed. O. Hammerich and B. Speiser, CRC Press, 5th edn, 2015, pp. 229–259 Search PubMed.
- P. Winget, E. J. Weber, C. J. Cramer and D. G. Truhlar, Phys. Chem. Chem. Phys., 2000, 2, 1871 RSC.
- P. Winget, E. J. Weber, C. J. Cramer and D. G. Truhlar, Phys. Chem. Chem. Phys., 2000, 2, 1231–1239 RSC.
- P. Winget, C. J. Cramer and D. G. Truhlar, Theor. Chem. Acc., 2004, 112, 217–227 CrossRef CAS.
- J. Moens, P. Jaque, F. De Proft and P. Geerlings, J. Phys. Chem. A, 2008, 112, 6023–6031 CrossRef CAS PubMed.
- D. H. Evans, Chem. Rev., 2008, 108, 2113–2144 CrossRef CAS PubMed.
- J. J. Guerard and J. S. Arey, J. Chem. Theory Comput., 2013, 9, 5046–5058 CrossRef CAS PubMed.
- W. A. Arnold, Environ. Sci.: Processes Impacts, 2014, 16, 832–838 CAS.
- P. R. Erickson, N. Walpen, J. J. Guerard, S. N. Eustis, J. S. Arey and K. McNeill, J. Phys. Chem. A, 2015, 119, 3233–3243 CrossRef CAS PubMed.
- M. Jonsson, J. Lind, T. E. Eriksen and G. Merenyi, J. Am. Chem. Soc., 1994, 116, 1423–1427 CrossRef CAS.
- W. A. Arnold, Y. Oueis, M. O'Connor, J. E. Rinaman, M. G. Taggart, R. E. McCarthy, K. A. Foster and D. E. Latch, Environ. Sci.: Processes Impacts, 2017 10.1039/C6EM00580B.
- P. Wardman, J. Phys. Chem. Ref. Data, 1989, 18, 1637–1657 CrossRef CAS.
- C. G. Zoski, Handbook of Electrochemistry, Elsevier, 2006 Search PubMed.
- L. Meites, Polarographic Techniques, Wiley Interscience, New York, 1965 Search PubMed.
- Organic Electrochemistry, ed. O. Hammerich and B. Speiser, CRC Press, 5th edn, 2015 Search PubMed.
- A. J. Bard and L. R. Faulkner, Electrochemical Methods. Fundamentals and Applications, Wiley, New York, 2001 Search PubMed.
- T. A. Enache, J. Electroanal. Chem., 2011, 655, 9–16 CrossRef CAS.
- D. Bejan and A. Duca, Croat. Chem. Acta, 1998, 71, 745–756 CAS.
- R. M. W. Amon, H.-P. Fitznar and R. Benner, Limnol. Oceanogr., 2001, 46, 287–297 CrossRef CAS.
- J. Wang, M. Jiang and F. Lu, J. Electroanal. Chem., 1998, 444, 127 CrossRef CAS.
- C. Cyrille, R. Marc and S. Jean-Michel, in Organic Electrochemistry, ed. O. Hammerich and B. Speiser, CRC Press, 5th edn, 2015, pp. 481–509, DOI:10.1201/b19122-17.
- C. Li and M. Z. Hoffman, J. Phys. Chem. B, 1999, 103, 6653–6656 CrossRef CAS.
- H. Li, L. S. Lee, D. G. Schulze and C. A. Guest, Environ. Sci. Technol., 2003, 37, 2686–2693 CrossRef CAS PubMed.
- M. Skarpeli-Liati, M. Jiskra, A. Turgeon, A. N. Garr, W. A. Arnold, C. J. Cramer, R. P. Schwarzenbach and T. B. Hofstetter, Environ. Sci. Technol., 2011, 45, 5596–5604 CrossRef CAS PubMed.
- M. Skarpeli-Liati, A. Turgeon, A. N. Garr, W. A. Arnold, C. J. Cramer and T. B. Hofstetter, Anal. Chem., 2011, 83, 1641–1648 CrossRef CAS PubMed.
- S. Steenken and P. Neta, J. Phys. Chem., 1982, 86, 3661–3667 CrossRef CAS.
- J. Q. Chambers, in The Chemistry of the Quinonoid Compounds, Interscience, New York, 1974, vol. 2, pp. 737–791 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6em00694a |
| This journal is © The Royal Society of Chemistry 2017 |