Radicals in carbonaceous residue deposited on mordenite from methanol

Abstract

It is shown that control of the degree of coking can lead to the observation of hyperfine structures in the carbonaceous residues deposited from methanol over mordenite (H-MOR) at temperatures relevant to the conversion of methanol to hydrocarbons. EPR measurements of the catalyst samples at various times on stream have been recorded, with a rich hyperfine splitting pattern observed in the early stages of the reaction. Interpretation of the EPR data with the aid of density functional theoretical calculations has afforded the first definitive assignment of the radical cations formed in high temperature coke. The results detail a shortlist of six species: 2,3/2,6/2,7-dimethylnaphthalenium, 2,3,6-trimethylnaphthalenium, 2,3,6,7-tetramethylnaphthalenium, and anthracenium radical cations whose proton hyperfine splitting profiles match the experimental spectra; 2,3,6,7-tetramethylnaphthalenium showed the best agreement. The observation of these particular isomers of polymethylnaphthalene suggest the formation of more highly branched polyaromatic species is less likely within the confines of the H-MOR 12-membered ring channel. These radicals formed when the catalyst is active may constitute key intermediates in the conversion of methanol to light olefins.

---

Introduction

The conversion of methanol over microporous materials is an area of both current and historical interest.^1–4 A number of inter-related processes have been the centre of attention, including methanol dehydration to yield dimethylether, MTO (the conversion of methanol to light olefins) and MTH (the conversion of methanol to hydrocarbons). Catalysis of the latter two processes can be achieved with a range of zeolite and zeotype materials but particular interest has centred upon SAPO-34 for MTO and H-ZSM-5 for MTH.^1,2 For both these processes, the so-called hydrocarbon pool mechanism has gained widespread acceptance in recent years.^5,6 In general, although subject to refinements, this mechanism is based upon the formation of an active hydrocarbon pool upon reaction. This hydrocarbon pool is proposed to be comprised of catalytically active alkylated aromatic species.^3,7

In concert with the formation of active hydrocarbon species MTH processes is the unavoidable generation of a carbonaceous residue (coke) chiefly composed of polyaromatics that coats the surface of the zeolite affecting catalyst deactivation.⁸ It has long been known this residue harbours radicals that have been identified by EPR spectroscopy, similar to coal and pitch.⁹ The signal typically manifests as a featureless line whose width is modulated by the radical concentration.¹⁰ It is not unsurprising that similar signals were observed in the undesirable formation of carbonaceous residues over acidic zeolite catalysts during MTH processes.^2,11 EPR spectroscopy has been sought to identify and elucidate the role of these radicals during methanol conversion. Seminal work by Karge and co-workers utilised in situ and ex situ EPR to monitor hydrocarbon deposited on mordenite from ethene and propene feeds.^12,13 Their study revealed short-lived olefinic radicals appearing in low temperature coke (<200 °C) and abundantly more stable radicals forming at reaction temperatures exceeding 250 °C. It was the observation of multiline hyperfine splitting in the spectra of the olefinic radicals that facilitated their identification, as structural information can only be obtained from hyperfine coupling interactions between the unpaired electron and the nuclear spin of protons. As such, they could only postulate that the nearly featureless high temperature coke derives from polymethylbenzene radicals,^12,13 consistent with previous studies that correlated the formation of aromatic radicals with zeolite acidity.^14–17

Within the past few years a degree of attention has centred upon the observation of radicals specific to the conversion of alcohols over zeolites.^18,19 Recent attempts have been made to correlate their existence to the mechanism and deactivation of ethanol transformation over HZSM-5,²⁰ however the absence of hyperfine features precluded identification of the radicals formed. Seo and co-workers determined hexamethylbenzenium radicals are generated on H-SAPO-34 and H-SSZ-13 a mere 30 minutes time on stream (TOS) when the catalyst was still active.²¹ The signal persisted for 3 h, there after narrowing as larger aromatics formed and the catalyst activity declined.²² Recently, they identified 1,2,4,5-tetramethylbenzenium radicals during MTO over a phosphorus modified H-ZSM-5.²³ The modification eliminated many acid sites thereby leaving the radicals sufficiently separated and free from effects of interspin coupling that extinguishes hyperfine features. Their assignment was neatly supported by collecting reference spectra of polymethylbenzenium radicals formed on mordenite at 200 °C.

Herein, we extend studies of the formation of EPR active radicals as formed over H-mordenite (H-MOR) samples coked using methanol. We concentrate upon establishing whether, or not, there are any relationships between coking profile and radical concentration by varying TOS for the samples generated with a 20% MeOH feed at 260 °C. The efficacy of H-MOR for the production of hydrocarbons has been established in previous studies,²² and investigations undertaken using a variety of techniques demonstrate that features consistent with the formation of a hydrocarbon pool to be formed.²⁴ We observe in spectra of samples with short TOS a rich hyperfine splitting profile, and with the aid of theoretical calculations are able to assign the radical species formed in high temperature coke residue.

Experimental section

Sample preparation

Approximately 0.28 of H-mordenite (H-MOR; Si/Al = 10) was held in a quartz fixed-bed reactor tube connected to a stainless steel reactor. All reactor lines were trace heated to 150 °C. The sample was heated under an Ar flow (22 mL min⁻¹; GHSV = 3000 h⁻¹) and heated to the desired reaction temperature. Once at temperature, the feed was switched to bypass mode and purged with liquid methanol (0.01 mL min⁻¹) pumped via Knauer HPLC pump in addition to the previous Ar feed. Once a constant feed of methanol was observed using a GC-TCD detector at the rear end of the rig, the methanol/Ar flow was directed towards the H-MOR for the desired length of time. Following the reaction period, the methanol feed was stopped, the heater switched off and the H-MOR was allowed to cool until <50 °C in an Ar flow (22 mL min⁻¹). Once cooled the reactor tube was immediately removed, plugged with rubber bungs and transferred into an inert atmosphere glove box.

EPR spectroscopy

Powder samples of H-MOR following carbon deposition from methanol were loaded to a height of 20 mm in a 4 mm (o.d.) quartz EPR tube. The tube was sealed with a J. Young Teflon stopcock under an atmosphere of Ar inside a glovebox. X-band EPR spectra were taken at ambient temperature (293 K) using a Bruker ELEXSYS E500 spectrometer equipped with a super high-Q cavity (ER 4122 SHQE). The experimental parameters for EPR spectra were as follows: microwave frequency = 9.786 GHz; microwave power = 0.63 mW; modulation amplitude = 0.05 mT; modulation frequency = 100 kHz; time constant = 10.24 ms; conversion time = 20.48 ms; number of scans = 20. Spectral simulations were generated using XSophe distributed by Bruker Biospin GmbH.²⁵

Other physical measurements

Carbon analyses were undertaken using an Exeter Analytical CE-440 elemental analyser. TGA profiles were measured using a TA Instruments Q500 instrument under a flow of air. The temperature was ramped from 20 to 1000 °C at a rate of 10 °C min⁻¹. Surface areas were determined by applying the Brunauer–Emmett–Teller (BET) method to the nitrogen physisorption isotherm obtained at −196 °C in a Micromeritics Gemini instrument. The sample was first heated up to 250 °C for 2 h under vacuum and degassed at 250 °C for 2 h prior to analysis. ¹³C MAS NMR data were acquired by the EPSRC NMR Service at the University of Durham using a Varian VNMRS spectrometer equipped with a 9.40 T magnet operating at 100.56 MHz. A 6 mm (rotor o.d.) magic angle spinning probe was utilised. Cross-polarisation spectra were obtained using a 1 s delay, a 1 ms contact time, a sample spin rate of 6.8 kHz and “TOSS” spinning side band suppression.

Calculations

The program package ORCA was used for all calculations.²⁶ The input geometry for the monocationic radicals was derived from their parent neutral molecule generated in ArgusLab. The geometries of all molecules were fully optimized by a spin-unrestricted DFT method employing the B3LYP functional.²⁷ Triple-ξ-quality basis sets with one set of polarization functions (def2-TZVP) were used all atoms.²⁸ The RIJCOSX approximation²⁹ combined with the appropriate Ahlrichs auxiliary basis set³⁰ was used to speed up the calculations. The self-consistent field calculations were tightly converged (1 × 10⁻⁸E_h in energy, 1 × 10⁻⁷E_h in the density charge, and 1 × 10⁻⁷ in the maximum element of the DIIS³¹ error vector). The geometry was converged with the following convergence criteria: change in energy < 10⁻⁵E_h, average force < 5 × 10⁻⁴E_h Bohr⁻¹, and the maximum force 10⁻⁴E_h Bohr⁻¹. The coordinates of the atoms are included in the ESI.† Spin density maps were visualised with the program Molekel.³²

Results and discussion

The coking profiles of the H-MOR sample after 5 h TOS run under four different partial pressures of methanol (20%, 50%, 60%, 90% with the balance in all cases being argon) are presented in Fig. 1.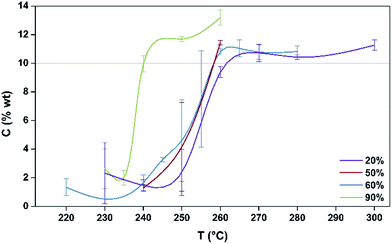

Fig. 1 Coking profiles, as C wt%, of post reaction samples produced at different reaction temperatures for different partial pressures of MeOH.

A pronounced step is evident in the profiles of the 20%, 50% and 60% MeOH partial pressures demonstrating that the samples progress from a regime of a relatively light degree of coke formation to one where much more severe coke formation occurs over a relatively narrow temperature range. This step occurs ∼20 °C lower for the 90% MeOH/Ar mixture than for the other reaction mixtures. Indeed, the sensitivity of the process is further underlined by the relatively large error bars associated with the degree of coking for temperatures which are within the range of the step in the profiles. The error bars were determined from replicate runs and they reflect the degree of sensitivity within these coking regimes. The step in coking behaviour is consistent with a change in selectivity as a function of temperature passing from a regime wherein dimethylether is formed by dehydration, associated with a low degree of coking, to one where the methanol to hydrocarbons reaction occurs which may be associated with the formation of an active hydrocarbon pool and the formation of waxes which deposit in the downstream cold spot of the reactor. Nitrogen physisorption analysis shows that the more heavily coked materials exhibit a type II isotherm which is indicative of micropore filling by carbonaceous species as indicated by the reduction in BET surface area (which strictly is not applicable to the type I isotherms of the fresh materials but which is used in comparative terms; Fig. S1†). In comparing the various profiles presented in Fig. 1 it can be seen that the degree of coking beyond the step is relatively independent of methanol partial pressure.

In terms of our aim to monitor the relationship between coking profile and the formation of EPR active radicals, we have selected the 20% methanol feed at 260 °C for further investigation. This temperature is close to the top of the step for this partial pressure as illustrated in Fig. 1. Accordingly, since the degree of coking could be controlled over a relatively wide range by variation of TOS for this temperature, it was felt that this would offer an opportunity to speciate the nature of the coke and to draw comparisons with the EPR behaviour.

EPR spectroscopy

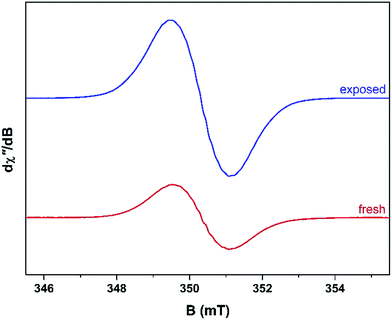
Unused catalyst produced no signal aside from an almost undiscernible peak at g ∼ 4.3 ascribed to Fe³⁺ impurities.^33,34 This resolution of this peak could have been improved with higher power and cryogenic temperatures, however, it had previously be determined that these transition metal impurities are not involved in coke radical formation.¹² Furthermore, this signal is extinguished during the course of the reaction at 260 °C.³⁵ The EPR signal evident for coked samples present relatively featureless spectra centred at a g-value of 2.0026 consistent with carbon-based radicals.⁹ The signal first emerges for a catalyst sample after 1 h on the stream. The spectrum is very weak indicating minimal coking at this time and commensurate with the lack of colour (light tan) in the sample (Fig. S2†). A more pronounced signal is observed after 2 h TOS. The “fresh” catalyst sample was taken directly from the reactor and loaded into the EPR tube under an inert atmosphere. The longevity of the radicals was explored by exposing the sample to atmosphere for 24 h and recording its effect on the EPR signal (labelled “exposed”). These spectra are presented in Fig. 2. The signal for the air contacted samples survived several weeks, though there was no further increase in intensity after 1–2 days stored in air. A wide sweep spectrum shows that in addition to the dominant carbon radical at g = 2.0026, a very broad feature is observed with g ∼ 2.17 (width 40 mT; Fig. S3†). This is signal most likely stems from amorphous iron oxide/hydroxide where the coking alters the geometry and relaxation properties of the Fe³⁺ centres.³³

Fig. 2 Comparison of the X-band EPR spectra for the fresh (red) and air-exposed (blue) catalyst recorded at ambient temperature on an aliquot collected after 2 h TOS with 20% MeOH/Ar at a reaction temperature of 260 °C.

The spectrum of the fresh catalyst after 2 h exhibits some fine structure attributed to hyperfine coupling through the crossing point. This spectrum is reminiscent of the signal of high temperature coke measured by Karge and co-workers over the temperature range 250–450 °C.^12,13 Most interesting is its nearly identical appearance to the signal from coke residue coating the external surface of H-UZM-12 zeolites under a methanol feed.²¹ The H-UZM-12 framework possesses ERI topology with large cages 13.0 Å long and 6.3 Å in diameter.³⁶ The hyperfine features are slightly attenuated but still visible in the air exposed sample, a consequence of the noticeable increase in the signal intensity. Further catalyst aliquots taken at 3, 4 and 5 h produced an almost identical profile to the spectra shown in Fig. 2. Extending the TOS afforded EPR spectral that were almost featureless (Fig. S2†), though some hyperfine structure is visible in the second derivative (Fig. S4†). Importantly, all signals have the same spectral width (∼0.6 mT), which suggests these radicals are of the same or similar chemical composition irrespective of their TOS. The signal is consistent with high temperature coke described by Karge and co-workers when carbonising ethylene and propylene over H-MOR at temperatures exceeding 200 °C.^12,13

The effects of exposure to air are displayed in Fig. 3 with a comparison of the absorption spectrum at different TOS intervals; the signal intensity given by the area under the absorption peak. Overall, the general form of the EPR profile is maintained, however the intensity of the air contacted spectra is considerably greater than their fresh catalyst counterparts, indicating further evolution of radicals. This is in contrast to carbon radicals adsorbed on a silica–alumina surface, where the introduction of oxygen reduced the signal intensity by approximately one-third and decreased the spin lattice relaxation times by an order of magnitude.³⁷

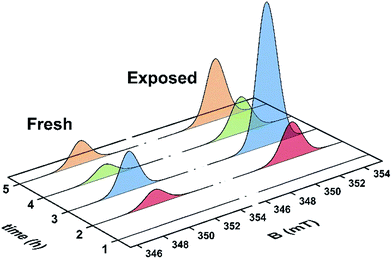Fig. 3 Comparison of the absorption spectra collected at ambient temperature for the fresh and air exposed catalyst at hourly time intervals (reactor conditions: 20% MeOH/Ar at 260 °C).

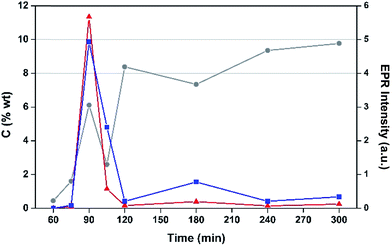
The effects of TOS upon both post-reaction carbon content and EPR signal intensity are displayed in Fig. 4. The list includes samples collected at 75, 90 and 105 min TOS in order to determine the approximate time frame for the evolution of coke radicals. Interestingly, EPR intensity data peak at 90 minutes, which then fall sharply with longer TOS. After 90 minutes the H-MOR still exhibits a high surface area (Fig. S1†), such that the radical content indicates high coverage of the acid sites (Si/Al = 10). For TOS beyond 2 h, the coking profile and surface area analysis is characteristic of pore blockage, which is mode of deactivation in monodimensional zeolites like H-MOR.³⁸ This has the effect of increasing coking of the catalyst surface, leading to clustering of radicals that would be fewer in number but more prone to the effects of spin–spin interactions on their EPR lineshape, such as the loss of hyperfine structure (Fig. S2†). We posit this pore blockage reduces the exposure of radicals in the channels from contact with oxygen, and the aforementioned impact of the EPR spectra. Therefore the increase in signal intensity for TOS >2 h arises from aerial oxidation of surface adsorbed coke,³⁹ and is proportional to the acid site content of the zeolite.³⁸ This conclusion is also consistent with the drop in signal intensity for the air-contacted samples at 90 and 105 min when oxygen has unimpeded access to the catalyst interior.

Fig. 4 Comparison of the radical content in the air deprived (red trace) and exposed (blue trace) samples derived from EPR signal intensity and the total C wt% (20% MeOH/Ar at 260 °C; gray trace) at various time intervals.

As anticipated, the degree of coking varies over a wide range. Inspection of the trend evident demonstrates that EPR signal intensity is not a simple function of carbon content, although with the exception of the 180 min TOS data, there does seem to be such a relationship, which is perhaps not surprising. At 180 min, there appears to be a reduction in the amount of coke deposited with respect to the two data points to either side and this is also associated with a significant enhancement in EPR signal intensity for this data point. This effect, which is outside that expected taking into experimental uncertainty, has been shown to be reproducible and could relate a change in the nature of coking at this reaction time.

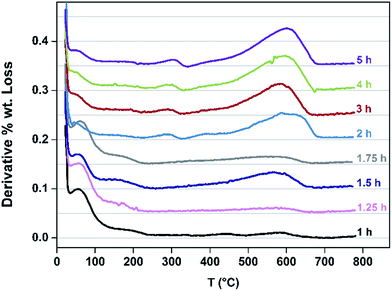
Speciation of the coke deposited upon the samples as a function of TOS at 260 °C was undertaken. TGA profiles undertaken in air are presented in Fig. 5. The mass losses occurring <130 °C correspond to the loss of water and the progressive diminution of this feature as a function of extended reaction time, and hence degree of coking, as would be expected can be seen. Furthermore, mass losses corresponding to species such as adsorbed methanol and/or dimethylether occur in the range ca. 150–230 °C. Upon extended reaction times, species which are lost in the 250–350 °C become evident – previous work has shown the losses in this range to be associated with desorption of carbonaceous species rather than oxidative processes.²⁴ The broad features in the range ca. 400–700 °C are associated with hard coke being lost through oxidation.²⁴

Fig. 5 TGA profiles for catalyst samples at indicated TOS.

DFT calculations

The concentration of cationic radicals was sufficiently low after 75 min TOS that the resulting spectrum exhibited resolved hyperfine splitting (Fig. 6). A similar spectral profile was measured for the 105 min sample. At these two time intervals, the radicals are sparsely deposited throughout the pores of H-MOR, minimising the spin–spin interaction between them. This allows their hyperfine features to remain visible. The impact of the spin–spin interaction is evidenced at higher radical concentration (longer reaction times) where the spectra are distinctly isotropic and featureless. However, despite the low radical concentration, the spin–spin interaction still manifests in the 75 min spectrum. Unpaired electrons interact with each in two ways: (i) exchange coupling which occurs through bonds, both covalent and non-covalent; and (ii) dipolar coupling which is a through space interaction.⁴⁰ These two couplings have an opposing effect in the EPR spectrum: the exchange interaction causes the hyperfine lines to collapse and the signal becomes narrower, whereas the dipolar interaction causes additional features to appear from a phenomenon known as zero-field splitting, which overall broadens the EPR signal.⁴¹ For the 75 min spectrum, ∼17 hyperfine lines are visible; the most prominent ones are in the centre of the spectrum as the line crosses the zero point best visualised in the second derivative plot (Fig. 6). The wings of the spectrum are less resolved which suggests dipolar broadening is dominant over exchange narrowing, commensurate with the low radical concentration. This is not unsurprising as the through bond interaction is attenuated by the lack of bona fide covalent bonds between radical cations, instead utilising less efficient π-stacking and other non-covalent pathways for neighbouring spins to communicate.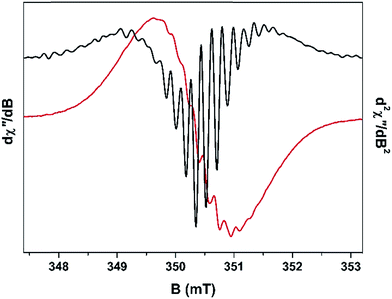

Fig. 6 X-band EPR first derivative spectrum (red line) overlaid with the second derivative spectrum (black line) of the fresh H-MOR catalyst sample after 75 min TOS.

The spectrum recorded after 75 min is reminiscent of polymethylaromatic radicals,^{14–17,21,23,42–47} and therefore a survey of potential candidates was undertaken to determine the likely species that were coating the pores of H-MOR. The survey was conducted as follows: the radical cation of a polymethylaromatic molecule was geometry optimised at the B3LYP level of DFT, and then the hyperfine coupling from each proton was calculated from the Mulliken spin population analysis. Proton hyperfine coupling constants (a_H) were calculated from the Mulliken spin density (ρ_H) distribution using the relationship a_H = ρ_H × 1419 (in MHz) derived from the McConnell equation.⁴⁸ Our theoretical estimate was compared with experimental data for authentic radical cations that were included in the survey, namely 1,2,4,5-tetramethylbenzenium, hexamethylbenzenium, anthracenium, 9,10-dimethylanthracenium, and pyrenium. The experimental are contrasted with the calculated a_H values in Table 1. Overall there is good agreement, especially for the anthracenium radical cation adsorbed on a silica–alumina surface.^16,47 It was noted that the a_H were only 4% larger for the surface absorbed anthracenium radical compared with chemically generated variant.

Table 1 Comparison of experimental and calculated proton hyperfine coupling constants (in MHz) for polyaromatic radical cations

Radical cation^a	Experimental	Calculated	Reference
a Each set of unique protons and their multiplicity are indicated.
1,2,4,5-Tetramethylbenzenium
CH3 (12)	22.8	21.9	49
3,6-H (2)	2.9	2.1
Hexamethylbenzenium
CH3 (18)	18.2	11.5	49
Anthracenium
9,10-H (2)	18.9	14.2	16
1,4,5,8-H (4)	9.0	6.4
2,3,6,7-H (4)	3.8	3.5
9,10-Dimethylanthracenium
9,10-H (2)	22.5	14.5	44
1,4,5,8-H (4)	7.0	6.4
2,3,6,7-H (4)	3.5	2.8
Pyrenium
1,3,6,8-H (4)	15.3	13.9	44
2,7-H (2)	6.0	4.0
4,5,9,10-H (4)	3.4	3.9

---

The monocationic radicals of the following polymethylaromatics where sampled: toluene, o-/m-/p-xylene, 1,2,3-/1,2,4-/1,3,5-trimethylbenzene, 1,2,3,4-/1,2,3,5-/1,2,4,5-tetramethylbenzene, pentamethylbenzene, hexamethylbenzene, indene, naphthalene, 1-/2-methylnaphthalene, 1,2-/1,4-/2,3-/2,6-/2,7-dimethylnaphthalene, 2,3,6-trimethylnaphthalene, 2,3,6,7-tetramethylnaphthalene, anthracene, 1-/2-/9-methylanthracene, 1,2-/2,3-/2,6-/2,7-/9,10-dimethylanthracene, 2,3,6-trimethylanthracene, 2,3,6,7-tetramethylanthracene, phenanthrene, and pyrene. The selected species has all been previously been identified in coke residue using a combination of solid state NMR and GC-MS;^6,36,50–52 several of the corresponding radical cations had been have been observed by EPR.^{12,13,16,21,23} Solid-state ¹³C NMR data reveal signals ascribed to benzenes (toluene, xylenes), naphthalenes and anthracenes were as constituents of the coke formed in the H-MOR pores (Fig. S5†).^{19,22,24,53,54} Moreover, the pores are large enough (6.5 × 7.0 Å) to accommodate polyaromatics of this size,⁵⁵ as demonstrated by the seminal work of Seo and co-workers who recorded representative spectra for a suite of di-, tri-, tetra-, penta- and hexa-methylbenzene radicals formed over mordenite.⁵⁴

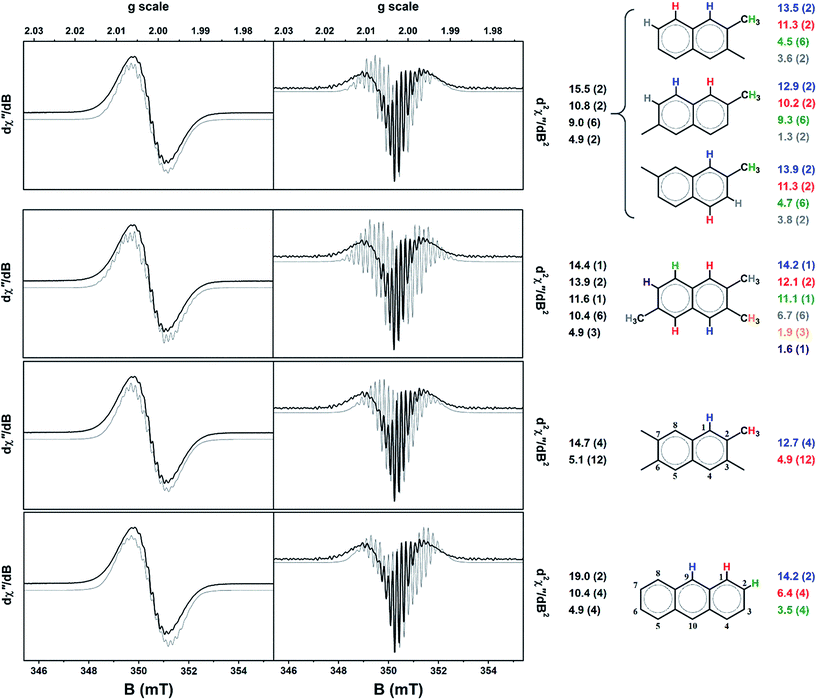
The calculated hyperfine parameters were used to compose a spectrum for each radical cation that could be compared to the experimental data. In order to reproduce the correct number of experimental lines, at least three types of protons are required. For example, the naphthalenium radical cation has two sets of four symmetrically equivalent protons (positions 1,4,5,8 and 2,3,6,7; standard numbering scheme shown in Fig. 7), and thus too few lines are generated. On the other hand, anthracenium has a three sets of protons: two in the 9,10 position, and the same two sets of four identified in naphthalenium, which is the minimum required to match the experiment. Secondly, the coupling of methyl protons is typically larger than the aromatic ones. The resonance structures for the radical cations of polymethylbenzenes deposit a large amount of spin density on the methyl carbon.^{15,23,43,44,49} The position of the substituent is also critical; the hyperfine coupling of methyl protons is larger in p-xylene than m-xylene because of the stability of the resonance structures in the former.²³ Based on these observations the monocationic radicals of all polymethylbenzenes, indene, 1-methylnaphthalene, 1,2-/1,4-dimethylnaphthalene, 1-/9-methylanthracene, and 1,2-/9,10-dimethylanthracene radicals were eliminated from the list as they were too broad due to the large coupling of the methyl protons. Three other contenders, 2-methylnaphthalenium, 2,3,6-trimethylanthracenium and 2,3,6,7-tetramethylanthracenium produced too many hyperfine lines and were similarly excluded. The outcome was a shortlist of six radical cations: 2,3-/2,6-/2,7-dimethylnaphthalenium, 2,3,6-trimethylnaphthalenium, 2,3,6,7-tetramethylnaphthalenium, and anthracenium. Phenanthrenium and pyrenium radicals, despite having four and three equivalent sets of protons, respectively, yielded an insufficient number of lines to match the spectrum profile (Fig. 7).

Fig. 7 Overlay of the experimental X-band EPR spectrum of catalyst mixture after 75 min TOS (solid line) with simulations (gray trace) derived from B3LYP-DFT calculations of the radical cations depicted right. Second derivative spectra shown adjacent the corresponding first derivative. The proton hyperfine coupling constants (in MHz) from the simulation are listed in black adjacent the corresponding spectrum with the number in parenthesis indicating the multiplicity of the nucleus. The DFT-derived proton coupling constants are colour-coded and their position is identified on the structural diagrams. The standard numbering scheme for these polyaromatics is provided for reference on the structures of 2,3,6,7-tetramethylnaphthalenium and anthracenium.

The Mulliken spin density analysis for each radical is shown in Fig. S6,† with the majority of the spin density is confined to the aromatic carbon atoms. The majority shareholders of the unpaired spin are the 1,4,5,8 carbons of naphthalene unit, and 1,4,5,8,9,10 carbons of anthracene unit; methyl groups attached at any of these positions would give large coupling constants. The proton splitting pattern for each of the shortlisted radicals was used to generate a simulation for the spectrum recorded after 75 min (Fig. 6). The spin-Hamiltonian, Ĥ = gμ_BBS + ∑aSI, was used, where the first term is the electron Zeeman splitting where the parameter g is the Landé g-factor (g = 2.0026), μ_B the Bohr magneton, B the magnetic field, S the total electron spin (S = 1/2 for these radical cations).⁴⁰ The second term is the hyperfine interaction as the sum of all protons (I = 1/2) in the system parameterised by the coupling constant a. The linewidth was fixed at 2 MHz being the smallest peak-to-peak distance in the spectrum.

For the dimethylnaphthalenium radical cations, a splitting pattern of 2 > 2 > 6 > 2 was used. In the case of 2,3-dimethyl substitution, the 1,4 protons have the largest coupling constants, then the 5,8, the six methyl protons and finally the 3,7 aromatic protons. The computed coupling constant for each set of protons is presented in Fig. 7. The 2,7-dimethylnaphthalenium radical gave the same magnitude of hyperfine splitting, whereas the 2,6 variant gave a significantly larger coupling of the methyl protons and concomitantly a miniscule one for the 3,7 protons. In generating these simulations, two simplifications have been employed. Firstly, an isotropic spin-Hamiltonian has been used even though the radicals are fixed to the surface of the H-MOR and unable to freely rotate.^13,14,56 This ignores the anisotropy of the proton hyperfine coupling, however the observed difference between parallel and perpendicular components, depending on the specific aromatic radical, can be rather small.^46,57 Moreover the motional averaging of both anisotropic hyperfine coupling and the g-matrix is improved at higher temperatures, i.e. room temperature.^17,45 Secondly, contributions to the lineshape from exchange narrowing and dipolar broadening have been ignored as these are not easily included in the simulation. The effect is that dipolar broadening may generate additional splitting from zero-field interaction,⁴⁰ such that not all the lines result from hyperfine coupling. The exchange interaction will compress the spacing between the hyperfine lines making these couplings appear smaller than they actually are.⁴¹ Nevertheless, the close agreement between simulated and computed proton coupling constants would seem to validate these assumptions. However, despite the closer agreement of the coupling constants for the 2,6-dimethylnaphthalenium radical compared with the other two isomers, we are unable to provide a more definitive assignment of the radical species in the sample. It is quite possible that these radicals are present in varying amounts and thus the EPR signal is a superposition of several spectra.

The lower symmetry of 2,3,6-trimethylnaphthalenium radical is expressed in the 1 > 2 > 1 > 6 > 3 > 1 splitting pattern (Fig. 7). The weakest coupled proton was ignored as this value of 1.6 MHz is smaller than the linewidth (2 MHz for each simulation). Despite the aforementioned requirement of a three sets of protons, the 4 > 12 pattern for 2,3,6,7-tetramethylnaphthalenium does produce the correct number of hyperfine lines, and in excellent agreement with the calculated coupling constants (Fig. 7). The final contender, the anthracenium radical cation, showed the largest disparity between experiment and theory. This species could probably be excluded as is it plausible that there is significantly less anthracene formed than naphthalene (and its derivatives) this stage of the reaction.

The observation of larger polymethylaromatic radical cations compared to those proposed for H-ZSM-5 is interesting. Structurally, the two zeolites differ in the size of their channel structures with larger 12-membered ring channels being present in H-MOR compared to the 10-membered ring channels in H-ZSM-5. Whilst 4- and 8-membered ring channels are present in the H-MOR structure, it is improbable that these could contain the aromatic cations evident in the EPR spectra presented within this manuscript which suggests that, as expected, the active hydrocarbon pool is restricted to the large channels. However, the confines of the pore-channels in these zeolites seemingly restrict the formation of branched aromatics, such as hexamethylbenzene, phenanthrene and pyrene that are frequently registered in H-SAPO-34 and related cage-like frameworks.^36,50,52 Although the results reported here do not preclude the formation of branched aromatics, it could be construed that the dimensions of H-MOR pores accelerate disproportion of these intermediates to the desired olefinic products.^22,58

Conclusions

This manuscript demonstrates that it is possible to observe hyperfine structures within the hydrocarbonaceous residue EPR spectra for H-MOR by careful control of the degree of coking with a low partial pressure of methanol. Through the application of experimentally calibrated DFT calculation of hyperfine coupling constants and sampling a large selection of potential polymethylaromatic species, we have been able to definitively assign the radical cations that constitute the EPR signal of high temperature coke.^12,13 In the case of H-MOR it has been shown that larger aromatic radical cations are formed compared to those expected in, for example, H-ZSM-5, however, both materials appear to disfavour the formation of the highly branched aromatics associated with MTO in H-SAPO-34.^36,52 The EPR signal is invariant over the course of the coking reaction, which demonstrates these methylated aromatic radicals are present in the active catalyst. Therefore it is conceivable these radicals, analogous to tetramethyl- and hexamethyl-benzene,^21,23 are also reaction intermediates in the formation of light olefins.

Acknowledgements

We are grateful to Mrs Kim Wilson for undertaking the C analyses. We wish to acknowledge access to the EPSRC NMR Service at University of Durham and thank Dr David Apperley and Mr Fraser Markam for acquiring the ¹³C MAS NMR spectra. JSJH and NAS gratefully acknowledge EPSRC (EP/J501979/1) and BP Chemicals for the generous provision of an Industrial CASE Award.

References

1. M. Stöcker, Microporous Mesoporous Mater., 1999, 29, 3.
2. M. Stöcker, in Zeolites and Catalysis: Synthesis, Reactions and Applications, ed. J. Čejka, A. Corma and S. Zones, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, 2010.
3. U. Olsbye, S. Svelle, M. Bjørgen, P. Beato, T. V. W. Janssens, F. Joensen, S. Bordiga and K. P. Lillerud, Angew. Chem., Int. Ed., 2012, 51, 5810.
4. U. Olsbye, S. Svelle, K. P. Lillerud, Z. H. Wei, Y. Y. Chen, J. F. Li, J. G. Wang and W. B. Fan, Chem. Soc. Rev., 2015, 44, 7155.
5. (a) M. Bjørgen, S. Akyalcin, U. Olsbye, S. Benard, S. Kolboe and S. Svelle, J. Catal., 2010, 275, 170; (b) I. M. Dahl and S. Kolboe, J. Catal., 1994, 149, 458; (c) J. F. Haw and D. M. Marcus, Top. Catal., 2005, 34, 41.
6. D. M. McCann, D. Lesthaeghe, P. W. Kletnieks, D. R. Guenther, M. J. Hayman, V. van Speybroeck, M. Waroquier and J. F. Haw, Angew. Chem., Int. Ed., 2008, 47, 5179.
7. J. F. Haw, W. Song, D. M. Marcus and J. B. Nicholas, Acc. Chem. Res., 2003, 36, 317.
8. M. Guisnet and P. Magnoux, Appl. Catal., 1989, 54, 1.
9. (a) D. J. E. Ingram, J. G. Tapley, R. Jackson, R. L. Bond and A. R. Murnaghan, Nature, 1954, 174, 197; (b) J. E. Bennett, D. J. E. Ingram and J. G. Tapley, J. Chem. Phys., 1955, 23, 215.
10. (a) L. S. Singer and I. C. Lewis, Carbon, 1978, 16, 417; (b) G. R. Eaton, S. S. Eaton, D. P. Barr and R. T. Weber, Quantitative EPR, Springer-Verlag, Wien, 2010.
11. (a) D. M. Bibby, R. F. Howe and G. D. McLellan, Appl. Catal., A, 1992, 93, 1; (b) P. M. M. Blauwhoff, J. W. Gosselink, E. P. Kieffer, S. T. Sie and W. H. J. Stork, in Catalysis and Zeolites: Fundamentals and Applications, ed. J. Weitkamp and L. Puppe, Springer-Verlag, Berlin, 1999.
12. J.-P. Lange, A. Gutsze and H. G. Karge, J. Catal., 1988, 114, 136.
13. H. G. Karge, J.-P. Lange, A. Gutsze and M. Łaniecki, J. Catal., 1988, 114, 144.
14. D. M. Brouwer, J. Catal., 1962, 1, 372.
15. P. L. Corio and S. Shih, J. Catal., 1970, 18, 126.
16. G. Muha, J. Phys. Chem., 1967, 71, 640.
17. G. M. Muha, J. Phys. Chem., 1967, 71, 633.
18. M. Hunger and J. Weitkamp, Angew. Chem., Int. Ed., 2001, 40, 2954.
19. M. Hunger, Microporous Mesoporous Mater., 2005, 82, 241.
20. K. B. Tayeb, L. Pinard, N. Touati, H. Vezin, S. Maury and O. Delpoux, Catal. Commun., 2012, 27, 119.
21. S. J. Kim, H.-G. Jang, J. K. Lee, H.-K. Min, S. B. Hong and G. Seo, Chem. Commun., 2011, 47, 9498.
22. J. W. Park, S. J. Kim, M. Seo, S. Y. Kim, Y. Sugi and G. Seo, Appl. Catal., A, 2008, 349, 76.
23. H.-G. Jang, H.-K. Min, S. B. Hong and G. Seo, J. Catal., 2013, 299, 240.
24. L. J. France, D. C. Apperley, E. J. Ditzel, J. S. J. Hargreaves, J. P. Lewicki, J. J. Liggat and D. Todd, Catal. Sci. Technol., 2011, 1, 932.
25. G. R. Hanson, K. E. Gates, C. J. Noble, M. Griffin, A. Mitchell and S. Benson, J. Inorg. Biochem., 2004, 98, 903.
26. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73.
27. (a) A. D. Becke, J. Chem. Phys., 1993, 98, 5648; (b) C. T. Lee, W. T. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785.
28. (a) R. Ahlrichs and K. May, Phys. Chem. Chem. Phys., 2000, 2, 943; (b) F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297.
29. F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98.
30. (a) K. Eichkorn, O. Treutler, H. Ohm, M. Haser and R. Ahlrichs, Chem. Phys. Lett., 1995, 242, 652; (b) K. Eichkorn, F. Weigend, O. Treutler and R. Ahlrichs, Theor. Chem. Acc., 1997, 97, 119.
31. (a) P. Pulay, Chem. Phys. Lett., 1980, 73, 393; (b) P. Pulay, J. Comput. Chem., 1982, 3, 556.
32. Molekel, Advanced Interactive 3D-Graphics for Molecular Sciences, Swiss National Supercomputing Center, http://www.cscs.ch/molekel.
33. (a) E. G. Derouane, M. Mestdagh and L. Vielvoye, J. Catal., 1974, 33, 169; (b) B. Wichterlová, Zeolites, 1981, 1, 181; (c) D. Goldfarb, M. Bernardo, K. G. Strohmaler, D. E. W. Vaughan and H. Thomann, J. Am. Chem. Soc., 1994, 116, 6344; (d) A. V. Kucherov, C. N. Montreuil, T. N. Kucherova and M. Shelef, Catal. Lett., 1998, 56, 173.
34. P. Wenquin, Q. Shilun, K. Qiubin, W. Zhiyun, P. Shaoyi, F. Guochuan and T. Di, Stud. Surf. Sci. Catal., 1989, 49, 281.
35. A. Brückner, U. Lohse and H. Mehner, Microporous Mesoporous Mater., 1998, 20, 207.
36. J. H. Lee, M. B. Park, J. K. Lee, H.-K. Min, M. K. Song and S. B. Hong, J. Am. Chem. Soc., 2010, 132, 12971.
37. C. P. Poole Jr, E. N. Dicarlo, C. S. Noble, J. F. Itzel Jr and H. H. Tobin, J. Catal., 1965, 4, 518.
38. M. Guisnet and P. Magnoux, Stud. Surf. Sci. Catal., 1994, 88, 53.
39. K. Moljord, P. Magnoux and M. Guisnet, Appl. Catal., A, 1995, 121, 245.
40. G. R. Eaton, S. S. Eaton and K. M. Salikhov, Foundations of Modern EPR, World Scientific Publishing Co., Singapore, 1998.
41. V. A. Atsarkin, G. A. Vasneva, V. V. Demidov, F. S. Dzheparov, B. M. Odintov and R. B. Clarkson, JETP Lett., 2000, 72, 369.
42. J. T. Cooper, W. F. Forbes and J. C. Robinson, Can. J. Chem., 1970, 48, 1942.
43. X.-G. Lei, S. Jockursch, M. F. Ottaviani and N. J. Turro, Photochem. Photobiol. Sci., 2003, 2, 1095.
44. I. C. Lewis and L. S. Singer, J. Chem. Phys., 1965, 43, 2712.
45. P. Kinell, A. Lund and A. Shimizu, J. Phys. Chem., 1969, 73, 4175.
46. T. Komatsu and A. Lund, J. Phys. Chem., 1972, 76, 1972.
47. J. J. Rooney and R. C. Pink, Trans. Faraday Soc., 1962, 58, 1632.
48. A. Carrington and A. D. McLachlan, Introduction to Magnetic Resonance, Harper & Row, New York, 1967.
49. R. M. Dessau, S. Shih and E. I. Heiba, J. Am. Chem. Soc., 1970, 92, 412.
50. B. Arstad and S. Kolboe, J. Am. Chem. Soc., 2001, 123, 8137.
51. (a) M. Bjørgen, F. Joensen, K. P. Lillerud, U. Olsbye and S. Svelle, Catal. Today, 2009, 142, 90; (b) M. Bjørgen, S. Svelle, F. Joensen, J. Nerlov, S. Kolboe, F. Bonino, L. Palumbo, S. Bordiga and U. Olsbye, J. Catal., 2007, 249, 195.
52. (a) D. M. Marcus, W. Song, L. L. Ng and J. F. Haw, Langmuir, 2002, 18, 8386; (b) S. Svelle, F. Joensen, J. Nerlov, U. Olsbye, K. P. Lillerud, S. Kolboe and M. Bjørgen, J. Am. Chem. Soc., 2006, 128, 14770.
53. (a) W. Wang, Y. Jiang and M. Hunger, Catal. Today, 2006, 113, 102; (b) W. Song, J. B. Nicholas and J. F. Haw, J. Phys. Chem. B, 2001, 105, 4317.
54. Y. Jiang, W. Wang, V. R. R. Marthala, J. Huang, B. Sulikowski and M. Hunger, J. Catal., 2006, 238, 21.
55. (a) K. Smith and G. A. El-Hiti, Green Chem., 2013, 13, 1579; (b) C. Baerlocher, W. M. Meier and D. H. Olson, Atlas of Zeolite Framework Types, Elsevier, Amsterdam, 5th edn, 2001.
56. I. R. Leith, J. Chem. Soc., Chem. Commun., 1972, 1282.
57. R. Erickson, N. P. Benetis, A. Lund and M. Lindgren, J. Phys. Chem. A, 1997, 101, 2390.
58. A. R. Pradhan, T.-S. Lin, W.-H. Chen, S.-J. Jong, J.-F. Wu, K.-J. Chao and S.-B. Liu, J. Catal., 1999, 184, 29.

---

Footnote

† Electronic supplementary information (ESI) available: Surface area analysis; ¹³C MAS NMR spectra; geometry optimized coordinates for all radical cations; Mulliken spin density plots, experimental EPR spectra. See DOI: 10.1039/c6ta01053a

---