Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Highly efficient rutile TiO2 photocatalysts with single Cu(II) and Fe(III) surface catalytic sites†
Susann
Neubert
a,
Dariusz
Mitoraj
a,
Stephen A.
Shevlin
b,
Petra
Pulisova
a,
Manuel
Heimann
a,
Yonghua
Du
c,
Gregory K. L.
Goh
d,
Michał
Pacia
e,
Krzysztof
Kruczała
e,
Stuart
Turner
f,
Wojciech
Macyk
e,
Zheng Xiao
Guo
b,
Rosalie K.
Hocking
g and
Radim
Beranek
*ah
aFaculty of Chemistry and Biochemistry, Ruhr University Bochum, Universitätsstr. 150, 44780 Bochum, Germany. E-mail: radim.beranek@rub.de; radim.beranek@uni-ulm.de; Fax: +49-731-5025409; Tel: +49-731-5026063
bDepartment of Chemistry, University College London, London WC1E 6BT, UK
cInstitute of Chemical and Engineering Sciences, Agency for Science, Technology and Research (A*STAR), 1 Pesek Road, 627833, Singapore
dInstitute of Materials Research and Engineering, Agency for Science, Technology and Research (A*STAR), 3 Research Link, 117602, Singapore
eFaculty of Chemistry, Jagiellonian University, Ingardena 3, 30-060, Kraków, Poland
fEMAT, University of Antwerp, Groenenborgerlaan 171, B-2020 Antwerp, Belgium
gMatter and Materials Group, College of Science, Technology and Engineering, James Cook University, Townsville, 4811, Australia
hInstitute of Electrochemistry, Ulm University, Albert-Einstein-Allee 47, 89069 Ulm, Germany
First published on 30th December 2015
Abstract
Highly active photocatalysts were obtained by impregnation of nanocrystalline rutile TiO2 powders with small amounts of Cu(II) and Fe(III) ions, resulting in the enhancement of initial rates of photocatalytic degradation of 4-chlorophenol in water by factors of 7 and 4, compared to pristine rutile, respectively. Detailed structural analysis by EPR and X-ray absorption spectroscopy (EXAFS) revealed that Cu(II) and Fe(III) are present as single species on the rutile surface. The mechanism of the photoactivity enhancement was elucidated by a combination of DFT calculations and detailed experimental mechanistic studies including photoluminescence measurements, photocatalytic experiments using scavengers, OH radical detection, and photopotential transient measurements. The results demonstrate that the single Cu(II) and Fe(III) ions act as effective cocatalytic sites, enhancing the charge separation, catalyzing “dark” redox reactions at the interface, thus improving the normally very low quantum yields of UV light-activated TiO2 photocatalysts. The exact mechanism of the photoactivity enhancement differs depending on the nature of the cocatalyst. Cu(II)-decorated samples exhibit fast transfer of photogenerated electrons to Cu(II/I) sites, followed by enhanced catalysis of dioxygen reduction, resulting in improved charge separation and higher photocatalytic degradation rates. At Fe(III)-modified rutile the rate of dioxygen reduction is not improved and the photocatalytic enhancement is attributed to higher production of highly oxidizing hydroxyl radicals produced by alternative oxygen reduction pathways opened by the presence of catalytic Fe(III/II) sites. Importantly, it was demonstrated that excessive heat treatment (at 450 °C) of photocatalysts leads to loss of activity due to migration of Cu(II) and Fe(III) ions from TiO2 surface to the bulk, accompanied by formation of oxygen vacancies. The demonstrated variety of mechanisms of photoactivity enhancement at single site catalyst-modified photocatalysts holds promise for developing further tailored photocatalysts for various applications.
Introduction
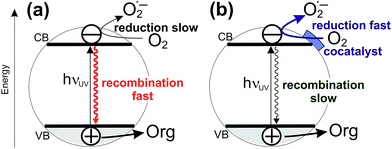
Sunlight-driven heterogeneous photocatalysis utilizing low-cost materials is potentially one of the most attractive methods for decontamination of water or air from toxic organic pollutants.1–8 However, real-life commercially viable applications of photocatalytic depollution are still rather scarce, due to insufficient performance stability and typically very low photocatalytic reaction rates. In terms of performance stability, the typical material of choice is titanium dioxide due to its excellent stability against photocorrosion, non-toxicity, low cost, and possibility for further functionalization.3,5,7,9,10 Efforts to improve the photoactivity of TiO2 have mainly focused on shifting the light absorption edge of pristine TiO2 (3.2 eV for anatase, 3.0 eV for rutile; ∼390–410 nm) into the visible range by doping TiO2 with metals or main group elements.4 However, this approach has only rarely led to activity enhancements under solar irradiation, mainly because of diminished oxidizing power of photogenerated holes and due to enhanced recombination via intra-bandgap states introduced by doping.4,11–17 In this context, it is important to realize that even under UV light irradiation the quantum yields of organic pollutant degradation reactions at pristine TiO2 are very low, typically only a few per cent.18 This means that majority of charges photogenerated by UV light in TiO2 are lost via recombination before they can induce redox reactions. Notably, it has long been suggested by Gerischer and Heller that the rate-limiting reaction in environmental photocatalysis is the reduction of oxygen by photogenerated electrons.1,19 Indeed, this has been recently confirmed by kinetic studies using transient absorption spectroscopy which have shown that the reduction of dioxygen by photogenerated electrons is much slower (∼μs timescale) than, for example, the oxidation of alcohols by photogenerated holes (∼ns timescale).20,21 This suggests that a very promising strategy for enhancing photodegradation rates at TiO2 is to improve the kinetics of oxygen reduction at the photocatalyst surface by depositing a cocatalyst which would catalyze the transfer of photogenerated electrons to oxygen molecules. Faster channeling of photogenerated electrons from TiO2 to oxygen molecules would diminish recombination and enhance charge separation (see Fig. 1).22The feasibility of this approach is well documented in the literature. For example, it is known that deposition of small amounts of platinum cocatalyst nanoparticles onto TiO2 leads to enhanced photocatalytic efficiencies for pollutant degradation.1,23–27 Obviously, for large-scale applications cocatalysts based on abundant, non-noble materials are needed. Notably, Ohno et al. observed enhancement of photocatalytic degradation rates of gaseous acetaldehyde under both UV and visible light on rutile TiO2 impregnated with Fe(III), Cu(II), Ni(II), and Cr(III) ions.28 Based on double-beam photoacoustic spectroscopy measurements, the authors concluded that the transition metal ions improved the efficiency by acting as electron acceptors and as electron donors under UV and visible light, respectively. Later, Hashimoto et al. reported enhanced visible light activity in photocatalytic decomposition of isopropanol in the gas phase at rutile TiO2 powders modified with small CuOx and FeOx clusters.29–32 The enhanced photoactivity in the gas phase was ascribed to visible light-mediated direct optical charge transfer from the valence band of TiO2 to energy levels in the co-catalyst clusters lying below the conduction band edge of TiO2, whereby the lower reducing power of visible-light photogenerated electrons towards oxygen was compensated by the ability of the cocatalyst to catalyze two-electron transfer to oxygen that occurs at more positive potentials (E0 = −0.16 V vs. NHE and +0.69 V vs. NHE for one-electron and two-electron reduction of oxygen, respectively).29–31,33–35 Similarly, improved degradation rate of gaseous acetaldehyde under visible light irradiation was reported for N-doped TiO2 loaded with copper ions by Morikawa et al. who suggested that the presence of Cu leads to prolonged lifetime of photogenerated charge carriers,36 and for WO3 photocatalysts impregnated with CuO by Sayama et al. who ascribed the activity enhancement to improved catalysis of oxygen reduction reaction.37
In the present work, we focus on the deposition of redox cocatalysts for oxygen reduction onto TiO2 in order to enhance the intrinsic UV light activity of TiO2 in degradation of aqueous organic pollutants. We assume that already boosting the reaction rates under UV light irradiation alone due to improved catalysis of the rate-limiting oxygen reaction would yield photocatalysts for commercially viable applications in solar water decontamination. In a similar vein to the work of Ohno et al.28 and Hashimoto et al.,29–32 we have recently impregnated rutile TiO2 powders with small amounts of copper(II) or iron(III) nitrate.38 After a mild heat treatment, such surface-modified rutile photocatalysts exhibited highly enhanced activity, as compared to pristine rutile TiO2, in photocatalytic degradation of 4-chlorophenol (4-CP) in aqueous phase under simulated solar light irradiation (λ > 320 nm). We tentatively suggested that small CuOx and FeOx clusters were formed on the TiO2 surface after impregnation and drying, and that these small clusters allowed for improved catalysis of dioxygen reduction by photogenerated electrons, leading to enhanced photoactivity.38 Herein we report our further detailed structural, spectroscopic, and theoretical investigations of these surface-modified rutile materials, and compare their photoactivity with rutile TiO2 modified by conventional deposition of platinum nanoparticles. Most importantly, we provide conclusive experimental evidence for the presence of single Cu(II) and Fe(III) cocatalytic sites in our highly active photocatalysts, which differentiates them from conventional composites of TiO2 with metal or metal oxide particles.29–32,36,37,39–43 The mechanistic aspects of the photoactivity enhancement at single ion-modified photocatalysts are discussed based on both theoretical DFT calculations and experimental (spectroscopic and photoelectrochemical) methods.
Results and discussion
Photocatalytic activity
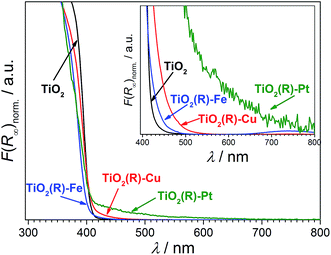
Highly active photocatalysts were prepared by simple impregnation of nanocrystalline rutile TiO2 powders with very small amounts of copper(II) and iron(III) nitrate. The optimum amount (actual loading) of Cu and Fe leading to maximum photocatalytic degradation rates of a test organic pollutant (4-chlorophenol, 4-CP) was found to be very low: 0.12 wt% for Cu and 0.13 wt% for Fe.38 For comparison, rutile TiO2 decorated with Pt nanoparticles (optimum Pt loading of 0.34 wt%) was prepared by conventional photoreduction method44–46 and served as a benchmark. After 3 hours of simulated solar irradiation (λ > 320 nm) the TiO2(R)–Cu and TiO2(R)–Fe induced 4-CP degradation of 80% and 54%, respectively (Fig. 2a), a significant enhancement as compared to the photoactivity of pristine rutile TiO2 (25%). The benchmark platinized TiO2(R)–Pt material showed degradation of 73%. The highest initial degradation rate of 2.8 × 10−8 mol L−1 s−1 was observed for TiO2(R)–Cu (Fig. 2c), a value higher by a factor of 7 than the pristine rutile TiO2, and is even higher than for TiO2(R)–Pt (by a factor of 5.5 vs. pristine TiO2). Furthermore, TiO2(R)–Fe also demonstrates an enhancement in degradation rate (by a factor of 4 vs. pristine TiO2), although this is less enhancement than for TiO2(R)–Cu. After purging the suspension with argon, the initial degradation rates decreased drastically, confirming the crucial role of dissolved oxygen as an electron acceptor in photocatalytic degradation. Complete mineralization of 4-CP molecules to carbon dioxide, water and chloride ions was confirmed by monitoring the TOC (Total Organic Carbon) values during the photocatalytic reaction (Fig. 2b). Interestingly, the platinized TiO2(R)–Pt sample seems to be more effective in inducing complete mineralization than TiO2(R)–Cu, which can be ascribed to the well-known high activity of platinized TiO2 in complete decarboxylation of carboxylic acids44–46 which are important intermediates in the mineralization process of 4-CP. It should be noted that the photoactivity enhancement of modified samples is not the result of enhanced activity in the visible range. Though TiO2(R)–Cu and TiO2(R)–Fe show a very slightly yellowish tint to the naked eye, their fundamental optical absorption edge is the same as in case of pristine TiO2 (Fig. 3). Accordingly, the photocatalytic degradation under visible light only (λ > 455 nm) was found to be negligible for all samples.38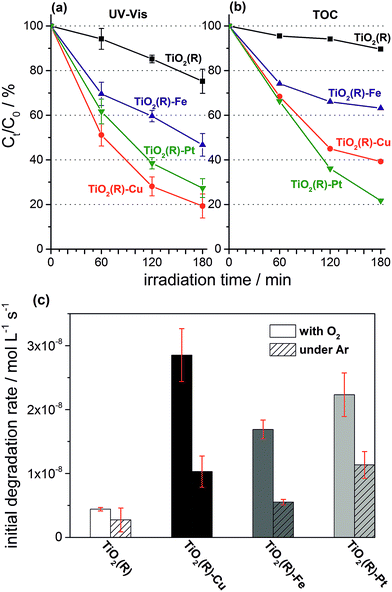 | ||
| Fig. 2 Comparison of 4-CP degradation monitored by UV-Vis spectroscopy (a) (for UV-Vis absorption spectra see ESI, Fig. S5†), complete mineralization followed by changes of TOC (b), and initial degradation rates (c) during photocatalytic degradation experiments using suspensions of TiO2(R), TiO2(R)–Cu, TiO2(R)–Fe and TiO2(R)–Pt under ambient and oxygen-free conditions. | ||
Two things are noteworthy. Firstly, simple physical mixtures of rutile TiO2 with CuO or Fe2O3 (in amounts corresponding to the optimum loading) prepared by grinding do not induce any photoactivity enhancement (see ESI, Fig. S6†). Secondly, while highly active TiO2(R)–Cu and TiO2(R)–Fe samples are obtained after a mild drying at 120–150 °C, after calcination at high temperatures (450 °C) the photoactivity is diminished drastically, though the Cu and Fe content is practically the same as in active samples. These results suggest that the chemical nature of Cu and Fe species at the surface of rutile TiO2 is of crucial significance for high photoactivity.
Structural characterization
Due to the low concentration of Cu and Fe species, both Raman spectra and X-ray diffractograms have shown only the typical pattern of rutile TiO2 (ESI, Fig. S7 and S8†). The primary crystallite sizes calculated using Scherrer's formula are 12–13 nm for all samples. High temperature treatment results in increase of rutile crystallite size to 20 nm and 15 nm for TiO2(R)–Cu (450 °C) and TiO2(R)–Fe (450 °C), respectively, which alone cannot explain the decrease of activity after calcination. We assumed that this is rather related to changes of the chemical nature of Cu and Fe species at the rutile surface.In this context, it is intriguing to realize that the optimum loading (0.12 wt% Cu and 0.13 wt% Fe) in TiO2(R)–Cu and TiO2(R)–Fe is very low, indeed. Given the BET specific surface area of rutile TiO2 (111 m2 g−1), such loading corresponds to the surface density of 0.10 Cu atoms per nm2 and 0.13 Fe atoms per nm2. This very low surface coverage let us to hypothesize that it could be single Cu(II) or Fe(III) sites which are present at the surface of rutile TiO2 and are responsible for the enhanced photoactivity of the novel materials. This suspicion was further deepened by the fact that electron energy loss spectroscopy (EELS), which in the setup we used has sensitivity at the single atom level, could only show a very weak signal for Cu, while no signal for Fe could be detected (ESI, Fig. S9†).
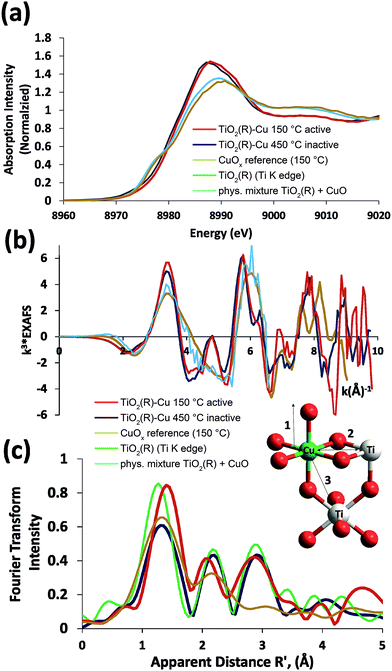
In order to gain further insight into the local chemical environment of Fe and Cu species and their oxidation states, we performed an X-ray absorption study. Fig. 4 presents the Cu K-edge XAS data (for the Fe data see ESI, Fig. S2†). The beamline did not have sufficient energy resolution to resolve pre-edge data, but the lack of intensity indicates that there is not too much deviation from centrosymmetry.47,48 The major peaks in the Fourier transform are labelled “1” to represent the 6 Cu–O distances @ 1.9–2.1 Å, “2” to represent the Cu–Ti distances @ 2.8–3.00 Å and “3” to represent the Cu–Ti distances at 3.4–3.6 Å. As the data was only suitable for interpretation to k = 10 Å−1 no attempt was made to split the coordination spheres further. A fit of the EXAFS data is given in the ESI (Fig. S1†). The peaks in the Fourier transform of TiO2(R)–Cu both before and after heating at 450 °C are consistent overall with Cu(II) sitting “on” or “in” the rutile structure. There are, however, minor differences in the structure of the materials before and after heating. Before heating there is a slight splitting of the coordination sphere, consistent with what one expects if the Cu(II) was decorating the surface of TiO2 in a well distributed form. After heating the material becomes more integrated into the TiO2 lattice, consistent with the slight shifts of R values of the Fourier transform peaks. Similar effects, though less pronounced, are noted at the Fe edge (ESI, Fig. S3†). Notably, the XAS data of bulk CuOx and a physical mixture of TiO2(R) with CuO show only two distinct peaks in the Fourier transform, and are thus clearly different from TiO2(R)–Cu. The XANES data of Cu are consistent with copper in oxidation state (II), the XANES data of Fe are consistent with Fe(III) with a high spin configuration.
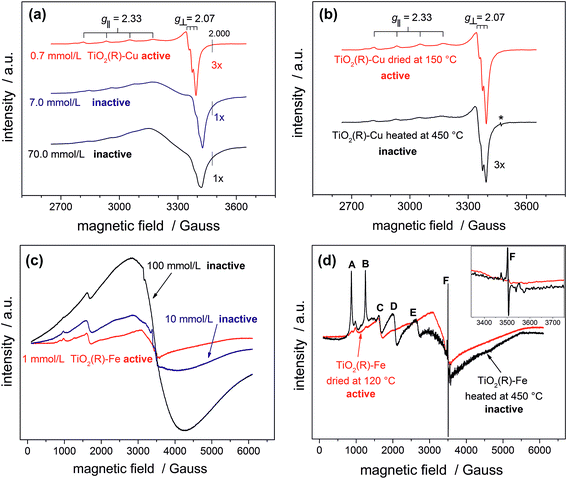
In order to provide conclusive evidence for the presence of single surface Cu(II) and Fe(III) sites in our photocatalysts, an EPR study was performed. EPR is a highly sensitive spectroscopic technique which can give valuable information about the nature of d9 Cu(II) and d5 Fe(III) paramagnetic species in our materials. The most active TiO2(R)–Cu sample exhibits an anisotropic signal with hyperfine structure due to I = 3/2 of Cu(II) typical for isolated mononuclear slightly axially distorted octahedral Cu(II) complexes,49 with resonance parameters A‖ = 11.9 mT, g‖ = 2.33 and g⊥ = 2.07 (Fig. 5a). This feature is a fingerprint of surface-bound single Cu(II) ions at rutile50 or anatase TiO2,49 or Cu(II) substituting lattice Ti(IV),51,52 both assumed to be spectroscopically equivalent. The increase of Cu(II) concentration during impregnation yields photocatalytically inactive powders containing small CuOx clusters and nanoparticles. This is apparent from broadening of spectral lines due to long-range dipolar interactions between Cu(II) ions which results in gradual disappearance of the anisotropic hyperfine structure (Fig. 5a). Following this trend, bulk CuO reference and the physical mixture of TiO2 and CuO show only a very broad EPR signal (ESI, Fig. S10†). The above results provide clear evidence for the presence of single isolated Cu(II) surface sites in highly active TiO2(R)–Cu.
After calcination of TiO2(R)–Cu at 450 °C the EPR resonance parameters stay the same, but the hyperfine structure is slightly less resolved (Fig. 5b). Importantly, an additional sharp signal with g = 2.005 (denoted by an asterisk in Fig. 5b) appears, which is associated with formation of oxygen vacancies upon migration of Cu(II) ions from the surface to the sub-surface layer where it substitutes Ti(IV).51 The same feature is observed upon heat treatment of copper complexes in the matrix of silicate glasses or on the surfaces of SnO2.53,54 Further evidence for migration of Cu(II) from surface to the bulk after heat treatment at 450 °C comes from a simple experiment using an aqueous ammonia solution. Before the heat treatment the Cu(II) ions in TiO2(R)–Cu are easily accessible for reaction with ammonia to form a typical blue tetraamminecopper(II) complex, while after the heat treatment at 450 °C the sample does not show blue coloration upon addition of ammonia. In this context it is important to recall that the high-temperature treated sample is not photoactive. Based on our results, we conclude that this loss of activity is both because of migration of catalytically active surface Cu(II) ions to the subsurface layer and concomitant formation of oxygen vacancies, which both give rise to recombination centers.
A similar broadening of EPR spectra upon increasing the amount of Fe(III) is observed for TiO2(R)–Fe (Fig. 5c). Transition at g = 4.31 (C) can be ascribed to the Fe(III) ions in orthorhombic sites at the surface of rutile TiO2.55 After calcination at 450 °C, the peaks A, B, D and E increased dramatically, suggesting that the Fe(III) ions migrated into the bulk. Indeed, the new EPR resonance transitions at g = 8.02 (A), 5.54 (B), 3.47 (D) and 2.26 (E) have been unambiguously assigned to Fe(III) ions located in substitutional tetragonal sites of distorted axial symmetry where the Fe(III) have substituted Ti(IV) in the TiO2 bulk lattice.55,56 And, similar to the case of TiO2(R)–Cu, the most prominent new EPR signal arising after the heat treatment at 450 °C (g ≈ 2.006, F) is related to substitutional Fe(III) ions accompanied by oxygen vacancies,57 which render the sample photocatalytically inactive.
Theoretical calculations
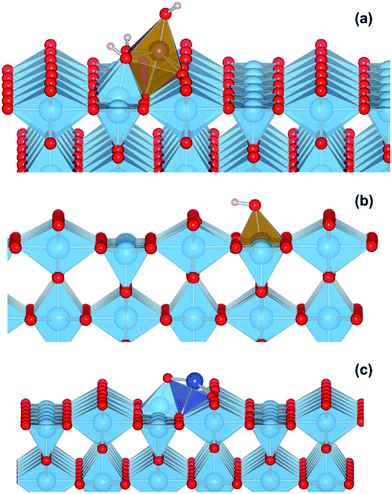
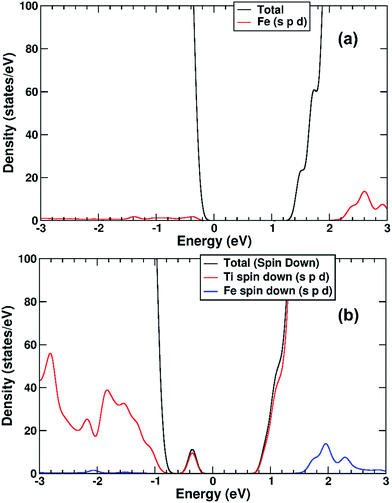
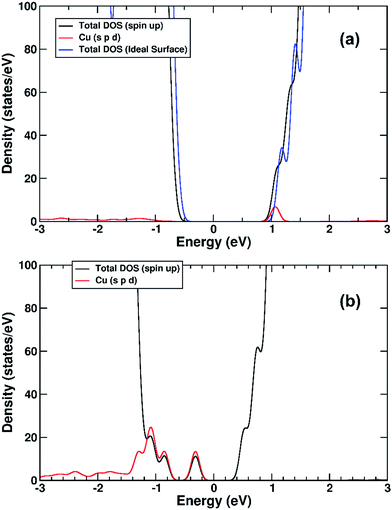
We performed a set of DFT calculations to understand the influence of single Cu(II) and Fe(III) ions on the electronic structure of the rutile TiO2 surface in order to estimate the effects on photogenerated charge separation. The (110) surface of rutile was used in calculations as it is the most commonly observed surface facet.58 First of all, we present the results for the effects of Fe-decoration. As for our previous work on Fe2O3 decoration of anatase TiO2,39 we investigated several different low energy adsorption sites on ideal rutile TiO2, the lowest of which is shown in Fig. 6a. The Fe(OH)3 cluster binds to the twofold oxygen row of the rutile surface in such a way that the Fe(III) cation becomes octahedral. This is a very stable structure, with an exothermic binding energy of 3.64 eV. The Fe(OH)3 cluster binds to two twofold oxygen atoms of the protruding row, and a surface threefold oxygen atom, resulting in a notable tilt. Furthermore, the Fe atom is not centrally located in the resultant FeO6 octahedra, with one short Fe–O bond of 1.82 Å pointing away from the surface, one long Fe–O bond of 2.46 Å pointing into the surface, and four equatorial Fe–O bonds of 2.03 to 2.11 Å.The electronic structure of TiO2(R)–Fe is shown in Fig. 7a. We focus on the spin-down DOS, as this is where the totality of the Fe contribution to the DOS resides. As can be seen, the Fe atom, and indeed the cluster as a whole does not strongly modify the electronic structure at the band edges, implying that the primary charge separation properties of rutile are not affected. The bandgap of this composite system is at 1.80 eV the same as the ideal surface, this value is slightly smaller than our calculated bulk theoretical bandgap of 2.00 eV. The band edge character is the same as the ideal rutile surface. To further investigate the effects of Fe(III) decoration on charge separation we determined the atomic and electronic structure of the charged system. We relaxed the charged system to observe whether the electron localizes onto a specific site, resulting in the formation of an electron polaron. This will occur in an absorber-cocatalyst system when the conduction band (or LUMO) of the cocatalyst is lower than that of the light absorber.43 Based on our analysis of the DOS of TiO2(R)–Fe we do not expect the extra electron to reside upon the Fe atom. There is a relaxation energy of 0.47 eV associated with the electron polaron, however upon inspection there is no strong structural rearrangement. Furthermore, from analysis of the DOS (see Fig. 7b), a state that does split off from the conduction band edge is not related to the Fe atom. Rather, this polaron state is associated with the Ti atoms that predominate at the conduction band edge (CBE). From analysis of the charge density difference, we observe that the excess electron localizes on a single Ti site in the middle of the slab, away from the surface. Specifically, this is an octahedral sixfold coordinated Ti directly below a surface fivefold coordinated Ti site, and exactly the same polaron localization as is observed for the ideal rutile TiO2-(110) surface.59 This suggests that single Fe(III) decoration, as depicted in Fig. 6a, does not improve the thermodynamics of charge separation in ideal rutile TiO2.
In order to account for possible different modes of Fe(III) incorporation into the rutile surface, we further considered the effects of Fe cation addition to defective surfaces of rutile TiO2-(110), specifically those where a single titanium surface vacancy is present. This defect was chosen as this provides a natural site for Fe(III) cations to reside, in comparison to other native point defects such as oxygen vacancies and titanium interstitials. Furthermore, under oxygen-rich conditions titanium vacancies (VTi) have a relatively low defect formation energy of 2.32 eV.60 We denote this system TiO2(R)–Fe(VTi). We modelled the adsorption of a FeOH unit on the vacancy; the single OH functional group is required to obtain Fe(III). The structure of the final relaxed geometry is shown in Fig. 6b. As can be seen, the titanium vacancy can easily accommodate the Fe atom, with the hydroxyl functional group pointing out of the surface. The Fe atom is displaced out of the centre of the vacancy, with Fe–O bond lengths of 1.94, 1.96, 2.05, and 2.10 Å with the rutile lattice oxygen atoms. There is bond length extension compared to the rutile Ti–O bonds lengths of 1.96 to 1.97 Å.
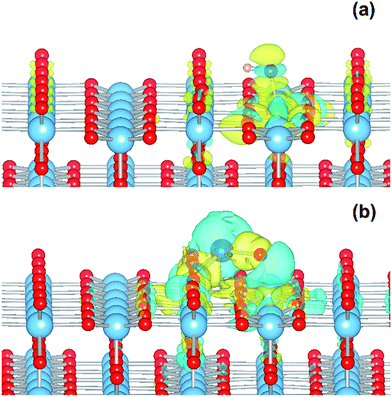
The electronic structure is shown as a DOS plot in Fig. 8. From inspection, it can be clearly seen that there is a significant iron presence in the spin-down channel near the CBE. More interesting, however, is that there is an acceptor state in the gap located above the Fermi level, specifically 0.26 eV above the VBE and 1.54 eV below the CBE. Upon photoexcitation this implies that there would be a thermodynamic driving force for the photoelectron to transfer from the rutile crystal to the Fe(III) cation, improving charge separation. In order to investigate whether this is the case, we determined the geometry and thus the electronic structure of the electron polaron (Fig. 8b). The main difference in the DOS with respect to the uncharged system is that the unoccupied state above the Fermi level is now shifted below the Fermi level, becoming occupied. The relaxation energy involved with this polaron formation is relatively tiny, at 0.022 eV, implying that at room temperature it will be easy for the electron to delocalize into the rutile lattice. Furthermore, although the charge density difference of the electron polaron shows that there is a concentration of electron density on the Fe(OH) site (see Fig. 9a), with closer examination we observe that there is a significant minority of charge on the oxygen twofold coordinated rows, providing further evidence that the electron polaron is not strongly localized on the Fe(OH) site.
In contrast to the TiO2(R)–Fe system, the charge separation properties of TiO2(R)–Cu are much simpler to analyze. We present results for a single CuO cluster adsorbed on the rutile TiO2–(110) surface, with the geometry shown in Fig. 6c. There is a strong binding between the CuO cluster and the rutile TiO2-(110) surface, with an exothermic binding energy of 2.82 eV. The Cu(II) cation is fourfold coordinated, with Cu–O bonds of length 1.89 Å, 1.93 Å, 1.98 Å, and 2.39 Å. We were unable to stabilize octahedral species on the surface. We ascribe the missing atoms that enable octahedral coordination to the solvent, which is missing in our calculations where the surface is exposed to vacuum. Furthermore, the oxygen atom of the cluster forms a short bond of 1.79 Å with a fivefold coordinated titanium atom of the surface, closing a TiO6 octahedra.
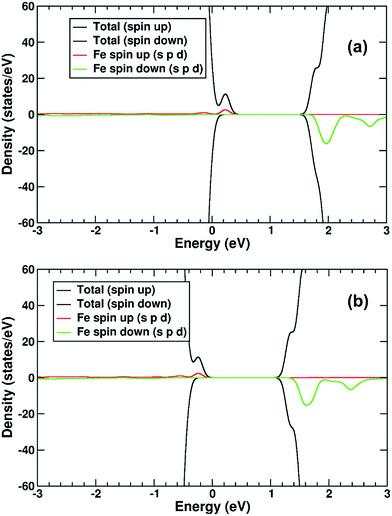
The electronic structure of TiO2(R)–Cu is shown in Fig. 10a. The Cu atom has a significant presence on the CBE. This is primarily due to the Cu d-states. Further, we compare the position of the decorated rutile TiO2 surface to the bare rutile surface, by comparison and alignment of the electrostatic potential in the vacuum region.61 When the alignment is taken into account, the Cu-state is marginally (∼0.1 eV) below the CBE of the ideal rutile surface. This would imply that any photoelectrons would transfer to the Cu(II), rather than stay in the rutile itself, although the thermodynamic driving force is quite weak.
As for the Fe(III)-decorated systems discussed above, we also determine the effects of the Cu(II) decorant on the photoelectron charge separation properties by investigating the thermodynamics for electron polaron formation. The addition of a single electron results in a substantial amount of reconstruction, with a reconstruction energy of 0.48 eV, very similar to the polaron in ideal rutile. As can be readily observed from inspection of the DOS, see Fig. 10b, the Cu-derived state is strongly stabilized by injection of the additional electron, with the state dropping by 1.0 eV and becoming occupied. This is related to the closure of the electronic state that is half-filled by the spare d-electron of the Cu atom. Furthermore, from calculation of the charge density difference we can directly determine where the excess electron, e.g. the photoelectron, resides. This photoelectron is strongly localized on the Cu atom, see Fig. 9b. In other words, Cu(II) decorants do aid charge separation by providing a thermodynamic trap, with a strong localization energy, for photoelectrons.
To summarize, we have shown that both Fe(III) and Cu(II) might improve the primary (thermodynamic) charge separation properties of rutile TiO2. However, the mechanism for charge separation is different for the two cations. For TiO2(R)–Fe, separation of the photoelectron from the rutile crystal does not occur for decoration by Fe(III), but for surface implantation. This therefore requires the presence of titanium vacancies, which are going to be a minority presence in any rutile sample. Additionally, the relaxation energy for electron polaron formation is very low at ∼0.02 eV, which may be overcome due to thermal fluctuations. In contrast, for TiO2(R)–Cu, separation of the photoelectron from the rutile crystal does occur for decoration by Cu(II). These decorated systems also strongly localize the photoelectron at the surface site with a high relaxation energy, potentially improving the kinetics of subsequent oxygen reduction reaction. From our calculations there are clearly different charge separation mechanisms for the two metal cations.
Mechanistic investigations
Notably, the DFT calculations corroborate the experimental results showing that the optical absorption of TiO2(R)–Cu and TiO2(R)–Fe is practically the same as for pristine TiO2, ∼3.0 eV (see Fig. 3). This is important since the redox cocatalysts at the surface of composite photocatalysts (see Fig. 1b) should not parasitically absorb light and diminish thus the light harvesting by the TiO2 light absorber. Clearly, single metal ion sites are sufficient to positively influence the charge separation, whereby blocking of the light by cocatalyst is avoided since an extended lattice structure such as in metal oxide particles, does not develop. The positive effect of decoration of TiO2 with single Cu(II) and Fe(III) sites on electron–hole separation is evidenced also by photoluminescence (PL) measurements (see ESI; Fig. S11†). The PL intensity of both TiO2(R)–Cu and TiO2(R)–Fe is significantly quenched as compared to pristine rutile TiO2, suggesting diminished radiative recombination both in the band-to-band mode (2.7–3.0 eV) and in the range typically attributed to surface state-mediated recombination (2.1–2.7 eV).62Though both Cu(II) and Fe(III) improve the photocatalytic performance (Fig. 2), the DFT results indicate that the reason for the improvement might be different for TiO2(R)–Cu and TiO2(R)–Fe. In order to shed light on the detailed mechanism of the photocatalytic degradation of 4-CP the reaction was conducted under different conditions. The 4-CP degradation is completely suppressed for all materials in the presence of EDTA acting as a strongly adsorbing hole scavenger (Fig. 11a). This underlines the substantial role of the oxidative pathway (holes and/or hydroxyl radicals) in the degradation reaction. In argon-purged suspension (see Fig. 2c) the photoactivity of all materials decreases. This finding confirms the essential role of oxygen as a primary electron acceptor. Residual photoactivity under argon can arise from the hole oxidation while electrons reduce residual traces of oxygen, lattice Ti(IV) ions in a rutile lattice, or Cu(II) and Fe(III) in TiO2(R)–Cu and TiO2(R)–Fe.
Degradation curves in the presence of oxygen or an alternative electron acceptor, namely tetranitromethane under argon, are shown in Fig. 11b. Pristine TiO2(R) degrades 4-CP much more efficiently in the presence of tetranitromethane as an electron scavenger than with oxygen. This means that, at pristine rutile, tetranitromethane scavenges the photogenerated electrons much faster as compared to dissolved oxygen, enabling the holes to oxidize efficiently the 4-CP molecules. This is in line with the reported reduction potential of tetranitromethane (+0.4 V vs. NHE)63 which is more positive than in case of O2 (−0.16 V vs. NHE).35 In contrast, the degradation rates for TiO2(R)–Cu are practically the same in the presence of tetranitromethane and oxygen. This finding is very significant. It confirms that the nature of reacting electrons in TiO2(R)–Cu is different from TiO2(R). The photogenerated electrons are apparently very efficiently trapped by Cu(II) sites, whereby the reactivity of Cu(II/I)-trapped electrons towards oxygen is enhanced, compensating kinetically the lower thermodynamic driving force for the reduction of oxygen as compared to the reduction of tetranitromethane. Moreover, the electron trapping at Cu(II) sites is clearly very fast, at least much faster than the reduction of tetranitromethane or oxygen by photoelectrons trapped by surface Ti(IV). Exactly as suggested by the DFT calculations, the charge separation in TiO2(R)–Cu will be dominated by the transfer of photogenerated electrons to surface Cu(II) ions. Rather different results were obtained for TiO2(R)–Fe which behaves quite similar to pristine TiO2(R), though the enhancement after addition of tetranitromethane is not so pronounced. This suggests that either a significant portion of reactive electrons in TiO2(R)–Fe might have a similar chemical nature (i.e., electrons trapped at Ti(IV/III) sites) to those in pristine TiO2(R), or the reactivity of electrons trapped at Fe(III/II) surface sites towards tetranitromethane is much higher than for Cu(II/I)-trapped electrons. In line with our DFT calculations, the primary charge separation due to electron transfer to Fe(III) in TiO2(R)–Fe is less effective than in case of TiO2(R)–Cu. The degradation rates for TiO2(R)–Fe in the presence of oxygen are lower than for TiO2(R)–Cu, yet still higher than for pristine rutile TiO2. However, the mechanism of the enhancement at TiO2(R)–Fe seems to be different than in case of TiO2(R)–Cu.
In this context it is important to realize that dissolved oxygen not only serves as an electron acceptor, but can also become a source of various reactive species, like superoxide anion, hydrogen peroxide or hydroxyl radical, which can take an active part in the degradation process. After addition of tert-butanol, which is typically taken as a preferential scavenger of hydroxyl radicals, the photoactivity of TiO2(R)–Fe hardly changed and that of TiO2(R)–Cu dropped only slightly (Fig. 11c). It should be noted that tert-butanol does not adsorb strongly onto TiO2 and therefore efficiently scavenges free hydroxyl radicals (˙OHf) but not surface-bound hydroxyl radicals (˙OHs).64 Moreover, it has been reported that, in contrast to anatase where ˙OHf forms efficiently, at rutile TiO2 mainly ˙OHs is produced.64 Our results therefore indicate that free ˙OHf radicals do not play any significant role in the enhancement of photocatalytic degradation rates of 4-CP molecules. However, the possibility that, apart from holes, also surface-bound ˙OHs radicals play some role cannot be completely ruled out. As a next step, we investigated the formation of hydroxyl radicals quantitatively. Fig. S12 (ESI†) shows fluorescence spectra of hydroxyterephthalic acid formed upon irradiation of the material suspensions in a terephthalic acid solution under the ambient conditions. The production of hydroxyl radicals for each sample is proportional to the formation of hydroxyterephthalic acid, and is linear with time (see ESI; Fig. S13†).65 No correlation between hydroxyl radical production and photoactivity was found. The most active material, TiO2(R)–Cu, exhibits the lowest hydroxyl radical production, even lower than pristine TiO2(R) by a factor of 2. This points to a minor role of the hydroxyl radicals in the photooxidation mechanism at TiO2(R)–Cu. In contrast, TiO2(R)–Fe shows the highest rate of hydroxyl radical formation, which is higher by a factor of 2 than in the case of pristine rutile. Since the chemical nature of holes in all samples should be the same, we assume that this enhanced formation of hydroxyl radicals at TiO2(R)–Fe has its origin in the reductive pathway (initiated by reduction of oxygen). H2O2 can be formed by a two-electron reduction of dioxygen catalyzed by Fe(III) sites. The H2O2 molecules formed can be converted to hydroxyl radicals by further reduction by photogenerated electrons. Furthermore, Fenton-type reactions might be at play, which would involve reaction of Fe(II) and/or Fe(III) with H2O2 under formation of highly oxidizing hydroxyl radicals (˙OH) or hydroperoxyl radicals (HOO˙), respectively. At any rate, apart from the quenching of PL mentioned above, the enhanced formation of (surface-bound) hydroxyl radicals is at present the only prominent feature of TiO2(R)–Fe which helps us to understand its enhanced photoactivity as compared to pristine rutile.
As it is known that the solubility of first-row transition metal cations increases upon reduction, we investigated also the operational stability of our materials during four successive photocatalytic degradation experiments (ESI, Fig. S14†). The activity of all modified samples, including TiO2(R)–Pt, decreased by ∼50% during four cycles, however still remaining higher than in case of pristine TiO2(R). As platinum clusters are not expected to undergo reductive photocorrosion, we attribute the decrease in activity of all samples to accumulation of decomposition intermediates at the surface of photocatalysts or to partial loss of photocatalyst during filtration after each cycle. These problems can be overcome by optimization of operational parameters and reactor design.
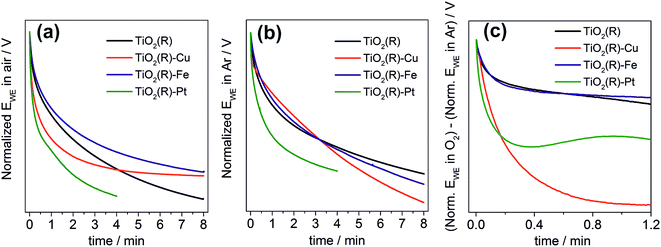
Finally, we performed a set of photopotential decay measurements which are a powerful tool for directly probing the dynamics of photogenerated electrons, including the kinetics of their reaction with dioxygen.66,67 During prolonged illumination under open-circuit conditions, the photoelectrons accumulate in the TiO2 and shift the quasi-Fermi level of the electrode to negative potentials, until a steady state is achieved. After switching off the light, the open-circuit potential starts to decay. Under our experimental conditions, the rate of the decay depends on the concentration of accumulated charges and on the rate constants for two processes: the electron–hole recombination, and the reaction of electrons with dioxygen dissolved in the solution. In the presence of oxygen both processes are at work (Fig. 12a), whereas in the absence of oxygen the recombination process is predominant and is chiefly responsible for the potential decay (Fig. 12b). A decay curve obtained by subtracting these two curves can serve as an indicator for the kinetics of dioxygen reduction (Fig. 12c). Our measurements clearly confirm the importance of fast dioxygen reduction for achieving high photocatalytic degradation rates. In the presence of oxygen the fastest potential decays are observed for the most photoactive materials, TiO2(R)–Cu and TiO2(R)–Pt. The fast decay is clearly due to enhanced rate of dioxygen reduction at TiO2(R)–Cu and TiO2(R)–Pt, as exemplified in Fig. 12c. In other words, Cu(II) sites act as efficient catalyst for O2 reduction in a similar way as Pt particles. For TiO2(R)–Fe the situation is very different, the decay curves are similar to TiO2(R). This again confirms that the mechanism of the photocatalytic rate enhancement at TiO2(R)–Fe is distinct from TiO2(R)–Cu. Since the kinetics of primary O2 reduction at TiO2(R)–Fe is apparently not improved as compared to TiO2(R), the enhancement is most probably due to new catalytic pathways to H2O2 and hydroxyl radicals, opened by the presence of Fe(III) catalytic sites, as we discussed above.
Conclusions
Our experimental results combined with theoretical calculations demonstrate that single ion catalytic sites at the surface of TiO2 photocatalysts are sufficient to considerably enhance the rate of photocatalytic decomposition of organic pollutants in water. The exact mechanism of the photoactivity enhancement can differ depending on the nature of the cocatalyst. For example, Cu(II)-decorated rutile photocatalysts exhibit fast transfer of photogenerated electrons to Cu(II/I) sites, followed by enhanced catalysis of dioxygen reduction, resulting in improved charge separation and higher photocatalytic degradation rates. On the other hand, at Fe(III)-modified rutile the rate of dioxygen reduction is not improved, and the photocatalytic enhancement is attributed to higher production of highly oxidizing hydroxyl radicals produced by alternative oxygen reduction pathways opened by the presence of catalytic Fe(III/II) sites. Importantly, we have shown that excessive heating (at 450 °C) of initially highly active photocatalysts leads to their deactivation due to migration of catalytically active Cu(II) and Fe(III) ions from TiO2 surface to the bulk, which is accompanied by formation of oxygen vacancies. In terms of light harvesting, single-site-modified photocatalysts capitalize on the intrinsic UV light absorption by TiO2, whereby the isolated nature of surface cocatalytic sites guarantees negligible losses due to parasitic light absorption by the cocatalyst. The improved photocatalytic performance is chiefly due to the electronic and redox properties of single ion sites, enhancing the charge separation, catalyzing “dark” redox reactions at the interface, and thus improving the typically very low quantum yields which represent the major bottleneck in environmental photocatalysis. These features make this type of materials distinct from more conventional visible light-active modified TiO2 (ref. 29, 30 and 36) or TiO2 composites with heterojunction structure,39–43 and also from “single site photocatalysts” based on light-absorbing metal ion species dispersed on the surface of zeolites or silica.68–70 As the photocatalytic activity of most photocatalysts is known to be highly substrate-specific6,71 and depending also on a complex interplay of many material properties (crystallinity, porosity, surface area, relative amounts of specific crystal facets, etc.),6 the demonstrated variety of mechanisms of photoactivity enhancement at single site catalyst-modified photocatalysts holds promise for developing many novel, tailored photocatalysts for various applications. Such efforts may also go beyond using TiO2 as light absorber and include photocatalytic transformations other than aerobic degradation of organic pollutants.Acknowledgements
Financial support by the EU-FP7 Grant “4G-PHOTOCAT” (Grant No. 309636) and by the MIWFT-NRW within the project “Anorganische Nanomaterialien für Anwendungen in der Photokatalyse: Wasseraufbereitung und Wasserstoffgewinnung“ is gratefully acknowledged. We thank the Sachtleben company for providing rutile TiO2 material. The support of the Center for Electrochemical Sciences (CES) is gratefully acknowledged. The authors also acknowledge the use of the UCL Legion High Performance Computing Facility (Legion@UCL), the IRIDIS High Performance Computing Facility and associated support services, and the ARCHER National Computing Service as facilitated by a Research Allocation Proposal (project e352), in the completion of this work. S. T. gratefully acknowledges the FWO Flanders for a post-doctoral scholarship under contract number G004413N. M. P. is indebted to the Foundation for Polish Science within the TEAM/2012-9/4 programme.References
- H. Gerischer and A. Heller, J. Phys. Chem., 1991, 95, 5261–5267 CrossRef CAS.
- M. R. Hoffmann, S. T. Martin, W. Choi and D. W. Bahnemann, Chem. Rev., 1995, 95, 69–96 CrossRef CAS.
- O. Carp, C. L. Huisman and A. Reller, Prog. Solid State Chem., 2004, 32, 33–177 CrossRef CAS.
- X. Chen and S. S. Mao, Chem. Rev., 2007, 107, 2891–2959 CrossRef CAS PubMed.
- A. Fujishima, X. Zhang and D. A. Tryk, Surf. Sci. Rep., 2008, 63, 515–582 CrossRef CAS.
- B. Ohtani, J. Photochem. Photobiol., C, 2010, 11, 157–178 CrossRef CAS.
- C. McCullagh, J. M. C. Robertson, D. W. Bahnemann and P. K. J. Robertson, Res. Chem. Intermed., 2007, 33, 359–375 CrossRef CAS.
- D. Friedmann, C. Mendive and D. Bahnemann, Appl. Catal., B, 2010, 99, 398–406 CrossRef CAS.
- A. Fujishima, T. N. Rao and D. A. Tryk, J. Photochem. Photobiol., C, 2000, 1, 1–21 CrossRef CAS.
- A. L. Linsebigler, G. Lu and J. T. Yates Jr, Chem. Rev., 1995, 95, 735–758 CrossRef CAS.
- B. Ohtani, Recent Pat. Eng., 2010, 4, 149–154 CrossRef CAS.
- D. Mitoraj and H. Kisch, Angew. Chem., Int. Ed., 2008, 47, 9975–9978 CrossRef CAS PubMed.
- D. Mitoraj, R. Beranek and H. Kisch, Photochem. Photobiol. Sci., 2010, 9, 31–38 CAS.
- J.-M. Herrmann, J. Disdier and P. Pichat, Chem. Phys. Lett., 1984, 108, 618–622 CrossRef CAS.
- W. Mu, J.-M. Herrmann and P. Pichat, Catal. Lett., 1989, 3, 73–84 CrossRef CAS.
- J. M. Herrmann, Sci. China: Chem., 2010, 53, 1831–1843 CrossRef CAS.
- M. D'Arienzo, N. Siedl, A. Sternig, R. Scotti, F. Morazzoni, J. Bernardi and O. Diwald, J. Phys. Chem. C, 2010, 114, 18067–18072 Search PubMed.
- A. Emeline, A. Salinaro and N. Serpone, J. Phys. Chem. B, 2000, 104, 11202–11210 CrossRef CAS.
- H. Gerischer and A. Heller, J. Electrochem. Soc., 1992, 139, 113–118 CrossRef.
- Y. Tamaki, A. Furube, M. Murai, K. Hara, R. Katoh and M. Tachiya, J. Am. Chem. Soc., 2006, 128, 416–417 CrossRef PubMed.
- L. Jing, Y. Cao, H. Cui, J. R. Durrant, J. Tang, D. Liu and H. Fu, Chem. Commun., 2012, 48, 10775–10777 RSC.
- P. V. Kamat, J. Phys. Chem. Lett., 2012, 3, 663–672 CrossRef CAS PubMed.
- D. W. Bahnemann, J. Mönig and R. Chapman, J. Phys. Chem., 1987, 91, 3782–3788 CrossRef.
- D. Hufschmidt, D. Bahnemann, J. J. Testa, C. A. Emilio and M. I. Litter, J. Photochem. Photobiol., A, 2002, 148, 223–231 CrossRef.
- J. Lee and W. Choi, J. Phys. Chem. B, 2005, 109, 7399–7406 CrossRef PubMed.
- A. A. Ismail and D. W. Bahnemann, Green Chem., 2011, 13, 428–435 RSC.
- A. A. Ismail and D. W. Bahnemann, J. Phys. Chem. C, 2011, 115, 5784–5791 CAS.
- N. Murakami, T. Chiyoya, T. Tsubota and T. Ohno, Appl. Catal., A, 2008, 348, 148–152 CrossRef CAS.
- H. Irie, K. Kamiya, T. Shibanuma, S. Miura, D. A. Tryk, T. Yokoyama and K. Hashimoto, J. Phys. Chem. C, 2009, 113, 10761–10766 CAS.
- H. Yu, H. Irie, Y. Shimodaira, Y. Hosogi, Y. Kuroda, M. Miyauchi and K. Hashimoto, J. Phys. Chem. C, 2010, 114, 16481–16487 CAS.
- X. Qiu, M. Miyauchi, K. Sunada, M. Minoshima, M. Liu, Y. Lu, D. Li, Y. Shimodaira, Y. Hosogi, Y. Kuroda and K. Hashimoto, ACS Nano, 2011, 6, 1609–1618 CrossRef PubMed.
- M. Liu, R. Inde, M. Nishikawa, X. Qiu, D. Atarashi, E. Sakai, Y. Nosaka, K. Hashimoto and M. Miyauchi, ACS Nano, 2014, 8, 7229–7238 CrossRef CAS PubMed.
- Y. Nosaka, S. Takahashi, H. Sakamoto and A. Y. Nosaka, J. Phys. Chem. C, 2011, 115, 21283–21290 CAS.
- M. Nishikawa, Y. Mitani and Y. Nosaka, J. Phys. Chem. C, 2012, 116, 14900–14907 CAS.
- P. Wardman, J. Phys. Chem. Ref. Data, 1989, 18, 1637–1755 CrossRef CAS.
- T. Morikawa, Y. Irokawa and T. Ohwaki, Appl. Catal., A, 2006, 314, 123–127 CrossRef.
- T. Arai, M. Horiguchi, M. Yanagida, T. Gunji, H. Sugihara and K. Sayama, J. Phys. Chem. C, 2009, 113, 6602–6609 CAS.
- S. Neubert, P. Pulisova, C. Wiktor, P. Weide, B. Mei, D. A. Guschin, R. A. Fischer, M. Muhler and R. Beranek, Catal. Today, 2014, 230, 97–103 CrossRef.
- S. J. A. Moniz, S. A. Shevlin, X. An, Z.-X. Guo and J. Tang, Chem.–Eur. J., 2014, 20, 15571–15579 CrossRef CAS PubMed.
- X. An, H. Liu, J. Qu, S. J. A. Moniz and J. Tang, New J. Chem., 2015, 39, 314–320 RSC.
- S. J. A. Moniz and J. Tang, ChemCatChem, 2015, 7, 1659–1667 CrossRef CAS.
- R. Marschall, Adv. Funct. Mater., 2014, 24, 2421–2440 CrossRef CAS.
- S. J. A. Moniz, S. A. Shevlin, D. J. Martin, Z.-X. Guo and J. Tang, Energy Environ. Sci., 2015, 8, 731–759 CAS.
- B. Kraeutler and A. J. Bard, J. Am. Chem. Soc., 1978, 100, 5985–5992 CrossRef CAS.
- B. Kraeutler and A. J. Bard, J. Am. Chem. Soc., 1978, 100, 4317–4318 CrossRef CAS.
- B. Kraeutler and A. J. Bard, J. Am. Chem. Soc., 1978, 100, 2239–2240 CrossRef CAS.
- T. E. Westre, P. Kennepohl, J. G. deWitt, B. Hedman, K. O. Hodgson and E. I. Solomon, J. Am. Chem. Soc., 1997, 119, 6297–6314 CrossRef CAS.
- R. Hocking and E. Solomon, in Molecular Electronic Structures of Transition Metal Complexes I, ed. D. M. P. Mingos, P. Day and J. P. Dahl, Springer, Berlin Heidelberg, 2012, pp. 155–184 Search PubMed.
- S. K. Poznyak, V. I. Pergushov, A. I. Kokorin, A. I. Kulak and C. W. Schläpfer, J. Phys. Chem. B, 1999, 103, 1308–1315 CrossRef CAS.
- A. Amorelli, J. C. Evans and C. C. Rowlands, J. Chem. Soc., Faraday Trans., 1989, 85, 4111–4118 RSC.
- G. Li, N. M. Dimitrijevic, L. Chen, T. Rajh and K. A. Gray, J. Phys. Chem. C, 2008, 112, 19040–19044 CAS.
- H. J. Gerritsen and E. S. Sabisky, Phys. Rev., 1962, 125, 1853–1859 CrossRef CAS.
- J. G. Darab and R. K. MacCrone, Phys. Chem. Glasses, 1991, 32, 91 CAS.
- P. G. Harrison, C. Bailey, W. Daniell, D. Zhao, I. K. Ball, D. Goldfarb, N. C. Lloyd and W. Azelee, Chem. Mater., 1999, 11, 3643–3654 CrossRef CAS.
- T. A. Egerton, E. Harris, E. John Lawson, B. Mile and C. C. Rowlands, Phys. Chem. Chem. Phys., 2001, 3, 497–504 RSC.
- A. Amorelli, J. C. Evans, C. C. Rowlands and T. A. Egerton, J. Chem. Soc., Faraday Trans., 1987, 83, 3541–3548 RSC.
- P.-O. Andersson, E. L. Kollberg and A. Jelenski, Phys. Rev. B: Solid State, 1973, 8, 4956–4965 CrossRef CAS.
- H. Perron, C. Domain, J. Roques, R. Drot, E. Simoni and H. Catalette, Theor. Chem. Acc., 2007, 117, 565–574 CrossRef CAS.
- N. A. Deskins, R. Rousseau and M. Dupuis, J. Phys. Chem. C, 2011, 115, 7562–7572 CAS.
- F. M. Hossain, G. E. Murch, L. Sheppard and J. Nowotny, Defect Diffus. Forum, 2006, 251–252, 1–12 CrossRef CAS.
- A. Walsh and C. R. A. Catlow, J. Mater. Chem., 2010, 20, 10438–10444 RSC.
- L. Kernazhitsky, V. Shymanovska, T. Gavrilko, V. Naumov, L. Fedorenko, V. Kshnyakin and J. Baran, J. Lumin., 2014, 146, 199–204 CrossRef CAS.
- L. Eberson and F. Radner, J. Am. Chem. Soc., 1991, 113, 5825–5834 CrossRef CAS.
- W. Kim, T. Tachikawa, G.-H. Moon, T. Majima and W. Choi, Angew. Chem., Int. Ed., 2014, 53, 14036–14041 CrossRef CAS PubMed.
- T. Hirakawa and Y. Nosaka, Langmuir, 2002, 18, 3247–3254 CrossRef.
- T. Berger, D. Monllor-Satoca, M. Jankulovska, T. Lana-Villarreal and R. Gómez, ChemPhysChem, 2012, 13, 2824–2875 CrossRef CAS PubMed.
- D. Monllor-Satoca and R. Gomez, J. Phys. Chem. C, 2008, 112, 139–147 CAS.
- M. Matsuoka and M. Anpo, J. Photochem. Photobiol., C, 2003, 3, 225–252 CrossRef CAS.
- H. Yamashita and M. Anpo, Curr. Opin. Solid State Mater. Sci., 2003, 7, 471–481 CrossRef CAS.
- J. Schneider, M. Matsuoka, M. Takeuchi, J. Zhang, Y. Horiuchi, M. Anpo and D. W. Bahnemann, Chem. Rev., 2014, 114, 9919–9986 CrossRef CAS PubMed.
- J. Ryu and W. Choi, Environ. Sci. Technol., 2007, 42, 294–300 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental and theoretical methods; XAS data; photocatalytic degradations with physical mixtures; UV-Vis spectra during 4-CP degradation; Raman spectra; XRD; HAADF-STEM images and EELS spectra; PL spectra; OH radical measurements; stability measurements. See DOI: 10.1039/c5ta07036h |
| This journal is © The Royal Society of Chemistry 2016 |