Particle detachment from fluid interfaces: theory vs. experiments†
Svetoslav E.
Anachkov‡
ab,
Ivan
Lesov‡
ab,
Michele
Zanini
a,
Peter A.
Kralchevsky
b,
Nikolai D.
Denkov
b and
Lucio
Isa
*a
aLaboratory for Interfaces, Soft matter and Assembly, Department of Materials, ETH Zurich, Vladimir-Prelog-Weg 5, CH-8093 Zurich, Switzerland. E-mail: lucio.isa@mat.ethz.ch; Tel: +41 44 633 63 76
bDepartment of Chemical and Pharmaceutical Engineering, Faculty of Chemistry and Pharmacy, Sofia University, 1 James Bourchier Ave., 1164 Sofia, Bulgaria
First published on 10th August 2016
Abstract
Microparticle adsorption and self-assembly at fluid interfaces are strongly affected by the particle three-phase contact angle θ. On the single-particle level, θ can be determined by several techniques, including colloidal-probe AFM, the gel-trapping technique (GTT) and the freeze-fracture shadow-casting (FreSCa) method. While GTT and FreSCa provide contact angle distributions measured over many particles, colloidal-probe AFM measures the wettability of an individual (specified) particle attached onto an AFM cantilever. In this paper, we extract θ for smooth microparticles through the analysis of force–distance curves upon particle approach and retraction from the fluid interface. From each retraction curve, we determine: (i) the maximal force, Fmax; (ii) the detachment distance, Dmax; and (iii) the work for quasistatic detachment, W. To relate Fmax, Dmax and W to θ, we developed a detailed theoretical model based on the capillary theory of flotation. The model was validated in three different ways. First, the contact angles, evaluated from Fmax, Dmax and W, are all close in value and were used to calculate the entire force–distance curves upon particle retraction without any adjustable parameters. Second, the model was successfully applied to predict the experimental force–distance curve of a truncated sphere, whose cut is positioned below the point of particle detachment from the interface. Third, our theory was confirmed by the excellent agreement between the particle contact angles obtained from the colloidal-probe AFM data and the ensemble-average contact angles measured by both GTT and FreSCa. Additionally, we devised a very accurate closed-form expression for W (representing the energy barrier for particle detachment), thus extending previous results in the literature.
1. Introduction
Particle adsorption and self-assembly at fluid interfaces have attracted considerable attention as these phenomena can be exploited in a vast range of materials and processes, including Pickering-stabilized emulsions and foams,1,2 drug-delivery vehicles,3,4 mineral recovery by flotation5 and fabrication of nanostructured materials.6–11 One of the main parameters controlling the particle interfacial behavior is its three-phase contact angle θ. Commonly, θ is defined as the angle of the tangent to the particle surface at the three-phase contact line, measured through the aqueous phase; therefore, we have θ < 90° for hydrophilic particles and θ > 90° for hydrophobic particles. The binding energy, ΔG, of a solid spherical colloid with radius R attached to a fluid interface with interfacial tension σ is given by ΔG = −πR2σ(1 − |cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ|)2; see ref. 12 and 13. Therefore, for microparticles with typical contact angles (θ = 45°–135°), the adsorption is practically irreversible since |ΔG| > 106kBT. By controlling particle immersion in each fluid phase, θ also affects particle self-assembly14 and dynamics15,16 at the interface. Furthermore, interparticle interactions, e.g., capillary17 forces that arise due to interfacial deformations around each particle, depend on particle wettability, i.e. on θ.
θ|)2; see ref. 12 and 13. Therefore, for microparticles with typical contact angles (θ = 45°–135°), the adsorption is practically irreversible since |ΔG| > 106kBT. By controlling particle immersion in each fluid phase, θ also affects particle self-assembly14 and dynamics15,16 at the interface. Furthermore, interparticle interactions, e.g., capillary17 forces that arise due to interfacial deformations around each particle, depend on particle wettability, i.e. on θ.
Different techniques have been developed to obtain θ for colloidal particles,18 based on direct visualization19–23 or indirect measurements.24–30 The gel-trapping technique (GTT)19,20 and freeze-fracture shadow-casting (FreSCa) cryo-SEM21,22 are applicable for contact-angle measurements of nano- and microparticles. FreSCa can be used only for oil–water interfaces, whereas GTT is applicable to both air–water and oil–water interfaces. Alternatively, for micron-sized particles at the air–water interface, θ can be measured directly by entrapping them in a poly(butylcyanoacrylate) film.23 For hydrophilic micrometer-sized particles, additional methods include contact-angle determination by optical microscopy using the film-trapping technique24 or the film-caliper method.25 Finally, θ can also be evaluated from global interfacial properties by applying appropriate theoretical models. For instance, using a Langmuir trough,26θ can be estimated from the pressure–area-isotherms differences between a surfactant and a surfactant–particle system, assuming there are no surfactant–particle interactions. Alternatively, using an ellipsometer27,28 and applying a two-layer model to describe a particle–laden interface, one can deduce the average particle position relative to the interface and then calculate θ.
The methods described above can be applied to measure contact angles either on a single-particle level,19–25 or to obtain an average26–28 value. Yet, none of these techniques permits direct force measurements associated with particle attachment and detachment – both related to θ. The only available method that does not impose any major restrictions in terms of the choice of both particles and fluids is colloidal-probe AFM.29–31 In general, by colloidal-probe AFM one measures the interaction forces between a probe particle and a surface as a function of separation, commonly referred to as force–distance curves (see Fig. 1a). The latter can provide valuable information on local material properties such as elasticity, adhesion and even surface charge densities.32
In this work, we apply colloidal-probe AFM to measure the interactions between colloidal particles and a fluid interface. More specifically, we attach smooth micron-sized silica particles to AFM cantilevers and measure their interactions with air–water and oil–water interfaces as a function of particle size and particle surface modification. The experimental data are analyzed using a detailed and self-consistent theoretical model, which relates θ to various measurable quantities. As demonstrated below, our model can predict the entire force–distance curves describing particle detachment without any adjustable parameters. To verify our results for θ, we compare them to contact-angle measurements from independent experimental methods such as GTT and FreSCa. The excellent agreement proves that our theoretical model is correct and self-consistent, and can be used to determine θ from AFM experimental data.
2. Theory
2.1. Theoretical background
Here, we present briefly the basic theoretical equations that describe the detachment of solid spherical particles from fluid interfaces. The geometrical representation in Fig. 1b depicts a solid sphere attached to an AFM cantilever at the oil–water (or air–water) interface. For a micrometer-sized particle (negligible particle weight and buoyancy) in its equilibrium position at the interface, the fluid–fluid phase boundary is flat and the net force acting on the particle is 0. By pulling the particle upwards, however, the interface deforms, which gives rise to a capillary force, F, acting on the colloidal probe. Due to the axial symmetry of the system, there is a net capillary force only in the vertical direction: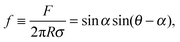 | (1) |
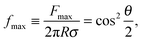 | (2) |
The detachment process is also characterized by the distance, D, between the particle center of mass and its equilibrium position expressed by:
 | (3) |
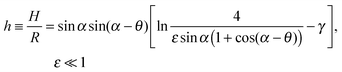 | (4) |
 | (5) |
For a given θ and ε = qR, the dimensionless force–distance curve f(d) can be calculated in the parametric form: f = f(α,θ) using eqn (1) and d = d(α,θ,ε) using eqn (3). Note that at fixed values of θ and ε, the functions |f(α)| and d(α) have maxima, which will be denoted by αmax,1 and αmax,2, respectively; see Fig. 2a. These maxima have the following physical meaning.
Let us consider a particle that is fixed to the cantilever (Fig. 1b). The particle is slowly (quasistatically) pulled upwards, so that the contact line slides downwards relative to the particle surface. By imposing different regimes on the cantilever, this quasistatic process can be carried out in two different ways.
(i) Force control: the force magnitude |f|, acting on the cantilever, is gradually increased with time, and correspondingly, α and d increase in accordance with eqn (1) and (3). In such a case, the particle detaches when the force becomes equal to fmax and the central angle is α = αmax,1.
(ii) Displacement control: the distance d is gradually increased with time, and then, α and f vary in accordance with eqn (3) and (1). At α = αmax,1, the maximal force is reached, but the particle remains attached. Upon further increase of d, the force decreases. At d = dmax ≡ Dmax/R (see Fig. 2a), corresponding to α = αmax,2, the particle detaches.
To sum up, the particle will detach at either α = αmax,1, or α = αmax,2, depending on whether the cantilever motion is carried out under force or displacement control. It should be noted that our experiments were performed under displacement control.
The area over the F(D) curve is equal to the work for particle detachment W. Physically, W represents the energy barrier for particle detachment into the upper phase (see Fig. 2b) and is analogous to the activation energy of chemical reactions. W is evaluated as follows:
 | (6) |
In the case of force control, the particle detaches from the interface at α = αmax,1 = (π + θ)/2 and w can be calculated analytically. Pitois & Chateau39,40 were the first to find an exact formula, hereby denoted by wPC:
 | (7) |
In the case of displacement control, the particle detaches from the interface at α = αmax,2, when D is maximal. This case was first considered by Scheludko et al.34 and W was evaluated numerically for particle detachment in the lower phase. Later, using perturbation methods, approximate closed-form formulae for αmax,2 and W were derived by Chateau & Pitois.40 In Section 2.2, we propose more accurate expressions with wider ranges of applicability.
2.2. Extension of the theory
The expressions derived here are applicable to both flotation separation processes34 and colloidal-probe AFM measurements that take place under displacement (distance) control. The starting point is the condition for maximal detachment distance dmax ≡ Dmax/R: | (8) |
 | (9) |
 | (10) |
 | (11) |
 | (12) |
 | (13) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ε. For the sake of comparison, we expand our result from eqn (13) in terms of 1/ln
ε. For the sake of comparison, we expand our result from eqn (13) in terms of 1/ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ε and obtain:
ε and obtain: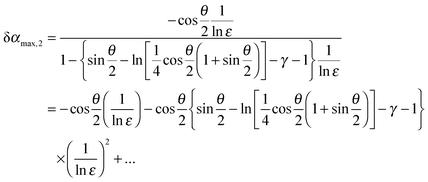 | (14) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ε)2 and its derivation is much simpler.
ε)2 and its derivation is much simpler.
Next, we will obtain the work w(1) for particle retraction under displacement control. First, it is useful to recast eqn (6) in the form:
 | (15) |
 | (16) |
 | (17) |
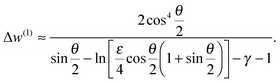 | (18) |
| w(1) = wPC + Δw(1) | (19) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ε:
ε: | (20) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ε terms should be minuses, not pluses. The latter error decreases the accuracy of eqn (31) from ref. 40 when compared to the exact numerical computations. As before, our formula for w(1) is more accurate since it incorporates the contributions of terms of order higher than (1/ln
ε terms should be minuses, not pluses. The latter error decreases the accuracy of eqn (31) from ref. 40 when compared to the exact numerical computations. As before, our formula for w(1) is more accurate since it incorporates the contributions of terms of order higher than (1/ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ε)2 and its derivation is straightforward.
ε)2 and its derivation is straightforward.
3. Materials and methods
3.1. Materials
This study focuses on the wettability of microparticles at fluid interfaces. As model particles, we used: (i) monodisperse silica spheres with diameters 6.27 ± 0.23 μm and 7.38 ± 0.23 μm (Microparticles GmbH, Germany); and (ii) polydisperse silica spheres with diameters between 2 and 20 μm (MSS-500; Kobo Products Inc., USA). To investigate the effect of surface chemistry on the particle wetting properties, we compared non-modified and hydrophobized silica spheres. The surface hydrophobization was carried out using 1H,1H,2H,2H-perfluorooctyltriethoxysilane (98%, Sigma-Aldrich, Germany). As the oil phase, we used n-hexadecane (>99%, Sigma-Aldrich, Germany) in both AFM and GTT experiments, whereas we used n-decane (>99%, Sigma-Aldrich, Germany) in FreSCa experiments. Both alkanes were purified from surface-active contaminants using an alumina column (MP EcoChrome™ Alumina B, Activity: Super I; MP Biomedicals, USA). The equilibrium interfacial tension of n-hexadecane against water was 52.5 ± 0.5 mN m−1 at 25 °C, measured by the pendant drop method (DSA100; Krüss GmbH, Germany) and later used in the numerical calculations.For particle trapping in GTT, we used gellan gum (AppliChem, Germany), which was purified from surface-active contaminants using a high-purity silica gel column (60 Å pores, 70–230 mesh; Fluka, Germany). The polydimethylsiloxane (PDMS) replica of the interface was created using Sylgard® 184 elastomer (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 base-to-curing-agent ratio by weight; Sigma-Aldrich, Germany), while the UV-glue replica was prepared using UV-curable glue (Norland Optical Adhesives 63, Norland Products Inc., USA). For particle spreading, we used isopropanol (≥99.5%, Fisher Chemical, USA), whereas for rinsing cantilevers and silicon wafers we used isopropanol, ethanol (≥99.8%, Fluka, Germany), and acetone (≥99.9%, Sigma-Aldrich, Germany). All solvents were used as received without further purification. For solution preparation and as the aqueous phase, we used high-purity MilliQ water.
1 base-to-curing-agent ratio by weight; Sigma-Aldrich, Germany), while the UV-glue replica was prepared using UV-curable glue (Norland Optical Adhesives 63, Norland Products Inc., USA). For particle spreading, we used isopropanol (≥99.5%, Fisher Chemical, USA), whereas for rinsing cantilevers and silicon wafers we used isopropanol, ethanol (≥99.8%, Fluka, Germany), and acetone (≥99.9%, Sigma-Aldrich, Germany). All solvents were used as received without further purification. For solution preparation and as the aqueous phase, we used high-purity MilliQ water.
3.2. Methods
All force measurements were conducted in a liquid cell at 25 °C. The cell consisted of a truncated metal cone (1.5 mm height and 2 mm diameter of the truncated upper part) and a glass petri dish (5 mm height and 25 mm diameter). The metal cone was glued to the bottom of the petri dish using the UV-curable glue. Prior to each measurement, the cone was filled with water up to its edge. For force measurements at the air–water interface, the petri dish was partially filled with water to reduce the evaporation from inside the cone. For force measurements at the oil–water interface, the petri dish was filled with n-hexadecane. In all cases, the fluid interface was practically flat and no curvature effects were considered. The liquid cell was then centered below the colloidal probe via an optical microscope and the cantilever speed was set to 1 μm s−1 to prevent any dynamic effects. At least 50 force–distance curves were collected for each automatic measurement.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 volume ratio was used. The silica particles were dispersed in the spreading solvent, so that their concentration was about 3 wt%.
1 volume ratio was used. The silica particles were dispersed in the spreading solvent, so that their concentration was about 3 wt%.
Next, 2.5 mL of hot gellan gum solution were poured in a UV-ozone-cleaned glass petri dish (5 mm height and 25 mm diameter) and 2 mL of purified n-hexadecane were added over the aqueous gellan gum solution. Then, ∼2 μL of the silica suspension were taken with a micropipette and spread at the oil–water interface. Afterwards, the petri dish was slowly cooled for about 1 hour at 0.5 °C min−1 to achieve complete setting of the gel. Successively, a PDMS or a UV-glue replica of the particle–laden interface was created at 23 °C. The PDMS replica was cured for at least 48 hours, whereas the UV-glue replica was cured by 366 nm UV-light for 15 minutes. After curing, all replicas were carefully peeled off from the jellified aqueous phase, rinsed with water, dried and then sputtered with ∼10 nm-thick gold or platinum layers.
Using an optical 3D profilometer (PLu Neox; Sensofar, Spain) equipped with 50× confocal objective, we measured the height of the protruding particles, Hp, in each replica. The UV-glue was used in the case of hydrophilic silica particles, because of their inferior adhesion to the PDMS; see Fig. A1 and Appendix A1 for details in the ESI.† The error of the height measurement, due to the replica surface roughness, was always less than 150 nm. For each particle, using the measured Hp and the average particle radius R given by the supplier, θ was calculated as follows:
 | (21) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K s−1, leading to water vitrification. After vitrification, the samples were mounted under liquid nitrogen onto a double fracture cryo-stage and were transferred under a cryo-high-vacuum with a shuttle (<5 × 10−7 mbar; VCT010; Bal-Tec AG/Leica, Germany) to a pre-cooled freeze-fracture device at −120 °C (BAF060; Bal-Tec AG/Leica, Germany). The samples were then fractured and partially freeze-dried at −100 °C for 1 min to remove residual water condensation and ice crystals. Successively, at −120 °C, the particle–laden interfaces were coated by unidirectional tungsten deposition at an elevation angle of 30° to a thickness of 3 nm and by extra 2 nm with a continuously varying angle between 90° and 30°. The second deposition is necessary to minimize charging effects during imaging.
000 K s−1, leading to water vitrification. After vitrification, the samples were mounted under liquid nitrogen onto a double fracture cryo-stage and were transferred under a cryo-high-vacuum with a shuttle (<5 × 10−7 mbar; VCT010; Bal-Tec AG/Leica, Germany) to a pre-cooled freeze-fracture device at −120 °C (BAF060; Bal-Tec AG/Leica, Germany). The samples were then fractured and partially freeze-dried at −100 °C for 1 min to remove residual water condensation and ice crystals. Successively, at −120 °C, the particle–laden interfaces were coated by unidirectional tungsten deposition at an elevation angle of 30° to a thickness of 3 nm and by extra 2 nm with a continuously varying angle between 90° and 30°. The second deposition is necessary to minimize charging effects during imaging.
The freeze-fractured and metal-coated samples were transferred under high vacuum (<5 × 10−7 mbar) at −120 °C to a pre-cooled (−120 °C) cryo-SEM (Leo 1530 Gemini; Zeiss, Germany). Images were taken with a secondary-electron detector and θ was extracted for individual particles as explained in ref. 22.
4. Results and discussion
4.1. Numerical results
Here, we summarize the basic numerical results obtained from the theory in Section 2. Our main attention is devoted to the process of particle detachment from fluid interfaces (air–water and oil–water). Fig. 3 shows a sketch of a force–distance curve for the particle retraction process. For small particles in mechanical equilibrium, the fluid interface is flat and the net capillary force is zero. By pulling the particle upwards, the interface deforms, which results in a non-zero capillary force. Upon further pulling, the particle detaches from the interface and goes into the upper phase. From the retraction force–distance curve, we can determine: (i) the maximal force, Fmax; (ii) the detachment distance, Dmax; and (iii) the work for quasistatic detachment, W; see Fig. 3. These parameters are all related to the three-phase contact angle θ: Fmaxviaeqn (2); Dmaxviaeqn (3), (4) and (8); and W viaeqn (6) – for explanations see Section 2.The dependence of Fmax on θ was first derived by Scheludko & Nikolov33 and is given by eqn (2). The distance Dmax is defined as the maximal distance travelled by the particle center of mass from its equilibrium position to the point of detachment. Having determined Dmax, we can calculate θ from eqn (3), (4) and (8). Fig. 4a shows the dimensionless detachment distance Dmax/R versus θ. As expected, Dmax/R is larger for hydrophilic particles than for hydrophobic particles. For superhydrophobic particles θ ≈ 180°, Dmax/R approaches zero. Dmax/R decreases also when the Bond number ε ≡ qR increases, that is, when either the particle radius, or the capillary length increase.
Another key parameter is the work for quasistatic detachment W, which is equal to the area over the F(D) force–distance curve. The relationship between W and θ follows from eqn (6). In Fig. 4b, we see the numerical results for W/(πR2σ) versus θ. Expectedly, W/(πR2σ) is a decreasing function of θ and it approaches zero for superhydrophobic particles. Similarly to Dmax/R, W/(πR2σ) decreases when R increases. Physically, W coincides with the energy barrier associated with particle detachment (Fig. 2b). In Fig. 2b, the initial state coincides with the equilibrium position of the particle at the interface, while the transition state represents the fully stretched meniscus formed prior to particle detachment. Thus, W is analogous to the activation energy of chemical reactions.
An analytical expression for W/(πR2σ) was found by Pitois & Chateau – eqn (7),39 for the case of particle detachment under force control. However, in the regime of displacement control, the detachment happens when the distance D becomes equal to Dmax. To take this difference into account (Fig. 5a), we derived the first-order correction Δw(1) expressed in eqn (15). Therefore, for quasistatic retraction under displacement control, W/(πR2σ) should be evaluated either numerically from eqn (6), or analytically from eqn (19).
 | ||
| Fig. 5 (a) The plot represents a theoretical force–distance curve calculated for a large hydrophilic particle with θ = 0°. The area over the curve (proportional to w) can be divided into two contributions: (i) up to the minimum – given by wPC from eqn (7); and (ii) from the minimum to the detachment position – given by Δw(1) in eqn (15). (b) The relative errors of the analytical formulae [eqn (7) and (19)] for w are plotted as a function of the Bond number ε. The solid lines are for hydrophilic particles, θ = 0°, and the dashed lines are for hydrophobic particles, θ = 135°. | ||
For the sake of comparison, in Fig. 5b, the analytical formulae for wPC and w(1) from eqn (7) and (19) are compared to the exact numerical results as a function of the Bond number ε. We see that the closed-form expressions are quite accurate for very small Bond numbers ε, i.e. for very small particles. However, for larger particles, wPC underestimates the quasistatic work for particle detachment by around 10%, whereas w(1) is more accurate and deviates less than 3% compared to the exact numerical calculations.
4.2. Colloidal-probe AFM results
Using colloidal-probe AFM, one can extract θ for individual smooth microparticles from various physical quantities. One of these quantities is the so-called jump-in distance δ,43 which can be measured directly from the force–distance curves upon particle approach. For a sphere in its equilibrium position at the air–water or oil–water interface (having ρoil < 1 g cm−3), δ represents the particle immersion depth into the aqueous phase and is related to θ as follows:43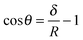 | (22) |
As explained in Section 4.1, the key parameters, which describe the particle retraction process, are: (i) the maximal force Fmax; (ii) the detachment distance Dmax; and (iii) the work for quasistatic detachment W. Hereafter, the receding contact angles obtained from these physical quantities are designated as: θf, θd and θw, respectively.
Table 1 summarizes the three-phase contact angles of silica microspheres at both oil–water and air–water interfaces. θ and Δθ are calculated from at least 50 force–distance curves, unless a limited number of manual measurements are performed (first and last row in the table). Additional comments on the sources of errors are reported in Appendix A.2 in the ESI.† Expectedly, the advancing contact angle θδ is always higher than the receding contact angles θf, θd and θw. Compared to δ, which can be affected by hydrodynamic instabilities, capillary waves and fast wetting phenomena, Fmax, Dmax, and W seem to be more reproducible. Accordingly, the receding contact angles θf, θd and θw can all be determined quite accurately. Moreover, θf, θd and θw are also very close in value, which proves that the theoretical model from Section 2 is robust and self-consistent. Here, we should point out that θd is especially reliable since Dmax depends only on the nanometric accuracy of the piezo-actuator and, in contrast to Fmax and W, is independent of the cantilever calibration method.
| R (μm) | θ δ (°) | Δθδ (°) | θ f (°) | Δθf (°) | θ d (°) | Δθd (°) | θ w (°) | Δθw (°) |
|---|---|---|---|---|---|---|---|---|
| a Native (UV-cleaned) silica surface. b In situ-glue-modified silica surface. c Hydrophobized (fluorosilanized) silica surface. d Estimated value, assuming 10% relative error of Fmax. | ||||||||
| Oil–water (OW) | ||||||||
| 5.62a | 56 | — | 28 | 18d | 42 | — | 33 | — |
| 1.50b | 125 | 4 | 90 | 1 | 93 | 2 | 91 | 1 |
| 6.34c | 142 | 2 | 120 | 1 | 121 | 1 | 117 | 2 |
| 3.75c | 154 | 5 | 135 | 3 | 131 | 5 | 132 | 2 |
| Air–water (AW) | ||||||||
| 3.69b | 71 | — | 58 | 10d | 56 | — | 54 | — |
Next, using Table 1, we will compare the wetting properties of the measured silica microspheres with different surface chemistry. The first silica particle, with R = 5.62 μm, is very hydrophilic since it was UV-ozone cleaned on the cantilever just before the AFM measurement. For such hydrophilic particles, part of the measurement was performed manually via a stepper-motor since Dmax exceeded the maximal extension of the piezo-actuator. We thus have few force–distance curves, no correction for the deflection baseline and no consistent estimate for Δθ. The second particle, with R = 1.50 μm, corresponds to a surface modified in situ by the UV-curable glue vapors during the colloidal probe preparation. This particle is more hydrophobic than native silica particles: θd = 93° versus θd = 42°. The former value is very close to θ = 80 ± 10° measured by DSA for water droplets on a glue-modified silicon wafer immersed in n-hexadecane. The third and fourth particles were hydrophobized following the procedure described in Section 3.2. Their average θd is 126 ± 7°, which agrees reasonably well with θ = 112 ± 10° measured by DSA for water droplets on a hydrophobized silicon wafer immersed in n-hexadecane. The last particle, with R = 3.69 μm, measured at the air–water interface, is in situ-modified and hydrophilic with θd = 56°. This contact angle is close to θ = 60 ± 6° obtained by DSA measurements of water droplets on either non-modified, or glue-modified silicon wafers in air.
To demonstrate the validity of our theoretical model from Section 2, we calculated the force–distance curves for the particle retraction process without any adjustable parameters. Fig. 6 illustrates the comparison of four theoretical versus experimental force–distance curves, for which θd varies in a wide interval from 42° to 135°. Note that, θf and θd are determined for each f(d) curve using only two points, and may slightly deviate from the average values in Table 1. The excellent agreement between theory and experiments (always within the experimental error) proves the adequacy of our model, which can be applied for contact-angle determination of individual microparticles.
To prove that the contact line motion on the particle surface before detachment fully determines the force–distance curves, we have produced a truncated silica sphere (Fig. 7a), cut by a focused ion beam (FIB), whose cut is positioned just below the expected detachment point. Fig. 7b shows that the theoretical and experimental force–distance curves practically coincide and θd = 101°. As expected, the theory holds since the FIB-cut, with αcut = 146°, is just below the detachment point, αmax,2 = 144°. Thus, the contact line slides and then detaches before reaching the cut. If the FIB-cut were above the detachment point corresponding to a sliding contact line, then one would expect pinning at the edge.44
4.3. Comparison of different methods (AFM, GTT, FreSCa)
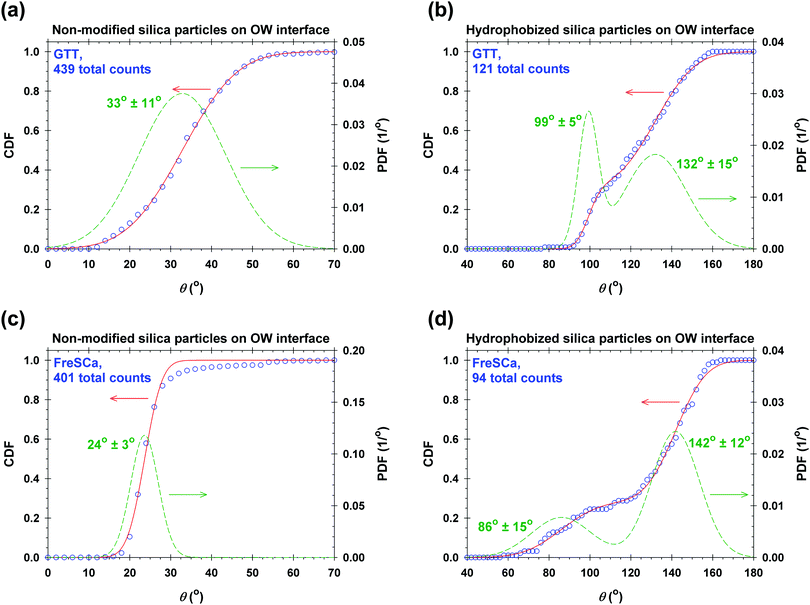
To verify the data obtained from colloidal-probe AFM, we applied two independent methods for contact-angle measurement: the gel-trapping technique (GTT) and the freeze-fracture shadow-casting (FreSCa) cryo-SEM method. Fig. 8 shows the three-phase contact angle distributions of non-modified and hydrophobized silica particles at the oil–water interface. The empty symbols represent the experimental points, whereas the solids lines are calculated assuming a normal distribution for θ: monomodal for the non-modified particles and bimodal for the hydrophobized particles. The presence of bimodal distributions can be ascribed to incomplete functionalization of a fraction of the particles. The cumulative distribution function (CDF) is:45 | (23) |
 | (24) |
| Silica particles | Contact angle, θ (°) | ||
|---|---|---|---|
| AFM | GTT | FreSCa | |
| Non-modified | 42 | 33 ± 11 | 24 ± 3 |
| Hydrophobized | 126 ± 7 | 99 ± 5 (θ1) | 86 ± 15 (θ1) |
| 132 ± 15 (θ2) | 142 ± 12 (θ2) | ||
From Table 2 and for a given surface modification (non-modified or hydrophobized particles), we see that the average contact angles obtained from GTT and FreSCa are in good agreement as they differ within the respective standard deviations. The next step is to compare the colloidal-probe AFM to GTT and FreSCa. Before that, however, it should be noted that using the colloidal-probe AFM we measure θ for individual particles, whereas using GTT and FreSCa we obtain contact angle distributions, thus also capturing particle-to-particle variations. Having that in mind, the contact angle θd for non-modified silica spheres is close to the average contact angle determined from GTT and is slightly higher than the one from FreSCa. For hydrophobized silica spheres, θd practically coincides with θ2, which corresponds to the completely fluorosilanized particle surface. During fluorosilane-vapor deposition, however, some of the particles are only partially hydrophobized and their average contact angle is given by θ1.
In summary, by applying independent experimental techniques, we prove that our theoretical model is robust and self-consistent, and can be used to determine θ in a reliable way.
5. Summary and conclusions
In this paper, we have developed a detailed theoretical model to interpret the experimental data from colloidal-probe AFM that describes the process of particle detachment from the interface. For small spherical particles in mechanical equilibrium, the fluid interface is flat and the net capillary force is zero. By pulling the particle upwards, the interface deforms, which results in a non-zero capillary force. At some point, the particle detaches from the interface and goes into the upper phase. From the force–distance curve, we can directly extract: (i) the maximal force Fmax; (ii) the detachment distance Dmax; and (iii) the work for quasistatic detachment W. These parameters are all related to the three-phase contact angle θ.F max is a decreasing function of θ and was first calculated by Scheludko & Nikolov.33 Similarly, Dmax/R and W/(πR2σ) decrease with θ and both approach zero for super-hydrophobic particles θ ≈ 180°. In contrast to Fmax, which is independent of the Bond number ε ≡ qR, Dmax/R and W/(πR2σ) both decrease when ε increases, namely, when the particle radius R increases. Physically, W can be interpreted as an energy barrier for particle detachment in analogy to the activation energy for chemical reactions. We devised a very accurate closed-form expression for W, which improves those found by Pitois & Chateau.39,40
Using Fmax, Dmax and W, as well as our theoretical model, we calculated the receding contact angles θf, θd and θw for non-modified and hydrophobized silica particles at both air–water and oil–water interfaces. The advancing contact angle θδ was evaluated from the so-called jump-in distance δ,43 which was measured upon particle approach. As expected, the advancing contact angle θδ is higher than the receding contact angles θf, θd and θw. It is important to stress here that θf, θd and θw can all be determined very accurately and are very close in value, which proves that our theoretical model is adequate and self-consistent.
Furthermore, our model was validated in three ways. First, we calculated the theoretical force–distance curves without using any adjustable parameters and they closely coincide with the experimental data for a wide range of contact angles. Second, as a proof of concept, the model was successfully applied to predict the experimental force–distance curve of an FIB-truncated sphere, whose FIB-cut is positioned below the point of particle detachment from the interface. Third, using independent experimental methods such as GTT, FreSCa and DSA, we verified the contact angle measurements by AFM.
The results contribute to the understanding of particle wetting, adhesion and detachment from fluid interfaces. Additionally, the theoretical model can be applied to predict both the force and interfacial deformation imparted by the colloidal probe, which is especially valuable when AFM is used as a tool for guided particle assembly. As an outlook, we foresee the extension of this model to the case of fixed contact line (pinned contact line),44 as this is commonly found in many particle systems used in applications, e.g. showing surface roughness for enhanced emulsion stability.46
Acknowledgements
I. L. and S. E. A. gratefully acknowledge the Sciex – Scientific Exchange Programme NMS.CH for the granted postdoctoral fellowships Sciex 14.081 and Sciex 14.082 at ETH Zurich. L. I. and M. Z. acknowledge the Swiss National Science Foundation (SNSF) grant PP00P2_144646/1 for financial support. The authors thank Dr Thomas Henze from JPK Instruments AG, Germany, for useful discussions about AFM calibration and force measurements. The authors acknowledge the support of the ETH microscopy center ScopeM and thank Prof. André Studart for SEM access.References
- S. U. Pickering, J. Chem. Soc., Trans., 1907, 91, 2001–2021 RSC.
- R. Aveyard, B. P. Binks and J. H. Clint, Adv. Colloid Interface Sci., 2003, 100–102, 503–546 CrossRef CAS.
- A. D. Dinsmore, M. F. Hsu, M. G. Nikolaides, M. Marquez, A. R. Bausch and D. A. Weitz, Science, 2002, 298, 1006–1009 CrossRef CAS PubMed.
- A. Verma and F. Stellacci, Small, 2010, 6, 12–21 CrossRef CAS PubMed.
- A. V. Nguyen, R. J. Pugh and G. J. Jameson, in Colloidal Particles at Liquid Interfaces, ed. B. P. Binks and T. S. Horozov, Cambridge University Press, Cambridge, 1st edn, 2006, ch. 9, pp. 328–382 Search PubMed.
- K. P. Velikov and O. D. Velev, in Colloidal Particles at Liquid Interfaces, ed. B. P. Binks and T. S. Horozov, Cambridge University Press, Cambridge, 1st edn, 2006, ch. 7, pp. 225–297 Search PubMed.
- D. J. Norris, E. G. Arlinghaus, L. Meng, R. Heiny and L. E. Scriven, Adv. Mater., 2004, 16, 1393–1399 CrossRef CAS.
- A. Böker, J. He, T. Emrick and T. P. Russell, Soft Matter, 2007, 3, 1231–1248 RSC.
- R. McGorty, J. Fung, D. Kaz and V. N. Manoharan, Mater. Today, 2010, 13, 34–42 CrossRef CAS.
- L. Isa, K. Kumar, M. Müller, J. Grolig, M. Textor and E. Reimhult, ACS Nano, 2010, 4, 5665–5670 CrossRef CAS PubMed.
- B. M. Rey, R. Elnathan, R. Ditcovski, K. Geisel, M. Zanini, M. A. Fernandez-Rodriguez, V. V. Naik, A. Frutiger, W. Richtering, T. Ellenbogen, N. H. Voelcker and L. Isa, Nano Lett., 2016, 16, 157–163 CrossRef CAS PubMed.
- A. F. Koretsky and P. M. Kruglyakov, Izv. Sib. Otd. Akad. Nauk SSSR, Ser. Biol. Nauk, 1971, 2, 139 Search PubMed.
- B. P. Binks and T. S. Horozov, in Colloidal Particles at Liquid Interfaces, ed. B. P. Binks and T. S. Horozov, Cambridge University Press, Cambridge, 1st edn, 2006, ch. 1, pp. 1–74 Search PubMed.
- T. S. Horozov, R. Aveyard, J. H. Clint and B. P. Binks, Langmuir, 2003, 19, 2822–2829 CrossRef CAS.
- Y. Peng, W. Chen, T. M. Fischer, D. A. Weitz and P. Tong, J. Fluid Mech., 2009, 618, 243–261 CrossRef CAS.
- J. T. Petkov, K. D. Danov, N. D. Denkov, R. Aust and F. Durst, Langmuir, 1996, 12, 2650–2653 CrossRef CAS.
- P. A. Kralchevsky and K. Nagayama, Langmuir, 1994, 10, 23–36 CrossRef CAS.
- M. Zanini and L. Isa, J. Phys.: Condens. Matter, 2016, 28, 313002 CrossRef PubMed.
- V. N. Paunov, Langmuir, 2003, 19, 7970–7976 CrossRef CAS.
- L. N. Arnaudov, O. J. Cayre, A. C. Stuart, D. Stoyanov, M. A. C. Stuart, S. D. Stoyanov and V. N. Paunov, Phys. Chem. Chem. Phys., 2010, 12, 328–331 RSC.
- L. Isa, F. Lucas, R. Wepf and E. Reimhult, Nat. Commun., 2011, 2, 438–457 CrossRef PubMed.
- L. Isa, Chimia, 2013, 67, 231–235 CrossRef CAS PubMed.
- N. Vogel, J. Ally, K. Bley, M. Kappl, K. Landfester and C. K. Weiss, Nanoscale, 2014, 6, 6879–6885 RSC.
- A. Hadjiiski, R. Dimova, N. D. Denkov, I. B. Ivanov and R. Borwankar, Langmuir, 1996, 12, 6665–6675 CrossRef CAS.
- T. S. Horozov, D. A. Braz, P. D. I. Fletcher, B. P. Binks and J. H. Clint, Langmuir, 2008, 24, 1678–1681 CrossRef CAS PubMed.
- D. O. Grigoriev, J. Krägel, V. Dutschk, R. Miller and H. Möhwald, Phys. Chem. Chem. Phys., 2007, 9, 6447–6454 RSC.
- B. P. Binks, J. H. Clint, A. K. F. Dyab, P. D. I. Fletcher, M. Kirkland and C. P. Whitby, Langmuir, 2003, 19, 8888–8893 CrossRef CAS.
- T. N. Hunter, G. J. Jameson and E. J. Wanless, Aust. J. Chem., 2007, 60, 651–655 CrossRef CAS.
- M. Preuss and H.-J. Butt, J. Colloid Interface Sci., 1998, 208, 468–477 CrossRef CAS PubMed.
- G. Gillies, K. Büscher, M. Preuss, M. Kappl, H.-J. Butt and K. Graf, J. Phys.: Condens. Matter, 2005, 17, S445–S464 CrossRef CAS.
- D. M. Kaz, R. McGorty, M. Mani, M. P. Brenner and V. N. Manoharan, Nat. Mater., 2011, 11, 138–142 CrossRef PubMed.
- H.-J. Butt, B. Cappella and M. Kappl, Surf. Sci. Rep., 2005, 59, 1–152 CrossRef CAS.
- A. D. Scheludko and A. D. Nikolov, Colloid Polym. Sci., 1975, 253, 396–403 Search PubMed.
- A. Scheludko, B. V. Toshev and D. T. Bojadjiev, J. Chem. Soc., Faraday Trans. 1, 1976, 72, 2815–2828 RSC.
- B. V. Derjaguin, Dokl. Akad. Nauk SSSR, 1946, 51, 517 Search PubMed.
- D. F. James, J. Fluid Mech., 1974, 63, 657–664 CrossRef.
- L. L. Lo, J. Fluid Mech., 1983, 132, 65–78 CrossRef.
- P. A. Kralchevsky, I. B. Ivanov and A. D. Nikolov, J. Colloid Interface Sci., 1986, 112, 108–121 CrossRef CAS.
- O. Pitois and X. Chateau, Langmuir, 2002, 18, 9751–9756 CrossRef CAS.
- X. Chateau and O. Pitois, J. Colloid Interface Sci., 2003, 259, 346–353 CrossRef CAS PubMed.
- G. E. Yakubov, O. I. Vinogradova and H.-J. Butt, J. Adhes. Sci. Technol., 2000, 14, 1783–1799 CrossRef CAS.
- J. L. Hutter and J. Bechhoefer, Rev. Sci. Instrum., 1993, 64, 1868–1873 CrossRef CAS.
- M. Preuss and H.-J. Butt, Int. J. Miner. Process., 1999, 56, 99–115 CrossRef CAS.
- J. Ally, M. Kappl and H.-J. Butt, Langmuir, 2012, 28, 11042–11047 CrossRef CAS PubMed.
- B. S. Everitt and D. J. Hand, Finite Mixture Distributions, Chapman & Hall, London, 1981 Search PubMed.
- R. Van Hooghten, L. Imperiali, V. Boeckx, R. Sharma and J. Vermant, Soft Matter, 2013, 9, 10791–10798 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available: Appendix A: additional figures, derivations and comments. See DOI: 10.1039/c6sm01716a |
| ‡ Both authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2016 |