Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A monometallic lanthanide bis(methanediide) single molecule magnet with a large energy barrier and complex spin relaxation behaviour†
Matthew
Gregson‡
a,
Nicholas F.
Chilton‡
 a,
Ana-Maria
Ariciu
b,
Floriana
Tuna
b,
Iain F.
Crowe
c,
William
Lewis
d,
Alexander J.
Blake
a,
Ana-Maria
Ariciu
b,
Floriana
Tuna
b,
Iain F.
Crowe
c,
William
Lewis
d,
Alexander J.
Blake
 d,
David
Collison
a,
Eric J. L.
McInnes
b,
Richard E. P.
Winpenny
*a and
Stephen T.
Liddle
*a
d,
David
Collison
a,
Eric J. L.
McInnes
b,
Richard E. P.
Winpenny
*a and
Stephen T.
Liddle
*a
aSchool of Chemistry, The University of Manchester, Oxford Road, Manchester, M13 9PL, UK. E-mail: steve.liddle@manchester.ac.uk; richard.winpenny@manchester.ac.uk
bSchool of Chemistry and Photon Science Institute, The University of Manchester, Oxford Road, Manchester, M13 9PL, UK
cSchool of Electrical and Electronic Engineering and Photon Science Institute, The University of Manchester, Oxford Road, Manchester, M13 9PL, UK
dSchool of Chemistry, University of Nottingham, University Park, Nottingham, NG7 2RD, UK
First published on 23rd November 2015
Abstract
We report a dysprosium(III) bis(methanediide) single molecule magnet (SMM) where stabilisation of the highly magnetic states and suppression of mixing of opposite magnetic projections is imposed by a linear arrangement of negatively-charged donor atoms supported by weak neutral donors. Treatment of [Ln(BIPMTMS)(BIPMTMSH)] [Ln = Dy, 1Dy; Y, 1Y; BIPMTMS = {C(PPh2NSiMe3)2}2−; BIPMTMSH = {HC(PPh2NSiMe3)2}−] with benzyl potassium/18-crown-6 ether (18C6) in THF afforded [Ln(BIPMTMS)2][K(18C6)(THF)2] [Ln = Dy, 2Dy; Y, 2Y]. AC magnetic measurements of 2Dy in zero DC field show temperature- and frequency-dependent SMM behaviour. Orbach relaxation dominates at high temperature, but at lower temperatures a second-order Raman process dominates. Complex 2Dy exhibits two thermally activated energy barriers (Ueff) of 721 and 813 K, the largest Ueff values for any monometallic dysprosium(III) complex. Dilution experiments confirm the molecular origin of this phenomenon. Complex 2Dy has rich magnetic dynamics; field-cooled (FC)/zero-field cooled (ZFC) susceptibility measurements show a clear divergence at 16 K, meaning the magnetic observables are out-of-equilibrium below this temperature, however the maximum in ZFC, which conventionally defines the blocking temperature, TB, is found at 10 K. Magnetic hysteresis is also observed in 10% 2Dy@2Y at these temperatures. Ab initio calculations suggest the lowest three Kramers doublets of the ground 6H15/2 multiplet of 2Dy are essentially pure, well-isolated |±15/2〉, |±13/2〉 and |±11/2〉 states quantised along the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Dy
Dy![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C axis. Thermal relaxation occurs via the 4th and 5th doublets, verified experimentally for the first time, and calculated Ueff values of 742 and 810 K compare very well to experimental magnetism and luminescence data. This work validates a design strategy towards realising high-temperature SMMs and produces unusual spin relaxation behaviour where the magnetic observables are out-of-equilibrium some 6 K above the formal blocking temperature.
C axis. Thermal relaxation occurs via the 4th and 5th doublets, verified experimentally for the first time, and calculated Ueff values of 742 and 810 K compare very well to experimental magnetism and luminescence data. This work validates a design strategy towards realising high-temperature SMMs and produces unusual spin relaxation behaviour where the magnetic observables are out-of-equilibrium some 6 K above the formal blocking temperature.
Introduction
Proposals have been made for devices employing the quantum effects of molecular magnets,1–3 and many remarkable experimental results have been reported involving single molecule magnets (SMMs).4–6 SMMs are molecules that show slow relaxation of magnetisation, which can lead to observation of magnetic hysteresis of a molecular origin.7 These addressable magnets operating at the scale of a few nm lay the groundwork for new, potentially revolutionary quantum-based devices; however until SMMs operate at much higher temperatures their exploitation seems unlikely.Many interesting SMMs have been reported based on a single lanthanide centre,8 and theoretical developments for their understanding are progressing at a rapid pace.9–11 Recently a design principle for a high-temperature SMM was proposed, in the form of a linear two-coordinate lanthanide complex.12,13 A linear arrangement of negatively charged donor atoms imposes a strong and purely axial ligand field (LF) potential, stabilising the maximal angular momentum projections of 4f ions with oblate electron densities such as dysprosium(III).14–16 This would result in electronic states that are widely separated in energy, leading to huge energy barriers, Ueff, for thermal relaxation processes. Furthermore, owing to the high symmetry of the LF potential there should be no mixing between components of opposite magnetic projection, therefore disallowing short-cuts through or under the barrier.17 Our design strategy is orthogonal to that required for 4f ions whose maximal angular momentum functions have prolate electron densities such as erbium(III), where equatorial LF potentials are required; this alternative approach has recently yielded an excellent result in the form of [Er(COT)2]−.18,19 We previously calculated that in a real system, where the symmetry is likely to be lower than ideal, even a near-axial LF imposed by anionic donors should be strong enough to produce large Ueff barriers.13 This remains experimentally unproven, but provides a promising direction towards high temperature SMMs.
Simple electrostatic considerations imply that the strength of the axial LF depends on the charge on the donor atoms on the axis, and hence we proposed that the use of dianionic methanediides would optimise Ueff.12,13 However, such complexes present a significant synthetic challenge; four decades after the first proposal of a lanthanide alkylidene,20 such a species remains elusive,21 let alone realising a bis(alkylidene) complex. The stabilisation of a two-coordinate lanthanide bis(dicarbanion) clearly represents a major challenge, even before control of molecular symmetry is considered. Our first step towards the synthesis of such a difficult target is to consider a complex stabilised by weak equatorial donors in a pincer framework. There has been a significant amount of work in recent years where the stabilisation of lanthanide complexes with carbanion donors is achieved with phosphorus substituents,22,23 where both mono- and di-anionic donors are known.24 Seeking inspiration, we noted that Cavell et al. reported the bis(methanediide) complex [Zr{C(PMe2NSiMe3)2}2], where the two ligands are orthogonal due to the ‘locking’ effect of the imino arms to avoid steric clashing.25 Such an arrangement is particularly important in the design of a SMM – whilst two-coordinate complexes are ideal, if stabilising donors atoms must be present they should at least be symmetrically disposed.
Here we report the synthesis, structure, theoretical characterisation and magnetic studies of a bis(methanediide) complex of dysprosium(III) which has a Ueff value of 813 K, the largest for any monometallic dysprosium(III) complex. This complex also possess rich magnetisation dynamics where out-of-equilibrium magnetisation is observed below 16 K yet TB appears to be 10 K. Although the bis(methanediide) complex is not a two-coordinate linear system, it is clear that there is significant charge accumulation along the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Dy
Dy![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C axis which effectively mimics the linear arrangement we ultimately seek. Thus, this work experimentally validates our proposition that a linear arrangement of negative charges in a dysprosium(III) complex should lead to very large energy barriers to magnetic relaxation, and provides a promising direction to making high-temperature SMMs a reality.
C axis which effectively mimics the linear arrangement we ultimately seek. Thus, this work experimentally validates our proposition that a linear arrangement of negative charges in a dysprosium(III) complex should lead to very large energy barriers to magnetic relaxation, and provides a promising direction to making high-temperature SMMs a reality.
Results
Synthesis and characterisation
The route to a bis(methanediide) dysprosium(III) complex is shown in Scheme 1. Treatment of [Dy(CH2Ph)3(THF)3]26 with two equivalents of BIPMTMSH2 [BIPMTMSH2 = H2C(PPh2NSiMe3)2] in toluene produces an orange solution, which when briefly heated fades to yellow. Work-up and recrystallisation from toluene affords colourless crystals of the mixed methanediide–methanide complex [Dy(BIPMTMS)(BIPMTMSH)] (1Dy) in 63% isolated yield. Alternatively, treatment of [Dy(BIPMTMS)(CH2Ph)(THF)] with one equivalent of BIPMTMSH2 also affords 1Dy in 63% yield. Complex [Dy(BIPMTMS)(CH2Ph)(THF)] was reported previously by us,26 but was not structurally authenticated; here we report its solid state structure (see ESI†). The orange colour during preparations is most likely due to the intermediate formation of [Dy(BIPMTMS)(CH2Ph)(THF)] that effects metallation of free BIPMTMSH2 when heated. We previously showed that early, large lanthanides (La–Gd) spontaneously form the mixed methanediide–methanide combination irrespective of reactant ratios, presumably via highly reactive [Ln(BIPMTMS)(CH2Ph)(THF)] complexes due to the large metal size, whereas the later, smaller lanthanides like Dy and Er form isolable methanediide–benzyl combinations. The formulation of 1Dy is supported by IR, CHN, and Evans method magnetic moment (μeff = 11 μB), but the 1H NMR spectrum is broad and uninformative due to the paramagnetic DyIII ion.With 1Dy in hand, we prepared the target bis(methanediide) derivative. Treatment of 1Dy with benzyl potassium in THF gave an orange suspension, which yielded a yellow solution after stirring. Following addition of 18-crown-6 ether (18C6) and concentration, yellow crystals of the bis(methanediide) complex [Dy(BIPMTMS)2][K(18C6)(THF)2]·2THF (2Dy) were obtained in 43% isolated yield. The identity of 2Dy is supported by IR, CHN, and Evans method magnetic moment data (μeff = 11 μB); however, as for 1Dy the 1H NMR spectrum of 2Dy is uninformative. For the purposes of doping 2Dy into a diamagnetic host we prepared the yttrium bis(methanediide) analogue [Y(BIPMTMS)2][K(18C6)(THF)2]·2THF (2Y) in 60% yield from [Y(BIPMTMS)(BIPMTMSH)] (1Y). The interaction of the methanediide centres in 2Y with yttrium can be seen in the 13C NMR spectrum, which exhibits a single triplet of doublets at 53.70 ppm (JPC = 210.86 Hz; JYC = 3.07 Hz) showing that the methanediides are magnetically equivalent on the NMR timescale; this can be compared to the 13C NMR spectrum of 1Y which exhibits a triplet at 19.87 ppm (JPC = 114.25 Hz) and a triplet of doublets at 66.50 ppm (JPC = 171.76 Hz; JYC = 6.90 Hz) for the methanide and methanediide centres respectively. This suggests a significant interaction between the yttrium and methanediide centres in 2Y, and by inference a similar situation for the dysprosium and methanediide centres in 2Dy, which is important for generating a largely axial LF at dysprosium.
Structural characterisations
The solid state structures of 1Dy and 2Dy were determined by X-ray crystallography and are illustrated in Fig. 1. The yttrium analogues can be found in the ESI.† Complex 1Dy crystallises as discrete monomers where the dysprosium centre is six-coordinate. The C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Dy–C angle is 158.25(6)°, and the N–Dy–N angles are 129.51(5) and 110.51(5)° for the methanediide and methanide ligands, respectively. The Dy
Dy–C angle is 158.25(6)°, and the N–Dy–N angles are 129.51(5) and 110.51(5)° for the methanediide and methanide ligands, respectively. The Dy![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and Dy–C bond lengths are 2.3640(17) and 2.9001(18) Å, respectively, which reflects the formal double and single bond character of these linkages. The Dy–N distances are longer in the methanediide [range: 2.4587(15)–2.4786(15) Å] than the methanide [range: 2.3903(15)–2.4092(15) Å]. The methanediide centre adopts an essentially T-shaped planar geometry [Σ∠ = 355.06(16)°] whereas the methanide is puckered to accommodate the hydrogen atom. Complex 1Dy does not approach the linear arrangement of highly charged donor atoms that we seek.
C and Dy–C bond lengths are 2.3640(17) and 2.9001(18) Å, respectively, which reflects the formal double and single bond character of these linkages. The Dy–N distances are longer in the methanediide [range: 2.4587(15)–2.4786(15) Å] than the methanide [range: 2.3903(15)–2.4092(15) Å]. The methanediide centre adopts an essentially T-shaped planar geometry [Σ∠ = 355.06(16)°] whereas the methanide is puckered to accommodate the hydrogen atom. Complex 1Dy does not approach the linear arrangement of highly charged donor atoms that we seek.
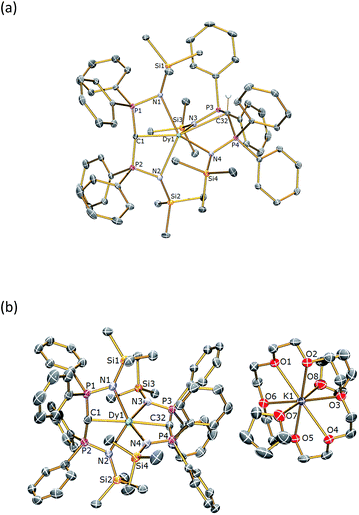 | ||
| Fig. 1 Molecular structures of (a) 1Dy and (b) 2Dy. Structures are shown with 30% probability displacement ellipsoids and with non-methanide hydrogen atoms and lattice solvent omitted for clarity. Selected bond lengths (Å) and angles (°): for 1Dy – C(1)–P(1) 1.6464(19), C(1)–P(2) 1.6437(19), C(32)–P(3) 1.7369(18), C(32)–P(4) 1.7251(18), P(1)–N(1) 1.6222(16), P(2)–N(2) 1.6281(15), P(3)–N(3) 1.6055(15), P(4)–N(4) 1.6077(15), Dy(1)–C(1) 2.3640(17), Dy(1)–C(32) 2.9001(18), Dy(1)–N(1) 2.4786(15), Dy(1)–N(2) 2.4587(15), Dy(1)–N(3) 2.4092(15), Dy(1)–N(4) 2.3903(15), P(1)–C(1)–P(2) 162.79(12), P(3)–C(32)–P(4) 138.32(12), N(1)–Dy(1)–N(2) 129.51(5), N(3)–Dy(1)–N(4) 110.51(5), C(1)–Dy(1)–C(32) 158.25(6); for 2Dy – C(1)–P(1) 1.630(7), C(1)–P(2) 1.651(7), C(32)–P(3) 1.645(6), C(32)–P(4) 1.634(6), P(1)–N(1) 1.620(5), P(2)–N(2) 1.617(5), P(3)–N(3) 1.619(5), P(4)–N(4) 1.607(5), Dy(1)–C(1) 2.434(6), Dy(1)–C(32) 2.433(6), Dy(1)–N(1) 2.460(5), Dy(1)–N(2) 2.480(5), Dy(1)–N(3) 2.473(5), Dy(1)–N(4) 2.489(4), P(1)–C(1)–P(2) 166.5(4), P(3)–C(32)–P(4) 167.4(4), N(1)–Dy(1)–N(2) 128.39(17), N(3)–Dy(1)–N(4) 128.00(17), C(1)–Dy(1)–C(32) 176.6(2). The structures of 1Y and 2Y (see ESI†) are essentially identical. | ||
Complex 2Dy crystallises as a solvent separated ion pair and there are no significant contacts between the [Dy(BIPMTMS)2]− anion and the [K(18C6)(THF)2]+ cation components. Complex 2Dy has the on-axis C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Dy
Dy![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C arrangement of highly charged donor atoms required to test our proposal for high-temperature SMMs. The dysprosium ion is six-coordinate and the C
C arrangement of highly charged donor atoms required to test our proposal for high-temperature SMMs. The dysprosium ion is six-coordinate and the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Dy
Dy![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C angle is almost linear at 176.6(2)°. The methanediide centres adopt planar T-shaped geometries [av. Σ∠ = 357.1(6)°] and, importantly, the two C(PN)2Dy planes are disposed essentially orthogonal to each other [89.47(12)°]. The Dy
C angle is almost linear at 176.6(2)°. The methanediide centres adopt planar T-shaped geometries [av. Σ∠ = 357.1(6)°] and, importantly, the two C(PN)2Dy planes are disposed essentially orthogonal to each other [89.47(12)°]. The Dy![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond distances of 2.434(6) and 2.433(6) Å are statistically identical, and longer than the Dy
C bond distances of 2.434(6) and 2.433(6) Å are statistically identical, and longer than the Dy![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C distance of 2.364(2) Å in four coordinate [Dy(BIPMTMS)(CH2Ph) (THF)] and in six-coordinate 1Dy, reflecting the trans-disposition of the two methanediide centres and the electron-rich, anionic formulation of the dysprosium fragment in 2Dy. The Dy–N bond lengths in 2Dy average 2.461(9) Å, which is consistent with the analogous methanediide-derived Dy–N bond lengths in 1Dy. All other bond distances and angles in the (BIPMTMS)2− are unexceptional for this ligand in its dianionic state.22–24
C distance of 2.364(2) Å in four coordinate [Dy(BIPMTMS)(CH2Ph) (THF)] and in six-coordinate 1Dy, reflecting the trans-disposition of the two methanediide centres and the electron-rich, anionic formulation of the dysprosium fragment in 2Dy. The Dy–N bond lengths in 2Dy average 2.461(9) Å, which is consistent with the analogous methanediide-derived Dy–N bond lengths in 1Dy. All other bond distances and angles in the (BIPMTMS)2− are unexceptional for this ligand in its dianionic state.22–24
Static and dynamic magnetism
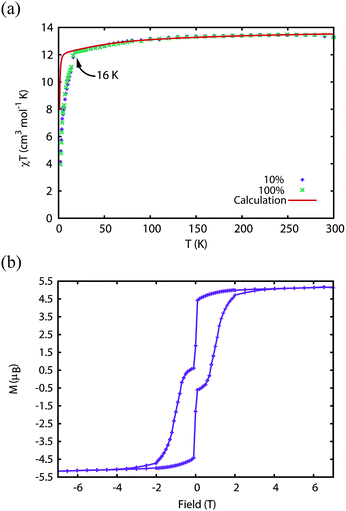
The magnetic properties of 1Dy and 2Dy were measured as neat polycrystalline powders dispersed in eicosane and flame sealed in a quartz NMR tube. The room temperature value of χmT of 2Dy is 13.5 cm3 mol−1 K, around 10% lower than expected for a free DyIII ion (14.2 cm3 mol−1 K, Fig. 2). Measuring in-field in a cooling cycle [FC(c)], χmT is weakly temperature dependent to 100 K below which the moment starts to fall gradually reaching a value of 12.6 cm3 mol−1 K by 50 K, suggesting that at this temperature only the |±15/2〉 doublet is populated. At 16 K χmT decreases precipitously, where equilibrium population cannot be achieved due to the barrier to magnetisation reversal (see below). Magnetisation (M) versus field (H) curves at 1.8 K saturate at a value of ∼5.1 μB mol−1, confirming a well isolated |±15/2〉 ground state.AC magnetic measurements performed on 2Dy in zero DC field show temperature and frequency dependent behaviour, characteristic of slow magnetic relaxation over two thermal barriers, Fig. 3a. Fitting these data to the generalised Debye equation yields temperature dependent relaxation times, Fig. 3b and c. The strong linear dependence of ln(τ) at high temperatures is indicative of a dominant Orbach relaxation mechanism, whilst at lower temperatures its curvature suggests competing relaxation processes are active. As a temperature independent regime is not reached, this cannot be attributed to QTM and we therefore interpret this as a second order Raman process.§
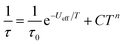 | (1) |
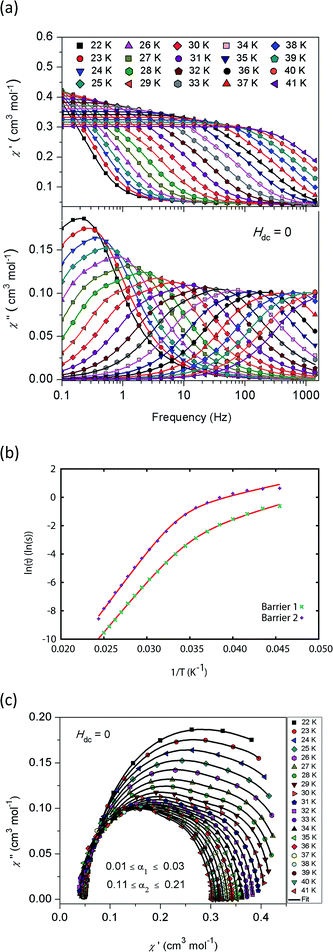 | ||
| Fig. 3 (a) In-phase χ′ (top) and out-of-phase χ′′ (bottom) AC magnetic susceptibility as a function of frequency in zero DC field for 2Dy. Solid lines are fits to the generalised Debye model. (b) Natural logarithm of the relaxation times for the two barriers observed in 2Dy as a function of reciprocal temperature. Red lines are fits to eqn (1), see text for parameters. (c) Cole plot for 2Dy recorded at different temperatures under zero DC field with an AC field of 1.55 Oe, at frequencies between 0.1 and 1400 Hz. Solid black lines are fits to the generalised Debye equation. | ||
Fitting the two data sets with eqn (1) yields Ueff(1) = 721(1) K (501 cm−1), τ0(1) = 1.11(3) × 10−12 s, C(1) = 3.01(7) × 10−11 s−1 K−8, n(1) = 8, α(1) = 0.01–0.03, Ueff(2) = 813(1) K (565 cm−1), τ0(2) = 5.65(20) × 10−13 s, C(2) = 3.55(10) × 10−9 s−1 K−6, n(2) = 6 and α(2) = 0.11–0.21. The values of τ0 are of the correct order of magnitude expected for an Orbach relaxation process over a large barrier (τ0 ∼ (10−5 to 10−3)/Ueff3)27 and the values of C and n are as expected for the second-order Raman process for Kramers ions.27¶ We have explored the possibilities that the measured relaxation data are due to the Raman process alone, or to a combination of two Orbach processes, but find that these cannot explain the data as the parameters required for such fits are physically unreasonable, see ESI and Fig. S1 and S2.† The same characteristic out-of-phase AC signals can be found in dilute samples (10% 2Dy@2Y and 3% 2Dy@2Y), Fig. S3,† therefore confirming the molecular origin of this phenomenon.
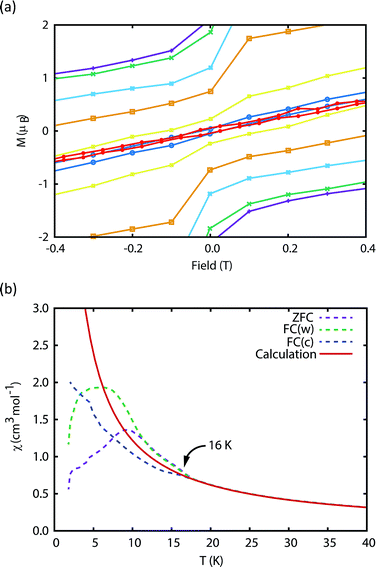
The blocking temperature (TB) is conventionally defined as the maximum in the ZFC susceptibility;7 Gatteschi et al. have pointed out that for SMMs a second temperature, TIRREV, is also important which is the point where the FC and ZFC susceptibilities diverge, as this is the temperature below which the magnetic observables are out-of-equilibrium and show history dependent behaviour.7 For most SMMs TB and TIRREV are very similar, and observed differences have been assigned to a distribution of relaxation times.7 Another proposed definition of TB is the temperature where the relaxation time is 100 s.7,18,28
We have used DC and AC magnetic measurements to establish both TB and TIRREV for 2Dy. Magnetic hysteresis is observed in M(H) loops for 10% 2Dy@2Y to at least 10 K for a sweep rate of 3.5 mT s−1 (Fig. 4a and S4†); the coercivity at 13 and 16 K is very small. Extrapolation of the fitted AC relaxation times for 2Dy gives a relaxation time of 100 s at 12 K. FC(c)/zero-FC (ZFC) measurements for 2Dy diverge at temperatures up to 16 K (Fig. 4b), with the ZFC maximum at ca. 10 K, depending on the heating/cooling rates. Therefore while TB for 2Dy is 10–12 K by conventional definitions, the magnetic observables are history dependent below 16 K. To investigate this further we have also measured FC(w); these data also diverge from FC(c) at temperatures up to 16 K depending on rates. Unusually, for any rate that we measured, the FC(w) data go above the FC(c) before reaching equilibrium. Such behaviour would normally be associated with a metastable state arising from the phenomenon of magnetostriction,29 but its origin here is unclear and will require extensive further studies.
Furthermore, the discrepancy of up to 6 K between TB and TIRREV, usually explained as owing to a range of relaxation times, is very large and does not appear to have precedent in SMMs. Accounting for these two observations, we can only suggest that multiple relaxation processes are competitive at low temperatures, including Raman and QTM mechanisms, which gives rise to this strange behaviour.
There remains a significant, sweep-rate dependent, loss of magnetisation at zero-field in M(H) even at the lowest temperature measured (1.8 K), Fig. S4 and S5.† This drop at zero-field is less pronounced in the dilute samples, indicating that there is an intermolecular contribution to the relaxation, but that the blocking is due to individual molecules. Measurements of the decay of magnetisation as a function of time, Fig. S6,† on the dilute samples shows there is a significant magnetisation that is retained for a very long time; in the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 sample M = 0.15 μB after 10 hours. This is only 3% of the saturation magnetisation, but clearly some component of the system has a very long lifetime.
20 sample M = 0.15 μB after 10 hours. This is only 3% of the saturation magnetisation, but clearly some component of the system has a very long lifetime.
The χmT of 1Dy is 13.7 cm3 mol−1 K at room temperature and is weakly temperature dependent until below 70 K where it starts to gradually fall, followed by a larger drop at very low temperatures (Fig. S7†). The M(H) at 1.8 K saturates at a value of ∼5.2 μB mol−1 (Fig. S8†) which is indicative of a well isolated |±15/2〉 ground state. AC magnetic measurements performed in zero DC field show temperature and frequency dependent behaviour above 10 K (Fig. S9†). Fitting these data to the generalised Debye equation (Fig. S10†), yields temperature dependent relaxation times which results in a linear ln(τ) vs. 1/T curve at high temperatures, whilst at lower temperatures we observe a transition to a temperature independent regime (Fig. S11†). This is indicative of a dominant Orbach relaxation mechanism at high temperature and QTM at lower temperatures. Application of an optimal 1 kG DC field can quench the temperature independent process (Fig. S9 and S12†) however the ln(τ) vs. 1/T plot still curves at lower temperatures (Fig. S11†). This curvature in the intermediate temperature regime also requires a second order Raman mechanism and we model the temperature dependent relaxation data for both zero field and 1 kG simultaneously with eqn (2), where the 1/τQTM term is omitted for the 1 kG relaxation data.
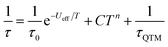 | (2) |
The best-fit parameters are Ueff = 255(1) K (177 cm−1), τ0 = 3.55(9) × 10−12 s, C = 1.46(3) × 10−5 s−1 K−7, n = 7, τQTM = 9.26(10) × 10−3 s and α = 0.06–0.22. The values of τ0 are of the correct order of magnitude expected for an Orbach relaxation process over a large barrier and the values of C and n are as expected for the second order Raman process for Kramers ions.27
Theoretical characterisation
Based on the X-ray crystal structures of 1Dy and 2Dy, we performed ab initio calculations of the CASSCF/RASSI/SINGLE_ANISO variety with MOLCAS 7.8.30–33 The calculated χmT vs. T plots for both compounds are almost identical to that obtained experimentally, save for the sub-16 K data for 2Dy (Fig. 2a and S7†), and require scaling factors of 0.981 and 0.968 for 1Dy and 2Dy, respectively, to reproduce the data above 200 K. Such scaling factors are modest compared to other works.34 As predicted, the linear coordination mode of the two methanediide centres in 2Dy with a large build-up of negative charge on the axis ensures a large energy gap between the |±15/2〉 ground state and all other doublets (see Tables 1 and S1†). In further agreement with our expectations, the three lowest energy Kramers doublets of the ground 6H15/2 multiplet of 2Dy are essentially the pure |±15/2〉, |±13/2〉 and |±11/2〉 states quantised along the main C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Dy
Dy![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C axis. The result of this is that thermal relaxation via the second and third states is quenched. The fourth and fifth doublets are strongly mixed, and have main magnetic axes perpendicular to that of the ground state, allowing efficient relaxation (Fig. 5 and Tables S2 and S3†). They are calculated to lie at energies of 742 K and 810 K, respectively, which is in excellent agreement with the experimentally determined energy barriers of Ueff(1) = 721 K and Ueff(2) = 813 K.
C axis. The result of this is that thermal relaxation via the second and third states is quenched. The fourth and fifth doublets are strongly mixed, and have main magnetic axes perpendicular to that of the ground state, allowing efficient relaxation (Fig. 5 and Tables S2 and S3†). They are calculated to lie at energies of 742 K and 810 K, respectively, which is in excellent agreement with the experimentally determined energy barriers of Ueff(1) = 721 K and Ueff(2) = 813 K.
| E (cm−1) | E (K) | g x | g y | g z | Angle (°) | Wavefunction |
|---|---|---|---|---|---|---|
| 0 | 0 | 0.00 | 0.00 | 19.88 | — | 100% |±15/2〉 |
| 168 | 242 | 0.00 | 0.00 | 17.19 | 3.89 | 99% |±13/2〉 + 1% |±11/2〉 |
| 399 | 574 | 0.09 | 0.14 | 14.27 | 1.56 | 97% |±11/2〉 + 1% |±13/2〉 + 1% |±9/2〉 + 1% |±3/2〉 |
| 516 | 742 | 2.09 | 5.61 | 14.11 | 85.37 | 48% |±1/2〉 + 18% |∓1/2〉 + 13% |±9/2〉 + 8% |±3/2〉 + 3% |∓3/2〉 + 3% |∓7/2〉 + 3% |∓9/2〉 + 2% |±7/2〉 + 2% |±5/2〉 + 1% |∓5/2〉 |
| 563 | 810 | 1.32 | 4.36 | 12.34 | 83.41 | 31% |±3/2〉 + 24% |∓3/2〉 + 23% |±5/2〉 + 5% |±1/2〉 + 5% |∓1/2〉 + 4% |±9/2〉 + 3% |∓5/2〉 + 3% |∓7/2〉 + 1% |±7/2〉 + 1% |∓9/2〉 |
| 593 | 853 | 0.67 | 2.33 | 9.34 | 11.48 | 75% |±9/2〉 + 10% |±1/2〉 + 5% |±3/2〉 + 3% |∓7/2〉 + 2% |∓3/2〉 + 1% |±11/2〉 + 1% |±7/2〉 + 1% |±5/2〉 + 1% |∓5/2〉 + 1% |∓9/2〉 |
| 652 | 939 | 2.74 | 7.54 | 11.41 | 83.98 | 46% |±7/2〉 + 18% |∓5/2〉 + 12% |±5/2〉 + 8% |±3/2〉 + 6% |∓1/2〉 + 5% |∓7/2〉 + 2% |∓3/2〉 + 1% |±9/2〉 + 1% |±1/2〉 + 1% |∓9/2〉 |
| 683 | 982 | 0.85 | 1.74 | 16.32 | 72.52 | 34% |±5/2〉 + 25% |∓7/2〉 + 14% |∓3/2〉 + 11% |±7/2〉 + 6% |∓5/2〉 + 5% |±1/2〉 + 3% |±3/2〉 + 1% |±9/2〉 + 1% |∓1/2〉 |
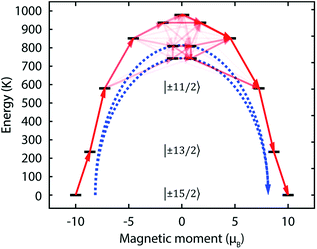 | ||
Fig. 5 Calculated magnetic relaxation barrier for 2Dy. The x-axis shows the magnetic moment of each state along the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Dy Dy![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C axis. Relaxation probabilities are calculated based on a magnetic perturbation and are normalised from each departing state.12 While the fourth state is strongly axial, its main magnetic axis is perpendicular to that of the ground state and when expressed along the C C axis. Relaxation probabilities are calculated based on a magnetic perturbation and are normalised from each departing state.12 While the fourth state is strongly axial, its main magnetic axis is perpendicular to that of the ground state and when expressed along the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Dy Dy![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C axis is composed mainly of 48% |±1/2〉 + 18% |∓1/2〉 + 13% |±9/2〉 where C axis is composed mainly of 48% |±1/2〉 + 18% |∓1/2〉 + 13% |±9/2〉 where 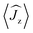 = ±0.65. Similarly, the fifth state has eigenfunctions mainly composed of 31% |±3/2〉 + 24% |∓3/2〉 + 23% |±5/2〉 where = ±0.65. Similarly, the fifth state has eigenfunctions mainly composed of 31% |±3/2〉 + 24% |∓3/2〉 + 23% |±5/2〉 where 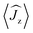 = ±0.63. = ±0.63. | ||
Whilst the RN−–P+(R)2–C2−–P+(R)2–N−–R resonance form of the (BIPMTMS)2− dianion is known to be the most appropriate way to formulate the formal charge distribution of this ligand,22 it should be noted that the phosphorus(V) centres withdraw electron charge from the nitrogen centres rendering them relatively soft donors more in keeping with the imino character that is drawn in Lewis-style depictions. Although the phosphorus(V) centres do polarise some of the methanediide charge, it is evident from extensive studies of early metal BIPMTMS chemistry that the majority of the dianion charge remains at carbon available for donation to a coordinated metal.35–42 Indeed, the experimental 13C NMR chemical shift of the methanediide centres in 2Y is consistent with charge accumulation at these carbon centres and by inference this should be the case for 2Dy also. Thus, and in accord with experimental observations, the symmetrical disposition of the four nitrogen donors, which reside away from the formal equatorial plane due to the bite angle of the BIPMTMS ligand, imposes an axially symmetric equatorial potential (approximate S4 symmetry) which reduces the strength of, but does not destroy, the axial potential of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Dy
Dy![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C motif in 2Dy. It is germane to note that although the dysprosium centre in 2Dy is of pseudo-octahedral geometry, an effectively linear charge build-up is obviously felt by the dysprosium centre, resulting in strong axial anisotropy, as evidenced by the magnetic behaviour of this system. If the pincer nitrogen donors could be replaced by more weakly coordinating groups, the Ueff value(s) would be even higher,12,13 providing obvious targets for subsequent studies.
C motif in 2Dy. It is germane to note that although the dysprosium centre in 2Dy is of pseudo-octahedral geometry, an effectively linear charge build-up is obviously felt by the dysprosium centre, resulting in strong axial anisotropy, as evidenced by the magnetic behaviour of this system. If the pincer nitrogen donors could be replaced by more weakly coordinating groups, the Ueff value(s) would be even higher,12,13 providing obvious targets for subsequent studies.
For 1Dy the ground doublet is largely |±15/2〉 with a small admixture of |±11/2〉, while the second doublet is more significantly mixed but still shows a dominant 81% |±13/2〉 contribution (see Table S4†). The compound has lower symmetry [C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Dy–C(H) angle = 158.3°] and has a weaker axial potential due to the mono- and di-anionic ligands vs. the bis(di-anionic) set of 2Dy. The result is that the third doublet has a main magnetic axis perpendicular to the ground state and shows significant transverse g-factors, thus providing an efficient thermal relaxation pathway, Fig. S13 and Tables S5 and S6.† The calculated Ueff value of 245 K agrees very well with the experimentally determined value of Ueff = 255 K.
Dy–C(H) angle = 158.3°] and has a weaker axial potential due to the mono- and di-anionic ligands vs. the bis(di-anionic) set of 2Dy. The result is that the third doublet has a main magnetic axis perpendicular to the ground state and shows significant transverse g-factors, thus providing an efficient thermal relaxation pathway, Fig. S13 and Tables S5 and S6.† The calculated Ueff value of 245 K agrees very well with the experimentally determined value of Ueff = 255 K.
Luminescence studies
To further test and corroborate the validity of our model, variable temperature optical emission spectroscopy has been performed for 2Dy; we report results recorded at 13 K. After excitation with UV irradiation, sensitised complexes of DyIII are known to exhibit luminescence in the optical region owing to radiative decay from the 4F9/2 multiplet to the 6HJ multiplets, with photon energies (wavelengths) of approximately 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 cm−1 (475 nm), 17
100 cm−1 (475 nm), 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1 (570 nm) and 15
500 cm−1 (570 nm) and 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 cm−1 (660 nm), for the J = 15/2, 13/2 and 11/2 multiplets, respectively.43 After excitation at 375 nm, 2Dy exhibits strong emission at 20
200 cm−1 (660 nm), for the J = 15/2, 13/2 and 11/2 multiplets, respectively.43 After excitation at 375 nm, 2Dy exhibits strong emission at 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–21
000–21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 (J = 15/2) and 16
000 cm−1 (J = 15/2) and 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700–17
700–17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 cm−1 (J = 13/2) but only weak signals are observed around 15
700 cm−1 (J = 13/2) but only weak signals are observed around 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 (J = 11/2), Fig. 6.
000 cm−1 (J = 11/2), Fig. 6.
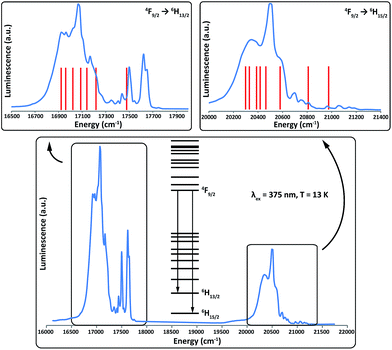 | ||
Fig. 6 Emission spectrum of 2Dy from 4F9/2 to 6HJ at 13 K (blue lines) and the calculated line positions (red lines). Calculated line positions are fixed at left-most shoulders (16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 920 cm−1 and 20 920 cm−1 and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 290 cm−1 for the 6H13/2 and 6H15/2 multiplets, respectively) and the relative energies are fixed from the ab initio calculations (Tables 1 and S5†). 290 cm−1 for the 6H13/2 and 6H15/2 multiplets, respectively) and the relative energies are fixed from the ab initio calculations (Tables 1 and S5†). | ||
As it is possible to observe emission from excited crystal field doublets of the 4F9/2 term, the only reliable transition is that of lowest energy into each multiplet, corresponding to a transition from the lowest lying 4F9/2 state into the highest energy states of the 6HJ multiplets. Therefore, using the low energy edge of the emission band to fix the location of the highest energy Kramers doublet in both the 6H15/2 and 6H13/2 multiplets, we compare the observed transitions to the calculated energy levels (Fig. 6). The most intense emissive feature in the 6H15/2 multiplet (∼20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 490 cm−1) corresponds well to the calculated position of the third excited state, which suggests that the strong mixing of this state results in an enhanced transition probability. Conversely, transitions into the first excited and ground states of the 6H15/2 multiplet are expected to be much weaker as these are virtually pure |±13/2〉 and |±15/2〉 states. These conclusions are supported by the ab initio calculated transition probabilities between the lowest lying 4F9/2 state and the eight Kramers doublets of the 6H15/2 multiplet (Table S7†).
490 cm−1) corresponds well to the calculated position of the third excited state, which suggests that the strong mixing of this state results in an enhanced transition probability. Conversely, transitions into the first excited and ground states of the 6H15/2 multiplet are expected to be much weaker as these are virtually pure |±13/2〉 and |±15/2〉 states. These conclusions are supported by the ab initio calculated transition probabilities between the lowest lying 4F9/2 state and the eight Kramers doublets of the 6H15/2 multiplet (Table S7†).
Both manifolds show more transitions than expected for a single emissive state and hence we assign these as a combination of transitions originating from excited states in the 4F9/2 multiplet and vibronic transitions. The presence of these additional transitions complicates the spectra sufficiently such that we cannot unequivocally determine experimental energy separations within the lowest lying multiplets. However, given the simplicity of the analysis with fixed theoretical line positions, the agreement with experiment for both multiplets is reasonably good, and only small shifts from the calculated line positions would be required to more closely match the experimental data.
Discussion
The ab initio calculations allow us to interpret the magnetic behaviour and propose that magnetisation relaxation is via the third doublet in 1Dy and fourth and fifth doublets in 2Dy. This behaviour matches our predictions that a strong axial LF should give rise to a large Ueff in lanthanide SMMs, accompanied by increased TB values. Compound 1Dy is an excellent SMM in its own right, and shows very similar behaviour to those seen previously.8,44 In particular, quantum tunnelling of magnetisation (QTM) within the ground doublet is clearly important. This is seen by the very small hysteresis loop, but more decisively by the temperature independent relaxation rate below 10 K. The unique electronic structure of 2Dy is responsible for generating a remarkably high Ueff value, and leads to non-equilibrium behaviour below 16 K, where the details of the relaxation dynamics remains to be fully understood.The AC data are unequivocal that relaxation between 20 and 40 K occurs by Orbach and Raman mechanisms alone; the Orbach process going via the fourth and fifth states at 721 and 813 K, respectively, which has been experimentally verified here for the first time. These are the largest Ueff barriers reported for any monometallic dysprosium(III) complex to date, where a Ueff of 481 K was previously the highest found in a Dy-salen-type Schiff base complex,44,45 but fall below 842 K for polymetallic Dy@[Y4K2O(OtBu)12],46 and 938 K for a [Tb(Pc)2] derivative.47 While Rajaraman and co-workers suggested that the slow magnetic relaxation of [Er(N(SiMe3)2)3]48 could proceed by the fifth state,49 the experimental Ueff = 122 K seems much more compatible with relaxation via the second state at a spectroscopically-determined 158 K.50
Below 16 K there are features we do not presently understand for 2Dy. Firstly, there is a large step at zero-field in M(H) plots, which is conventionally explained as the hallmark of QTM. Our calculations predict a virtually pure |±15/2〉 ground state and for such a state QTM should have a vanishingly small probability, therefore more work is required to investigate the relaxation mechanisms which cause this phenomenon. This step remains in the 3% diluted sample, and therefore it is possible that this is not dilute enough to completely remove transverse dipolar fields from nearby paramagnetic complexes. An alternative explanation is that nuclear hyperfine interactions may be responsible for this fast relaxation – a mechanism not accounted for in our purely electronic calculations. Such arguments have been made in Ho-SMMs,51 and have been studied recently by Pointillart et al., who show that isotopic enrichment with nuclear-spin-free 164Dy provides a significant opening of the hysteresis loop compared to the I = 5/2 161Dy isotope.52 Synthesis and study of the isotopically enriched species is planned.
Conclusions
In the continued absence of true two-coordinate bis(alkylidene) lanthanide complexes, we have prepared complex 2Dy which contains two methanediide centres that are disposed trans to one another. Although the pincer arms coordinate in off-axial positions, and in principle may carry some charge, it is clear that overall the dysprosium(III) bis(methanediide) complex 2Dy possess a strong axial LF due to significant negative charge accumulation along the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Dy
Dy![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C axis. We find that the weak equatorial donors do not destroy this strong axial LF; this is in contrast to the recent report of Zhang et al. who show that erbium(III) complexes (which require strong equatorial LFs) are strongly affected by weak axial donors, lowering the Ueff = 122 K of [Er{N(SiMe3)2}3] to Ueff = 34 K for [Er{N(H)Dipp}3(THF)2].48
C axis. We find that the weak equatorial donors do not destroy this strong axial LF; this is in contrast to the recent report of Zhang et al. who show that erbium(III) complexes (which require strong equatorial LFs) are strongly affected by weak axial donors, lowering the Ueff = 122 K of [Er{N(SiMe3)2}3] to Ueff = 34 K for [Er{N(H)Dipp}3(THF)2].48
AC magnetic measurements of 2Dy in zero DC field show temperature- and frequency-dependent SMM behaviour. Orbach relaxation dominates at high temperature, but a second-order Raman process becomes important as the temperature is lowered. We find thermal energy barriers (Ueff) of 721 and 813 K for two distinct processes, the largest Ueff values reported for any monometallic dysprosium(III) complex.45
Ab initio calculations, which independently model the magnetic data remarkably well and are in good agreement with experimental optical spectra, suggest that the bottom three Kramers doublets of the ground 6H15/2 multiplet of 2Dy are essentially pure, well-isolated |±15/2〉, |±13/2〉 and |±11/2〉 states quantised along the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Dy
Dy![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C axis. Thermal relaxation via the second and third states is quenched, and relaxation occurs via the fourth and fifth states because they are strongly mixed, with calculated Ueff values of 742 and 810 K that compare very well to experimental values.
C axis. Thermal relaxation via the second and third states is quenched, and relaxation occurs via the fourth and fifth states because they are strongly mixed, with calculated Ueff values of 742 and 810 K that compare very well to experimental values.
Magnetic measurements of 2Dy suggest that TB = 10–12 K, yet the FC/ZFC data show a clear divergence at TIRREV = 16 K. Compound 2Dy is therefore a peculiar molecule where the magnetism is history dependent at a temperature significantly above the conventional “blocking” temperature. Previous in-depth studies to assess the competing relaxation mechanisms53,54 have provided valuable insight into SMMs with conventional coordination numbers and geometries, and hence less extreme electronic structures. Compounds such as 2Dy move us into a new area where chemical control of molecular geometry generates new and intriguing electronic structures. Despite a mature understanding of the microscopic origins of magnetic relaxation in complexes of the 3d metals,7,55–57 it is clear that more experimental and theoretical work is required to come to understand magnetic relaxation in 4f complexes and determine how chemistry may play a role in its control.58
Given the properties of the molecules presented herein, realised by following a simple design strategy, we anticipate that such motifs could be employed with other contemporary Ln chemistry, using the idea of ‘building-block engineering’.59 For example, the recent report of a near-linear Dy–F–Dy linkage by Murugesu and co-workers60 suggests a tantalising molecular design with a linear C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Dy–F–Dy
Dy–F–Dy![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C unit, which should provide a platform to examine in great detail the exchange interactions between pure mJ states.61 Alternatively, two collinear formal C
C unit, which should provide a platform to examine in great detail the exchange interactions between pure mJ states.61 Alternatively, two collinear formal C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Dy
Dy![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C units could be coupled through a radical ligand bridge which also represents a promising direction for Ln SMMs.62
C units could be coupled through a radical ligand bridge which also represents a promising direction for Ln SMMs.62
Experimental section
General considerations
All manipulations were carried out using Schlenk techniques, or an MBraun UniLab glovebox, under an atmosphere of dry nitrogen. Solvents were dried by passage through activated alumina towers and degassed before use or were distilled from calcium hydride. All solvents were stored over potassium mirrors except for THF which was stored over activated 4 Å sieves. Deuterated solvent was distilled from potassium, degassed by three freeze–pump–thaw cycles and stored under nitrogen. BIPMTMSH2, [K(CH2Ph)], [Ln(CH2Ph)3(THF)3] and [Ln(BIPMTMS)(CH2Ph)(THF)] were prepared as described previously.261H, 13C, 29Si, and 31P NMR spectra were recorded on a Bruker 400 spectrometer operating at 400.2, 100.6, 79.5, and 162.0 MHz respectively; chemical shifts are quoted in ppm and are relative to TMS (1H, 13C, 29Si) and 85% H3PO4 (31P). FTIR spectra were recorded on a Bruker Tensor 27 spectrometer. Variable-temperature magnetic moment data for 2Dy, 10% 2Dy@2Y and 3% 2Dy@2Y were recorded in an applied dc field of 0.1 T on a Quantum Design MPMS XL5 superconducting quantum interference device (SQUID) magnetometer using doubly recrystallised powdered samples. Samples were carefully checked for purity and data reproducibility between several independently prepared batches for each compound examined. Care was taken to ensure complete thermalisation of the sample before each data point was measured and samples were immobilised in an eicosane matrix to prevent sample reorientation during measurements. Diamagnetic corrections were applied using tabulated Pascal constants and measurements were corrected for the effect of the blank sample holders (flame sealed Wilmad NMR tube and straw) and eicosane matrix. Solution magnetic moments were recorded at room temperature using the Evans method. CHN microanalyses were carried out by Tong Liu at the University of Nottingham. The compounds described herein can be classed as moderately air-/moisture-sensitive, but with adequate precautions they can be handled under a dry nitrogen atmosphere for extended periods with no sign of decomposition.Acknowledgements
We thank the Royal Society, EPSRC, ERC, COST, University of Nottingham and University of Manchester for generous funding and support. N. F. C. thanks The University of Manchester for a President's Doctoral Scholarship and Prof. Hans U. Güdel for helpful conversations. I. F. C thanks Mr Eric Whittaker for engineering a novel sample mount and general assistance with the luminescence measurements.This work is dedicated to and in memory of Prof. Malcolm Chisholm, with thanks for much friendly advice and encouragement.
Notes and references
- M. N. Leuenberger and D. Loss, Nature, 2001, 410, 789–793 CrossRef CAS PubMed.
- P. Santini, S. Carretta, F. Troiani and G. Amoretti, Phys. Rev. Lett., 2011, 107, 230502 CrossRef CAS PubMed.
- C. J. Wedge, G. A. Timco, E. T. Spielberg, R. E. George, F. Tuna, S. Rigby, E. J. L. McInnes, R. E. P. Winpenny, S. J. Blundell and A. Ardavan, Phys. Rev. Lett., 2012, 108, 107204 CrossRef CAS PubMed.
- S. Thiele, F. Balestro, R. Ballou, S. Klyatskaya, M. Ruben and W. Wernsdorfer, Science, 2014, 344, 1135–1138 CrossRef CAS PubMed.
- M. Ganzhorn, S. Klyatskaya, M. Ruben and W. Wernsdorfer, Nat. Nanotechnol., 2013, 8, 165–169 CrossRef CAS PubMed.
- M. Urdampilleta, S. Klyatskaya, J.-P. Cleuziou, M. Ruben and W. Wernsdorfer, Nat. Mater., 2011, 10, 502–506 CrossRef CAS PubMed.
- D. Gatteschi, R. Sessoli and J. Villain, Molecular Nanomagnets, Oxford University Press, 2006 Search PubMed.
- S.-D. Jiang, B.-W. Wang and K. A. Gschneidner Jr., Molecular Nanomagnets and Related Phenomena, in Structure and Bonding, ed. S. Gao, Springer, Berlin, Heidelberg, 2014, pp. 111–141 Search PubMed.
- J. J. Baldoví, J. M. Clemente-Juan, E. Coronado and A. Gaita-Ariño, Inorg. Chem., 2014, 53, 11323–11327 CrossRef PubMed.
- P. Zhang, L. Zhang and J. Tang, Dalton Trans., 2015, 44, 3923–3929 RSC.
- S. Gómez-Coca, D. Aravena, R. Morales and E. Ruiz, Coord. Chem. Rev., 2015, 289–290, 379–392 CrossRef.
- N. F. Chilton, C. A. P. Goodwin, D. P. Mills and R. E. P. Winpenny, Chem. Commun., 2015, 51, 101–103 RSC.
- N. F. Chilton, Inorg. Chem., 2015, 54, 2097–2099 CrossRef CAS PubMed.
- J. Sievers, Z. Phys. B: Condens. Matter Quanta, 1982, 45, 289–296 CrossRef CAS.
- J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078–2085 RSC.
- N. F. Chilton, D. Collison, E. J. L. McInnes, R. E. P. Winpenny and A. Soncini, Nat. Commun., 2013, 4, 2551 RSC.
- S. T. Liddle and J. van Slageren, Chem. Soc. Rev., 2015, 44, 6655–6669 RSC.
- K. R. Meihaus and J. R. Long, J. Am. Chem. Soc., 2013, 135, 17952–17957 CrossRef CAS PubMed.
- L. Ungur, J. J. le Roy, I. Korobkov, M. Murugesu and L. F. Chibotaru, Angew. Chem., Int. Ed., 2014, 53, 4413–4417 CrossRef CAS PubMed.
- H. Schumann and J. Müller, J. Organomet. Chem., 1979, 169, C1–C4 CrossRef CAS.
- O. T. Summerscales and J. C. Gordon, RSC Adv., 2013, 3, 6682–6692 RSC.
- S. T. Liddle, D. P. Mills and A. J. Wooles, Chem. Soc. Rev., 2011, 40, 2164–2176 RSC.
- T. Cantat, N. Mézailles, A. Auffrant and P. L. Floch, Dalton Trans., 2008, 1957–1972 RSC.
- N. D. Jones and R. G. Cavell, J. Organomet. Chem., 2005, 690, 5485–5496 CrossRef CAS.
- K. Aparna, R. P. Kamalesh Babu, R. McDonald and R. G. Cavell, Angew. Chem., Int. Ed., 2001, 40, 4400–4402 CrossRef CAS.
- A. J. Wooles, D. P. Mills, W. Lewis, A. J. Blake and S. T. Liddle, Dalton Trans., 2009, 500–510 Search PubMed.
- A. Abragam and B. Bleaney, Electron Paramagnetic Resonance of Transition Ions, Oxford University Press, 1970 Search PubMed.
- J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, J. Am. Chem. Soc., 2011, 133, 14236–14239 CrossRef CAS PubMed.
- J. D. Moore, G. K. Perkins, K. Morrison, L. Ghivelder, M. K. Chattopadhyay, S. B. Roy, P. Chaddah, K. A. G. Jr, V. K. Pecharsky and L. F. Cohen, J. Phys.: Condens. Matter, 2008, 20, 465212 CrossRef.
- G. Karlström, R. Lindh, P.-Å. Malmqvist, B. O. Roos, U. Ryde, V. Veryazov, P.-O. Widmark, M. Cossi, B. Schimmelpfennig, P. Neogrady and L. Seijo, Comput. Mater. Sci., 2003, 28, 222–239 CrossRef.
- V. Veryazov, P. Widmark, L. Serrano-Andrés, R. Lindh and B. O. Roos, Int. J. Quantum Chem., 2004, 100, 626–635 CrossRef CAS.
- F. Aquilante, L. de Vico, N. Ferré, G. Ghigo, P. Malmqvist, P. Neogrády, T. B. Pedersen, M. Pitoňák, M. Reiher, B. O. Roos, L. Serrano-Andrés, M. Urban, V. Veryazov and R. Lindh, J. Comput. Chem., 2010, 31, 224–247 CrossRef CAS PubMed.
- L. F. Chibotaru and L. Ungur, J. Chem. Phys., 2012, 137, 064112 CrossRef CAS PubMed.
- R. Marx, F. Moro, M. Dörfel, L. Ungur, M. Waters, S. D. Jiang, M. Orlita, J. Taylor, W. Frey, L. F. Chibotaru and J. van Slageren, Chem. Sci., 2014, 5, 3287–3293 RSC.
- S. T. Liddle, J. McMaster, J. C. Green and P. L. Arnold, Chem. Commun., 2008, 1747–1749 RSC.
- D. P. Mills, A. J. Wooles, J. McMaster, W. Lewis, A. J. Blake and S. T. Liddle, Organometallics, 2009, 28, 6771–6776 CrossRef CAS.
- A. J. Wooles, O. J. Cooper, J. McMaster, W. Lewis, A. J. Blake and S. T. Liddle, Organometallics, 2010, 29, 2315–2321 CrossRef CAS.
- O. J. Cooper, D. P. Mills, J. McMaster, F. Moro, E. S. Davies, W. Lewis, A. J. Blake and S. T. Liddle, Angew. Chem., Int. Ed., 2011, 50, 2383–2386 CrossRef CAS PubMed.
- D. P. Mills, O. J. Cooper, F. Tuna, E. J. L. McInnes, E. S. Davies, J. McMaster, F. Moro, W. Lewis, A. J. Blake and S. T. Liddle, J. Am. Chem. Soc., 2012, 134, 10047–10054 CrossRef CAS PubMed.
- O. J. Cooper, D. P. Mills, J. McMaster, F. Tuna, E. J. L. McInnes, W. Lewis, A. J. Blake and S. T. Liddle, Chem.–Eur. J., 2013, 19, 7071–7083 CrossRef CAS PubMed.
- M. Gregson, E. Lu, J. McMaster, W. Lewis, A. J. Blake and S. T. Liddle, Angew. Chem., Int. Ed., 2013, 52, 13016–13019 CrossRef CAS PubMed.
- L. Orzechowski, G. Jansen and S. Harder, J. Am. Chem. Soc., 2006, 128, 14676–14684 CrossRef CAS PubMed.
- J.-C. G. Bünzli and S. V. Eliseeva, in Lanthanide Luminescence, ed. P. Hänninen and H. Härmä, Springer Berlin Heidelberg, Berlin, Heidelberg, 2010, vol. 7, pp. 1–45 Search PubMed.
- D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110–5148 CrossRef CAS PubMed.
- W.-B. Sun, P.-F. Yan, S.-D. Jiang, B.-W. Wang, Y.-Q. Zhang, H.-F. Li, P. Chen, Z.-M. Wang and S. Gao, Chem. Sci., 2016 10.1039/C5SC02986D.
- R. J. Blagg, L. Ungur, F. Tuna, J. Speak, P. Comar, D. Collison, W. Wernsdorfer, E. J. L. McInnes, L. F. Chibotaru and R. E. P. Winpenny, Nat. Chem., 2013, 5, 673–678 CrossRef CAS PubMed.
- C. R. Ganivet, B. Ballesteros, G. de la Torre, J. M. Clemente-Juan, E. Coronado and T. Torres, Chem.–Eur. J., 2013, 19, 1457–1465 CrossRef CAS PubMed.
- P. Zhang, L. Zhang, C. Wang, S. Xue, S.-Y. Lin and J. Tang, J. Am. Chem. Soc., 2014, 136, 4484–4487 CrossRef CAS PubMed.
- S. K. Singh, T. Gupta, M. Shanmugam and G. Rajaraman, Chem. Commun., 2014, 42, 14045–14048 Search PubMed.
- S. Jank, H.-D. Amberger and N. M. Edelstein, Spectrochim. Acta, Part A, 1998, 54, 1645–1650 CrossRef.
- N. Ishikawa, M. Sugita and W. Wernsdorfer, J. Am. Chem. Soc., 2005, 127, 3650–3651 CrossRef CAS PubMed.
- F. Pointillart, K. Bernot, S. Golhen, B. le Guennic, T. Guizouarn, L. Ouahab and O. Cador, Angew. Chem., Int. Ed., 2015, 54, 1504–1507 CrossRef CAS PubMed.
- E. Lucaccini, L. Sorace, M. Perfetti, J.-P. Costes and R. Sessoli, Chem. Commun., 2014, 50, 1648–1651 RSC.
- K. S. Pedersen, L. Ungur, M. Sigrist, A. Sundt, M. Schau-Magnussen, V. Vieru, H. Mutka, S. Rols, H. Weihe, O. Waldmann, L. F. Chibotaru, J. Bendix and J. Dreiser, Chem. Sci., 2014, 5, 1650–1660 RSC.
- J. Villain, F. Hartman-Boutron, R. Sessoli and A. Rettori, Europhys. Lett., 1994, 27, 159–164 CrossRef CAS.
- J. Liu, E. del Barco and S. Hill, Molecular Magnets, in NanoScience and Technology, ed. J. Bartolomé, F. Luis and J. F. Fernández, Springer, Berlin, Heidelberg, 2014, pp. 77–110 Search PubMed.
- M. Atanasov, D. Aravena, E. Suturina, E. Bill, D. Maganas and F. Neese, Coord. Chem. Rev., 2015, 289–290, 177–214 CrossRef CAS.
- K. S. Pedersen, J. Dreiser, H. Weihe, R. Sibille, H. V. Johannesen, M. A. Sørensen, B. E. Nielsen, M. Sigrist, H. Mutka, S. Rols, J. Bendix and S. Piligkos, Inorg. Chem., 2015, 54, 7600–7606 CrossRef CAS PubMed.
- K. S. Pedersen, J. Bendix and R. Clérac, Chem. Commun., 2014, 50, 4396–4415 RSC.
- G. Brunet, F. Habib, I. Korobkov and M. Murugesu, Inorg. Chem., 2015, 54, 6195–6202 CrossRef CAS PubMed.
- N. Iwahara and L. F. Chibotaru, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 174438 CrossRef.
- S. Demir, I.-R. Jeon, J. R. Long and T. D. Harris, Coord. Chem. Rev., 2015, 289–290, 149–176 CrossRef CAS.
- B. O. Roos, R. Lindh, P.-Å. Malmqvist, V. Veryazov and P.-O. Widmark, J. Phys. Chem. A, 2005, 109, 6575–6579 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Magnetism, calculations, and crystallographic details. CCDC 1054027–1054031. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c5sc03111g |
| ‡ These authors contributed equally. |
| § The first-order process should not be active for a Dy(III) Kramers ion in the absence of a static magnetic field. A second-order Raman process is invoked because measurements were performed in zero DC field. |
| ¶ The Raman pre-factor ranges are wide but are close to predictions. The theoretical framework is based on simple crystal lattices with Debye-like phonon spectra; here we have an isolated 6-coordinate Dy(III) complex where the phonon spectrum is likely to be more complex. The fitted data were measured over a temperature range of 22–41 K where the approximations inherent to the phonon spectrum treatment mean that a simple T9 law cannot be expected to hold for the two-phonon process of a Kramers ion. For further details see pg 564–565 of ref. 27. For Raman processes typical values of the exponent n are: non-Kramers doublet, n = 7; Kramers doublet, n = 9; multiplet with small splitting, n = 5. These exponents are based on a number of approximations that are parameterised overall by two numbers and thus represent a guide and not absolutes. For further details see pg 65–66 of ref. 27. |
| This journal is © The Royal Society of Chemistry 2016 |