Detection and quantification of food colorant adulteration in saffron sample using chemometric analysis of FT-IR spectra†
Sadegh Karimi*a,
Javad Feizyb,
Fatemeh Mehrjoa and
Maryam Farrokhniac
aDepartment of Chemistry, College of Science, Persian Gulf University, Bushehr, Iran. E-mail: sakarimi@pgu.ac.ir; karimi.sadegh@gmail.com
bResearch Institute of Food Science and Technology, P. O. Box 91735-147, Mashhad, Iran
cThe Persian Gulf Marine Biotechnology Research Center, Bushehr University of Medical Sciences, Bushehr, Iran
First published on 19th February 2016
Abstract
The aim of present study is to investigate the combination of Fourier transform infrared (FT-IR) spectroscopy with pattern recognition to recognize the standard saffron from those which have been adulterated with various types of food colorants. Transmittance FT-IR spectra have been obtained for standard saffron and six mixed samples with food colorants including Tartrazine, Sunset yellow, Azorubine, Quinoline-yellow, Allura red and Sudan II. Genetic algorithm-linear discriminant analysis (GA-LDA) based on the concept of clustering of variables has been applied to transmittance FT-IR spectra for classification of standard saffron from fraudulent samples. Analysis of the selected clusters of variables indicates that three bands corresponding to 1800–1830, 2600–2900 and 3700–3850 cm−1 are responsible for differentiation of standard samples from fraudulent ones. Regression analysis has been introduced in order to obtain information related to the amount of food colorant. A combination of FT-IR and the concept of clustering of variables resulted in the best performances for calibration and an external test set with 100% sensitivity and specificity.
1. Introduction
Food quality control (authenticity) is one of the increasingly important and sometimes vital subjects for consumers, regulatory agencies and the food industry. One of the main characteristics of authentication is to find a way for finding economically motivated adulteration in food products which are usually more readily available and less expensive substitutes. However their identification is very difficult by routine analytical methodologies.1 Meanwhile fraud detection by routine analytical methodologies is usually time-consuming.Saffron has long been used as a coloring and flavoring agent in food. It is also known for a wide range of health benefits.2,3 It consists of dried stigmas of the cultivated species Crocus sativus L. On the other hand, saffron is one the most expensive species in food industry. In addition, this product is just produced in a few countries such as Iran and Spain. These two factors cause that the saffron can be good a candidate for adulteration conducted for economic gain and has been subjected to various types of adulteration over the centuries.4,5 A good review of the different types of saffron adulteration has been collected by Consonni and coworkers.6 As they mentioned, different spectroscopic (UV-vis) and several chromatographic methods have been used for the detection of saffron adulteration, however, each method has its limitation.
Food colorants like Azorubine, Quinoline, Sunset yellow, Sudan II, Allura red and Tartrazine are another area for authentication of saffron samples. Regardless of the experimental practice and design, the detection of food colorant frauds in saffron is a challenging task since changes in physical and color properties are not always easily identifiable. FT-IR spectroscopy is a simple analytical technique largely applied for its rapidity and reproducibility in food fraud detection.7 Another characteristic of FT-IR spectroscopy is the potential for high-throughput analysis with minimal sample pretreatment.8,9 Transmittance FT-IR spectroscopy based fingerprinting may identify the differences that often exist between authentic samples and normal products. As an example, Fourier-transform mid-infrared (FT-MIR) spectroscopy has been recently used to investigate how the typical FT-MIR spectrum of saffron changes as a result of storage under different conditions.10 However the FT-IR spectra of samples have complexity and limitations for analysis. For example a FT-IR spectrum, usually consists of hundreds or even thousands of measurements or channels, containing information for a classification. Almost all of these measurements contain redundant or irrelevant information. Therefore, powerful methods should be used to extract the fingerprint of the analytes or properties from the total signal.
Due to high similarities between transmittance FT-IR spectra of samples, it is impossible to discriminate them using visual inspection of the spectra. This problem encouraged us to apply powerful multivariate pattern recognition for analysis of such a data set.7 On the other hand transmittance FT-IR spectra have high throughput for each sample. This subject led to the problem of small sample sizes (the ratio of variable to sample is high) for the pattern recognition analysis method. In this condition, classification methods such as LDA have a tendency to show over-fitting results.11 This subject can be solved using the concept of clustering of variables for transmittance FT-IR spectra before LDA analysis. Finally, most of the wavenumbers are irrelevant to class distinction and should be discarded or removed. The current study presents an approach to discriminate adulterations in saffron by means of transmittance FT-IR and pattern recognition method. The efficiency of a new pattern recognition algorithm11 which has been created by clustering of variables is demonstrated in the present study. GA-LDA based on a self-organizing map (SOM) approach is based on a combination of data dimension reduction and variable selection algorithms. In addition, the obtained results have been compared using partial least square-discriminant analysis (PLS-DA) as a conventional pattern recognition method. Different studies related to chemical composition and geographic origin has been done in saffron study.12–14 To the best of our knowledge, there are no published reports providing information about discrimination and quantification of standard saffron samples from food colorant adulteration using FT-IR spectroscopy.
2. Materials and methods
2.1. Preparation of fraudulent saffron samples
Stigma (without styles attached) of pure Iranian saffron have been collected from flowers from Torbat Heydariyeh farms (harvest 2014) in the Khorasan Razavi province. All of the standard saffron samples and food colorants, were finely ground in a mortar. In order to create the adulterated (synthetic data set) saffron samples, artificial mixtures containing 0.5% up to 30.0% (w/w) of food colorant were prepared. Overall, 20 mixtures with different amounts of food colorant were used for each adulterant and seven classes were defined, including the standard and authentic saffron samples. The chemical structures and their FT-IR spectra of six food colorants can be found in Fig. S1 and S2 in the ESI.† As we can see from Fig. S2† the FT-IR spectral data of food colorants are very similar and fraudulent sample detection is not so straightforward. On the other hand, the spectra look similar but they do show some differences (the height and area of the peaks are different) when compared in detail, because different quantities of food colorant were added to each sample. In other words the differences exist in the intensity of spectra not in the shape.Saffron can be considered as a complex compound, so its FT-IR (transmittance or absorbance) spectrum shows extensive overlap of various compounds. The FT-IR spectra of a representative saffron sample from the investigated ones is shown in Fig. 2a. As reported in the literature,14–18 the broad peak which is centered around 3400 cm−1 is due to hydroxyl (–OH) groups. The spectral region related to 3000–2830 cm−1 presents two peaks (2929 and 2851 cm−1) which correspond to C–H stretching.19,20 Moreover the spectral region 1800–1500 cm−1 is the characteristic groups region. The carbonyl (–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) group (esters, ketones, aldehydes), the non-removed water and the aromatic ring absorb in this region.19,20 The region 1500–800 cm−1 is the ‘fingerprint region’. The peaks in this region are associated with the skeletal vibrations of the components and have been attributed to –CH2–, CH3–, –OH, C–C, C–O and C–O–C groups.17,18 Particularly, the 1200–800 cm−1 spectral region has been correlated with the presence of sugars and polysaccharides.21
O) group (esters, ketones, aldehydes), the non-removed water and the aromatic ring absorb in this region.19,20 The region 1500–800 cm−1 is the ‘fingerprint region’. The peaks in this region are associated with the skeletal vibrations of the components and have been attributed to –CH2–, CH3–, –OH, C–C, C–O and C–O–C groups.17,18 Particularly, the 1200–800 cm−1 spectral region has been correlated with the presence of sugars and polysaccharides.21
2.2. Transmittance spectral measurements
Fourier transform infrared (FT-IR) spectra have been recorded using a Bruker Vector22 spectrometer, operating in the region of 4000–400 cm−1 in the transmittance mode. A total of 16 scans with 4 cm−1 resolution were acquired for each spectrum. For FT-IR transmittance measurements, all samples were mixed with KBr (suitable ratio (w/w)) and homogenized. This mixture for each synthetic sample was then compressed under a pressure of ca. 200 MPa for 1 min to form a thin KBr disc. Also the spectrum of a clean KBr disc (without saffron) was used for background subtraction. It is worth mentioning that the time required for the preparation of a KBr pellet for each sample is approximately 5 minutes and totals 10 minutes with scanning the wavenumber. So, in comparison with other methods for example HPLC, ELISA etc. this one is simple, economical and isn’t a time consuming approach. The spectrometer was located in an air-conditioned room (25 °C). The spectra were stored using the OPUS software supplied from the same manufacturer.2.3. Multivariate data analysis
Principal components analysis (PCA) and GA-LDA based on SOM have been performed with auto scaling as a preprocessing algorithm. The basic idea behind the PCA is to visualize the data in the low dimensional space. For this purpose, PCA transforms the data from a high dimensional space onto lower dimensional ones, without losing much information. The principal components are constructed in such a way that the first explains most of the data variance; the second is orthogonal to the first and describes most of the variance not explained by the first PC, and so on. Finally, samples are distributed in this low space (two and three) based on their similarities.2.4. Linear discriminant analysis
Among traditional classifier algorithms, linear discriminant analysis is probably the most known method.22 The method can be considered as the probabilistic parametric classification technique which separates objects into classes by maximizing the between-class variance and minimizing the within-class variance. Furthermore LDA makes the assumption that the classes have identical covariance matrices and fits a multivariate normal density to each group with a pooled estimate of the covariance. Because a pooled covariance matrix is calculated, the number of objects must be significantly greater than the number of variables. In other words, when the class object sizes are small compared to the dimension of the measurement space (the number of variables), the inversion of covariance matrices became difficult.23 Also in the case of highly correlated variables, i.e. in presence of multicollinearity, discriminant analysis led to over-fitting results.2.5. Partial least square-discriminant analysis
Partial least square-discriminant analysis (PLS-DA) can be considered an extension of the LDA algorithm which uses the latent variables for predicting one (or several) binary responses(s) y from a set of variables in D.23 Similar to PLS regression, PLS-DA performs a dimension reduction; however the extracted scores are used to discriminate the calibration and prediction samples. Thus, PLS-DA needs the class-variable of the objects and extracted scores not only retain the maximal variances of the original variables but also are correlated with the class-variable.2.6. Kohonen self-organizing map (SOM)
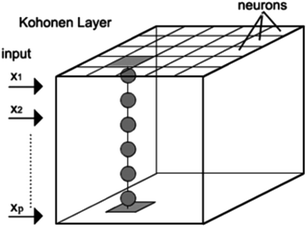
A Kohonen self-organizing map (SOM) is a two dimensional array of neurons, with each neuron containing a weight vector that has the same dimension as the experimental variable data set. A SOM is trained to reflect as much as possible the relationship between individual pieces of data. They are able to map multidimensional information into a surface (the 2D array). Similarly to principal component analysis, SOMs reduce multidimensional information to two dimensions with maintaining the topology of information. However, in contrast to PCA, SOMs have advantages such as the use of nonlinear relationships between variables in data matrices. Fig. 1 shows the structural design of a Kohonen network. Each column in the grid map represents a neuron and each box in such a column represents a weight (a number). In this case, the objects are the samples and the variables are the wavenumbers. Before starting the training, the weights take random values. It should be noted that the learning is a competitive and iterative process. This step includes the adjustment of the weight during the training phase. The procedure of a SOM can be summarized as follows. (1) A variable from a training set is introduced to the network. (2) The neuron with the weight vector most similar (determined using the Euclidean distance) to the input variable is called the wining neuron or the best matching unit (BMU). (3) The weights of winning neurons are modified by the network to become much more similar to the input variables. (4) With the same aim, neighborhood neurons are also corrected. However the amount of these corrections depends on their distance from the winning neuron. (5) All these steps repeat iteratively to reach a predefined number of cycles (epoch) and then the process stops. Finally, when all the wavenumbers are entered in the Kohonen network and the process is completed, similar input (in our case similar spectral information) vectors are clustered based on their similarities.112.7. Description of GA-LDA based on SOM
Almost all chemical data which has been obtained from a laboratory have more variables in comparison with samples. For analysis (multivariate calibration and classification) of such data sets, we should be careful about over-fitting the problem. Suppose we have a data matrix (D) with m rows (the samples) and n columns (the wavenumbers). The proposed algorithm can be illustrated using the subsequent steps:(1) In the first part, the number of wavenumbers has been divided into a q cluster using a Kohonen self-organizing map (SOM). Clustering of wavenumbers into different sub-matrices (Di) has been performed according to their similarities in information.
| D = [[D1][D2]…[Dq]] | (1) |
(2) Afterwards, in order to obtain the principal components and loadings of each sub-matrix, PCA can be applied to each sub-matrix (Di) separately.
Di = TiPTi, i = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) q q
| (2) |
The matrices Ti and Pi are the principal components and loadings of the each sub-matrix (Di) respectively. The superscript “T” indicates the matrix transpose notation.
(3) Substitution of eqn (2) into eqn (1) gives the reduced data set (Dr):
| Dr = [[T1PT1][T2PT2]…[TqPTq]] | (3) |
Obviously the column of this reduced data set, Dr, consists of all the obtained principal components, PCs, from different clusters. So that, the dimensions of Dr are (m × r), where m is the number of samples and r is the total number of principal components obtained from the previous step. Eqn (3) indicates that one is able to separate the PCs and loadings of different clusters. By this approach, three main purposes have been obtained. The first one is that most of the information from the original data matrix has been maintained. The second one, which is the most important for LDA analysis, is that the dimensions of the data have been reduced. Lastly, the information in the PCs of the original data set has been divided into different, useful and redundant, parts.
(4) Finally the LDA classifier has been applied, on the reduced data set (Dr) and the classification score for the training sample (xi) is defined as:
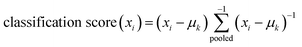 | (4) |
where 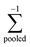 , is the inverse of the class covariance matrix and μk is the mean vector of class k.
, is the inverse of the class covariance matrix and μk is the mean vector of class k.
It should be noted again that, for ill-condition situations, the number of wavenumbers is higher than the number of objects and the estimations of the class covariance matrix becomes highly uncertain, which is not true in our case.
(5) The reduced data (Dru), for the prediction step,11 can be constructed as:
| tu = [t1ut2u…tqu] = DuV+ | (5) |
The superscript ‘+’ represents the matrix pseudo-inversion.
Two important subjects must be considered in the mentioned algorithm. The first one is the type of clustering algorithms and the second one is the cluster size (q). Recently we have shown that non-linear clustering such as Kohonen SOM has superiority with respect to other clustering algorithms for regression modeling.24 The cluster size (q) should be optimized by trial and error such that all classification models have been performed on any network size and the obtained results have been compared for their prediction abilities. The performance evaluation of each cluster size from LDA classification models has been used based on Not-Error Rate (NER) values, evaluated both on cross-validation groups and external test samples. The validation of the presented classification models is based on leave many out (LMO) cross-validation (1/5 being excluded during each run).
As noted previously, the PCs of different clusters and corresponding loadings contain the useful and redundant information for classification. Our effort is to get rid of second ones which reduce the calibration and prediction efficiency of our models. On the other hand the useful PCs which can improve the classification model should be extracted. This can be done by applying a PC selection algorithm such as a genetic algorithm (GA) on the reduced data set (Dr). For any network size of SOM, the classification models have been constructed based on selected PCs and statistical parameters have been used to compare the network sizes. The variable selection algorithm (GA) used in this paper is described by Leardi et al.,25 in PLS regression, except that in the proposed algorithm, GAs are coupled directly with LDA to improve the power of the classification algorithm. The selection of variables is performed by repeating the GA, t times and then including the variables on the basis of the frequencies of selection.
2.8. Clustering of variable-PLS regression
Recently we have introduced a new strategy for variable selection in PLS regression using the concept of clustering of variables.26 This algorithm which we called clustering of variables-partial least square, CLoVA-PLS, consists of two steps. Like the first step of the GA-LDA based SOM (eqn (1)), in this algorithm the whole spectral region has been divided into some clusters based on their similarities using a Kohonen self-organizing map. As we mentioned in Section 2.7 the number of clusters can be varied from 1 to the number of variables. For example if one set of the number of the cluster size (q) is 1, all the variables contribute in model building and can be considered as the conventional PLS. In practice, the number of the cluster size can be optimized by gradually increasing the cluster size (q) and following the statistical parameter can find a model with the satisfied result. In other word, for each cluster size, in order to find the most useful cluster of variables, all of the produced sub-matrices (clusters) have to be investigated using PLS regression separately. The statistical parameters, usually RMSCV and RMSEP, of the constructed model from each cluster, are used as judgment for selecting the informative one(s). It is worth mentioning that calibration samples are responsible for training and selecting the useful variables, while test samples are never used during the optimization stage and are subsequently predicted by means of the models optimized in the training samples. For more details about this algorithm, the interested readers can refer to our previous publication.26Data analysis has been performed in a MATLAB environment (MathWorks, Inc., Natick, MA, USA, version 7.2). GA-LDA is based on the GA-PLS of Leardi which is modified for classification. The LDA classification and Kohonen self-organizing map toolboxes provided by Ballabio were downloaded for free from the website of Milano Chemometrics and QSAR research group (http://michem.disat.unimib.it/chm/download/kohoneninfo.htm). PLS calibrations were based on the PLS Toolbox version 4 from Eigenvector Research.
3. Result and discussion
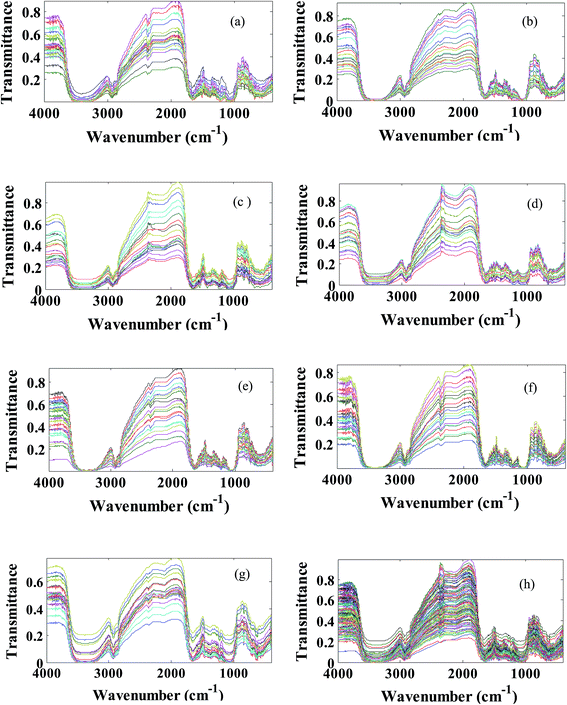
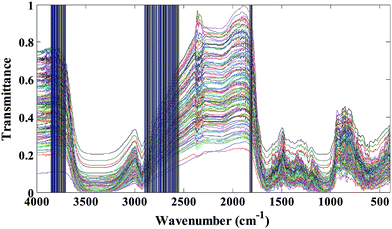
The transmittance FT-IR spectra of all studied saffron samples (standard and fraudulent) have been collected in data matrix D of the dimension of (ns × nw), where ns and nw are the number of samples and wavenumbers respectively. Thus, each row of D (di) is the transmittance FT-IR spectrum of a specified sample. Since we have obtained 20 spectra for each kind of saffron adulteration, size ns is considered 140. The applicability of transmittance FT-IR spectroscopy in combination with multivariate pattern recognition for discrimination between standard and fraudulent saffron samples has been investigated. The data matrix (D) has been divided into the calibration and prediction sets using the DUPLEX algorithm.27 In summary, the DUPLEX algorithm starts as follows: first the two points which are furthest away from each other are selected for the calibration set; from the remaining points, the two objects which are furthest away from each other are included in the prediction set; then the remaining point which is furthest away from the two previously selected for the calibration set is included in the calibration set. The procedure is repeated for the test set which is furthest from the existing points in that set. In conclusion, points representing both training and test sets were distributed uniformly within the whole space which is constructed using the entire dataset. Based on the DUPLEX strategy, one can assure that the composition of the training set and the test set is representative, at the same time the imbalance of the two datasets is avoided.In our case 98 samples have been included in the training set and the remaining 42 samples have been selected as the test set. The transmittance FT-IR spectra of the standard saffron samples and fraudulent ones are represented in Fig. 2. As is evident from these figures they are very similar spectra to each other; so that visual inspection of the spectra is impossible. The major bands in the typical FT-IR spectra of saffron samples can be found in Table S1 in the ESI.† Considering that saffron is a complex mixture of different chemical compounds it is difficult to assign all of the bands directly to specific constituents. On the other hand, since our goal was to identify wavenumber region(s) with high effect on discrimination of standard saffron from fraudulent ones, we investigated all spectral region(s) in the infrared data using LDA based on the concept of clustering of variables.
3.1. PCA overview of transmittance FT-IR data
To get an overview of the saffron data set, PCA has been applied to extract the meaningful PCs. The results of application of PCA on the transmittance spectral data matrix of the whole sample set are given in Table S2 in the ESI section.† Different strategies exist for adequate PC selection in the literature.28 Therefore, in this table, the Eigen value and percentage of variances in the data matrix are explained by each PC and the cumulative percent of variances (CPV) are reported. The first five principal components could explain 98.45% of variance in the data set. In other words, 42 saffron (standard and fraudulent) samples can be visualized in four principal components instead of 1868 dimension wavenumbers. A plot of the first two principal component scores for auto scaled data, which corresponds to 94.92% of the original variance, is shown in Fig. 3. Due to high similarity between the transmittance FT-IR spectra of the saffron samples (standard and different fraudulent ones) there is no evidence of discrimination between the seven classes along with the first two principal components. Because, most of the wavenumbers are unrelated to a class of our samples, more extraction of PCs is not useful. Although PCA is the powerful and versatile method, it just uses transmittance data matrix and consequently gives an overview of the complex multivariate data.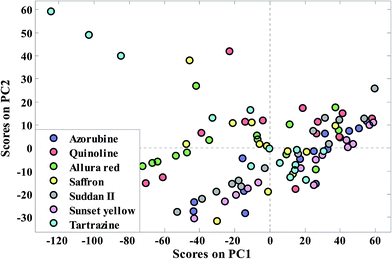 | ||
| Fig. 3 Distribution pattern of the saffron samples in the PCA factor spaces of their transmittance FTIR spectra for extended multiplicative scatter correction. | ||
3.2. GA-LDA based on SOM: combining data dimension reduction and classification
The transmittance FT-IR spectra of saffron samples data matrix is composed of 1868 variables (wavenumber). Not all parts of the presented wavenumber have useful information about the class information of samples. In the first step of GA-LDA based on a SOM, a Kohonen SOM is applied to cluster wavenumbers based on their similarity. Different clustering algorithms can be used in this step, but we have shown that a Kohonen SOM has superiority with respect to other clustering algorithms.24One of the important parameters of a Kohonen SOM which should be optimized is the number of Kohonen sizes (nodes). Each n-node Kohonen SOM model leads to (n × n) clusters of variables. Therefore, the number of clusters (q) produced by each Kohonen map model is equal to n2. The wavenumbers which are located in each cluster are considered as one cluster of variables that has similar information. In order to characterize the obtained results of the Kohonen map, each cluster is given nomenclature as Si,j, where i and j are the row and column of the cluster, respectively. Seven Kohonen SOM networks from the node sizes of 2 × 2 to 8 × 8 have been checked. Fig. S3 in the ESI† shows the distribution of wavenumbers in the (4 × 4) Kohonen SOM network. In spite of other interval based pattern recognition methods7 which divide the variables equally, in the clustering of variables strategy each cluster includes a different number of variables. This is clearly identified in Fig. S3.† As is shown in this figure clusters S2,1, S1,2, S1,3 and S4,3 contain a high number of wavenumbers and some of them, such as S3,2, S4,2 and S3,4, have a low number of wavenumbers. This is due to the fact that the variables have been clustered based on their similarities (similar information). In the next stage, the meaningful PCs and corresponding loadings of each cluster are extracted by applying the PCA on each cluster separately. The extracted PC of whole clusters builds a new data matrix (Dr, step 3 of GA-LDA based SOM theory) where the columns are significant principal components retained from produced clusters. In other words the columns of the original data matrix (wavenumbers) have been replaced with principal components which are extracted from different clusters. This procedure has been done for all Kohonen network sizes. This new data set (Dr) along with an LDA algorithm, have been used to construct the classification algorithms using linear relation by genetic algorithm PC selection. Table 1 lists the statistical classification parameters of the models obtained from a different number of clusters through the Kohonen SOM method. This table includes the number of total PCs which are extracted from the clusters (NEPC) and the number of selected PCs in the final LDA model (NSPC) using a genetic algorithm. The statistical parameters (NERcal, NERval and NERpre) obtained from different GA-LDA based SOM models for saffron discrimination has been shown in the last three columns of Table 1. Now the question is which of them is the best model? We had a complete discussion in our previous publication related to best model selection.11 In summary both calibration and prediction results should be considered for optimum model selections. Based on the obtained results shown in Table 1, it is evident that the number of extracted PCs is increased (from 30 to 86) when the number of clusters or Kohonen nodes is increased (from 4 to 64). However, the number of selected PCs in the LDA analysis remains relatively constant (3 to 4) and are independent of the number of clusters. The Not Error Rate (NER) of calibration, validation and prediction statistics shown in Table 1 reveal that the GA-LDA model obtained from Kohonen nodes q = 4, (16 cluster) is the optimum one for both calibration and prediction of classification. This 16-cluster GA-LDA model which uses three PCs out of 64 extracted PCs, has a very high degree of correctly assigned samples (NER) 1.000, 1.000 and 1.000 for calibration, cross-validation and prediction, respectively. The same conclusion can be achieved by looking at Table 2. According to the results presented in this table, GA-LDA of network size 4 has higher values of sensitivity (sensitivity describes the model’s ability to correctly recognize objects belonging to gth class) and specificity for both cross-validation and test set samples than other network sizes.
| Number of segments (Kohonen nodes) | NEPCa | NSPCb | NERcalc | NEvald | NERpree |
|---|---|---|---|---|---|
| a Number of the extracted PCs from all clusters.b Number of selected PC.c Not error rate based on leave many out cross validation for calibration set.d Not error rate based on leave many out cross validation for validation set.e Not error rate based on leave many out cross validation for prediction set. | |||||
| 4 (2 × 2) | 30 | 2 | 0.94 | 0.84 | 0.80 |
| 9 (3 × 3) | 41 | 3 | 1.00 | 0.86 | 0.85 |
| 16 (4 × 4) | 64 | 3 | 1.00 | 1.00 | 1.00 |
| 25 (5 × 5) | 70 | 3 | 1.00 | 0.93 | 0.92 |
| 36 (6 × 6) | 75 | 3 | 1.00 | 0.87 | 0.85 |
| 49 (7 × 7) | 80 | 4 | 0.98 | 0.84 | 0.80 |
| 64 (8 × 8) | 86 | 4 | 0.97 | 0.82 | 0.75 |
| PLS-DA model | — | 4 | 1.00 | 0.93 | 0.91 |
| (2 × 2) | (3 × 3) | (4 × 4) | (5 × 5) | (6 × 6) | (7 × 7) | (8 × 8) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CVc | Test | CV | Test | CV | Test | CV | Test | CV | Test | CV | Test | CV | Test | |
| a Class sensitivity (Sn) describes the model’s ability to correctly recognize samples belonging to the gth class, i.e. if all the samples belonging to g are correctly assigned, Sn is equal to 1.b Class specificity (Sp) describes the model’s ability to reject samples of all the other classes from class gth, i.e. if samples not belonging to g are never assigned to g, Sp is equal to 1.c Cross validation. | ||||||||||||||
| Specificity | 0.85 | 0.75 | 0.87 | 0.79 | 1.0 | 1.0 | 0.91 | 0.85 | 0.88 | 0.80 | 0.85 | 0.75 | 0.82 | 0.70 |
| Sensitivity | 0.86 | 0.85 | 0.90 | 0.88 | 1.0 | 1.0 | 0.95 | 0.93 | 0.93 | 0.88 | 0.86 | 0.85 | 0.80 | 0.75 |
The clusters and their selected PCs used in the GA-LDA based on SOM modeling of saffron data are presented in Table 3. Fig. S3† reveals that the first segment (S1,2) is located at the top-left, and S4,1 is located at the bottom left corner of the distribution plane of the wavenumbers. Interestingly, selected PCs cluster S4,1 of variables do not have the highest variable and they are chosen based on their correlations with class information. The selected PCs are representative of the wavenumbers that appeared in these clusters. These wavenumbers have spectral information that is more correlated with class information. To know which subset of wavenumbers are more useful for classification of the saffron samples from adulteration ones, the corresponding loadings of the selected PCs have been searched for variables (wavenumbers) of the highest loading values and those detected are shown in the last column of Table 3. It should be noted that GA-LDA based on SOM does not build a classification model based on the selected wavenumbers and uses all wavenumbers of the selected clusters for model building. However, it has the ability to identify the most important ones.
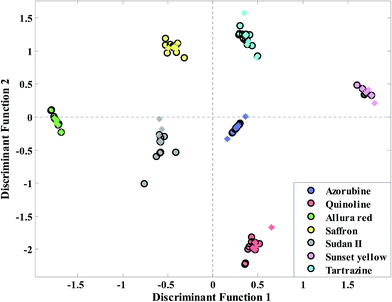
Selected regions of wavenumbers have been shown in Fig. 4. As we can see from this figure wavenumbers 1800–1830, 2600–2900 and 3700–3850 cm−1 corresponding to C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching of aldehyde and ketone, stretching H-acidic and –OH phenolic can be proposed for food colorant adulteration detection. Finally, the discriminant function plot (DF1) of Kohonen network size q = 4 is given in Fig. 5. It is evident that a clear separation between samples from the LDA plot of this cluster size is observed. That is, the selected wavenumbers in Fig. 4 have high efficiency related to detection of adulteration in saffron samples. Moreover the statistical parameters of PLS-DA have been reported in the last row of Table 2. As we can see the PLS-DA analysis (Fig. S4†) also led to promising results but three main purposes have been obtained using the proposed algorithm. The first one is that most information from the original data matrix has been maintained. The second one, which is the most important, is that the dimension of data has been reduced. Lastly, the information in the PCs of the original data set has been divided into different parts. Moreover with this strategy the small sample size problem of LDA classifier can be solved.
O stretching of aldehyde and ketone, stretching H-acidic and –OH phenolic can be proposed for food colorant adulteration detection. Finally, the discriminant function plot (DF1) of Kohonen network size q = 4 is given in Fig. 5. It is evident that a clear separation between samples from the LDA plot of this cluster size is observed. That is, the selected wavenumbers in Fig. 4 have high efficiency related to detection of adulteration in saffron samples. Moreover the statistical parameters of PLS-DA have been reported in the last row of Table 2. As we can see the PLS-DA analysis (Fig. S4†) also led to promising results but three main purposes have been obtained using the proposed algorithm. The first one is that most information from the original data matrix has been maintained. The second one, which is the most important, is that the dimension of data has been reduced. Lastly, the information in the PCs of the original data set has been divided into different parts. Moreover with this strategy the small sample size problem of LDA classifier can be solved.
 | ||
| Fig. 4 Selection the important variables using GA-LDA based dimension reduction for discrimination of saffron samples. | ||
3.3. Regression analysis based on the concept of clustering of variables
Finally, in order to have the information related to amount of food colorants in saffron samples, regression analysis has been introduced. Since the absorbance spectra has the linear relation with concentration (Beer’s law), the infrared absorbance spectral data has been used for regression proposal. Fig. S5† shows the absorbance spectral data of saffron samples which have been contaminated with different amounts of food colorants. Here, seven SOM network sizes (2–8) have been examined. The maximum latent variables were set to 10, and the optimum number of latent variables was obtained by five-fold cross validation. In accordance with the results of Table 4, cluster S4,4 from Kohonen network size q = 4 has lower error especially for the prediction step and can been considered as the most informative ones. This cluster possesses root mean square errors of 0.084, 0.112 and 0.087 for calibration, cross-validation and prediction, respectively. In other words, the variables of this cluster are more informative than the full spectral data for the regression model. Finally we found that the obtained prediction error of this cluster decreases (13.8%) in comparison with conventional PLS regression.4. Conclusion
In the present study, the application of the concept of clustering of variables combined with transmittance FT-IR spectra has been used in the quality control of standard saffron samples from food colorant adulteration. The effect of six typical and well known food colorants (Tartrazine, Sunset yellow, Azorubine, Quinoline-yellow, Allura red and Sudan II) has been investigated. Powerful pattern recognition as a useful alternative way, instead of more complex analytical tools for the detection of adulteration has been proposed. Moreover the analysis of such a “highly correlated” dataset has been introduced for quality control diagnosis and food chemistry using the proposed method. The obtained results demonstrate that it is possible to split the information in transmittance FT-IR spectra into informative and redundant information.References
- E. A. Petrakis, L. R. Cagliani, M. G. Polissiou and R. Consonni, Evaluation of saffron (Crocus sativus L.) adulteration with plant adulterants by 1H NMR metabolite fingerprinting, Food Chem., 2015, 173, 890–896 CrossRef CAS PubMed.
- J. P. Melnyk, S. Wang and M. F. Marcone, Chemical and biological properties of the world’s most expensive spice: Saffron, Food Res. Int., 2010, 43(8), 1981–1989 CrossRef CAS.
- P. Winterhalter and M. Straubinger, Saffron renewed interest in an ancient spice, Food Res. Int., 2000, 16(1), 39–59 CrossRef CAS.
- S. Hagh-Nazari and N. Keifi, in Saffron and various fraud manners in its production and trades, II International Symposium on Saffron Biology and Technology, 2006, vol. 739, pp. 411–416 Search PubMed.
- A. Torelli, M. Marieschi and R. Bruni, Authentication of saffron (Crocus sativus L.) in different processed, retail products by means of SCAR markers, Food Control, 2014, 36, 126–131 CrossRef CAS.
- A. Eleftherios, L. R. C. Petrakis, G. P. Moschos and C. Roberto, Evaluation of saffron (Crocus sativus L.) adulteration with plant adulterants by 1H NMR metabolite fingerprinting, Food Chem., 2015, 173, 890–896 CrossRef PubMed.
- K. Javidnia, M. Parish, S. Karimi and B. Hemmateenejad, Discrimination of edible oils and fats by combination of multivariate pattern recognition and FT-IR spectroscopy: A comparative study between different modeling methods, Spectrochim. Acta, Part A, 2013, 104, 175–181 CrossRef CAS PubMed.
- S. T. H. Sherazi, A. Kandhro, S. A. Mahesar, M. I. Bhanger, M. Y. Talpur and S. Arain, Application of transmission FT-IR spectroscopy for the trans fat determination in the industrially processed edible oils, Food Chem., 2009, 114, 323–327 CrossRef CAS.
- H. Yang, J. Irudayaraj and M. M. Paradkar, Discriminant analysis of edible oils and fats by FTIR, FT-NIR and FT-Raman spectroscopy, Food Chem., 2005, 93, 25–32 CrossRef CAS.
- S. A. Ordoudi, M. de los Mozos Pascual and M. Z. Tsimidou, On the quality control of traded saffron by means of transmission Fourier-transform mid-infrared (FT-MIR) spectroscopy and chemometrics, Food Chem., 2014, 150, 414–421 CrossRef CAS PubMed.
- S. Karimi and M. Farrokhnia, Leukemia and small round blue-cell tumor cancer detection using microarray gene expression data set: Combining data dimension reduction and variable selection technique, Chemom. Intell. Lab. Syst., 2014, 139, 6–14 CrossRef CAS.
- E. Anastasaki, C. Kanakis, C. Pappas, L. D. Maggi, C. P. Campo, M. Carmona, G. L. Alonso and M. G. Polissiou, Differentiation of saffron from four countries by mid-infrared spectroscopy and multivariate analysis, Eur. Food Res. Technol., 2010, 230, 571–577 CrossRef CAS.
- L. R. Cagliani, N. Culeddu, M. Chessa and R. Consonni, NMR investigations for a quality assessment of Italian PDO saffron (Crocus sativus L.), Food Control, 2015, 50, 342–348 CrossRef CAS.
- A. Zalacain, S. A. Ordoudi, E. M. Doaz-Plaza, M. Carmona, I. Blazquez, M. Z. Tsimidou and G. L. Alonso, Near-infrared spectroscopy in saffron quality control: determination of chemical composition and geographical origin, J. Agric. Food Chem., 2005, 53, 9337–9341 CrossRef CAS PubMed.
- J. Coates, Interpretation of infrared spectra, a practical approach, in Encyclopedia of analytical chemistry, John Wiley & Sons Ltd, 2000, pp. 10815–10837 Search PubMed.
- M. Kanou, K. Nakanishi, A. Hashimoto and T. Kameoka, Influences of monosaccharides and its glycosidic linkage on infrared spectral characteristics of disaccharides in aqueous solutions, Appl. Spectrosc., 2005, 59, 885–892 CrossRef CAS PubMed.
- N. A. Nikonenko, D. K. Buslov, N. I. Sushko and R. G. Zhbankov, Spectroscopic manifestation of stretching vibrations of glycosidic linkage in polysaccharides, J. Mol. Struct., 2005, 752, 20–24 CrossRef CAS.
- D.-W. Sun, Infrared spectroscopy for food quality analysis and control, Elsevier, New York, 1st edn, 2009, ch. 4 Search PubMed.
- K. Nakanishi, Solomon PA Infrared absorption spectroscopy, Holden-Day, San Francisco, 1977 Search PubMed.
- G. Socrates, Infrared characteristic group frequencies, Wiley, Chichester, 1997 Search PubMed.
- C. S. Pappas, P. A. Tarantilis, P. C. Harizanis and M. G. Polissiou, New method for pollen identification by FT-IR spectroscopy, Appl. Spectrosc., 2003, 57, 23–27 CrossRef CAS PubMed.
- G. McLachlan, Discriminant analysis and statistical pattern recognition, Wiley.com, 2004 Search PubMed.
- D. Ballabio, T. Skov, R. Leardi and R. Bro, Classification of GC-MS measurements of wines by combining data dimension reduction and variable selection techniques, J. Chemom., 2008, 22, 457–463 CrossRef CAS.
- B. Hemmateenejad, S. Karimi and N. Mobaraki, Clustering of variables in regression analysis: a comparative study between different algorithms, J. Chemom., 2013, 27, 306–317 CrossRef CAS.
- R. Leardi and A. Lupiz Gonzalez, Genetic algorithms applied to feature selection in PLS regression: how and when to use them, Chemom. Intell. Lab. Syst., 1998, 41, 195–207 CrossRef CAS.
- M. Farrokhnia and S. Karimi, Variable selection in multivariate calibration based on clustering of variable concept, Anal. Chim. Acta, 2016, 902, 70–81 CrossRef CAS PubMed.
- R. D. Snee, Validation of regression models: methods and examples, Technometrics, 1977, 19, 415–428 CrossRef.
- R. B. A. K. Smilde, Principal component analysis, Anal. Methods, 2014, 6, 2812–2831 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra25983e |
| This journal is © The Royal Society of Chemistry 2016 |