Tubular optical microcavities of indefinite medium for sensitive liquid refractometers†
Shiwei
Tang
a,
Yangfu
Fang
a,
Zhaowei
Liu
b,
Lei
Zhou
cd and
Yongfeng
Mei
*a
aDepartment of Materials Science, Fudan University, Shanghai 200433, China. E-mail: yfm@fudan.edu.cn
bDepartment of Electrical and Computer Engineering, University of California, San Diego, 9500 Gilman Drive, La Jolla, California 92093-0407, USA
cState Key Laboratory of Surface Physics and Key Laboratory of Micro and Nano Photonic Structures (Ministry of Education), Fudan University, Shanghai 200433, China
dCollaborative Innovation Center of Advanced Microstructures, Fudan University, Shanghai 200433, China
First published on 9th November 2015
Abstract
Optical microcavities enable circulated light to intensively interact with a detecting liquid, thus promising high sensitivity in fluidic refractometers. Based on Mie scattering theory, we propose a tubular metamaterial device for liquid sensing, which utilizes anisotropic metamaterials with hyperbolic dispersion called indefinite media (IM). Besides traditional whispering gallery modes (WGMs), such tubular cavities can support surface plasmon polariton (SPP) WGMs, enabling high sensitivity liquid detection. Three configurations of such metamaterial tubes for sensing are discussed: tube-in-liquid, hollow-tube-in-liquid and liquid-in-tube; these are analyzed using numerical formulas and compared with dielectric and metal materials. Compared with traditional dielectric media (DM), the IM tubular cavity exhibits a higher sensitivity (S), which is close to that of a metal tubular cavity. However, compared with metal media, such an IM cavity can achieve higher quality (Q) factors similar to the DM tubular cavity. Therefore, the IM tubular cavity can offer the highest figures of merit (QS) for the sensing performance among the three types of materials. Our results suggest a novel tubular optofluidic device based on metamaterials, which could be useful for liquid refractometers.
Introduction
Optofluidics takes advantage of optics and fluidics, thus offering unique devices and systems for interesting applications such as oil-immersion microscopes,1 liquid mirrors,2 liquid-crystal displays,3 biomolecular detectors4–6 and electrowetting lenses.7 Optical cavities serving as liquid refractometers can detect resonance mode shifts when the refractive indices of liquids (nL) change; examples include photonic crystal microcavities,8 ring-resonators,9 microdisk cavities10 and microtube cavities.11 Tubular microcavities can hold liquids and support optical resonance with whispering gallery modes (WGMs); these are recognized as one of the more interesting optofluidic devices.12–18 However, WGM-microcavities, including tubular cases composed of traditional dielectric material (DM), present slightly low sensitivities (S = dλr/dnL11) but high quality (Q) factors due to the excellent light confinement inside the cavity. Therefore, it would be desirable if new materials and/or designs can be developed that deliver both high sensitivity and high Q-factors in optical microcavities for liquid sensing.Metamaterials are being extensively studied with many exciting new phenomena, properties, and devices are being predicted or demonstrated such as a negative index of refraction,19,20 super lensing21 and invisibility cloaks.22–24 Metamaterials applied in subwavelength cavities25,26 can be anisotropic with a hyperbolic dispersion;27–29 these are known as indefinite media (IM). Various interesting effects have been demonstrated in such IM metamaterials, including subwavelength imaging,30–33 focusing33,34 and lifetime engineering.27,28,35 Tubular IM metamaterials composed of multilayered superlattices with numerous material layers of subwavelength thicknesses36 can be rolled up into a hollow cylinder and made into a tubular cavity by rolled-up nanotechnology.13,16,37
Herein, we implement the Mie scattering theory to explore optical resonances and liquid sensing capability of IM tubular cavities, which normally confine electromagnetic fields into an extremely small volume.27,38 In addition to traditional WGMs, such IM tubular cavities can also support surface plasmon polariton (SPP) WGMs, which enable high sensitivity for liquid detection. We employed analytical formulas to calculate the resonant wavelengths λr, Q factors, sensitivities (S) and figures of merit (QS) in tubular cavities formed by dielectric materials, metal and indefinite media under three types of sensing configurations: tube-in-liquid, hollow-tube-in-liquid and liquid-in-tube. Compared with metal tubular cavities, the proposed IM tubular cavities support SPP WGMs with higher Q factors. Compared with DM, the resonance mode shift of IM tubular cavities presents an opposite variation trend when we modulate the tube wall thickness (t) and therefore higher QS can be achieved when the wall thickness is optimized. Thus, unlike DM and metal tubes, the IM cavity can achieve the highest QS under the liquid-in-tube configuration.
Theory
Effective medium theory
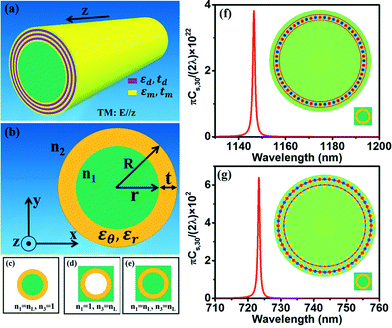
Fig. 1(a) shows a new type of tubular cavity consisting of a periodic bilayer superlattice, in which a single bilayer is composed of a layer of dielectric and a layer of metal, where εd and εm are the permittivities of the dielectric and metal and td and tm are their thicknesses. Herein, we take εd = 4, which is close to that of silicon oxides.39 To describe the dielectric constant of the metal, we adopted the Drude model εm(ω) = ε∞ − ω2pl/(ω2 − iωωcol) with plasmon frequency ωpl = 1.37 × 1016 rad s−1, damping parameter ωcol = 2.73 × 1013 rad s−1 and ε∞ = 3.7.40 When the individual bilayer thickness is much smaller than the wavelength, an effective permittivity can be approximated using an effective medium theory.41–43 The effective medium theory allows us to calculate the radial and tangential permittivity of the bilayered hollow cylinder structure in the following way: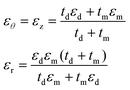 | (1) |
As a result, the bilayered hollow cylinder structure can be treated as an anisotropic metamaterial [Fig. 1(b)], whose permittivities can be approximated with the effective medium theory. The dielectric permittivity of the effective media is characterized by two values: εθ along the angular direction of the cylinder geometry and εr along the radial direction. To satisfy the IM conditions εr > 0 and εθ < 0, we take td/tm = 4 in the following discussion. Herein, we take the refractive indices of the core and background of the hollow cylinder structure as n1 and n2. The tubular cavity has outer radius R, inner radius r and wall thickness t. To systemically study the properties of tubular cavities composed of IM, DM and metal, we designed three configurations: liquid-in-tube, hollow-tube-in-liquid and tube-in-liquid [see Fig. 1(c)–(e)]. Rigorous formulas are presented to calculate four parameters of the tubular cavity: resonant wavelength, λr, Q factor, sensitivity, S = dλr/dnL and figures of merit QS.
Mie scattering method
We employ rigorous Mie scattering theory to quantitatively study the optical properties of the proposed tubular cavities formed by different media. The tubular cavity can be viewed as a multilayered structure in cylindrical geometry with (N − 1) layers and the layer indexed by i. The indices of the core and background are 1 and (N + 1), respectively. The ith layer has an outer radius ri and a dielectric constant εi, while the tubular cavity is along the z direction for simplicity.We consider transverse magnetic (TM) waves that are propagating in the r − θ plane with the magnetic field along the z direction. When the TM waves impact the cavity, the magnetic field in the ith layer can be expressed as:
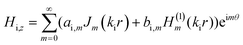 | (2) |
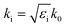 . The origin of the cylindrical coordinates (r,θ) is at the center of the tubular cavity and the Bessel function Jm and Hankel function H(1)m of the first type stand for the incident and scattering waves, respectively. The resonances occur in the tubular cavity when the following condition is met,
. The origin of the cylindrical coordinates (r,θ) is at the center of the tubular cavity and the Bessel function Jm and Hankel function H(1)m of the first type stand for the incident and scattering waves, respectively. The resonances occur in the tubular cavity when the following condition is met,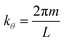 | (3) |
Using continuities of Hz and 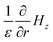 , we have
, we have
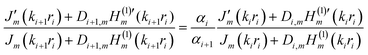 | (4) |
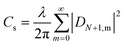 | (5) |
Results
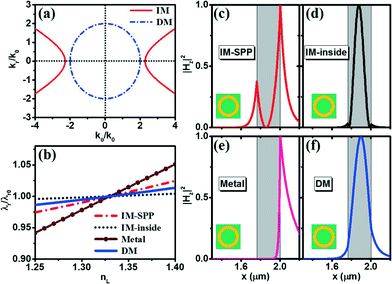
We studied the resonant modes of the angular momentum for a typical IM tubular microcavity with R = 2000 nm and t = 240 nm. Fig. 1(f) shows the partial scattering cross section Cs,m (m is the angular momentum mode number) for the microtube formed from IM and immersed in water. From Cs,30, we can obtain the resonant wavelength at 1146.5 nm for the TM resonance with m = 30. The magnetic field intensity |Hz|2 of the resonant mode is shown in the inset of Fig. 1(f), which is mainly confined in the tube wall with a few evanescent fields penetrating into the water. From the partial scattering cross section Cs,30 plotted in Fig. 1(g), we can find another type of TM WGM mode (m = 30) at 723.3 nm for such an IM-based microtube when the tube is immersed in water. We can identify that this WGM mode is based on surface plasmon from the magnetic field intensity |Hz|2, shown in the inset of Fig. 1(g). Such surface plasmon WGMs have more evanescent fields, which can enter into the water and are expected to enhance interaction. It is commonly known that a higher evanescent field is usually associated with a higher sensitivity.45–47 As a result, such an IM microtube supports two types of WGM modes; one can confine the electromagnetic field inside the tube wall (IM-inside mode) and the other one is the SPP WGM mode (IM-SPP mode).Furthermore, for the TM waves, the electric field vector can be divided into two components (along and transverse to the optical axis). So both εθ and εr play a role in the dielectric response. Using the effective medium theory, the dispersion relation for TM polarization is given by
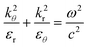 | (6) |
We noted that the SPP WGM can also be found in microcavities made from metal,48,49 and therefore it was interesting to compare the IM-based and metal-based microcavities. We showed the resonance and sensing parameters (such as resonant wavelength λr, Q factors, sensitivities S and figures of merit QS) of the microtube composed of metal (blue symbols in Fig. 3) and compared these with those of the IM microtube (red symbols in Fig. 3). Herein, we adopted the same geometrical parameters (i.e. R = 2000 nm, nL = 1.33 and t = 240 nm) for the metal-based microcavity to make the comparison fair. The resonant wavelength of the metal-based cavity is located 610 nm under the tube-in-liquid setup. Judging from the resonant behaviour plotted in Fig. 2(e), the magnetic field intensity |Hz|2 does not easily enter into the tube wall and almost all of the evanescent waves are distributed into the water outside the tube wall. As a result, for the hollow-tube-in-liquid and tube-in-liquid setups, the sensitivity S can be almost equal to Smax [see Fig. 3(b)]. However, for the liquid-in-tube setup, the sensitivity S tends to zero because no field can enter the core of the metal microtube. Moreover, from Fig. 3(c) we find that the Q factor of metal microtubes is very low, which can also be attributed to the fact that very few field components can penetrate the tube wall. On the other hand, we find from Fig. 2(c) that the magnetic field intensity of the IM-SPP tubular cavity exponentially decays from the edge of the tube wall to both sides, which provides both a high sensitivity S and a high Q factor. As a result, although the microtube made from metal has a higher sensitivity S, its figure of merit QS is much lower than that of the IM microtube [see Fig. 3(d)].
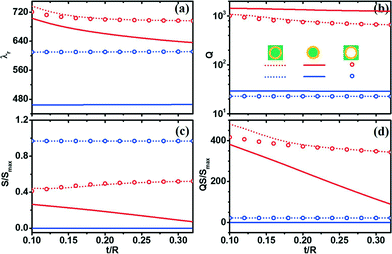 | ||
| Fig. 3 (a) Resonant wavelength λr, (b) Q-factors, (c) sensitivities S = dλr/dnL and (d) figures of merit QS for the m = 30 resonant modes of the microtubes made from IM-SPP with absorption (red symbols) and metal (blue symbols). All three setups in Fig. 1(c), (d) and (e) are shown with different symbols: tube-in-liquid (dotted line), liquid-in-tube (solid line) and hollow-tube-in-liquid (circles). | ||
In the following section, we compare the resonance and sensing properties of an IM microtube (supporting SPP WGM) and a DM microtube. Fig. 4 shows the resonant and sensing parameters (such as resonant wavelength λr, Q factors, sensitivities S and figures of merit QS) of microtubes made from IM (red symbols) and DM (blue symbols) with different wall thicknesses t. We also maintain the outer radius R = 2000 nm and nL = 1.33 for consistency. The permittivity of the DM is taken as εDM = εd = 4. For convenience, we did not consider the loss of metal and surface imperfections.11 Comparing Fig. 4 with Fig. 3, we can observe that although ideal microtubes and real microtubes with metal loss have quite different Q factors, they exhibit almost the same resonance peak positions and sensitivities. From Fig. 4(a), we find that the resonant wavelengths of IM microtubes are blue-shifted when we increase the wall thickness, which does not occur with traditional DM microtubes. Interestingly, both Fig. 3(a) and Fig. 4(a) show almost the same WGM resonance wavelengths for two setups: tube in liquid and hollow tube in liquid in the tubular cavity made from IM. Based on the magnetic field intensities of the WGM resonant modes shown in Fig. 2, we find that most of the fields are distributed in the outer wall of the IM tubular cavity and few fields are distributed in the inner wall of the IM tubular cavity. This means that there is a stronger interaction between the liquid outside and the outer wall of the tubular cavity than between the liquid with the inner wall, which thus mainly influences the resonance modes (e.g. wavelength). However, the “tube-in-liquid” and “hollow-tube-in-liquid” setups present close and even almost identical resonance wavelengths.
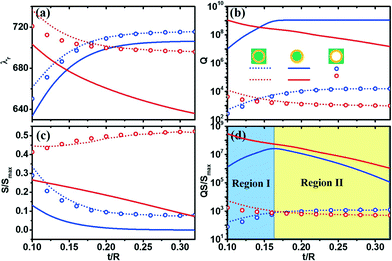 | ||
| Fig. 4 (a) Resonant wavelength λr, (b) Q-factors, (c) sensitivities S = dλr/dnL and (d) figures of merit QS for the resonant modes m = 30 of the microtubes made from IM-SPP without absorption (red symbols) and DM (blue symbols). All three setups in Fig. 1(c), (d) and (e) are shown with different symbols: tube-in-liquid (dotted line), liquid-in-tube (solid line) and hollow-tube-in-liquid (circles). | ||
As with the resonant wavelengths, the Q factors show an opposite variation tendency between IM and DM microtubes. When we reduce the wall thickness, the Q factor becomes higher for the IM-SPP microtubes but lower for DM tubes [see Fig. 4(b)]. From Fig. 4(b) we can also observe that the highest Q factors can be found in the liquid-in-tube setup for both DM and IM-SPP microtubes.
The sensitivity S is our main concern for the liquid refractometers. Compared with the DM microtubes, the IM-SPP microtubes present a much higher sensitivity S for the tube-in-liquid and hollow-tube-in-liquid setups, which is shown in Fig. 4(c). From Fig. 2(f) we can observe that the magnetic fields are confined to the DM tube wall and few evanescent waves can enter the water, which has contributed to the small sensitivity in DM microtubes. When we increase the thickness of the tube wall, the sensitivity S of the DM microtube becomes much lower but the S of the IM-SPP microtube does not change significantly. On the other hand, the Q factor of the DM microtube becomes higher when the thickness of the tube wall is increased. As a result, the DM microtube should have the highest figure of merit QS. From Fig. 4(d), we can observe that the DM microtubes with t = 0.16 R reach the highest QS value in the liquid-in-tube setup. However, the highest QS values for the DM microtubes are still lower than the values for the IM-SPP microtubes under the same setup. By taking t = 0.16 R as a division line, Fig. 4(d) can be divided into two regions. In Region II, the QS values for both DM and IM-SPP decreases when we increase the thickness of the tube wall. However, in Region I, when we reduce the thickness of the tube wall, the QS value of the DM microtube is decreased, whereas the QS value of the IM-SPP microtube increases, which presents a unique sensing capability for optofluidics.
Therefore, the metal tubular microcavity has a high sensitivity S but a low Q-factor, whereas the DM tubular microcavity has a high Q-factor but a low sensitivity S. The IM metamaterial microcavity with SPP WGMs exhibits both a high Q-factor and high sensitivity S, which can be used in hypersensitive liquid sensing and is a good candidate for optofluidic devices. The IM microtube with a high QS value shows great promise for potential application in hypersensitive liquid sensing.
Such indefinite media microtubular cavities can be obtained using self-assembly rolled-up nanotechnology.12,13,37,50 The metal–dielectric multilayered structure is a good candidate for indefinite media microtubular cavities. As a metal in such metal-dielectric multilayered IM structures, silver is an excellent candidate due to its low losses compared to other metals. Crystalline semiconductors such as silicon and GaAs are good choices for dielectrics as they have high refractive indices and can be fabricated as indefinite media with a very thin geometry.51 It is more convenient and simple to prepare silicon dioxide and titanium dioxide thin films by electron-beam evaporation or other methods than by high quality deposition52 but the quality and refractive index of the dielectrics become lower. However, silver-semiconductor bilayers could be an ideal structure for IM microcavities and silver-oxide bilayers could be chosen as well due to practical feasibility and simplicity. It has been proposed and demonstrated that by releasing a strained bilayer of metal and dielectric, rolled-up metamaterials can be developed to be used for plasmonic devices, including hyperlenses and metamaterial fiber optics.32,51,53 A recent study experimentally demonstrated that pronounced surface-enhanced Raman scattering can be observed in a rolled-up Ag/SiOx microcavity,52 wherein there exists a large plasmonic density of states along with an enhanced local electromagnetic field. Therefore, it can be expected that an IM microtubular cavity for liquid refractometers can be achieved from rolled-up metal-dielectric multilayers.
To fulfil a comprehensive study on the IM tubular microcavity, we characterize the resonance property inside the tube wall (as shown in Fig. 1d) with radial resonance modes (N), where the fields are almost completely confined inside the tube wall. We keep the angular momentum mode as m = 30 for the higher order along the radial direction. The partial scattering cross sections of N = 1 to N = 6 are calculated and their magnetic field distributions are shown in Fig. 5(a). Herein, we fix R = 2000 nm, t = 320 nm and nL = 1.33 for consistency. From the resonant wavelength λr plotted in Fig. 5(b), we find that the higher-order radial resonance mode oscillates at a longer wavelength, which is different from traditional DM microcavities. Such radial resonance is in relation to the anomalous dispersion (see Fig. 2(a)) due to the opposite signs of the principal components of the permittivity tensor.27 Because of the absorption of metal, the higher radial resonance mode has lower Q factors (see Fig. 5(c)), and the sensitivities have the same variation tendency because the fields are confined to the tube wall. As a result, the QS value also decreases as the radial resonance mode increases (Fig. 5(e)). Based on the abovementioned discussion, the magnetic fields for high radial resonance modes are well confined inside the tube wall, which makes them unsuitable for liquid sensing but may be promising for low threshold lasing.54,55
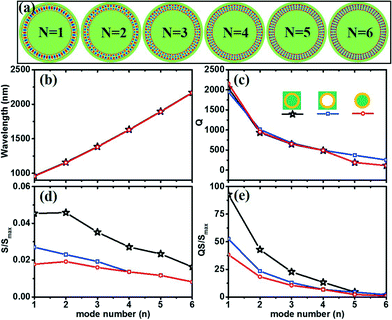 | ||
| Fig. 5 (a) Calculated magnetic field distributions of different modes; (b) resonant wavelength λr, (c) Q-factors, (d) sensitivities S = dλr/dnL and (e) figures of merit QS for different resonant modes of the microtubes made from IM. All three setups in Fig. 1(c), (d) and (e) are shown with different symbols. | ||
Conclusions
We apply the Mie scattering method and effective medium theory to explore the optical resonance and liquid sensing properties in tubular cavities in various media such as IM, metal and DM. Analytical formulas are presented to calculate the resonant wavelength λr, Q factors, sensitivities S = dλr/dnL and figures of merit QS. The IM cavity achieves high Q factors, as does the DM tubular cavity and exhibits high sensitivity similarly to the metal cavity. However, the IM tubular cavity offers the highest figures of merit QS for sensing performance in contrast to DM and metal tubes. Our results can lead to new designs of unique optical devices based on metamaterials and inspire interesting demonstrations with fluidic applications.Acknowledgements
This study is supported by the Natural Science Foundation of China (No. 51322201, 11474057, 11174055), the Project Based Personnel Exchange Program with CSC and DAAD, the Specialized Research Fund for the Doctoral Program of Higher Education (No. 20120071110025) and the Science and Technology Commission of Shanghai Municipality (14JC1400200).References
- V. Ronchi, Physis Riv. Int. Stor. Sci., 1969, 11, 520–533 CAS.
- R. W. Wood, Astrophys. J., 1909, 29, 164–176 CrossRef.
- W. E. Haas, Mol. Cryst. Liq. Cryst., 1983, 94, 1–31 CrossRef CAS.
- X. Wu, M. K. K. Oo, K. Reddy, Q. Chen, Y. Sun and X. Fan, Nat. Commun., 2014, 5, 1–7 Search PubMed.
- M. Li, X. Wu, L. Liu, X. Fan and L. Xu, Anal. Chem., 2013, 85, 9328–9332 CrossRef CAS PubMed.
- K. H. Kim and X. Fan, Appl. Phys. Lett., 2014, 105, 191101 CrossRef.
- S. Kuiper and B. Hendriks, Appl. Phys. Lett., 2004, 85, 1128–1130 CrossRef CAS.
- E. Chow, A. Grot, L. W. Mirkarimi, M. Sigalas and G. Girolami, Opt. Lett., 2004, 29, 1093–1095 CrossRef CAS PubMed.
- A. Ksendzov and Y. Lin, Opt. Lett., 2005, 30, 3344–3346 CrossRef CAS PubMed.
- A. M. Armani and K. J. Vahala, Opt. Lett., 2006, 31, 1896–1898 CrossRef CAS PubMed.
- F. Zhao, T. Zhan, G. Huang, Y. Mei and X. Hu, Lab Chip, 2012, 12, 3798–3802 RSC.
- O. G. Schmidt and K. Eberl, Nature, 2001, 410, 168 CrossRef CAS PubMed.
- Y. F. Mei, G. S. Huang, A. A. Solovev, E. B. Ureña, I. Mönch, F. Ding, T. Reindl, R. K. Y. Fu, P. K. Chu and O. G. Schmidt, Adv. Mater., 2008, 20, 4085–4090 CrossRef CAS.
- T. Kipp, H. Welsch, C. Strelow, C. Heyn and D. Heitmann, Phys. Rev. Lett., 2006, 96, 077403 CrossRef CAS PubMed.
- C. Strelow, H. Rehberg, C. Schultz, H. Welsch, C. Heyn, D. Heitmann and T. Kipp, Phys. Rev. Lett., 2008, 101, 127403 CrossRef PubMed.
- G. Huang, V. A. Bolaños Quiñones, F. Ding, S. Kiravittaya, Y. Mei and O. G. Schmidt, ACS Nano, 2010, 4, 3123–3130 CrossRef CAS PubMed.
- E. J. Smith, S. Schulze, S. Kiravittaya, Y. Mei, S. Sanchez and O. G. Schmidt, Nano Lett., 2011, 11, 4037–4042 CrossRef CAS PubMed.
- G. Huang, Y. Mei, D. J. Thurmer, E. Coric and O. G. Schmidt, Lab Chip, 2009, 9, 263–268 RSC.
- V. G. Veselago, Phys.-Usp., 1968, 10, 509–514 CrossRef.
- D. R. Smith, W. J. Padilla, D. C. Vier, S. C. Nemat-Nasser and S. Schultz, Phys. Rev. Lett., 2000, 84, 4184–4187 CrossRef CAS PubMed.
- J. B. Pendry, Phys. Rev. Lett., 2000, 85, 3966–3969 CrossRef CAS PubMed.
- D. Schurig, J. J. Mock, B. J. Justice, S. A. Cummer, J. B. Pendry, A. F. Starr and D. R. Smith, Science, 2006, 314, 977–980 CrossRef CAS PubMed.
- J. Luo, P. Xu, H. Y. Chen, B. Hou, L. Gao and Y. Lai, Appl. Phys. Lett., 2012, 100, 221903–221905 CrossRef.
- J. B. Pendry, D. Schurig and D. R. Smith, Science, 2006, 312, 1780–1782 CrossRef CAS PubMed.
- H. Li, J. Hao, L. Zhou, Z. Wei, L. Gong, H. Chen and C. T. Chan, Appl. Phys. Lett., 2006, 89, 104101 CrossRef.
- N. Engheta, IEEE Antenn. Wireless Propag. Lett., 2002, 1, 10–13 CrossRef.
- X. Yang, J. Yao, J. Rho, X. Yin and X. Zhang, Nat. Photonics, 2012, 6, 450–454 CrossRef CAS.
- D. Lu, J. J. Kan, E. E. Fullerton and Z. Liu, Nat. Nanotechnol., 2014, 9, 48–53 CrossRef CAS PubMed.
- J. Yao, X. Yang, X. Yin, G. Bartal and X. Zhang, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 11327–11331 CrossRef CAS PubMed.
- Z. Liu, H. Lee, Y. Xiong, C. Sun and X. Zhang, Science, 2007, 315, 1686 CrossRef CAS PubMed.
- J. Rho, Z. Ye, Y. Xiong, X. Yin, Z. Liu, H. Choi, G. Bartal and X. Zhang, Nat. Commun., 2010, 1, 143 CrossRef PubMed.
- E. J. Smith, Z. Liu, Y. F. Mei and O. G. Schmidt, Appl. Phys. Lett., 2009, 95, 083104 CrossRef.
- S. Ishii, A. V. Kildishev, E. Narimanov, V. M. Shalaev and V. P. Drachev, Laser Photonics Rev., 2013, 7, 265–271 CrossRef CAS.
- D. R. Smith, D. Schurig, J. J. Mock, P. Kolinko and P. Rye, Appl. Phys. Lett., 2004, 84, 2244–2246 CrossRef CAS.
- H. N. S. Krishnamoorthy, Z. Jacob, E. Narimanov, I. Kretzschmar and V. M. Menon, Science, 2012, 336, 205–209 CrossRef CAS PubMed.
- A. Poddubny, I. Iorsh, P. Belov and Y. Kivshar, Nat. Photonics, 2013, 7, 948–957 CrossRef CAS.
- G. S. Huang and Y. F. Mei, Adv. Mater., 2012, 24, 2517–2546 CrossRef CAS PubMed.
- C. Bacco, P. Kelly and L. Kuznetsova, in Proc. SPIE, Metamaterials, Metadevices, and Metasystems, 2015, p. 954419 Search PubMed.
- E. D. Palik, Handbook of optical constants of solids, Academic press, 1998 Search PubMed.
- P. B. Johnson and R. Christy, Phys. Rev. B: Solid State, 1972, 6, 4370–4379 CrossRef CAS.
- V. M. Agranovich and V. E. Kravtsov, Solid State Commun., 1985, 55, 85–90 CrossRef CAS.
- S. Tang, B. Zhu, M. Jia, Q. He, S. Sun, Y. Mei and L. Zhou, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 174201 CrossRef.
- A. V. Kildishev, U. K. Chettiar, Z. Jacob, V. M. Shalaev and E. E. Narimanov, Appl. Phys. Lett., 2009, 94, 071102 CrossRef.
- H. C. Hulst, Light scattering by small particles, Dover Publications, 1981 Search PubMed.
- H. Zhu, I. M. White, J. D. Suter, P. S. Dale and X. Fan, Opt. Express, 2007, 15, 9139–9146 CrossRef CAS PubMed.
- J. Zhang, J. Zhong, Y. F. Fang, J. Wang, G. S. Huang, X. G. Cui and Y. F. Mei, Nanoscale, 2014, 6, 13646–13650 RSC.
- J. Trommer, S. Bottner, S. Li, S. Kiravittaya, M. R. Jorgensen and O. G. Schmidt, Opt. Lett., 2014, 39, 6335–6338 CrossRef PubMed.
- B. Min, E. Ostby, V. Sorger, E. Ulin-Avila, L. Yang, X. Zhang and K. Vahala, Nature, 2009, 457, 455–458 CrossRef CAS PubMed.
- Y. Chen, C. Zou, Y. Hu and Q. Gong, Phys. Rev. A At. Mol. Opt. Phys, 2013, 87, 023824 CrossRef.
- J. Wang, T. Zhan, G. Huang, P. K. Chu and Y. Mei, Laser Photonics Rev., 2014, 8, 521–547 CrossRef.
- S. Schwaiger, M. Bröll, A. Krohn, A. Stemmann, C. Heyn, Y. Stark, D. Stickler, D. Heitmann and S. Mendach, Phys. Rev. Lett., 2009, 102, 163903 CrossRef PubMed.
- Y. Zhang, D. Han, D. Du, G. Huang, T. Qiu and Y. Mei, Plasmonics, 2015, 10, 949–954 CrossRef CAS.
- E. J. Smith, Z. Liu, Y. Mei and O. G. Schmidt, Nano Lett., 2010, 10, 1–5 CrossRef CAS PubMed.
- S. M. Spillane, T. J. Kippenberg and K. J. Vahala, Nature, 2002, 415, 621–623 CrossRef CAS PubMed.
- S. I. Shopova, H. Zhou, X. Fan and P. Zhang, Appl. Phys. Lett., 2007, 90, 221101 CrossRef.
Footnote |
| † Published as part of a themed issue on optofluidics. |
| This journal is © The Royal Society of Chemistry 2016 |