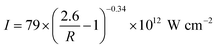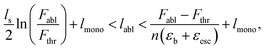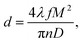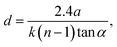Femtosecond laser-induced breakdown spectroscopy

Abstract

The presented review summarizes nearly two decades of studies on femtosecond laser-induced breakdown spectrometry (fs-LIBS). When an ultra-short (<1 ps) laser pulse is used for ablation, the physics of laser-induced plasma changes dramatically in comparison with ablation by pico or nanosecond pulses. A femtosecond laser pulse interacts only with the electron subsystem, while nanosecond pulses continuously interact with different thermodynamic states of material, starting from solid through liquid into plasma. The properties of ultra-short laser radiation, the timescale of fs-laser ablation and the radiative properties of fs plasma are briefly described. We consider the advantages of fs-LIBS, namely, low ablation thresholds, high-spatial resolution, and rapid analysis of samples, which require minimal invasion and allow high-efficiency transportation of laser radiation in filamentation mode for remote analysis. Moreover, we discussed possible limitations of the technique and different approaches to overcome such constraints while retaining the unique possibilities of fs-LIBS.

---

Timur A. Labutin

Timur Labutin is a senior researcher at the Department of Chemistry of Lomonosov Moscow State University in Russia. He has been studying laser sampling and laser-enhanced ionization, obtaining his PhD in 2007. His research interests range from laser–matter interaction to chemometrics and development of laser-based methods for analytical chemistry (mostly LIBS). He was awarded by the Scientific Council on Analytical Chemistry of the Russian Academy of Sciences in 2014 for the applications of LIBS to environmental sample analysis. Currently, his main activity focuses on the combination of LIBS and Raman spectroscopy for the analysis of complex oxide systems such as minerals and pigments.

Vasily N. Lednev

Vasily N. Lednev is a researcher at the National University of Science and Technology MISiS in Russia. His research interests range from the fundamentals of laser–matter interaction (laser ablation and laser plasma) to laser remote sensing diagnostics by laser induced breakdown spectroscopy (LIBS), Raman scattering and laser induced fluorescence (LIF). During the last five years his main activity has focused on laser pulse interaction (femto, pico, nano) with nanosized objects (nanoparticles and nanotubes) and express diagnostics of nanomaterials by LIBS and Raman spectroscopies.

Alexey A. Ilyin

Alexey Ilyin is a senior researcher at the Institute of Automation and Control Processes of the Far East Branch of the Russian Academy of Sciences and Far Eastern Federal University. After graduating with honors at Far Eastern Federal University in 1999, he investigated laser-induced plasma and physics of shock waves. After obtaining his PhD degree in 2003, his mainstream research activities are in the field of femtosecond LIBS and laser filamentation, laser ablation and laser-induced gas breakdown.

Andrey M. Popov

Andrey Popov is a senior researcher at the Department of Chemistry of Lomonosov Moscow State University, Russia. After graduating in Chemistry at Moscow University in 2003, he continued his research on the correction of matrix effects in laser ablation-based methods and obtained his PhD in Chemistry from Lomonosov Moscow State University in 2007. Later, he worked at the Frascati Centre of ENEA in Italy. His research interests are focused on approaches to improve LIBS sensitivity for quantitative detection of traces in soils and ores. He awarded by the Scientific Council on Analytical Chemistry of the Russian Academy of Sciences in 2014 for applications of LIBS to analyze environmental samples.

---

1 Introduction

A pulsed solid-state Nd:YAG laser with nanosecond pulse duration is a typical “workhorse” for a laser-induced breakdown spectrometry setup. A perspective tool became available for novel LIBS applications with the development of a new generation of ultra-short laser systems with femtosecond pulse duration in the late 1980s. Femtosecond laser-induced breakdown spectrometry (fs-LIBS) can improve figures of merit for LIBS quantitative analysis (e.g. better reproducibility, absence of fractional evaporation and reduction in damage) due to changes in laser–matter interaction.

Fs-LIBS has made a long “journey” of more than 25 years from the generation of the first ultrashort pulses to elemental analysis. The first generation of femtosecond laser pulses was demonstrated in 1970s;¹ the invention of Ti:Sapphire laser in the 1980s attracted growing attention to femtosecond systems.² The invention of the chirped-pulse amplification technique in 1985 was a revolutionary breakthrough in femtosecond laser systems, resulting in the appearance of powerful femtosecond laser pulses.³ The first plasma spectroscopy studies induced by femtosecond pulses (700 fs) were carried out four years later and were mainly focused on plasma physics problems.⁴ The rapid growth of publications on femtosecond laser plasma started when powerful commercial laser systems became available. The first emission spectrum for femtosecond laser plasma was ascribed to controlled laser machining in 1998.⁵ The first application of femtosecond pulses to analytical chemistry problems was demonstrated only in 2000 by Margetic et al.⁶ Seven years later, Gurevich and Hergenröder⁷ presented the first review on the achievements and future perspectives of fs-LIBS. After this review, numerous studies on fs-LIBS have been published. In the current review, we summarized the state-of-the-art findings in studies of femtosecond ablation and plasma physics, instrumentation and applications.

Ultrashort pulse duration gave numerous benefits with respect to fs-LIBS: low ablation threshold, absence of fractionation vaporization, improved spatial resolution for 3D mapping applications, small ablated mass, and reduced sample damage. All these benefits originate from the physics of femtosecond ablation and plasma, which are described in Section 2. In Section 3, we summarize the analytical performance of fs-LIBS and discuss its perspectives. The possibility of high-efficiency transportation of laser radiation in filamentation mode for remote analysis and applications of filaments in LIBS, which is also called filament-induced breakdown spectroscopy (FIBS), are discussed in Section 4. Special attention is given to the comparison of analytical figures of merit (sensitivity, accuracy, and precision) as well as unique applications (filament-induced breakdown spectroscopy).

2 Fundamentals of femtosecond laser-induced plasmas

2.1 Properties of ultra-short laser radiation and typical equipment

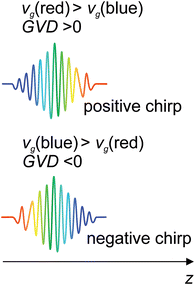
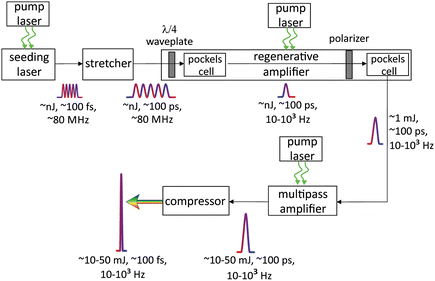
Femtosecond pulse generation is based on Kerr lensing in the gain medium^8,9 and a Ti:Sapphire crystal is commonly used for this purpose. In contrast to a nanosecond laser (Q-switched), the output energy of femtosecond oscillators (∼1 nJ) is clearly insufficient to exceed a threshold for plasma generation. Therefore, a femtosecond laser for LIBS is supposed to use one or more additional amplifiers to a seeding laser, as shown in Fig. 1. Normally, the seeding laser produces a train of femtosecond pulses with a central wavelength near 800 nm and a repetition rate of ∼80 MHz. A femtosecond pulse can be broadened due to a self-phase modulation in the media with a nonlinear refractive index and group velocity dispersion (GVD) by optical elements of the laser. The pulse duration of the seeding laser can be tuned by modifying the GVD of the cavity, which is determined as follows:
where k(ω) is the wave vector and v_g is the group velocity. One can easily see that the group velocity is different for various wavelengths. The influence of the dispersion properties of a material on the instantaneous frequency of a femtosecond pulse is characterized by a chirp. The pulse is said to be positively “chirped” when the instantaneous frequency is red-shifted in a pulse front and blue-shifted in a trail, as shown in Fig. 2.

Fig. 1 Typical scheme of femtosecond laser system. Pulse repetition rate is reduced to 1–10 Hz for systems with pulse energy exceeding 10 mJ.

Fig. 2 Chirp and GVD.

The positive chirp of intracavity elements can be compensated by the media with a negative GVD-like grating or prism pairs to obtain short output pulses.

To avoid damage to the Ti:Sapphire crystal, it is essential to keep the power density in the amplifier below the Ti:Sapphire damage threshold. This can be achieved using a chirped pulse amplification technique, which incorporates a stretcher that reduces power and broadening pulses before they enter a regenerative amplifier with consequent narrowing of pulses by a compressor after amplification. Usually, the stretcher and compressor represent a pair of gratings or prisms. The pulse repetition rate is reduced to 10 to 10³ Hz by Pockels cells to provide maximal amplification without overheating the gain medium in a regenerative amplifier. Thus, the pulse energy increases from several nJ to roughly mJ level. The amplification in a multipass amplifier is limited by the number of passes (usually 2–8) due to difficulties in focusing into a single Ti:Sapphire rod. Finally, a pulse is usually compressed down to a duration of 30–500 fs, although sub-4 fs pulses can be obtained in specially designed laser systems.^10,11 Femtosecond pulses are also broadened by optical components of the LIBS system. The output pulse duration for a Gaussian transform-limited pulse is determined as follows:⁹

where τ₀ is the incoming pulse duration and L is the length of the dispersive material. For example, an initially unchirped 30 fs pulse at 800 nm becomes broadened to 40 fs after passing through a 6 mm-thick focusing BK-7 lens (GVD = 44.6 fs² mm⁻¹ at 800 nm).

The temporal profile of the femtosecond laser pulse and the intensities of the pulse components are of key importance in laser–target interaction. During generation, amplification, and spectral and temporal shaping, a number of physical processes affect the temporal shape of the pulse. The final pulse may consist of pre-pulses, post-pulses and a main pulse on top of a very broad pedestal (see Fig. 3).^12,13 This nanosecond pedestal or amplified spontaneous emission (ASE), corresponds to noise photons amplifying in the same way as the main pulse. The ASE duration does not exceed 10 ns and may contain up to 25% of the total pulse energy,¹⁴ with the ratio of the peak intensity of the main pulse to the peak intensity of the ASE ∼ 10⁵ to 10⁸ (contrast ratio).^12,13 Pre- and post-pulses are caused by Fresnel reflections in optical elements^12,13 and radiation leakage out of the regenerative amplifier on each pass of a beam in a cavity.⁷ Their durations are greater than or equal to the main pulse, and the contrast ratio varies over a wide range from 10² to 10⁸, depending on the laser system. Pre-pulses can create plasma before the arrival of a main pulse, leading to a reduction in the main pulse energy deposition in an analyzed sample.¹³ Saturable absorbers, frequency doubling and additional Pockels cells can be used to correct temporal shape and improve contrast ratio. Usually, pulse duration and temporal shape are controlled by fast photodiodes, streak cameras and auto- and cross-correlation methods.⁹

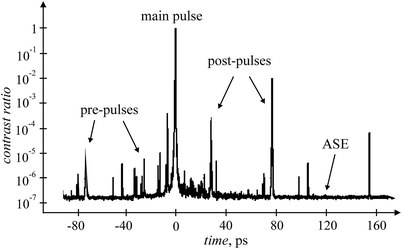Fig. 3 Temporal profile of fs laser pulse with ASE, pre- and post-pulses obtained by a 3^rd order cross-correlator.

2.2 Filamentation

Visually, a laser-induced filament in air represents a long, luminous thread due to emission of the first negative system of N₂⁺ B²Σ_u⁺ → X²Σ_g⁺ and the second positive system of N₂ C³Π_u → B³Π_g. A filament can appear at a high peak laser intensity. A theoretical estimation was carried out by Chiao et al.¹⁵ in 1964. Although the first filament was induced in liquids by powerful nanosecond pulses in 1965,¹⁶ it was observed in air only in 1995 when powerful femtosecond laser systems with a peak power of several GW became available.¹⁷ Therefore, filamentation in the atmosphere has been a subject of intensive investigation over the past two decades. Generally, these investigations are related to the self-focusing of laser beams, conical emission, and supercontinuum generation.^18–20 A detailed description of filament physics and applications can be found in several reviews.^21–24

Filamentation arises due to strong spatiotemporal self-modulation of femtosecond pulses, i.e. self-focusing initiates a plasma that defocuses the propagating laser beam. A series of self-focusing events from the front part of the pulse gives rise to the luminous plasma channel or so-called filament. The back part of the pulse experiences self-phase modulation and self-stepping, resulting in strong spectral broadening (supercontinuum). On average, the filamentation area is 50–200 μm in diameter and its length varies depending on pulse power, medium and laser wavelength.^23,25 A continuous filament was observed with a length of ∼100 m (ref. 26) and, more recently, up to 1 km.²⁷ It should be noted that tuning of pulse chirping allows precise control of filament initiation at desired distances up to 20 km.²⁸

For a laser radiation, the power of which exceeds a self-focusing threshold in the air (1.7–10 GW for λ = 800 nm),^29–31 many filaments emerge due to non-homogeneity of intensity distribution in the cross-section of the laser beam^21,22 and (pre-)post-pulse filamentation.³² For weakly focused laser beams, intensity clamping is observed as a consequence of balance between Kerr-type self-focusing and plasma induced defocusing. In an air filament, the intensity does not exceed the threshold value of ∼5 × 10¹³ W cm⁻² even with an increase in the femtosecond pulse energy.^23,33 This situation corresponds to a low NA (numerical aperture < 3–5 × 10⁻³) or a nonlinear focusing regime in filamentation.³⁴ In the case of a high-NA or a linear focusing regime, geometrical focusing and plasma defocusing are the primary contributors to the filamentation process, while Kerr-type self-focusing plays a secondary role. In this case, the intensity exceeds the threshold value of 5 × 10¹³ W cm⁻².^33,35 Xu et al.³³ suggested a simple formula for the estimation of the intensity of the laser radiation in the filament:

where R is the intensity ratio (391.2 nm/337 nm) of nitrogen molecule lines.

Electron density in plasma filaments varies from 10¹⁴ to 10¹⁸ cm⁻³, depending on the experimental conditions.^29,36–38 Basically, electrons appear due to multiphoton ionization (MPI); the ionization rate is proportional to I^K, where K is the number of absorbed photons necessary to ionize molecules. Ionization potentials of air molecules are 15.6 eV (N₂) and 12.1 eV (O₂). Therefore, K(O₂) = 8 and K(N₂) = 11 for λ = 800 nm (photon energy is 1.55 eV). Kasparian et al.³⁹ have shown that K(O₂) ≈ 6.5 and K(N₂) ≈ 7.5 for intensity I < 10¹⁴ W cm⁻², indicating the occurrence of tunnel ionization (TI). In other words, at such intensities, electrons in a molecule pass through the potential barrier and escape from the molecule. Electron avalanche ionization is characteristic of plasma induced by ns pulses. Seed electrons starting an avalanche arise due to MPI of impurities with low ionization potential.⁴⁰ The energy of the electrons is then increased by an inverse Bremsstrahlung effect, i.e. electrons absorb photons in the field of ions or atoms (molecules). This process requires approximately 350 fs in air.⁴¹ Thus, electron avalanche ionization can also take place in filaments induced by laser pulses with durations exceeding this value. For I < 2 × 10¹⁴ W cm⁻², photoelectrons ejected from molecules have an initial kinetic energy of a few eV, which corresponds to an initial free-electron temperature of ∼10⁴ to 10⁵ K.^42,43 These values are much smaller than initial temperature (60 eV) of plasma induced by ns pulse with I = 2 × 10¹¹ W cm⁻².⁴⁴ This is why electron density in filaments is less than that of nanosecond plasma, which can reach critical values of 1.7 × 10²¹ cm⁻³ (at λ = 800 nm). It is interesting to note that the velocity of filament expansion is 2 × 10⁸ m s⁻¹,³² which is close to the speed of light. In the case of a ns pulse, plasma expanding due to single photon UV and avalanche ionization has velocity = ∼10⁵ m s⁻¹.⁴⁵

In contrast to extensive studies on self-focusing, harmonics and supercontinuum generation, molecular and atomic emission of plasma generated by laser filamentation is less investigated. Temporal characteristics of atomic and molecular emission of laser plasma filaments can be found in ref. 21 and 46–48. The application of laser filamentation to spectrochemical analysis will be considered in Section 4.

2.3 Interaction of femtosecond pulses with condensed matter

Negligible heat transfer from the irradiated area and an absence of plasma–laser interactions are the main features of femtosecond laser ablation in comparison with its nanosecond equivalent. Therefore, absorbed laser energy is localized in a relatively small (even less than a μm for near-field focusing⁴⁹) region with simply-controlled dimensions.^50,51 Moreover, the absorption wave moving towards the laser beam is absent in femtosecond plasma.

Interaction of a femtosecond pulse with matter involves many physical phenomena, such as light absorption, non-linear ionization, plasma formation, thermal conduction, and ablation. Comprehensive reviews of these phenomena can be found in recently published studies.^52,53 In regards to LIBS, plasma and ablation dynamics are very important. First, let us consider the early stage of plasma evolution. Free electrons in a metal absorb laser photons via the inverse Bremsstrahlung process at the very beginning of the irradiation and do not obey the Fermi–Dirac distribution in the absorption region of laser radiation (∼10 nm depth). The non-thermalized ballistic electrons transfer absorbed laser energy to deeper sample layers (∼100 nm).⁵⁴ A few femtoseconds is required to establish a thermal equilibrium through electron–electron collisions in the electron subsystem.⁵³ Hot electrons overcome the potential barrier⁵² and are emitted from the surface. Moreover, photo-induced electrons overcome the barrier due to multiphoton absorption, because barrier energy exceeds photon energy at λ = 800 nm for most materials. At this time period, the ions of the lattice are cold because electron–lattice thermalization occurs on a picosecond time scale. Electrons emitted from the surface create an electrostatic field, which pulls ions out of the surface. This fast ion ejection is known as the double layer effect⁵⁵ or electrostatic ion removal.⁵² It was shown that approximately several tens of femtoseconds are necessary to remove ions.⁵² After free electrons and ions are generated, electrons can increase their energy due to a “parachute effect”⁵⁶ and impact ionization is also started.⁵⁷

Another mechanism of plasma formation is realized for dielectrics and semiconductors because additional energy is needed to create free carriers in a conduction band. Absorption of one or two photons is enough for electron transition from valence band to conduction band due to a relatively narrow bandgap. When the electron density reaches ∼10¹⁸ to 10¹⁹ cm⁻³, an electron avalanche is launched. At this stage, electrons absorb energy via inverse Bremsstrahlung effect, and avalanche ionization prevails over other ionization mechanisms.⁵³ Seed electrons in the conduction band are generated by MPI in dielectrics. As soon as a definite density of these electrons is achieved, avalanche ionization is initiated. In the case of high laser intensities, TI also takes place in the superficial layer of a sample.^53,58 Another mechanism of plasma formation typically observed for dielectrics is Coulomb explosion (CE). Emission of electrons from a surface leads to accumulation of an excessive positive charge in the superficial layer of the sample. For a strong field, electrostatic repulsive forces between ions disintegrate this layer (to several nanometers depth), resulting in CE during the first hundreds of femtoseconds.⁵³ Coulomb explosion was observed at extreme intensities of ∼10¹⁹ W cm⁻² for metals,⁵⁸ whereas it is still debated for semiconductors at high intensities (I ≥ 10¹⁴ W cm⁻²).⁵³

In ambient conditions, the gas layer in the vicinity of a sample can be ionized by laser radiation and/or high-energy free electrons ejected from the sample. It should be noted that the front part of the laser beam reflected from the sample can interfere with the trail of the beam, resulting in an increase in the laser intensity by a factor of 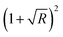above a surface with reflectivity R.⁵⁹ Free electrons from gas and electrons removed from the sample can become seed electrons for avalanche ionization,⁶⁰ which can be supported by post-pulses.

The early stage of plasma evolution was investigated both experimentally and theoretically in ref. 60–62. In the case of a vacuum (4 × 10¹³ W cm⁻², 50 fs, 800 nm), the electron cloud above the surface of Cu is split into fast-moving (∼10⁷ m s⁻¹) and slow-moving (∼10⁴ m s⁻¹) parts, and this can be explained by the generation of a repulsive electric field within the electron cloud. Electron density in the fast-moving cloud decreases from ∼10²⁰ to ∼10¹⁷ to 10¹⁶ cm⁻³ during the first 4–12 ps. In the case of ambient gas, target plasma with air breakdown is observed (100 fs, ∼4 × 10¹⁴ W cm⁻², 800 nm). For target plasma formation, a simulation reveals the existence of double layers (electrons and ions) with a maximum electron density of 10²⁰ cm⁻³. The electron front in the air breakdown area moves faster than electrons near the target surface due to attraction of a lesser quantity of ions. Air molecules are ionized primarily due to MPI with consequent electron avalanche, while impact ionization by target electrons plays a secondary role. Electron density is about 10²⁰ cm⁻³ near the target and 10¹⁹ cm⁻³ at the electron front. Zhao and Shin⁶² claim that emission of Si⁺ and Si²⁺ ions is observed from several tens to 150 fs due to CE, whereas electrostatic ion removal and thermal ejection are characteristic for Cu⁺ and Cu²⁺ ions. It should be noted that the air breakdown threshold by femtosecond pulses is ∼2 to 4 × 10¹⁴ W cm⁻² at λ = 800 nm.^63–65 The above mentioned mechanisms of plasma formation can be treated as non-thermal mechanisms, which launch ablation on a femtosecond time scale. A brief description of laser–matter interactions related to thermal and mechanical effects will be given below. These processes occur on a picosecond time scale and result in a larger amount of ejected material.

Laser–matter interaction at the femtosecond scale is usually described by a two-temperature model,⁶⁶ where electrons and lattice are characterized by different temperatures. Electrons transfer absorbed laser energy to an initially cold lattice through electron–phonon interactions, which lead to electron–lattice thermalization over a few picoseconds.^67–69 The temperature of the lattice also increases after the laser pulse, resulting in melting of the irradiated layer. Heating to melting temperature requires tens of picoseconds.^70,71 The melting depth reaches hundreds of nanometers and depends on laser fluence and material. It should be stressed that ultrafast melting is observed for semiconductors on a time scale of ∼100 fs at intensities of ∼10¹² W cm⁻².⁶⁸ Transfer of ∼10% to 15% valence electrons to conduction band leads to lattice instability and disordering.⁷² Because ultrafast disordering occurs at temperatures below the melting point, it is also called non-thermal or cold melting. A high temperature in superficial layers (tens of nanometers in depth) up to 3 × 10⁴ K can lead to direct evaporation to gas phase with a phase trajectory lying above the critical point (supercritical regime or atomization).^67,73 Critical point phase separation is observed at temperatures close to the critical point. In this case, the phase trajectory of the sample layer crosses the liquid branch of the binodal and enters into the region of metastable liquid.^67,74 The lifetime of this state is only several picoseconds and the substance instantaneously disintegrates into a gas–liquid mixture.^67,74,75

Tensile stress caused by thermoelastic and shock waves leads to formation of voids at a certain depth. Some of the voids coalesce, resulting in mechanical layer decomposition and spallation over tens of picoseconds.^70,76 This mechanism arises if the lifetime of a metastable liquid state exceeds the time of mechanical fracture at temperatures below the critical point. Otherwise, phase explosion occurs with disintegration of matter into gas and droplets.^74,75 This mechanism is similar to critical point phase separation but unlike this, phase explosion is observed at lower temperatures. Although ∼80% of the ablated mass of metals at irradiance of ∼10¹³ to 10¹⁴ W cm⁻² is ejected by mechanical decomposition,^67,74 this mechanism can be suppressed by recoil pressure of the vapour/cluster plume at high laser fluences.⁵³ Finally, plasma expansion and intensive ejection of vapor and droplets lead to shock wave formation in the surrounding gas.^69,77 Summarizing our considerations, the main processes of plasma formation and ablation at laser intensities of ∼10¹³ to 10¹⁵ W cm⁻² are shown in Fig. 4.

Fig. 4 Sketch of the main physical phenomena, leading to plasma formation and ablation. CPPS is critical point phase separation and SCR means supercritical regime.

The competing processes lead to the formation of several fractions in a plasma plume. Three different velocity populations can be distinguished during plasma expansion. Coulomb explosion first produces ions with high kinetic energy, which are followed by neutrals formed by adiabatic expansion with velocities in the nanosecond regime and finally those from nanoscale clusters.⁷⁸ These nanoparticles produce broadband continuum radiation in the plasma similar to black body emission from a macroscopic object.⁷⁹ Moreover, different ablation mechanisms for various types of solids lead to considerable variation in the fractional composition of ejected matter and nanoparticles. Noël et al.⁸⁰ and Axente et al.⁸¹ considered plasma composition during femtosecond ablation of copper and fused silica. A ‘‘slow’’ component of high intensity is located close to the target, whereas a ‘‘fast’’ component of lower emission intensity is observed at a larger distance. It was shown that with the use of fast imaging and optical emission spectroscopy, two clouds of nanoparticles were generated during femtosecond laser ablation in vacuum (10⁻⁴ Pa): a fast frontal plume component mainly consisted of small clusters (“fast” component) and larger particles were located mostly at the back (“slow” component). Spectra registered during metal ablation revealed that the emission from the “fast” component consisted of mainly spectral lines of neutral atoms and ions, whereas a blackbody-like continuum dominates the emission of the “slow” component (Fig. 5a). Unlike metal ablation, the plasma generated by a femtosecond laser on a fused silica target had only a “fast” component (Fig. 5b). The characteristic expansion velocity of this unique component was about one order of magnitude higher than that of the “fast” component in the case of metals.

Fig. 5 Plume emission intensity vs. distance and wavelength: (a) recorded 20 ns after the laser pulse for ablation of copper with fluence of 4 J cm⁻² (reproduced from Noël et al.⁸⁰ with the permission of Elsevier Science); (b) fused silica for different delay times between the laser pulse and the observation gate (reproduced from Axente et al.⁸¹ with the permission of IOP Publishing).

Because a sufficient part of the pulse energy presents ASE, this can influence the ablation process.^14,69,82 It was shown that ASE can create a relatively thick melt layer on a surface before the main pulse with an increasing ejected volume of material. A schematic view of femtosecond ablation with ASE is shown in Fig. 6 (time τ = 0 corresponds to a main pulse with duration t_p).⁶⁹ A sample surface is heated (Fig. 6a) and can be melted by the pre-pulse or ASE before the main pulse. Main pulse interaction leads to hot plasma formation with emission of electrons and breakdown in the ambient gas (Fig. 6b). After electron and lattice temperatures become similar at τ ≈ τ_eq, different layers of material can be evaporated, melted or maintained in a plasma or metastable state. Homogeneous nucleation then occurs in the superheated melt (Fig. 6d). Some delay in phase explosion or mechanical decomposition can be explained by boiling crisis (Fig. 6e),⁶⁹ observed earlier for ablation by nanosecond pulses because of the formation of a continuous vapor layer or film over the liquid melt.^83,84 Phase explosion starts at τ = 700 ps to 1 ns, when pressure decreases due to vapor expansion. A shock wave can be detected up to τ ≈ 100 ns (Fig. 6f). Vapor and sub-micrometer particles are ejected up to 500–700 ns (Fig. 6g). Sometimes continuous liquid jets or melt droplets with a size of several micrometers are observed up to τ ≈ 1 μs.

Fig. 6 Schematic view of plasma formation and ablation. t_p is the duration of the main fs pulse and τ_eq is the characteristic time of the equilibrium established between electrons and lattice.

Thus, the features of femtosecond pulses are durations less than thermalization in any medium, chirping and controlled filamentation, which permit laser energy transfer over a long distance in the atmosphere. At the same time, the mechanism of ablation and plasma formation strongly depend on material, laser fluence, wavelength, pulse duration, and layer depth. In contrast to nanosecond pulses, there is no shielding effect or absorption wave of laser radiation in ambient gas, resulting in a smaller initial temperature and electron density and, as a result, in reduced continuum radiation. In combination with smaller ablation thresholds, this leads to considerable ejection of material on a picosecond time scale. A minimally heat-affected zone, sputtering and mechanical deformation can provide high depth/spatial resolution and precise machining due to negligible heat transfer from the energy absorption area.

3 Analytical performance of femtosecond LIBS

3.1 Depth profiling

A unique feature of femtosecond laser ablation is a small amount of melting in comparison with ablation produced by nanosecond pulses. As a result, the craters produced by an fs laser have more even walls without the clear rims than those produced by ns lasers,⁸⁵ and the structure, diameter and depth of craters are accurately reproduced. Lopez-Claros et al.⁸⁶ recently studied the thresholds for single-shot femtosecond ablation of different metals (Pb, Ag, Zn, Sn, Cr, Cu, W, Ni and Fe). The craters exhibited a similar size (∼40 μm at 4–9 J cm⁻²) and shape, regardless of the sample type, energy range (for energies per pulse <400 μJ) and accumulated energy dosage (<500 laser shots on the same sample position). Such a peculiarity allows the use of fs-LIBS to accurately construct in-depth profiles of metallic alloys. Because the goal of a quantitative in-depth analysis is to obtain the local concentration of an analyte as a function of the layer depth with respect to a distance perpendicular to the solid surface,⁸⁷ analysts have to solve two tasks. It is essentially important to find a conversion function from the dependence of LIBS intensity on pulse number, i.e. “measured profile”, into a relation between content and depth, i.e. “true” depth profile. Another obstacle for in-depth measurements by LIBS is accuracy validation by means of independent methods, ideally non-destructive techniques that do not involve removing material from a surface. To quantitatively describe the ability of a technique to distinguish the local content between two depth profiles, the term depth resolution is used. According to IUPAC terminology, this is “the distance between the 84 and 16 percent level of the depth profile of an element in a perfect sandwich sample with an infinitesimally small overlap of the compounds.”⁸⁸

The general practice for estimating depth resolution for techniques with laser ablation is to calculate the average value of the ablation rate from pulse-to-pulse measurements of crater deepening by several profilometry techniques in terms of μm per pulse or nm per pulse.⁸⁹ Ideally, this should be permanent and the crater is linearly deepened under the fixed fluence. An ablation depth per pulse, l_abl, for ultrafast laser processing of metallic alloys can be estimated by the following inequality:⁵²

where F_abl and F_thr are ablation and threshold fluences, respectively, the depth of the one surface atomic layer, l_mono, can be estimated as ∼n_a^−1/3, l_s is the depth of a thin layer in which the energy of the fs pulse is absorbed and, finally, ε_b and ε_esc are the energy spent on breaking bonds and the kinetic energy of ablated atoms, respectively. It is obvious that the lower the ablation fluence used, the shallower the crater will be. This means that the distribution of energy across a beam defines the ablation rate; thus, a beam profile influences the crater shape, its diameter and depth. Using a Gaussian beam, the crater shape becomes cone-like and can be applied to make, for example, grooves with a regular shape.⁹⁰ In such a way, a Gaussian beam can be considered as a ‘knife’ to produce deeper craters. On the other hand, a flat-top beam profile is capable of producing straight-wall craters with a flat bottom.⁹¹ For example, Banerjee et al.⁹² recently demonstrated that the ablation rates for Gaussian and flat-top beams differed by 30-fold (1 μm per pulse vs. 30 nm per pulse, respectively) similar to the ratio of the laser fluences of the beams, 42 J cm⁻²vs. 1.4 J cm⁻². Like an ‘awl’, a Gaussian beam can quickly (<30 shots) drill an upper thick layer of silicon (32 μm) to reach to buried layers of Cu and Cr (about several μm). Only two or three pulses of this laser were needed to reach the thin layers of copper and chromium. Unlike the Gaussian beam, the flat-top beam allowed the improvement of depth resolution down to 30 nm with prolongation of ablation for up to 1200 pulses.

Another way of deeply penetrating a sample is provided by non-diffracting Bessel beams. These have an intensity distribution across a beam, which can be described by a Bessel function of the nth-order J_n:⁹³ the beam shape has a central core with a series of concentric rings. A unique feature of such a beam is that the intensity profile of its central core propagates without experiencing appreciable spreading. A circular slit⁹⁴ or a conical axicon⁹⁵ are the usual tools for generating Bessel beams. The most spectacular demonstration of the ability of Bessel beams is drilling λ/4 = 200 nm channels with an aspect ratio of ∼100 by a single shot of a 650 nJ to 230 fs pulse in glass.⁹⁶ The robustness of Bessel beams to the presence of obstacles and their self-healing ability makes them very attractive for laser processing of dielectrics with powerful femtosecond pulses. Because there have been, to the best of our knowledge, no studies on the use of LIBS techniques for spectral monitoring of ablation processes with Bessel beams of zeroth or first order, we suggest that this field of LIBS application should prove promising, especially in micromachining and material processing.

Generally, LIBS is applied to the measurement of the thickness of coatings⁹⁷ and layers as an auxiliary tool to detect a transition between two different layers. In this case, to decide whether the crater bottom crossed the interface between two layers, analysts should observe a sharp change in the pulse-to-pulse variations of a LIBS signal. If it increases (or decreases), the layer containing an analyte has begun (or ended). However, mixing of layers of different materials due to melting and resolidification during a multiple shot depth profiling can lead to worsening of the resolution with respect to the ablation rate. This means that the changes between two consecutive single shot LIBS spectra cannot reflect the changes in the average depth composition, and the ablation rate will be an inaccurate estimation of the depth resolution. Recently, Banerjee and Fedosejevs⁹⁸ introduced the concept of “depth sensitivity” to describe an approach for estimating the accuracy of distinguishing the boundary between a two-layer system by the use of single-shot LIBS signals from each component. As an example, they calculated depth sensitivity as “the Cu layer depth where the Si emission falls to 1/e from its pure Si value” for a thin Cu–Si interface layer. This was 2.5–4 nm for crater depths of 25–100 nm. This term can be interpreted as the minimum change in depth that can be reliably detected by changes in the LIBS signal of the sample constituents. Evidently, the depth sensitivity is preferable as a measure of the ability to perform depth profiling by LIBS techniques because of the simplicity of its measurement, compared with the ablation rate.

The very first study on the application of femtosecond LIBS to measure the thickness of multilayered coatings of Cu–Ag sandwiches was performed by Margetic et al.⁸⁹ Two types of Cu–Ag samples were prepared by thermal deposition of Cu and Ag layers on a Si wafer: double and triple sandwiches of alternating Cu and Ag layers. The thickness of each copper and silver layer was ∼600 nm. With a fluence of about 1 J cm⁻², they detected five boundaries between layers after ∼25–30 laser shots. Because the depth profiles of Cu and Ag were constructed by the accumulation of 10 pulses, an accurate estimation of depth resolution in terms of “depth sensitivity” has to give a larger value of at least 200 nm, instead of an ablation rate of 15–30 nm per pulse. By comparing ns-LIBS with fs-LIBS, Pouli et al.⁹⁹ measured the thickness of different types of thin organic films used as protective coatings on historical and archaeological metal objects. They established that ns pulses were inadequate to assess the polymer coating on an Al–Mg substrate because of their weak absorption, while fs pulses yielded well-resolved profiles with a depth resolution of 1 μm. More recently, de Bonis et al.¹⁰⁰ compared 40 ns pulses vs. 40 fs pulses to measure the depth of a patina to clean corroded bronzes. Because the ablation rate of a 40 ns laser was four times larger than that for a 40 fs laser, the resolution of femtosecond LIBS depth profiling was better and accuracy with respect to the Cu/Sn ratio was also better due to minimal fractionation.

Unlike the depth profile with a sharp leap due to the interface between two layers, this accuracy problem of LIBS should be overcome to construct “continuous” depth profiles. In principal, LIBS is a microdestructive technique¹⁰¹ because analyzed material in the plasma is removed from a surface. In spite of attempts to analyze the ablated particles,¹⁰² it is not possible to accurately establish the local composition of the material after it has been removed from the sample. Therefore, it is necessary to compare the results of in-depth measurements by LIBS with other analytical techniques. Accuracy can be proved by in-depth measurements of the same area by non-destructive techniques before ablation. Electron spectroscopy for chemical analysis or Auger electron spectroscopy can be applied for non-destructive profiling of ultrathin layers (0.5–5 nm). For larger sampling depths (up to several μm), there is Rutherford backscattering spectroscopy (RBS) of low mass and high energy ions in the MeV range with a depth resolution of about 1–5 nm.¹⁰³ RBS depth profiles are infrequently matched to fs-LIBS data because of the cost of the technique (requiring a He⁺ source), although it is suitable for determining the thickness of a specific coating or deposition. At the same time, in-depth results of LIBS are sometimes compared with other microdestructive techniques such as glow-discharge OES, electron probe microanalysis (EPMA), SIMS, and laser ablation ICP-MS due to their low cost and simplicity in comparison with RBS. To assure accuracy in quantitative analysis, such a comparison demands an assumption of either sample homogeneity or that the depth profiles are the same at different points of a sample surface. Recently, Galmed et al.¹⁰⁴ examined the ability of fs-LIBS to achieve depth profiling for a Ti thin film deposited onto a Si substrate during thermal annealing. They estimated the thickness of a Ti coating after annealing to be 213 nm. Because such a depth corresponded to the intersection between Si and Ti signals, they established that LIBS can be considered as a rapid analytical technique for accurately estimating the thickness of coatings.

However, there was only one study on the comparison of a “continuous” profile obtained by fs-LIBS with the in-depth measurements by other techniques. Das et al.¹⁰⁵ also tried to quantitatively locate the interfaces of an interdiffusion zone (depth = ∼20–25 μm) in a thermal barrier-coated sample using 150 fs laser pulses with a fluence of 18 J cm⁻². The average ablation rate was less than 200 nm per pulse. It is interesting to note that each layer was prepared by different techniques: a β-(Ni,Pt)Al bond coat was prepared through a combination of electroplating, high temperature diffusion and chemical vapor deposition processes, while a ceramic outer layer was deposited on the bond coat by an electron beam physical vapor deposition technique. This provided an interdiffusion zone below the bond coat. By comparing an fs-LIBS depth profile for an Al line with the one obtained by EPMA, they found that LIBS could indicate the ceramic layer/bond coat interface, while the absence of sharp changes in the Al intensity across the β layer/interdiffusion zone and interdiffusion zone/substrate interfaces meant that it was not possible to identify these interfaces from the spectral intensity profile of Al.

Although it is possible to achieve a very shallow ablation depth per pulse, such as ≤2 nm per pulse, with the use of ns-LIBS, for example, due to angle-resolved laser ablation,¹⁰⁶ the main advantage of femtosecond pulses is still the production of more reproducible craters with an even bottom. By measuring in-depth profiles of Ti ultrathin layers on a steel sheet with the use of doubled 12 ns pulses, Kratochvíl et al.¹⁰⁷ recently showed that the roughness of a crater bottom was about 50 nm at a depth of 150 nm after a single laser shot. The technique was capable of measuring the surface density of Ti on a sheet at a level of several hundreds of pg mm⁻² only for a single shot because of the etching of the Ti layer by the first pulse. This means that the “depth sensitivity” of fs-LIBS is better, at least by two orders of magnitude, than that provided by ns-LIBS due to the even bottom as a result of low melting.

3.2 Lateral resolution

Chemical mapping, i.e. the distribution of a component across a sample surface, requires high spatial resolution, ideally, at near-atomic level or, at least, at the nanoscale level. Because of low melting, focusing ultrafast laser pulses onto a sample surface can produce a crater without high rims and other irregularities (e.g. droplets), which are usually observed for nanosecond laser ablation. Therefore, their applications to construct a map are limited by the crater size, which is slightly wider than a spot. The diffraction-limited beam diameter d at the focus of a lens with focal length f and aperture D is given by the following relation:⁵²
where M² is a propagation constant characterizing the deviation from the ideal Gaussian beam and n is the refractive index of the lens. Gaussian beams give a spot with a minimal diameter (because M² ≈ 1), while the beams with flat-top profiles, which are widely used for in-depth measurements, give a wider spot because they have an M² value much higher than 10. As a result, the crater diameters from the two beams differ significantly and spatial resolution for ablation with a flat-top beam is worsened. As an example, Banerjee et al.⁹² demonstrated that a Gaussian beam produced craters with a diameter of ∼7–9 μm, while craters made by a flat-top beam had a size of ∼90 μm. Because the vast majority of available femtosecond lasers provide a Gaussian distribution across a beam, several studies reporting such a beam profile for mapping can be mentioned; these studies include mapping of sunflower cells,¹⁰⁸ leaves,^109,110 films on silicon^111,112 and aluminium alloys.¹¹³ There are several studies on attempts to achieve micromachining on alloys. Tong et al.¹¹⁴ examined the use of an fs-LIBS system as a diagnostics instrument for real-time control of femtosecond micromachining in the fabrication of microheater structures on thermally sprayed materials. Recently, the spectacular demonstration performed by Wessel et al.¹¹⁵ involved searching microcracks or defects in Ti–Al alloys. The spatial resolution of 2 μm allowed the detection of long and narrow cracks and microindentation zones. By comparing SEM and Ti line-LIBS images of an area under investigation, one can see in Fig. 7 that fs-LIBS allows the detection of a crack of such a length. Due to the high repetition rate of an fs laser (1 kHz), the operation of mapping is not very time-consuming. Another interesting idea related to chemical mapping by fs-LIBS is the production of precise 3D maps. More recently, Hou et al.¹¹⁶ combined 2D cross-sectional contour maps with layer-by-layer measurements. They obtained the enrichment of two surface layers by Li and Al for stuffed lithium garnets Li₇La₃Zr₂O₁₂. High depth resolution (∼700 nm) allowed this demonstration in the first instance, while the lateral resolution achieved was moderate (crater size of ∼40 μm), although a Gaussian beam was used. It may be noted that the analyte in these cases of fs-LIBS mapping was the major or, at least, a minor component.

Fig. 7 (a) SEM micrograph of Ti–Al sample surface before ablation and (b) fs-LIBS map constructed on the intensity of the Ti I line. Reproduced from Wessel et al.¹¹⁵ with the permission of Elsevier Science.

Unlike diffraction-limited beams, non-diffracting Bessel beams have a central core with diameter d expressed as follows:¹¹⁷

where a is a constant of order unity and α and n are the wedge angle of the axicon and its refraction index, respectively. Therefore, the larger the wedge angle of axicon is, the narrower the crater will be. As an example, Courvoisier et al.⁹⁶ recently demonstrated the formation of long channels with diameters of 200 nm and 400 nm, which were smaller than the laser wavelength. Moreover, the conical geometry of energy delivery from the rings to the central lobe offers high resistance to filamentation due to the nonlinear Kerr effect when compared with Gaussian beams. One more class of laser beams providing high lateral resolution is cylindrical vector beams, which are described by a solution to the vector Helmholtz equation with cylindrical boundary conditions. The mathematical aspects of cylindrical beams with radial or azimuthal polarization and experimental methods of generating such vector beams are thoroughly described in the comprehensive review by Zhan.¹¹⁸ A feature of these beams is that the polarization direction in vector beams spatially varies and affects the intensity distribution in the focus of high-NA optics. As an example, intensity distributions of a radially (TM) and azimuthally (TE) polarized beam in the focal plane of an NA = 0.9 objective, simulated by Hnatovsky et al.,¹¹⁹ are shown in Fig. 8. SEM images of craters produced by each type of pulse are also presented. Note that the crater produced by the beam possessing a longitudinal z-component of the 30 nJ single TM pulse has the size of ∼0.1λ. Thus, the small diameter of the crater that was provided by either Bessel beams or radially polarized cylindrical vector beams will allow high spatial resolution for LIBS investigations of sub-micron objects.

Fig. 8 (a) and (b) Simulated intensity distributions in vacuum of TM and TE polarized beams, respectively. SEM images of irradiation of borosilicate Corning 0211 glass samples with (c) the longitudinal component of a 30 nJ single TM pulse; (d) the transverse component of a 120 nJ single TE pulse; (e) multiple 80 nJ TM pulses; and (f) multiple 40 nJ TE pulses. The scale bar is the same for (c)–(f). Reproduced from Hnatovsky et al.¹¹⁹ with permission of the American Physical Society.

To overcome a diffraction limit in far-field optical spectroscopy, near-field microscopy is developed to observe objects on the nanometer scale.¹²⁰ The main concept of near-field scanning optical microscopy (NSOM) is to place a detector very close to the sample surface at a distance much smaller than the irradiation wavelength. To realize such a configuration, an incident beam passes through a narrow fiber probe (∼100 nm) and radiation reflected from a surface is collected by the same probe. The first demonstration of the NSOM technique with respect to LIBS measurements was carried out by Russo's group.⁴⁹ By ablating a silicon wafer with 100 fs to 0.18 nJ single laser pulse, they obtained a crater on a silicon wafer with a diameter of only 30 nm but a weak LIBS spectrum of silicon was detected with 5.9 nJ pulses, which produced a crater size of ∼1 μm. They then observed emission lines from sodium and potassium in a mica sample using a NSOM tool for a 40 nJ single pulse and the crater size was ∼450 nm.^121,122 The sensitivity of such a low energy effect was poor; for example, the average single-shot limit of detection for Na was 2700 ppm. To improve sensitivity, they incorporated a double-pulse fs to ns scheme for micrometer resolution.¹²³ By comparing NSOM technology and far-field propagation of a cylindrical beam for LIBS purposes, one can see that the latter produces a crater with a diameter of ∼80 nm, while the former can achieve craters with a size of ∼30 nm. However, the energy delivered to a surface by the two techniques is significantly different: 30 nJ in the cylindrical beam vs. 0.18 nJ for NSOM. Because LIBS spectra were detected for 40 nJ in the NSOM configuration, the capability of a cylindrical beam for higher spatial resolution in LIBS appears to be reasonable.

3.3 Signal enhancement in femtosecond LIBS

In the pioneering study⁶ on the use of a characteristic emission of femtosecond laser plasma for analytical studies, the pulse energy did not exceed 400 μJ. Based on the calibration plots, it is possible to conclude that the useful signal is roughly comparable with the experimental error in the case of the samples containing a few percent of Zn. When comparing the emission properties of laser-induced plasma, generated by pulses of various duration, it was demonstrated that, after a period of time of 10 ns, the emission intensity is basically determined by the pulse energy.¹²⁴ Sabsabi et al.¹²⁵ used a laser with an energy of 50 mJ. As a consequence, the detection limit of Ag in aluminium alloys was reported to be ∼2 ppm at pulse durations of 80 fs, 2 ps and 270 ps. However, the cost of femtosecond laser systems with an energy of dozens of mJ is very high. Moreover, an advantage of femtosecond evaporation is that a small-sized crater with minimal thermal effects can be implemented when the fluence is slightly above the ablation threshold. Under these conditions, the spectral lines of the major and some minor constituents are usually observed in the spectra of laser plasma. Although it was shown that the emission signal is proportional to the pulse energy due to the absence of plasma shielding,^126,127 an improvement in the sensitivity of fs-LIBS is more urgent compared to a conventional LIBS technique operating with nanosecond lasers. We first consider various options for optimization and improvement of the single pulse scheme.

Optical configuration. Location of the focus relative to a surface has a considerable impact on the emission signal, because it influences the crater size, spectral density, and the mechanism of laser breakdown. In the case of ns-LIBS, focusing onto the surface of a sample is preferable.¹²⁸ In a pioneering study⁶ focused on the analysis of brasses, it was shown that, in the case of fs-LIBS, the best signal-to-noise ratio was achieved when the focus was located slightly above the surface (so called prefocus). Schiffern et al.¹²⁹ demonstrated that the highest intensity of the Si I line at 288.16 nm can be observed when the laser beam is focused both under the sample surface (so called postfocus) and for a prefocus depending on the fluence. Santos et al.¹³⁰ discovered that the maximum intensity of a spectrum of a laser plume from animal tissue is referred to a focus position 1–2 mm below the sample surface.

Scaffidi et al.¹³¹ proposed that in the case of a collinear double-pulse for fs to ns LIBS, the highest intensity of a spectrum of pure Fe is observed at a focus position of 2.5 mm both above and below the sample surface. This was in good agreement with results, according to which the maximal signal was detected at a focus of 0.5 mm above/below the surface. Sometimes, the laser beam is focused directly on the surface of samples,^132–134 assuming that this leads to the maximal fluence and, as a consequence, to the highest intensity of spectra.

Finally, Zuhlke et al.¹³⁵ performed a fundamental investigation on the influence of focusing conditions on the fs-LIBS signal of silicon in a vacuum and in atmosphere. They found out that under vacuum conditions (2 Pa), there were two peaks of similar magnitude of Si I, intensity = 288.16 nm, corresponding to pre- and post-focus and a local minimum at the focus. At 1 atm, the LIBS signal had a single prefocus peak and a continual drop-off in signal through and beyond the focus. This phenomenon was attributed to continuum generation in air plasma, diminishing the energy per pulse and effectively lowering the fluence due to an increase of the total divergence angle in near and post-focus regions. The available data led to the conclusion that at the optimal fluence for the materials and semiconductors, the maximal signal can be achieved at a focus above the surface. It is also recommended to determine lens-to-sample distance (LTSD) before the analytical measurements. Despite numerous studies, it is still of great importance to continue investigations into the influence of fluence and focusing on the analytical signal as well as on the form and size of craters of dielectric samples.

Ambient atmosphere. The nature of the gas and its pressure significantly affect the laser ablation process, laser plasma evolution, and the analytical emission signal. Numerous studies devoted to the influence of an ambient atmosphere on ns-ablation have shown that the best sensitivity of LIBS can be achieved at low pressures in an atmosphere of Ar or He, depending on the element under investigation.¹⁰¹ Generally, the abovementioned factor also applies when operating with fs pulses, which is probably related to the fact that in both cases analytical measurements are performed after the end of a laser pulse and plasma interacts for quite a long period of time with the atmosphere or expands into a vacuum. It was shown that emission signal enhancement and background reduction occur under low pressures (130–530 Pa) for both lines of main (Al) and minor (Mg) components of aluminum alloys with the use of Ti:Sapphire laser (130 fs, 800 nm, 20 μJ).¹³⁰ Mateo et al.¹³⁶ observed the maximal enhancement of LIBS intensity and SNR for lines of Cu, Zn, Si, and Al at 3 kPa measured in copper, brass, silicon and aluminum alloy, respectively. The difference in optimal pressure is most likely due to the higher laser energy in the latter case (KrF excimer, 450 fs, 248 nm, 900 μJ). Higher enhancement is observed in an argon atmosphere in terms of signal intensity, while the maximum values of SNR are obtained when helium is employed for most of the studied lines. Maximal values of signal intensity or SNR are reached at 0.5 atm for both helium and argon. Nakimana et al.¹³⁷ demonstrated that temperature and electron density of laser-induced plasma determined the signal enhancement of Al and Mg lines under reduced pressure in a noble gas atmosphere (50 fs, 800 nm, 3.5 mJ). Hotter and denser plasma was observed in argon than in air and helium. They also noted that plasma parameters at relatively low pressures of argon (1 kPa) are similar to those obtained at relatively high pressures of helium (80 kPa). In fact, argon provides the best environment for femtosecond laser-induced breakdown spectroscopy only at relatively low pressures, while helium constitutes a good environment only at relatively high pressures.

A somewhat different situation was described by Harilal et al.¹³⁸ although the optimal value of SNR was observed at 2.5–6.5 kPa, the signal intensities were maximal at a pressure level of about 0.5 atm. Apparently, this is because the plasma core did not fit into the area of the plasma used for observation (1 mm above surface) within selected temporal parameters of registration (delay 100 ns, gate 1 μs). Moreover, time resolved images of the laser plume clearly demonstrated that the plasma core had been expanded and had moved rapidly away from the surface under reduced pressure and the maximal intensity of plasma emission was observed at a height significantly higher than 1 mm above the surface. To sum up, the ambient atmosphere influences the fs-plasma in the same way as it influences the ns-plasma, thus the maximal signal enhancement can be obtained at a reduced pressure in noble gases. One should keep in mind that the pulse energy obviously influences the plasma dynamics and, as a consequence, the optimal pressure value can vary. Most likely, the intensity increase of a certain line depends on electron density and temperature, for instance, the emission intensity of a plasma on a Zn target was maximal at 530–1300 Pa, depending on whether the line was atomic or ionic.¹³⁹

Pulse shaping. The above mentioned approaches to signal enhancement were not specific to fs-LIBS, although there were some differences compared to ns-LIBS. There are still some phenomena related only to the use of femtosecond laser pulses. The first of these is related to temporal or phase modulation of a laser pulse. Gunaratne et al.¹²⁶ studied the influence of pulse duration, its bandwidth and phase shaping on a LIBS signal during laser ablation of copper and aluminium (35 fs, 800 nm, 750 μJ per pulse). Pulse duration and bandwidth were varied by a box shaper and changing the number of slits, respectively; frequency domain was modified either by a sine phase function, leading to a shift in the mask with respect to the spectrum of the pulse, or by applying a variety (512) of binary phase functions. The LIBS signal was relatively insensitive to pulse duration, while it was highly dependent on the bandwidth (up to 40% signal increase). The effects of sinusoidal and binary modulation showed more modest enhancements with differences between aluminum and copper—in copper, non-modified pulses yielded the highest LIBS signal, while aluminum required greater pulse modulation, presumably due to the aluminum-oxide layer. It should also be noted that pulse shape affected the LIBS signal for gentle ablation with pulse energies three to five times higher than the breakdown threshold, when the intensity was increased to 30 times the threshold; the effect of modulation was decreased to less than 10%. Guillermin et al.¹⁴⁰ developed a sophisticated system for pulse shaping including a spatial light modulator, which allowed controlled retardation of spectral components; it tailored in turn the temporal shape of the pulse, and a closed loop with feedback to the result of the laser action. They applied an adaptive optimization loop to lock up temporal shapes for increasing the intensity of selected aluminium lines. They attempted to simplify the optimal pulse shape as two components: a pair of fs-pulses with delays of 5–15 ps and a “long” pulse with a width of 6 ps. A multiplication factor up to 3.64 was obtained due to the reduction of the neutral species emission as a consequence of femtosecond pulses and augmentation of the ionic emission by a distribution of energy in the picosecond timescale. The latter also allowed an enhancement of the total luminosity of the plasma. Subsequently, the same authors provided additional experimental data and numerical calculations to provide a deeper understanding of signal enhancement with shaped pulses.¹⁴¹ They demonstrated that an optimized pulse shape resulted in an increase in distance between the surface and the front of the plasma, maintenance of the same temperature (2600 K) in the vicinity of the surface, a higher excitation state with a smaller area associated with neutrals, and a high front temperature (∼34 000 K), producing a majority of multiple ionized aluminium atoms and a larger Al II area with the density state more than one order of magnitude higher (∼10²³ m⁻³) than for a single pulse. The same results were obtained for an fs-LIBS study of a brass alloy with pulse shape optimization.¹⁴² The regions of neutral and ionized species were formed due to an increasing temperature profile together with the corresponding ionization degrees. Neutral Cu and Zn atoms were mainly located in the vicinity of the surface, while ions were located closer to the plasma front. Hartig et al.¹⁴³ compared the effect of pulse width (45 fs to 1.5 ps) and shape resulting from application of both positive and negative chirp on SNR and peak-to-peak signal variations in fs-LIBS of copper and uranium. Although the intensities of specific lines depended on both the sign of the chirp and the pulse duration, an increase of only 27% and 18% in the SNR for uranium and copper, respectively, was observed compared to the SNR measured at the shortest pulse duration. The SNR and peak intensity were decreased for pulse durations longer than 1 ps, regardless of the chirp sign. Thus, on the basis of these relevant papers, we may conclude that pulse shaping can give some enhancement of figures of merit of LIBS measurements, especially if the technique is adapted to a specific analyte. It should also be noted that simple pulse width variation does not provide a significant increase in signal or SNR.

Continuous emission. We conclude the consideration of the potential merits of fs plasma for analytical measurements with a discussion on a continuous background signal and its ratio to atomic lines. In earlier studies on fs-LIBS, it was noted that there was a relatively low background level in emission spectra. Moreover, it was shown that a combination of non-gated detection of LIBS and high pulse rates, up to 1000 Hz, was effective in increasing the LIBS signal for a given measurement time.¹⁴⁴ Thereafter this was considered as the one of the advantages of fs-LIBS in numerous studies. However, some remarks are needed to obtain a clear description of the impact of the background on analytical results in fs-LIBS. First, the ablation thresholds are considerably lower for fs pulses than for ns ones and, as a consequence, plasma can be generated even with a pulse energy of several μJ. Second, the pulse energy is often hundreds of μJ and rarely more than few mJ. These features, together with the absence of beam–plasma interaction, result in a relatively low plasma temperature, which is apparently the main reason for the low continuum radiation level. Third, signal enhancement in fs-LIBS is usually studied on individual substances or binary alloys and, therefore, the lines of main components are considered. Taking into account that fs plasma may be denser than ns plasma, spectral interference increases for non-gated registration and lines of minor components can be strongly overlapped with lines of the main component. le Drogoff et al.¹⁴⁵ demonstrated theoretically and experimentally that dependence on the continuum emission appears to be similar for different pulse durations (fs to ns) for pulses with high-energy (50 mJ). They concluded that laser-produced plasmas evolve through similar transient states, the only difference being that these states were reached at different delays after the laser shot. Thus, the temporal gating parameters are still important for analytical measurements and it is preferable to choose them for each laser pulse duration if possible.

This observation is also in agreement with a study of fs and ns LIBS of brasses by Freeman et al.¹⁴⁶ The intensity of background radiation was high for at least 100 ns after an ns pulse, while it became negligible after 25 ns for an fs pulse. Moreover, there were attempts to reduce continuum radiation by a specific process in fs laser plasma. In particular, Liu et al.¹⁴⁷ reported that continuum emission of the plasma produced in femtosecond ablation of Si could be polarized. Later, the same authors tried to apply this effect to LIBS measurements of aluminium,¹⁴⁸ copper and graphite¹⁴⁹ to cut off continuum emission and enhance signal-to-background ratio (SBR) with the use of a polarizer. Unfortunately, mainly scattered laser light (s- or p-polarized) was removed by the polarizer, while only approximately 15% of the continuum was polarized due to its reflection by the target surface and polarization of the outgoing radiation in accordance with the Fresnel equations.¹⁵⁰

Molecular fragments. Low plasma temperatures and low thermal effects during ejection of matter, especially near an ablation threshold, result in the production of molecular fragments of the ablated substance. This is evidently a drawback for most elemental analysis but this makes it possible to correlate the emission of molecular species to the organic content in ablated material.¹⁵¹ Thus, the generation of molecular fragments enhances the possibilities of LIBS for the analysis of organic materials. Primarily, this feature of fs-LIBS was applied to the detection of explosives on a surface.^152–156 A high yield of molecular species is an undoubted improvement for isotopic elemental analysis, since molecular isotopic shifts are usually larger than the atomic ones. Yee et al.¹⁵⁷ used the characteristic molecular spectra of two boron isotopes to reconstruct the boron isotopic ratio by fs-LIBS. More recently, Russo's group,^158,159 developing laser ablation molecular isotopic spectrometry (LAMIS), suggested the use of fs-LIBS for the isotopic analysis of five Zr isotopes in the form of their oxides.

Double pulse. The use of a double pulse (DP) regime is one of the most common and efficient techniques for signal enhancement in LIBS.^160,161 This can be used in fs LIBS to some extent. The results of the studies devoted to the use of a DP regime in fs LIBS for signal enhancement are summarized in Table 1. In most cases, an enhancement factor was calculated as a ratio of the line intensity in a DP regime to that in an SP regime. Although all possible DP configurations were considered (collinear, orthogonal with pre-spark and reheating), there are some limitations due to the high cost of an fs laser and low pulse energy. First, all studies with a pair of fs pulses employed one laser with either temporal shaping of a pulse inside a laser or optical delay. As a result, a delay varied within the range of 0–1 ns. Second, the energy of re-heating an fs pulse was relatively low in comparison with that of re-heating an ns pulse. The latter limitation was successfully overcome by the use of an additional ns laser, which was reported for the first time by Scaffidi et al.¹³¹ An orthogonal ns pulse can deliver enough energy to reheat plasma while preserving the advantages of fs ablation. Moreover, such a combination provided the highest enhancement of signal intensity, up to 360-fold (see Table 1). A collinear scheme can provide much lower signal enhancement, which is presumably due to low pulse energy. Unfortunately, the majority of studies involving the use of a DP regime in fs-LIBS covered only ablation of individual substances and often monitoring of resonance atomic lines. Thus, the effect of a DP regime on signal enhancement can be mixed with the effects of self-absorption, and the possible spectral interference was also not evaluated. Only a few studies, for example ref. 162, have examined the influence of a DP regime on figures of merit of an analytical procedure. The leading mechanism of signal enhancement can be related to plasma reheating¹⁶³ and atomization of nanoparticles,¹⁶⁴ of which the generation by fs-LIBS was discussed earlier in Part 2.

Table 1 Emission signal enhancement with the use of a DP regime^{123,127,129,173–200}

Sample	Analytical line, nm	Lasers in DP combination	Optical scheme, interpulse delay, other conditions^a	Enhancement factor
a O – orthogonal scheme, C – collinear scheme. b This value was obtained in terms of a decrease in a signal detection threshold. c This value was obtained near the ablation threshold. d In terms of electron density and excitation temperature.
Pure copper	Cu I 515.32	100 fs, 800 nm, 6 mJ + 7 ns, 1064 nm, 30 mJ	O (ns spark 1 mm height), 5 μs	30
	Cu I 324.75	80 fs, 800 nm, 1 mJ + 1 mJ	C, 106 ps	11
	Cu I 324.75	120 fs, 800 nm, 50 J cm^−2 + 50 J cm^−2	C, 106 ps	9
	Cu I 510.55, 515.32, 521.82	250 fs, 527 nm, 0.6 J cm^−2 + 0.6 J cm^−2	C, 2 ns, 200 ps, 10^−9 bar	4.5–6.5
	Cu I	100 fs, 800 mm, 25 μJ + 25 μJ	C, 300 ps, 10^−4 Pa	4
	Cu II 490 (unresolved), Cu II 505.18	250 fs, 527 nm, 0.6 J cm^−2 + 0.6 J cm^−2	C, 2 ns, 200 ps, 10^−9 bar	6.5–11
Bronze, brass	Cu I 282.44, 465.11	250 fs, 527 nm, 3 mJ + 7 ns, 532 nm, 45 mJ	O (ns spark 0.5 mm height), 8 μs	70–280
	Cu I 465.11, 510.55, 515.32, 521.82	100 fs, 800 nm, 0.5 mJ + 0.5 mJ	C, 27 ps	3.5–5
	Cu I 521.82	100 fs, 800 nm, 10 mJ + 5 ns, 1064 nm, 150 mJ	O (fs spark 0.6 mm height), 3.5 μs	2.5–4
	Cu I 450.94	450 fs, 248 nm, 0.5 mJ + 0.5 mJ	C, 200–400 ps	9.5 (2^b)
	Zn I 481.05	450 fs, 248 nm, 0.5 mJ + 0.5 mJ	C, 200–400 ps	7.2 (2^b)
	Zn I 481.01, 472.21, 481.05	100 fs, 800 nm, 0.5 mJ + 0.5 mJ	C, 27 ps	3.5–5
	Zn I 472.21	250 fs, 527 nm, 3 mJ + 7 ns, 532 nm, 45 mJ	O (ns spark 0.5 mm height), 8 μs	14
	Sn I 284.00	250 fs, 527 nm, 3 mJ + 7 ns, 532 nm, 45 mJ	O (ns spark 0.5 mm height), 8 μs	30
	Pb I 280.20	250 fs, 527 nm, 3 mJ + 7 ns, 532 nm, 45 mJ	O (ns spark 0.5 mm height), 8 μs	10–15
Pure gold	Au I	100 fs, 800 mm, 25 μJ + 25 μJ	C, 200 ps, 10^−4 Pa	5.3
Pure aluminum	Al I 394.40, Al I 396.15	100 fs, 800 nm, 6 mJ + 7 ns, 1064 nm, 30 mJ	O (ns spark 1 mm height), 5 μs	80
	Al I 396.15	100 fs, 800 nm, 10 mJ + 5 ns, 1064 nm, 150 mJ	O (fs spark 0.6 mm height), 55 μs	3–3.5
	Al I 394 + 396 (unresolved)	30 fs, 785 nm, 125 nJ + 125 nJ	C, 800 ps	6
	Al I 394.4, 396.15	150 fs, 800 nm, 0.5 mJ + 0.5 mJ	C, 9 ps, 10^−5 Pa	0.5
	Al II 358.7, 466.3, 559.32	150 fs, 800 nm, 0.5 mJ + 0.5 mJ	C, 9 ps, 10^−5 Pa	1.7–3.5
	Al II 281.62	450 fs, 248 nm, 0.5 mJ + 0.5 mJ	C, 400 ps	5.6
Aluminum alloy	Al I 396.152	50 fs, 800 nm, 40 μJ + 40 μJ	C, 150 ps	4.3
	Al I 396.152	50 fs, 800 nm, 40 μJ + 40 μJ	C, 150 ps, Ar jet	3
	Mg I 518.36	50 fs, 800 nm, 40 μJ + 40 μJ	C, 150 ps	7.5
	Mg I 518.36	50 fs, 800 nm, 40 μJ + 40 μJ	C, 150 ps, Ar jet	2
Pure titanium	Integral Ti I (430.6, 445.7, 453.6)	100 fs, 620 nm, 2 mJ + 2 mJ	C, 0.9 ns, 10^−6 Torr	2–7
	Ti I 451.80	250 fs, 527 nm, 0.8 mJ + 7 ns, 532 nm, 25 mJ	O (ns spark 1 mm height), 500 μs	35
	Ti I 453.3 + 453.5 (unresolved)	30 fs, 785 nm, 125 nJ + 125 nJ	C, 800 ps	2.5
	Integral Ti II (334.9, 368.5, 375.9, 376.1)	100 fs, 620 nm, 2 mJ + 2 mJ	C, 0.9 ns, 10^−6 Torr	2–7
	Ti II 346.15	250 fs, 527 nm, 0.8 mJ + 7 ns, 532 nm, 25 mJ	O (ns spark 1 mm height), 500 μs	500
	Ti III 251.60	250 fs, 527 nm, 0.8 mJ + 7 ns, 532 nm, 25 mJ	O (ns spark 1 mm height), 500 μs	900
Pure iron	Fe II 274.65	450 fs, 248 nm, 0.5 mJ + 0.5 mJ	C, 400 ps	9.1
Steel	Fe I 438.41, Fe II 419.95	350 fs, 257.5 nm, 10 μJ + 1030 nm, 10 μJ	C, 40 ps	3–5
	Cr I 425.48, Cr II 449.71	350 fs, 257.5 nm, 10 μJ + 1030 nm, 10 μJ	C, 40 ps	3–5
CMSX-4 superalloy	Ni I 352.45	150 fs, 775 nm, 160 μJ + 640 μJ	O (2^nd fs spark 30 μm height), 10.36 ns	∼500^c (9^b)
	Cr I 425.44	150 fs, 775 nm, 160 μJ + 640 μJ	O (2^nd fs spark 30 μm height), 10.36 ns	∼500^c (9^b)
	Al I 394.40	150 fs, 775 nm, 160 μJ + 640 μJ	O (2^nd fs spark 30 μm height), 10.36 ns	∼500^c (9^b)
Pure nickel	Ni I 447.047, 464.865, 478.653, 547.691	33 fs, 810 nm, 0.2 mJ + 0.2 mJ	C, 50 ps	5–13
Bilayer Ag/Al plate	Al I 394.40, 396.15	60 fs, 800 nm, 0.3–30 μJ + 0.3–30 μJ	C, 104 ps	7–3.5
	Ag I 405.85, 421.62, 431.32, 520.91, 546.54	60 fs, 800 nm, 0.3–30 μJ + 0.3–30 μJ	C, 104 ps	13–3
Pure silicon	Si I 288.16	450 fs, 248 nm, 0.5 mJ + 0.5 mJ	C, 400 ps	4.3
	Si I 288.16	800 μJ pulses with 50 fs, 800 nm, 125 μJ + 125 μJ	C, 0–80 ps	1.1–2
	Si I 288.16	100 fs, 800 nm, 28 μJ + 28 μJ	C, 60 ps	2
	Si I 212.41, 221.67, 243.52, 251.61, 288.16	100 fs, 800 nm, 1 mJ + 1 mJ	C, 70 ps	1.2^d
	Si II 505.6	80 fs, 800 nm, 1 mJ + 1 mJ	C, 106 ps	6
	Si II 505.6	100 fs, 800 nm, 28 μJ + 28 μJ	C, 60 ps	2
Single-crystalline silicon	Si I 252 (unresolved), 288.16	500 fs, 343 nm, 400 nJ + 6 ns, 355 nm, 1.5–3 mJ	O (ns spark 45 μm height), 500 ns	360
Pure boron	B II 412, 477, 497, 700	150 fs, 800 nm, 0.5 mJ + 0.5 mJ	C, 15 ps, 10^−5 Pa	1–1.4
BaSO4	Ba II 455.40	450 fs, 248 nm, 0.5 mJ + 0.5 mJ	C, 400 ps	8.1
CaF2	Ca II 317.93	80 fs, 800 nm, 1 mJ + 1 mJ	C, 106 ps	2
Gd2O3	Gd I 419.08, Gd II 409.86	100 fs, 800 nm, 2 mJ + 532 nm, 10 ns, 30 mJ	O (ns spark 0.9 mm height), 2–4 μs	10–25
Polymethyl methacrylate-PMMA	Ca II 393.4, 396.8	45 fs, 800, 300 μJ + 300 μJ	C, 80 ps	6.5
	Ca I 422.6, Na I 589.0, 589.6	45 fs, 800, 300 μJ + 300 μJ	C, 80 ps	4
	CN 388.3, C2 516.5	45 fs, 800, 300 μJ + 300 μJ	C, 80 ps	2
	CH 431.4	45 fs, 800, 300 μJ + 300 μJ	C, 80 ps	1.5
Air	Intensity at 400, 450, 500	120 fs, 800 nm, 86 μJ + 26 μJ	C, 40 ps	5
	N II 500.5	33 fs, 810 nm, 0.8 mJ + 1.0 mJ	O, 0 fs	32
	H I 656.2	33 fs, 810 nm, 0.8 mJ + 1.0 mJ	O, 0 fs	8
	N I 746.8	33 fs, 810 nm, 0.8 mJ + 1.0 mJ	O, 0 fs	7.5
	O I 777.2	33 fs, 810 nm, 0.8 mJ + 1.0 mJ	O, 0 fs	6

---

Besides traditional applications of a DP regime for signal enhancement, there are a number of studies^165–168 that describe the use of a second pulse as a probe to study the evolution of plasma, including the evaluation of nanoparticle compositions.

3.4 Self-absorption

Self-absorption effect is stronger for the fs-LIBS technique than its ns equivalent. By comparing ablation of copper alloys by 80 fs and 270 ps pulses, le Drogoff et al.¹²⁵ observed the strong deviation of a calibration curve for an Ag resonance line from linearity in the range of 100–450 ppm. They tried to achieve the best sensitivity with high energy pulses of ∼50 mJ per pulse and a fluence of ∼20 J cm⁻² due to the absence of plasma shielding with the use of femtosecond pulses. However, self-reversal of a resonance Mg line as well as self-absorption of a resonance Ag line were considerably more pronounced as the laser pulse duration was reduced. To explain this behavior, the authors assumed that two factors acted in combination: the higher ablation efficiency of femtosecond laser ablation¹⁶⁹ resulted in a higher number density of atoms, while a lower plasma temperature¹⁷⁰ increased the population density of the ground-state species. Elhassan et al.¹⁷¹ demonstrated similar behavior with Zn/Cu, Sn/Cu, and Pb/Cu ratios in the ablation of bronze alloys by 500 fs pulses of 11.2 mJ. At the same time, there were no significant differences in the plasma temperature and the electron density between nanosecond and femtosecond ablation under their experimental conditions. Fornarini et al.¹⁷² observed that calibration graphs for lead and tin had a tendency to show lower than linear dependences regardless of pulse duration. They used two fs-systems with fluences of 6.5 J cm⁻² (8.2 mJ per pulse) and 15 J cm⁻² (3.0 mJ per pulse). In this case, the authors have attributed their observations to the so-called phenomenon of “fractionation” because calibration curves for Zn/Cu ratios were close to linear for nanosecond and femtosecond ablation of bronze alloys. Similarly, Margetic et al.⁶ demonstrated the absence of a non-linear trend in a calibration curve for Zn/Cu ratios for brass alloy ablation at different pressures and laser fluences. In any case, possible strong self-absorption should be taken into account when choosing between fs-LIBS and ns-LIBS as an analytical method.

4 Filament-induced breakdown spectrometry (FIBS)

4.1 Filament-induced breakdown spectrometry basics

The unique LIBS capability to perform express elemental analysis of a remote sample makes this method very suitable for military and safety applications as well as space exploration missions (ChemCam instrument in the Curiosity mission by NASA). However, conventional ns-LIBS is limited to a distance of a hundred meters due to the difficulty in delivering high laser intensities that are sufficient to induce ablation and ionization of the remote target. There are two main limiting factors: diffraction from focusing optics and fluctuation of atmospheric optical properties. Ideally, the focal plane of a lens should be equal to the distance between the laser and sample but even high quality optics suffer from spherical aberrations at a distance of several tens of meters. To overcome this, a large and heavy optical system should be constructed that limits the mobility of a remote LIBS system. A second problem that cannot be solved, even with an ideal optical system, is the fluctuation of atmospheric optical properties for an optical path length of several tens of meters. Fluctuation in the refractive index of air (turbulence vortexes) is generally combined with aerosol particle movements, which together completely distort a laser beam at a distance of several tens of meters.²⁰¹ Increasing the efficiency and measurement range and improving the signal-to-noise ratio are important issues for LIBS applications.

To the best of our knowledge, conventional remote sensing of a solid target with fs laser pulses was only studied by Rohwetter et al.²⁰² They used positive chirping to prevent filamentation. Such a variant of remote LIBS appears to be unproductive because it offers no benefits compared to nanosecond remote LIBS, bearing in mind the increase in complexity and the cost of the fs system. A new era of laser-assisted remote elemental analysis was started when filaments were used to produce plasma on a solid sample surface. The capability of filamentation to overcome diffraction limits and deliver high laser intensities at long distances without focusing was demonstrated in the early 2000s.^39,203,204 However, the first application²⁰⁵ of filaments to the remote induction of laser plasma was made by Teramobile's team in 2004 for samples located at a distance of 90 m. Teramobile's system consists of a terra-watt laser and a detection system installed in a 20-foot standard freight container, allowing field measurement campaigns. A detailed description of the system and the main results of the project can be found in numerous studies^206–211 as well as at Teramobile's official site.²¹²

Thereafter, such a variant of LIBS was more frequently named filament-induced breakdown spectrometry (FIBS), and we will also use this term in this review. In the above mentioned pioneer study, the femtosecond non-focused laser beam (800 nm, 80 fs, 250 mJ) initiated multiple filaments (up to 30) at 7 m from the pure metal samples (Cu and Al), which were located 90 m from the system.²⁰⁵ Filament-induced plasma emission was collected by a 20 cm telescope and guided to a spectrograph equipped with a gated detector. The spectra revealed the absence of broad–band emission within the first 100 ns, indicating a low temperature and electron density in the plasma. Atomic lines of Cu I and Fe I were clearly observed with a better contrast compared to a nanosecond LIBS system. In the next Teramobile study on FIBS,²¹³ the length and initiation point of a filament from a target was optimized by varying the beam diameter and chirp. Line emission from a metallic target was registered at distances up to 180 m from the laser. Moreover, the authors assumed that this distance could be extended up to 1 km and is restricted only by the collecting optics and the detector efficiency. This is the principal advantage of FIBS over remote ns LIBS systems with laser beam focusing, which is of great interest with respect to the remote sensing of dangerous or unreachable sites like explosives or chemical pollutants.

4.2 Filament-induced ablation

Filament-induced ablation can be defined as the ablation of a solid/liquid surface by a femtosecond pulse with a power density above the filamentation threshold in surrounding media. In other words, ablation is induced by both the filaments and the femtosecond laser pulse. It should be noted that filaments contain only a small fraction of energy compared to a laser pulse (less than 1%)^21,36,205 but plasma channels (filaments) change laser–matter interaction. The majority of studies on FIBS were focused on the feasibility proof of remote analysis for different types of samples, i.e. the detection of atomic/molecular spectra from a large distance for major sample components. The physics of filament-induced ablation and the resulting plasma have been studied superficially in a few studies.

Crater studies were carried out for a 5 cm diameter femtosecond laser beam that ablated a remote copper target.²¹³ Multiple craters (up to 30) with 100–200 μm diameters were formed by individual filaments. The authors studied the influence of optical path length on crater properties. They compared craters produced on metallic plates located at 25 and 90 m from the laser by a beam producing multiple filaments (each ∼100 μm in diameter). The diameter of the first crater was about 5 mm (compare with 50 mm laser beam at laser output), while the second crater diameter was significantly larger (about 30 mm). The authors explained this as being due to a random walk of the filament around its mean position due to fluctuations in the air and the stochastic nature of multifilamentation. For smaller distances (up to 50 m) in air, the crater diameter did not change, as was shown for filament-induced (800 nm, 180 fs, 25 mJ) ablation of GaAs.²¹⁴ A direct comparison of femtosecond and filament-induced ablation has been carried out by Valenzuela et al.²¹⁵ Under the same experimental conditions Ti:Sapphire laser pulses (800 nm, 100 fs, 25 mJ) were sharply focused (no filamentation), slightly focused (assisted filamentation) and self-focused (filamentation) on steel and titanium targets. A crater study revealed a substantial decrease in evaporated mass for filament-induced ablation compared to femtosecond (sharply focused) ablation.

Plasma emission duration did not exceed several hundred nanoseconds, compared to a time scale of a few microseconds for non-filament ablation by femtosecond or nanosecond pulses. For example, filament-induced plasma on a copper target could be detectable for the first 130 ns (conditions: 800 nm, 80 fs, 250 mJ per pulse, 10 Hz); this did not depend significantly on the distance between laser and target.²¹³ A twelve times longer plasma emission duration (1 μs) was detected for molecular species in the case of organic film sampling.²¹⁶

Broadband emission for femtosecond induced plasma is significantly lower compared to pico/nano-second cases.²⁰² However, FIBS provided the smallest continuum background emission compared to fs/pico/nano second pulses.^205,217 First, fs-LIBS provides a colder plasma with faster decay compared to ns-LIBS.¹⁴⁶ Second, the electron density in filaments is two-three orders lower compared to fs-LIBS, thus reducing broadband emission from plasma. The continuum emission for filament-induced plasma can originate from supercontinuum generation during filament propagation in air. Nevertheless, supercontinuum emission spreads within a narrow cone and its intensity is linearly proportional to the propagation distance. Consequently, this process can be effectively controlled by a chirping technique (see further in the text). In addition, the background emission level can be substantially decreased when strong and short filaments are formed to induce plasma, thus even non-gated detectors can be used.²¹⁷

Filament-induced plasma temperature and electron density was measured by Xu et al.²¹⁸ The electron density was measured by Stark broadening of Pb I lines to decrease within 200 ns from 8 × 10¹⁷ to 1 × 10¹⁷ cm⁻³. The plasma temperature was measured by the Boltzmann plot method and was shown to decrease from 7000 to 4500 K during the first 100 ns. Judge et al.²¹⁹ studied the plasma temperature induced by a filament on composite graphite samples at a distance of 6 m. A significant difference in plasma temperature (9000 vs. 5500 K) calculated from atomic lines (Al I, K I) and molecular bands of C₂ (Swan system) was obtained. The authors explained this fact to be due to non-equilibrium plasmas formed on different micro domains in the samples that were superimposed by multiple filaments.

Ambient air properties (air turbulence and aerosols) influenced filament properties and consequently filament-induced plasma. The total area of sampling by multiple filaments strongly depends on air turbulence.^213,214 The influence of temperature, pressure, humidity and precipitation (snow) on FIBS signals has been investigated by Xu et al.²²⁰ A compact laser system was used to perform an FIBS study under polar conditions. Femtosecond laser pulses (800 nm, 45 fs, 225 mJ) induced filaments in air at temperatures below −10 °C under clear sky and snowy conditions. Strong turbulence in the air was observed due to a 40 degree temperature gradient between the measuring system and the target. Moreover, dense snow fall and weak fog lowered the air visibility to 3.2 km, and therefore significantly suppressed measured signals. Despite the adverse conditions, resonance Al I lines were detected with a high signal-to-noise ratio at a distance of 60 m. The maximum distance was estimated to be 730 m for clear-sky conditions.

4.3 Optimizing filament-induced breakdown spectrometry

Laser wavelength. Although near infrared (IR) Ti:Sapphire lasers are common in FIBS due to their availability, there are a few studies with ultraviolet (UV) ones. The results of impact on plasma properties are contradictory. UV filament ablation resulted in more effective atomization and molecule collapse in the case of complex inorganic or organic material,²²¹ while a sufficient increase in molecular fragment (CN, NH₂) formation in comparison with IR radiation was observed for dinitrotoluene and ammonium perchlorate.²²² It is obvious that systematic study of the mechanisms by which wavelength influences filament-induced ablation would be extremely desirable.

Pulse chirping. Tuning of pulse chirping allows precise control of filament initiation.²¹ Optimization of chirping was performed by Rohwetter et al.²¹³ Detailed experimental studies (800 nm, 80 fs, 250 mJ per pulse, 10 Hz) revealed that filament-induced plasma atomic emission increases significantly if the filament is initiated several meters from the target. The optimal chirp duration was explained by the dynamic nature of multiple filamentation.

Laser beam energy is not effectively used for the excitation of filament-induced plasma due to defocusing and lowering peak intensity of the laser beam at filament clamps, resulting in slight conversion of pulse energy into plasma. Zeng et al.²²³ suggested spatio-temporal chirping to increase peak intensity in a filament core. Two cylindrical lenses (concave and convex) confined the beam to an elliptical profile. The filament length was significantly shorter than for the initial laser beam. This was explained by the spatial separation of different components at the focus and a chirp-free pulse in the focal spot. Nitrogen molecule ionization increased by one order of magnitude in the filament core. The suggested technique can be of great interest for improving the spatial resolution for LIDAR applications while retaining the capability of filament initiation at any position for long distances. The same authors observed²²⁴ a significant (3–5 times) intensity increase in atomic lines of Al and Fe with the use of a spatio-temporal chirped pulse (800 nm, 50 fs, 8 mJ) for FIBS of aluminum and steel samples. Consequently, the spatio-temporal chirping technique allows initiation of the filament at longer distances and more effective conversion of laser energy.

Focusing optics. An alternative method is to use focusing optics to control filament initiation at a short range (less than 500 m). Formation of short and intense filaments near the target resulted in low-level continuum emission of plasma, allowing the use of non-gated detectors.²¹⁷

4.4 Applications

Most applications of FIBS are associated with the unique capability of filamentation to conserve laser beam divergence without any optical systems at distances up to 20 km.²⁸ Moreover, it was demonstrated that remote analysis of a distant object can be performed by FIBS even under snowy conditions.²²⁰

Filament-induced breakdown spectrometry applications. Teramobile team initiated FIBS by a demonstration of plasma formation with a filament on a remote target.²⁰⁵ In subsequent studies, they tested a variety of pure metals (such as Al and Ti) as a target, while other research groups focused on various complex samples like biological or cultural heritage objects. The main experimental parameters and results for remote sensing by filaments are summarized in Table 2.

Table 2 Remote sensing applications by filament-induced fluorescence and plasma spectroscopies. For better view, the data was sorted for ascending laser to sample distance

Analyte	Matrix	Distance (estimated)^a, m	Laser parameters	Conditions	Reference
a Experimental distance between laser system and sample is presented first, while the estimated maximum distance is shown in brackets.
Cu I, Fe I	Copper, steel	180 (up to 1000)	800 nm, 80 fs, 250 mJ	Open air; field conditions	205 and 213
Al I	Aluminum	60 (730)	800 nm, 45 fs, 225 mJ	Open air, −20 °C, snowing	220
Al I, Mg II	Aluminum	50 (1900)	800 nm, 90 fs, 108 mJ	Lab air	217
Ca I, PH2, NH2, CN	White egg, yeast	50 (1500)	800 nm, 45 fs, 7 mJ	Lab air	225
K I, Al I, C2	Composite graphite	6	800 nm, 60 fs, 3 mJ	Lab air	219
Mg I	White marble, red clay	6 (not estimated)	248 nm, 450 fs, 20 mJ	Air	221
Pb I	Lead	5 (325)	800 nm, 45 fs, 12 mJ	Lab air	218
Cr I	Leaves, soil	0.95–1.03	800 nm, 50 fs, 4 mJ	Lab air
Si I, Mg I, Ca I, Al I, C2, CN	Corn, barley wheat	4 (not estimated)	800 nm, 45 fs, 12 mJ	Air; laboratory conditions	226
CN, NH2	Dinitrotoluene, ammonium perchlorate	1.5 (not estimated)	266 and 800 nm, 100 fs, 15 mJ	Lab air	222

---

Tzortzakis et al.²²¹ made the first step towards FIBS analysis of cultural heritage, studying elemental compositions of typical materials in sculptures and large monuments (white marble, red clay, and limestone) at a distance of 4.5 m. The authors were able to distinguish these materials by small differences in their spectral features (for example, Mg I lines for red clay).

The feasibility of FIBS classification of biological objects was described in ref. 225. Egg white and yeast were sampled by filaments at a distance of 6 m. The spectra had low levels of broadband emission (continuum) and contained atomic lines (Ca, Na) and molecular bands (NH₂, PH₂, CN) of major components. The more complex goal of agricultural sample differentiation (wheat, barley and corn) by FIBS was undertaken in ref. 226. Samples were pressed into pellets and then sampled by FIBS at a distance of 4 m. The spectra were quite similar (C₂ and CN molecular bands and Si, C, Mg, Al, Na, Ca, Mn, Fe, Sr and K lines) due to the samples having almost the same elemental composition. Despite this, the authors were able to distinguish three types of samples from intensity ratios in the plasma spectra. Recently, it was demonstrated that FIBS can be used for monitoring of toxic metals such as Cr in leaves²²⁷ and soils²²⁸ but this was only tested at a short distance (∼1 m).

Detection of explosive material (dinitrotoluene and ammonium perchlorate) on metal plates by UV FIBS was demonstrated in ref. 222. Molecular bands of CN and NH₂ were detected at a distance of 50 m. However, the authors have not described any attempts to identify explosive/non-explosive materials by FIBS. Another team has tried to identify organic films as test samples for detection of explosive materials.²¹⁶ Two polymers, namely, poly methyl methacrylate (PMMA) and Futurex were ablated by a filament in air. Surprisingly, the authors detected strong CN molecular bands without any molecular nitrogen emission in PMMA plasma spectra. These results indicate that, despite a unique capability to induce plasma at long distances by filaments, a lot of investigations have to be carried out towards meaningful explosive discrimination by FIBS.

Isotopic analysis of zirconium by FIBS was recently performed at distances up to 7 m by Russo's group.¹⁵⁹ Besides semi-quantitative isotopic analysis without the use of calibration standards, they investigated the properties of plasmas generated at different filament propagation distances.

Filament-induced fluorescence spectrometry applications. Similar to FIBS and a prospective application of filaments is the use of plasma initiation in the atmosphere itself to study the fluorescence of gas species. Multigas pollutants at the sub-ppm level were quantitatively detected by this technique (800 nm, 45 fs, 6 mJ).²²⁹ Mixtures were analyzed using a genetic algorithm, showing good concentration agreement within an error of 25%. Laboratory vs. field measurements of methane in air were directly compared at a distance of 10–30 m.²³⁰ The authors detected at least 1% CH₄ added to air at a distance of 20 m with filaments produced by a Ti:Sapphire laser (800 nm, 45 fs, 190 mJ, 10 Hz) in the laboratory, while field measurements in open air showed worse results for CH₄ analysis (reproducibility and sensitivity) due to the strong influence of turbulence vortexes on filament formation. Filament-induced fluorescence spectrometry proved to be an effective tool for detecting different objects: gases,²³¹ water clouds,²³² and aerosols.²³³ A series of review studies can be recommended for further reading on remote sensing of gases by filaments.^21,234,235

5 Conclusion

In conclusion, femtosecond laser pulses are believed to provide a brighter future for numerous LIBS applications due to the absence of fractionation; improved spatial resolution; and lower ablation threshold. This can be useful for applications, where minimal invasion is required, such as analysis of artefacts^{171,236–238} and biological samples,²³⁹ or even bacterial classification.^240,241 Besides this, the fs-LIBS technique can be successfully used as an assistant monitoring tool in such applications as micromachining or surgery,^242,243 where fs lasers are used. However, to date, femtosecond laser systems with single pulse energy in the range of a few mJ are still very expensive and very complex for conventional LIBS measurements. Because femtosecond lasers provide low ablation thresholds, the plasma near the threshold has a low level of background emission; unlike nanosecond ablation, one could expect an improvement in LIBS sensitivity in terms of better limits of detection (LOD). The typical repetition rate of femtosecond lasers is in the kHz range, thus a long exposure time for a non-gated detector can be applied to sum thousands of spectra in a CCD matrix over several seconds, which significantly increases the signal-to-noise ratio, thus improving the sensitivity of fs-LIBS. However, a lower plasma temperature and a shorter plasma life for fs-LIBS should limit the total intensity. In Table 3, we have collected the best LODs available in the literature to weigh the pros and cons of detection capabilities of fs- and ns-LIBS. To avoid matrix effects, we gathered LOD values for matrices matched as closely as possible. For example, LODs given for “Thin films or coatings” were retrieved for films of oil or other coatings on the substrate. Moreover, such a division allows the elimination of spectral interferences of main components. Indeed, comparison of LODs for Mn between Cu alloys for fs-LIBS and Fe-alloys for ns-LIBS appears to be unreasonable. We have also tried to gather values obtained for the same analytical line of an element. However, several elements (such as Fe) are presented by different lines. Because there is a large amount of data on enhancing LIBS sensitivity, in Table 3, data for single-pulse LIBS are given only to avoid inappropriate comparison between techniques. This means that no values for double-pulse techniques, laser-induced fluorescence, resonance ablation or sorption on a specific matter are listed. Because values for laser fluence are not given by some authors, we compared laser energy per pulse only. Fs-LIBS at approximately the same pulse energy has, in general, higher values of LODs than ns-LIBS in spite of the higher ablation efficiency, i.e. the sensitivity of fs-LIBS is, at least, the same as of ns-LIBS. Therefore, such an expensive tool as fs-LIBS cannot be considered as the best practical way to improve sensitivity.

Table 3 Comparison of the best LODs (in ppm) known for femtosecond and nanosecond single-pulse LIBS. The total number of laser shots delivered to a sample and used to accumulate spectra is given in brackets

Element	Femtosecond LIBS			Nanosecond LIBS
Alloys
Ag	1.4	50 mJ (400)	Ref. 125	0.2	60 mJ (100)	Ref. 244
Cu	3.2			1
Si	30			8
Ni	10			7	60 mJ (1000)	Ref. 245
Fe	22	50 mJ (100)	Ref. 170	3.7	60 mJ (100)	Ref. 244
Mg	2.1			0.13	60 mJ (1000)	Ref. 245
Mn	6.7			2	60 mJ (50)	Ref. 246
Water
Al	0.19	1.1 mJ (4000)	Ref. 247	0.7	≤100 mJ	Ref. 248
Ca	0.01			0.003	16 mJ (12)	Ref. 249
Mg	1			0.1	150 mJ ()	Ref. 250
Na	0.0009			0.0004	16 mJ (12)	Ref. 249
Zn	2.5			0.05	14 mJ (30)	Ref. 251
Ba	0.08	1 mJ (4000)	Ref. 252	0.007	16 mJ (12)	Ref. 249
Cu	0.78			0.39	90 mJ (500)	Ref. 253
Fe	2.6	7 mJ (10 000)	Ref. 254	37	40 mJ (100)	Ref. 255
Tissue
Al	29	840 μJ (500)	Ref. 256	0.82	80 mJ (1200)	Ref. 257
Thin films or coatings
Mg	3010	221 μJ (1)	Ref. 258	0.24	90 mJ (200)	Ref. 259
Leaves
Ca	0.007	1.5 mJ (15)	Ref. 260	0.007	70 mJ (15)	Ref. 260
Cu	7			1
Fe	12			3
Mg	0.02			0.01
Mn	2			1
P	0.4			0.1
Zn	80			4

---

Improved resolution in 2D and 3D mapping applications was demonstrated by fs-LIBS. Under the best conditions, conventional ns-LIBS systems can provide spatial resolution of ∼50 μm.²⁶¹ Other problems associated with “long” laser pulses are thermal ablation effects and higher ablation thresholds, which are responsible for “matrix effects”. As a result, spatial resolution for ns-LIBS is limited by materials, their surface morphology and their compositions.²⁶² Craters with sizes less than diffraction-limited laser beam diameters can be produced due to the absence of a heat-affected zone for femtosecond laser ablation. NSOM technology combined with femtosecond laser ablation can achieve crater diameters as small as 450 nm,¹²¹ which are visible on an fs-LIBS spectrum. Interesting achievements in operating with ultrafast laser beams, especially cylindrical vector beams,¹¹⁹ give expectations of a new breakthrough for fs-LIBS with a spatial resolution below 80 nm. Another unique capability of fs-LIBS is high-resolution depth profiling of layers or coatings. For example, a depth sensitivity of about 3 nm (ref. 98) has been recently reported in thickness measurements of buried layers. However, either high depth sensitivity or high spatial resolution can be achieved in fs-LIBS. Thus, a Gaussian beam provides small and deep craters, while a flat-top beam produces wider and shallower ablation craters. It should be noted that the higher the spatial resolution, the lower the sensitivity will be because an increasingly smaller mass (and number of atoms) is ablated with an increasing concentration of beam energy in a space.

In spite of the poor detectability of single pulse fs-LIBS, the spatial resolution allows microanalytical measurements that result in minimal sample damage. For example, fs-LIBS was recently tested with respect to the detection of cancer antigen 125 in blood plasma.²⁶³ The combination of efficient energy coupling and a lower ablation threshold for femtosecond laser sampling is very suitable for the analysis of biological materials such as bacteria, cells, and leaves and cultural heritage objects such as ceramics, bronze statues, glasses and coatings, where minimal damage is a primary concern. Fs-LIBS can also be an auxiliary tool to monitor material processing by femtosecond lasers for cleaning of corroded alloys and preparing sub-micron grooves on a layered surface. In this case, LIBS provides spectral information for stopping or continuing material processing.

The low emissivity of plasma due to relatively low fs laser pulse energy can be overcome by the use of an additional ns laser in an orthogonal configuration, which can deliver enough energy to reheat plasma while preserving the advantages of fs ablation.

A new era of laser remote sensing has been started by filament-induced breakdown spectrometry (FIBS), which utilizes the unique capability of powerful femtosecond laser pulses to initiate filamentation in air. Filamentation makes it possible to overcome laser beam diffraction and to conserve the laser beam diameter at long distances (up to 20 km) without any focusing optics. This allows laser pulses to be delivered with the high power density needed to induce ablation of remote samples. Conventional focusing systems for remote LIBS utilize focusing optics to achieve the power density needed for analytically meaningful plasma. Ideally, the focal length of a lens should be proportional to the distance between laser and sample, resulting in an optical system with a large dimension and mass. Nevertheless, even ideally focusing optics cannot deliver a sufficiently powerful laser beam at a distance beyond several tens of meters due to fluctuation of atmospheric properties (refraction index fluctuation and interaction with aerosol particles). Filamentation allows a laser beam to be delivered with enough power density to induce plasma breakdown, even under heavy meteorological conditions (e.g. snow). Currently, the maximum distance for FIBS measurements is determined by collecting optics efficiency and detector system sensitivity. It was demonstrated that state-of-the-art FIBS systems can perform measurements at a distance of ∼200 m, while the maximum estimated distance can reach up to 2 km with the use of more sensitive gated detectors.

The feasibility of elemental remote sensing by filaments was demonstrated for metallic, inorganic and organic samples. FIBS measurements published in the literature were motivated by remote sensing of dangerous materials (e.g. explosives and drugs), cultural heritage objects, and isotopic analysis. To date, FIBS studies were mainly focused on feasibility demonstration rather than on quantitative analysis. The analytical figures of merit for FIBS were roughly estimated at the tenth ppm level in one study presented in the literature.²¹⁷ The estimated limits of detection were at a level of a tenth to hundreds of ppm for additives in aluminum samples located at a distance of 50 m. The high cost and complexity of powerful femtosecond laser systems are the main limiting factors for the deployment of filament-induced breakdown spectrometry in everyday practice.

Acknowledgements

Labutin T. A. and Popov A. M. thank the Russian Science Foundation for the financial support (agreement No. 14-13-01386) in the preparation of Section 3. Lednev V. N. gratefully acknowledges the financial support of the Ministry of Education and Science of the Russian Federation in the framework of Increase Competitiveness Program of NUST «MISiS» (agreement No. K4-2015-052) for the preparation of Section 4. Ilyin A. A. thanks the Russian Science Foundation for financial support (agreement No. 14-50-00034) for the preparation of Section 2. Some results presented in this section were obtained using scientific equipment from TsKP LaMI of IACP FEB RAS.

References

1. C. V. Shank and E. P. Ippen, Sub-picosecond kilowatt pulses from a mode locked cw dye laser, Appl. Phys. Lett., 1974, 24, 373.
2. P. F. Moulton, Ti-doped Sapphire Tunable Solid State Laser, Optics News, 1982, 8, 9.
3. D. Strickland and G. Mourou, Compression of amplified chirped optical pulses, Opt. Commun., 1985, 56, 219.
4. J. A. Cobble, G. A. Kyrala, A. A. Hauer, A. J. Taylor, C. C. Gomez, N. D. Delamater and G. T. Schappert, Kilovolt X-ray spectroscopy of a subpicosecond-laser-excited source, Phys. Rev. A: At., Mol., Opt. Phys., 1989, 39, 454.
5. B.-M. Kim, M. D. Feit, A. M. Rubenchik, B. M. Mammini and L. B. Da Silva, Optical feedback signal for ultrashort laser pulse ablation of tissue, Appl. Surf. Sci., 1998, 127–129, 857.
6. V. Margetic, A. Pakulev, A. Stockhaus, M. Bolshov, K. Niemax and R. Hergenroder, A comparison of nanosecond and femtosecond laser-induced plasma spectroscopy of brass samples, Spectrochim. Acta, Part B, 2000, 55, 1771.
7. E. L. Gurevich and R. Hergenröder, Femtosecond laser-induced breakdown spectroscopy: physics, applications, and perspectives, Appl. Spectrosc., 2007, 61, 233A.
8. J. Herrmann, Theory of Kerr-lens mode-locking – role of self-focusing and radially varying gain, J. Opt. Soc. Am. B, 1994, 11, 498.
9. Femtosecond Laser Pulses. Principles and Experiments, ed. C. Rulliere, Springer-Verlag, 2005.
10. K. Yamane, Z. Zhang, K. Oka, R. Morita, M. Yamashita and A. Suguro, Optical pulse compression to 3.4 fs in the monocycle region by feedback phase compensation, Opt. Lett., 2003, 28, 2258.
11. G. Steinmeyer and G. Stibenz, Generation of sub-4-fs pulses via compression of a white-light continuum using only chirped mirrors, Appl. Phys. B, 2006, 82, 175.
12. O. A. Konoplev, Temporal high-contrast structure of ultrashort pulses: a plea for standardization of nomenclature and conventions, Proc. SPIE, 2000, 3934, 102.
13. S. Fourmaux, S. Payeur, S. Buffechoux, P. Lassonde, C. St-Pierre, F. Martin and J. C. Kieffer, Pedestal cleaning for high laser pulse contrast ratio with a 100 TW class laser system, Opt. Express, 2011, 19, 8486.
14. V. V. Semak, J. G. Thomas and B. R. Campbell, Drilling of steel and HgCdTe with the femtosecond pulses produced by a commercial laser system, J. Phys. D: Appl. Phys., 2004, 37, 2925.
15. R. Y. Chiao, E. Garmire and C. H. Townes, Self-trapping of optical beams, Phys. Rev. Lett., 1964, 13, 479.
16. N. F. Pilipetskii and A. R. Rustamov, Observation of self-focusing of light in liquids, JETP Lett., 1965, 2, 55.
17. A. Braun, G. Korn, X. Liu, D. Du, J. Squier and G. Mourou, Self-channeling of high-peak-power femtosecond laser pulses in air, Opt. Lett., 1995, 20, 73.
18. P. Béjot and J. Kasparian, Conical emission from laser filaments and higher-order Kerr effect in air, Opt. Lett., 2011, 36, 4812.
19. V. P. Kandidov, O. G. Kosareva and A. A. Koltun, Nonlinear-optical transformation of a high-power femtosecond laser pulse in air, Quantum Electron., 2003, 33, 69.
20. Y. E. Geints and A. A. Zemlyanov, Self-focusing of a focused femtosecond laser pulse in air, Appl. Phys. B: Lasers Opt., 2010, 101, 735.
21. S. L. Chin, T. J. Wang, C. Marceau, J. Wu, J. S. Liu, O. Kosareva, N. Panov, Y. P. Chen, J. F. Daigle, S. Yuan, A. Azarm, W. W. Liu, T. Seideman, H. P. Zeng, M. Richardson, R. Li and Z. Z. Xu, Advances in intense femtosecond laser filamentation in air, Laser Phys., 2012, 22, 1.
22. A. Couairon and A. Mysyrowicz, Femtosecond filamentation in transparent media, Phys. Rep., 2007, 441, 47.
23. V. P. Kandidov, S. A. Shlenov and O. G. Kosareva, Filamentation of high-power femtosecond laser radiation, Quantum Electron., 2009, 39, 205.
24. S. L. Chin, S. A. Hosseini, W. Liu, Q. Luo, F. Théberge, N. Aközbek, A. Becker, V. P. Kandidov, O. G. Kosareva and H. Schröder, The propagation of powerful femtosecond laser pulses in optical media: physics, applications, and new challenges, Can. J. Phys., 2005, 83, 863.
25. D. V. Apeksimov, O. A. Bukin, E. E. Bykova, Yu. E. Geints, S. S. Golik, A. A. Zemlyanov, A. A. Il’in, A. M. Kabanov, G. G. Matvienko, V. K. Oshlakov, A. V. Petrov and E. B. Sokolova, Filamentation of the focused Ti:Sapphire laser pulse in air at two harmonics, Plasma Phys. Rep., 2013, 39, 1074.
26. G. Mechain, C. D. Amico, Y.-B. Andre, S. Tzortzakis, M. Franco, B. Prade, A. Mysyrowicz, A. Couairon, E. Salmon and R. Sauerbrey, Range of plasma filaments created in air by a multi-terawatt femtosecond laser, Opt. Commun., 2005, 247, 171.
27. M. Durand, A. Houard, B. Prade, A. Mysyrowicz, A. Durécu, B. Moreau, D. Fleury, O. Vasseur, H. Borchert and K. Diener, Kilometer range filamentation, Opt. Express, 2013, 21, 26836.
28. M. Rodriguez, R. Bourayou, G. Méjean, J. Kasparian, J. Yu, E. Salmon, A. Scholz, B. Stecklum, J. Eislöffel and U. Laux, Kilometer-range nonlinear propagation of femtosecond laser pulses, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 036607.
29. A. A. Ionin, S. I. Kudryashov, S. V. Makarov, L. V. Seleznev and D. V. Sinitsyn, Multiple filamentation of intense femtosecond laser pulses in air, JETP Lett., 2009, 90, 423.
30. A. A. Ilyin and S. S. Golik, Absorption of laser-radiation energy by femtosecond laser spark in air, Tech. Phys. Lett., 2014, 40, 1.
31. W. Liu and S. L. Chin, Direct measurement of the critical power of femtosecond Ti:Sapphire laser pulse in air, Opt. Express, 2005, 13, 5750.
32. N. Zhang, W.-X. Bao, J.-H. Yang and X.-N. Zhu, Determination of the temporal structure of femtosecond laser pulses by means of laser-induced air plasma, Chin. Phys. B, 2013, 22, 054209.
33. S. Xu, X. Sun, B. Zeng, W. Chu, J. Zhao, W. Liu, Y. Cheng, Z. Xu and S. L. Chin, Simple method of measuring laser peak intensity inside femtosecond laser filament in air, Opt. Express, 2012, 20, 299.
34. K. Lim, M. Durand, M. Baudelet and M. Richardson, Transition from linear-to nonlinear-focusing regime in filamentation, Sci. Rep., 2014, 4, 7217.
35. P. P. Kiran, S. Bagchi, S. R. Krishnan, C. L. Arnold, G. R. Kumar and A. Couairon, Focal dynamics of multiple filaments: microscopic imaging and reconstruction, Phys. Rev. A: At., Mol., Opt. Phys., 2010, 82, 013805.
36. Y. E. Geints, A. A. Ionin, A. A. Zemlyanov, S. I. Kudryashov, L. V. Seleznev, D. V. Sinitsyn and E. S. Sunchugasheva, Features of focused propagation of intense femtosecond laser pulses in air under low pressure, Atmos. Oceanic Opt., 2012, 25, 185.
37. A. Couairon and A. Mysyrowicz, in Progress in Ultrafast Intense Laser Science, ed. K. Yamanouchi, S. L. Chin, P. Agostini and G. Ferrante, Springer, 2006, vol. I, pp. 235–258.
38. F. Théberge, W. Liu, P. T. Simard, A. Becker and S. L. Chin, Plasma density inside a femtosecond laser filament in air: strong dependence on external focusing, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 036406.
39. J. Kasparian, R. Sauerbrey and S. L. Chin, The critical laser intensity of self-guided light filaments in air, Appl. Phys. B: Lasers Opt., 2000, 71, 877.
40. N. B. Delone, Basics of interaction of laser radiation with matter, Editions Frontieres, 1993.
41. H. L. Xu, A. Azarm, J. Bernhardt, Y. Kamali and S. L. Chin, The mechanism of nitrogen fluorescence inside a femtosecond laser filament in air, Chem. Phys., 2009, 360, 171.
42. J. Yu, D. Mondelain, J. Kasparian, E. Salmon, S. Geffroy, C. Favre, V. Boutou and J.-P. Wolf, Sonographic probing of laser filaments in air, Appl. Opt., 2003, 42, 7117.
43. G. N. Gibson, R. R. Freeman and T. J. McIlrath, Dynamics of the high-intensity multiphoton ionization of N2, Phys. Rev. Lett., 1991, 67, 1230.
44. Y. P. Raizer, Laser-Induced Discharge Phenomena, Consultants Bureau, 1977.
45. A. A. Ilyin, I. G. Nagorny and O. A. Bukin, Supersonic regimes of plasma expansion during optical breakdown in air, Appl. Phys. Lett., 2010, 96, 171501.
46. A. A. Ilyin, S. S. Golik and K. A. Shmirko, Absorption and emission characteristics of femtosecond laser plasma filaments in the air, Spectrochim. Acta, Part B, 2015, 112, 16.
47. F. Martin, R. Mawassi, F. Vidal, I. Gallimberti, D. Comtois, H. Pépin, J. C. Kieffer and H. P. Mercure, Spectroscopic study of ultrashort pulse laser-breakdown plasmas in air, Appl. Spectrosc., 2002, 56, 1444.
48. B. R. Arnold, S. D. Roberson and P. M. Pellegrino, Excited state dynamics of nitrogen reactive intermediates at the threshold of laser induced filamentation, Chem. Phys., 2012, 405, 9.
49. V. Zorba, X. Mao and R. E. Russo, Optical far- and near-field femtosecond laser ablation of Si for nanoscale chemical analysis, Anal. Bioanal. Chem., 2010, 396, 173.
50. S.-S. Wellershoff, J. Hohlfeld, J. Güdde and E. Matthias, The role of electron–phonon coupling in femtosecond laser damage of metals, Appl. Phys. A: Mater. Sci. Process., 1999, 69, S99.
51. F. Korte, S. Nolte, B. N. Chichkov, T. Bauer, G. Kamlage, T. Wagner, C. Fallnich and H. Welling, Far-field and near-field material processing with femtosecond laser pulses, Appl. Phys. A: Mater. Sci. Process., 1999, 69, S7.
52. E. G. Gamaly and A. V. Rode, Physics of ultra-short laser interaction with matter: from phonon excitation to ultimate transformations, Prog. Quantum Electron., 2013, 37, 215.
53. Ultrafast Laser Processing: From Micro- to Nanoscale, ed. K. Sugioka and Y. Cheng, Pan Stanford Publishing, 2013.
54. M. Lisowski, P. A. Loukakos, U. Bovensiepen, J. Stahler, C. Gahl and M. Wolf, Ultra-fast dynamics of electron thermalization, cooling and transport effects in Ru(001), Appl. Phys. A: Mater. Sci. Process., 2004, 78, 165.
55. N. M. Bulgakova, A. V. Bulgakov and O. F. Bobrenok, Double layer effects in laser-ablation plasma plumes, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 5624.
56. A. Brantov, W. Rozmus, R. Sydora, C. E. Capjack, V. Y. Bychenkov and V. T. Tikhonchuk, Enhanced inverse Bremsstrahlung heating rates in a strong laser field, Phys. Plasmas, 2003, 10, 3385.
57. W. Hu, Y. C. Shin and G. King, Energy transport analysis in ultrashort pulse laser ablation through combined molecular dynamics and Monte Carlo simulation, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 094111.
58. N. M. Bulgakova, R. Stoian and A. Rosenfeld, Laser-induced modification of transparent crystals and glasses, Quantum Electron., 2010, 40, 966.
59. N. M. Bulgakova, V. P. Zhukov, A. Y. Vorobyev and C. Guo, Modeling of residual thermal effect in femtosecond laser ablation of metals: role of a gas environment, Appl. Phys. A: Mater. Sci. Process., 2008, 92, 883.
60. W. Hu, Y. C. Shin and G. King, Early-stage plasma dynamics with air ionization during ultrashort laser ablation of metal, Phys. Plasmas, 2011, 18, 093302.
61. J. Li, X. Wang, Z. Chen, R. Clinite, S. S. Mao, P. Zhu, Z. Sheng, J. Zhang and J. Cao, Ultrafast electron beam imaging of femtosecond laser-induced plasma dynamics, J. Appl. Phys., 2010, 107, 083305.
62. X. Zhao and Y. C. Shin, Coulomb explosion and early plasma generation during femtosecond laser ablation of silicon at high laser fluence, J. Phys. D: Appl. Phys., 2013, 46, 335501.
63. X.-L. Liu, X. Lu, X. Liu, T.-T. Xi, F. Liu, J.-L. Ma and J. Zhang, Tightly focused femtosecond laser pulse in air: from filamentation to breakdown, Opt. Express, 2010, 18, 26007.
64. A. E. Martirosyan, C. Altucci, A. Bruno, C. de Lisio, A. Porzio and S. Solimeno, Time evolution of plasma afterglow produced by femtosecond laser pulses, J. Appl. Phys., 2004, 96, 5450.
65. V. V. Bukin, N. S. Vorob'ev, S. V. Garnov, V. I. Konov, V. I. Lozovoi, A. A. Malyutin, M. Y. Shchelev and I. S. Yatskovskii, Formation and development dynamics of femtosecond laser microplasma in gases, Quantum Electron., 2006, 36, 638.
66. S. I. Anisimov, B. L. Kapeliovich and T. L. Perel’man, Electron-emission from surface of metals induced by ultrashort laser pulses, Soviet Physics – JETP, 1975, 39, 375.
67. M. E. Povarnitsyn, T. E. Itina, M. Sentis, K. V. Khishchenko and P. R. Levashov, Material decomposition mechanisms in femtosecond laser interactions with metals, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 23, 235414.
68. B. Rethfeld, K. Sokolowski-Tinten, D. von der Linde and S. I. Anisimov, Timescales in the response of materials to femtosecond laser excitation, Appl. Phys. A: Mater. Sci. Process., 2004, 79, 767.
69. I. Mingareev, Ultrafast dynamics of melting and ablation at large laser intensities, PhD thesis, RWTH- Aachen, 2009.
70. D. S. Ivanov and L. V. Zhigilei, Combined atomistic-continuum modeling of short-pulse laser melting and disintegration of metal films, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 064114.
71. B. Rethfeld, K. Sokolowski-Tinten, D. von der Linde and S. I. Anisimov, Ultrafast thermal melting of laser-excited solids by homogeneous nucleation, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 092103.
72. A. Rousse, C. Rischel, S. Fourmaux, I. Uschmann, S. Sebban, G. Grillon, P. Balcou, E. Förster, J. P. Geindre, P. Audebert, J. C. Gauthier and D. Hulin, Non-thermal melting in semiconductors measured at femtosecond resolution, Nature, 2001, 410, 65.
73. J. P. Colombier, P. Combis, R. Stoian and E. Audouard, High shock release in ultrafast laser irradiated metals: scenario for material ejection, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 104105.
74. M. E. Povarnitsyn, K. V. Khishchenko and P. R. Levashov, Phase transitions in femtosecond laser ablation, Appl. Surf. Sci., 2009, 255, 5120.
75. A. A. Ionin, S. I. Kudryashov, L. V. Seleznev, D. V. Sinitsyn, A. F. Bunkin, V. N. Lednev and S. M. Pershin, Thermal melting and ablation of silicon by femtosecond laser radiation, J. Exp. Theor. Phys., 2013, 116, 347.
76. M. E. Povarnitsyn, T. E. Itina, P. R. Levashov and K. V. Khishchenko, Simulation of ultrashort double-pulse laser ablation, Appl. Surf. Sci., 2011, 257, 5168.
77. I. Mingareev and A. Horn, Time-resolved investigations of plasma and melt ejections in metals by pump-probe shadowgrpahy, Appl. Phys. A: Mater. Sci. Process., 2008, 92, 917.
78. O. Albert, S. Roger, Y. Glinec, J. C. Loulergue, J. Etchepare, C. Boulmer-Leborgne, J. Perriere and E. Millon, Time-resolved spectroscopy measurements of a titanium plasma induced by nanosecond and femtosecond lasers, Appl. Phys. A: Mater. Sci. Process., 2003, 76, 319.
79. D. Scuderi, R. Benzerga, O. Albert, B. Reynier and J. Etchepare, Spectral and temporal characteristics of metallic nanoparticles produced by femtosecond laser pulses, Appl. Surf. Sci., 2006, 252, 4360–4363.
80. S. Noël, J. Hermann and T. Itina, Investigation of nanoparticle generation during femtosecond laser ablation of metals, Appl. Surf. Sci., 2007, 253, 6310.
81. E. Axente, S. Noël, J. Hermann, M. Sentis and I. N. Mihailescu, Correlation between plasma expansion and damage threshold by femtosecond laser ablation of fused silica, J. Phys. D: Appl. Phys., 2008, 41, 105216.
82. I. Mingareev and A. Horn, Melt dynamics of aluminum irradiated with ultrafast laser radiation at large intensities, J. Appl. Phys., 2009, 106, 013513.
83. N. M. Bulgakova and A. V. Bulgakov, Pulsed laser ablation of solids: transition from normal vaporization to phase explosion, Appl. Phys. A: Mater. Sci. Process., 2001, 73, 199.
84. A. A. Ilyin, I. G. Nagorny, O. A. Bukin, A. V. Bulanov and K. A. Shmirko, Features of development of optical breakdown on an inclined aluminum surface, Tech. Phys. Lett., 2012, 38, 975.
85. B. N. Chichkov, C. Momma, S. Nolte, F. Yon Alvensleben and A. Tünnermann, Femtosecond, picosecond and nanosecond laser ablation of solids, Appl. Phys. A: Mater. Sci. Process., 1996, 63, 109.
86. M. Lopez-Claros, J. M. Vadillo and J. J. Laserna, Determination of plasma ignition threshold fluence during femtosecond single-shot laser ablation on metallic samples detected by optical emission spectroscopy, J. Anal. At. Spectrom., 2015, 30, 1730.
87. S. Hofmann, Quantitative Depth Profiling in Surface Analysis: A Review, Surf. Interface Anal., 1980, 2, 148.
88. Compendium of Analytical Nomenclature: Orange Book of IUPAC. Definitive Rules; 1997. Part 17.4 Terms related to surface analysis.
89. V. Margetic, M. Bolshov, A. Stockhaus, K. Niemax and R. Hergenröder, Depth profiling of multi-layer samples using femtosecond laser ablation, J. Anal. At. Spectrom., 2001, 16, 616.
90. A. Baskevicius, A. Alesenkov, G. Chozevskis, J. Litvaityte, O. Balachninaite, D. Paipulas, A. Melninkaitis and V. Sirutkaitis, Optimization of Laser-Ablation Micromachining by Choice of Scanning Algorithms and Use of Laser-Induced-Breakdown Spectroscopy, J. Laser Micro/Nanoeng., 2013, 8, 24.
91. O. Samek, V. Hommes, R. Hergenröder and S. V. Kukhlevsky, Femtosecond pulse shaping using a liquid-crystal display: applications to depth profiling analysis, Rev. Sci. Instrum., 2005, 76, 086104.
92. S. P. Banerjee, Z. Chen, I. Utkin and R. Fedosejevs, Detection of buried layers in silicon devices using LIBS during hole drilling with femtosecond laser pulses, Appl. Phys. A: Mater. Sci. Process., 2013, 111, 791.
93. D. McGloin and K. Dholakia, Bessel beams: diffraction in a new light, Contemp. Phys., 2005, 46, 15.
94. J. Durnin, J. J. Miceli Jr and J. H. Eberly, Diffraction-free beams, Phys. Rev. Lett., 1987, 58, 1499.
95. J. Arlt and K. Dholakia, Generation of high-order Bessel beams by use of an axicon, Opt. Commun., 2000, 177, 297.
96. F. Courvoisier, J. Zhang, M. K. Bhuyan, M. Jacquot and J. M. Dudley, Applications of femtosecond Bessel beams to laser ablation, Appl. Phys. A: Mater. Sci. Process., 2013, 112, 29.
97. D. E. Roberts, A. du Plessis, J. Steyn, L. R. Botha, C. A. Strydom and I. J. van Rooyen, Femtosecond laser induced breakdown spectroscopy of silver within surrogate high temperature gas reactor fuel coated particles, Spectrochim. Acta, Part B, 2010, 65, 918.
98. S. P. Banerjee and R. Fedosejevs, Single shot depth sensitivity using femtosecond Laser Induced Breakdown Spectroscopy, Spectrochim. Acta, Part B, 2014, 92, 34.
99. P. Pouli, K. Melessanaki, A. Giakoumaki, V. Argyropoulos and D. Anglos, Measuring the thickness of protective coatings on historic metal objects using nanosecond and femtosecond laser induced breakdown spectroscopy depth profiling, Spectrochim. Acta, Part B, 2005, 60, 1163.
100. A. de Bonis, B. de Filippo, A. Galasso, A. Santagata, A. Smaldone and R. Teghil, Comparison of the performances of nanosecond and femtosecond Laser Induced Breakdown Spectroscopy for depth profiling of an artificially corroded bronze, Appl. Surf. Sci., 2014, 302, 275.
101. D. W. Hahn and N. Omenetto, Laser-Induced Breakdown Spectroscopy (LIBS), Part II: Review of Instrumental and Methodological Approaches to Material Analysis and Applications to Different Fields, Appl. Spectrosc., 2012, 66, 347.
102. C. Liu, X. L. Mao, S. S. Mao, X. Zeng, R. Greif and R. E. Russo, Nanosecond and Femtosecond Laser Ablation of Brass:  Particulate and ICPMS Measurements, Anal. Chem., 2004, 76, 379.
103. C. Jeynes, N. P. Barradas and E. Szilagyi, Accurate Determination of Quantity of Material in Thin Films by Rutherford Backscattering Spectrometry, Anal. Chem., 2012, 84, 6061.
104. A. H. Galmed, A. K. Kassem, H. von Bergmann and M. A. Harith, A study of using femtosecond LIBS in analyzing metallic thin film–semiconductor interface, Appl. Phys. B: Lasers Opt., 2011, 102, 197.
105. D. K. Das, J. P. McDonald, S. M. Yalisove and T. M. Pollock, Depth-profiling study of a thermal barrier coated superalloy using femtosecond laser-induced breakdown spectroscopy, Spectrochim. Acta, Part B, 2008, 63, 27.
106. C. C. García, M. Corral, J. M. Vadillo and J. J. Laserna, Angle-resolved laser-induced breakdown spectrometry for depth profiling of coated materials, Appl. Spectrosc., 2000, 54, 1027.
107. T. Kratochvíl, T. Černohorský, P. Knotek, L. Kalina, J. Návesník, M. Pouzar and M. Zvolská, Fast determination of the surface density of titanium in ultrathin layers using LIBS spectrometry, J. Anal. At. Spectrom., 2014, 29, 1806.
108. A. Assion, M. Wollenhaupt, L. Hag, F. Mayorov, C. Sarpe-Tudoran, M. Winter, U. Kutschera and T. Baumert, Femtosecond laser-induced-breakdown spectrometry for Ca²⁺ analysis of biological samples with high spatial resolution, Appl. Phys. B: Lasers Opt., 2003, 77, 391.
109. O. Samek, J. Lambert, R. Hergenröder, M. Liška, J. Kaiser, K. Novotný and S. Kukhlevsky, Femtosecond laser spectrochemical analysis of plant samples, Laser Phys. Lett., 2006, 3, 21.
110. J. Kaiser, O. Samek, L. Reale, M. Liška, R. Malina, A. Ritucci, A. Poma, A. Tucci, F. Flora, A. Lai, L. Mancini, G. Tromba, F. Zanini, A. Faenov, T. Pikuz and G. Cinque, Monitoring of the Heavy-Metal Hyperaccumulation in Vegetal Tissues by X-ray Radiography and by Femto-Second Laser Induced Breakdown Spectroscopy, Microsc. Res. Tech., 2007, 70, 147.
111. M. T. Taschuk, Y. Y. Tsui and R. Fedosejevs, Detection and Mapping of Latent Fingerprints by Laser-Induced Breakdown Spectroscopy, Appl. Spectrosc., 2006, 60, 1322.
112. S. P. Banerjee, Z. Chen and R. Fedosejevs, High resolution scanning microanalysis on material surfaces using UV femtosecond laser induced breakdown spectroscopy, Optic Laser Eng., 2015, 68, 1.
113. I. V. Cravetchi, M. T. Taschuk, Y. Y. Tsui and R. Fedosejevs, Evaluation of femtosecond LIBS for spectrochemical microanalysis of aluminium alloys, Anal. Bioanal. Chem., 2006, 385, 287.
114. T. Tong, J. Li and J. P. Longtin, Real-time control of ultrafast laser micromachining by laser-induced breakdown spectroscopy, Appl. Opt., 2004, 43, 1971.
115. W. Wessel, A. Brueckner-Foit, J. Mildner, L. Englert, L. Haag, A. Horn, M. Wollenhaupt and T. Baumert, Use of femtosecond laser-induced breakdown spectroscopy (fs-LIBS) for micro-crack analysis on the surface, Eng. Fract. Mech., 2010, 77, 1874.
116. H. Hou, L. Cheng, T. Richardson, G. Chen, M. Doeff, R. Zheng, R. E. Russo and V. Zorba, Three-Dimensional Elemental Imaging of Li-ion Solid-State Electrolytes Using fs-Laser Induced Breakdown Spectroscopy (LIBS), J. Anal. At. Spectrom., 2015, 30, 2295.
117. M. Duocastella and C. B. Arnold, Bessel and annular beams for materials processing, Laser Photonics Rev., 2012, 6, 607.
118. Q. Zhan, Cylindrical vector beams: from mathematical concepts to applications, Adv. Opt. Photonics, 2009, 1, 1.
119. C. Hnatovsky, V. Shvedov, W. Krolikowski and A. Rode, Revealing Local Field Structure of Focused Ultrashort Pulses, Phys. Rev. Lett., 2011, 106, 123901.
120. E. Betzig and J. K. Trautman, Near-Field Optics: Microscopy, Spectroscopy, and Surface Modification Beyond the Diffraction Limit, Science, 1992, 257, 189.
121. V. Zorba, X. Mao and R. E. Russo, Ultrafast laser induced breakdown spectroscopy for high spatial resolution chemical analysis, Spectrochim. Acta, Part B, 2011, 66, 189.
122. R. E. Russo, T. W. Suen, A. A. Bol'shakov, J. Yoo, O. Sorkhabi, X. Mao, J. Gonzalez, D. Oropeza and V. Zorba, Laser plasma spectrochemistry, J. Anal. At. Spectrom., 2011, 26, 1596.
123. Y. Lu, V. Zorba, X. Mao, R. Zheng and R. E. Russo, UV fs to ns double-pulse laser induced breakdown spectroscopy for high spatial resolution chemical analysis, J. Anal. At. Spectrom., 2013, 28, 743.
124. G. W. Rieger, M. Taschuk, Y. Y. Tsui and R. Fedosejevs, Comparative study of laser-induced plasma emission from microjoule picosecond and nanosecond KrF-laser pulses, Spectrochim. Acta, Part B, 2003, 58, 497.
125. B. le Drogoff, M. Chaker, J. Margot, M. Sabsabi, O. Barthélemy, T. W. Johnston, S. Laville and F. Vidal, Influence of the Laser Pulse Duration on Spectrochemical Analysis of Solids by Laser-Induced Plasma Spectroscopy, Appl. Spectrosc., 2004, 58, 122.
126. T. Gunaratne, M. Kangas, S. Singh, A. Gross and M. Dantus, Influence of bandwidth and phase shaping on laser induced breakdown spectroscopy with ultrashort laser pulses, Chem. Phys. Lett., 2006, 423, 197.
127. V. Piñon and D. Anglos, Optical emission studies of plasma induced by single and double femtosecond laser pulses, Spectrochim. Acta, Part B, 2009, 64, 950.
128. E. Tognoni, V. Palleschi, M. Corsi and G. Cristoforetti, Quantitative micro-analysis by laser-induced breakdown spectroscopy: a review of the experimental approaches, Spectrochim. Acta, Part B, 2002, 57, 1115.
129. J. T. Schiffern, D. W. Doerr and D. R. Alexander, Optimization of collinear double-pulse femtosecond laser-induced breakdown spectroscopy of silicon, Spectrochim. Acta, Part B, 2007, 62, 1412.
130. D. Santos, R. E. Samad, L. C. Trevizan, A. Z. de Freitas, N. D. Vieira and F. J. Krug, Evaluation of Femtosecond Laser-Induced Breakdown Spectroscopy for Analysis of Animal Tissues, Appl. Spectrosc., 2008, 62, 1137.
131. J. Scaffidi, W. Pearman, J. C. Carter and S. M. Angel, Observations in collinear femtosecond–nanosecond dual-pulse laser-induced breakdown spectroscopy, Appl. Spectrosc., 2006, 60, 65.
132. Ş. Yalçın, Y. Y. Tsui and R. Fedosejevs, Pressure dependence of emission intensity in femtosecond laser-induced breakdown spectroscopy, J. Anal. At. Spectrom., 2004, 19, 1295.
133. L. A. Emmert, R. C. Chinni, D. A. Cremers, C. R. Jones and W. Rudolph, Comparative study of femtosecond and nanosecond laser-induced breakdown spectroscopy of depleted uranium, Appl. Opt., 2011, 50, 313.
134. A. W. Schill, D. A. Heaps, D. N. Stratis-Cullum, B. R. Arnold and P. M. Pellegrino, Characterization of near-infrared low energy ultra-short laser pulses for portable applications of laser induced breakdown spectroscopy, Opt. Express, 2007, 15, 14044.
135. C. A. Zuhlke, J. Bruce III, T. P. Anderson, D. R. Alexander and C. G. Parigger, A Fundamental Understanding of the Dependence of the Laser-Induced Breakdown Spectroscopy (LIBS) Signal Strength on the Complex Focusing Dynamics of Femtosecond Laser Pulses on Either Side of the Focus, Appl. Spectrosc., 2014, 68, 1021.
136. M. P. Mateo, V. Piñon, D. Anglos and G. Nicolas, Effect of ambient conditions on ultraviolet femtosecond pulse laser induced breakdown spectra, Spectrochim. Acta, Part B, 2012, 74–75, 18.
137. A. Nakimana, H. Tao, X. Gao, Z. Hao and J. Lin, Effects of ambient conditions on femtosecond laser-induced breakdown spectroscopy of Al, J. Phys. D: Appl. Phys., 2013, 46, 285204.
138. S. S. Harilal, N. Farid, J. R. Freeman, P. K. Diwakar, N. L. LaHaye and A. Hassanein, Background gas collisional effects on expanding fs and ns laser ablation plumes, Appl. Phys. A: Mater. Sci. Process., 2014, 117, 319.
139. N. Smijesh and R. Philip, Emission dynamics of an expanding ultrafast-laser produced Zn plasma under different ambient pressures, J. Appl. Phys., 2013, 114, 093301.
140. M. Guillermin, C. Liebig, F. Garrelie, R. Stoian, A.-S. Loir and E. Audouard, Adaptive control of femtosecond laser ablation plasma emission, Appl. Surf. Sci., 2009, 255, 5163.
141. M. Guillermin, J. P. Colombier, S. Valette, E. Audouard, F. Garrelie and R. Stoian, Optical emission and nanoparticle generation in Al plasmas using ultrashort laser pulses temporally optimized by real-time spectroscopic feedback, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 035430.
142. M. Guillermin, A. Klini, J. P. Colombier, F. Garrelie, D. Gray, C. Liebig, E. Audouard, C. Fotakis and R. Stoian, Tuning spectral properties of ultrafast laser ablation plasmas from brass using adaptive temporal pulse shaping, Opt. Express, 2010, 18, 11159.
143. K. C. Hartig, J. P. McNutt, P. Ko, T. W. Jacomb-Hood and I. Jovanovic, Pulse chirp effects in ultrafast laser-induced breakdown spectroscopy, J. Radioanal. Nucl. Chem., 2013, 296, 135.
144. S. M. Angel, D. N. Stratis, K. L. Eland, T. Lai, M. A. Berg and D. M. Gold, LIBS using dual- and ultra-short laser pulses, Fresenius' J. Anal. Chem., 2001, 369, 320.
145. B. le Drogoff, J. Margot, F. Vidal, S. Laville, M. Chaker, M. Sabsabi, T. W. Johnston and O. Barthélemy, Influence of the laser pulse duration on laser-produced plasma properties, Plasma Sources Sci. Technol., 2004, 13, 223.
146. J. R. Freeman, S. S. Harilal, P. K. Diwakar, B. Verhoff and A. Hassanein, Comparison of optical emission from nanosecond and femtosecond laser produced plasma in atmosphere and vacuum conditions, Spectrochim. Acta, Part B, 2013, 87, 43.
147. Y. Liu, S. Singha, T. E. Witt, Y. Cheng and R. J. Gordon, Observation of near total polarization in the ultrafast laser ablation of Si, Appl. Phys. Lett., 2008, 93, 161502.
148. J. S. Penczak, Y. Liu and R. J. Gordon, Polarization Resolved Laser-Induced Breakdown Spectroscopy of Al, J. Phys. Chem. A, 2009, 113, 13310.
149. Y. Zhao, S. Singha, Y. Liu and R. J. Gordon, Polarization-resolved laser-induced breakdown spectroscopy, Opt. Lett., 2009, 34, 494.
150. J. S. Penczak, Y. Liu, R. D. Schaller, D. H. Rich and R. J. Gordon, The mechanism for continuum polarization in laser induced breakdown spectroscopy of Si(111), Spectrochim. Acta, Part B, 2012, 74–75, 3.
151. J. Serrano, J. Moros and J. J. Laserna, Exploring the Formation Routes of Diatomic Hydrogenated Radicals Using Femtosecond Laser-Induced Breakdown Spectroscopy of Deuterated Molecular Solids, J. Anal. At. Spectrom., 2015, 30, 2343.
152. Y. Dikmelik and J. B. Spicer, Femtosecond laser-induced breakdown spectroscopy of explosives and explosive-related compounds, Proc. SPIE, 2005, 5794, 757.
153. Y. Dikmelik, C. McEnnis and J. B. Spicer, Femtosecond and nanosecond laser-induced breakdown spectroscopy of trinitrotoluene, Opt. Express, 2008, 16, 5332.
154. F. C. de Lucia Jr, J. L. Gottfried and A. W. Miziolek, Evaluation of femtosecond laser-induced breakdown spectroscopy for explosive residue detection, Opt. Express, 2009, 17, 419.
155. S. Sunku, M. K. Gundawar, A. K. Myakalwar, P. P. Kiran, S. P. Tewari and S. V. Rao, Femtosecond and nanosecond laser induced breakdown spectroscopic studies of NTO, HMX, and RDX, Spectrochim. Acta, Part B, 2013, 79–80, 31.
156. S. Sunku, E. N. Rao, G. M. Kumar, S. P. Tewari and S. V. Rao, Molecular formation dynamics of 5-nitro-2,4-dihydro-3H-1,2,4-triazol-3-one,1,3,5-trinitroperhydro-1,3,5-triazine, and 2,4,6-trinitrotoluene in air, nitrogen, and argon atmospheres studied using femtosecond laser induced breakdown spectroscopy, Spectrochim. Acta, Part B, 2013, 87, 121.
157. B. Yee, K. C. Hartig, P. Ko, J. McNutt and I. Jovanovic, Measurement of boron isotopic ratio with non-gated molecular spectroscopy of femtosecond laser-produced plasma, Spectrochim. Acta, Part B, 2013, 79–80, 72.
158. H. Hou, G. C.-Y. Chan, X. Mao, V. Zorba, R. Zheng and R. E. Russo, Femtosecond Laser Ablation Molecular Isotopic Spectrometry for Zirconium Isotope Analysis, Anal. Chem., 2015, 87, 4788.
159. H. Hou, G. C.-Y. Chan, X. Mao, R. Zheng, V. Zorba and R. E. Russo, Femtosecond filament-laser ablation molecular isotopic spectrometry, Spectrochim. Acta, Part B, 2015, 113, 113.
160. V. I. Babushok, F. C. de Lucia Jr, J. L. Gottfried, C. A. Munson and A. W. Miziolek, Double pulse laser ablation and plasma: laser induced breakdown spectroscopy signal enhancement, Spectrochim. Acta, Part B, 2006, 61, 999.
161. E. Tognoni and G. Cristoforetti, Basic mechanisms of signal enhancement in ns double-pulse laser-induced breakdown spectroscopy in a gas environment, J. Anal. At. Spectrom., 2014, 29, 1318.
162. A. Santagata, R. Teghil, G. Albano, D. Spera, P. Villani, A. de Bonis, G. P. Parisi and A. Galasso, fs/ns dual-pulse LIBS analytic survey for copper-based alloys, Appl. Surf. Sci., 2007, 254, 863.
163. M. E. Povarnitsyn, T. E. Itina, K. V. Khishchenko and P. R. Levashov, Suppression of Ablation in Femtosecond Double-Pulse Experiments, Phys. Rev. Lett., 2009, 103, 195002.
164. S. Noël, E. Axente and J. Hermann, Investigation of plumes produced by material ablation with two time-delayed femtosecond laser pulses, Appl. Surf. Sci., 2009, 255, 9738.
165. R. Teghil, A. Santagata, A. de Bonis, G. Albano, P. Villani, D. Spera, G. P. Parisi and A. Galasso, Applications of ultra-short pulsed laser ablation: thin films deposition and fs/ns dual-pulse laser-induced breakdown spectroscopy, Phys. Scr., 2008, 78, 058113.
166. A. Santagata, G. Albano, D. Spera, R. Teghil, P. Villani, G. P. Parisi, A. de Bonis and D. J. Sordelet, Emission spectra investigation of fs induced NPs probed by the ns laser pulse of a fs/ns DP-LIBS orthogonal configuration, Appl. Surf. Sci., 2009, 255, 5159.
167. J. Hermann, L. Mercadier, E. Axente and S. Noël, Properties of plasmas produced by short double pulse laser ablation of metals, J. Phys.: Conf. Ser., 2012, 399, 012006.
168. A. Guarnaccio, G. P. Parisi, D. Mollica, A. de Bonis, R. Teghil and A. Santagata, Fs to ns double-pulse Laser Induced Breakdown Spectroscopy of copper-based-alloys: generation and elemental analysis of nanoparticles, Spectrochim. Acta, Part B, 2014, 101, 261.
169. A. Semerok, C. Chaléard, V. Detalle, J.-L. Lacour, P. Mauchien, P. Meynadieκ, C. Nouvellon, B. Sallé, P. Palianov, M. Perdrix and G. Petite, Experimental investigations of laser ablation efficiency of pure metals with femto, pico and nanosecond pulses, Appl. Surf. Sci., 1999, 138–139, 311.
170. B. le Drogoff, J. Margot, M. Chaker, M. Sabsabi, O. Barthélemy, T. W. Johnston, S. Laville, F. Vidal and Y. von Kaenel, Temporal characterization of femtosecond laser pulses induced plasma for spectrochemical analysis of aluminum alloys, Spectrochim. Acta, Part B, 2001, 56, 987.
171. A. Elhassan, A. Giakoumaki, D. Anglos, G. M. Ingo, L. Robbiola and M. A. Harith, Nanosecond and femtosecond Laser Induced Breakdown Spectroscopic analysis of bronze alloys, Spectrochim. Acta, Part B, 2008, 63, 504.
172. L. Fornarini, R. Fantoni, F. Colao, A. Santagata, R. Teghil, A. Elhassan and M. A. Harith, Theoretical Modeling of Laser Ablation of Quaternary Bronze Alloys: Case Studies Comparing Femtosecond and Nanosecond LIBS Experimental Data, J. Phys. Chem. A, 2009, 113, 14364.
173. J. Scaffidi, J. Pender, W. Pearman, S. R. Goode, B. W. Colston Jr, J. C. Carter and S. M. Angel, Dual-pulse laser-induced breakdown spectroscopy with combinations of femtosecond and nanosecond laser pulses, Appl. Opt., 2003, 42, 6099.
174. J. Scaffidi, W. Pearman, M. Lawrence, J. C. Carter, B. W. Colston Jr and S. M. Angel, Spatial and temporal dependence of interspark interactions in femtosecond–nanosecond dual-pulse laser-induced breakdown spectroscopy, Appl. Opt., 2004, 43, 5243.
175. J. Scaffidi, W. Pearman, J. C. Carter, B. W. Colston Jr and S. M. Angel, Temporal dependence of the enhancement of material removal in femtosecond–nanosecond dual-pulse laser-induced breakdown spectroscopy, Appl. Opt., 2004, 43, 6492.
176. D. Scuderi, O. Albert, D. Moreau, P. P. Pronko and J. Etchepare, Interaction of a laser-produced plume with a second time delayed femtosecond pulse, Appl. Phys. Lett., 2005, 86, 071502.
177. A. Santagata, A. de Bonis, P. Villani, R. Teghil and G. P. Parisi, Fs/ns-dual-pulse orthogonal geometry plasma plume reheating for copper-based-alloys analysis, Appl. Surf. Sci., 2006, 252, 4685.
178. A. Santagata, R. Teghil, A. de Giacomo, M. Dell’Aglio, G. P. Parisi, A. de Bonis and A. Galasso, Optical emission spectroscopy investigation of an ultra-short laser induced titanium plasma reheated by a ns laser pulse, Appl. Surf. Sci., 2007, 253, 7792.
179. J. P. McDonald, D. K. Das, J. A. Nees, T. M. Pollock and S. M. Yalisove, Approaching non-destructive surface chemical analysis of CMSX-4 superalloy with double-pulsed laser induced breakdown spectroscopy, Spectrochim. Acta, Part B, 2008, 63, 561.
180. V. Piñon, C. Fotakis, G. Nicolas and D. Anglos, Double pulse laser-induced breakdown spectroscopy with femtosecond laser pulses, Spectrochim. Acta, Part B, 2008, 63, 1006.
181. V. Piñón, D. Anglos and G. Nicolás, Improvement of laser induced breakdown spectroscopy technique using double pulse schemes, Opt. Pura Apl., 2010, 43, 113.
182. S. Singha, Z. Hu and R. J. Gordon, Ablation and plasma emission produced by dual femtosecond laser pulses, J. Appl. Phys., 2008, 104, 113520.
183. S. Amoruso, R. Bruzzese and X. Wang, Plume composition control in double pulse ultrafast laser ablation of metals, Appl. Phys. Lett., 2009, 95, 251501.
184. S. Amoruso, R. Bruzzese, X. Wang, G. O'Connell and J. G. Lunney, Multidiagnostic analysis of ultrafast laser ablation of metals with pulse pair irradiation, J. Appl. Phys., 2010, 108, 113302.
185. S. Noël and J. Hermann, Reducing nanoparticles in metal ablation plumes produced by two delayed short laser pulses, Appl. Phys. Lett., 2009, 94, 053120.
186. O. Balachninaitė, A. Baškevičius, K. Stankevičiūtė, K. Kuršelis and V. Sirutkaitis, Double-pulse laser-induced breakdown spectroscopy with 1030 and 257.5 nm wavelength femtosecond laser pulses, Lith. J. Phys., 2010, 50, 105.
187. M. Oba, Y. Maruyama, K. Akaoka, M. Miyabe and I. Wakaida, Double-pulse LIBS of gadolinium oxide ablated by femto- and nano-second laser pulses, Appl. Phys. A: Mater. Sci. Process., 2010, 101, 545.
188. F. Bourquard, J.-P. Colombier, M. Guillermin, A.-S. Loir, C. Donnet, R. Stoian and F. Garrelie, Temporal pulse shaping effects on aluminium and boron ablation plumes generated by ultrashort pulsed laser ablation and analyzed by time- and space-resolved optical spectroscopy, Appl. Surf. Sci., 2012, 258, 9374.
189. J. Guo, T. Wang, J. Shao, T. Sun, R. Wang, A. Chen, Z. Hu, M. Jin and D. Ding, Emission enhancement ratio of the metal irradiated by femtosecond double-pulse laser, Opt. Commun., 2012, 285, 1895.
190. A. Chen, S. Li, S. Li, Y. Jiang, J. Shao, T. Wang, X. Huang, M. Jin and D. Ding, Optimally enhanced optical emission in laser-induced air plasma by femtosecond double-pulse, Phys. Plasmas, 2013, 20, 103110.
191. S. S. Harilal, P. K. Diwakar and A. Hassanein, Electron-ion relaxation time dependent signal enhancement in ultrafast double-pulse laser-induced breakdown spectroscopy, Appl. Phys. Lett., 2013, 103, 041102.
192. J. Penczak, R. Kupfer, I. Bar and R. J. Gordon, The role of plasma shielding in collinear double-pulse femtosecond laser-induced breakdown spectroscopy, Spectrochim. Acta, Part B, 2014, 97, 34.
193. J. Mildner, C. Sarpe, N. Götte, M. Wollenhaupt and T. Baumert, Emission signal enhancement of laser ablation of metals (aluminium and titanium) by time delayed femtosecond double pulses from femtoseconds to nanoseconds, Appl. Surf. Sci., 2014, 302, 291.
194. A. Semerok and C. Dutouquet, Analytical performances of laser-induced micro-plasma of Al samples with single and double ultrashort pulses in air and with Ar-jet: a comparative study, Spectrochim. Acta, Part B, 2014, 99, 163.
195. X. Liu, S. Sun, X. Wang, Z. Liu, Q. Liu, P. Ding, Z. Guo and B. Hu, Effect of laser pulse energy on orthogonal double femtosecond pulse laser-induced breakdown spectroscopy, Opt. Express, 2013, 21, A704.
196. H. Qi, S. Li, Y. Qi, A. Chen, Z. Hu, X. Huang, M. Jin and D. Ding, Effect of sample position on collinear femtosecond double-pulse laser-induced breakdown spectroscopy of silicon in air, J. Anal. At. Spectrom., 2014, 29, 1105.
197. Y. Qi, H. Qi, Q. Wang, Z. Chen and Z. Hun, The influence of double pulse delay and ambient pressure on femtosecond laser ablation of silicon, Opt. Laser Technol., 2015, 66, 68.
198. X. Zhao and Y. C. Shin, Laser–plasma interaction and plasma enhancement by ultrashort doublepulseablation, Appl. Phys. B: Lasers Opt., 2015, 120, 81.
199. J. Shen, Z. Yang, X. Liu, Y. Shi, P. Zhao, S. Sun and B. Hu, Analysis of Enhanced Laser-Induced Breakdown Spectroscopy with Double Femtosecond Laser Pulses, Plasma Sci. Technol., 2015, 17, 147.
200. M. Wang, S. Wang, Z. Cao, P. Wang and C. Wang, Investigation of double-pulse femtosecond laser induced breakdown spectroscopy of polymethyl methacrylate (PMMA), Proc. SPIE, 2015, 9351, 93511Q.
201. J. J. Laserna, R. Fernández Reyes, R. González, L. Tobaria and P. Lucena, Study on the effect of beam propagation through atmospheric turbulence on standoff nanosecond laser induced breakdown spectroscopy measurements, Opt. Express, 2009, 17, 10265.
202. P. Rohwetter, J. Yu, G. Mejean, K. Stelmaszczyk, E. Salmon, J. Kasparian, J.-P. Wolf and L. Woste, Remote LIBS with ultrashort pulses: characteristics in picosecond and femtosecond, J. Anal. At. Spectrom., 2004, 19, 437.
203. K. Y. Andrianov, V. P. Kandidov, O. G. Kosareva, S. L. Chin, A. Talebpur, S. Petit, W. Liu, A. Ivasaki and M. C. Nadeau, Influence of beam quality on filamentation of high-power femtosecond laser pulses in air, Izv. Akad. Nauk SSSR, Ser. Fiz., 2002, 66, 1091.
204. V. P. Kandidov, O. G. Kosareva, S. A. Shlenov, N. A. Panov, V. Y. Fedorov and A. E. Dormidonov, Dynamic small-scale self-focusing of a femtosecond laser pulse, Quantum Electron., 2005, 35, 59.
205. K. Stelmaszczyk, P. Rohwetter, G. Mejean, J. Yu, E. Salmon, J. Kasparian, R. Ackermann, J. P. Wolf and L. Woste, Long-distance remote laser-induced breakdown spectroscopy using filamentation in air, Appl. Phys. Lett., 2004, 85, 3977.
206. H. Wille, M. Rodriguez, J. Kasparian, D. Mondelain, J. Yu, A. Mysyrowicz, R. Sauerbrey, J. P. Wolf and L. Woste, Teramobile: a mobile femtosecond-terawatt laser and detection system, Eur. Phys. J., 2002, 20, 183.
207. R. S. Hatzes, Kilometer-range non-linear propagation of fs laser pulses, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 036607.
208. C. D'Amico, A. Houard, M. Franco, B. Prade and A. Mysyrowicz, Coherent and incoherent radial THz radiation emission from femtosecond filaments in air, Opt. Express, 2007, 15, 15274.
209. G. Méchain, T. Olivier, M. Franco, A. Couairon, B. Prade and A. Mysyrowicz, Femtosecond filamentation in air at low pressures. Part II: laboratory experiments, Opt. Commun., 2006, 261, 322.
210. J. Kasparian, R. Ackermann, Y.-B. Andre, G. Mechain, G. Mejean, B. Prade, P. Rohwetter, E. Salmon, K. Stelmaszczyk, J. Yu, A. Mysyrowicz, R. Sauerbrey, L. Woste and J.-P. Wolf, Progress towards lightning control using lasers, Journal of the European Optical Society: Rapid Publications, 2008, 3, 08035.
211. Y. Petit, S. Henin, J. Kasparian, J.-P. Wolf, P. Rohwetter, K. Stelmaszczyk, Z. Q. Hao, W. M. Nakaema, L. Wöste and A. Vogel, Influence of pulse duration, energy, and focusing on laser-assisted water condensation, Appl. Phys. Lett., 2011, 98, 041105.
212. http://www.teramobile.org .
213. P. Rohwetter, K. Stelmaszczyk, L. Wöste, R. Ackermann, G. Méjean, E. Salmon, J. Kasparian, J. Yu and J.-P. Wolf, Filament-induced remote surface ablation for long range laser-induced breakdown spectroscopy operation, Spectrochim. Acta, Part B, 2005, 60, 1025.
214. M. Weidman, K. Lim, M. Ramme, M. Durand, M. Baudelet and M. Richardson, Stand-off filament-induced ablation of gallium arsenide, Appl. Phys. Lett., 2012, 101, 034101.
215. A. Valenzuela, C. Munson, A. Porwitzky, M. Weidman and M. Richardson, Comparison between geometrically focused pulses versus filaments in femtosecond laser ablation of steel and titanium alloys, Appl. Phys. B: Lasers Opt., 2014, 116, 485.
216. M. Weidman, M. Baudelet, M. Fisher, C. Bridge, C. Brown, M. Sigman, P. J. Dagdigian and M. Richardson, Molecular signal as a signature for detection of energetic materials in filament-induced breakdown spectroscopy, Proc. SPIE, 2009, 7304, 73041G.
217. W. Liu, H. L. Xu, G. Méjean, Y. Kamali, J.-F. Daigle, A. Azarm, P. T. Simard, P. Mathieu, G. Roy and S. L. Chin, Efficient non-gated remote filament-induced breakdown spectroscopy of metallic sample, Spectrochim. Acta, Part B, 2007, 62, 76.
218. H. L. Xu, J. Bernhardt, P. Mathieu, G. Roy and S. L. Chin, Understanding the advantage of remote femtosecond laser-induced breakdown spectroscopy of metallic targets, J. Appl. Phys., 2007, 101, 033124.
219. E. J. Judge, G. Heck, E. B. Cerkez and R. J. Levis, Discrimination of Composite Graphite Samples Using Remote Filament-Induced Breakdown Spectroscopy, Anal. Chem., 2009, 81, 2658.
220. H. L. Xu, P. T. Simard, Y. Kamali, J.-F. Daigle, C. Marceau, J. Bernhardt, J. Dubois, M. Châteauneuf, F. Théberge and G. Roy, Filament-induced breakdown remote spectroscopy in a polar environment, Laser Phys., 2012, 22, 1767.
221. S. Tzortzakis, D. Anglos and D. Gray, Ultraviolet laser filaments for remote laser-induced breakdown spectroscopy (LIBS) analysis: applications in cultural heritage monitoring, Opt. Lett., 2006, 31, 1139.
222. D. Mirell, O. Chalus, K. Peterson and J.-C. Diels, Remote sensing of explosives using infrared and ultraviolet filaments, J. Opt. Soc. Am. B, 2008, 25, B108.
223. B. Zeng, W. Chu, H. Gao, W. Liu, G. Li, H. Zhang, J. Yao, J. Ni, S. L. Chin and Y. Cheng, Enhancement of peak intensity in a filament core with spatiotemporally focused femtosecond laser pulses, Phys. Rev. A: At., Mol., Opt. Phys., 2011, 84, 063819.
224. B. Zeng, T.-J. Wang, S. Hosseini, Y. Cheng, Z. Xu, W. Liu and S. L. Chin, Enhanced remote filament-induced breakdown spectroscopy with spatio-temporally chirped pulses, J. Opt. Soc. Am. B, 2012, 29, 3226.
225. H. L. Xu, W. Liu and S. L. Chin, Remote time-resolved filament-induced breakdown spectroscopy of biological materials, Opt. Lett., 2006, 31, 1540.
226. H. L. Xu, G. Méjean, W. Liu, Y. Kamali, J.-F. Daigle, A. Azarm, P. T. Simard, P. Mathieu, G. Roy and J.-R. Simard, Remote detection of similar biological materials using femtosecond filament-induced breakdown spectroscopy, Appl. Phys. B: Lasers Opt., 2007, 87, 151.
227. Y.-W. Zhang, X. Gao, Y. Zhang, C. Song and J.-Q. Lin, Analysis of heavy metals in poplar leaves by femtosecond filament-induced breakdown spectroscopy, Acta Phys. Sin., 2015, 64, 175203.
228. X. Gao, C. Du, C. Li, L. Liu, C. Song, Z.-Q. Hao and J.-Q. Lin, Detection of heavy metal Cr in soil by the femtosecond filament induced breakdown spectroscopy, Acta Phys. Sin., 2014, 63, 095203.
229. H. L. Xu, Y. Kamali, C. Marceau, P. T. Simard, W. Liu, J. Bernhardt, G. Méjean, P. Mathieu, G. Roy and J.-R. Simard, Simultaneous detection and identification of multigas pollutants using filament-induced nonlinear spectroscopy, Appl. Phys. Lett., 2007, 90, 101106.
230. Y. Kamali, J.-F. Daigle, F. Théberge, M. Châteauneuf, A. Azarm, Y. Chen, C. Marceau, S. C. Lessard, F. Lessard and G. Roy, Remote sensing of trace methane using mobile femtosecond laser system of T&T Lab, Opt. Commun., 2009, 282, 2062.
231. Q. Luo, H. L. Xu, S. A. Hosseini, J.-F. Daigle, F. Théberge, M. Sharifi and S. L. Chin, Remote sensing of pollutants using femtosecond laser pulse fluorescence spectroscopy, Appl. Phys. B: Lasers Opt., 2005, 82, 105.
232. J.-F. Daigle, G. Méjean, W. Liu, F. Théberge, H. L. Xu, Y. Kamali, J. Bernhardt, A. Azarm, Q. Sun and P. Mathieu, Long range trace detection in aqueous aerosol using remote filament-induced breakdown spectroscopy, Appl. Phys. B: Lasers Opt., 2007, 87, 749.
233. J.-F. Daigle, Y. Kamali, G. Roy and S. L. Chin, Remote filament-induced fluorescence spectroscopy from thin clouds of smoke, Appl. Phys. B: Lasers Opt., 2008, 93, 759.
234. S. L. Chin, H. L. Xu, Q. Luo, F. Théberge, W. Liu, J. F. Daigle, Y. Kamali, P. T. Simard, J. Bernhardt and S. A. Hosseini, Filamentation ‘remote’ sensing of chemical and biological agents/pollutants using only one femtosecond laser source, Appl. Phys. B: Lasers Opt., 2009, 95, 1.
235. J. Odhner and R. Levis, Optical Spectroscopy Using Gas-Phase Femtosecond Laser Filamentation, Annu. Rev. Phys. Chem., 2014, 65, 605.
236. A. de Giacomo, M. Dell'Aglio, O. de Pascale, R. Gaudiuso, A. Santagata and R. Teghil, Laser Induced Breakdown Spectroscopy methodology for the analysis of copper-based-alloys used in ancient artworks, Spectrochim. Acta, Part B, 2008, 63, 192.
237. S. Almaviva, R. Fantoni, L. Caneve, F. Colao, L. Fornarini, A. Santagata and R. Teghil, Use of ns and fs pulse excitation in laser-induced breakdown spectroscopy to improve its analytical performances: a case study on quaternary bronze alloys, Spectrochim. Acta, Part B, 2014, 99, 185.
238. M. Oujja, M. Sanz, F. Agua, J. F. Conde, M. García-Heras, A. Dávila, P. Oñate, J. Sanguino, J. R. Vázquez de Aldana, P. Moreno, M. A. Villegas and M. Castillejo, Multianalytical characterization of Late Roman glasses including nanosecond and femtosecond laser induced breakdown spectroscopy, J. Anal. At. Spectrom., 2015, 30, 1590.
239. R. K. Gill, F. Knorr, Z. J. Smith, M. Kahraman, D. Madsen, D. S. Larsen and S. Wachsmann-Hogiu, Characterization of Femtosecond Laser-Induced Breakdown Spectroscopy (fsLIBS) and Applications for Biological Samples, Appl. Spectrosc., 2014, 68, 949.
240. L. Guyon, M. Baudelet, J. Yu, J. Wolf, T. Amodeo, E. Frejafon and P. Laloi, Laser-Induced Breakdown Spectroscopy Analysis of Bacteria: What Femtosecond Lasers Make Possible, in 15th International Conference on Ultrafast Phenomena, OSA Technical Digest Series, 2006.
241. M. Baudelet, J. Yu, M. Bossu, J. Jovelet, J.-P. Wolf, T. Amodeo, E. Fréjafon and P. Laloi, Discrimination of microbiological samples using femtosecond laser-induced breakdown spectroscopy, Appl. Phys. Lett., 2006, 89, 163903.
242. D. C. Jeong, P. S. Tsai and D. Kleinfeld, Prospect for feedback guided surgery with ultra-short pulsed laser light, Curr. Opin. Neurobiol., 2012, 22, 24–33.
243. H. Huang, L.-M. Yang, S. Bai and J. Liu, Smart surgical tool, J. Biomed. Opt., 2015, 20, 028001.
244. M. Sabsabi, R. Héon and L. St-Onge, Critical evaluation of gated CCD detectors for laser-induced breakdown spectroscopy analysis, Spectrochim. Acta, Part B, 2005, 60, 1211.
245. P. Fichet, D. Menut, R. Brennentot, E. Vors and A. Rivoallan, Analysis by laser-induced breakdown spectroscopy of complex solids, liquids, and powders with an echelle spectrometer, Appl. Opt., 2003, 42, 6029.
246. M. Sabsabi and P. Cielo, Quantitative Analysis of Aluminum Alloys by Laser-Induced Breakdown Spectroscopy and Plasma Characterization, Appl. Spectrosc., 1995, 49, 499.
247. A. A. Ilyin and S. S. Golik, Femtosecond laser-induced breakdown spectroscopy of sea water, Spectrochim. Acta, Part B, 2013, 87, 192.
248. P. Fichet, M. Tabarant, B. Salle and C. Gautier, Comparisons between LIBS and ICP/OES, Anal. Bioanal. Chem., 2006, 385, 338.
249. K. M. Lo and N. H. Cheung, ArF Laser-Induced Plasma Spectroscopy for Part-per-Billion Analysis of Metal Ions in Aqueous Solutions, Appl. Spectrosc., 2002, 56, 682.
250. F.-Y. Yueh, R. C. Sharma, J. P. Singh, H. Zhang and W. A. Spencer, Evaluation of the Potential of Laser-Induced Breakdown Spectroscopy for Detection of Trace Element in Liquid, J. Air Waste Manage. Assoc., 2002, 52, 1307.
251. S. T. Järvinen, S. Saari, J. Keskinen and J. Toivonen, Detection of Ni, Pb and Zn in water using electrodynamic single-particle levitation and laser-induced breakdown spectroscopy, Spectrochim. Acta, Part B, 2014, 99, 9.
252. S. S. Golik, O. A. Bukin, A. A. Il’in, E. B. Sokolova, A. V. Kolesnikov, M. Y. Babiy, Y. N. Kul'chin and A. A. Gal'chenko, Determination of detection limits for elements in water by femtosecond laser-induced breakdown spectroscopy, J. Appl. Spectrosc., 2012, 79, 471.
253. J. Xiu, S. Zhong, H. Hou, Y. Lu and R. Zheng, Quantitative Determination of Manganese in Aqueous Solutions and Seawater by Laser-Induced Breakdown Spectroscopy (LIBS) Using Paper Substrates, Appl. Spectrosc., 2014, 68, 1039.
254. S. S. Golik, A. A. Ilyin, M. Y. Babiy, Y. S. Biryukova, V. V. Lisitsa and O. A. Bukin, Determination of Iron in Water Solution by Time-Resolved Femtosecond Laser-Induced Breakdown Spectroscopy, Plasma Sci. Technol., 2015, 17, 975.
255. H. Loudyi, K. Rifaï, S. Laville, F. Vidal, M. Chaker and M. Sabsabi, Improving laser-induced breakdown spectroscopy (LIBS) performance for iron and lead determination in aqueous solutions with laser-induced fluorescence (LIF), J. Anal. At. Spectrom., 2009, 24, 1421.
256. D. Santos Jr, R. E. Samad, L. C. Trevizan, A. Z. de Freitas, N. D. Vieira Jr and F. J. Krug, Evaluation of Femtosecond Laser-Induced Breakdown Spectroscopy for Analysis of Animal Tissues, Appl. Spectrosc., 2008, 62, 1137.
257. M. D. Adamson and S. J. Rehse, Detection of trace Al in model biological tissue with laser-induced breakdown spectroscopy, Appl. Opt., 2007, 46, 5844.
258. T. Owens, S. S. Mao, E. K. Canfield, C. P. Grigoropoulos, X. Mao and R. E. Russo, Ultrafast thin-film laser-induced breakdown spectroscopy of doped oxides, Appl. Opt., 2010, 49, C67.
259. J. Xiu, V. Motto-Ros, G. Panczer, R. Zheng and J. Yu, Feasibility of wear metal analysis in oils with parts per million and sub-parts per million sensitivities using laser-induced breakdown spectroscopy of thin oil layer on metallic target, Spectrochim. Acta, Part B, 2014, 91, 24.
260. G. G. Arantes de Carvalho, J. Moros, D. Santos Jr, F. J. Krug and J. J. Laserna, Direct determination of the nutrient profile in plant materials by femtosecond laser-induced breakdown spectroscopy, Anal. Chim. Acta, 2015, 876, 26.
261. Ş. Yalçın, S. Örer and R. Turan, 2-D analysis of Ge implanted SiO₂ surfaces by laser-induced breakdown spectroscopy, Spectrochim. Acta, Part B, 2008, 63, 1130.
262. I. Lopez-Quintas, V. Pinon, M. P. Mateo and G. Nicolas, Effect of surface topography in the generation of chemical maps by laser-induced plasma spectroscopy, Appl. Surf. Sci., 2012, 258, 9432.
263. Y. Markushin, P. Sivakumar, D. Connolly and N. Melikechi, Tag-femtosecond laser-induced breakdown spectroscopy for the sensitive detection of cancer antigen 125 in blood plasma, Anal. Bioanal. Chem., 2015, 407, 1849.

---