Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Substituent effects on fluoride binding by lanthanide complexes of DOTA-tetraamides†
Octavia A.
Blackburn
a,
Jack D.
Routledge
a,
Laura B.
Jennings
a,
Nicholas H.
Rees
a,
Alan M.
Kenwright
b,
Paul D.
Beer
a and
Stephen
Faulkner
a
aUniversity of Oxford, Chemistry Research Laboratory, 12 Mansfield Road, Oxford OX1 3TA, UK. E-mail: Stephen.Faulkner@chem.ox.ac.uk
bDepartment of Chemistry, University of Durham, South Road, Durham DH1 3LE, UK
First published on 4th January 2016
Abstract
Fluoride binding by a series of europium and ytterbium complexes of DOTA-tetraamide ligands derived from primary, secondary and tertiary amides has been studied by NMR and luminescence spectroscopies. In all the systems studied, fluoride binding results in a change in the nature of the magnetic anisotropy at the metal centre from an easy axis, to an easy plane anisotropy. This results in reversal of the peaks in the NMR spectra, and in changes to the fine structure of the luminescence spectra. Furthermore, changes to the periphery of the binding cavity are implicated in determining the affinity constant for fluoride. There are clear differences in the entropic contribution to the free energy of activation between systems with benzylic amides and those with methylamides.
The spectroscopic and magnetic properties of lanthanide complexes have been widely exploited over the course of many years, particularly in magnetic resonance imaging contrast agents and in time-resolved bioassays, and more recently in the field of molecular magnetism. In all of these areas, optimisation of the properties of these lanthanide containing systems is contingent on the fundamental understanding of their electronic structure, and the interaction of open shell f-electrons with their surroundings.
Bleaney's approach to understanding the effect of lanthanide magnetism on surrounding nuclear spins has underpinned the development of the field for almost fifty years.1 Defining these theories required a number of approximations to be made; and, while many have pointed out discrepancies between theoretical prediction and experimental observations (particularly in low symmetry systems), it is only recently that supporting theoretical methods have become available to study and interpret more unusual aspects of lanthanide behaviour in molecular systems.
We recently investigated the binding of fluoride ions to lanthanide complexes of the tetraamide ligand DTMA and determined that the replacement of water with fluoride induces a change in the nature of the magnetic anisotropy and in the sign of the crystal field parameter B20.2,3 The change resulted in dramatic changes to NMR, EPR and luminescence spectra, and the phenomenon was further understood using ab initio calculations. These results, taken together with a number of recent studies on single molecule magnets4 and luminescent complexes,5 provide a rapidly growing body of data that reveal the subtleties inherent to the magnetic behaviour of lanthanide complexes.
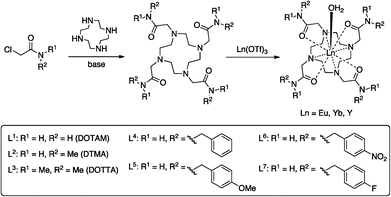
In this manuscript we seek to determine how the nature of the ligand affects the fluoride-binding event in symmetric DOTA tetraamide complexes. To this end we have synthesised and studied the fluoride binding by a number of complexes related to DTMA (L1, L3–L7), shown in Scheme 1. This array of related complexes has allowed us to explore the effect of variations in amide structure and hydrophobicity on fluoride binding and its spectroscopic consequences.
Results and discussion
Synthesis
A series of tetraamide ligands derived from a variety of different amines, were synthesised by the well-established procedure outlined in Scheme 1. The chloroacetamides were synthesised from the appropriate primary or secondary amine and reacted with cyclen to give the 8-coordinate ligands. The complexes were formed by reaction of the ligands with the appropriate lanthanide triflate salts and characterised by NMR, mass spectrometry and CHN analysis (see ESI†).NMR studies
Proton NMR studies focussed on the Yb3+ complexes of ligands L1–7 due to the dominance of the pseudocontact shift for this ion. The 1H NMR spectra in D2O, and the effect of addition of fluoride on the spectra are shown in Fig. 1. All of the Yb3+ complexes apart from YbL3 appear to only be present as the SAP isomer. YbL3 contains approximately 7% TSAP in D2O at 298 K. Upon addition of fluoride, all Yb complexes display a new set of peaks in slow exchange with the original set, as originally observed with YbL2 (YbDTMA).2 In all cases, EXSY spectra show a reversal of the peak order between hydrated and fluoride-bound forms, implying a change of sign of B20 (see ESI†). In our earlier studies, we rationalised these observations by a change in the order of the mJ states arising from ligand field splitting of the 2F7/2 ground state giving rise to a change in the nature of the magnetic anisotropy at the lanthanide centre, and it is reasonable to infer that this phenomenon is general across this series of complexes. The observation of such dramatic changes to the NMR spectra upon fluoride coordination must be explained in terms of changes to the Boltzmann populations within the mJ manifold as a result of changing the relative energies of the various mJ states, and it is clear that the overall anisotropy of the metal ion must reflect all of these states.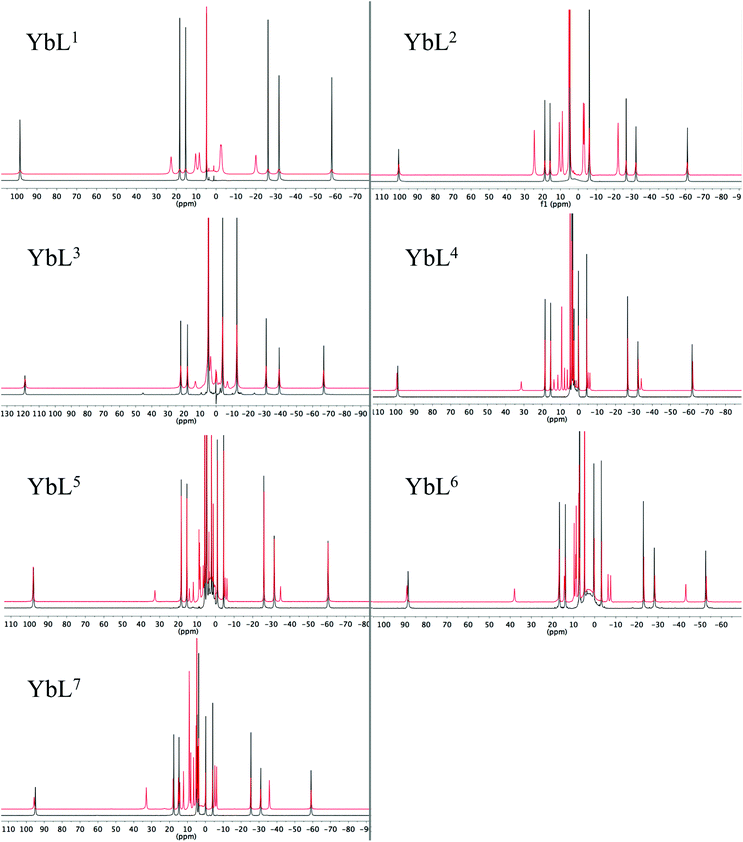 | ||
| Fig. 1 1H NMR of complexes YbL1–7 in the absence (black) and presence (red) of an excess of sodium fluoride (D2O, 400 MHz, 298 K). | ||
Inspection of the spectra in Fig. 1 reveals that while the range of chemical shifts observed for the hydrated complexes are fairly similar, those for the fluoride-bound species show significant differences between complexes. Differences in the spread of observed 1H chemical shifts between complexes reflect the relative magnitudes of the axial magnetic anisotropy resulting from the effects of different ligand fields. For systems with axial symmetry and negligible contact shift contribution, the effect of the crystal field on the observed shifts is conveniently expressed using the Bleaney equation1 and the crystal field parameter, B20:
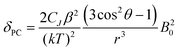 | (1) |
The crystal field coefficient, CJ, and the parameters B20β, k and T are often grouped together into one parameter labelled D1 to give:
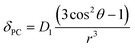 | (2) |
Plots of δPCvs. (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2
cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ − 1)/r3, yield lines with gradients corresponding to D1 (eqn (2)), which are proportional to B20. δPC are approximated from δobs by subtraction of 2.9 ppm (the average shift for the protons on the ligand) to take account of the diamagnetic contribution and (3
θ − 1)/r3, yield lines with gradients corresponding to D1 (eqn (2)), which are proportional to B20. δPC are approximated from δobs by subtraction of 2.9 ppm (the average shift for the protons on the ligand) to take account of the diamagnetic contribution and (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2
cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ − 1)/r3 values are taken from closely related crystal structures.6,7 These experimentally derived D1 values are given in Table 1 for each complex in both hydrated and fluoride-bound forms (plots are given in ESI†) along with the difference between the two. The reported values are uncorrected for changes in the bulk magnetic anisotropy with the lanthanide: the same method was used for both the fluoride-free and fluoride bound systems, and the relative change between the two can be assumed to be correct.
θ − 1)/r3 values are taken from closely related crystal structures.6,7 These experimentally derived D1 values are given in Table 1 for each complex in both hydrated and fluoride-bound forms (plots are given in ESI†) along with the difference between the two. The reported values are uncorrected for changes in the bulk magnetic anisotropy with the lanthanide: the same method was used for both the fluoride-free and fluoride bound systems, and the relative change between the two can be assumed to be correct.
| YbLx–OH2 | YbLx–F | ΔD1 | |
|---|---|---|---|
| YbL1 | 3027 | −791 | 3818 |
| YbL2 | 3216 | −890 | 4106 |
| YbL3 | 3613 | −356 | 3969 |
| YbL4 | 3382 | −1350 | 4732 |
| YbL5 | 3329 | −1379 | 4708 |
| YbL6 | 2976 | −1666 | 4642 |
| YbL7 | 3234 | −1404 | 4638 |
For the hydrated species, the magnitudes of D1 fall within a relatively narrow range. Observed differences correlate with variations in electron demand, although solvation is also expected to play a role. The nature of the para-benzyl substituent has a small but significant influence on the crystal field, with the NO2 group giving the smallest B20 of the benzyl-substituted complexes.
It is possible to use the data in Table 1 to estimate the degree of anisotropy in each of the complexes. Since:
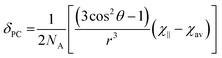 | (3) |
| χav = (χ∥ + 2χ⊥)/3 | (4) |
It is possible to define both χ∥ and χ⊥ from D1 provided we know χav. In previous studies, we modelled χav for Yb·L2–OH2 and for Yb·L2–F− obtaining values for χavT at 300 K of 2.49 and 2.51 cm3 mol−1 K respectively, while the free ion χav would be expected to be 2.57 cm3 mol−1 K.2 In our previous study, theoretical models were also used to support the hypothesis that axial ligand exchange (i.e. replacing water with fluoride) did not alter the structure of the macrocyclic ligand significantly. In the case of this work, it is reasonable to assume that axial ligand exchange occurs- since substitution of a fluoride ligand for one of the other donor atoms to Ln would break the observed symmetry inferred from the NMR spectra.
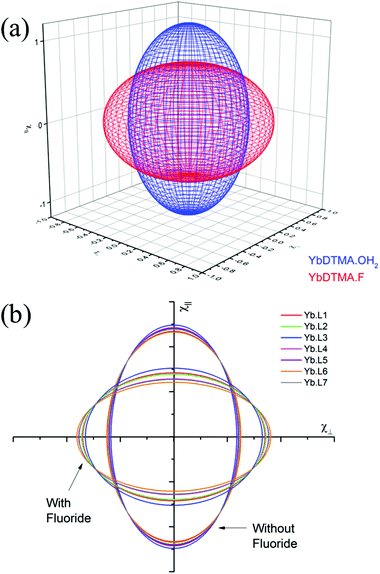
Thus the crystal field of the ligands undoubtedly has an effect upon the value of χav, albeit a small one. For the purposes of this study, a qualitative map of the anisotropy can be obtained by estimating χav as 2.5 cm3 mol−1 K for the systems studied in this manuscript. The results of applying this approach can be seen in Fig. 2, which represents the magnetic susceptibilities as a series of spheroids in which the z-axis defines the molecular axis. Values for χ∥ and χ⊥ are tabulated in the ESI† to this paper. From Fig. 2, it should be clear that the anisotropy takes very different forms in the water-bound and fluoride-bound complexes, while much smaller (though still significant) differences in anisotropy are observed between complexes with different macrocyclic ligands. It should be noted that, at the ambient temperatures studied in this work, free rotation about the Ln–O bond in the aquated complex results in averaging of χX and χY on the timescale of the NMR experiment (meaning that the anisotropy can be treated as a spheroid rather than an ellipsoid on these timescales).
YbL1 and YbL2 behave similarly on addition of fluoride. YbL3–F has anomalous chemical shift ranges and a much less negative D1, which are likely to be a consequence of YbL3 being the only tertiary tetraamide studied. The change in slope of the Bleaney plot on binding fluoride is however similar to YbL1,2, being in the range 3800–4100 ppm Å3, so although the magnetic anisotropy in YbL3–F is smaller than the other complexes, this is due to the axial fluoride offsetting a stronger equatorial ligand field. The fluoride bound benzylamide derivatives, YbL4–7, have more negative D1 than YbL1–3 while all show changes in D1 in the range 4600–4700 ppm Å3. This would argue that exchange of water for fluoride has a greater impact on the crystal field for YbL4–7 compared with YbL1–3. This is likely to be a consequence of reduced solvation of the fluoride in the binding cavity making the fluoride a better donor. The observed value of D1 does, however, vary from complex to complex as a consequence of the electronic influences of the peripheral substituents on the benzyl groups. YbL6–F has a more negative gradient than the other benzylamides, however this is a consequence of a weaker equatorial ligand field (as indicated by the trend in the series of hydrated benzylamide complexes).
Analogous effects of fluoride binding are also observed in the NMR spectra of the europium complexes, although chemical shifts are significantly affected by the contact shift and so eqn (1) cannot be employed. Furthermore, EuL1–3 are present as mixtures of SAP and TSAP isomers in solution.7 The exchange between isomers in these cases causes broadening of the 1H NMR spectra and cooling is required to distinguish the peaks. The benzyl-substituted Eu(III) complexes however display much sharper NMR spectra since only the SAP isomer appears to be present (see ESI†), as has been previously noted for larger secondary substituents of this nature.8 EuL3 is a mixture of SAP and TSAP in ca. 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio and two new sets of 1H signals appear on addition of fluoride, in a ratio of ca. 1
2 ratio and two new sets of 1H signals appear on addition of fluoride, in a ratio of ca. 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (Fig. 3), presumably corresponding to fluoride bound SAP and TSAP isomers.
3 (Fig. 3), presumably corresponding to fluoride bound SAP and TSAP isomers.
During our previous study we observed the 19F signals corresponding to bound fluoride for several different lanthanide complexes of ligand L2.3 In the case of the pseudo-lanthanide yttrium the signal is a doublet due to coupling between 19F and 89Y nuclei, as confirmed by HMQC.3 Bound fluoride resonances are reported here for Y3+, Eu3+ and Yb3+ complexes (Table 2). In the case of EuL3, two bound fluoride signals are observed and integration indicates that the peak at −500 ppm (298 K) corresponds to the major isomer of the fluoride-bound form.
| Y | Eu | Yb | |
|---|---|---|---|
| L1 | −62 (59) | −487 | −833 |
| L2 | −59 (61) | −481 | −859 |
| L3 | −60 (57) | −414, −500 | −721 |
| L4 | −54 (65) | −483 | −993 |
| L5 | −54 (65) | −479 | −1016 |
| L6 | −52 (66) | −477 | −1098 |
| L7 | −54 (66) | −483 | −1023 |
The yttrium complexes allow us to assess the diamagnetic contributions to the 19F chemical shift. Complexes of L1–3 have bound fluoride shifts of a similar magnitude to one another, while complexes of L4–7 give less negative bound fluoride shifts. Y–F coupling constants are also separated into these two groups. The larger coupling constants and less negative chemical shifts (a larger shift from free fluoride) would imply a significant difference to the nature of the interaction between fluoride and the benzylamide-based complexes.
In the paramagnetic complexes, the diamagnetic contribution to the shift is small relative to the effect of the paramagnetic metal centres. The europium complexes have bound fluoride chemical shifts that are broadly similar, with the exception of EuL3. Here the lanthanide induced shift (LIS) is dominated by the contact shift, especially considering that the fluoride is directly coordinated to the metal. The phenomenon of spin–spin coupling between fluorine and spatially adjacent nuclei by virtue of orbital overlap (“through-space couplings”) is well known and has been extensively studied.9 Note that this does not imply any “formal” bond between the fluoride ion and the metal, nor does it necessarily tell us anything about the contribution of the contact shift for other nuclei (such as protons) in the complex. The similarity of the lanthanide induced fluoride shifts therefore indicates that the contact shift felt by the fluoride ion is relatively constant across the series of complexes studied and implies that the nature of the contact interaction is insensitive to the substituents.
Conversely, the bound fluoride shifts of the ytterbium complexes are dominated by the pseudocontact shift,3 and therefore vary with the size of the crystal field coefficient. A plot of D1 for the fluoride-bound Yb3+ complexes taken from Table 1vs. LIS of the ytterbium bound fluoride gives a straight line (Fig. 4). The shifts of the yttrium analogues are used to subtract the diamagnetic contributions. The linear correlation would imply that the geometric factor, (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2
cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ − 1)/r3, remains constant across the series of complexes and since we can assume that θ is also constant, we can infer that the distance between fluoride and lanthanide does not vary with the identity of the ligand.
θ − 1)/r3, remains constant across the series of complexes and since we can assume that θ is also constant, we can infer that the distance between fluoride and lanthanide does not vary with the identity of the ligand.
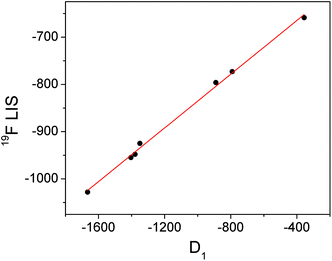 | ||
| Fig. 4 Graph of D1 (derived from Bleaney plots of 1H shifts of YbL1–7) vs. the observed LIS of bound fluoride for YbL1–7 with linear fit in red. | ||
Luminescence studies
We also studied the effects of fluoride binding on the luminescence properties of the europium complexes since information regarding the ligand field can readily be extracted from fine structure.10 Changes to the shape of the spectrum are observed in all bands (see ESI†) upon addition of fluoride. The ΔJ = 1 band is the most appropriate to analyse since in axial symmetry we would expect the band to consist of two peaks as a result of the 2J + 1 degeneracy being lifted by the ligand field. The parameter B20 can be extracted directly from the splitting of this band. The fine structure of the ΔJ = 1 bands in the presence and absence of fluoride are shown for EuL1–7 in Fig. 5.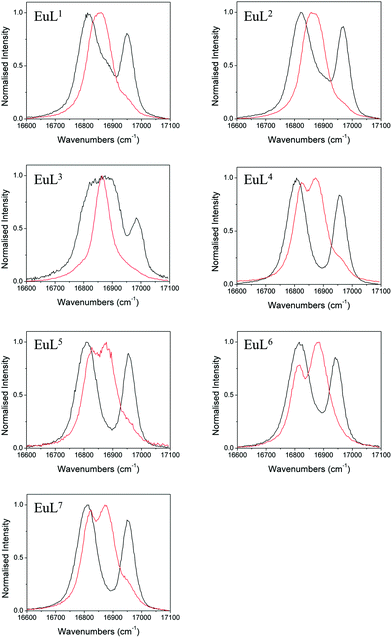 | ||
| Fig. 5 Normalised emission bands for the 5D0–7F1 transitions of EuL1–7 in the absence (black) and presence (red) of an excess of sodium fluoride (exit slit = 0.2 nm). | ||
In the absence of fluoride, the ΔJ = 1 regions of EuL1–3 appear to consist of more than two transitions, especially for EuL3 which displays a particularly broad band. For EuL4–7, ΔJ = 1 is split into two easily distinguishable peaks. This correlates with the presence of two conformational isomers with significantly different ligand field splitting, SAP and TSAP, for EuL1–3 and the predominance of SAP in EuL4–7. Therefore, while the shape of the ΔJ = 1 band for EuL1–3 is complicated by the presence of multiple isomers, the shape of this band for Eu·L4–7 is determined only by B20 of the SAP isomer. It is instantly apparent from the splitting of ΔJ = 1 that L6 invokes a smaller crystal field splitting than L4,5,7, which correlates with the 1H NMR studies of the Yb3+ complexes (Table 1).
Upon addition of fluoride, the emission spectra of the Eu complexes change shape in accordance with a change in the ligand field (see ESI†). The change is similar for all complexes with a decrease in the magnitude of splitting within the ΔJ = 1 band (Fig. 5). For Eu·L1–3 the ΔJ = 1 peaks merge into one, corresponding to the reduction in the magnitude of B20 in the fluoride bound complexes. EuL3 displays a particularly narrow band, which correlates with the small magnitude of D1 of YbL3 compared with YbL1−2 (Table 1). The magnitude of the splitting is unresolvable in the Eu·L1–3 emission spectra.
For the benzyl substituted complexes in the presence of fluoride, the splitting of ΔJ = 1 is resolvable and is small compared with the original complex, in line with the observations from 1H NMR of the Yb complexes. The fact that the splitting is resolvable for EuL4–7 but not EuL1–3 tallies with the larger magnitude of D1 observed for the former (Table 1). The peak separation is larger for EuL6 than EuL4–5 in line with the more negative D1 for the former. Furthermore, while it is not possible to clearly identify the A and E components of the ΔJ = 1 band in EuL4,5,7, for EuL6 the transition from 5D0 to the doubly degenerate E level of 7F1 (which appears broader in the spectrum) is now at higher energy than the A level. The energetic ordering of the A and E levels is thus reversed with respect to the hydrated complex, presenting further direct evidence of a change in sign of B20.
The luminescence lifetimes of the Eu-based emission were measured in the presence and absence of fluoride in both H2O and D2O and are given along with q values in Table 3.11 Lifetimes are lengthened on addition of fluoride corresponding to a change in the number of bound water molecules from one to zero, confirming the displacement of water by fluoride in each case.
| EuLx–OH2 | EuLx–F | |||||
|---|---|---|---|---|---|---|
| τ D2O (ms) | τ H2O (ms) | q | τ D2O (ms) | τ H2O (ms) | q | |
| a Previously published.3 | ||||||
| EuL1 | 2.22 | 0.51 | 1.0 | 2.50 | 0.96 | 0.0 |
| EuL2a | 1.72 | 0.54 | 0.9 | 2.41 | 1.07 | 0.0 |
| EuL3 | 1.88 | 0.61 | 1.0 | 2.29 | 1.34 | 0.1 |
| EuL4 | 2.27 | 0.59 | 0.8 | 2.60 | 1.01 | 0.1 |
| EuL5 | 2.31 | 0.57 | 0.9 | 2.61 | 1.10 | 0.0 |
| EuL6 | 2.17 | 0.54 | 1.0 | 2.37 | 1.07 | 0.0 |
| EuL7 | 1.92 | 0.54 | 0.9 | 2.56 | 1.13 | 0.0 |
Association constants
The association constants for fluoride with EuL1–7 were determined both by tracking changes in the emission spectra and by following changes in 1H and/or 19F NMR intensities as a function of fluoride concentration, which provide a direct measure of the concentrations of each species. The data was fitted using a one to one binding model in Dynafit12 and the values are given in Table 4 with associated confidence intervals. NMR titrations provided K values within error of those obtained from the luminescence titrations.| Luminescence | NMR | |
|---|---|---|
| a Using 1H NMR data. b Previously published.3 c At 278 K using 1H and 19F data from the same titration. d Following the 19F resonance of the ligand. | ||
| EuL1 | 90.9 [82.5–100.4] | 82.8 [72.7–94.7]a |
| EuL2 | 59.9 [57.1–62.7] | 57.5 [47.7–69.5]b |
| EuL3 | 33.3 [31.4–35.3] | 17.7 [16.0–19.5]c |
| EuL4 | 21.0 [19.5–22.6] | 21.7 [19.3–24.4]a |
| EuL5 | 20.8 [18.2–23.8] | 19.9 [16.8–23.5]a |
| EuL6 | 83.4 [77.4–89.9] | 85.2 [73.5–99.6]a |
| EuL7 | 40.7 [37.9–43.9] | 43.7 [37.8–50.7]d |
The titration data shows that there are significant differences in K with varying the ligand substituents, although they are of a similar magnitude. As we incorporate methyl groups from L1 to L3, the K value decreases. Similarly, as the electron withdrawing nature of the benzyl substituent is increased, the K value increases. This would indicate that residual charge on the metal plays a major role in determining the association constant. Correlation of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K with the D1 values (for the hydrated Yb3+ complexes) from Table 1 reveals a broadly negative correlation (Fig. S17†), although a lack of linearity would imply that there are additional factors contributing. The introduction of hydrophobic benzyl substituents does not appear to have a significant effect of the magnitude of K.
K with the D1 values (for the hydrated Yb3+ complexes) from Table 1 reveals a broadly negative correlation (Fig. S17†), although a lack of linearity would imply that there are additional factors contributing. The introduction of hydrophobic benzyl substituents does not appear to have a significant effect of the magnitude of K.
Rates of exchange
We previously determined that the rate of exchange of fluoride at the metal centre is relatively slow compared with, for example, water exchange. Qualitative information about the relative rates of exchange can be gleaned by observing the change in the proton NMR spectra of the Lu3+ complexes as the fluoride concentration is increased. Here the differences in chemical shifts of the aliphatic protons are small between complexes unlike in the paramagnetic complexes. Furthermore, exchange is not complicated by the presence of multiple isomers. The exchange rate of fluoride at the lanthanide appears fast in LuL1–3 (see ESI and ref. 3†) since all 1H peaks are seen to shift upfield with increasing fluoride concentration. Whereas in LuL4 the exchange rate is slower, with the spectra exhibiting coalescence and line shape changes upon heating in the “intermediate” exchange regime (see ESI†).A quantitative assessment of the exchange rate is achieved by using a selective inversion NMR technique appropriate for a system in slow exchange. In a sample containing a mixture of the fluoride-bound and hydrated complexes, the effects of exchange on a pair of resonances is monitored following selective inversion of one of the signals. The evolution of the magnetisations is governed by both the exchange rate (k) and the spin-lattice relaxation rates (R1 = 1/T1). A second experiment monitors the magnetisation following a non-selective inversion pulse and fitting of all data is performed by varying k and R1 using the CIFIT2 program.13 In order to extract k, an appropriate pair of resonances is required and in this case the main difficulty is that R1 is very fast for nuclei near the paramagnetic centres. The 19F nuclei of the L7 ligand are ideal for this study since they are far enough from the lanthanide to have reasonable R1s and other 19F resonances do not overlap. The methyl protons of L2 have much faster R1s than the 19F of L7, but fortunately the rate of exchange is large enough to compensate in the case of YbL2.
The rate of fluoride exchange measured with EuL7 is significantly slower than with YbL7 at 298 K (Table 5). This tallies with our previous observation that the process is faster for LuL2 compared with YL2,3 and indicates that the difference in rates is linked with the ionic size of the lanthanide ion. The ligand is able to envelop the smaller metal ions (Yb3+, Lu3+) more extensively, accelerating the dissociation of the axial ligand, as suggested by Aime et al. with DOTA complexes.14
| k (298 K) (s−1) | ΔH‡ (kJ mol−1) | ΔS‡ (J K−1 mol−1) | ΔG‡ (298 K) (kJ mol−1) | |
|---|---|---|---|---|
| YbL2 | 215.7 ± 3.0 | 47.2 ± 1.5 | −41.8 ± 5.1 | 59.7 ± 3.0 |
| YbL7 | 61.2 ± 3.6 | 45.5 ± 0.8 | −58.1 ± 2.9 | 62.8 ± 1.7 |
| EuL7 | 0.41 ± 0.01 | — | — | — |
There is also a significant difference in k measured between Yb3+ complexes of ligands L2 and L7, with the aromatic substituents conferring a slower rate of exchange between species. This corroborates our qualitative observations with Lu complexes of L2 and L4 above. A similar observation is made for the exchange rate of water at lanthanide centres in related complexes– hydrophobic groups tend to slow the rate of water exchange.15 In order to explore the origins of the ligand effect on the rate, k was measured for YbL2 and YbL7 at a range of temperatures (see ESI†). Eyring plots display good linear correlations and are shown in Fig. 6.
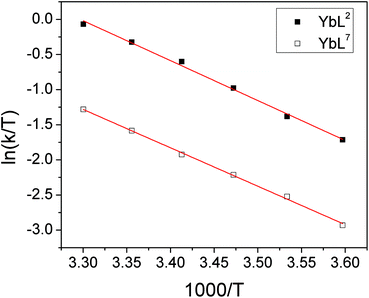 | ||
| Fig. 6 Eyring plots for YbL2 and YbL7 in D2O for the exchange of fluoride-bound and hydrated complexes. | ||
The thermodynamic parameters extracted from the slopes and intercepts of the plots are given in Table 5. It is clear from the data that the ΔH‡ values for the two complexes are the same within error and thus that the electrostatic interaction between Yb3+ and F− is independent of the ligand framework in this instance. However, the ΔS‡ values extracted from the plots are significantly different, with the benzyl-appended complex having a more negative value. This implies that the interaction of fluoride with lanthanide tetraamide complexes is appreciably affected by the nature of the ligand substituents and that the rearrangement of solvent in the vicinity of the metal centre plays a key role. The change in solvation around the complex decorated with hydrophobic groups incurs a greater entropic cost during fluoride binding, resulting in a slower rate of exchange. Calculated ΔG‡ values at 298 K are within error of one another.
Conclusions
From these results, several things become clear. Firstly, the effect of fluoride on the magnetic anisotropy of lanthanide tetraamide complexes appears to be a general phenomenon: in all the systems studied fluoride binding results in a change in the anisotropy from a prolate to an oblate electron distribution as a consequence of the effect of the axial fluoride donor atom. Further, Eyring analysis of the data shows that entropy plays a large part in defining the free energy of activation. The results highlight the complexity of the influences on the fluoride binding event, even within complexes of similar chemical structure, with electrostatics, sterics and solvation clearly playing intricate roles in the nature of the interaction.This study adds further weight to the increasing body of evidence that the ligand field is important in lanthanide coordination chemistry, and that the relative populations (and indeed ordering) of the Stark sub-levels of the ground state are critical to defining the spectroscopic properties of the complexes.
Acknowledgements
The Authors acknowledge the Universities of Oxford and Durham for support. The research leading to these results has received funding from the European Research Council under the European Union's seventh Framework Programme (FP7/2007_2013)/ERC-Advanced Grant Agreement Number 267426.Notes and references
- (a) B. Bleaney, J. Magn. Reson., 1972, 8, 91–100 CAS; (b) B. Bleaney, C. M. Dobson, B. A. Levine, R. B. Martin, R. J. P. Williams and A. V. Xavier, J. Chem. Soc., Chem. Commun., 1972, 791b–7793 RSC.
- O. A. Blackburn, N. F. Chilton, K. Keller, C. E. Tait, W. K. Myers, E. J. L. McInnes, A. M. Kenwright, P. D. Beer, C. R. Timmel and S. Faulkner, Angew. Chem., Int. Ed., 2015, 54, 10783–10786 CrossRef CAS PubMed.
- O. A. Blackburn, A. M. Kenwright, P. D. Beer and S. Faulkner, Dalton Trans., 2015, 44, 19509–19517 RSC.
- (a) M.-E. Boulon, G. Cucinotta, J. Luzon, C. Degl'Innocenti, M. Perfetti, K. Bernot, G. Calvez, A. Caneschi and R. Sessoli, Angew. Chem., Int. Ed., 2012, 52, 350–354 CrossRef PubMed; (b) N. F. Chilton, D. Collison, E. J. L. McInnes, R. E. P. Winpenny and A. Soncini, Nat. Commun., 2013, 4, 1–7 Search PubMed, 1AD; (c) J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078 RSC.
- (a) A. M. Funk, P. Harvey, K.-L. N. A. Finney, M. A. Fox, A. M. Kenwright, N. J. Rogers, P. K. Senanayake and D. Parker, Phys. Chem. Chem. Phys., 2015, 17, 16507–16511 RSC; (b) A. M. Funk, K.-L. N. A. Finney, P. Harvey, A. M. Kenwright, E. R. Neil, N. J. Rogers, P. Kanthi Senanayake and D. Parker, Chem. Sci., 2015, 6, 1655–1662 RSC; (c) L. Di Bari, G. Pintacuda, P. Salvadori, R. S. Dickins and D. Parker, J. Am. Chem. Soc., 2000, 122, 9257 CrossRef CAS; (d) L. Di Bari and P. Salvadori, Coord. Chem. Rev., 2005, 249, 2854 CrossRef CAS; (e) S. Di Pietro, S. Lo Piano and L. Di Bari, Coord. Chem. Rev., 2011, 255, 2810 CrossRef CAS; (f) R. Berardozzi and L. Di Bari, Inorg. Chem., 2013, 52, 11514 CrossRef CAS PubMed.
- R. S. Dickins, J. A. K. Howard, C. W. Lehmann, J. Moloney, D. Parker and R. D. Peacock, Angew. Chem., Int. Ed., Engl., 1997, 36, 521–523 CrossRef CAS.
- S. Aime, A. Barge, J. I. Bruce, M. Botta, J. A. K. Howard, J. M. Moloney, D. Parker, A. S. de Sousa and M. Woods, J. Am. Chem. Soc., 1999, 121, 5762–5771 CrossRef CAS.
- (a) G. Zucchi, R. Scopelliti, P.-A. Pittet, J.-C. G. Bünzli and R. D. Rogers, J. Chem. Soc., Dalton Trans., 1999, 931–938 RSC; (b) M. Woods, S. Zhang, V. H. Ebron and A. D. Sherry, Chem. – Eur. J., 2003, 9, 4634–4640 CrossRef CAS PubMed.
- J. Hilton and L. H. Sutcliffe, Progr. NMR Spectrosc, 1975, 10, 27 CrossRef.
- K. Binnemans and C. Görller-Walrand, Chem. Phys. Lett., 1995, 245, 75 CrossRef CAS.
- A. Beeby, I. M. Clarkson, R. S. Dickins, S. Faulkner, D. Parker, L. Royle, A. S. de Sousa, J. A. G. Williams and M. Woods, J. Chem. Soc., Perkin Trans. 2, 1999, 493–504 RSC.
- P. Kuzmic, Anal. Biochem., 1996, 237, 260–273 CrossRef CAS PubMed.
- A. D. Bain and J. Cramer, J. Magn. Reson., Ser. A, 1996, 118, 21–27 CrossRef CAS.
- S. Aime, M. Botta, M. Fasano, M. P. M. Marques, C. F. Geraldes, D. Pubanz and A. E. Merbach, Inorg. Chem., 1997, 36, 2059–2068 CrossRef CAS PubMed.
- S. Aime, A. Barge, A. S. Batsanov, M. Botta, D. D. Castelli, F. Fedeli, A. Mortillaro, D. Parker and H. Puschmann, Chem. Commun., 2002, 1120–1121 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Synthetic procedures, Bleaney plots, χ∥ and χ⊥ values, EXSY spectra, EuLx 1H NMR spectra, emission spectra, binding isotherms, LuLx 1H NMR spectra, inversion recovery plots, exchange rate data. See DOI: 10.1039/c5dt04349b |
| This journal is © The Royal Society of Chemistry 2016 |