Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Fundamental growth principles of colloidal metal nanoparticles – a new perspective†
Jörg
Polte
Humboldt-Universität zu Berlin, Department of Chemistry, Brook-Taylor-Str. 2, 12489 Berlin, Germany. E-mail: joerg.polte@hu-berlin.de
First published on 23rd June 2015
Abstract
In the past few decades, much effort was put into the development of synthetic strategies to produce nanoparticles of different sizes and morphologies and a large number of scientific contributions is dedicated to the characterization and application of metal nanoparticles. In contrast, only few studies deal with particle formation mechanisms. As a consequence, theoretical concepts that describe particle growth processes are very rare and the few existing models are hardly able to explain how synthesis parameters influence the final particle size distribution. This contribution discusses recent experimental results from which a novel growth concept based on colloidal stability is deduced. The growth concept is in contrast to nucleation models and allows a description of colloidal growth processes from a different perspective. It states that for most syntheses the minimal particle size is rather determined by colloidal than thermodynamic stability making a nucleation model irrelevant.
1 Introduction
In the past 50 years, the development of colloidal nanoparticle syntheses has been pursued intensively due to the enormous technological applications and fundamental scientific interest. Colloidal nanoparticles (NPs) exhibit interesting electrical, optical, magnetic, and chemical properties different from their bulk counterparts. These properties are determined by parameters such as size, shape, composition or crystalline structure. Their unique properties qualify them for a wide range of potential applications in fields such as medicine, biotechnology and catalysis, placing colloidal NPs among the most intensely studied nanoscale materials. In principle, it is possible to adjust their properties in the desired manner by controlling one of the above listed parameters which essentially requires the understanding of the formation processes. The foundations of metal colloid science were laid by Michael Faraday in the 19th century with his ground-breaking experiments on gold sols.1 Faraday attributed the red color of a solution to the presence of colloidal gold, obtained by reduction of dissolved chloroaurate using white phosphorus.2 Further important progress in the description of NP behavior was achieved by Wilhelm Ostwald at the end of 19th century, in particular by his theory of particle growth via Ostwald ripening.3 His son Wolfgang Ostwald became one of the most influential scientists in the field of colloidal chemistry in the beginning of the 20th century and is the founder of the German Colloid Society. In 1925, Richard Zsigmondy received a Nobel Prize for his work on colloids and the invention of the ultra microscope, which enabled the direct observation of particles contained in colloidal solutions. Since Faraday's ground-breaking work in 1857, numerous experimental methods for the synthesis of metal, metal oxide and semiconductor NPs have been developed,1 such as the classical reduction of chloroauric acid in aqueous solution by trisodium citrate.4 This synthetic procedure became popular upon the work by John Turkevich in the 1950s, a professor of chemistry in Princeton and a pioneer in the field of catalysis. To explain the underlying processes of colloidal formation of such syntheses, the classical nucleation theory (developed by Becker and Döring in the 1930s)5 with its transformation to NPs by LaMer and co-workers in the 1950s6,7 is still seen as the basic model. Nevertheless, several studies demonstrated that the classical nucleation theory (CNT) fails to describe nanoparticle growth.8 Accordingly, Oxtoby noted that “nucleation theory is one of the few areas of science in which agreement of predicted and measured rates to within several orders of magnitude is considered as major success”.9 As a result, even after more than 150 years of research in the field of metal colloids, formation mechanisms of NPs are still discussed controversially. No theory or theoretical model exists so far that is able to describe or predict the evolution of the particle size or size distribution comprehensively. Moreover, only limited information of the different underlying physicochemical processes like the reduction process or the stability of the colloids are available.8 Xia et al. described this situation very appropriately by stating that “at the current stage of development, it is not an exaggeration to say that the chemical synthesis of metal nanocrystals (as well as for other solid materials) remains an art rather than a science”.20 Exemplarily, different and also contradictory mechanisms are derived for the classical citrate synthesis of gold NPs (Turkevich method).4,10–19 In fact, it is impressive what kind of nanostructure can be synthesized without having a deep understanding of the underlying principles but it does not need much imagination what would be possible with a profound mechanistic knowledge.In my opinion, the main reason for that lack of knowledge was the absence of reliable experimental information about the particle growth process, in particular of the particle size and concentration during the growth process. Thus, the development of experimental setups for time resolved in situ measurements which allow the determination of that demanded information represents the most capable approach to reveal the key steps of NP formation. In the past 5–6 years, my colleagues and I could show that setups applying small angle X-ray scattering (SAXS) can exactly deliver the required information.18,19,21–23 In these publications several metal NP (mainly Au–NP and Ag–NP) syntheses were investigated applying these novel techniques and setups. For each investigated synthetic procedure, a detailed growth mechanism could be deduced.
The aim of this paper is to elucidate a major issue in colloidal science by analyzing and comparing the different growth mechanisms: the identification of fundamental principles of colloidal NP growth.
The structure of this paper is as follows: (i) a brief description of NPs, their properties and theoretical approaches to describe particle growth (section 2); (ii) a short introduction to the concept of colloidal stability necessary to understand the herein proposed concept of particle growth (section 3); (iii) a summary of the important results and findings from the recent studies comprising the mechanistic interpretations (section 4.1); (iv) a discussion of growth mechanisms for syntheses with a monomer-supplying chemical reaction faster than the actual particle growth (section 4.2.1); (v) an introduction of new concept of colloidal growth (section 4.2.2 and 4.2.3); (vi) a discussion of Ostwald ripening processes in metal colloidal syntheses (section 4.3); (vii) a discussion of growth mechanisms of syntheses for which the monomer-supplying reaction governs the growth kinetics using the Turkevich method as an example (section 4.4); and (viii) critical discussion of the suitability of nucleation models and the herein introduced growth concept with focus on metal colloids (section 5). The following two sections (i.e. 2 and 3) comprise a summary of common approaches to synthesize (metal) colloids and describe colloidal growth and a brief introduction of colloidal stability. These briefly summarized subjects need to be understood to follow the discussion of this contribution.
2 Brief description of colloidal nanoparticles, their properties and theoretical approaches to describe nanoparticle growth
The preparation of NPs can be realized by numerous physical and chemical methods. For NPs, physical methods often rely on a “top–down” approach by subdividing some bulk (precursor) material into smaller units. In contrast, chemical procedures are mainly “bottom–up” approaches that start with a chemical reaction delivering the metal atoms, followed or accompanied by controlled aggregation of atoms into particles. In general, chemical routines (i.e. reduction, thermal decomposition or sol–gel syntheses) are more suitable to obtain small and uniform particles. This publication focuses on metal NPs prepared via wet chemical reduction processes – the probably most common synthetic procedure for metal NPs.For these syntheses, metal NPs (Au, Ag, Pd, Pt, Cu…) are often prepared in aqueous or non-aqueous solutions by the reduction of a dissolved metal precursor (typically a metal salt) with a reducing agent such as sodium borohydride, ascorbic acid, trisodium citrate or alcohols.24 This procedure is often carried out in the presence of a stabilizing agent, which influences the aggregation behavior of clusters and NPs. Stabilizing agents adsorb on a NP surface and provide via repulsive forces an electrostatic stabilization (like citrate ions) or a steric stabilization (as for polymers such as PVA (poly(vinyl alcohol)) and PVP (poly(vinylpyrrolidone))). Furthermore, organic ligands with a strong affinity to metal surfaces via phosphine or thiol functionalities can suppress NP aggregation. Thiols used as capping agents include disulfides, polymers with mercapto groups and dendrimers.1,25,26 Micelles or droplets in emulsion can be employed as nano-reactors which confine the precursor solution locally; hence, spatial separation precedes NP formation.27
Size control of NPs can be obtained via thermodynamic, kinetic or stoichiometric means. Strategies can rely on strongly adsorbed stabilizer on the NP surface, arresting a limited amount of reactants in micelles (i.e. stoichiometric control), suppressing further “nucleation events” (e.g. seeded-growth), or subsequent treatments that increase NP size homogeneity (digestive ripening). A common approach for size control is the use of capping agents that typically adsorb on the nanocrystal surface, creating a nanoparticle–stabilizer entity which then represents a thermodynamically very stable NP configuration. As reported for several metal nanoparticle syntheses, a variation of the capping agent type or concentration (i.e. stoichiometry) enables a size variation of the derived NPs. In the case of thiol-stabilized Au–NP, this results in a size variation between 1 and 4 nm in diameter, but often fails for larger particles since significantly wider size distributions are obtained.1 In general, the thermodynamic approach of NP size control, i.e. forming stable bonding between protective agents and NPs, can generate problems in applications such as catalysis, where e.g. sulfur originating from the capping agents thiol groups is difficult to remove and acts detrimentally by blocking catalytically active sites. Access to larger NPs with narrow size distribution is usually gained via “seeded-growth”.26,28 In the case of noble metal NPs, typically small seeds are generated by fast reduction (e.g. HAuCl4 + NaBH4) in the presence of a stabilizing agent (e.g. sodium citrate), succeeded by addition of a weak reducing agent (e.g. ascorbic acid) and a second stabilizer (e.g. CTAB).25,26,28–35 The particle growth is induced by adding repeatedly small amounts of precursor. To avoid further generation of new (small) particles, the reduction of added precursor is often relatively slow because of the use of a “mild reducing agent”.26,28 In practice, size control is rather based on extensive experimental trial-and-error strategies than on a directed design of a synthesis process.
2.1 Nucleation
Nucleation is a purely thermodynamic model which describes the process of the first step in a first order phase transition. It describes the appearance of a new phase – the nucleus – in the metastable primary phase.The vast majority of the available theoretical work on nucleation applying equilibrium thermodynamics are based on the classical nucleation theory (CNT) developed by Becker and Döring more than 70 years ago.5 The CNT applies that a thermodynamic system tends to minimize its Gibbs free energy (i.e. to maximize the entropy of the whole system). Originally a thermodynamic approach describing the condensation of liquid from the vapor phase,9 it was extended to other types of phase transitions,36,37 thus making it an apparent ideal candidate for precipitation processes as well as crystallization of solids. This thermodynamic theory was also transferred to growth processes of NPs such as LaMer's theory.6 The CNT only describes the nucleation; particle growth is separated as a subsequent process. The further growth can be explained via different growth processes such as diffusion limited growth, aggregation or Oswald ripening. Further approaches to characterize the particle growth are models using rate equations that are able to describe the size evolution of NPs via the use of rates for certain changes such as a rate of monomer attachment. Formulating and solving (in general numerically) these expressions evolve a particle size distribution with respect to time.38
The concept of CNT is based on the macroscopic Gibbs capillary effect, meaning that macroscopic entities such as the surface energy are taken to develop expressions for the nucleation rate.5 In this context, it is important to distinguish between homogeneous and heterogeneous nucleation. Nucleation which occurs at nucleation sites on solid surfaces contacting the liquid or vapor is referred to as heterogeneous nucleation. Exemplarily, a heterogeneous nucleation in the field of NP growth occurs at the surface of particles in solution providing nucleation sites, used in seeded-growth syntheses. In contrast, homogeneous nucleation occurs spontaneously and randomly, but requires a supercritical state such as a supersaturation.
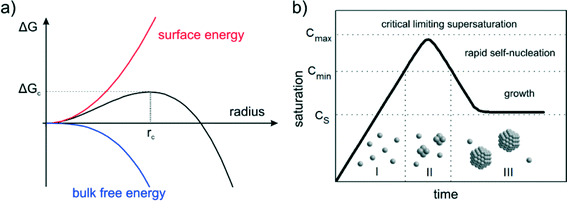
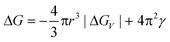 | (1) |
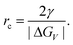 | (2) |
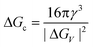 | (3) |
The nucleation rate J(T,ΔGc) can be expressed using the Arrhenius equation since the energy barrier is an activation energy and thus nucleation a statistical process:
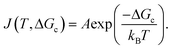 | (4) |
2.2 LaMer's nucleation theory
The concept of CNT was transferred to NP syntheses by LaMer and his colleagues back in the 1950s proposing the concept of burst nucleation.6,7 The pioneering concept was developed from their research on various oil aerosols and sulfur hydrosols. In the burst nucleation process, nuclei are generated at the same time due to homogeneous nucleation and subsequently grow without additional nucleation. The basic idea of that NP formation concept is to separate nucleation and growth. It can been interpreted as a separation of a homogeneous from a heterogeneous phase. Such a process enables control of the particle size distribution during growth. The mechanism, displayed in Fig. 1b, is as follows: (I) the concentration of monomers is increasing (in the case of metallic NPs most likely due to reduction) and reaches, at a certain time, a certain critical supersaturation level (CS) at which homogeneous nucleation is possible but “effectively infinite”;6 (II) the saturation increases and reaches a level (Cmin) at which the energy barrier (activation energy) for nucleation can be overcome leading to a rapid self-nucleation – the burst nucleation; and (III) due to the burst nucleation, the supersaturation level lowers immediately below this self-nucleation level ending the nucleation period; growth then occurs by diffusion of further monomers in solution towards particle surfaces which can be interpreted as heterogeneous nucleation/growth. The expected corresponding particle concentration with respect to time would increase fast at the self-nucleation stage (II) and a more or less constant value during the final growth stage (III).The LaMer model and its modifications are still the only commonly accepted models describing the general mechanism of the NP formation process. In principle, the model rationalizes also conventional strategies for size adjustment of colloidal NPs, i.e. fast reduction to induce a rapid build-up of supersaturation. As a consequence, many nucleation events lead to many small NPs, and few events to less and bigger particles. Moreover, the principles of “seeded-growth” are derived from the concept of classical nucleation, i.e. suppressing further nucleation by slow reduction to use reduced monomers exclusively for growth of already formed particles. However, the LaMer model is not able to predict or characterize the evolution of NP size distributions. It only describes the process of nucleation followed by a growth of the stable nuclei, but the characteristics of the growth remain more or less unspecific. Accordingly, LaMer stated: “…the process of growth of stable nuclei to form discrete particles can proceed by diffusion of molecularly dissolved sulfur to the nuclei”.6
2.3 Theoretical approaches describing particle growth
The model of LaMer interpreted for the synthesis of monodisperse particles is a concept of separating nucleation and growth. Thus, theoretical models for the actual growth of the nuclei forming the NPs are needed to predict the final size distribution. Soon after LaMer proposed his mechanism, Reiss developed a growth model known as “growth by diffusion” in which the growth rate of spherical particles depends solely on the monomer flux supplied to the particles.39Reiss deduced that if the diffusional growth is only dependent on the monomer flux, smaller particles will then grow faster in the presence of larger particles, leading to a size focusing (narrowing of size distribution). However, this is a very simplified mechanism since it does not include other effects such as aggregation, coalescence or dissolution (Ostwald ripening). Sugimoto et al. extended Reiss's model qualitatively by including dissolution effects obtaining a size dependent growth rate by considering the Gibbs–Thomson equation.40 As a consequence, broadening of the size distribution due to NP dissolution is also possible (dependent on the monomer concentration). Experimentally, Alivisatos and co-workers deduced a focusing and defocusing behavior of the size distribution for the hot-injection synthesis of CdSe NPs.41
Alternative approaches to characterize particle growth are models using rate equations that are able to describe the size evolution of NPs by means of rates for certain changes, such as a rate for a monomer attachment. Formulating and solving (in general numerically) these mathematical expressions evolves the size distribution of the particles with respect to the time. Several publication developed kinetic models using only rate equations to describe the nucleation and growth of NPs.38,42 Additionally, it was theoretically shown that diffusion limitation is not necessarily required for the size focusing effect.38 A further approach was introduced by Privman et al. who developed a model consisting of two steps: a burst nucleation step, followed by an aggregation of the primary particles into micron-sized colloidal agglomerates.43 The model incorporated the CNT for the first step and rate equations for the second step.
In summary, several approaches including CNT, single particle growth laws or rate equations are typically used to characterize particle growth. Numerous other studies exist that extend, improve or combine these models (as Privman did).43
The common problem of all theoretical models is the severely limited availability of experimental time-resolved in situ data for rates of NP formation and growth. Such data enable the determination of particle growth mechanisms and kinetics and thus would allow verifying theoretical models.
Moreover, the chemical aspect of creating monomers (e.g. due to reduction) which are able to grow onto the NP surface is often strongly simplified or neglected. Hence, models that can describe quantitatively the formation, growth and coalescence of colloidal metal or metal oxide nanocrystals and are able to reproduce the changes induced by variation of the synthesis conditions, i.e. concentrations, pH, temperature and stabilizers, do not exist. In a nutshell, the lack of profound experimental data is one of the major obstacles8 to change the current state of colloidal synthesis “from “alchemy” to chemistry”.44
3 Brief introduction to the concepts of colloidal stability
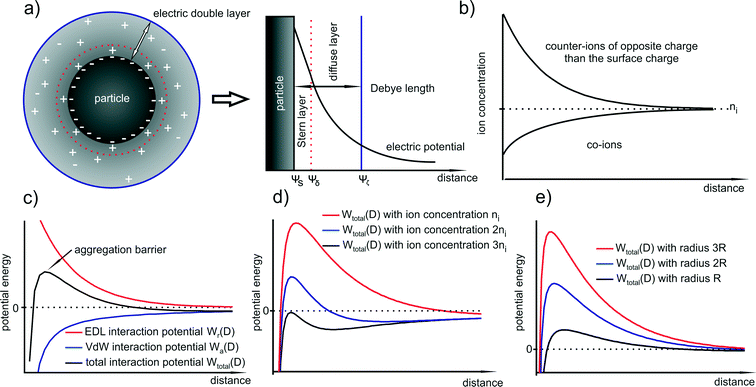
One of the most important aspects in colloid science is the mechanism of (metal) NP stabilization in the dispersing medium. In general, particles at the nanoscale are unstable and tend to agglomerate because at short interparticle distances they are attracted to each other by van der Waals, electrostatic or magnetic forces. Without any counteractive repulsive forces NPs aggregate, agglomerate or undergo coalescent processes. Exemplarily, such repulsive forces can be achieved by electrostatic or steric stabilization.45Electrostatically stabilized NPs are described to have at least one electrical double layer due to a surface charging. The resulting Coulomb repulsion forces between the particles decay exponentially with particle to particle distance. If the electrostatic repulsion is sufficiently high, it prevents the particles from any kind of coagulation.
In the following section, important particle interactions are discussed briefly (a more detailed description can be found in S1 in the ESI†).
3.1 van der Waals interaction – nanoparticle attraction force
A common way to describe intermolecular forces is to use the Lennard-Jones potential which is an expression for the interaction energy of the pair potential W(r) of two molecules at a distance r: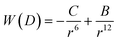 | (5) |
The van der Waals interaction energy Wa(D) between two particles with radius R1 and R2 can be theoretically obtained by integrating over all intermolecular forces between all constituent molecules of the particles, which finally yields for two spherical particles:
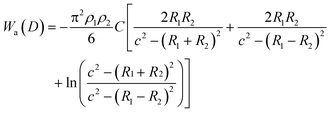 | (6) |
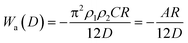 | (7) |
3.2 Electrostatic interaction – nanoparticle repulsion force
The attractive van der Waals interactions discussed beforehand can promote reversible agglomeration or even irreversible aggregation of suspended particles. The preparation of stable NPs demands forces opposing the van der Waals attraction. For metal NPs this is often provided by the particle surface charge resulting in repulsive interparticle forces.In solution, solvated ions surround the particles and shield their surface charge. This can be described using the Stern–Gouy–Chapman theory in which the surface potential decreases within two layers known as the electric double layer (EDL) – a compact inner and a diffuse outer layer. The thickness of this double layer is called Debye length λ (κ−1) and can be quantified using simple electrostatics. Obviously, the distribution of the electric surface potential ψ(x) is required for the description of the double layer. The Poisson equation states:
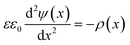 | (8) |
Applying the known Debye–Hückel linearization of exponential functions (exp(±x) = 1 ± x + …), the Poisson equation can be approximated as:
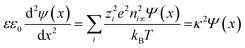 | (9) |
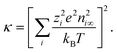 | (10) |
The Debye screening length λD which measures the diffuse layer thickness is defined as λD = κ−1. The simple solution for the differential equation (eqn (8)) is:
| ψ(x) = ψ0(x)exp(−κx) | (11) |
| F(D) = −2πεε0κRψ2δ exp(−κD) | (12) |
| WR(D) = 2πεε0Rψ2δ exp(−κD) | (13) |
3.3 DLVO theory
More than 70 years ago, two Russian (Derjaguin and Landau) and two Dutch (Verwey and Overbeek) scientists developed a theory of colloidal stability which is still seen as one of the groundbreaking characterization models in the physics and chemistry of colloids – the DLVO theory.48 The basic assumption is that the total force between colloidal particles is the addition of the van der Waals (attractive) and the EDL (repulsive) forces. In the DLVO theory the effect of the van der Waals and double layer forces are combined, so that the potential interaction energy between two particles or two surfaces in a liquid is assumed to be the sum of the van der Waals and EDL interaction energies:| Wtotal(D) = Wa(D) + Wr(D) | (14) |
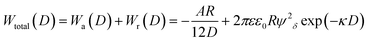 | (15) |
Note that in particular the second term changes with different assumptions (constant surface potential or surface charge, thin EDL compared to the particle size and vice versa, etc.)
A representative resulting total interaction potential (TIP) is displayed in Fig. 2c. The TIP demonstrates some fundamental features that become important in the explanation of particle growth processes. The shape of the curve is the consequence of the exponential and steep decay of the repulsive and attractive terms, respectively. The resulting maximum of the curve represents the aggregation barrier and determines the colloidal stability. The barrier creates effectively an activation energy for aggregation that two particles have to overcome when they collide.
In this picture, several parameters affect the stability of the system (i.e. the barrier): (i) the ion type and concentration, (ii) the value of the surface potential and (iii) the particle size. Although, eqn (12) is limited to two identical particles, it describes the properties of the whole system quite well since expressions for spherical particles with different sizes show in general similar dependencies with respect to size, surface charge, and ion concentration. The van der Waals attraction is relatively independent of the ion concentration, but the repulsive term strongly depends on it since the counter-ions are the dominant ions in the Stern and diffuse layers. The ion concentration is directly proportional to κ and thus to the exponential decrease in the surface potential. This means that the higher the ion concentration (in particular the counter-ion concentration), the smaller is the EDL. In Fig. 2d it is shown how the ion concentration in principle affects the TIP.
Moreover, eqn (15) (i.e. with the assumption of a constant surface potential and a thin EDL), reveals that in close proximity the particle size is proportional to both the attractive and repulsive terms. Consequently, the TIP is directly proportional to the radius which means that with increasing size, the shape of the curve and the position of the maximum do not shift to another distance whereas the aggregation barrier increases. As a more general rule, one can state that in almost all cases of charge stabilized particles, the aggregation barrier increases with increasing size and therefore also the colloidal stability. In other words, larger particles are in general colloidally more stable than smaller particles. This is illustrated in Fig. 2e.
3.4 Steric stabilization
Steric stabilization is a process in which colloidal particles are prevented from aggregating by adsorption of large molecules at the particle surface, such as polymers or surfactants, providing a protective layer. The prevention of coagulation of these large molecules can be explained via simple mechanisms. The density of the adsorbed molecules in the interparticle space would increase tremendously, if the interparticle distance would become smaller and smaller. This would cause a decrease in entropy, thus an increase of the Gibbs free energy which is thermodynamically not favorable. Due to the increased density, osmotic repulsive forces would also increase. Furthermore, a higher solubility of the stabilizing molecule counteracts agglomeration.49As an approximation, the interaction potential described in the DLVO theory can be extended by a further term describing the repulsive forces due to the steric stabilization Wsteric:
| Wtotal(D) = Wa(D) + Wr(D) + Wsteric | (16) |
The repulsive interaction potential Wsteric is not a long range interaction and does not significantly depend on the particle size since the stability is mainly determined by parameters such as polymer concentration, temperature, average chain length and the solubility of the polymer.46,50
4 Principles of metal colloidal growth
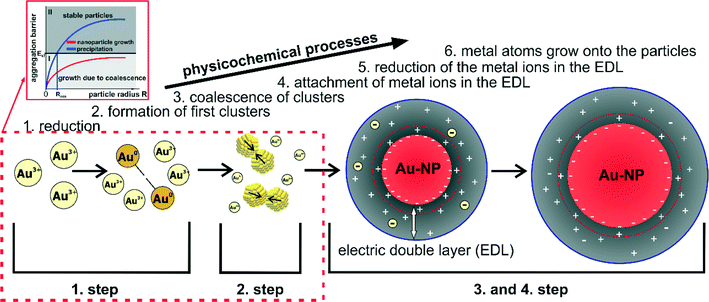
In some of my recent contributions, two main topics and scientific issues were addressed: (1) the development of techniques and experimental setups that enable the investigation of NP growth processes; and (2) the study of different NP syntheses (in parts with these novel techniques and setups) to reveal their corresponding growth mechanisms.19,21–23,51–56 Several metal NP syntheses were investigated time-resolved and in situ. For each of these systems, a growth mechanism could be deduced. In the following, the findings and mechanistic interpretations of Au–NP and Ag–NP syntheses with sodium borohydride (a relatively strong reducing agent) and sodium citrate (a relatively mild reducing agent) are briefly summarized. Comparing the results, similarities can be identified that allow evaluating the governing principles of the particle growth. Moreover, a general mechanism and growth concept for syntheses of colloidal metal NPs in which the monomer-supplying chemical reaction is faster than the actual growth can be derived. It is shown, that this concept of colloidal NP growth allows a more sophisticated interpretation of syntheses with mild reducing agents such as the reduction of tetrachloroauric acid with sodium citrate – known as the Turkevich method.4.1 Summary of the findings from recent studies of the growth mechanisms of colloidal metal nanoparticles
The growth process of Au–NPs obtained via the reduction of tetrachloroauric acid (HAuCl4) with sodium borohydride (NaBH4) which in the following statements is denoted as Au-System 1 proceeds in two steps (see Fig. 7 in ref. 21). The first step is the reduction of the ionic gold to Au monomers within less than 200 ms accompanied by the formation of primary particles. In a second step, these primary particles grow due to coalescence along with a corresponding decrease in the number of particles. In consequence, particle growth in Au-System 1 is driven only by coalescence in the experimentally accessible time.The growth mechanism of Ag–NPs obtained via the reduction of silver perchlorate (AgClO4) with NaBH4 (denoted as Ag-System in the succeeding statements) is actually the same but consist of two well-separated steps of coalescence. The growth mechanism can be divided into four steps as illustrated in Fig. 6 in ref. 23. The first two steps are the same as in the growth mechanism of the described growth mechanism of Au-System 1 beforehand. The third step is a metastable state which is related to the hydrolysis of BH4− to B(OH)4−. At a certain point in the hydrolysis (when most of the BH4− is converted), the colloidal stability of the particles decreases initiating a further coalescence process which is the final step of the synthesis.22 Furthermore, it is shown that the addition of a steric stabilizing agent (in that case, PVP) affects the particle size at each step, the long term stability of the silver colloids and the duration of the metastable state, but not the growth mechanism itself. In a recent publication it is shown that the excess of NaBH4 after the metal precursor reduction determines if growth proceeds in one or two coalescent steps.74
The Turkevich method refers to the reduction of HAuCl4 with sodium citrate (Na3Ct) at elevated temperatures and is the most common synthesis to produce monodisperse gold colloids in aqueous solution,57,58 which in the following statements is denoted as Au-System 2. In contrast to NaBH4, sodium citrate is a mild reducing agent. As a consequence, the monomer-supplying chemical process in the Turkevich method is not separated from the NP growth as it is the case for Au-System 1 and Ag-System. The growth mechanism of Au-System 2 was investigated with a novel coupling of analytical methods – a combination of SAXS and X-ray absorption near-edge structure (XANES) which allowed a simultaneous determination of the mean oxidation state of gold (XANES) as well as the size, number and polydispersity of formed particles (SAXS).51 The measurements were conducted using a levitated droplet with samples being extracted from a batch mix at different reaction times. In addition, a SAXS setup applying a free liquid jet was developed to be able to measure particle growth containerless with a high time-resolution.19 From the investigations, a growth mechanism which consists of four steps could be deduced as illustrated in Fig. 4 in ref. 51. The first step incorporates a fast reduction of a small amount of gold precursor and the formation of first small clusters (step 1). Resulting clusters undergo coalescence processes (step 2) forming particles with radii larger than 1.5 nm. This is followed by a diffusional growth to a mean radius of about 4–5 nm (step 3). Finally, particles grow rapidly until the gold precursor is consumed (step 4). The rate of chemical reduction changes and is coupled to the four physical steps of particle formation and vice versa.
4.2 Category 1 syntheses: monomer-supplying chemical reaction faster than the actual particle growth
For the investigated systems, the use of NaBH4 as reducing agent results in a reduction much faster than the actual growth (few milliseconds or less vs. several seconds). Consequently, the monomer-supplying chemical reaction, i.e. the reduction, is separated from the actual particle growth. In the following statements, syntheses with this characteristic are denoted as Category 1 syntheses.The mechanistic studies of Category 1 syntheses (Au-System 1 and Ag-System) revealed growth mechanisms which are always governed by coalescence, even after the addition of a steric stabilizing agent. A process of coalescence (merging of particles) is followed by the process of aggregation which is the result of insufficient colloidal stability. As a result, it is found that the particle growth and thus the final size distribution is primarily governed by colloidal stability and thus independent from any kind of classical or non-classical nucleation process.23 The following discussion is separated in three subsections. The first subsection discusses the general growth mechanism of Category 1 syntheses. In the second, a general concept of NP formation for idealized syntheses is deduced. In the last subsection, the validity of that idealized growth concept for “real” syntheses is discussed.
In the case of metal clusters, the probability of metal bonds breaking at room temperature is very low. Melting points of small metallic clusters in the gas phase are in general above 500 K.59–62 As a result, the Ostwald ripening process is very unlikely to occur during the commonly used syntheses of metal colloids (most are conducted below 400 K) but are often claimed without a conclusive explanation or any profound experiment. This issue is discussed in section 4.3.
The electrostatic and steric stabilization of the investigated systems also explains the slower particle growth kinetics as known from precipitation kinetics of systems without a significant colloidal stability.63 Without a significant aggregation barrier between the particles (e.g. due to electrostatic or steric stabilization), the probability that two particles aggregate in each collision process (which occurs due to their Brownian movement and their van der Waals attraction) is very high and decreases with an increasing repulsive potential. Time-resolved precipitation studies using SAXS show for selected systems in which a significant barrier does not evolve that within few milliseconds the particle size is already around 20–30 nm in radius.63,64 The results of these publications are also of great importance to understand NP growth. In contrast to precipitation, the investigated NP growth processes with NaBH4 as reducing agent (Au-System 1 and Ag-System) have final particle sizes in a range of 2–8 nm in radius and proceed on a time scale of a few seconds. Furthermore, the particles have a size distribution with mean radii below 1 nm at around 200 ms (also in the absence of any stabilizing agent).21,23 This indicates that even very small clusters with radii below 1 nm have already a substantial colloidal electrostatic stabilization that decelerates the growth. Actually, it is completely unclear at which size an electrostatic stabilization evolves that affects the growth. It might already be the metal dimer or probably correlated with the size of the metal transition.
In the idealized thought experiment, the growth of NPs is only due to aggregation and coalescence if the reduction is much faster than the actual growth, i.e. reduction is well-separated from particle growth. This finding is supported by our experimental results and appears to be a fundamental principle of NP formation.23
Furthermore, it is assumed that the duration for mixing the reactants and the reduction process is infinitely small which is obviously not the case for any real synthetic system. It is known that mixing conditions can have an influence on the final size. In the case of Au-System 1, a significant change in the final particle size distribution was not observed if the solutions were mixed with a micro-structured mixer (mixing time in the range of 50 μs) or mixing the solutions 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 with two Eppendorf Tips (mixing time in the range of a second). In contrast, for the Ag-System, mixing conditions clearly have an influence on the growth and therefore on the final size.22 However, for the investigated systems the mixing conditions might change the final particle size but not the growth mechanism itself. Thus, the findings of the thought experiment are also valid without the assumption of an infinitely fast mixing. In contrast, the reduction rate is not negligible with respect to the mechanism. This is obvious when comparing the deduced growth mechanisms of Au-System 1 and Au-System 2. The influence of the reduction and in particular of the reduction rate (i.e. the monomer-supplying rate) will be discussed later in this contribution.
1 with two Eppendorf Tips (mixing time in the range of a second). In contrast, for the Ag-System, mixing conditions clearly have an influence on the growth and therefore on the final size.22 However, for the investigated systems the mixing conditions might change the final particle size but not the growth mechanism itself. Thus, the findings of the thought experiment are also valid without the assumption of an infinitely fast mixing. In contrast, the reduction rate is not negligible with respect to the mechanism. This is obvious when comparing the deduced growth mechanisms of Au-System 1 and Au-System 2. The influence of the reduction and in particular of the reduction rate (i.e. the monomer-supplying rate) will be discussed later in this contribution.
As pointed out in the thought experiment and deduced in recent publications, the growth mechanisms of syntheses with fast reduction (Au-System 1 and Ag System) is primarily correlated with colloidal stabilization (the relation of attractive and repulsive forces between clusters/nanoparticles). Thus, a generalized particle growth model demands a description of colloidal stability such as the commonly used DLVO theory derived in the 1940s.48,65 As already stated, the basic assumption of the DLVO theory is that the total force between colloidal particles is the sum of the attractive van der Waals and the repulsive EDL forces. The steric stabilization is not considered in the classical DLVO approach. In the case of spherical symmetry, the total interaction potential between two identical particles with radius R in close proximity can be written as in eqn (15) (note that the DLVO approach as well as the derivation of the equation consists of idealizations and approximations). The resulting total potential and the influence of the radius and the ion concentration are shown in Fig. 2.
For simplification, it can be assumed that in case of syntheses with NaBH4, the total ion concentration is constant after mixing the solutions. The metal precursors are immediately reduced and the chemical conversion of residual BH4− into B(OH)4− occurs on a time scale of several minutes to hours (for details see experiment S4 in the ESI† in Wuithschick et al.22). Moreover, a size dependence of the surface potential is at first also neglected. The constant ion concentrations appear to be reasonable but the constant surface potential might be too rigorous (one could also keep the surface charge density constant). However, it will be shown that this simplification does not affect the general interpretation of the growth processes.
In this above described simplified DLVO model, the interaction energy between two identical spherical particles is directly proportional to their size (see eqn (15)) which means that with increasing size also the aggregation barrier increases (see Fig. 2e). As a consequence, the probability of aggregation between two particles decreases with increasing size. In other words, the probability of a coalescence process between two smaller particles is higher than between two larger particles. At a certain particle size the aggregation barrier has increased so that the thermal energy of these particles is too low to overcome the barrier which makes the process of aggregation or coalescence very unlikely. This particle size in turn corresponds to the minimum stable particle size and primarily determines the final size distribution.
Summarizing, the beforehand discussion leads to two major conclusions concerning the metal NP growth of syntheses with fast reducing agents (Category 1 syntheses):
1. The actual NP growth is only due to aggregation and coalescence.
2. The final size distribution strongly depends on the increase of the aggregation barrier with increasing particle size.
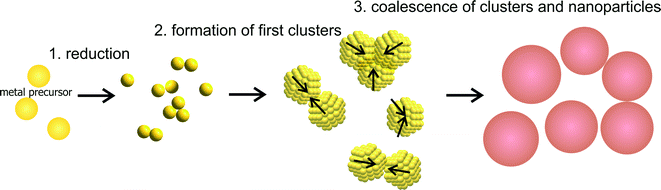
The consequential general mechanism for the growth of metal NPs with fast reducing agents can be expressed with three steps displayed in Fig. 3. The first step is a fast reduction of the metal ions. The metal atoms will form dimers and small clusters which marks the second step. In the final and third step, the clusters grow due to aggregation and coalescence until reaching a final particle size at which the particles are sufficiently stabilized. It must be noted, that the second step is consciously not referred to as nucleation whereby the reason for this is following discussed.
Based on the experimental results with the fast reducing agent NaBH4, two fundamental aspects (see the two enumerated statements above) and a generalized mechanism of NP growth (see Fig. 3) are deduced in the previous section.
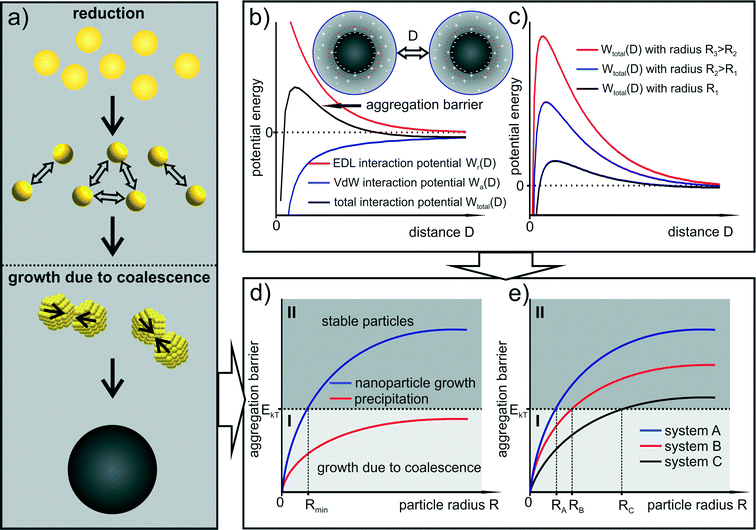
This leads to a picture of NP growth, for which the concept of nucleation is nonessential because the final particle size distribution is determined by the increase in colloidal stability (i.e. the increase in the size depends on the interaction potential between the particles). The formation of any primary cluster that overcomes a certain critical radius is irrelevant. With focus on metal NP syntheses, the concept of nucleation, and in particular the classical nucleation theory, is discussed in section 5. The general principle of the growth mechanism due to coalescence is displayed in Fig. 4a. Typical interaction potentials between two identical spherical particles with their dependence on the particle size due to the concept of electrostatic stabilization are displayed in Fig. 4b and c.
For a simplified picture of growth, it is at first assumed that coalescence occurs only between particles with similar size although this is not the case in reality. Subsequently, this model is extended to real systems. However, at least for Au-System 1 the probability that only particles with similar size undergo a coalescence process is much higher than between particles of different sizes. This can be deduced from the constantly low polydispersity of 10–15% during the growth.
In this simplified model, the increase in the aggregation barrier with increasing particle size (as shown in Fig. 4c) indicates that at a certain particle size the thermal energy is not sufficient to overcome the increasing barrier of aggregation. The criterion for stability can be assumed to be the primary maximum of the aggregation barrier curve since the corresponding distance represents the highest interaction energy. This situation is displayed in Fig. 4d. It shows an anticipated increase in the primary maximum of the total interaction potential between identical particles with respect to particle size. In the following statements, this curve will be denoted as “stability curve”. Note that the stability curves displayed in Fig. 4d and e are only qualitative.
The diagram in Fig. 4d is separated in two sections by the thermal energy of the particles EkT. If the aggregation barrier is below that energy (section I) the particles can aggregate and subsequently coalesce. If the barrier is above that energy (section II), the colloidal stability is sufficient to prevent further growth. Thus, section I represents the area in which aggregation and coalescence (therefore growth) is possible and section II represents the area of colloidally stable particles. The blue curve in Fig. 4d displays NP growth since the stability curve reaches section II at which aggregation and coalescence stops. In contrast, the red curve represents a process of precipitation as the stability curve remains in section I. As a consequence, the radius at which the aggregation barrier curve crosses the boundary between the two sections (denoted as RkT) is the particle size at which a further growth becomes energetically unfavored and therefore very unlikely. In this idealized image, the critical radius RkT represents the smallest particle size of the final size distribution since same-sized particles slightly smaller than RkT still coalesce and reach the stability region at radii larger than RkT. In Fig. 4e three stability curves with different slopes are displayed leading to three different final average radii.
The stability curve can also be transferred to a size dependent probability function for particle coalescence. The probability of coalescence decreases the closer the aggregation barrier curve comes to the boundary between section I and II. In this simplified image, the particle formation process of the Au-System 1 can be described with system A of Fig. 4e. It is a growth process only due to coalescence producing monodisperse stable particles.
The corresponding Ag–NP synthesis without PVP as steric stabilizer (Ag-System) can be represented by systems B and C. In the beginning of the synthesis, particle growth can be described with system B because the particles formed in the first step are slightly bigger than for the Au–NPs of system 1. The BH4− conversion during the metastable phase and its influence on the surface chemistry leads to a rapid change in colloidal stability (the end of the metastable phase). The aggregation barrier decreases which can be depicted by a change in the aggregation barrier curve from system B to C. This represents further growth due to coalescence. Accordingly, the Ag–NP synthesis with PVP as additional steric stabilizer can be described with a change of system A to C.
So far, the proposed growth model is limited to a growth in which only particles with same or similar size undergo coalescence processes as it is roughly the case for Au-System 1. It also demands an instant coalescence subsequent to an aggregation since only interaction of spherical particles is considered. In the following, several idealizations are discussed and the more general validity of this idealized growth concept is demonstrated.
(i) Influence of coalescence kinetics on particle size. In the simplified image described beforehand only coalescence of spherical particles is assumed. Thus, the merging of two aggregated particles into one larger spherical particle needs to be almost infinitely fast. Otherwise, the subsequent coalescence process of this entity is obviously not between spherical particles. The second coalescence step in the Ag–NP synthesis (Ag-System) is not infinitely fast. It is in the range of several seconds which can be deduced from UV-vis and SEM experiments. The UV-vis spectra during the second coalescence step reveal a broadening of the plasmon resonance band and an increased absorption at higher wavelengths characteristic of non-spherical particles and aggregates (see Fig. 2c in ref. 23). In addition, SEM images showed aggregated particles for that growth stage (see Fig. 4c in ref. 23). Actually, a simple eye-experiment also indicates the existence of aggregates for 30–60 s during the metastable state (see photographs in Fig. 2a in ref. 23). Thus, also non-spherical particles are existent and probably also merge with each other during the second coalescence step in the Ag-System. Consequently, merging of only spherical particles cannot be assured even for syntheses with spherical final particles. Although, it does not change the general picture of growth, it remains an open question if it has an influence on the final particle size distribution. For a purely electrostatic stabilization, it is hard to predict if a non-spherical aggregate has a higher colloidal stability than a spherical particle with the same volume. Concerning only the (geometric) Derjaguin approximation (i.e. assuming a constant surface potential or surface charge density), the aggregation barrier would be dependent on the geometric arrangement of the two particles (i.e. their relative orientation and position).67 Depending on the geometric arrangements, the colloidal stability of a non-spherical aggregate might be higher or lower compared to a spherical particle with same volume. Hence, the kinetics of coalescence, merging or crystal reorganization (i.e. the kinetics of free energy minimization of the particle) does not change the picture of growth but might influence the final particle size. Indeed, it was shown that the second coalescence step in which non-spherical aggregates are present causes the lack of size control in the Ag–NP synthesis. Eliminating the second coalescence step reveals a size-controlled Ag–NP synthesis.22
(ii) Primary maximum as criterion for particle stability. A common scientific approach to describe a certain process is an argumentation via an energy barrier. In this publication the interaction energy was discussed for particle growth processes. The value of the primary maximum was taken as a criterion for stability which simplifies the issue, but provides an useful approximation. The average thermal (or kinetic) energy of a colloidal particle in Brownian motion is EkT = (3/2)kBT whereas a particle can have a kinetic energy Ekin below or above this value. However, the higher the difference between Ekin and EkT, the lower the probability for such a particle state. The Brownian motion results from arbitrary collision with molecules of the surrounding medium or other particles. In general, colloidal solutions of metal NPs are very dilute and particles are large and heavy compared to the solvent molecules. Therefore, the kinetic energy of the particles will not differ much from EkT and for the herein described systems it is very unlikely (although not impossible) that a particle will have a thermal energy of 10kBT or more. As a consequence, the particles should be colloidally stable if the aggregation barrier (Wmax) is approximately the average thermal energy. In this contribution Wmax = EkT as a criterion for a sufficient colloidal stability is assumed to be reasonable (i.e. a ratio of 1). Even if the ratio is higher, it would not change the principles of the growth concept.
(iii) Coalescence limited to same-sized nanoparticles. So far, the proposed growth concept is limited to a growth in which only particles with same or similar size can undergo a coalescent process as it was roughly the case for the Au-System 1. The assumption of similarity is necessary to illustrate the simplified image of growth (see Fig. 4). In the following, it is discussed why that principal idea of particle growth does not change if aggregation or coalescence can occur between particles of different sizes.
In real systems particles of different sizes undergo aggregation or coalescence processes. Thus, in addition to the interparticle energy barrier between two dissimilar particles, one needs to consider the probability that two colloidal particles of arbitrary size collide. In the simplified image beforehand, the particle concentration does not need to be considered since only same-sized particles undergo coalescence.
A broad range of publications deal with theoretical descriptions of coagulation of dissimilar sized particles. To the best of my knowledge, the principal theoretical approaches always comprise population balanced equations. Each equation concerns the concentration of a single entity (particles of specific size) which can increase or decrease due to aggregation or decomposition. Depending on the described system, the mathematical incorporation of physical effects such as particle diffusion, thermodynamic stability or particle interactions is required. In most publications about coagulation, decomposition is not considered since in general it is intended to describe the coagulation of larger particles for which decomposition due to non-sufficient thermodynamic stability is very unlikely. Actually, the ground-breaking work in this field was done by Smoluchowski almost 100 years ago which describes the kinetics of particle coagulation caused by binary aggregation but without decomposition or fragmentation. Smoluchowski derived a set of non-linear differential equations:
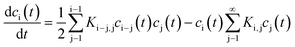 | (17) |
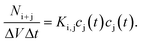 | (18) |
Several years after Smoluchowski, Müller extended this theory for continuous cluster mass distributions by introducing a particle mass density c(x,t) whereby c(x,t)dx represents the average number of particles with a mass between x and x + dx.68 Thus, the term c(c,t)c(y,t)K(x,y)dxdy represents the average numbers of coagulation processes between particles of mass x to x + dx with particles of mass y to y + dy during the time interval dt. This converts the discrete Smoluchowski model into integro-differential equations:68
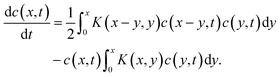 | (19) |
In general, the set of the differential equations (eqn (17) or (19)) cannot be solved analytically and demand numerical approaches. For simulations of NP growth a stochastic method is commonly applied. Anyway, the scope of this contribution is to deduce general growth characteristics and not to provide a further mathematical approach using the Smoluchowski approach. However, the Smoluchowski approach is correlated with the experimental results of Au-System 1 and Ag-System. At first, discussed for non-interacting particles and subsequently extended for particle interaction.
In any Smoluchowski approach, the type of particle interaction is specified with the coagulation kernel. Therefore, a broad range of different kernels is described in the literature in the past 100 years. The simplest case is the non-interacting spherical particles (i.e. without attractive or repulsive forces) with Brownian movement. For such particle coagulation, Smoluchowski deduced the kernel as
| Ki,j = const. × (ri + rj)(1/ri + 1/rj). | (20) |
Since x ~ r3, eqn (20) can be rewritten in terms of masses to:
| K(x, y) = const. × (x1/3 + y1/3)(1/x1/3 + 1/y1/3). | (21) |
As a consequence of eqn (20) and (21), this purely Brownian kernel has a parabolic shape. It means that the kernel is higher for particles with different sizes than for particles of the same size. For example, the kernel value of a coalescence process between particles with a size ratio of 10 (i.e. r2 = 10r1 or vice versa) is approximately three times larger than the kernel value for coalescence of same-sized particles. For the Au-System 1 and the Ag-System, a size ratio of 10 is approximately also the size range of their particle growth (in the first coalescence step) since the size after the first coalescence step is approximately 1.5 nm (in radius) and the hydrodynamic radius of a single gold atom is around 0.15 nm. Thus, the probability for a single atom to coalesce with a 1.5 nm particle is around 3 times higher than with another atom but only if (I) the concentrations of both species are the same and (II) no interaction between the particles exist (see eqn (22)). Both these limitations are not the case for the growth of charged NPs and therefore the following statements are discussed.
(I) For the NaBH4 syntheses, the metal precursor is completely reduced within the mixing time of the solutions leading to high concentrations of metal atoms and molecular-like metal clusters in the beginning of the synthesis. The concentrations of these small entities will be much higher than the concentrations of the larger particles because larger particles in this synthesis consist of around 500–1000 atoms. Consequently, the particle concentration decreases during the synthesis due to the increasing particle size which has been investigated with time-resolved SAXS experiments. The coalescence probability is proportional to the kernel and the respective particle concentrations (see eqn (18)). Consequently, the probability of metal atoms or molecular-like metal clusters to coalesce with larger particles can decrease by 2–3 orders of magnitude (as the concentration does).
(II) As for any synthesis, the final NPs are colloidally stable due to the particle interaction forces whereby the repulsive forces become dominant with increasing particle size (otherwise one would not have a stable colloidal solution). In 1934, Nicolai Albertovich Fuchs described this phenomenon for the coagulation of aerosol particles69 and introduced a ratio W (later known as the Fuchs stability ratio) as a correction factor which describes the coagulation probability of two charged particles if the coagulation probability of uncharged particles is 1. Applying the Fuchs stability ratio, the kernel can be modified to:69
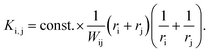 | (22) |
The general form of the Fuchs stability ratio is given by:
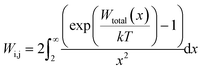 | (23) |
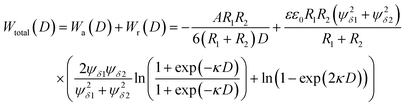 | (24) |
 . For eqn (24) a constant surface potential (eqn (24) can also be rewritten for a constant surface charge) and particle radii much larger than the thickness of the EDL (i.e. assumption of a thin electrical double layer (κr > 10)) are assumed. For particles which are governed by the increasing Coulomb repulsion forces, Reerink and Overbeek pointed out that the primary maximum of the interaction potential (Wmax) is the dominant factor in restricting aggregation.71 They described a reasonable approximation for the stability ratio Wij using the primary maximum:
. For eqn (24) a constant surface potential (eqn (24) can also be rewritten for a constant surface charge) and particle radii much larger than the thickness of the EDL (i.e. assumption of a thin electrical double layer (κr > 10)) are assumed. For particles which are governed by the increasing Coulomb repulsion forces, Reerink and Overbeek pointed out that the primary maximum of the interaction potential (Wmax) is the dominant factor in restricting aggregation.71 They described a reasonable approximation for the stability ratio Wij using the primary maximum: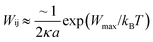 | (25) |
The integral in eqn (23) or Wmax in eqn (25) can be positive or negative depending on the forces between the two particles. Simplifying, if the integral or Wmax is positive, the repulsive forces dominate the particle interaction which leads to a decrease in the coagulation probability (the kernel) over the probability of the purely Brownian coagulation (vice versa if the attractive forces dominate). As a rule of thumb for most particle syntheses, the particle interaction decreases the probability of particle coalescence during the particle growth since the aggregation barrier increases with increasing size of the interacting particles. For the herein discussed NaBH4 syntheses, the repulsive forces dominate the growth at least for the larger particles (with radii between 1 and 2 nm). Three cases of particle interaction provide a good image of the coagulation probability: (1) between two “large” particles (with radii of 1.5–2 nm); (2) between a “large” and a “small” particle (below 1 nm in radius) and (3) between two “small” particles. Obviously, the repulsion forces will be the highest for case 1 and the smallest for case 3. Thus, the coagulation probability will very likely decrease most for case 1 and least for case 3.
Summarizing the discussion of the limitations (I) and (II), it can be concluded that both – the particle concentration and the particle interaction – tremendously increase the probability of coalescence between particles of similar size. As a consequence, the particle coalescence of charged NPs leads to final particles with relatively low polydispersity which is in contrast to the often referred publication of Sugimoto.40 For the skeptical reader: exactly this growth characteristic could be measured with time-resolved SAXS experiments for syntheses with growth due to coalescence.21,23 For aerosol particles (which are typically in the μm size range), Friedlander and co-workers have already described a similar growth characteristic in the 1960s with their theory of the self-preserving size distribution.72,73
A simple experiment which illustrates the influence of particle concentration and interaction on the NP size distribution is the separation of the Au-System 1 synthesis into several growth steps. A detailed description of that experiment can be found in S1 in the ESI.† The experiment comprises three different mixing conditions of precursor and reducing agent solution whereby all three colloidal solutions have the same final gold concentration. The first mixing conditions is the standard synthesis with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixing of the two reactants to obtain 10 ml of colloidal solution with a final gold concentration of 0.25 mM (e.g. mixing 0.5 mM HAuCl4 and 3 mM NaBH4 solution with Eppendorf pipettes in a time scale of a second). The particles grow due to coalescence to a size of approx. 1.5 nm in radius and are colloidally stable for minutes (i.e. within further 60 min they grow to a size of approx. 1.8 nm in radius).21 To prevent further growth to 1.8 nm, PVP as stabilizing agent is added to the “final” colloids (i.e. after approx. 5 min). The second mixing comprises a synthesis in two steps. At first 5 ml of a colloidal gold solution with the standard synthesis (with 1
1 mixing of the two reactants to obtain 10 ml of colloidal solution with a final gold concentration of 0.25 mM (e.g. mixing 0.5 mM HAuCl4 and 3 mM NaBH4 solution with Eppendorf pipettes in a time scale of a second). The particles grow due to coalescence to a size of approx. 1.5 nm in radius and are colloidally stable for minutes (i.e. within further 60 min they grow to a size of approx. 1.8 nm in radius).21 To prevent further growth to 1.8 nm, PVP as stabilizing agent is added to the “final” colloids (i.e. after approx. 5 min). The second mixing comprises a synthesis in two steps. At first 5 ml of a colloidal gold solution with the standard synthesis (with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixing) is prepared (leading to 1.5 nm particles) and subsequently, at first 2.5 ml of 3 mM NaBH4 and then 2.5 ml of a 0.5 mM HAuCl4 solution is added. For the third order, at first 2.5 ml of 3 mM NaBH4 is added to 5 ml of a colloidal gold solution (also prepared with the standard procedure). Subsequently, the 2.5 ml of HAuCl4 solution is added in 30 steps with additions of around 40 μl every 5–10 s (note that every growth step comprises around 3–4 s). The final particles of the first mixing conditions (standard 1
1 mixing) is prepared (leading to 1.5 nm particles) and subsequently, at first 2.5 ml of 3 mM NaBH4 and then 2.5 ml of a 0.5 mM HAuCl4 solution is added. For the third order, at first 2.5 ml of 3 mM NaBH4 is added to 5 ml of a colloidal gold solution (also prepared with the standard procedure). Subsequently, the 2.5 ml of HAuCl4 solution is added in 30 steps with additions of around 40 μl every 5–10 s (note that every growth step comprises around 3–4 s). The final particles of the first mixing conditions (standard 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixing) have a mean radius of 1.44 nm at a polydispersity of 10%. For the second mixing conditions in which HAuCl4 is reduced in the presence of existing particles (with a mean radius of 1.44 nm), the final mean radius increased to 1.64 nm. The experiment reveals that around 50% of the added HAuCl4 grow on existing particles, with the remaining 50% forming new particles. Therefore, the final particle concentration in the second procedure equates to approx. 75% of the concentration in the first procedure. The growth mechanism of the second mixing procedure can be deduced from the mechanistic knowledge of the standard synthesis. The existing particles with a mean radius of 1.44 nm are colloidally stable. The addition of HAuCl4 (to the colloidal solution with sufficiently BH4− ions) leads to an almost immediate reduction. The gold atoms can either grow on existing particles or form small metal clusters (dimers etc.) which are not colloidally stable. The probability for the growth on existing particles is much lower than the formation of small clusters which is caused by the higher aggregation barrier but mainly due to the relatively low concentration of the existing particles. With the same argumentation, the formed small molecular-like metal clusters grow further due to coalescent with themselves whereby the corresponding aggregation probability decreases with increasing size caused by the increasing aggregation barrier and decreasing concentration. According to this argumentation, the probability for an aggregation process between colloidally unstable particles decreases more with increasing size than the probability between unstable and existing particles. Consequently, with the second mixing conditions less and larger particles are created than with the standard synthesis. This effect is reinforced with the increase of subsequent additions. For each of the subsequent growth steps the concentration of the unstable particles is decreased and the concentration is directly proportional to the aggregation probability. This concentration influence can be observed for the third mixing conditions (i.e. 30 additions of around 40 μl) in which the final mean radius is 1.75 nm and around 90% of the added gold salt grows onto the existing particles.
1 mixing) have a mean radius of 1.44 nm at a polydispersity of 10%. For the second mixing conditions in which HAuCl4 is reduced in the presence of existing particles (with a mean radius of 1.44 nm), the final mean radius increased to 1.64 nm. The experiment reveals that around 50% of the added HAuCl4 grow on existing particles, with the remaining 50% forming new particles. Therefore, the final particle concentration in the second procedure equates to approx. 75% of the concentration in the first procedure. The growth mechanism of the second mixing procedure can be deduced from the mechanistic knowledge of the standard synthesis. The existing particles with a mean radius of 1.44 nm are colloidally stable. The addition of HAuCl4 (to the colloidal solution with sufficiently BH4− ions) leads to an almost immediate reduction. The gold atoms can either grow on existing particles or form small metal clusters (dimers etc.) which are not colloidally stable. The probability for the growth on existing particles is much lower than the formation of small clusters which is caused by the higher aggregation barrier but mainly due to the relatively low concentration of the existing particles. With the same argumentation, the formed small molecular-like metal clusters grow further due to coalescent with themselves whereby the corresponding aggregation probability decreases with increasing size caused by the increasing aggregation barrier and decreasing concentration. According to this argumentation, the probability for an aggregation process between colloidally unstable particles decreases more with increasing size than the probability between unstable and existing particles. Consequently, with the second mixing conditions less and larger particles are created than with the standard synthesis. This effect is reinforced with the increase of subsequent additions. For each of the subsequent growth steps the concentration of the unstable particles is decreased and the concentration is directly proportional to the aggregation probability. This concentration influence can be observed for the third mixing conditions (i.e. 30 additions of around 40 μl) in which the final mean radius is 1.75 nm and around 90% of the added gold salt grows onto the existing particles.
(iv) Commonly used idealization. As common in science, theoretical descriptions of certain processes or states are made by using idealizations, approximations or measurements of experimental quantities. For the theoretical description of charged colloidal particles this includes typically idealizations or approximations of the charged surface, the resulting electrical potential, the double layer dimensions, the adsorption behavior of ions or the interaction of charged surfaces. In addition, the measurements of certain experimental quantities are often necessary for the description of colloidal stability such as the zeta potential.
For particles during the growth, any of the beforehand mentioned idealization can hardly be made which makes a theoretical description very difficult. Exemplarily, neither will the surface charge density of small metal clusters be similar as of larger metal NPs nor will the surface potential be the same. The dimensions of the double layer with respect to the particle size also differ during growth (i.e. the final metal NP might have a thin double layer with respect to the NP size but for small clusters this is very unlikely the case). Also a time-resolved zeta potential measurement of particles during growth is experimentally not possible. Consequently, the herein used mathematical equations to describe particle interactions are only used to support the qualitative explanation of the experimental results and should be seen as those.
4.3 Ostwald ripening of metal clusters – an unlikely process?
Experimentally, it is very difficult to distinguish between growth due to coalescence and growth due to Ostwald ripening. In both cases the particle concentration decreases with increasing particle size. Although the growth kinetics can indicate that one or the other process is more likely, it remains in most cases rather speculative. In this and some of my former contributions, it is stated that a growth due to Ostwald ripening is very unlikely since it can be assumed that at room temperature small NPs are thermodynamically stable. However, a broad range of publications make a contrary assumption. In a recent study, my colleagues and I tried to investigate the thermodynamic stability of metal clusters with a rather uncommon approach – a growth study of NPs in standard soda lime glasses. The idea was that in a solid glass matrix, particle movement is inhibited even for extremely small clusters. Actually, only atoms can diffuse in the glass matrix. As a result, growth can only occur via monomer addition (i.e. atoms). In that growth study, it could be shown that molecular silver clusters in a glass matrix which are predominantly silver dimers are stable up to about 410 °C.52 These results revealed that small molecular-like metal clusters (in a glass matrix) are thermodynamically stable even at elevated temperatures. Indeed, the surrounding matrix has an influence on the thermal stability of a metal cluster but one would not expect a dissolution of metal clusters in aqueous and non-aqueous solutions in the temperature range of most synthetic procedures (<150 °C). Obviously, this is not true if the solution contains chemical additives such as corrosive acids (e.g. HNO3) or ligands that can etch the particle surface. Thus, for metal colloidal syntheses aggregation or coalescence caused by nonsufficient colloidal stability is a much more likely process than Ostwald ripening due to non-sufficient thermodynamic stability. Nevertheless, Ostwald ripening is an often claimed growth mechanism for (metal) NPs but to the best of my knowledge not a single publication exists which provides convincing experimental indications of an Ostwald ripening growth for syntheses in common temperature ranges (<200 °C). This includes colloidal metal, metal–oxide and semiconductor NP syntheses.4.4 Category 2 syntheses – kinetics of monomer-supplying reaction determines growth kinetics
So far, the discussion is limited to synthetic systems with a monomer-supplying chemical reaction much faster than the actual growth. For almost all synthetic procedures this is not the case. The borohydride reduction represents an exception. In general, the kinetics of the chemical reaction govern the particle growth kinetics. As a consequence, one could assume for the majority of syntheses that a nucleation and growth model to describe the particle formation can be a promising approach. However, the following discussion demonstrates that a nucleation and growth approach might not be as helpful as often assumed. It rather reveals that the the beforehand discussed growth model which is governed by colloidal stability can be extended to a broad range of colloidal syntheses. In this contribution, this is exemplarily discussed for the most common Au–NP synthesis – the classical Turkevich method.In particular the SAXS experiments applying a free-liquid jet revealed that the four steps occur concomitant to four different steps of the reduction kinetics.19 In the first step, the reduction rate is rather high, the number of particles increases and initial particles of about 1–2 nm in radius are rapidly formed. In the second step, reduction continues, but at a much lower rate, and the freshly formed particles that are likely to have a weak stabilization undergo coalescence processes leading to a decrease in the number of particles. When the particle size reaches a mean radius of about 2.5 nm, the number of particles remains constant, but particles keep growing in size. Taking the polydispersity into account, the smaller particles in that size distribution have radii of around 1.5 nm. One can deduce that at this particle size the electrostatic stabilization of the citrate-capped colloids is sufficient to prevent further coalescence. Subsequently, the Au–NPs grow due to the diffusion of the gold atoms reduced in solution (as stated in the mechanism). Hence, a diffusional growth comprises the third step of the growth process which further decreases the polydispersity. When the particles reach a radius of around 4–5 nm, the growth rate increases drastically and the remaining 70–80% of the gold salt is reduced rapidly. In this fourth step, particle size increases to the final radius.
The first two steps correspond in first place to a growth due to coalescence whereby a fast reduction occurs in the first minutes after mixing the solutions. The amount of particles formed in the first two steps remains constant in the following two steps of growth. Indeed, the first two steps can also be described by a nucleation process with subsequent growth due to aggregation. However, this nucleation model would describe a quite unimportant process concerning the evolution of the final particle size. The formation of the gold dimer or probably slightly larger clusters (which are thermodynamically stable) does not affect the outcome of the first two steps and therefore also of the final particles. The particle size distribution and concentration at the end of the first two steps is determined by the amount of reduced gold and the colloidal stability since this will define the seed particle size and concentration. Actually, from the time-resolved SAXS experiments it appears that the amount of gold is defined already in the first 2–3 minutes whereby the coalescence kinetics is slightly slower.
The third step of the growth mechanism is interpreted as a growth by diffusion, meaning that gold ions are reduced anywhere in solution and grow onto the existing particles. In the fourth step the reduction rate increases tremendously leading to a fast reduction of the remaining gold salt (interpreted as autocatalytic surface reduction) and the reduced gold grows onto the existing particles. Again, no further particles form. For both steps, it might be possible that as an intermediate step some gold atoms form small gold clusters which subsequently coalesce with the particles. The probability for such a process is dependent on size and concentration of the existing particles as well as on the formed clusters. This issue is discussed in section 3.2.3 (iii). Consequently, if or if not new particles are formed is mainly determined by the reduction rate which is relatively low during the third step. However, the difference in reduction rate between the first step in which the primary particles are formed and the third step is not as big as further particle formation can be excluded. In the fourth step the reduction rate increases tremendously leading to a fast reduction of the remaining gold salt and is even higher than in the first step. Actually, in each of the last two steps a small amount of newly formed particles could be expected, in particular in the final step. This becomes evident when comparing these two final steps with the first two steps or with the Au-System 1. For the Au-System 1, the experiment under the different mixing conditions (see 3.2.3 (iii) or S1†) reveals that even very slow additions of gold precursor can lead to particle formation although the existing particles in the Au-System 1 are much smaller and their concentration much higher (both decrease the probability that further particles are created).
In fact, the particle growth without further particle formation in the last two steps could be explained with four different processes: I. the existence of an energy or concentration barrier to the formation of small NPs as it is predicted in the CNT; II. the diffusional growth as presumed in the existing growth mechanism; III. the formation of gold clusters that subsequently undergo coalescence processes with the particles formed in the first two steps; and IV. the reduction in proximity or directly at the particle surface with subsequent growth onto the particle.
The first process (I) of an energy barrier is very unlikely since in the first two steps such an energy barrier would not allow the fast formation of particles. In addition, it is previously discussed that dissolution of small gold clusters/nanoparticles is very improbable. The second and third process (II and III) appear to be very reasonable especially in the third step of the synthesis in which they could occur, both consecutively and parallel. However, these two processes can hardly explain the fourth step of the growth mechanism. In the fourth step, the reduction rate increases tremendously (higher than in the first step) and even for such a relatively high reduction rate (see Fig. 2c in ref. 19) no further particles are formed. Consequently, the most probable explanation for the final two growth steps is a reduction of gold ions which are attached in the proximity of the particle surfaces (i.e. as co-ions in the EDL). Hence, the reduction in the third and fourth step is most likely a catalytic reaction at the NP surface making process IV the most probable explanation for particle growth without further particle formation.
The enrichment of gold ions in the EDL can also be deduced from a subsequent addition of HAuCl4 solution to the final Au–NP. The plasmon band slightly shifts towards higher wavelengths leading to a color change (in standard UV-vis cuvettes) from red to violet. As shown in previous publications the color change is neither caused by any aggregation54 nor by the absorption of the gold ions themselves.53 Consequently, the red-shift is most likely due to the adsorption of HAuCl4 on the NP surface influencing the surface chemistry or the dielectric constant of the surrounding medium. The same argument explains the grey and later purple color of the colloidal solution in the course of the reaction. The ruby red color of the the final colloid represents the state without any gold ions in solution (i.e. without gold ions in the EDL).
The tremendous change in the reduction rate between step 3 and step 4 (although it has no impact on the final particle size since the particle concentration is constant) remains unclear. It appears that the fourth step occurred for all the investigated citrate-reduced Au–NP systems (at different concentrations and temperatures) if the average radius is about 4 nm. However, such a size-dependent effect would lead to an increase in the polydispersity or even to a bimodal size distribution because particles that reach this size at first (sufficient for such a fast surface reduction) would grow much faster than the existing smaller particles. In contrast, the polydispersity remains low or even decreases further which makes the size-dependent effect very unlikely. Thus, the change in the reduction rate seems to relate to the changing chemical composition of the solution during the reaction (probably caused by product(s) of the reduction).
The preceding discussion leads to a refinement of the four-step growth mechanism described in ref. 19 and 51. Actually, six different sequential physicochemical processes occur during the growth of a particle which are displayed in Fig. 5. The first process is the reduction of gold salt. Subsequently, the metal atoms form small clusters (second process) which undergo coalescence processes to form first NPs (third process). As a consequence, gold ions are attached near the surface in the EDL as co-ions (fourth process), get reduced (fifth process) and grow onto the existing NPs (sixth process). Step 1 of the growth mechanism consists of the first two processes (reduction and formation of first clusters) and the third process (coalescence of clusters) represents step 2. The last three processes (gold ion attachment, reduction and growth) occur in step 3 and 4 whereby the two steps are only separated by a slow and fast reduction in the fifth process.
For the Turkevich method, the resulting final monodisperse Au–NPs are basically determined by two factors. The first factor is the change in reduction chemistry and kinetics between the seed particle formation and the actual seeded growth. The reduction chemistry in the beginning of the reaction enables the seed formation and a change in the reduction chemistry terminates it. Subsequently, reduction occurs in the vicinity of the particle surface. Thus, less than 3% of the gold amount is available for the seed particle formation. The SAXS experiments applying a free-liquid jet even revealed that the four steps of growth occur concomitant to four different steps of the reduction kinetics.19 However, the kinetic changes between step 3 and 4 seem to have no influence on the final size. The second factor is the colloidal stability of the seed particles. At any time during the synthesis the colloidal stability determines the minimum particle size. Thus, the lower the colloidal stability the larger the seed particles which leads to a lower seed particle concentration and therefore larger final particles. Without a sufficient colloidal stability, too few seed particles are formed leading to relatively large final particles or even precipitation. Indeed, the colloidal stability can change during the growth. The minimum particle size in the beginning of the Turkevich synthesis is about 1.5 nm in radius (i.e. smaller particles are not detected) which corresponds approximately to the particle size of the NaBH4 systems.
Summarizing, for the Turkevich method the interplay of several physicochemical processes leads to an almost ideal seeded growth process in a one-pot synthesis with a seed particle formation in the beginning and a subsequent seeded growth most likely driven by a surface enhanced reduction.
5 Nanoparticle growth: thermodynamic stability vs. colloidal stability
As stated in the beginning, nucleation is a thermodynamic model which describes the first step in a first order phase transition with the appearance of a new phase – the nucleus – in the metastable primary phase. In general, most nucleation models are described with the classical nucleation theory (CNT) which applies equilibrium thermodynamics and was originally developed for vapor condensation.66In the following, the previous mechanistic findings for metal NP syntheses are discussed concerning the classical nucleation approach and subsequently extended for the general case of nucleation and NP growth.
The CNT and its extension to NP syntheses from LaMer predicts a certain degree of saturation (supersaturation) of monomers necessary for the formation of first stable particles (nuclei) that are larger than a minimum critical size. Below that critical size the particles or clusters are thermodynamically not stable. Due to the particle formation, this saturation decreases below that certain saturation degree. Subsequently, the formed and stable particles (nuclei) are in the growth stage (for instance due to a monomer supply) until reaching their final size. Following this theoretical paradigm, an ideal nucleation and growth process (i.e. growth without aggregation) leads to an increase in the number of particles in the beginning, which remains constant in the growth stage. If such a growth behavior is measured, it is often concluded that the formation process is described at best with a nucleation model. However, this is in general not as straightforward as usually assumed since if A implies B it does not follow that B implies A. Again, the underlying basic concept of CNT is the process of nucleation. What does this effectively mean for the herein discussed metal NP syntheses?
The CNT and its extension to NP syntheses from LaMer6 presumes the need of a certain concentration of reduced metal atoms in solution which allows the formation of first small clusters/nanoparticles – the nuclei. The solubility of the metal atoms in a solvent such as water is not exactly known, but should be extremely small (effectively 0). So, it can be assumed that such a supersaturation effectively occurs as long as metal atoms are in the solution (i.e. as long as all the reduced metal atoms are not part of a cluster or particle). Furthermore, it was discussed that a dissolution of small clusters (r < 0.5 nm) for common synthesis temperatures is very unlikely. Therefore, a supersaturation already exists at extremely low concentrations since very small metal clusters consisting of a few atoms are already thermodynamically stable. For common synthesis temperatures (<200 °C) even the metal dimer is very likely to be thermodynamically stable. In this case the critical cluster size would be the metal atom. In contrast, the size at which a cluster or particle is colloidally stable is in general in the range of nanometers (i.e. clusters/particles consisting of several hundred or thousand atoms).
For the herein described syntheses, the aggregation and coalescence steps are the first size determining steps. For the syntheses with NaBH4 as a reducing agent, the growth is solely due to aggregation and coalescence and consequently the increasing colloidal stability determines the final size distribution. For the Turkevich synthesis, a fast reduction and coalescence growth step (steps 1 and 2) determine the size of the seed particles. The concentration of the formed seed particles determines the number of particles on which the gold salt is distributed and therefore the final size.
Even if a nucleation-like process in these syntheses really occurs as the first step of the phase transition, it has no impact on the growth process and therefore on the final size. It would probably only describe the formation of a metal dimer or another very small metal cluster. These small metal clusters might be thermodynamically stable but they are not colloidally stable. Thus, the clusters grow further by aggregation and coalescence until they reach a colloidally stable size. In this case, it is irrelevant if the first thermodynamic stable cluster is the dimer or another slightly larger cluster. From a physical point of view, the concept of NP growth with a minimum particle size governed by colloidal stability as proposed herein can hardly connect with the CNT, the LaMer model or any other nucleation model since these theories have a contrary concept of “energy barrier”. The basic idea behind any nucleation model is that clusters/nanoparticles have to overcome an free energy barrier due to a certain particle size (particles with a critical radius) to be able to grow in size. In contrast, the growth governed by colloidal stability states that clusters/nanoparticles always grow at least to a size, at which they cannot overcome an energy barrier of aggregation. In other words, a nucleation model deals with something like an activation energy to form first thermodynamically stable particles, whereas the growth governed by colloidal stability deals with a deactivation energy (an energy barrier at which aggregation or coalescence stops) – hence, two theoretical approaches with two contrary basic assumptions (note that CNT is actually an approach of maximizing entropy).
For a broad range of NP syntheses (i.e. also for metal–oxide and semiconductor NPs), the colloidal stability and not the thermodynamic stability determine the minimum particle size. For these syntheses a theoretical model describing the first relevant particle formation step demands the description of the colloidal stability and also of the monomer-supplying reaction if this reaction is not faster than the actual growth. The two synthetic systems discussed herein are classified in two categories and can be seen as model systems for this broad range of colloidal syntheses. The almost ideal separation between monomer supply and actual growth of Category 1 syntheses leads to a particle growth which is only due to aggregation and coalescence. Even for very low concentrations, particles grow at least to the minimal particle size by aggregation and coalescence. Thus, to obtain very small NPs in aqueous solution (below 2 nm in radius), synthethic protocols almost always use NaBH4 as reducing agent. This is not caused by any “fast” nucleation step. Only, the exclusive growth due to coalescence leads to final particle sizes close to the minimal particle size determined by colloidal stability. For Category 2 syntheses in which the monomer-supplying reaction is governing the growth kinetics, the first stable particles are also growing to or slightly above the minimal particle size by aggregation and coalescence. The Turkevich method as an almost perfect seeded growth in a one-pot synthesis represents a model system for Category 2 synthesis. The first particles are formed by a fast coalescence step whereby the largest proportion of the gold monomers is evenly distributed on the previously formed (seed) particles. As discussed, this must result from a change in the reduction chemistry during the synthesis. Indeed, most syntheses neither will have a perfect separation between monomer supply and growth nor will they consist of an ideal seeded growth. However, they can be described by a combination of the herein discussed synthetic model systems since (i) the first relevant growth step will be a growth due to aggregation and coalescence and (ii) the following growth is either due to a monomer supply or a further growth due to aggregation and coalescence. The growth due to aggregation or coalescence in (ii) is either between colloidal unstable particles or between a colloidal unstable and a colloidal stable particle. The particle growth due to the subsequent additions of HAuCl4 and NaBH4 to colloidal gold (see 3.2.3 (iii)) illustrates these possible growth processes. The subsequent additions lead either to the formation of new particles formed solely by coalescence or to the growth of the preformed NPs which are colloidally stable. The growth of preformed NPs occurs due to monomer addition or due to coalescence with colloidally unstable metal clusters.
Hence, theoretical growth descriptions of most colloidal NP syntheses demand basic knowledge of the underlying growth mechanism, the minimal particle size (determined by the colloidal stability) and the chemical reactions occurring during the syntheses but not a description of a nucleation event.
6 Conclusion
This contribution provides a detailed discussion of growth principles for colloidal metal NPs which is based on time-resolved experimental investigations of several gold and silver NP syntheses. The syntheses are classified in two categories. The first category comprises colloidal syntheses for which the monomer-supplying reaction is faster than the actual growth. This category is mainly covered by syntheses with BH4− as a reducing agent. It is deduced that the growth mechanism of Category 1 syntheses is only due to aggregation and coalescence and therefore governed by colloidal stability. For these syntheses, an idealized concept of NP growth is presented which is in contrast to the commonly applied LaMer model.For most syntheses, the monomer-supplying reaction is much slower and governs the kinetics of particle growth. These syntheses are classified as Category 2 syntheses and discussed using the most popular gold NP synthesis as an example – the Turkevich method. For the Turkevich method, an interplay of several physicochemical processes leads to an almost ideal seeded growth process in a one-pot synthesis. The seed particles are formed in the beginning of the synthesis with a subsequent seeded growth which is most likely driven by a surface reduction. The seeded growth mechanism with the resulting final monodisperse gold NPs is caused by two factors: a change in the reduction chemistry and the colloidal stability.
For both synthetic classes the minimal particle size is in general determined by the colloidal and not by the thermodynamic stability making a nucleation model irrelevant. For Category 1 syntheses, the minimal particle size corresponds to the smallest final size and for Category 2 syntheses to the smallest seed particle size. Furthermore, it is discussed why Ostwald ripening is a very unlikely growth process for most metal colloid syntheses.
The herein discussed growth mechanisms can be seen as model cases of synthetic systems. Other synthetic systems might not have a distinct separation of the monomer-supplying reaction and particle growth as it is in the case with Category 1 syntheses or might not comprise a perfect seed-mediated growth as Category 2 syntheses. Nevertheless, the growth of most syntheses can be described by a combination of the herein discussed synthetic model systems and the growth concept based on colloidal stability.
Abbreviation
| CNT | classical nucleation theory |
| EDL | electric double layer |
| TIP | total interaction potential |
| NPs | nanoparticles |
| SAXS | small angle X-ray scattering |
| XANES | X-ray Absorption near edge structure |
Acknowledgements
J. P. acknowledges generous funding by the Deutsche Forschungsgemeinschaft within the project PO 1744/1-1. J. P. also acknowledges the discussions with Dr. Franziska Emmerling, Dr. Ralph Krähnert, Prof. Klaus Rademann, Prof. Nicola Pinna, Dipl. Chem. Maria Wuithschick and Dipl. Chem. Frieder Kettemann.References
- J. Park, J. Joo, S. G. Kwon, Y. Jang and T. Hyeon, Synthesis of Monodisperse Spherical Nanocrystals, Angew. Chem. Int. Ed., 2007, 46, 4630–4660, DOI:10.1002/anie.200603148.
- M. Faraday, The bakerian lecture: Experimental relations of gold (and other metals) to light, Philos. Trans. R. Soc. Lond., 1857, 147, 145–181 CrossRef.
- W. Ostwald, Über die vermeintliche Isomerie des roten und gelben Quecksilberoxyds und die Oberflächenspannung fester Körper, Z. Phys. Chem., 1900, 34, 495 Search PubMed.
- J. Turkevich, P. C. Stevenson and J. Hillier, A study of the nucleation and growth processes in the synthesis of colloidal gold, Discuss. Faraday Soc., 1951, 11, 55, 10.1039/df9511100055.
- R. Becker and W. Doring, Kinetic treatment of germ formation in supersaturated vapour, Ann. Phys., 1935, 24, 719–752 CrossRef CAS PubMed.
- V. K. LaMer, Nucleation in Phase Transitions, Ind. Eng. Chem., 1952, 44, 1270–1277, DOI:10.1021/ie50510a027.
- V. K. LaMer and R. H. Dinegar, Theory, Production and Mechanism of Formation of Monodispersed Hydrosols, J. Am. Chem. Soc., 1950, 72, 4847–4854, DOI:10.1021/ja01167a001.
- E. E. Finney and R. G. Finke, Nanocluster nucleation and growth kinetic and mechanistic studies: A review emphasizing transition-metal nanoclusters, J. Colloid Interface Sci., 2008, 317, 351–374, DOI:10.1016/j.jcis.2007.05.092.
- X. C. Zeng and D. W. Oxtoby, Gas–liquid nucleation in Lennard-Jones fluids., J. Chem. Phys., 1991, 94, 4472, DOI:10.1063/1.460603.
- K. Takiyama, Formation and aging of precipitates. VIII. Formation of monodisperse particles (1) Gold sol particles by sodium citrate method, Bull. Chem. Soc. Jpn., 1958, 31, 944–950 CrossRef CAS.
- M. K. Chow and C. F. Zukoski, Gold Sol Formation Mechanisms: Role of Colloidal Stability, J. Colloid Interface Sci., 1994, 165, 97–109, DOI:10.1006/jcis.1994.1210.
- L. Pei, K. Mori and M. Adachi, Formation Process of Two-Dimensional Networked Gold Nanowires by Citrate Reduction of AuCl4- and the Shape Stabilization, Langmuir, 2004, 20, 7837–7843, DOI:10.1021/la049262v.
- X. Ji, X. Song, J. Li, Y. Bai, W. Yang and X. Peng, Size Control of Gold Nanocrystals in Citrate Reduction: The Third Role of Citrate., J. Am. Chem. Soc., 2007, 129, 13939–13948, DOI:10.1021/ja074447k.
- S. Kumar, K. S. Gandhi and R. Kumar, Modeling of Formation of Gold Nanoparticles by Citrate Method, Ind. Eng. Chem. Res., 2007, 46, 3128–3136, DOI:10.1021/ie060672j.
- B.-K. Pong, H. I. Elim, J.-X. Chong, W. Ji, B. L. Trout and J.-Y. Lee, New Insights on the Nanoparticle Growth Mechanism in the Citrate Reduction of Gold(III) Salt:Formation of the Au Nanowire Intermediate and Its Nonlinear Optical Properties., J. Phys. Chem. C, 2007, 111, 6281–6287, DOI:10.1021/jp068666o.
- Y. Mikhlin, A. Karacharov, M. Likhatski, T. Podlipskaya, Y. Zubavichus, A. Veligzhanin and V. Zaikovski, Submicrometer intermediates in the citrate synthesis of gold nanoparticles: New insights into the nucleation and crystal growth mechanisms, J. Colloid Interface Sci., 2011, 362, 330–336, DOI:10.1016/j.jcis.2011.06.077.
- S. K. Sivaraman, S. Kumar and V. Santhanam, Monodisperse sub-10 nm gold nanoparticles by reversing the order of addition in Turkevich method – The role of chloroauric acid., J. Colloid Interface Sci., 2011, 361, 543–547, DOI:10.1016/j.jcis.2011.06.015.
- J. Polte, T. T. Ahner, F. Delissen, S. Sokolov, F. Emmerling, A. F. Thünemann and R. Kraehnert, Mechanism of Gold Nanoparticle Formation in the Classical Citrate Synthesis Method Derived from Coupled in situ XANES and SAXS Evaluation, J. Am. Chem. Soc., 2010, 132, 1296–1301, DOI:10.1021/ja906506j.
- J. Polte, R. Erler, A. F. Thünemann, F. Emmerling and R. Kraehnert, SAXS in combination with a free liquid jet for improved time-resolved in situ studies of the nucleation and growth of nanoparticles, Chem. Commun., 2010, 46, 9209, 10.1039/c0cc03238g.
- Y. Xia, Y. Xiong, B. Lim and S. E. Skrabalak, Shape-Controlled Synthesis of Metal Nanocrystals: Simple Chemistry Meets Complex Physics?, Angew. Chem. Int. Ed., 2008, 48, 60–103, DOI:10.1002/anie.200802248.
- J. Polte, R. Erler, A. F. Thünemann, S. Sokolov, T. T. Ahner, K. Rademann, F. Emmerling and R. Kraehnert, Nucleation and Growth of Gold Nanoparticles Studied via in situ Small Angle X-ray Scattering at Millisecond Time Resolution, ACS Nano, 2010, 4, 1076–1082, DOI:10.1021/nn901499c.
- M. Wuithschick, B. Paul, R. Bienert, A. Sarfraz, U. Vainio, M. Sztucki, R. Kraehnert, P. Strasser, K. Rademann and F. Emmerling, et al. Size-Controlled Synthesis of Colloidal Silver Nanoparticles Based on Mechanistic Understanding, Chem. Mater., 2013, 25, 4679–4689, DOI:10.1021/cm401851g.
- J. Polte, X. Tuaev, M. Wuithschick, A. Fischer, A. F. Thünemann, K. Rademann, R. Kraehnert and F. Emmerling, Formation Mechanism of Colloidal Silver Nanoparticles: Analogies and Differences to the Growth of Gold Nanoparticles, ACS Nano, 2012, 6, 5791–5802, DOI:10.1021/nn301724z.
- N. Toshima and T. Yonezawa, Bimetallic nanoparticles—novel materials for chemical and physical applications, New J. Chem., 1998, 22, 1179–1201, 10.1039/a805753b.
- M.-C. Daniel and D. Astruc, Gold Nanoparticles: Assembly, Supramolecular Chemistry, Quantum-Size-Related Properties, and Applications toward Biology, Catalysis, and Nanotechnology, Chem. Rev., 2004, 104, 293–346, DOI:10.1021/cr030698+.
- N. R. Jana, L. Gearheart and C. J. Murphy, Seeding Growth for Size Control of 5–40 nm Diameter Gold Nanoparticles, Langmuir, 2001, 17, 6782–6786, DOI:10.1021/la0104323.
- A. Guiet, T. Reier, N. Heidary, D. Felkel, B. Johnson, U. Vainio, H. Schlaad, Y. Aksu, M. Driess and P. Strasser, et al. A One-Pot Approach to Mesoporous Metal Oxide Ultrathin Film Electrodes Bearing One Metal Nanoparticle per Pore with Enhanced Electrocatalytic Properties, Chem. Mater., 2013, 25, 4645–4652, DOI:10.1021/cm401135z.
- N. R. Jana, L. Gearheart and C. J. Murphy, Seed-Mmediated Ggrowth Aapproach for Sshape-Ccontrolled Ssynthesis of Sspheroidal and Rrod-like Ggold Nnanoparticles Uusing a Ssurfactant Ttemplate, Adv. Mater., 2001, 13, 1389–1393, DOI:10.1002/1521-4095(200109)13:18<1389:AID-ADMA1389>3.0.CO;2-F.
- S. D. Perrault and W. C. W. Chan, Synthesis and Surface Modification of Highly Monodispersed, Spherical Gold Nanoparticles of 50–200 nm, J. Am. Chem. Soc., 2009, 131, 17042–17043, DOI:10.1021/ja907069u.
- K. R. Brown, D. G. Walter and M. J. Natan, Seeding of Colloidal Au Nanoparticle Solutions. 2. Improved Control of Particle Size and Shape, Chem. Mater., 2000, 12, 306–313, DOI:10.1021/cm980065p.
- N. R. Jana, L. Gearheart and C. J. Murphy, Evidence for Seed-Mediated Nucleation in the Chemical Reduction of Gold Salts to Gold Nanoparticles, Chem. Mater., 2001, 13, 2313–2322, DOI:10.1021/cm000662n.
- X. Ji, X. Song, J. Li, Y. Bai, W. Yang and X. Peng, Size Control of Gold Nanocrystals in Citrate Reduction: The Third Role of Citrate, J. Am. Chem. Soc., 2007, 129, 13939–13948, DOI:10.1021/ja074447k.
- J. Niu, T. Zhu and Z. Liu, One-step seed-mediated growth of 30–150 nm quasi-spherical gold nanoparticles with 2-mercaptosuccinic acid as a new reducing agent, Nanotechnology, 2007, 18, 325607, DOI:10.1088/0957-4484/18/32/325607.
- J. Rodríguez-Fernández, J. Pérez-Juste, F. J. G. de Abajo and L. M. Liz-Marzán, Seeded Growth of Submicron Au Colloids with Quadrupole Plasmon Resonance Modes, Langmuir, 2006, 22, 7007–7010, DOI:10.1021/la060990n.
- T. Zhu, K. Vasilev, M. Kreiter, S. Mittler and W. Knoll, Surface Modification of Citrate-Reduced Colloidal Gold Nanoparticles with 2-Mercaptosuccinic Acid, Langmuir, 2003, 19, 9518–9525, DOI:10.1021/la035157u.
- D. B. Dickens and J. J. Sloan, The Nucleation and Freezing of Dilute Nitric Acid Aerosols, J. Phys. Chem. A, 2002, 106, 10543–10549, DOI:10.1021/jp0259566.
- G. W. Turner and L. S. Bartell, On the Probability of Nucleation at the Surface of Freezing Drops, J. Phys. Chem. A, 2005, 109, 6877–6879, DOI:10.1021/jp058098x.
- J. Y. Rempel, M. G. Bawendi and K. F. Jensen, Insights into the Kinetics of Semiconductor Nanocrystal Nucleation and Growth, J. Am. Chem. Soc., 2009, 131, 4479–4489, DOI:10.1021/ja809156t.
- H. Reiss, The Growth of Uniform Colloidal Dispersions, J. Chem. Phys., 1951, 19, 482, DOI:10.1063/1.1748251.
- T. Sugimoto, Preparation of monodispersed colloidal particles, Adv. Colloid Interface Sci., 1987, 28, 65–108, DOI:10.1016/0001-8686(87)80009-X.
- X. Peng, J. Wickham and A. P. Alivisatos, Kinetics of II-VI and III-V Colloidal Semiconductor Nanocrystal Growth: “Focusing” of Size Distributions, J. Am. Chem. Soc., 1998, 120, 5343–5344, DOI:10.1021/ja9805425.
- J. Van Embden, J. E. Sader, M. Davidson and P. Mulvaney, Evolution of Colloidal Nanocrystals: Theory and Modeling of their Nucleation and Growth, J. Phys. Chem. C, 2009, 113, 16342–16355, DOI:10.1021/jp9027673.
- V. Privman, Mechanisms of Diffusional Nucleation of Nanocrystals and Their Self-Assembly into Uniform Colloids, Ann. N. Y. Acad. Sci., 2009, 1161, 508–525, DOI:10.1111/j.1749-6632.2008.04323.x.
- C. Engelbrekt, P. S. Jensen, K. H. Sørensen, J. Ulstrup and J. Zhang, Complexity of Gold Nanoparticle Formation Disclosed by Dynamics Study, J. Phys. Chem. C, 2013, 117, 11818–11828, DOI:10.1021/jp401883h.
- J. T. G. Overbeek and J. W. Goodwin, Colloidal Dispersions, 1983 Search PubMed.
- R. J. Hunter, Foundations of Colloid Science, 1st edition, Oxford University Press, Oxford, 1987 Search PubMed.
- T. Cosgrove, Colloid Science: Principles, Methods and Applications, 2nd Edition, Wiley-Blackwell, Oxford, 2010 Search PubMed.
- E. J. W. Verwey and J. T. G. Overbeek, Theory of the Stability of Lyophobic Colloids, Elsevier, Amsterdam, 1948 Search PubMed.
- A. D. Pomogailo and V. N. Kestelman, Metallopolymer Nanocomposites, Springer-Verlag Berlin Heidelberg, Berlin/Heidelberg, 2005, vol. 81 Search PubMed.
- D. H. Napper, Polymeric Stabilization of Colloidal Dispersions, Academic Press, London, 1983 Search PubMed.
- J. Polte, T. T. Ahner, F. Delissen, S. Sokolov, F. Emmerling, A. F. Thünemann and R. Kraehnert, Mechanism of Gold Nanoparticle Formation in the Classical Citrate Synthesis Method Derived from Coupled in situ XANES and SAXS Evaluation, J. Am. Chem. Soc., 2010, 132, 1296–1301, DOI:10.1021/ja906506j.
- A. Simo, J. Polte, N. Pfänder, U. Vainio, F. Emmerling and K. Rademann, Formation Mechanism of Silver Nanoparticles Stabilized in Glassy Matrices, J. Am. Chem. Soc., 2012, 134, 18824–18833, DOI:10.1021/ja309034n.
- T. Hendel, M. Wuithschick, F. Kettemann, A. Birnbaum, K. Rademann and J. Polte, In situ Ddetermination of Ccolloidal Ggold Cconcentrations with UV-–vVis Sspectroscopy: Llimitations and Pperspectives, Anal. Chem., 2014, 86, 11115–11124, DOI:10.1021/ac502053s.
- J. Polte, M. Herder, R. Erler, S. Rolf, A. Fischer, C. Würth, A. F. Thünemann, R. Kraehnert and F. Emmerling, Mechanistic insights into seeded growth processes of gold nanoparticles, Nanoscale, 2010, 2, 2463, 10.1039/c0nr00541j.
- J. Polte, R. Kraehnert, M. Radtke, U. Reinholz, H. Riesemeier, A. F. Thünemann and F. Emmerling, New insights of the nucleation and growth process of gold nanoparticles via in situ coupling of SAXS and XANES, J. Phys.: Conf. Ser., 2010, 247, 012051, DOI:10.1088/1742-6596/247/1/012051.
- J. Polte, F. Emmerling, M. Radtke, U. Reinholz, H. Riesemeier and A. F. Thünemann, Real-Time Monitoring of Copolymer Stabilized Growing Gold Nanoparticles, Langmuir, 2010, 26, 5889–5894, DOI:10.1021/la903829q.
- M. Doyen, K. Bartik and G. Bruylants, UV–vis and NMR study of the formation of gold nanoparticles by citrate reduction: Observation of gold–citrate aggregates., J. Colloid Interface Sci., 2013, 399, 1–5, DOI:10.1016/j.jcis.2013.02.040.
- J. Kimling, M. Maier, B. Okenve, V. Kotaidis, H. Ballot and A. Plech, Turkevich Method for Gold Nanoparticle Synthesis Revisited, J. Phys. Chem. B, 2006, 110, 15700–15707, DOI:10.1021/jp061667w.
- T. X. Li, Y. L. Ji, S. W. Yu and G. H. Wang, Melting properties of noble metal clusters., Solid State Commun., 2000, 116, 547–550, DOI:10.1016/S0038-1098(00)00373-2.
- L. Miao, V. R. Bhethanabotla and B. Joseph, Melting of Pd clusters and nanowires: a comparison study using molecular dynamics simulation, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 134109, DOI:10.1103/PhysRevB.72.134109.
- B. S. de Bas, M. J. Ford and M. B. Cortie, Melting in small gold clusters: a density functional molecular dynamics study, J. Phys.: Condens. Matter, 2006, 18, 55–74, DOI:10.1088/0953-8984/18/1/004.
- F. Baletto and R. Ferrando, Structural properties of nanoclusters: energetic, thermodynamic, and kinetic effects, Rev. Mod. Phys., 2005, 77, 371, DOI:10.1103/RevModPhys.77.371.
- W. Schmidt, P. Bussian, M. Lindén, H. Amenitsch, P. Agren, M. Tiemann and F. Schüth, Accessing Ultrashort Reaction Times in Particle Formation with SAXS Experiments: ZnS Precipitation on the Microsecond Time Scale, J. Am. Chem. Soc., 2010, 132, 6822–6826, DOI:10.1021/ja101519z.
- H. Haberkorn, D. Franke, T. Frechen, W. Goesele and J. Rieger, Early stages of particle formation in precipitation reactions–quinacridone and boehmite as generic examples, J. Colloid Interface Sci., 2003, 259, 112–126, DOI:10.1016/S0021-9797(03)00024-9.
- B. Derjaguin and L. Landau, Theory of the stability of strongly charged lyophobic sols and of the adhesion of strongly charged particles in solutions of electrolytes, Prog. Surf. Sci., 1941, 43, 30–59, DOI:10.1016/0079-6816(93)90013-L.
- R. Becker and W. Döring, Kinetic treatment of germ formation in supersaturated vapour, Ann. Phys., 1935, 24, 719–752 CrossRef CAS PubMed.
- Z. Adamczyk and P. Weroński, Application of the DLVO theory for particle deposition problems, Adv. Colloid Interface Sci., 1999, 83, 137–226 CrossRef CAS.
- H. Müller, Zur allgemeinen Theorie der raschen Koagulation, Kolloidchem. Beih., 1928, 27, 223–250, DOI:10.1007/BF02558510.
- N. Fuchs, Theory of coagulation, Z. Phys. Chem., 1934, 171, 199–208 Search PubMed.
- R. Hogg, T. W. Healy and D. W. Fuerstenau, Mutual coagulation of colloidal dispersions, Trans. Faraday Soc., 1966, 62, 1638, 10.1039/tf9666201638.
- H. Reerink and J. T. G. Overbeek, The rate of coagulation as a measure of the stability of silver iodide sols, Discuss. Faraday Soc., 1954, 18, 74–84, 10.1039/DF9541800074.
- S. K. Friedlander and C. S. Wang, The self-preserving particle size distribution for coagulation by Brownian motion, J. Colloid Interface Sci., 1966, 22, 126–132, DOI:10.1016/0021-9797(66)90073-7.
- D. L. Swift and S. K. Friedlander, The coagulation of hydrosols by Brownian motion and laminar shear flow, J. Colloid Sci., 1964, 19, 621–647, DOI:10.1016/0095-8522(64)90085-6.
- M. Wuithschick, S. Witte, F. Kettemann, K. Rademann and J. Polte, Phys. Chem. Chem. Phys., 2015 10.1039/C5CP02219C.
- M. Wuithschick, A. Birnbaum, S. Witte, M. Sztucki, U. Vainio, N. Pinna, K. Rademann, F. Emmerling, R. Kraehnert and J. Polte, ACS Nano, 2015 DOI:10.1021/acsnano.5b01579.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ce01014d |
| This journal is © The Royal Society of Chemistry 2015 |