Open Access Article
Open Access ArticleStructure and dynamics of 3′-aminoacetophenone and 4′-aminoacetophenone from rotational spectroscopy†
Giovanna
Salvitti
 a,
Silvia
Sigismondi
a,
Silvia
Sigismondi
 a,
Sonia
Melandri
a,
Sonia
Melandri
 a,
Juan Carlos
López
a,
Juan Carlos
López
 b,
Susana
Blanco
b,
Susana
Blanco
 *b and
Assimo
Maris
*b and
Assimo
Maris
 *a
*a
aDepartment of Chemistry G. Ciamician, University of Bologna, I-40126 Bologna, Italy. E-mail: assimo.maris@unibo.it; Tel: +39 0512099502
bDepartment of Physical Chemistry and Inorganic Chemistry, IU-CINQUIMA, University of Valladolid, E-47011 Valladolid, Spain. E-mail: susana.blanco@uva.es
First published on 19th December 2023
Abstract
The rotational spectra of 4′-aminoacetophenone, and those of two conformers (Z and E arrangement of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and NH2 groups) of 3′-aminoacetophenone and their 13C and 15N isotopologues were investigated both in the microwave (2–8 GHz) and millimetre (59.6–74.4 GHz) frequency regions using chirped pulse Fourier transform and free-jet absorption techniques, respectively. The spectra consist of μa and μb type lines that show a hyperfine structure due to both the nuclear quadrupole coupling of the 14N nucleus and the methyl internal rotation. Relative intensity measurements show that the Z form in 3′-aminoacetophenone is favoured with respect to E and the measured energy difference upper limit is about 5.5(1) kJ mol−1. Barriers to methyl internal rotation are V3 = 7.04(2) and 6.530(6) kJ mol−1 for 3′(Z)- and 4′-aminoacetophenone, respectively. Flexible model analyses of the amino inversion motion based on ab initio potential energy paths, suggest that the corresponding vibrational splitting increases up to 78% from aniline to 3′(E)-, 3′(Z), and 4-aminoacetophenone. However, due to supersonic expansion cooling, no splitting related to amine inversion is observed.
O and NH2 groups) of 3′-aminoacetophenone and their 13C and 15N isotopologues were investigated both in the microwave (2–8 GHz) and millimetre (59.6–74.4 GHz) frequency regions using chirped pulse Fourier transform and free-jet absorption techniques, respectively. The spectra consist of μa and μb type lines that show a hyperfine structure due to both the nuclear quadrupole coupling of the 14N nucleus and the methyl internal rotation. Relative intensity measurements show that the Z form in 3′-aminoacetophenone is favoured with respect to E and the measured energy difference upper limit is about 5.5(1) kJ mol−1. Barriers to methyl internal rotation are V3 = 7.04(2) and 6.530(6) kJ mol−1 for 3′(Z)- and 4′-aminoacetophenone, respectively. Flexible model analyses of the amino inversion motion based on ab initio potential energy paths, suggest that the corresponding vibrational splitting increases up to 78% from aniline to 3′(E)-, 3′(Z), and 4-aminoacetophenone. However, due to supersonic expansion cooling, no splitting related to amine inversion is observed.
1 Introduction
Molecules are not rigid bodies but flexible objects characterized by internal motions leading to both vibrational modes and conformational complexity, which is related to the torsional degrees of freedom. The ensemble of the torsional angle's values define the so-called molecular conformational space and the energy of a molecule as a function of this ensemble is defined as the potential energy space (PES). Conformers correspond to the PES local minima, and their population at equilibrium is dependent on the temperature and quantified by the Boltzmann distribution. The interconversion between conformers is expected to occur along minimum energy paths, where their maxima are the transition states of the PES.PES can be investigated through theoretical methods: quantum mechanics is used for small systems whereas molecular dynamics techniques are introduced as the molecular size increases (i.e. macromolecules). To determine the molecular structure of the most stable species, diffraction, nuclear magnetic resonance, and rotational spectroscopy are the most used experimental techniques. However, obtaining information on the interconversion pathways is challenging. High-resolution spectroscopy can provide indirect information by measuring precise energy values for transitions between quantum-mechanical states. Actually, if two or more equivalent conformers exist and the interconversion barrier between them is small enough, the corresponding vibration states couple and the energy levels split due to the tunnelling effect. Using spectroscopic tools, it is possible to determine the size of this splitting and since it depends on the energy pathway, appropriate modelling can be used to characterize the interconversion energy barrier. Equivalent conformers can arise from the internal rotation of symmetric tops or planar frames, such as methyl and phenyl groups, respectively.1 They can also originate from the inversion of a tetrahedral torsion angle, like the umbrella motion of ammonia.2 Sometimes, interconversion occurs upon combined motions, as in the case of ring-puckering and pseudorotation in cyclic molecules.3
The gas phase constitutes the ideal medium to identify coupling effects because the torsional motions are not hindered by intermolecular interactions and high-resolution spectroscopy measurements are possible. In this respect, rotational and ro-vibrational spectroscopies, which also allow molecular structure characterization, have been proven to be valuable tools. For instance, from the free-jet millimetre-wave spectrum of methacrylamide,4 which is a small organic molecule with two C–C rotatable bonds (CH3–C(CH2)–CONH2), two conformers (one planar and the other with non-planar doubly degenerate skeletal arrangement) were detected and their energy difference was determined (4 kJ mol−1). Moreover, splittings due to the torsion around both the C–C bonds were observed and analyzed with appropriate Hamiltonian models5,6 achieving the barrier for the methyl internal rotation of both planar and non-planar conformers (10.2 and 7.4 kJ mol−1, respectively) as well as the interconversion barrier between the two equivalent non-planar forms (3.6 kJ mol−1). It is worth noting that in methacrylamide the amino group is part of an amide group and therefore its inversion motion is hindered because of resonance with the carbonyl group.
In addition to intramolecular effects, also intermolecular interactions can prevent the amine group inversion: when ammonia-like molecules form a non-covalent bond through their nitrogen lone pair the motion is blocked. This has been clearly observed in several molecular complexes, for instance, the hexafluorobenzene complexes with ammonia7 and trimethylamine,8 where the nitrogen lone pair points toward the σ-hole at the centre of the ring. Interestingly, in these species, another large amplitude motion is generated and observed: the free rotation between the monomers, which results in an overall symmetric-top geometry of the complex. Differently, in the absence of constraints, the amino group undergoes an inversion motion: the barrier and the splitting depending on the kind of groups bound to the nitrogen atom.
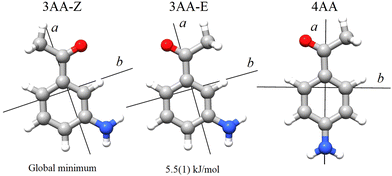
The term aminoacetophenone identifies a series of molecules constituted by a phenyl ring attached to an amine and acetyl side groups which are both characterized by large amplitude motions: the rotation inversion of the amine and the internal rotation of the whole acetyl group as well as its methyl group. In a previous paper, we studied 2′-aminoacetophenone (2AA) by chirped pulsed Fourier transform microwave spectroscopy and no effects due to large amplitude vibrations were observed.9 Indeed, our study shows that due to the proximity of the amino and acetyl groups, an NH–O intramolecular hydrogen bond is formed that stiffens the overall molecular structure. However, as the two substituents are spaced on the ring and can not directly interact a different behaviour is expected, mainly affected by resonance and inductive effects. For this reason, we decided to investigate the rotational spectrum of meta and para isomers: 3′-aminoacetophenone (3AA) and 4′-aminoacetophenone (4AA) respectively, shown in Fig. 1.
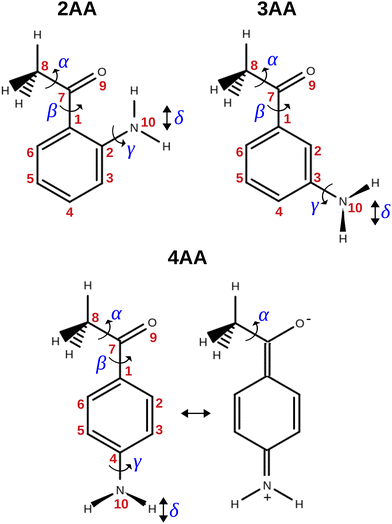 | ||
| Fig. 1 Structure, atoms’ numbering and torsional degrees of freedom of the isomers of aminoacetophenone and zwitterionic form of 4AA. | ||
2 Experimental methods
Commercial samples (Sigma Aldrich) of 3AA (C8H9NO, CAS no. 99-03-6, purity 97%, mp 367–371 K, bp 562–563 K) and 4AA (C8H9 NO, CAS no. 99-92-3, purity 99%, mp 376–380 K, bp 565–563 K) were used without further purification. The gas phase compounds were studied in two different spectral regions using supersonic expansion conditions, in which the molecules reach very low rotational temperatures and the most stable forms are trapped in their energy minima. The broadband spectra were recorded using a chirped-pulse Fourier transform microwave spectrometer (CP-FTMW) with a heatable nozzle in the 2–8 GHz frequency interval.10 The experimental conditions are briefly described. The supersonic jet was formed by the pulsed expansion of a Ne flow (2 bar) which drag the heated 3AA (408 K) or 4AA (403 K) vapour through a 0.8 mm nozzle with a repetition rate of 5 Hz. The sample was polarized by a 5 μs chirped pulse amplified to 20 W, then the subsequent transient molecular emission spanning 40 μs is recorded, and Fourier transformed to the frequency domain. For each gas pulse 8 polarization/detection frames were repeated. The accuracy of the frequency measurements is better than 10 kHz. The good signal-to-noise ratio obtained by the accumulation of 1.6 million spectra allowed us to measure the weak lines belonging to the 13C and 15N isotopologues observed in natural abundance. The spectrum in the 59.6–74.4 GHz frequency region was investigated using a Stark modulated free-jet absorption millimeter-wave (FJ-AMMW) spectrometer, the details of which have been described previously.11–13 The 3AA and 4AA samples were heated to 408 and 403 K, respectively while a stream of argon at a stagnation pressure of 10 kPa flowed over it. The mixture was then expanded to about Pb = 0.5 Pa through a 0.3 mm diameter pinhole nozzle. The rotational temperature of the molecules in the jet was estimated to be 5–10 K.13 The estimated uncertainty for the measurements is about 50 kHz and lines separated by more than 300 kHz are distinguishable.3 Computational methods
Geometry optimization and harmonic vibrational frequency calculations were run in order to characterize the minima on the PES. The potential energy functions of the internal motions were obtained through relaxed scans varying the involved coordinate on a regular grid. All calculations were performed with the Gaussian16® software package (G16, Rev. A.03‡). Density functional theory (DFT) was applied for preliminary calculations. Valence triple-ζ quality Karlsruhe polarized type basis set (def2-TZVP)14 was used in combination with Becke-three-parameters Lee–Yang–Parr hybrid density functional theory (B3LYP)15,16 corrected by the D3 version of Grimme's empirical dispersion with Becke–Johnson (BJ) damping.17,18Ab initio calculations were performed using valence triple-ζ quality Dunning correlation consistent polarized type basis set augmented with diffuse functions (aug-cc-pVTZ)19 in combination with Møller–Plesset second-order perturbation theory (MP2).204 Results
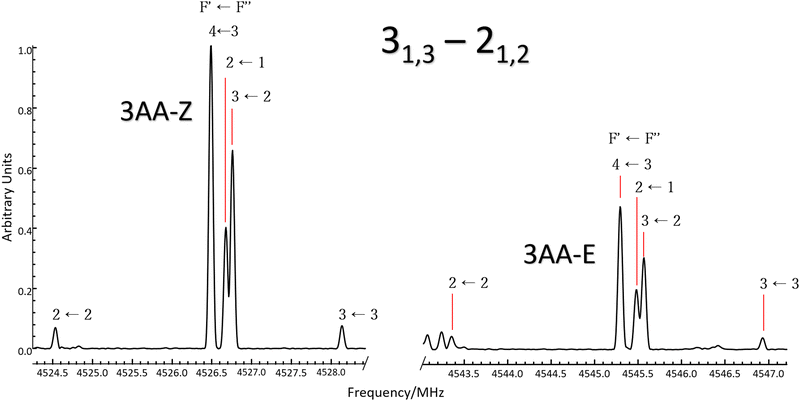
According to quantum-mechanical calculations, the structures of 4AA and 3AA are characterized by the acetyl symmetry plane being coplanar to the phenyl ring and the amine having a pyramidal arrangement, as shown in Fig. 2. Only one species is expected for 4AA, whereas for 3AA, depending on the orientation of the acetyl group, two conformers are possible, where the carbonyl and amine groups are on the same or opposite sides with respect to the C7C1C2C3 skeletal frame. Extending the meaning of zusammen and entgegen configurations, we will label these conformers as 3AA-Z and 3AA-E, respectively.The simulations based on the predicted spectroscopic parameters and energy values listed in Tables 1–3 allowed us to identify, for each of the three species, several μa and μb-type rotational transition lines. In agreement with the calculated relative energies and dipole moment component values, the spectrum of 3AA-Z is more intense than the spectrum of 3AA-E. All the rotational transition lines recorded by CP-FTMW in the 2–8 frequency region show a hyperfine structure (see for instance Fig. 3) due to the interaction of the 14N nuclear quadrupole with the electric field gradient at nitrogen. Also, it is worth noting that, despite the not negligible value expected for the electric dipole moment along the c direction (0.8–1 D), no corresponding transition lines were observed.
| Calc. | Exp. (Ir-representation) | |||
|---|---|---|---|---|
| B3LYP-D3(BJ)/def2-TZVP | MP2/aug-cc-pVTZ | SPFIT | XIAM | |
a
A, B and C are the rotational constants. DJ, DJK and DK are the quartic centrifugal distortion constants. 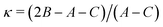 is the Ray parameter. Mgg (g = a, b or c) are the planar moments of inertia. μg (g = a, b or c) are the electric dipole moment components, Yes or No indicated if a-, b- or c-type transitions have been observed. χaa, χbb and χcc are the quadrupole coupling tensor diagonal elements for 14N atom. V3 is the internal rotation barrier for the methyl top. N is the number of quadrupole hyperfine components fitted. σ is the rms deviation of the fit. Ee is the electronic energy. E0 is the zero point energy.
b Standard errors in parentheses in units of the last digits.
c The value of is the Ray parameter. Mgg (g = a, b or c) are the planar moments of inertia. μg (g = a, b or c) are the electric dipole moment components, Yes or No indicated if a-, b- or c-type transitions have been observed. χaa, χbb and χcc are the quadrupole coupling tensor diagonal elements for 14N atom. V3 is the internal rotation barrier for the methyl top. N is the number of quadrupole hyperfine components fitted. σ is the rms deviation of the fit. Ee is the electronic energy. E0 is the zero point energy.
b Standard errors in parentheses in units of the last digits.
c The value of 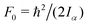 , where Iα is the inverse of the moment of inertia of the methyl top, and the angle between the methyl top axis and the a-axis δ were fixed to the ab initio values in the fit: F0 = 159.533 GHz, δ = 1.02965 rad. , where Iα is the inverse of the moment of inertia of the methyl top, and the angle between the methyl top axis and the a-axis δ were fixed to the ab initio values in the fit: F0 = 159.533 GHz, δ = 1.02965 rad.
|
||||
| A/MHza | 3673.126 | 3658.635 | 3651.3631(11)b | 3651.3557(7) |
| B/MHz | 794.961 | 794.400 | 790.8414(2) | 790.8412(2) |
| C/MHz | 656.416 | 655.698 | 653.3018(2) | 653.3013(2) |
| D J/kHz | 0.011 | 0.011 | 0.010(1) | 0.0120(5) |
| D JK/kHz | 0.005 | 0.005 | — | — |
| D K/kHz | 0.351 | 0.346 | 0.327(8) | 0.358(5) |
| χ aa/MHz | 2.437 | 2.315 | 2.424(7) | 2.425(4) |
| χ bb−χcc/MHz | 6.890 | 5.900 | 6.155(13) | 6.152(9) |
| V 3/cm−1 | 411 | 514 | — | 545.7(5)c |
| σ/MHz | — | — | 0.019 | 0.019 |
| N | — | — | 193 | 266 |
| κ | −0.908 | −0.908 | −0.908 | |
| M aa /uÅ2 | 634.02 | 634.40 | 637.10 | |
| M bb /uÅ2 | 135.88 | 136.35 | 136.47 | |
| M cc /uÅ2 | 1.70 | 1.78 | 1.94 | |
| μ a/D | 4.3720 | 3.58 | Ye | |
| μ b/D | −2.3984 | −2.32 | Yes | |
| μ c/D | 0.7817 | 0.93 | No | |
| E e/a.u. | −440.462662 | −439.405081 | — | |
| E 0/a.u. | −440.309057 | −439.250214 | — | |
| Exp. | 13C1 | 13C2 | 13C3 | 13C4/7 | 13C5 | 13C6 | 13C4/7 | 13C8 | 15N |
|---|---|---|---|---|---|---|---|---|---|
| A/MHz | 3651.05(46) | 3613.11(44) | 3614.05(41) | 3649.30(51) | 3612.43(41) | 3613.94(45) | 3653.21(52) | 3615.04(41) | 3651.09(57) |
| B/MHz | 790.328(1) | 790.852(1) | 788.241(1) | 785.178(1) | 788.355(1) | 790.859(2) | 785.200(1) | 780.231(1) | 775.790(2) |
| C/MHz | 652.954(2) | 652.079(2) | 650.341(1) | 649.446(2) | 650.363(1) | 652.112(2) | 649.429(2) | 644.894(1) | 642.997(2) |
| σ/MHz | 0.006 | 0.003 | 0.005 | 0.002 | 0.004 | 0.006 | 0.006 | 0.008 | 0.003 |
| N | 13 | 13 | 14 | 13 | 16 | 12 | 13 | 15 | 8 |
| Calc. | Exp. (Ir-representation) | |||
|---|---|---|---|---|
| B3LYP-D3(BJ)/def2-TZVP | MP2/aug-cc-pVTZ | SPFIT | XIAM | |
a Constants as defined in Table 1.
b Standard errors in parentheses in units of the last digits.
c The value of 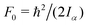 , where Iα is the inverse of the moment of inertia of the methyl top, and the angle between the methyl top axis and the a-axis δ were fixed to the ab initio values in the fit: F0 = 159.485 GHz, δ = 0.74466 rad. , where Iα is the inverse of the moment of inertia of the methyl top, and the angle between the methyl top axis and the a-axis δ were fixed to the ab initio values in the fit: F0 = 159.485 GHz, δ = 0.74466 rad.
|
||||
| A/MHza | 2624.8909 | 2610.4854 | 2608.2950(8)b | 2608.2906(4) |
| B/MHz | 945.4848 | 946.8023 | 941.2898(2) | 941.2916(1) |
| C/MHz | 698.4934 | 698.2762 | 695.4869(2) | 695.4865(1) |
| D J/kHz | 0.018 | 0.018 | — | 0.020(1) |
| D JK/kHz | −0.005 | -0.007 | — | — |
| D K/kHz | 0.226 | 0.229 | 0.228(5) | 0.201(3) |
| χ aa/MHz | 2.333 | 2.057 | 2.137(6) | 2.138(3) |
| χ bb−χcc/MHz | 7.084 | 6.236 | 6.42(1) | 6.423(5) |
| V 3/cm−1 | 494 | 535 | — | 594(1)c |
| σ/MHz | — | — | 0.014 | 0.012 |
| N | — | — | 187 | 214 |
| κ | −0.744 | −0.740 | −0.743 | |
| M aa/uÅ2 | 532.76 | 531.97 | 534.90 | |
| M bb/uÅ2 | 190.77 | 191.79 | 191.76 | |
| M cc/uÅ2 | 1.76 | 1.81 | 2.00 | |
| μ a/D | 2.4523 | −2.1083 | Yes | |
| μ b/D | 1.8427 | 1.9609 | Yes | |
| μ c/D | 0.8605 | −0.9341 | No | |
| E e/a.u. | −440.460357 | −439.404382 | — | |
| E 0/a.u. | −440.306262 | −439.248600 | — | |
| Exp. | 13C1 | 13C2 | 13C3 | 13C4 | 13C5 | 13C6 | 13C7 | 13C8 |
|---|---|---|---|---|---|---|---|---|
| A/MHz | 2608.162(1) | 2598.9568(8) | 2605.6951(8) | 2597.225(1) | 2562.3250(8) | 2579.098(1) | 2606.5724(8) | 2602.7929(9) |
| B/MHz | 940.8055(2) | 940.9482(2) | 935.6319(2) | 933.4727(2) | 939.1341(2) | 941.2031(2) | 934.6065(2) | 924.8912(2) |
| C/MHz | 695.2140(1) | 694.6367(1) | 692.20992(9) | 690.4305(1) | 691.0080(1) | 693.3461(1) | 691.7082(1) | 686.1184(1) |
| σ/MHz | 0.005 | 0.004 | 0.005 | 0.004 | 0.005 | 0.004 | 0.006 | 0.004 |
| N | 19 | 22 | 23 | 23 | 22 | 24 | 20 | 22 |
| B3LYP-D3(BJ)/def2-TZVP | MP2/aug-cc-pVTZ | Exp. (Ir-representation) | |
|---|---|---|---|
| a Constants as defined in Table 1. b Standard errors in parentheses in units of the last digits. | |||
| A/MHza | 2538.7929 | 2529.4959 | 2524.9246(7)b |
| B/MHz | 958.7647 | 959.3986 | 953.5975(3) |
| C/MHz | 699.3411 | 699.0664 | 696.0654(3) |
| D J/kHz | 0.018 | 0.018 | 0.015(4) |
| D JK/kHz | −0.001 | −0.002 | — |
| D K/kHz | 0.225 | 0.225 | 0.22(1) |
| χ aa/MHz | 2.350 | 2.073 | 2.125(7) |
| χ bb −χcc/MHz | 7.052 | 6.204 | 6.38(1) |
| σ/MHz | — | — | 0.013 |
| N | — | — | 174 |
| κ | −0.718 | −0.716 | −0.718 |
| μ a /D | 3.6642 | 3.3222 | Yes |
| μ b /D | −2.6636 | −2.4291 | Yes |
| μ c /D | 0.9192 | 0.9758 | No |
| M aa /μÅ2 | 525.350 | 524.95 | 527.93 |
| M bb /μÅ2 | 197.30 | 197.98 | 198.12 |
| M cc /μÅ2 | 1.76 | 1.81 | 2.04 |
| ΔEe/cm−1 | 245 | 235 | — |
| ΔE0/cm−1 | 244 | 224 | — |
| E e/a.u. | −440.459242 | −439.403311 | — |
| E 0/a.u. | −440.305148 | −439.248600 | — |
Ray's asymmetry parameter21 is κ ≃ −0.9 for 4AA and κ ≃ −0.7 for 3AA-Z and 3AA-E, classifying the observed species as asymmetric prolate rotors. As a first approach, the lines were assigned using the CALPGM program suite22 through direct diagonalization of the following Hamiltonian:
| Ĥ = ĤROT + ĤCD + ĤNQC | (1) |
4.1 Rotational spectrum of 4AA
The broadband spectrum of 4AA is shown in Fig. S1 of the ESI.† 22 intense R–μa-type transition lines with rotational quantum numbers from J′′ = 1 to J′′ = 5, 7 R–μb with rotational quantum numbers J′′ =0–7 and 14 Q–μb-type transition lines with rotational quantum numbers J′′ = 1–9 were assigned in the 2–8 GHz spectral region. The 32-22 and 42-32μa-type transition lines, and the 72,5-71,6μb-type transition line, are further split due to the methyl internal rotation effect (A/E components) and six μb-type transition lines show a splitting of about 0.05 MHz. Several Ka-asymmetry degenerate or almost degenerate R–μb-type transition lines with J′′ = 8–19 and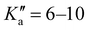 were assigned in the 59.6–74.4 GHz frequency region. Due to methyl internal rotation, each is a triplet with a central line and two weaker side peaks that have been assigned to E-type μc-forbidden lines.
were assigned in the 59.6–74.4 GHz frequency region. Due to methyl internal rotation, each is a triplet with a central line and two weaker side peaks that have been assigned to E-type μc-forbidden lines.
The overall set of detected lines was analysed using the combined axis method (CAM)23 implemented in the XIAM program,5 which fits a set of spectroscopic constants common to both the A and E states and directly supplies the methyl internal rotation barrier. The values of the reduced internal rotation constant (F0) and the angle between the internal rotation axis and the a principal inertial axis (∠ia) were fixed to those of the MP2/aug-cc-pVTZ calculated structure, whereas ∠ic was arbitrarily fixed to 0. A complete line list can be found in the ESI† (Table S1) while the determined rotational constants are given in Table 1.
4.2 Rotational spectrum of 3AA-Z
The broadband spectrum of 3AA is shown in Fig. S2 of the ESI.† 18 intense R–μa-type transition lines with rotational quantum numbers from lower J′′ = 1 to J′′ = 4, 10 R–μb type transition lines with rotational quantum numbers from J′′ = 0 to J′′ = 5 and 17 Q–μb-type transition lines with rotational quantum numbers from J′′ = 2 to J′′ = 8 were assigned in the 2–8 GHz spectral region. 5 transition lines are further split due to the methyl internal rotation effect and 9 transition lines show an additional splitting of about 0.05 MHz. Additional 9 R–μb-type transition lines with J′′ = 11–16 and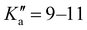 were detected in the 59.6–74.4 GHz frequency region. As for 4AA, they are characterised by methyl internal rotation hyperfine structure. The overall set of lines was fitted with the XIAM program, determining the spectroscopic constants given in Table 2. A complete line list can be found in the ESI† (Table S2).
were detected in the 59.6–74.4 GHz frequency region. As for 4AA, they are characterised by methyl internal rotation hyperfine structure. The overall set of lines was fitted with the XIAM program, determining the spectroscopic constants given in Table 2. A complete line list can be found in the ESI† (Table S2).
4.3 Rotational spectrum of 3AA-E
17 R–μa-type transition lines with rotational quantum numbers from J′′ = 1 to J′′ = 4, 10 R–μb with rotational quantum numbers from J′′ = 0 to J′′ = 5 and 20 Q–μb-type transition lines with rotational quantum numbers from lower J = 2 to J = 7 were assigned. Few weak R–μb-type transition lines with J′′= 13–17 and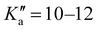 were assigned in the 59.6–74.4 GHz frequency region. A complete line list can be found in the ESI† (Table S3) while the determined rotational constants are given in Table 3.
were assigned in the 59.6–74.4 GHz frequency region. A complete line list can be found in the ESI† (Table S3) while the determined rotational constants are given in Table 3.
4.4 Isotopologues
Thanks to the good signal-to-noise ratio of CP-FTMW spectrometer, some transition lines of the 13C isotopologues of 4AA (μa-type) and 3AA-Z (μa- and μb-type) were observed in natural abundance. Their rotational constants were determined using the CALPGM program suite,22 fixing the value of nuclear coupling constants to those determined for the parent species. Unsplitted 15N-isotoplogue lines were also observed and assigned for 4AA. A complete line list can be found in the ESI† (Tables S4–S20) while the determined rotational constants are given in the bottom part of Tables 1 and 2, respectively for 4AA and 3AA-Z.5 Discussion
5.1 Molecular structure
First inspection of the rotational constants, shows that there is a reasonable agreement between the theoretical values, which refer to the equilibrium geometry (re) in the PES, and the experimental ones, which describe the molecule in its vibrational ground state (r0). The theoretical values of the B and C rotational constants calculated at the B3LYP-D3(BJ)/def2-TZVP and MP2/aug-cc-pVTZ levels of calculations differ by about 1 MHz or less, whereas the values for A differ by about 10–15 MHz.The ab initio values are closer to the experimental data than the DFT ones. Because of the vibration motions, the observed rotational constants are smaller than those computed in the harmonic approximation, the difference being about 1–9‰ with respect to the ab initio results. This effect can perhaps be better appreciated by comparing the planar moments of inertia (Tables 1 and 2), which are linear combinations of the moment of inertia that measure the distribution of the atoms’ masses (mi) along the principal inertial axes (a, b and c), i.e.:
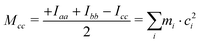 | (2) |
As regards the value of Mcc, it provides rough information on the out-of-plane atoms, even if the ab plane does not coincide exactly with that of the phenyl ring. The Mcc value is 1.79 uÅ2 for acetophenone24 due to the methyl group contribution and 0.20 uÅ2 for aniline25 due to that of the amine group. The sum of these values (1.99 uÅ2) should give us a rough estimation for aminoacetophenones. Consistently, the experimental values are 2.04, 2.00 and 1.94 uÅ2 for 3AA-E, 3AA-Z and 4AA, respectively. The lower value of 4AA could depend on the mesomeric effect for which a zwitterionic resonant planar structure exists as depicted in Fig. 1. However, for 2AA a smaller value similar to that of acetophenone was determined (1.80 uÅ2) and ascribed to a planar arrangement of the amine group constrained by an intramolecular hydrogen bond.9
Experimental information on the atoms’ position was achieved using Kraitchmans's method based on the assumption that different isotopologues share the same geometry.26 The resulting substitution coordinates (rs), the sign of which cannot be determined, are listed and compared to the computed equilibrium ones (re) in Tables 4 and 5 for 4AA and 3AA-Z, respectively. Usually, the knowledge of the absolute value of the substitution coordinates allows for a straightforward assignment of the coordinates themselves to the appropriate atom. This was shown for example for cis-verbenol whose ten carbon atoms positions are clearly distinguishable.27 However, despite the absence of any element of symmetry, it can happen that, apart from the sign, two atoms have similar coordinates, making the assignment difficult. In 4AA, we find three pairs of this kind: C2/C6, C3/C5 and C4/C7. Comparison with theoretical data allows for a reliable assignment of C2/C6 and C3/C5, whereas concerning C4 and C7 the assignment remains uncertain.
| |rs| | r e | |rs| | r e | ||
|---|---|---|---|---|---|
| C1 | C1 | C8 | C8 | ||
| a | 0.640(7) | −0.6657 | a | 2.951(1) | −2.9279 |
| b | 0.06(7) | 0.0208 | b | 1.193(4) | −1.2030 |
| c | 0.09(5) | 0.0006 | c | i·0.05(9) | −0.0055 |
| C2 | C2 | C6 | C6 | ||
| a | i·0.11(4) | 0.0678 | a | i·0.13(3) | 0.0297 |
| b | 1.212(4) | 1.2128 | b | 1.198(4) | −1.1933 |
| c | 0.05(8) | −0.0014 | c | 0.06(8) | −0.0033 |
| C3 | C3 | C5 | C5 | ||
| a | 1.451(3) | 1.4527 | a | 1.419(3) | 1.4188 |
| b | 1.197(4) | 1.1928 | b | 1.224(4) | −1.2159 |
| c | 0.09(5) | −0.0005 | c | 0.08(6) | 0.0052 |
| C4 | C4 | C7 | C7 | ||
| a | 2.140(1) | 2.1504 | a | 2.158(2) | −2.1501 |
| b | 0.18(3) | −0.0233 | b | i·0.16(3) | 0.0913 |
| c | 0.22(2) | 0.0065 | c | i·0.21(2) | 0.0006 |
| N | N | ||||
| a | 3.539(2) | 3.5405 | |||
| b | 0.07(8) | −0.0418 | |||
| c | 0.08(8) | −0.0534 | |||
| |rs| | r e | |rs| | r e | ||
|---|---|---|---|---|---|
| C1 | C1 | C8 | C8 | ||
| a | 0.526(3) | 0.5531 | a | 3.0899(5) | 3.0728 |
| b | 0.010(2) | 0.1201 | b | 0.648(2) | 0.6552 |
| c | 0.02(7) | −0.0007 | c | 0.06(3) | 0.0204 |
| C2 | C2 | C6 | C6 | ||
| a | 0.441(3) | −0.4670 | a | 0.223(7) | 0.2372 |
| b | 0.836(2) | −0.8338 | b | 1.485(1) | 1.4832 |
| c | 0.03(5) | 0.0010 | c | i·0.02(8) | −0.0052 |
| C3 | C3 | C5 | C5 | ||
| a | 1.8054(8) | −1.8077 | a | 1.107(1) | −1.1005 |
| b | 0.443(3) | −0.4480 | b | 1.8722(8) | 1.8720 |
| c | i·0.0(4) | −0.0030 | c | i·0.03(6) | −0.0093 |
| C4 | C4 | C7 | C7 | ||
| a | 2.1226(7) | −2.1147 | a | 1.9638(8) | 1.9634 |
| b | 0.917(2) | 0.9202 | b | 0.362(4) | −0.3670 |
| c | 0.0(1) | −0.0062 | c | i·0.03(4) | −0.0014 |
5.2 Relative intensity of 3AA conformers
Conformer 3AA-Z is calculated to be more stable than 3AA-E by 235 cm−1 at the MP2/aug-cc-pVTZ level and the inclusion of zero-point vibrational contribution slightly decreases this value to 224 cm−1. Evaluation of the free energy values in the harmonic and rigid rotor approximations further lowers the difference between conformers to 201 cm−1.It is worth noting that similar values are estimated at the B3LYP-GD3(BJ)/def2-TZVP level of calculation (245, 244 and 224 cm−1, respectively). At the thermal equilibrium, in the experimental pre-expansion conditions (T = 408 K), the ab initio free energy difference corresponds to a relative abundance NZ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NE= 1
NE= 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5. According to the theoretical electric dipole moment components, the intensity ratio of the rotational transition lines can be estimated as IaZ
0.5. According to the theoretical electric dipole moment components, the intensity ratio of the rotational transition lines can be estimated as IaZ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) IaE = 1
IaE = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.2 and IbZ
1.2 and IbZ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) IbE = 1
IbE = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.8. Actually, if we compare the same rotational transition lines (see for instance Fig. 3), those of 3AA-Z are always more intense than the 3AA-E ones: IaZ
0.8. Actually, if we compare the same rotational transition lines (see for instance Fig. 3), those of 3AA-Z are always more intense than the 3AA-E ones: IaZ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) IaE = 1
IaE = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5 and IbZ
0.5 and IbZ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) IbE = 1
IbE = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.3, confirming that 3AA-Z is the most stable conformer. The reason behind this preferred arrangement is uncertain, but it is worth noting that the electric dipole moment is less in the most stable species (μZ = 3.0 and μE = 4.3 D).
0.3, confirming that 3AA-Z is the most stable conformer. The reason behind this preferred arrangement is uncertain, but it is worth noting that the electric dipole moment is less in the most stable species (μZ = 3.0 and μE = 4.3 D).
However, the experimental evidence and theoretical landscape do not match perfectly, meaning that either the calculated energy difference is underestimated or that a partial conformational relaxation occurs during the supersonic expansion. In the hypothesis that no relaxation takes place, the relative energy of 3AA-E derived from the relative intensity measurements is about 460(10) cm−1. Interestingly, an X-ray diffraction study identified 3AA-Z as a ligand of the apo form cyclophilin-D isomerase, see https://doi.org/10.2210/pdb3R59/pdb.28
5.3 Nuclear quadrupole coupling interaction
The 14N nuclear quadrupole coupling constants of the aminoacetophenone isomers are compared to those of aniline in Table 6. The values of 4AA and aniline are similar, due to the analogous orientation of the principal axis system with respect to the amine group. As regards 3AA, the rotation of the ab inertial plane is reflected by the change on the χaa and χbb values, whereas the χcc values, which refer to the direction approximately perpendicular to the ring are only slightly modified.| Aniline25 | 4AA | 3AA-Z | 3AA-E | 2AA | |
|---|---|---|---|---|---|
| χ aa/MHz | 2.34(6) | 2.424(7) | 2.137(6) | 2.125(7) | 1.193(7) |
| χ bb/MHz | 1.86(6) | 1.866(2) | 2.143(9) | 2.126(5) | 2.608(4) |
| χ cc/MHz | −4.20(6) | −4.289(2) | −4.279(9) | −4.251(5) | −3.801(4) |
5.4 Internal molecular dynamics
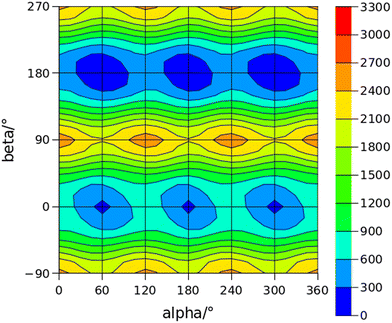
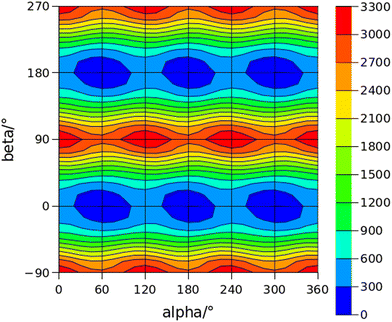
The conformational space of aminoacetophenones is described by the four torsion coordinates shown in Fig. 1 and labelled α, β, γ and δ. The dihedral angles α = HC8C7C1 and β = C8C7C1C2 concern the internal rotation of the methyl and the acetyl groups, respectively. The corresponding DFT 2D-PESs are shown in Fig. 5 and 6 for the two isomers. As regards the methyl internal rotation, a threefold path is found where barriers are approximately 494, 464 and 411 cm−1 for 3AA-Z, 3AA-E and 4AA, respectively. Further ab initio investigations raise these values by about 100 cm−1, in particular: 535, 556 and 514 cm−1, respectively. For a threefold path, splitting of the energy levels into a non-degenerate A-level and a doubly degenerate E-level is expected. Accordingly, several split lines were detected, allowing us to determine the methyl internal rotation barriers of both 3AA-Z (V3 = 595(1) cm−1) and 4AA (V3 = 545.7(5) cm−1). Comparison with the analogous compound acetophenone (V3 = 7.50(3) kJ mol−1 corresponding to 627(3) cm−124) suggests that insertion of an amine group in the phenyl ring lowers the methyl internal rotation barrier and that substitution in para is more effective than substitution in meta. The A/E energy difference has been estimated to be 37 and 58 MHz for 3AA-Z and 4AA, respectively.The dihedral angle β = C8C7C1C2, concerns the rotation of the acetyl group. Rotation around the C1–C7 bond leads to conformers Z (β = 180°) and E (β = 0°) separated by a 2100 cm−1 barrier for 3AA (Fig. 5) and to two equivalent species separated by a 2800 cm−1 barrier for 4AA (Fig. 6). The fundamental band for this torsion in acetophenone has been observed at 49.5 cm−1 and a twofold potential model barrier provided a barrier of 1103 cm−1.29 A subsequent microwave spectroscopy study confirmed that the acetyl group is coplanar to the phenyl ring.30
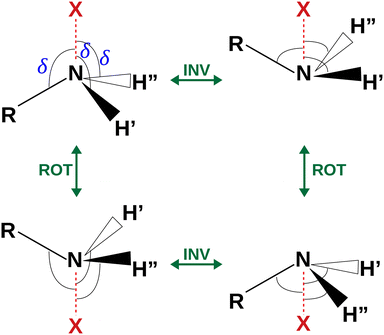 | ||
| Fig. 4 Sketch of the four equivalent minima arising from the rotoinversion of the amine group. δ is the angle used to describe the inversion of the amine group. | ||
The coordinates γ = XNCC and δ = ∠XNC = ∠XNH describe the amine group's rotation and inversion, respectively. To define them, we introduced a point X (see Fig. 1) whose position is determined by the constraint that the N–X direction makes equal angles (δ) with the three amine bonds. In the case of C3v molecular symmetry (i.e. ammonia), the N–X direction is that of the C3 symmetry axis. According to this definition, δ can be used as the inversion coordinate. For δ = (π/2) the amino group is planar whereas for δ = (π/2 ± x) two equivalent non-planar geometries are generated. x is called the pyramidalization angle. It is worth noting that two equivalent non-planar geometries are also generated upon rotation of the amino group around the N–C bond. Hence, four equivalent conformers exist, corresponding to the position of the amine hydrogen atoms above and below the phenyl plane. However, a comparison of the ab initio potential energy paths for the rotation (Fig. 7) and inversion (Fig. 8) motions, shows that the energy barrier for the amine rotation (about 2000 cm−1) is larger than that of amine inversion (about 400 cm−1). The estimated inversion barriers are similar to those of other amine compounds for which values spanning the 200–2000 cm−1 range were determined by PES modelling based on the experimental observations (see Table 7). For most of them a double minimum model has been used but for methylamine31 and aminocyclobutane32 a two-dimensional model taking into account also the amine rotation had to be used to explain all the observed spectral features. Moreover, it is worth noting that depending on the used model, different values can be determined. For instance, the barrier for aniline was estimated to be 525 cm−1 by Larsen et al.33 and 392 cm−1 by Fehrensen et al.,34 respectively. Interestingly, the ab initio value (472 cm−1) lies in between the experimental findings, indicating that the calculations are quite reliable. For this reason, we decided to apply the one-dimensional flexible model of Meyer35 to the theoretical parameters in order to estimate the inversion splitting in 3AA and 4AA, using aniline as a benchmark.
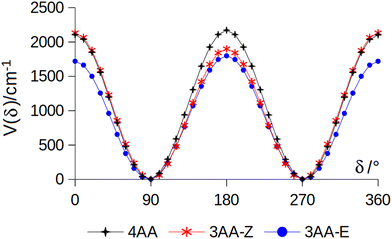 | ||
| Fig. 7 Potential energy function for the amine internal rotation calculated at the MP2/aug-cc-pVTZ level using a sample step of 10°. | ||
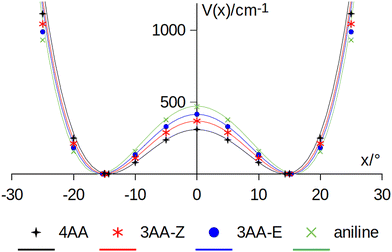 | ||
| Fig. 8 Amine inversion potential energy function. Points are calculated at the MP2/aug-cc-pVTZ level using a sample step of 5°. Lines correspond to the double minimum function described in eqn (3) using the theoretical barriers and pyramidalization angles (x) listed in Table 8. | ||
5.5 Flexible model
A double minimum non-periodic function based on two parameters was used to describe the amine inversion potential path: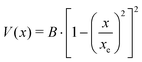 | (3) |
| B/cm−1 | x e/° | ΔE/cm−1 | |
|---|---|---|---|
| Aniline | 472 | 15.8 | 42 |
| 3AA-E | 415 | 15.3 | 51 |
| 3AA-Z | 368 | 14.9 | 61 |
| 4AA | 309 | 14.3 | 75 |
A numerical simulation was performed by exploring a 100° range with 80 grid mesh points, obtaining the vibrational splitting (ΔE) also given in Table 8. The model satisfactorily reproduces the ground state splitting of aniline, the experimental value being 40.9 cm−1 and the modelled one 41.6 cm−1. Ab initio calculations suggest that the inversion barrier and the pyramidalization angle decrease in going from aniline to 3AA-E, 3AA-Z and 4AA. Notably, this kind of planarization of the amine group is in agreement with the trend of the observed planar moment of inertia along the c-axis: Mcc (3AA-E) = 2.04, Mcc (3AA-Z) = 2.00 and Mcc (4AA) = 1.94 uÅ2. Accordingly, the predicted splittings increase up to 75 cm−1 for 4AA.
Considering that the split eigenstates are symmetric and antisymmetric with respect to the inversion coordinate and that the μc electric dipole moment component changes its sign along the same inversion coordinate, then the selection rules imply that μa- and μb-intrastate and μc-interstate type transitions lines should be observed. According to the flexible model results, interstate transitions will lie in the far-infrared spectral region and only intrastate transitions will take place in the microwave range. Actually, in the case of aniline, two series of lines separated by a few MHz have been observed and assigned to the symmetric and antisymmetric states.36 Differently, in the spectra of 3AA and 4AA we only observed a small splitting in some of the μb-type transition lines, which is not consistent with the expected trend. Therefore, we suppose that molecular cooling takes place during the supersonic expansion, depopulating the antisymmetric state. To support this interpretation, it is crucial to mention that splitting is usually observed in conventional microwave spectroscopy performed in a static cell (see compounds listed in Table 7), while there was no splitting observed in other substituted anilines that underwent examination in supersonic jets, including 3-aminophenol37 and 4-aminobenzonitrile.38
6 Conclusions
The rotational spectra of 4AA, two conformers of 3AA and 17 isotopologues were observed and assigned for the first time under supersonic expansion conditions. The rotational, quartic centrifugal distortion and 14N nuclear quadrupole coupling constants were determined, opening future investigations in higher frequency regions as well as molecular detection in the astrophysical and analytical fields. Even though the acetyl and amine groups cannot directly interact, both quantum mechanical calculations and relative intensity measurements clearly show that the preferred arrangement in 3AA is the one with the smaller electric dipole moment. This conformation is the one with the carbonyl and amine groups on the same side with respect to the phenyl ring.Ab initio calculations suggest that the amine inversion barrier of the amino group decreases upon the substitution of a hydrogen atom with an acetyl group and that substitution in para position is more effective than substitution in meta, probably due to the mesomeric effect. The results also show that the orientation of the acetyl group in 3AA plays a role since the barrier is lower for 3AA-E with respect to the one in 3AA-Z. Furthermore, theoretical and experimental evidence shows that amine substitution affects the methyl internal rotation motion, lowering the hindering barrier. Again the substitution in para position is more effective.
Author contributions
Conceptualization: SB and AM. Data curation: GS, SS, SM, JCL, SB and AM. Formal analysis: GS, SS, SM, JCL, SB and AM. Funding acquisition: SB and AM. Investigation: GS, SS, SM, JCL, SB and AM. Resources: SB and AM. Supervision: SB and AM. Validation: GS, SS, SM, JCL, SB and AM. Visualization: GS, AM. Writing – original draft preparation: AM. Writing – review and editing: GS, SS, SM, JCL, SB and AM.Conflicts of interest
There are no conflicts to declare.Acknowledgements
JCL and SB acknowledge the Ministerio de Ciencia e Innovación (Grant PID2021-125207NB-C33), and the Junta de Castilla y León (Grant INFRARED-FEDER IR2020-1-UVa02). AM acknowledges the University of Bologna (Ricerca Fondamentale Orientata) for support, the CINECA award under the ISCRA initiative for the availability of high-performance computing resources, and the author community of REVTeX.Notes and references
- D. R. Herschbach, J. Chem. Phys., 1959, 31, 91–108 CrossRef CAS.
- J. D. Swalen and J. A. Ibers, J. Chem. Phys., 1962, 36, 1914–1918 CrossRef.
- R. Meyer, J. C. López, J. L. Alonso, S. Melandri, P. G. Favero and W. Caminati, J. Chem. Phys., 1999, 111, 7871–7880 CrossRef CAS.
- A. Maris, S. Melandri, L. Evangelisti, A. Vigorito, S. Sigismondi, C. Calabrese and I. Usabiaga, J. Mol. Struct., 2022, 1248, 131391 CrossRef CAS.
- H. Hartwig and H. Dreizler, Z. Naturforsch., 1996, 51A, 923–932 CrossRef.
- L. Paoloni and A. Maris, J. Phys. Chem. A, 2021, 125, 4098–4113 CrossRef CAS PubMed.
- W. Li, I. Usabiaga, C. Calabrese, L. Evangelisti, A. Maris, L. B. Favero and S. Melandri, Phys. Chem. Chem. Phys., 2021, 23, 9121–9129 RSC.
- D. Lv, W. Li, L. Evangelisti, I. Usabiaga, C. Calabrese, A. Maris, S. Melandri, G. Wang and M. Zhou, J. Phys. Chem. Lett., 2023, 14, 5335–5342 CrossRef CAS PubMed.
- G. Salvitti, S. Blanco, J. C. Lòpez, S. Melandri, L. Evangelisti and A. Maris, J. Chem. Phys., 2022, 157, 144303 CrossRef CAS PubMed.
- P. Pinacho, S. Blanco and J. C. López, Phys. Chem. Chem. Phys., 2019, 21, 2177–2185 RSC.
- C. Calabrese, A. Maris, L. Evangelisti, L. Favero, S. Melandri and W. Caminati, J. Phys. Chem. A, 2013, 1117, 13712–13718 CrossRef PubMed.
- C. Calabrese, A. Vigorito, A. Maris, S. Mariotti, P. Fathi, W. D. Geppert and S. Melandri, J. Phys. Chem. A, 2015, 119, 11674–11682 CrossRef CAS PubMed.
- A. Vigorito, C. Calabrese, S. Melandri, A. Caracciolo, S. Mariotti, A. Giannetti, M. Massardi and A. Maris, A&A, 2018, 619, A140 Search PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456 CrossRef CAS PubMed.
- T. Dunning Jr., J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- C. Møller and M. Plesset, Phys. Rev., 1934, 46, 618–622 CrossRef.
- B. S. Ray, Z. Phys., 1932, 78, 74–91 CrossRef CAS.
- H. M. Pickett, J. Mol. Spectrosc., 1991, 148, 371–377 CrossRef CAS.
- R. Woods, J. Mol. Spectrosc., 1966, 21, 4–24 CrossRef CAS.
- J. Lei, J. Zhang, G. Feng, J.-U. Grabow and Q. Gou, Phys. Chem. Chem. Phys., 2019, 21, 22888–22894 RSC.
- A. Hatta, M. Suzuki and K. Kozima, Bull. Chem. Soc. Jpn., 1973, 46, 2321–2323 CrossRef CAS.
- J. Kraitchman, Am. J. Phys., 1953, 21, 17–25 CrossRef CAS.
- S. Blanco, J. C. López and A. Maris, Phys. Chem. Chem. Phys., 2020, 22, 5729–5734 RSC.
- A. Ahmed-Belkacem, L. Colliandre, N. Ahnou, Q. Nevers, M. Gelin, Y. Bessin, R. Brillet, O. Cala, O. Douguet, W. Bourguet, I. Krimm, J.-M. Pawlotsky and J.-F. Guichou, Nat. Commun., 2016, 7, 1326–1328 Search PubMed.
- J. Durig, H. Bist, K. Furic, J. Qiu and T. Little, J. Mol. Struct., 1985, 129, 45–56 CrossRef CAS.
- M. Onda, Y. Kohama, K. Suga and I. Yamaguchi, J. Mol. Struct., 1998, 442, 19–22 CrossRef CAS.
- M. Kreglewski, J. Mol. Spectrosc., 1989, 133, 10–21 CrossRef CAS.
- L. B. Favero, B. Velino, A. Maris and W. Caminati, J. Mol. Struct., 2002, 612, 357–367 CrossRef CAS.
- N. Larsen, E. Hansen and F. Nicolaisen, Chem. Phys. Lett., 1976, 43, 584–586 CrossRef CAS.
- B. Fehrensen, D. Luckhaus and M. Quack, Z. Phys. Chem., 1999, 209, 1–19 CrossRef CAS.
- R. Meyer, J. Mol. Spectrosc., 1979, 76, 266–300 CrossRef CAS.
- E. Ye, K. Chandrasekaran and R. P. Bettens, J. Mol. Spectrosc., 2005, 229, 54–56 CrossRef CAS.
- F. Filsinger, K. Wohlfart, M. Schnell, J.-U. Grabow and J. Küpper, Phys. Chem. Chem. Phys., 2008, 10, 666–673 RSC.
- T. Betz, S. Zinn, J. B. Graneek and M. Schnell, J. Phys. Chem. A, 2014, 118, 5164–5169 CrossRef CAS PubMed.
- J. E. Wollrab and V. W. Laurie, J. Chem. Phys., 1968, 48, 5058–5066 CrossRef CAS.
- H. Vinh Lam Nguyen and W. Stahl, J. Chem. Phys., 2011, 135, 024310 CrossRef PubMed.
- L. B. Favero, P. Moreschini, W. Caminati, M. Becucci, I. López-Tocón and G. Pietraperzia, Phys. Chem. Chem. Phys., 2000, 2, 1351–1355 RSC.
- R. Kydd, Spectrochim. Acta, Part A, 1979, 35, 409–413 CrossRef.
- R. Kydd and A. Dunham, J. Mol. Struct., 1983, 98, 39–47 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: List of the observed rotational transition lines and optimized geometries. See DOI: https://doi.org/10.1039/d3cp05608b |
| ‡ Gaussian is a registered trademark of Gaussian, Inc. 340 Quinnipiac St. Bldg. 40 Wallingford, CT 06492 USA. |
| This journal is © the Owner Societies 2024 |