Interactions and reactivity in crystalline intermediates of mechanochemical cyclorhodation reactions

Abstract

There is experimental evidence that solid mixtures of the rhodium dimer [Cp*RhCl₂]₂ and benzo[h] quinoline (BHQ) produce two different polymorphic molecular cocrystals called 4α and 4β under ball milling conditions. The addition of NaOAc to the mixture leads to the formation of the rhodacycle [Cp*Rh-(BHQ)Cl], where the central Rh atom retains its tetracoordinate character. Isolate 4β reacts with NaOAc leading to the same rhodacycle while isolate 4α does not under the same conditions. We show that the puzzling difference in reactivity between the two cocrystals can be traced back to fundamental aspects of the intermolecular interactions between the BHQ and [Cp*RhCl₂]₂ fragments in the crystalline environment. To support this view, we report a number of descriptors of the nature and strength of chemical bonds and intermolecular interactions in the extended solids and in a cluster model. We calculate formal quantum mechanical descriptors based on electronic structure, electron density, and binding and interaction energies including an energy decomposition analysis. Without exception, all descriptors point to 4β being a transient structure higher in energy than 4α with larger local and global electrophilic and nucleophilic powers, a more favorable spatial and energetic distribution of the frontier orbitals, and a more fragile crystal structure.

---

1 Introduction

Among the major sources of external energy under which chemical reactions take place heat (thermochemistry), electromagnetic radiation (photochemistry), mechanical waves (sonochemistry), electrochemistry and mechanical forces (mechanochemistry) are prominent. Mechanochemistry, in particular, is a current intensive area of research with several highly desirable consequences:^1–4 it offers the possibility of environmentally safer and cleaner reactions with minimal energy consumption,⁵ often with the capability of yielding final reaction products whose traditional synthesis are extremely hard.^6–10

Most chemists are familiar with the idea that reaction mechanisms describing the bond breaking and formation in thermal and radiation driven reactions are quite different, an observation that readily extends to the other types of ways to induce chemical reactions listed above. Indeed, understanding the mechanisms of mechanochemical reactions is an important theoretical problem currently under intensive research with several methods and strategies that were summarized elsewhere,^11–17 however, what seems clear, as specifically stated by kulik¹⁸ in a recent review of methods used to model mechanochemistry from first principles is that “Through the use of force as stimulus, it is now established that the expected thermal or photochemical response of a molecule is different from what occurs in conditions under force”.

Popular alternatives to understand how chemical reactions occur under external forces include exploration of potential energy surfaces via ab initio methods by pulling or compressing molecular systems,^19–24 that is, by analyzing the change in the molecular energy as a function of an arbitrary coordinate describing the molecular distortion and then finding the point of minimum force required to break specific bonds, this may be achieved in a number of different ways, for example, by calculating relaxed scans of the geometries changing the distances between two specific atoms or groups. Other approaches available are steered molecular dynamics^25,26 and writing the total force on the molecular bonds as F^tot = F^ab initio + F^ext and recalculating force-modified potential energy surfaces (FMPES).²⁷ In all of the previous cases, conceptual DFT has been adapted to study the changes in reactivity along the reaction paths.²⁸

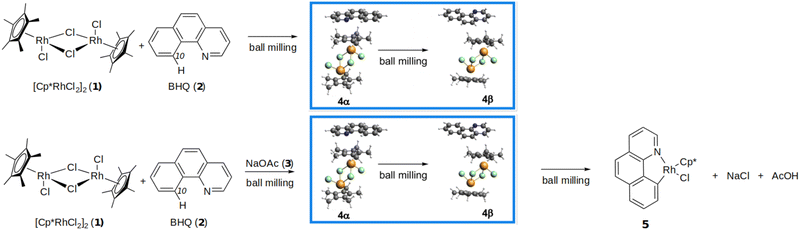
All those methods have their own shortcomings and virtues which have been judiciously analyzed,^{19,27,29–36} however, we call the attention to the fact that most of them are applied to single molecules considering continuous variations of the properties of chemical bonds as a function of atom separation (or, more precisely, a continuous reaction path), which is a risky proposition if the external forces are very large and if the systems under consideration are extended solids. Notwithstanding, all those methods point to a couple of important facts: the thermal energy required to break chemical bonds is reduced when subjected to external forces and, if the hypothetical mechanism under these external forces was the same as in their absence, activation energies are lowered and reaction rates are increased. In this work, we take an alternative, complementary strategy: we calculate formal descriptors of chemical reactivity provided by a number of quantum mechanical methods to rationalize the sequential detection of two cocrystals labeled 4α and 4β with a marked higher reactivity of the 4β form on the mechanochemical reactions undergone by the cocrystals conformers [Cp*RhCl₂]₂ (Rc, 1) with benzo[h] quinoline (BHQ, 2), as shown in Fig. 1. It is worth noticing that as a general case, cocrystals are separated by small energy differences, nonetheless, are able to sensibly influence solid state reactivity.^37–39 The present work is an attempt to understand this preferential reactivity using the formalism of quantum mechanics.

Fig. 1 Ball milling of the rhodium dimer 1 and the benzo[h] quinoline 2 (top) leads to the formation of the 4α and 4β cocrystals. If NaOAc 3 is added to the mixture (bottom) the ball milling instigates the production of the rhodacycle 5.

2 Computational methods

Hernández et al.⁴⁰ reported that in situ analysis of the ball milling of mixtures of 1 and 2 yielded the 4α cocrystal after 3 minutes and the 4β cocrystal after 18 minutes, then the two phases coexisted for about 20 minutes gradually exhausting 4α so that after about 40 minutes only 4β remained. (For in situ monitoring of mechanochemical reactions, see ref. 41–43). In a previous experiment Ardila-Fierro et al.³⁷ with ex situ analysis showed that 4α first and then 4β were transiently obtained in their way to finally yielding the rhodacycle 5 when solid NaOAc was added to the mixture from the onset (see Fig. 1 and the corresponding papers for the experimental conditions). Notice that in addition to the rupture of Rh–Cl bonds from the rhodium dimer 1, the production of 5 requires the activation and rupture of the C_10(sp²)–H bond and the formation of one C–Rh with the same carbon atom. Additionally, there is the formation of one N–Rh bond with no change in the oxidation state of Rh. Importantly, similar crystalline intermediates were detected before the C–H activation step in mechanochemical cyclorhodations of substrates different from BHQ such as phenylpyridine and 2-phenylquinoline.³⁷

In order to understand why 4α is the first cocrystal produced by the milling and why only 4β seems to lead to 5, we took the reported Cartesian coordinates of all needed species from the above cited experimental works^37,40 and proceeded with two alternative approaches: first, we relaxed the reported crystal geometries to locate the nearest equilibrium structure and to optimize the lattice parameters under periodic boundary conditions and then calculated all reactivity indices on the extended solids (we call this the extended solid approach), second, we took the structures of the rhodium dimer 1 (Rc) and of the 2Rc + 3BHQ fragment within the 4α and 4β optimized crystals (Fig. 2) and calculated the reactivity indices (we call this the cluster approach). Notice that changes in reactivity arising from systematically growing the clusters in the Rc + BHQ, Rc + 2BHQ, 2Rc + 2BHQ, 2Rc + 3BHQ stoichiometries using the non-optimized geometries have been already reported,⁴⁰ we focus on the 2Rc + 3BHQ fragment because it afforded geometries that were the closest to those of the extended solids, and because the difference in energy between the 4α and 4β fragments closely matched the difference in energy between the two solids. All electronic structure calculations (solid and cluster approaches) were carried out using the empirically dispersion corrected⁴⁴ PBE-D3/DZP model chemistry.^45–48 This choice of functional/basis set has proven accurate for this particular problem.⁴⁰ For solid state calculations we used the same functional and empirical dispersion correction with a plane-wave basis sets with an energy cut-off of 400 eV. Core electrons were modeled with the projected augmented plane wave method (PAW) as implemented in VASP.^49–52 The Fukui function in the solid state was computed with the interpolation method developed by Cárdenas et al.^53–57

Fig. 2 Fragments of the extended solids of the 4α and 4β cocrystals produced by the ball milling of mixtures of the rhodium dimer 1 and the BHQ 2. Atom color code: C: grey, H: white, Rh: orange, Cl: green, N: blue.

To help understand the differences in reactivity between 4α and 4β under ball milling conditions we calculated the following quantities in the cluster and/or solid geometries as needed: (i) Energy related descriptors: Binding energies (BE), energy decomposition analysis under periodic conditions (pEDA),⁵⁸ (ii) Electronic structure descriptors: band gaps, density of states, Fukui functions for electrophilic and nucleophilic attacks,^54,59–62 structures and energies of molecular orbitals, electrostatic potentials (iii) Electron density descriptors: Non-covalent interaction (NCI) surfaces,^63,64 properties of the chemical bonds and intermolecular interactions as derived from the bond critical points obtained after topological analysis of the electron densities under the Quantum Theory of Atoms In Molecules (QTAIM).^65–67 The following programs were used to accomplish our goals: VASP,^49–52,68 AMS,⁶⁹ AMS-BAND,^70,71 AMS-QTAIM,⁷² NCIPLOT,⁷³ Critic2.^74,75

We emphasize that our calculations do not provide a specific reaction mechanism, in other words, we do not know what bonds break first or late or what is the set of primitive processes involved in the production of 5 + NaCl + AcOH and if they occur simultaneously or in a sequence. Rather, recall that as mentioned in the introduction, in the hypothetical case that the mechanism remains the same within the limits imposed by the external force, the net effect of this force is to reduce the activation energy by weakening the chemical bonds,^{19,27,29–36} however, this hypothesis fails if the external force is too large. Thus, our results lead us to postulate that in analogy with the role of heating in solution chemistry, when the temperature reached is sufficiently high the internal energy gained by the reactant molecules is such that the activation energy is overcome, then, when the external force in the ball milling is sufficiently large, the chemical bonds are simply broken exposing the reacting centers and the reaction mechanism may change.^1,76 Notwithstanding, our calculations provide valuable insight into the relative reactivity of the species.

3 Results

Let us make an inventory of the chemical bonds that need to be broken/formed in the reaction depicted in Fig. 1. Each Rh center in 1 substitutes two bridging Rh–Cl (labeled in the literature as Rh–μCl) bonds with one Rh–C and one Rh–N bonds, for this to happen two Rh–μ Cl, one C–H and one Na–O bonds need to be broken and one of each Rh–C, Rh–N, NaCl and O–H bonds are formed. We attempt to provide a formal picture of the relative strengths of the bonds to be broken and calculate additional reactivity indices to help explain the experimental observations exposed at the beginning of the Computational methods section.

3.1 Structures and energies

4α has triclinic symmetry while 4β is monoclinic. The unit cell in 4β has exactly twice as many fragments as 4α and almost twice the volume of the unit cell (21 512.84, 42 904.37 a.u. for 4α and 4β, respectively). It has been pointed out by Ardila-Fierro et al.³⁷ that the main geometrical differences between 4α and 4β are the relative positions of the Cp* rings leading to a dominant contribution from C–H⋯Cl over C–H⋯π interactions in 4α. Fig. 2 shows that the fragments within the 4α units are better organized and that there is a larger degree of lateral displacement among the fragments in 4β. Another important geometrical difference is the relative positions of the N corners on the BHQ units: all nitrogen atoms (highlighted in blue) are aligned in the same direction in 4α but alternate from left to right to left and so on in 4β.

As a general rule, the rhodium dimer and BHQ fragments are spatially closer in 4α (see below) leading to larger magnitudes for every component of the repulsive and attractive terms in the PEDA as shown in Table 1. 4α is more tightly bound by about 6.4 kcal mol⁻¹ while having the largest Pauli repulsion term, nonetheless, all attractive terms in the PEDA favor the more negative energy of 4α, so, the dispersion, electrostatic and orbital terms in the PEDA more than compensate in favor of 4α despite the larger Pauli repulsion. The largest contributors on almost equal amounts to the cohesion of the solids are the dispersion and electrostatic terms, however, the orbital terms are not negligible. Notice that 4α and 4β are non-covalent solids and that interaction energies were calculated as the difference between the energy of the solid and the energy of the fragments, as a result, 4α and 4β have very large interaction energies >240 kcal mol⁻¹, which are in the range of ionic solids. This is not uncommon for organometallic solids. We rationalize these puzzling interaction energies as due to the very large number of individual non–covalent contacts, each one providing a small amount of stabilization energy between the rhodium dimer and BHQ fragments.

Table 1 Main bond energy terms and interaction energies for the 4α and 4β cocrystals at PBE-D3/DZP. Because of the stoichiometry of the unit cells ΔE_int calculated as E_4α − 0.5 E_4β. All energies in kcal mol⁻¹

Term	Unit cell			2Rc + 3BHQ clusters
	4α	4β	ΔE	4α	4β	ΔE
E Pauli	217.5	201.7	15.8	39.6	36.2	3.4
E disp	−177.5	−174.5	−3.1	−41.0	−35.9	−5.1
E elstat	−181.7	−168.1	−13.6	−40.5	−35.6	−4.9
E orb	−105.0	−99.5	−5.5	−29.1	−25.4	−3.7
E int	−246.8	−240.4	−6.4	−70.9	−60.7	−10.2
Enthalpy				−24 473.9	−24 460.9	−13.0
Gibbs				−24 620.7	−24 607.6	−13.1

---

It is gratifying that the cluster approach using the 3BHQ + 2Rc stoichiometry yields the exact same qualitative trends in the PEDA, but, more importantly, it yields differences in interaction energies between 4α and 4β that are very close to the extended solid, thus, the cluster model may be used to extract meaningful reactivity information. Within the limitations of the computational model, the Gibbs free energies computed at room conditions afford a difference of 13.1 kcal mol⁻¹ in favor of 4α, further decomposition into the ΔH − TΔS terms reveals that this difference is exclusively due to the ΔH term. Since the molar Gibbs energies are directly related to the chemical potentials, this observation has the important consequence that the difference in reactivity between 4α and 4β may be analyzed from the intermolecular interactions between the Rc and BHQ fragments.

3.2 Electronic structure

The electronic structure of the extended solids and of the 3 : 2 (BHQ : Rc) clusters afford a compelling picture of the relative reactivity of the rhodium dimer as well as of the 4α and 4β cocrystals, which we attempt to relate to global and local reactivity descriptors.

3.2.1 Global descriptors. A number of global descriptors derived from frontier orbitals for the rhodium dimer 1 and for the 3 : 2 (BHQ : Rc) clusters are listed in Table 2. In a quite broad initial assessment, since 4α and 4β are cocrystal polymorphs and since ε^4α_HOMO > ε^4β_HOMO, the electrons in 4α are more labile and thus in orbital controlled reactions 4α should be a slightly better nucleophile than 4β. Similarly, since ε^4α_LUMO > ε^4β_LUMO, then 4β should be a slightly better electrophile. This, however, is an incomplete picture: it turns out that within the limitations provided by the DZP basis set, 4α has 25 unoccupied molecular orbitals with negative energies while 4β has 31, thus, both cocrystals should be excellent electrophiles with a clear preference for 4β. This is a relevant result because, as the experiments show, the reaction with NaOAc indeed heavily favors 4β, which can be explained by its larger affinity towards the charged AOc⁻.

Table 2 Global descriptors in eV for the rhodium dimer 1 (Fig. 1) and for the 4α and 4β cocrystals in the 3 : 2 (BHQ : Rc) clusters (Fig. 2) and in the extended solids. All regular values from the AMS-BAND calculations, all values within parentheses from the VASP calculations. Chemical hardness, net electrophilicity, and chemical potentials derived from approximations involving the frontier orbitals within the formalism of conceptual DFT as shown elsewhere.^77–80

Quantity	1	4α	4β
a Indirect band gap.
3 : 2 (BHQ : Rc) clusters
ε HOMO	−4.87	−4.73	−4.85
ε LUMO	−3.08	−3.15	−3.20
Chemical hardness η	1.80	1.58	1.64
Net Electrophilicity	17.85	19.67	19.70
Chemical potential μ	−3.97	−3.92	−4.00
Extended solids
AMS-BAND
Top of valence band	−6.48	−6.44	−6.48
Bottom of conduction band	−4.82	−4.64	−4.62
Chemical hardness (band gap, εg)	1.66^a	1.80	1.86
Chemical potential (Fermi energy, εF)	−4.93	−5.57	−6.26
Electrophilicity	9.62	8.53	8.28
VASP
Chemical hardness (band gap, εg)	1.90	1.98	2.00
Chemical potential (Fermi energy, εF)	−7.56	−7.54	−7.63
Electrophilicity	15.04	14.36	14.55

---

In the same line of reasoning, the energies of the HOMO and LUMO orbitals indicate that 1 has a larger chemical hardness and that there is only a slight difference between the two cocrystals (Δη_(4β−4α) = 0.06 eV). The global net electrophilicities reveal a similar difference of 0.03 in favor of 4β, however, the chemical potentials are not as resolutive. Thus, an initial cluster-based coarse view of the relative reactivity suggests that 1 is less reactive than the evenly matched 4α and 4β. This broad generalization is fully consistent with the experimental observation that the rupture of dimer 1 is only achieved once BHQ is added to the mixture under ball milling conditions which leads to the transient formation of 4α and then 4β, in other words, the global descriptors are consistent with the observation that mixtures of solid 1 and NaOAc are unreactive under ball milling.

The corresponding descriptors calculated in the extended solids and listed in Table 2 provide a complementary picture or the relative reactivity of 1, 4α and 4β as the one provided by analyzing the 3 : 2 (BHQ : Rc) clusters. Notice that according to these descriptors 4α is more electrophilic than 4β, however, with the VASP alignment of the energy levels, the relative electrophilicity matches the results obtained from the cluster model. These results suggest that the differences in reactivity are due to local rather than to global properties. It is interesting to notice that the conduction and valence bands in all solids (Fig. S1 in the (ESI†)) have large components from the p orbitals in the Cl centers and Cp* units and from d orbitals in Rh atoms. Then, again as an initial coarse assessment, the role of the nucleophilic chlorine atoms should not be ignored.

3.2.2 Local descriptors. The structures of the HOMO, LUMO and LUMO+1 orbitals depicted in Fig. 3 provide additional insight to understand the relative reactivity between 4α and 4β. When both cocrystals act as electrophiles, the ability to accept electrons into the LUMO in 4α is 80% localized in the aromatic BHQ unit, while in 4β the LUMO is 86% concentrated in the rhodium dimer region with 27% contributions arising right from d orbitals in Rh atoms. Notice that none of these orbitals contain contributions from the dangling chlorine atoms in 1 in 4α or 4β, therefore, these atoms are not good electrophilic centers.

Fig. 3 Frontier orbitals of the rhodium dimer 1 and for the 3 : 2 (BHQ : Rc) clusters of 4α and 4β.

The spatial distribution of the LUMOs provides a plausible explanation for the otherwise puzzling formation of the cationic intermediate^81,82 [Cp*Rh(OAc)]⁺, (experimentally detected in ref. 82) and used as the starting point for hypothetical mechanisms leading to 5, suggested by them and by other authors when the reaction takes place in solution.^83,84 If our analysis is correct, the molecular geometry of the rhodacycle 5 with two new Rh–BHQ bonds (with the C and N atoms) coming from the transformation of two Rh–O bonds from the intermediate 4 of Li et al.,⁸² suggests that either in solution or under ball milling, the LUMO of 4β has a prominent role in this reaction. Notice that you have to go to the LUMO+1 in 4α to achieve the same qualitative reactivity at the Rh center, however, this orbital still has a significant 32% concentration at the BHQ fragment. Similarly, in orbital controlled reactions, the structure of the HOMO gives away the nucleophilic sites (this is important because one of the reaction products is NaCl): in 1, the contributions from the two non-bridge chlorine atoms amount to 48% while the remaining of the orbital is split into the entire rhodium dimer. In 4α the HOMO is >99% delocalized along the rhodium dimer with 43% of the orbital concentrated at just one of the non-bridge Cl atoms. Finally, the HOMO in 4β is 100% distributed along the rhodium dimer with large contributions (25% and 15%) from two non-bridge Cl atoms. In summary, all HOMO and LUMO derived descriptors of reactivity heavily favor 4β.

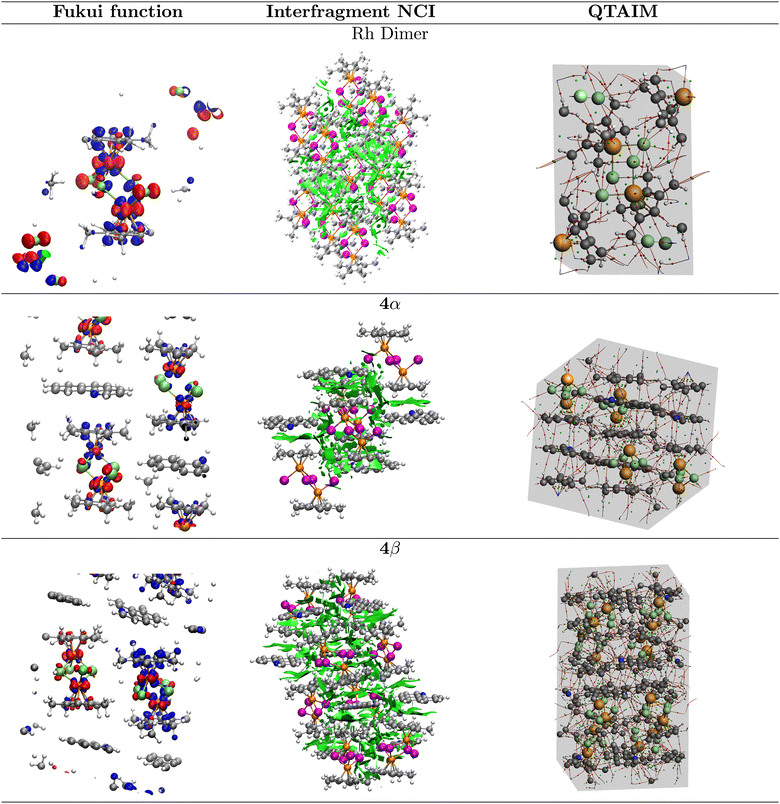
All the previous calculations on the extended solids were carried out using the 2022.02 version of the AMS-BAND program.^69,70 The largest deviation in the calculated cell parameters obtained for all solids (rhodium dimer 1, 4α and 4β) from the experimental geometries was <2.5%. As shown in Table 1, the extended 4β solid is favored over the 4α form by 6.4 kcal mol⁻¹. We now turn our attention to the Fukui functions, which, unfortunately, are not available in AMS-BAND, therefore we used the algorithm developed by Cerón et al.⁵⁴ in the VASP suite⁶⁸ for these calculations under periodic boundary conditions. The corresponding surfaces are plotted in Fig. 4. The optimization of the solids resulted in cell parameters with a maximum deviation from the experimental geometries of 4.5% and a difference of 2.7 kcal mol⁻¹ still in favor of 4β.

Fig. 4 Electronic structure derived descriptors on the extended solids. Isosurfaces of the Fukui functions f⁺(r) in blue and f⁻(r) in red in the left panel (in all cases the isosurfaces correspond to a value 0.012 Å⁻³ (unit formula)⁻¹). Reduced density gradient (RDG) surfaces in the middle panel within a 0.3 isosurface. QTAIM molecular graphs in the right panel.

In good agreement with the descriptors previously mentioned, the Fukui functions calculated on the extended rhodium dimer solid show that both Rh atoms have electrophilic and nucleophilic powers, the bridging Cl atoms are strong electrophiles and the dangling chlorines are strong nucleophiles.

Recall that the unit cells of 4α and 4β contain four and eight rhodium dimer units respectively and that all differences in reactivity are due to the interaction with the BHQ units that lead to the two molecular solids. What we observe, in summary, is that the Fukui function of the [Cp*RhCl₂]₂ crystal 1 more closely resembles the Fukui function of the 4α phase. The solid arrangements are such that the four and eight units split into two sets of non-equivalent units within each cell with overall strong ambiphilic potential in both cases. The two non-equivalent units in the 4α phase exhibit nucleophilic and electrophilic potential at all Rh atoms with the dimer at the bottom left (Fig. 4) showing larger differences between the two Rh of the same unit. In addition, there are two Cl atoms at the unit in the bottom left that are stronger nucleophiles than all other chlorines and both units have Cl atoms with electrophilic power. Thus, for the 4α phase, the [Cp*RhCl₂]₂ molecule on the left has an overall larger nucleophilic character than the one on the upper right. The differences between non-equivalent units are much more marked in the 4β phase, namely, two Cl atoms in the [Cp*RhCl₂]₂ unit to the right are strong electrophiles and this unit is much more electrophilic overall that the one on the left. This description adds additional support to the idea that the overall role of the reactivity of the Cl atoms should not be ignored.

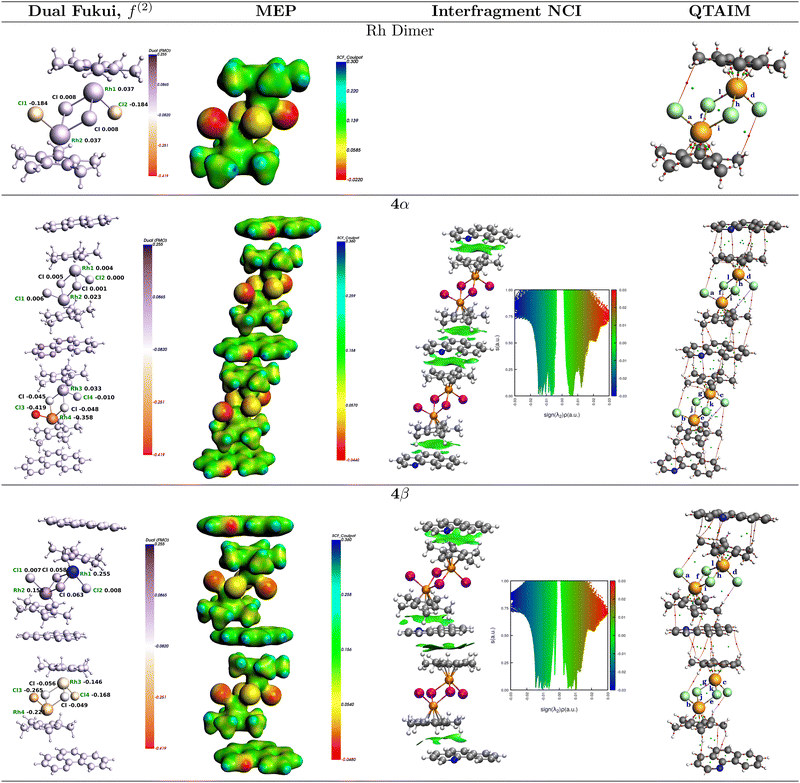
The condensed dual Fukui functions,^61,62f⁽²⁾(r) = f⁺(r) − f⁻(r), calculated on the bare rhodium dimer 1, and on the 4α and 4β 3 : 2 (BHQ : Rc) clusters are shown in Fig. 5. The results of these calculations yield a picture of reactivity that is quite consistent with the analysis of the Fukui functions on the extended solids just discussed: Both Rh atoms and the two bridging chlorides in the rhodium dimer are electrophiles while the dangling chlorides are nucleophiles. Cocrystallization with BHQ affects the reactivity in such a way that it leads to two non-equivalent units in each of the 4α and 4β forms with various degrees of electrophilicity and nucleophilicity which are in line with the results obtained for the extended solids in that 4β seems to enhance both the electrophilic character of the Rh atoms and the nucleophilic character of the Cl centers. This again suggests that the nucleophilic role of the chlorine atoms is significant.

Fig. 5 Reactivity and structural descriptors on the 3 : 2 (BHQ : Rc) clusters. From left to right: Dual Fukui functions, molecular electrostatic potentials (MEP), 3D and 2D reduced density gradient (RDG) surfaces for intermolecular interactions and QTAIM molecular graphs with Rh–Cl bond labels.

The degree of contribution from electrostatic charges to the overall reaction leading to 5 from mixtures of 1, 2 and NaOAc should be reflected in the cluster electrostatic potentials shown in Fig. 5 and listed in Table 3 along with atom charges derived from three different schemes, namely, QTAIM, Mulliken, and Hirshfeld. All these electrostatic criteria show even smaller differences between the relative reactivities of 1 against 4α and 4β but nonetheless lead to the same coarse view as when analyzing the electronic structure derived chemical hardness and electrophilicity. Overall, the dangling chlorines are stronger nucleophiles than the ones in the bridges, also, the rhodium centers in all cases 1, 4α and 4β have positive electrostatic potentials and positive charges, slightly favoring 4α and 4β as active electrophiles over the bare rhodium dimer. However, despite the fact that all charge schemes yield the same trends, the differences between 1, 4α and 4β are so small that a plausible conclusion is that mechanochemical assisted reactions for these species are actually controlled by orbital interactions.

Table 3 Molecular electrostatic potentials (MEP) and atom charges derived from three different calculation schemes: QTAIM (Q), Mulliken (M), and Hirshfeld (H) for the cluster models. All quantities in atomic units. See Fig. 2 for atom numbering

Atom	1				4α				4β
	MEP	q Q	q M	q H	MEP	q Q	q M	q H	MEP	q Q	q M	q H
Rh1	0.13	0.66	1.27	0.28	0.13	0.66	1.27	0.26	0.14	0.66	1.25	0.25
Rh2	0.13	0.66	1.27	0.28	0.15	0.65	1.24	0.25	0.15	0.67	1.25	0.25
Rh3					0.13	0.66	1.27	0.26	0.14	0.66	1.25	0.25
Rh4					0.14	0.65	1.24	0.25	0.15	0.67	1.25	0.25
Cl1	−0.01	−0.56	−0.46	−0.31	−0.02	−0.55	−0.45	−0.32	−0.01	−0.56	−0.46	−0.32
Cl2	−0.01	−0.56	−0.46	−0.31	−0.01	−0.57	−0.47	−0.30	−0.01	−0.57	−0.47	−0.32
Cl3					−0.02	−0.55	−0.45	−0.32	−0.02	−0.56	−0.46	−0.33
Cl4					−0.01	−0.57	−0.47	−0.30	−0.02	−0.57	−0.47	−0.32

---

3.3 Electron density derived descriptors

The descriptors for this section are plotted in Fig. 4 and 6 for the extended solids and in Fig. 5 for the 3 : 2 (BHQ : Rc) clusters.

Fig. 6 2D Reduced density gradient (RDG) plots for the extended solids. From top to bottom: rhodium dimer 1, 4α, 4β and their superposition showing the points of contact with the line of zero reduced gradient.

3.3.1 Non-covalent interactions (NCI). The NCI surfaces for all solids in Fig. 4 calculated using promolecular densities show that all crystals are stabilized by attractive fluxional walls of discontinuous patches of charge transferred from the fragments to the interstitial regions. The NCI color code (green surfaces) places these walls in the category of weak, long range interactions, a classification that is reinforced by analyzing the ranges in which the reduced gradients touch the zero line in Fig. 6: all reduced gradients cover very small intervals ([−0.0130, 0.0072] a.u. for 1, [−0.0120,0.0093] a.u. for 4α and [−0.0110,0.0086] a.u. for 4β) around Sign(λ₂)ρ = 0. Notice that it is the cumulative effect of a large number of these weak interactions that provides the large interaction energies for the molecular crystals listed in Table 1. The weak character of these interactions is further emphasized when comparing against the [−0.0230,0.0150] a.u. interval for the archetypal hydrogen bond in the water dimer,⁸⁵ which, while still a weak interaction, accumulates about twice as much electron density at the points in which the reduced gradient vanishes. The larger the accumulation of electron density at the point of Zero reduced gradient, the more electron density is shared between the two fragments, thus increasing the degree of covalency of the interaction and its strength, accordingly, the strength of the interaction increases moving to the left, away from the Sign(λ₂)ρ = 0. Consequently, according to this criterion, it is evident from the superposition plot (Fig. 6, bottom) that the units in the rhodium dimer 1 are more strongly bound than in 4α, which in turn are more strongly bound than in 4β.

Let us now focus our attention on the 3 : 2 (BHQ : Rc) model clusters from which we draw additional quantitative insight. The green surfaces stabilizing the vertically grown clusters are shown in Fig. 5. Notice that for the vertically stabilized clusters, the lines of Zero reduced gradient are touched at Sign(λ₂)ρ = −0.0145, −0.0144 for 4α and 4β, respectively, thus there is only a small difference in favor of 4α. Nonetheless, integrating the charges of the surfaces over the entire enclosed volumes affords 8.97 and 7.87 × 10⁻⁴ a.u., thus, 10% more charge is transferred to the interstitial region between fragments in 4α than in 4β. To account for both the vertical and lateral interactions and to directly quantify the lateral contributions, we considered the 2BHQ + Rc and one of the geometrically possible 6BHQ + Rc fragments, as shown in Fig. 7. The integrations afford 3.1 and 2.6 × 10⁻⁴ a.u. for the 4α and 4β forms of 2BHQ + Rc, thus, in this stoichiometry, the vertical contributions are ≈17% larger for the 4α. Similarly, 4.7 and 3.8 × 10⁻⁴ a.u. for the 4α and 4β forms of 6BHQ + Rc were obtained, thus, the integration with both vertical and lateral contributions yields ≈19% in favor of the 4α form. The lateral components are calculated to be 35% in 4α and 32% in 4β. The fact that the NCI surfaces are larger for the 4α form suggests that there are more interfragment interactions in the 4α clusters than in 4β.

Fig. 7 Reduced models showing the vertical and lateral Reduced density gradient (RDG) surfaces.

3.3.2 Quantum theory of atoms in molecules (QTAIM). The reader is directed to the specialized literature^65–67 for a detailed analysis of how the calculated descriptors are related to the nature and strength of bonding interactions, which we briefly describe next. Larger accumulations of electron densities, ρ(r_c), at bond critical points (BCPs) indicate that the atoms share more electron density and therefore equate to larger covalent character. Positive Laplacians of the electron density, ∇²ρ(r_c) > 0, signal local minima, thus the electron density for these interactions tends to concentrate around the nuclei, which are indicative of either highly ionic or of long range inductive and dispersive interactions. 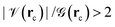Local virial ratios indicate an excess of local electron density at the BCP and are clear signs of formal covalent interactions, in the same line, indicate anionic or long range interactions and the region describes interactions with both covalent and anionic contributions. Negative total energy densities at BCPs, [script letter H](r_c) indicate a local dominance of the attractive potential energy leading to favorable accumulation of electron density while positive total energy densities indicate a local dominance of the repulsive kinetic energy leading to unfavorable conditions for accumulation of electron densities; alternatively, energy densities have units of pressure (E/V = F/A = P), then, energy densities can be related to the quantum pressures that electrons face within electron distributions, consequently, local negative energy densities (local negative pressures) suck electrons to the BCP and describe highly covalent interactions while positive local energy densities (local positive pressures) drive electrons away from the BCP and describe ionic or long range interactions.

Using periodic boundary conditions we analyzed the topology of the electron densities and derived the descriptors of bonding related above for all bond critical points in the extended solids of the rhodium dimer 1 and the 4α and 4β crystals. See Fig. 4 for the molecular graphs containing all the topological features of the unit cells in the extended solids and Table 4 for an inventory of all interactions corresponding to well defined bonding paths: besides the obvious C–C, C–N, C–H, Rh–C and Rh–Cl formal bonds, we obtained C⋯C and C⋯N interactions corresponding to π–π stacking, which determine the geometry of the unit cells and a large number of assorted weaker interactions that are consequence of the geometrical arrangement.

Table 4 Number of well defined bond critical points in the unit cells of the extended solids and in the 3 : 2 (BHQ : Rc) clusters

	Contact	Unit cell			Cluster 3 : 2 (BHQ : Rc)
		1	4α	4β	1	4α	4β
∇^2ρ(rc) > 0 and [script letter H](rc)<0	Rh–Cl	12	24	24 (48)	6	12	12
∇^2ρ(rc) > 0 and [script letter H](rc) > 0	Cl⋯HCp*	35	34	46 (92)	—	6	4
	Cl⋯HBHQ	—	31	28 (56)	—	—	—
	Cl⋯CCp*	—	2	—	2	—	—
	CCp*⋯HCp*	16	18	16 (33)	—	—	—
	CBHQ⋯HCp*	—	32	44 (87)	—	14	16
	CBHQ ⋯HBHQ	—	2	—	—	—	—
	CCp*⋯HBHQ	—	4	6 (12)	—	—	—
	CCp*⋯CCp*	—	2	6 (12)	—	—	—
	CCp*⋯CBHQ	—	8	8 (16)	—	—	2
	CCp*⋯N	—	2	—	—	2	—
	N⋯HCp*	—	6	6 (13)	—	2	—
	N⋯HBHQ	—	—	(8)	—	—	—
	HCp*⋯HCp*	8	14	20 (41)	—	2	2
	HBHQ⋯HBHQ	—	2	2 (4)	—	—	—
	HCp*⋯HBHQ	—	18	18 (37)	—	4	—
Sum		71	199	229 (459)	8	42	36

---

All BCPs exhibit positive Laplacians. The Rh–Cl bond critical points have negative energy densities, then, these bonds should be considered as to have simultaneous large ionic and covalent components. In addition to the positive Laplacians, all the inter fragment interactions have positive energy densities and thus are characterized as strictly long range. Fig. 8 summarizes our results. The BCPs for the Rh–Cl bonds indicate that the 4α solid accumulates more electron density, has more negative energy densities and larger virial ratios than in the 4β form, thus, all criteria point to them being stronger than in 4β. Among the several types of intermolecular interactions, the natural logarithm as a function of the atom–atom distance plot is quite revealing. The following hierarchy of interaction strength based on the accumulation of electron density at the BCPs is obtained: C⋯C and C⋯N > Cl⋯H > C⋯H > N⋯H > H⋯H. The logarithmic dependence of the electron charge with the atom separation yields two physically insightful results: first, there can not be negative electron densities for large enough distances as linear density vs. distance correlations suggested in early works,⁸⁶ second, the fact that each group of interactions has its own trend line indicates that the electron density at bond critical points suffices as a stand alone criterion to fully establish the strength of a particular set of interactions.^85,87,88

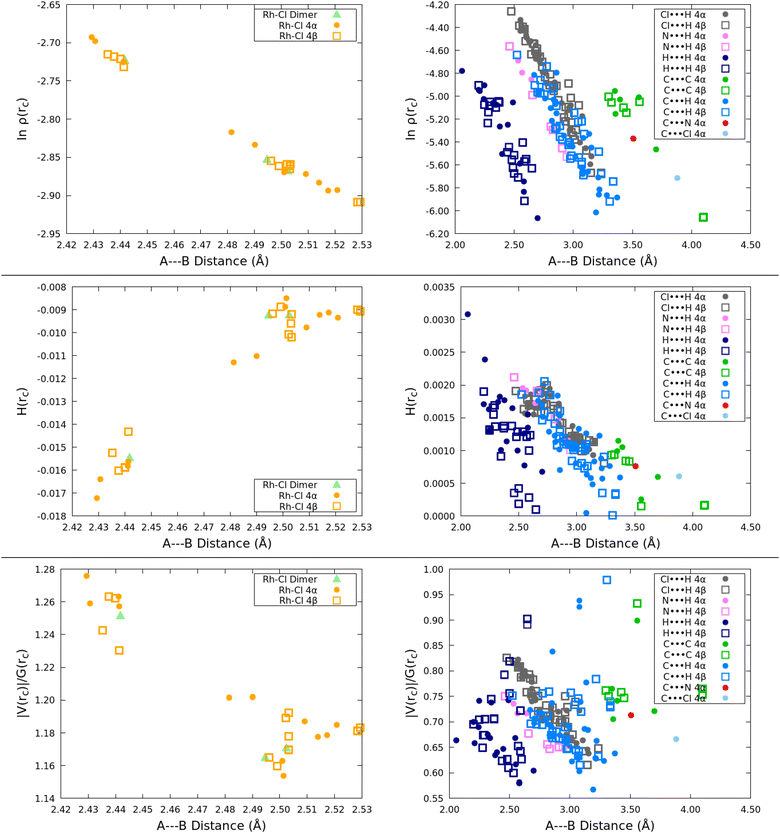Fig. 8 QTAIM derived descriptors of the nature and strength of formal bonds and of interactions as a function of atom separation for the extended solids.

In order to understand the specific contributions to each solid, we separated each set of interactions into subsets as shown in Fig. S2 of the ESI.† Take for example the C⋯C intermolecular interactions responsible for the π–π stacking, they were separated into C_Cp*⋯C_Cp* and C_Cp*⋯C_BHQ. We found small but non-negligible differences between them, however, there is little difference between their contributions to the 4α and 4β forms. Similar results were obtained for all the other sets of intermolecular interactions, therefore, since the weaker interactions cannot be convincingly separated between the two cocrystals, it follows that the most appropriate criterion to establish their relative reactivity is the properties of the Rh–Cl bonds. The very close values obtained for all bonding descriptors other than the logarithmic correlation between electron density at the BCP and atom separation are the source of the somewhat fuzzier plots of the virial ratios and the energy densities, therefore, neither of them are as resolutive although yielding the same overall general trends.

Calculations of the same bond descriptors for the Rh–Cl bonds on the 3 : 2 (BHQ : Rc) clusters shown in Fig. 5 with the proper labels reinforce the idea that the relative reactivity depends on the properties of these bonds: Fig. 9 shows that every single descriptor supports the 1 > 4α > 4β hierarchy of Rh–Cl bond strengths. Moreover, the bridging chlorides (involved in bonds labeled e–k) are weaker according to all descriptors than the dangling chlorides (involved in bonds labeled a–d), which, in addition, exhibit well defined Cl⋯H long range interactions with the hydrogens in Cp*.

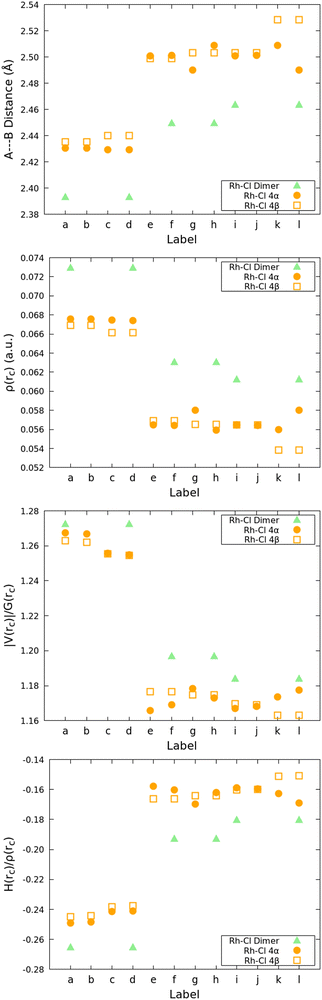Fig. 9 QTAIM descriptors on the Rh–Cl bonds of the 3 : 2 (BHQ : Rc) clusters. See Fig. 5 for the proper labels.

In summary, all bonding descriptors in the extended solids point to 4β having the potential of being more reactive than 4α and to the strength of the Rh–Cl bonds and the ability of either the Rh or Cl atoms to act as electrophiles and nucleophiles as the major contributors to the differences in reactivity. On formal grounds, since all these descriptors correspond to non-observable properties, there are no well defined quantum operators that can be used to unequivocally calculate them, then approximate methods must be used which may yield contradictory results even when calculating the same property as is well known for example in the calculation of atom charges with several schemes, then it is quite remarkable that the wide variety of descriptors used in this work, which differ not only in the methodology used but also in the basic variables used (wave functions vs. electron densities) yield consistent results.

4 Summary and conclusions

The experimental evidence gathered from previous reports that motivated the present work may be summarized as follows: the rhodium dimer 1 reacts with sodium acetate and BHQ in solution to produce the rhodacycle 5via an experimentally characterized intermediate in which explicit Rh–O bonds replace Rh–Cl bonds. The same final product 5 may be obtained from solid mixtures of 1 and BHQ via the formation of the 4α and then 4β polymorphic cocrystals under neat ball milling conditions, which, after further addition of NaOAc exhaust 4α and 4β, without the observation (or detection) of such an intermediate. Also, neither isolate 1 nor 4α react with NaOAc, however, adding NaOAc to isolate 4β leads to 5. We attempt to find the sources of these differences in reactivity with our computations.

Our calculations indicate that 4β is more structurally distorted, appears more fragile both vertically and horizontally, and is higher in energy than 4α by ≈10 kcal mol⁻¹ depending on the method of calculation. In addition, if the molecular orbitals play any role in the reaction, not only is the LUMO of 4β more susceptible to accept electrons because it is lower in energy than the LUMO of 4α, but the number of unoccupied negative energy orbitals in 4β is larger than in 4α. Similarly, if the distribution of charge plays a role in the reaction, all descriptors of the nature and strength of bonds suggest that 4β is more reactive than 4α towards NaOAc because the dangling Cl centers in 4β are stronger nucleophiles (stronger Na⁺ attractors) and that the Rh centers in 4β are stronger electrophiles (stronger AcO⁻ attractors). In both 4α and 4β the dangling chlorine atoms are involved in Rh–Cl bonds that have simultaneously larger covalent and ionic character compared to the bridging Rh–Cl bonds, with all descriptors giving 4β a larger reactivity. The cocrystals are stabilized by several types of intermolecular interactions, among them, C⋯C and C⋯N interactions responsible for π–π stacking, which are the major factors determining the geometrical arrangements, which in turn originate many other interactions which are consequence of the geometries.

With all the experimental and computational evidence we venture a hypothesis of how the reactive mixtures evolve: the ball milling of 1 and BHQ mixtures takes the system first to a deep energy well where 4α resides and then to a more energetic, more structurally fragile and distorted 4β form. Addition of NaOAc to isolate 4α leads to two possible reaction channels, namely, producing 4β or producing 5, since for this experiment production of 5 is not observed, then there are both reactivity and energetic insurmountable obstacles for the further chemical evolution of 4α. Conversely, the addition of NaOAc to 4β leads to the formation of 5, thus, this reaction channel is heavily favored both, energetically and reactivity wise over falling back to 4α. This difficulty in revisiting 4α is easily explained by the continuous energy input from the ball milling, that is, inasmuch as when transferring heat to a reacting mixture favors one direction of the reaction. Once the Cl and Rh reactive sites are exposed by the ball milling of 4β, most likely by overpowering the weaker lateral interfragment interactions, AcO⁻ anions have expedite access to Rh centers and Na⁺ have access to Cl centers effectively leading to 5.

Given the precedent that cocrystalline intermediates such as 4α and 4β have been observed in cyclometallations with other substrates,³⁷ the above mentioned rationalization might be general for many C–H activation reactions under ball milling conditions.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We gratefully acknowledge the Center for High Performance Computing (CHPC) at SNS for providing the computational infrastructure. Partial funding from Universidad de Antioquia via “Estrategia para la sostenibilidad” is also acknowledged. C. C. and T. G. acknowledge FONDECYT through project No. 1220366, Center for the Development of Nanosciences and Nanotechnology, CEDENNA AFB 220001, and Powered@NLHPC: this research was partially supported by the supercomputing infrastructure of the NLHPC (ECM-02).

Notes and references

1. R. T. O’Neill and R. Boulatov, Nat. Rev. Chem., 2021, 5, 148–167.
2. V. Martinez, T. Stolar, B. Karadeniz, I. Brekalo and K. Užarević, Nat. Rev. Chem., 2023, 7, 51–65.
3. J. G. Hernández, Beilstein J. Org. Chem., 2022, 18, 1225–1235.
4. X. Liu, Y. Li, L. Zeng, X. Li, N. Chen, S. Bai, H. He, Q. Wang and C. Zhang, Adv. Mater., 2022, 34, 2108327.
5. K. J. Ardila-Fierro and J. G. Hernández, ChemSusChem, 2021, 14, 2145–2162.
6. M. Arhangelskis, D.-K. Bučar, S. Bordignon, M. R. Chierotti, S. A. Stratford, D. Voinovich, W. Jones and D. Hasa, Chem. Sci., 2021, 12, 3264–3269.
7. R. F. Koby, T. P. Hanusa and N. D. Schley, J. Am. Chem. Soc., 2018, 140, 15934–15942.
8. F. Cuccu, L. De Luca, F. Delogu, E. Colacino, N. Solin, R. Mocci and A. Porcheddu, ChemSusChem, 2022, 15, e202200362.
9. J. G. Hernández and C. Bolm, J. Org. Chem., 2017, 82, 4007–4019.
10. J.-L. Do and T. Friščić, ACS Cent. Sci., 2017, 3, 13–19.
11. M. K. Beyer and H. Clausen-Schaumann, Chem. Rev., 2005, 105, 2921–2948.
12. K. S. Suslick and G. J. Price, Annu. Rev. Mater. Sci., 1999, 29, 295–326.
13. M. M. Caruso, D. A. Davis, Q. Shen, S. A. Odom, N. R. Sottos, S. R. White and J. S. Moore, Chem. Rev., 2009, 109, 5755–5798.
14. J. Ribas-Arino and D. Marx, Chem. Rev., 2012, 112, 5412–5487.
15. T. Stauch and A. Dreuw, Chem. Rev., 2016, 116, 14137–14180.
16. D. E. Makarov, J. Chem. Phys., 2016, 144, 030901.
17. G. S. Kochhar, G. S. Heverly-Coulson and N. J. Mosey, in Theoretical Approaches for Understanding the Interplay Between Stress and Chemical Reactivity, ed. R. Boulatov, Springer International Publishing, Cham, 2015, pp. 37–96.
18. H. J. Kulik, Modeling Mechanochemistry From First Principles, John Wiley & Sons, Ltd, 2018, ch. 6, pp. 265–311.
19. W. Kauzmann and H. Eyring, J. Am. Chem. Soc., 1940, 62, 3113–3125.
20. H. Eyring, J. Walter and G. Kimball, Quantum Chemistry, J. Wiley & Sons, Incorporated, 1944.
21. M. Ferguson, M. S. Moyano, G. A. Tribello, D. E. Crawford, E. M. Bringa, S. L. James, J. Kohanoff and M. G. D. Pópolo, Chem. Sci., 2019, 10, 2924–2929.
22. S. Amirjalayer, H. Fuchs and D. Marx, Angew. Chem., Int. Ed., 2019, 58, 5232–5235.
23. B. S. Pladevall, A. de Aguirre and F. Maseras, ChemSusChem, 2021, 14, 2763–2768.
24. D. De Chavez, H. Kobayashi, A. Fukuoka and J.-Y. Hasegawa, J. Phys. Chem. A, 2020, 125, 187–197.
25. S. Izrailev, S. Stepaniants, B. Isralewitz, D. Kosztin, H. Lu, F. Molnar, W. Wriggers and K. Schulten, Computational Molecular Dynamics: Challenges, Methods, Ideas: Proceedings of the 2nd International Symposium on Algorithms for Macromolecular Modelling, Berlin, May 21–24, 1997, 1999, pp. 39–65.
26. B. Isralewitz, J. Baudry, J. Gullingsrud, D. Kosztin and K. Schulten, J. Mol. Graphics Modell., 2001, 19, 13–25.
27. M. T. Ong, J. Leiding, H. Tao, A. M. Virshup and T. J. Martnez, J. Am. Chem. Soc., 2009, 131, 6377–6379.
28. S. Liu, Conceptual density functional theory: Towards a new chemical reactivity theory, John Wiley & Sons, 2022.
29. S. Zhurkov, Int. J. Fract., 1984, 26, 295–307.
30. G. I. Bell, Science, 1978, 200, 618–627.
31. S. S. M. Konda, J. N. Brantley, C. W. Bielawski and D. E. Makarov, J. Chem. Phys., 2011, 135, 164103.
32. E. Evans and K. Ritchie, Biophys. J., 1997, 72, 1541–1555.
33. M. K. Beyer, J. Chem. Phys., 2000, 112, 7307–7312.
34. K. Wolinski and J. Baker, Mol. Phys., 2009, 107, 2403–2417.
35. K. Wolinski and J. Baker, Mol. Phys., 2010, 108, 1845–1856.
36. G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904.
37. K. J. Ardila-Fierro, M. Rubčić and J. G. Hernández, Chem. – Eur. J., 2022, 28, e202200737.
38. S. Lukin, M. Tireli, I. Lončarić, D. Barišić, P. Šket, D. Vrsaljko, M. di Michiel, J. Plavec, K. Užarević and I. Halasz, Chem. Commun., 2018, 54, 13216–13219.
39. M. Kralj, S. Lukin, G. Miletić and I. Halasz, J. Org. Chem., 2021, 86, 14160–14168.
40. J. G. Hernández, K. J. Ardila-Fierro, S. Gómez, T. Stolar, M. Rubčić, E. Topić, C. Z. Hadad and A. Restrepo, Chem. Eur. J., 2023, 29, e202301290.
41. S. Lukin, L. S. Germann, T. Friščić and I. Halasz, Acc. Chem. Res., 2022, 55, 1262–1277.
42. A. A. Michalchuk and F. Emmerling, Angew. Chem., Int. Ed., 2022, 61, e202117270.
43. P. A. Julien and T. Friščić, Cryst. Growth Des., 2022, 22, 5726–5754.
44. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
45. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
46. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
47. E. Van Lenthe and E. J. Baerends, J. Comput. Chem., 2003, 24, 1142–1156.
48. D. P. Chong, E. Van Lenthe, S. Van Gisbergen and E. J. Baerends, J. Comput. Chem., 2004, 25, 1030–1036.
49. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558.
50. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
51. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
52. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
53. C. Cardenas, M. Munoz, J. Contreras, P. W. Ayers, T. Gomez and P. Fuentealba, Wuli Huaxue Xuebao/Acta Phys.-Chim. Sin., 2018, 34, 631–638.
54. M. L. Cerón, T. Gomez, M. Calatayud and C. Cárdenas, J. Phys. Chem. A, 2020, 124, 2826–2833.
55. C. Cárdenas, A. Echeverry, T. Novoa, A. Robles-Navarro, T. Gomez and P. Fuentealba, The Fukui Function in Extended Systems: Theory and Applications, John Wiley & Sons, Ltd, 2022, ch. 27, pp. 555–571.
56. C. Cárdenas, N. Rabi, P. W. Ayers, C. Morell, P. Jaramillo and P. Fuentealba, J. Phys. Chem. A, 2009, 113, 8660–8667.
57. P. Fuentealba and C. Cárdenas, Chemical Modelling: Volume 11, The Royal Society of Chemistry, 2014, ch. Density functional theory of chemical reactivity, pp. 151–174.
58. M. Raupach and R. Tonner, J. Chem. Phys., 2015, 142, 194105.
59. R. G. Parr and W. Yang, J. Am. Chem. Soc., 1984, 106, 4049–4050.
60. F. Guégan, P. Mignon, V. Tognetti, L. Joubert and C. Morell, Phys. Chem. Chem. Phys., 2014, 16, 15558–15569.
61. C. Morell, A. Grand and A. Toro-Labbé, J. Phys. Chem. A, 2005, 109, 205–212.
62. F. Zielinski, V. Tognetti and L. Joubert, Chem. Phys. Lett., 2012, 527, 67–72.
63. G. A. DiLabio and A. Otero-de-la Roza, Noncovalent Interactions in Density Functional Theory, John Wiley & Sons, Ltd, 2016, ch. 1, pp. 1–97.
64. E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506.
65. R. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, Oxford, 1990.
66. P. L. Popelier, Atoms in Molecules: An Introduction, Prentice Hall, London, 2000.
67. S. J. Grabowski, Chem. Rev., 2011, 111, 2597–2625.
68. J. Hafner, J. Comput. Chem., 2008, 29, 2044–2078.
69. E. Baerends and et al., AMS (version 2022.102), Software for Chemistry & Materials, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, 2022, https://www.scm.com.
70. P. Philipsen, G. te Velde, E. Baerends, J. Berger, P. de Boeij, M. Franchini, J. Groeneveld, E. Kadantsev, R. Klooster, F. Kootstra, M. Pols, P. Romaniello, M. Raupach, D. Skachkov, J. Snijders, C. Verzijl, J. Celis Gil, J. M. Thijssen, G. Wiesenekker, C. A. Peeples, G. Schreckenbach and T. Ziegler, BAND (version 2022.102), Software for Chemistry & Materials, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, 2022, https://www.scm.com.
71. G. Te Velde and E. Baerends, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 7888.
72. J. I. Rodrguez, J. Comput. Chem., 2013, 34, 681–686.
73. J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625–632.
74. A. Otero-de-la Roza, M. Blanco, A. M. Pendás and V. Luaña, Comput. Phys. Commun., 2009, 180, 157–166.
75. A. Otero-de-la Roza, E. R. Johnson and V. Luaña, Comput. Phys. Commun., 2014, 185, 1007–1018.
76. A. E. Beedle, M. Mora, C. T. Davis, A. P. Snijders, G. Stirnemann and S. Garcia-Manyes, Nat. Commun., 2018, 9, 3155.
77. H. Chermette, J. Comput. Chem., 1999, 20, 129–154.
78. P. Geerlings, F. De Proft and W. Langenaeker, Chem. Rev., 2003, 103, 1793–1874.
79. P. K. Chattaraj, A. Chakraborty and S. Giri, J. Phys. Chem. A, 2009, 113, 10068–10074.
80. G. Hoffmann, V. Tognetti and L. Joubert, J. Mol. Model., 2018, 24, 1–12.
81. D. L. Davies, O. Al-Duaij, J. Fawcett, M. Giardiello, S. T. Hilton and D. R. Russell, Dalton Trans., 2003, 4132–4138.
82. L. Li, W. W. Brennessel and W. D. Jones, Organometallics, 2009, 28, 3492–3500.
83. A. P. Walsh and W. D. Jones, Organometallics, 2015, 34, 3400–3407.
84. A. I. VanderWeide, W. W. Brennessel and W. D. Jones, J. Org. Chem., 2019, 84, 12960–12965.
85. N. Rojas-Valencia, S. Gómez, D. Guerra and A. Restrepo, Phys. Chem. Chem. Phys., 2020, 22, 13049–13061.
86. O. Knop, R. J. Boyd and S. C. Choi, J. Am. Chem. Soc., 1988, 110, 7299–7301.
87. I. Alkorta, I. Rozas and J. Elguero, Struct. Chem., 1998, 9, 243–247.
88. F. Ramrez, C. Hadad, D. Guerra, J. David and A. Restrepo, Chem. Phys. Lett., 2011, 507, 229–233.

---

Footnote

† Electronic supplementary information (ESI) available: Band structure and Density of states of the solids, Logarithmic relationships for [r,ρ(r_c)] in some subsets of the interactions. See DOI: https://doi.org/10.1039/d3cp04201d

---