Topology versus porosity: what can reticular chemistry tell us about free space in metal–organic frameworks?†
Alexander P.
Shevchenko
abc,
Eugeny V.
Alexandrov
 abc,
Andrey A.
Golov
abc,
Andrey A.
Golov
 ab,
Olga A.
Blatova
ab,
Alexandra S.
Duyunova
a and
Vladislav A.
Blatov
ab,
Olga A.
Blatova
ab,
Alexandra S.
Duyunova
a and
Vladislav A.
Blatov
 *ab
*ab
aSamara Center for Theoretical Materials Science (SCTMS), Samara University, Ac. Pavlov St. 1, 443011 Samara, Russian Federation. E-mail: blatov@topospro.com
bSamara Center for Theoretical Materials Science (SCTMS), Samara State Technical University, Molodogvardeyskaya St. 244, 443100 Samara, Russian Federation
cSamara Branch of P. N. Lebedev Physical Institute of the Russian Academy of Sciences, Novo-Sadovaya St. 221, 443011 Samara, Russian Federation
First published on 16th July 2020
Abstract
We present the results of a comprehensive geometrical and topological analysis of 3D coordination networks in 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 790 coordination polymers. We have found relations between topological descriptors and free space of the networks, and have revealed topological types that promote high porosity of metal–organic frameworks.
790 coordination polymers. We have found relations between topological descriptors and free space of the networks, and have revealed topological types that promote high porosity of metal–organic frameworks.
Historically, the main class of chemical compounds, for which the methods of crystal design1 were developed and applied, was coordination polymers and their important subclass metal–organic frameworks (MOFs). It was MOFs that promoted the appearance of reticular chemistry2 – a part of chemical science, where the crystal structures and their assembly from predetermined building blocks are described in terms of periodic nets. The theory and methods of reticular chemistry originate from the 1950s,3 but their renaissance came at the very beginning of this century right after the explosive growth of MOF chemistry.4 Reticular chemistry is inherently topological science and its important feature for crystal design is that the periodic nets encode the methods of assembling crystal structures from atoms and polyatomic building units.5 Such periodic nets are called underlying nets6 as they characterize the architecture of the whole structure. To date, MOFs remain the central point of application of reticular chemistry thanks to the extreme diversity of their building units and assembly. Topological properties of coordination polymers and MOFs have been discussed many times,5,6 and the topological motifs that occur in MOFs have been described and collected in electronic databases.7 Recently, a number of papers were published where the correlations between local and overall topological parameters, for example, between coordination of building units and the underlying topology, were explored, and prediction schemes ‘chemical composition – local topology – overall topology’ were proposed for the coordination polymers.8 On the other hand, practical interest in MOFs is mainly caused by their high porosity and surface area, although the relations between the topological parameters of MOFs and the characteristics of their free space were not thoroughly explored. However, methods of geometrical analysis of the free space are intensively being developed,9,10 and a plethora of information on the porosity parameters has been collected for MOFs.11
The topological method for the description of the free space in crystals is based on the concept of periodic natural tiling, where each natural tile corresponds to a minimal framework cage.12 In particular, all known 252 topologically distinct zeolite frameworks stored in the IZA database‡ are characterized by their natural tilings, which were studied in detail, and 405 types of zeolite natural tiles are stored in the ToposPro TTT collection.9 However, the tiling representation was never explored for a comprehensive analysis of MOFs.
In this work, we have studied for the first time the relations between topological properties of MOFs and the geometrical parameters of free space in their structures. We have used the topological models of periodic net and natural tiling as well as the methods of their analysis, which are implemented in our program package ToposPro13 and described in detail in the ESI.† We have applied these tools to 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 790 crystal structures of 3D coordination polymers, which are collected in the Cambridge Structural Database (Table S1, ESI†).14 This amount is five times bigger than in the latest overview of the underlying topology of coordination polymers6 and more than twice as big as the CoRE MOF 2019 collection.15 Out of this amount we have computed the porosity parameters for 17
790 crystal structures of 3D coordination polymers, which are collected in the Cambridge Structural Database (Table S1, ESI†).14 This amount is five times bigger than in the latest overview of the underlying topology of coordination polymers6 and more than twice as big as the CoRE MOF 2019 collection.15 Out of this amount we have computed the porosity parameters for 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 857 completely determined structures (Tables S1 and S2, ESI†). The main question to be answered was: can the framework topology predetermine the framework porosity and to what extent? This general question implied more specific issues, which are discussed below.
857 completely determined structures (Tables S1 and S2, ESI†). The main question to be answered was: can the framework topology predetermine the framework porosity and to what extent? This general question implied more specific issues, which are discussed below.
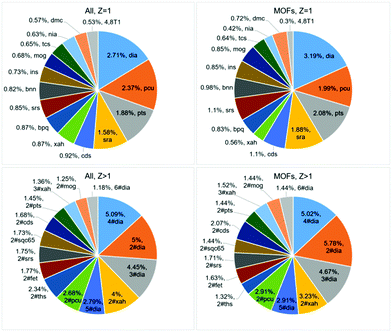
Are there ‘suitable’ or ‘forbidden’ topologies? The distribution of the underlying topologies in general fits the statistics published almost 10 years ago.6 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 747 single coordination frameworks are arranged into 8555 topological types (Table S1, ESI†), and the most abundant types (dia, pcu) remain the same (Fig. 1 top; Tables S2 and S3, ESI†). The scattering of the distribution is very wide: the most frequent topology, dia, composes only 2.71% of the total sample, and 7178 topological types occur only in a single crystal structure. Thus, some underlying topologies are suitable for many combinations of metal atoms and ligands, while other topological motifs can be realized only for a special chemical composition (Table S1, ESI†). Moreover, the number of topological types of coordination networks amounts to only 10% of all 3D network topologies gathered in the ToposPro TTD collection.§ The other 90% can hardly be considered as ‘forbidden’, but they need a unique combination of structural groups to be realized. Efforts of many research groups in searching for new such combinations result in the discovery of hundreds of new topologies every year (Fig. S6, ESI†).
747 single coordination frameworks are arranged into 8555 topological types (Table S1, ESI†), and the most abundant types (dia, pcu) remain the same (Fig. 1 top; Tables S2 and S3, ESI†). The scattering of the distribution is very wide: the most frequent topology, dia, composes only 2.71% of the total sample, and 7178 topological types occur only in a single crystal structure. Thus, some underlying topologies are suitable for many combinations of metal atoms and ligands, while other topological motifs can be realized only for a special chemical composition (Table S1, ESI†). Moreover, the number of topological types of coordination networks amounts to only 10% of all 3D network topologies gathered in the ToposPro TTD collection.§ The other 90% can hardly be considered as ‘forbidden’, but they need a unique combination of structural groups to be realized. Efforts of many research groups in searching for new such combinations result in the discovery of hundreds of new topologies every year (Fig. S6, ESI†).
How does interpenetration influence the porosity? It is known that just a few nets form interpenetrating arrays;6 however, there is no strict prohibition for a particular net to be interpenetrated. In total, we have found 5043 interpenetrating arrays belonging to 1032 topological types compared to 975 interpenetrating arrays and 91 topological types in our last review.6 Self-dual nets, such as dia, ths, pcu, cds, or srs especially tend to form interpenetrated pairs (Fig. 1 bottom; Tables S3 and S4, ESI†) since one net strictly follows the cages and channels of the other net. However, out of 38 self-dual nets contained in the RCSR database, only 25 are presented in coordination polymers (Table S5, ESI†), while 1007 out of the 1032 interpenetrated motifs are not self-dual. In most cases, interpenetration should be avoided when designing porous materials, and thus the underlying topologies, which are not prone to interpenetration, are especially valuable. However, interpenetration also enables one to tune the porous space, and some interpenetrated (for example, n-fold diamondoid; Fig. S7, ESI†) arrays can provide high porosity; moreover, high-porous motifs can even be more preferable for them.
Are there ‘porous’ or ‘dense’ topologies? Porosity is a geometrical property and at first glance, it should not depend on the topological properties of the coordination network. Some authors16 reported about ‘foldable’ and ‘rigid’ topologies, but no strict topological criteria to recognize foldability or rigidity were proposed. We have explored the correlations between underlying topology and porosity in four groups of coordination compounds with ‘low’ (P < 0.25), ‘normal’ (P = 0.25–0.50), ‘high’ (P = 0.50–0.75), and ‘extremely high’ porosity (P > 0.75%). The following conclusions can be made (Table S6, ESI†):
(i) There are topologies that provide only low-porous or only high-porous frameworks, while many other topologies can describe frameworks of any porosity. For example, the most abundant primitive cubic topology (pcu) has high probabilities to be realized in all groups, while rht or tbo topologies are found in the frameworks with high or extra-high porosity, and the ith-3,9-R3m underlying nets fall only under the ‘low-porous’ group.
(ii) Most topologies have average porosity of about 0.40–0.45 and large scattering (3σ > 0.30) that covers the whole porosity range. Such topologies can be considered as ‘deformable’ as they can be preserved at a strong geometrical distortion of the network thus providing a variety of the free space. The deformability of tiles and nets is considered in this work in a general way, without any restriction of their distortion. Thus, the network foldability,16 which intends only rotation between the network nodes while keeping the angles and edge lengths around each node, can be considered as a special case of the network deformability. All most frequent topologies belong to this group (Fig. 1), and this can explain their abundance: indeed, the topology should be more realizable the more different geometrical configurations of the network it can fit. The topologies with small porosity scattering (3σ > 0.06) can be considered ‘rigid’; they are all not frequent (no more than 17 structures of a given topology, Table S6, ESI†), which reflects their inadaptability to geometrical variations of the networks of different composition. Most of such networks have ‘normal’ porosity within the 0.25–0.50 range, but there are examples from other porosity groups, and these examples are most interesting in practice.
(iii) A detailed analysis shows that all groups of structures with small porosity scattering represent a series of isostructural compounds with either the same ligand (usually these complexes are monoligand) or structurally similar ligands and metal atoms. This means that rare topologies are realized at a special combination of complexing atoms and ligands, which have suitable shape and coordination. To select the appropriate structural groups (metal atoms, polynuclear complex groups and ligands) one needs information about their structural role (typical coordination numbers and figures), which can be obtained by machine analysis of their topological descriptors.8
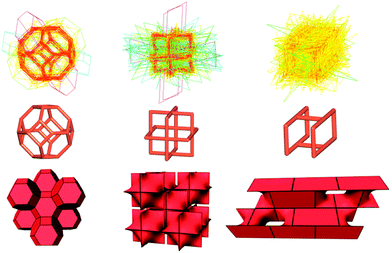
How can topology describe the crystal free space? Total porosity characterizes the volume of the crystal free space, but provides no information about details of its structure. Such information can be derived from natural tiling, which represents a topological model of the system of pores. The building units of the natural tiling, (natural) tiles, characterize the combinatorial topology, the smallest cages in the framework, and the tiling as a whole encodes the method of connection of the cages through common tile faces (channels) (Fig. 2).17 The algorithm of constructing natural tiling for a given net12 is rigorous and implemented in the ToposPro package. We have constructed natural tilings for 1966 topological types of the underlying nets of coordination frameworks, and collected 2507 distinct topological types of tiles, which do not occur in zeolites. We used the following descriptors derived from natural tiling to find correlations between the structure topology and porosity:
(i) Tile topology. The graph of the tile vertices and edges bears the information on the cage architecture irrespective of the possible cage distortion. However, even this purely topological information can be useful when designing porous materials. For this purpose, one can select the tiles that are typical for porous structures. Thus, while the porosity does not directly correlate with the topological size of the tile, i.e., with the number of the tile vertices (Fig. S8, ESI†), it does correlate with the topological type of the tile, and some tiles provide high porosity thanks to their topology (Fig. S9, ESI†). Another topological descriptor, connectivity index (CI), is equal to the ratio of the number of tile edges (e) and the number of tile vertices (v): CI = e/v; the larger CI, the more rigid the tile framework. By definition, CI > 1; CI = 3/2 corresponds to a tile, in which the average coordination number of the vertices is three, which can be considered minimal for a stable construction. For example, the tile in the sodalite-type (sod) network has CI = 3/2, while many underlying nets have tiles with CI < 3/2 (Fig. 2 and Fig. S5, ESI†). If the coordination network is assembled from only one type of tile, i.e., its tiling is isohedral, the tile properties can characterize the whole structure. Many abundant underlying nets admit isohedral tilings, and CI < 3/2 is typical for most of them (Table S7, ESI†).
(ii) Tile distortion (Σ). If the underlying net in the most symmetrical embedding is accepted as the standard, all other embeddings can be considered as distortions of the standard; the same concerns the natural tiles of the nets. We have found that some tiles can be strongly distorted, while other tiles remain close to the standard in most cases (Fig. 2 and Fig. S4, ESI†). Moreover, the realization of interpenetrating nets requires, as a rule, a higher distortion of the net than in single nets (Fig. S4 inset, ESI†). This can indicate that the deformable net topologies are more prone to interpenetration. If the net is ‘rigid’, it can interpenetrate only if a rare combination of factors gave rise to its distortion like in the only example of two interpenetrating sod nets (Fig. S10, ESI†). We suppose that this descriptor can also recognize ‘deformable’ topologies and can be used to design the ‘breathing’ frameworks in combination with the algorithm of identifying the duplicated (i.e., having the same composition and topology and thus forming the same series) frameworks18 and the descriptors of porosity (P, Rf, Ri, Rfi and PC; see the ESI† for details).9 Thus, we have identified 4428 duplicated frameworks arranged into 1306 series; 1366 of these frameworks (Table S8, ESI†) arranged into 479 series essentially differ by their porosity parameters. These 479 series can be considered as potentially ‘breathing’; they are distributed over 157 different underlying topologies, of which pcu, dia, and bpq are the most frequent, as well as over 27 topologically different interpenetrating arrays. Many of these topologies are deformable according to the tile distortion criterion (Fig. S11, ESI†). For example, in the bpq frameworks of the MIL-53 series, the flexibility is provided by squashing the rhombic tiles along the main diagonal (Fig. S11 left, ESI†).
(iii) Topology of the channel system. Our data on porosity contain the information about the periodicity of the channel system and the number of independent channel systems (Table S2, ESI†). Depending on the radius of the probe molecule, one can select different channel systems in the same structure. If one ignores too narrow channels, which cannot admit even small molecules like the hydrogen molecule with the radius of 1.2 Å, most of the channel systems remain 3-periodic or lose their periodicity after splitting into separate cages. However, there are topologies that intrinsically provide a special periodicity of pores. For example, the MOFs with the 4,8T1 underlying topology have only one-periodic systems of channels thanks to a special tiling structure with large 12-membered tile faces aligned in the same direction (Fig. S12, ESI†).
The topological descriptors discussed above together with the correlations between them and the framework porosity form a knowledge database, which can be used in the practical design of new porous coordination networks (Tables S1 and S2, ESI†). All this information enables us to discuss the last and most practical issue.
What can topology predict in porosity? We see that the topological information can be useful for understanding some details of the structure of pores in coordination polymers. What practical tasks of the design of coordination networks can be solved within the topological approach, and how can topology help in the synthesis of new porous structures? Below, we enumerate some features of the crystal structure of a coordination polymer, which can be envisaged using topological descriptors.
(i) Dimensionality of the network. Since low-dimensional materials, like nanotubes or nanosheets, become more and more popular among coordination polymers, it is important to know the conditions, which provide chain or layered motifs. On the contrary, if one aims to obtain a 3D MOF, he/she should avoid low-dimensional structures. In both cases, the prediction of a lower or higher dimensionality of the coordination network gains value even without other topological details. The combination of local topological descriptors used in this work enables one to successfully solve this task.8
(ii) Underlying topology of the network. This is the second overall topological parameter, which can be successfully predicted with machine learning methods using the same set of descriptors as for the prediction of dimensionality.8 As was shown above, some underlying topologies tend to form porous structures, while other topologies are typical for dense networks. Thus the synthetic chemist can try to choose such set of structural units, whose coordination numbers, modes and figures provide the framework with the desired porosity.
(iii) Framework cages and channels. Natural tiles completely describe the geometrical properties of the cages and channels; hence, the underlying net topology, which predetermines the natural tiling, bears the information about the size and shape of all framework pores.
(iv) Interpenetration. As was mentioned above, self-duality is an important purely topological property, which favours interpenetration; however, it does not explain the existence of n-fold interpenetrating arrays with n > 2 and the interpenetration of non-self-dual nets. We show here that a high deformability of the network is another property, which leads to interpenetration. Overall, the set of interpenetrating structures (Table S1, ESI†) can serve as a reference list when planning the design of porous frameworks.
(v) ‘Breathing’ frameworks. The ‘breathing’ phenomenon, which is especially important for the design of porous sorbents with specific mechanical properties, can also be predicted resting upon the underlying net topology.19 The deformable topologies discussed above can play an important role in obtaining new ‘breathing’ frameworks.
(vi) Topology of the porous space. The topological properties of the system of pores are completely described by the framework tiling, which is in turn determined by the underlying net. One could be interested in the frameworks, which contain isolated cages, or channels (pores) spreading in a particular direction, or several systems of non-crossing channels. All such frameworks can be found in our knowledge database (Tables S1 and S2, ESI†).
This list does not exhaust all structural features, which could be considered and at least, partially predicted by the synthetic chemist prior to the experiment. The knowledge database developed in this work can answer both special and more general questions of the user concerning the design problems. In fact, this database mimics the experience of an expert in this field, but contains much more knowledge than the human brain can store. This knowledge can and should be extended with other data, which characterize porosity, for example, with experimental measurements, but the topological information can serve as a ‘skeleton’ thus supporting all other data and providing the predictive power of the database.
The authors thank the Russian Foundation for Basic Research (grants no. 18-07-00183, 18-29-04010) for financial support.
Conflicts of interest
There are no conflicts to declare.Notes and references
- O. M. Yaghi, M. J. Kalmutzki and C. S. Diercks, Introduction to Reticular Chemistry: Metal-Organic Frameworks and Covalent Organic Frameworks, Wiley-VCH, Weinheim, Germany, 2019 Search PubMed.
- O. M. Yaghi, M. O'Keeffe, N. W. Ockwig, H. K. Chae, M. Eddaoudi and J. Kim, Nature, 2003, 423, 705 CrossRef CAS PubMed.
- A. F. Wells, Acta Crystallogr., 1954, 7, 535 CrossRef CAS.
- N. Stock and S. Biswas, Chem. Rev., 2012, 112, 933 CrossRef CAS PubMed.
- N. W. Ockwig, O. Delgado-Friedrichs, M. O’Keeffe and O. M. Yaghi, Acc. Chem. Res., 2005, 38, 176 CrossRef CAS PubMed.
- E. V. Alexandrov, V. A. Blatov, A. V. Kochetkov and D. M. Proserpio, CrystEngComm, 2011, 13, 3947 RSC.
- V. A. Blatov, E. V. Alexandrov and A. P. Shevchenko, Topology: ToposPro, Reference Module in Chemistry, Molecular Sciences and Chemical Engineering, Elsevier, 2019 DOI:10.1016/b978-0-12-409547-2.14576-7.
- A. P. Shevchenko, R. A. Eremin and V. A. Blatov, CrystEngComm, 2020 10.1039/D0CE00265H.
- O. A. Blatova, A. A. Golov and V. A. Blatov, Z. Kristallogr., 2019, 234, 421 CAS , https://topospro.com/databases/ttt/.
- I. G. García and M. Haranczyk, CrystEngComm, 2020 10.1039/C9CE01753D.
- Y. G. Chung, M. Haranczyk, B. J. Sikora, W. Bury, V. Krungleviciute, T. Yildirim, O. K. Farha, D. S. Sholl and R. Q. Snurr, Chem. Mater., 2014, 26, 6185 CrossRef CAS.
- V. A. Blatov, O. Delgado-Friedrichs, M. O’Keeffe and D. M. Proserpio, Acta Crystallogr., Sect. A: Found. Crystallogr., 2007, A63, 418 CrossRef PubMed.
- V. A. Blatov, A. P. Shevchenko and D. M. Proserpio, Cryst. Growth Des., 2014, 14, 3576 CrossRef CAS , https://topospro.com/.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171 CrossRef CAS PubMed.
- Y. G. Chung, E. Haldoupis, B. J. Bucior, M. Haranczyk, S. Lee, H. Zhang, K. D. Vogiatzis, M. Milisavljevic, S. Ling, J. S. Camp, B. Slater, J. I. Siepmann, D. S. Sholl and R. Q. Snurr, J. Chem. Eng. Data, 2019, 64, 5985 CrossRef CAS.
- F. M. Amombo Noa, E. S. Grape, S. M. Brülls, O. Cheung, P. Malmberg, A. Ken Inge, C. J. McKenzie, J. Mårtensson and L. Öhrström, J. Am. Chem. Soc., 2020, 142, 9471 CrossRef CAS PubMed.
- O. Delgado-Friedrichs and M. O’Keeffe, Acta Crystallogr., Sect. A: Found. Crystallogr., 2005, 61, 358 CrossRef PubMed.
- S. Barthel, E. V. Alexandrov, D. M. Proserpio and B. Smit, Cryst. Growth Des., 2018, 18, 1738 CrossRef CAS PubMed.
- E. V. Alexandrov, A. V. Goltsev, R. A. Eremin and V. A. Blatov, J. Phys. Chem. C, 2019, 123, 24651 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: An Excel file (Tables S1, S2, S8), which contains information on all crystal structures studied; a pdf file, which contains the description of the methods, Fig. S1–S12, and Tables S3–S7. See DOI: 10.1039/d0cc04004e |
| ‡ http://www.iza-structure.org/databases/. |
| § https://topospro.com/databases/ttd/. |
| This journal is © The Royal Society of Chemistry 2020 |