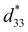Enhanced electromechanical response in Dy³⁺-doped PNN–PZT relaxor ferroelectrics

Abstract

Ferroelectric ceramics with both high piezoelectric coefficients and a wide operational temperature range are in high demand for advanced electromechanical applications. However, since these properties are often mutually exclusive, achieving both exceptional performance and robust thermal stability remains a significant challenge. Here, we report achieving high piezoelectricity (d₃₃ = 840 pC N⁻¹, k_p = 0.73, T_C = 180 °C) and excellent temperature stability (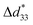 less than 10% within 20–160 °C) in 0.39Pb(Ni_1/3Nb_2/3)O₃–0.59Pb(Zr_0.356Ti_0.644)O₃–0.02Pb(Mg_1/2W_2/3)O₃ ceramics doped with 0.2 wt% Dy₂O₃, outperforming those of other typical piezoceramics. Rayleigh analysis, domain writing of PFM, and calculation of the activation energy of domain wall motion reveal that high piezoelectric properties result from enhanced internal contribution and easier domain wall motion. Excellent temperature stability is mainly attributed to the stable domain structure. This work provides a promising direction for the development of piezoelectric materials with both high piezoelectric performance and good temperature stability.

---

Ting Zheng

Ting Zheng is currently an associate researcher in the College of Materials Science and Engineering of Sichuan University. She received her Ph.D. degree in 2019 from Sichuan University. Her main research interest is lead-free ferroelectric/piezoelectric ceramics and devices.

1. Introduction

Ferroelectrics are renowned for their exceptional ability to convert mechanical energy into electrical energy and vice versa. This characteristic has positioned them as promising candidates for a variety of applications, including sensors, actuators, ultrasonic devices, and energy harvesting systems.^1–3 In recent years, there has been a high demand for ferroelectrics with high piezoelectric coefficients and a wide operating temperature range for advanced electromechanical applications, such as high-temperature sensors, piezoelectric transducers, and so on.^4–7 However, the contradiction between high d₃₃ and high T_C limits the practical application of ferroelectrics.

Among all ferroelectrics, Pb(Zr,Ti)O₃ (PZT)-based relaxors with a morphotropic phase boundary (MPB) have been the mainstay ferroelectrics in the last 70 years.^2,8 Typical PZT-based relaxor systems include Pb(Mg,Nb)O₃–Pb(Zr,Ti)O₃ (PMN–PZT),^9,10 Pb(Zn,Nb)O₃–Pb(Zr,Ti)O₃ (PZN–PZT),¹¹ and Pb(Ni,Nb)O₃–Pb(Zr,Ti)O₃ (PNN–PZT), among them, the PNN–PZT system has garnered significant research interest due to its ability to achieve an extremely high piezoelectric coefficient by tuning the MPB without doping. The outstanding properties near MPB composition are due to the coexistence of two or more competing ferroelectric phases leading to a flattened free energy profile.⁸ In pursuit of superior piezoelectric performance, researchers have conducted a series of methods on the PNN–PZT system, including the construction of MPB,^12,13 doping modification,^14–16 and texturing.¹⁷ However, adjusting the MPB phase boundary or doping modification typically results in a significant deterioration of the Curie temperature (T_C) while enhancing piezoelectric performance (d₃₃).^13–17 Also, the texturing process is complex and production costs are high.

To achieve a balance between high d₃₃ and high T_C, we introduced the high T_C element (Pb(Mg,W)O₃, PMW) into the PNN–PZT systems.^18–21 According to literature reports, the PNN–PMW–PZT system has a Curie temperature of around 300 °C, which is much higher than other PNN–PZT systems. However, although the PNN–PMW–PZT system has been reported to have a Curie temperature of around 300 °C, the piezoelectric performance is not high.

Therefore, Dy³⁺ was doped into the PNN–PMW–PZT system with the aim of balancing high d₃₃ and high T_C. This inspiration comes from the numerous recent literature reports on the promotional effect of rare earth ion doping on the enhancement of performance in relaxor ferroelectric ceramics. The rare earth ions that have been extensively studied include Sm³⁺,^22–25 Eu³⁺,²⁶ La³⁺,^27,28 and others. Li et al.²⁴ believe that the high piezoelectric performance obtained in Sm³⁺-doped Pb(Mg,Nb)O₃–PbTiO₃ (PMN–PT) ceramics is due to the fact that Sm³⁺ is the smallest ion with an effective ionic radius that can fully occupy the A-site in PMN–PT, inducing a significant local structural heterogeneity. We found that Dy³⁺ has an even smaller ionic radius compared to Sm³⁺, and it is also possible for it to enter the A-site of the perovskite structure. There are relatively few research reports on Dy³⁺ doping in PZT-based relaxor ferroelectrics. However, some studies²⁹ have explored the performance differences caused by doping PZT ceramics with different rare earth elements, with Dy³⁺ doping reported to have a higher relative permittivity (ε_r) and remanent polarization (P_r) compared to Sm³⁺ and Eu³⁺ doping. For perovskite ferroelectrics, d₃₃ is directly proportional to the product of ε_r and P_r.³⁰ Therefore, theoretically, Dy³⁺ doping should also effectively improve the piezoelectric performance of PZT relaxor ferroelectrics.

In this work, Dy³⁺ was doped into the PNN–PMW–PZT system, introducing local structural heterogeneity and achieving excellent comprehensive performance with the d₃₃ of 840 pC N⁻¹ and the T_C of 180 °C. In order to explore the origin of the high piezoelectric performance, we conducted Rayleigh analysis under a small electric field to analyze the internal and external contributions, using PFM domain writing to analyze the electric field-induced domain wall motion, and calculated the activation energy for domain wall motion. This work not only enriches the understanding of the role of rare earth doping in relaxor ferroelectrics but also provides a promising direction for the development of high-performance piezoelectric materials.

2. Experimental procedure

The 0.39Pb(Ni_1/3Nb_2/3)O₃–0.59Pb(Zr_0.356Ti_0.644)O₃–0.02Pb(Mg_1/2W_2/3)O₃ + xwt%Dy₂O₃ ceramics were prepared by the traditional solid-state sintering method. The required raw materials were accurately weighed according to the chemical ratio, including Pb₃O₄ (95%), ZrO₂ (99%), TiO₂ (98%), NiO (99%), Nb₂O₅ (99.5%), MgO (99.99%), WO₃ (99%) and Dy₂O₃ (99.9%). After the ingredients were prepared, the raw materials were mixed with zirconia balls and anhydrous ethanol and then placed in a planetary ball mill for grinding for 8 hours. After the ball milling was completed, the evenly mixed slurry was dried and pre-sintered at 820 °C for 2 hours. After grinding the pre-sintered powder for another 8 hours, polyvinyl alcohol (PVA) aqueous solution was added as a binder for granulation, and then a powder tablet press was used to press and form the tablets under a pressure of 5 MPa to obtain a round sheet with a diameter of 12 mm. In order to reduce the volatilization of lead, the matrix powder was buried during the sintering process to create a sintering atmosphere, and then the crucible was covered and placed in the muffle furnace at a temperature of 1200 °C for 2 hours. The ceramic discs prepared by the solid-state sintering method needed to be metallized on their surfaces to undergo electrical property testing. The specific operation first involves polishing the surface of the sintered ceramic discs to make them smooth, then applying silver paste to the top and bottom surfaces of the discs. The discs were then placed in a muffle furnace to sinter at 600 °C for 10 minutes to plate the silver electrodes. The ceramic discs were immersed in silicone oil at 130 °C, and a direct current (DC) electric field of 30 kV cm⁻¹ was applied to the samples for 15 minutes to polarize them, after which subsequent electrical property testing could be conducted.

The crystal structures of the samples were analyzed using an X-ray diffraction (XRD) analyzer (Bruker D8 Advanced XRD, Bruker AXS Inc., Madison, WI, CuKα) and a Raman spectrometer (DXR2xi, Thermo Fisher Scientific, USA). The PXRD data of the PNN–PZT–PMW–xDy ceramic powder were evaluated by Rietveld refinement using the GSAS software. After polishing the samples, they were thermally etched at 1050 °C for 3 minutes, and their microstructure was observed using a scanning electron microscope (SEM) (JSM-7500LV, Japan Electronics Corporation, Japan). Piezoelectric response force microscopy (PFM) (MFP-3D, Asylum Research, Goleta, CA) was used to observe the domain structure of the polished sample, as well as domain writing. The piezoelectric constant d₃₃ is measured using a quasi-static d₃₃ tester (ZJ-3A, Institute of Acoustics, Chinese Academy of Sciences). In situ temperature-dependent d₃₃ was obtained using a high-temperature piezoelectric tester (TZQD-600, Mydream, Shanghai, China). The planar electromechanical coupling coefficient k_p was obtained using an impedance analyzer (HP 4194A, Agilent, Palo Alto, CA, USA). The relative dielectric constant ε_r and dielectric loss tan δ were determined using an LCR analyzer (HP 4980, Agilent, USA). The temperature dependence of the dielectric parameters (ε_r/tan δ − T curve) was measured by the dielectric temperature spectroscopy test system (TZDM-200–300, Harbin Julang Technology Co, Ltd, Harbin, China) with a heating rate of 2 °C min⁻¹ and a temperature range from room temperature to 300 °C. The room temperature and temperature-dependent P–E, unipolar S–E, and bipolar S–E curves were measured at a frequency of 10 Hz using a ferroelectric analyzer (aixACCT TF Analyzer 2000, Germany).

3. Results and discussion

3.1. Crystal structure

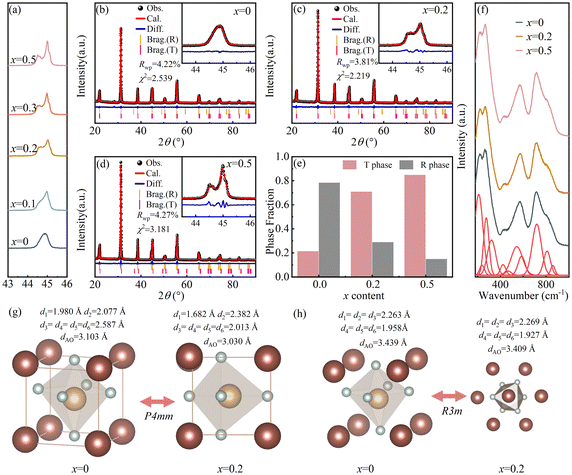
The XRD patterns of the PNN–PZT–PMW–xDy ceramics reveal that all the ceramics exhibit a standard perovskite structure without other impurity phases, indicating that Dy³⁺ ions are completely incorporated into the PNN–PZT–PMW lattice (Fig. S1†). To facilitate the observation of phase structure variations in samples with different Dy³⁺ doping content, Fig. 1(a) presents enlarged XRD patterns within the 2θ range of 43°–46°. When x ranges from 0.1 to 0.5, the splitting of the (200) peak indicates the coexistence of the rhombohedral (R) phase and the tetragonal (T) phase.³¹ To further deduce the crystal structure information, the Rietveld refinement analysis of PNN–PZT–PMW–xDy ceramic powders for x = 0, 0.2, and 0.5 using the GSAS software is shown in Fig. 1(b–e) and Table S1.† During the refinement process, the initial crystal structures were assumed to be tetragonal (P4mm) and rhombohedral (R3m) phases, ultimately achieving relatively low R_wp and goodness-of-fit indicators (χ²), suggesting that the refinement results can be considered reliable. From Fig. 1(b–d), it can be seen that the structures of the three compositions contain coexisting T and R phases. Fig. 1(e) presents the phase fraction of the three compositions. With the increase of x content, the fraction of the T phase increases, while the R phase decreases correspondingly. This may be due to the increase in Dy₂O₃ concentration, causing lattice distortion. To substantiate the reliability of the Rietveld results, Fig. 1(f) presents the Raman spectra of the ceramics for x = 0, 0.2, and 0.5, along with their Gaussian peak fitting. Eleven peaks within the range of 200 to 1000 cm⁻¹ are obtained, corresponding to eleven distinct lattice vibrational modes. The intensity of the Raman spectral peaks is related to the lattice symmetry. The ionic radius of Dy³⁺ is 0.912 Å, compared to r_Pb²⁺ (1.49 Å) and r_Nb⁵⁺ (0.64 Å), and it is possible to replace the Pb²⁺ and Zr⁴⁺/Ti⁴⁺ ions, respectively. Considering the changes in the lattice constants and unit cell volume provided in Table S1,† the doping of Dy³⁺ leads to a contraction of the unit cell volume, indicating that Dy³⁺ ions preferentially replace Pb²⁺ ions in the perovskite structure.²⁴Fig. 1(g) and (h) illustrate the R and T crystal structures of the compositions with x = 0 and 0.2, respectively, as derived from the Rietveld refinement results. In Fig. 1(g and h), the bond lengths of the A–O and the six B–O bonds within the perovskite octahedral structure are also indicated, further verifying that the Dy³⁺ ions replace the A-site ions.

Fig. 1 (a) The enlarged XRD patterns around the Bragg peak position of (200)/(002) with the 2θ range of 43°–46°. (b and c) Rietveld refinements of the PNN–PZT–PMW–xDy (x = 0, 0.2, and 0.5) ceramic powders. (e) Phase fraction as a function of x (x = 0, 0.2, and 0.5) content. (f) Raman spectra of the PNN–PZT–PMW–xDy (x = 0, 0.2, and 0.5) ceramics. (g and h) Variation of the crystal structure with Dy³⁺ doping.

3.2. Microstructure

Fig. 2(a–c) present the surface SEM images of the samples with x = 0, 0.2, and 0.5, and Fig. 2(d–f) display the particle size distribution charts of the ceramics. All ceramics exhibit a dense microstructure with few pores and contain both large and small grains. Notably, the grain size significantly increases at x = 0.2, which shows the maximum average grain size (G_ave) of 3.98 μm. This may be due to the substitution of Dy³⁺ for Pb²⁺, introducing vacancies at the A-site of the lattice, which facilitates the diffusion and migration of ions, thereby promoting grain growth and densification of the ceramic.³² When x = 0.5, the grain size becomes smaller, suggesting that the doping threshold has been reached, inhibiting further grain growth.

Fig. 2 Surface microstructure, grain size distribution and PFM phase images for the PNN–PZT–PMW–xDy ceramics with (a, d and g) x = 0, (b, e and h) x = 0.2, and (c, f and i) x = 0.5. The insets of (d–f) denote the average grain size.

Fig. 2(g–i) characterize the phase images of the domain structure of samples with x = 0, 0.2 and 0.5. The domains appear as irregular blocks, with a clear contrast between purple and yellow phase colors visible in Fig. 2(g–i). By comparing the sizes of the irregular blocks, it can be observed that when x = 0.2, the domain size is the largest. It can be inferred that the difference in domain size is related to the difference in grain size. The increase in grain size reduces the pinning effect of grain boundaries on domain wall motion, leading to a more pronounced piezoelectric response.¹⁴

3.3. Dielectric properties

To accurately determine the phase transition temperature and investigate the effect of Dy³⁺ doping on the dielectric properties, the temperature dependence of the dielectric spectra was tested for different compositions at various frequencies. Fig. 3(a–c) show the temperature dependence of the ε_r and tan δ for PNN–PZT–PMW–xDy ceramics, measured at f = 0.1, 1, 10, 100 and 1000 kHz. When the ceramics undergo a phase transition from the ferroelectric to the paraelectric phase, there will be an abrupt change in the relative permittivity with temperature; that is, a dielectric anomaly peak appears, and the temperature corresponding to this peak is the Curie temperature T_C. In this work, the temperature corresponding to the maximum permittivity T_m is used as an approximation for T_C. From Fig. 3(a–c), with the increase of Dy₂O₃ content, T_C does not show a significant change, and the sample with x = 0.2 exhibits a notably higher dielectric constant compared to other compositions.

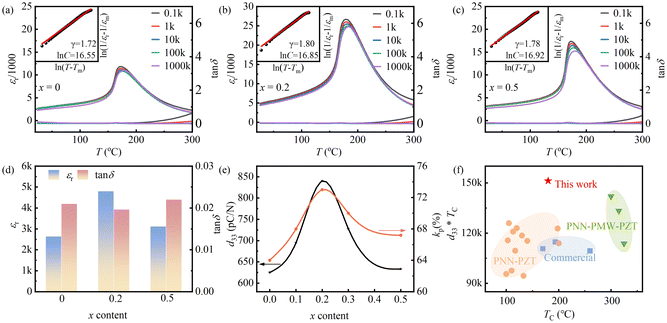Fig. 3 (a–c) Temperature dependence of ε_r/1000 and tan δ of unpoled PNN–PZT–PMW–xDy ceramics, measured at f = 0.1, 1, 10, 100 and 1000 kHz: (a) x = 0, (b) x = 0.2, (c) x = 0.5. The insets show the plots of ln (1/ε_r − 1/ε_m) versus ln (T − T_m) of PNN–PZT–PMW–xDy ceramics. (d) ε_r and tan δ values of poled PNN–PZT–PMW–xDy ceramics measured at f = 1 kHz. (e) d₃₃ and k_p values varying with x. (f) Comparison of d₃₃ and T_C values of PZT-based ceramics.^{1,3,13–16,36–43}

Since the high piezoelectric performance of lead-based relaxor ferroelectrics is closely related to their relaxor behavior,¹⁴ the influence of Dy₂O₃ content on the relaxor characteristics of PNN–PZT–PMW–xDy ceramics was further studied. The relaxor behavior of PNN–PZT–PMW–xDy ceramics was analyzed using the modified Curie–Weiss law, the equation for which is:

1/ε_r − 1/ε_m = (T − T_m)^γ/C (1)

where, C represents the Curie–Weiss constant, and γ indicates the dispersion factor. The insets in Fig. 3(a–c) present the fitting curves of the Curie–Weiss law for different x contents, along with the corresponding dispersion factor γ and Curie–Weiss constant C. The dispersion factor γ of all compositions is between 1.72 and 1.80. The γ of a classical ferroelectric is 1, and that of a completely relaxor ferroelectric is equal to 2.³³ The closer γ is to 2, the stronger the relaxor characteristics the material exhibits. Therefore, the PNN–PZT–PMW–xDy ceramics are all strong relaxor ferroelectrics. As the content of x increases, γ shows a trend of first increasing and then decreasing, with the x = 0.2 ceramic having the maximum relaxation (γ = 1.80). There have been many literature reports on the existence of polar nanoregions (PNRs) in lead-based relaxor ferroelectric systems doped with rare earth elements, and doping with high-valence rare earth elements leads to an increase in PNRs and enhanced local structural heterogeneity.^34,35 It is inferred that doping Dy³⁺ into PNN–PZT–PMW ceramics would also lead to an increase in PNRs, enhancing local structural heterogeneity, thereby improving piezoelectric performance. The increase in the relaxation degree of the x = 0.2 sample can provide some evidence for this inference.

Fig. 3(d) and (e) illustrate the variation of dielectric properties (ε_r and tan δ) and piezoelectric properties (d₃₃ and k_p) with the content of x. As the content of Dy₂O₃ increases, ε_r, d₃₃, and k_p all exhibit a trend of first increasing and then decreasing, reaching their maximum values when x = 0.2, while tan δ shows the opposite trend. Fig. 3(f) compares the T_C and 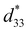T_C of the current work with those of other related lead-based piezoelectric ceramics. It can be seen from Fig. 3(f) that this work has effectively achieved a balance between d₃₃ and T_C for PNN–PZT-based ceramics, with a comprehensive performance superior to other similar lead-based ceramics.

3.4. Ferroelectric properties

Fig. 4(a–c) depict the room-temperature P–E curves, S–E curves, and unipolar S–E curves of the PNN–PZT–PMW–xDy ceramics. All compositions exhibit saturated P–E loops and typical butterfly-shaped S–E curves, indicating that the samples possess good ferroelectricity. Fig. 4(d) and (e) display the ferroelectric parameters extracted from the P–E loops and bipolar S–E curves, including the remanent polarization P_r and the coercive field E_c, as well as the positive strain S_pos, negative strain S_neg, and strain at peak-to-peak S_p–p. The P_r increases and then decreases with the increase of x content, reaching a maximum at x = 0.2, while the trend for E_c is opposite, with the smallest value at x = 0.2. The changes in P_r and E_c can be correlated with the previous SEM results, where at x = 0.2, the larger grain size reduces the pinning effect on domain wall motion, making the non-180° domains easier to switch, thus increasing P_r and decreasing E_c.⁴⁴ The S_pos, S_neg, and S_p–p all exhibit a trend of increasing first and then decreasing with the increase of x content. At x = 0.2, S_pos = 0.14%, S_neg = 0.17%, and S_p–p = 0.31%, demonstrating the best strain performance. As mentioned above, this is also because the larger the grain size, the stronger the constraint on domain wall switching during the reversal of domains, making it more difficult to flip, and the ease of domain wall switching plays a decisive role in the strain performance of piezoelectric materials.⁴⁵Fig. 4(c) shows that the unipolar strain S_uni initially increases with the content of x, reaching the best strain value (0.177%) at x = 0.2, and then decreases. To further describe the unipolar strain, the inverse piezoelectric coefficient ( = S_uni/E_max, where S_uni is the maximum unipolar strain corresponding to the maximum electric field E_max) and strain hysteresis (H = ΔS_Emax/2/S_uni, where ΔS_Emax/2 is the strain difference at 1/2 of the maximum electric field strength E_max) were calculated based on the data in Fig. 4(c), and the changes in 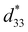and H values with the content of x are shown in Fig. 4(f). When x = 0.2, the 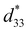reaches its maximum value of 712 pm V⁻¹, which is inferred to be the result of the increase in both the content of the T phase and the average grain size. In PNN–PZT ceramics, the T phase is more prone to polarization reversal compared to the R phase.⁴⁶ The main source of strain hysteresis is the non-intrinsic contribution from irreversible domain wall motion within the piezoelectric ceramics. Based on the reduction of strain hysteresis, it is speculated that the doping of Dy₂O₃ enhances the contribution of the intrinsic piezoelectric response strain.

Fig. 4 Ferroelectric and strain properties of the PNN–PZT–PMW–xDy ceramics: (a) P–E loops; (b) bipolar S–E curves. (c) Unipolar S–E curves. Composition-dependent (d) P_r, E_c, (e) S_pos, S_neg, S_p–p, (f) , and H values.

3.5. Origin of piezoelectric properties

In order to explore the origin of the high piezoelectric performance of the PNN–PZT–PMW–0.2Dy ceramic, we conducted an analysis on samples with different compositions using the Rayleigh model. Rayleigh analysis has been proven to be a method for quantifying the contributions of intrinsic lattice distortion and extrinsic domain wall motion to the piezoelectric effect.^47,48 The Rayleigh model is shown in the following formula:

S(E₀) = (d_init + αE₀) E₀ (2)

d₃₃(E₀) = d_init + αE₀ (3)

In the formula, E₀ represents the applied electric field strength, αE₀ represents the irreversible external contribution from non-180° domain wall motion, and d_init represents the reversible piezoelectric contribution, which includes both the internal lattice distortion contribution and the external contribution from reversible domain wall motion. Under high electric fields, the piezoelectric coefficient is mostly derived from the lattice distortion contribution, and the reversible domain wall motion can be neglected. Therefore, d_init can be considered the internal contribution, and αE₀ represents the external contribution. Typically, the electric field range responsive to the Rayleigh model is about one-third to one-half of the coercive field, which is well below the coercive field and does not form new domains, exhibiting linear Rayleigh behavior.⁴⁹ Since the electric field range is not sufficient for domain flipping, the strain curve of the sample does not exhibit a “butterfly shape”.

The inverse piezoelectric coefficient can be calculated based on the maximum and minimum strains measured at E₀, using the following formula:

d₃₃(E₀) = (S_max − S_min)/2E₀ (4)

Fig. 5(a) shows the S–E curves of the x = 0.2 sample tested under different electric fields. The variation of the inverse piezoelectric coefficient 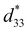with the applied electric field for different compositions, calculated according to the aforementioned formula, is shown in Fig. 5(b). Linear fitting of the data in Fig. 5(b) yields the intercept and slope of the linear function, which correspond to the d_init and α values, representing the internal and external contributions, respectively. The extraction of the fitting results for different compositions is shown in Fig. 5(c), where both d_init and α values exhibit a trend of increasing first and then decreasing, reaching their maximum values at x = 0.2. This indicates that the internal and external contributions to the ceramic increase when x = 0.2, leading to a significant enhancement in piezoelectric performance. The enhancement of the internal lattice distortion contribution is related to the increase in PNRs caused by the doping of the rare earth ion Dy³⁺, while the enhancement of irreversible external contribution is related to the fact that non-180° domain walls become more prone to switching, which is due to the increased grain size and the lead vacancies resulting from the A-site substitution by the high-valence ions.³² In perovskite ferroelectrics, the piezoelectric coefficient d₃₃ can be expressed by the following formula:

d₃₃ = 2 × Q × ε_r × P_r (5)

where, Q is the electrostrictive coefficient, P_r is the remanent polarization, and ε_r is the dielectric constant.³⁰ The Q value is generally relatively stable; hence, the piezoelectric coefficient d₃₃ is proportional to the product of ε_r × P_r, which follows the same trend with composition variation as shown in Fig. 5(d). Since the sample with x = 0.2 has the highest values of ε_r and P_r, it exhibits the best piezoelectric performance.

Fig. 5 (a) P–E loops of the ceramics with x = 0.2 measured at f = 10 Hz. (b) Electric field-dependent as a function of x; (c) d_init and α values varying with x; (d) d₃₃ and ε_rP_r values varying with x. ε_r measured at f = 1 kHz.

Domain writing can be performed using PFM to analyze the electric field-induced domain switching process. Fig. 6(a) and (b) are the domain writing results for the undoped sample and the x = 0.2 sample, respectively. Different voltages of 5, 10, 15, and 20 V were applied to the four regions of the sample during the test, as shown in Fig. 6(a) and (b). When the applied voltage is 5 V, the undoped sample does not exhibit significant domain switching, whereas the x = 0.2 sample has already completed the majority of domain switching under the low voltage drive of 5 V. This indicates that the x = 0.2 sample has easier domain switching at low voltages, with lower domain wall motion activation energy, which is conducive to improving piezoelectric performance. Additionally, the local domain switching is analyzed using switching spectroscopy PFM (SS-PFM) loops. Both the undoped sample and the x = 0.2 sample exhibit butterfly-shaped amplitudes, indicating benign local domain switching. The amplitude of the x = 0.2 ceramic is higher than that of the undoped sample, consistent with their macroscopic ferroelectric/piezoelectric properties. Combined with the results of the Rayleigh analysis in Fig. 5(a–c), it can be concluded that the enhanced internal and external contributions and easier domain wall motion are the sources of the high piezoelectric performance of the x = 0.2 sample.

Fig. 6 PFM amplitude and phase images under different electric fields in a square area, and ss-PFM for the ceramics: (a) x = 0; (b) x = 0.2.

In order to further verify the origin of the high piezoelectric performance of the x = 0.2 sample, the activation energy for domain wall motion (E_a) was calculated using the following formula:

P_sr = P₀exp(−E_a/k_BT) (6)

In the formula, P_sr represents the reverse switching polarization intensity, defined as P_sr = P_s − P_r, where P₀ and k_B are the fitting constant and the Boltzmann constant, respectively. The polarization reverse switching effect describes that after the removal of the externally applied electric field, the originally highly polarized domains tend to be depolarized to a certain extent under the action of the residual depolarization field, resulting in lower system energy.⁵⁰ By measuring the temperature-dependent P–E curves of samples with different compositions, the P_sr at different temperatures can be obtained. Fig. 7(a–e) show scatter plots with the vertical coordinate as ln (P_sr) and the horizontal coordinate as 1000/T, with the black lines representing linear fits obtained. The absolute value of the slope is the activation energy E_a. The variation of E_a with the content of x is given in Fig. 7(f). When x = 0.2, the sample has the lowest E_a, and the trend of E_a with Dy₂O₃ content is exactly opposite to the trend of the piezoelectric performance d₃₃. This is because a lower E_a is conducive to domain wall motion, making polarization reversal easier, which is consistent with the analysis of the previous PFM domain writing results.

Fig. 7 (a–e) Plot of ln (P_sr) as a function of 1000/T for x = 0–0.5. (f) E_a as a function of x.

3.6. Temperature stability

Fig. 8(a) and (d) present the temperature stability of the unipolar strain for the x = 0.2 sample under electric fields of 10 kV cm⁻¹ and 25 kV cm⁻¹, with the temperature range extending from 20 °C to 160 °C. Under 10 kV cm⁻¹, the maximum value of the unipolar strain S_uni continuously decreases with the increase of temperature, with the maximum S_uni at 20 °C being 0.096%. However, under the 25 kV cm⁻¹ electric field, S_uni reaches its maximum value at 120 °C, with a maximum of 0.169%. S_uni shows little change in the measured temperature range. The amplitudes of the strain extremum variation with temperature for the x = 0.2 sample under 10 and 25 kV cm⁻¹ electric fields are 0.018 and 0.024, respectively, indicating excellent strain temperature stability.

Fig. 8 Unipolar S–E curves of the PNN–PZT–PMW–0.2Dy ceramics from 20 °C to 160 °C: (a) E = 10 (kV cm⁻¹); (d) E = 25 (kV cm⁻¹). Temperature- and electric field-dependent (b) S_uni and (e) of the PNN–PZT–PMW–0.2Dy ceramics. Comparison of the temperature stability of (c) and (f) d₃₃ for several reported PZT-based ceramics.^{4,12,37,51,52}

To further determine how S_uni values change with temperature and the applied electric field, the relationship among S_uni, temperature, and electric field for the x = 0.2 ceramic is shown in Fig. 8(b), and the relationship among the , temperature, and electric field is shown in Fig. 8(e). It can be seen from Fig. 8(b) that there is good strain temperature stability under different applied electric fields. From Fig. 8(e), it can be observed that is significantly greater within the 20–100 °C range and under an electric field of less than 15 kV cm⁻¹. The strain in piezoelectric materials is equal to the sum of the strains caused by the inverse piezoelectric effect and the electrostrictive effect.³⁷ The smaller 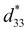under high electric fields is because the strain caused by the piezoelectric effect is greater than the strain caused by the electrostrictive effect at this time.¹² When a lower electric field is applied, the strain of the x = 0.2 ceramic is significantly reduced at high temperatures above 120 °C, which is related to the lower strain caused by the inverse piezoelectric effect, and the sample undergoes thermal depolarization.

Fig. 8(c) and (f) compare the temperature stability of and d₃₃ for the x = 0.2 sample in this work with those reported in other literature studies for PNN–PZT and the typical commercial ceramic PZT-5H. It can be seen that the strain temperature stability of the x = 0.2 sample is better than the temperature stability of d₃₃. The variation of within the wide temperature range of 20–160 °C is less than ±10%; however, d₃₃ also exhibits good temperature stability over a broad temperature range, indicating that the x = 0.2 ceramic has excellent temperature stability. The reason for the decrease in d₃₃ with increasing temperature can be explained by thermal depolarization, which can be illustrated by the temperature-dependent PFM after domain writing. Fig. 9(a) and (b) show the PFM phase images of the domain after temperature variation and the temperature variation after domain writing, respectively. The domains of the x = 0.2 sample are essentially unaffected by temperature within the range of 25–100 °C, exhibiting good temperature stability. Furthermore, the temperature variation after domain writing can reflect the temperature stability of d₃₃. It is only when the temperature rises to 100 °C that the domain response significantly weakens, indicating the occurrence of thermal depolarization.

Fig. 9 PFM phase images for the PNN–PZT–PMW–0.2Dy ceramics of (a) the domain after temperature variation (4 × 4 μm) and (b) the temperature variation after domain writing (3 × 3 μm).

4. Conclusions

In this work, 0.39Pb(Ni_1/3Nb_2/3)O₃–0.59Pb(Zr_0.356Ti_0.644)O₃–0.02Pb(Mg_1/2W_2/3)O₃ + xwt%Dy₂O₃ piezoelectric ceramics are synthesized using a two-step precursor method. High levels of piezoelectric properties (d₃₃ = 840 pC N⁻¹, k_p = 0.73, T_C = 180 °C) and temperature stability ( less than 10% within 20–160 °C) are obtained in the ceramics with x = 0.2, superior to those of reported PZTs and commercially available PZT-5H ceramics. The origin of the high piezoelectricity is attributed to the enhanced internal and external contributions and easier domain wall motion. While good temperature stability originates from a relatively stable domain structure. These advantages make this new material system well-suited for high-performance piezoelectric sensor or actuator applications requiring excellent temperature stability.

Data availability

Data available on request from the authors. The data that support the findings of this study are available from the corresponding author upon reasonable request.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors gratefully acknowledge the support of the National Science Foundation of China (NSFC No. U23A20567) and the Natural Science Foundation Project of Sichuan Province (2024NSFJQ). The authors appreciate the support from Dr. Xiaoshan Zhang (College of Materials Science and Engineering of Sichuan University) for measuring the temperature dependence of piezoelectric coefficient.

References

1. Y. Saito, H. Takao and T. Tani, et al., Lead-free piezoceramics, Nature, 2004, 432(7013), 84–87.
2. B. Jaffe, R. S. Roth and S. Marzullo, Piezoelectric Properties of Lead Zirconate–Lead Titanate Solid–Solution Ceramics, J. Appl. Phys., 1954, 25(6), 809–810.
3. T. Bove, W. Wolny and E. Ringgaard, et al., New piezoceramic PZT–PNN material for medical diagnostics applications, J. Eur. Ceram. Soc., 2001, 21(10), 1469–1472.
4. F. Li, Z. Xu and X. Wei, et al., Temperature- and dc bias field- dependent piezoelectric effect of soft and hard lead zirconate titanate ceramics, J. Electroceram., 2010, 24(4), 294–299.
5. L. Li, S. Zhang and Z. Xu, et al., 1–3 piezoelectric composites for high-temperature transducer applications, J. Phys. D: Appl. Phys., 2013, 46(16), 165306.
6. W. Liu, T. Zheng and F. Zhang, et al., Achieving High Piezoelectricity and Excellent Temperature Stability in Pb(Zr,Ti)O3-Based Ceramics via Low-Temperature Sintering, ACS Appl. Mater. Interfaces, 2022, 14(45), 51113–51121.
7. H. Shi, M. Zhao and D. Zhang, et al., Effect of Sb-induced oxygen octahedral distortion on piezoelectric performance and thermal stability of Pb(In,Nb)O3-Pb(Hf,Ti)O3 ceramics, J. Mater. Sci. Technol., 2023, 161, 101–110.
8. T. R. Shrout and S. J. Zhang, Lead-free piezoelectric ceramics: Alternatives for PZT, J. Electroceram., 2007, 19(1), 113–126.
9. J. S. Park, K. Y. Huh and M.-S. Kim, et al., A relaxor-ferroelectric PMN-PZT thin-film-based drop-on-demand printhead for bioprinting applications with high piezoelectricity and low heat dissipation, Sens. Actuators, B, 2024, 417, 136194.
10. T. Mingyang, L. Xin and Z. Shuguang, et al., Electric field control of piezoelectricity in textured PMN-PZT ceramics, J. Mater. Sci. Technol., 2024, 224, 10–18.
11. Chen, Hao and Pu, et al., Enhancement of Piezoelectric Properties in Low-Temperature Sintering PZN–PZT Ceramics by Sr2+ Substitution, J. Electron. Mater., 2022, 51, 1261–1271.
12. H. Wang, F. Zhang and Y. Chen, et al., Giant piezoelectric coefficient of PNN-PZT-based relaxor piezoelectric ceramics by constructing an R-T MPB, Ceram. Int., 2021, 47(9), 12284–12291.
13. L. Bian, X. Qi and K. Li, et al., High-performance Pb(Ni_1/3Nb_2/3)O₃-PbZrO₃-PbTiO₃ ceramics with the triple point composition, J. Eur. Ceram. Soc., 2021, 41(14), 6983–6990.
14. T. Pu, H. Chen and J. Xing, et al., High piezoelectricity of low-temperature sintered Li₂CO₃-added PNN–PZT relaxor ferroelectrics, J. Mater. Sci.: Mater. Electron., 2022, 33(8), 4819–4830.
15. F. Guo, S. Zhang and W. Long, et al., SnO₂ modified PNN-PZT ceramics with ultra-high piezoelectric and dielectric properties, Ceram. Int., 2022, 48(16), 23241–23248.
16. F. Guo, S. Zhang and R. Qiu, et al., Dramatical improvement in temperature stability of ZnO modified PNN-PZT ceramics via synergistic effect of doping and composite, Ceram. Int., 2023, 49(11, Part B), 18878–18884.
17. L. Bian, K. Zhu and Q. Wang, et al., Performance enhancement of ultrasonic transducer made of textured PNN-PZT ceramic, J. Adv. Dielectr., 2022, 12, 2244003.
18. S. Dursun, A. E. Gurdal and S. Tuncdemir, et al., Material and device design for the high performance low temperature co-fired multilayer piezoelectric transformer, Sens. Actuators, A, 2019, 286, 4–13.
19. Y. K. Oh, J. Yoo and M. H. Park, et al., Dielectric and piezoelectric properties of PMW-PNN-PZT ceramics sintered at low temperatures with high d₃₃ piezoelectric coefficients; Proceedings of ISAF-ECAPD-PFM 2012, F 9–13 July 2012, 2012 [C].
20. J. Yoo, Y. Kim and H. Cho, et al., High piezoelectric d₃₁ coefficient and high TC in PMW-PNN-PZT ceramics sintered at low temperature, Sens. Actuators, A, 2017, 255, 160–165.
21. J. Yoo, K. Yoo and H. Lee, et al., Dielectric and Piezoelectric Properties of Low-Temperature-Sintering Pb(Mg_1/2W_1/2)O₃-Pb(Ni_1/3Nb_2/3)O₃-Pb(Zr,Ti)O₃ Ceramics for Multilayer Piezoelectric Actuator, Jpn. J. Appl. Phys., 2005, 44(9S), 7042.
22. F. Li, D. Lin and Z. Chen, et al., Ultrahigh piezoelectricity in ferroelectric ceramics by design, Nat. Mater., 2018, 17(4), 349–354.
23. Q. Guo, F. Li and F. Xia, et al., High-Performance Sm-Doped Pb(Mg_1/3Nb_2/3)O₃-PbZrO₃-PbTiO₃-Based Piezoceramics, ACS Appl. Mater. Interfaces, 2019, 11(46), 43359–43367.
24. C. Li, B. Xu and D. Lin, et al., Atomic-scale origin of ultrahigh piezoelectricity in samarium-doped PMN-PT ceramics, Phys. Rev. B, 2020, 101(14), 140102.
25. S. Dong, F. Guo and H. Zhou, et al., Phase structures and electrical properties of Sm doped PSN-PMN-PT ceramics, J. Alloys Compd., 2021, 881, 160621.
26. Q. Guo, L. Hou and F. Li, et al., Investigation of dielectric and piezoelectric properties in aliovalent Eu³⁺-modified Pb(Mg_1/3Nb_2/3)O₃-PbTiO₃ ceramics, J. Am. Ceram. Soc., 2019, 102(12), 7428–7435.
27. M. N. Al-Aaraji, W. N. Hasan and K. Al-Marzoki, Effects of La+3 and Sc+3 Ions on Structure and Microstructure of PZT Ceramics for Energy Storage Applications, Solid State Phenomena, 2023, 341, 65–76.
28. F. Yang, X. Cheng and Y. Zhang, Domain orientation distributions in La,Nb-doped PZT ceramics based on in situ polarization angle analysis by Raman spectroscopy, J. Mater. Sci.: Mater. Electron., 2022, 33, 19405–19419.
29. S. R. Shannigrahi, R. N. P. Choudhary and H. N. Acharya, et al., Structural, electrical and piezoelectric properties of rare-earth doped PZT ceramics, Indian J. Pure Appl. Phys., 1999, 37, 359–362.
30. S. Trolier-McKinstry, S. Zhang and A. J. Bell, et al., High-Performance Piezoelectric Crystals, Ceramics, and Films, Annu. Rev. Mater. Res., 2018, 48, 191–217.
31. Q. Liu, Q. Sun and W. Ma, et al., Large-strain 0.7Pb(Zr_xTi_1−x)O₃–0.1Pb(Zn_1/3Nb_2/3)O₃–0.2Pb(Ni_1/3Nb_2/3)O₃ piezoelectric ceramics for high-temperature application, J. Eur. Ceram. Soc., 2014, 34(5), 1181–1189.
32. W. Liu, F. Zhang and T. Zheng, et al., Ultra-broad temperature insensitive Pb(Zr, Ti)O₃-based ceramics with large piezoelectricity, J. Mater. Sci. Technol., 2024, 192, 19–27.
33. R. A. Malik, A. Hussain and A. Zaman, et al., Correction: Structure–property relationship in lead-free A- and B-site co-doped Bi_0.5(Na_0.84K_0.16)_0.5TiO₃–SrTiO₃ incipient piezoceramics, RSC Adv., 2015, 5(125), 103315–103315.
34. F. Li, S. Zhang and D. Damjanovic, et al., Local Structural Heterogeneity and Electromechanical Responses of Ferroelectrics: Learning from Relaxor Ferroelectrics, Adv. Funct. Mater., 2018, 28(37), 1801504.
35. J. Chen, H. M. Chan and M. P. Harmer, Ordering Structure and Dielectric Properties of Undoped and La/Na-Doped Pb(Mg_1/3Nb_2/3)O₃, J. Am. Ceram. Soc., 1989, 72(4), 593–598.
36. J. Du, J. Qiu and K. Zhu, et al., Effects of Fe₂O₃ doping on the microstructure and piezoelectric properties of 0.55Pb(Ni_1/3Nb_2/3)O₃–0.45Pb(Zr_0.3Ti_0.7)O₃ ceramics, Mater. Lett., 2012, 66(1), 153–155.
37. X. Gao, J. Wu and Y. Yu, et al., Giant Piezoelectric Coefficients in Relaxor Piezoelectric Ceramic PNN-PZT for Vibration Energy Harvesting, Adv. Funct. Mater., 2018, 28(30), 1706895.
38. Y. Yue, Q. Zhang and R. Nie, et al., Influence of sintering temperature on phase structure and electrical properties of 0.55Pb(Ni_1/3Nb_2/3)O₃–0.45Pb(Zr_0.3Ti_0.7)O₃ ceramics, Mater. Res. Bull., 2017, 92, 123–128.
39. H. Liu, R. Nie and Y. Yue, et al., Effect of MnO₂ doping on piezoelectric, dielectric and ferroelectric properties of PNN–PZT ceramics, Ceram. Int., 2015, 41(9, Part A), 11359–11364.
40. C.-W. Ahn, S. Nahm and J. Ryu, et al., Effects of CuO and ZnO Additives on Sintering Temperature and Piezoelectric Properties of 0.41Pb(Ni_1/3Nb_2/3)O₃-0.36PbTiO₃-0.23PbZrO₃ Ceramics, Jpn. J. Appl. Phys., 2004, 43(1R), 205.
41. C.-H. Nam, H.-Y. Park and I.-T. Seo, et al., Low-Temperature Sintering and Piezoelectric Properties of 0.65Pb(Zr_1−xTi_x)O₃–0.35Pb(Ni_0.33Nb_0.67)O₃ Ceramics, J. Am. Ceram. Soc., 2011, 94(10), 3442–3448.
42. Y. Xia, Z. Li and Y. Yan, et al., Excellent piezoelectric properties of PNN-PHT ceramics sintered at low temperature with CuO addition, Int. J. Appl. Ceram. Technol., 2020, 17(2), 707–712.
43. Y. Yan, Z. Li and Y. Xia, et al., Ultra-high piezoelectric and dielectric properties of low-temperature-sintered lead hafnium titanate-lead niobium nickelate ceramics, Ceram. Int., 2020, 46(4), 5448–5453.
44. H. Li, L. Xie and Z. Tan, et al., Utilization of Nonstoichiometric Nb⁵⁺ to Optimize Comprehensive Electrical Properties of KNN-Based Ceramics, Inorg. Chem., 2022, 61(46), 18660–18669.
45. X. Ren, Z. Peng and B. Chen, et al., A compromise between piezoelectricity and transparency in KNN-based ceramics: The dual functions of Li₂O addition, J. Eur. Ceram. Soc., 2020, 40(6), 2331–2337.
46. T. Wang, C. Wu and J. Xing, et al., Enhanced piezoelectricity and temperature stability in LaFeO₃-modified KNN-based lead-free ceramics, J. Am. Ceram. Soc., 2019, 102(10), 6126–6136.
47. D. Damjanovic, Chapter 4 - Hysteresis in Piezoelectric and Ferroelectric Materials [M]//Bertotti GMayergoyz ID, in The Science of Hysteresis, Academic Press, Oxford, 2006, pp. 337–465.
48. F. Li, S. Zhang and Z. Xu, et al., Composition and phase dependence of the intrinsic and extrinsic piezoelectric activity of domain engineered (1−x)Pb(Mg1/3Nb2/3)O3–xPbTiO3 crystals, J. Appl. Phys., 2010, 108(3), 034106.
49. R. E. Eitel, T. R. Shrout and C. A. Randall, Nonlinear contributions to the dielectric permittivity and converse piezoelectric coefficient in piezoelectric ceramics, J. Appl. Phys., 2006, 99(12), 124110.
50. A. Picinin, M. H. Lente and J. A. Eiras, et al., Theoretical and experimental investigations of polarization switching in ferroelectric materials, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69(6), 064117.
51. W. Peng, J. Chang and J. Zhao, et al., Enhanced piezoelectric properties and thermal stability of LiNbO₃-modified PNN–PZT ceramics, J. Materiomics, 2024, 10(5), 995–1003.
52. D. Wang, Y. Fotinich and G. P. Carman, Influence of temperature on the electromechanical and fatigue behavior of piezoelectric ceramics, J. Appl. Phys., 1998, 83(10), 5342–5350.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr04839c

---