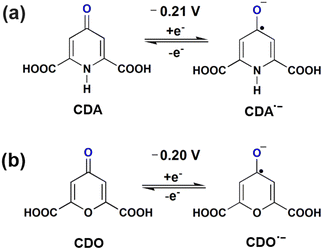
Open Access Article
Open Access ArticleTautomerism and nucleophilic addition influence the performance of aqueous organic redox flow batteries of chelidamic acid and chelidonic acid†
Surya
Prakash
a,
Alagar
Ramar
a,
Fu-Ming
Wang
 *abcd,
Kefyalew Wagari
Guji
a,
Citra Deliana Dewi
Sundari
*abcd,
Kefyalew Wagari
Guji
a,
Citra Deliana Dewi
Sundari
 e and
Laurien
Merinda
a
e and
Laurien
Merinda
a
aGraduate Institute of Applied Science and Technology, National Taiwan University of Science and Technology, No. 43, Sec. 4, Keelung Road, Taipei 106, Taiwan, Republic of China. E-mail: mccabe@mail.ntust.edu.tw; Fax: +886 2 27303733; Tel: +886 2 27303755
bR&D Center for Membrane Technology, Chung Yuan Christian University, Taoyuan, Taiwan
cSustainable Energy Center, National Taiwan University of Science and Technology, Taipei, Taiwan
dDepartment of Chemical Engineering, Chung Yuan Christian University, Taoyuan, Taiwan
eDepartment of Chemistry Education, UIN Sunan Gunung Djati Bandung, Bandung, Indonesia
First published on 5th September 2024
Abstract
The redox flow battery is a cost-effective solution for grid-scale energy storage. Its special feature of separate reservoirs and electrodes makes it easy to adjust the electrolyte volume and electrode size, improving safety and scalability. In this work, we explore two organic anolytes, chelidamic acid (CDA) and chelidonic acid (CDO), which share similar molecular weight but differ in their heteroatoms: pyridone and pyrone. The half-cell potentials of the CDA and CDO anolytes enable them to exhibit theoretical cell voltages of 0.49 V and 0.48 V, respectively, when coupled with K4[FeII(CN)6] catholyte. CDA demonstrated a stable discharge capacity of 650 mA h L−1 over 17 days in a basic medium without any degradation. In contrast, CDO gradually loses its capacity over successive cycles. The mechanism for the decomposition of CDO was analysed through cyclic voltammetry, 1H-NMR, and FTIR spectroscopy techniques. The analytical results revealed that there was a significant impact of tautomerization in CDA and nucleophilic addition in CDO on the performance in ARFBs.
Introduction
The global demand for energy increases significantly every decade due to the overpopulation and economic growth. This is driven by the depletion of highly consumed non-renewable energy sources such as coal, oil, and gas. Numerous researchers are striving to provide sustainable energy solutions by expanding renewable sources like solar and wind. However, the intermittent nature of these sources poses challenges in storing and transporting large amounts of energy to end-users. In recent years, the redox flow battery has shown remarkable growth surpassing the Li-ion battery, attracting researchers due to its environmentally friendly nature, cost-effectiveness, and high endurance.1,2 Moreover, the redox flow battery offers scalability and adaptability through the flexibility to adjust the volume and electrode area to precisely meet the requirements of consumers. Various types of redox systems have been introduced, including all-vanadium, Zn/Br, and Fe/Cr. However, some inorganic materials face challenges such as corrosive electrolytes, high costs, toxic materials, and low conductivity solvents.3 To overcome these hurdles, researchers have turned to aqueous organic redox-active materials as they use highly conductive solvents like water. In addition, these materials are low-cost, offer safety, and use less corrosive supporting electrolytes such as KOH. For instance, quinone, extracted from coal and wood tar, has been successfully used as an anolyte active material in Quino energy.4 While various electrolytes like phenazine,1 alloxazine,5 and flavin6,7 have been explored, only a few meet the criteria for stability, solubility, capacity, and power density. Enhancing material performance in commercial electrolytes has been accomplished by two primary approaches. Firstly, structural chemistry is modified to improve potential, solubility, and stability. Secondly, pH adjustments, electrochemical regeneration, and modifications in the potential window are implemented to overcome degradation mechanisms or side reactions of electrolytes, ensuring successive stability.2,6–8Bo Yang et al. identified a voltage drop of 150 mV in the anthraquinone-2,6-disulfonic acid-4,5-dihydroxybenzene-1,3-disulfonic acid aqueous redox flow battery (ARFB) after the first few cycles, which was attributed to Michael addition reactions to form additional hydroxy substitutions on the benzene.9 In 2017, Sanford et al. reported that low-potential pyridinium anolyte degrades in a neutral solution (NaCl) due to catalytic proton reduction.8 In 2023, Grey et al. reported an FMN/K4[FeII(CN)6] ARFB where hydrolysis products of 4-(D-ribo-2,3,4-trihydroxypentyl-5′-phosphate)-3-oxo-3,4-dihydroquinoxaline-2-carboxylate under basic conditions caused a change in the charge plateau without loss in the voltage.7 Additionally, in 2022, the degradation of 2,6-dihydroxy androne (DHAQ) to DHA(L)2− (double charging plateau) was identified via in situ1H-NMR, with subsequent electrochemical regeneration back to DHAQ2−.6 Furthermore, the discovery of tautomerization in 2,3-dimethylquinoxaline-6-carboxylic acid via Bayesian inference coupled with density functional theory (DFT) analysis provided valuable insights for filtering and selecting appropriate electrolytes for ARFBs.2
Chelidamic acid (dihydro-4-oxo-2,6-pyridone-dicarboxylic acid) and chelidonic acid (4-oxo-4H-pyran-2,6-dicarboxylic acid) are renowned for their ability to form stable organic complexes or dimers with various metals including vanadium, copper, and calcium.10–12 Furthermore, CDA has been utilized as an additive in the catholyte of vanadium-based ARFBs.13 Recent research in 2020 revealed that dipicolinic acid, similar in structure to CDA, serves as an effective ligand when paired with chromium in a neutral redox flow battery, demonstrating a solubility of 0.7 M and consistent performance over 120 cycles.14
The present work investigates two redox-active materials, chelidamic acid (CDA) and chelidonic acid (CDO), as anolytes in an aqueous redox flow battery under alkaline conditions. Despite their comparable molecular weights, they were subtly differentiated by the presence of distinct heteroatoms, specifically the structure of pyridone and pyrone. Both are fully conjugated aromatic compounds with carbonyl groups in their six-membered rings. Compared to pyridone, pyrone possesses a higher electron withdrawing characteristic due to the presence of an oxygen hetero atom. Generally, structures containing carbonyl groups have great potential in energy storage applications.4,9,15 Compounds like CDA and CDO, which feature a two-electron withdrawing group (–COOH), significantly impact solubility in aqueous media.2,16 Previously, these materials were optimized as composite anode materials for Li-ion energy storage devices, showing remarkable capacities of 740.2 mA h g−1 (CDA) and 562.8 mA h g−1 (CDO) over 250 cycles without capacity degradation.17 Given their promising performance in Li-ion anode materials, CDA and CDO were chosen as redox-active anolytes in ARFBs. The impact of heteroatoms in CDA and CDO was investigated by constructing ARFBs with potassium hexacyanoferrate(II) trihydrate. Additionally, our investigation reveals novel insights into nucleophilic addition at α,β unsaturated carbon (CDO), as evidenced by FTIR and 1H-NMR analysis. Furthermore, CDA demonstrates stable charge–discharge behaviour, underscoring the impact of tautomerism in alkaline ARFBs.
Experimental procedure
Materials and characterisation
Potassium hydroxide (KOH, molecular weight: 56.11 g mol−1, purity: 85%), potassium hexacyanoferrate(II) trihydrate (K4[FeII(CN)6]3H2O, molecular weight: 422.39 g mol−1, purity: 98.5%), chelidamic acid hydrate (CDA, molecular weight: 183.12 g mol−1, purity: ≥97%), and chelidonic acid (CDO, molecular weight: 184.10 g mol−1, purity: 97%) were purchased from Sigma Aldrich and Merck Limited, Taiwan. Deuterium oxide (D2O, molecular weight: 20.027 g mol−1, purity: 99.8% D) was purchased from Thermo Scientific Chemicals. The Sustainion X-37 FA membrane was obtained from Dioxide Materials, a CO2 recycling company. Carbon felt (thickness – 6.5 mm) was purchased from Clean Energy Technology. A BioLogic VMP3 multichannel Potentiostat was employed for electrochemical measurements, while SP-150e was used for ARFB testing. A Bruker AVANCE III HD 600 MHz nuclear magnetic resonance (NMR) spectrometer was utilized for 1H-NMR analysis. UV-visible analysis in the range of 190 to 800 nm was conducted using a V-670 JASCO spectrometer. FT/IR – 6700, JASCO Fourier transform infrared spectroscopy (FTIR) was performed with powdered samples in the range of 4000–400 cm−1. Pin flow energy storage devices were employed in this study.Solubility test
CDA and CDO were added in 5 ml of 1 M KOH solution until saturation was achieved. The solution was left overnight, and then filtration was used to eliminate insoluble residues. The soluble anolyte obtained was diluted to lower concentrations to compare it against known concentration standards. This process helps to determine the maximum solubility of both CDA and CDO.Electrochemical measurement
Cyclic voltammetry (CV) and linear sweep voltammetry (LSV) were measured by using a three-electrode system in a closed environment at 25 °C. A three-electrode system consisting of glassy carbon (with an active surface area – 0.196 cm2) as a working electrode, a platinum wire (99.99%) as a counter electrode, and an Ag/AgCl electrode soaked in a 3 M AgCl solution serving as a reference electrode was employed to perform CV and LSV measurements. Before each measurement, the glassy carbon electrode surface was polished using alumina suspension and then sonicated for 3 minutes, followed by cleaning with ethanol. Electrochemical characterizations were performed using a BioLogic VMP3 multichannel Potentiostat. A 5 mM sample of CDO and CDA dissolved in 1 M KOH was employed, with a scan rate of 10 mV s−1. LSV measurement was carried out by a rotating disc electrode (RDE) fixed with a Pine rotating shaft. A 5 mM sample of CDO/CDA dissolved in 1 M KOH was tested at various rotation speeds from 300–2700 rpm, with a potential sweep value of 10 mV s−1, from 0 to −0.6 V. LSV measurements of 5 mM of K4[FeII(CN)6] in 1 M KOH were carried out in the potential range from 0 to 0.6 V.Redox flow battery tests
The anolyte and catholyte were prepared in a ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, due to the quasi-reversible nature of CDO and CDA. A solution containing 50 mM of CDA or CDO with 100 mM of K4[FeII(CN)6] dissolved in 1 M KOH was used. The flow of the electrolyte was controlled at 25 rpm using a peristaltic pump via the flow-by method.18 To enhance the wettability of the carbon felt (active surface area – 5 cm2), it was sintered for 12 h at a stable temperature of 400 °C in a high-temperature furnace before assembling a battery. This process increased the electrochemical surface area of the carbon felt, improving its contact with the electrolyte. An imidazolium-functionalized styrene and vinyl benzyl chloride polymer membrane (X-37 FA membrane) was used as an anion exchange membrane to separate the anolyte and catholyte. The membrane was immersed in 1 M KOH to convert Cl− ions into OH− ions, making it suitable for use in an ARFB. After assembling the battery, a potentiostat SP-150e was used to apply a constant current of 0.4 mA cm−2 and monitor the performance of the ARFB.
2, due to the quasi-reversible nature of CDO and CDA. A solution containing 50 mM of CDA or CDO with 100 mM of K4[FeII(CN)6] dissolved in 1 M KOH was used. The flow of the electrolyte was controlled at 25 rpm using a peristaltic pump via the flow-by method.18 To enhance the wettability of the carbon felt (active surface area – 5 cm2), it was sintered for 12 h at a stable temperature of 400 °C in a high-temperature furnace before assembling a battery. This process increased the electrochemical surface area of the carbon felt, improving its contact with the electrolyte. An imidazolium-functionalized styrene and vinyl benzyl chloride polymer membrane (X-37 FA membrane) was used as an anion exchange membrane to separate the anolyte and catholyte. The membrane was immersed in 1 M KOH to convert Cl− ions into OH− ions, making it suitable for use in an ARFB. After assembling the battery, a potentiostat SP-150e was used to apply a constant current of 0.4 mA cm−2 and monitor the performance of the ARFB.
Computational method
Geometry optimizations and single point frequency calculations for all structures were conducted in the Orca 4.2.0 software package. The initial structures of chelidamic acid (CDA) and chelidonic acid (CDO) were constructed using Avogadro software. Density functional theory (DFT) calculations were performed using the B3LYP hybrid functional and 6-311++G(d,p) basis set. Spin-unrestricted calculations are used to allow for any possible bond cleavage during geometry optimization of the radical species. The solvent effect was included in the calculations by employing the conductor-like polarizable continuum model (CPCM), using a dielectric constant of 70, to implicitly account for solvent effects of 1 M KOH. The optimized molecular geometries and HOMO–LUMO isosurfaces were visualized using Chemcraft.Results and discussion
Electrochemical characterization
Cyclic voltammetry measurements were performed to determine the standard potential of the redox active material. Additionally, the reversibility was assessed by evaluating the ratio of peak current between the anode and cathode. The value of ratio 1 indicates a reversible electrochemical reaction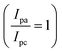 . In our study, the initial three cycles of CDO and CDA were analyzed, revealing a quasi-reversible
. In our study, the initial three cycles of CDO and CDA were analyzed, revealing a quasi-reversible 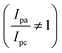 rate of electron transfer between the electrode and the redox material, as indicated by the unequal peak current values of Ipa and Ipc in the negative potential range.19 The standard redox potentials of CDA and CDO were calculated from the anodic and cathodic peak potential ((Epa + Epc)/2), yielding values of −0.21 and −0.20 V vs. Ag/AgCl, respectively (Fig. 1). In both cases, the ketone served as the active site for the electrochemical reduction, similar to quinone, and anthraquinone in Fig. 2.15 The reduction behavior of CDA (pyridone) is evident in compounds like benzo[g]quinoline-4,5,10(1H)-trione, which contains a pyridone substructure. This reduction is observed when the compound is dissolved in DMSO (dimethyl sulfoxide).20 The reduction behavior of CDO is demonstrated in the xanthone structure, where the carbonyl group (C
rate of electron transfer between the electrode and the redox material, as indicated by the unequal peak current values of Ipa and Ipc in the negative potential range.19 The standard redox potentials of CDA and CDO were calculated from the anodic and cathodic peak potential ((Epa + Epc)/2), yielding values of −0.21 and −0.20 V vs. Ag/AgCl, respectively (Fig. 1). In both cases, the ketone served as the active site for the electrochemical reduction, similar to quinone, and anthraquinone in Fig. 2.15 The reduction behavior of CDA (pyridone) is evident in compounds like benzo[g]quinoline-4,5,10(1H)-trione, which contains a pyridone substructure. This reduction is observed when the compound is dissolved in DMSO (dimethyl sulfoxide).20 The reduction behavior of CDO is demonstrated in the xanthone structure, where the carbonyl group (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) is reduced by hydride (H−) transfer, resulting in the formation of a hydroxyl radical (C–OH). In this process, the pyrone ring acts as the redox center.21 When coupled with K4[FeII(CN)6] as a redox-active organo-metallic catholyte, CDA and CDO exhibited a theoretical potential window of 0.49 and 0.48 V, respectively.
O) is reduced by hydride (H−) transfer, resulting in the formation of a hydroxyl radical (C–OH). In this process, the pyrone ring acts as the redox center.21 When coupled with K4[FeII(CN)6] as a redox-active organo-metallic catholyte, CDA and CDO exhibited a theoretical potential window of 0.49 and 0.48 V, respectively.
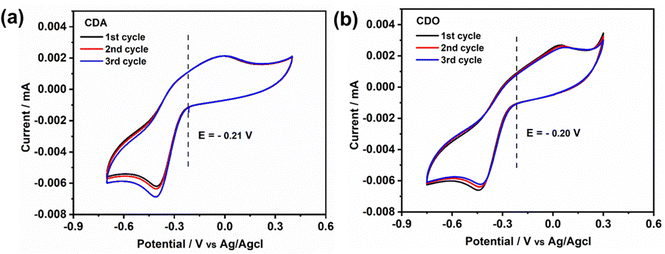 | ||
| Fig. 1 Cyclic voltammetry of 5 mM of (a) CDA and (b) CDO at the scan rate of 10 mV s−1 in 1 M KOH supporting solution. | ||
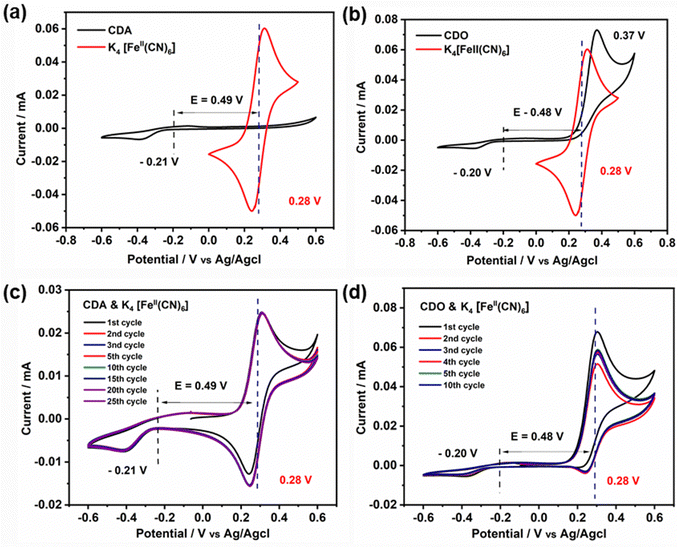
To demonstrate the reversibility of CDA and CDO, a long-term cyclability test was conducted using cyclic voltammetry, as shown in Fig. S1 (ESI†). Over 100 cycles, CDA exhibited more stable cyclic reversibility compared to CDO. In the case of CDA, the observed increase in reduction current and the shift with the number of cycles may be attributed to the deposition of CDA on the glassy carbon electrode surface, facilitated by the contact of the amine group.22,23 This organic molecule deposition increases capacitance, which in turn leads to a higher reduction current as the number of cycles increases, a finding supported by previous research.24 Additionally, chelidamic acid forms polymeric or dimeric structures with metal ions and hydrogen bonds with water, creating water clusters. This phenomenon, reported in previous research, provides evidence for the rise in reduction current as the number of cycles increases.25 In contrast, due to low conjugation, CDO becomes irreversible within a few cycles, leading to a decrease in current and a loss of reversibility as the number of cycles increases.
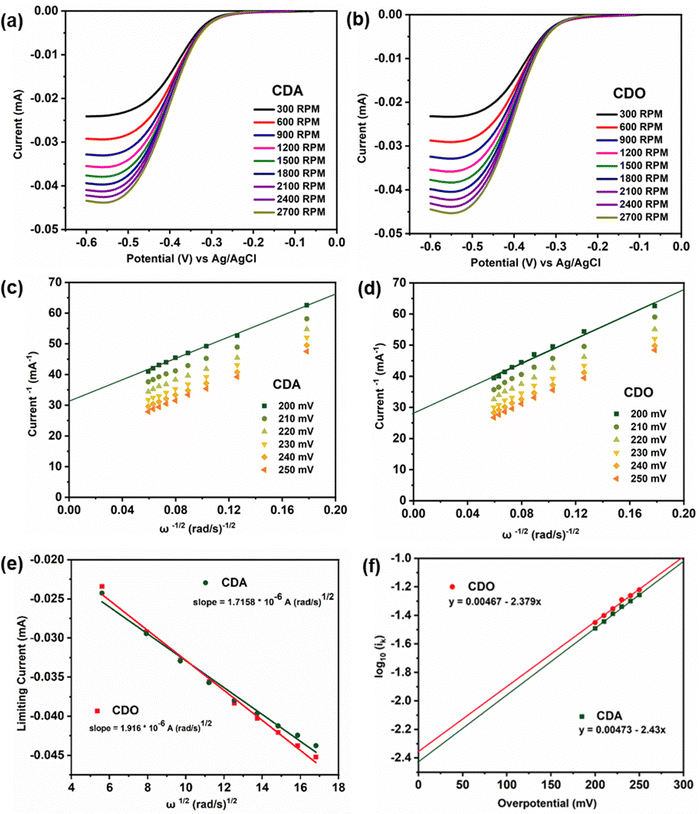
In LSV measurements (Fig. 3a, b and Fig. S2a, ESI†), the limiting current value elucidates the transition of active material from a stable state to a charged state.9 This transition results in a limiting current (iL) that varies with the square root of the angular velocity (ω1/2), as explained by the Levich eqn (1).19 The observed linear inverse relationship between the limiting current decreases and the increase in rotation speed suggests that the electrochemical reduction was controlled by diffusion. The kinetics of diffused redox-active species are crucial for the optimal performance of redox flow batteries. Ensuring fast diffusion rates helps in achieving higher current densities and lower overpotentials, leading to more efficient and effective energy storage and delivery. The kinetic rate constant of the redox active materials was then calculated by using the diffusion coefficient value obtained from eqn (1), with the slope value of CDA, and CDO recorded as 1.7158 × 10−6 and 1.916 × 10−6 mA rad−1 s−1, from the Koutecky Levich plot (Fig. 3e and Fig. S2b, ESI†),
| iL = 0.625nFAD2/3ω1/2ν−1/6C0 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485 C mol−1), A represents the surface area of the electrode (0.196 cm2), D signifies the diffusion coefficient of the redox active material, ν denotes the kinetic viscosity of 1 M KOH (1.07 × 10−2 cm2 s−1) and C0 represents the concentration of the active material (0.005 × 10−3 mol cm−3). Consequently, the diffusion coefficient (D) values for CDA and CDO were calculated as 5.09 × 10−8, and 5.998 × 10−8 cm2 s−1. To minimize error, the diffusion coefficient value of the known K4[FeII(CN)6] was determined from Fig. S2 (ESI†) and compared with previously published research papers.15,26
485 C mol−1), A represents the surface area of the electrode (0.196 cm2), D signifies the diffusion coefficient of the redox active material, ν denotes the kinetic viscosity of 1 M KOH (1.07 × 10−2 cm2 s−1) and C0 represents the concentration of the active material (0.005 × 10−3 mol cm−3). Consequently, the diffusion coefficient (D) values for CDA and CDO were calculated as 5.09 × 10−8, and 5.998 × 10−8 cm2 s−1. To minimize error, the diffusion coefficient value of the known K4[FeII(CN)6] was determined from Fig. S2 (ESI†) and compared with previously published research papers.15,26
In the Koutecky Levich plot, the inverse limiting current value 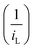 was plotted against the inverse square root of various overpotentials
was plotted against the inverse square root of various overpotentials 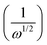 , showing a linear relationship (Fig. 3c, d and Fig. S2c, ESI†). The logarithm of the kinetic current (log
, showing a linear relationship (Fig. 3c, d and Fig. S2c, ESI†). The logarithm of the kinetic current (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ik) value was extracted from the intercept of the y-axis
ik) value was extracted from the intercept of the y-axis 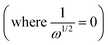 or it can be calculated from eqn (2). Additionally, the Tafel plot was plotted with various over potentials against their corresponding log
or it can be calculated from eqn (2). Additionally, the Tafel plot was plotted with various over potentials against their corresponding log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ik values (Fig. 3f and Fig. S2d, ESI†) and the antilogarithm of the intercept (where the overpotential is zero) of the y-axis is equal to nFA k0C0, which is used to calculate the kinetic rate constant,19,27,28
ik values (Fig. 3f and Fig. S2d, ESI†) and the antilogarithm of the intercept (where the overpotential is zero) of the y-axis is equal to nFA k0C0, which is used to calculate the kinetic rate constant,19,27,28
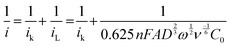 | (2) |
| ik = nFAk0C0 | (3) |
From eqn (3), the calculated kinetic rate constants (k0) for CDA, and CDO were found to be 2.66 × 10−4, and 2.26 × 10−4 cm s−1, respectively (Table 1). The derived kinetic rate constant of K4[FeII(CN)6] (Fig. S2, ESI†) aligns well with those reported in the literature, indicating a high level of comparability.29 However, it is noteworthy that the kinetic rate constants of CDA and CDO were larger than those of vanadium redox flow battery electrolytes such us V2+/V3+ and VO2+/VO2+, which were reported as 1.75× 10−5 and 7.5 × 10−4 cm s−1.30,31 Additionally, the CDA and CDO exhibited a maximum solubility of 0.55 M and 0.59 M in 1 M KOH, as determined by UV-visible spectra (Fig. S3, ESI†).
| Anolyte | Half-cell potential (V) | Diffusion coefficient (cm2 s−1) | Kinetic rate constant (cm s−1) |
|---|---|---|---|
| CDA | −0.21 | 5.09 × 10−8 | 2.26 × 10−4 |
| CDO | −0.20 | 5.998 × 10−8 | 2.66 × 10−4 |
Charge–discharge and structural characterization
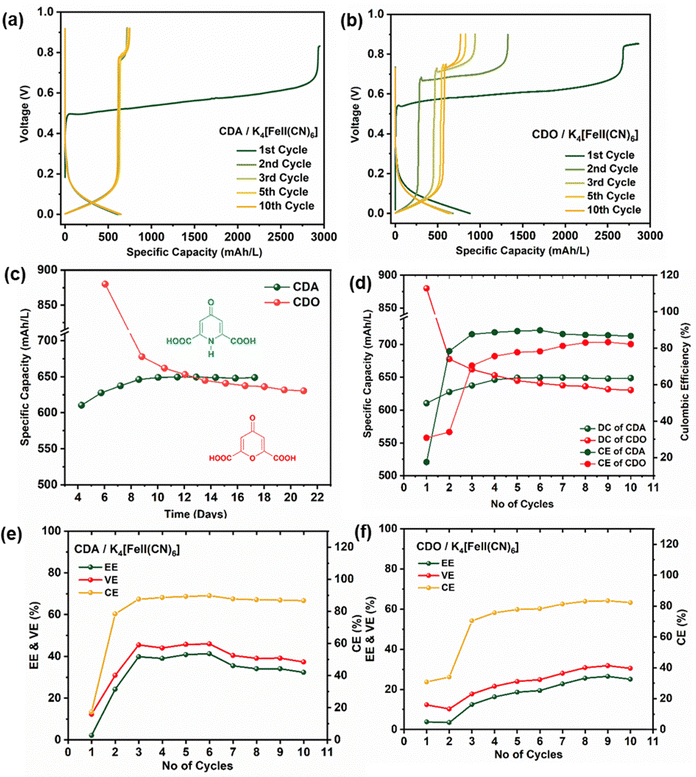
The ARFB of CDA/K4[FeII(CN)6] and CDO/K4[FeII(CN)6] underwent charge–discharge cycles over 10 cycles within the voltage range of 0 to 0.9 V (Fig. 4(a) and (b)). Notably, the charge–discharge characteristics of both CDA and CDO displayed an unusual charge–discharge plateau, indicating their dependence on structural characteristics. The discharge capacity of CDA/K4[FeII(CN)6] started at approximately 630 mA h L−1 in the first cycle, gradually increasing to around 650 mA h L−1 and remaining stable for up to 17 days. Conversely, CDO/K4[FeII(CN)6] displayed its discharge capacity at approximately 880 mA h L−1 but linearly declined to 630 mA h L−1 by the end of 21 days (Fig. 4c and d). This indicates that the pyridone heterocyclic compound in CDA offers greater stability compared to the pyrone compound in CDO. Regarding the energy efficiency (EE), coulombic efficiency (CE), and voltage efficiency (VE), CDA exhibited an average value of 36%, 87%, and 41%, respectively, while CDO showed an average value of 19%, 74%, and 24%, respectively (Fig. 4e and f).32 These outcomes suggest the superior performance of CDA compared to CDO. The performance of redox flow batteries at low current density often results in lower coulombic efficiency (CE) due to uneven ion and electron transfer, unlike the more efficient charge transfer observed at higher current densities. Additionally, the voltage window during charge–discharge testing also impacts coulombic efficiency.33In the first cycle of CDA/K4[FeII(CN)6] and CDO/K4[FeII(CN)6], a single charge plateau was observed alongside a corresponding discharge plateau. Interestingly, in this initial cycle, the capacity of the charge plateau was three times higher than the discharge capacity, resulting in a lower CE of approximately 20% (Fig. 4c and d). The high Charge capacity in the first cycle is related to the total electron withdrawal from the 0.1 M K4[FeII(CN)6]. However, the low discharge capacity is linked to the limited reversible electron release process from CDA and CDO. This discrepancy leads to low coulombic efficiency in the first cycle. However, from the second cycle, the charging process exhibited two distinct plateaus, the first one at 0 V and the next at approximately 0.7 V, while a single discharge plateau remained. Notably, these two plateaus reversibly appeared from the second cycle to the tenth cycle in CDA, maintaining a stable capacity. In contrast, in CDO, the voltage of the plateaus (∼0.7 V) increases with each cycle, resulting in a decrease in both charge and discharge capacity.
X-37 FA membranes were subjected to FTIR analysis before and after 10 cycles of CDA/K4[FeII(CN)6] and CDO/K4[FeII(CN)6] to assess their stability, which could potentially impact the voltage drop in the ARFB. The membrane primarily comprised tetra methyl imidazole along with a copolymer of styrene and vinyl benzyl chloride (VBC). The presence of O–H stretching at 3400 cm−1 indicated the OH group of KOH or K4[FeII(CN)6], while the small peak at 2040 cm−1 denoted the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N peak from K4[FeII(CN)6].30,31 Additionally, peaks observed at 2923, 2850, and 3021 cm−1 represent the C–H (sp3) and
N peak from K4[FeII(CN)6].30,31 Additionally, peaks observed at 2923, 2850, and 3021 cm−1 represent the C–H (sp3) and ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–H (sp2) stretching of tetramethyl imidazole, as depicted in Fig. S4 (ESI†). Peaks at 1647 and 1561 cm−1 were attributed to the C
C–H (sp2) stretching of tetramethyl imidazole, as depicted in Fig. S4 (ESI†). Peaks at 1647 and 1561 cm−1 were attributed to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N or N
N or N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–N stretching vibration of the imidazole ring structure.34 The persistent appearance of the stretching bands of imidazole C
C–N stretching vibration of the imidazole ring structure.34 The persistent appearance of the stretching bands of imidazole C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N+ and C–N+ at 1495 and 1445 cm−1 (Fig. 3),35 before and after 10 cycles, suggests that the X-37 FA membrane was not associated with the emerging new plateau in the second cycle.
N+ and C–N+ at 1495 and 1445 cm−1 (Fig. 3),35 before and after 10 cycles, suggests that the X-37 FA membrane was not associated with the emerging new plateau in the second cycle.
To understand the difference in stability between CDA and CDO, cyclic voltammetry measurements were conducted from −0.6 V to 0.6 V and compared with K4[FeII(CN)6] (Fig. 5(a) and (b)). Notably, no peak appeared in the CDA within the positive potential range, whereas a significant oxidation peak appeared at 0.37 V in CDO, closely aligned with the oxidation peak of K4[FeII(CN)6]. This prompts curiosity about the compatibility of CDA and CDO anolytes with K4[FeII(CN)6] in basic solution, especially when cross-over occurs in ARFB. Consequently, an investigation was initiated to explore the cyclic voltammetry stability of the anolyte when paired with an equal amount of catholyte.27 The cyclic voltammetry of equimolar mixed CDA and K4[FeII(CN)6] exhibited stable cyclic behavior over 25 cycles at a scan rate of 5 mV s−1 (Fig. 5c). However, employing the same approach with CDO revealed a quasi-reversible K4[FeII(CN)6] cyclic behavior, accompanied by a reduction in current values with an increasing number of cycles (Fig. 5d). This observation sheds light on the reason for the notable loss of discharge capacity in CDO/K4[FeII(CN)6] systems. However, it doesn’t explain the mechanism behind the unstable CDO in the basic medium.
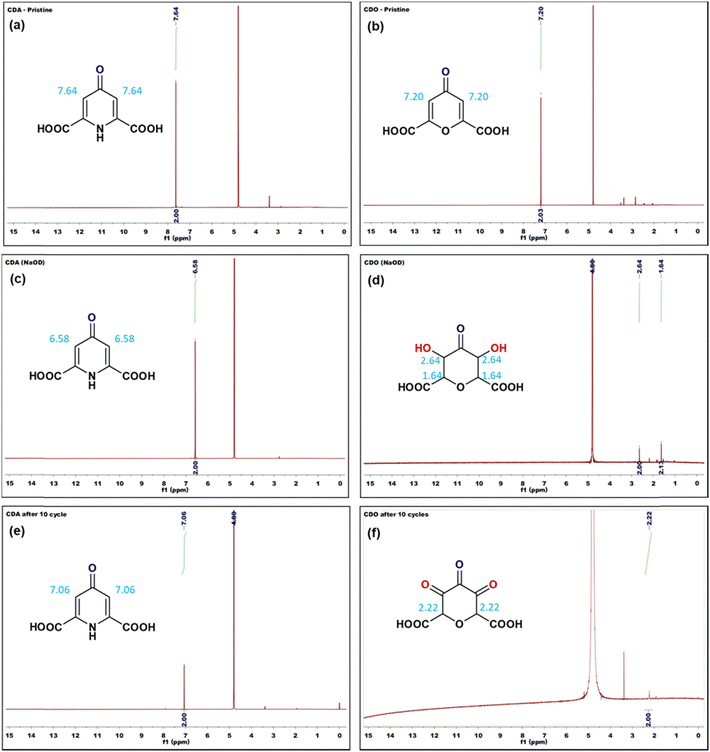
In addition, to gain insight into the structural changes in CDA and CDO before and after reaction, 1H-NMR spectroscopy was employed. As depicted in Fig. 6, the olefinic proton peaks of CDA and CDO (in D2O solvent) were observed at 7.64 and 7.20 ppm (Fig. 6a and b), respectively. Upon dissolution of pristine CDA and CDO in a solution containing 40% NaOH + D2O, their stability in basic conditions was varied. Interestingly, the absence of the proton peak at 7.20 ppm was noted in CDO, while the proton peaks of CDA shifted to 6.58 ppm due to the high molarity of 3 M NaOD.36 The observed shift of the proton signal belonging to CDA indicates the occurrence of tautomerism in the basic medium (Fig. 6c).37 Subsequent 1H-NMR data of CDO after 10 cycles of discharge showed no peaks around 7 ppm. However, it is supported by the presence of a proton peak at 2.22 ppm (Fig. 6f). The absence of a proton peak in CDO suggests a nucleophilic addition reaction in the basic medium, which is supported by the proton peaks at 2.64 and 1.64 ppm (Fig. 6d). However, CDA retained its proton peak at 7.06 ppm even after 10 cycles (Fig. 6e), indicating its stability in the basic medium over multiple cycles.
Tautomerization is a chemical reaction that results in the rearrangement of bonds in a compound. This process creates an equilibrium between the keto form, characterized by a carbon–oxygen double bond (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), and the enol form, which features a carbon–oxygen single bond (C–OH). In CDA (Fig. 7a), tautomerization involves the shifting of a proton between amine nitrogen to carbonyl oxygen, leading to keto (C
O), and the enol form, which features a carbon–oxygen single bond (C–OH). In CDA (Fig. 7a), tautomerization involves the shifting of a proton between amine nitrogen to carbonyl oxygen, leading to keto (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) – enol (C–OH) tautomerization. This process involves the conversion of dihydro-4-oxo-2,6-pyridone-dicarboxylic acid (CDA) into 4-hydroxy pyridone-2,6-dicarboxylic acid (4-HPD).37,38 In the RFB environment, particularly in an alkaline solution, nucleophiles like H2O and OH− are predominant. In CDO (Fig. 7b), a carbon–carbon double bond is located adjacent to an α,β-unsaturated ketone (carbonyl ketone). The carbon atom directly attached to the carbonyl group is known as the α carbon, followed by the β carbon. The electron-withdrawing nature of the carbonyl group makes this double bond highly reactive towards nucleophiles (–OH) in an alkaline medium. The nucleophiles directly add to the α carbon, forming a saturated ketone (carbonyl ketone), as shown in Fig. 7b.39,40 This process involves the conversion of 4-oxo-4H-pyran-2,6-dicarboxylic acid (CDO) into tetrahydro-3,5-dihydroxy-4-oxo-2H-pyran-2,6-dicarboxylic acid (TOHD). The structure of TOHD is further supported by the 1H-NMR spectra in Fig. 6d (CDO-NaOD). In Fig. 7c, the presence of tetrahydro-3,4,5-trioxo-2H-pyran-2,6-dicarboxylic acid (THD) is evidenced by an oxidation peak at 0.37 V in the cyclic voltammetry (Fig. 5b). These oxidation behaviours have been previously reported in quinoxaline derivatives in an alkaline medium.41 Furthermore, the presence of THD is confirmed by the 1H-NMR spectra of CDO after 10 cycles of discharge, as shown in Fig. 6d. These findings help to support the tautomerization and nucleophilic addition reaction in CDA and CDO in Fig. 7.
O) – enol (C–OH) tautomerization. This process involves the conversion of dihydro-4-oxo-2,6-pyridone-dicarboxylic acid (CDA) into 4-hydroxy pyridone-2,6-dicarboxylic acid (4-HPD).37,38 In the RFB environment, particularly in an alkaline solution, nucleophiles like H2O and OH− are predominant. In CDO (Fig. 7b), a carbon–carbon double bond is located adjacent to an α,β-unsaturated ketone (carbonyl ketone). The carbon atom directly attached to the carbonyl group is known as the α carbon, followed by the β carbon. The electron-withdrawing nature of the carbonyl group makes this double bond highly reactive towards nucleophiles (–OH) in an alkaline medium. The nucleophiles directly add to the α carbon, forming a saturated ketone (carbonyl ketone), as shown in Fig. 7b.39,40 This process involves the conversion of 4-oxo-4H-pyran-2,6-dicarboxylic acid (CDO) into tetrahydro-3,5-dihydroxy-4-oxo-2H-pyran-2,6-dicarboxylic acid (TOHD). The structure of TOHD is further supported by the 1H-NMR spectra in Fig. 6d (CDO-NaOD). In Fig. 7c, the presence of tetrahydro-3,4,5-trioxo-2H-pyran-2,6-dicarboxylic acid (THD) is evidenced by an oxidation peak at 0.37 V in the cyclic voltammetry (Fig. 5b). These oxidation behaviours have been previously reported in quinoxaline derivatives in an alkaline medium.41 Furthermore, the presence of THD is confirmed by the 1H-NMR spectra of CDO after 10 cycles of discharge, as shown in Fig. 6d. These findings help to support the tautomerization and nucleophilic addition reaction in CDA and CDO in Fig. 7.
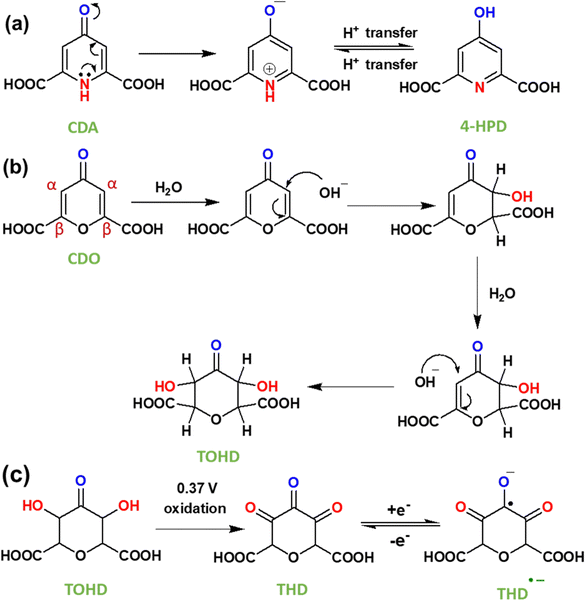 | ||
| Fig. 7 (a) Tautomerization reaction mechanism in CDA, (b) nucleophilic addition mechanism in CDO and (c) electrochemical reaction in CDO after nucleophilic addition. | ||
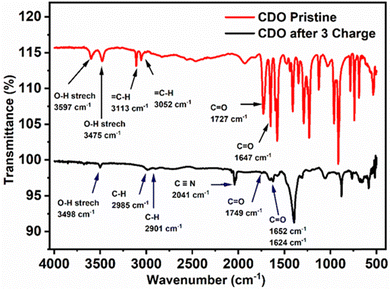
To further confirm the nucleophilic addition to CDO, the FTIR spectra of pristine and after three charge cycles of electrolyte samples were obtained. In pristine CDO (Fig. 8), the O–H stretching was observed at 3597 and 3475 cm−1, corresponding to the –COOH group, while the ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–H (sp2) modes of CDO were noted at 3113 and 3052 cm−1. The C
C–H (sp2) modes of CDO were noted at 3113 and 3052 cm−1. The C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O conjugated functional group was located at 1727 cm−1, indicating that the –COOH, and the C
O conjugated functional group was located at 1727 cm−1, indicating that the –COOH, and the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O redox-active site was found at 1647 cm−1.
O redox-active site was found at 1647 cm−1.
After three charge cycles of CDO, a peak shift of the O–H stretch was observed at 1498 cm−1, transitioning from ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–H (sp2) to –C–H (sp3).17,42 Additionally, the peak at 2040 cm−1 represents the C
C–H (sp2) to –C–H (sp3).17,42 Additionally, the peak at 2040 cm−1 represents the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N peak from K4[FeII(CN)6], which denotes cross-over in the battery.31 The C
N peak from K4[FeII(CN)6], which denotes cross-over in the battery.31 The C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching of –COOH shifts to 1749 cm−1 due to the reduced conjugation in CDO. Notably, the presence of two carbonyl peaks at 1652 and 1623 cm−1 provides evidence of two hydroxyl groups or nucleophilic additions after the first cycle. This is further supported by the absence of the proton peak in 40% NaOH + D2O and after ten cycles, as observed in the 1H-NMR of CDO, along with the presence of an oxidation peak in CV.43
O stretching of –COOH shifts to 1749 cm−1 due to the reduced conjugation in CDO. Notably, the presence of two carbonyl peaks at 1652 and 1623 cm−1 provides evidence of two hydroxyl groups or nucleophilic additions after the first cycle. This is further supported by the absence of the proton peak in 40% NaOH + D2O and after ten cycles, as observed in the 1H-NMR of CDO, along with the presence of an oxidation peak in CV.43
The nucleophilic addition at α,β- unsaturated carbon (concerning carboxylic acid) not only explains the loss of discharge capacity but also accounts for the appearance of a new plateau in CDO after the first cycle in an alkaline medium. In contrast, the stability of CDA in the basic medium is attributed to tautomerism. Simply, tautomerism in CDA refers to the transfer of a proton from an amine nitrogen to a carbonyl oxygen. Due to this proton transfer in CDA, nucleophilic addition predominantly does not occur at the pyridone heteroatoms. As a result of enaol-1 reduction, two stable charge plateaus appear over 10 cycles (17 days).11 Additionally, the performance of a high concentration ARFB with 0.4 M CDA and CDO analysed using a current density of 40 mA cm−2, is shown in Fig. S5 and S6 (ESI†). CDA demonstrates stable cycling performance over 230 cycles, significantly outperforming CDO at high current density, with an average coulombic efficiency of 98%. This observation suggests that CDA exhibits better performance in ARFB compared to CDO in a basic medium.
To further support the findings on electrolyte stability and conductivity, the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) value of CDA, CDO, and their charged forms (CDA− and CDO−) were calculated using DFT analysis, as shown in Fig. 9. The energy gaps of CDA, CDO, CDA− and CDO− are 4.64, 4.8, 1.53 and 1.73 eV, respectively. According to frontier molecular orbital analysis, molecules with a small energy gap tend to exhibit greater electrolyte stability and higher conductivity. The smaller energy gap in CDA and CDA− anions compared to CDO and CDO− suggests that CDA is more stable than CDO. Additionally, the DFT analysis of the molecular charge distribution for CDA, CDO, 4-HPD−, and THD−, as shown in Fig. S7 (ESI†), provides further insights into their molecular reactivity. This analysis highlights regions of negative (blue) and positive (green) charges, which indicates potential sites for nucleophilic and electrophilic reactions. In CDA, CDO, and THD−, a significant negative charge is concentrated on the carbonyl group at the 4-position, suggesting this as the primary site for reduction reactions. For 4-HPD−, the negative charge concentration is located on the nitrogen atom, indicating the site of the reduction reaction.44,45
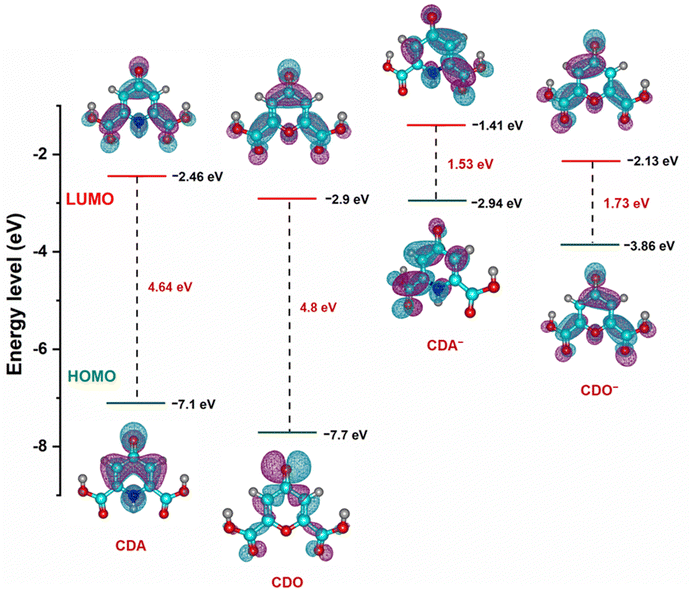 | ||
| Fig. 9 Optimized structure and calculated energy levels of CDA, CDO and charged CDA−, CDO− from DFT simulations. | ||
The deterioration of the CDO capacity at the beginning of the charge–discharge cycles is supported by cyclic voltammetry and DFT analysis, as shown in Fig. S8 (ESI†). The performance of CDA and CDO is compared with previously published ARFBs, as presented in Table 2. To enhance the efficiency of ARFBs, future research should focus on improving the reduction potential, resistance to side reactions and reversible characteristics of CDA and CDO by fine-tuning their molecular structure. In particular, a high conjugated structure is crucial, as it contributes life span and better performance at high current density.
| Electrolyte | Current density | Average CE (%) | D (cm2 s−1) | K 0 (cm s−1) | No. of cycles | Ref. |
|---|---|---|---|---|---|---|
| Anthrarufin/K4[FeII(CN)6] | 20 mA cm−2 | 88 | 1.87 × 10−6 | 2.63 × 10−3 | 20 cycles | 15 |
| Anthraquinone 2-sulfonic acid/BQDS | 8 mA cm−2 (200 mA) | — | 3.71 × 10−6 | 2.2 × 10−4 | 12 cycles | 46 |
| Benzoylpyridinuim salt/K4[FeII(CN)6] | 7.85 mA cm−2 | 95 | — | — | 10 cycles | 8 |
| CDA/K4[FeII(CN)6] | 0.04 mA cm−2 | 87 | 5.09 × 10−8 | 2.66 × 10−4 | 10 cycles | Present work |
| 40 mA cm−2 | 98 | 230 cycles | ||||
| CDO/K4[FeII(CN)6] | 0.04 mA cm−2 | 74 | 5.99 × 10−8 | 2.26 × 10−4 | 10 cycles | |
| 40 mA cm−2 | 96 | 230 cycles |
Conclusion
In this study, we explore the aqueous soluble anolytes of CDA and CDO, which share comparably similar molecular weights but are different in heteroatoms pyridone and pyrone. Although they initially display similar charge plateaus, their cycling stability diverges from the second cycle onwards. To unravel their stability in the basic medium and when paired with K4[FeII(CN)6]. We utilized CV, revealing stable behavior for CDA-K4[FeII(CN)6] but not for CDO-K4[FeII(CN)6]. Their structural characteristics were further analyzed during charging and discharging using 1H-NMR, FTIR spectroscopy and DFT analysis. The results indicate nucleophilic addition in CDO, evidenced by the absence of proton peaks in 1H-NMR and FTIR analysis after three charges, which correlates with decreased discharge capacity in subsequent cycles. Additionally, the redox stability of CDA and the deterioration of CDO are supported by HOMO–LUMO energy levels and molecular charge distribution plots. In contrast, CDA exhibits tautomerism in the basic medium, contributing to stable cycling over 17 days. These findings underscore the significant influence of heteroatoms on the stability of ARFBs, emphasizing the importance of active sites and heteroatoms in determining stability.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
The author is grateful for the financial support from the National Science and Technology Council (NSTC) of Taiwan, R.O.C., under grant numbers 110-2923-E-007-005, 111-2622-E-011-013, 111-3116-F-011-005, 112-2923-E-007-005, 112-2622-E-011-026, and 112-2221-E-011-013-MY3.References
- A. Hollas, X. L. Wei, V. Murugesan, Z. M. Nie, B. Li, D. Reed, J. Liu, V. Sprenkle and W. Wang, Nat. Energy, 2018, 3, 508–514 CrossRef CAS.
- S. V. Modak, D. Pert, J. L. Tami, W. Shen, I. Abdullahi, X. Huan, A. J. McNeil, B. R. Goldsmith and D. G. Kwabi, J. Am. Chem. Soc., 2024, 146, 5173–5185 CrossRef CAS PubMed.
- C. Sun and H. Zhang, ChemSusChem, 2022, 15, e202101798 CrossRef CAS PubMed.
- F. Hasan, V. Mahanta and A. A. A. Abdelazeez, Adv. Mater. Interfaces, 2023, 10 Search PubMed.
- K. X. Lin, R. Gómez-Bombarelli, E. S. Beh, L. C. Tong, Q. Chen, A. Valle, A. Aspuru-Guzik, M. J. Aziz and R. G. Gordon, Nat. Energy, 2016, 1 Search PubMed.
- D. Hey, R. B. Jethwa, N. L. Farag, B. L. D. Rinkel, E. W. Zhao and C. P. Grey, Nat. Commun., 2023, 14 Search PubMed.
- Y. Jing, E. W. Zhao, M. A. Goulet, M. Bahari, E. M. Fell, S. Jin, A. Davoodi, E. Jonsson, M. Wu, C. P. Grey, R. G. Gordon and M. J. Aziz, Nat. Chem., 2022, 14, 1103–1109 CrossRef CAS PubMed.
- C. S. Sevov, K. H. Hendriks and M. S. Sanford, J. Phys. Chem. C, 2017, 121, 24376–24380 CrossRef CAS.
- B. Yang, L. Hoober-Burkhardt, S. Krishnamoorthy, A. Murali, G. K. S. Prakash and S. R. Narayanan, J. Electrochem. Soc., 2016, 163, A1442–A1449 CrossRef CAS.
- D. C. Crans, M. Mahroof-Tahir, M. D. Johnson, P. C. Wilkins, L. Yang, K. Robbins, A. Johnson, J. A. Alfano, M. E. Godzala, L. T. Austin and G. R. Willsky, Inorg. Chim. Acta, 2003, 356, 365–378 CrossRef CAS.
- A. Wojciechowska, J. Janczak, K. N. Jarzembska, T. Rojek, A. Gorzsás, Ü. Kersen, T. K. Olszewski and J. Jezierska, Polyhedron, 2023, 230 Search PubMed.
- E. Avdeeva, E. Shults, T. Rybalova, Y. Reshetov, E. Porokhova, I. Sukhodolo, L. Litvinova, V. Shupletsova, O. Khaziakhmatova, I. Khlusov, A. Guryev and M. Belousov, Biomolecules, 2019, 9 Search PubMed.
- H. G. Han, Z. X. He, J. L. Liu, Y. Chen and S. Q. Liu, Ionics, 2015, 21, 167–174 CrossRef CAS.
- W. Ruan, J. Mao, S. Yang, C. Shi, G. Jia and Q. Chen, Chem. Commun., 2020, 56, 3171–3174 RSC.
- C. Mirle, V. Medabalmi and K. Ramanujam, Catal. Today, 2021, 370, 173–180 CrossRef CAS.
- K. Lin, R. Gómez-Bombarelli, E. S. Beh, L. Tong, Q. Chen, A. Valle, A. Aspuru-Guzik, M. J. Aziz and R. G. Gordon, Nat. Energy, 2016, 1, 1–8 CrossRef.
- F.-M. Wang, K. Wagari Guji, A. Ramar, L. Merinda and W.-C. Chien, ACS Sustainable Chem. Eng, 2021, 9, 12286–12299 CrossRef CAS.
- P. Leung, X. H. Li, C. P. de León, L. Berlouis, C. T. J. Low and F. C. Walsh, RSC Adv., 2012, 2, 10125–10156 RSC.
- H. Wang, S. Y. Sayed, E. J. Luber, B. C. Olsen, S. M. Shirurkar, S. Venkatakrishnan, U. M. Tefashe, A. K. Farquhar, E. S. Smotkin, R. L. McCreery and J. M. Buriak, ACS Nano, 2020, 14, 2575–2584 CrossRef CAS PubMed.
- M. d M. Blanco, A. Marcos, M. A. Ruiz, C. Avendano, J. C. Menendez, C. Pedrega and J. M. Pingarron, Heterocycl. Commun., 2000, 6, 295–300 Search PubMed.
- X. Yan, L. Zhang, Q. Liu, G. Wang, X. Liu and W. Yang, Polymer Chem., 2017, 8, 6356–6361 RSC.
- H. Thissen, R. A. Evans and V. Ball, Processes, 2021, 9, 82 CrossRef CAS.
- M.-A. Goulet, M. Skyllas-Kazacos and E. Kjeang, Carbon, 2016, 101, 390–398 CrossRef CAS.
- R. P. Gautam and C. J. Barile, J. Phy. Chem. C, 2021, 125, 8177–8184 CrossRef CAS.
- M. Mirzaei, H. Eshtiagh-Hosseini, Z. Karrabi, B. Notash, A. Bauzá Riera and A. Frontera Beccaria, J. Mol. Struct, 2015, 1080, 30–36 CrossRef CAS.
- S. Jung, R. Kortlever, R. J. Jones, M. F. Lichterman, T. Agapie, C. C. McCrory and J. C. Peters, Anal. Chem., 2017, 89, 581–585 CrossRef CAS PubMed.
- B. G. Tegegne, D. M. Kabtamu, Y.-Z. Li, Y.-T. Ou, Z.-J. Huang, N.-Y. Hsu, H.-H. Ku, Y.-M. Wang and C.-H. Wang, J. Energy Storage, 2023, 61, 106753 CrossRef.
- B. G. Tegegne, D. M. Kabtamu, Y.-T. Ou, G.-C. Chen, Z.-J. Huang, N.-Y. Hsu, H.-H. Ku, Y.-M. Wang and C.-H. Wang, J. Energy Storage, 2023, 73, 109201 CrossRef.
- Z. M. Bhat, R. Thimmappa, M. C. Devendrachari, S. P. Shafi, S. Aralekallu, A. R. Kottaichamy, M. Gautam and M. O. Thotiyl, J. Phys. Chem. Lett., 2017, 8, 3523–3529 CrossRef CAS PubMed.
- J. J. Kaczur, H. Yang, Z. Liu, S. D. Sajjad and R. I. Masel, C, 2020, 6, 33 CAS.
- K. Dimos, I. Panagiotopoulos, T. Tsoufis, R. Y. Gengler, A. Moukarika, P. Rudolf, M. A. Karakassides, T. Bakas and D. Gournis, Langmuir, 2012, 28, 10289–10295 CrossRef CAS.
- B. Liu, C. W. Tang, H. Jiang, G. Jia and T. Zhao, J. Power Sources, 2020, 477, 228985 CrossRef CAS.
- G. S. Nambafu, K. Siddharth, C. Zhang, T. Zhao, Q. Chen, K. Amine and M. Shao, Nano Energy, 2021, 89, 106422 CrossRef CAS.
- L. C. Jheng, C. Y. Hsu and H. Y. Yeh, Membranes (Basel), 2021, 11, 901 CrossRef CAS.
- G. Das, B. J. Park, J. Kim, D. Kang and H. H. Yoon, Sci. Rep., 2019, 9, 9572 CrossRef PubMed.
- M. G. Marino and K. D. Kreuer, ChemSusChem, 2015, 8, 513–523 CrossRef CAS.
- B. Chen, J. Lu, W. Mu, Y. Yang, B. Liu, Y. Yang, H. Wei, S. Peng and X. Li, J. Solut. Chem., 2022, 51, 1187–1198 CrossRef CAS.
- H. B. Schlegel, P. Gund and E. M. Fluder, J. Am. Chem. Soc., 1982, 104, 5347–5351 CrossRef CAS.
- K. Wedege, E. Dražević, D. Konya and A. Bentien, Sci. Rep., 2016, 6, 39101 CrossRef CAS PubMed.
- M. Schuchmann, J. Sonntag and C. Sonntag, J. Chem. Soc., Perkin Transact. 2, 1998, 791–796 RSC.
- C. Wang, Y. Wang, M. Tao, B. Yu, K. Zhang, J. Wei, Y. Liu, P. Zhang, G. Ding and Z. Tie, ACS Appl. Energy Mater., 2022, 5, 10379–10384 CrossRef CAS.
- S. S. Malaganvi, J. Tonannavar Yenagi and J. Tonannavar, Heliyon, 2019, 5, e01586 CrossRef PubMed.
- P. Kumar and K. K. Dubey, New Future Dev. Microb. Biotechnol. Bioeng., 2018, 165–181, DOI:10.1016/B978-0-444-63504-4.00013-X.
- Y. Zhen, C. Zhang, J. Yuan, Y. Zhao and Y. Li, J. Power Sources, 2020, 480, 229132 CrossRef CAS.
- C. Mirle and K. Ramanujam, ACS Appl. Energy Mater., 2022, 5, 9711–9721 CrossRef CAS.
- B. Yang, L. Hoober-Burkhardt, F. Wang, G. S. Prakash and S. Narayanan, J. Electrochem. Soc., 2014, 161, A1371 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ya00331d |
| This journal is © The Royal Society of Chemistry 2024 |