Unconventional stoichiometric two-dimensional potassium nitrides with anion-driven metallicity and superconductivity†
Qiuping
Yang
a,
Ying
Zhao
a,
Xue
Jiang
 *a,
Baotian
Wang
*a,
Baotian
Wang
 bc and
Jijun
Zhao
a
bc and
Jijun
Zhao
a
aKey Laboratory of Materials Modification by Laser, Ion and Electron Beams (Ministry of Education), Dalian University of Technology, Dalian 116024, China. E-mail: jiangx@dlut.edu.cn
bInstitute of High Energy Physics, Chinese Academy of Sciences, Beijing 100049, China
cSpallation Neutron Source Science Center, Dongguan 523803, China
First published on 23rd November 2023
Abstract
The design of compounds with interesting coordination geometries, exotic oxidation states, and intriguing properties is of fundamental interest in physics, chemistry, and materials science. Herein, first-principle swarm-intelligence structure search calculations identify two unconventional stoichiometric KN2 and KN4 monolayers, in which the coordination number of K atoms increases from 6 to 12, becoming two-dimensional (2D) metal nitrides with the highest coordination number. Nitrogen motifs in stable K–N monolayers depend on the nitrogen content (e.g., N2− dimer in KN2 and N20.5− dimer in KN4), and are accompanied by an electronic transition from superconducting to metallic. Intriguingly, the KN2 monolayer shows a unique superconducting energy gap with a calculated critical temperature (Tc) of 4.3 K under ambient conditions. The superconductivity is mainly derived from strong electron–phonon coupling (EPC) of the N 2p electrons and low- and mid-frequency K and N atomic vibrational modes. Our work provides key insight into 2D metal-bearing nitrides and the correlation between non-stoichiometry and conductivity mechanisms.
Introduction
Since the discovery of superconductivity in metallic mercury at 4.2 K in 1911, the exploration of superconductors and understanding of microscopic mechanisms have become important and challenging issues in condensed matter physics.1,2 Inspired by theoretical calculations, great breakthroughs have been achieved in H3S3,4 (203 K at 155 GPa) and LaH105,6 (260 K at 188 GPa) to fulfill the dream of high-temperature superconductivity. Although these materials display high superconducting transition temperature (Tc), high pressure and complicated experimental equipment greatly limit their practical applications.7In addition to pressure-induced superconductivity, the role of dimensionality reduction on superconductivity has also attracted massive attention. Compared with bulk superconducting materials, 2D superconductors play a critical and irreplaceable role in small portable magnetic resonance imagers, high-precision micro-magnetic field and low-dissipation integrated circuits.8–10 The 2D superconductivity state has recently been observed in graphene,11,12 transition-metal dichalcogenides (NbS2,13 MoS2,14 NbSe2,15 TiSe216), ZrNCl surface,17,18 single Pb layer,19etc., with the help of electron/hole doping, intercalation, gating, and substrate proximity effects. Their superconducting transition temperatures were estimated to be 1–30 K. However, the number of 2D intrinsic superconductors is rather limited and there is a pressing task to expand the family of 2D superconductors.
Nitrogen, as one of the major components of the atmosphere,20 is a fascinating element. But the understanding of nitrogen chemistry is very limited due to the extremely high stability of the triple-bond in the N2 molecule. For a long time, only nitride N3− and azide N3− nitrogen motifs were known. It was not until 2001 that Kniep et al. demonstrated the diazenides N22− in the deprotonated diazene N2H2 with a N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond.21 In the same year, binary diazenides SrN2 and BaN2 were synthesized for the first time.22 Subsequently, stable homoatomic ions N5− and N5+ were successfully discovered,23,24 greatly expanding the chemical richness of nitrogen. Lately, the study of N-rich nitrides revealed the ubiquity of charged [N2]x− (x = 1, 2, 3 or 4) dimers with N–N bond lengths from 1.15 to 1.35 Å in binary metal nitrides (e.g., LiN2,25 Li2N2,26 CrN2,27 IrN228).
N bond.21 In the same year, binary diazenides SrN2 and BaN2 were synthesized for the first time.22 Subsequently, stable homoatomic ions N5− and N5+ were successfully discovered,23,24 greatly expanding the chemical richness of nitrogen. Lately, the study of N-rich nitrides revealed the ubiquity of charged [N2]x− (x = 1, 2, 3 or 4) dimers with N–N bond lengths from 1.15 to 1.35 Å in binary metal nitrides (e.g., LiN2,25 Li2N2,26 CrN2,27 IrN228).
Introducing metal elements into nitrogen is an effective way to discover interesting nitrogen configurations and enrich the understanding of nitrogen evolution behavior. Specifically, 2D metal-bearing nitrogen-based materials exhibit diverse geometric structures and unique electronic properties, which are closely correlated with metal species and metal/nitrogen ratio. For 2D alkaline-earth metal nitrides (IIANs), a honeycomb BeN2 monolayer with direct bandgap and high mobility is expected to be useful for field-effect transistors (FETs).29 Interestingly, Ca2N, Sr2N and Ba2N sheets are electrides, in which the excess electrons are localized at the interstitial region and act as anions.30–32 On the other hand, 2D IIIANs (AlN, GaN, InN and TlN) with graphene-like honeycomb structures are semiconductors,33–35 while penta-AlN2 with Cairo pentagonal tiling geometry is a half-metal and shows ferromagnetism.36 Later, the prediction of 2D alkali metal nitrides (IANs) enriched the family of metal nitrides. In particular, a series of stable cation-deficient 2D K2N monolayers are p-type ferromagnetic metals or half metals with high Curie temperature of 480–1180 K.37
Encouraged by the aforementioned advance in 2D metal nitrides, we perform a systematic search for 2D N-rich KNx (x = 1–4) compounds via the particle swarm optimization algorithm.38,39 We have identified two stable KN2 and KN4 monolayers with unconventional stoichiometries, in which all N atoms form quasi-molecular N2 dimers. In the KN4 monolayer, the K atom reaches 12-fold hypercoordination, which is the highest one reported in 2D metal nitrides. The electronic properties of 2D KNx (x = 2, 4) monolayers are closely related to the nitrogen motif, that is, KN4 contains N20.5−, which is metallic, while KN2 containing N2− is superconducting with Tc of 4.3 K.
Computational details
Structural evolution algorithms play a key role in accelerating the discovery of novel 2D materials and broadening their application.40–45 The stable 2D K–N structural prediction was based on a global minimization of free energy surfaces merging ab initio total-energy calculations as implemented in the CALYPSO code.38,39,46 A vacuum space of more than 15 Å was added to avoid interaction between a layer and its periodic images along the c-axis. The structural relaxation and electronic property calculations were carried out by employing the Vienna ab initio Simulation Package (VASP),47,48 with electron–ion interactions described by the augmented wave potentials49 (3s23p64s1 and 2s22p3 valence states for K and N atoms, respectively) and plane-wave basis with a kinetic energy cutoff of 600 eV. The Monkhorst–Pack scheme50 with a dense k-point grid spacing of 2π × 0.03 Å−1 was chosen to ensure good convergence of the total energy. Dynamic stability was assessed by the supercell method51 implemented in the Phonopy code.52 Electron–phonon coupling (EPC) calculations were performed with density functional perturbation theory (DFPT) using the Quantum ESPRESSO package.53,54 Anisotropic superconducting properties were investigated by solving the fully anisotropic Migdal–Eliashberg equations as implemented in the electron–phonon Wannier (EPW) code.55–57 More details can be found in the Supplemental Material.Results and discussion
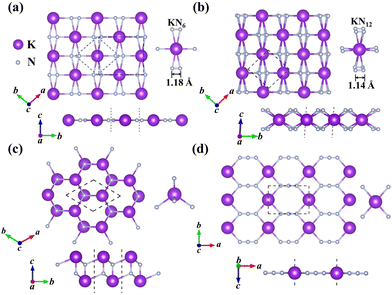
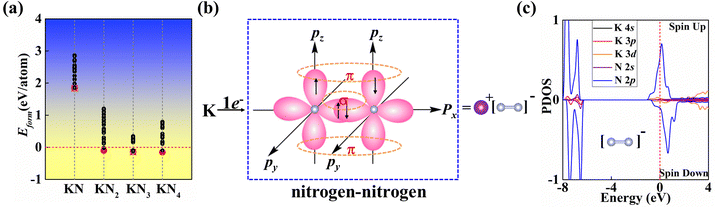
In this work, we mainly focus on the lowest-energy structural identification of changes in nitrogen proportion (KNx, where x = 1–4). We have successfully identified two hitherto unknown 2D thermodynamically and dynamically stable structures, i.e., superconducting KN2 (space group Cmmm, Fig. 1a) and metallic KN4 (space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , Fig. 1b) monolayers with unconventional stoichiometry. Up to now, several 2D non-stoichiometric compounds (e.g., Na2Cl, Na3Cl, and CaCl) have been synthesized.58 Both KN2 and KN4 monolayers have negative formation enthalpies with respect to the elemental solid of K59 and the molecular crystal of N260 (Fig. 2a), indicating that the synthetic reactions by converting K and N2 into KN2 and KN4 are thermodynamically favorable and experimentally feasible. The cohesive energies of KN2 and KN4 monolayers are 5.69 and 6.70 eV per atom, respectively, which surpasses the experimentally synthesized silicene (3.48 eV per atom)61 and phosphorene (3.30 eV per atom)62 and is comparable to MoS2 (5.05 eV per atom).63 Phonon dispersions of KN2 and KN4 with no imaginary frequencies in the whole Brillouin zone demonstrate that they are dynamically stable (Fig. S1, ESI†). According to the derived elastic constants (Table S1, ESI†), KN2 and KN4 satisfy the criteria for mechanical stability. We also calculate the Young's modulus E(θ) and Poisson's ratio v(θ) (Fig. S2, ESI†), which show anisotropy in both cases. Other stoichiometric formulas of KNx (x = 1, 3) (see Fig. 1c and 1d for structures) are incompatible with thermodynamic or dynamical stability (Fig. 2a and Fig. S3, ESI†); thus they are not conducive to experimental synthesis and will not be further considered thereafter.
, Fig. 1b) monolayers with unconventional stoichiometry. Up to now, several 2D non-stoichiometric compounds (e.g., Na2Cl, Na3Cl, and CaCl) have been synthesized.58 Both KN2 and KN4 monolayers have negative formation enthalpies with respect to the elemental solid of K59 and the molecular crystal of N260 (Fig. 2a), indicating that the synthetic reactions by converting K and N2 into KN2 and KN4 are thermodynamically favorable and experimentally feasible. The cohesive energies of KN2 and KN4 monolayers are 5.69 and 6.70 eV per atom, respectively, which surpasses the experimentally synthesized silicene (3.48 eV per atom)61 and phosphorene (3.30 eV per atom)62 and is comparable to MoS2 (5.05 eV per atom).63 Phonon dispersions of KN2 and KN4 with no imaginary frequencies in the whole Brillouin zone demonstrate that they are dynamically stable (Fig. S1, ESI†). According to the derived elastic constants (Table S1, ESI†), KN2 and KN4 satisfy the criteria for mechanical stability. We also calculate the Young's modulus E(θ) and Poisson's ratio v(θ) (Fig. S2, ESI†), which show anisotropy in both cases. Other stoichiometric formulas of KNx (x = 1, 3) (see Fig. 1c and 1d for structures) are incompatible with thermodynamic or dynamical stability (Fig. 2a and Fig. S3, ESI†); thus they are not conducive to experimental synthesis and will not be further considered thereafter.
The primitive cell of the KN2 monolayer consists of three atoms—one K atom and two equivalent N atoms. The optimized cell lattice parameters are a = b = 4.42 Å, in which the K atom is coordinated by six N atoms, forming planar K-centered nitrogen wheels (K@N6, Fig. 1a). The K–N bond lengths are 2.76 Å and 2.95 Å, respectively, which are comparable to those in 2D K–N compounds37 (e.g., 2.790 Å in H-K2N, 2.785 Å in T-K2N, and 2.922 Å in I-K2N). The most striking structural feature is that all N atoms exist in quasi-molecular N2 dimers with a nitrogen–nitrogen distance of 1.18 Å, which is much shorter than the N–N single bond length of 1.40 Å in the crystalline phase of the elemental solid.64 The nitrogen–nitrogen bond length of our KN2 monolayer is between the N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N triple bond length (e.g., 1.10 Å in hexagonal N265) and the N
N triple bond length (e.g., 1.10 Å in hexagonal N265) and the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N double bond lengths, such as 1.23 Å in penta-PtN2 monolayer,66 1.22 Å in IrN2 monolayer67 and 1.24 Å for bulk BaN2.68 N2 dimers in KN2 may show an overlap between the double and triple bonds consisting of σ and π bonds, where pz orbitals form localized π bonds (Fig. 2b). To decipher the nature of bonding and determine the charge state of quasi-molecular N2, Bader charge analysis was performed. Each K atom loses 0.82 e, having a formal oxidation of +1, while the Bader partial charge is −0.40 e for N. These results confirm that this species is [N2]− wherein all of the N atoms assume a −0.5 formal oxidation state. Obviously, [N2]− in KN2 contains an unpaired p electron that produces a paramagnetic state, which is further confirmed by the analysis of the spin-polarized projected density of states (PDOS) in Fig. 2c.
N double bond lengths, such as 1.23 Å in penta-PtN2 monolayer,66 1.22 Å in IrN2 monolayer67 and 1.24 Å for bulk BaN2.68 N2 dimers in KN2 may show an overlap between the double and triple bonds consisting of σ and π bonds, where pz orbitals form localized π bonds (Fig. 2b). To decipher the nature of bonding and determine the charge state of quasi-molecular N2, Bader charge analysis was performed. Each K atom loses 0.82 e, having a formal oxidation of +1, while the Bader partial charge is −0.40 e for N. These results confirm that this species is [N2]− wherein all of the N atoms assume a −0.5 formal oxidation state. Obviously, [N2]− in KN2 contains an unpaired p electron that produces a paramagnetic state, which is further confirmed by the analysis of the spin-polarized projected density of states (PDOS) in Fig. 2c.
The N-richer KN4 (Fig. 1b) consists of K atoms sandwiched between two layers of N atoms. Interestingly, as the N content increases, the coordination environment of the N atom becomes 12-fold hypercoordinated, that is, each K atom is located at the center of twelve surrounding N atoms (K@N12, Fig. 1b). For comparison, in the reported 2D metal nitrides, the Be atom coordinates with three N atoms to form sp2 hybridization in the BeN2 monolayer,29 and the transition metal atoms in 1H-TMN2 (TM = Ti, Zr, Hf and W) and 1T-TMN2 (TM = Zr, Hf, Nb, Ta and Mn) coordinate with six N atoms.69 To the best of our knowledge, the KN4 monolayer has the highest coordination number among the known 2D metal nitrides. The K–N bond lengths (2.87–3.25 Å) in KN4 are moderately longer than those in KN2 (2.75–2.95 Å), indicating that the K–N interaction is weakened. The nitrogen–nitrogen bond length (1.14 Å) is slightly shorter than that in KN2 (1.18 Å). The average Mulliken overlap population of the nitrogen–nitrogen bond in KN4 (1.35) is larger than that in KN2 (1.20), indicating that the nitrogen–nitrogen bond in KN4 is stronger. Accordingly, the highest phonon frequency (65.2 THz) is higher than that of KN2 (57.5 THz) (Fig. S1, ESI†), reflecting stronger nitrogen–nitrogen interaction in KN4. The calculated Bader partial charge for K (0.85 e) is comparable to 0.80 e in the KN2 monolayer. Based on the nitrogen–nitrogen distance and Bader charge (Table S2, ESI†), the KN4 monolayer contains N20.5− motifs. As mentioned above, the introduction of K not only greatly enriches the coordination geometry of N, but also contributes to structural stability. In the successive contents, we mainly discuss the KN2 monolayer with superconductivity, and a more detailed analysis of the structural information and electronic properties of the KN4 monolayer is given in the ESI.†
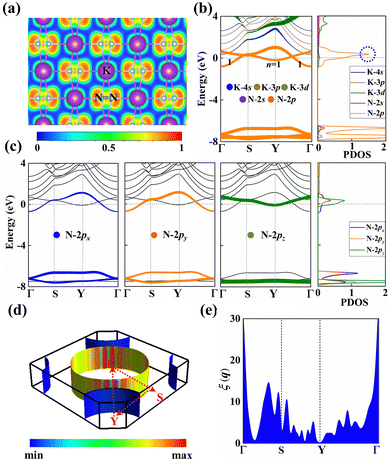
The electron localization function (ELF) in KN2 reveals electronic depletion around the K atoms and accumulation nearby N atoms (Fig. 3a), signifying a certain degree of ionicity between N2 dimers and K atoms, which is further supported by Bader charge analysis (Table S2, ESI†). On the contrary, there appears prominent electron localization between the N–N bonds as a signature of strong covalent bonding. Moreover, the non-bonding electrons located around the N atoms form lone electron pairs. Inspired by the unusual N-rich stoichiometry, interesting coordination geometries and exotic oxidation states, the projected electronic bands, PDOS, and Fermi surface of KN2 are also calculated. KN2 is one electron formula unit per cell short of the insulator electron count. As expected, KN2 is a metal with one band (denoted as n = 1, Fig. 3b) crossing the Fermi level, which is in sharp contrast with the non-metallic 2D metal nitrides (e.g., BeN2;29 PtN270 and Mg3N271), but similar to the metallic O-YN272 and H-ReN2.73 Below the Fermi level, there is a sizeable energy gap from −0.8 eV to −7.8 eV. Hence, the system can be tuned into an insulator by doping one hole per cell (Fig. S4, ESI†). Additionally, the metallicity of KN2 is further confirmed by more accurate HSE06 calculations (Fig. S5, ESI†). The coexistence of the “flat band-steep band” feature (e.g., Γ → S; Y → Γ and around Y) emerges around the Fermi level, which induces the high density of states near the Fermi level, forming a prominent van Hove singularity (vHs) (Fig. 3b) that is shown to be favorable for the formation of stable Cooper pairs.74 PDOS analysis reveals that its metallicity stems mainly from the contribution of N 2p, which is the typical anion-driven (N2−) metallicity. Further decomposition of PDOS indicates that the contribution of N 2pz to metallicity is much higher than that of N 2px and 2py (Fig. 3c), which promotes the in-plane conductivity. The Fermi surface plotted in Fig. 3d shows two electron pockets at the Γ and Y points, ascribable mainly to the N 2p orbitals, and the Fermi velocity has small values on the surface surrounding the Y point. In addition, details of Fermi surface (FS) nesting can be calculated by the nesting function ξ(q):
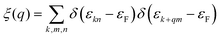 | (1) |
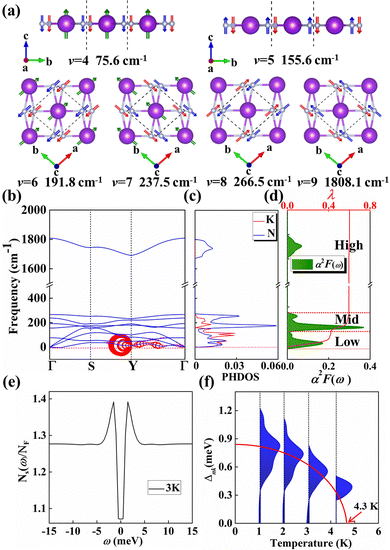
Motivated by the strong PDOS peak near the Fermi level, we examined the electron–phonon coupling calculations. KN2 with three atoms per primitive cell has nine phonon modes: three acoustic and six optical branches. Obviously, as shown in Fig. 4b, there is a large phonon gap (∼1400 cm−1) between mid- and high-frequency optical branches, where the vibration modes of K and N atoms together dominate the mid-frequency optical branches, whereas high-frequency phonon modes are merely characterized by the vibration of N atoms (Fig. 4c). In order to better reveal the relative motions of K and N atoms, the vibration modes of six optical branches at the Γ point are investigated (Fig. 4a). The fourth vibration mode (v = 4) at 75.6 cm−1 is mainly derived from the out-of-plane vibrations of K and N atoms. At 155.6 cm−1, the out-of-plane vibration of N atoms governs the fifth mode (v = 5). On the contrary, the optical branch vibrations (v = 6, 7) are mainly derived from the in-plane vibrations of K and N atoms along the a and b directions, respectively. Modes 8 and 9 (v = 8, 9) along the a and b directions are bending and stretching vibrations between N–N, respectively, which is a direct consequence of the large frequency difference between modes 8 and 9.
The magnitude of the EPC λq,v can be calculated by:
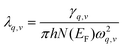 | (2) |
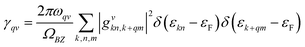 | (3) |
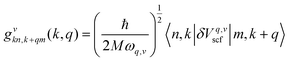 | (4) |
The Eliashberg spectral function for the electron–phonon interaction and the frequency-dependent EPC can be calculated by:
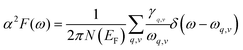 | (5) |
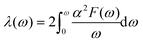 | (6) |
In the KN2 monolayer, the calculated EPC parameter λ is 0.6, which is comparable to 0.61 in MgB2.75 The low- and mid-frequency vibrations below 300 cm−1 give 97% contribution to λ (Fig. 4d), which is different from the high-frequency H-derived vibrations of high-Tc LaH105,6 and YH10.76 In particular, based on the phonon dispersion curves with λ weights (Fig. 4b) nearby the Y point contribute significantly to the EPC. The strong EPC originates from its low velocity near the Y point. Low Fermi velocity corresponds to the “flat band” in the band structure, which significantly increases the density of electron states and further facilitates EPC. On the other hand, the strong EPC is also ascribed to phonon softening along S → Y and Y → Γ. Subsequently, we have estimated the superconducting critical temperatures Tc of KN2 using the Allen–Dynes modified McMillan equation on the basis of Bardeen–Cooper—Schrieffer (BCS) theory with a typical choice of μ* = 0.1.55,77–79 The Tc of KN2 is predicted to be 2 K at ambient pressure, suggesting that it is a phonon-mediated superconductor. The present Tc value is comparable to 0.86 K for 1T-TaN2,80 1.3 K for 1H-TaN2,80 and 3.4 K for Ba2N monolayer.81
Compared to the traditional McMillan approximation, solving the Migdal–Eliashberg equation is more reliable for layered or low-dimensional systems.82 We also employ anisotropic Migdal–Eliashberg equations with subsequent analytic continuation to the real axis using Padé functions to explore the superconduction of the KN2 monolayer. The calculated the normalized quasiparticle superconducting density of states at 3 K, which is given in Fig. 4e, showing only a pair of peaks corresponding to a single superconducting gap. This is in sharp contrast with multigap superconductors like MgB2 solid83,84 and LiBC85 monolayer. The anisotropic superconducting gap vanishes at about 4.3 K (Fig. 4f), which is slightly higher than the value from the McMillan–Allen–Dynes formula (2 K). Similar situations occurred in other systems,86,87 indicating that our results on the superconductivity of KN2 monolayer are reasonable. KN4 monolayer is metallic rather than superconducting, probably because the N2 dimer in KN4 (N20.5−) is less charged than that in KN2 (N2−). Furthermore, the high electronic density of states leads to the emergence of unique vHs near the Fermi level in the KN2 monolayer, which is conducive to the formation of stable Cooper pairs, playing a crucial role in enhancing the EPC.
Conclusions
To summarize, we uncover two stable non-stoichiometric 2D materials, KN2 and KN4 monolayers, using a combination of swarm-intelligence structural search and ab initio calculation. Their negative formation energies, high cohesive energies and dynamical stabilities suggest the synthetic feasibility. As the nitrogen content increases, the ligand N atom increases from 6 to 12. Meanwhile, the nitrogen motifs evolve from N2− to N20.5−. The unique coordination geometries and exotic oxidation states induce distinct electronic properties. KN4 is metallic, while KN2 exhibits superconductivity with a Tc value of 4.3 K. The N 2p electrons and low- and mid-frequency atomic vibrations of K and N atoms are mainly responsible for the strong electron–phonon coupling. These findings not only deepen the understanding of the hypercoordination and oxidation state of nitrogen, but also promote future efforts in exploring the superconductivity of 2D metal nitrides.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This work was supported by the National Natural Science Foundation of China (12274050 and 91961204) and the Fundamental Research Funds for the Central Universities (DUT22LAB104 and DUT22ZD103). The authors also acknowledge the Supercomputing Center of the Dalian University of Technology and Tianjin for providing the computing resources.References
- H.-K. Mao, X.-J. Chen, Y. Ding, B. Li and L. Wang, Rev. Mod. Phys., 2018, 90, 15007 CrossRef CAS.
- J. A. Flores-Livas, L. Boeri, A. Sanna, G. Profeta, R. Arita and M. Eremets, Phys. Rep., 2020, 856, 1–78 CrossRef CAS.
- A. P. Drozdov, M. I. Eremets, I. A. Troyan, V. Ksenofontov and S. I. Shylin, Nature, 2015, 525, 73–76 CrossRef CAS.
- D. Duan, Y. Liu, F. Tian, D. Li, X. Huang, Z. Zhao, H. Yu, B. Liu, W. Tian and T. Cui, Sci. Rep., 2014, 4, 6968 CrossRef CAS.
- H. Liu, I. I. Naumov, R. Hoffmann, N. W. Ashcroft and R. J. Hemley, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 6990–6995 CrossRef CAS.
- A. P. Drozdov, P. P. Kong, V. S. Minkov, S. P. Besedin, M. A. Kuzovnikov, S. Mozaffari, L. Balicas, F. F. Balakirev, D. E. Graf, V. B. Prakapenka, E. Greenberg, D. A. Knyazev, M. Tkacz and M. I. Eremets, Nature, 2019, 569, 528–531 CrossRef CAS.
- Z. Zhang, T. Cui, M. J. Hutcheon, A. M. Shipley, H. Song, M. Du, V. Z. Kresin, D. Duan, C. J. Pickard and Y. Yao, Phys. Rev. Lett., 2022, 128, 47001 CrossRef CAS.
- J. Delahaye, J. Hassel, R. Lindell, M. Sillanpää, M. Paalanen, H. Seppä and P. Hakonen, Science, 2003, 299, 1045–1048 CrossRef CAS PubMed.
- O.-P. Saira, M. Meschke, F. Giazotto, A. M. Savin, M. Möttönen and J. P. Pekola, Phys. Rev. Lett., 2007, 99, 27203 CrossRef.
- E. J. Romans, E. J. Osley, L. Young, P. A. Warburton and W. Li, Appl. Phys. Lett., 2010, 97, 222506 CrossRef.
- M. Xue, G. Chen, H. Yang, Y. Zhu, D. Wang, J. He and T. Cao, J. Am. Chem. Soc., 2012, 134, 6536–6539 CrossRef CAS PubMed.
- B. M. Ludbrook, G. Levy, P. Nigge, M. Zonno, M. Schneider, D. J. Dvorak, C. N. Veenstra, S. Zhdanovich, D. Wong, P. Dosanjh, C. Straßer, A. Stöhr, S. Forti, C. R. Ast, U. Starke and A. Damascelli, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 11795–11799 CrossRef CAS.
- I. Guillamón, H. Suderow, S. Vieira, L. Cario, P. Diener and P. Rodière, Phys. Rev. Lett., 2008, 101, 166407 CrossRef.
- J. T. Ye, Y. J. Zhang, R. Akashi, M. S. Bahramy, R. Arita and Y. Iwasa, Science, 2012, 338, 1193–1196 CrossRef CAS.
- M. M. Ugeda, A. J. Bradley, Y. Zhang, S. Onishi, Y. Chen, W. Ruan, C. Ojeda-Aristizabal, H. Ryu, M. T. Edmonds, H.-Z. Tsai, A. Riss, S.-K. Mo, D. Lee, A. Zettl, Z. Hussain, Z.-X. Shen and M. F. Crommie, Nat. Phys., 2016, 12, 92–97 Search PubMed.
- L. J. Li, E. C. T. O’Farrell, K. P. Loh, G. Eda, B. Özyilmaz and A. H. Castro Neto, Nature, 2016, 529, 185–189 CrossRef CAS PubMed.
- Y. Saito, Y. Kasahara, J. Ye, Y. Iwasa and T. Nojima, Science, 2015, 350, 409–413 CrossRef CAS PubMed.
- J. T. Ye, S. Inoue, K. Kobayashi, Y. Kasahara, H. T. Yuan, H. Shimotani and Y. Iwasa, Nat. Mater., 2010, 9, 125–128 CrossRef CAS.
- T. Zhang, P. Cheng, W.-J. Li, Y.-J. Sun, G. Wang, X.-G. Zhu, K. He, L. Wang, X. Ma, X. Chen, Y. Wang, Y. Liu, H.-Q. Lin, J.-F. Jia and Q.-K. Xue, Nat. Phys., 2010, 6, 104–108 Search PubMed.
- C. J. Stevens, Science, 2019, 363, 578–580 CrossRef CAS.
- P. A. Giguère and I. D. Liu, J. Chem. Phys., 1952, 20, 136–140 CrossRef.
- G. Auffermann, Y. Prots and R. Kniep, Angew. Chem., Int. Ed., 2001, 40, 547–549 CrossRef CAS PubMed.
- K. O. Christe, W. W. Wilson, J. A. Sheehy and J. A. Boatz, Angew. Chem., Int. Ed., 1999, 38, 2004–2009 CrossRef CAS.
- C. Zhang, C. Sun, B. Hu, C. Yu and M. Lu, Science, 2017, 355, 374–376 CrossRef CAS PubMed.
- D. Laniel, G. Weck and P. Loubeyre, Inorg. Chem., 2018, 57, 10685–10693 CrossRef CAS PubMed.
- S. B. Schneider, R. Frankovsky and W. Schnick, Angew. Chem., Int. Ed., 2012, 51, 1873–1875 CrossRef CAS.
- K. Niwa, T. Yamamoto, T. Sasaki and M. Hasegawa, Phys. Rev. Mater., 2019, 3, 53601 CrossRef CAS.
- A. F. Young, C. Sanloup, E. Gregoryanz, S. Scandolo, R. J. Hemley and H. Mao, Phys. Rev. Lett., 2006, 96, 155501 CrossRef PubMed.
- C. Zhang and Q. Sun, J. Phys. Chem. Lett., 2016, 7, 2664–2670 CrossRef CAS PubMed.
- K. Lee, S. W. Kim, Y. Toda, S. Matsuishi and H. Hosono, Nature, 2013, 494, 336–340 CrossRef CAS PubMed.
- S. Guan, S. A. Yang, L. Zhu, J. Hu and Y. Yao, Sci. Rep., 2015, 5, 12285 CrossRef PubMed.
- J. Wang, L. Li, Z. Shen, P. Guo, M. Li, B. Zhao, L. Fang and L. Yang, Materials, 2018, 11, 2462 CrossRef CAS.
- H. Şahin, S. Cahangirov, M. Topsakal, E. Bekaroglu, E. Akturk, R. T. Senger and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 155453 CrossRef.
- H. L. Zhuang, A. K. Singh and R. G. Hennig, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 165415 CrossRef.
- A. K. Singh, H. L. Zhuang and R. G. Hennig, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 245431 CrossRef.
- J. Li, X. Fan, Y. Wei, H. Liu, S. Li, P. Zhao and G. Chen, Sci. Rep., 2016, 6, 33060 CrossRef CAS PubMed.
- X. Jiang, Q. Liu, J. Xing and J. Zhao, J. Phys. Chem. Lett., 2019, 10, 7753–7759 CrossRef CAS.
- Y. Wang, J. Lv, L. Zhu and Y. Ma, Comput. Phys. Commun., 2012, 183, 2063–2070 CrossRef CAS.
- Y. Wang, J. Lv, L. Zhu and Y. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 94116 CrossRef.
- Y. Yang, S.-C. Liu, W. Yang, Z. Li, Y. Wang, X. Wang, S. Zhang, Y. Zhang, M. Long, G. Zhang, D.-J. Xue, J.-S. Hu and L.-J. Wan, J. Am. Chem. Soc., 2018, 140, 4150–4156 CrossRef CAS.
- S. Zhao, Z. Li and J. Yang, J. Am. Chem. Soc., 2014, 136, 13313–13318 CrossRef CAS PubMed.
- W. Ming, M. Yoon, M.-H. Du, K. Lee and S. W. Kim, J. Am. Chem. Soc., 2016, 138, 15336–15344 CrossRef CAS PubMed.
- H. Zhang, Y. Li, J. Hou, K. Tu and Z. Chen, J. Am. Chem. Soc., 2016, 138, 5644–5651 CrossRef CAS PubMed.
- C. Tang, G. Kour and A. Du, Chin. Phys. B, 2019, 28, 107306 CrossRef CAS.
- T. Yu, Z. Zhao, L. Liu, S. Zhang, H. Xu and G. Yang, J. Am. Chem. Soc., 2018, 140, 5962–5968 CrossRef CAS PubMed.
- B. Gao, P. Gao, S. Lu, J. Lv, Y. Wang and Y. Ma, Sci. Bull., 2019, 64, 301–309 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192 CrossRef.
- K. Parlinski, Z. Q. Li and Y. Kawazoe, Phys. Rev. Lett., 1997, 78, 4063–4066 CrossRef CAS.
- A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106 CrossRef.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef.
- S. Baroni, S. de Gironcoli, A. Dal Corso and P. Giannozzi, Rev. Mod. Phys., 2001, 73, 515–562 CrossRef CAS.
- P. B. Allen and R. C. Dynes, Phys. Rev. B: Solid State, 1975, 12, 905–922 CrossRef CAS.
- A. B. Migdal, Sov. Phys. JETP, 1968, 35, 996 Search PubMed.
- S. Poncé, E. R. Margine, C. Verdi and F. Giustino, Comput. Phys. Commun., 2016, 209, 116–133 CrossRef.
- G. Shi, L. Chen, Y. Yang, D. Li, Z. Qian, S. Liang, L. Yan, L. H. Li, M. Wu and H. Fang, Nat. Chem., 2018, 10, 776–779 CrossRef CAS.
- M. I. McMahon, R. J. Nelmes, U. Schwarz and K. Syassen, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 140102 CrossRef.
- J. Donohue, Acta Crystallogr., 1961, 14, 1000–1001 CrossRef CAS.
- A. Fleurence, R. Friedlein, T. Ozaki, H. Kawai, Y. Wang and Y. Yamada-Takamura, Phys. Rev. Lett., 2012, 108, 245501 CrossRef PubMed.
- J. Guan, Z. Zhu and D. Tománek, Phys. Rev. Lett., 2014, 113, 46804 CrossRef CAS PubMed.
- C. Ataca, M. Topsakal, E. Aktürk and S. Ciraci, J. Phys. Chem. C, 2011, 115, 16354–16361 CrossRef CAS.
- J. Zhao, Phys. Lett. A, 2007, 360, 645–648 CrossRef CAS.
- A. F. Schuch and R. L. Mills, J. Chem. Phys., 1970, 52, 6000–6008 CrossRef CAS.
- K. Zhao, X. Li, S. Wang and Q. Wang, Phys. Chem. Chem. Phys., 2019, 21, 246–251 RSC.
- J. Jia, S. Wei, Q. Cai and J. Zhao, J. Colloid Interface Sci., 2021, 600, 711–718 CrossRef CAS PubMed.
- M. Wessel and R. Dronskowski, J. Am. Chem. Soc., 2010, 132, 2421–2429 CrossRef CAS.
- J. Liu, Z. Liu, T. Song and X. Cui, J. Mater. Chem. C, 2017, 5, 727–732 RSC.
- L. Liu, D. Wang, S. Lakamsani, W. Huang, C. Price and H. L. Zhuang, J. Appl. Phys., 2019, 125, 204302 CrossRef.
- P.-F. Liu, L. Zhou, T. Frauenheim and L.-M. Wu, Phys. Chem. Chem. Phys., 2016, 18, 30379–30384 RSC.
- S. Gong, C. Zhang, S. Wang and Q. Wang, J. Phys. Chem. C, 2017, 121, 10258–10264 CrossRef CAS.
- S.-H. Zhang and B.-G. Liu, Nanotechnology, 2018, 29, 325401 CrossRef.
- X. Zhang, Y. Yao, S. Ding, A. Bergara, F. Li, Y. Liu, X.-F. Zhou and G. Yang, Phys. Rev. B, 2023, 107, L100501 CrossRef CAS.
- H. J. Choi, D. Roundy, H. Sun, M. L. Cohen and S. G. Louie, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 20513 CrossRef.
- F. Peng, Y. Sun, C. J. Pickard, R. J. Needs, Q. Wu and Y. Ma, Phys. Rev. Lett., 2017, 119, 107001 CrossRef.
- W. L. McMillan, Phys. Rev., 1968, 167, 331–344 CrossRef CAS.
- J. P. Carbotte, Rev. Mod. Phys., 1990, 62, 1027–1157 CrossRef CAS.
- L. N. Oliveira, E. K. U. Gross and W. Kohn, Phys. Rev. Lett., 1988, 60, 2430–2433 CrossRef PubMed.
- L. Yan, B.-T. Wang, X. Huang, Q. Li, K. Xue, J. Zhang, W. Ren and L. Zhou, Nanoscale, 2021, 13, 18947–18954 RSC.
- X.-L. Qiu, J.-F. Zhang, H.-C. Yang, Z.-Y. Lu and K. Liu, Phys. Rev. B, 2022, 105, 165101 CrossRef CAS.
- F. Giustino, M. L. Cohen and S. G. Louie, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 165108 CrossRef.
- H. J. Choi, D. Roundy, H. Sun, M. L. Cohen and S. G. Louie, Nature, 2002, 418, 758–760 CrossRef CAS.
- Y. An, J. Li, K. Wang, G. Wang, S. Gong, C. Ma, T. Wang, Z. Jiao, X. Dong, G. Xu, R. Wu and W. Liu, Phys. Rev. B, 2021, 104, 134510 CrossRef CAS.
- P. Modak, A. K. Verma and A. K. Mishra, Phys. Rev. B, 2021, 104, 54504 CrossRef CAS.
- J.-Y. You, B. Gu, G. Su and Y. P. Feng, Phys. Rev. B, 2021, 103, 104503 CrossRef CAS.
- D. Wu, Y. Lin, L. Xiong, J. Li, T. Luo, D. Chen and F. Zheng, Phys. Rev. B, 2021, 103, 224502 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3tc03718e |
| This journal is © The Royal Society of Chemistry 2024 |